经典流体力学与空气动力学建立在连续介质假设之上,即宏观微元中需包含足够多的微观分子。与之相反,稀薄气体动力学描述的则是在此假设不成立时气体的流动与热力学等性质。克努森数
由此,不难发现,稀薄气体流动广泛存在于航空航天、工业技术和能源环境等重要的国防、民生领域,如返回舱再入大气层以及临近空间飞行器高空域飞行时的绕流[1-5]、微机电系统中的气体流动[6-9]以及页岩气开采中甲烷在复杂多孔介质中的流动[10]等。相关科学技术的发展对我国国防、国民经济和社会发展意义重大,如下所述:
1)临近空间飞行器既可以避免绝大部分的地面攻击,同时也能够有效实施对地攻击和对航天器的打击,因此临近空间是进行空中军事活动的理想区域,发展潜力极大,我国和不少其他国家已经将其纳入信息化武器装备体系[11]。在70 km以上的飞行空域,复杂构型的高超声速飞行器表面存在极为复杂的流动,因而需要建立新的流动模型和计算方法,来预测复杂的稀薄气体效应、高温真实气体效应以及解决激波/膨胀波与黏性作用的耦合干扰等问题。深入研究上述实际应用中的稀薄气体流动规律是优化飞行器设计的关键所在,具有重要意义。
2)机电系统微小集成化是提高能源利用效率的重要手段,因为微小化可大幅度减少传热传质阻力从而显著提高工质的相关输运能力。近年来,微流动系统在电子、化学、生物等领域已经取得了巨大的发展并得到了广泛的应用,但是微尺度下的空气动力学理论和模拟方法仍不完善,还存在许多亟待解决的问题[12]:如在电容式膜片压力计中,当被测气体的温度与压力计的温度不同时,稀薄气体自动从低温区向高温区蠕动,从而导致压力测量偏差,需要考虑稀薄气体效应进行修正[13];工作在低压风洞的测量设备也需要考虑相应的稀薄气体效应修正以提高测量精度。
3)随着自然资源逐渐枯竭和环境破坏愈发严重,能源转型和能源利用效率提升成为各国科技发展的重要目标。相较于传统化石能源,以甲烷为主要成分的页岩气,因其具有弥补常规能源储量及产量、减少温室气体排放的巨大潜力,在世界能源供给中变得愈发重要。值得一提的是,我国页岩气储备位列全球第一,但复杂的地质条件要求对其输运机制有更清晰深入的理解,才能实现经济有效的开采;虽然页岩气埋藏在地表深处,气体压力大,但是页岩孔隙直径在纳米尺度,因而同样需要考虑稀薄气体效应[14]。
图1列举了典型稀薄气体流动中纳维-斯托克斯方程的数值预测结果与实验测量存在明显差距的例子。由此可以看出,基于连续性假设得到的流体力学方程不再适用于此类问题,其根本原因在于,在稀薄效应较强的区域内,由宏观量的一阶导数构成的线性本构关系不再准确。另一方面,直接模拟所有气体分子运动与相互作用的分子动力学方法,提供了一个更为准确地模拟稀薄气体流动的途径。然而,因其庞大的计算量,该方法仅能用于极小时空尺度下的气体输运问题。因此,对于更为广泛存在的介观尺度下稀薄气体流动,如何建立准确的动理论模型方程并有效求解,则是目前最为关切与亟待解决的两个问题。

|
图 1 典型稀薄气体流动及纳维-斯托克斯方程的预测误差:第一列图显示,当马赫数大于2时,纳维-斯托克斯方程低估正激波的厚度[15];第二列图显示,当声波振动频率接近气体分子碰撞频率时,纳维-斯托克斯方程低估声波接收器的声强[16-17];第三列图显示,低压下纳维-斯托克斯方程可能远远低估微纳米通道的质量流量[18] Fig.1 Typical rarefied gas flows and the incapability of Navier-Stokes equations. Figures in the first column show that, when the Mach number is larger than 2, the Navier-Stokes equations underpredict the thickness of normal shock wave[15]. Figures in the second column show that the Navier-Stokes equations underpredict the sound pressure at the receiver[16-17]. Figures in the last column show that the Navier-Stokes equations might underestimate the mass flow rate significantly[18] |
(1)研究现状。
一般来说,传统的纳维-斯托克斯方程只能描述连续流区(
作为最为重要的气体动理论方程,玻尔兹曼方程描述了单原子气体的速度分布函数在时间与空间中的演化规律。玻尔兹曼方程的求解,在航空航天、微机电系统和页岩气开发等领域中都发挥着重要作用。其中,基于统计随机方法的DSMC计算,是模拟稀薄气体流动的重要工具[24]。对于单原子气体的模拟,DSMC方法已在数学上被证明在粒子数趋于无穷的条件下,收敛于玻尔兹曼方程的解[25-26]。玻尔兹曼方程中气体分子的速度分布函数是定义在平均自由程尺度上,由于DSMC方法将气体分子自由运动与相互碰撞这两个过程进行了解耦,因此该方法的模拟中要求空间网格尺寸小于气体平均自由程,且时间步长小于平均碰撞时间。而这直接导致了DSMC方法对近连续流模拟的低效性。此外,由于流场的宏观量信息需要通过统计抽样得到,因此DSMC模拟中需进行大量系综平均去除噪声,特别地,当宏观物理量自身数值相对于其统计微观量的涨落较小时,例如低速流动或较小温差的系统,DSMC方法的时间成本将变得难以负担。
相比于DSMC等统计模拟方法,确定性数值方法在近几十年得到快速发展并展现出强大优势,我国学者在此方面贡献良多。但由于玻尔兹曼方程碰撞项的复杂性,除了少数方法可以求解玻尔兹曼方程外[27-31],大部分确定性方法求解的是简化模型方程,如BGK模型[32]、ES-BGK模型[33-34]和Shakhov模型[35]等。中国空气动力研究与发展中心的李志辉和张涵信[36]最早应用气体动理论统一数值算法求解模型方程,并建立了三维复杂飞行器高马赫数绕流问题的统一算法大规模并行计算研究平台,已应用于返回舱回收和天宫一号离轨、再入、解体等航天工程[37-39]。香港科技大学徐昆首创的统一气体动理论格式(unified gas kinetic scheme,UGKS)耦合处理了模型方程的迁移项和碰撞项,相对于传统离散速度方法而言,在网格离散尺度远大于分子平均自由程时依然可以在连续流时恢复纳维-斯托克斯方程的解,从而在计算多尺度问题时可以采用更粗粒化的时空离散[40]。华中科技大学的郭照立、西北工业大学的钟诚文、新加坡国立大学舒昌等课题组在UGKS的基础上做了进一步发展[41-43]。最近,苏微和吴雷等提出的合成迭代算法(general synthetic iterative scheme,GSIS)耦合了宏观方程以实现全流场信息交换,具有良好的“渐近保持”和“快速收敛”性质,不但可以使用大空间网格和时间步长,而且可以在短短几十步迭代内找到稳态解,极大地提高了数值精度和效率[44-47]。更重要的是,该方法对碰撞项的具体形式没有要求,可以直接针对玻尔兹曼方程进行快速求解。
(2)存在的一些问题。
稀薄气体研究主要涉及动理学建模和多尺度计算两个方面,本文仅关注分子气体动理论模型中存在的一些问题。众所周知,目前大部分气体动理论方程是针对单原子气体提出的[48-50],而实际气体大多是分子气体,即一个气体分子包含两个或两个以上的原子,例如占据地球大气绝大部分比例的N2和O2,占据火星大气绝大部分比例的CO2等。相对于仅具有平动自由度的单原子气体,分子气体中还存在转动与振动的内能形式,并且各类型自由度的能量可以相互转化。对于常见气体,其转动能在室温下已充分激发,而振动能也在上千度高温下逐渐激发。随着温度的继续升高,分子气体的离解与电离也将逐渐发生,与此同时,化学反应也通常存在于此。此时,高温真实气体效应显著。而单原子玻尔兹曼方程无法包含这些过程,因此需要更复杂的模型方程来给出相应的模拟。目前,大部分以此为目标的建模工作是针对连续流提出的,例如对高超声速飞行器周围气体的模拟。由于分子气体的热流由平动能量和内部能量的输运与相互转换共同作用导致,因此需要通过额外的能量方程来描述高温气体能量输运,并且保证能量交换速率和总热导率与实验数值一样,此类连续流下的模拟方法就可以较为准确地模拟高温真实气体效应,国内外学者在这方面已经做了大量工作方面已经开展了大量工作[51]。
然而,对于临近空间飞行器等类似问题而言,稀薄气体效应也非常显著[19],因此有必要将稀薄气体效应和高温真实气体效应结合起来考虑。对此,王承书和乌伦贝克建立的WCU方程[52]给出了相对完备的描述,该方程以经典力学方式描述平动能量,而以量子力学方式描述内部(转动与振动)能量,并对每个能级下的速度分布函数建立方程。显然,该方法使得方程组自由度过于庞大,致使其求解变得相当困难从而难以应用于实际问题。因此建立相对简化的模型方程尤为必要。与此同时,由于各类自由度的特征碰撞时间不同,导致稀薄气体效应的程度也不同,因此动理论建模难度也大为增加。
对于分子气体的动理论建模,如何在模型方程中准确反应气体的各个输运系数是首要问题。相对于单原子气体,由于更多内部自由度的存在,分子气体中出现了更多的输运过程及相应参数。其一为体积黏性,其表征了气体在膨胀压缩的做功过程中能量与内部自由度转换的阻力,这一阻力来源于有限时间的能量弛豫过程;其二为转动、振动热导率,即内部自由度同时参与了热流的传递,与热流的弛豫速率紧密相关。实际上,在分子气体动理论的建模中,正确的体积黏性是容易实现的,只需保证正确的内部能量(转动、振动等)和平动能量的弛豫速率即可。但是,实现正确的平动、转动和振动热导率却非常困难。本文以仅有转动自由度的分子气体为例说明问题所在。历史上,Eucken首先将气体总热导率
| $ \begin{split} \frac{\kappa m}{\mu k_B}& = \frac{\kappa_{tr} m}{\mu k_B}+\frac{\kappa_{rot} m}{\mu k_B}\\ &\equiv\frac{3}{2}f_{tr}+\frac{d_r}{2}f_{rot}\\ &\equiv\frac{3+d_r}{2}f_{eu}\end{split}$ | (1) |
其中:
| $ f_{tr} = \frac{5}{2}, \quad f_{rot} = 1 $ | (2) |
后来,人们意识到气体内部热导率与分子扩散有关,将内部Eucken因子改写为:
| $ f_{tr} = \frac{5}{2}, \quad f_{rot} = \frac{\rho{D}}{\mu}\equiv\frac{1}{{Sc}} $ | (3) |
其中
WCU方程的复杂性限制了其在实际问题中的应用,而DSMC方法则相对容易地从单原子气体模拟推广至分子气体的输运。即便如此,对于极为复杂的分子气体碰撞过程,DSMC方法依然采用了适当简化的模型来处理,从而提高计算效率。目前通用的分子碰撞模型最早由Borgnakke和Larsen提出[55]。此后,人们提出各种各样的改进,主要目的均在于正确实现分子各能级间的能量交换速率,从而获得正确的分子气体的体积黏性[56-58]。然而,当前的DSMC方法并没有包含可以单独调节热导率的相应机制与参数。与此同时,在实际中使用DSMC模拟分子气体流动时,该碰撞模型对应得到的平动和转动热导率是否正确尚未可知。因此,有必要对DSMC模拟分子气体的相应模型进行检查,这里的检查有双重意义:1)检查DSMC模拟得到的总热导率是否与实验测量数据一致,若不一致,则DSMC即便在近连续流下也会给出错误解。2)即使DSMC能给出正确的总热导率,也还需要检查
在近连续流条件下,能量在平动自由度与内部自由度的分配趋于一致,因而平动温度与转动和振动温度的差别极小,此时保证总体热导率的正确性,即可得到相应正确的结果。因而,在稀薄效应较强的区域,保证各个热导率分量的正确性就显得尤为关键。例如,爱因斯坦等很早就发现,对于热蠕动等稀薄气体流动,温度梯度引起的气体流动只与
(3)本文目的和结构。
分子气体稀薄效应的准确刻画是稀薄气体动理学和高温气体动力学研究的前沿和热点,在这个背景下,本文首先介绍分子气体动理论建模的思路和最新研究进展,并讨论现有的分子气体模型方程在稀薄气体流动中的适用性与准确性,为今后多组分分子气体和化学反应的非平衡流动的建模和模拟奠定坚实的理论基础。以下第1节介绍单原子气体玻尔兹曼方程的基本性质、输运系数的严格推导以及动理学建模的基本思路。特别地,我们指出,几乎所有的简化模型都可以从Gross-Jackson模型非线性化而来。第2节介绍王承书和乌伦贝克提出的WCU方程,推导分子气体的体积黏性和平动、转动热导率系数,并指出DSMC碰撞模型的缺陷。第4节介绍WCU方程的线性化Hanson-Morse模型以及主流的非线性模型,并在经典的稀薄气体流动中测试模型的精度。第4节和第5节分别讨论热弛豫速率的不确定性对稀薄气体流动的影响,以及从分子动力学模拟和实验中减小甚至消除热弛豫速率不确定性的方法。最后做总结和展望。
1 单原子气体玻尔兹曼方程及其简化模型在气体动理论中,单原子气体在相空间中的概率密度由速度分布函数
| $ \begin{split} &n(t,{\boldsymbol{x}}) = \int{}f(t,{\boldsymbol{x}},{\boldsymbol{v}}){\rm{d}}{\boldsymbol{v}} \\ &{\boldsymbol{u}}(t,{\boldsymbol{x}}) = \frac{1}{n(t,{\boldsymbol{x}})}\int{\boldsymbol{v}}f(t,{\boldsymbol{x}},{\boldsymbol{v}}){\rm{d}}{\boldsymbol{v}}\\ &T(t,{\boldsymbol{x}}) = \frac{m}{3k_Bn(t,{\boldsymbol{x}})}\int{}c^2f(t,{\boldsymbol{x}},{\boldsymbol{v}}){\rm{d}}{\boldsymbol{v}} \\ &p_{ij}(t,{\boldsymbol{x}}) = {}m\int{}c_ic_jf(t,{\boldsymbol{x}},{\boldsymbol{v}}){\rm{d}}{\boldsymbol{v}} \\ &{\boldsymbol{q}}(t,{\boldsymbol{x}}) = \frac{m}{2}\int{}c^2{\boldsymbol{c}}f(t,{\boldsymbol{x}},{\boldsymbol{v}}){\rm{d}}{\boldsymbol{v}} \end{split} $ | (4) |
其中,
| $ \sigma_{ij} = p_{ij}-p\delta_{ij} $ | (5) |
其中,
对于稀疏气体(分子间距远远大于分子直径),在外部施加的加速度
| $ \frac{\partial f}{\partial t}+{\boldsymbol{v}}\cdot\frac{\partial f}{\partial {\boldsymbol{x}}}+{\boldsymbol{a}}\cdot\frac{\partial f}{\partial {\boldsymbol{v}}} = {Q(f)}$ | (6) |
方程(6)左边的三项分别表示速度分布函数在时间上的变化、在速度作用下在物理空间的变化以及在外力作用下在速度空间的变化,右边表示使得分布函数趋于平衡态的气体分子的碰撞过程。在玻尔兹曼方程中,两体碰撞的形式为:
| $ Q(f) = \iint{}B(\theta,{v}_r) \Big [f({\boldsymbol{v}}'_*)f({\boldsymbol{v}}')-f({\boldsymbol{v}}_*)f({\boldsymbol{v}})\Big]{\rm{d}}{{\boldsymbol{\varOmega}}}{\rm{d}}{\boldsymbol{v}}_* $ | (7) |
其中,
| $ \begin{split} {\boldsymbol{v}}' =& \frac{{\boldsymbol{v}}+{\boldsymbol{v}}_\ast}{2}+\frac{|{\boldsymbol{v}}-{\boldsymbol{v}}_\ast|}{2}{\boldsymbol{\varOmega}}\\ {\boldsymbol{v}}'_\ast = &\frac{{\boldsymbol{v}}+{\boldsymbol{v}}_\ast}{2}-\frac{|{\boldsymbol{v}}-{\boldsymbol{v}}_\ast|}{2}{\boldsymbol{\varOmega}}\end{split} $ | (8) |
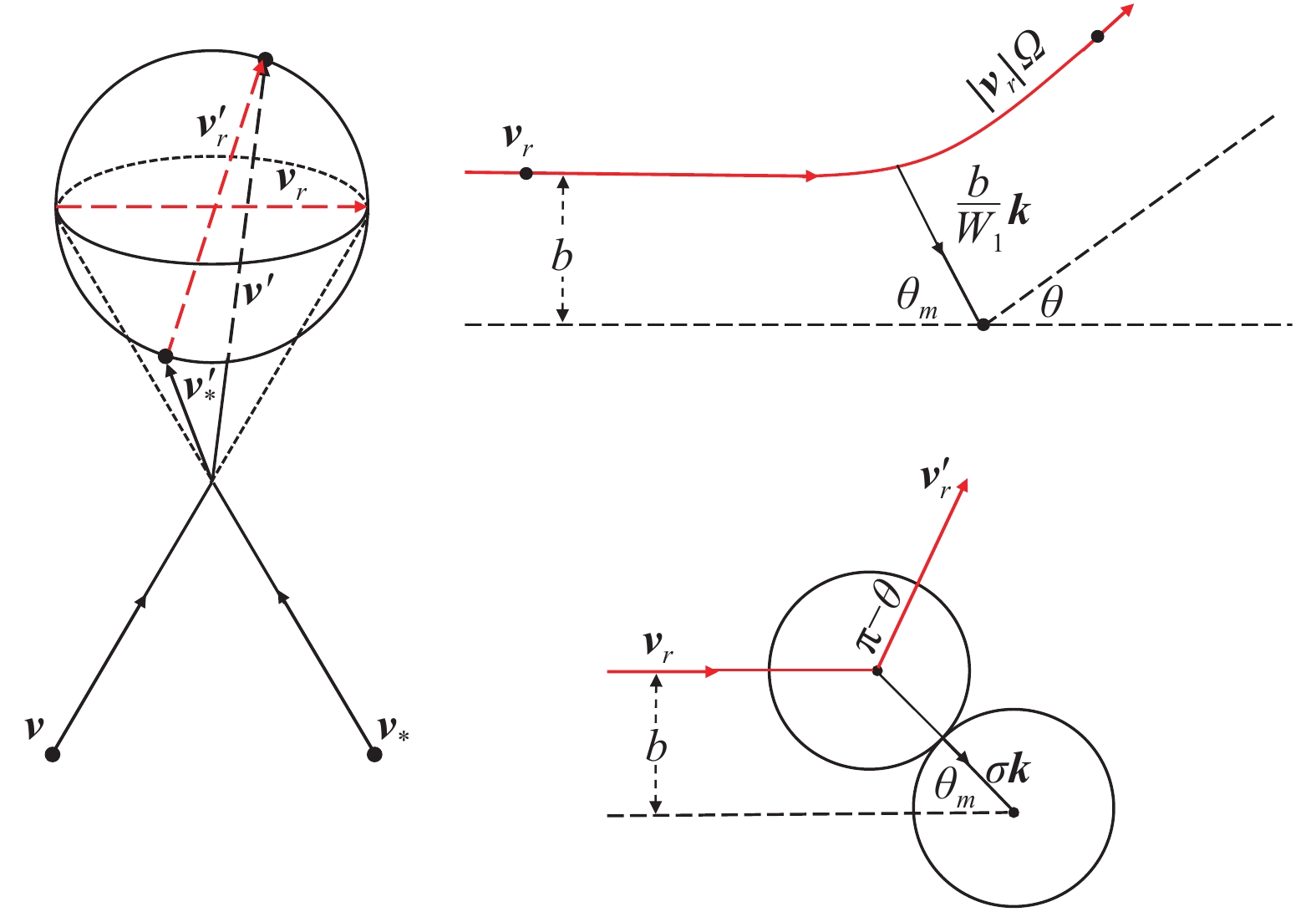
碰撞示意图见图2。其中,碰撞前两分子的相对速度为
| $ \cos\theta ={\boldsymbol{ \varOmega}}\cdot\frac{{\boldsymbol{v}}_r}{{v}_r} $ | (9) |
最后,碰撞核
|
图 2 (左)两体碰撞前后的速度分布:由于动量和能量守恒,碰撞前后的相对速度分布在球体上并且通过球心;(右上)中心力场作用下的经典两体碰撞示意图,其中 |
假设分子间通过中心力场作用,作用势
| $ \theta(b,{v}_r) = {\text {π}}-2\int_0^{W_1}\left[1-W^2-\frac{4\phi(r)}{m{v}_r^2}\right]^{-\frac{1}{2}}{\rm{d}}W $ | (10) |
其中,
在气体动理论中,经常考虑如下形式的逆幂律分子作用势:
| $ \phi(r) = \frac{K}{\eta-1}r^{1-\eta} $ | (11) |
其中,K表征分子间相互作用的强度。从式(10)可知,偏转角只与变量
| $ s = \left[\frac{m(\eta-1)}{4K}\right]^{\frac{1}{\eta-1}}bv^{\frac{2}{\eta-1}}_r $ | (12) |
微分散射截面定义为:
| $ \sigma_{_D} = \frac{b\;\big|{\rm{d}}b\big|}{\sin\theta\;\big|{\rm{d}}\theta\big|} = \left[\frac{m(\eta-1)}{4K}\right]^{\frac{2}{1-\eta}}v^{\frac{4}{1-\eta}}_r \frac{s{\rm{d}}s}{\sin\varTheta{{\rm{d}}\varTheta}} $ | (13) |
而碰撞核为:
| $ B(\theta,v_r) = v_r \sigma_{_D} $ | (14) |
当式(11)中
对于任意关于分子速度的函数
| $ \begin{split} \int\varPsi({\boldsymbol{v}})Q({\boldsymbol{v}}){\rm{d}}{\boldsymbol{v}} = &\frac{1}{4}\iiint {\rm{d}}{\boldsymbol{\varOmega}} {\rm{d}}{\boldsymbol{v}}_\ast{{\rm{d}}{\boldsymbol{v}}} \Delta[\varPsi] B(\theta,v_r) \cdot \\ & \left[f({\boldsymbol{v}}'_{\ast})f({\boldsymbol{v}}')-f({\boldsymbol{v}}_{\ast})f({\boldsymbol{v}})\right] \end{split} $ | (15) |
其中
定义
| $ H = -\iint {f\ln}f{\rm{d}}{\boldsymbol{v}}{\rm{d}}{\boldsymbol{x}} $ | (16) |
H是与气体系统的熵相关的标量。在无外力的情况下,H的时间导数可写为:
| $ \begin{split} \frac{\partial H}{\partial t} = & -\iint(1+{\ln}f)\frac{\partial{f}}{\partial{t}}{\rm{d}}{\boldsymbol{v}}{\rm{d}}{\boldsymbol{x}}\\ = &\iint{{\boldsymbol{v}}\cdot\frac{\partial{f}\ln{f}}{\partial{\boldsymbol{x}}}}{\rm{d}}{\boldsymbol{v}}{\rm{d}}{\boldsymbol{x}}-\iint(1+\ln{f}){Q} {\rm{d}}{\boldsymbol{v}}{\rm{d}}{\boldsymbol{x}}\\ = &\oint \int{{\boldsymbol{v}}\cdot{\boldsymbol{n}} {f}\ln{f}}{\rm{d}}{\boldsymbol{v}}{\rm{d}}S-\iint(1+\ln{f}){Q} {\rm{d}}{\boldsymbol{v}}{\rm{d}}{\boldsymbol{x}}\end{split} $ |
式中,
| $ \begin{split} \frac{1}{4}\iiint{}&{\rm{d}}{\boldsymbol{\varOmega}} {\rm{d}}{\boldsymbol{v}}_\ast{{\rm{d}}{\boldsymbol{v}}} B \left[f({\boldsymbol{v}}'_{\ast})f({\boldsymbol{v}}')-f({\boldsymbol{v}}_{\ast})f({\boldsymbol{v}})\right]\\ &\times \Big\{ \ln[f({\boldsymbol{v}}'_{\ast})f({\boldsymbol{v}}')] -\ln[f({\boldsymbol{v}}_{\ast})f({\boldsymbol{v}})] \Big\} \end{split} $ |
因为碰撞核
| $ \frac{\partial H}{\partial t}\geqslant 0 $ | (17) |
式(17)表明孤立系统的
| $ F_{eq}(T) = n\left(\frac{m}{2{\text{π}} k_BT}\right)^{\frac{3}{2}}\exp\left(-\frac{mc^2}{2k_BT}\right) $ | (18) |
线性化玻尔兹曼方程在气体动理论中具有重要地位。第一,线性化玻尔兹曼碰撞项的本征值与本征函数,不仅在渐近展开推导纳维-斯托克斯方程的过程中至关重要,而且是发展简化动理学模型方程的源头理论。第二,在许多微机电系统中,气体的压力梯度与温度梯度非常小,因此使用线性化方程可以高效准确地模拟微流动。第三,虽然玻尔兹曼方程是单粒子速度分布函数确定性演化的平均方程,但是在某些问题中(例如:第5.2节中的瑞利-布里渊散射)可以通过线化玻尔兹曼方程研究粒子涨落带来的影响。
通常将速度分布函数在全局平衡态
| $ f_{eq} = n_0\left(\frac{m}{2{\text{π}} k_BT_0}\right)^{\frac{3}{2}}\exp\left(-\frac{mv^2}{2k_BT_0}\right) $ | (19) |
下展开为:
| $ f(t,{\boldsymbol{x}},{\boldsymbol{v}}) = f_{eq}({\boldsymbol{v}})\left[1+\phi(t,{\boldsymbol{x}},{\boldsymbol{v}})\right] $ | (20) |
其中扰动量
| $ \begin{split} \frac{\partial\phi}{\partial t}+{\boldsymbol{\xi}}\cdot\frac{\partial\phi}{\partial {\boldsymbol{x}}} & = \frac{\ell}{v_m}{J}(\phi)\\ &\equiv -\frac{\ell}{v_m}\iint B \Delta[\phi]f_{eq}({\boldsymbol{v}}_{\ast}){\rm{d}}{\boldsymbol{\varOmega}} {\rm{d}}{\boldsymbol{v}}_\ast \end{split} $ | (21) |
这里的速度和空间坐标分别通过最概然速率
| $ {\boldsymbol{\xi}} = \frac{{\boldsymbol{c}}}{v_m(T_0)} $ | (22) |
其中:
| $ v_m(T) = \sqrt{\frac{2k_BT}{m}} $ | (23) |
为气体分子的最概然速率,即与麦克斯韦速率分布的极大值对应的速率。
对于麦克斯韦分子,线性化玻尔兹曼碰撞项的本征值与本征函数为[52]:
| $\begin{split} J({{\varPhi} _{rlm}}) =& n{\lambda _{rl}}{{\varPhi} _{rlm}}\\ {{\varPhi} _{rlm}} =& {g_{rl}}({\xi} )Y_l^m(\hat {\xi} )\\ =& \sqrt {\frac{{2{{\text{π}} ^{\frac{3}{2}}}r!}}{{\left( {r + l + \dfrac{1}{2}} \right)!}}} S_{l + \frac{1}{2}}^{(r)}({{\xi} ^2}){{\xi} ^l}Y_l^m(\hat {\xi} )\\ {\lambda _{rl}} =& 2{\text{π}} \sqrt {\frac{{2K}}{m}} \int_0^{\text{π}} {\rm{d}} {\theta} \sin {\theta} B({\theta} )\times\\& \Bigg [ - 1 + {\cos ^{2r + l}}\frac{{\theta} }{2}{P_l}\left( {\cos \frac{{\theta} }{2}} \right)-\\& {\delta _{r0}}{\delta _{l0}} + {\sin ^{2r + l}}\frac{{\theta} }{2}{P_l}\left( {\sin \frac{{\theta} }{2}} \right)\Bigg] \end{split} $ | (24) |
式中,
前三项本征值为
| $ \begin{split} & {{\lambda} _{02}} = \left( { - \frac{3}{2}} \right){\text{π}} \sqrt {\frac{{2K}}{m}} \int_0^{\text{π}} {{\rm{d}}{\theta} } {\sin ^3}{\theta} B({\theta} )\\& {{\lambda} _{11}} = \frac{2}{3}{{\lambda} _{02}} \end{split} $ | (25) |
这两个本征值决定了剪切黏性系数和热导率的大小。若归一化的速度
| $ \begin{split}& \varPhi_{000} = 1 ,\; \varPhi_{010} = \sqrt{2}\xi_z \\& \varPhi_{100} = \sqrt{\dfrac{2}{3}}\left(\dfrac{3}{2}-\xi^2\right) \\& \varPhi_{020} = \dfrac{1}{3\sqrt{3}}\left(\xi^2_z-\dfrac{\xi^2}{3}\right) \\& \varPhi_{110} = \dfrac{2}{\sqrt{5}}\left(\dfrac{5}{2}-\xi^2\right)\xi_z \end{split} $ |
其与气体的分子数密度、速度、温度、压力和热流的扰动密切相关:
| $ \begin{split} &[{n},{\boldsymbol{u}}, T] = \int\left[1,{\boldsymbol{\xi}},\frac{2}{3}\left(\xi^2-\frac{3}{2}\right)\right] {f_{eq}\phi}{\rm{d}}{\boldsymbol{\xi}} \\ &[\sigma_{ij},{\boldsymbol{q}}] = \int \left[2\xi_{\langle i}\xi_{j\rangle}, \left(\xi^2 -\frac{5}{2}\right){\boldsymbol{\xi}}\right] f_{eq}\phi{}{\rm{d}}{\boldsymbol{\xi}}\end{split} $ | (26) |
式(26)中,下标中的尖括号表示该张量是无迹张量,即
玻尔兹曼方程和纳维-斯托克斯方程分别在介观和宏观尺度上描述气体系统的演化,它们之间的关系一直是数学家和力学家研究的重要课题[63]。对玻尔兹曼方程求守恒量
| $ \begin{array}{c} \dfrac{\partial \rho}{\partial t}+\dfrac{\partial(\rho{}u_j) }{\partial x_j} = 0 \\ \dfrac{\partial (\rho{u_i})}{\partial t}+\dfrac{\partial (\rho{}u_iu_j+p_{ij})}{\partial x_j} = \rho{}a_i\\ \dfrac{\partial \left(\rho{}E\right)}{\partial t}+\dfrac{\partial \left(\rho{}{E}u_j+u_i{p}_{ij}+q_j\right)}{\partial x_j} = \rho{}a_ju_j \end{array} $ | (27) |
其中
在Chapman和Enskog[65-66]方法中,首先将玻尔兹曼方程改写为:
| $ \frac{\partial f}{\partial t}+{\boldsymbol{v}}\cdot\frac{\partial f}{\partial {\boldsymbol{x}}}+{\boldsymbol{a}}\cdot\frac{\partial f}{\partial {\boldsymbol{v}}} = \frac{Q(f)}{\varepsilon} $ | (28) |
然后将分布函数和玻尔兹曼碰撞项展开为
| $ \begin{split}&\qquad\qquad\qquad f = \sum_{k = 0}^\infty {\varepsilon^k} f^{(k)}\\& Q = \sum_{k = 0}^\infty {\varepsilon^k} Q^{(k)} = Q(f^{(0)}) +\varepsilon{}{J}(f^{(1)})+{O}(\varepsilon^2)\end{split} $ | (29) |
值得注意的是,
同时,压力和热流也相应展开如下:
| $ \begin{split} p_{ij} = \sum_{k = 0}^\infty {\varepsilon^k} p_{ij}^{(k)} \equiv \sum_{k = 0}^\infty {\varepsilon^k} \; m\int{}c_ic_jf^{(k)}{\rm{d}}{\boldsymbol{v}} \\ {\boldsymbol{q}} = \sum_{k = 0}^\infty {\varepsilon^k} {\boldsymbol{q}}^{(k)} \equiv \sum_{k = 0}^\infty {\varepsilon^k} \; \frac{m}{2}\int{}{\boldsymbol{c}}c^2f^{(k)}{\rm{d}}{\boldsymbol{v}} \end{split} $ | (30) |
但是,碰撞不变量对应的宏观量
| $ \Big [{\rho},{\rho}{\boldsymbol{u}}, 3k_B{\rho}{}T \Big ] = m\int{} \Big [1,{\boldsymbol{v}},mc^2 \Big ]f^{(0)}{\rm{d}}{\boldsymbol{v}} $ | (31) |
而各个高阶展开对
将式(30)代入式(27),可知时间导数亦可表示为
| $ \frac{\partial}{\partial{} t} = \sum_{k = 0}^\infty \varepsilon^k \frac{\partial}{\partial{} t_k} $ | (32) |
且对于零阶近似,可得到:
| $ \begin{array}{c}\dfrac{\partial \rho}{\partial t_0}+\dfrac{\partial(\rho{}u_j) }{\partial x_j} = 0 \\ \dfrac{\partial (\rho{u_i})}{\partial t_0}+\dfrac{\partial (\rho{}u_iu_j+nk_BT\delta_{ij})}{\partial x_j} = \rho{}a_i\\ \dfrac{\partial \left(\rho{}E\right)}{\partial t_0}+\dfrac{\partial \left(\rho{}{E}u_j+u_ink_BT\delta_{ij}\right)}{\partial x_j} = \rho{}a_ju_j\end{array} $ | (33) |
从式(28)和式(29)易知
| $ f^{(0)} = F_{eq} $ | (34) |
而速度分布函数的一阶近似
| $ \begin{split} {J}(\phi) =& \frac{1}{F_{eq}}\left[\frac{\partial F_{eq}}{\partial t_0}+{\boldsymbol{v}}\cdot\frac{\partial F_{eq}}{\partial {\boldsymbol{x}}}+{\boldsymbol{a}}\cdot\frac{\partial F_{eq}}{\partial {\boldsymbol{v}}} \right]\\ =& 2\xi_{\langle{i}} \xi_{j\rangle} \frac{\partial u_{\langle i}}{\partial x_{j\rangle}} +\left(\xi^2-\frac{5}{2}\right)\xi_i\sqrt{\frac{2k_BT}{m}}\frac{\partial \ln{T}}{\partial x_i}\end{split} $ | (35) |
其中,方程的推导过程中用到
| $ \frac{\partial F_{eq}}{\partial t_0} = \frac{\partial F_{eq}}{\partial C_M} \frac{\partial C_M}{\partial t_0}, \quad \frac{\partial F_{eq}}{\partial {\boldsymbol{x}}} = \frac{\partial F_{eq}}{\partial C_M} \frac{\partial C_M}{\partial {\boldsymbol{x}}} $ |
以及式(33)。注意式(21)中的
积分方程(35)的解可分为齐次部分与非齐次部分。齐次部分满足
| $ \phi = -A(\xi)\xi_i\sqrt{\frac{2k_BT}{m}}\frac{\partial \ln{T}}{\partial x_i} -B(\xi)\xi_{\langle{i}} \xi_{j\rangle}\frac{\partial u_{\langle i}}{\partial x_{j\rangle}} $ | (36) |
其中,
| $ {J}(A\xi_i) = -\left(\xi^2-\frac{5}{2}\right)\xi_i, \;\; {J}(B\xi_{\langle{i}} \xi_{j\rangle}) = -2\xi_{\langle{i}} \xi_{j\rangle} $ | (37) |
且兼容性条件要求
一旦得到
| $ \sigma^{(1)}_{ij} = -2\mu\frac{\partial u_{\langle i}}{\partial x_{j\rangle}},\quad q^{(1)}_i = -\kappa \frac{\partial T}{\partial x_i} $ | (38) |
且剪切黏性与热导率分别为:
| $ \begin{split}& \mu = \frac{2p}{15{\text{π}}^{\frac3 2}}\int\exp(-\xi^2)B(\xi)\xi^4 {\rm{d}}{\boldsymbol{\xi}} \\& \kappa = \frac{2p}{3{\text{π}}^{\frac3 2}} \frac{k_B}{m} \int\exp(-\xi^2)A(\xi)\xi^4 {\rm{d}}{\boldsymbol{\xi}}\end{split} $ | (39) |
一般将
| $ \begin{split} A(\xi)& = -\sum_{r = 1}^{n_a}a_rS^{(r)}_{\frac{3}{2}}(\xi^2) \\ B(\xi)& = \sum_{r = 0}^{n_b}b_rS^{(r)}_{\frac{5}{2}}(\xi^2)\end{split} $ | (40) |
然后通过式(37)和索南多项式的正交性求解输运系数。对于麦克斯韦分子,取第一项展开可得到准确的剪切黏性和热导率,即取
| $ \sigma_{\mu} = \int \frac{B(\theta,v_r)}{v_r}\sin^2\theta {{\rm{d}}\varOmega} $ | (41) |
则剪切黏性为:
| $ \mu = \frac{5\sqrt{{\text{π}}{m}k_BT}}{8\left(\dfrac{m}{4k_BT}\right)^4\displaystyle\int_0^\infty {}v_r^7\sigma_{\mu}\exp\left(-\dfrac{mv^2_r}{4k_BT}\right){\rm{d}}v_r} $ | (42) |
而热导率为:
| $ {\kappa} = \frac{15}{4}\frac{k_B}{m}\mu $ | (43) |
从而单原子气体的普朗特数为:
| $ \begin{split} Pr & = {c_p}\frac{\mu}{\kappa} = \frac{5k_B}{2m}\frac{\mu}{\kappa} = \frac{2}{3}\end{split} $ | (44) |
对于逆幂律分子间相互作用势(式(11)),可以得出气体黏性和温度的关系:
| $\mu(T)\propto{T^\omega}, \quad \omega=\frac{\eta+3}{2(\eta-1)}$ | (45) |
其中
将式(38)代回式(27),即可获得纳维-斯托克斯方程。若继续计算Chapman-Enskog展开的高阶近似,可以得到Burnett、super-Burnett等宏观方程组[21]。但是可能由于应力和热流与宏观量
值得一提的是,对于麦克斯韦分子,在空间均匀系统中,本征值
| $ \begin{split}& \frac{\partial \sigma_{ij}}{\partial t} = n\lambda_{02} \sigma_{ij} = -\frac{p}{\mu}\sigma_{ij}\\& \frac{\partial q_{i}}{\partial t} = n\lambda_{11} q_{i} = -\frac{2}{3}\frac{p}{\mu}q_{i}\end{split} $ | (46) |
可以认为这些弛豫过程是本质,而黏性系数和热导率则为表象:在稀薄气体流动中,本构关系式(38)和等效输运系数会随着克努森数的改变而改变,但一旦分子作用势确定,弛豫系数就会确定不变。
利用弛豫时间和输运系数的关系,可以大大简化模型方程中输运系数的推导过程。即,如果应力偏量的弛豫时间为
玻尔兹曼方程碰撞项的复杂性给数值求解带来极大挑战[31],因此,学者建议使用简化的碰撞模型来代替。在简化玻尔兹曼方程的碰撞项时,一般认为需要满足以下几点:
1)动理学模型必须保证质量、动量、能量守恒;
2)理想气体的局部平衡态速度分布函数为麦克斯韦分布;
3)从模型方程导出的黏性系数与热导率应与玻尔兹曼方程导出的结果保持一致;
4)满足熵增定理,当且仅当孤立系统处于平衡态时熵增为零,并达到其最大值。
其中,前两项是基本要求,第三项要求在连续流区域通过Chapman-Enskog展开恢复出纳维-斯托克斯方程。而第四项仅为从物理角度出发的考量,并不能保证模型方程的精度:如果一个动理学模型方程与玻尔兹曼方程完全一致,那么熵增速率也应该相同,然而这通常是不可能做到的。实际上,大多数时候,仅在线性化情况下满足熵增定理的Shakhov模型的精度优于完全满足熵增定理的ES-BGK模型。
由于玻尔兹曼碰撞项在形式上可记为
| $ Q = \frac{f_{r}-f}{\tau} $ | (47) |
其中:
BGK模型是最著名的气体动理学简化模型,由Bhatnagar、Gross和Krook提出[32],其参考速度分布函数是局部麦克斯韦分布:
| $ f^{BGK}_r = F_{eq} $ | (48) |
易见此模型满足三大守恒律,且给出了在平衡态下的正确解
| $ \begin{split}\frac{\partial H}{\partial t} = & -\int \frac{F_{eq}-f}{\tau}\ln{f} {\rm{d}}{\boldsymbol{v}}\\ = &-\int \frac{F_{eq}-f}{\tau}(\ln{}F_{eq}-\ln{f}) {\rm{d}}{\boldsymbol{v}}\\ \geqslant &\; 0 \end{split} $ | (49) |
空间均匀系统中应力偏量和热流的弛豫时间均为
Holway[33]提出了ES-BGK模型以修正BGK模型中错误的普朗特数,其中参考速度分布函数是在给定质量、动量、能量和应力张量条件下,通过最大化熵函数式(16)而来:
| $ f_r^{ES} = \frac{n}{\sqrt{{\rm{det}} [2\pi{\boldsymbol{\lambda}}_{ij}]}}\exp\left(-\frac{1}{2}{\boldsymbol{\lambda}}_{ij}^{-1}c_i{c_j}\right) $ | (50) |
其中:
| $ {\boldsymbol{\lambda}}_{ij} = (1-b)\frac{k_BT}{m}\delta_{ij}+b\frac{p_{ij}}{nm} = \frac{p\delta_{ij}+b\sigma_{ij}}{nm} $ | (51) |
若
容易证明,应力偏量的弛豫时间为
| $ \mu = \frac{1}{1-b}{p\tau}, \;\; Pr = \frac{1}{1-b} $ | (52) |
为确保弛豫时间为正,则有
| $ b = -\frac{1}{2} $ | (53) |
可以看出,当碰撞项为零时,ES-BGK方程给出
Andries等[34]证明了ES-BGK模型满足熵增定理,使之成为唯一满足熵增定理且能正确恢复各输运系数的动理学模型,因此,ES-BGK模型受到广泛关注。
1.5.3 Shakhov模型不同于ES-BGK模型在参考速度分布函数中引入应力修正项,Shakhov模型通过在参考速度分布函数中引入热流修正项来恢复正确的输运系数:
| $ f_r^S = F_{eq}\left[1+(1-{Pr})\frac{2m{\boldsymbol{q}}\cdot {\boldsymbol{c}}}{5n(k_BT)^2}\left(\frac{mc^2}{2k_BT}-\frac{5}{2}\right)\right] $ | (54) |
此模型同样满足三大守恒律。从偏应力和热流的弛豫时间可以看出,该模型的黏性为
线性化的Shakhov模型满足熵增定理。而对于非线性流动,熵增定理未被证明但也无从证伪;另外,速度分布函数可能出现非物理的负值。尽管如此,Shakhov模型仍能在许多问题中给出准确结果,因此得到了广泛应用。
1.5.4 Gross-Jackson模型及其非线性化针对麦克斯韦分子,根据线化玻尔兹曼碰撞项的本征值与本征函数,Gross和Jackson提出的以下形式的动理学模型去逼近线性化玻尔兹曼碰撞项
| $ \begin{split} {L}_{GJ} = &\lambda_{st}\phi+\sum_{nl}(\lambda_{nl}-\lambda_{st})\frac{2l+1}{4\pi} \cdot \\ &\int{}P_l(\cos\theta')g_{nl}(\xi)g_{nl}(\xi_1)\phi({\boldsymbol{\xi}}_1) {\rm{d}}{\boldsymbol{\xi}}_1 \end{split} $ | (55) |
式中,
Gross和Jackson将
| $ \begin{split} {L}_{GJ}^{(N)} = &\lambda_{0N}\phi -\lambda_{0N}\sum_{2n+l\leqslant{N}} \left(1-\frac{\lambda_{nl}}{\lambda_{0N}}\right)g_{nl}(\xi)\cdot \\ &\frac{2l+1}{4\pi} \int{}P_l(\cos\phi')g_{nl}(\xi_1)\phi({\boldsymbol{\xi}}_1) {\rm{d}}{\boldsymbol{\xi}}_1 \end{split} $ | (56) |
即保留了所有阶数小于或等于
在线性化情况下,即把速度分布函数在全局平衡态下根据式(20)展开,BGK、ES-BGK和Shakhov模型有如下形式:
| $ \begin{split} &\frac{\partial \phi}{\partial{}t} +{{\boldsymbol{\xi}}}\cdot\frac{\partial \phi}{\partial {\boldsymbol{x}}} = \frac{\ell}{v_m}{L} \\ &{L}_{BGK} = \frac{p}{\mu}\left[{n}+2{\boldsymbol{u}}\cdot{\boldsymbol{\xi}}+T\left(\xi^2-\frac{3}{2}\right)-\phi\right] \\ &{L}_{ES} = \frac{2}{3}{L}_{BGK}-\frac{2p}{3\mu} \frac{\sigma_{ij}}{2}\xi_{\langle i}\xi_{j\rangle} \\ &{L}_{S} = {L}_{BGK} +\frac{p}{\mu}\frac{4(1-{Pr})}{5}{\boldsymbol{q}}\cdot{\boldsymbol{\xi}}\left(\xi^2-\frac{5}{2}\right) \end{split} $ | (57) |
其中扰动宏观物理量的定义可参考式(26)。它们都可以看作是Gross-Jackson模型的特例。当
| $ \lambda_{03} = \frac{3}{2}\lambda_{02} = \frac{3p}{2\mu} $ | (58) |
从而式(56)给出:
| $ \begin{split} {L}_{GJ}^{(3)} = &\frac{3}{2}L_{BGK}+\frac{p}{\mu}\left[\frac{\sigma_{ij}}{2}\xi_{\langle i}\xi_{j\rangle} +\frac{2}{3}{\boldsymbol{q}}\cdot{\boldsymbol{v}}\left( \xi^2-\frac{5}{2}\right)\right]f_{eq} \\ = &-\frac{3}{2}{L}_{ES}+\frac{5}{2}{L}_{S}\end{split} $ |
虽然,这既不符合线性化ES-BGK模型,也不符合线性化Shakhov模型,但是可将其视为这两个模型的线性组合。另一方面,若给定约束
因此,通过Gross-Jackson模型和线性化BGK、ES-BGK、Shakhov模型的关系,可以反推出各种形式的非线性动理学模型。例如,陈松泽等将ES-BGK模型与Shakhov模型线性组合为一个复合模型,通过改变两模型所占的比例和普朗特数,复合模型能够分别恢复到BGK、ES-BGK和Shakhov模型式[68]。类似地,吴雷在博士论文也提出一个带有自由参数
| $ \begin{split} f_r = &F_{eq} \left\{1+ \frac{\sigma_{ij}}{p} \frac{c_{\langle i}c_{j\rangle}}{2k_B\frac{T}{m}} +\right.\\ &\left.\Bigg[1-{Pr}(1-b)\Bigg]\frac{2m{\boldsymbol{q}}\cdot {\boldsymbol{c}}}{5n(k_BT)^2}\left(\frac{mc^2}{2k_BT}-\frac{5}{2}\right) \right\}\\ \tau = &(1-b)\frac{\mu}{p} \end{split} $ | (59) |
该模型实际上是在Gross-Jackson模型(55)中取
| $ \begin{split} {n}+2{\boldsymbol{u}}\cdot{\boldsymbol{\xi}}+T\left(\xi^2-\frac{3}{2}\right)-\phi \rightarrow& {F_{eq}}-f\\ \sigma_{ij}\frac{\xi_{\langle i}\xi_{j\rangle}}{2} \rightarrow& \frac{\sigma_{ij}}{p}\frac{c_{\langle i}c_{j\rangle}}{2k_BT} F_{eq} \\ {\boldsymbol{q}}\cdot{\boldsymbol{\xi}}\left(\xi^2-\frac{5}{2}\right) \rightarrow& \frac{m{\boldsymbol{q}}\cdot {\boldsymbol{c}}}{2n(k_BT)^2}\left(\frac{mc^2}{2k_BT}-\frac{5}{2}\right)F_{eq} \end{split} $ | (60) |
需要注意到,含有应力偏量的项既可以被吸收到指数函数里使参考分布函数变成类似式(50)的形式,也可以放在外面(此时对
玻尔兹曼方程是仅针对单原子气体提出的,为模拟具有两个或多个原子的分子结构的气体的动力学行为,则需要在气体动理论层面重新建模。对于分子气体,两体碰撞保持动量守恒,但是能量却可以在各形式自由度和能级之间进行交换。因此,相比于仅具有剪切黏性的单原子气体,分子气体还存在体积黏性。另外,除了由分子平动引起的平动热导率外,还有由分子转动和振动引起的内部热导率。复杂的物理过程和更多的输运参数都给分子气体动理论建模带来挑战。
分子的内能可以表示为转动能量、振动能量以及电离能之和,分子气体内部自由度导致了更加复杂的碰撞项。王承书和乌伦贝克从量子力学角度出发建立了WCU方程,定义
| $\begin{aligned}[b] Q_i=&\sum_{jkl}\iint P_{ij}^{kl}B(\theta,{v_r}) {\rm{d}}{\boldsymbol{\varOmega}} {\rm{d}}\boldsymbol{v}_\ast \cdot \\ &\left[\omega_{ij}^{kl}f_l(\boldsymbol{v}'_{\ast})f_k(\boldsymbol{v}')-f_j(\boldsymbol{v}_{\ast})f_i(\boldsymbol{v})\right] \end{aligned}$ | (61) |
其中,
| $ |{\boldsymbol{v}}'_r|^2 = |{\boldsymbol{v}}_r|^2+\frac{4}{m}(e_{i}+e_{j}-e_{k}-e_{l})>0 $ | (62) |
碰撞后的分子速度为:
| $ {\boldsymbol{v}}' = \frac{{\boldsymbol{v}}+{\boldsymbol{v}}_\ast}{2}+\frac{v'_r}{2}{\boldsymbol{\varOmega}}, \; \; {\boldsymbol{v}}'_\ast = \frac{{\boldsymbol{v}}+{\boldsymbol{v}}_\ast}{2}-\frac{v'_r}{2}{\boldsymbol{\varOmega}} $ | (63) |
碰撞核和跃迁概率的具体表达式是非常复杂的。这里以N2为例,在只存在转动自由度的情况下,对WCU方程的计算复杂性进行说明。在Lennard-Jones作用势下,转动能可表达为:
| $ e_{i} = 2.9{i}(i+1)\; {K} $ |
而转动能级的简并度为:
| $ g_i = 2i+1, \quad i = (0,1,\cdots,\infty) $ |
| $ \begin{split} P_{ij}^{kl} = P_0\omega_{ij}^{kl}&\left[\frac{2e_{tot}}{5e_{tr0}}\exp(-\varDelta_1-\varDelta_2-\varDelta_3-\varDelta_4)+\right.\\ &\left.\frac{5e_{tr0}}{2e_{tot}}\exp(-\varDelta_3-\varDelta_4)\right] \end{split} $ |
其中,
| $ \begin{split}& \varDelta_1 = \dfrac{|e_{i}+e_{j}-e_{k}-e_{l}|}{e_{tr0}} \\& \varDelta_2 = 2\dfrac{|e_{i}+e_{l}-e_{k}-e_{j}|}{e_{tot}} \\& \varDelta_3 = 4\dfrac{|e_{i}-e_{k}|}{e_{tr0}+e_{i}} \\& \varDelta_4 = 2\dfrac{|e_{j}-e_{l}|}{e_{tr0}+e_{j}} \\& e_{tr0} = \dfrac{m}{4}v_r^2 \\& e_{tot} = \dfrac{m}{4}v_r^2+e_{i}+e_{j} \end{split}$ |
显然,如果总能级数为
根据碰撞过程中平动动能是否守恒,WCU方程中的碰撞项可以分为弹性碰撞与非弹性碰撞。若处在
| $ \begin{split} Q_i = &\sum_{j}\iint P_{ij}^{ij}B \left[f_j({\boldsymbol{v}}'_{\ast})f_i({\boldsymbol{v}}')-f_j({\boldsymbol{v}}_{\ast})f_i({\boldsymbol{v}})\right]{\rm{d}}{\boldsymbol{\varOmega}} {\rm{d}}{\boldsymbol{v}}_\ast + \\ &\sum_{jkl}(1-\delta_{jk}\delta_{il}) \iint P_{ij}^{kl}B \left[f_k({\boldsymbol{v}}'_{\ast})f_l({\boldsymbol{v}}')-f_j({\boldsymbol{v}}_{\ast})f_i({\boldsymbol{v}})\right]{\rm{d}}{\boldsymbol{\varOmega}} {\rm{d}}{\boldsymbol{v}}_\ast \end{split} $ |
对于弹性碰撞和非弹性碰撞,可以分别引入两个等效的弛豫时间[72]:
| $ \begin{split} \frac{1}{\tau_{el}} = &\sum_{j}\iint P_{ij}^{ij}B f_j({\boldsymbol{v}}_{\ast}){\rm{d}}{\boldsymbol{\varOmega}} {\rm{d}}{\boldsymbol{v}}_\ast \\ \frac{1}{\tau_{in}} = &\sum_{jkl}(1-\delta_{jk}\delta_{il})\iint P_{ij}^{kl}B f_j({\boldsymbol{v}}_{\ast}){\rm{d}}{\boldsymbol{\varOmega}} {\rm{d}}{\boldsymbol{v}}_\ast \end{split} $ |
而将WCU碰撞项形式地改写为:
| $ \begin{split} Q_i = &\sum_{j}\iint P_{ij}^{ij}B f_j({\boldsymbol{v}}'_{\ast})f_i({\boldsymbol{v}}'){\rm{d}}{\boldsymbol{\varOmega}} {\rm{d}}{\boldsymbol{v}}_\ast + \\ &\sum_{jkl}(1-\delta_{jk}\delta_{il})\iint P_{ij}^{kl}B f_k({\boldsymbol{v}}'_{\ast})f_l({\boldsymbol{v}}'){\rm{d}}{\boldsymbol{\varOmega}} {\rm{d}}{\boldsymbol{v}}_\ast - \frac{f_i({\boldsymbol{v}})}{\tau_{el}}-\frac{f_i({\boldsymbol{v}})}{\tau_{in}} \end{split} $ |
这两个等效的碰撞时间,表征着能量在各种自由度或能级间的弛豫速度,因而与下面将讨论的分子气体输运系数、体积黏性、平动/转动热导率等,有着直接的关联。
2.1 体积黏性体积黏性表征了气体无剪切膨胀或压缩时所受的阻力,对于稀疏气体,这种阻力来自于气体分子平动动能与内能的交换过程:在膨胀或者压缩过程中,压力做功会立刻改变平动动能,但在一定的延迟后才会通过非弹性碰撞来改变内能。为方便起见,在下述推导中,假设只存在一个转动能级。
引入非弹性碰撞所对应的平动能与转动能交换的弛豫时间
| $ \frac{\partial{T_r}}{\partial t} = \frac{T_t-T_r}{\tau_r} $ | (64) |
式中,
| $ T = \frac{3T_t+d_rT_r}{3+d_r} $ | (65) |
忽略剪切黏性和热传导的影响,通过膨胀压缩过程中能量守恒可得到:
| $ \begin{split} \frac{3nk_B}{2}\frac{{\rm{D}}T_t}{{\rm{D}}t} = -p_t\nabla\cdot{\boldsymbol{u}}-\frac{d_r}{2}nk_B\frac{T_t-T_r}{\tau_r}\\ \frac{d_r}{2}nk_B\frac{{\rm{D}}T_r}{{\rm{D}}t} = \frac{d_r}{2}nk_B\frac{T_t-T_r}{\tau_r} \end{split} $ | (66) |
式中,
| $ \frac{{\rm{D}}}{{\rm{D}}t}(T_t-T_r) = -\frac{2}{3}T_t\nabla\cdot{\boldsymbol{u}}-\frac{3+d_r}{3}\frac{T_t-T_r}{\tau_r} $ | (67) |
将
| $ T_t-T_r\approx-\frac{2\tau_r}{3+d_r}{T_t\nabla\cdot{\boldsymbol{u}}}\approx-\frac{2\tau_r}{3+d_r}{T\nabla\cdot{\boldsymbol{u}}} $ | (68) |
这说明,内能弛豫的影响将压力从原始压力
| $ p_t = nk_BT_t = p_0\left[1-\frac{2d_r}{(3+d_r)^2}\tau_r\nabla\cdot{\boldsymbol{u}}\right] $ | (69) |
式中速度散度前的系数即为体积黏性
| $ Z = \frac{3}{d_r+3}\frac{\tau_r}{\tau} $ | (70) |
其中由分子平动引起的平均碰撞时间定义为
| $ \frac{\mu_b}{\mu} = \frac{2d_rZ}{3(d_r+3)} $ | (71) |
从式(70)和式(71)可知,体积黏性正比于能量交换时间。对于单原子气体,若不考虑电离,不存在内部能量的交换,因此体积黏性为零。而对于一些分子气体,例如CO2,体积黏性可以是剪切黏性的上千倍[73]。但是,需要强调的是,式(68)成立的条件是
| $ {\mu}_b = 2n_0k_BT_t\dfrac{\dfrac{{d_r} {\tau_r}}{1+\varpi^2\tau^2_r}}{\Bigg(3+\dfrac{d_r}{1+\varpi^2\tau^2_r}\Bigg)^2} $ | (72) |
也就是说,在
分子气体的热流由两部分组成,一部分是由分子的平动引起的动能传递,一部分是由分子的扩散引起的内能的传递。由于气体分子迁移过程中存在动能和内能交换,这一非弹性碰撞改变了能量在不同自由度下的分布,从而间接改变了动能传递与内能随扩散传递的结果。因而,平动热流和转动热流的弛豫过程是相互耦合的。于是,在空间均匀系统中,类似于式(46),平动热流
| $ \begin{split}& \frac{\partial{\boldsymbol{q}}_{t}}{\partial{t}} = -\frac{p}{\mu}( A_{tt}{\boldsymbol{q}}_{t}+A_{tr}{\boldsymbol{q}}_{r}) \\& \frac{\partial{\boldsymbol{q}}_{r}}{\partial{t}} = -\frac{p}{\mu}( A_{rt}{\boldsymbol{q}}_{t}+A_{rr}{\boldsymbol{q}}_{r}) \end{split} $ | (73) |
而通过Chapman-Enskog展开得到的连续流下的平动热导率
| $ \begin{split}& A_{tt}\kappa_{tr}+A_{tr}\kappa_{rot} = \frac{5}{2}\frac{k_B\mu}{m} \\& A_{rt}\kappa_{tr}+A_{rr}\kappa_{rot} = \frac{d_r}{2}\frac{k_B\mu}{m} \end{split} $ | (74) |
将方程(74)代入方程(1),就可以通过热弛豫系数求解如下方程,得到对应的Eucken系数:
| $ \begin{bmatrix} f_{tr} \\ f_{rot} \end{bmatrix} = {\begin{bmatrix} 3A_{tt} & d_rA_{tr} \\ 3A_{rt} & d_rA_{rr} \end{bmatrix}}^{-1} \begin{bmatrix} 5 \\ d_r \end{bmatrix} $ | (75) |
基于WCU方程(61),Manson和Manchick通过修正的Chapman-Enskog展开推导出四个无量纲热弛豫系数的具体形式:
| $ \begin{split}& A_{tt} = \frac{2}{3}+\frac{5}{6Z}\frac{d_r}{3+d_r} \\& A_{rr} = \frac{\mu}{\rho{D'}}+\frac{3}{2(3+d_r)Z} \\& A_{tr} = -\frac{5}{2(3+d_r)Z} \\& A_{rt} = -\frac{d_r}{2(3+d_r)Z} \end{split} $ | (76) |
其中
| $ \begin{split}& f_{tr} = \frac{5}{2}\left[1-\frac{5d_r}{4(d_r+3)Z}\left(1-\frac{2\rho{D'}}{5\mu}\right)\right] \\& f_{rot} = \frac{\rho{D'}}{\mu}\left[ 1+\frac{15}{4(d_r+3)Z}\left(1-\frac{2\rho{D'}}{5\mu}\right) \right] \end{split} $ | (77) |
注意到,
Mason与Monchick的解析解依然存在的一个问题,即无法保证通过式(76)推导而来的无量纲热弛豫系数
对于单原子气体,在粒子数和空间网格足够多的情况下,DSMC已被证明收敛于玻尔兹曼方程的解[25]。实际上,由于DSMC中两体碰撞后粒子速度的更新方式与玻尔兹曼方程一致,式(43)在可接受的误差范围内恒成立,即DSMC可确保平动Eucken因子
我们通过提取DSMC中的热弛豫速率
| $ Z = \frac{1}{\varLambda}\frac{{\alpha}(5-2\omega)(7-2\omega)}{5({\alpha}+1)({\alpha}+2)} $ | (78) |
式中,
| $ {Sc} = \frac{\mu}{\rho{D}} = \frac{5(2+{\alpha})}{3(7-2\omega){\alpha}} $ | (79) |
使用开源软件SPARTA在空间均匀系统中提取DSMC方法中的热弛豫系数矩阵
|
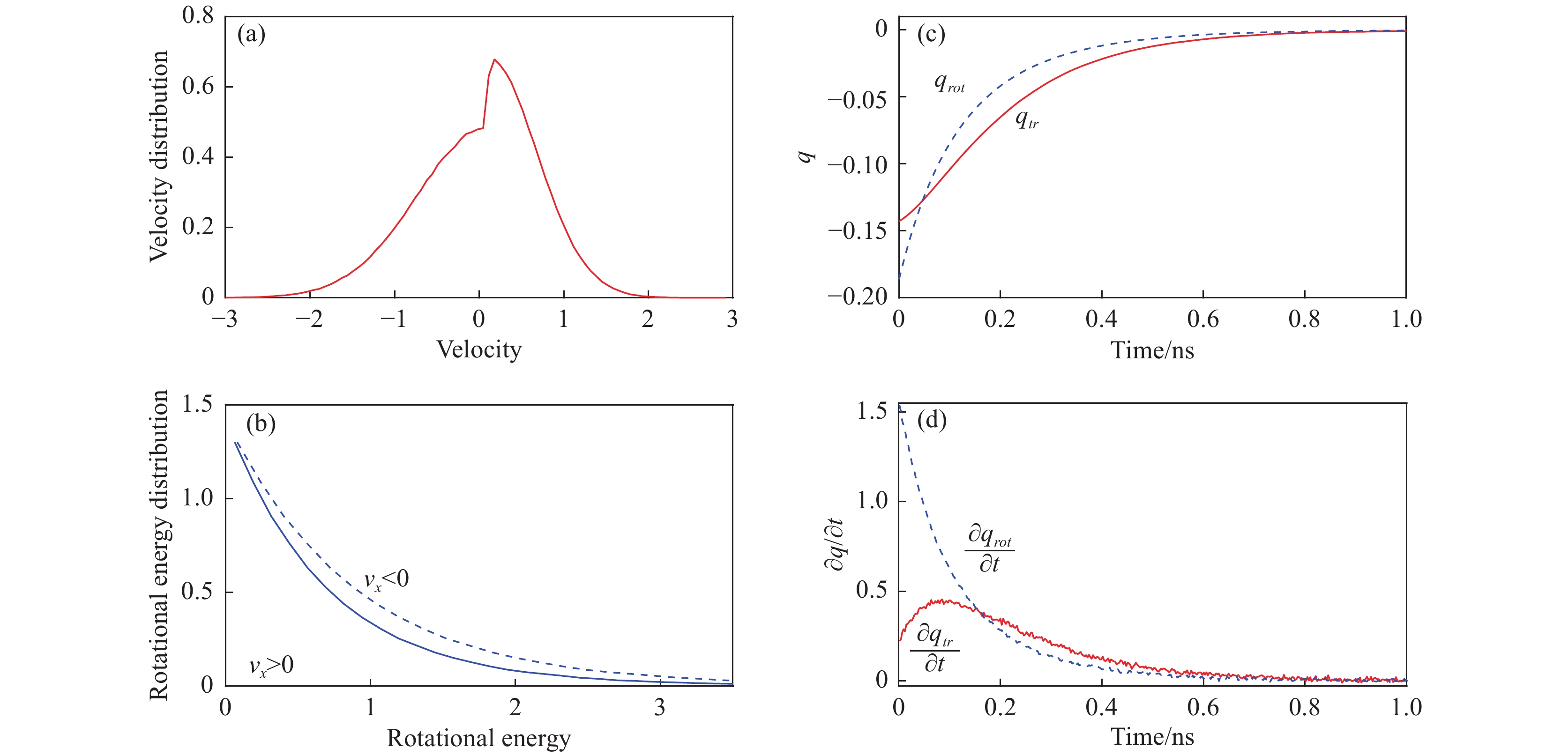
图 3 从DSMC模拟中提取热流的弛豫速率:(a)初始状态用于激发平动热流的速度分布函数,横坐标由最概然速率 |
图3(d)给出N2的热流变化率的演化过程,可以看出平动热流的时间导数随时间先增加后减小,这可以解释为平动热流与转动热流之间存在强耦合效应,即在平动热流衰减的同时得到了转动热流的补偿,且根据式(73)可知,
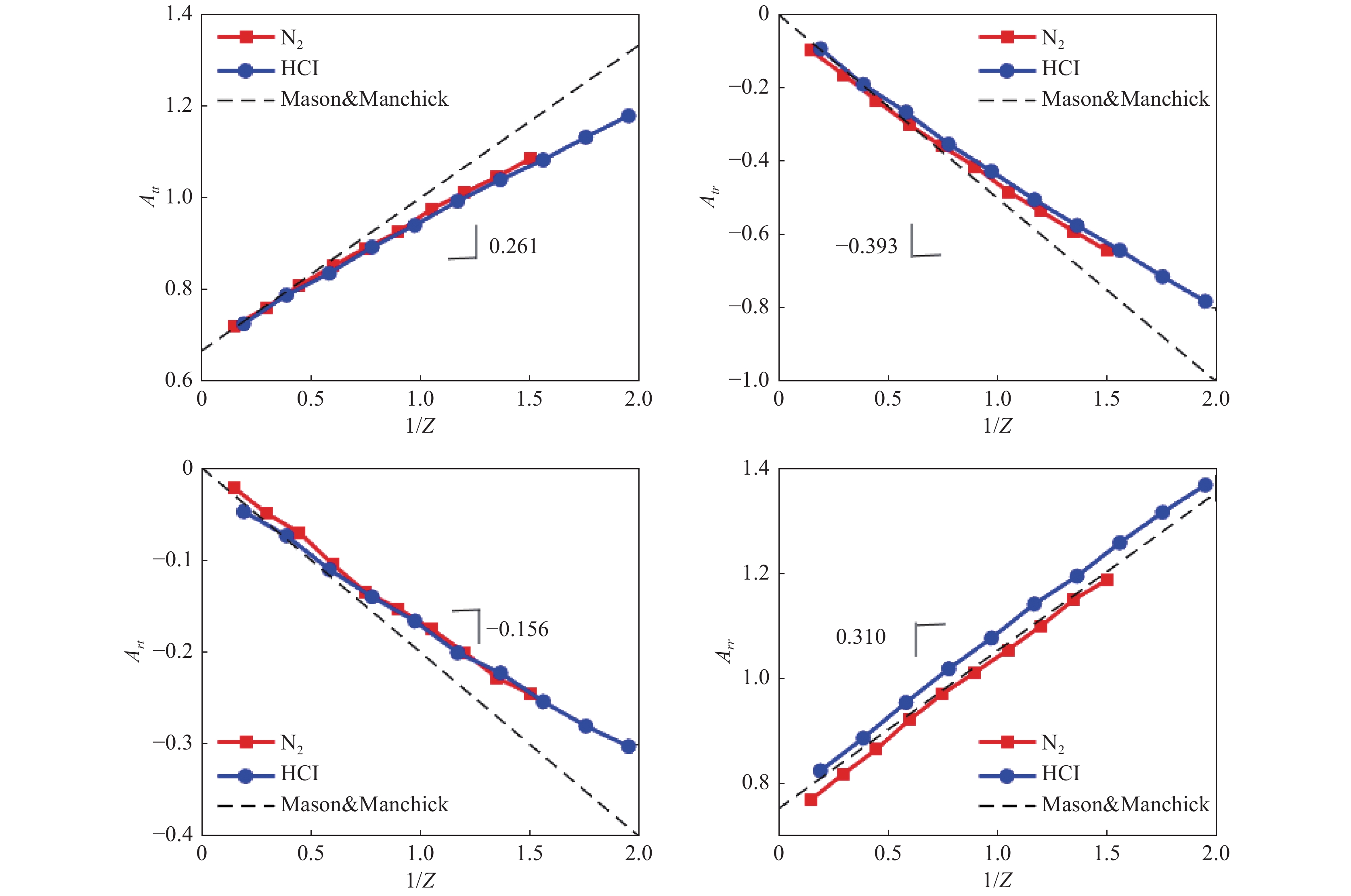
图4显示通过最小二乘法求解线性回归问题(式73)得到的热流弛豫速率A。可以看出,在相同的转动碰撞数Z和斯密特数下,N2与HCl气体的热弛豫速率几乎相同。另外,当
|
图 4 根据理论公式(76)从DSMC模拟中提取的热弛豫速率. 施密特数为 |
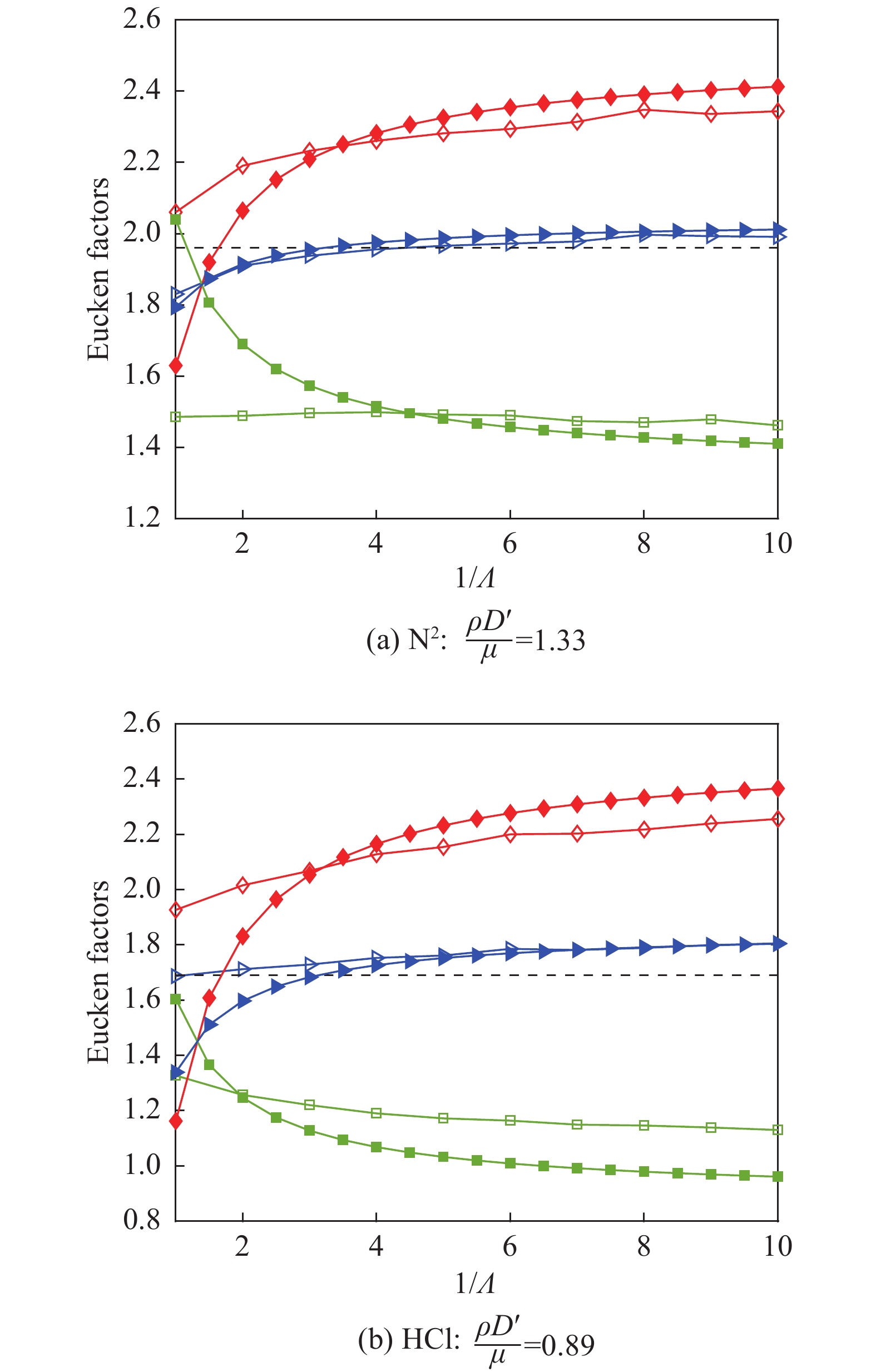
图5给出根据式(74)和式(75)计算得到的Eucken式因子,并与常温下的实验结果对比。对于N2,当施密特数取
|
图 5 室温下Eucken因子的解析解(77)与DSMC数值解的对比. DSMC中使用可变软球模型,自扩散系数 D取值为 D',菱形、正方形、三角形分别表示平动、内能和总Eucken因子,实心点为解析解,空心点为DSMC结果,虚线表示300 K温度下实验测量的总Eucken因子,图中数据来源于文献[54] Fig.5 The thermal conductivity obtained from the analytical solution (77) and the DSMC at room temperature, as a function of the inelastic collision probability |
从式(77)可得,当气体种类确定时,转动碰撞数决定了体积黏性,因此可以通过调整DSMC中的扩散系数以恢复总热导率,见图5(b)。然而,即便在体积黏性与总热导率均与实验值相同的情况下,方程(77)的近似解与使用Larsen-Borgnakke模型的DSMC方法得到的平动热导率
WCU方程的每一个内能能级都对应一个速度分布函数,因而计算代价巨大。对于强激波问题,N2的能级数可达到70,给数值求解带来了极大的困难[71]。因此对WCU方程进行简化是非常必要的,而简化的基本原则与单原子气体相同,即需要满足必要的守恒律和平衡态分布,还需要尽量使各物理量的输运系数与WCU方程保持一致,如扩散系数、剪切黏性、体积黏性、热导率及其在各自由度下的分量等。更接近本质的说法是,各输运系数对应的物理量的弛豫速率与实际气体保持一致。学者们提出了许多描述分子气体稀薄效应的动理学模型方程,如Rykov模型和ES-BGK模型等。与在单原子气体中Gross-Jackson模型可以视为所有模型的源头类似,在分子气体中可以认为Hanson-Morse模型[78]是所有动理论模型的源头。
3.1 Hanson-Morse线性化模型此模型在线性化情况下逼近WCU方程(61)的碰撞项。这种构造方法类似于单原子气体的Gross-Jackson模型[79],即通过对玻尔兹曼碰撞项进行正交多项式展开,并保证各多项式对应的宏观量的弛豫速率与WCU方程一致而获得。对于分子气体,关于分子速度的多项式仍由麦克斯韦分子的本征函数(24)给出;关于内部能量的多项式的前两项取为1和
分子气体的平衡态速度分布函数可表示为
| $ o_i = \frac{g_i\exp\Bigg(\dfrac{-e_i}{k_BT}\Bigg)}{\displaystyle\sum_j g_j\exp\Bigg(\dfrac{-e_j}{k_BT}\Bigg)} $ | (80) |
表征了内能为
| $ f_i(t,{\boldsymbol{x}},{\boldsymbol{\xi}}) = o_if_{eq}({\boldsymbol{\xi}})\left[1+\phi_i(t,{\boldsymbol{x}},{\boldsymbol{\xi}})\right] $ | (81) |
其中每个内部能级对应的扰动分布函数
| $ \begin{array}{c} {n}_i = \displaystyle\int{f_{eq}}\phi_i{\rm{d}}{\boldsymbol{\xi}} \\ \bar{e} = \displaystyle\sum_io_ie_i \\ [{\boldsymbol{u}},\sigma_{{\alpha}\beta}] = \displaystyle\sum_io_i\int{f_{eq}}\phi_i[{\boldsymbol{\xi}},\xi_{\langle {\alpha}}\xi_{\beta\rangle}]{\rm{d}}{\boldsymbol{\xi}} \quad\\ T_{t} = \displaystyle\sum_io_i\int{f_{eq}}\phi_i \left(\frac{2}{3}\xi^2-1\right){\rm{d}}{\boldsymbol{\xi}} \\ {\boldsymbol{q}}_{t} = \displaystyle\sum_io_i\int{f_{eq}}\phi_i \left(\xi^2-\frac{5}{2}\right){\boldsymbol{\xi}}{\rm{d}}{\boldsymbol{\xi}} \\ [T_{r},{\boldsymbol{q}}_{r}] = \displaystyle\sum_io_i\int{f_{eq}}\phi_i\varepsilon_i \left[\frac{2}{d_r},{\boldsymbol{\xi}}\right]{\rm{d}}{\boldsymbol{\xi}} \end{array} $ | (82) |
同时,总扰动密度为
若加速度为小量,WCU方程的线性化形式为:
| $ \frac{\partial \phi_i}{\partial{}t} +{{\boldsymbol{\xi}}}\cdot\frac{\partial \phi_i}{\partial {\boldsymbol{x}}} -2{{\boldsymbol{a}}}\cdot{\boldsymbol{\xi}} = \frac{\ell}{v_m}{J}_i $ | (83) |
其中
| $ \begin{split} {J}_i = &-J_{030}(n_i+2{\boldsymbol{\xi}}\cdot{\boldsymbol{u}}-\phi_i) +{2\sigma_{{\alpha}\beta}}(J_{020}-J_{030}) \xi_{\langle {\alpha}}\xi_{\beta\rangle}+\\ & T_{t}\left[ (-J_{030}+J_{100})\left(\xi^2-\frac{3}{2}\right)-\frac{3}{d_r}J_{100}{\varepsilon} \right] +\\ & 2{\boldsymbol{\xi}}\cdot{\boldsymbol{q}}_{t}\left[ (J_{110}-J_{030})\frac{2}{5}\left(\xi^2-\frac{5}{2}\right) -J_{011}^{110}\sqrt{\frac{4}{5d_r}}{\varepsilon} \right]+\\ & T_{r}\left[ -J_{100}\left(\xi^2-\frac{3}{2}\right) +\left( \frac{3}{d_r}J_{100}-{J}_{030} \right){\varepsilon} \right]+\\& 2{\boldsymbol{\xi}}\cdot{\boldsymbol{q}}_{r}\left[ -{J}_{011}^{110}\sqrt{\frac{4}{5d_r}}\left(\xi^2-\frac{5}{2}\right) +2(J_{011}-J_{030})\frac{{\varepsilon}}{d_r} \right] \end{split} $ |
Hanson-Morse模型假设各内部能级的弛豫时间相同,则与式(76)对应的弛豫率为:
| $ \begin{split}& \tau = \frac{\mu}{p_t} \\& J_{020} = -\tau^{-1} \\& J_{030} = -\frac{3}{2}\tau^{-1} \\& J_{100} = -\frac{1}{Z\tau}\frac{d_r}{3+d_r} \\& J_{110} = -\frac{2}{3\tau}-\frac{5}{6Z\tau}\frac{d_r}{3+d_r} \\& J_{011}^{110} = -\sqrt{\frac{5}{4d_r}}\frac{1}{Z\tau}\frac{d_r}{3+d_r} \\& J_{011} = -\frac{\mu}{\rho{D'}}-\frac{3}{2(3+d_r)Z}\end{split} $ | (84) |
在自发瑞利-布里渊散射中,如果模型中包含应力偏量
当在Hanson-Morse模型中移除应力偏量,为了复现应力偏量、能量弛豫、热流的弛豫过程,式(84)中的
| $ J_{011} = -\dfrac{2d_r}{3(3+d_r)\tau} \dfrac{\dfrac{1}{5}(3+d_r)+\dfrac{6+d_r}{4Z}+\dfrac{9}{16Z^2}f_u} {\dfrac{2}{15}f_u\left(3+d_r\right)+\dfrac{d_r}{6Z}f_u-1} $ | (85) |
为了减小计算量,引入如下两个约化速度分布函数:
| $ g = \sum_i{o_i}f_{eq}{\phi_i}, \;\;r = \sum_i{o_i}f_{eq}{\phi_i}(e_i-\bar{e}) $ | (86) |
消去内能自由度,则Hanson-Morse模型可以简化为:
| $ \begin{split}& \frac{\partial g}{\partial{}t} +{{\boldsymbol{\xi}}}\cdot\frac{\partial g}{\partial {\boldsymbol{x}}} -2{{\boldsymbol{a}}}\cdot{\boldsymbol{\xi}} = \frac{\ell}{v_m}{J}_g \\& \frac{\partial r}{\partial{}t} +{{\boldsymbol{\xi}}}\cdot\frac{\partial r}{\partial {\boldsymbol{x}}} -2{{\boldsymbol{a}}}\cdot{\boldsymbol{\xi}} = \frac{\ell}{v_m}{J}_r \end{split} $ | (87) |
其中:
| $ \begin{split} {J}_g =& -J_{030}\left[ {n}+2{\boldsymbol{\xi}}\cdot{\boldsymbol{u}}+{\boldsymbol{\xi}}\cdot{\boldsymbol{q}}_{t} \frac{4}{15}\left(\xi^2-\frac{5}{2}\right)-g\right]-\\ &J_{030}T_{t}\left(\xi^2-\frac{3}{2}\right)+{2\sigma_{{\alpha}\beta}}(J_{020}-J_{030}) \xi_{\langle {\alpha}}\xi_{\beta\rangle} -\\ &(T_{r}-T_{t})J_{100}\left(\xi^2-\frac{3}{2}\right)-\\ &{\boldsymbol{\xi}}\cdot\left[{\boldsymbol{q}}_{t} \frac{2d_r}{3Z\tau(3+d_r)} +2{\boldsymbol{q}}_{r} {J}_{011}^{110}\sqrt{\frac{4}{5d_{r}}} \right]\left(\xi^2-\frac{5}{2}\right) \end{split} $ | (88) |
| $ \begin{split} {J}_r = & -{J}_{030}\left(\frac{d_r}{2}T_{r}+2{\boldsymbol{\xi}}\cdot{\boldsymbol{q}}_{r}-r\right)-\\ &\frac{3}{2}J_{100}(T_{t}-T_{r})-\\ & 2{\boldsymbol{\xi}}\cdot{\boldsymbol{q}}_{t}J_{011}^{110}\sqrt{\frac{d_{r}}{5}} +2{\boldsymbol{\xi}}\cdot{\boldsymbol{q}}_{r} J_{011} \end{split} $ | (89) |
至此,注意到单原子气体中Gross-Jackson模型与BGK、ES-BGK、Shakhov等模型的关系,可以通过类似于式(60)中展示的非线性化程序构造出分子气体的动理学模型。即,首先写出扰动量
| $ \begin{split} &G(t,{\boldsymbol{x}},{\boldsymbol{v}}) = \sum_i{o_i}{f_i}\\ &R(t,{\boldsymbol{x}},{\boldsymbol{v}}) = \sum_i{o_i}{f_i}e_i \end{split} $ | (90) |
并定义宏观量如下:
| $ \begin{split} &[n,{\boldsymbol{u}},T_t] = \int{}\left[1,\frac{{\boldsymbol{v}}}{n}, \frac{mc^2}{3nk_B}\right]G{\rm{d}}{\boldsymbol{v}} \\ &[p_{ij},{\boldsymbol{q}}_{t}] = \int{}\left[mc_i{c_j},\frac{{mc^2}{\boldsymbol{c}}}{2}\right]G{\rm{d}}{\boldsymbol{v}} \\ &[T_r,{\boldsymbol{q}}_{r}] = \int{}\left[\frac{2}{d_rnk_B},{\boldsymbol{c}}\right]R {\rm{d}}{\boldsymbol{v}}\end{split} $ | (91) |
总热流定义为
| $ \begin{split} \frac{\partial G}{\partial t}+{\boldsymbol{v}}\cdot \frac{\partial G}{\partial {\boldsymbol{x}}} +{\boldsymbol{a}}\cdot \frac{\partial G}{\partial {\boldsymbol{v}}}& = \underbrace{\frac{G_t-G}{ \tau }}_{{\rm{弹性}}}+\underbrace{\frac{G_r-G_t}{ Z\tau}}_{{\rm{非弹性}}} \\ \frac{\partial R}{\partial t}+{\boldsymbol{v}}\cdot \frac{\partial R}{\partial {\boldsymbol{x}}} +{\boldsymbol{a}}\cdot \frac{\partial R}{\partial {\boldsymbol{v}}}& = \underbrace{\frac{R_t-R}{ \tau }}_{{\rm{弹性}}}+\underbrace{\frac{R_r-R_t}{ Z\tau}}_{{\rm{非弹性}}} \end{split} $ | (92) |
最后,根据式(88)和式(89)中的碰撞项,类比式(60),写出四个参考分布函数
例如,考虑Hanson-Morse模型中不出现应力偏量。式(88)中的第一行和第二行即为线性化Shakhov模型的碰撞项,可以非线性化为:
| $\begin{split}& \frac{p_t}{\mu} \left\{ F_{eq}(T_t)\left[1+\frac{2m{\boldsymbol{q}}_{t} \cdot {\boldsymbol{c}}}{15k_BT_tp_t}\left(\frac{mc^2}{2k_BT_t}-\frac{5}{2}\right)\right]-G \right\}\\&\qquad= \frac{p_t}{\mu} (G_t-G) \end{split} $ | (93) |
结合非线性模型(式92)中的非弹性碰撞项
| $ \begin{split}& G_r = F_{eq}(T)\left[1+\frac{2m{\boldsymbol{q}}' \cdot {\boldsymbol{c}}} {15k_BTp}\left(\frac{mc^2}{2k_BT}-\frac{5}{2}\right)\right] \\& {\boldsymbol{q}}' = \left[1-\frac{5d_r}{2(3+d_r)}\right]{\boldsymbol{q}}_{t} +\frac{15}{2(3+d_r)}{\boldsymbol{q}}_{r} \end{split} $ | (94) |
以在线性化情况下退化为式(88)中的后两项,其中能量交换由
然而,历史并没有选择非线性化路线,而是由许多学者各自提出了非线性动理学模型[33-34,50,61,83-87]。下面先介绍主要的Rykov模型和ES-BGK模型,并揭示与Hanson-Morse模型的内在联系,最后介绍吴模型。
3.3.1 Rykov模型原始的Rykov模型[61]仅适用于无振动模态的双原子气体,但是构造思想可以直接拓展至多原子分子气体建模[83]。在该模型中,四个参考速度分布函数定义为:
| $ \begin{split}& G_t = F_{eq}(T_t)\left[1+\frac{2m{\boldsymbol{q}}_{t} \cdot {\boldsymbol{c}}}{15k_BT_tp_t}\left(\frac{mc^2}{2k_BT_t}-\frac{5}{2}\right)\right] \\& G_r = F_{eq}(T)\left[1+\omega_0\frac{2m{\boldsymbol{q}}_{t} \cdot {\boldsymbol{c}}} {15k_BTp}\left(\frac{mc^2}{2k_BT}-\frac{5}{2}\right)\right] \\& R_t = \frac{d_rk_BT_r}{2}G_t+F_{eq}(T_t)(1-{Sc})\frac{m{\boldsymbol{q}}_{r} \cdot {\boldsymbol{c}}}{p_t} \\& R_r = \frac{d_rk_BT}{2}G_r+F_{eq}(T)\omega_1(1-{Sc})\frac{m{\boldsymbol{q}}_{r} \cdot {\boldsymbol{c}}}{p} \end{split} $ | (95) |
选取弹性碰撞弛豫时间
| $ \begin{split} &A_{tt} = \frac{2}{3}\left(1+\frac{1-\omega_0}{2Z}\right) \\ &A_{rr} = {Sc}+\frac{(1-{Sc})(1-\omega_1)}{Z} \\ &A_{tr} = A_{rt} = 0 \end{split} $ | (96) |
因此通过式(75)可以得到Eucken因子的表达式如下:
| $ \begin{split} f_{tr}& = \frac{5}{2}\left(1+\frac{1-\omega_0}{2Z}\right)^{-1} \\ f_{rot}& = \left[{Sc}+\frac{(1-{Sc})(1-\omega_1)}{Z}\right]^{-1} \end{split} $ | (97) |
这说明,在Rykov模型中,可通过调整自由参数
当
Holway通过最大熵原理提出了ES-BGK模型,该模型保留了标准BGK模型的数学简便性,并且能够恢复正确的普朗特数,同时满足熵增定理[33-34]。速度分布函数的演化方程为:
| $ \begin{split}& \frac{\partial G}{\partial t}+{\boldsymbol{v}}\cdot \frac{\partial G}{\partial x} +{\boldsymbol{a}}\cdot \frac{\partial G}{\partial {\boldsymbol{v}}} = \frac{1}{ \tau }\left(f_r^{ES}-G\right) \\& \frac{\partial R}{\partial t}+{\boldsymbol{v}}\cdot \frac{\partial R}{\partial x}+{\boldsymbol{a}}\cdot \frac{\partial R}{\partial {\boldsymbol{v}}} = \frac{1}{ \tau }\left(\frac{d_r}{2}k_BT_{rel}f_r^{ES}-R\right) \end{split} $ | (98) |
其中,弛豫温度
| $ T_{rel} = \left(1-\frac{1}{Z}\right){T_r}+\frac{T}{Z} $ | (99) |
参考分布函数
| $ \lambda_{ij} = \left(1-\frac{1}{Z}\right) \left[(1-b)\frac{k_BT_t}{m}\delta_{ij}+b\frac{p_{ij}}{nm}\right] +\frac{k_BT}{Zm}\delta_{ij} $ | (100) |
当
取弹性碰撞弛豫时间
| $ Pr = \frac{1}{1-b+\frac{b}{Z}} $ | (101) |
为使参考分布函数有界且在物理上有意义,要求
与Rykov模型一样,ES-BGK模型的平动热流和转动热流的弛豫过程互不干涉;从其弛豫率可知,Eucken因子可以表达为:
| $ \begin{split} &f_{tr} = \frac{5}{3Pr} \\ &f_{rot} = \frac{1}{Pr} = \frac{3+d_r}{5+d_r}f_{eu} \end{split} $ | (102) |
注意到,对于多原子ES-BGK模型,平动Eucken因子与转动Eucken因子的比值始终为
上述气体动理学模型的弛豫时间
吴模型的演化方程为:
| $ \begin{split} &\frac{\partial G}{\partial t}+{\boldsymbol{v}}\cdot \frac{\partial G}{\partial x}+{\boldsymbol{a}}\cdot \frac{\partial G}{\partial {\boldsymbol{v}}} = Q(G)+\frac{G_r-G_t}{ Z\tau } \\& \frac{\partial R}{\partial t}+{\boldsymbol{v}}\cdot \frac{\partial R}{\partial x} +{\boldsymbol{a}}\cdot \frac{\partial R}{\partial {\boldsymbol{v}}} = \frac{R_t'-R}{ \tau }+\frac{R_r-R_t}{ Z\tau } \end{split} $ | (103) |
式中,
| $ \begin{split}& G_t = F_{eq}(T_t)\left[1+\frac{2m{{\boldsymbol{q}}_{t}} \cdot {\boldsymbol{c}}}{15k_BT_tp_t}\left(\frac{mc^2}{2k_BT_t}-\frac{5}{2}\right)\right] \\& G_r = F_{eq}(T)\left[1+\frac{2m{\boldsymbol{q}}' \cdot {\boldsymbol{c}}} {15k_BTp}\left(\frac{mc^2}{2k_BT}-\frac{5}{2}\right)\right] \\& R_t = \frac{d_rk_BT_r}{2}G_t \\& R_r = \frac{d_rk_BT}{2}G_r+F_{eq}(T)\frac{m{\boldsymbol{q}}'' \cdot {\boldsymbol{c}}}{p} \end{split} $ | (104) |
为了恢复热流弛豫过程(式(73)),选取
| $ \begin{split}& {\boldsymbol{q}}' = \left[-3Z( A_{tt}-\frac{2}{3})+1\right]{\boldsymbol{q}}_{t}-3ZA_{tr}{\boldsymbol{q}}_{r} \\& {\boldsymbol{q}}'' = -Z\left[A_{rt} q_t+(A_{rr}-1){\boldsymbol{q}}_{r}\right] \end{split} $ | (105) |
当
本节以正激波结构、库特流、热蠕动、二维热驱动问题为例,比较不同模型描述稀薄气体流动的精度。模拟中,分子气体为N2,转动自由度
|
表 1 不同动理学模型和DSMC模拟中所使用的Eucken因子与热弛豫速率. N2的Eucken因子为
|
|
|
引入参考密度
| $ {Kn} = \frac{\mu(T_0)}{n_0\ell}\sqrt{\frac{\text{π}}{2mk_BT_0}} $ | (106) |
用于表征流动的稀薄程度,其中
在以下各研究问题中,气体在固体表面的反射均用完全漫反射作为边界条件,即气体反射速度分布为满足固体表面宏观量的麦克斯韦分布。在数值解法上,使用离散速度法求解动理学模型,快速谱方法求解玻尔兹曼碰撞项[31],开源软件SPARTA进行DSMC模拟。
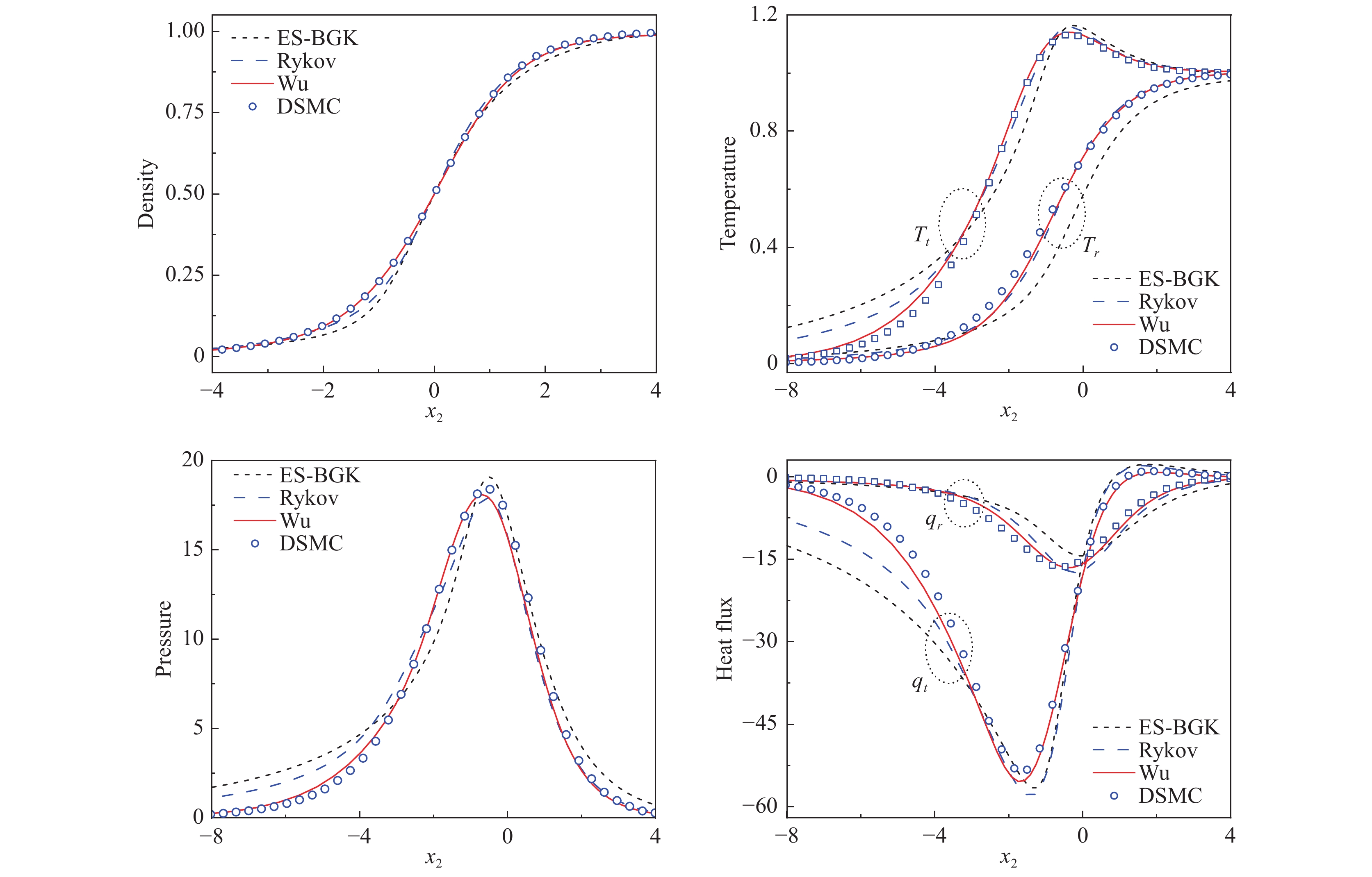
3.4.1 正激波图6给出马赫数为7的一维N2正激波的结构。空间坐标用激波上游的分子平均自由程
|
图 6 不同动理学模型预测的马赫数为7的氮气正激波的密度、温度、应力偏量σ22和热流的对比 Fig.6 Comparisons in the density, temperature, stress, and heat flux between different kinetic models for a normal shock in Nitrogen gas with Mach number 7 |
平板库特流动的上下两板温度相同,处在

|
图 7 平板库特流动中的密度、温度和垂直于流动方向的热流分布. 第一行和第二行的克努森数分别为 |
考察处在两平行静止的无限长平板间的分子气体,每个气体分子受到与其速度相关的水平外力的作用:
| $a_{x_1}=a_0\left(\frac{v^2}{v^2_m}-\frac{3}{2}\right)$ | (107) |
在此例中,取
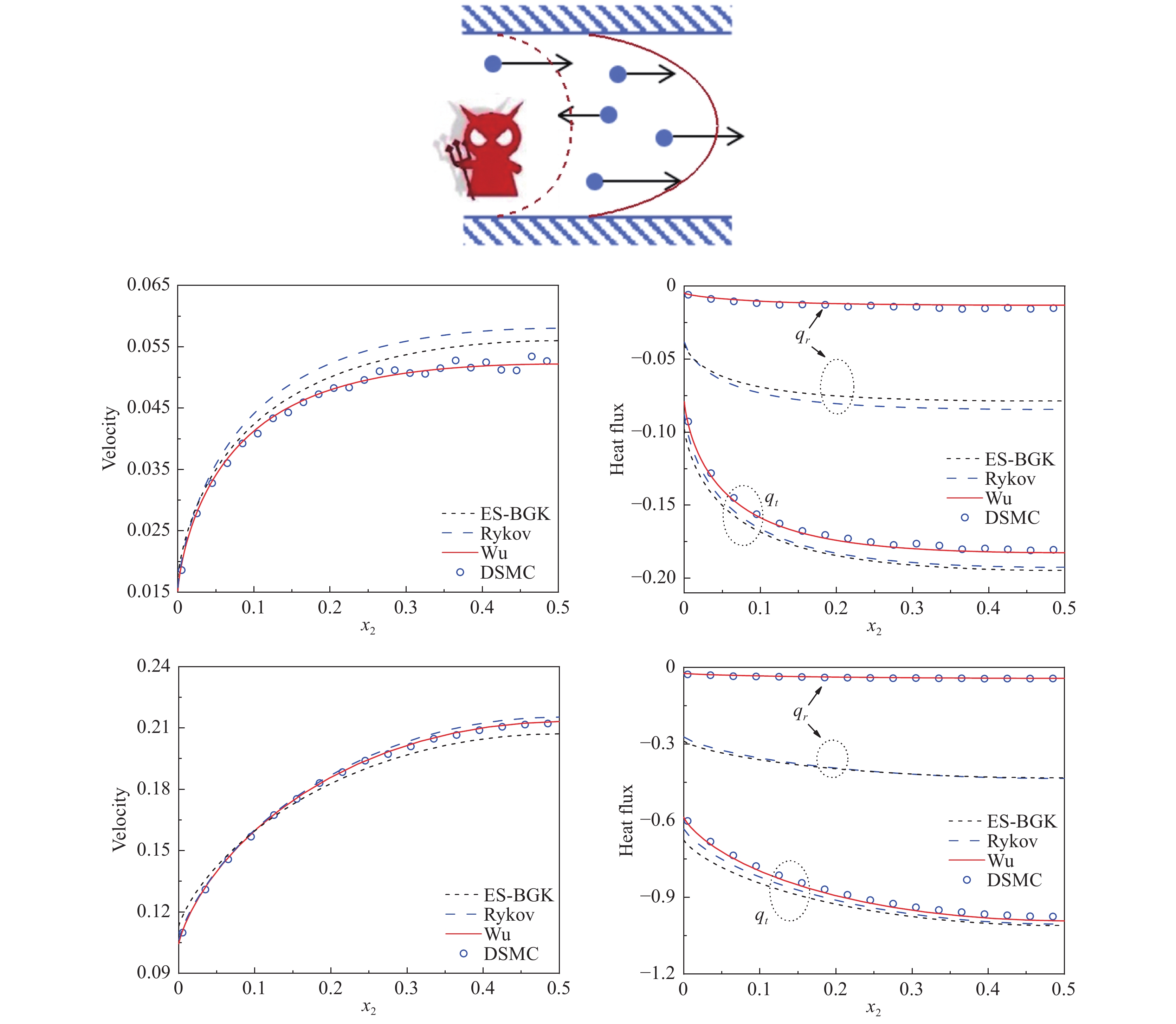
|
图 8 麦克斯韦妖驱动下的稀薄气体热蠕动, 其中速度和热流均沿 |
图8给出克努森数分别为0.1和1的模拟结果对比。吴模型与DSMC非常符合,速度剖面与热流分布的最大误差仅为
最后,考察二维封闭方腔内的热蠕动问题。方腔宽度与高度比值为5,固定左板和右板的温度分别为200 K和400 K,而上下两板的温度在此间线性分布。由于此问题以
图9中给出各个动理学模型方程与DSMC结果的比较。吴模型的热流云图与速度剖面均与DSMC结果相符,而ES-BGK模型热流与速度剖面的解与DSMC的解有非常大的偏离,并且ES-BGK模型计算得到的中心涡更偏向右侧的高温区,且结构范围更小。另外,Rykov模型在预测热流方面存在一定误差。

|
图 9 克努森数为0.6的稀薄气体在二维方腔内的热蠕动 Fig.9 Rarefied gas flow driven by temperature gradient in the solid walls: (a) The streamlines and the contour of translational heat flux in the x1 direction; (b) Velocity profiles at x2 = 0 and 0.5; (b) Velocity profiles at x2 = 0.5; (d) The translational and rotational heat fluxes along the bottom wall |
为了准确地预测稀薄分子气体的非平衡行为,气体动理学的建模过程应实现正确的剪切黏性、体积黏性、平动热导率、转动热导率。分子气体的热导率比剪切黏性和体积黏性更加复杂,实验通常只能确定总热导率,但是难以分辨其平动与转动分量。虽然在连续流极限下,气体动力学行为取决于气体黏性与总热导率,但是在稀薄流区,分子气体的平动与内能热导率可能对非平衡效应有各自不同的影响。
上文的算例表明,热弛豫速率在稀薄气体流动中也起着重要作用。尽管在DSMC和其他分子气体动理学模型中[33,72,88-89],已有大量关于温度弛豫效应(与体积黏性相关)的研究工作,却从未有过关于热弛豫速率矩阵A对稀薄气体非平衡效应的影响的相关研究。通过实验可以直接测量总热导率,并且在某些情况下,还可以提取平动热导率[54,59,90-91]。然而,根据式(73),弛豫系数矩阵A中至少有两个元素不能确定,即不同的系数矩阵A可以对应一致的热导率及其分量。因此有必要量化在输运系数都一致的前提下,由系数A的变化所带来的宏观量的不确定性。
在DSMC中,因碰撞模型的原因,固定体积黏性后,热弛豫系数也随之确定。在吴模型中,可以通过独立修改
给定
考察一维正激波问题,
接着,保持总热导率不变,且选择
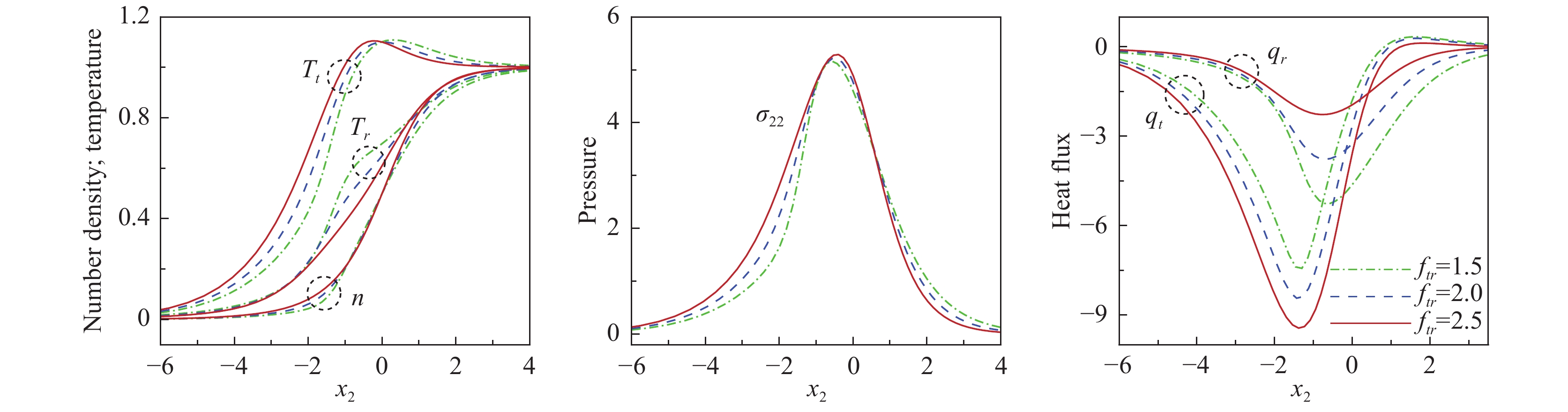
|
图 10 总Eucken因子不变时,不同平动Eucken因子对马赫数为4的正激波结构的影响. 图中数据来源于文献[60] Fig.10 Influence of the translational Eucken factor on the structure of normal shock wave with Mach number 4. The figures are from Ref. [60] |
由此,在正激波问题中,由热弛豫系数
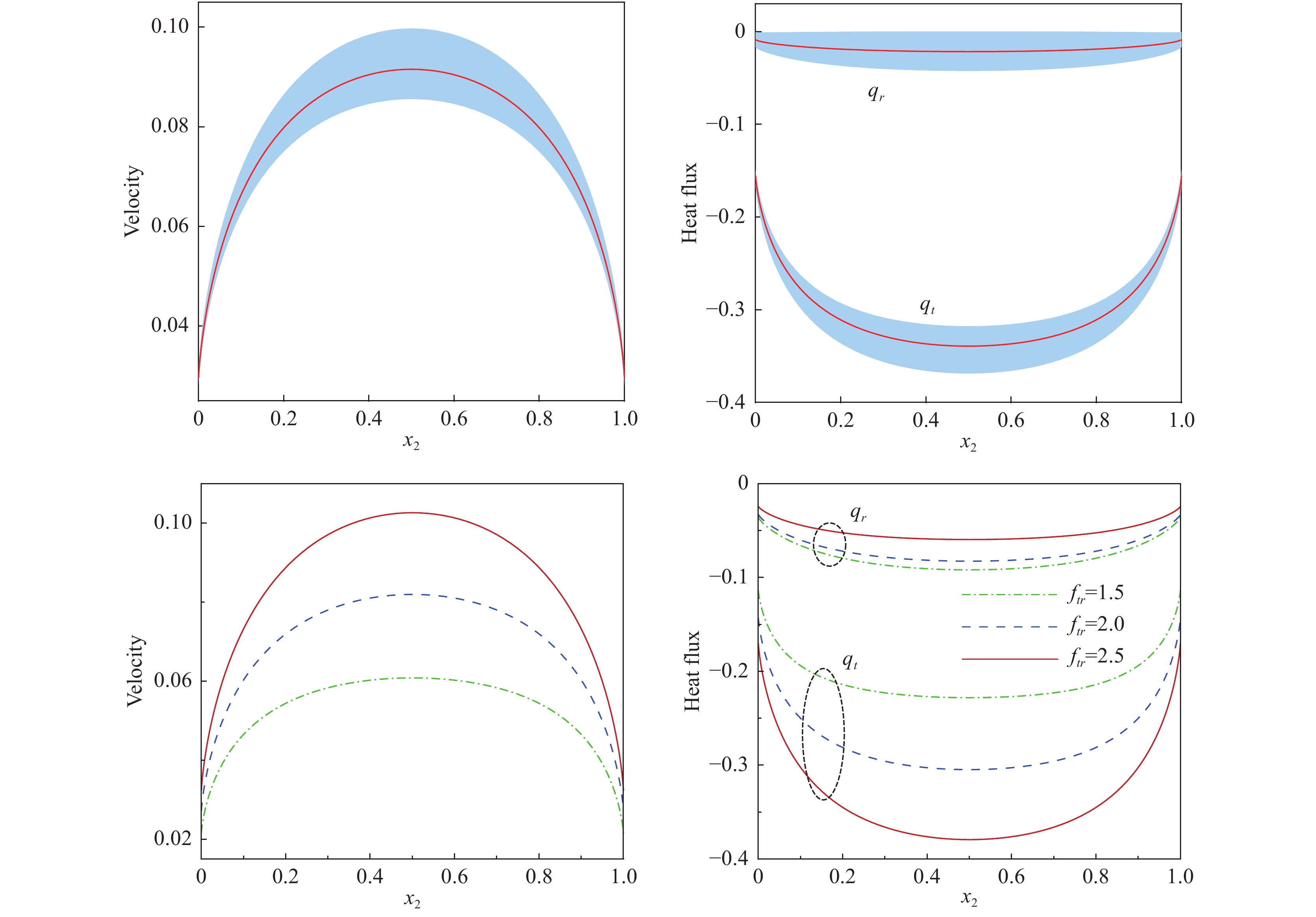
使用与正激波算例中相同的系数矩阵A,使
|
图 11 (第一行)热流弛豫速率对麦克斯韦妖驱动的热蠕动速度和热流分布的影响,以及吴模型中改变热弛豫速率的结果对比. 红色实线对应的 |
为进一步研究平动Eucken因子的影响,考察Eucken因子
平动Eucken因子在此问题中的重要性可得到如下解释:从方程(73)可以看出,热弛豫系数
上文的研究结果揭示了热流弛豫速率不确定性对稀薄气体流动的影响,因此有必要通过获取并使用正确的相应系数,来减少或消除模型的不确定性。我们认为可以尝试以下两种方法。
5.1 分子动力学模拟从物理上来说,只要知道了分子间的相互作用势,根据牛顿第二运动定律,就可以通过分子动力学方法模拟气体的行为。由此,输运系数能够通过Green-Kubo公式获得[92-93]:
| $ \mu = \frac{1}{V}\frac{1}{k_BT}\int_0^\infty \langle J_{xy}^p(0)J_{xy}^p(\tau) \rangle {\rm{d}}\tau $ | (108) |
| $ \frac{4}{3}\mu+\mu_b = \frac{1}{V}\frac{1}{k_BT}\int_0^\infty \langle J_{xx}^p(0)J_{xx}^p(\tau) \rangle {\rm{d}}\tau $ | (109) |
| $ \kappa = \frac{1}{V}\frac{1}{k_BT^2}\int_0^\infty \langle J_{x}^q(0)J_{x}^q(\tau) \rangle {\rm{d}}\tau $ | (110) |
其中,
然而,对于如何获得热流弛豫矩阵系数尚不清楚。一个可行的方法是仿照第2.3节中介绍的DSMC方法,即在分子动力学中设置带有初始热流的状态,模拟低密度气体的演化过程,然后通过拟合公式(73)获得弛豫系数。虽然目前尚未有相关工作的报道,但是原理上是可行的。
5.2 瑞利-布里渊散射瑞利-布里渊散射指的是光在气体中传播时,被气体分子的自发密度涨落散射。由于散射光谱包含气体信息,因此可以用来无损测量声速、流速、温度和体积黏性[94-96]。例如,欧洲航天局于2018年发射的ADM-Aeolus卫星,测量从地球表面到30 km高度的全球风速,用于提高天气预报精度。
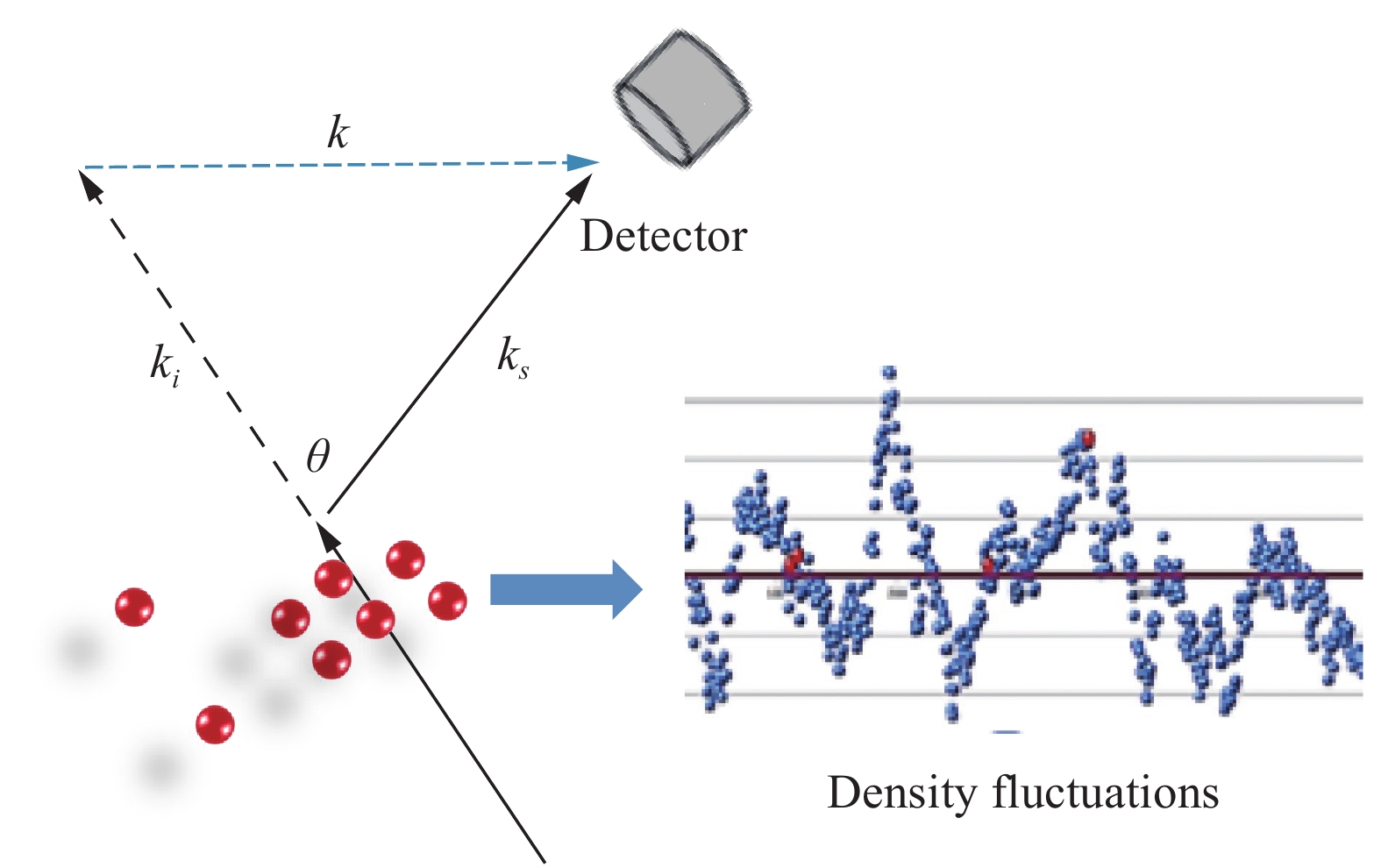
如图12所示,波矢为
| $ G(x_2,t) = \int_{-\infty}^{\infty}{n}(l+x_2,t){n}(l,0){\rm{d}}l $ | (111) |
因此,频谱为:
| $ S(f_s) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}G(x_2,t){\rm{e}}^{{\rm{i}}(kx_2-2\pi{f_s}t)}{\rm{d}}x_2{\rm{d}}t $ | (112) |
式中,i为虚数单位,
对于短波长和高散射频率,应该使用气体动理论来描述密度扰动的演化过程。以单原子气体为例说明瑞利-布里渊散射的计算。密度扰动量与式(20)中分布函数扰动量
| $ 2{\text {π}}{{\rm{i}}}(f_s-v_2)\hat{\phi} = \frac{\ell}{v_m}J(\hat{\phi})+1 $ | (113) |
其中方程右端的1来自于初始密度扰动对应的拉普拉斯变换,
| $ S(f_s) = \Re\left(\int \hat{\phi} f_{eq}({\boldsymbol{\xi}}){\rm{d}}{\boldsymbol{\xi}}\right) $ | (114) |
其中
|
图 12 自发瑞利-布里渊散射示意图[54],在气体中传播的光被气体分子自发的密度涨落散射 Fig.12 Schematic of the spontaneous Rayleigh-Brillouin scattering[54], where the light is scattered by the spontaneous density fluctuations in the gas |
此例中,我们根据荷兰自由大学的实验数据[91]来提取N2的体积黏性和平动Eucken因子。其中,激光波长为
| 表 2 自发瑞利-布里渊散射实验中,N2相关参数汇总以及根据吴模型从实验数据中提取的体积黏性与平动/转动Eucken因子(剪切黏性与总热导率均使用国际单位制) Table 2 Experimental conditions in the spontaneous Rayleigh-Brillouin scattering, and the extracted bulk viscosity, translational/rotational Eucken factors from the Wu model. The SI units are adopted for the shear viscosity and thermal conductivity |
|
|
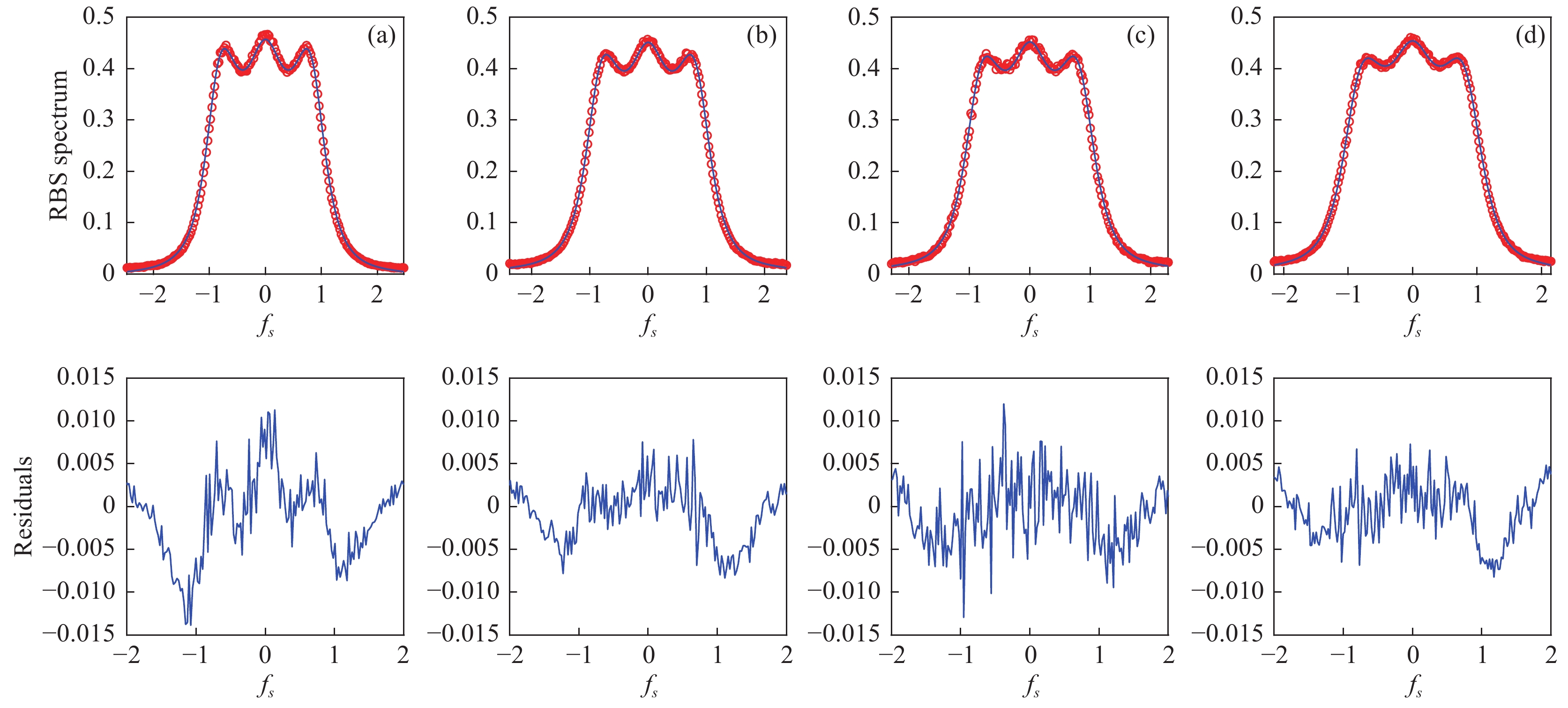
实验数据与吴模型最佳预测的比较如图13所示。实验[99]测得N2在标准温度和压力下的转动弛豫时间为
|
图 13 基于实验频谱(圆圈)和吴模型预测结果(线条),提取N2的体积黏性与平动Eucken因子[54]:第一行的实线为计算光谱,通过计算给定 |
| $ \mu_b = 2p\tau_r\frac{d_r}{(3+d_r)^2} = 1.18\times10^{-5}{\rm{kg\cdot{m^{-1}}\cdot{s^{-1}}}} $ |
这一结果与实验值吻合较好。另外,提取的平动Eucken因子也在合理的范围。
6 总结与展望本文回顾了国内外学者在稀薄效应动理学建模中所取得的进展,包括单原子气体与分子气体。由于高温真实气体效应,当分子内自由度增加时,分子间复杂的相互作用通常伴随着更加新颖、复杂的物理现象,这对稀薄分子气体动理学建模提出了很高的要求。我们指出,应力偏量、能量交换、热流的弛豫过程是输运现象的本质,而剪切黏性、体积黏性、平动/内部热导率等输运系数则是表象,即,随着克努森数的变化,这些输运系数对应的本构关系会失效,而相应的弛豫过程和速率不会改变。为了准确预测稀薄分子气体的非平衡行为,气体动理学的建模过程应尽可能准确地捕捉应力偏量、能量交换、热流的弛豫过程和速率。
本文还介绍了DSMC中提取热弛豫速率的方法,并讨论了DSMC方法恢复热导率的能力。虽然经典的Larsen-Borgnakke模型可以通过调整非弹性碰撞概率改变体积黏性,但是很难同时调整热导率及其分量。而这些分量的比例以及本质的热流弛豫时间对稀薄气体流动的影响巨大。因此,非常有必要对DSMC碰撞模型进行修改和优化。
非常有意思的是,基于王承书等的工作,分子气体的线性化理论和方法已经非常成熟。而非线性模型虽然五花八门,但都与线性化模型存在着本质联系,即所有的非线性模型都可以通过对线性化Gross-Jackson模型和Hanson-Morse模型的非线性化而来。本文首次给出一个非线性化方案。
对于临近空间高超声速飞行器而言,其周围的空气动力学非常复杂。如何建立描述多组分气体、化学反应的稀薄气体动理学模型是个极大的挑战。本文提出的弛豫过程本质论、输运系数表象论、从线性化模型中反推非线性模型的方法,以及从分子动力学和相关实验中提取弛豫速率的设想,将为解决此类问题提供极大助力。
致谢:感谢爱丁堡大学苏微博士的有益讨论。
| [1] |
VOTTA R, SCHETTINO A, BONFIGLIOLI A. Hypersonic high altitude aerothermodynamics of a space re-entry vehicle[J]. Aerospace Science and Technology, 2013, 25(1): 253-265. DOI:10.1016/j.ast.2012.02.001 |
| [2] |
IVANOV M S, GIMELSHEIN S F. Computational hypersonic rarefied flows[J]. Annual Review of Fluid Mechanics, 1998, 30: 469-505. DOI:10.1146/annurev.fluid.30.1.469 |
| [3] |
SCANLON T J, WHITE C, BORG M K, et al. Open-source direct simulation Monte Carlo chemistry modeling for hypersonic flows[J]. AIAA Journal, 2015, 53(6): 1670-1680. DOI:10.2514/1.j053370 |
| [4] |
李志辉, 梁杰, 李中华, 等. 跨流域空气动力学模拟方法与返回舱再入气动研究[J]. 空气动力学学报, 2018, 36(5): 826-847. LI Z H, LIANG J, LI Z H, et al. Simulation methods of aerodynamics covering various flow regimes and applications to aerodynamic characteristics of re-entry spacecraft module[J]. Acta Aerodynamica Sinica, 2018, 36(5): 826-847. (in Chinese) |
| [5] |
梁杰, 李志辉, 李齐, 等. 返回舱再入跨流域气动及配平特性数值研究[J]. 空气动力学学报, 2018, 36(5): 848-855. LIANG J, LI Z H, LI Q, et al. Numerical simulation of aerodynamic and trim characteristics across different flow regimes for reentry module[J]. Acta Aerodynamica Sinica, 2018, 36(5): 848-855. (in Chinese) |
| [6] |
WANG X W, SU T Y, ZHANG W Q, et al. Knudsen pumps: a review[J]. Microsystems & Nanoengineering, 2020, 6: 26. DOI:10.1038/s41378-020-0135-5 |
| [7] |
AOKI K, TAKATA S, TATSUMI E, et al. Rarefied gas flows through a curved channel: application of a diffusion-type equation[J]. Physics of Fluids, 2010, 22(11): 112001. DOI:10.1063/1.3496315 |
| [8] |
KUGIMOTO K, HIROTA Y, KIZAKI Y, et al. Performance prediction method for a multi-stage Knudsen pump[J]. Physics of Fluids, 2017, 29(12): 122002. DOI:10.1063/1.5001213 |
| [9] |
WANG P, SU W, WU L. Thermal transpiration in molecular gas[J]. Physics of Fluids, 2020, 32(8): 082005. DOI:10.1063/5.0018505 |
| [10] |
WU L, HO M T, GERMANOU L, et al. On the apparent permeability of porous media in rarefied gas flows[J]. Journal of Fluid Mechanics, 2017, 822: 398-417. DOI:10.1017/jfm.2017.300 |
| [11] |
叶友达. 高超声速空气动力学研究进展与趋势[J]. 科学通报, 2015, 60(12): 1095-1103. YE Y D. Advances and prospects in hypersonic aerodynamics[J]. Chinese Science Bulletin, 2015, 60(12): 1095-1103. DOI:10.1360/N972014-01180 (in Chinese) |
| [12] |
庄逢甘, 黄志澄. 未来高技术战争对空气动力学创新发展的需求[C]//2003空气动力学前沿研究学术研讨会论文集, 中国空气动力学会, 2003: 73–79.
|
| [13] |
DAUDÉ B, ELANDALOUSSI H, JANSSEN C. On the gas dependence of thermal transpiration and a critical appraisal of correction methods for capacitive diaphragm gauges[J]. Vacuum, 2014, 104: 77-87. DOI:10.1016/j.vacuum.2014.01.002 |
| [14] |
WU L, LIU H H, REESE J M, et al. Non-equilibrium dynamics of dense gas under tight confinement[J]. Journal of Fluid Mechanics, 2016, 794: 252-266. DOI:10.1017/jfm.2016.173 |
| [15] |
ALSMEYER H. Density profiles in argon and nitrogen shock waves measured by the absorption of an electron beam[J]. Journal of Fluid Mechanics, 1976, 74(3): 497-513. DOI:10.1017/s0022112076001912 |
| [16] |
SCHOTTER R. Rarefied gas acoustics in the noble gases[J]. The Physics of Fluids, 1974, 17(6): 1163-1168. DOI:10.1063/1.1694859 |
| [17] |
WU L, GU X J. On the accuracy of macroscopic equations for linearized rarefied gas flows[J]. Advances in Aerodynamics, 2020, 2: 2. DOI:10.1186/s42774-019-0025-4 |
| [18] |
EWART T, PERRIER P, GRAUR I A, et al. Mass flow rate measurements in a microchannel, from hydrodynamic to near free molecular regimes[J]. Journal of Fluid Mechanics, 2007, 584: 337-356. DOI:10.1017/s0022112007006374 |
| [19] |
JIANG D W, MAO M L, LI J, et al. An implicit parallel UGKS solver for flows covering various regimes[J]. Advances in Aerodynamics, 2019, 1: 8. DOI:10.1186/s42774-019-0008-5 |
| [20] |
李志辉, 蒋新宇, 吴俊林, 等. 转动非平衡玻尔兹曼模型方程统一算法与全流域绕流计算应用[J]. 力学学报, 2014, 46(3): 336-351. LI Z H, JIANG X Y, WU J L, et al. Gas-kinetic unified algorithm for Boltzmann model equation in rotational nonequilibrium and its application to the whole range flow regimes[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(3): 336-351. (in Chinese) |
| [21] |
CHAPMAN S, COWLING T G, CERCIGNANI C. The mathematical theory of non-uniform gases[M]. Cambridge University Press, 1970.
|
| [22] |
GRAD H. On the kinetic theory of rarefied gases[J]. Communications on Pure and Applied Mathematics, 1949, 2(4): 331-407. DOI:10.1002/cpa.3160020403 |
| [23] |
GU X J, EMERSON D R. A high-order moment approach for capturing non-equilibrium phenomena in the transition regime[J]. Journal of Fluid Mechanics, 2009, 636: 177-216. DOI:10.1017/s002211200900768x |
| [24] |
BIRD G A. Molecular gas dynamics and the direct simulation of gas flows[M]. New York : Oxford Science Publications, Oxford University Press Inc, 1994.
|
| [25] |
WAGNER W. A convergence proof for Bird's direct simulation Monte Carlo method for the Boltzmann equation[J]. Journal of Statistical Physics, 1992, 66(3-4): 1011-1044. DOI:10.1007/BF01055714 |
| [26] |
LI Z H, FANG M, JIANG X Y, et al. Convergence proof of the DSMC method and the Gas-Kinetic Unified Algorithm for the Boltzmann equation[J]. Science China Physics, Mechanics and Astronomy, 2013, 56(2): 404-417. DOI:10.1007/s11433-013-4999-3 |
| [27] |
HADJICONSTANTINOU N G, GARCIA A L, BAZANT M Z, et al. Statistical error in particle simulations of hydrodynamic phenomena[J]. Journal of Computational Physics, 2003, 187(1): 274-297. DOI:10.1016/S0021-9991(03)00099-8 |
| [28] |
TCHEREMISSINE F G. Solution to the Boltzmann kinetic equation for high-speed flows[J]. Computational Mathematics and Mathematical Physics, 2006, 46(2): 315-329. DOI:10.1134/s0965542506020138 |
| [29] |
WU L, REESE J M, ZHANG Y H. Solving the Boltzmann equation deterministically by the fast spectral method: application to gas microflows[J]. Journal of Fluid Mechanics, 2014, 746: 53-84. DOI:10.1017/jfm.2014.79 |
| [30] |
WU L, WHITE C, SCANLON T J, et al. Deterministic numerical solutions of the Boltzmann equation using the fast spectral method[J]. Journal of Computational Physics, 2013, 250: 27-52. DOI:10.1016/j.jcp.2013.05.003 |
| [31] |
吴雷, 张勇豪, 李志辉. Boltzmann方程碰撞积分建模与稀薄空气动力学应用研究[J]. 中国科学 (物理学 力学 天文学), 2017, 47(7): 28-45. WU L, ZHANG Y H, LI Z H. Computable model on the collision integral of Boltzmann equation and application to rarefied aerodynamics[J]. SCIENTIA SINICA Physica, Mechanica & Astronomica, 2017, 47(7): 28-45. (in Chinese) |
| [32] |
BHATNAGAR P L, GROSS E P, KROOK M. A model for collision processes in gases. I. small amplitude processes in charged and neutral one-component systems[J]. Physical Review, 1954, 94(3): 511-525. DOI:10.1103/physrev.94.511 |
| [33] |
HOLWAY L H. New statistical models for kinetic theory: methods of construction[J]. The Physics of Fluids, 1966, 9(9): 1658-1673. DOI:10.1063/1.1761920 |
| [34] |
ANDRIES P, LE TALLEC P, PERLAT J P, et al. The Gaussian-BGK model of Boltzmann equation with small Prandtl number[J]. European Journal of Mechanics - B/Fluids, 2000, 19(6): 813-830. DOI:10.1016/S0997-7546(00)01103-1 |
| [35] |
SHAKHOV E M. Approximate kinetic equations in rarefied gas theory[J]. Fluid Dynamics, 1968, 3(1): 112-115. DOI:10.1007/BF01016254 |
| [36] |
LI Z H, ZHANG H X. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[J]. Journal of Computational Physics, 2004, 193(2): 708-738. DOI:10.1016/j.jcp.2003.08.022 |
| [37] |
LI Z H, PENG A P, MA Q, et al. Gas-kinetic unified algorithm for computable modeling of Boltzmann equation and application to aerothermodynamics for falling disintegration of uncontrolled Tiangong-No. 1 spacecraft[J]. Advances in Aerodynamics, 2019, 1: 4. DOI:10.1186/s42774-019-0009-4 |
| [38] |
WU J L, LI Z H, ZHANG Z B, et al. On derivation and verification of a kinetic model for quantum vibrational energy of polyatomic gases in the gas-kinetic unified algorithm[J]. Journal of Computational Physics, 2021, 435: 109938. DOI:10.1016/j.jcp.2020.109938 |
| [39] |
LI Z H, ZHANG H X. Gas-kinetic numerical studies of three-dimensional complex flows on spacecraft re-entry[J]. Journal of Computational Physics, 2009, 228(4): 1116-1138. DOI:10.1016/j.jcp.2008.10.013 |
| [40] |
XU K, HUANG J C. A unified gas-kinetic scheme for continuum and rarefied flows[J]. Journal of Computational Physics, 2010, 229(20): 7747-7764. DOI:10.1016/j.jcp.2010.06.032 |
| [41] |
YANG L M, SHU C, YANG W M, et al. An improved discrete velocity method (DVM) for efficient simulation of flows in all flow regimes[J]. Physics of Fluids, 2018, 30(6): 062005. DOI:10.1063/1.5039479 |
| [42] |
YUAN R F, ZHONG C W. A conservative implicit scheme for steady state solutions of diatomic gas flow in all flow regimes[J]. Computer Physics Communications, 2020, 247: 106972. DOI:10.1016/j.cpc.2019.106972 |
| [43] |
GUO Z L, XU K, WANG R J. Discrete unified gas kinetic scheme for all Knudsen number flows: low-speed isothermal case[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2013, 88(3): 033305. DOI:10.1103/PhysRevE.88.033305 |
| [44] |
SU W, ZHU L H, WANG P, et al. Can we find steady-state solutions to multiscale rarefied gas flows within dozens of iterations?[J]. Journal of Computational Physics, 2020, 407: 109245. DOI:10.1016/j.jcp.2020.109245 |
| [45] |
SU W, ZHU L H, WU L. Fast convergence and asymptotic preserving of the general synthetic iterative scheme[J]. SIAM Journal on Scientific Computing, 2020, 42(6): B1517. DOI:10.1137/20m132691x |
| [46] |
ZHU L H, PI X C, SU W, et al. General synthetic iterative scheme for nonlinear gas kinetic simulation of multi-scale rarefied gas flows[J]. Journal of Computational Physics, 2021, 430: 110091. DOI:10.1016/j.jcp.2020.110091 |
| [47] |
SU W, ZHANG Y H, WU L. Multiscale simulation of molecular gas flows by the general synthetic iterative scheme[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 373: 113548. DOI:10.1016/j.cma.2020.113548 |
| [48] |
ANDRIES P, BOURGAT J F, LE TALLEC P, et al. Numerical comparison between the Boltzmann and ES-BGK models for rarefied gases[J]. Computer Methods in Applied Mechanics and Engineering, 2002, 191(31): 3369-3390. DOI:10.1016/S0045-7825(02)00253-0 |
| [49] |
MIEUSSENS L, STRUCHTRUP H. Numerical comparison of Bhatnagar-Gross-Krook models with proper Prandtl number[J]. Physics of Fluids, 2004, 16(8): 2797-2813. DOI:10.1063/1.1758217 |
| [50] |
GORJI M H, TORRILHON M, JENNY P. Fokker–Planck model for computational studies of monatomic rarefied gas flows[J]. Journal of Fluid Mechanics, 2011, 680: 574-601. DOI:10.1017/jfm.2011.188 |
| [51] |
欧阳水吾, 谢中强. 高温非平衡空气绕流[M]. 北京: 国防工业出版社, 2001.
|
| [52] |
WANG-CHANG C S, UHLENBECK G E. Transport phenomena in polyatomic gases[R]. University of Michigan, UMR4405, 1951. http://deepblue.lib.umich.edu/bitstream/2027.42/8195/5/bad7743.0001.001.pdf
|
| [53] |
MASON E A, MONCHICK L. Heat conductivity of polyatomic and polar gases[J]. The Journal of Chemical Physics, 1962, 36(6): 1622-1639. DOI:10.1063/1.1732790 |
| [54] |
WU L, LI Q, LIU H H, et al. Extraction of the translational Eucken factor from light scattering by molecular gas[J]. Journal of Fluid Mechanics, 2020, 901: A23. DOI:10.1017/jfm.2020.568 |
| [55] |
BORGNAKKE C, LARSEN P S. Statistical collision model for Monte Carlo simulation of polyatomic gas mixture[J]. Journal of Computational Physics, 1975, 18(4): 405-420. DOI:10.1016/0021-9991(75)90094-7 |
| [56] |
BOYD I D. Rotational-translational energy transfer in rarefied nonequilibrium flows[J]. Physics of Fluids A:Fluid Dynamics, 1990, 2(3): 447-452. DOI:10.1063/1.857740 |
| [57] |
HAAS B L, HASH D B, BIRD G A, et al. Rates of thermal relaxation in direct simulation Monte Carlo methods[J]. Physics of Fluids, 1994, 6(6): 2191-2201. DOI:10.1063/1.868221 |
| [58] |
GIMELSHEIN N E, GIMELSHEIN S F, LEVIN D A. Vibrational relaxation rates in the direct simulation Monte Carlo method[J]. Physics of Fluids, 2002, 14(12): 4452-4455. DOI:10.1063/1.1517297 |
| [59] |
PORODNOV B T, KULEV A N, TUCHVETOV F T. Thermal transpiration in a circular capillary with a small temperature difference[J]. Journal of Fluid Mechanics, 1978, 88(4): 609-622. DOI:10.1017/s002211207800230x |
| [60] |
LI Q, ZENG J N, SU W, et al. Uncertainty quantification in rarefied dynamics of molecular gas: rate effect of thermal relaxation[J]. Journal of Fluid Mechanics, 2021, 917: A58. DOI:10.1017/jfm.2021.338 |
| [61] |
RYKOV V A, SKOBELKIN V N. Macroscopic description of the motions of a gas with rotational degrees of freedom[J]. Fluid Dynamics, 1978, 13(1): 144-147. DOI:10.1007/BF01094479 |
| [62] |
SHARIPOV F. Influence of quantum intermolecular interaction on internal flows of rarefied gases[J]. Vacuum, 2018, 156: 146-153. DOI:10.1016/j.vacuum.2018.07.022 |
| [63] |
SONE Y. Kinetic Theory and Fluid Dynamics[M]. Boston, MA: Birkhäuser Boston, 2002. DOI: 10.1007/978-1-4612-0061-1
|
| [64] |
HILBERT D. Begründung der kinetischen gastheorie[J]. Mathematische Annalen, 1912, 72(4): 562-577. DOI:10.1007/BF01456676 |
| [65] |
CHAPMAN S. VI. On the law of distribution of molecular velocities, and on the theory of viscosity and thermal conduction, in a non-uniform simple monatomic gas[J]. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character, 1916, 216(538-548): 279-348. DOI:10.1098/rsta.1916.0006 |
| [66] |
ENSKOG D. Kinetische theorie der vorgänge in mässig verdünnten gasen (German edition)[M]. University of Michigan Library, 1917. (in German)
|
| [67] |
STRUCHTRUP H. Macroscopic transport equations for rarefied gas flows: approximation methods in Kinetic theory[M]// Interaction of Mechanics and Mathematics, Heidelberg, Germany: Springer, 2021. doi: 10.1007/3-540-32386-4
|
| [68] |
CHEN S Z, XU K, CAI Q D. A comparison and unification of ellipsoidal statistical and shakhov BGK models[J]. Advances in Applied Mathematics and Mechanics, 2015, 7(2): 245-266. DOI:10.4208/aamm.2014.m559 |
| [69] |
WU L. Deterministic numerical simulation of the Boltzmann and kinetic model equations for classical and quantum dilute gases[D]. Glasgow: University of Strathclyde, 2013.
|
| [70] |
BEYLICH A. An interlaced system for Nitrogen gas[R]//Proceedings of CECAM Workshop, ENS de Lyon, France, 2000.
|
| [71] |
TCHEREMISSINE F G, AGARWAL R K, ABE T. Computation of hypersonic shock waves in diatomic gases using the generalized Boltzmann equation[C]//AIP Conference Proceedings 1084, Kyoto, Japan, 2008: 427-433. doi: 10.1063/1.3076515
|
| [72] |
MORSE T F. Kinetic model for gases with internal degrees of freedom[J]. The Physics of Fluids, 1964, 7(2): 159-169. DOI:10.1063/1.1711128 |
| [73] |
李馨东, 胡宗民, 姜宗林. 可压缩流体体积黏性的连续介质理论[J]. 中国科学 (物理学 力学 天文学), 2016, 46(3): 034701. LI X D, HU Z M, JIANG Z L. The continuum theory of bulk viscosity in compressible fluids[J]. SCIENTIA SINICA Physica, Mechanica & Astronomica, 2016, 46(3): 034701. (in Chinese) |
| [74] |
BRUNO D, FREZZOTTI A, GHIROLDI G P. Oxygen transport properties estimation by classical trajectory-direct simulation Monte Carlo[J]. Physics of Fluids, 2015, 27(5): 057101. DOI:10.1063/1.4921157 |
| [75] |
MEADOR W E, MINER G A, TOWNSEND L W. Bulk viscosity as a relaxation parameter: fact or fiction?[J]. Physics of Fluids, 1996, 8(1): 258-261. DOI:10.1063/1.868833 |
| [76] |
MEIJER A S, DE WIJN A S, PETERS M F E, et al. Coherent Rayleigh-Brillouin scattering measurements of bulk viscosity of polar and nonpolar gases, and kinetic theory[J]. The Journal of Chemical Physics, 2010, 133(16): 164315. DOI:10.1063/1.3491513 |
| [77] |
JAEGER F, MATAR O K, MÜLLER E A. Bulk viscosity of molecular fluids[J]. The Journal of Chemical Physics, 2018, 148(17): 174504. DOI:10.1063/1.5022752 |
| [78] |
HANSON F B, MORSE T F. Kinetic models for a gas with internal structure[J]. The Physics of Fluids, 1967, 10(2): 345-353. DOI:10.1063/1.1762114 |
| [79] |
GROSS E P, JACKSON E A. Kinetic models and the linearized Boltzmann equation[J]. The Physics of Fluids, 1959, 2(4): 432-441. DOI:10.1063/1.1724415 |
| [80] |
BOLEY C D, DESAI R C, TENTI G. Kinetic models and Brillouin scattering in a molecular gas[J]. Canadian Journal of Physics, 1972, 50(18): 2158-2173. DOI:10.1139/p72-286 |
| [81] |
TENTI G, BOLEY C D, DESAI R C. On the kinetic model description of Rayleigh–Brillouin scattering from molecular gases[J]. Canadian Journal of Physics, 1974, 52(4): 285-290. DOI:10.1139/p74-041 |
| [82] |
PAN X G, SHNEIDER M N, MILES R B. Coherent Rayleigh-Brillouin scattering in molecular gases[J]. Physical Review A, 2004, 69(3): 033814. DOI:10.1103/physreva.69.033814 |
| [83] |
WU L, WHITE C, SCANLON T J, et al. A kinetic model of the Boltzmann equation for non-vibrating polyatomic gases[J]. Journal of Fluid Mechanics, 2015, 763: 24-50. DOI:10.1017/jfm.2014.632 |
| [84] |
WANG Z, YAN H, LI Q B, et al. Unified gas-kinetic scheme for diatomic molecular flow with translational, rotational, and vibrational modes[J]. Journal of Computational Physics, 2017, 350: 237-259. DOI:10.1016/j.jcp.2017.08.045 |
| [85] |
彭傲平, 李志辉, 吴俊林, 等. 含振动能激发Boltzmann模型方程气体动理论统一算法验证与分析[J]. 物理学报, 2017, 66(20): 204703-214. PENG A P, LI Z H, WU J L, et al. Validation and analysis of gas-kinetic unified algorithm for solving Boltzmann model equation with vibrational energy excitation[J]. Acta Physica Sinica, 2017, 66(20): 204703-214. DOI:10.7498/aps.66.204703 (in Chinese) |
| [86] |
TITAREV V A, FROLOVA A A. Application of model kinetic equations to calculations of super- and hypersonic molecular gas flows[J]. Fluid Dynamics, 2018, 53(4): 536-551. DOI:10.1134/s0015462818040110 |
| [87] |
MATHIAUD J, MIEUSSENS L. BGK and Fokker-Planck models of the Boltzmann equation for gases with discrete levels of vibrational energy[J]. Journal of Statistical Physics, 2020, 178(5): 1076-1095. DOI:10.1007/s10955-020-02490-7 |
| [88] |
RYKOV V A. A model kinetic equation for a gas with rotational degrees of freedom[J]. Fluid Dynamics, 1975, 10(6): 959-966. DOI:10.1007/BF01023275 |
| [89] |
GORJI M H, JENNY P. A Fokker-Planck based kinetic model for diatomic rarefied gas flows[J]. Physics of Fluids, 2013, 25(6): 062002. DOI:10.1063/1.4811399 |
| [90] |
MASON E A. Molecular relaxation times from thermal transpiration measurements[J]. The Journal of Chemical Physics, 1963, 39(3): 522-526. DOI:10.1063/1.1734288 |
| [91] |
GUPTA A D, STORVICK T S. Analysis of the heat conductivity data for polar and nonpolar gases using thermal transpiration measurements[J]. The Journal of Chemical Physics, 1970, 52(2): 742-749. DOI:10.1063/1.1673048 |
| [92] |
GREEN M S. Markoff random processes and the statistical mechanics of time-dependent phenomena. II. irreversible processes in fluids[J]. The Journal of Chemical Physics, 1954, 22(3): 398-413. DOI:10.1063/1.1740082 |
| [93] |
KUBO R. Statistical-mechanical theory of irreversible processes. I. general theory and simple applications to magnetic and conduction problems[J]. Journal of the Physical Society of Japan, 1957, 12(6): 570-586. DOI:10.1143/jpsj.12.570 |
| [94] |
PAN X G, SHNEIDER M N, MILES R B. Coherent Rayleigh-Brillouin scattering[J]. Physical Review Letters, 2002, 89(18): 183001. DOI:10.1103/physrevlett.89.183001 |
| [95] |
VIEITEZ M O, VAN DUIJN E J, UBACHS W, et al. Coherent and spontaneous Rayleigh-Brillouin scattering in atomic and molecular gases and gas mixtures[J]. Physical Review A, 2010, 82(4): 043836. DOI:10.1103/physreva.82.043836 |
| [96] |
GU Z Y, UBACHS W. Temperature-dependent bulk viscosity of nitrogen gas determined from spontaneous Rayleigh-Brillouin scattering[J]. Optics Letters, 2013, 38(7): 1110-1112. DOI:10.1364/OL.38.001110 |
| [97] |
SUGAWARA A, YIP S, SIROVICH L. Spectrum of density fluctuations in gases[J]. The Physics of Fluids, 1968, 11(5): 925-932. DOI:10.1063/1.1692060 |
| [98] |
REICHL L E. A Modern Course in Statistical Physics[M]. Weinheim, Germany: Wiley-VCH Verlag GmbH & Co. KGaA, 2016. doi: 10.1002/9783527690497
|
| [99] |
DAGDIGIAN P J. Vibrational and rotational relaxation in gases (Lambert J D)[J]. Journal of Chemical Education, 1979, 56(1): A42. https://pubs.acs.org/doi/pdf/10.1021/ed056pA42.1 doi: 10.1021/ed056pA42.1
|
 2022, Vol. 40
2022, Vol. 40


