2. 天津市现代工程力学重点实验室,天津 300354
2. Tianjin Key Laboratory of Modern Engineering Mechanics, Tianjin 300354, China
湍流大尺度运动的研究一直是湍流研究的热点之一。Kim和Adrian[1]在充分发展的圆管湍流流向脉动速度的前乘波谱中,发现其具有两个峰值—与小尺度运动相关的高波数模态和与超大尺度相关的低波数模态。Guala 和Adrian等[2]在充分发展的圆管湍流外区中使用热膜测量流向瞬时速度序列,得到超大尺度运动存在于对数律区,且波长可达
关于大尺度运动对于湍流能量的贡献,Balakumar和Adrian[5]在零压力梯度的湍流边界层和槽道流中以
湍流实验测量常用方法有基于单点的热线测量[9]、激光多普勒测量[10]、基于场测量的PIV方法[11-12]。通过热线测量和激光多普勒测量得到单点瞬时速度序列,并使用傅里叶变换、小波变换、希尔伯特–黄变换等,将时间信息变为不同频率信息(波长),利用泰勒冻结假设[13]:空间点定义为
| $ u\left( {x + r,t + \tau } \right) = u\left( {x + r - {{\boldsymbol{U}}}\tau ,t} \right) $ | (1) |
其中
泰勒冻结假设一般适用于迁移速度为常数的均匀各向同性湍流。而对于剪切湍流,由于湍流结构非各向同性,时间尺度转化为空间尺度可能由于相关性变弱等原因,造成相干运动的失真,因此用泰勒冻结假设测出的相干运动空间尺度要比真实相干运动的空间尺度要小。
单点数据常用的尺度分析方法有傅里叶变换、小波分解[14-16]、希尔伯特–黄变换[17-18]等。傅里叶变换得到的是频谱信息,对于非稳态或非周期性信号,其结果不能反映局部突变信息。而小波变换既可得到频域信息,又可得到时域信息。基于PIV图像的分析方法有本征正交分解(POD)[19-23]、动力学模态分解(DMD)[24]、线性随机估计等。这些方法虽然可以同时得到时空信息,但很难将相邻尺度的运动区分开来。
本文使用高时间分辨率粒子图像测速技术,通过拼接4个高速相机得到足够大视场的速度场时间序列。从同一流向位置不同法向高度的脉动速度时间序列提取的大尺度结构,使用小波变换将其重构到空间结构,并与从空间直接提取的对应空间大尺度结构进行对比,分析两者差异。
1 实验设置 1.1 实验设备实验在天津大学流体力学实验室重力溢流式低湍流度循环水洞中进行。水洞实验段长度
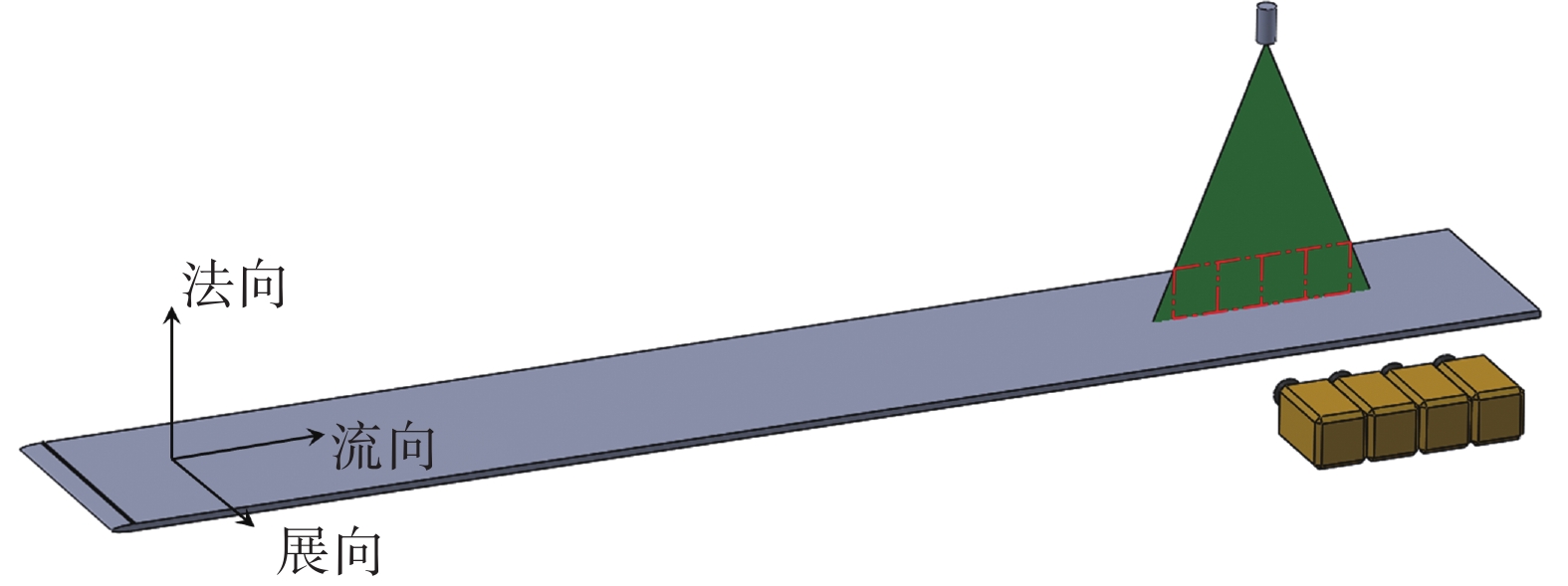
|
图 1 实验示意图 Fig.1 Schematic of the experiment setup |
| 表 1 实验参数 Table 1 Experiment parameters |
|
|
小波变换最早由法国科学家Morlet 于1980年分析地震数据时首创。与傅里叶变换相比,小波变换能保持信号中的局域性特征。就湍流情况而言,连续小波变换通过空间和尺度提供连续的和冗余的开折,因此我们能够跟踪相干结构的动力学情况并测量其对能谱的贡献[16]。在湍流边界层中使用小波变换的方法辨识相干结构已有丰富研究[14,25-27]。
本文使用“db3”小波函数,将脉动速度分解为不同尺度部分(如图2所示),红色实线为尺度函数(父小波),绿色实线为小波母函数(母小波)。
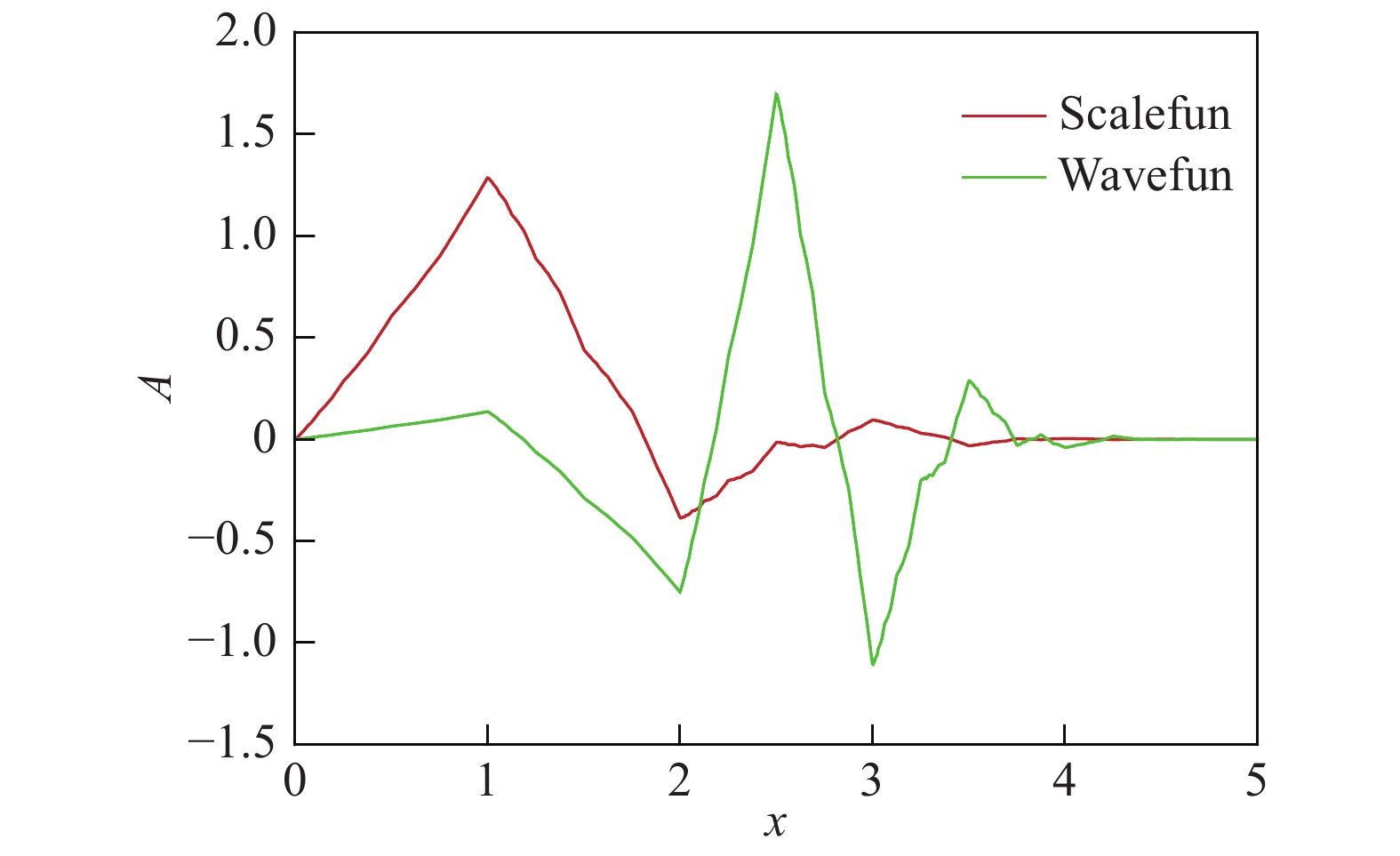
|
图 2 “db3”小波形状 Fig.2 Wavelet shape of ‘db3’ |
壁面摩擦速度是湍流边界层的一个重要参数,是衡量流动控制效果的常用指标,也是进行湍流分析的重要物理量。然而这个量在水洞中很难直接测得,也难以测得准确,因此本文使用间接测量方法来得到壁面摩擦阻力。Spalding[28]提出了可以同时使用黏性底层和对数律区的平均速度剖面来计算壁面摩擦速度的方法,计算公式如式(2)。同时对得到的粒子图像进行标定、拼接、去噪并计算出速度场,然后对速度场进行沿时间和流向的平均可以得到平均速度剖面。根据Spalding给出的黏性底层和对数律区的平均速度与法向位置的关系,使用最小二乘方法拟合壁面摩擦速度。
| $ {y^ + } = {u^ + } {\rm{e}}^{- \kappa B} \Bigg[ {\rm{e}}^{ \kappa {u^ + }} - 1 - \kappa {u^ + } - \frac{{{{\left( {\kappa {u^ + }} \right)}^2}}}{2} - \frac{{{{(\kappa {u^ + })}^3}}}{6}\Bigg] $ | (2) |
式(2)中,内尺度无量纲化后的壁面法向高度
在获得壁面摩擦速度后,可以衡量流场的基本量在湍流边界层内的分布。图3与图4分别为内尺度无量纲化后的平均速度剖面与二阶量剖面,其中
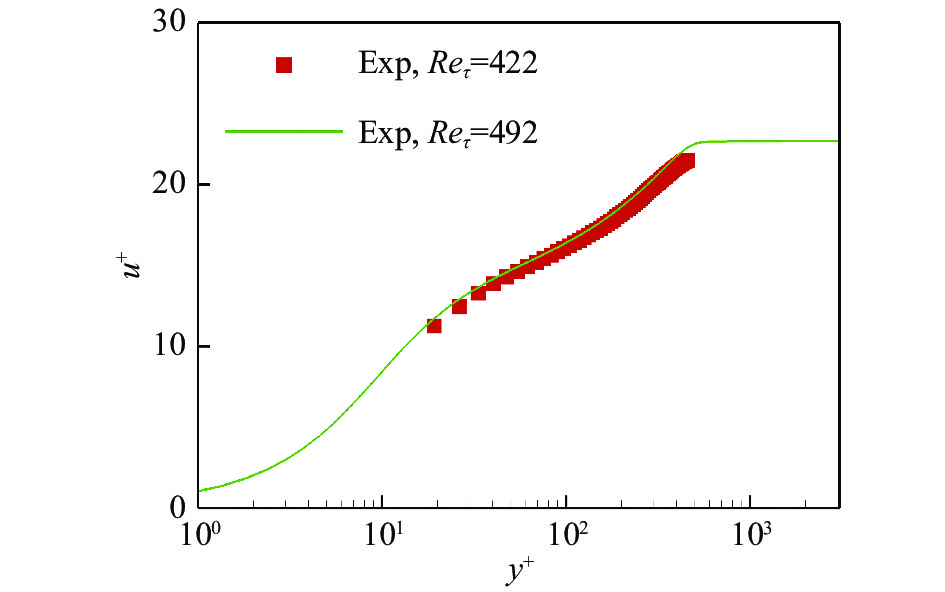
|
图 3 平均速度剖面 Fig.3 Profiles of the mean velocity |
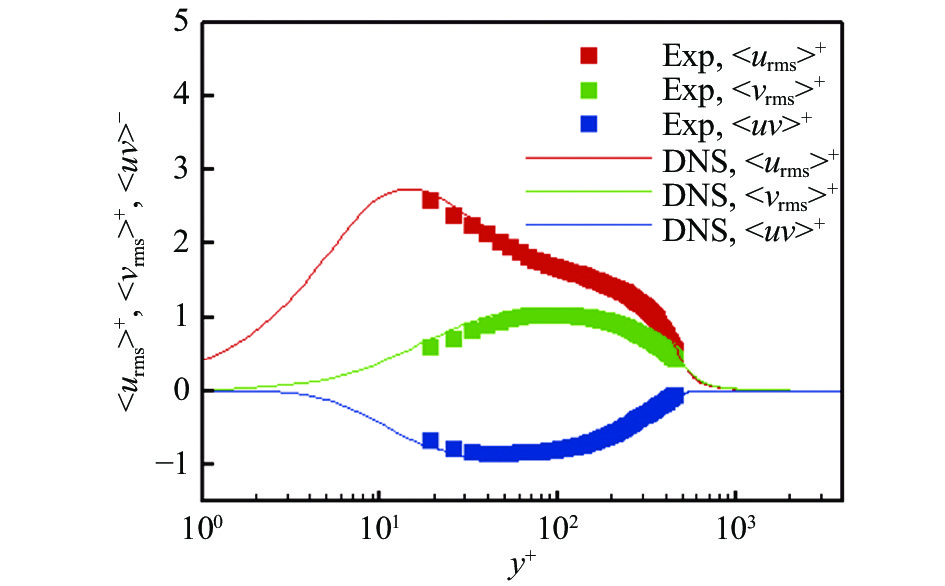
|
图 4 雷诺应力剖面 Fig.4 Profiles of the Reynold stress |
湍流可以分解为平均速度、相干部分和完全随机部分。相干结构是湍流的主要特征。Marusic[30]将主要的湍流结构分为三类:与近壁循环相关的展向尺度约为100个黏性尺度的条带;尺度为边界层厚度量级的大尺度运动;尺度为10倍边界层厚度量级的超大尺度运动。随着雷诺数变化,不同尺度湍流结构所起的作用也发生变化,因此本文将使用小波分解的方法计算不同尺度结构占湍动能的比例。
利用沿流向的空间小波分解方法得到不同空间尺度所包含的脉动速度,并由此计算出流场的总湍动能以及每个空间尺度所包含的湍动能,进而得到不同尺度对湍动能贡献的比例。将每一法向层不同流向尺度携带的湍动能占比按照顺序排列,可以得到不同流向尺度湍动能占比随法向位置变化的云图(图5),其中
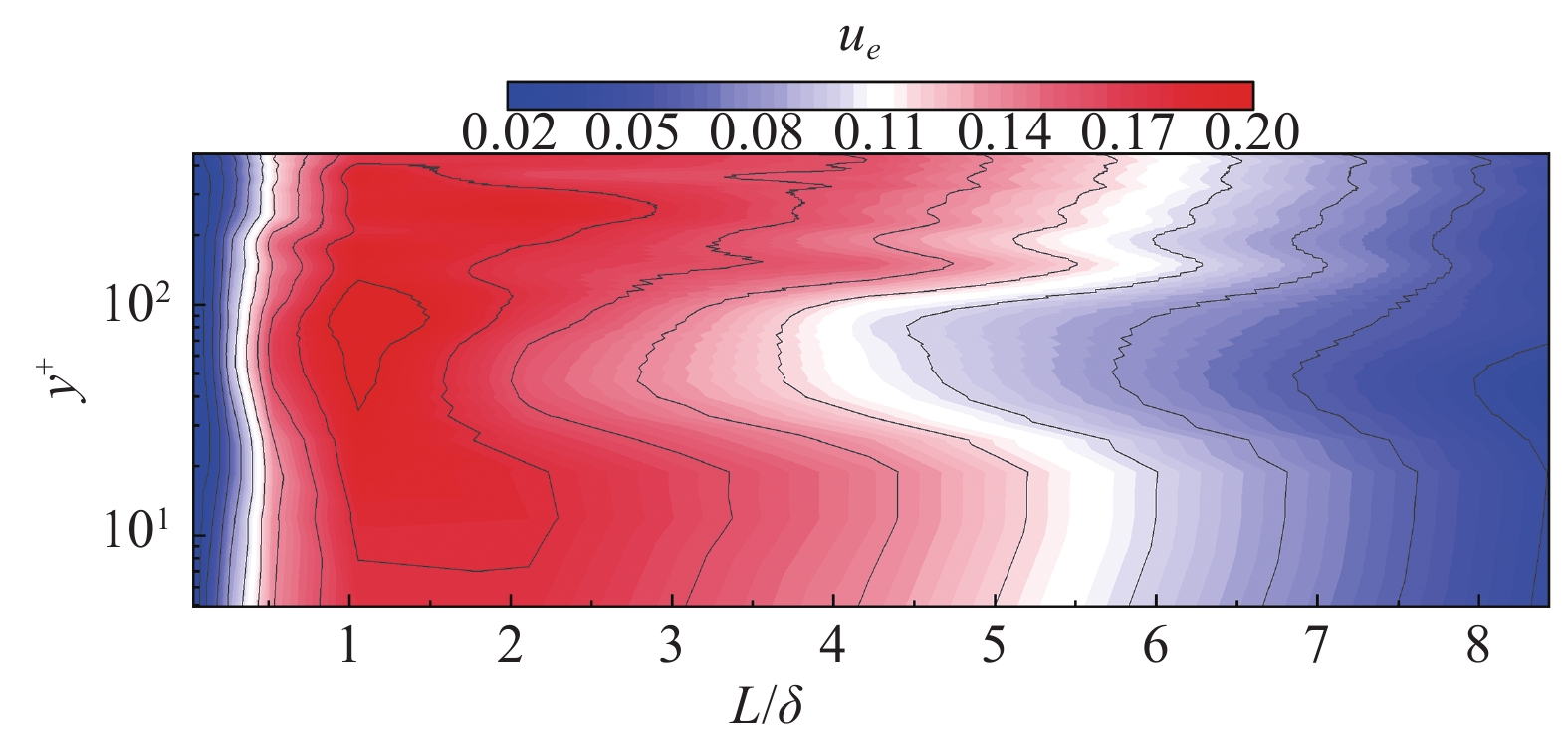
|
图 5 不同尺度所占湍动能比例 Fig.5 Turbulent kinetic energy fraction for different scales |
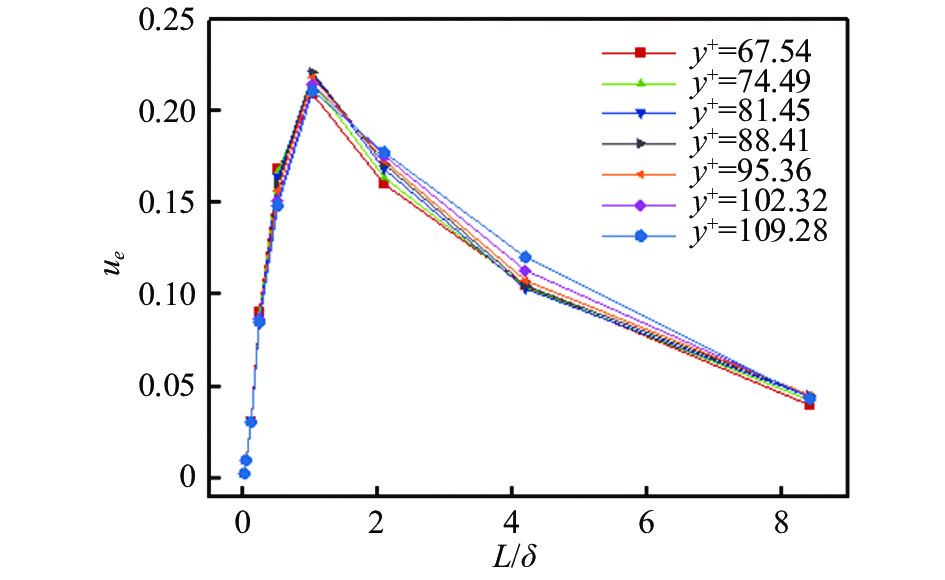
|
图 6 峰值附近不同尺度所占湍动能比例 Fig.6 Turbulent kinetic energy fraction in different scales near the peak location |
相干运动在湍流边界层中起到了决定性的作用,而大尺度相干运动在中高雷诺数的情况下对流向雷诺正应力和雷诺切应力的贡献占所有相干运动贡献的一半以上。当前,关于如何检测湍流边界层中的大尺度相干运动是一个基础内容。在有关湍流边界层的实验研究中,常用的测量手段有单点测量的热线方法和多点测量的PIV方法。热线可以得到单点时间序列,而 PIV方法,特别是具有高时间分辨率的TRPIV方法,可以得到全场多点的时间序列。对于热线测量,通过检测时间序列中的相干结构,并使用泰勒冻结假设可以得到相干结构的空间结构。而对于PIV结果,则可以对流场内每个点的时间序列进行尺度分解以提取流场内的空间结构。本文采用连续小波变换的方法来进行尺度分解,其中小波基函数为“amor”。通过以
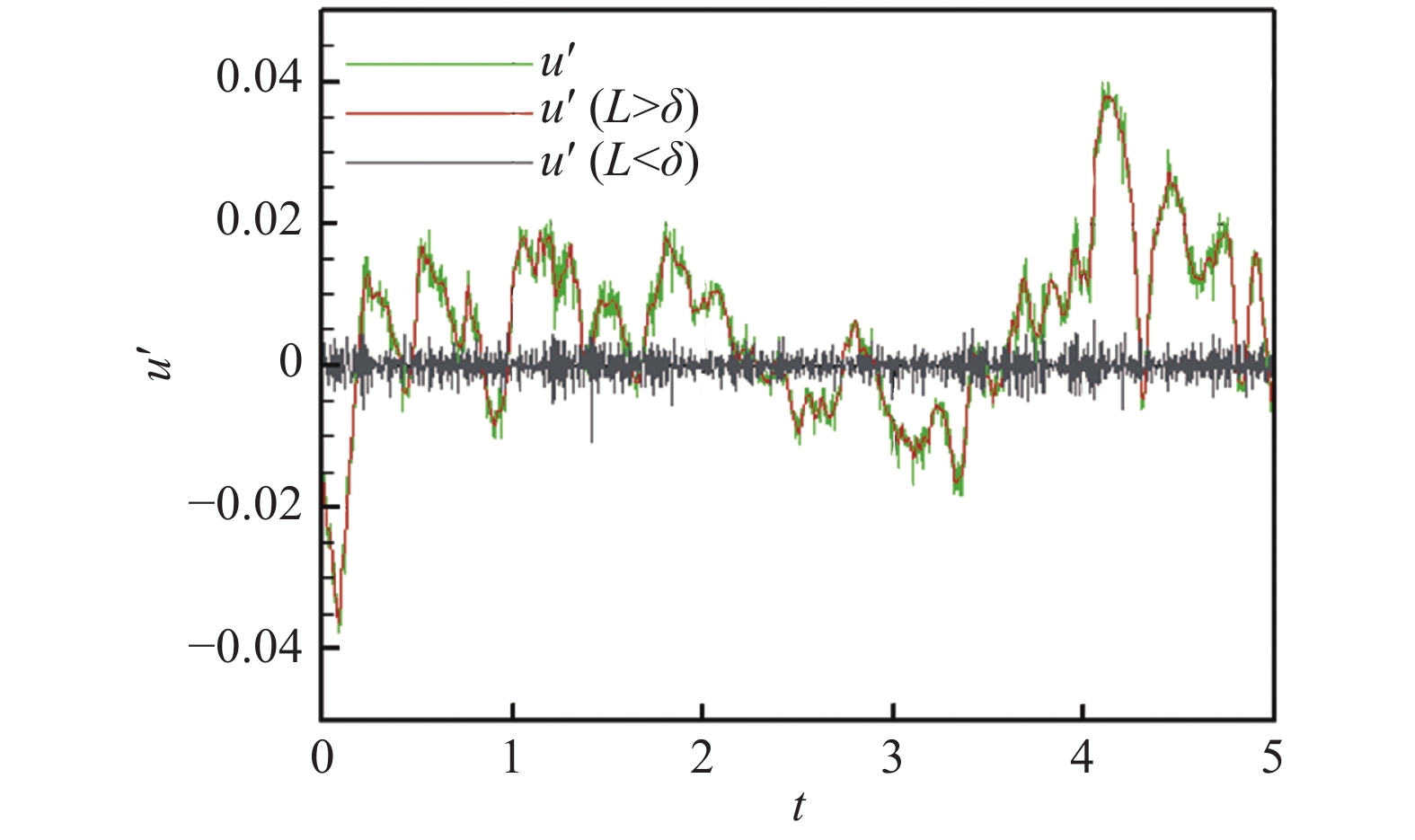
|
图 7 单点原始流向脉动速度与尺度分解后大小尺度分量的时间序列 Fig.7 One-point time series of the original, large-scale and small-scale streamwise velocity fluctuations |

|
图 8 原始流向脉动速度和尺度分解后大小尺度分量云图 Fig.8 Contours of the origin, large-scale and small-scale streamwise velocity fluctuations |
由小波分解重构得到的是大、小尺度分开的脉动速度场的时间序列,可以将这些速度场看作由排列在流向-法向平面的二维热线探针阵列得到的脉动速度时间序列。取其中一点的大尺度脉动速度序列,使用传统的Mu-level方法提取大尺度结构。Mu-level方法是检测猝发事件的经典方法之一。由于流向脉动速度与猝发事件的相关程度更大,因此其主要通过流向脉动速度与其均方根的比值来判断是否发生猝发事件,只有当比值达到给定的门限值时才会认为发生了猝发事件。其中喷射事件检测准则如下:
| $ D(t) = \left\{ {\begin{array}{*{20}{l}} { - 1,\;\;\;\;{u_{_{L}}} \leqslant -{L_{_{m}}} {u_{{\rm{rms}}}}} \\ { - 1,\;\;\; - {L_{_{m}}}{u_{{\rm{rms}}}} < {u_{_{L}}} < - 0.25{u_{{\rm{rms}}}} \; \& \; D(t - 1) = - 1} \\ {0,\;\;\;\;\;\;\;{u_{_{L}}} \geqslant - 0.25{u_{{\rm{rms}}}} } \\ {0,\;\; \;\;\;\; - {L_{_{m}}}{u_{{\rm{rms}}}} < {u_{_{L}}} < - 0.25{u_{{\rm{rms}}}} \; \& \; D(t - 1) = 0} \end{array}} \right. $ | (3) |
式中,Lm为门限值,在本文中取0.6;

|
图 9 时间序列重构出的相干结构 Fig.9 Coherent structures reconstructed from the time series of signals |
可以看到,时间序列重构得到的猝发事件与速度矢量场的符合程度较高。此外,在空间中会存在一个与通过时间序列重构出的脉动速度场相对应的原始速度场,对空间上的脉动速度场使用象限分裂的方法可以直接提取大尺度相干运动。根据流向和法向脉动速度的符号可以将其分为四个象限,Ⅰ:
| $ D(t) = \left\{ {\begin{array}{*{20}{l}} { - 1,\;\;\;{u_{_{L}}} \leqslant - {L_{_{m}}}{u_{{\rm{rms}}}} } \\ { - 1,\;\;\; - {L_{_{m}}}{u_{{\rm{rms}}}} < {u_{_{L}}} < - 0.25{u_{{\rm{rms}}}} \; \& \; D(x - 1) = - 1} \\ {0,\;\;\;\;\;\;{u_{_{L}}} \geqslant - 0.25{u_{{\rm{rms}}}} } \\ {0,\;\;\;\;\; - {L_{_{m}}}{u_{{\rm{rms}}}} < {u_{_{L}}} < - 0.25{u_{{\rm{rms}}}} \; \& \; D(x - 1) = 0} \end{array}} \right. $ | (4) |
式中,

|
图 10 空间提取的相干结构 Fig.10 Coherent structure extracted from the spatial domain |
为了验证从时间检测出的相干结构的可靠性,将时间和空间中检测出的相干结构进行对比(图11),其中黑色实线标出的为从空间上提取的相干结构,而有颜色的区域代表从时间中提取出的相干结构。可以看出,时间重构检测出的结构基本上与空间矢量场一致,不过在剪切层和展向涡附近会出现偏差,同时从时间上得到的相干结构比空间结构要小些。检测结果的对比,证明了从时间上提取相干运动的可靠性。
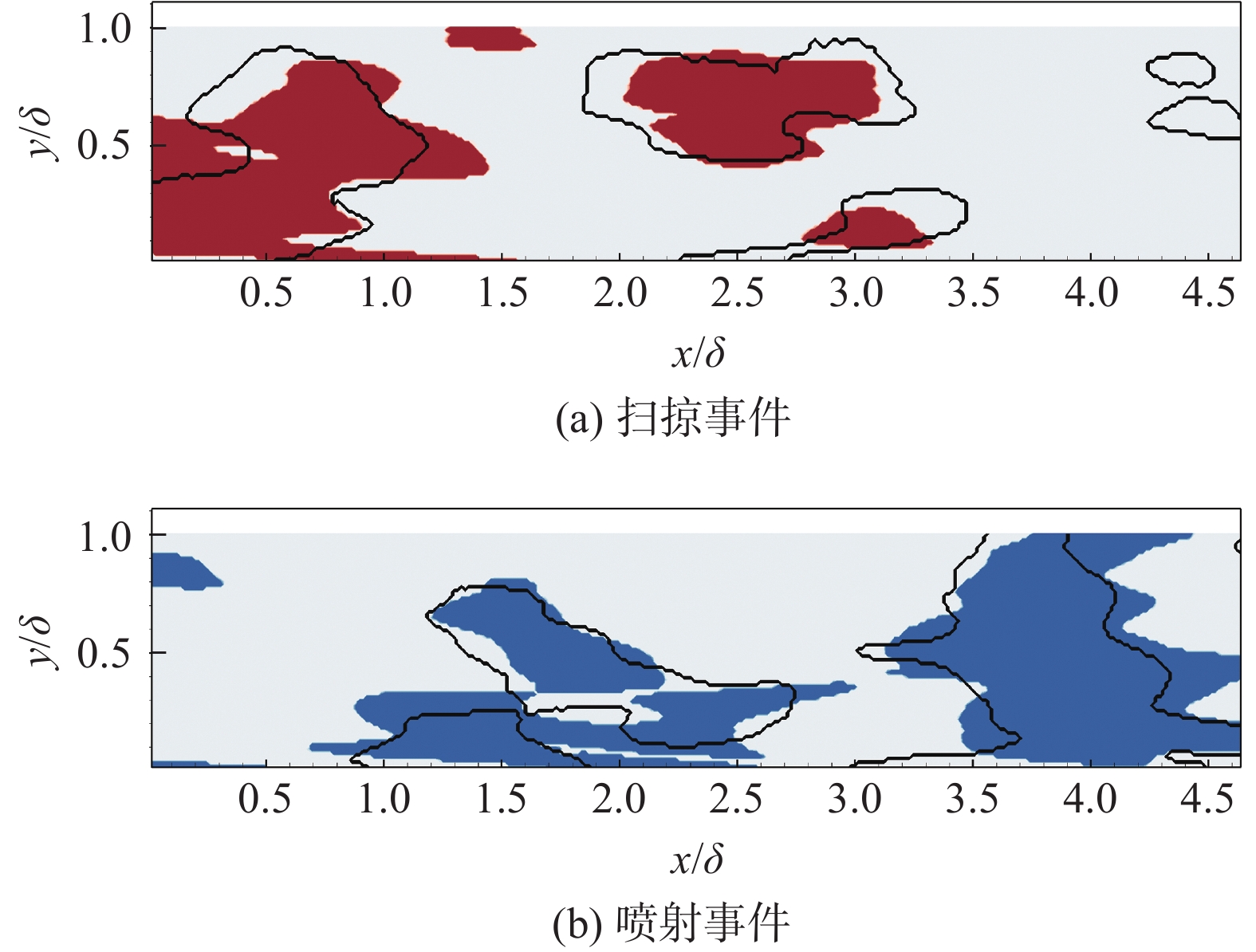
|
图 11 从时间和空间提取的喷射和扫掠事件对比 Fig.11 Comparison of the ejection and sweep events between the temporal and spatial extraction |
空间条件相位平均是提取相干结构空间拓扑形态的经典方法。从时间和空间中提取的相干结构的结果对比可以说明,时间重构的相干结构与直接检测原始空间速度场相干结构的统计特性存在差异。
为了研究这一差异,以
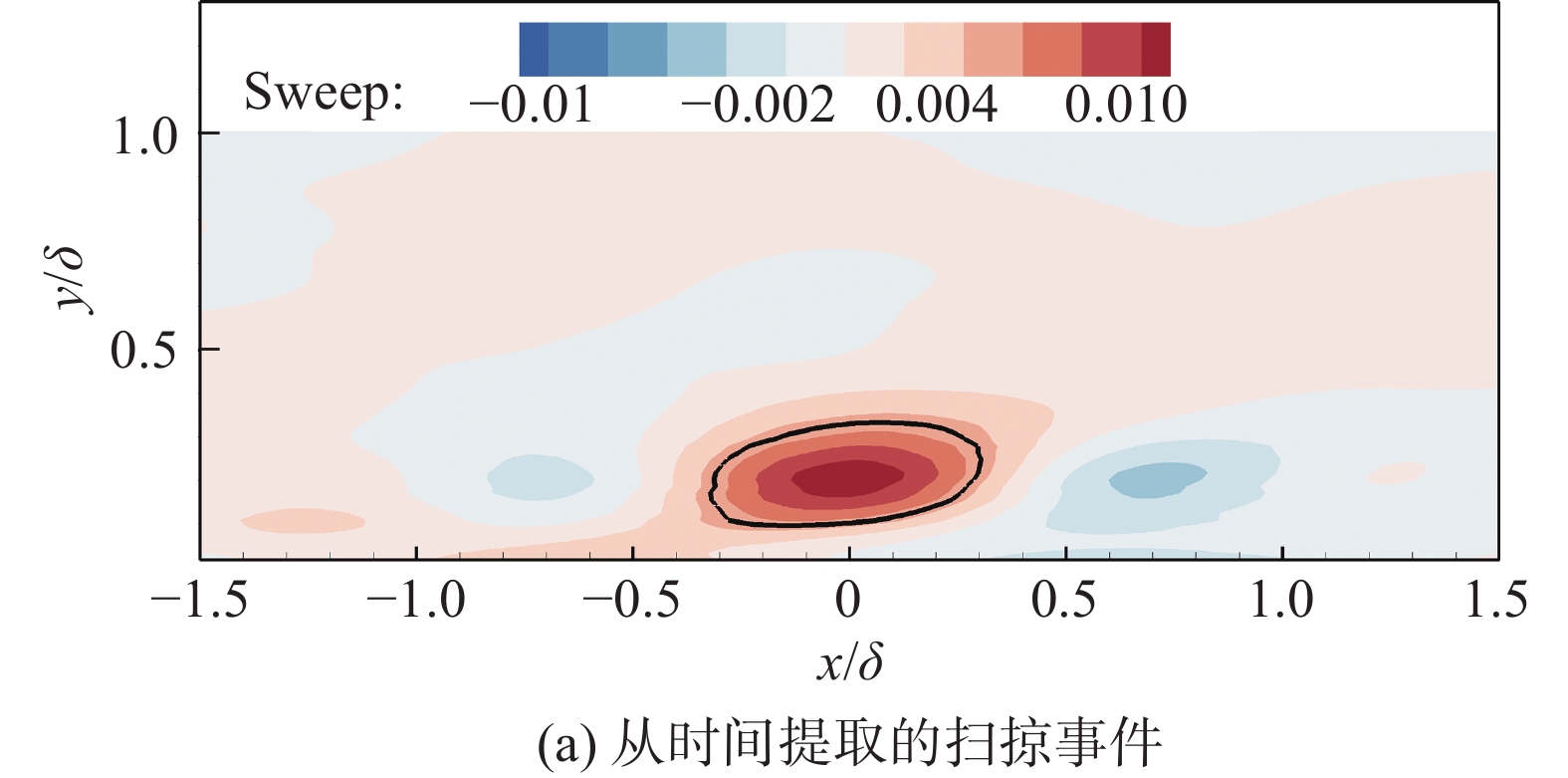
|
图 12 |

|
图 12 从时间和空间提取的猝发事件 Fig.12 Burst events extracted from the temporal and spatial domains |
通过对时间和空间提取的猝发事件给定阈值(扫掠事件给定流向脉动速度最大值的0.25倍,喷射事件给定值与扫掠事件给定值的符号相反),并使用椭圆拟合的方法找到流向间距最大的两点坐标,以分别提取猝发事件的流向尺度。如图13和图14所示,可以看出在0.2δ~0.6δ的法向区域内,猝发事件的尺度基本是不变的。计算不同法向位置,时间猝发事件与空间猝发事件的流向尺度比例,可以看出,时间和空间提取的喷射事件流向尺度比例在0.9~1.0,扫掠事件比例在0.75~0.85。可以说明,时间提取猝发事件尺度要小于空间提取的猝发事件,喷射事件两者更接近,扫掠事件相差更大。这种不一致是喷射和扫掠事件的时空相关强度不同或者迁移速度差异造成的。
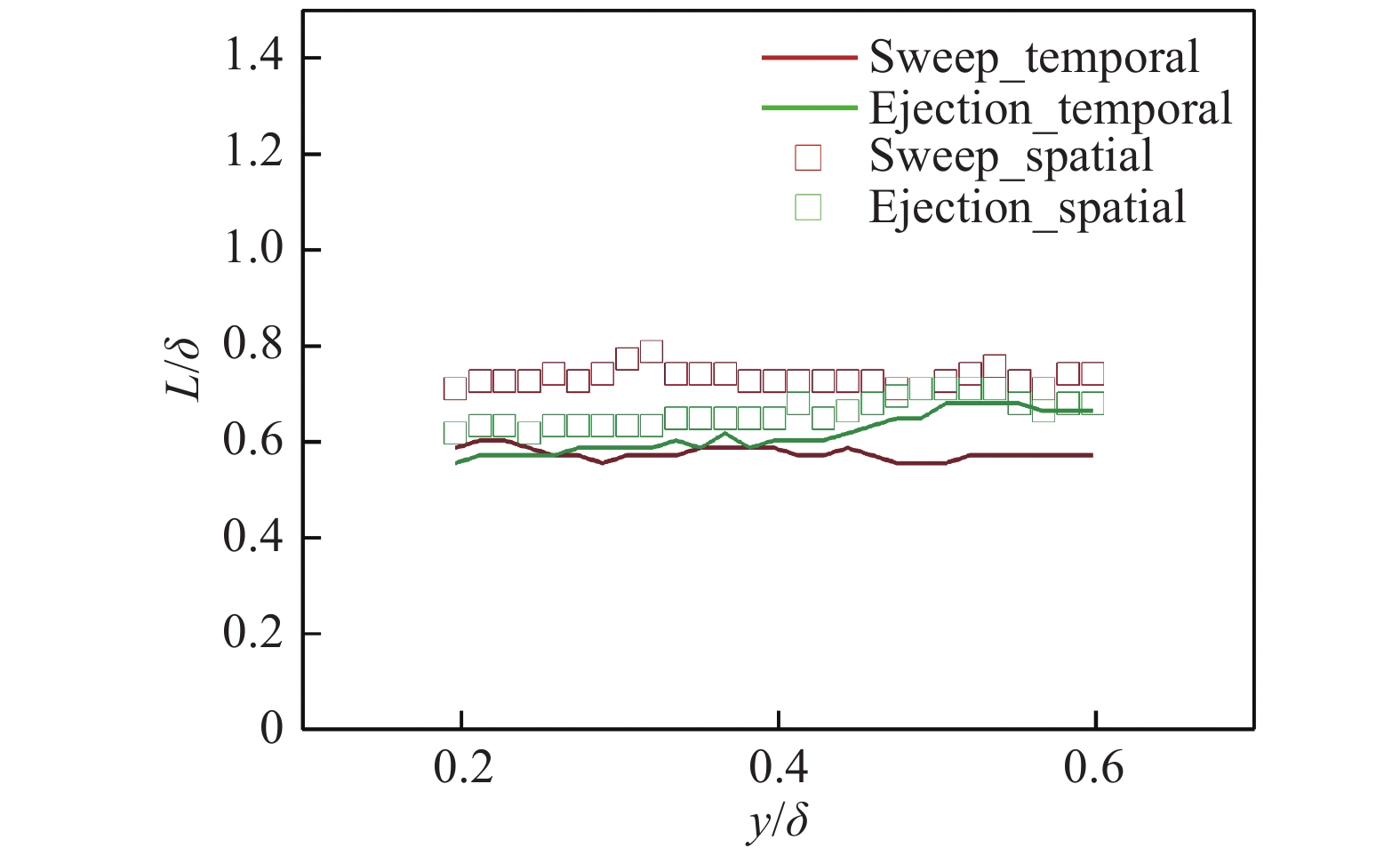
|
图 13 从时间和空间中提取的不同法向位置猝发事件流向长度尺度 Fig.13 Streamwise length scales of the burst events extracted from the temporal and spatial domains along different wall-normal locations |
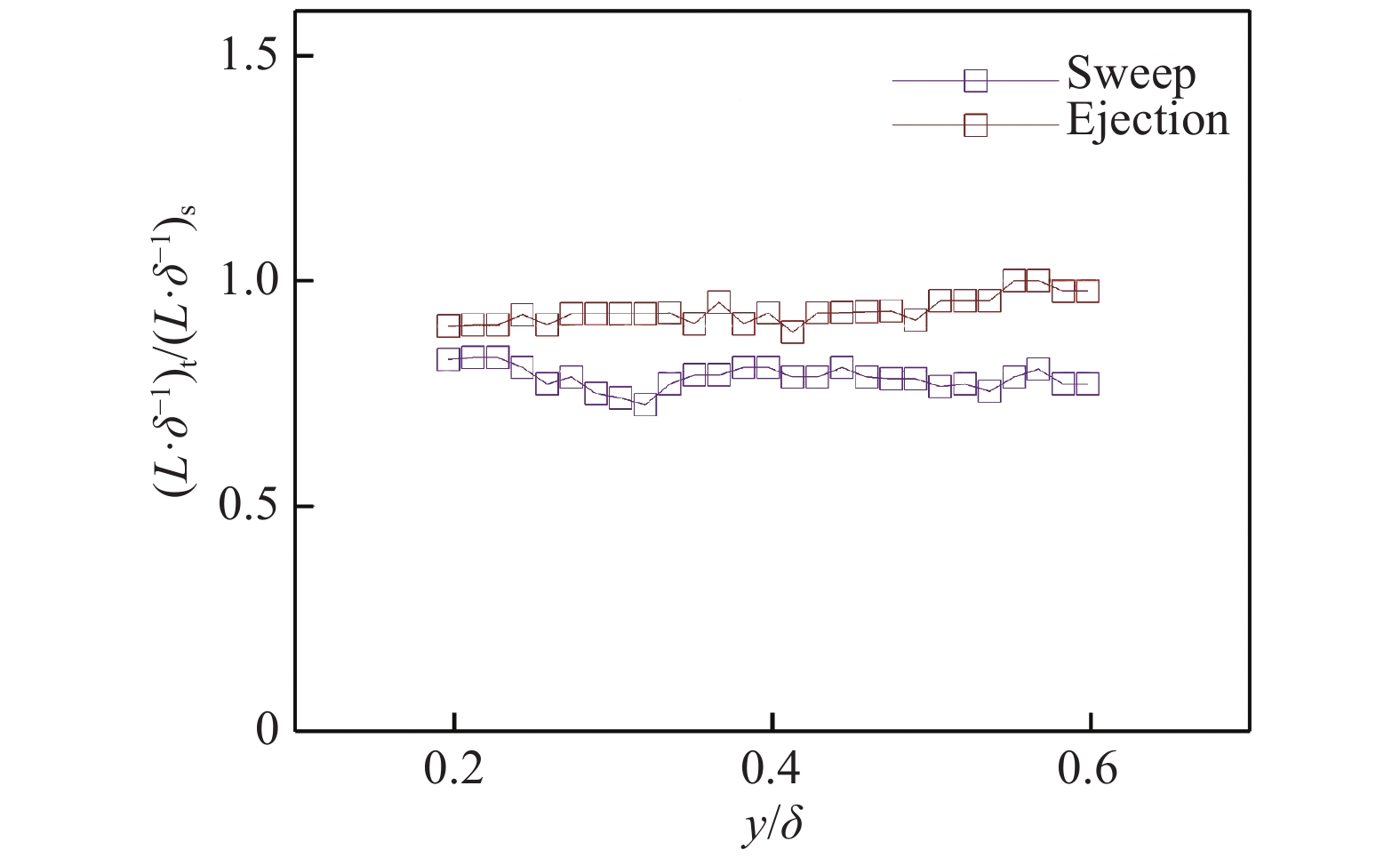
|
图 14 从时间、空间提取的不同法向位置猝发事件流向长度比值 Fig.14 Ratio of the streamwise lengths of burst events extracted from the temporal and spatial domains along different wall-normal locations |
使用相机阵列在湍流边界层中得到流法向尺度大小为
1)通过小波变换将大范围流场按照所含湍动能的占比划分为不同尺度,发现在湍流边界层中存在流向能量最大尺度,其峰值位置对应的尺度约为1倍边界层厚度。
2)利用泰勒冻结假设在时间维度上提取出的相干结构重构到原流场,可以找到与之对应的真实空间结构,且两种不同方法提取的结构基本一致。
3)从时间维度提取的高速条带(扫掠事件)尺度要小于空间提取的高速条带尺度,在
| [1] |
KIM K C, ADRIAN R J. Very large-scale motion in the outer layer[J]. Physics of Fluids, 1999, 11(2): 417-422. DOI:10.1063/1.869889 |
| [2] |
GUALA M, HOMMEMA S E, ADRIAN R J. Large-scale and very-large-scale motions in turbulent pipe flow[J]. Journal of Fluid Mechanics, 2006, 554: 521. DOI:10.1017/s0022112006008871 |
| [3] |
BAILEY S C C, SMITS A J. Experimental investigation of the structure of large- and very-large-scale motions in turbulent pipe flow[J]. Journal of Fluid Mechanics, 2010, 651: 339-356. DOI:10.1017/s0022112009993983 |
| [4] |
WANG W K, PAN C, WANG J J. Energy transfer structures associated with large-scale motions in a turbulent boundary layer[J]. Journal of Fluid Mechanics, 2021, 906: A14. DOI:10.1017/jfm.2020.777 |
| [5] |
BALAKUMAR B J, ADRIAN R J. Large- and very-large-scale motions in channel and boundary-layer flows[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2007, 365(1852): 665-681. DOI:10.1098/rsta.2006.1940 |
| [6] |
LEE J H, SUNG H J. Very-large-scale motions in a turbulent boundary layer[J]. Journal of Fluid Mechanics, 2011, 673: 80-120. DOI:10.1017/s002211201000621x |
| [7] |
WANG G H, ZHENG X J. Very large scale motions in the atmospheric surface layer: a field investigation[J]. Journal of Fluid Mechanics, 2016, 802: 464-489. DOI:10.1017/jfm.2016.439 |
| [8] |
LIU H Y, WANG G H, ZHENG X J. Three-dimensional representation of large-scale structures based on observations in atmospheric surface layers[J]. Journal of Geophysical Research: Atmospheres, 2019, 124(20): 10753-10771. DOI:10.1029/2019JD030733 |
| [9] |
NAKA Y, STANISLAS M, FOUCAUT J M, et al. Space-time pressure-velocity correlations in a turbulent boundary layer[J]. Journal of Fluid Mechanics, 2015, 771: 624-675. DOI:10.1017/jfm.2015.158 |
| [10] |
MICHIOKA T, SATO A, SADA K. Wind-tunnel experiments for gas dispersion in an atmospheric boundary layer with large-scale turbulent motion[J]. Boundary-Layer Meteorology, 2011, 141(1): 35-51. DOI:10.1007/s10546-011-9633-1 |
| [11] |
OSKOUIE R N, TACHIE M F, WANG B C. Investigation of large-scale coherent structures and momentum interference of twin rectangular jets[J]. Experimental Thermal and Fluid Science, 2020, 119: 110214. DOI:10.1016/j.expthermflusci.2020.110214 |
| [12] |
郭延昂, 董祥瑞, 蔡小舒, 等. 基于MSFLE与Liutex的涡合并实验研究[J]. 空气动力学学报, 2020, 38(3): 432-440. GUO Y A, DONG X R, CAI X S, et al. Experimental studies on vortices merging based on MSFLE and Liutex[J]. Acta Aerodynamica Sinica, 2020, 38(3): 432-440. DOI:10.7638/kqdlxxb-2020.0012 (in Chinese) |
| [13] |
HE G W, JIN G D, YANG Y. Space-time correlations and dynamic coupling in turbulent flows[J]. Annual Review of Fluid Mechanics, 2017, 49(1): 51-70. DOI:10.1146/annurev-fluid-010816-060309 |
| [14] |
姜楠, 王振东, 舒玮. 子波分析辨识壁湍流猝发事件的能量最大准则[J]. 力学学报, 1997, 29(4): 406-411. JIANG N, WANG Z D, SHU W. The maximum energy criterion for identifying burst events in wall turbulence using wavelet analysis[J]. Acta Mechanica Sinica, 1997, 29(4): 406-411. DOI:10.3321/j.issn:0459-1879.1997.04.003 (in Chinese) |
| [15] |
JIANG N, ZHANG J. Detecting multi-scale coherent eddy structures and intermittency in turbulent boundary layer by wavelet analysis[J]. Chinese Physics Letters, 2005, 22(8): 1968-1971. DOI:10.1088/0256-307x/22/8/041 |
| [16] |
FARGE M. Wavelet transforms and their applications to turbulence[J]. Annual Review of Fluid Mechanics, 1992, 24(1): 395-458. DOI:10.1146/annurev.fl.24.010192.002143 |
| [17] |
HUANG Y X, SCHMITT F G, LU Z M, et al. An amplitude-frequency study of turbulent scaling intermittency using Empirical Mode Decomposition and Hilbert Spectral Analysis[J]. EPL (Europhysics Letters), 2008, 84(4): 40010. DOI:10.1209/0295-5075/84/40010 |
| [18] |
YANG S Q, JIANG N. Tomographic TR-PIV measurement of coherent structure spatial topology utilizing an improved quadrant splitting method[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(10): 1863-1872. DOI:10.1007/s11433-012-4887-2 |
| [19] |
WU Y, CHRISTENSEN K T. Spatial structure of a turbulent boundary layer with irregular surface roughness[J]. Journal of Fluid Mechanics, 2010, 655: 380-418. DOI:10.1017/s0022112010000960 |
| [20] |
BERKOOZ G, HOLMES P, LUMLEY J L. The proper orthogonal decomposition in the analysis of turbulent flows[J]. Annual Review of Fluid Mechanics, 1993, 25(1): 539-575. DOI:10.1146/annurev.fl.25.010193.002543 |
| [21] |
WANG W K, PAN C, WANG J J. Quasi-bivariate variational mode decomposition as a tool of scale analysis in wall-bounded turbulence[J]. Experiments in Fluids, 2017, 59(1): 1-18. DOI:10.1007/s00348-017-2450-7 |
| [22] |
YIN Z Y, STÖHR M. Time-frequency localisation of intermittent dynamics in a bistable turbulent swirl flame[J]. Journal of Fluid Mechanics, 2020, 882: A30. DOI:10.1017/jfm.2019.762 |
| [23] |
WU Y H. A study of energetic large-scale structures in turbulent boundary layer[J]. Physics of Fluids, 2014, 26(4): 045113. DOI:10.1063/1.4873199 |
| [24] |
KORDA M, MEZIĆ I. On convergence of extended dynamic mode decomposition to the Koopman operator[J]. Journal of Nonlinear Science, 2018, 28(2): 687-710. DOI:10.1007/s00332-017-9423-0 |
| [25] |
舒玮, 姜楠. 湍流中涡的尺度分析[J]. 空气动力学学报, 2000, 18(S1): 89-95. SHU W, JIANG N. Eddy scale analysis in turbulence[J]. Acta Aerodynamica Sinica, 2000, 18(S1): 89-95. (in Chinese) |
| [26] |
李栎, 许春晓, 崔桂香, 等. 壁湍流结构的二维子波分析[J]. 力学学报, 2001, 33(4): 433-441. LI L, XU C X, CUI G X, et al. 2-D wavelet analysis of structures in wall turbulence[J]. Acta Mechanica Sinica, 2001, 33(4): 433-441. DOI:10.3321/j.issn:0459-1879.2001.04.001 (in Chinese) |
| [27] |
陈子赟, 孙鉴泞, 袁仁民, 等. 对流槽湍流涡旋结构特征的小波分析[J]. 地球物理学报, 2004, 47(6): 964-970. CHEN Z Y, SUN J N, YUAN R M, et al. An analysis of convective boundary layer eddy structure in water tank by orthonormal wavelet[J]. Chinese Journal of Geophysics, 2004, 47(6): 964-970. DOI:10.3321/j.issn:0001-5733.2004.06.005 (in Chinese) |
| [28] |
SPALDING D B. A single formula for the "law of the wall"[J]. Journal of Applied Mechanics, 1961, 28(3): 455-458. DOI:10.1115/1.3641728 |
| [29] |
SCHLATTER P, ÖRLÜ R. Assessment of direct numerical simulation data of turbulent boundary layers[J]. Journal of Fluid Mechanics, 2010, 659: 116-126. DOI:10.1017/s0022112010003113 |
| [30] |
MARUSIC I, MCKEON B J, MONKEWITZ P A, et al. Wall-bounded turbulent flows at high Reynolds numbers: Recent advances and key issues[J]. Physics of Fluids, 2010, 22(6): 065103. DOI:10.1063/1.3453711 |
 2022, Vol. 40
2022, Vol. 40


