2. 中国空气动力研究与发展中心 空气动力学国家重点实验室,绵阳 621000;
3. 天津市现代工程力学重点实验室,天津 300354
2. State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center, Mianyang 621000, China;
3. Tianjin Key Laboratory of Modern Engineering Mechanics, Tianjin 300354, China
流动分离往往会带来阻力增大和剧烈的风噪。Ga-el Hak(2000)和Willians(2009)归纳和总结了各种主动和被动流动控制方法的发展历程,指出,主动控制方法利用激励器输出的小扰动和流动的不稳定性可达到“四两拨千斤”的效果,缺点是需要携带大质量的供能设备,被动流动控制方法虽然不需要能量输入,但所获得的扰动信号的传播路径较为单一。如果采用类似于羽毛的柔性锯齿形设计旋涡发生器,则可以利用湍流的非定常性自适应地控制流动分离。
仿生学是一座巨大的宝藏,其中蕴藏着数不胜数的“黑科技”。大自然中的动植物经过日积月累的进化,会以巧妙的生物构造适应于自然界的“物理法则”。猫头鹰作为一种“寂静”的猎手,它们的飞行高效且低噪声。Gruschka最早在1971年分析了猫头鹰的生理构造与其“无声飞行”的本领。Hans[1]在2012年详细研究了猫头鹰的翅膀骨架和羽毛的独特构造,分析了它们的飞行模式。Klan[2]在2012年模仿猫头鹰翅膀的横截面设计了一款翼型,其表面柔性绒毛结构具有优秀的扰流效果。Thomas[3]在2015年通过实验研究了仓枭的翅膀结构及其扑翼飞行原理。Li[4]在2017年通过仿真比较了两种长耳猫头鹰翅膀模型的控制分离和降噪效果。
猫头鹰柔软的锯齿形覆羽会在大攻角下向上抬起,同时自适应地通过变形调整扰动传播的方向、振幅和频率,有效地控制流动分离。Markus(2004)[5]设计了一种刚性的“自激励的运动襟翼”可以在大攻角下获得10%的增升效果,Gotz(2002)[6]在S824翼型上研究了自激励扰流板优良的分离控制效果。Jorg(2010)[7]模仿海鸥设计了一种在大攻角下发生运动的铰接襟翼,将其安装于各种翼型进行实验,研究了其控制流动分离的效果,Wang(2012)[8]通过有限翼模型内置的力传感器研究了不同长度自激励襟翼在不同位置处的增升减阻效果。Marco(2017)[9]通过仿真得到了“自适应可动平板”产生扰流涡的流向结构,这些扰流涡传播到尾流区诱导了剪切层面积的缩小。
从猫头鹰的“无声飞行”能力中得到启发,各种用于减小噪声的仿生学扰流器被设计出来,其所具有的优良降噪能力被仿真、实验结果所证实。Justin(2013)[10]研究了多孔材料的降噪效果。Jones(2012)[11]、Huang(2017)[12]通过建模仿真证明了锯齿形具有优秀的降噪效果,许影博(2012)[13]通过风洞实验验证了锯齿形安装在尾缘时可以有效地降低噪声。Avallone(2016)[14]通过层析PIV实验研究了锯齿形尾缘的降噪原理,得到了锯齿形产生的扰动涡的空间结构。乔渭阳(2018)[15]对气动噪声控制的仿生学方法进行了总结和展望。
本文从猫头鹰的覆羽结构得到启发,设计出了一种新型的柔性可变形的锯齿形旋涡发生器,以铰接的方式安装在机翼不同弦长位置处(90%、50%等),进行风洞实验。通过热线风速仪单点扫掠的方法得到尾流区流场的湍动能分布特征,通过小波变换的方法在时域、频域同时分析流场中各尺度分离涡的破碎和掺混过程,然后通过双通道热线同时测量,得到不同空间点的同步流场信号,通过互相关函数得到欧拉速度场中不同空间点涡包结构之间在时域和频域上的相互作用效果,结合不同柔性材料的变形和振动差异,分析其控制流动分离和降噪的效果和原理。
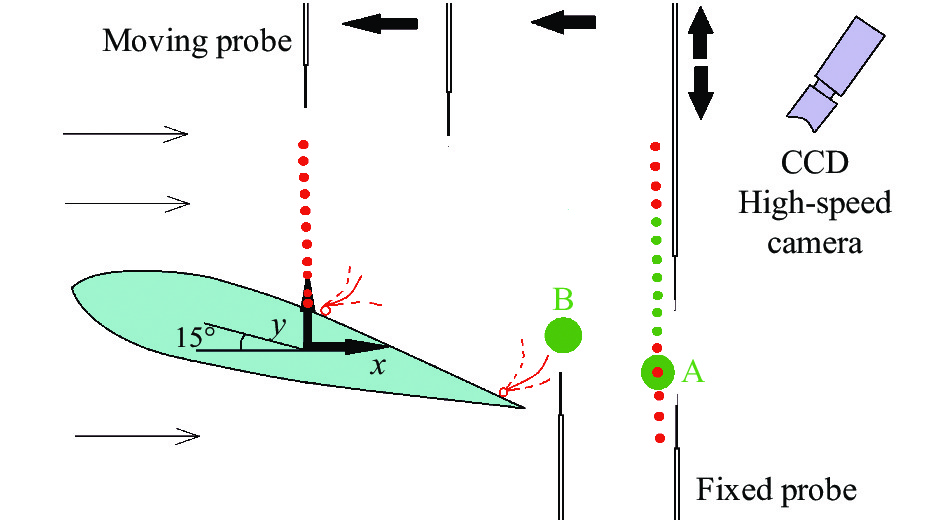
1 实验设备实验在天津大学直流式风洞中进行,实验段尺寸为600 mm(长)×250 mm(宽)×250 mm(高),来流速度u∞ = 15.2 m/s,湍流度I0 = 1%。采用NACA0018二维翼型,弦长c = 0.1 m,雷诺数Re = 1×105。通过示踪粒子的流动显示结合翼型表面测压数据,得到攻角α = 15°下翼型前缘发生流动分离,利用IFA300热线风速仪,以5000 Hz的频率采样52 s,得到高分辨率并收敛的湍流脉动信号,所使用的探头为TSI-1210-T1.5型单丝热线探头,热线为直径5 μm的钨丝,过热比为1.5。建立如图1所示的平面直角坐标系,坐标原点(x/c, y/c) = (0,0)对应着二维翼型50%弦长处的中心位置。在进行单通道测量时,在x/c = 0处移动探针从近壁点开始以5 mm的步长扫掠11个红色测点;在x/c = 0.75的尾流区以5 mm的步长扫掠16个红色测点;在进行双探针同时测量时,固定探针放置于A点或B点分别作为尾缘剪切层湍动能峰值位置及扰动源的参考点,移动探针同步在x/c = 0.75剖面以步长5 mm扫掠前缘剪切层的7个绿色测点。通过内置CCD芯片的高速相机以800 Hz的频率拍摄柔性锯齿的振动图像,该频率足够捕捉不同柔性材料随来流自适应振动的幅度、频率和柔性变形,通过分析旋涡发生器的柔性形变规律结合热线结果分析扰动的传播和作用原理。
|
图 1 实验装置示意图 Fig.1 Schematic diagram of experimental setup |
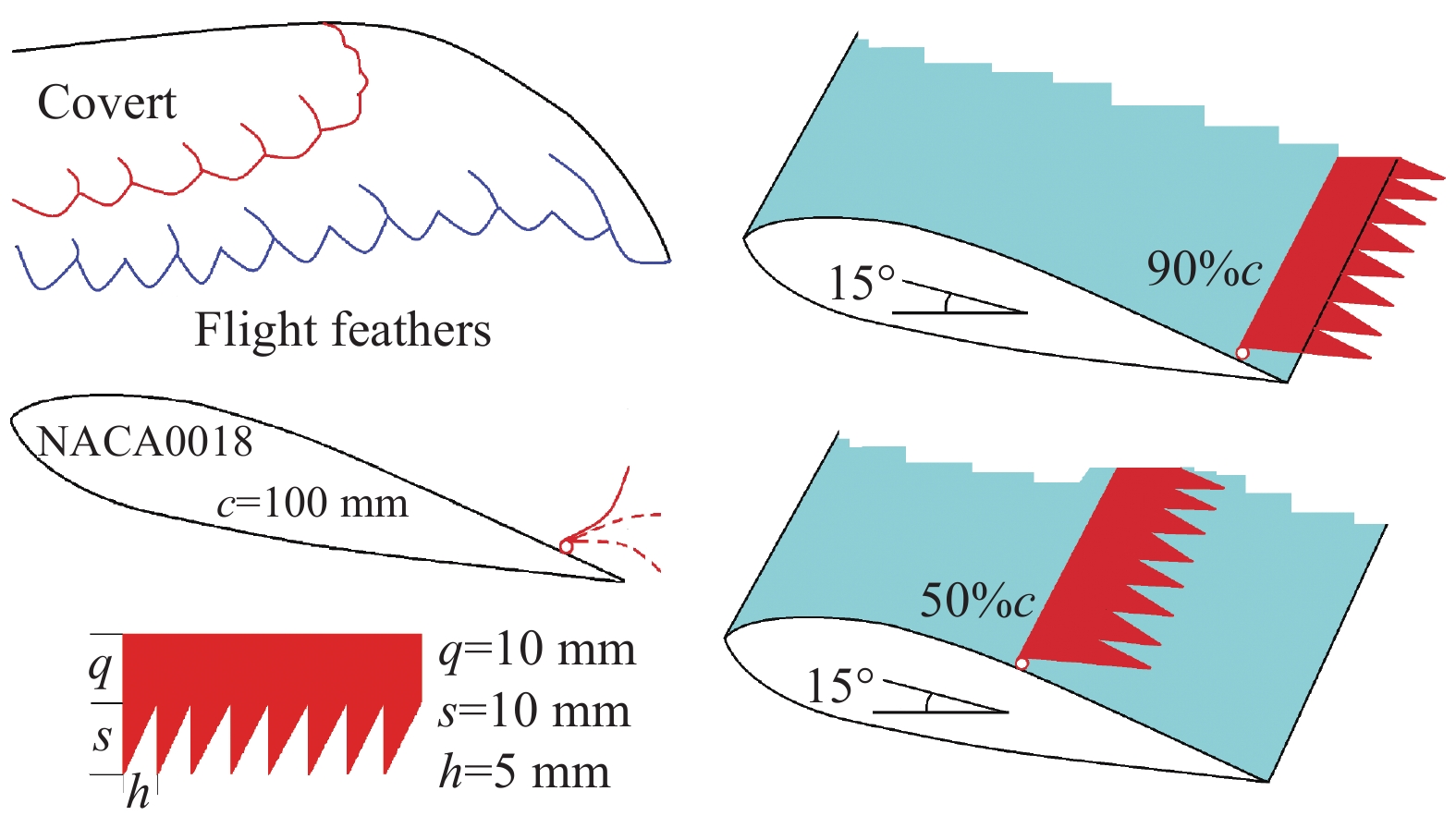
铰接式柔性锯齿的灵感来源于猫头鹰的翅膀构造,如图2所示,翅膀上红色的锯齿状羽毛为覆羽[3],其质地非常柔软,在大攻角飞行的时候就会随来流自适应地向上掀起发生颤振,同时羽毛呈锯齿形会产生柔性形变,这一独特的翅膀构造使得猫头鹰单次振翅滑行的距离非常远,且在飞行过程中几乎不发出噪声。图2中q部分为覆羽根部重叠的区域,s部分为覆羽的齿形尖端,铰接的连接方式使得整排“羽毛”可以向上抬起。在非定常湍流的激励下,铰接结构通过自适应地颤振产生一定频率的扰流涡控制流动分离[5, 16],同时柔性材料随流动产生形变,改变旋涡尺度并扩大扰动范围,锯齿形的结构进一步破碎和掺混湍涡实现降噪的功能[17-18]。
郑小波(2021)[19]在实验中发现以不同频率振动的翼型会产生不同尺度结构、不同脱落频率的旋涡传递到尾流区。本文的柔性旋涡发生器可以看作一系列可以自适应振动的微型机翼,在非定常来流的激励下,利用其产生的一定频率带宽的扰动达到控制流动分离的目的。锯齿形参数q、s会影响噪声的强度和分布[17-18]。我们在前期的实验工作中[20]对比了大齿、小齿和无齿柔性旋涡发生器的扰流效果,得到了相近雷诺数下扰流效果较好的小齿形参数,如图2所示。
|
图 2 柔性锯齿自适应振动的仿生学原理 Fig.2 Bionic principle of adaptive vibration of flexible sawteeth |
猫头鹰的覆羽沿翅尖方向越来越靠近于翅膀前缘,所以本实验将柔性锯齿的铰接位置从90%c处逐渐向前缘移动到50%c处,分析旋涡发生器在不同弦长位置处对分离的控制效果。
在旋涡发生器自适应变形颤振的过程中,材料过于柔软会导致扰流效率的降低,过于厚重则可能会产生特定频率的噪声。本文通过面密度σ(即单位面积的质量,单位:g/cm2)和厚度d(单位:mm)来分类不同的柔性材料,式(1)中ρ(单位:g/cm3)为体密度:
| $ \sigma =\rho d/10 $ | (1) |
图3为高速相机拍摄的柔性尾缘在实验中的振动图像。可以发现,面密度和厚度较大的柔性材料的颤振行程越短,齿尖的形变范围较小,回弹恢复较快,各相位姿态之间的过渡较为连续;面密度较低、厚度较小的材料,铰接振动的幅度较大,齿尖大部分时间处于向上或向下翻折的大形变状态,难以维持某个伸直的相位姿态。这种形变状态与柔性薄膜[21]的风洞实验结论相吻合。

|
图 3 CCD高速相机拍摄的实验图像 Fig.3 Experimental images captured by high-speed CCD camera |
通过对多种柔性锯齿进行高速拍摄和热线测量,最终选取了表1所示的最具代表性的低、中、高三种面密度的柔性材料(后文中的密度均指面密度)。它们的面密度和厚度均大约相差一个量级:高密度(High Density,HD)柔性材料在颤振过程中形变较小;中等密度(Medium Density,MD)柔性材料的振动和变形较为适中;低密度(Low Density,LD)柔性材料形变较大并呈现翻折状态。
| 表 1 三种柔性材料的面密度和厚度 Table 1 Areal density and thickness of three flexible materials |
|
|
对比不同母函数的小波能谱图可以发现,对于Re = 1×105的分离区剪切湍流数据,采样频率fs = 5000 Hz,能够还原的信号最高频率为2500 Hz(Nyquist,1924),足够分析其中的各尺度结构。选取‘db4’作为母函数的连续和正交小波变换都具有较好的鲁棒性,且在时域、频域同时分解和重构脉动速度时具有足够的分辨率。
| $ {W}_{ab}\left(t\right)=\frac{1}{\sqrt{a}}W\left(\frac{t-b}{a}\right) $ | (2) |
| $ {W}_{u'}\left(a,b\right)={\int }_{-\infty }^{+\infty }u'\left(t\right){W}_{ab}\left(t\right){\rm{d}}t $ | (3) |
式中,W为子波母函数,Wab为对应时间和频率的窗函数,同时从时间b和频率a尺度分解和重构脉动速度
| $ u(t)=\bar{u}+{u}'(t)=\bar{u}(t)+\sum\limits_{a}{W}_{u'}\left(a,b\right) $ | (4) |
式中,每个测点的速度可以分解为平均速度
分尺度小波能量E(a)和脉动速度能量之间的关系如下,式(7)为小波变换的反演条件。
| $ E\left(a\right)=\frac{2}{{C}_{w}}{\int }_{-\infty }^{+\infty }{\left|{W}_{u'}\left(a,b\right)\right|}^{2}{\rm{d}}b $ | (5) |
| $ {\int }_{-\infty }^{+\infty }{\left|u'\left(t\right)\right|}^{2}dt={\int }_{0}^{+\infty }\frac{E\left(a\right)}{{a}^{2}}{\rm{d}}a $ | (6) |
| $ {C}_{w}={\int }_{-\infty }^{+\infty }\frac{{\left|{W}'\left(f\right)\right|}^{2}}{\left|f\right|}{\rm{d}}f < \infty $ | (7) |
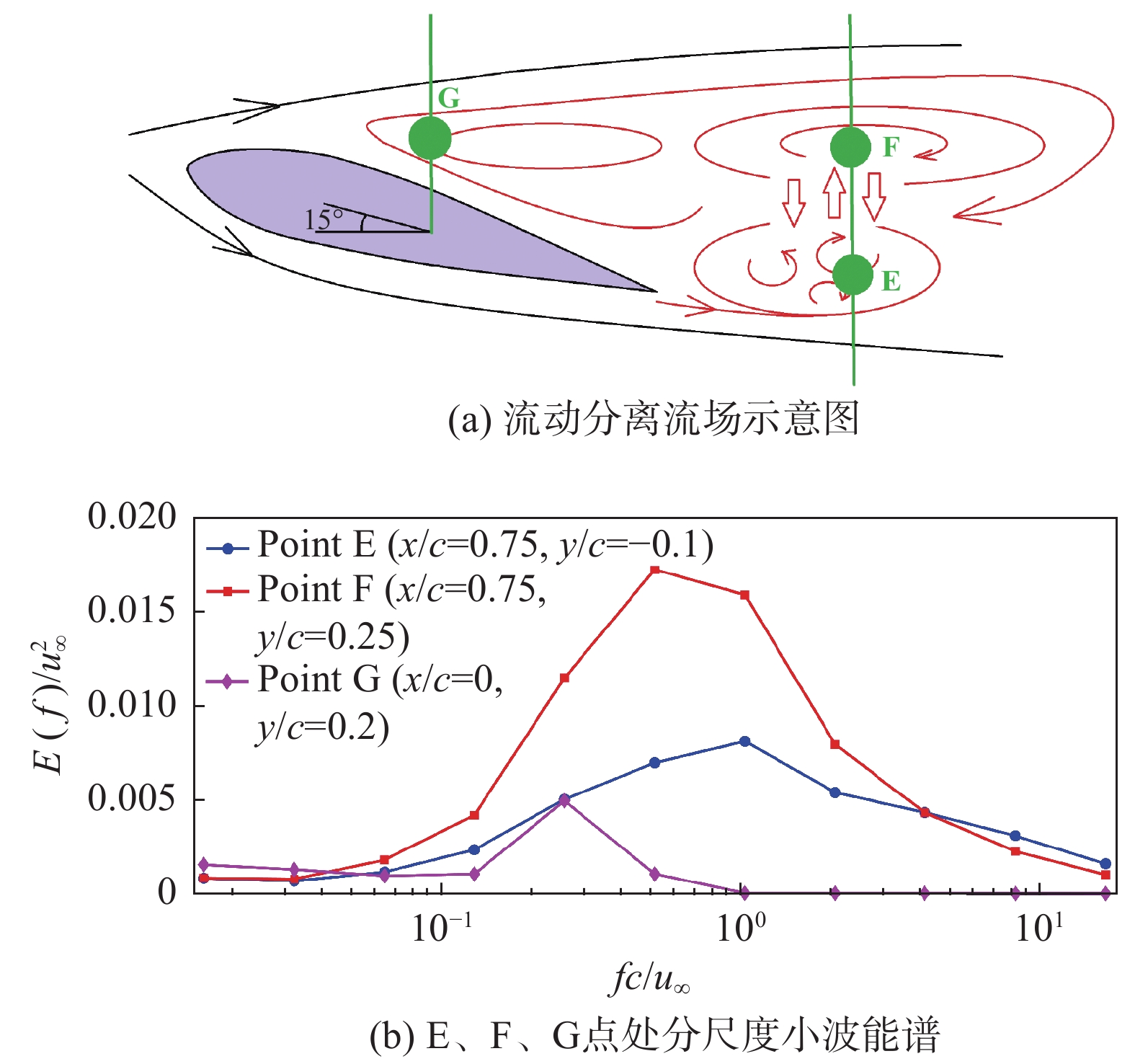
图4(a)中点E(0.75, −0.1)、F(0.75, 0.25)分别为尾流区x/c = 0.75处的尾缘和前缘剪切层的湍动能峰值点,点G(0, 0.2)为上游x/c = 0处的湍动能峰值点。图4(b)采用正交小波变换Mallat(1988)方法以指数率调整小波窗口函数的长度用于划分频率尺度,可以减少计算量,削弱脉动数据相对于窗函数两端的冗余量。
| $ {A}_{0}\left(b\right)=u'(t) $ | (8) |
| $ {A}_{j}\left(b\right)=\sum\limits_{t}H(2b-t){A}_{j-1}(b) $ | (9) |
| $ {D}_{j}\left(b\right)=\sum\limits_{t}L(2b-t){A}_{j-1}(b) $ | (10) |
式中H和L分别为对应于W的低通和带通分解滤波器,每次仅对低频部分继续划分尺度得到低频子波系数Aj和高频子波系数Dj,接下来划分合适的参数a来衡量剪切层中的脱落涡尺度。
|
图 4 分离泡的脱落涡尺度分布 Fig.4 Scale distribution of the separation bubble |
图4(b)三条曲线分别表示4(a)中E、F、G三个测点处的各频率尺度的小波能量分布。根据最大能量法则[22],上游点G的分离涡尺度较大fc/u∞ = 0.26,由于还未充分发展所以湍动能相较于点E、F较低。点F峰值处fc/u∞ = 0.5,点E则多为高频小尺度结构fc/u∞ = 1,说明上游的大尺度旋涡从上翼面发展至尾流区后,与尾缘卷起的小尺度旋涡相互扰动,形成尺度适中的分离涡,其湍动能主要集中在前缘剪切层点F,这与相近雷诺数的翼型实验[23-24]和仿真[25]结果相吻合。三条曲线最高能量激发态对应的峰值频率各自相差一个尺度,说明划分的11个频率尺度足够表现出旋涡脱落的尺度变化情况。
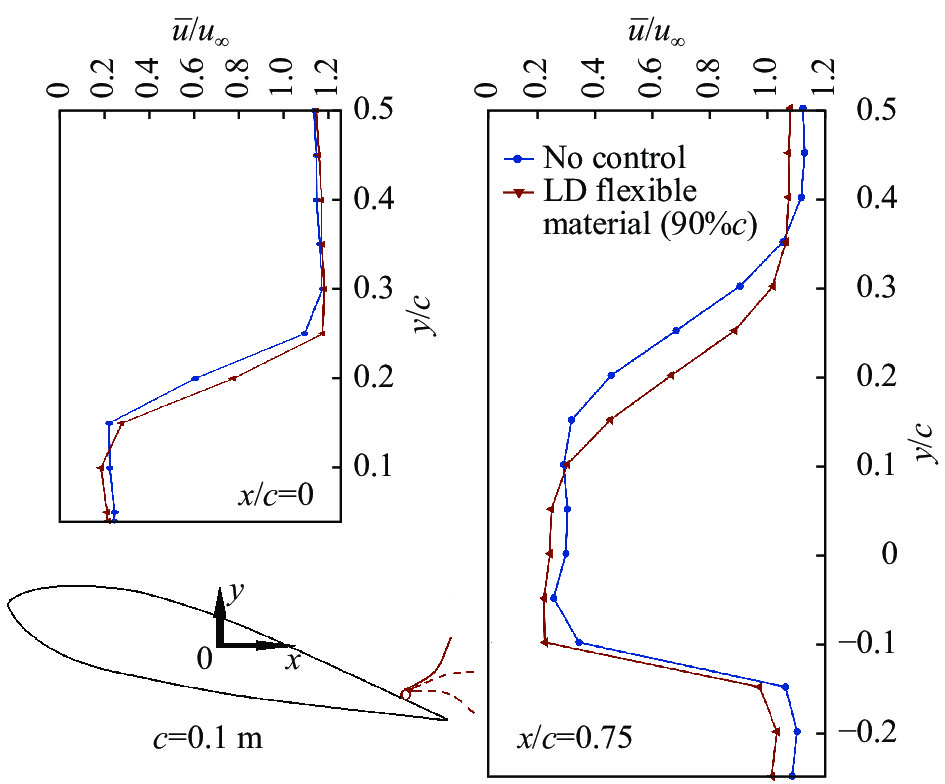
3.2 柔性锯齿的控制分离效果图5表示在加装低密度(LD)尾缘前后上游x/c = 0和尾流x/c = 0.75处的平均速度曲线,x/c = 0.75处的剪切层上边界下移了0.05c,随着绝对不稳定性扰动的传播,上游x/c = 0处的边界也略有下降。
|
图 5 尾缘加装控制前后x/c = 0、0.75处的平均速度剖面 Fig.5 Average velocity profiles at x/c = 0, 0.75 compared before and after the control |
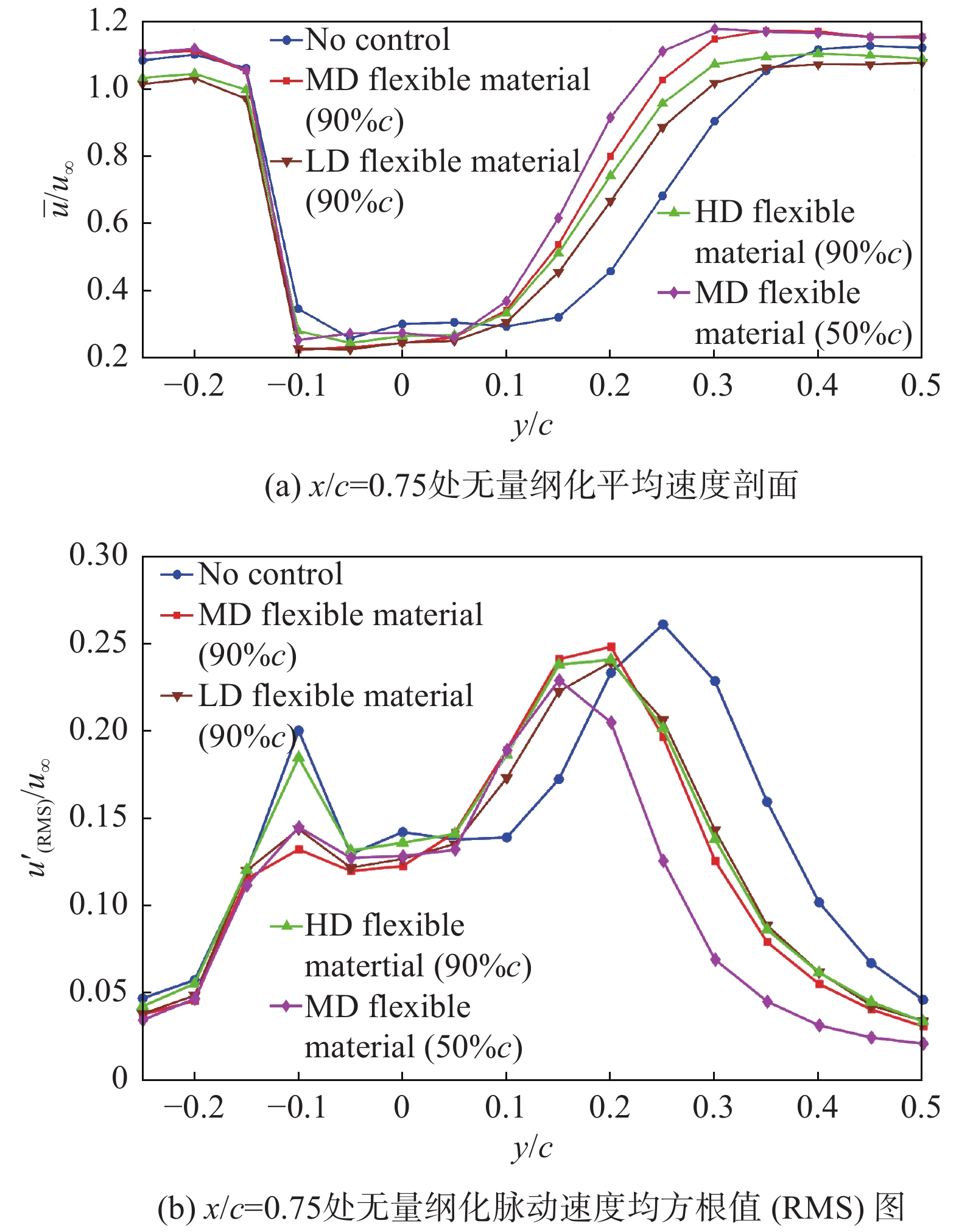
图6为尾流x/c = 0.75处平均速度和脉动速度均方根值(湍动能)的分布。通过图6(b)可以发现在尾缘90%c加装控制时,中等密度(MD)柔性材料的效果最好,分离区上边界下移超过了0.05c,尾缘和前缘剪切层的湍动能峰值下降了34%和5%;将其安装位置移动到50%c处时,上边界下移接近0.1c,尾缘和前缘剪切层的湍动能峰值下降了27.6%和12.2%,这与自适应平板控制流动分离的仿真结果[9]相似。各工况中高密度(HD)柔性材料对尾缘剪切层湍动能峰值的削弱效果较差。
|
图 6 尾流区平均速度和湍动能分布 Fig.6 Average velocity and turbulent kinetic energy distributions in the wake region |
表2为不同工况下前缘剪切层的平坦因子峰值。随着旋涡发生器向前缘移动,平坦因子提高率从5%变为22%,即前缘剪切层中的湍流-非湍流比例(间歇性)得到提高。说明相较于90%c的安装位置,柔性锯齿在50%c处产生的不稳定性扰动湍流更多地影响到了前缘剪切层,所以图6(b)的粉色曲线相较于红色曲线的湍动能峰值降低率在尾缘剪切层较为逊色,而在前缘剪切层较为优异。
| 表 2 前缘剪切层的平坦因子峰值变化情况 Table 2 Peak value of the flatness factor in theleading-edge shear layer |
|
|
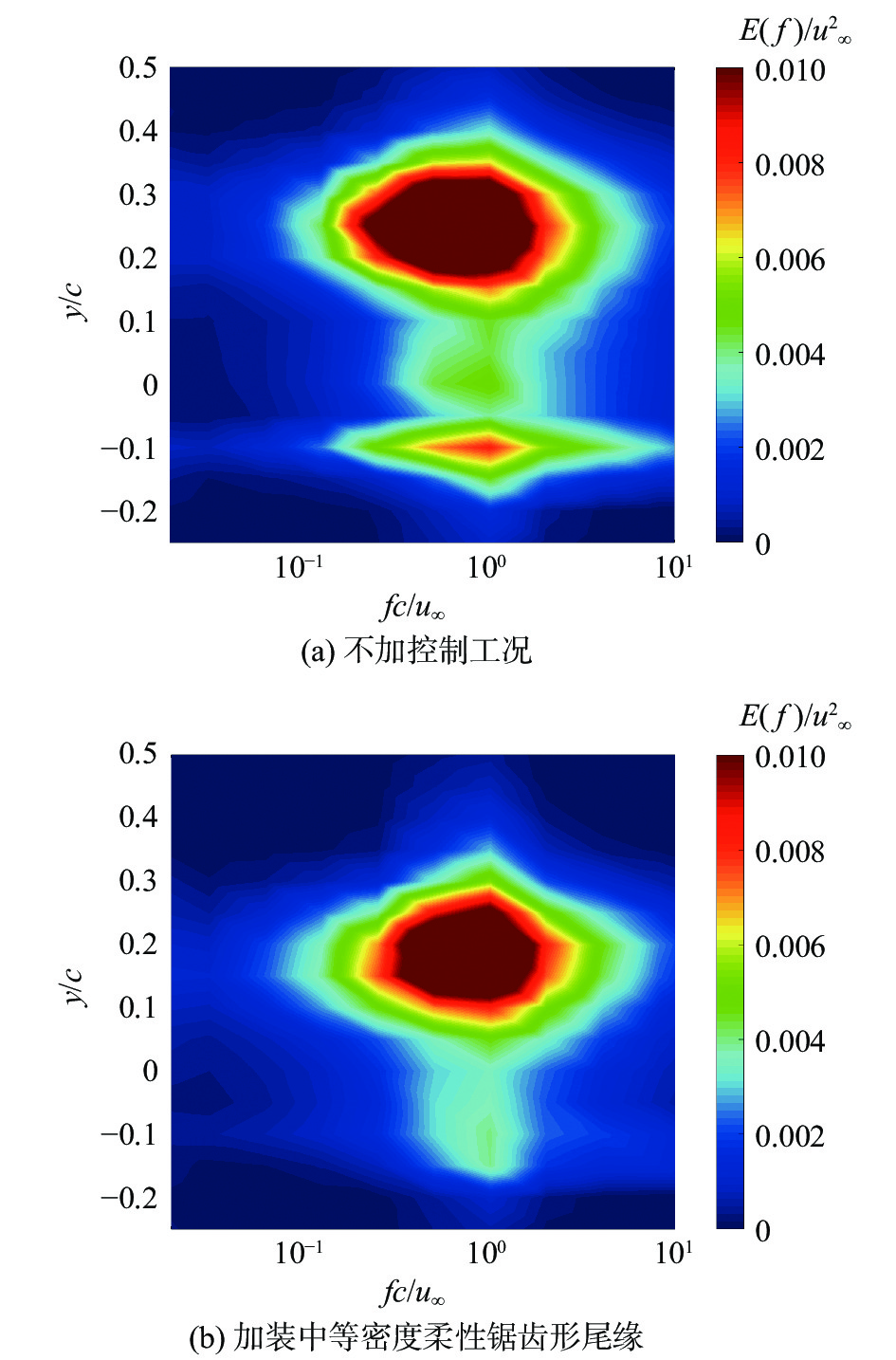
图7表示不同空间位置和频率尺度的小波能量云图,可以发现,加装中等密度尾缘后,尾缘剪切层的红色区域消失,前缘剪切层的深红色区域向高频收缩变窄的同时向下移动,说明分离区边界下移,旋涡的频率带宽变窄,部分低频大涡得到消除,这与之前的柔性尾缘实验结果相似[20, 26]。
|
图 7 小波能谱的空间和尺度分布 Fig.7 Spatial and scale distribution of wavelet energy spectrum |
| $\begin{split}& \left(\frac{1}{{c}^{2}}\frac{{\partial }^{2}}{\partial {t}^{2}}-\frac{{\partial }^{2}}{\partial {{x}_{i}}^{2}}\right){p}'\left(x,t\right)=\frac{\partial }{\partial t}\left[({\rho }_{0}{v}_{n})\delta (\psi )\right]\\&\qquad-\frac{\partial }{\partial {x}_{i}}\left[{l}_{i}\delta (\psi )\right]+\frac{{\partial }^{2}}{\partial {x}_{i}{x}_{j}}\left[{T}_{ij}H(\psi )\right] \end{split}$ | (11) |
式中:c表示声速,
FW-H(1969)声比拟公式中控制体外观测点(x, t)的声压
|
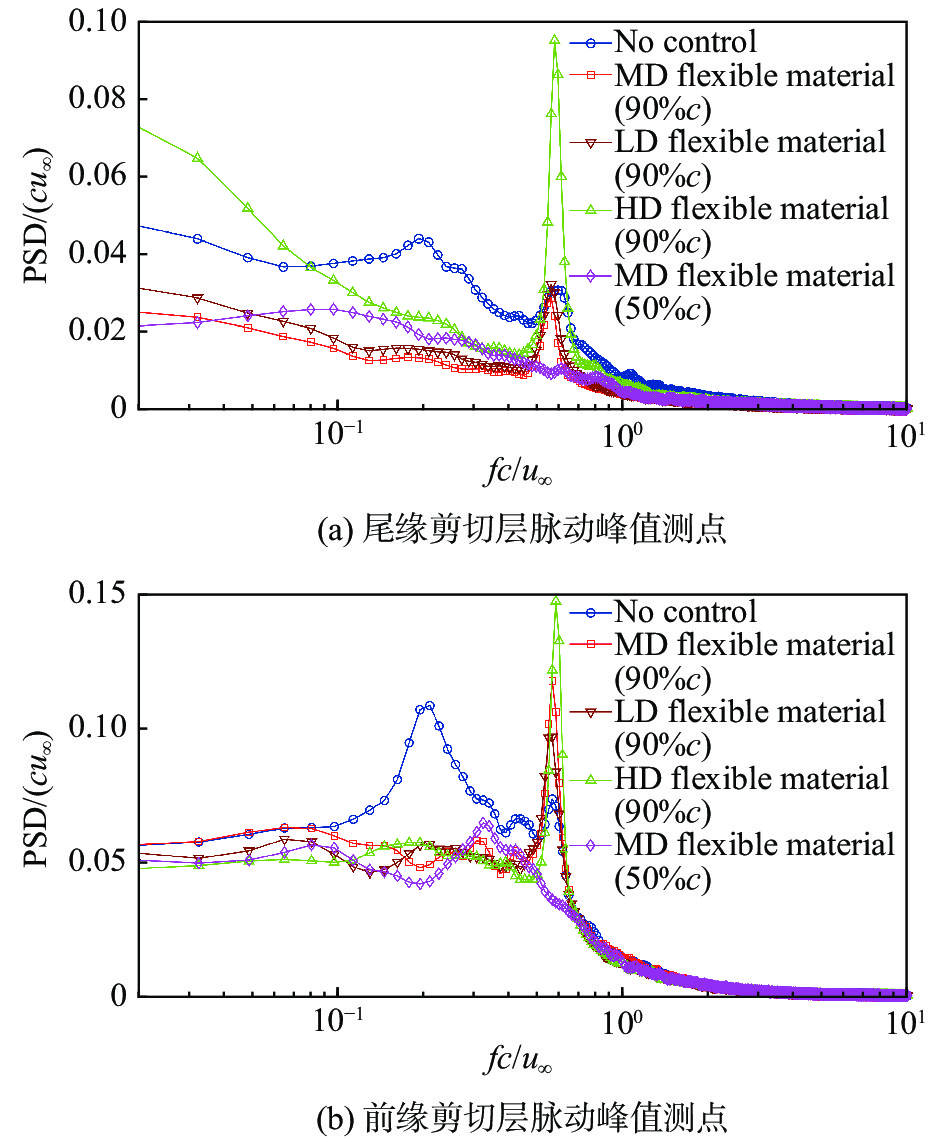
图 8 无量纲化功率谱密度(PSD)图 Fig.8 Dimensionless power spectral density (PSD) |
图8(a)、(b)中蓝色曲线低频fc/u∞ = 0.2处的峰值都消失了。当锯齿形安装在90%c时,高密度材料在尾缘剪切层会产生高强度的高频fc/u∞ = 0.6和低频fc/u∞ = 0.02的峰值,低密度和中等密度材料产生的高频扰动强度较低,且对低频段PSD峰值的削弱非常明显,中等密度锯齿在尾缘和前缘剪切层分别达到了70%和50%。将中等密度锯齿移到50%c时,受到x/c = 0(50%c)处大尺度分离涡的激励,其产生的扰动传递到下游分别在尾缘和前缘剪切层会提高fc/u∞ = 0.1和0.3附近的低频PSD,带宽较宽,强度较低,消除了fc/u∞ = 0.6的高频峰值,产生了强度相对较低的低频脉动。锯齿形在流动分离发生的条件下可以有效地控制不稳定的噪声源,类似的结论在刚性锯齿形尾缘的降噪实验[17-18]中也被证实。
在前缘剪切层,图8(b)中安装在90%c位置时,三种柔性材料都在前缘剪切层存在高频峰值,说明原本分离涡的低频段信号转移到了高频,其对应的旋涡尺度变化情况见3.3.1节。在尾缘剪切层,加装中等或低面密度旋涡发生器之后,各频率脉动信号均得到削减,详细的能量传递低频段和能量耗散高频段的分析见3.3.2节。
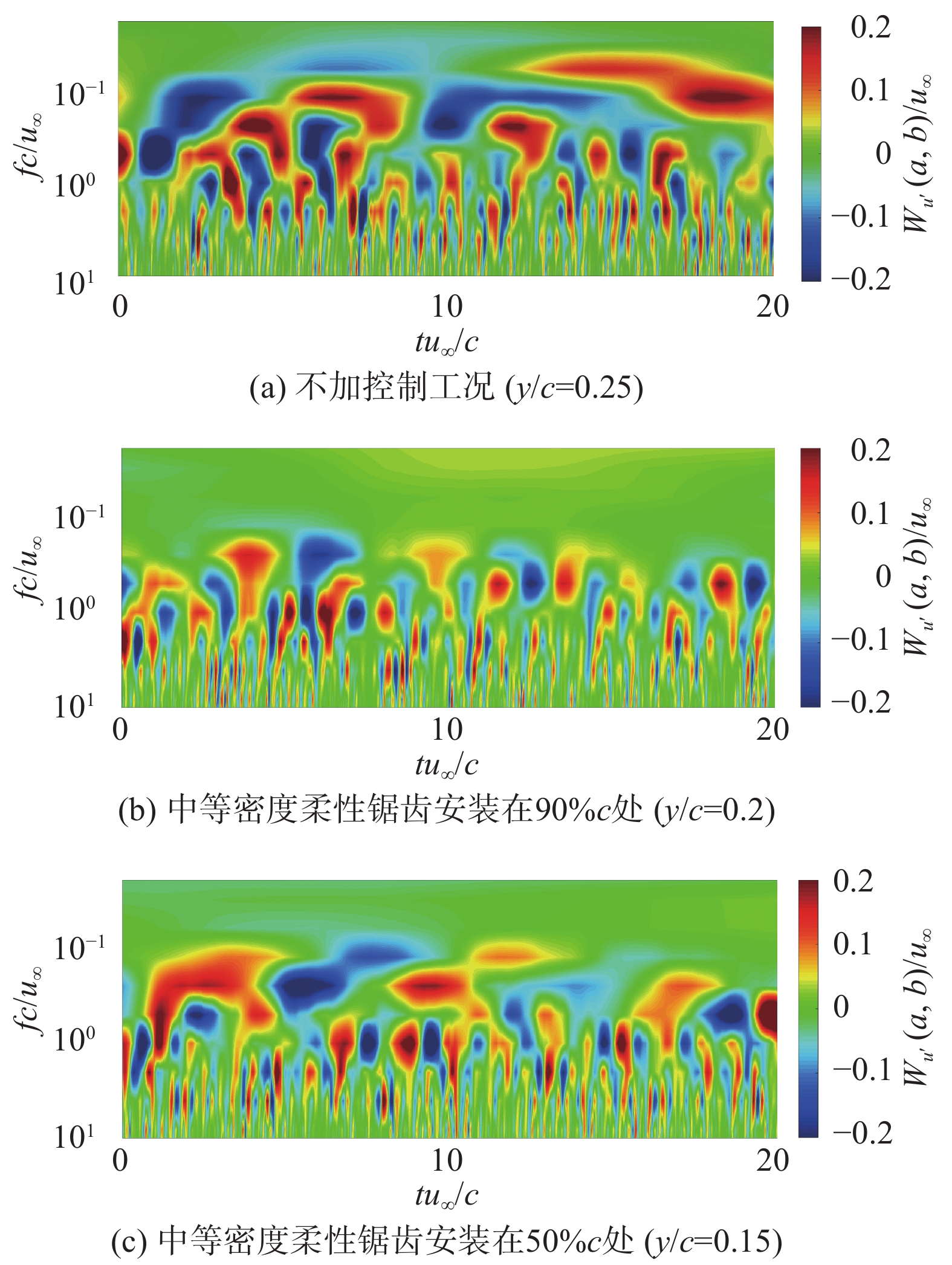
3.3.1 前缘剪切层的脱落涡尺度图9为前缘剪切层脉动峰值点的子波系数云图,在各个瞬时分析旋涡尺度的变化过程。图9(a)不加控制工况下大致可分为三级相互包含的“倒U”结构,这与相近雷诺数的实验结果[20]吻合,时间轴上从左至右表示小尺度湍涡掺混为大尺度涡包,最后再破碎为小尺度结构,其连接部分对应的尺度分别为fc/u∞ = 0.5、0.26、0.13,表示三种不同尺度旋涡组合成的大型涡包结构,云图中涡包结构紧密,动量交换剧烈。在90%c加装控制后图9(b)的涡包得到破碎,仅剩一级小尺度结构fc/u∞ = 0.26。在50%c处加装控制后,扰动传递到前缘剪切层同样也破碎了部分涡包结构,大致包含两级较低频的“倒U”结构fc/u∞ = 0.5、0.26。
|
图 9 前缘剪切层脉动峰值点无量纲化子波系数云图 Fig.9 Wavelet coefficient contour for the peak fluctuation point in the leading-edge shear layer |
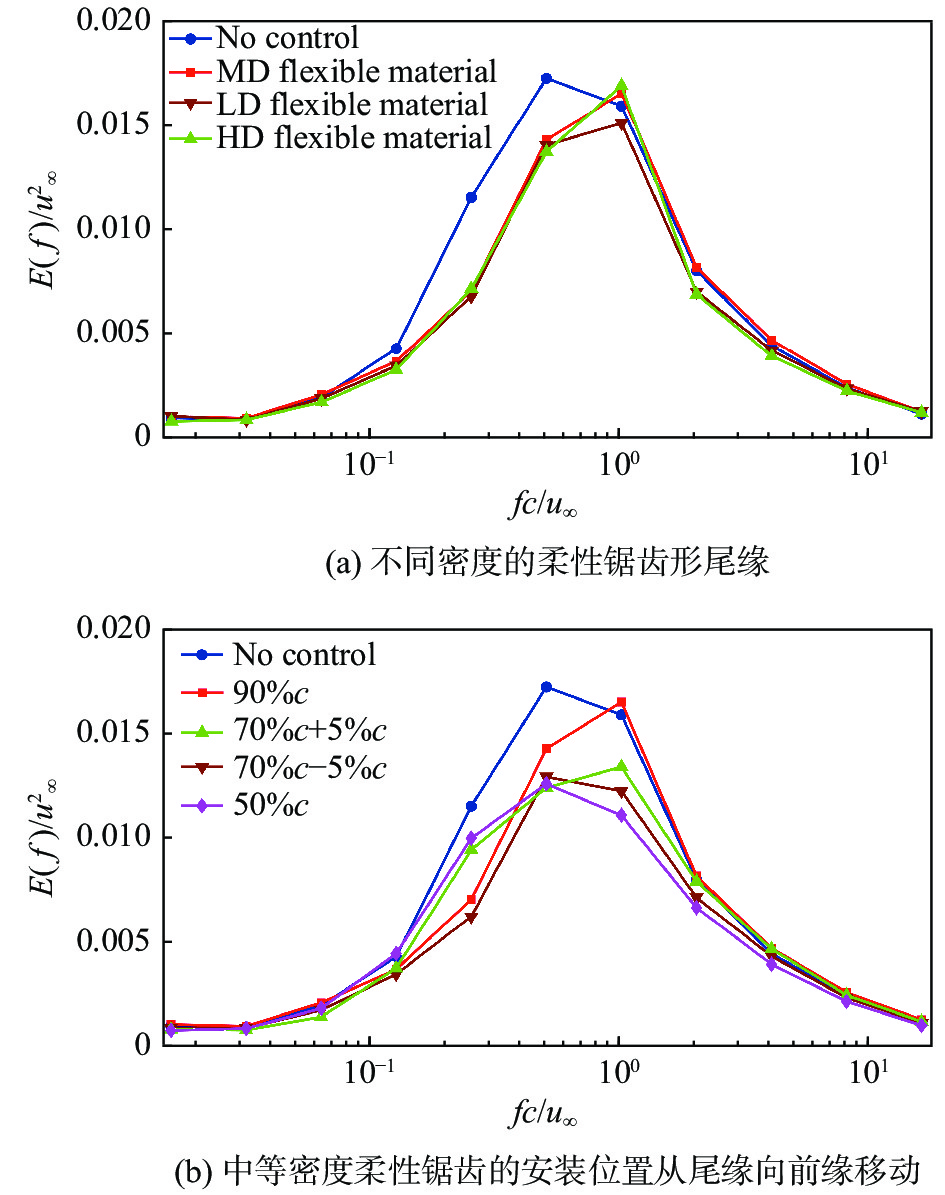
图10表示在时域上积分后的分尺度小波能谱,图10(a)中三种不同密度的柔性材料均可以将前缘剪切层的分离涡降低一个尺度,从fc/u∞ = 0.5变为1,说明柔性锯齿在90%c处产生的扰动传播到前缘剪切层可以起到破碎低频大尺度涡包的作用,具有消除低频气动噪声的潜力。
|
图 10 前缘剪切层脉动峰值点分尺度小波能谱 Fig.10 Wavelet energy spectrum for the peak fluctuation point in the leading-edge shear layer |
图10(b)为中等密度柔性锯齿从尾缘向前缘移动过程中的的小波能谱,玫红色曲线峰值降低了27%,含能尺度仍然为低频fc/u∞ = 0.5,说明安装在50%c处的锯齿吸收了点E处同尺度低频旋涡(图4)的能量,产生的扰流涡尺度较大。绿色和棕色曲线的峰值点分别降低了22%和25%,且尺度从fc/u∞ = 1变为0.5,发生了迁移,说明柔性锯齿从尾缘向前缘移动的过程中,在70%c左右前缘剪切层的分离涡发生明显的尺度变化,湍动能逐渐降低。
3.3.2 尾缘剪切层的能量级串现象能量级串[30]在复杂的剪切湍流中往往难以分析,因为翼型近场尾流区受壁面逆压梯度和自由剪切湍流共同影响,结构复杂,非定常性较强,间歇性差异较大,耗散率难以在时域上取得系综平均,所以各能谱的波数空间分布(标度率)难以确定。通过时域展开的方法可以分析各个瞬时的波数空间。
| $ k(t)=\frac{2{\text{π}} f}{u(t)} $ | (12) |
| $ \lambda (t)=\frac{2{\text{π}} }{k(t)}=\frac{u(t)}{f} $ | (13) |
| $ l(t)=\frac{1}{k(t)}=\frac{\lambda (t)}{2{\text{π}} } $ | (14) |
式中:k(t)表示瞬时波数,
预乘能谱
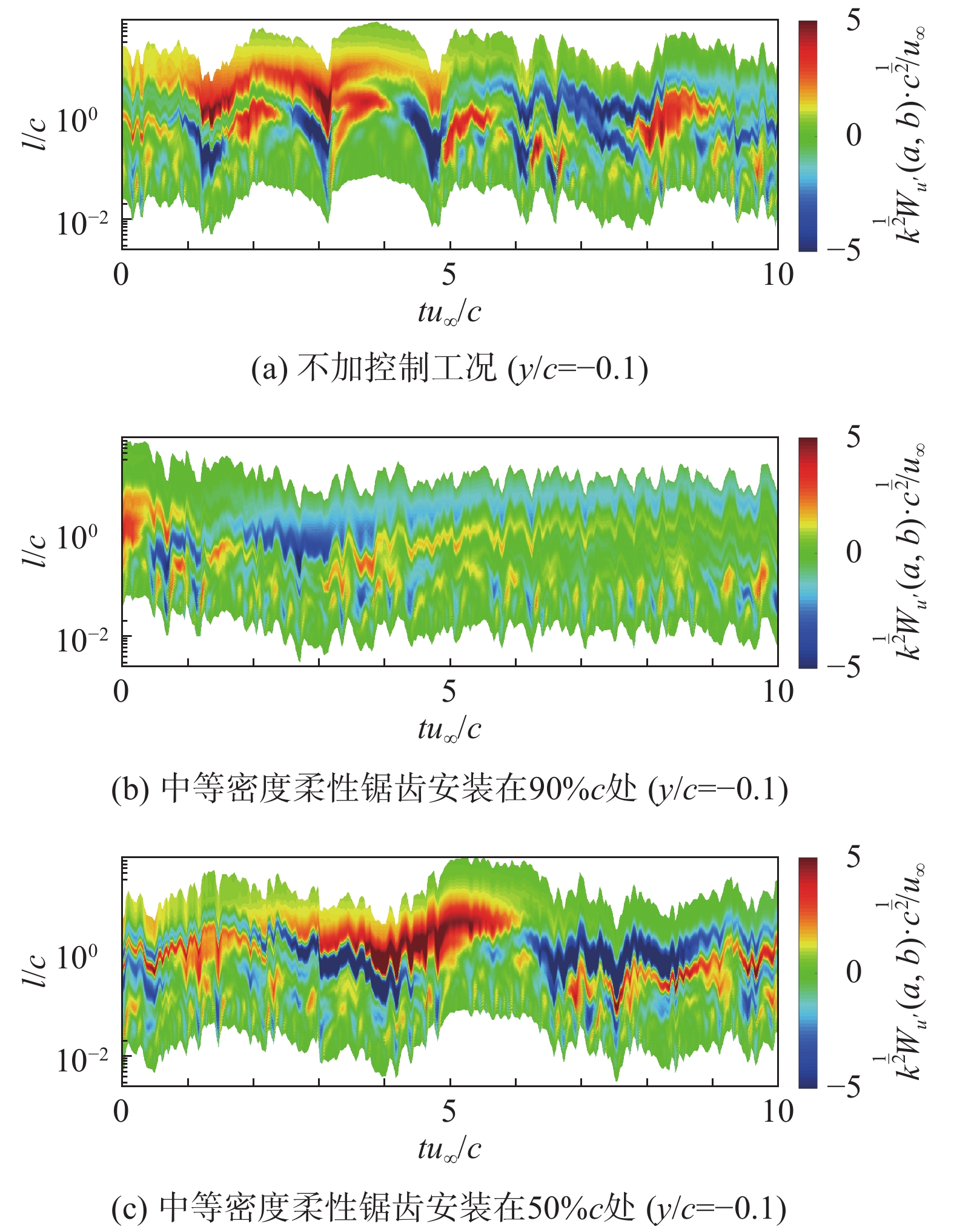
图11反映了尾缘剪切层的湍动能级串现象,能量由含能尺度[31]输入。在惯性影响下能量向小尺度传递并最终表现为各项同性状态在耗散区耗散消失,间接反映了载荷声源产生的低频偶极子噪声和湍动能输运并耗散导致的四极子噪声。
|
图 11 尾缘剪切层脉动峰值点预乘谱的时域展开 Fig.11 Expansion of pre-multiplied spectrum in time domain for the peak fluctuation point in the trailing-edge shear layer |
对比图11(a)-(c)三图,发现图(b)中从含能尺度输入的能量的强度很低,所以被柔性尾缘有效地吸收了。从能量级串的角度来看,不加控制时图11(a)的能量条带呈“V”字形,快速传递到耗散尺度,沿长度尺度的变化梯度非常大。图11(b)、图11(c)加装控制之后蓝红色带得到显著延长,原本的“V”字形被拆分成了多层长条带,能量从大尺度输入,再利用惯性转移到耗散尺度的过程层级增加,能量得以缓慢地逐级串级。从速度场的欧拉观点来看,瞬时的红色“V”字形结构代表沿流向的各长度尺度旋涡集合而成的涡包。在“V”字形两端时刻涡包集中表现为大尺度旋涡,在“V”字形尖端涡包破碎,能量迅速向小尺度湍涡注入。重叠的红蓝条带则表示在较长时间内,涡包都表现为沿流向大尺度结构和逆流向较小尺度结构(或逆流向大尺度结构和沿流向较小尺度结构)相互掺混的状态。无控工况下较大的红色“V”字形可能反映了某瞬时由于强烈脉动导致的气动噪声。加装控制后的红蓝条带在较长时间范围内包含着相反方向交错的多尺度结构,避免了瞬时的强烈脉动,具有降噪的潜力。
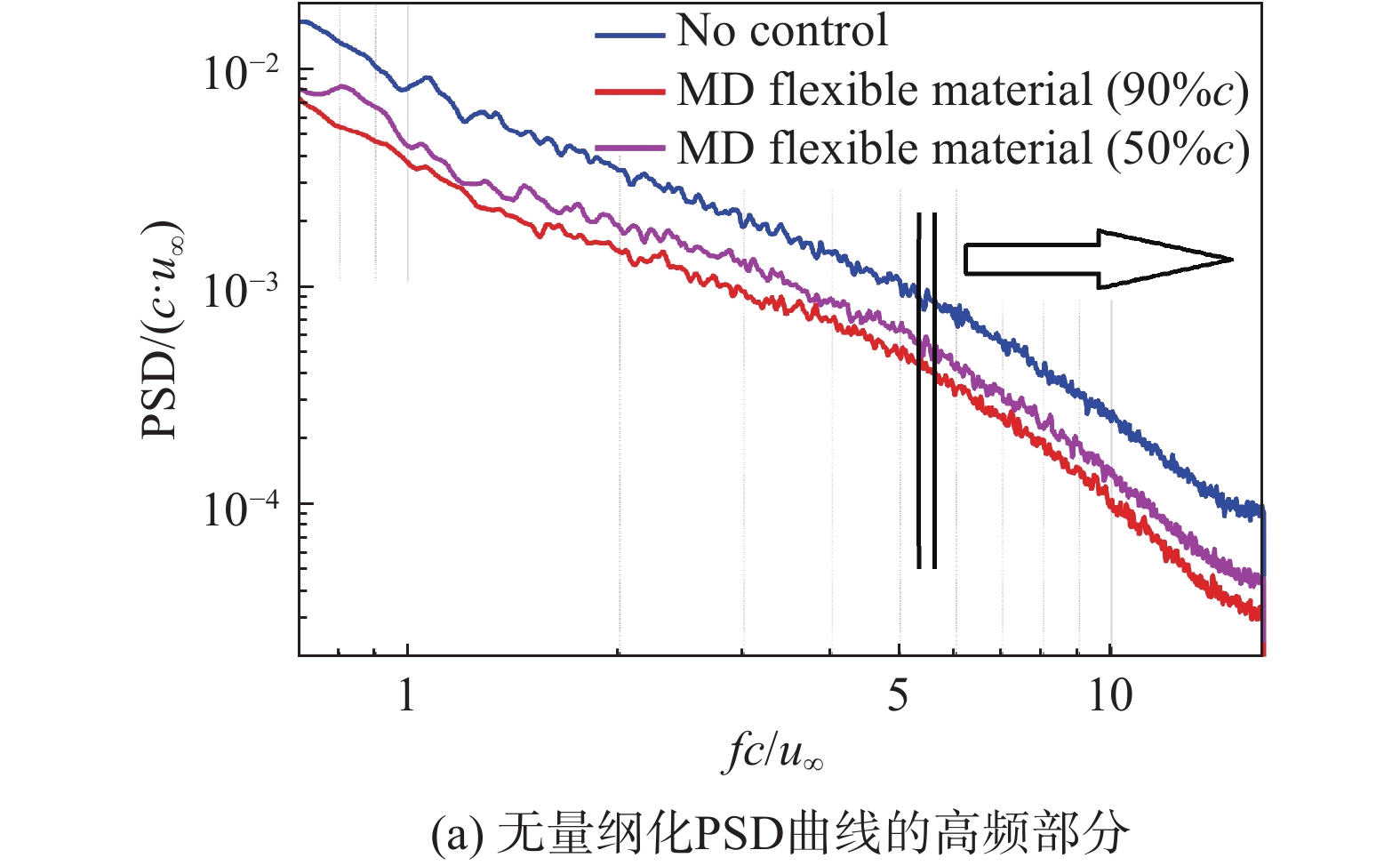
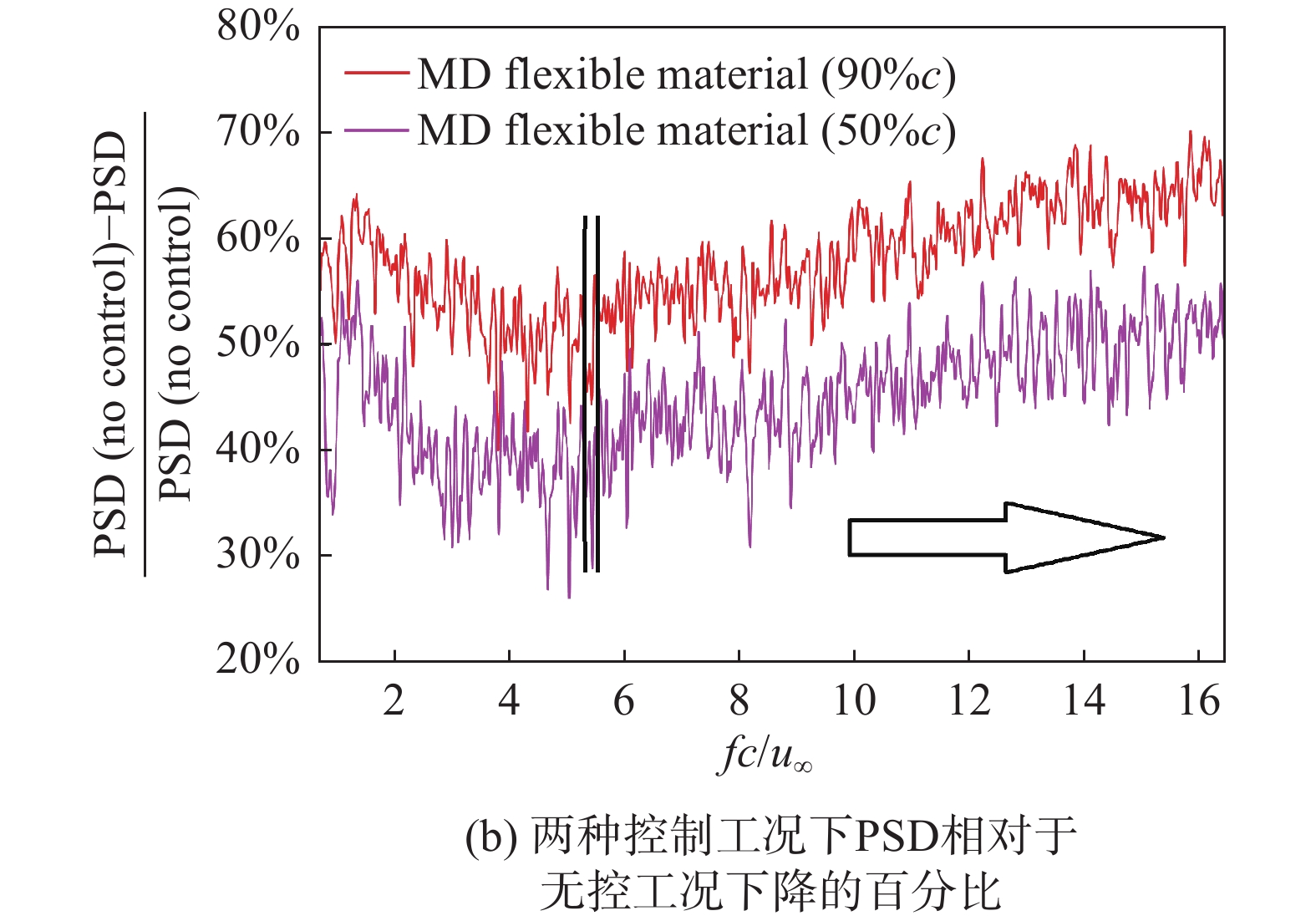
由于剪切层中的分离涡频率fc/u∞主要集中在1以下,图11难以着重表示出更高频更小尺度湍涡的耗散情况。图12(a)仅显示了图8(a)无量纲化PSD曲线的fc/u∞ > 0.7高频部分,采用双对数坐标观察PSD的下降趋势。图12(b)采用双线性坐标表示了两种控制工况下PSD相对于无控工况下降的百分比。可以发现在fc/u∞ > 5.5的区间内,图12(a)的三条曲线以相近的斜率下降,加装控制前后相应的PSD差值近似不变,相应的图12(b)的减小率曲线开始上升,说明含能尺度旋涡不断破碎到该特征尺度[30-31]湍涡后,其携带的能量在黏性作用下耗散消失。对于中等密度的旋涡发生器,在50%c加装后区间fc/u∞ > 5.5的PSD的减小比率在50%~60%,在90% c加装后的减小比率在40%~50%,这与锯齿形结构有效降噪的仿真结果[11-14]符合。
|
图 12 |
|
图 12 控制前后的功率谱及减小比率 Fig.12 Power spectral density and its reduction ratio compared between the controlled and uncontrolled conditions |
通过双通道热线的测量方法可以同时记录下不同空间位置的流场脉动信号,从而研究扰动从旋涡发生器出发传播到前缘剪切层,最终诱导其上边界下移的扰流过程,这种互相关的分析方法可以有效识别出旋涡间的相互作用关系[32]。
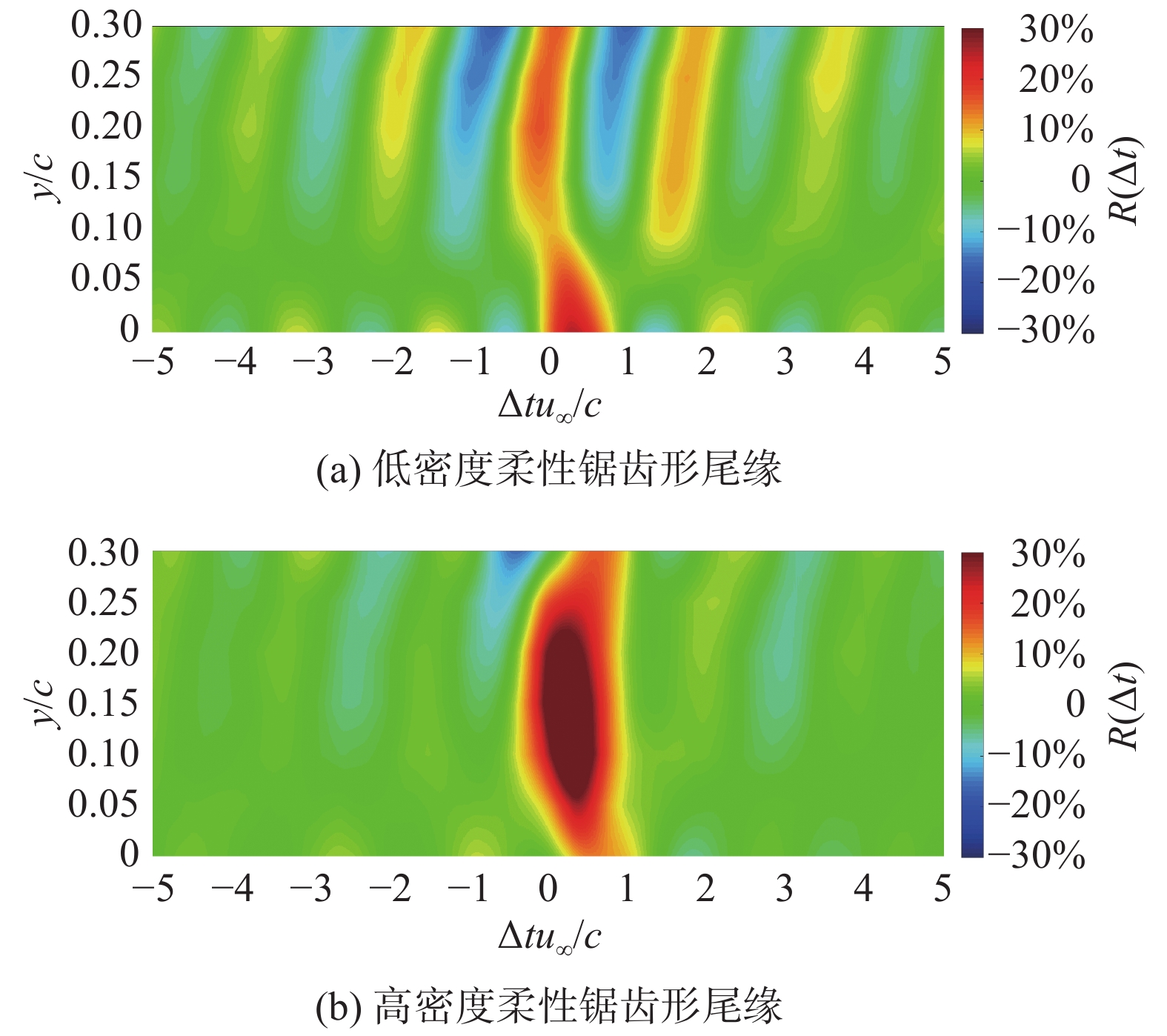
3.4.1 扰动的传播原理图13为x/c = 0.75处前缘剪切层各测点相对于尾缘扰动源附近(点B)的互相关函数,横轴为无量纲化的时间延迟,表示前缘剪切层测点的脉动信号相对于扰动源信号的相位差。图13(b)色带集中于前缘和尾缘剪切层的交汇区,图13(a)色带分为前缘和尾缘剪切层两部分,在y/c = 0.05附近发生相位突变向右上方倾斜。向右上方倾斜是因为扰动在当地平均速度的带动下传播,在靠近剪切层边界的地方会较快。色带分成两部分说明低密度材料产生的扰流涡很难传播到两剪切层的交汇区,导致扰动在两剪切层之间有相位差,产生错位。扰动向下游传播后在两剪切层内分别产生作用。
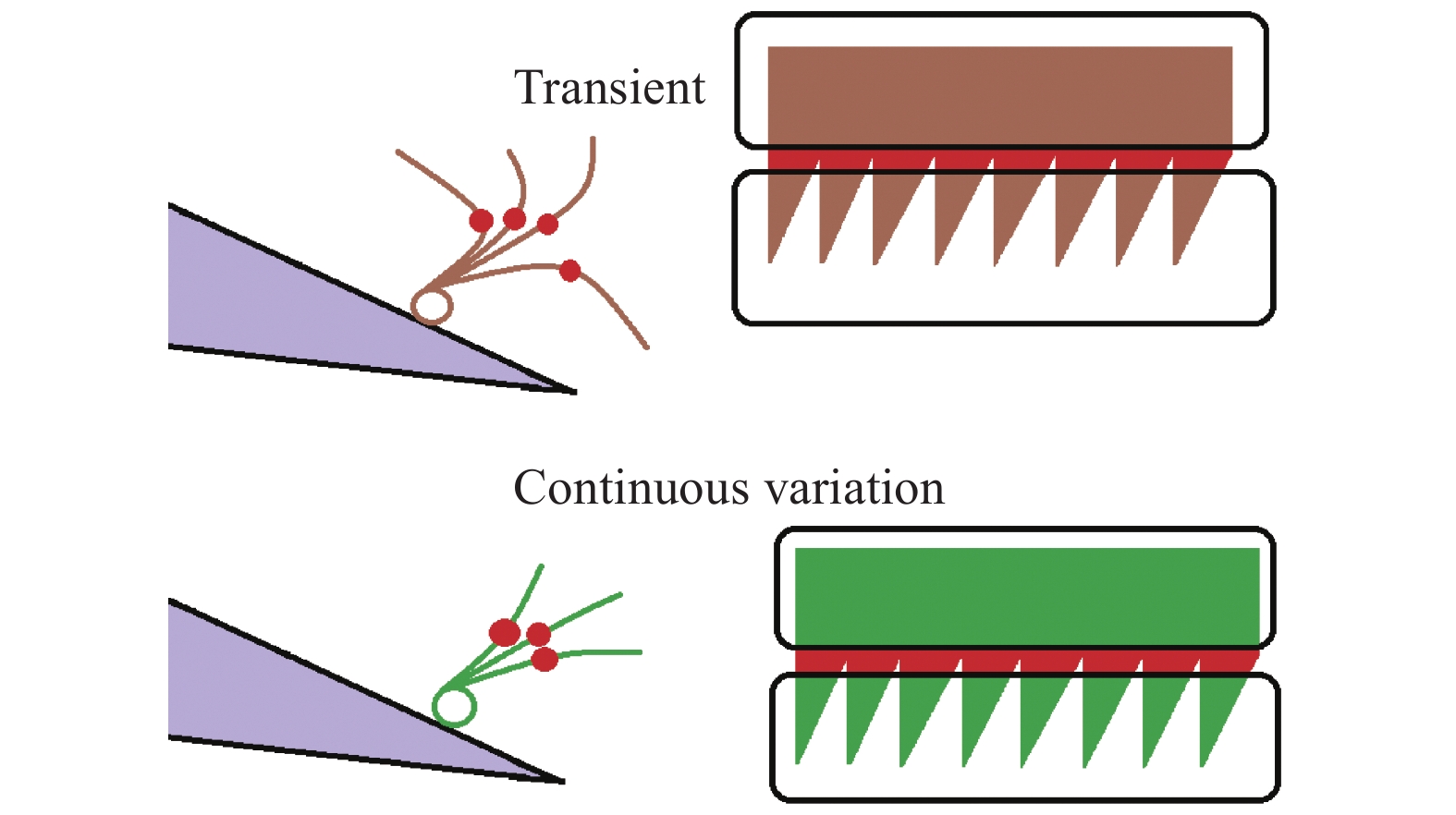
低密度柔性材料无法向交汇区y/c = 0.1处传播扰动,是因为其质地较软无法维持伸直状态。不同于铰接式刚性旋涡发生器处于不同翻折角度时会产生各尺度和传播方向的扰流涡[16]。本实验的旋涡发生器由柔性材料制成。通过观察CCD高速相机的拍摄的如图3所示的旋涡发生器各瞬时的扰流姿态,可以总结得到图14各柔性材料的形变规律。不同柔性锯齿根部和齿间的形变角度变化会导致受力边界条件、相对前缘分离点距离和相对壁面距离等参数的较大差异,从而产生频率、幅值、传播方向差异较大的扰动。低密度锯齿在红色的翻折点位置会发生大角度形变,在变换相位姿态的过程中会突然从向上翻折的状态突变为向下翻折,所以其产生的扰流涡扩散角度较大,只能分别向前缘和尾缘剪切层传播扰动。高密度柔性材料变形较小,变形过程较为连续,所以扰动传播的范围较为集中。
|
图 13 相对于扰动源(点B)的互相关函数 Fig.13 Cross-correlation function relative tothe perturbation source point B |
|
图 14 扰动传播方式 Fig.14 Disturbance propagation modes |
图13(b)图的相关性较高,色带较为粗短,图13(a)色带形状较为细长。将y/c = 0.2前缘剪切层脉动峰值点处的互相关函数在时域和频域上分别展开得到图15,图15(a)两条曲线的峰值点相位差较大(Δt·u∞/c = 0.27),棕线和绿线的相关函数峰值分别为16%和36%,可以推测出高密度材料产生的扰动向前缘剪切层传播的速度较快且强度较高。
| $ {\gamma }_{xy}(f)=\frac{{G}_{xy}(f)}{\sqrt{{G}_{xx}(f){G}_{yy}(f)}} $ | (15) |
式(15)定义了相干函数
图15(b)曲线实际提取出了前缘剪切层中与扰流涡结构相似的部分。在高频部分(f·c/u∞ = 0.6)两曲线的相干性均达到了46%。绿色曲线除了高频峰值,在低频(f·c/u∞ = 0.16)处的相干性为43%,并且在很大的低频带宽内相干性均维持在25%左右,而棕色曲线趋近于0,说明高密度材料较为厚重,产生的扰动含有多种尺度结构,造成了能量冗余,分离控制效率较低,在振动过程中会同时产生高频和低频两类扰流涡,可能会导致不必要的低频噪声。

|
图 15 前缘剪切层脉动峰值点相对于扰动源(点B)的相关性 Fig.15 Correlation between the peak fluctuation point in the leading-edge shear layer and the perturbation source point B |
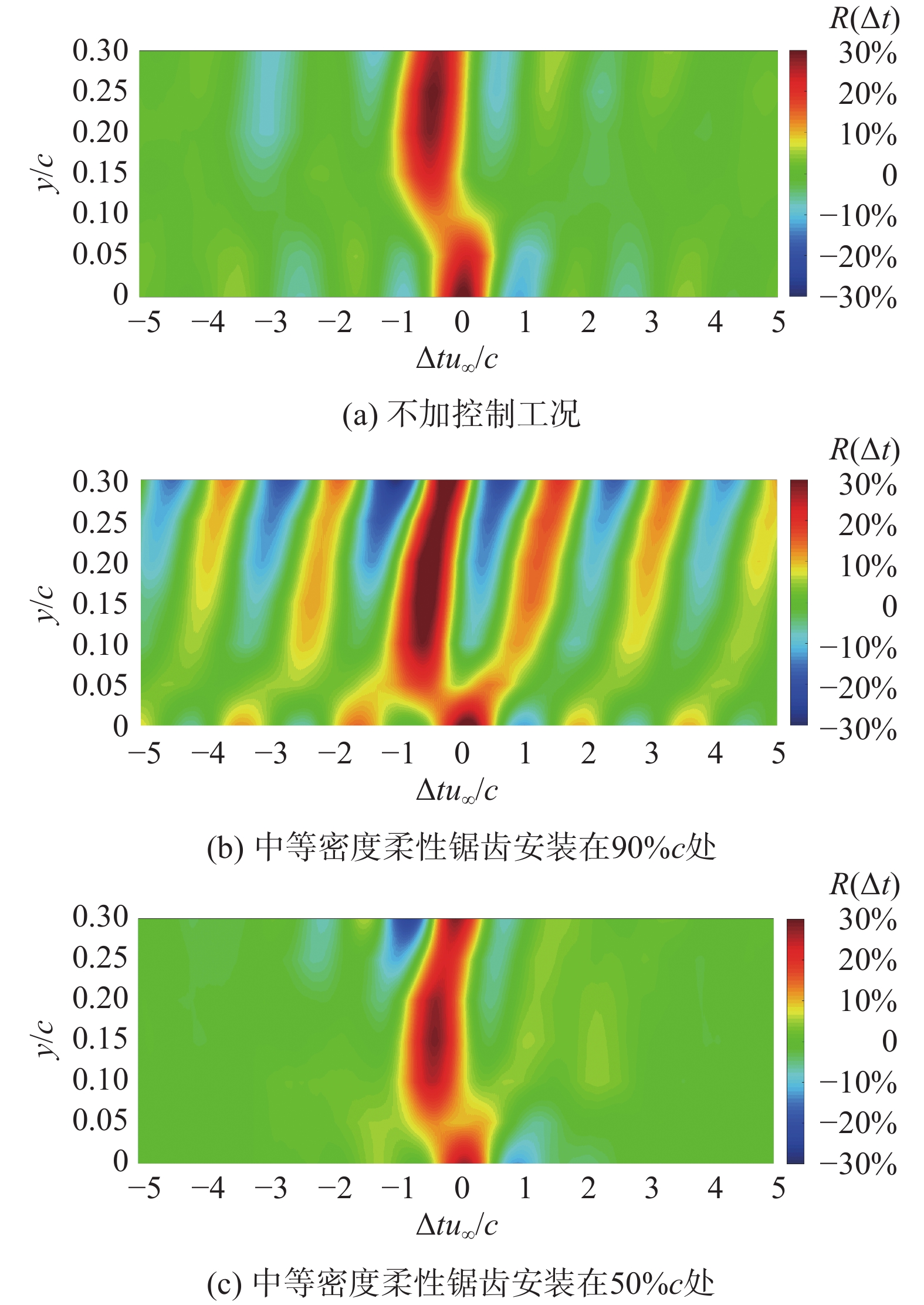
图16为前缘剪切层各测点和尾缘y/c = −0.1脉动峰值点A的互相关函数,可以分析不同安装位置处产生的扰动对两个剪切层相关性的影响。横轴所示的相位差若为正,则前缘剪切层该测点的信号提前于尾缘剪切层的点A,反之则落后。可以发现,红色条带向右上方偏斜,且在交汇区y/c = 0.05附近存在相位突变,因为点A与其附近的尾缘剪切层测点相位较为接近,且相关性随着距离缩短逐渐趋近于100%。而尾缘剪切层与前缘剪切层相互作用时会存在时间差,因为两剪切层从边界开始接触交换动量,相互挤压、掺混,通过拉格朗日结构传递压缩和拉伸应力,其传递动量的强度和速度决定了两剪切层之间相关性及其相位差。
在90%c处加装控制之后,图16(b)中的深红色区域显著延长了,红色条带在交汇区都连接在一起,表明前缘剪切层从下边界就开始受到显著的扰动调制作用,与尾缘剪切层在很长一段空间距离上都维持了较高的相关性,跟随尾缘剪切层同步挤压或是拉伸,沿y方向不同位置具有一定的时间滞后。在50%c处加装控制后,图16(c)红色条带仅发生下移,色带结构变化不明显,说明上游产生的大尺度扰动传播到尾流区可以诱导前缘剪切层继续下移,没有明显提高两剪切层之间的相关性。
|
图 16 相对于尾缘剪切层脉动峰值点(点A)的互相关函数 Fig.16 Cross-correlation function relative to the peak flucatuation point A in the trailing-edge shear layer |
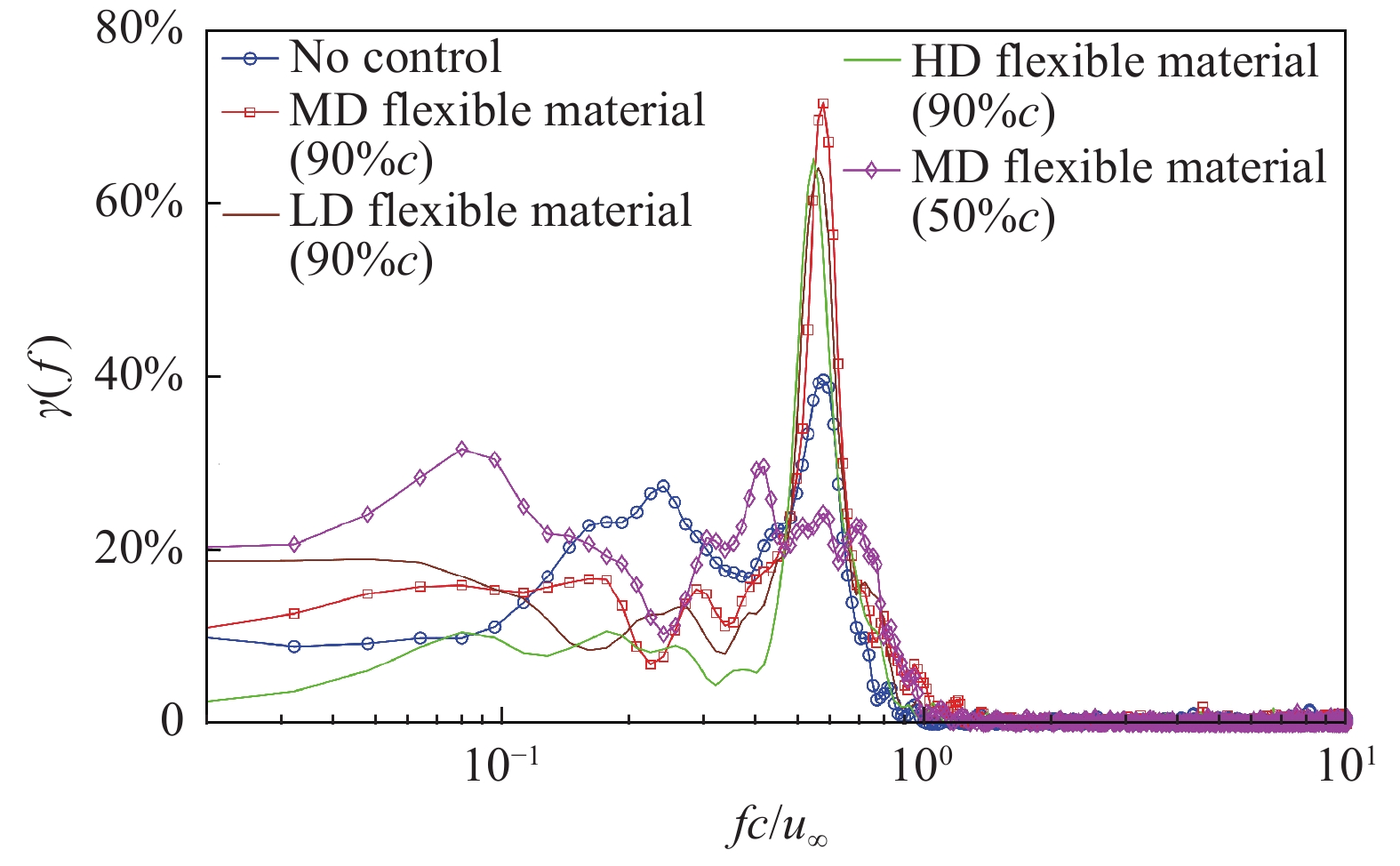
图16(b)图中含有大量规律的红蓝条带,说明两剪切层之间共同作用的周期性非常强,以某一确定频率进行动量交换,同步挤压、拉伸。通过图17所示的相干性分析,可以识别出其相干频率,红色曲线表示在90%c加装控制后,两剪切层在高频fc/u∞ = 0.6的相干性从40%提升到了72%。不加控制时,两剪切层之间低频fc/u∞ = 0.24的动量交换从27%被抑制到了7%;玫红色曲线表示在50%c加装控制,两剪切层相互作用的两个特征频率峰值分别向低频移动至fc/u∞ = 0.1和0.42,相互作用的强度变化并不显著,相干性均保持在30%左右。
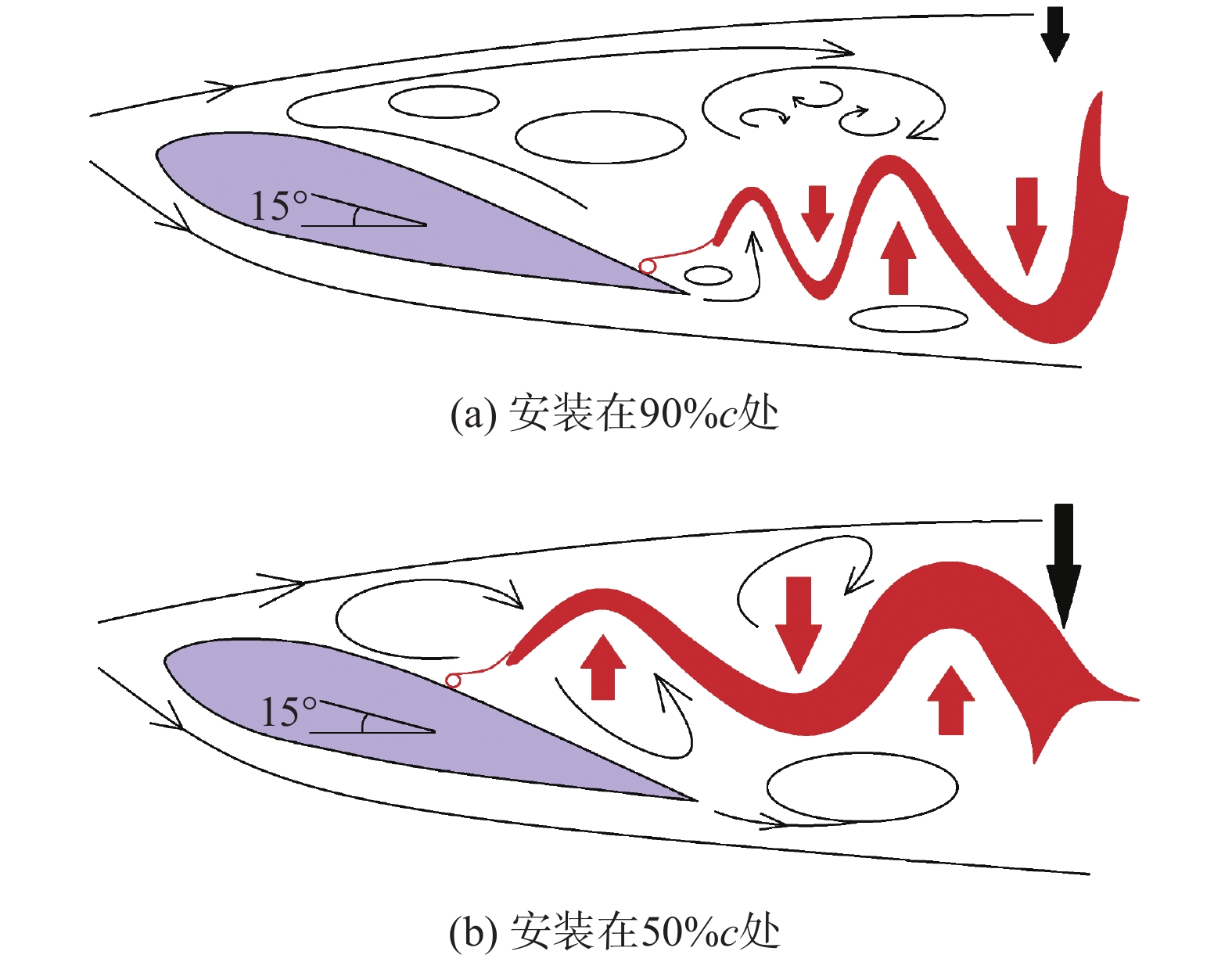
柔性锯齿通过改变前缘和尾缘剪切层之间相互挤压、拉伸的强度和频率,使得两剪切层相互靠近,同步运动,从而诱导前缘剪切层的上边界向下移动,这与Meyer[5]和Marco[9]所作的“自适应可动平板”的扰流涡传播过程的仿真结果相似。如图18所示,中等密度柔性锯齿在90%c处产生的高频小尺度扰动,可以有效加快两剪切层之间相互作用的速率和强度,破碎前缘剪切层的大尺度涡包,从而控制流动分离并降低低频脉动。在50%c处受逆压梯度产生的低频大尺度扰动充分发展和作用的时间较长,传播至尾流区后可以降低两剪切层相互作用的频率,增大相互作用的空间幅度,有效拉近两剪切层,交汇区产生的湍涡被掺混为大尺度旋涡,促使两剪切层的重叠区变大,剪切层的上边界从而显著下降,有效控制流动分离现象。
|
图 17 前缘相对于尾缘剪切层(点A)的频域相干性 Fig.17 Coherence between the leading-edge point and point A in the trailing-edge shear layer in the frequency domain |
|
图 18 柔性锯齿控制分离示意图 Fig.18 Schematic diagram of flow separation control via flexible sawteeth |
本文通过风洞实验,验证了仿生学覆羽“高效率、低噪声”的控制流动分离的效果,并分析了不同柔性材料的锯齿形在不同安装位置处产生扰动的传播和作用原理。得出以下结论:
1)中等面密度的柔性材料具有适中的变形和回弹效果,可以有效吸收尾缘脱落涡的湍动能并诱导剪切层边界下移;
2)柔性锯齿安装在90%c时,可以将前缘层的大尺度涡包破碎为小尺度湍涡并耗散,显著降低了低频脉动,通过产生高频小尺度的扰动提高两剪切层之间相干性的频率和强度,控制流动分离;
3)柔性锯齿安装在50%c时,剪切层边界继续向下移动,产生的低频大尺度扰动增大了两剪切层相互作用的空间幅度,通过促进两剪切层之间重叠和掺混,控制流动分离。
| [1] |
FÖRSCHING H, HENNINGS H. Aeroelastic mysteries in avian flight[J]. CEAS Aeronautical Journal, 2012(3): 135-143. DOI:10.1007/s13272-012-0048-6 |
| [2] |
KLÄN S, BURGMANN S, BACHMANN T, et al. Surface structure and dimensional effects on the aerodynamics of an owl-based wing model[J]. European Journal of Mechanics - B/Fluids, 2012, 33: 58-73. DOI:10.1016/j.euromechflu.2011.12.006 |
| [3] |
WOLF T, KONRATH R. Avian wing geometry and kinematics of a free-flying barn owl in flapping flight[J]. Experiments in Fluids, 2015, 56(2): 1-18. DOI:10.1007/s00348-015-1898-6 |
| [4] |
LI D, LIU X M. A comparative study on aerodynamic performance and noise characteristics of two kinds of long-eared owl wing models[J]. Journal of Mechanical Science and Technology, 2017, 31(8): 3821-3830. DOI:10.1007/s12206-017-0726-8 |
| [5] |
SCHATZ M, KNACKE T, THIELE F, et al. Separation control by self-activated movable flaps[C]//42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2004. doi: 10.2514/6.2004-1243
|
| [6] |
BRAMESFELD G, MAUGHMER M D. Experimental investigation of self-actuating, upper-surface, high-lift-enhancing effectors[J]. Journal of Aircraft, 2002, 39(1): 120-124. DOI:10.2514/2.2905 |
| [7] |
SCHLUTER J U. Lift enhancement at low Reynolds numbers using self-activated movable flaps[J]. Journal of Aircraft, 2010, 47(1): 348-351. DOI:10.2514/1.46425 |
| [8] |
WANG C H J, SCHLÜTER J. Stall control with feathers: Self-activated flaps on finite wings at low Reynolds numbers[J]. Comptes Rendus Mécanique, 2012, 340(1-2): 57-66. DOI:10.1016/j.crme.2011.11.001 |
| [9] |
ROSTI M E, KAMPS L, BRUECKER C, et al. The PELskin project-part V: towards the control of the flow around aerofoils at high angle of attack using a self-activated deployable flap[J]. Meccanica, 2017, 52(8): 1811-1824. DOI:10.1007/s11012-016-0524-x |
| [10] |
AYTON L J. Acoustic scattering by a finite rigid plate with a poroelastic extension[J]. Journal of Fluid Mechanics, 2016, 791: 414-438. DOI:10.1017/jfm.2016.59 |
| [11] |
JONES L E, SANDBERG R D. Acoustic and hydrodynamic analysis of the flow around an aerofoil with trailing-edge serrations[J]. Journal of Fluid Mechanics, 2012, 706: 295-322. DOI:10.1017/jfm.2012.254 |
| [12] |
HUANG X. Theoretical model of acoustic scattering from a flat plate with serrations[J]. Journal of Fluid Mechanics, 2017, 819: 228-257. DOI:10.1017/jfm.2017.176 |
| [13] |
许影博, 李晓东. 锯齿型翼型尾缘噪声控制实验研究[J]. 空气动力学学报, 2012, 30(1): 120-124. XU Y B, LI X D. An experiment study of the serrated trailing edge noise[J]. Acta Aerodynamica Sinica, 2012, 30(1): 120-124. DOI:10.3969/j.issn.0258-1825.2012.01.021 (in Chinese) |
| [14] |
AVALLONE F, PRÖBSTING S, RAGNI D. Three-dimensional flow field over a trailing-edge serration and implications on broadband noise[J]. Physics of Fluids, 2016, 28(11): 117101. DOI:10.1063/1.4966633 |
| [15] |
乔渭阳, 仝帆, 陈伟杰, 等. 仿生学气动噪声控制研究的历史、现状和进展[J]. 空气动力学学报, 2018, 36(1): 98-121. QIAO W Y, TONG F, CHEN W J, et al. Review on aerodynamic noise reduction with bionic configuration[J]. Acta Aerodynamica Sinica, 2018, 36(1): 98-121. (in Chinese) |
| [16] |
HAO W X, DING Q W, LI C. Optimal performance of adaptive flap on flow separation control[J]. Computers & Fluids, 2019, 179: 437-448. DOI:10.1016/j.compfluid.2018.11.010 |
| [17] |
CHONG T P, VATHYLAKIS A. On the aeroacoustic and flow structures developed on a flat plate with a serrated sawtooth trailing edge[J]. Journal of Sound and Vibration, 2015, 354: 65-90. DOI:10.1016/j.jsv.2015.05.019 |
| [18] |
CHONG T P, JOSEPH P, VATHYLAKIS A, et al. On the noise and wake flow of an airfoil with broken and serrated trailing edges[C]//17th AIAA/CEAS Aeroacoustics Conference (32nd AIAA Aeroacoustics Conference), Portland, Oregon. Reston, Virginia: AIAA, 2011. doi: 10.2514/6.2011-2860
|
| [19] |
ZHENG X B, PRÖBSTING S, WANG H L, et al. Characteristics of vortex shedding from a sinusoidally pitching hydrofoil at high Reynolds number[J]. Physical Review Fluids, 2021, 6(8): 084702. DOI:10.1103/physrevfluids.6.084702 |
| [20] |
巩绪安, 张鑫, 马兴宇, 等. 柔性锯齿形尾缘流动分离控制实验的多尺度相干结构研究[J]. 实验流体力学, 2021 (已录用). GONG X A, ZHANG X, MA X Y, et al. Experimental study on flow separation control by flexible serrated trailing edge based on multi-scale coherent structure analysis[J]. Journal of Experiments in Fluid Mechanics, 2021(accepted). (in Chinese) |
| [21] |
SHI S X, NEW T H, LIU Y Z. Flapping dynamics of a low aspect-ratio energy-harvesting membrane immersed in a square cylinder wake[J]. Experimental Thermal and Fluid Science, 2013, 46: 151-161. DOI:10.1016/j.expthermflusci.2012.12.007 |
| [22] |
姜楠, 王振东, 舒玮. 子波分析辨识壁湍流猝发事件的能量最大准则[J]. 力学学报, 1997, 29(4): 406-412. JIANG N, WANG Z D, SHU W. The maximum energy criterion for identifying burst events in wall turbulence using wavelet analysis[J]. Acta Mechanica Sinica, 1997, 29(4): 406-412. DOI:10.3321/j.issn:0459-1879.1997.04.003 (in Chinese) |
| [23] |
王皓田, 朱杨柱, 车学科, 等. S1223翼型低雷诺数下分离泡及气动特性[J]. 空气动力学学报, 2021, 39(3): 90-98. WANG H T, ZHU Y Z, CHE X K, et al. Separation bubble and aerodynamic characteristics of S1223 airfoil at low Reynolds numbers[J]. Acta Aerodynamica Sinica, 2021, 39(3): 90-98. DOI:10.7638/kqdlxxb-2020.0075 (in Chinese) |
| [24] |
吴鋆, 王晋军, 李天. NACA0012翼型低雷诺数绕流的实验研究[J]. 实验流体力学, 2013, 27(6): 32-38. WU J, WANG J J, LI T. Experimental investigation on low Reynolds number behavior of NACA0012 airfoil[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(6): 32-38. DOI:10.3969/j.issn.1672-9897.2013.06.006 (in Chinese) |
| [25] |
MARTINAT G, BRAZA M, HOARAU Y, et al. Turbulence modelling of the flow past a pitching NACA0012 airfoil at 105 and 106 Reynolds numbers
[J]. Journal of Fluids and Structures, 2008, 24(8): 1294-1303. DOI:10.1016/j.jfluidstructs.2008.08.002 |
| [26] |
李彪辉, 范子椰, 刘丽霞, 等. 柔性旋涡发生器对翼型前缘分离的自适应控制[J]. 气体物理, 2020, 5(5): 56-62. LI B H, FAN Z Y, LIU L X, et al. Adaptive control of wing leading edge separation by flexible vortex generator[J]. Physics of Gases, 2020, 5(5): 56-62. (in Chinese) |
| [27] |
CASALINO D. An advanced time approach for acoustic analogy predictions[J]. Journal of Sound and Vibration, 2003, 261(4): 583-612. DOI:10.1016/S0022-460X(02)00986-0 |
| [28] |
MOREAU S, ROGER M, CHRISTOPHE J. Flow features and self-noise of airfoils near stall or in stall[C]//15th AIAA/CEAS Aeroacoustics Conference (30th AIAA Aeroacoustics Conference), Miami, Florida. Reston, Virginia: AIAA, 2009. doi: 10.2514/6.2009-3198
|
| [29] |
LARATRO A, ARJOMANDI M, CAZZOLATO B, et al. Self-noise of NACA 0012 and NACA 0021 aerofoils at the onset of stall[J]. International Journal of Aeroacoustics, 2017, 16(3): 181-195. DOI:10.1177/1475472x17709929 |
| [30] |
SHE Z S, LEVEQUE E. Universal scaling laws in fully developed turbulence[J]. Physical Review Letters, 1994, 72(3): 336-339. DOI:10.1103/physrevlett.72.336 |
| [31] |
佘振苏, 苏卫东. 湍流中的层次结构和标度律[J]. 力学进展, 1999, 29(3): 289-303. SHE Z S, SU W D. Hierarchical structures and scalings in turbulence[J]. Advances in Mechanics, 1999, 29(3): 289-303. DOI:10.3321/j.issn:1000-0992.1999.03.001 (in Chinese) |
| [32] |
TANG Z Q, JIANG N. Scale interaction and arrangement in a turbulent boundary layer perturbed by a wall-mounted cylindrical element[J]. Physics of Fluids, 2018, 30(5): 055103. DOI:10.1063/1.5022670 |
 2021, Vol. 39
2021, Vol. 39


