翼型对飞机气动性能有极其重要的作用,翼型设计技术是飞机公司的核心技术之一。目前跨声速飞行的大型客机普遍采用的超临界翼型,其概念是20世纪60年代美国NASA提出的。经过了超过半个世纪的发展,超临界翼型设计技术不断革新,而计算流体力学技术的长足发展更为翼型的精细设计和性能权衡创造了良好的条件。
超临界翼型最大的优势在于,当来流马赫数高于临界马赫数后仍有理想的阻力发散性能。但在机翼设计中,随着翼型相对厚度、来流速度或攻角的增加,带来的激波变强甚至引发激波诱导流动分离等问题仍然是限制气动性能提升的关键。在更大的厚度、速度或升力系数下,有效控制激波强度、降低激波阻力和提升抖振边界仍然是超临界翼型设计的努力方向。20世纪70年代初,NASA在风洞实验中,发现增加超临界翼型后缘厚度可以降低跨声速阻力[1],该实验研究了后缘厚度与边界层位移厚度的相关性,结论是当后缘厚度超过边界层位移厚度后,后缘厚度对气动性能的影响规律将相反。麦道公司研究结果[2-3]表明当超临界翼型后缘厚度增加时(直至0.7%c),跨声速阻力降低而亚声速阻力没有不明显增加。如果后缘形状设计得好,这种效果可以持续到后缘厚度增加1%c。这种翼型称为后缘发散翼型(DTE,Divergent Trailing Edge)。DTE是格尼襟翼的一种进化产物[4],学者们对其增升减阻机理进行了大量研究[5-9]。较为一致的结论是:后缘发散使得后缘回流区长度增加,拓展了翼型有效弦长,进而实现增升减阻的效果。但后缘发散设计带来的问题也是比较突出的,一是靠近后缘增加的升力会使低头力矩明显增加,由此带来的更大的配平损失会抵消减阻效果;二是尾迹区的增大会带来更大的底部阻力,这一缺点在无激波的亚声速状态下更为明显。为了弥补这些不足,学者们也开展了相关研究,比如使用喷流流动控制技术[10-11]。在研究手段上,除了传统的风洞实验,学者们也研究了数值计算技术[12-13]。实际应用中,DTE的雷诺数效应问题和对抖振边界的作用也成为研究者关注的领域[14-16]。国内发表的相关研究资料较少,北京航空航天大学在风洞实验中通过测量压力分布和尾迹速度型,研究了后缘发散翼型和格尼襟翼的增升机理[17]。沈阳航空工业学院陆超,研究了超临界翼型后缘简单加厚对气动性能的影响规律[18]。
本文使用计算流体力学手段研究后缘发散概念在宽体客机机翼设计中的应用价值。计算分析修形参数对超临界翼型性能的影响规律,提出针对宽体客机机翼设计的应用思路。流场计算使用内部CFD(Computational Fluid Dynamics)程序SFlow[19],该程序在多块结构化网格上以有限体积法求解雷诺平均N-S方程,无黏通量项用Roe平均迎风通量差分分裂格式(FDS)离散,黏性通量项用中心差分格式离散,时间推进计算采用隐式LU-SGS方法,计算选用SST两方程湍流模型。SFlow程序经过大量标准模型的验证计算,其计算精度也在很多工程项目中确认。计算网格使用ICEM-CFD软件生成,翼型网格如图1所示,总单元数2.8万,远场取30倍弦长,后缘网格流向尺度为弦长的2‰;机翼-机身-短舱-吊挂构型的计算网格总单元数800万,物面第一层网格的尺寸可满足y+平均值在1左右,边界层内网格法向增长率为1.2。

|
图 1 翼型计算网格 Fig.1 Computational grid of the airfoil |
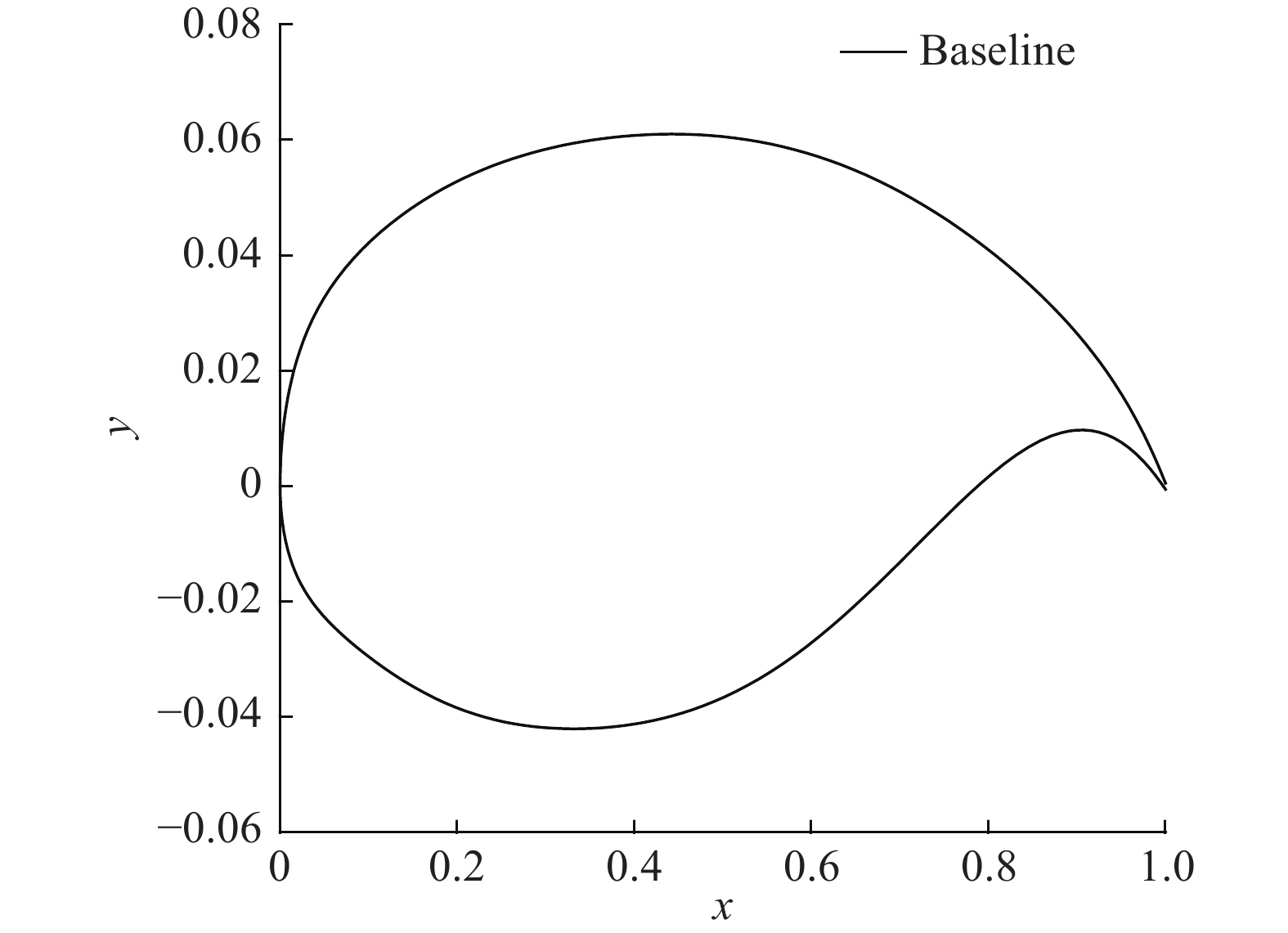
初始翼型(图2)取自某宽体客机机翼70%半翼展处,按1/4弦线后掠角转换为二维翼型后的相对厚度10.2%,后缘厚度为弦长的1‰,本节的后缘发散修形设计都在该翼型基础上进行。这里使用式(1)中幂函数表达的扰动量对下表面后缘附近实施后缘发散修形设计:
| $ \Delta y\left(x\right) = \left\{\begin{array}{c}\begin{array}{cc}0& \begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}\end{array}\;\;\;\;\quad,0\leqslant x < {x}_{\text{ref}}\\ \begin{array}{cc}-\Delta {y}_{1}{{\displaystyle \left(\frac{x-{x}_{\text{ref}}}{1.0-{x}_{\text{ref}}}\right)}}^{N}& ,{x}_{\text{ref}}\leqslant x\leqslant 1\end{array}\end{array}\right. $ | (1) |
其中x为弦向位置,
|
图 2 初始翼型 Fig.2 Baseline airfoil |
图3对比了
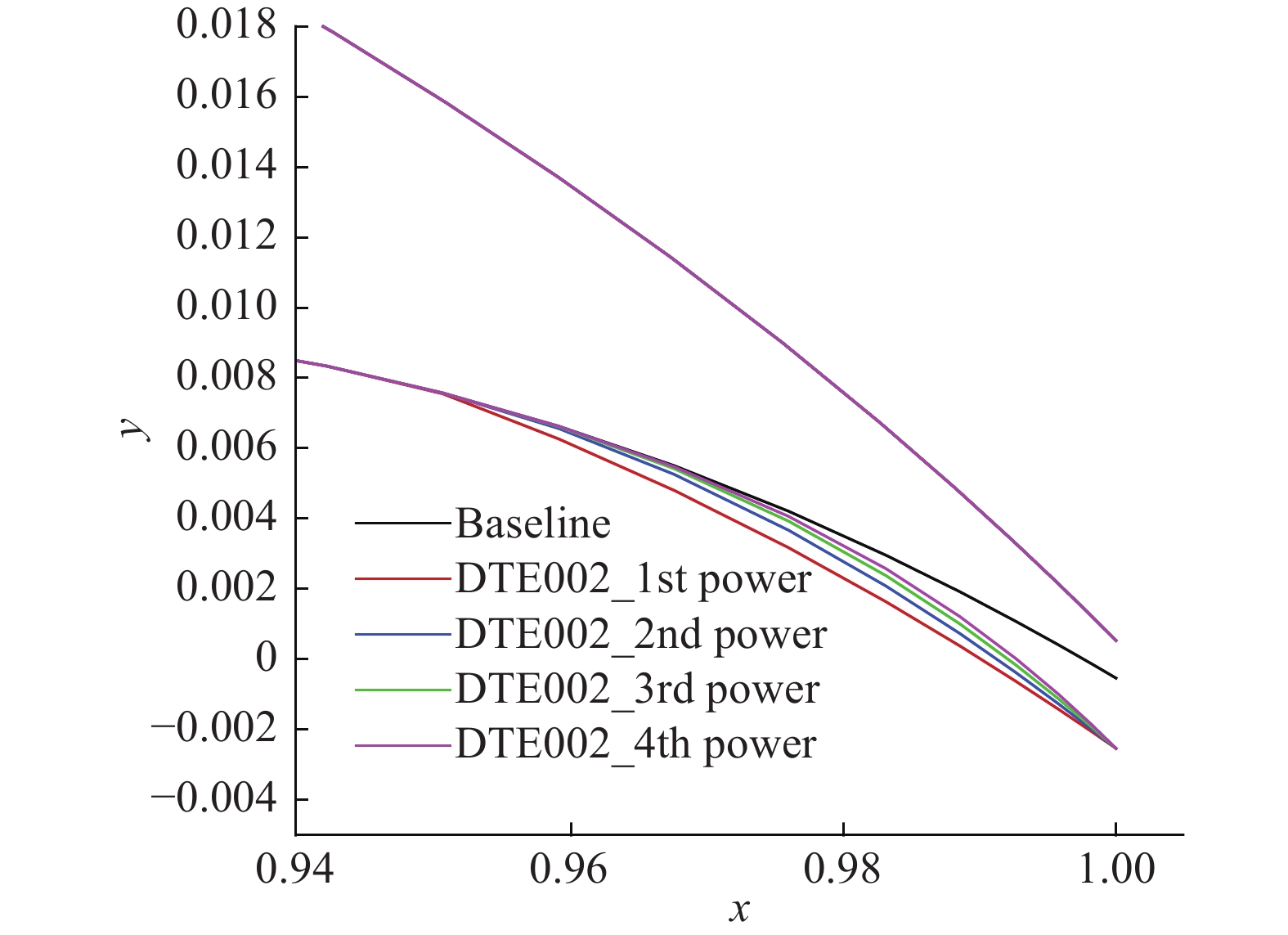
|
图 3 不同幂次后缘发散修形对比 Fig.3 Comparison of the trailing-edge shapes for different N |
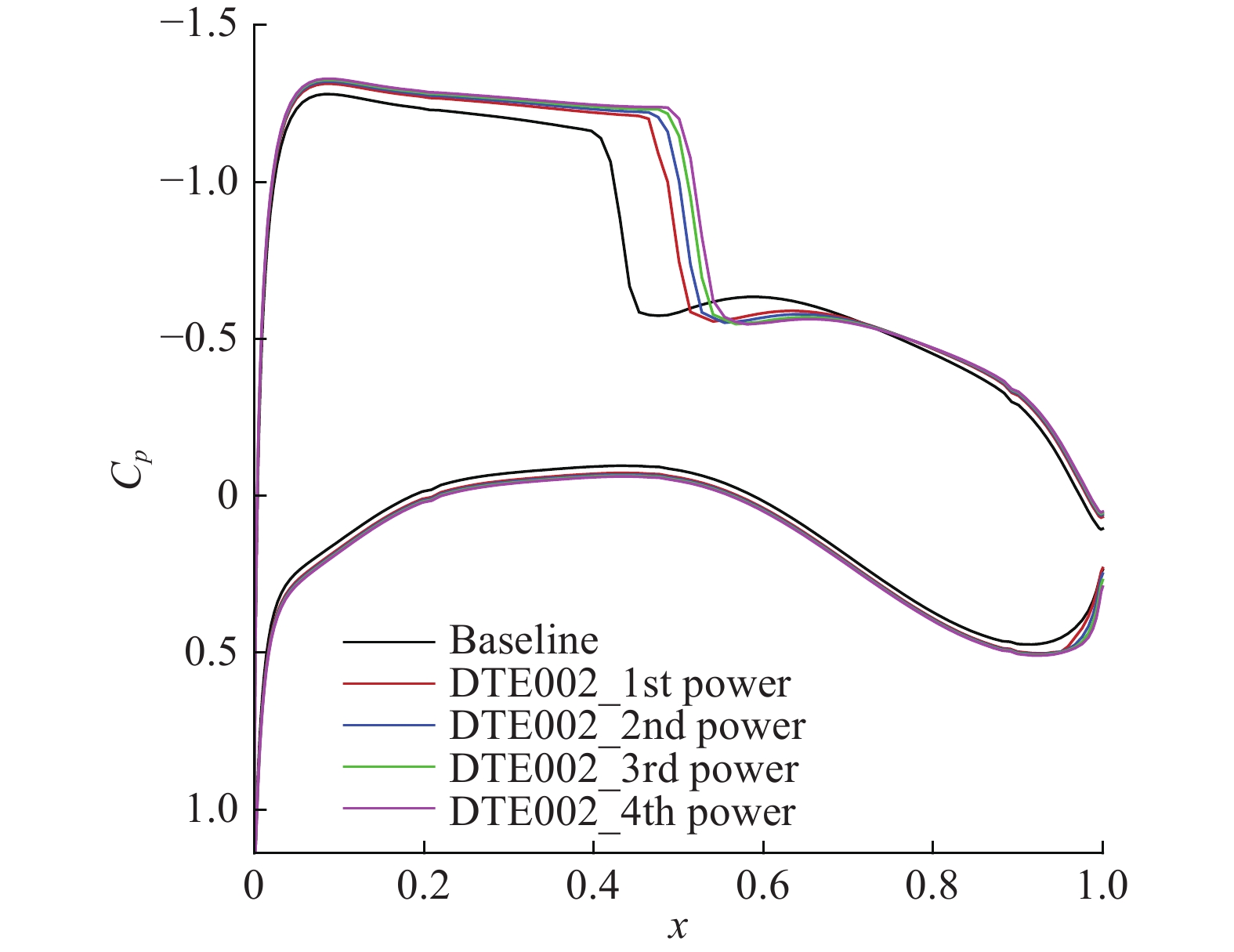
|
图 4 不同幂次后缘发散修形压力分布对比(α = 1.5°) Fig.4 Comparison of pressure distributions on the airfoils for different N (α = 1.5°) |
| 表 1 不同修形幂次力系数对比 Table 1 Force coefficients for differentN |
|
|
图5对比了
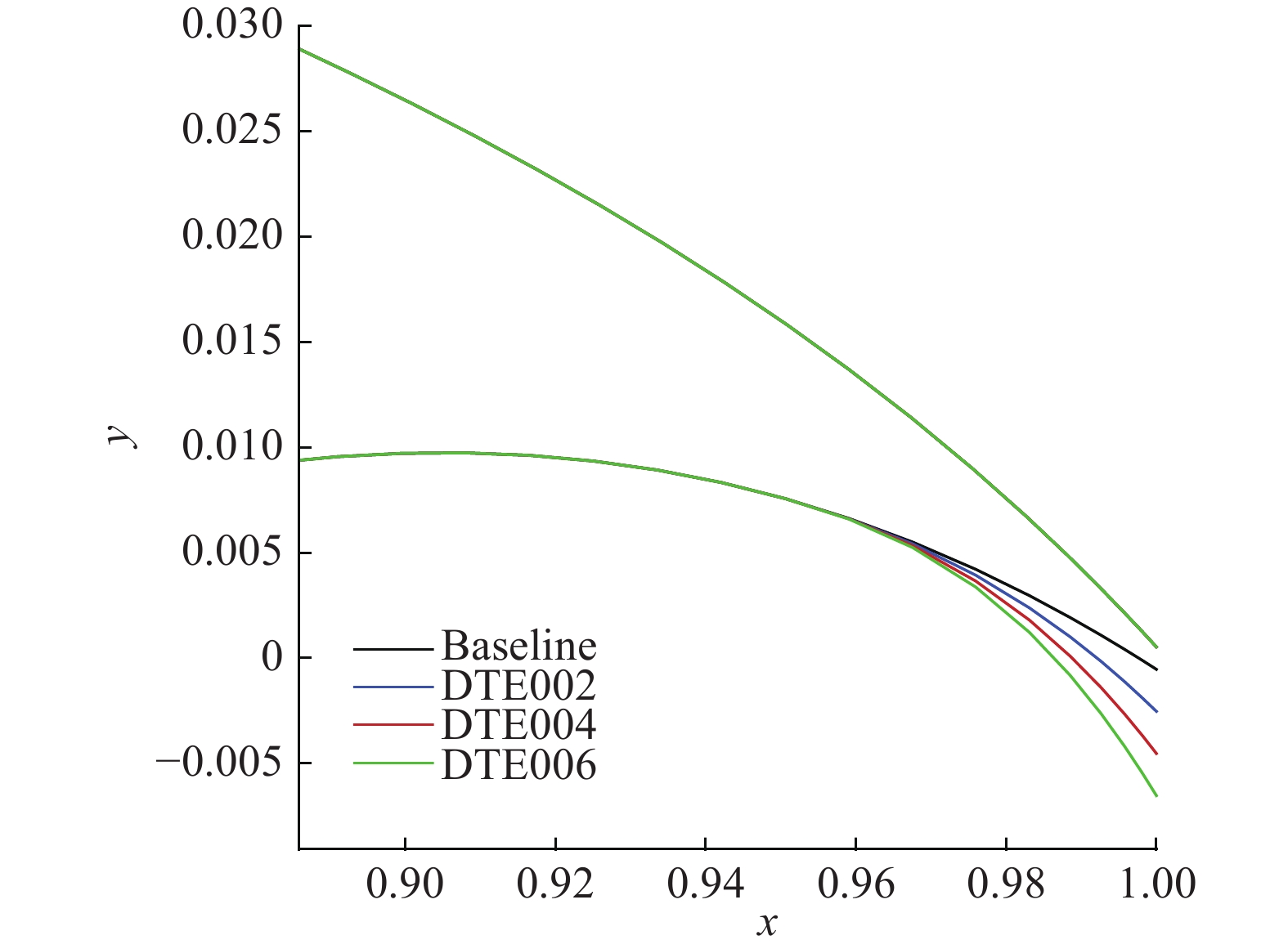
|
图 5 不同后缘厚度的后缘发散对比 Fig.5 Comparison of the trailing edges for different thickness |

|
图 6 不同后缘厚度的压力分布对比(CL = 0.97) Fig.6 Comparison of pressure distributionsfor different trailing-edge thickness Δy1 (CL = 0.97) |
| 表 2 不同后缘厚度的力系数对比 Table 2 Force coefficients for different thickness Δy1 |
|
|
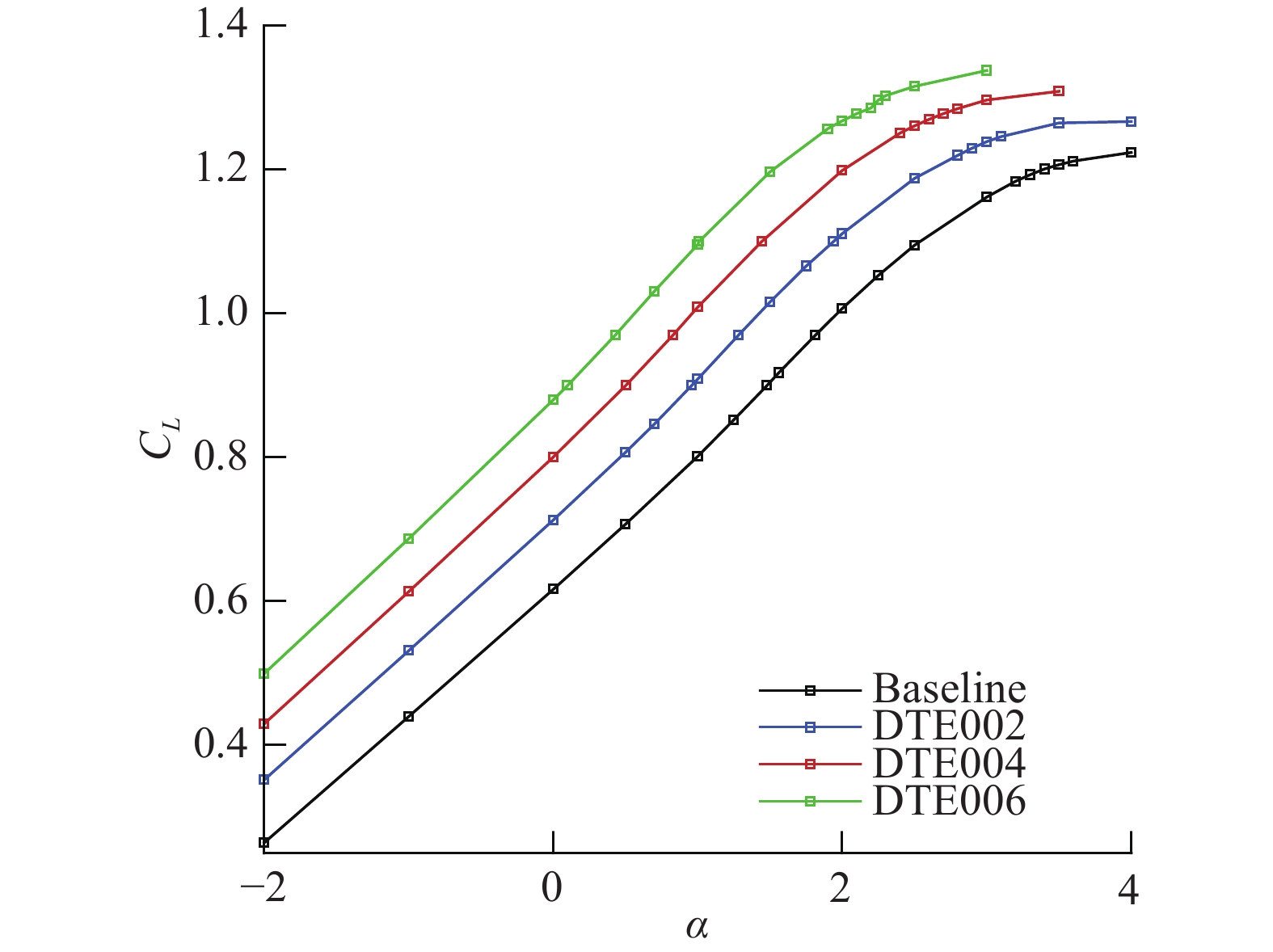
|
图 7 不同后缘厚度的升力线对比 Fig.7 Lift force comparison for different trailing-edge thickness |
图8、图9分别在雷诺数4×106、2×107(CL = 0.97)下,对比了不同后缘厚度增量的阻力发散曲线。马赫数0.5时后缘厚度增加使阻力增加。马赫数大于0.7后,在雷诺数4×106下,后缘厚度一直到弦长的7‰都可以取得较为明显的减阻效果,这与参考文献的结论吻合;而在雷诺数2×107下,后缘厚度由5‰增加到7‰减阻效果不及雷诺数4×106时明显。为了进一步分析后缘厚度对雷诺数的敏感性,图10、图11分别给出了马赫数0.72和0.5的阻力系数差量(相比初始)随后缘厚度增量

|
图 8 不同后缘厚度的阻力发散曲线对比(Re = 4×106) Fig.8 Drag divergence comparison for different trailing-edge thickness (Re=4×106) |
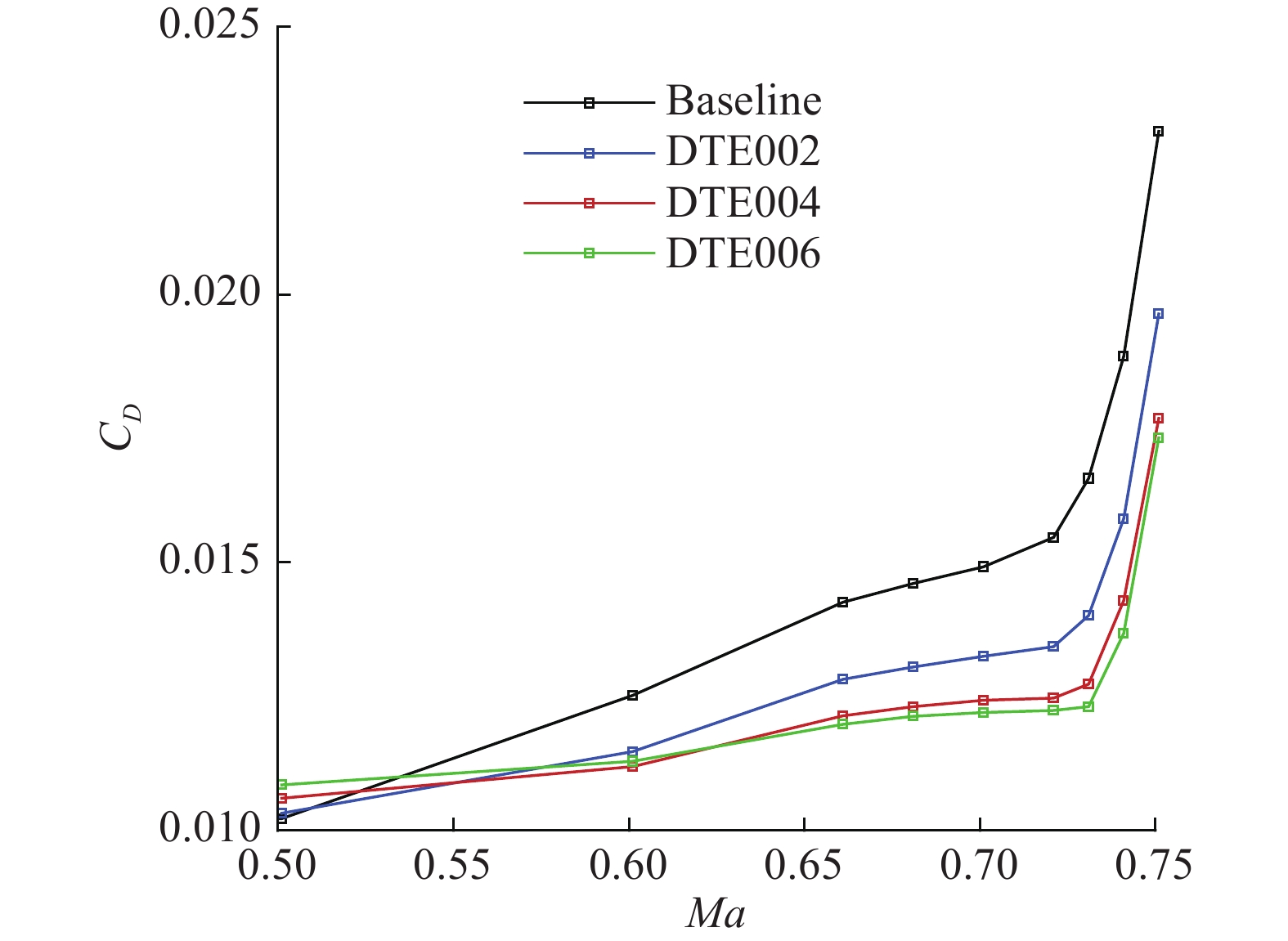
|
图 9 不同后缘厚度的阻力发散曲线对比(Re = 2×107) Fig.9 Drag divergence curve comparison for different trailing-edge thickness (Re=2×107) |
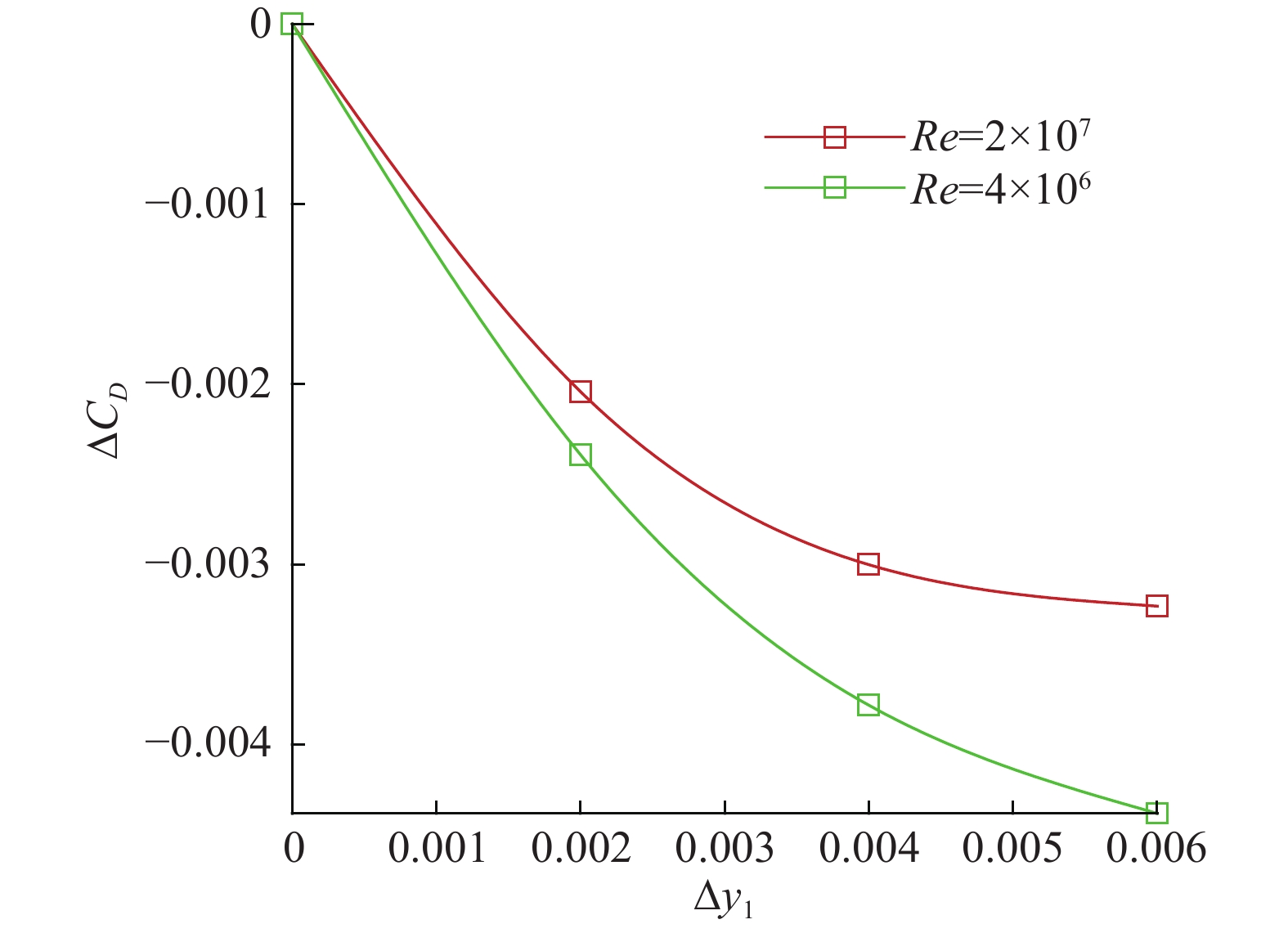
|
图 10 不同后缘厚度减阻效果的雷诺数效应(Ma = 0.72) Fig.10 Reynolds number effect for the drag reduction of airfoils with different trailing-edge thickness (Ma = 0.72) |
后缘发散翼型这样的雷诺数效应主要源于边界层厚度的不同。基于上述计算分析可以发现,后缘发散翼型后缘厚度对其性能有重要影响。风洞实验常见的雷诺数4×106下,后缘厚度一直到弦长的7‰都可以在跨声速下取得理想的减阻效果。而在宽体客机实际飞行的2×107甚至更高雷诺数下,由于边界层更薄,尾迹区更小,综合考虑跨声速减阻、亚声速增阻和低头力矩因素,后缘厚度取3‰左右较为合适。

|
图 11 不同后缘厚度减阻效果的雷诺数效应(Ma = 0.5) Fig.11 |
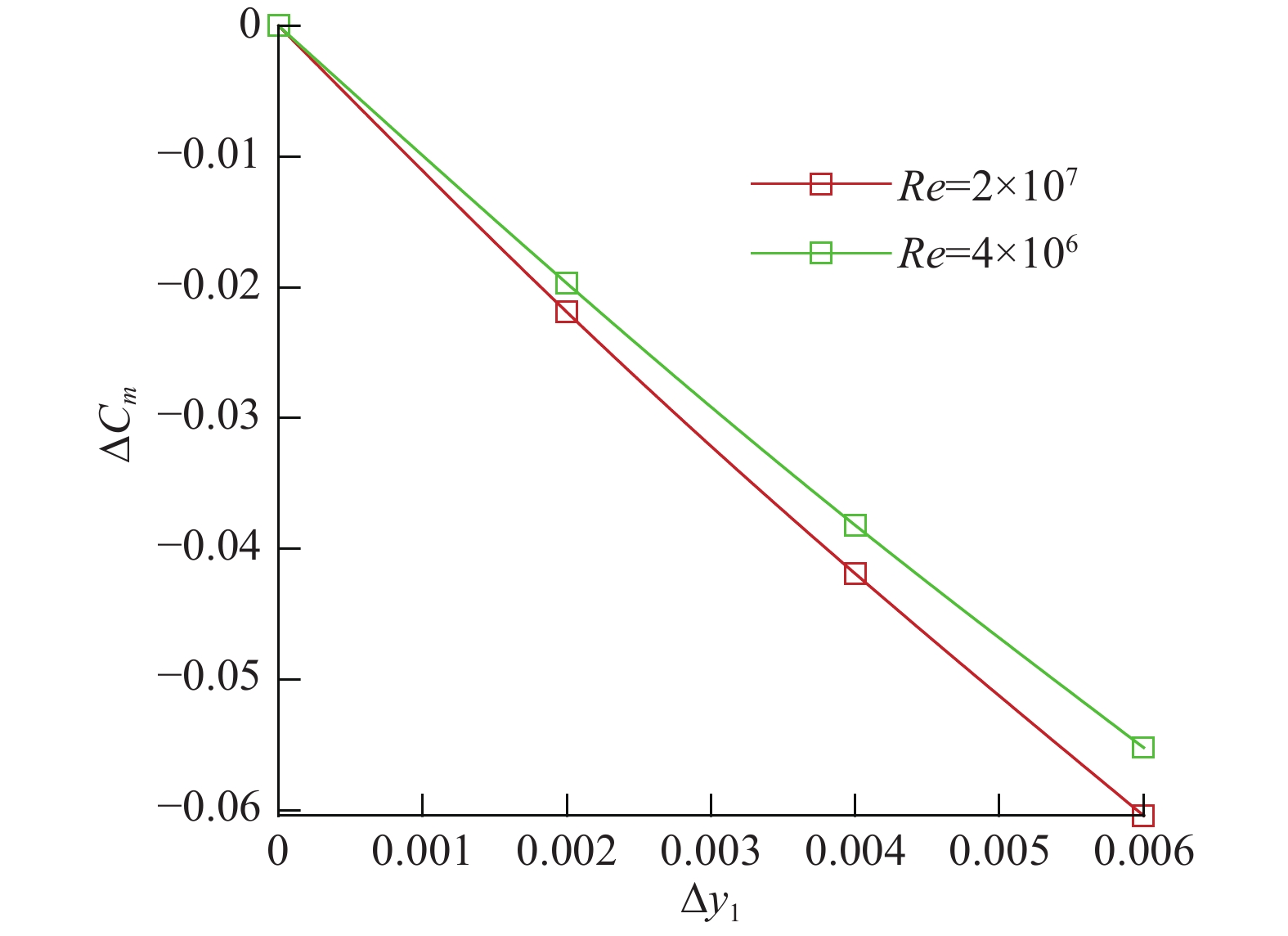
|
图 12 不同后缘厚度增加低头力矩的雷诺数效应(Ma = 0.72) Fig.12 Reynolds number effect for the pitching moment incre-ment of airfoils with different trailing-edge thickness (Ma = 0.72) |
通过第1节的计算分析发现,利用后缘发散概念,在已有超临界翼型后缘进行微小修形设计,即可有效控制激波强度,降低巡航阻力,改善抖振和阻力发散性能。但在实际飞机气动设计中如何利用后缘发散概念提升性能,本章提出了两个应用方向。
2.1 使用后缘发散设计换取厚度机翼厚度是气动设计的重要约束,同时对结构设计也至关重要。机翼厚度越大,型阻越大,激波强度越难以控制,气动设计的难度也越大。但厚度增大不仅意味着更充裕的内部空间,对降低结构重量提高结构效率也有重要意义。
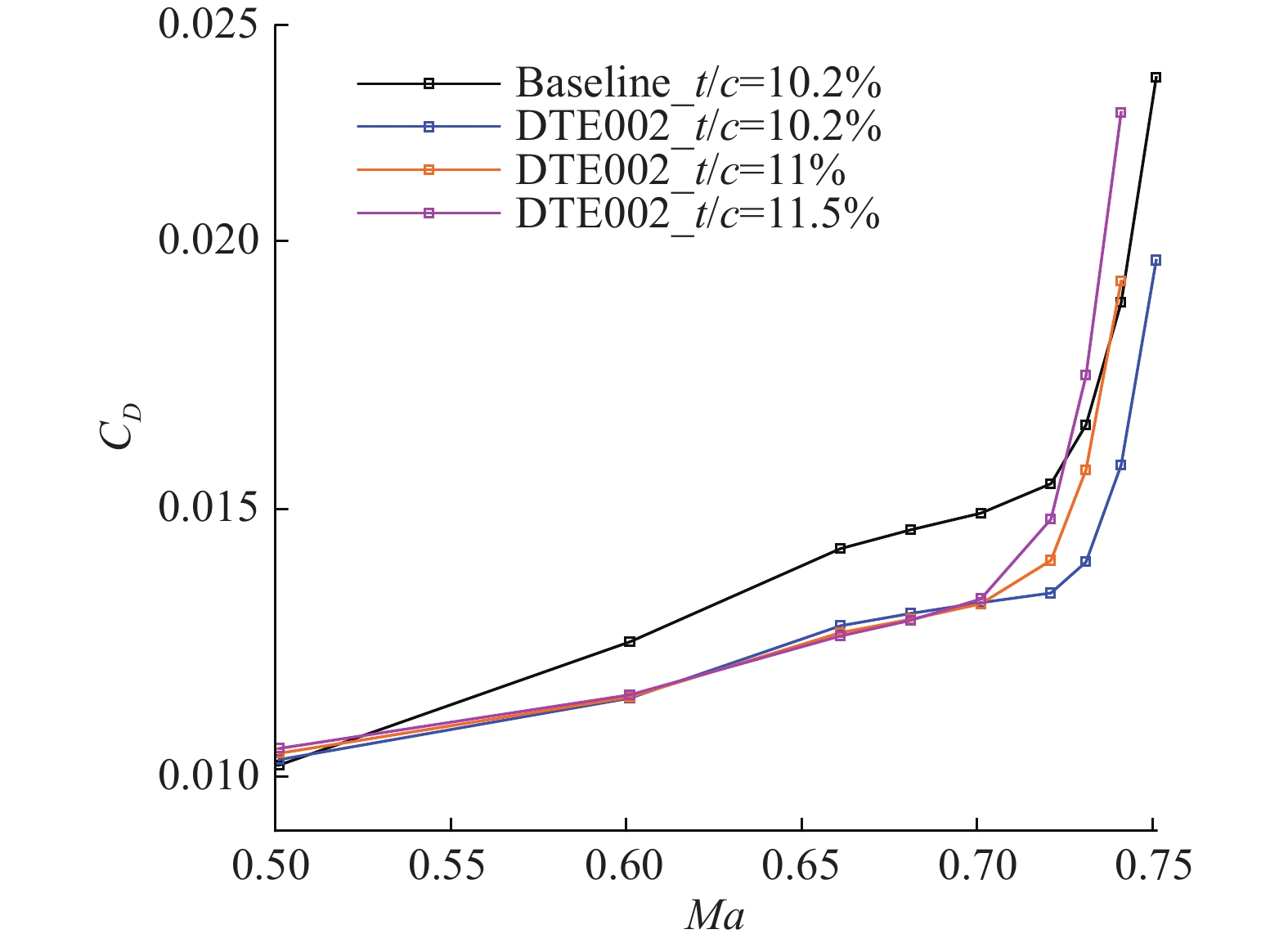
通过缩放将初始翼型相对厚度由10.2%分别增加到11%、11.5%,然后对厚度不同的三个翼型使用相同的后缘发散参数开展修形设计,

|
图 13 不同厚度的翼型对比 Fig.13 Comparison of airfoil shapes with different thickness |

|
图 14 不同翼型厚度的压力分布对比(CL = 0.97) Fig.14 Comparison of pressure distributions for airfoils with different thickness (CL = 0.97) |

|
图 15 不同翼型厚度的升阻极曲线对比(Ma = 0.72) Fig.15 Lift-drag polar curve comparison for airfoils with different thickness (Ma = 0.72) |
|
图 16 不同翼型厚度的阻力发散曲线对比(CL = 0.97) Fig.16 Drag divergence curve comparison for airfoils with different thickness (CL = 0.97) |
在某宽体客机高速机翼方案上实施后缘发散修形设计,针对机翼-机身-短舱-吊挂构型评估减阻收益和其他性能变化。设计巡航马赫数Ma = 0.85和升力系数CL_D下,初始方案表面等压线分布如图17所示。修形参数

|
图 17 初始方案表面等压线分布 Fig.17 Cp contour of baseline wing-fuselage-nacelle-pylon shape |

|
图 18 机翼后缘厚度增量沿展向分布 Fig.18 Variation of the trailing-edge thickness increment along the spanwise direction |

|
图 19 机翼后缘发散修形前后展向升力系数分布对比 Fig.19 Comparison of spanwise lift coefficient distributions before and after the DTE modification |
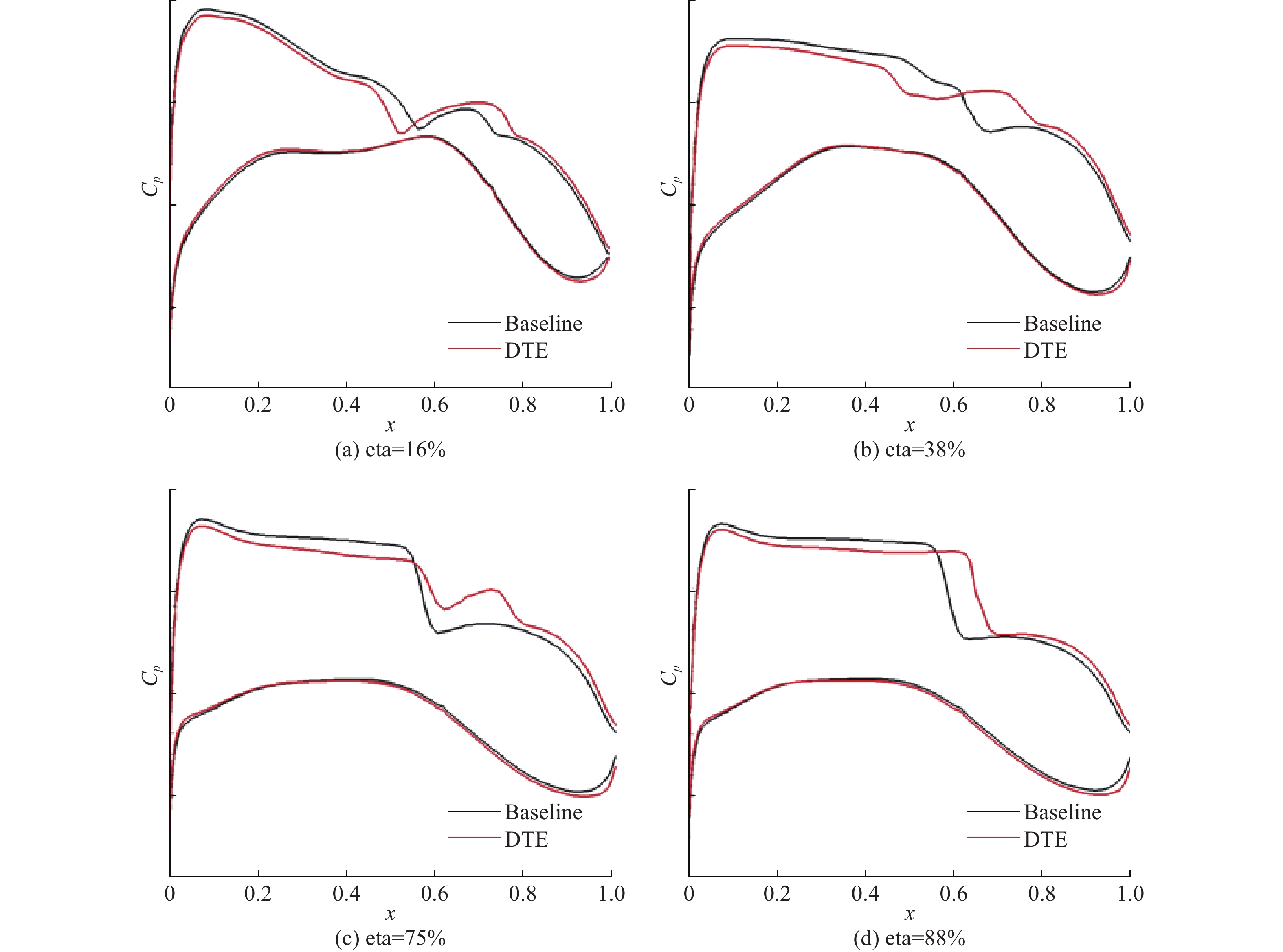
设计工况下四处机翼截面压力分布对比如图20,得益于攻角下降,修形后外翼部分激波强度降低,可降低波阻。表3列出了力系数的定量对比,由于仅使用了含800万单元的网格,阻力计算的绝对量偏大。根据文献[19]的研究结论,这样的网格密度对于评估修形前后阻力差量是足够的。后缘发散带来的性能变化量包括:Ma = 0.85、CL_D下减阻2.3 counts,低头力矩增加17%;Ma = 0.85、CL_D+0.02下减阻4.5 counts,低头力矩增加11%;Ma = 0.87、CL_D下减阻2.4 counts,低头力矩增加13%;从马赫数0.85到0.87的阻力蠕增量来看,修形前后阻力发散性能相当。值得注意的是在收获这些减阻收益的同时,低头力矩也明显增加,这将抵消一部分减阻收益。后经对全机外形进行配平计算后发现,Ma = 0.85、CL_D下减阻收益仅剩下1.1 counts,可见应用后缘发散减阻和配平阻力增加需要细致的权衡。相比之下,设计巡航马赫数、升力系数较大时,减阻效果更好,且低头力矩增加幅度也较小。
|
图 20 机翼后缘发散修形前后截面压力分布对比 Fig.20 Comparison of pressure distributions before and after the DTE modification |
| 表 3 机翼-机身-短舱-吊挂构型气动性能对比 Table 3 Comparison of aerodynamic characteristics of the wing-fuselage-nacelle-pylon configuration |
|
|
本文提出了一种幂函数表达的后缘发散修形设计方法,并在某宽体客机超临界翼型上开展了修形参数研究。增加修形幂次N或后缘厚度都可以控制激波强度,达到增升减阻的目的,但增加后缘厚度更加有效。具体的研究结论如下:
1) 后缘发散翼型有明显的雷诺数效应。雷诺数4×106下,后缘厚度一直增加到弦长的7‰都可以在跨声速下取得理想的减阻效果。而雷诺数2×107时,相同后缘厚度增量的跨声速减阻效果稍弱,同时低头力矩增加和亚声速增阻效果更显著。综合考量,雷诺数2×107下,后缘厚度增量取3‰c左右较为合适。
2) 在翼型设计应用中,发现后缘发散设计可以用来换取厚度增加。若要求设计点激波强度、升阻特性与初始翼型相当,后缘厚度3‰c的修形设计允许相对厚度从10.2%增至11.5%。
3) 在某宽体客机机翼方案上实施了内翼1‰c外翼2‰c后缘厚度增量的修形设计,在厚度和阻力发散性能不变的情况下,机翼-机身-短舱-吊挂构型可获得超过2 counts的阻力下降。
4) 在收获这些减阻收益的同时,后缘发散设计使低头力矩和亚声速阻力增加的副作用不容忽视,后缘发散减阻和配平阻力增加两个方面需要细致的权衡。后续还将尝试对整个翼型形状的优化设计来缓解低头力矩增加的问题。
| [1] |
HARRIS C D. Wind-tunnel investigation of effects of trailing-edge geometry on a NASA supercritical airfoil section[R]. NASA TM-X-2336, 1971. https://ntrs.nasa.gov/api/citations/19780019136/downloads/19780019136.pdf
|
| [2] |
GREGG R D, HOCH R W, HENNE P A. Application of divergent trailing edge airfoil technology to the design of a derivative wing[R]// SAE Transactions 98 (1989): 1587-1599. SAE TP 892288, 1989. doi: 10.4271/892288
|
| [3] |
HENNE P, GREGG R. A new airfoil design concept[C]//7th Applied Aerodynamics Conference, Seattle, WA, USA. Reston, Virigina: AIAA, 1989. AIAA 89-2201. doi: 10.2514/6.1989-2201
|
| [4] |
EL-GAMMAL M, NAUGHTON J W, HANGAN H. Drag force balance of a blunt and divergent trailing-edge airfoil[J]. Journal of Aircraft, 2010, 47(1): 345-348. DOI:10.2514/1.46308 |
| [5] |
KOSS D, BAUMINGER S, SHEPSHELOVICH M, et al. Pilot test of a low Reynolds number DTE-airfoil[C]//31st Aerospace Sciences Meeting, Reno, NV. Reston, Virginia: AIAA, 1993. AIAA 93-0643. doi: 10.2514/6.1993-643
|
| [6] |
THOMPSON B E, LOTZ R D. Divergent-trailing-edge airfoil flow[J]. Journal of Aircraft, 1996, 33(5): 950-955. DOI:10.1017/s0022112098002699 |
| [7] |
THOMPSON B, LOTZ R. Flow around a blunt and divergent trailing edge[J]. Experiments in Fluids, 2002, 33(3): 374-383. DOI:10.1007/s00348-002-0421-z |
| [8] |
EL-GAMMAL M, HANGAN H. Three-dimensional wake dynamics of a blunt and divergent trailing edge airfoil[J]. Experiments in Fluids, 2008, 44(5): 705-717. DOI:10.1007/s00348-007-0428-6 |
| [9] |
HUNTER A, THOMPSON B E. Turbulent separated flow over a rounded divergent trailing edge[C]//45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2007. AIAA 2007-274. doi:10.2514/6.2007-274
|
| [10] |
SEFCOVIC J A, SMITH D R. Aerodynamic control of a semi-span wing with a divergent trailing edge using synthetic jets[C]//27th AIAA Applied Aerodynamics Conference, San Antonio, Texas. Reston, Virginia: AIAA, 2009. AIAA 2009-3621. doi: 10.2514/6.2009-3621
|
| [11] |
SEFCOVIC J A, SMITH D R. Proportional aerodynamic control of a swept divergent trailing edge wing using synthetic jets[C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, Florida. Reston, Virginia: AIAA, 2010. AIAA 2010-92. doi: 10.2514/6.2010-92
|
| [12] |
HENNE P A. Innovation with computational aerodynamics: the divergent trailing-edge airfoil[M]//Applied Computational Aerodynamics. Washington DC: AIAA, 1990: 221-261. doi: 10.2514/5.9781600865985.0221.0261
|
| [13] |
YOO N S. Aerodynamic performance improvement by divergent trailing edge modification to a supercritical airfoil[J]. KSME International Journal, 2001, 15(10): 1434-1441. DOI:10.1007/BF03185685 |
| [14] |
THOMPSON B E, LOTZ R D. Reynolds number effects on divergent trailing edge airfoils in transonic flow[C]//ASME Fluids Engineering Division Summer Meeting, 1997.
|
| [15] |
CARUANA D, MIGNOSI A, ROBITAILLIÉ C, et al. Separated flow and buffeting control[J]. Flow, Turbulence and Combustion, 2003, 71(1-4): 221-245. DOI:10.1023/B:APPL.0000014918.93432.4f |
| [16] |
CARUANA D, MIGNOSI A, CORRÈGE M, et al. Buffet and buffeting control in transonic flow[J]. Aerospace Science and Technology, 2005, 9(7): 605-616. DOI:10.1016/j.ast.2004.12.005 |
| [17] |
LI Y C, WANG J J, HUA J. Experimental investigations on the effects of divergent trailing edge and Gurney flaps on a supercritical airfoil[J]. Aerospace Science and Technology, 2007, 11(2-3): 91-99. DOI:10.1016/j.ast.2006.01.006 |
| [18] |
陆超. 翼型改型对超临界翼型气动性能影响的研究[D]. 沈阳: 沈阳航空工业学院, 2009.
|
| [19] |
薛帮猛, 张文升, 张志雄. 民机飞发集成构型中机翼多目标优化设计[J]. 空气动力学学报, 2018, 36(6): 941-948. XUE B M, ZHANG W S, ZHANG Z X. Multi-objective wing optimization of civil aircrafts in engine-aircraft integration configuration[J]. Acta Aerodynamica Sinica, 2018, 36(6): 941-948. DOI:10.7638/kqdlxxb-2016.0126 (in Chinese) |
 2021, Vol. 39
2021, Vol. 39

