2. 西北工业大学 翼型、叶栅空气动力学国家级重点实验室,西安 710072;
3. 中国空气动力研究与发展中心 高超声速冲压发动机技术重点实验室,绵阳 621000;
4. 北京空天技术研究所,北京 100074
2. National Key Laboratory of Science and Technology on Aerodynamic Design and Research, NWPU, Xi'an 710072, China;
3. Science and Technology on Scramjet Laboratory, CARDC, Mianyang 621000, China;
4. Beijing Institute of Aerospace Technology, Beijing 100074, China
宽速域高超声速飞行器(如高超声速飞机、空天飞机),是一种具备常规跑道水平起降、高超声速巡航和可重复使用的飞行器。相比常规飞行器,此类飞行器具有明显的速度和飞行高度优势,而且可重复使用、效费比高,因而成为21世纪航空航天领域的前沿研究热点和各国竞相抢占的新的战略制高点。宽速域高超声速飞行器的飞行包线具有宽速域和大空域的特点,这就要求飞行器的飞行性能具有宽速域、全包线的适应性[1],气动设计需要兼顾整个速域内的飞行性能。然而,适合不同速域下的气动布局差别巨大,通常情况下,同一构型在不同速域下的气动性能往往是相互矛盾的[2-3]。因此,宽速域气动设计是一项极具挑战性的工作,是宽速域高超声速飞行器工程研制中亟需突破的瓶颈技术之一。
目前,提升高超声速飞行器宽速域综合气动性能的思路主要有两类。第一类是通过气动布局设计与优化,设计出兼顾不同速域气动特性的新概念布局,如:李世斌等[4]提出了宽速域“串联”飞行器和“并联”飞行器的设计方案,可以实现高超声速飞行器在宽速域范围内性能的兼顾;刘传振等[5]提出了涡波效应宽速域气动外形设计,通过定制乘波体平面形状在低速时利用涡效应改善了乘波体的低速性能。第二类思路是对翼型和机翼进行设计。然而,传统观点认为,高超声速机翼一般具有小展弦比和大后掠角的布局特征,三维效应较强,导致亚、跨声速下三维机翼各站位处的压力分布相比二维翼型压力分布会产生畸变[6],二维翼型设计将失去意义。另外,根据无黏流动的超声速线化理论,在超声速状态下翼型升力只与迎角有关,弯度和厚度都不产生升力,只产生阻力[7]。因而传统观点认为翼型的外形研究意义不大,一般采用对称薄翼型即可获得较好的气动性能。针对上述不支持开展翼型研究的观点,国内外学者开展了深入研究,结果表明:1)在亚、跨声速状态下,虽然三维效应会使机翼相对二维翼型的压力分布产生畸变,然而翼型特征对空气动力学特性影响的主要规律却不会改变。二维情况下气动性能更优的翼型在配置到三维机翼上也会有一定的收益,一般不会反而变差。2)超声速线化理论并不适用于高超声速,因而并不能在理论上支持高超声速条件下也应采用对称翼型的观点。事实上,在高超声速状态下,由于流动速度高,可有效压制三维横流效应,三维机翼不同站位处的压力分布和二维翼型表现出高度相似性。3)大多数超声速、高超声速飞行器采用的是对称的四边形或双弧形薄翼型,这种翼型具有很好的超声速和高超声速气动性能,但其亚、跨声速气动性能欠佳,亟待发展具有更好宽速域气动性能的翼型。总之,从空气动力学的角度分析,设计出一种具有良好宽速域气动性能的翼型,在理论上是可行的,在工程上也有迫切需要。
为了实现高超声速飞行器在不同速域下具有良好的综合气动特性,近年来有部分研究者开展了兼顾不同速域气动性能的宽速域翼型设计研究。日本JAXA的研究人员采用梯度优化方法,针对其提出的两级入轨空天飞机方案开展了大量宽速域翼型气动优化设计研究工作。其中,Ueno等[8]于2008年开展了兼顾跨声速气动性能的高超声速运载机机翼翼型的宽速域气动优化设计,并将优化翼型配置到了三维机翼上进行综合评估。结果表明,配置优化翼型后机翼的宽速域气动性能得到明显提升。2009年,Ueno等[9]又采用梯度优化方法开展了机翼的宽速域气动优化设计研究。文章指出,优化的二维翼型配置到机翼上可以明显改善机翼的宽速域气动性能。尽管对大后掠角、小展弦比的机翼而言,最终应该对剖面直接进行三维优化设计,但由宽速域翼型配置的机翼能够提供一个更理想的初始外形,可以帮助设计人员更快地找到优化解。在国内,2018年西北工业大学孙祥程、韩忠华等[10]开展了高超声速宽速域翼型分析与设计研究,并发明了一种能够兼顾跨声速和高超声速气动特性的新概念翼型。2019年,西北工业大学柳斐、韩忠华等[11]发展了基于代理模型的宽速域气动优化设计方法,并成功应用于宽速域翼型/机翼优化设计。2019年,西北工业大学张阳、韩忠华等[12]开展了高超声速飞行器宽速域翼型多目标优化设计研究,得到了优化翼型关于不同速域下升阻比的Pareto前沿。2020年,张阳、韩忠华等[13]进一步开展了考虑升力匹配的双后掠机翼宽速域气动优化设计研究,结果表明,剖面翼型设计对于提升机翼宽速域气动性能十分重要。
综上所述,目前国内外针对宽速域翼型设计已取得了一定的研究成果,表明剖面翼型设计对于宽速域高超声速飞行器仍具有重要意义。对于小展弦比、大后掠角的高超声速机翼,宽速域翼型设计及其流动机理的研究可以为三维机翼剖面设计提供理论指导和更优的初始外形。然而,现有研究缺乏关于翼型几何特征及其协调宽速域气动性能的流动机理的分析,未能澄清翼型设计对于高超声速飞行器的是否仍有重要意义这个问题,并且对宽速域翼型气动外形工程设计的指导意义不足。因此,本文拟针对高超声速飞行器宽速域翼型气动设计难题,开展宽速域翼型高效全局气动优化设计研究。
1 翼型宽速域气动优化设计方法 1.1 数值模拟程序有效性验证选取DLR F6翼身组合体标模以及方形弹体标模对RANS方程求解器的精度进行验证。
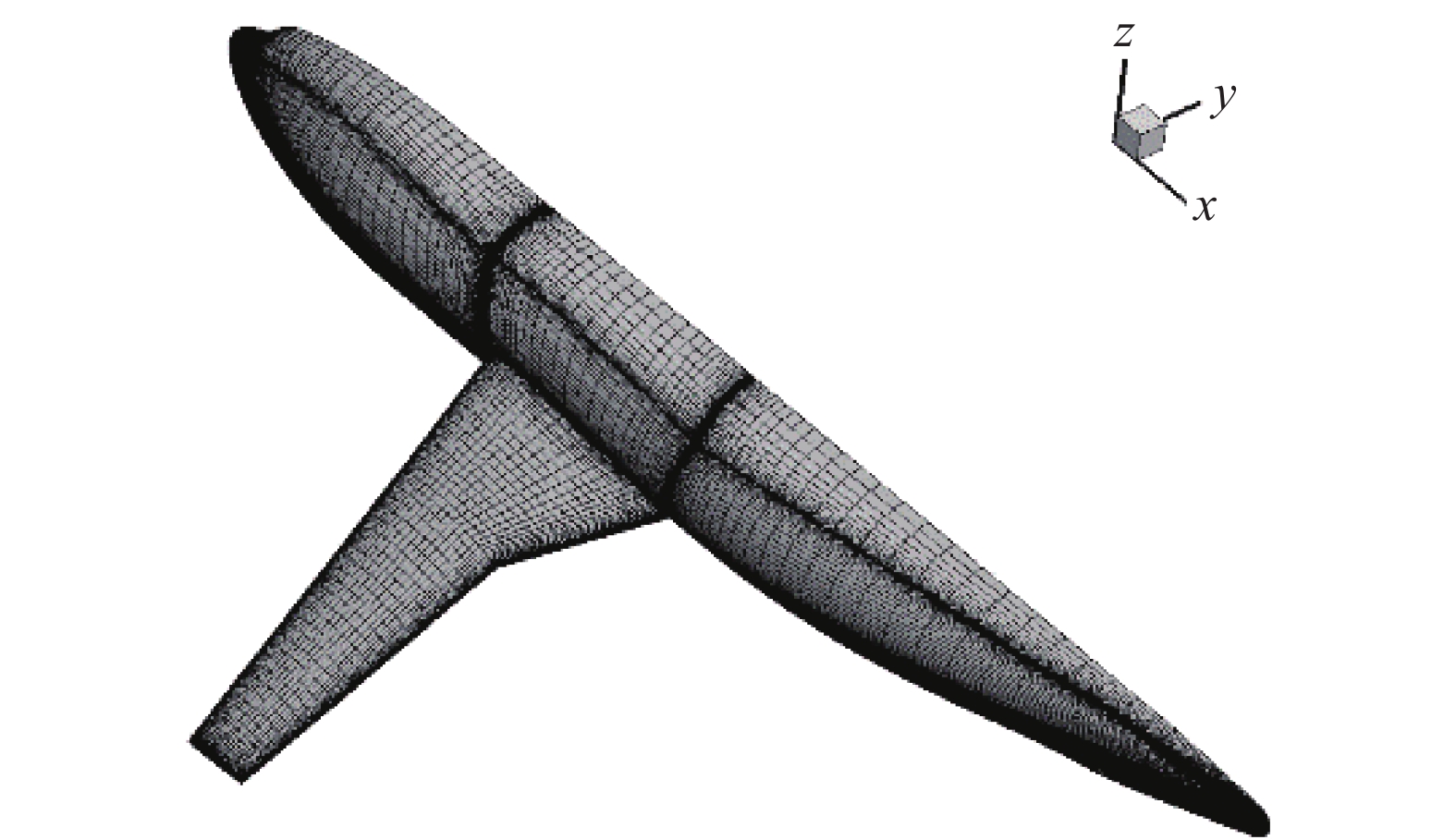
1.1.1 三维跨声速流动数值模拟验证DLR F6翼身组合体计算状态为
|
图 1 DLR F6翼身组合体表面网格 Fig.1 Surface grids for the transonic DLR F6 configuration |
|
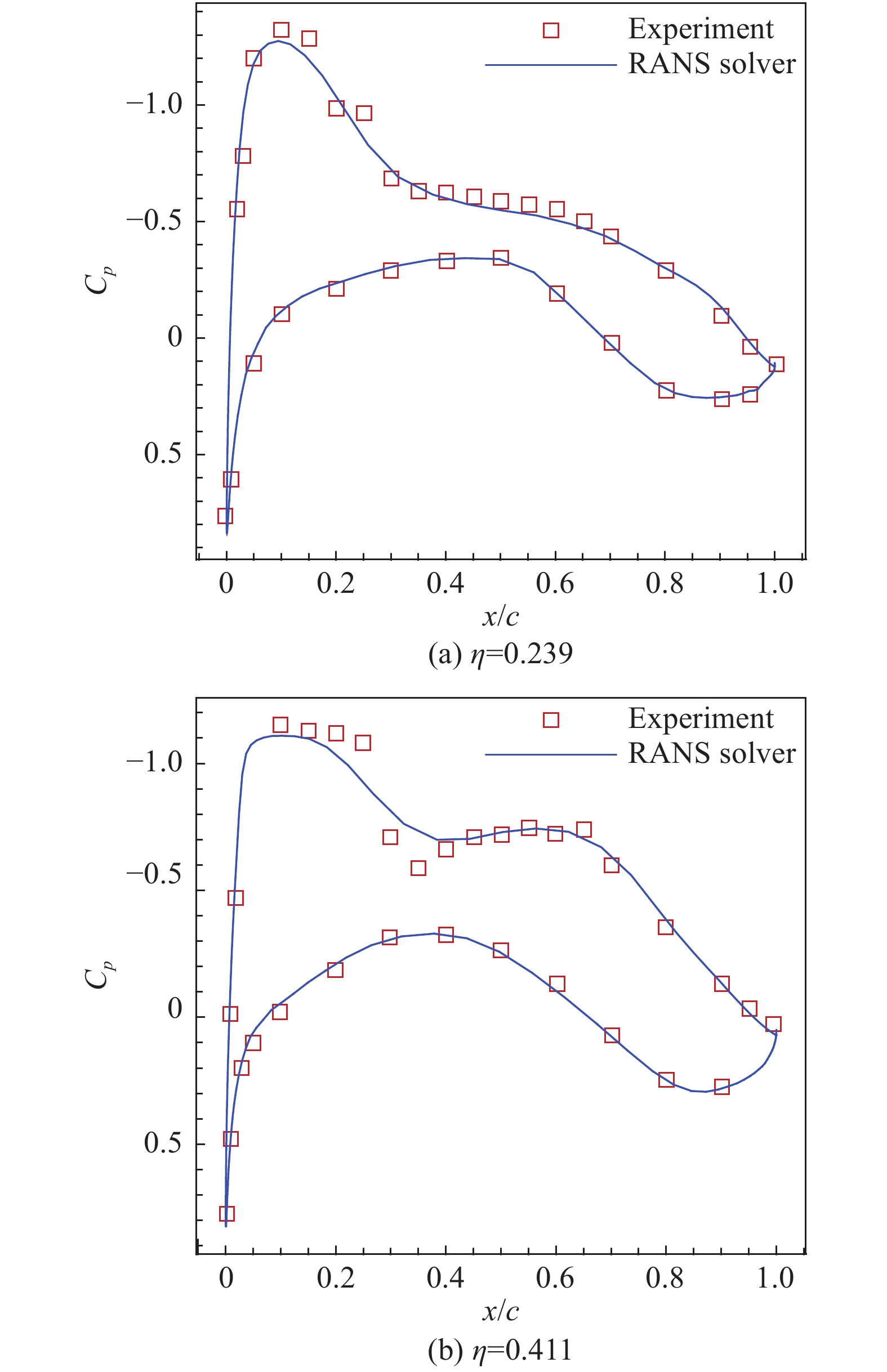
图 2 机翼不同展向站位压力系数分布的计算值与实验值对比 |
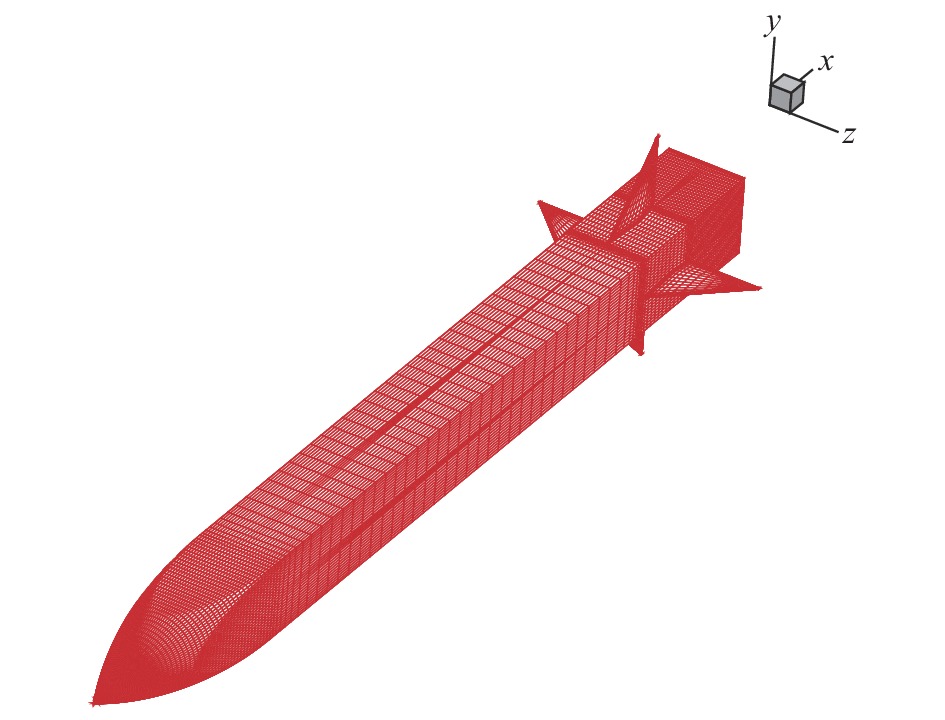
对方形弹体绕流进行数值模拟:计算状态为
|
图 3 方形弹体表面网格示意图 Fig.3 Surface grids for a square-section-shape missile |
|
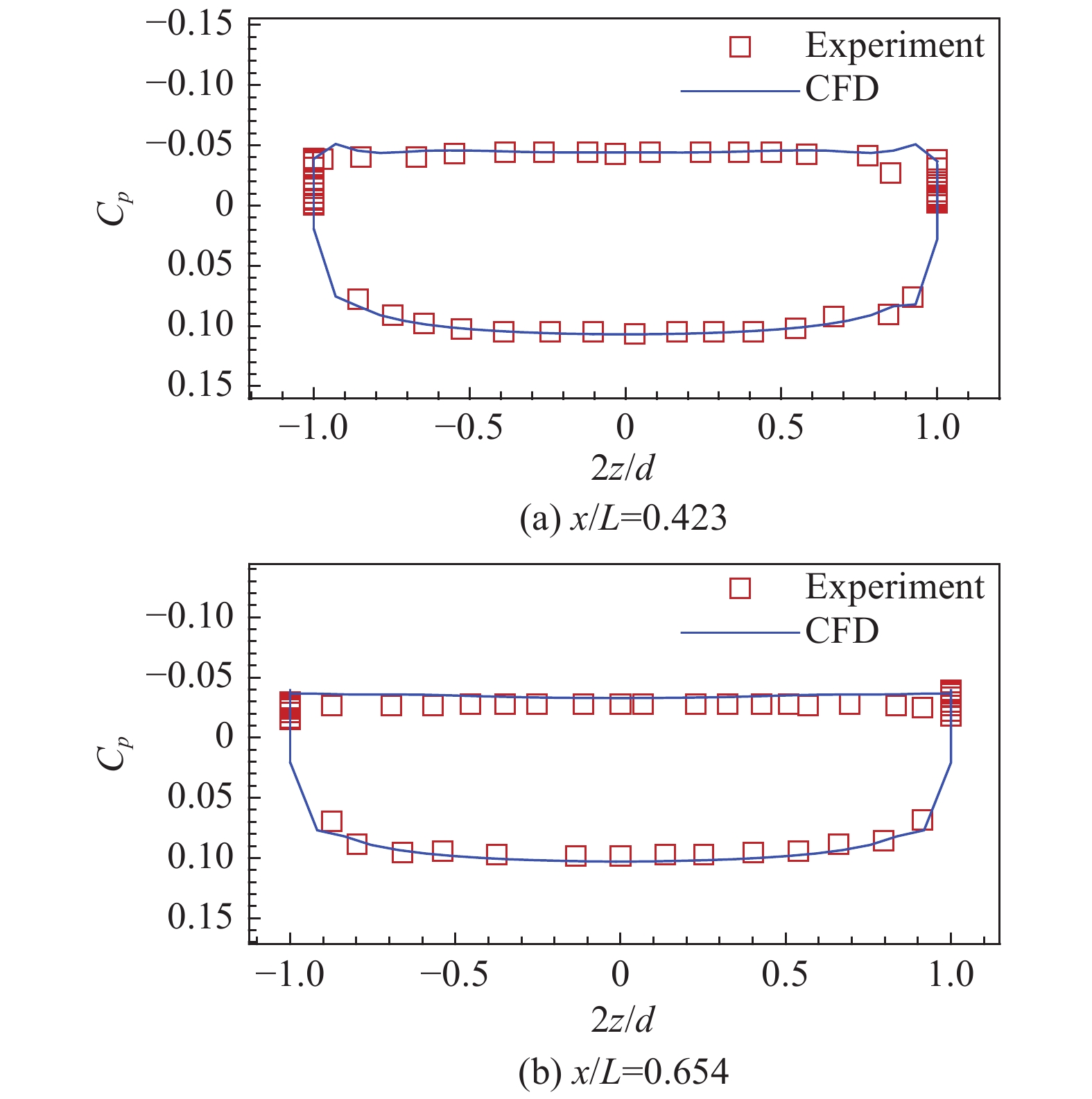
图 4 弹体不同流向站位压力系数分布的计算值与实验值对比 |
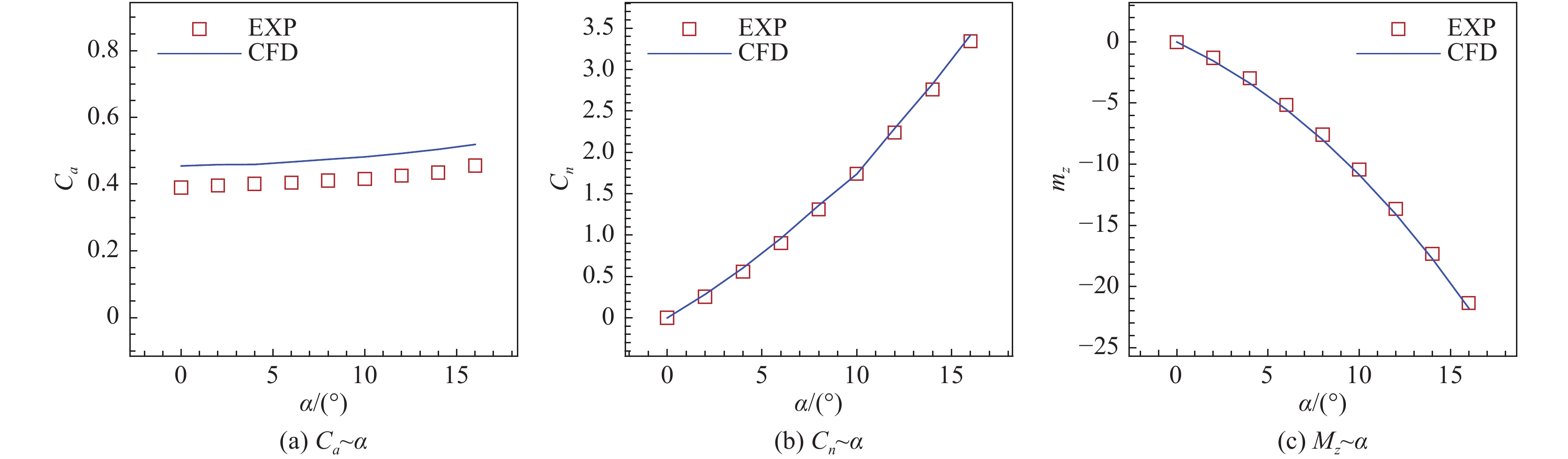
|
图 5 方形弹体力系数的计算值与实验值的对比 |
采用Kulfan[16-17]提出的Class function/Shape function Transformation (CST)方法进行翼型参数化。该方法采用一个类函数
上表面:
| $ {y_u} = C(x) {S_u}(x) + x {y_{_{{\rm{TEu}}}}} $ | (1) |
下表面:
| $ {y_l} = C(x) {S_l}(x) + x {y_{_{{\rm{TEl}}}}} $ | (2) |
其中:
采用8阶CST方法对翼型进行参数化,参数化一个翼型需要18个设计变量。
1.3 高效全局气动优化设计方法采用了课题组自主开发的基于代理模型的多目标多约束高效通用优化软件“SurroOpt”[18-22]开展宽速域翼型优化设计,其基本框架如图6 所示。
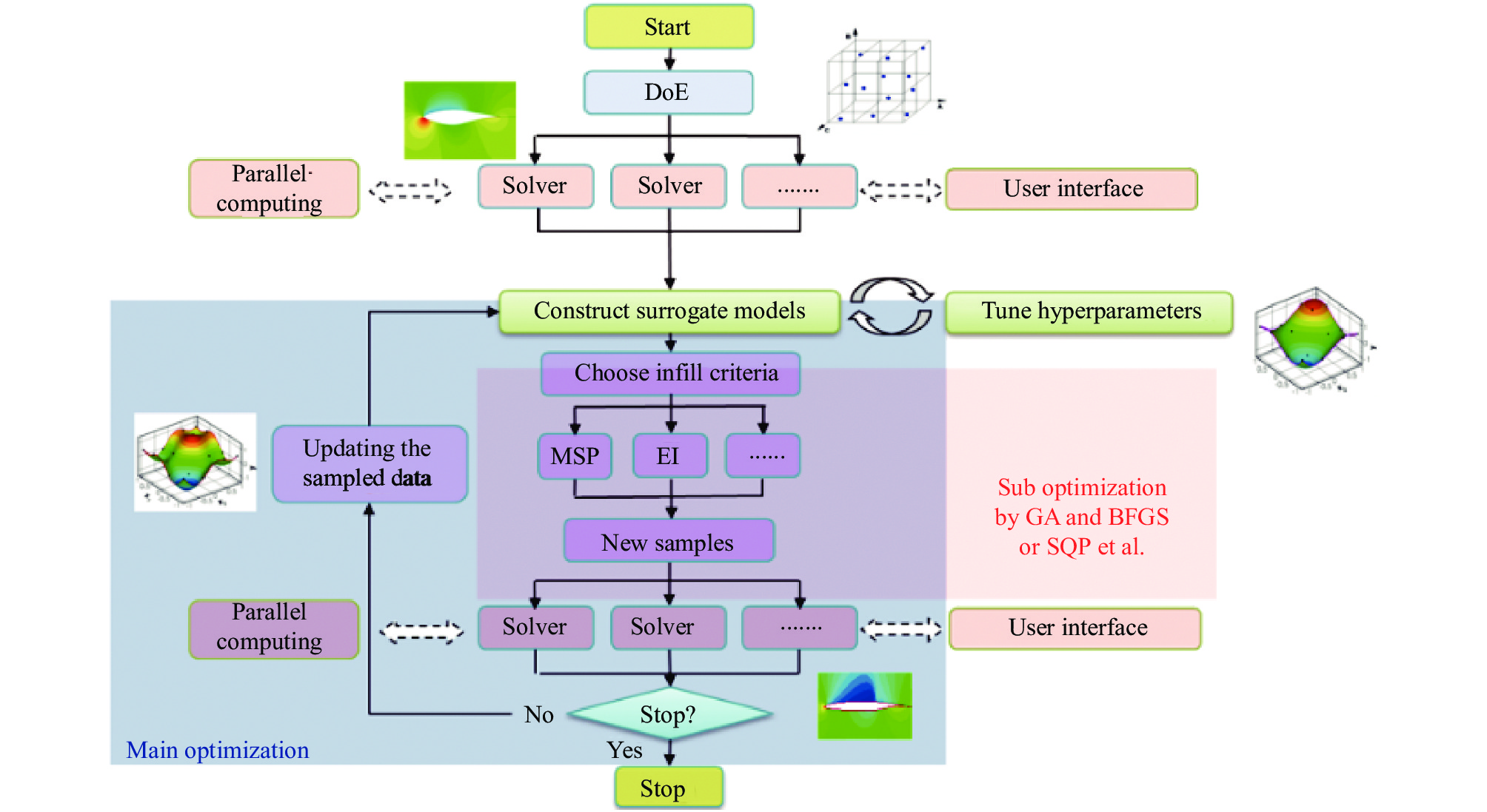
|
图 6 基于代理模型的通用优化软件SurroOpt流程图[18] Fig.6 Flowchart of a generic surrogate-based optimization software “SurroOpt”[18] |
首先,对设计空间进行实验设计,并进行数值模拟分析得到初始样本点的响应值,建立初始代理模型。其次,按照一定的加点准则,采用传统优化算法求解子优化问题,并以很小的计算代价对优化解进行预测。最后,对预测得到的最优解再次进行数值模拟分析,将结果作为样本点数据添加进已有的样本点集中,不断更新代理模型,直到所产生的样本点序列收敛于局部或全局最优解。有关该方法的具体描述,可参见文献[23-25]。
2 兼顾跨声速与高超声速气动性能的宽速域翼型优化设计对于宽速域高超声速飞行器的气动设计,既需要足够的高超声速升阻比以保证良好的巡航飞行效率,也需要高的跨声速升阻比以获得良好的加速性能。需要进行兼顾高超声速和跨声速气动性能的翼型宽速域气动优化设计研究。
2.1 翼型宽速域气动优化设计与评估将NACA64A-204翼型作为基准翼型,开展兼顾高超声速和跨声速气动性能的翼型宽速域气动优化设计。以提升高超声速下的升阻比为优化目标,将跨声速时的升阻比作为约束。设计工况为:高度9 km,马赫数0.8,雷诺数7.6×106,迎角1.5°;高超声速设计状态:高度26 km,马赫数6,雷诺数4.23×106,迎角5°。
优化问题的数学模型为:
| $ \begin{split} {\text{max}}\;\;&{\left( {{C_L}/{C_D}} \right)_{Ma = 6}} \\ {\text{s}}{\text{.t}}{\text{.}}\;\;&{\left( {{C_L}/{C_D}} \right)_{Ma = 0.8}} > {\left( {{C_L}/{C_D}} \right)_{0,Ma = 0.8}} \\& {C_{L,Ma = 0.8}} > \;{C_{{L_0},Ma = 0.8}}\; \\& {C_{L,Ma = 6}} > \;{C_{{L_0},Ma = 6}} \\& \left| {t - {t_0}} \right| < 0.02{t_0} \end{split} $ | (3) |
其中,
图7 给出了基准翼型与修形后优化翼型的几何外形对比图。与基准翼型NACA64A204相比,优化翼型头部的前缘半径明显减小,最大厚度位置后移至约50%弦长处。优化翼型上表面型线与双弧形翼型类似,下表面呈“双S”形,即靠近翼型前后缘各有一个局部的反弯。表1 为基准翼型和优化翼型在计算迎角下的气动系数对比。与基准翼型相比,优化翼型跨声速升阻比增加了15.9%,高超声速升阻比增加了121.6%,宽速域综合性能得到明显提升。
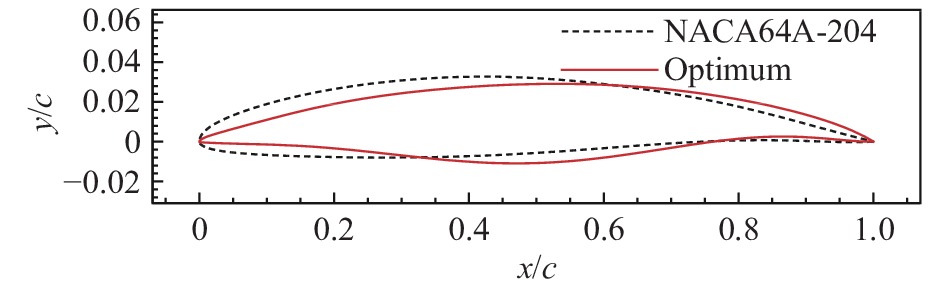
|
图 7 基准翼型与优化翼型几何外形对比 Fig.7 Comparison of geometric shapes between the optimal and baseline airfoils |
| 表 1 优化翼型与基准翼型的气动力系数对比 Table 1 Comparison of aerodynamic coefficients between the optimal and baseline airfoils |
|
|
对比优化翼型与常规超声速翼型的宽速域气动性能,选取的对比翼型是对称的四边形和双弧形翼型。两种对称翼型的厚度均为4%弦长,最大厚度位置为50%弦长处,前缘倒圆半径为0.1%弦长。优化翼型与四边形、双弧形翼型的几何外形对比如图8所示。

|
图 8 优化翼型与常规高超声速翼型几何外形对比 Fig.8 A comparison of airfoil geometries between the optimized and conventional hypersonic airfoils |
表2和表3是低速状态(
| 表 2 不同速域下优化翼型与四边形翼型气动特性对比 Table 2 Comparison of aerodynamic coefficients between the optimal and quadrilateral airfoils at different Mach numbers |
|
|
| 表 3 不同马赫数下优化翼型与双弧形翼型气动特性对比 Table 3 Comparison of aerodynamic coefficients between the optimal and double-arc airfoils at different Mach numbers |
|
|
图9 为基准翼型与优化翼型在跨声速
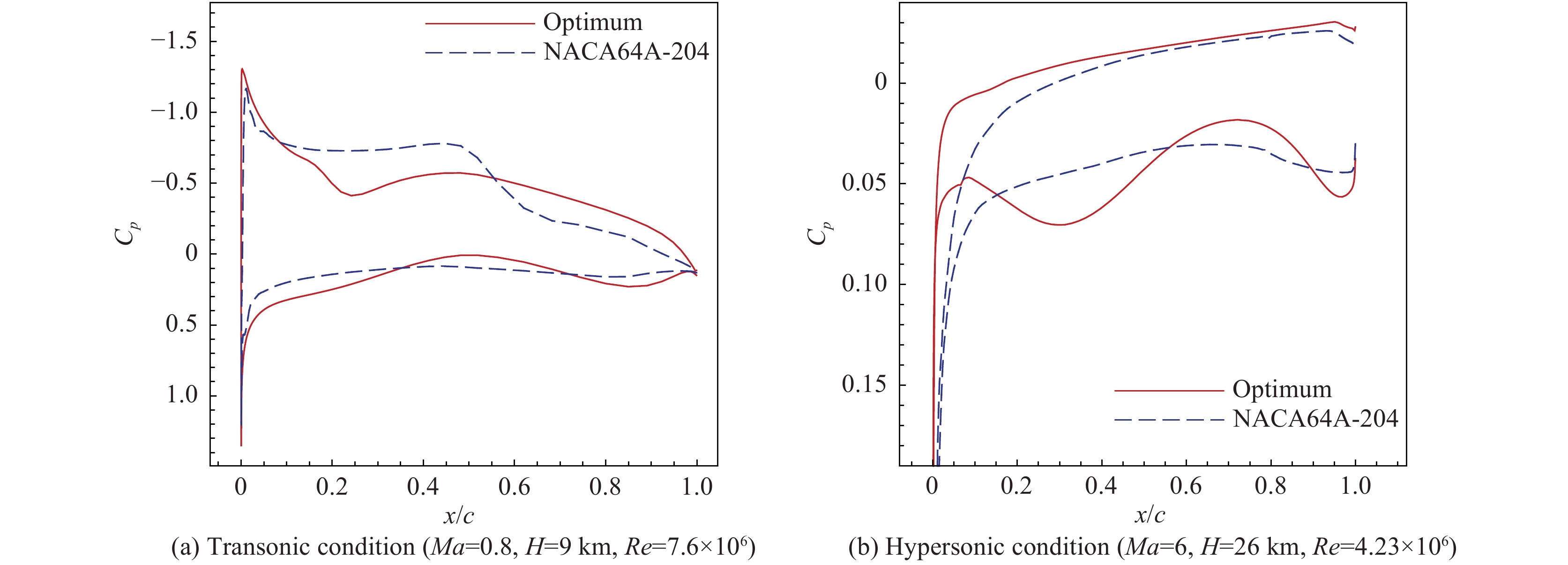
|
图 9 优化翼型与基准翼型压力系数分布对比图 Fig.9 Comparisons of pressure-coefficient distributions between the baseline and optimized airfoils |
|
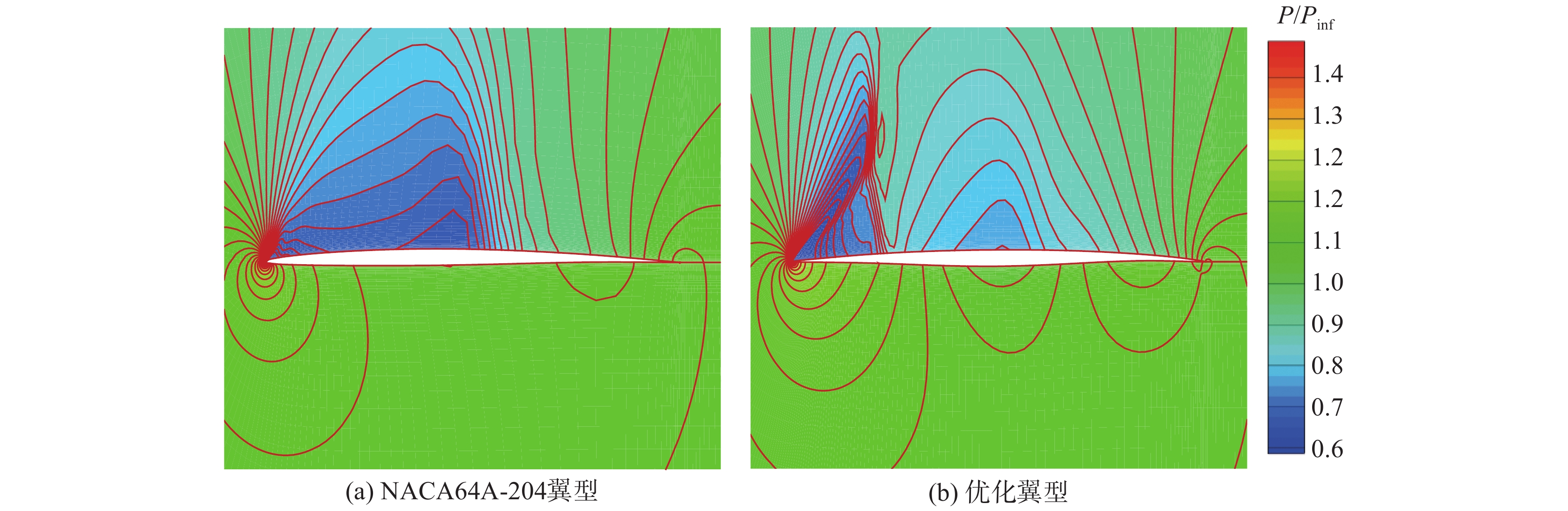
图 10 跨声速状态下优化翼型与NACA64A-204翼型的压力云图对比(Ma = 0.8, α = 1.5°, Re = 7.6×106) Fig.10 Comparison of pressure contours between the baseline and optimized airfoils in a transonic flow (Ma = 0.8, α = 1.5°, Re = 7.6×106) |

|
图 11 高超声速状态下优化翼型与NACA64A-204翼型的压力云图对比(Ma = 6, α = 5°, Re = 4.23×106) Fig.11 Comparison of pressure contours between the baseline and optimized airfoils in a hypersonic flow (Ma = 6, α = 5°, Re = 4.23×106) |
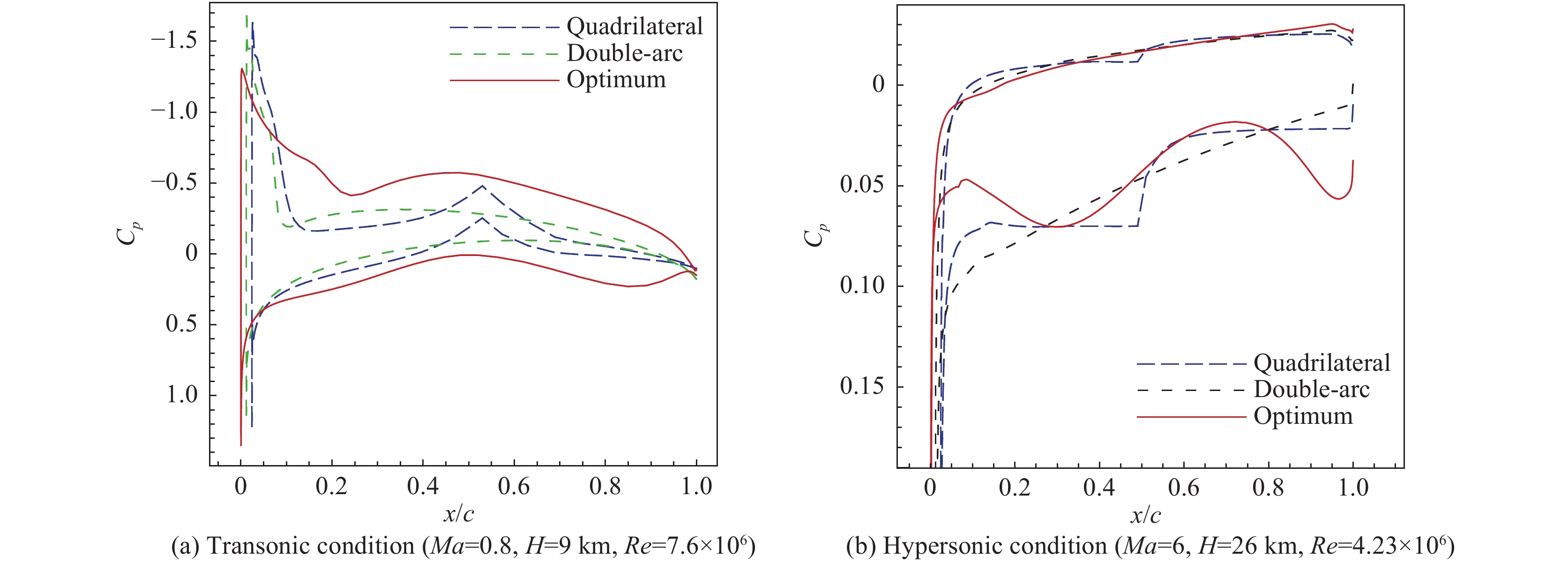
图12 是优化翼型与四边形翼型和双弧形翼型在跨声速和高超声速设计点的压力系数分布对比。图13和图14 是在跨声速和高超声速状态下的压力云图对比。对称四边形翼型和双弧形翼型没有弯度,根据线化理论,超声速状态下翼型弯度不产生升力,只产生阻力,因而对称四边形翼型和双弧形翼型具有较好的超声速气动性能。但对称翼型在亚/跨声速状态下的升力特性较差,如图13 所示,在跨声速设计点两种对称翼型的上表面低压区面积明显小于优化翼型,因此跨声速升力系数也显著小于优化翼型。在跨声速状态下,优化翼型与对称四边形翼型、双弧形翼型的阻力系数相差不大,但升力系数的差异使得优化翼型的跨声速升阻比显著优于四边形翼型和双弧形翼型。如图12(b),在高超声速状态下,优化翼型的下表面呈现出多次压缩特征,这是由其独特的下表面双“S”形导致的:自由来流接触到翼型前缘经历第一次压缩,下表面前缘点后经历第一个“S”弯,流动首先膨胀,这使得前缘附近激波强度减弱,有利于减小阻力,但同时也损失了升力。在膨胀之后,下表面流动再先后经历一次压缩和一次膨胀,最后在下表面后缘,流动经历第三次压缩。由图12(b)所示,最后一次压缩增加了额外的升力,部分弥补了下表面前缘膨胀导致的升力损失。高超声速状态下,表面多次压缩的特征也使气动载荷在弦向的分布更加均匀,相比常规对称翼型,优化翼型的抬头力矩更小。
|
图 12 优化翼型与传统高超声速翼型压力系数分布对比图 Fig.12 Comparisons of pressure-coefficient distributions between the optimized and conventional hypersonic airfoils |

|
图 13 跨声速状态下优化翼型与传统高超声速翼型的压力云图对比(Ma = 0.8, α = 1.5°, Re = 7.6×106) Fig.13 Comparison of pressure contours between the optimized and conventional hypersonic airfoils in a transonic flow (Ma = 0.8, α = 1.5°, Re = 7.6×106) |

|
图 14 高超声速状态下优化翼型与传统高超声速翼型的压力云图对比 (Ma = 6, α = 5°, Re = 4.23×106) Fig.14 Comparison of pressure contours between the optimized and conventional hypersonic airfoils in a hypersonic flow (Ma = 6, α = 5°, Re = 4.23×106) |
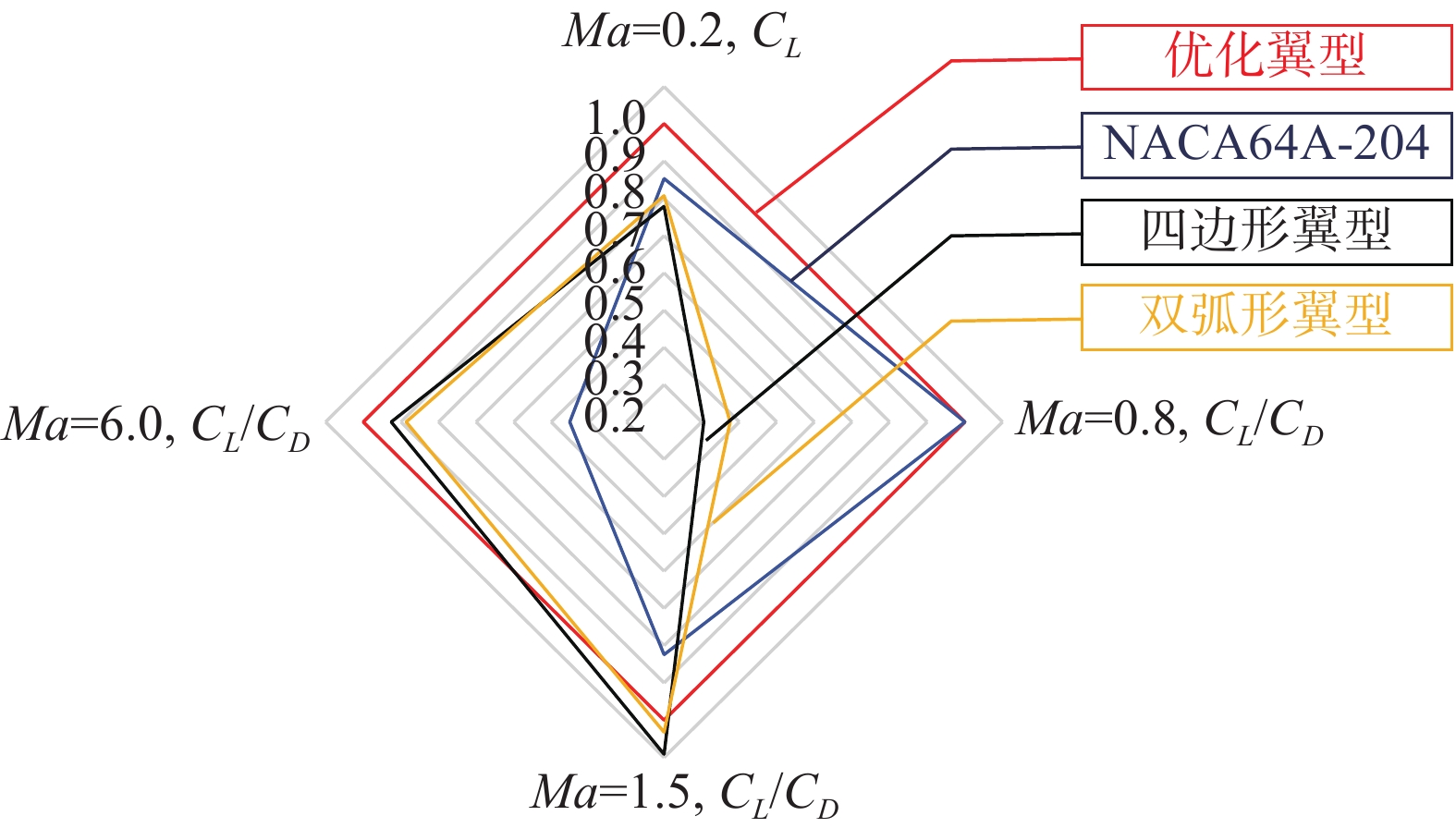
为了综合评估不同翼型的宽速域气动性能,图15给出了优化翼型与NACA64A-204翼型、四边形翼型及双弧形翼型在不同马赫数下气动特性对比的雷达图。可以看出:相对于亚、跨声速气动性能较好的NACA64A-204翼型,优化翼型的低速升力系数和跨声速升阻比略有优势;而在超声速和高超声速状态,优化翼型的升阻比显著优于NACA64A-204翼型。相对于超声速、高超声速气动性能较好的对称四边形翼型和双弧形翼型,优化翼型在超声速设计状态的升阻比略小,但差距均在10%以内,在高超声速设计状态下,优化翼型的升阻比略大于四边形翼型和双弧形翼型;但在亚声速和跨声速状态,优化翼型相应的指标显著优于四边形翼型和双弧形翼型。宽速域翼型设计时寻求全速域内气动性能的综合最优,而不是过分追求某一速域气动性能而严重损害其他速域的气动性能。从图15 可以看出优化翼型的各指标围成的雷达图面积明显大于其他常规翼型,说明优化翼型具有最好的宽速域气动性能。
|
图 15 不同翼型的升阻比雷达图(关于优化翼型的各指标作归一化处理) Fig.15 Radar-chart of the aerodynamic performance of different airfoils (values normalized by those of the optimal airfoil at each point) |
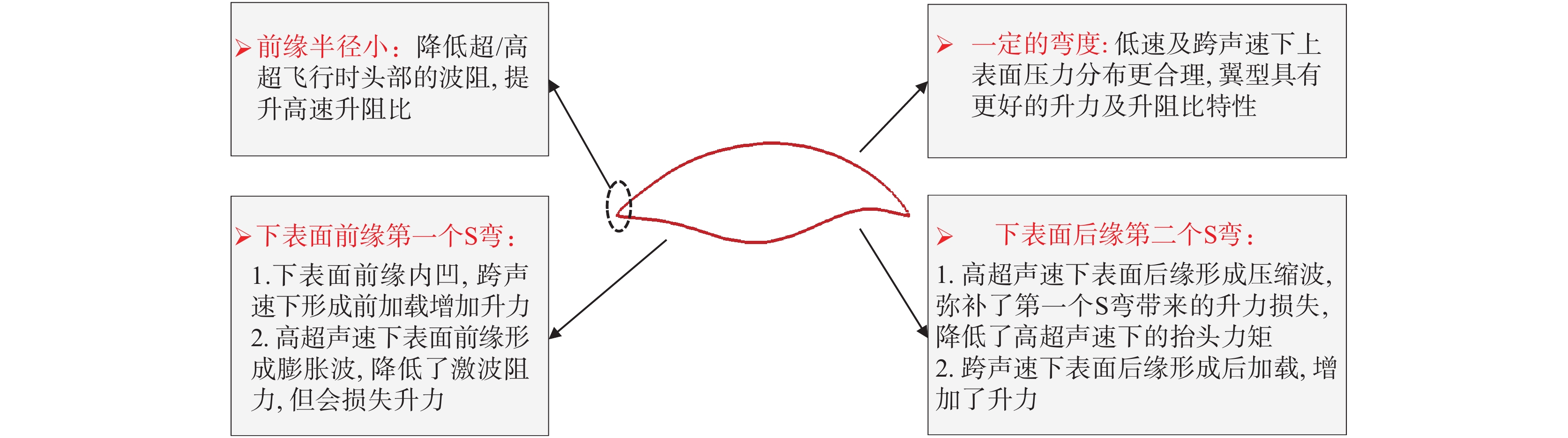
图16 是对优化翼型的几何外形协调宽速域气动性能的空气动力学原理的分析示意图。
|
图 16 优化翼型的几何外形与流动机理分析 Fig.16 Analyses of geometry and flow mechanism of the optimal airfoil |
总结为如下几点:
(1)优化翼型具有比较尖的前缘。由于需要进行高超声速飞行,在满足防热特性前提下,翼型需要小的前缘半径以削弱头部激波的强度,减小激波阻力,提升超声速、高超声速升阻比。
(2)优化翼型具有一定的弯度。在亚、跨声速状态下,翼型上表面产生的吸力是升力的重要来源,翼型具有一定的弯度,可以显著改善亚、跨声速的升力和升阻比特性,但超声速阻力会略有增加。
(3)优化翼型下表面具有“双S”形特征。其中,下表面前段第一个“S”:在跨声速下,翼型下表面前缘向内凹,来流经过前缘点后在下表面压缩形成前加载,可以增加亚、跨声速下的升力,减小低头力矩;而高超声速下使自由来流在前缘点后膨胀,使得前缘附近的激波被削弱,有利于减小阻力,但代价是损失了部分的升力。下表面后段第二个“S”:在跨声速下,类似于超临界翼型形成后加载增加升力;而在高超声速下会形成压缩波增加升力,弥补了前缘第一个“S”弯带来的升力损失,并使弦向气动力分布更加均匀,减小了抬头力矩。
3 宽速域翼型多目标优化设计为了进一步解释宽速域翼型兼顾不同速域气动性能的原理,开展了宽速域翼型Pareto多目标气动优化设计。优化目标为跨声速和高超声速设计状态下的升阻比,将两个状态的下升阻比、升力系数以及翼型厚度作为约束。优化问题的数学模型表述为:
| $ \begin{split} {\text{max}}\;\;&{\left( {{C_L}/{C_D}} \right)_{Ma = 6}} \\ {\text{max}}\;\;&{\left( {{C_L}/{C_D}} \right)_{Ma = 0.8}} \\ {\text{s}}{\text{.t}}{\text{.}}\;\;&{\left( {{C_L}/{C_D}} \right)_{Ma = 0.8}} > {\left( {{C_L}/{C_D}} \right)_{0,Ma = 0.8}} \\& {\left( {{C_L}/{C_D}} \right)_{Ma = 6}} > {\left( {{C_L}/{C_D}} \right)_{0,Ma = 6}} \\& {C_{L,Ma = 0.8}} > \;{C_L}_{_0,Ma = 0.8}\; \\& {C_{L,Ma = 6}} > \;{C_L}_{_0,Ma = 6} \\& \left| {t - {t_0}} \right| < 0.02{t_0} \end{split} $ | (4) |
基准翼型仍采用NACA64A-204翼型,采用CST参数化方法,设计空间取为基准翼型设计变量上下浮动50%。
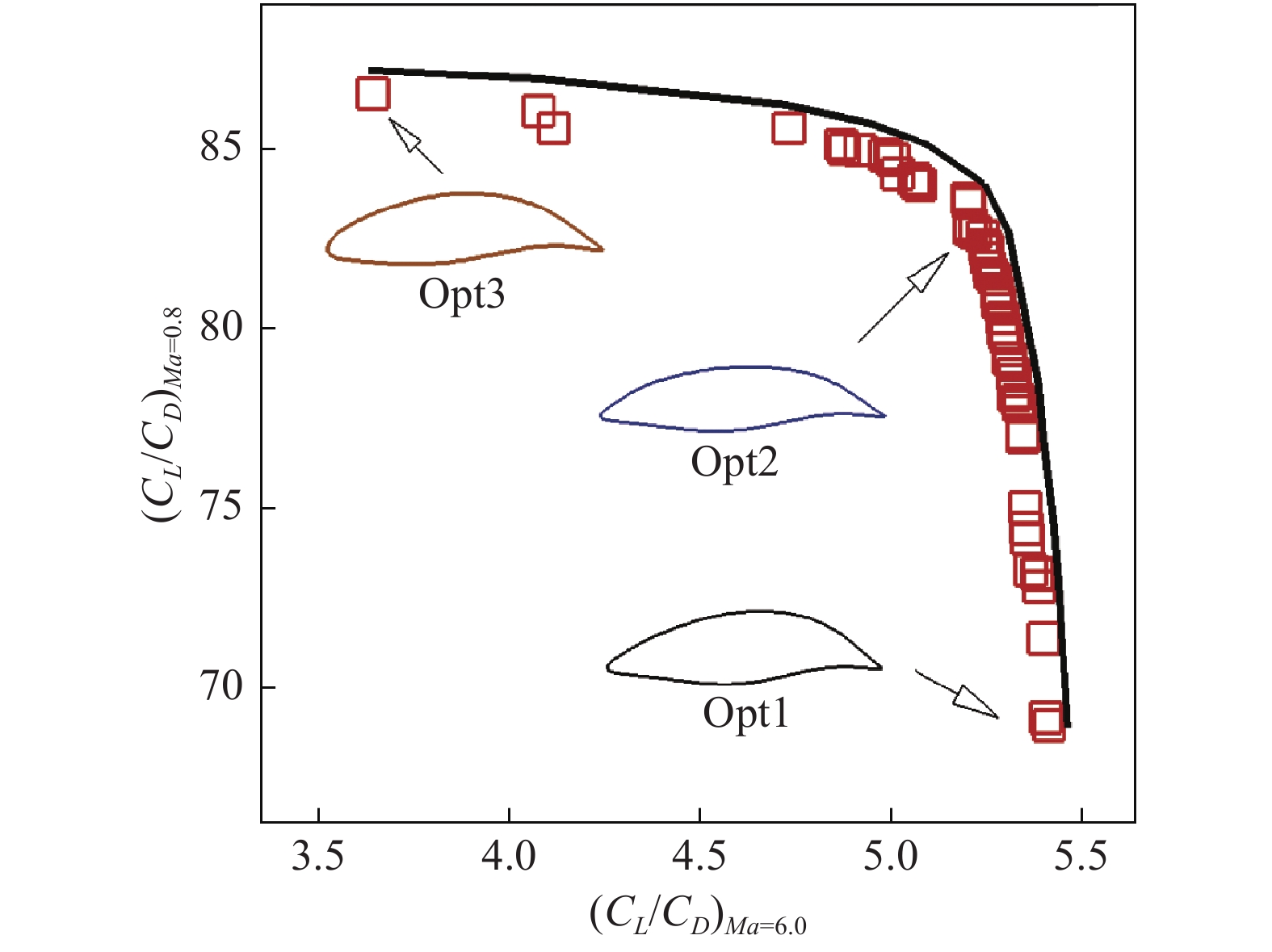
图17 给出了多目标优化所得的Pareto前沿,其中红色空心方块代表的是Pareto前沿上的各优化翼型在目标空间的位置,蓝色实心点代表基准翼型NACA64A-204在目标空间的位置。可见,相比基准翼型,Pareto前沿已向目标空间右上角大幅推进,说明Pareto前沿上优化翼型的宽速域气动性能显著优于基准翼型。图中黑色实线是对Pareto前沿外形的拟合线,Pareto前沿右侧拟合线急剧下降,说明相对于右上角区域的优化翼型,若要进一步提升它们的高超声速升阻比,必须损失更多的跨声速升阻比;Pareto前沿左侧拟合线接近水平,说明对于右上角区域的优化翼型,若要进一步提升它们的跨声速升阻比,必须损失更多的高超声速升阻比。对于宽速域翼型,追求的是宽速域下气动性能的综合最优,Pareto前沿右上角区域的优化翼型达到了跨声速和高超声速气动性能的最佳折中,而位于Pareto前沿上两侧的点则由于过分追求某一速域的气动性能,而导致其他速域气动性能严重恶化,不符合宽速域翼型的设计要求。

|
图 17 多目标优化得到的Pareto前沿 Fig.17 Pareto front obtained by a multi-objective optimization |
从图17 中的Pareto前沿上两侧以及右上角区域各选取一个翼型作为代表性翼型进行评估和分析。如图18 ,选取的三个翼型分别记为Opt1、Opt2和Opt3。从三个翼型位于Pareto前沿上的位置可知:Opt1翼型侧重于高超声速气动性能,Opt2翼型较好地兼顾了跨声速和高超声速气动性能,Opt3翼型则侧重于跨声速气动性能。图19 是Pareto前沿上的三个优化翼型的几何外形对比,可以发现:Opt1和Opt2的下表面具有双“S”形,且具有一定的弯度,其外形特征与第2节中优化所得翼型十分相似。Opt1与Opt2外形的差异主要在上表面前缘,相比Opt2翼型,Opt1的上表面前缘附近略向下凹陷。优化翼型Opt3的下表面的型线与基准翼型NACA64A-204接近,而上表面的型线分布具有一定的差异。
|
图 18 从Pareto前沿上选取的三个优化翼型示意图 Fig.18 Three optimized airfoils selected from the Pareto front obtained by optimization |

|
图 19 基准翼型和Pareto前沿上三个典型翼型的外形对比 Fig.19 Comparison of shapes between the baseline and three optimized airfoils selected from the Pareto front |
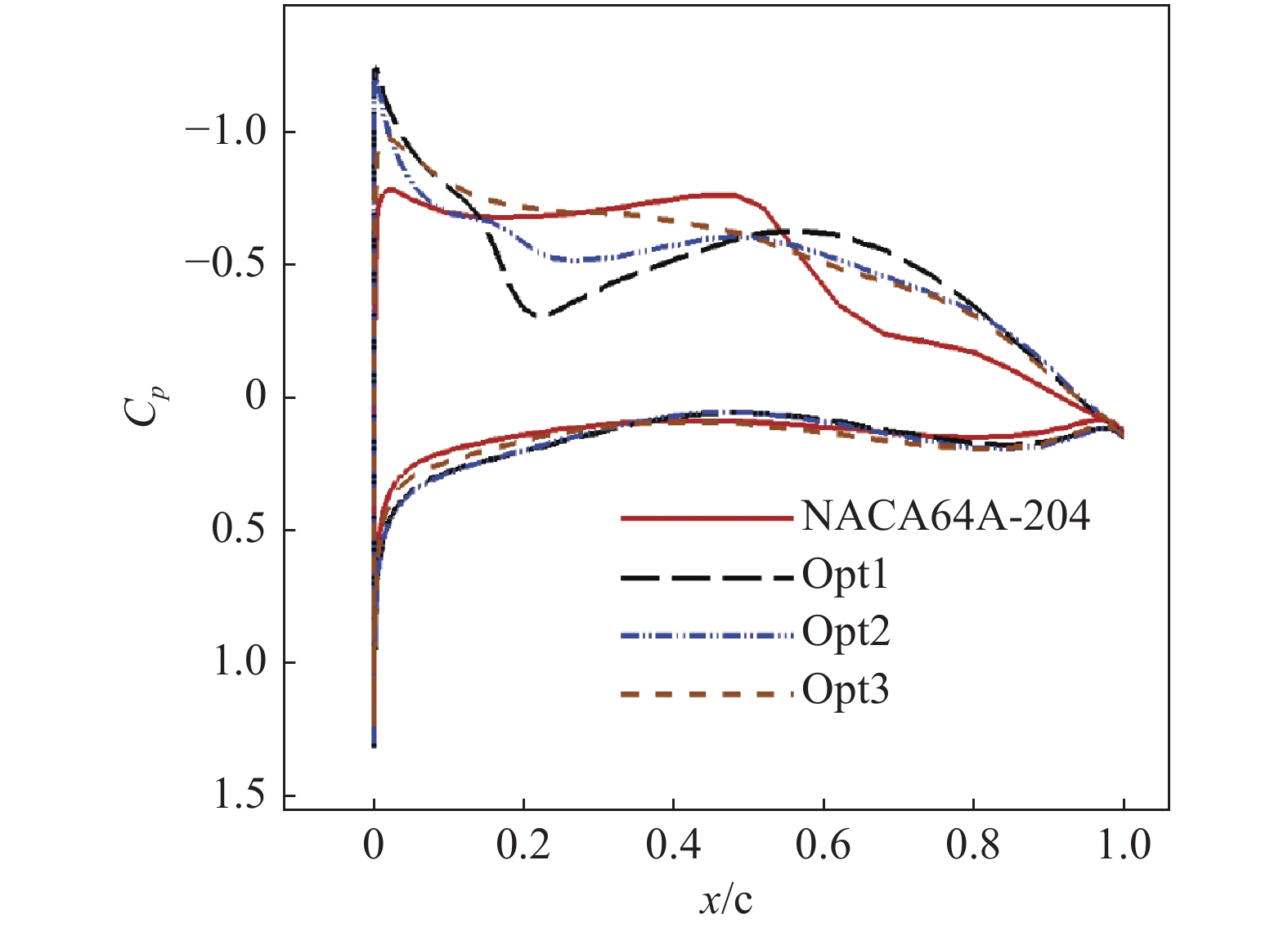
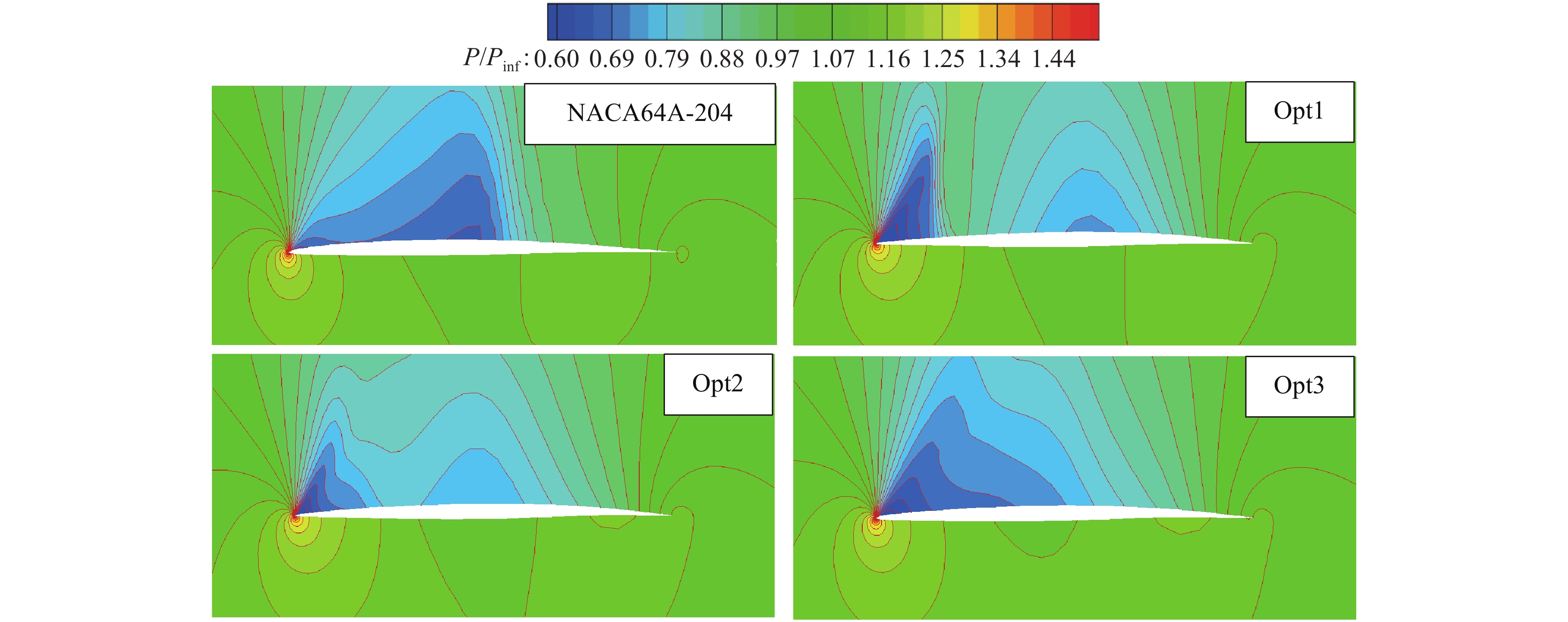
图20 和图21 是Opt1、Opt2、Opt3和基准翼型NACA64A-204在跨声速和高超声速设计状态的压力分布对比,图22 和图23 是压力云图对比,表4是气动性能对比。可以发现,跨声速状态下,NACA64A-204翼型前缘饱满,流动在上表面前缘附近形成大范围低压区,有利于增加升力,然而在上表面中部靠后位置,型面收缩过快,形成一道激波,增加了阻力。Opt1翼型更偏重高超声速气动性能,其前缘半径小,且上表面向内凹,上表面前缘点后流动急剧压缩,在大约20%弦长处形成一道激波,增加了阻力。Opt2翼型上表面前缘内凹不如Opt1明显,所以上表面并未形成激波,阻力特性好于Opt1。Opt3翼型的上表面前缘相比Opt1和Opt2更加饱满,上表面低压区大,且没有形成激波,其升力大、阻力小,因而跨声速状态下有最大的升阻比。高超声速状态下,NACA64A-204翼型和Opt3翼型由于头部前缘半径大,激波阻力大,导致升阻比相对较小;而Opt1与Opt2翼型前缘半径小,头部激波弱,高超声速升阻比大。
|
图 20 跨声速状态下优化翼型与基准翼型的压力分布对比(Ma = 0.8, α = 1.5°, Re = 7.6×106) Fig.20 Pressure distributions of the baseline and optimized airfoils at a transonic state (Ma = 0.8,α = 1.5°, Re = 7.6×106) |

|
图 21 高超声速状态下优化翼型与基准翼型的压力分布对比(Ma = 6, α = 5°, Re = 4.23×106) Fig.21 Pressure distributions of the baseline and optimized airfoils at a hypersonic state (Ma = 6, α = 5°, Re = 4.23×106) |
|
图 22 跨声速状态下Pareto前沿上的优化翼型与基准翼型的压力云图对比(Ma = 0.8, α = 1.5°, Re = 7.6×106) Fig.22 Comparison of pressure contours between the baseline and optimal airfoils at a transonic state (Ma = 0.8, α = 1.5°, Re = 7.6×106) |

|
图 23 高超声速状态下Pareto前沿上的优化翼型与基准翼型的压力云图对比(Ma = 6, α = 5°, Re = 4.23×106) Fig.23 Comparison of pressure contours between the baseline and optimal airfoils at a hypersonic state (Ma = 6, α = 5°, Re = 4.23×106) |
| 表 4 Pareto前沿上选取的三个优化翼型与基准翼型的力系数与翼型厚度对比 Table 4 Comparison of aerodynamic performance between the baseline and optimized airfoils |
|
|
通过宽速域翼型多目标优化设计研究,获得了不同马赫数下的翼型气动性能随几何外形变化的演化规律,并进一步验证了所设计的下表面“双S”形的小弯度翼型可以兼顾不同速域气动性能。同时发现,翼型上表面的外形设计对于提高跨声速升阻比很关键,若能形成大范围低压区,并控制上表面激波的强度,就可以增升、减阻,获得好的跨声速升阻比。需要注意的是上表面前缘附近的设计,若鼓起较多,有助于改善跨声速升力特性,但会增加高超声速的激波阻力,如Opt3;若上表面前缘内凹较多,如Opt1,虽然可以小幅改善高超声速升阻特性,但在跨声速状态下,上表面前缘点之后,可能导致流动急剧压缩,一方面损失了升力,若形成激波则还会增加阻力,使跨声速性能有较大损失。
4 三维构型下翼型宽速域气动优化设计本节开展三维构型下的翼型宽速域气动优化设计,以进一步检验该宽速域流动机理在考虑三维效应时的适用性。由于NACA64A-204翼型前缘半径大,并不适用于高超声速飞行,其外形与最终的优化翼型相差太大,故三维优化中以双弧形翼型为基准翼型。
选取的机翼平面外形如图24 所示。该机翼是一个梯形机翼,前缘后掠角为56°,后缘前掠8°,平均气动弦长为1 m。采用该平面外形,顺流向配置翼型获得完整机翼,此类中等后掠角的机翼可直接应用于宽速域飞行器,或应用于后掠角小的外翼段。对该机翼的翼型开展宽速域气动优化设计。由于机翼的平均气动弦长为1 m,因此雷诺数与第3节、第4节中二维翼型优化的雷诺数保持一致。Ma<1时,机翼的俯仰力矩参考点位于平均气动弦的1/4弦长处;Ma>1时,参考点位于1/2弦长处;俯仰力矩抬头为正,低头为负。为了使优化结果更具有工程实用性,考虑气动热防护的要求,在优化中采取前缘倒圆的方式约束机翼前缘半径为0.001 m。由于机翼的翼根和翼尖弦长不一样,而机翼前缘倒圆统一为0.001 m,会导致展向不同站位处的翼型有细微差异,因此约定结果展示时只对平均气动弦站位处的翼型进行展示。

|
图 24 梯形机翼平面外形示意图 Fig.24 Planform of a trapezoidal wing |
宽速域设计工况与二维翼型优化时的工况保持一致。优化目标为跨声速和高超声速设计状态下的升阻比。优化问题的数学模型表述为:
| $ \begin{split} {\text{max}}\;\;&{\left( {{C_L}/{C_D}} \right)_{Ma = 6}} \\ {\text{max}}\;\;&{\left( {{C_L}/{C_D}} \right)_{Ma = 0.8}} \\ {\text{s}}{\text{.t}}{\text{.}}\;\;&{\left( {{C_L}/{C_D}} \right)_{Ma = 0.8}} > {\left( {{C_L}/{C_D}} \right)_{0,Ma = 0.8}} \\& {\left( {{C_L}/{C_D}} \right)_{Ma = 6}} > {\left( {{C_L}/{C_D}} \right)_{0,Ma = 6}} \\& {C_{L,Ma = 0.8}} > \;{C_{{L_0},Ma = 0.8}}\; \\& {C_{L,Ma = 6}} > \;{C_{{L_0},Ma = 6}} \\& \left| {t - {t_0}} \right| < 0.02{t_0} \end{split} $ | (5) |
基准翼型采用双弧形翼型,使用CST参数化方法,设计空间取为基准翼型设计变量上下浮动30%。
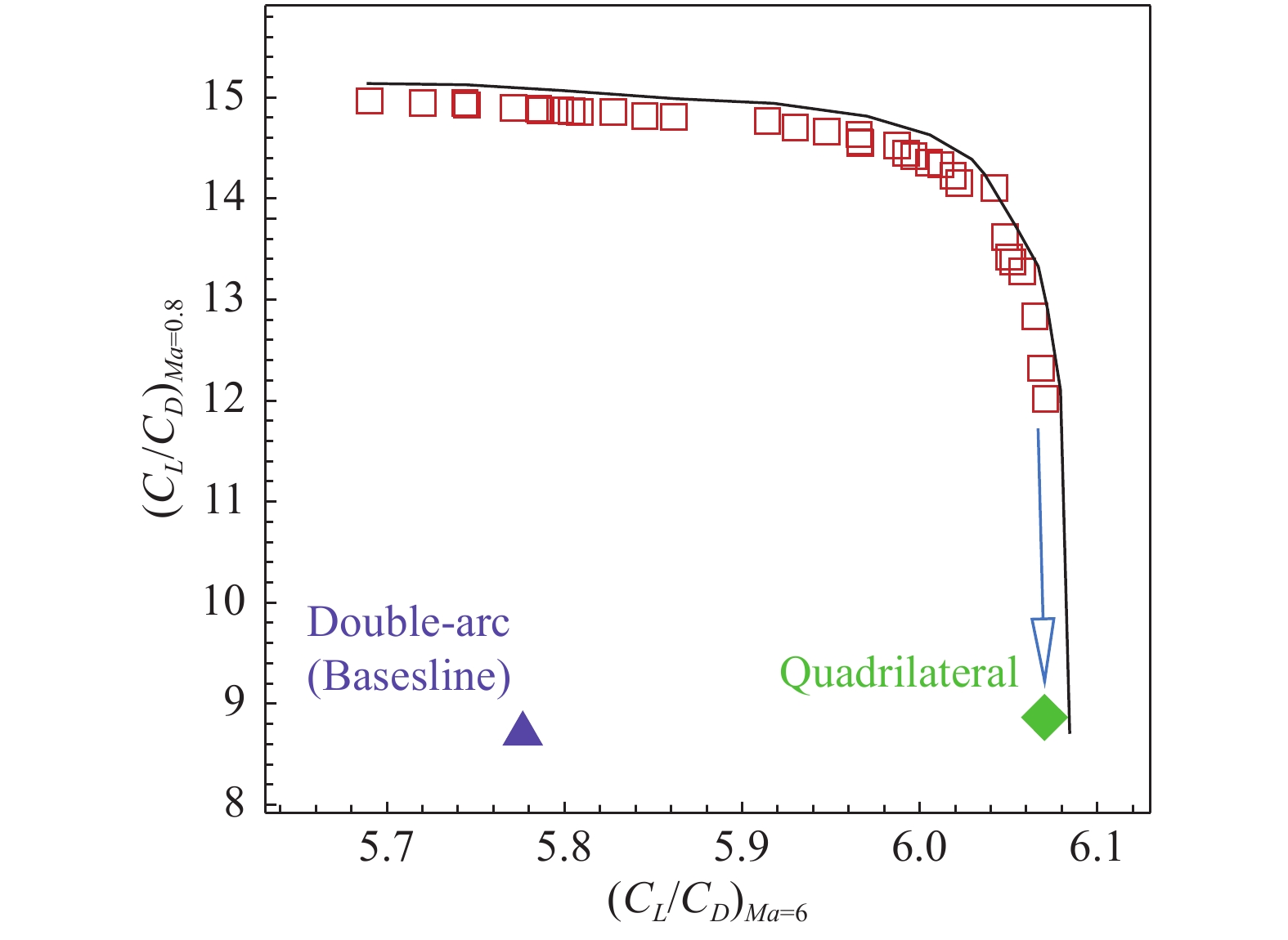
图25 是通过多目标优化所得的Pareto前沿,其中红色空心方块代表Pareto前沿上的各优化翼型对应的机翼在目标空间的位置,绿色的菱形块代表剖面为四边形翼型的机翼在目标空间的位置,紫色的三角形代表剖面为双弧形翼型的机翼在目标空间位置。相比基准的双弧形翼型,Pareto前沿已向目标空间右上角大幅推进。而剖面为四边型翼型的机翼位于优化所得Pareto前沿的右侧延伸线上,说明剖面为四边形翼型的机翼相比配置Pareto前缘上的机翼具有最大的高超声速升阻比。然而,若将Pareto前沿上最右侧的点沿箭头标示的方向移动到四边形翼型的位置,则该点的高超声速升阻比提升不到1%,然而其跨声速升阻比却减小超过30%。对于宽速域气动设计,追求的是宽速域下气动性能的综合最优,Pareto前沿右上拐角区域的点更符合宽速域气动设计的要求。注意到Pareto前沿线上四边形翼型附近有一段较长的区域未找到优化解,这是因为优化中采用的CST参数化方法所得翼型是光滑可导的,对四边形翼型这类表面有导数不连续点的翼型无法很好地进行拟合。
|
图 25 四边形和双弧形翼型在目标空间的位置的示意图 Fig.25 Quadrilateral and double-arc airfoils in the objective space |
从Pareto前沿上选取三个翼型作为代表性翼型进行分析,如图26(a)所示 ,选取的三个翼型分别记为Opt4、Opt5和Opt6。由三个翼型位于Pareto前沿上的位置可知:配置Opt4翼型的机翼更侧重于高超声速气动性能,配置Opt5翼型的机翼能较好地兼顾跨声速和高超声速气动性能,配置Opt6翼型的机翼则更侧重于跨声速气动性能。图26 (b)、(c)、(d)分别是优化翼型Opt4、Opt5、Opt6与双弧形翼型(基准翼型)的外形对比。相比双弧形翼型,各优化翼型的弯度显著增加了,Opt5和Opt6的下表面具有明显双“S”形特征,Opt4翼型下表面后缘S形特征不明显。

|
图 26 从Pareto前沿上选取三个优化翼型的示意图 Fig.26 Three optimized airfoils selected from the Pareto front obtained by a multi-objective optimization |
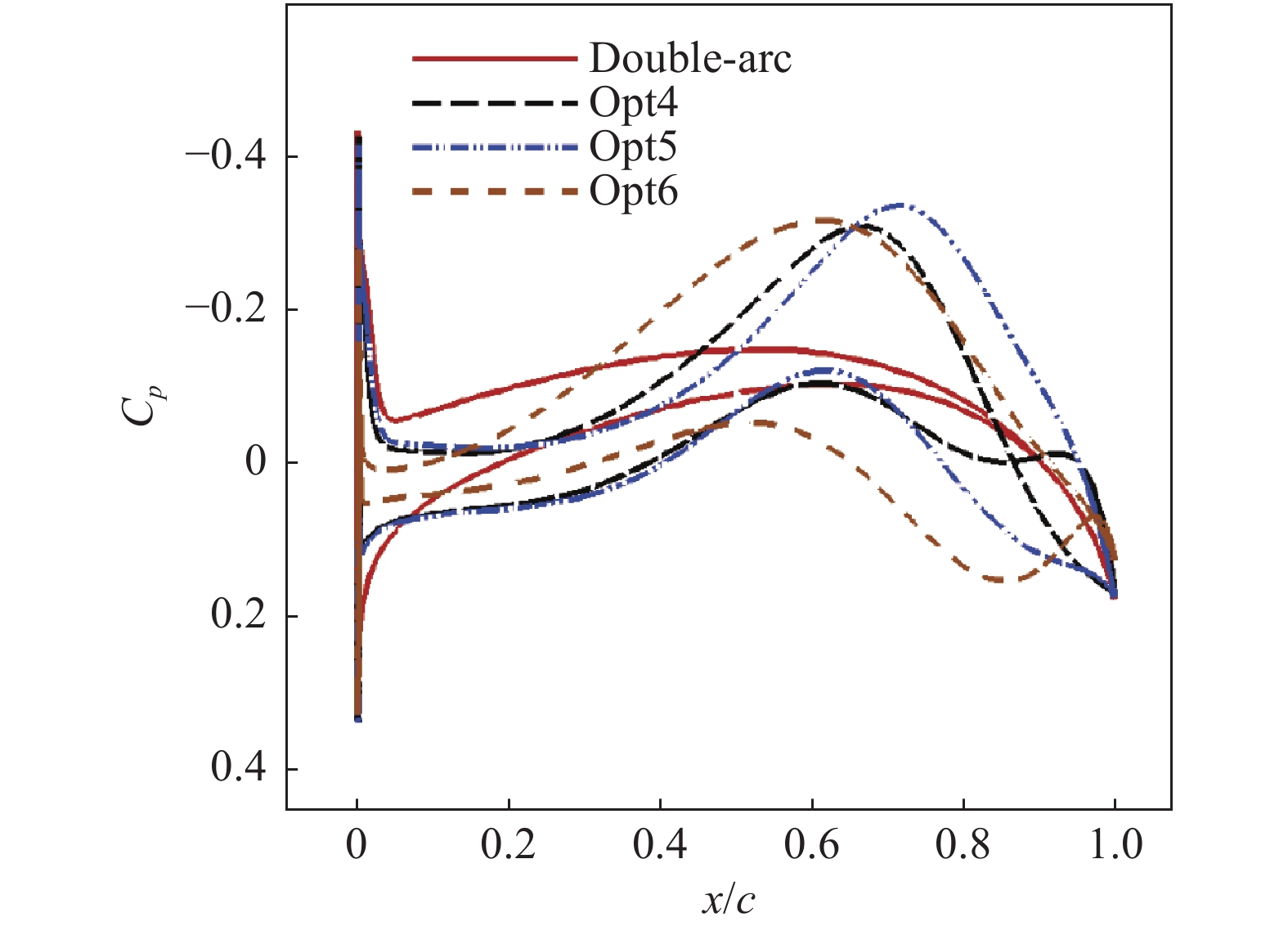
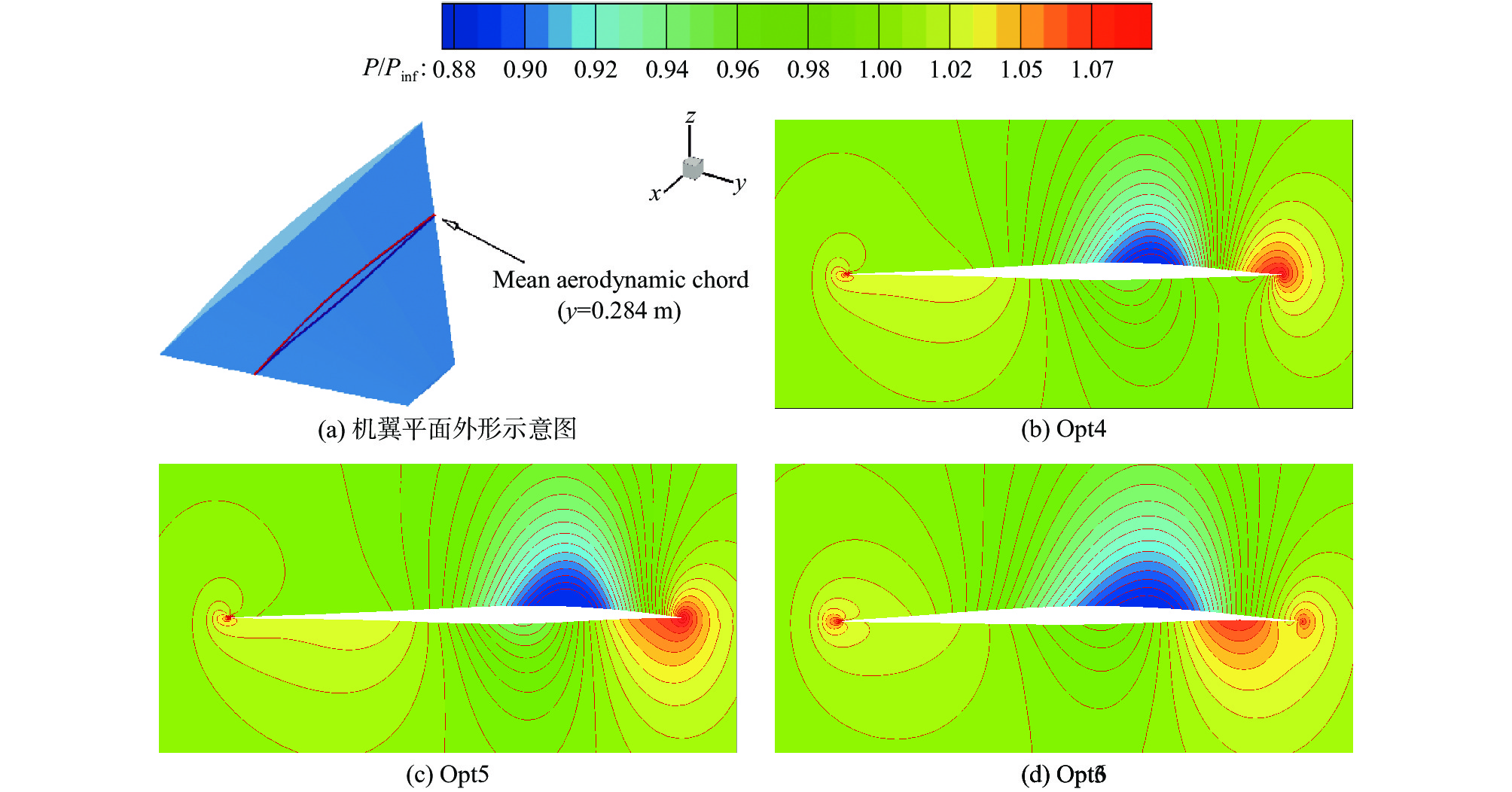
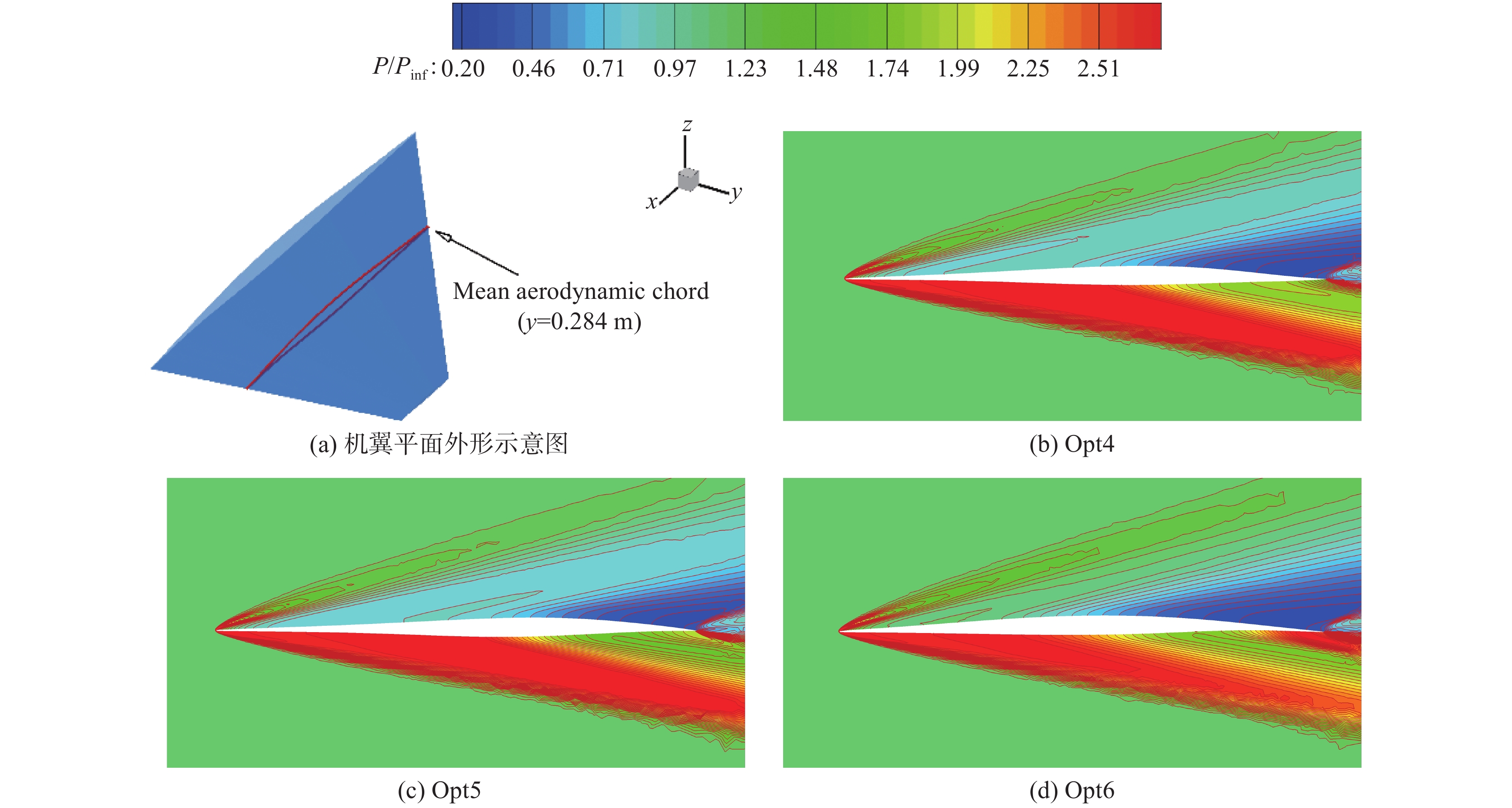
图27 和图28 分别是配置优化翼型Opt4、Opt5、Opt6和双弧形翼型的机翼平均气动弦所在站位处在跨声速(Ma = 0.8,α = 1.5°,Re = 7.6×106)和高超声速设计状态(Ma = 6,α = 5°,Re = 4.23×106)下的压力分布对比,图29 和图30 是压力云图对比,表5是气动性能对比。可以发现,在跨声速状态下,双弧形由于没有弯度,其上、下表面的压力分布差异很小,导致剖面为双弧形翼型的机翼升力严重不足。优化翼型Opt4、Opt5和Opt6都具有一定的弯度,配置优化翼型的机翼,上表面在跨声速下产生了明显的低压区(如图29),有利于增大升力。Opt6机翼后缘的反弯程度最大,其跨声速升力和升阻比特性较好。如图28 所示,高超声速下由于来流速度快,三维横流效应一定程度上被压制了,优化翼型对应的下表面压力分布有明显的多次压缩特征,与二维翼型的压力分布有很高的相似性。Opt6翼型的整体弯度和后缘弯度都很大,高超声速下压差阻力大,因此配置Opt6翼型的机翼的高超声速升阻比最小。Opt4翼型在下表面后缘弯度小,这有效削弱了尾缘激波,降低了阻力,使得配置Opt4翼型的机翼有很好的高超声速升阻比。Opt5翼型较好地兼顾了跨声速和高超声速气动性能,Opt5翼型几何特征与二维结果相似,说明下表面“双S”形的小弯度薄翼型兼顾亚、跨、超和高超声速气动性能的宽速域流动机理同样适用于三维情况。
|
图 27 跨声速状态下机翼剖面的压力分布对比(Ma = 0.8, α = 1.5°, Re = 7.6×106) Fig.27 Comparison of pressure distributions between different wing profiles at a transonic state (Ma = 0.8, α = 1.5°, Re = 7.6×106) |

|
图 28 高超声速状态下典型优化翼型的压力分布对比(Ma = 6, α = 5°, Re = 4.23×106) Fig.28 Comparison of pressure distributions between different wing profiles at a hypersonic state (Ma = 6, α = 5°, Re = 4.23×106) |
|
图 29 跨声速状态下Pareto前沿上优化机翼典型剖面的压力云图(Ma = 0.8, α = 1.5°, Re = 7.6×106) Fig.29 Pressure contours of typical optimal airfoils on the Pareto front at transonic state (Ma = 0.8, α = 1.5°, Re = 7.6×106) |
|
图 30 高超声速状态下Pareto前沿上优化机翼典型剖面的压力云图(Ma = 6,α = 5°,Re = 4.23×106) Fig.30 Pressure contours of typical optimal airfoils on the Pareto front at hypersonic state (Ma = 6, α = 5°, Re = 4.23×106) |
| 表 5 基准翼型和选取的三个优化翼型在两个设计状态下的力系数与翼型厚度对比 Table 5 Comparison of aerodynamic performance for the baseline and optimized profiles |
|
|
图31是在跨声速(Ma = 0.8,α = 1.5°,Re = 7.6×106)和高超声速(Ma = 6,α = 5°,Re = 4.23×106)状态,优化翼型Opt5在单独翼型以及配置到三维梯形机翼上时的压力分布对比。可见,对于大后掠角、小展弦比机翼,跨声速状态下,三维机翼的压力分布与二维的有显著不同,但配置优化翼型的机翼的跨声速升力仍然明显大于配置对称双弧形翼型的机翼,因此翼型几何特征对气动性能的影响规律不会改变。而在高超声速状态下,三维效应被有效压制,三维机翼与二维翼型的压力分布十分接近。

|
图 31 优化翼型在三维与二维情况下的压力分布对比 Fig.31 Comparisons of pressure distributions of the optimized airfoil in three-dimensional and two-dimensional cases |
本节采用梯形机翼平面外形,开展了三维构型下的翼型宽速域气动优化设计。可以发现,跨声速状态下,由于三维效应的影响,机翼的压力分布相比二维产生了畸变,但是翼型弯度和下表面后缘产生后加载增加升力的规律没变;而高超声速下,可以发现三维构型的压力分布与二维翼型有很强的相似性。结果表明,三维构型下的翼型优化结果也呈现出具有一定弯度、下表面具有“双S”形特征,这说明二维翼型优化所获得的翼型几何特征及其宽速域流动机理在三维情形下仍然成立。
5 结 论针对高超声速飞行器宽速域翼型气动设计问题,本文采用所发展的基于代理模型的宽速域翼型高效全局气动优化设计方法,开展了兼顾跨声速和高超声速气动性能的宽速域翼型优化设计研究,设计出一种下表面具有“双S”形特征的宽速域新翼型,并分析了该翼型协调不同速域气动性能的流动机理。其次,开展了宽速域翼型的多目标优化设计,得到了关于跨声速和高超声速气动特性的Pareto前沿。通过分析Pareto解集中翼型的宽速域气动性能随其几何外形变化的演化规律,解释了宽速域新翼型在协调跨声速与高超声速气动性能方面的原理。最后,采用平面外形为梯形的机翼,进行了三维构型下的机翼剖面宽速域翼型多目标优化设计,并验证了所得结论在三维流动环境下的适用性。研究结论如下:
1)所设计的下表面具有“双S”形的小弯度的薄翼型在保持超声速、高超声速良好的气动性能前提下,亚、跨声速性能比四边形翼型和双弧形对称翼型有明显提升。
2)对新翼型的流动机理分析表明:高超声速下,翼型下表面流动呈现多次压缩,不仅减小了头部激波阻力,且使升力分布更加均匀,力矩特性也得到改善;亚、跨声速下,下表面形成前加载和后加载,可改善升力与力矩特性;超声速下,由于翼型具有一定弯度,根据线化理论,超声速阻力略有增加。
3)小展弦比、大后掠三维机翼构型下的宽速域翼型优化设计研究表明,三维优化机翼的剖面几何特征和压力分布与二维结果相似,说明通过下表面双“S”形的小弯度翼型来兼顾亚、跨、超、高超声速气动性能的宽速域流动机理同样适用于三维情况,从而证实了翼型设计对于宽速域高超声速飞行器设计仍具有重要意义。
| [1] |
李宪开, 王霄, 柳军, 等. 水平起降高超声速飞机气动布局技术研究[J]. 航空科学技术, 2020, 31(11): 7-13. LI X K, WANG X, LIU J, et al. Research on the aerodynamic layout design for the horizontal take-off and landing hypersonic aircraft[J]. Aeronautical Science & Technology, 2020, 31(11): 7-13. (in Chinese) |
| [2] |
BERTIN J J, CUMMINGS R M. Fifty years of hypersonics: where we've been, where we're going[J]. Progress in Aerospace Sciences, 2003, 39(6-7): 511-536. DOI:10.1016/s0376-0421(03)00079-4 |
| [3] |
SZIROCZAK D, SMITH H. A review of design issues specific to hypersonic flight vehicles[J]. Progress in Aerospace Sciences, 2016, 84: 1-28. DOI:10.1016/j.paerosci.2016.04.001 |
| [4] |
李世斌. 新概念宽速域飞行器气动外形设计与优化[D]. 长沙: 国防科学技术大学, 2012. LI S B. Design and optimization of aerodynamic configuration for the novel-concept vehicle with the wide-range Mach numbers[D]. Changsha: National University of Defense Technology, 2012 (in Chinese). |
| [5] |
刘传振, 刘强, 白鹏, 等. 涡波效应宽速域气动外形设计[J]. 航空学报, 2018, 39(7): 121824. LIU C Z, LIU Q, BAI P, et al. Aerodynamic shape design integrating vortex and shock effects for width-velocity-range[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(7): 121824. (in Chinese) |
| [6] |
张锡金, 主编. 气动设计[M]//《飞机设计手册》总编委会, 编. 飞机设计手册, 第6册, 北京: 航空工业出版社, 2002.
|
| [7] |
ANDERSON J D. Fundamentals of aerodynamics[M]. New York: McGRaw-Hill. , 2007.
|
| [8] |
UENO A, SUZUKI K. CFD-based shape optimization of hypersonic vehicles considering transonic aerodynamic performance[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2008: 288. doi: 10.2514/6.2008-288
|
| [9] |
UENO A, SUZUKI K. Two-dimensional shape optimization of hypersonic vehicles considering transonic aerodynamic performance[J]. Transactions of the Japan Society for Aeronautical and Space Sciences, 2009, 52(176): 65-73. DOI:10.2322/tjsass.52.65 |
| [10] |
孙祥程, 韩忠华, 柳斐, 等. 高超声速飞行器宽速域翼型/机翼设计与分析[J]. 航空学报, 2018, 39(6): 121737. SUN X C, HAN Z H, LIU F, et al. Design and analysis of hypersonic vehicle airfoil/wing at wide-range Mach numbers[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(6): 121737. (in Chinese) |
| [11] |
LIU F, HAN Z H, ZHANG Y, et al. Surrogate-based aerodynamic shape optimization of hypersonic flows considering transonic performance[J]. Aerospace Science and Technology, 2019, 93: 105345. DOI:10.1016/j.ast.2019.105345 |
| [12] |
张阳, 韩忠华, 柳斐, 等. 高超声速飞行器宽速域翼型多目标优化设计研究[J]. 气体物理, 2019, 4(4): 26-40. ZHANG Y, HAN Z H, LIU F, et al. Multi-objective aerodynamic shape optimization of wide-Mach-number-range airfoil[J]. Physics of Gases, 2019, 4(4): 26-40. (in Chinese) |
| [13] |
ZHANG Y, HAN Z H, LIU F, et al. Aerodynamic design optimization of hypersonic wing over wide Mach-number range considering lift matching[C]//32nd Congress of the International Council of the Aeronautic Sciences, ICAS Paper 2020-0476, 2021.
|
| [14] |
GODARD J L. F6 model tests in the ONERA S2MA wind tunnel[C]// 2nd AIAA CFD Drag Prediction Workshop, 2003.
|
| [15] |
WILCOX F, BIRCH T, ALLEN J. Force, surface pressure, and flowfield measurements on a slender missile configuration with square cross-section at supersonic speeds[C]// 22nd Applied Aerodynamics Conference and Exhibit, Providence, Rhode Island. Reston, Virginia: AIAA, 2004 doi: 10.2514/6.2004-5451
|
| [16] |
KULFAN B M, BUSSOLETTI J E. “Fundamental” parameteric geometry representations for aircraft component shapes[C]//11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, Virginia. Reston, Virginia: AIAA, 2006. https://www.brendakulfan.com/docs/CST1.pdf doi: 10.2514/6.2006-6948
|
| [17] |
KULFAN B. A universal parametric geometry representation method - “CST”[C]//45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2007. AIAA-2007-62. doi: 10.2514/6.2007-62
|
| [18] |
HAN Z H. SurroOpt: A generic surrogate-based optimization code for aerodynamic and multidisciplinary design[C]//30th Congress of the International Council of the Aeronautical Sciences, Daejeon, South Korea, 2016. ICAS 2016-0281. https://www.icas.org/ICAS_ARCHIVE/ICAS2016/data/papers/2016_0281_paper.pdf
|
| [19] |
HAN Z H, GÖRTZ S. Hierarchical Kriging model for variable-fidelity surrogate modeling[J]. AIAA Journal, 2012, 50(9): 1885-1896. DOI:10.2514/1.J051354 |
| [20] |
HAN Z H, ZHANG Y, SONG C X, et al. Weighted gradient-enhanced kriging for high-dimensional surrogate modeling and design optimization[J]. AIAA Journal, 2017, 55(12): 4330-4346. DOI:10.2514/1.J055842 |
| [21] |
HAN Z H, XU C Z, ZHANG L, et al. Efficient aerodynamic shape optimization using variable-fidelity surrogate models and multilevel computational grids[J]. Chinese Journal of Aeronautics, 2020, 33(1): 31-47. DOI:10.1016/j.cja.2019.05.001 |
| [22] |
HAN Z H, CHEN J, ZHANG K S, et al. Aerodynamic shape optimization of natural-laminar-flow wing using surrogate-based approach[J]. AIAA Journal, 2018, 56(7): 2579-2593. DOI:10.2514/1.J056661 |
| [23] |
韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225. HAN Z H. Kriging surrogate model and its application to design optimization: a review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225. (in Chinese) |
| [24] |
韩忠华, 许晨舟, 乔建领, 等. 基于代理模型的高效全局气动优化设计方法研究进展[J]. 航空学报, 2020, 41(5): 623344. HAN Z H, XU C Z, QIAO J L, et al. Recent progress of efficient global aerodynamic shape optimization using surrogate-based approach[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(5): 623344. (in Chinese) |
| [25] |
夏露, 王丹, 张阳, 等. 基于自适应代理模型的气动优化方法[J]. 空气动力学学报, 2016, 34(4): 433-440. XIA L, WANG D, ZHANG Y, et al. Aerodynamic optimization method based on adaptive surrogate model[J]. Acta Aerodynamica Sinica, 2016, 34(4): 433-440. DOI:10.7638/kqdlxxb-2014.0121 (in Chinese) |
 2021, Vol. 39
2021, Vol. 39


