0 引　言

2020年8月SpaceX使用载人龙飞船完成NASA首次商业载人任务，民用航天迈入新的阶段。商用航天的快速发展，以及降低飞行成本、保证飞行安全的迫切需求，对高超声速飞行器气动和防热设计提出了更高要求。高超声速飞行的典型特征是激波，导致飞行器周围空气强烈压缩，产生大量热量，转化为内能后使得空气温度急剧升高，引起飞行器表面的严重气动加热现象^[1-3]。为保证飞行安全，降低飞行器防热系统体积和重量，需要对飞行器气动热环境进行准确预测。

高超声速气动热研究方法主要有工程算法、数值模拟、风洞试验以及飞行试验^[4-5]。工程算法通常只适用于简单构型，且计算误差较大；飞行试验时间和经费成本高昂，通常作为地面气动热预测的验证手段。在当前和可预见的未来，风洞试验和数值模拟是气动热地面预测的主要手段。当前，气动热试验^[4]研究一般在激波风洞等高焓设备中进行，其能够获取较为复杂外形飞行器的大面积和局部气动热数据，但地面风洞条件下无法完全复现真实飞行环境。而且，地面气动热试验时间较短，模型并未充分加热，与飞行器的长时间飞行存在显著差异，因而试验获得的热流数据也与真实飞行情况存在较大差异。

随着对高超声速流动机理的深入认知和计算技术与资源的快速发展，数值模拟成为高超声速气动力/热研究的重要手段。对于连续流区，基于N-S方程的计算体系已经较为成熟^[6-7]。在本文重点关注的稀薄过渡流区，直接模拟蒙特卡罗^[8-10]（Direct Simulation Monte Carlo，DSMC）方法是研究非平衡流动问题最为有效的手段之一，常用于高超声速飞行器的气动力/热计算。在DSMC方法中，气体分子与壁面碰撞后，以一定的方式^[11]（如漫反射、CLL(Cercignani，Lampis and Lord)模型）发生反射并进入流场，而确定分子反射行为的一个重要因素就是壁面温度。在工程实践中，通常采用人为设定的恒温壁面（冷壁或热壁），而反射后的分子速度等重要信息则根据初始设定的恒温壁面抽样给出。然而，飞行器在临近空间的长时间飞行，必然导致壁面温度的显著变化，任何初始设定的壁面恒温都不会准确，甚至飞行器不同部位的温度也会存在明显差异，因而壁面温度的恒温处理必将导致气动热环境预测的较大偏差。

从物理上讲，飞行器在受热后，壁面温度将逐渐升高，并将热流传导到飞行器内部，同时壁面将以黑体辐射的形式将部分能量辐射出去。可以假设：当飞行器温度达到平衡后，来自绕流气体的气动加热，将与辐射释放出去的能量达到平衡，即壁面辐射平衡。正是基于这一假设，国内外在壁面辐射平衡方面开展了大量研究工作。在连续流N-S方程方面，Edquist^[12]基于LAURA软件，发展了辐射平衡壁面温度条件，研究了热力学非平衡下的火星飞行器后体热流分布；周欣欣^[13]对壁面热传导下辐射平衡的温度边界条件进行了研究，发现壁面假设对数值计算热流结果影响较大，采用辐射平衡壁面温度边界可以正确计算钝头体沿轨道驻点的温度和热流变化；董维中等^[14]基于表面热辐射效应、催化效应和烧蚀效应，使用AEROPH_Flow软件，对球锥模型进行了计算，分析了壁面温度分布对气动热环境的影响；原志超^[15]采用等温和辐射平衡壁面，计算了高超声速圆柱完全催化下的表面热流，验证了其提出的“松弛”方法的有效性。目前，与DSMC方法相关的壁面辐射平衡研究工作处于起步阶段，屈程^[16-17]的工作具有重要意义，他发展了一种基于辐射平衡的壁面温度边界条件，并以简单外形进行了验证分析。然而，该方法初始分布时需要分布较多模拟分子，无法应用于真实飞行器气动热计算中。

受上述工作启发，本文将在对传统DSMC修正极小、计算量成本增量可控的约束条件下，发展DSMC方法壁面辐射平衡边界条件，在此基础上开发具有一定工程实用性的轴对称构型DSMC求解器，以钝锥构型验证其正确性。重点考察双锥构型试验条件（冷壁）和辐射平衡条件下的分离区、壁面压力、热流和温度分布，找寻对飞行器气动和防热设计有指导意义的普遍规律。

1 基于壁面辐射平衡的DSMC方法 1.1 DSMC气动热计算方法

DSMC方法计算气动热，需要先确定温度边界条件以及气体分子-表面相互作用模型。目前，DSMC方法常采用恒温壁面温度边界条件，在此边界条件下，壁面温度为恒定壁面温度，由初始设定给出，气体分子与物面作用反射进入流场的能量信息由该恒温确定。

气体分子-表面相互作用有多种模型，目前使用广泛的包括镜面反射模型、完全漫反射模型和Maxwell反射模型等^[8-9]。对于镜面反射模型，分子与物面碰撞后平行于物面的切向速度分量保持不变，而法向速度分量的大小不变，方向与碰撞前相反；对于漫反射模型，气体分子与壁面碰撞后的速度与碰撞前的速度没有关系，反射分子作为一个整体在速度上满足Maxwell速度分布，即:

$ f\left({c}'\right)={\left(\frac{m}{2\pi k{T}_{r}}\right)}^{\frac{3}{2}}\cdot {{\rm{e}}}^{-\frac{m{c'}^{2}}{2k{T}_{r}}} $

(1)

式中， $ {c}' $ 为分子的热运动速度， $ k $ 为Boltzmann常数， $ m $ 为分子质量， $ {T}_{r} $ 为反射温度，基于完全漫反射边界以及恒温物面条件， $ {T}_{r}={T}_{w} $ 。根据分布函数取样，反射后分子的速度如下:

$ \begin{split}& {{{v'}_r} = {r_1}{V_{mp}}}\\& {{{u'}_r} = {r_2}{\rm{cos}}\theta\;{V_{mp}}}\\& {{{w'}_r} = {r_2}{\rm{sin}}\theta\; {V_{mp}}} \end{split} $

(2)

式中， $r=\sqrt{{\rm{-ln}}\left({R}_{f}\right)}$ ， $ \theta =2\pi {R}_{f} $ ， $ {R}_{f} $ 为0～1之间的随机数， $ {V}_{mp} $ 为平衡气体的最概然速率，取为 $ {V}_{mp}=　\sqrt{2k{T}_{r}/m} $ 。

对于Maxwell反射模型，物面反射由漫反射和镜面反射组成，假设气体分子发生漫反射和镜面反射比例为 $ \sigma :(1-\sigma ) $ ，本文计算中σ取为0.85。

根据DSMC计算的基本原理，表面热流密度 $ {q}_{w} $ 定义为:

$ {q}_{w}=\frac{\displaystyle\sum {E}_{i}-\displaystyle\sum {E}_{r}}{\Delta t\cdot A} $

(3)

式中，下标i、r分别代表入射分子和反射分子；E代表分子总能量，包括平动、转动、振动三种能量； $ \Delta t $ 、 $ A $ 分别为作用时间与作用面积。

1.2 辐射平衡壁面边界

考虑表面热辐射效应、催化效应、烧蚀效应和热传导效应，利用准定常假设，由交界面一直延伸到物体深处的能量守恒方程^[14,18]为:

$ {q}_{w}={q}_{c}+\varepsilon \sigma {T}_{w}^{4}+{\dot{m}}_{w}\left({H}_{w}-{H}_{a}\right) $

(4)

式中， $ {q}_{w} $ 为表面热流， $ {q}_{c} $ 为通过热传导从表面传到壁面深处热流，ε是表面发射系数，若为绝对黑体，则 $ \varepsilon =1 $ ，σ为Stefan-Boltzmann常数，其值为 $ 5.670\;4\times $ $ {10}^{-8}\;\mathrm{J}{\mathrm{s}}^{-1}{\mathrm{m}}^{-2}{\mathrm{K}}^{-4} $ ， $ {T}_{w} $ 为壁面温度， $ {\dot{m}}_{w} $ 为表面烧蚀率， $ {H}_{w} $ 和 $ {H}_{a} $ 分别为表面总焓和材料生成焓。

Hirschel^[19]研究得出在来流速度小于8 km/s，飞行高度小于100 km时，对流换热占主导地位，来自激波层的辐射热流可忽略不计，本研究中 $ {q}_{w} $ 为非催化条件下的对流热流。加热一段时间后，壁面处在完全“热透”状态，不再往壁面深处传热，表面热传导热流 $ {q}_{c} $ = 0。因此对于非烧蚀表面，不考虑表面催化效应条件下，方程（4）可化简为:

$ {q}_{w}=\varepsilon \sigma {T}_{w}^{4} $

(5)

式（5）所表示的即为辐射平衡边界条件。本文主要研究DSMC方法在该边界条件下的热流、压力和温度以及与恒温物面边界的计算差异。

1.3 辐射平衡壁面建模及实现

根据DSMC方法热流计算流程，考虑完全将壁面“热透”最终状态，采用稳定取样的热流值作为式（5）中 $ {q}_{w} $ 值，经过几次迭代后，得出最终平衡时表面温度和热流值，该边界条件结合恒温冷壁边界条件，可以确定出实际飞行器表面热流的范围。具体实现步骤如下：

（1）根据来流条件进行初始化，将壁面初始温度 $ {T}_{w,0} $ 设为恒温冷壁温度；

（2）由辐射平衡温度边界式（5），在壁面边界编号为m的单元，表面的气动加热热流与该壁面辐射出的热流相等，流动经充分长的n₁时间步进入稳态，通过合理的n₂时间步后抽样得到流场及壁面热流、压力等信息。壁面温度由:

$ {q}_{w}^{i}=\varepsilon \sigma {\left({T}_{w,m}^{i+1}\right)}^{4} $

(6)

计算得到，并将该温度作为下一次迭代的初值。

在本文研究中，假设物面为绝对黑体，即 $ \varepsilon =1 $ ；根据来流条件和计算模型，确定流动稳定时间步长n₁和抽样时间步长n₂；若式（6）得到的壁面温度低于 ${T}_{{\rm{min}}}$ ，将壁面温度设为 ${T}_{{\rm{min}}}$ ，其中 ${T}_{{\rm{min}}}$ 为迭代初始温度和壁面温度的最小值；收敛条件为迭代的壁面温度两次之间的相对误差在1%以内。

结合上述步骤更新壁面温度的边界条件，基于辐射平衡的壁面热流DSMC方法计算流程如图1。

在此基础上，课题组开发了一套基于流场笛卡尔网格及自适应技术的MPI并行轴对称构型DSMC求解器（简称为DSMC2A）。

2 基于钝锥构型的算例验证

稀薄气体壁面辐射平衡研究文献较少，可以参考的是高超声速钝锥绕流^[17]。钝锥长1 m，头部半径35 mm，半锥角为5°，如图2所示。来流条件对应飞行高度为100 km，速度7000 m/s，其他自由来流条件如表1所示。计算时，空气取为N₂和O₂双组分气体，其摩尔百分比为0.763∶0.237，初始壁面温度为350 K，采用辐射平衡温度边界和Maxwell反射模型。

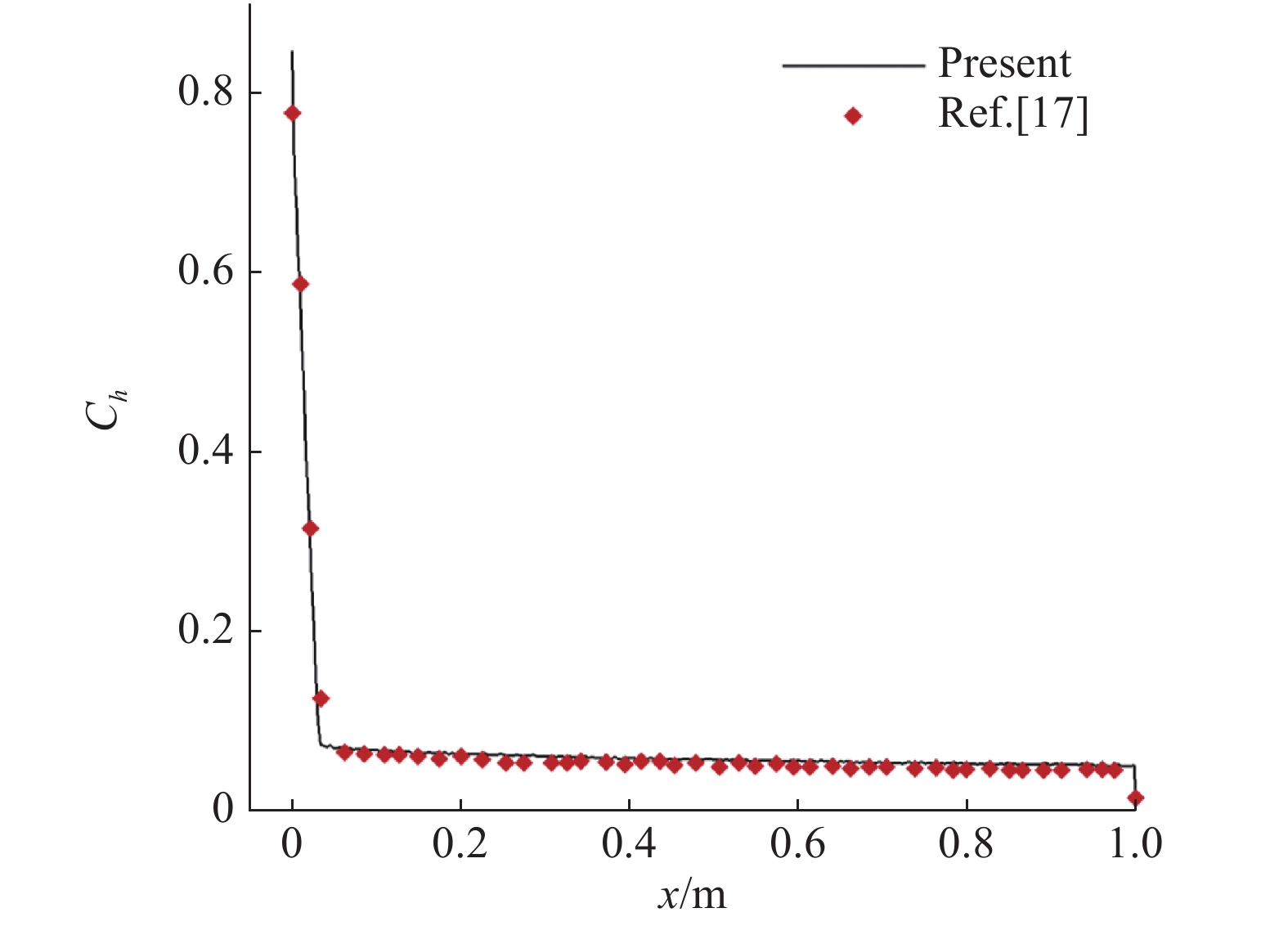
图3给出了辐射平衡条件下的物面热流系数C_h，并和文献[17]中结果进行了比较，可以看出两者吻合较好，验证了轴对称程序和辐射平衡壁面建模和实现的正确性。

同时，还计算了恒温冷壁（壁面温度为350 K）完全漫反射条件下的驻点热流值，为93.9 kW/m²，与辐射平衡下Maxwell模型的热流值81.32 kW/m²进行了比较，两者偏差达13.397%，表明壁面辐射平衡下的热流值较冷壁情况显著降低。

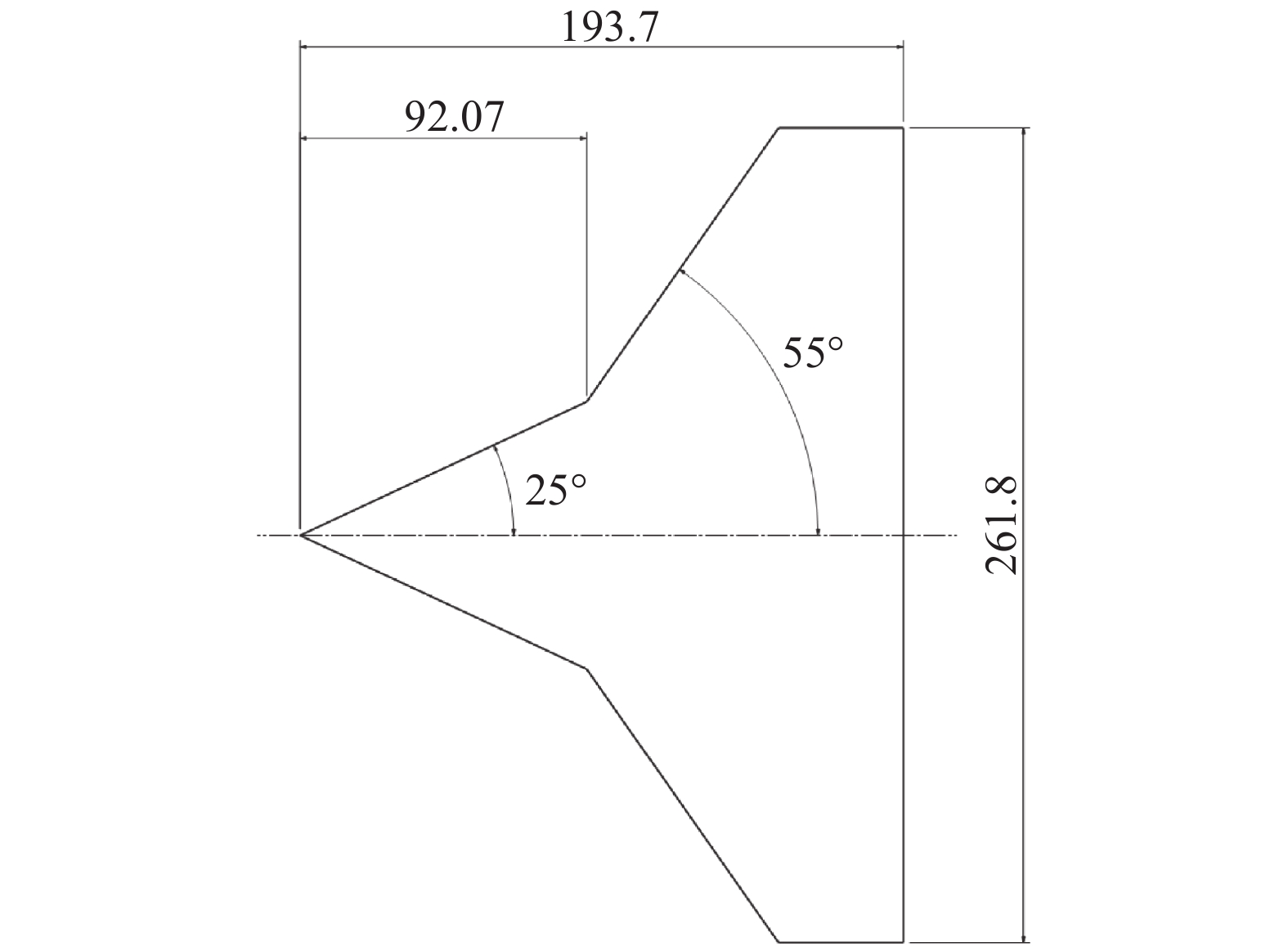
3 在双锥构型中的应用 3.1 计算条件

采用CUBRC 48英寸激波风洞中进行试验的25°/55°双锥构型^[20-22]，如图4所示，试验气体为N₂，来流马赫数为15.6。

计算迎角0°的试验状态，试验来流条件如表2所示。分子碰撞采用VHS模型，考虑平动能、转动能和振动能之间的能量交换，动能和内能能量交换采用Larsen-Borgnakke模型，使用无化学反应气体模型，壁面采用完全漫反射模型，转动弛豫碰撞次数取为5，振动弛豫碰撞次数^[8-9]取为温度T的表达式：

$ {{Z}}_{v}=\left({C}_{1}/{T}^{\omega }\right)\mathrm{e}\mathrm{x}\mathrm{p}\left({C}_{2}{T}^{-1/3}\right) $

(7)

式中， $ \omega $ 为黏性指数，C₁和C₂为常数。对于氮气，C₁取为9.1，C₂取为220.0。

3.2 试验条件下的结果分析

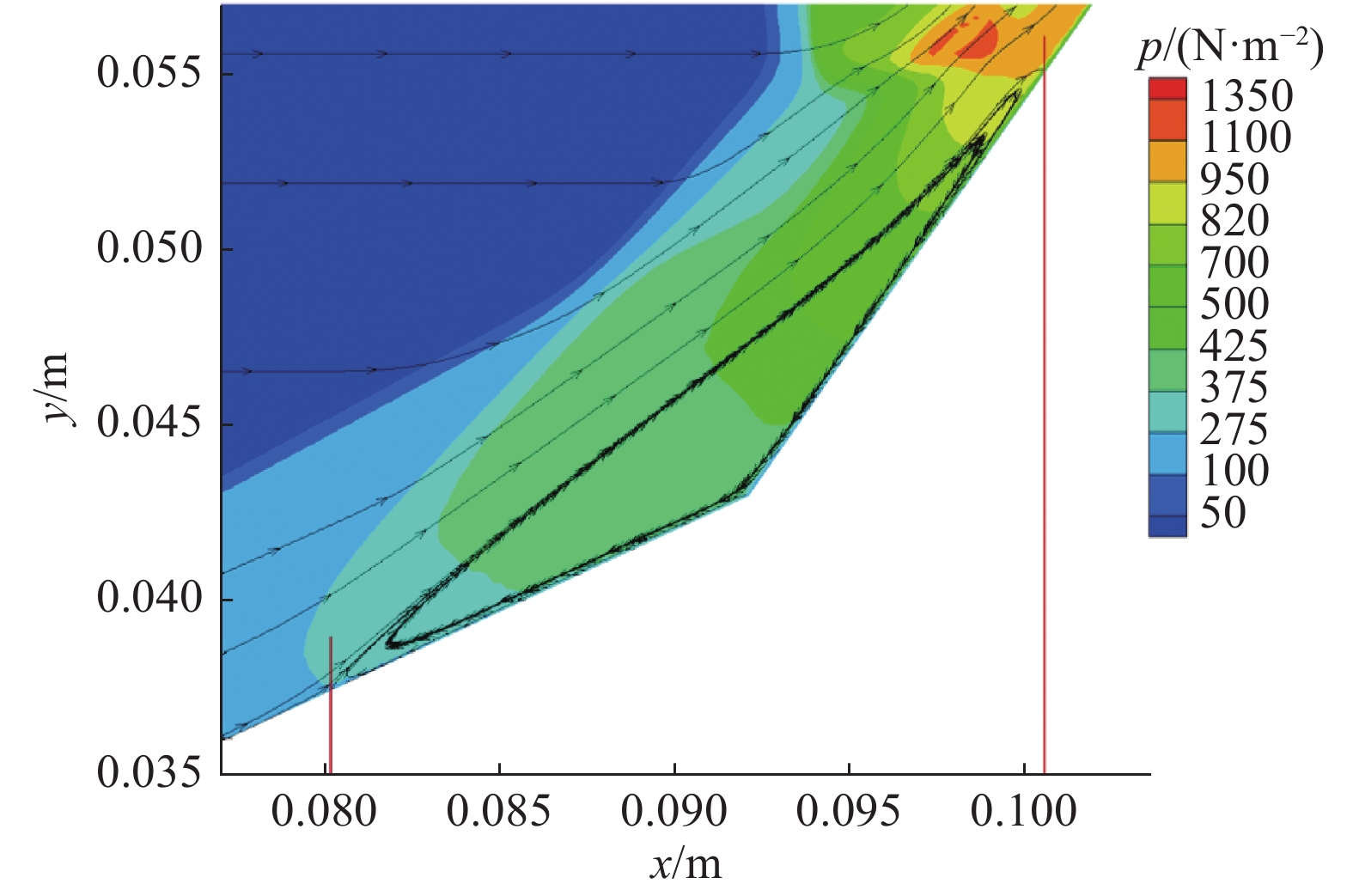
激波风洞试验时间短，模型壁面加热并不严重，可以将初始壁面温度下（即图1中辐射平衡计算尚未开始）的计算视为试验工况。图5给出了流场分离区压力云图和流线，从中可以看到左、右分离点以及分离区范围；与软件SMILE和DS2V计算结果^[21]进行比较，见表3，可以看出三种手段计算出的分离区范围和大小，并无明显差异。

图6给出了模型壁面沿中轴线的压力分布DSMC计算和CUBRC Run 7风洞试验结果对比，可以看出压力在锥前体、分离区、由于激波/激波相互作用产生的高压区以及第二段锥上均与试验值吻合得很好。

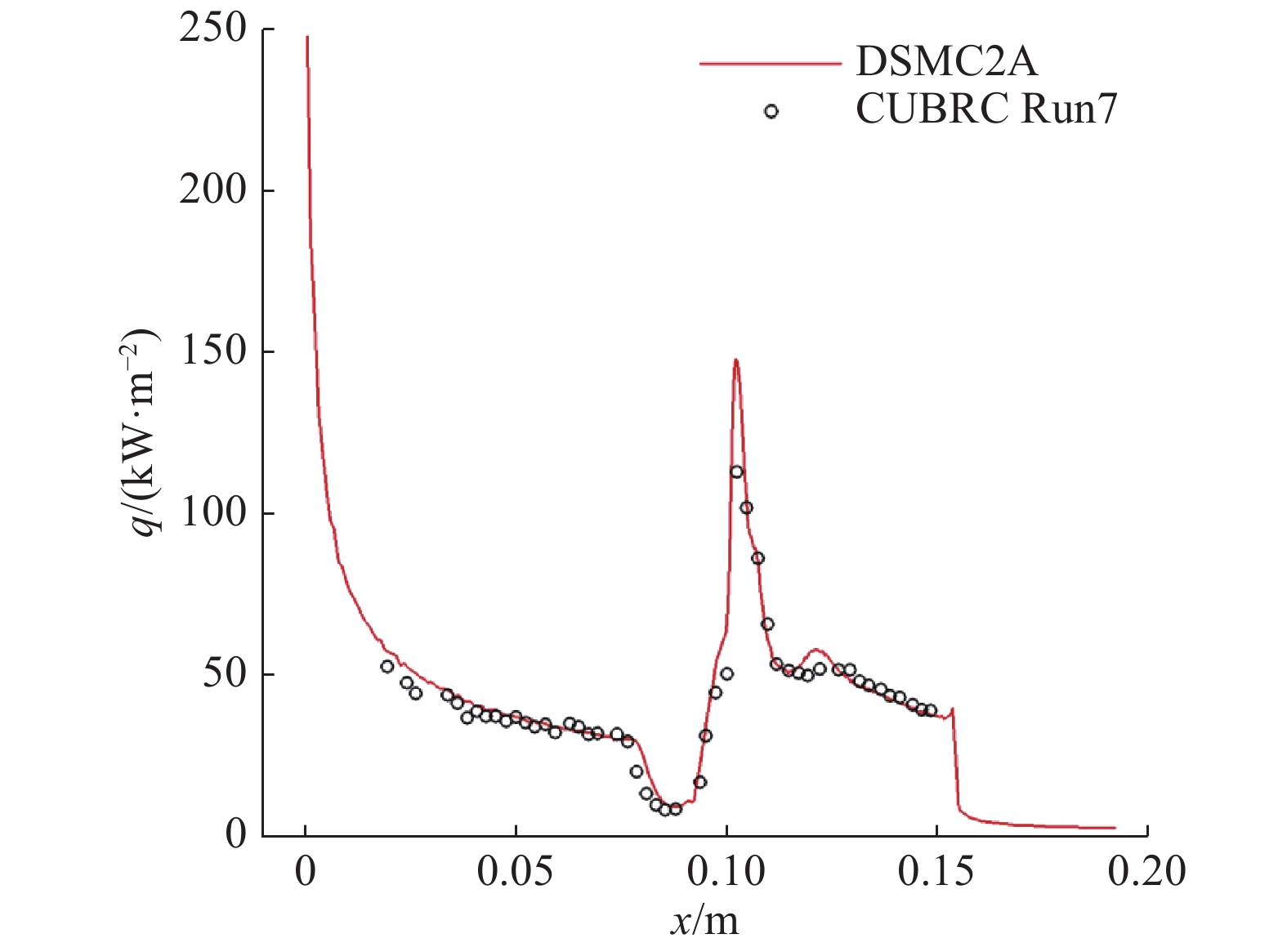
图7给出了DSMC方法预测的壁面中轴线热流和风洞试验结果，两者在绝大部分测量点处表现出良好的一致性，DSMC计算的干扰区热流峰值稍高于试验测量值，但在可以接受的合理范围内。

3.3 辐射平衡下的结果分析

图8给出了辐射平衡（对应图1中的迭代结束）条件下分离区与冷壁计算对比，可以看出辐射平衡条件下的左分离点为75.8 mm，相对于冷壁条件下前移；右分离点为103.9 mm，相对于冷壁条件下后移；分离区大小为28.1 mm，较冷壁条件下显著增大。该图还表明，相对于冷壁，辐射平衡条件下的分离区附近压力下降。

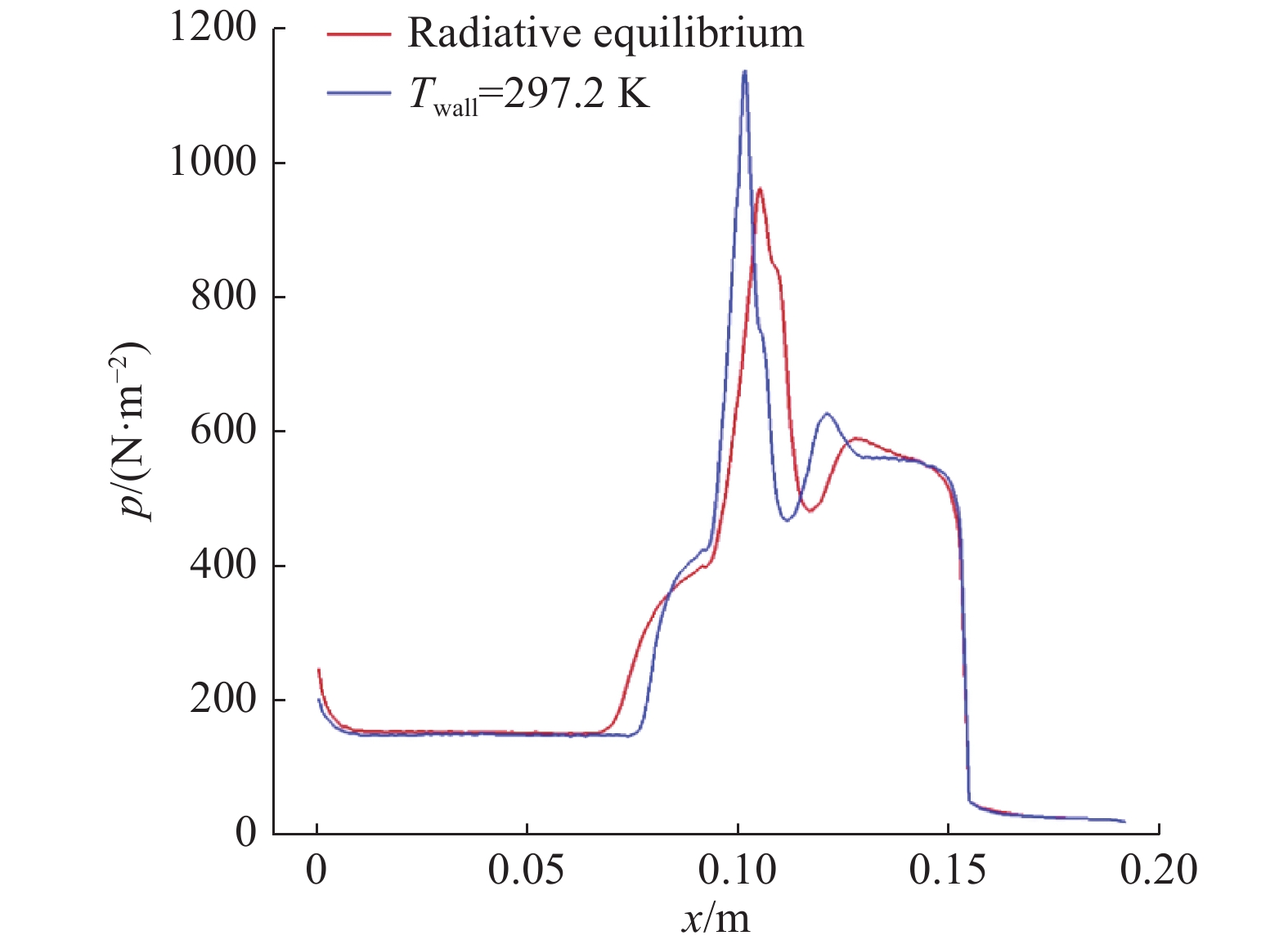
图9给出了冷壁和辐射平衡表面压力沿中轴线的计算结果，可以看出辐射平衡条件下的压力峰值明显低于冷壁条件压力峰值，两者差异约为15.4%，同时压力峰值后移。在两种边界条件下，压力在分离区和再附点处差异较大，但在锥前段和锥后凸台段基本相同。

表4给出了冷壁和辐射平衡条件下的阻力系数（凸台表面面积为参考面积），两种壁面条件下的阻力系数差异约为0.33%，表明壁面温度变化不会导致飞行器整体气动力特性的显著差异。

图10给出了辐射平衡条件下的中轴线壁面温度，是来流对壁面充分加热，达到完全“热透”的结果。可以看到，辐射平衡下的壁面温度显著高于冷壁温度（297.2 K），但前缘和再附点处的温度峰值均显著低于来流总温（2116 K）。对于整个模型而言，前缘位置温度最高，再附点次之，这与直观理解相吻合。这意味着，对于高超声速飞行器，防热系统设计的重点应该放在上述两个区域。

图11给出了从冷壁迭代到辐射平衡的表面热流结果，可以看出，受壁温的影响，冷壁热流与辐射平衡壁面热流的差别非常大，后者远小于前者，前缘处的热流峰值比试验状态低约50%，再附点处的热流峰值比试验状态低2/3左右。即使真实飞行中的壁面没有达到辐射平衡，至少长时间的飞行也使得壁面充分加热，即飞行条件下的热流也应该显著低于激波风洞给出的预测值。在实际应用中，可以认为真实热流值在冷壁和辐射平衡壁面的计算结果之间，因此两种条件相结合，可以给出真实飞行的热流预测范围估计。

4 结　论

本文在传统CFD方法辐射平衡壁面模型基础上，提出了适用于DSMC方法的辐射平衡壁面温度条件，开发了轴对称构型DSMC求解器，以钝锥构型验证了其正确性。基于双锥构型，重点考察了恒温冷壁（试验条件）和辐射平衡条件下的壁面压力分布和热流。数值计算结果表明：恒温冷壁条件得到的壁面压力分布和热流与风洞试验结果吻合，两种温度边界下的压力峰值差异约为15.4%，但是整体气动力特性差异仅约为0.33%。相对于冷壁，辐射平衡计算得到的前缘处热流峰值降低约50%，再附点处的热流峰值降低约三分之二；两种条件相结合，可以给出壁面热流的预测范围。该项研究可应用于真实飞行器外形和飞行条件下的表面热流和温度分布预测，为临近空间长航时飞行器设计提供可靠依据。本文研究并未考虑气体辐射、壁面催化/氧化/烧蚀等其他复杂过程对壁面热流大小的影响，后续将深入研究。