扑翼获能器作为一种较新的获能装置,由于其结构简单、鲁棒性好、噪音低以及对浅层、低速水流能量利用率高等方面的优势[1-3],成为了风力机与水轮机等传统旋转透平的有力竞争者,得到了越来越多研究者的关注[4]。
传统的旋转透平要求流动依附在叶片表面以实现较高的获能效率,扑翼结构可利用翼型失速产生的前缘涡,使其在叶片扑动过程中始终不脱离叶片表面,从而产生高升力牵动叶片进行做功[5-8]。通过扑动运动从流体中汲取能量的理念在1972年由Wu等[9]提出。随后,McKinney和DeLaurier等[10]首次通过实验的方式,利用扑翼结构以升沉运动与俯仰运动实现了从流体中获取能量。为了研究扑翼结构的获能特性,众多学者对扑翼在不同的几何、运动参数下展开了大量的模拟与实验研究。Jones等[11]通过对扑翼俯仰幅值、缩减频率以及俯仰运动、升沉运动的相位角等参数的研究,指出仅当俯仰幅值大于诱导迎角时,且升沉运动及俯仰运动的相位差在
尾缘襟翼(Trailing-Edge Flap,TEF)是一种广泛应用于航空航天领域的增升机构,其结构简单、鲁棒性强、增升效果好[14-15]。目前对于尾缘襟翼在单一叶片以及垂直轴风力机上应用的研究已经较为成熟[16-18],而应用于扑翼获能方面的研究则主要局限于格尼襟翼[19-20],朱兵的研究结果[20]表明格尼襟翼的应用影响了尾缘涡的演化,通过增大扑翼上下表面的压差,提高了升力,使获能效率得到了21%的提升,但文中并未提及格尼襟翼自身摆动带来的额外能量消耗。Totpai等[21]以实验方式探究了低缩减频率下被动式前缘襟翼对扑翼获能的影响,其结果表明:这种被动式的前缘变形增强了前缘涡强度,有助于提高升沉力,但该部分提高主要集中在升沉速度较小的扑动周期前期,力与速度同步性较差,难以对扑翼整体的获能效果带来显著提升。也有相关研究利用尾缘襟翼使扑翼在高风速下维持正常的升沉、俯仰运动[22],但并未对其在提高扑翼获能效果上进一步展开研究。
对于其他形式的襟翼在扑翼获能上的应用,目前的研究十分有限。为提高扑翼获能器的获能效率,本文提出了一种可摆动的尾缘襟翼模型,襟翼在扑翼运动过程中始终向翼型压力面偏转,通过增加翼型弯度以提高升沉力,从而达到提高扑翼获能效率的目的。这种形式的襟翼在扑翼获能器上的应用目前还未见相关报道,本文通过动网格技术与非定常数值模拟方法,对该模型的扑动过程和获能特性进行研究,发现对提升效率有显著效果,表明这是一种有应用前景的新型扑翼式获能器。此外,文章还详细计算分析了翼型厚度对具有尾缘襟翼扑翼的获能特性的影响,为今后这种新型带尾缘襟翼扑翼获能器的设计及其工程应用进行了有益的探索。
1 计算模型与验证 1.1 扑翼运动模型扑翼获能器的运动模型可以简化为升沉运动
| $ \begin{split} h(t) = &{h_{\rm{0}}}\sin (2{\rm{{\text{π}} }}ft + \varphi ) \\& \to {V_y}(t) = 2{\rm{{\text{π}} }}f{h_{\rm{0}}}\cos (2{\rm{{\text{π}} }}ft + \varphi ) \end{split} $ | (1) |
| $ \begin{split} \theta (t) =& {\theta _{\rm{0}}}\sin (2{\rm{{\text{π}} }}ft) \\& \to \omega (t) = 2{\rm{{\text{π}} }}f{\theta _{\rm{0}}}\cos (2{\rm{{\text{π}} }}ft) \end{split} $ | (2) |
其中,
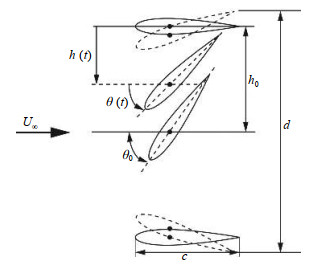
|
图 1 扑翼运动模型 Fig.1 The heaving and pitching motions of a flapping airfoil |
扑翼从流体中获取的总能量由升沉运动和俯仰运动做功之和求得[6-7, 12]。升沉运动做功
| $ {P_Y}(t) = Y(t){V_y}(t) $ | (3) |
| $ {P_\theta }(t) = M(t)\omega (t) $ | (4) |
扑翼在一个运动周期内的平均获能系数
| $ {\overline C _P}{\rm{ = }}\frac{{\overline P }}{{1/2\rho U_\infty ^3c}} $ | (5) |
式中,
| $ \begin{split} {\overline C _P}{\rm{ = }}{\overline C _{PY}} + {\overline C _{P\theta }} = \int_{\rm{0}}^{\rm{1}} {\left( {{C_Y}(t)\frac{{{v_y}(t)}}{{{U_\infty }}} + {C_M}(t)\frac{{\omega (t)c}}{{{U_\infty }}}} \right){\rm{d}}\left( {t/T} \right)} \end{split} $ | (6) |
式中,
为计算扑翼的获能效率,我们将其定义为流体对扑翼做的平均总功率
| $ \eta {\rm{ = }}\frac{{\overline P }}{{{{\overline P }_a}}} = \frac{{{{\overline P }_Y} + {{\overline P }_\theta }}}{{1/2\rho U_\infty ^3d}} = {\overline C _P}\frac{c}{d} $ | (7) |
其中,
本文所提出的尾缘襟翼模型如图2所示,图中
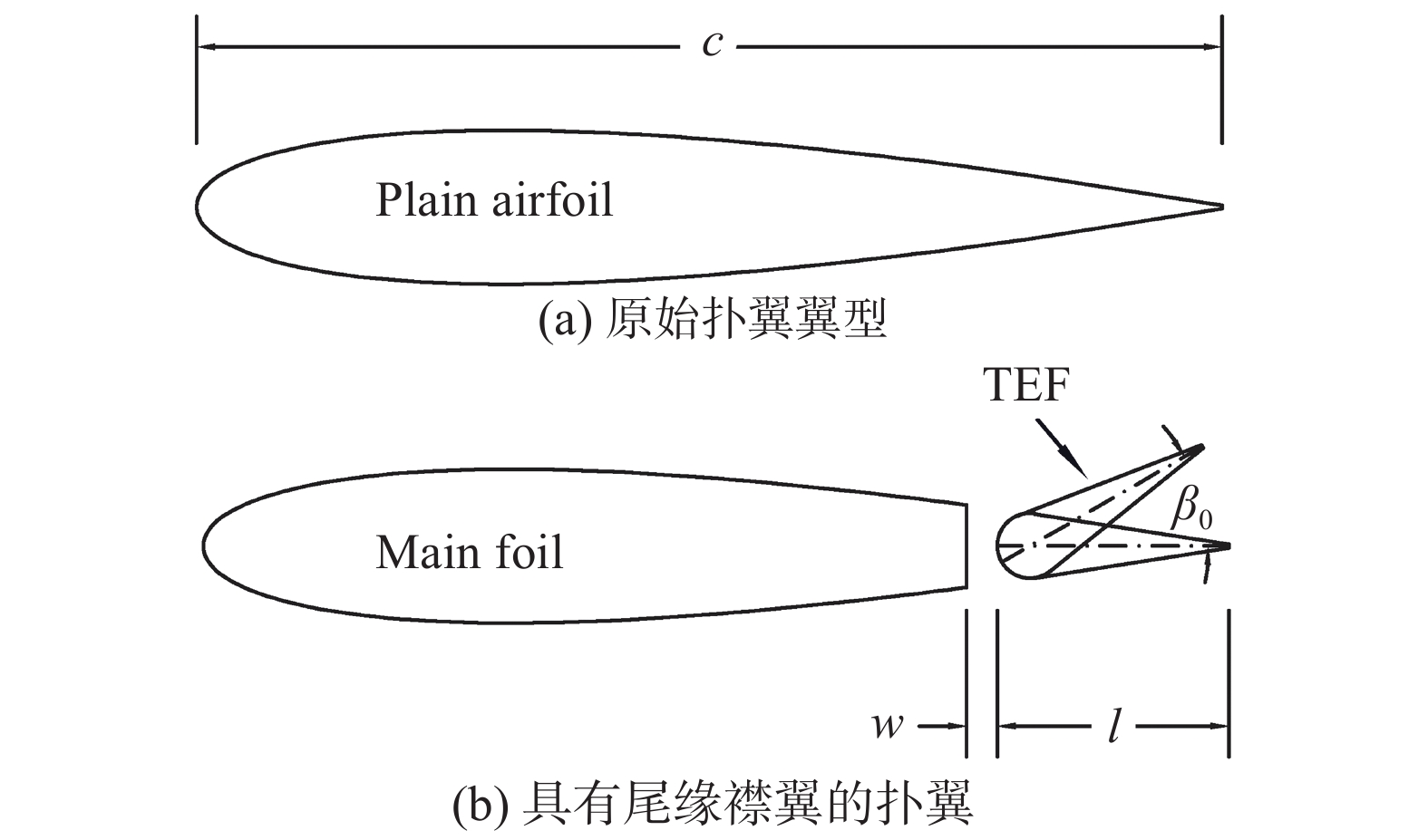
|
图 2 NACA0015基本翼型与加装尾缘襟翼后的扑翼 Fig.2 The NACA0015 airfoil and the flapping airfoil with a trailing-edge flap |
| $ \begin{split} \beta (t) = {\beta _{\rm{0}}}\sin (2{\rm{{\text{π}} }}ft + \varphi ) \to {\omega _t}(t) = 2{\rm{{\text{π}} }}f{\beta _{\rm{0}}}\cos (2{\rm{{\text{π}} }}ft) \end{split} $ | (8) |
其中,
尾缘襟翼绕自身俯仰轴产生的俯仰力矩系数
| $ {\overline C _P}{\rm{ = }}{\overline C _{PY}} + {\overline C _{P\theta }} + {\overline C _{P\theta t}} $ | (9) |
其中,
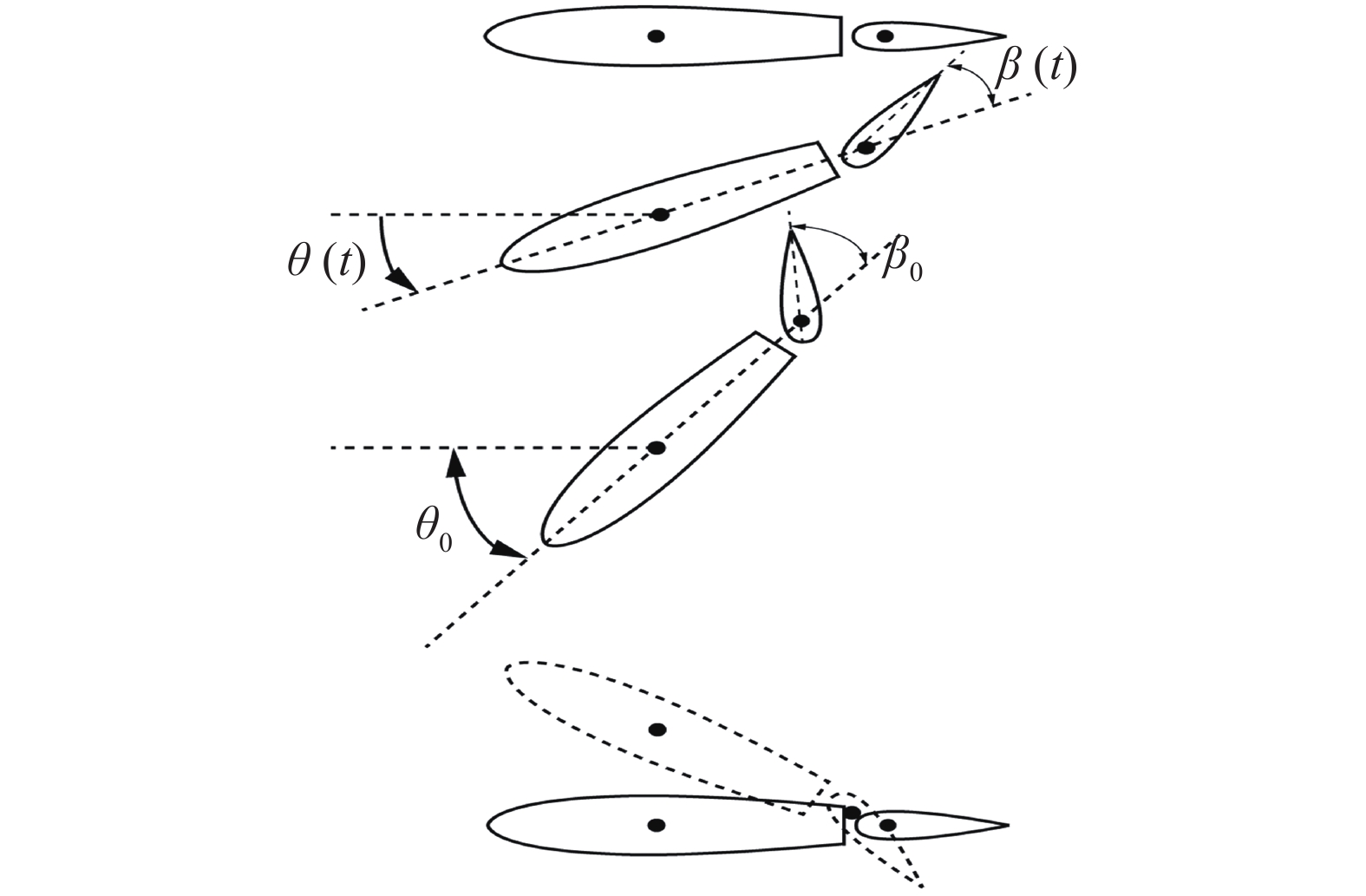
|
图 3 具有尾缘襟翼扑翼的运动模型 Fig.3 A sketch of imposed oscillating motions of the trailing-edge flap |
为了更全面地了解具有尾缘襟翼的扑翼运动过程中的获能特性,除研究其获能效率外,本文还计算了其耗能与获能的比值,定义为
| $ k = \frac{{\left| {\displaystyle\int_{\rm{0}}^{\rm{1}} {\left[ {{C_{PY - }}(t) + {C_{P\theta - }}(t) + {C_{P\theta t - }}(t)} \right]{\rm{d}}t} } \right|}}{{\displaystyle\int_{\rm{0}}^{\rm{1}} {\left[ {{C_{PY + }}(t) + {C_{P\theta + }}(t) + {C_{P\theta t + }}(t)} \right]{\rm{d}}t} }} $ | (10) |
式中
本文采用商用CFD软件ANSYS Fluent,在绝对坐标系下对扑翼周围的二维、非稳态、不可压缩流场展开了数值模拟。空间项和时间项采用二阶格式离散,计算格式采用二阶精度,残差的收敛精度为
图4所示为计算域网格和边界条件的示意图。
本研究采用结构—非结构的网格布局:利用非结构网格划分半径为3倍弦长的内部区域,进行网格重构以实现扑翼的升沉运动与俯仰运动;外围静止域为结构网格,半径为30倍弦长。静止域和动网格域之间通过交界面连接,进口边界采用速度入口条件,出口边界条件采用压力出口。

|
图 4 扑翼计算网格和边界条件 Fig.4 The mesh and boundary conditions for the numerical simulation |
为了保证计算结果的准确性,本文对原始扑翼的数值模拟结果分别进行了网格无关性和时间步长无关性验证。基于以往对于刚性扑翼获能特性的研究,数值模拟中选用NACA0015翼型,工质为液态水。各参数分别固定为:弦长
| 表 1 网格、时间步及湍流模型无关性验证 Table 1 Sensitivity studies of mesh size, time step, and turbulence model |
|
|
从表1中可以看出,当网格数取
为验证前文提出模型的准确度,对其在缩减频率
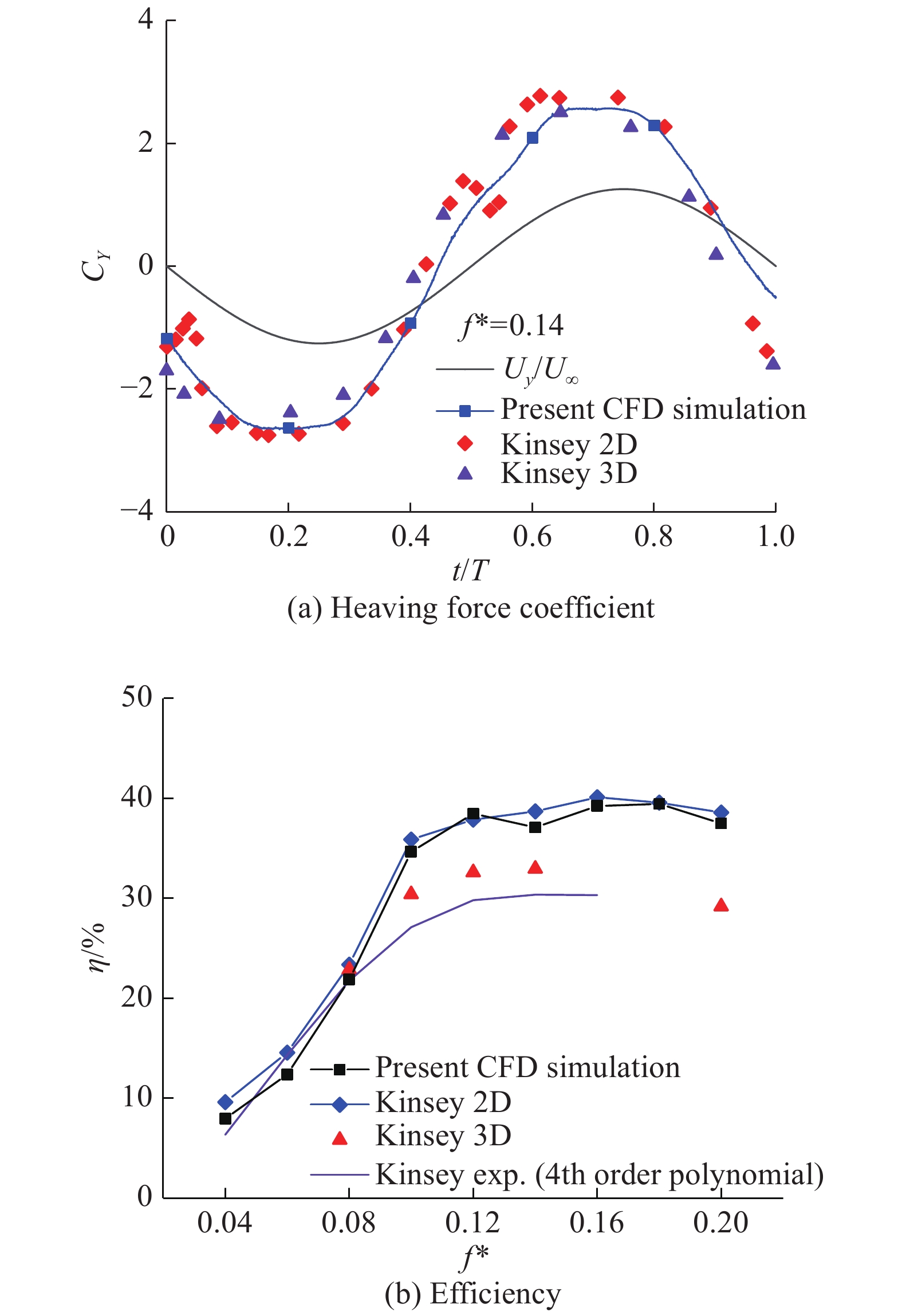
|
图 5 本文数值模拟与参考文献结果[13, 23-24]对比 Fig.5 A comparison between the present numerical results and Refs. [13,23-24] |
由图中可以看出,本研究的升沉力系数模拟结果与Kinsey的模拟结果十分接近,获能效率与Kinsey的二维模拟结果较为接近,其曲线形状能与三维结果较好吻合。获能效率的二维模拟结果均高于三维模拟以及实验结果,则是由于三维情况下翼型的有限展长所致。综上,可认为本研究所使用的的数值模型具有较高的准确性和可信度。
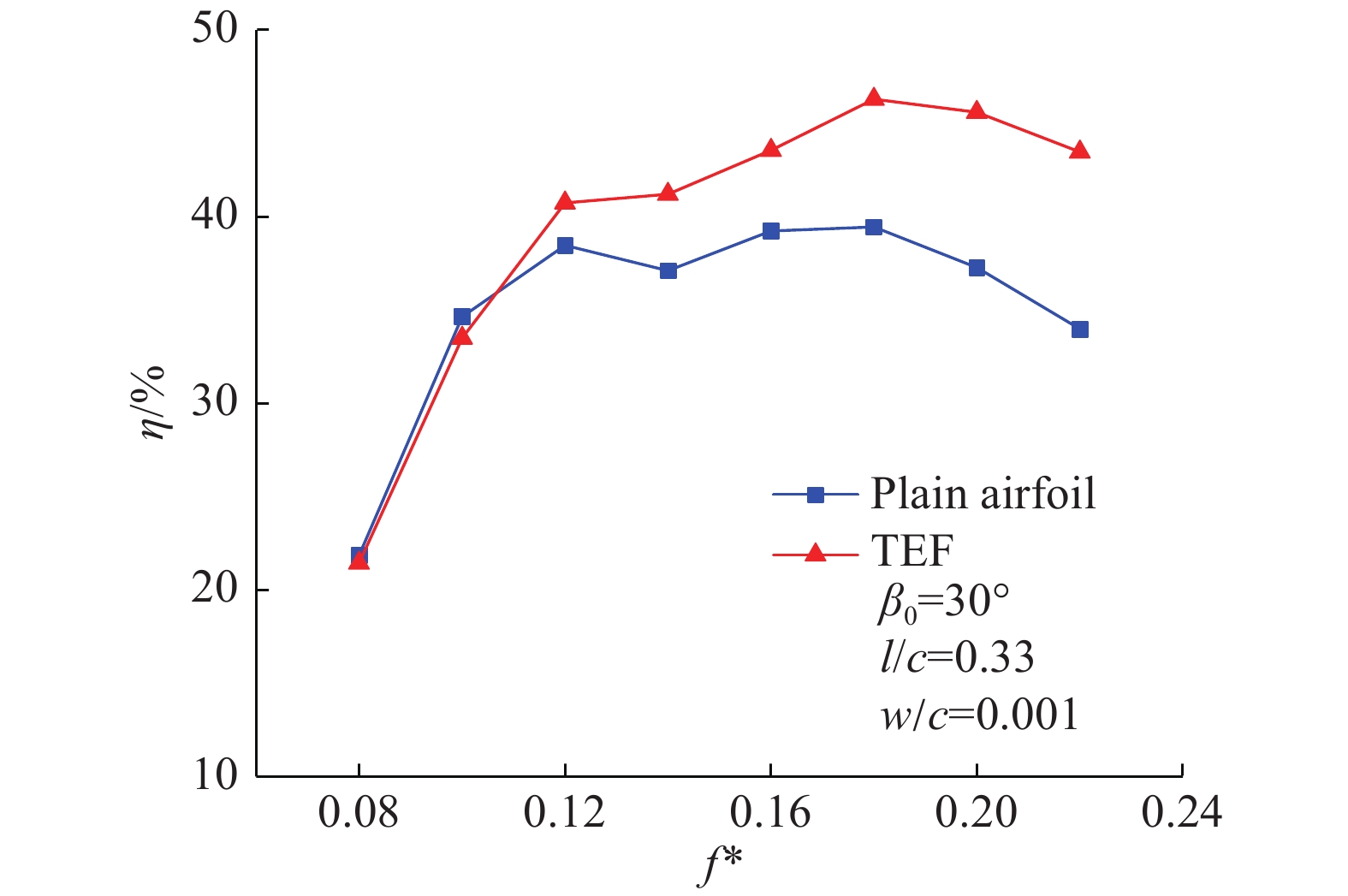
3 结果与讨论 3.1 尾缘襟翼对扑翼获能的影响图6为原始扑翼与带有尾缘襟翼的扑翼在不同缩减频率下的获能效率曲线图。图中选取的尾缘襟翼参数如下:襟翼偏转角度幅值
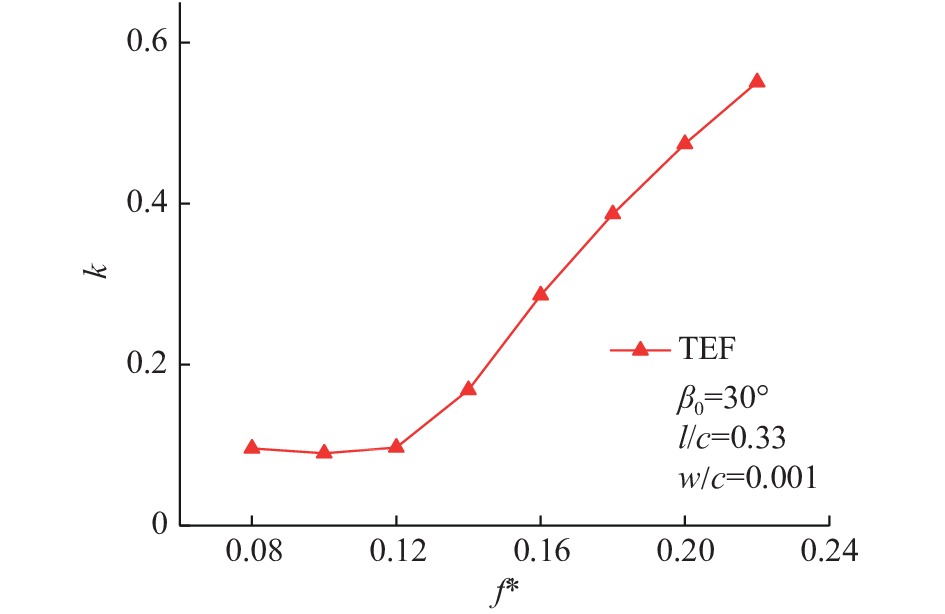
图7为具有尾缘襟翼的扑翼在不同缩减频率下的
为探究尾缘襟翼提升扑翼获能效率的作用机理,本节中以缩减频率
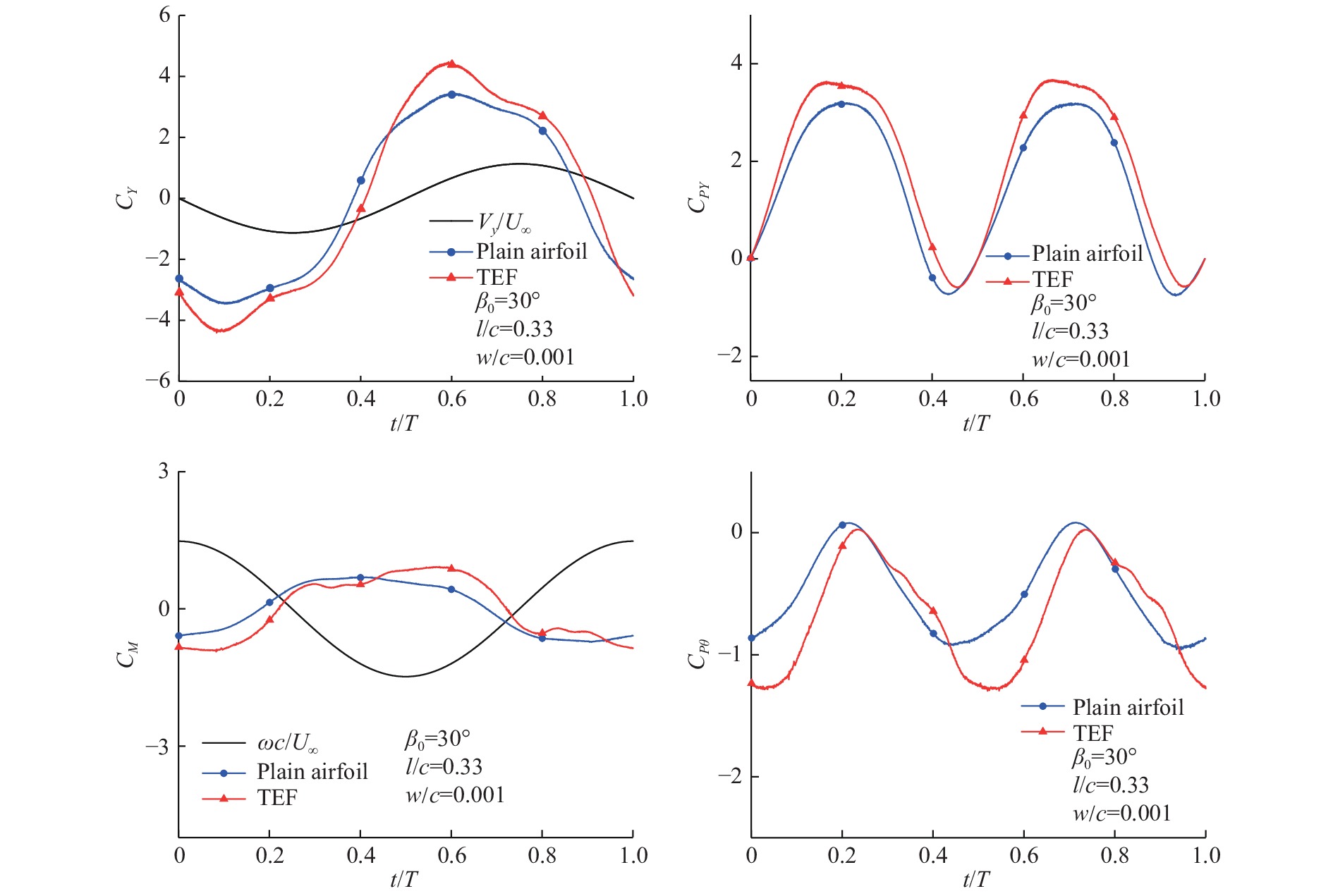
如前文所述,扑翼的总获能由升沉力做功和俯仰力矩做功两部分组成(见公式(6)),故可通过分析原始扑翼和带有尾缘襟翼的扑翼在一个运动周期内的升沉力系数、俯仰力矩系数及其做功情况(如图8所示),进而得到扑翼的获能规律。
|
图 6 原始扑翼与具有尾缘襟翼扑翼的获能效率曲线对比图 Fig.6 Comparison of efficiency at different reduced frequencies |
|
图 7 具有尾缘襟翼扑翼的耗能与获能比值曲线 Fig.7 The ratio of energy input to output of a flapping airfoil with a TEF at different reduced frequencies |
|
图 8 |
由图8可知,缩减频率
为解释升沉力做功与俯仰力矩做功的差异,下面选择

|
图 9 |
由图6可知,当缩减频率超过0.18继续增大时,两种扑翼的获能效率均呈现出下降趋势。本节以
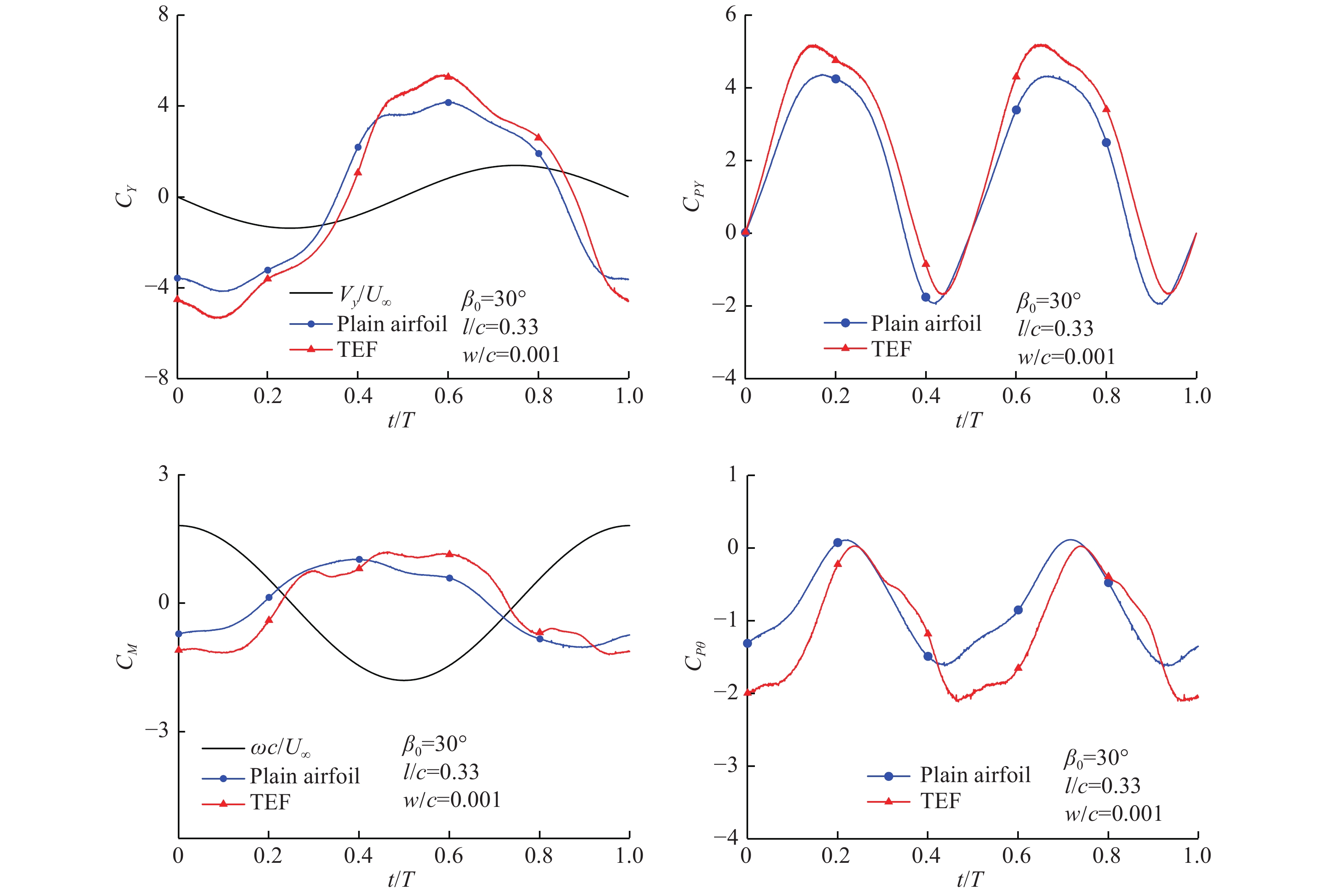
图10为缩减频率
|
图 10 |
图11给出了

|
图 11 |
本节探讨了翼型厚度对具有尾缘襟翼扑翼获能特性的影响。翼型选择NACA0005、NACA0010、NACA0015、NACA0020、NACA0025、NACA0030六种NACA系列标准对称翼型,在雷诺数
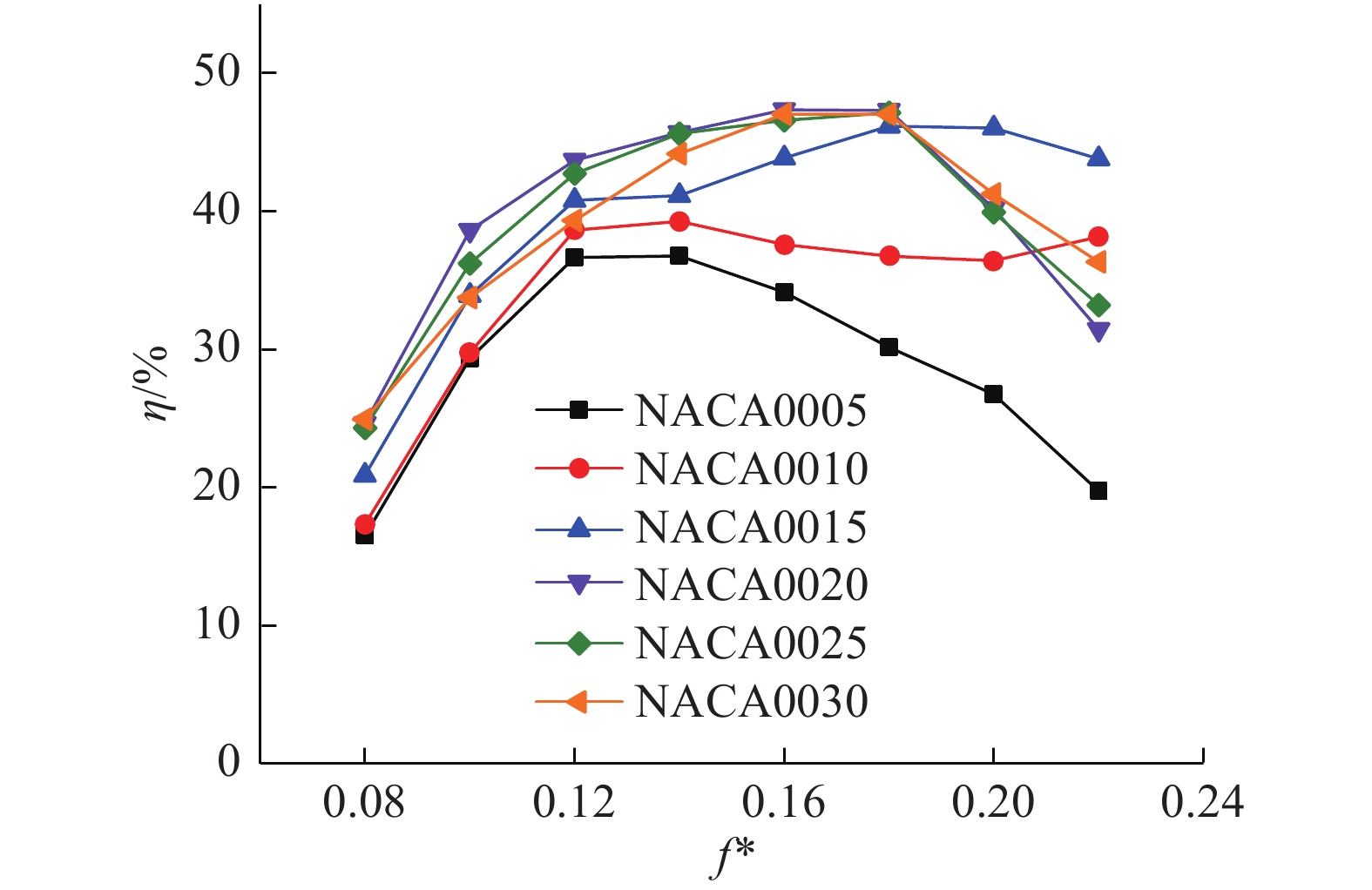
图12给出了不同缩减频率下翼型厚度对具有尾缘襟翼扑翼的获能效率的影响规律。从图中可以得出,最薄的翼型NACA0005的获能性能最差,随着翼型厚度的增大,获能的峰值与高效区范围逐渐增大,NACA0020翼型在中低缩减频率范围内的获能效率达到最大,但此时在高缩减频率下效率开始急剧下降,翼型厚度进一步增大,扑翼的高效工况区逐渐减小。
|
图 12 翼型厚度对尾缘襟翼扑翼获能效率的影响 Fig.12 The effects of airfoil thickness on the energy-extraction efficiency |
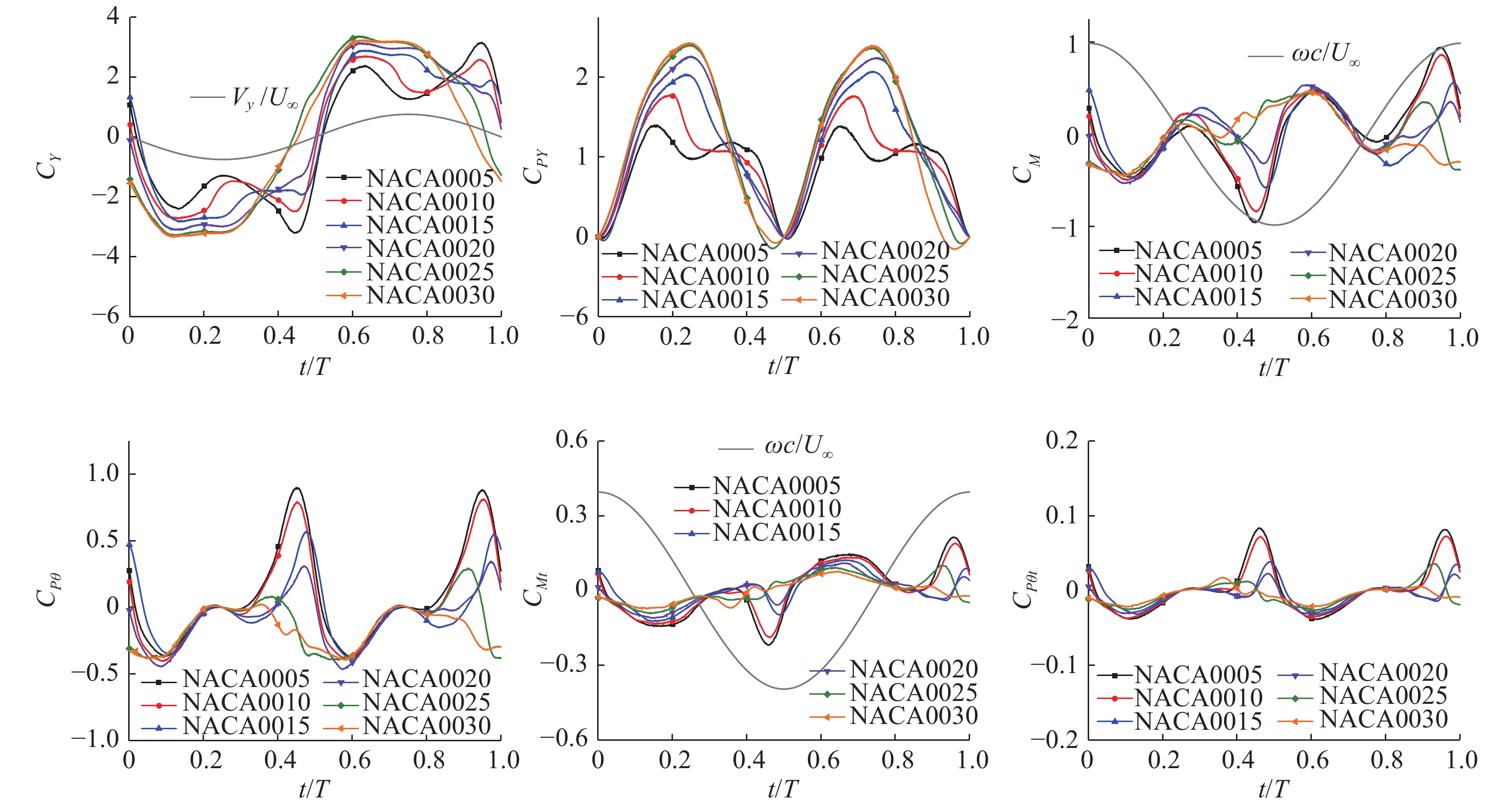
缩减频率取
|
图 13 不同厚度翼型襟翼扑翼的瞬时升沉力系数、俯仰力矩系数及功率系数( |
此外,从图7的结果中可以发现高缩减频率时的
图14选取NACA0005、NACA0015、NACA0025三种不同厚度翼型的襟翼扑翼在

|
图 14 不同时刻下翼型厚度不同的襟翼扑翼的涡量云图对比 Fig.14 The temporal evolution of vorticity around flapping airfoils with trailing-edge flaps (The three airfoils have different thicknesses) |
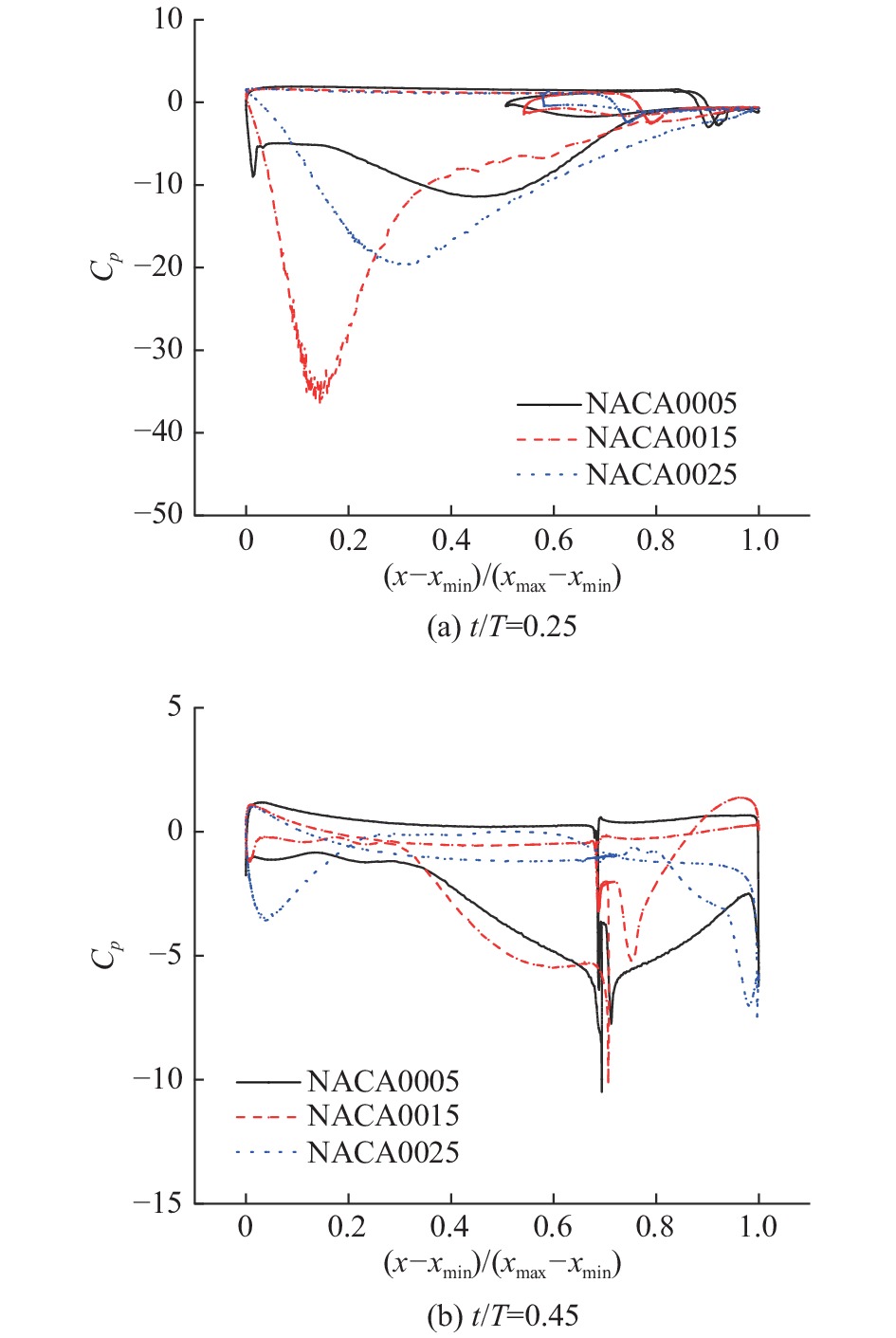
NACA0005、NACA0015、NACA0025三种翼型的襟翼扑翼在缩减频率
|
图 15 厚度不同的翼型襟翼扑翼的表面压力系数对比( |
本文提出了一种在扑翼式获能器上应用摆动尾缘襟翼的思路,通过增大翼型的弯度以提高升沉力及其做功,从而达到增大扑翼获能效率的目的。本文研究发现这种尾缘襟翼对提升效率有显著效果,表明是一种有应用前景的新型扑翼式获能器,并在此基础上探究了翼型厚度对具有尾缘襟翼扑翼获能特性的影响。主要结论可概括如下:
1)在扑翼上添加尾缘襟翼可提高扑翼所受的升沉力,有利于增强扑翼运动与受力方向的协同性,从而提高扑翼的升沉力做功和获能效率。尾缘襟翼对扑翼获能效率的提升在高缩减频率下尤为明显,效率相对原始扑翼最多可提高23.5%。超过最佳缩减频率后,俯仰力矩的负功增幅相比升沉力的正功增幅更大,因此获能效率开始降低。
2)具有尾缘襟翼的扑翼耗能与获能之比
3)翼型厚度对扑翼前缘涡的演化形态存在明显的影响,获能效率整体上呈现随翼型厚度增大先增加后降低的规律,此外,较大厚度翼型的获能特性在高缩减频率下出现了急剧劣化的现象。
本文提供了一种提高扑翼式获能器获能效率的新思路,研究结果具有一定的理论意义和实际应用价值。在后续的工作中,可以考虑进行三维数值模拟或可视化实验,揭示扑翼前缘涡演化过程中更多的流动细节,更深入地探讨尾缘襟翼的增升机理。此外,由于目前的研究大多着眼于扑翼的气动性能,还需要对控制、结构等学科交叉问题进行探索,以期为将来工程化应用提供可行性参考。
| [1] |
LIU Z, QU H L, SHI H D. Performance evaluation and enhancement of a semi-activated flapping hydrofoil in shear flows[J]. Energy, 2019, 189: 116255. DOI:10.1016/j.energy.2019.116255 |
| [2] |
常兴华, 马戎, 张来平. 海鸥翼折转运动的数值模拟及分析[J]. 空气动力学学报, 2018, 36(1): 135-143. CHANG X H, MA R, ZHANG L P. Numerical study on the folding mechanism of seagull's flapping wing[J]. Acta Aerodynamica Sinica, 2018, 36(1): 135-143. DOI:10.7638/kqdlxxb-2017.0168 (in Chinese) |
| [3] |
LAHOOTI M, KIM D. Multi-body interaction effect on the energy harvesting performance of a flapping hydrofoil[J]. Renewable Energy, 2019, 130: 460-473. DOI:10.1016/j.renene.2018.06.054 |
| [4] |
WU X, ZHANG X T, TIAN X L, et al. A review on fluid dynamics of flapping foils[J]. Ocean Engineering, 2020, 195: 106712. DOI:10.1016/j.oceaneng.2019.106712 |
| [5] |
POLHAMUS E C. Predictions of vortex-lift characteristics by a leading-edge suctionanalogy[J]. Journal of Aircraft, 1971, 8(4): 193-199. DOI:10.2514/3.44254 |
| [6] |
XIAO Q, ZHU Q. A review on flow energy harvesters based on flapping foils[J]. Journal of Fluids and Structures, 2014, 46: 174-191. DOI:10.1016/j.jfluidstructs.2014.01.002 |
| [7] |
YOUNG J, LAI J C S, PLATZER M F. A review of progress and challenges in flapping foil power generation[J]. Progress in Aerospace Sciences, 2014, 67: 2-28. DOI:10.1016/j.paerosci.2013.11.001 |
| [8] |
SIALA F F, LIBURDY J A. Power estimation of flapping foil energy harvesters using vortex impulse theory[J]. Renewable Energy, 2020, 154: 894-902. DOI:10.1016/j.renene.2020.03.067 |
| [9] |
WU T. Extraction of flow energy by a wing oscillating in waves[J]. Journal of Ship Research, 1972, 16(1): 66-78. DOI:10.5957/jsr.1972.16.1.66 |
| [10] |
MCKINNEY W, DELAURIER J. Wingmill: an oscillating-wing windmill[J]. Journal of Energy, 1981, 5(2): 109-115. DOI:10.2514/3.62510 |
| [11] |
JONES K, PLATZER M, JONES K, et al. Numerical computation of flapping-wing propulsion and power extraction[C]//the 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 1997. doi: 10.2514/6.1997-826
|
| [12] |
KINSEY T, DUMAS G. Parametric study of an oscillating airfoil in a power-extraction regime[J]. AIAA Journal, 2008, 46(6): 1318-1330. DOI:10.2514/1.26253 |
| [13] |
KINSEY T, DUMAS G, LALANDE G, et al. Prototype testing of a hydrokinetic turbine based on oscillating hydrofoils[J]. Renewable Energy, 2011, 36(6): 1710-1718. DOI:10.1016/j.renene.2010.11.037 |
| [14] |
LEE T, SU Y Y. Unsteady airfoil with a harmonically deflected trailing-edge flap[J]. Journal of Fluids and Structures, 2011, 27(8): 1411-1424. DOI:10.1016/j.jfluidstructs.2011.06.008 |
| [15] |
VISCONTI U, EUN W, SIM J, et al. Design improvements and flap deflection evaluations with considering centrifugal load on active trailing edge flap[J]. Aircraft Engineering and Aerospace Technology, 2018, 91(1): 10-19. DOI:10.1108/aeat-10-2016-0165 |
| [16] |
韩中合, 贾亚雷, 李恒凡, 等. 尾缘襟翼长度对风力机翼型气动性能的影响[J]. 空气动力学学报, 2015, 33(6): 835-842. HAN Z H, JIA Y L, LI H F, et al. The effect of trailing edge flaps length on aerodynamics of wind turbine airfoil[J]. Acta Aerodynamica Sinica, 2015, 33(6): 835-842. (in Chinese) |
| [17] |
季康, 李春, 阳君, 等. 尾缘襟翼动态气动特性与控制策略研究[J]. 太阳能学报, 2017, 38(7): 1912-1920. JI K, LI C, YANG J, et al. Research on dynamic aerodynamic performance and flow control of airfoil with flap[J]. Acta Energiae Solaris Sinica, 2017, 38(7): 1912-1920. (in Chinese) |
| [18] |
贾亚雷, 韩中合, 安鹏, 等. 尾缘襟翼缝隙大小对风力机翼型气动性能的影响[J]. 空气动力学学报, 2018, 36(1): 41-46. JIA Y L, HAN Z H, AN P, et al. Influence of gap size of trailing-edge-flap on aerodynamic performance of wind turbine airfoil[J]. Acta Aerodynamica Sinica, 2018, 36(1): 41-46. DOI:10.7638/kqdlxxb-2015.0209 (in Chinese) |
| [19] |
XIE Y H, JIANG W, LU K, et al. Numerical investigation into energy extraction of flapping airfoil with Gurney flaps[J]. Energy, 2016, 109: 694-702. DOI:10.1016/j.energy.2016.05.039 |
| [20] |
ZHU B, HUANG Y, ZHANG Y M. Energy harvesting properties of a flapping wing with an adaptive Gurney flap[J]. Energy, 2018, 152: 119-128. DOI:10.1016/j.energy.2018.03.142 |
| [21] |
TOTPAL A D, SIALA F F, LIBURDY J A. Energy harvesting of an oscillating foil at low reduced frequencies with rigid and passively deforming leading edge[J]. Journal of Fluids and Structures, 2018, 82: 329-342. DOI:10.1016/j.jfluidstructs.2018.04.022 |
| [22] |
FRUNZULICA F, DUMITRACHE A, STOIA M, et al. Harvesting the wind energy through an actively controlled pitch-plunge flapping wing[J]. Renewable Energy and Power Quality Journal, 2016, 1002-1006. DOI:10.24084/repqj14.549 |
| [23] |
KINSEY T, DUMAS G. Computational fluid dynamics analysis of a hydrokinetic turbine based on oscillating hydrofoils[J]. Journal of Fluids Engineering, 2012, 134(2): 021104. DOI:10.1115/1.4005841 |
| [24] |
KINSEY T, DUMAS G. Three-dimensional effects on an oscillating-foil hydrokinetic turbine[J]. Journal of Fluids Engineering, 2012, 134(7): 071105. DOI:10.1115/1.4006914 |
 2021, Vol. 39
2021, Vol. 39


