2. 成都流体动力创新中心,成都 610072
2. Chengdu Fluid Dynamics Innovation Center, Chengdu 610072, China
在稠密大气环境下,当高速轮轨列车运行速度超过400 km/h时,其诱发的气动噪声、气动阻力等问题十分突出,因此传统高速列车进一步提速的代价很大且十分不经济[1]。从交通工具的变革历程来看,人类一直在追求更高速、更安全、更环保的交通出行方式。若“高速列车”在低真空管道中运行,传统高速轮轨列车面临的气动力、气动噪声等问题迎刃而解,“高速列车”进一步提速具备了可能性[2]。值得注意的是,这里的“高速列车”不再是传统的轮轨列车而是安全性更高、舒适性更好的磁浮车[3]。“磁浮车”与“真空管道”相结合的交通模式正逐渐成为国内外专家和学者的研究热点[4-6]。
尽管“磁浮车”与“真空管道”相结合的交通模式可以解决气动阻力、气动噪声等传统高速列车面临的气动问题,但管内高速列车仍然面临着一些新的气动问题。与大气环境相比,真空管道高速列车受管壁限制,其产生的流场与阻塞比有着密切联系[7]。在真空管道高速列车气动问题研究初期,大量研究主要集中在真空度、阻塞比、车速、环境压力及温度等参数对管内气动力的影响[8-10]以及这些系统参数的匹配设计[11-12]。随着管内列车速度增大,管内气流可能达到跨声速或超声速状态,气动热、激波等复杂的气动现象逐渐成为研究热点[13-14]。当管内列车以跨声速运行时,列车前后方会出现正激波、尾流会出现膨胀波及激波相互作用的超声速区域[15]。由于管壁限制,管内气流可能出现流动壅塞现象,进而诱发激波[16-17],激波的出现使得管内气动热效应会更加明显[18]。管内气动热效应主要表现为两方面,其一是管内空气受列车高速压缩,环境中气流温度很快增大,当激波出现时,波后气流温度急剧增大;其二是由于气流黏性列车表面温度边界层较薄,温度梯度大,列车表面温度很高[19]。管内环境温度对管内运输系统的设备会有明显影响。张俊博等[20]建立了低真空管道常导磁悬浮列车计算模型,指出了悬浮导向电磁铁存在超温现象。
当单列高速列车在真空管道内运行时,其经过之处必然出现复杂的气动热变化。这种气动热变化必然对管内环境温度造成很大影响,管内的气动热若不及时通过某种手段进行处理,其对后续通过列车气动特性会产生明显的影响。因此,本文建立了含动边界的准二维真空管道列车数值计算模型,研究了不同初始环境温度对真空管道高速列车气动特性的影响。
1 数值计算模型 1.1 模型假设由于实际的三维列车模型结构、环境条件及运行过程较为复杂,数值求解过程较慢。为便于分析真空管道高速列车诱发的气动问题,这里对模型进行一定的假设:
1)忽略加减速过程,列车以马赫数1速度匀速直线运动;
2)在垂直于车运动方向的平面内,流场参数的切向梯度较小,可以忽略,同时车地间隙较大,忽略地面效应,计算域可简化为准二维轴对称模型;
3)真空管道气密性好,真空度能实现且维持在特定值;
4)管壁绝热性好,与外界不存在热交换;
5)列车运动前,管内气流均匀混合且压力、温度等参数均匀分布,无初始湍流。
1.2 数学模型 1.2.1 连续性介质条件在真空管道内,列车的运行环境不是绝对真空,而是在一定范围内的低压环境。当管内气压很低时,管内可能出现稀薄气体。Knudsen数是判断管内气流是否会出现稀薄效应的主要依据[21],其表示为:
| $ Kn = \frac{\lambda }{l} $ | (1) |
| $ \lambda {\text{ = }}\frac{{{k_B}T}}{{\sqrt 2 \pi {d^2}p}} $ | (2) |
式中,
在本文中,设置列车运行时的环境压力为0.001 atm,环境初始温度T0分别为271.15 K、300 K、350 K、400 K,空气分子直径为3.874×10−10,流动特征长度取车高3.15 m,由上述得到的Knudsen数在1.771×10−5~2.595×10−5之间变化,远小于0.01,管内气流满足连续介质条件。
1.2.2 空气物质属性当列车在管内跨声速运动时,管内气流的密度、动力黏度、热导率等物性参数发生变化。为了描述这些物性参数变化,可以通过Sutherland方程、分子动理论模型等建立起其与温度、压力等宏观物理量的关系。
这里通过理想状态方程建立密度与温度、压力之间的关系:
| $ \rho {\text{ = }}\frac{{p{M_w}}}{{RT}} $ | (3) |
式中,
通过分子动理论模型建立比热比、动力黏度、热导率与温度之间的关系[22],
| $ {c_p} = \frac{R}{{2{M_w}}}(f + 2) $ | (4) |
| $ \mu = 2.67 \times {10^{ - 6}}\frac{{\sqrt {{M_w}T} }}{{\sigma _{L - J}^2{\varOmega _\mu }(T,{E_{L - J}})}} $ | (5) |
| $ \kappa = \frac{{15R\mu }}{{4{M_w}}}\left( {\frac{{4{c_p}{M_w}}}{{15R}} + \frac{1}{3}} \right) $ | (6) |
式中,
含动边界的准二维轴对称非定常N-S积分方程为[24]:
| $ \begin{split}& \frac{\partial }{{\partial t}}\iiint\limits_W {\rho \varphi }{\text{d}}W + \mathop{{\int\int}\mkern-21mu \bigcirc}\limits_S {\rho \varphi \left( {{\boldsymbol{V}} - {{\boldsymbol{V}}_g}} \right)} \cdot {\text{d}}{\boldsymbol{S}} = \\&\quad \mathop{{\int\int}\mkern-21mu \bigcirc}\limits_S {\varGamma \nabla \varphi } \cdot {\text{d}}{\boldsymbol{S}} + \iiint\limits_W {{J_\varphi }}{\text{d}}W \end{split} $ | (7) |
式中,
雷诺数是判断气流为湍流态、过渡态、层流态的依据。假设列车静止,无穷远来流速度为列车运动速度,则雷诺数可以示为:
| $ Re = \frac{{{\rho _\infty }{v_\infty }l}}{{{\mu _\infty }}} $ | (8) |
式中,
对于简单的管道流,临界雷诺数约为2300,而对于简单的平板流,临界雷诺数约为5×105[25]。对于真空管道列车绕流,不属于简单的管道流及平板流,其临界雷诺数尚不明确。在本文中,不同初始环境温度下,由上述得到的管内来流雷诺数在3.01×104~3.65×104之间变化,管内气流可能存在层流到湍流的过渡态。为了更加精确捕捉尾车附近的分离流及从层流-湍流之间的过渡流,引入Menter提出的SST
| $ \begin{split}& \frac{{\partial \left( {\rho {\gamma _{{\text{inter}}}}} \right)}}{{\partial t}} + \frac{{\partial ( {\rho {u_j}{\gamma _{{\text{inter}}}}} )}}{{\partial {x_j}}} = {P_{\gamma 1}} - {E_{\gamma 1}} + \\& {P_{\gamma 2}} - {E_{\gamma 2}} + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _{{\gamma _{{\text{inter}}}}}}}}} \right)\frac{{\partial {\gamma _{{\text{inter}}}}}}{{\partial {x_j}}}} \right] \end{split} $ | (9) |
| $ \begin{split} & \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}k} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\& {\gamma _{{\text{eff}}}}{{\tilde G}_k} - \min \left( {\max \left( {{\gamma _{{\text{eff}}}},0.1} \right),1.0} \right){Y_k} + {S_k} \end{split} $ | (10) |
| $ {\gamma _{{\text{eff}}}} = \max \left( {{\gamma _{{\text{inter}}}},{\gamma _{{\text{sep}}}}} \right) $ | (11) |
| $ {\gamma _{{\text{sep}}}} = \min \left( {{C_{s1}}\max \left( {\frac{{R{e_v}}}{{3.235R{e_{\theta c}}}} - 1,0} \right){F_{{\text{reattch}}}},2} \right){F_{\theta t}} $ | (12) |
式中,标量
列车模型采用头车-中间车-尾车三编组形式的组合模型,头尾车完全相同,其中流线型长度为16.3 m,车身长度为12.09 m,而中间车长度为24.52 m,列车高度H为3.15 m。
由于采用动网格方法模拟列车的运动过程,为保证列车周围流场充分发展,计算域必须有足够的运动空间。在计算域中,头车鼻尖到前方边界水平距离为1500 m,尾车鼻尖到后方边界水平距离为80 m,如图1所示。列车运行的阻塞比为0.3,计算域高度为5.75 m。空间坐标原点位于头车鼻尖处。

|
图 1 计算域几何模型及边界条件示意图(单位:mm) Fig.1 Schematic of the geometric model and boundary conditions of the computational domain(unit: mm) |
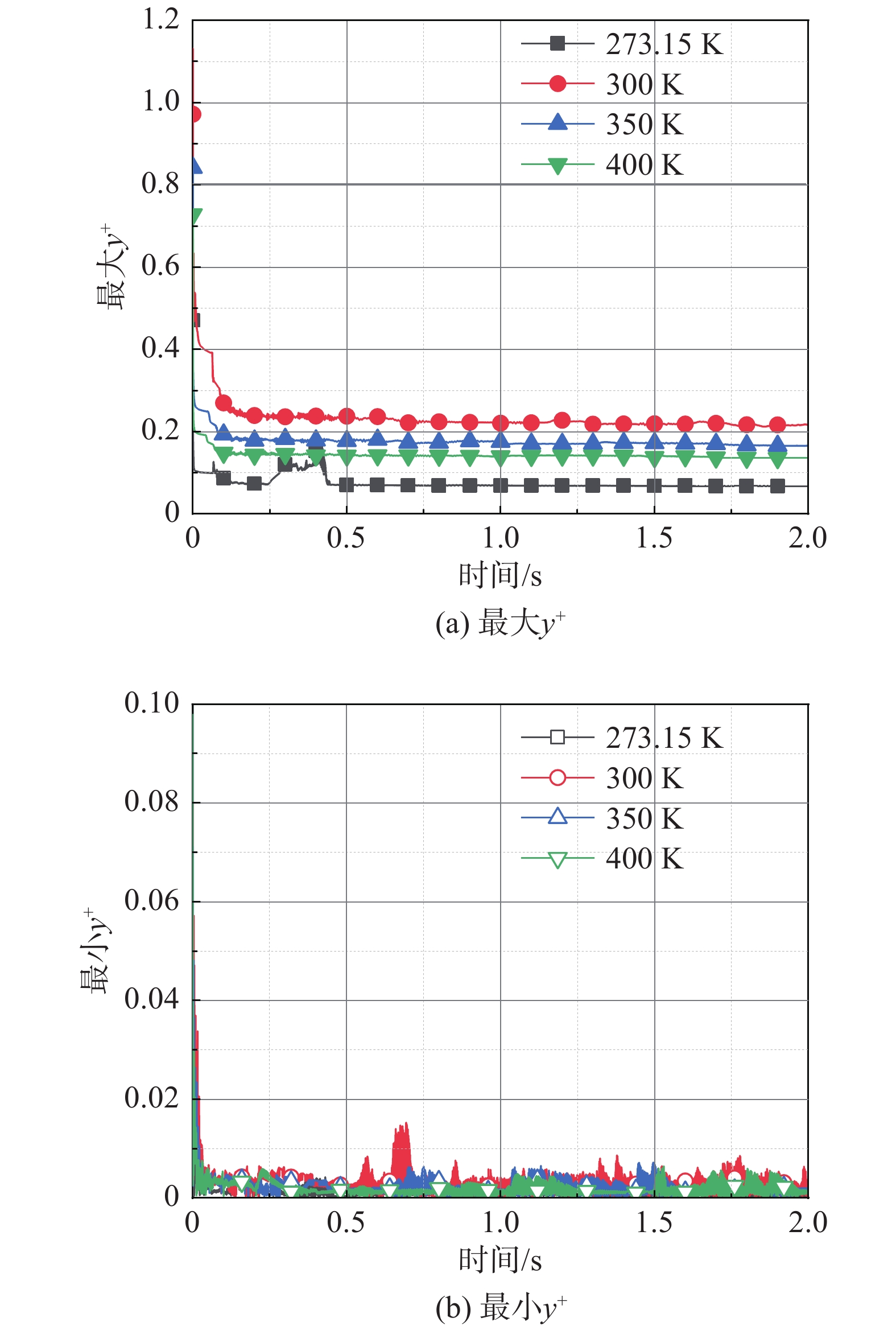
为保证网格具有较高质量且便于动态分层法更新计算域网格,计算域采用四边形的全结构化网格进行填充,如图2所示。网格精度对流场结构(尤其是激波)捕捉精度尤为重要,因此需要对网格精度进行检验。值得注意的是,激波是非常薄的,网格尺寸足够小,其捕捉效果才好,但限于计算资源,如此大的计算域只能降低捕捉激波的分辨率。Sui等[18]已经对管内列车准二维计算模型进行了网格独立性检验并指出当列车表面网格尺寸为10 mm时,能够满足网格精度要求。这里列车表面最大网格尺寸为10 mm,整个计算域最大网格尺寸为500 mm,网格总量约1.70×106。列车边界层内至少保证15层网格,网格增长率为1.1,第一层网格到列车表面法向距离为0.3 mm。图3给出了不同初始环境温度下列车壁面y+值随时间的变化曲线。可以看出,不同初始环境温度下,当列车运动足够时间时,列车壁面y+值逐渐趋于稳定,其中最大y+值不超过1,最小y+值不低于0.001。

|
图 2 列车周围网格分布 Fig.2 Grid distribution around the train |
|
图 3 不同初始环境温度下列车壁面y+分布 Fig.3 y+ value distribution on the train surface at different initial ambient temperatures |
列车前后方计算域边界均为非反射压力出口边界,边界处压力及温度值均与环境初始值保持一致,其中压力值为0.001 atm,温度值根据不同工况分别为273.15 K、300 K、350 K、400 K。列车与管壁均为无滑移壁面边界,其中列车运动速度为1马赫。对称轴(如图1所示)为轴对称边界类型。初始环境中,管内气流均匀充分混合,处于层流状态,无湍流运动。
1.6 求解方法伴随着管内列车高速运动,管内出现的激波等复杂流动现象可能造成收敛困难。为提高求解稳定性及收敛性,采用隐式求解器,通量采用Roe格式进行分裂。空间格式采用二级迎风格式对密度、动量、能量、湍流项等物理项进行离散。非定常时间项仍采用对偶时间步来推进,仿真时间步长为2×10−5 s,保证最大库朗数不超过1.0。整个仿真时间为2 s,能够保证列车周围流场充分发展并趋于稳定,同时能够防止波在计算域边界发生反射现象。在每个时间步内,最大迭代次数为20,流动方程及湍流方程的残差设置为1×10−4 。当列车开始运动时,流场变化大,残差标准难以满足,但随着列车运动,迭代步数增多,各指标的残差标准均满足。
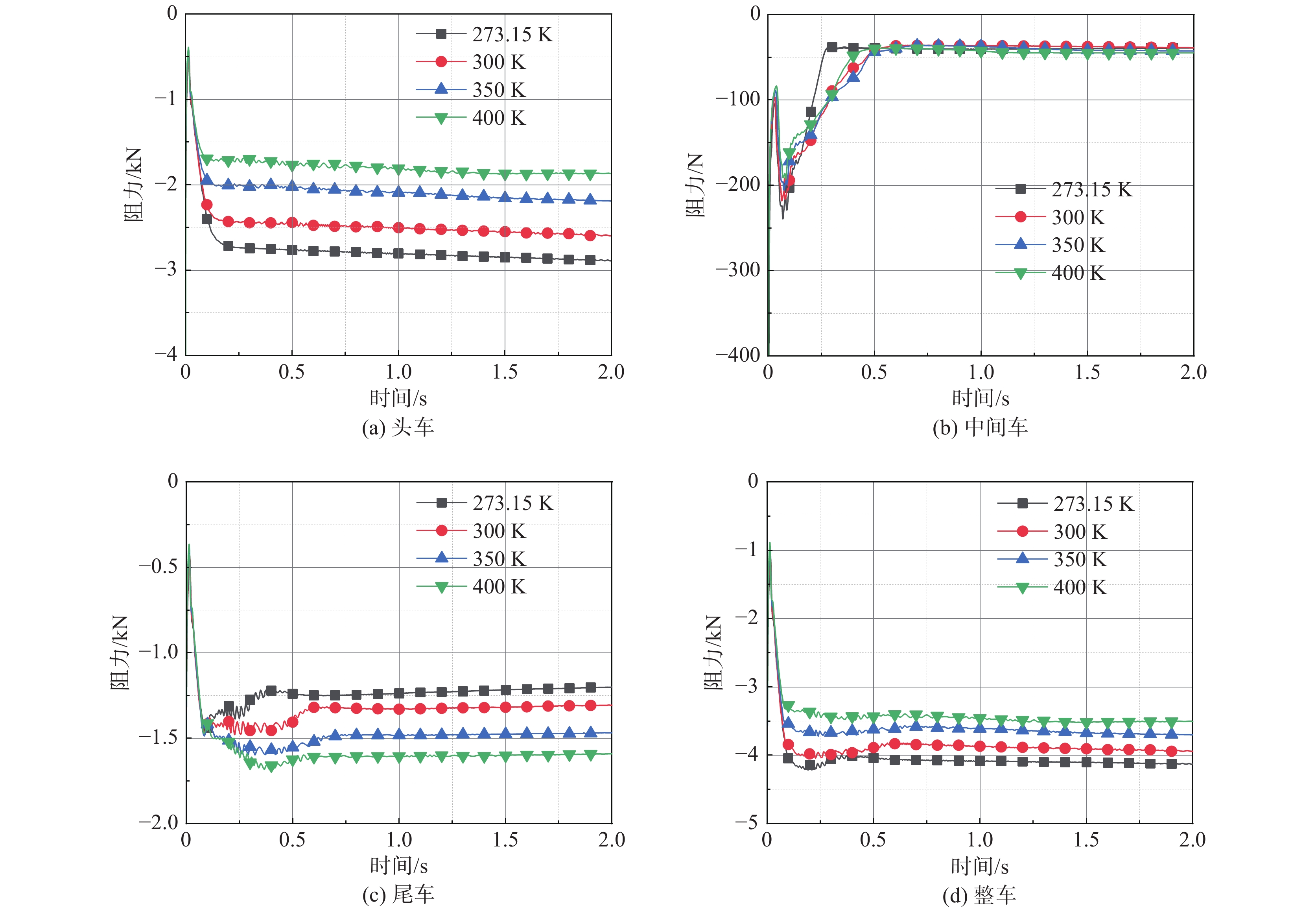
2 仿真结果与分析 2.1 列车气动荷载变化 2.1.1 阻力变化当列车刚开始运动时,列车周围流场变化剧烈,其气动阻力变化较大,但随着列车运动,其周围流场逐渐趋于稳定,气动力也趋于稳定,如图4所示。
|
图 4 不同初始环境温度下各车厢及整车阻力变化 Fig.4 Drag variation of each single car and the whole train at different initial ambient temperatures |
表1给出了当列车运动2 s时,各车厢及整车阻力值。可以看出,随着初始环境温度增大,头车阻力值减小,尾车阻力值增大,而中间车阻力值变化不到10 N。由于头车受前方较强的正激波作用,相同环境条件下,头车的阻力值比尾车的大。由于中间车壁面与来流方向平行,其阻力主要来源于黏性力,在不同环境温度下的阻力值大小几乎不变。随着初始环境温度增大,整车阻力值逐渐减小。整车阻力值与初始环境温度值之间呈二次多项式变化关系,可表示为:
| 表 1 各车厢及整车阻力值(列车运动时间2 s) Table 1 Drag values of each single car and the whole train (t= 2 s) |
|
|
| $ {F_{{\text{drag}}}} = {10^{ - 5}}T_{{\text{em}}}^2 - 0.0145{T_{{\text{em}}}} + 7.0169 $ | (13) |
式中,
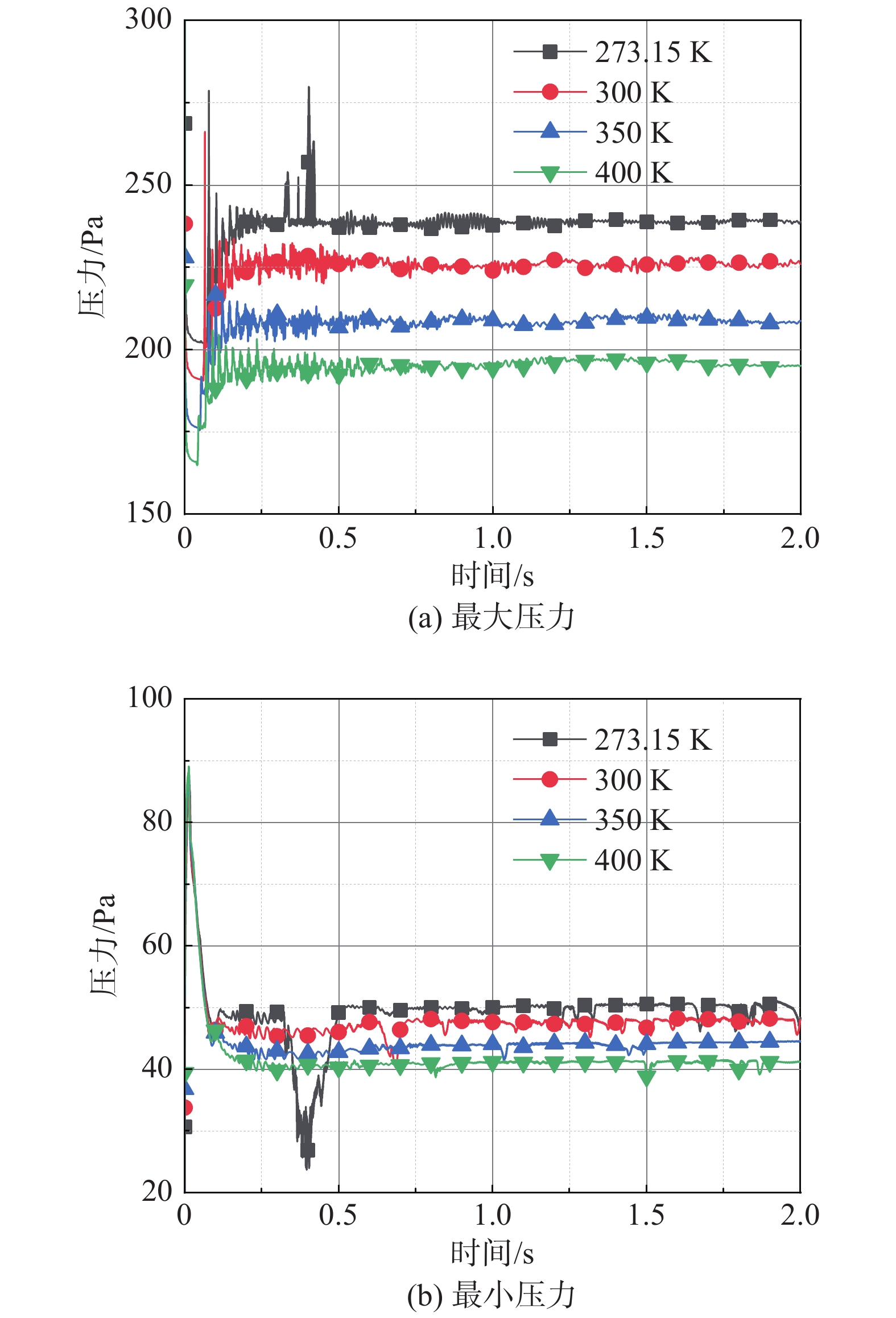
图5给出了不同初始环境温度下列车表面压力最大值最小值随时间的变化规律。可以看出,随着列车运动,列车表面压力最大值最小值趋于稳定。随着初始环境温度增大,列车表面压力最大值最小值越小。值得注意的是,在初始环境温度为273.15 K的工况下,列车运动时间在0.32 ~0.50 s之间,由于列车周围流场未充分发展,列车表面压力的最大值最小值出现较大幅度的波动,最大值超过250 Pa,而最小值接近20 Pa。
|
图 5 不同初始环境温度下列车表面最大最小压力变化 Fig.5 Maximum and minimum pressure variation on the train surface at different initial ambient temperatures |
当列车周围流场充分发展后,列车压力最大值出现在头车鼻尖,而最小值出现在尾车流线型部位的边界层分离处,如图6所示。当列车运动2 s时,在初始环境温度分别为273.15 K、300 K、350 K、400 K的工况下,列车表面压力最大值分别为238.8 Pa、225.9 Pa、208.7 Pa、195.1 Pa,分别超过初始环境压力值137.5 Pa、124.6 Pa、107.4 Pa、93.8 Pa,而列车表面压力最小值分别为48.2 Pa、47.9 Pa、44.5 Pa、41.3 Pa,分别低于初始环境压力值53.1 Pa、53.4 Pa、56.8 Pa、60.0 Pa。
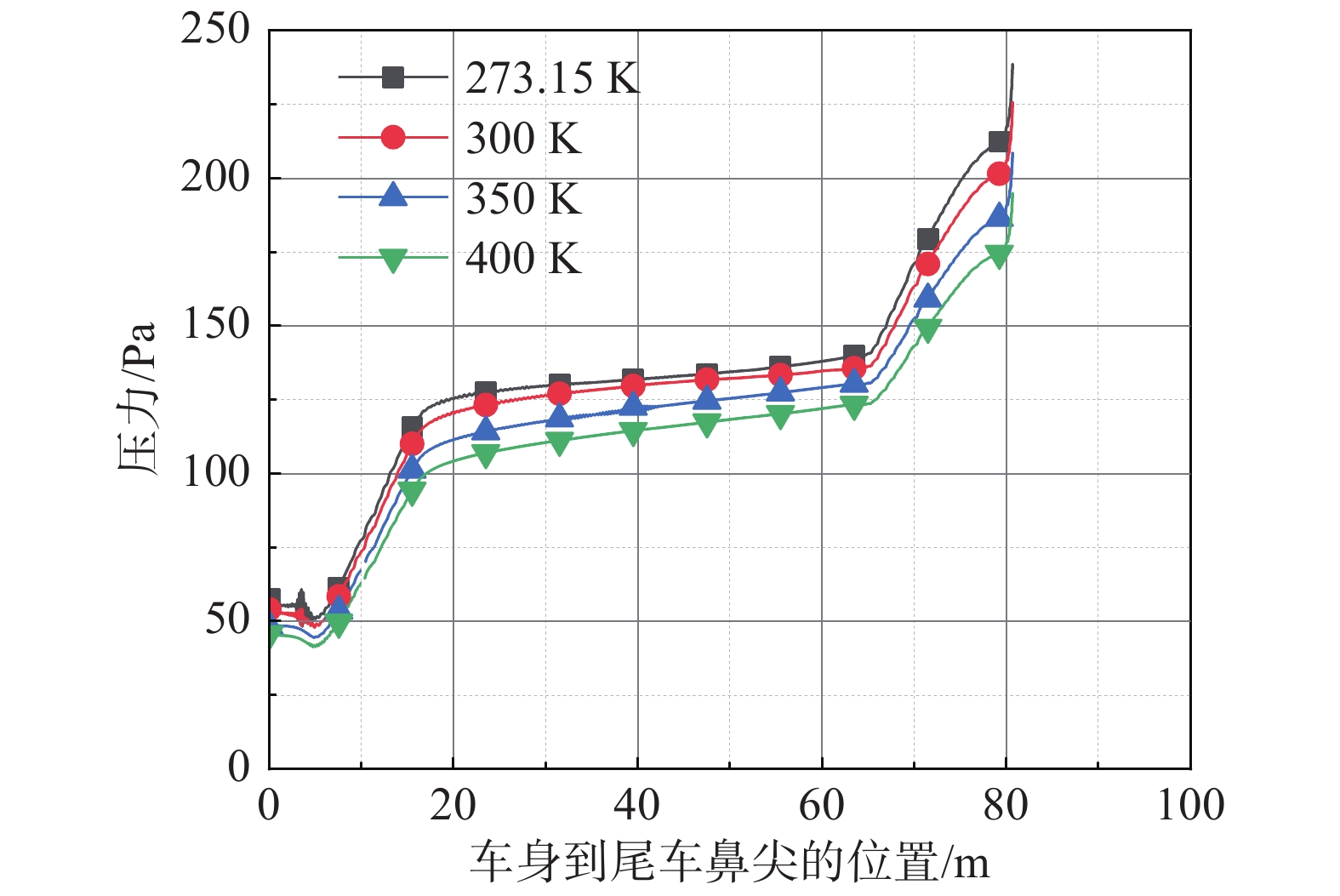
|
图 6 不同初始环境温度下列车表面压力分布(t = 2 s) Fig.6 Pressure distribution on the train surface at different initial ambient temperatures (t= 2 s) |
图7给出了不同初始环境温度下列车表面温度最大值最小值随时间的变化规律。可以看出,随着初始环境温度增大,列车表面温度最大值越大,但温度最小值变化不具有单调性。在初始环境温度为273.15 K的工况下,其列车表面温度最小值比初始环境温度为300 K的大。值得注意的是,在初始环境温度为273.15 K的工况下,列车运动时间在0.32~0.50 s之间,由于列车周围流场未充分发展,列车表面温度最大值最小值的分布位置有所变化,其值波动较大。
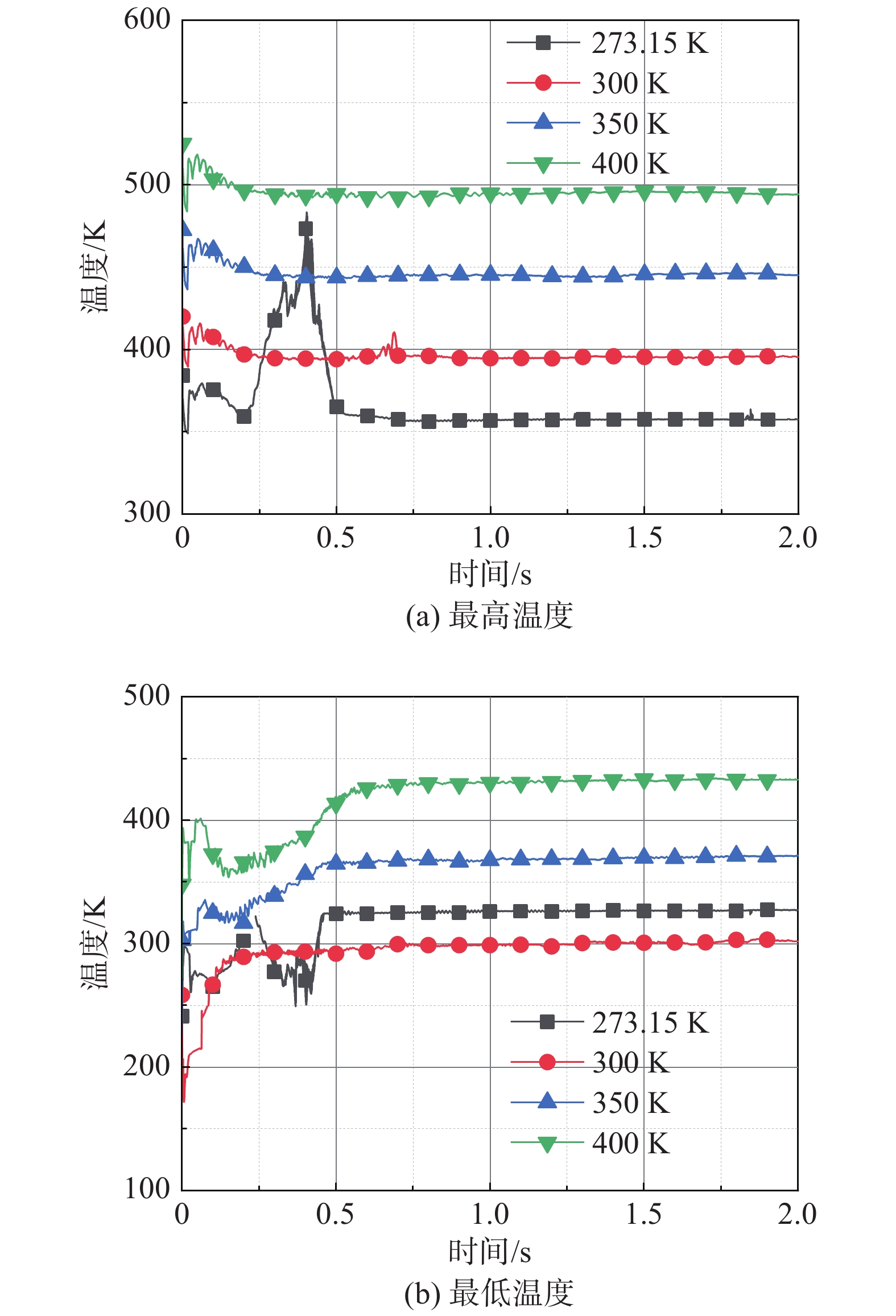
|
图 7 不同初始环境温度下列车表面最高最低温度变化 Fig.7 Maximum and minimum temperature variation on the train surface at different initial ambient temperatures |
当列车周围流场充分发展后,列车温度最大值最小值均出现在头车流线型部位,如图8所示。当列车运动2 s时,在初始环境温度分别为273.15 K、300 K、350 K、400 K的工况下,列车表面温度最大值分别为357.4 K、395.3 K、445.1 K、494.3 K,分别超过初始环境温度值84.3 K、95.3 K、95.1 K、94.3 K,而列车表面温度最小值分别为327.2 K、301.5 K、371.3 K、432.8 K,分别低于初始环境温度值54.1 K、1.5 K、21.3 K、32.8 K。
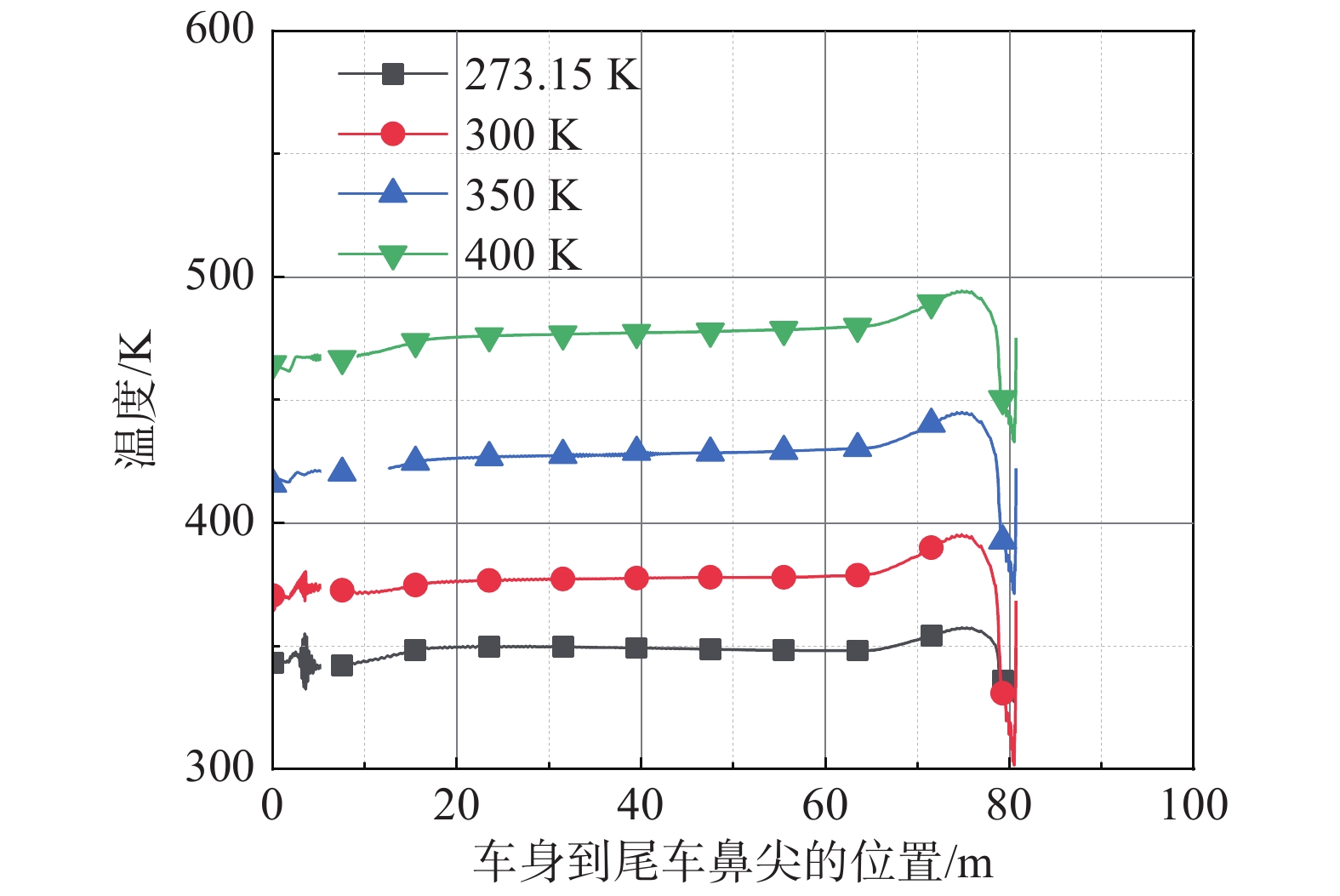
|
图 8 不同初始环境温度下列车表面温度分布(t = 2 s) Fig.8 Temperature distribution on the train surface at different initial ambient temperatures (t= 2 s) |
图9给出了列车运动2 s时,不同初始环境温度下,列车周围空间压力分布云图。可以看出,在不同初始环境温度下,列车诱发的流场具有相似结构,尾流均伴随着激波、膨胀波的反射、且列车前后方均有正激波形成。但随着初始环境温度增大,在相同时间段内,尾流扰动区(尾流正激波与尾车鼻尖之间的区域)的范围逐渐缩小,且低压区域的压力值逐渐减小,这与Bao等[27]研究结果保持一致。车前扰动区(列车前方正激波与头车鼻尖之间的区域)的范围逐渐扩大,且高压区域的压力值逐渐减小。可见,提高初始环境温度,可以延缓尾流波系的发展过程,而加快车前正激波的发展过程。当列车运动2 s时,在初始环境温度分别为273.15 K、300 K、350 K、400 K的工况下,尾流扰动区的长度分别为173 m、153 m、118 m、90 m,车前扰动区的长度分别为190 m、210 m、241 m、274 m,而整个流场扰动区(含列车旁侧区域)的长度分别为445 m、444 m、440 m、445 m。
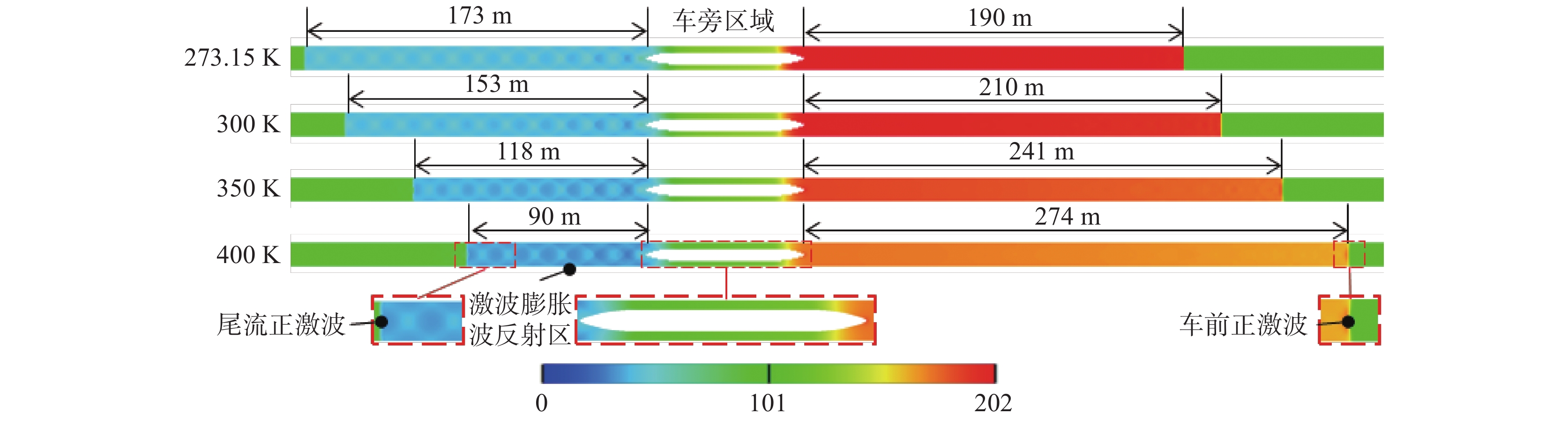
|
图 9 不同初始环境温度下列车周围空间压力分布(列车运动2 s,单位:Pa) Fig.9 Pressure distribution around the train at different initial ambient temperatures (t= 2 s, unit: Pa) |
图10给出了列车运动2 s时,不同初始环境温度下,列车周围空间温度分布云图。可以看出,随着初始环境温度增大,整个扰动区的温度越大。在不同初始环境温度下,列车诱发的空间温度分布具有相似结构。与压力分布不同,尾流轴线附近出现局部高温带(图中红色实线框圈出)。尾车流线型部分出现边界层分离而形成脱落涡,局部温度会降低,但由于尾车鼻尖附近产生的斜激波使得局部温度会升高,因此,尾车鼻尖附近区域的温度相对于尾流其它区域的温度更高。
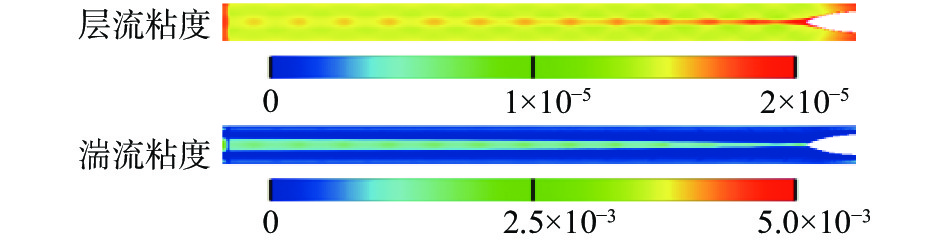
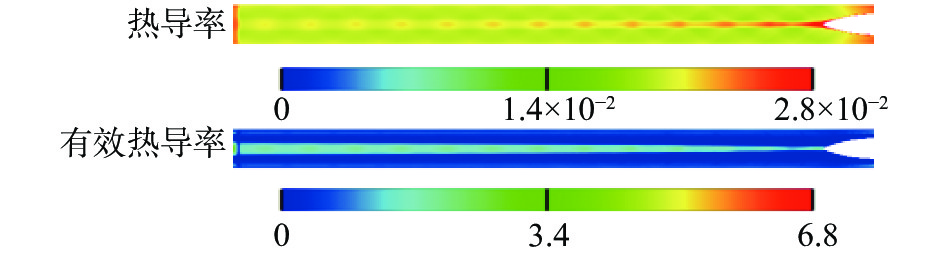
为了分析温度对空气物质属性的影响,以初始环境温度273.15 K为例,图11、图12分别给出了列车运动2 s时,尾流动力黏度、热导率的分布。可以看出,气流动力黏度、热导率的分布与温度分布保持一致,温度对空气物质属性影响十分明显。在尾流高温带中,层流黏度、热导率较大,且湍流黏度、有效热导率(热导率与湍流热导率之和)也较大。
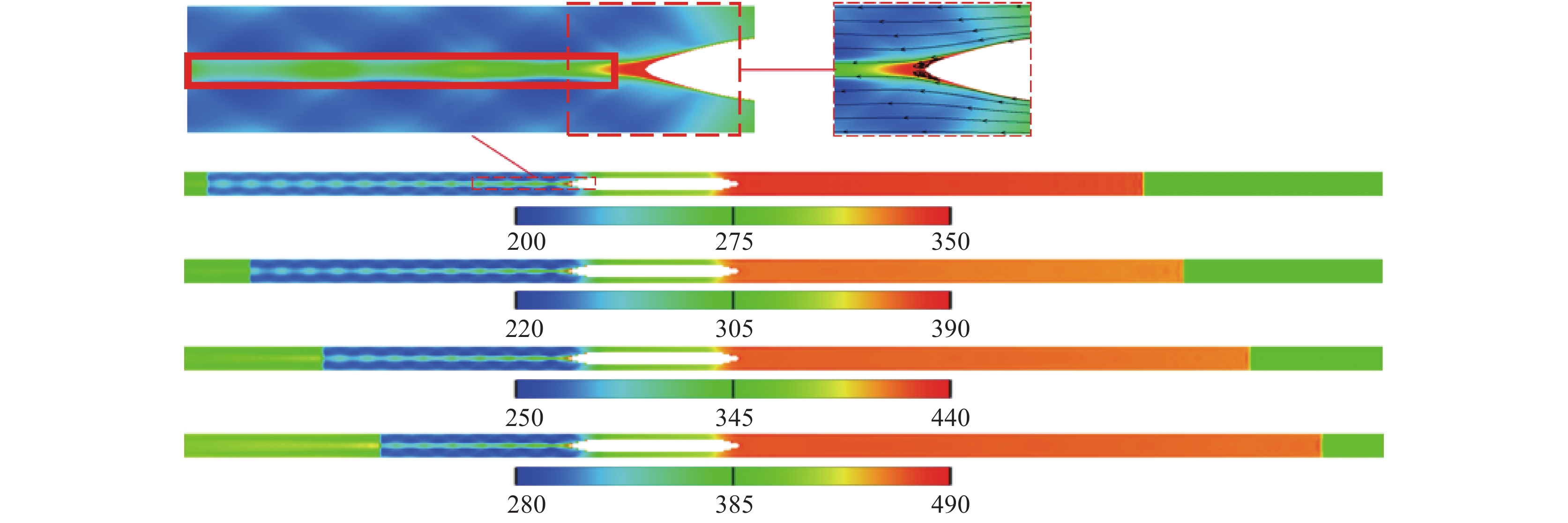
|
图 10 不同初始环境温度下列车周围空间温度分布(列车运动2 s,单位:K) Fig.10 Temperature distribution around the train at different initial ambient temperatures (t= 2 s, unit: K) |
|
图 11 尾流动力黏度分布(列车运动2 s,单位:N·s/m2) Fig.11 Dynamic viscosity distribution in the wake region (t= 2 s, unit: N·s/m2) |
|
图 12 尾流热导率分布(列车运动2 s,单位:W/(m·K)) Fig.12 Thermal conductivity distribution in the wake region (t= 2 s, unit: W/(m·K)) |
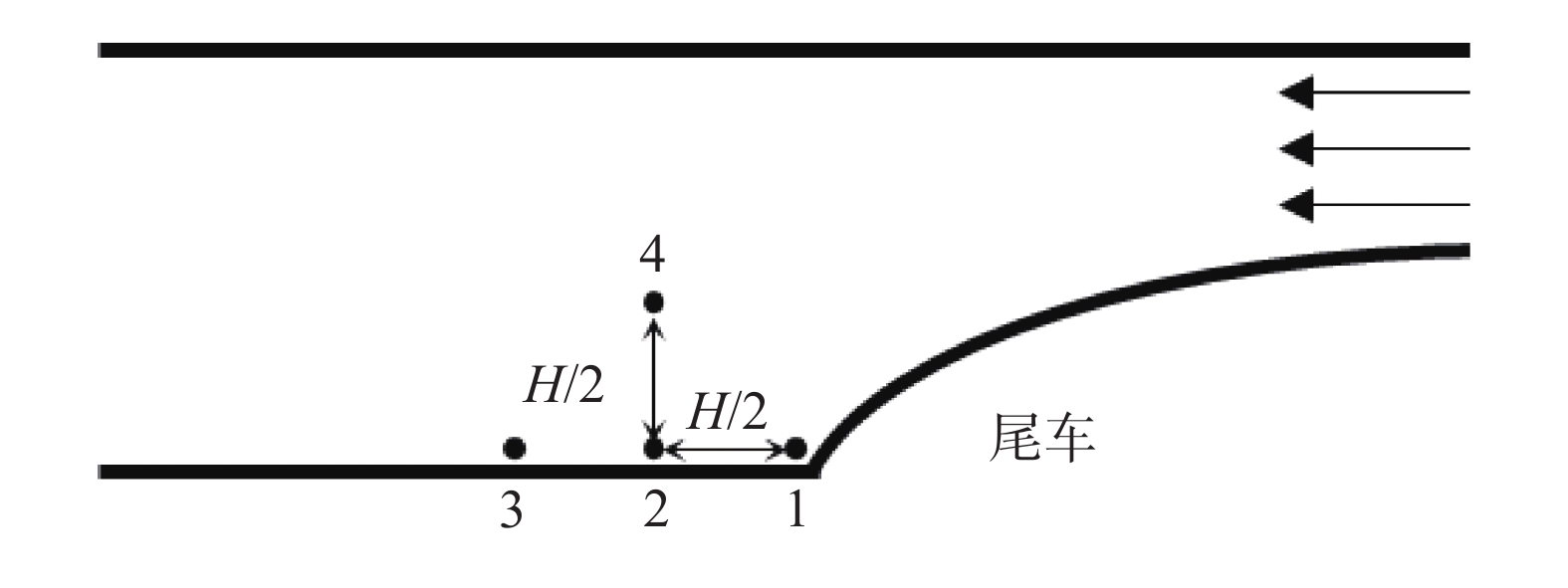
为监测尾流随时间的变化情况,图13给出了尾流区4个监测点的布置示意图。各监测点间隔H/2,监测点1刚好位于尾车鼻尖附近,且监测点1、2处于脱落涡作用范围内。监测点1-3位于对称轴上方1 mm处。当列车运动时,监测点随之运动,且保持监测点与列车的相对位置不变化。
|
图 13 尾流区监测点布置示意图 Fig.13 Schematic diagram of the monitoring point layout in the wake region |
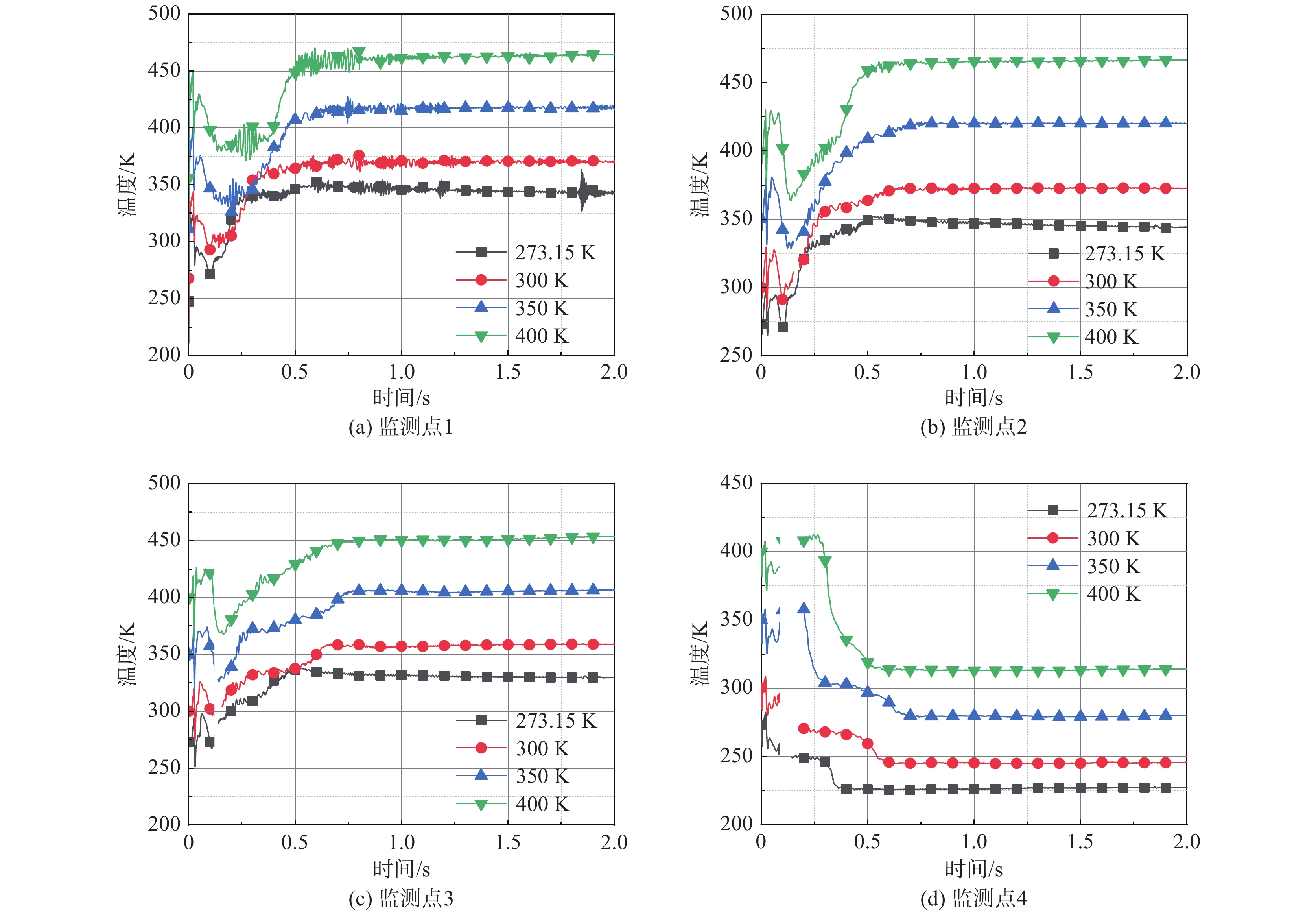
图14给出了不同初始环境温度下,各监测点温度随列车运动时间的变化曲线。当列车运动1 s时,各监测点温度变化开始趋于稳定的小幅度波动。由于监测点1、2处于脱落涡作用范围,其波动幅度较大。此外,在不同初始环境温度下,各监测点温度变化趋势一致,由于监测点1-3处于尾流高温带,在相同时刻,其温度均比监测点4的高,且监测点2的温度最高。
|
图 14 不同初始环境温度下各监测点温度变化 Fig.14 Temperature variation of all the monitoring points at different initial ambient temperatures |
表2给出了列车运动时间1~2 s内,不同初始环境温度下各监测点温度波动情况统计结果。各监测点温度波动的主频为甚低频0.76 Hz,监测点2的温度时均值最大,监测点4的温度时均值最小。监测点主频对应的主振幅不超过2 K,说明尾流区域流场趋于稳定。
| 表 2 不同初始环境温度下各监测点温度波动信息统计 Table 2 Statistics of the temperature fluctuation for each monitoring point at different initial ambient temperatures |
|
|
本文借助动网格方法实现了真空管道高速列车在不同初始环境温度下的运动过程,研究了初始环境温度变化对管内流场分布及列车气动特性的影响,能够为未来真空管道高速列车的气动设计提供一定参考。
本文通过分子动理论模型考虑了管内气流的物理属性变化,气流温度增大会导致热导率与动力粘度增大。不同初始环境温度下,气流热导率及动力粘度的空间分布结构相似。初始环境温度变化会导致管内列车表面压力、温度、列车阻力等参数的明显变化。随着初始环境温度增大,在同一时刻,头车阻力值减小,尾车阻力值增大,而中间车阻力值几乎不变,整车阻力值减小。随着初始环境温度增大,列车表面压力最大值最小值均减小,列车表面温度最大值增大,但温度最小值变化不具有单调性。通过频域数据分析,不同初始环境温度对尾涡脱落频率几乎无影响,且温度波动的主频很低,这可能是由本文采用几何较为简单的轴对称列车模型造成的。
伴随着列车运动,其周围空气受到强烈扰动,扰动区域范围随着列车运动而不断扩大。与Bao等[27]三维列车模型的计算结果类似,尾流扰动区范围随着初始环境温度增大而缩小,同时本文还发现了车前扰动区范围随初始环境温度增大而扩大,整个流场扰动区的长度变化不大。
本文只是初步研究不同初始环境温度对管内气动特性的影响,文中几何较为简单且仅考虑了管内对流传热过程。偏向实际工程应用的三维列车模型及管内辐射传热过程有待被进一步研究。
| [1] |
沈志云. 高速列车的动态环境及其技术的根本特点[J]. 铁道学报, 2006, 28(4): 1-5. SHEN Z Y. Dynamic environment of high-speed train and its distinguished technology[J]. Journal of the China Railway Society, 2006, 28(4): 1-5. DOI:10.3321/j.issn:1001-8360.2006.04.001 (in Chinese) |
| [2] |
沈志云. 关于我国发展真空管道高速交通的思考[J]. 西南交通大学学报, 2005, 40(2): 133-137. SHEN Z Y. On developing high-speed evacuated tube transportation in China[J]. Journal of Southwest Jiaotong University, 2005, 40(2): 133-137. DOI:10.3969/j.issn.0258-2724.2005.02.001 (in Chinese) |
| [3] |
邓自刚, 张勇, 王博, 等. 真空管道运输系统发展现状及展望[J]. 西南交通大学学报, 2019, 54(5): 1063-1072. DENG Z G, ZHANG Y, WANG B, et al. Present situation and prospect of evacuated tube transportation system[J]. Journal of Southwest Jiaotong University, 2019, 54(5): 1063-1072. DOI:10.3969/j.issn.0258-2724.20180204 (in Chinese) |
| [4] |
NØLAND J K. Prospects and challenges of the hyperloop transportation system: a systematic technology review[J]. IEEE Access, 2021, 9: 28439-28458. DOI:10.1109/ACCESS.2021.3057788 |
| [5] |
熊嘉阳, 邓自刚. 高速磁悬浮轨道交通研究进展[J]. 交通运输工程学报, 2021, 21(1): 177-198. XIONG J Y, DENG Z G. Research progress of high-speed maglev rail transit[J]. Journal of Traffic and Transportation Engineering, 2021, 21(1): 177-198. (in Chinese) |
| [6] |
CHAIDEZ E, BHATTACHARYYA S P, KARPETIS A N. Levitation methods for use in the hyperloop high-speed transportation system[J]. Energies, 2019, 12(21): 4190. DOI:10.3390/en12214190 |
| [7] |
贾文广, 董晨光, 周艳, 等. 基于阻塞比的真空管道交通系统热压耦合研究[J]. 工程热物理学报, 2013, 34(9): 1745-1748. JIA W G, DONG C G, ZHOU Y, et al. Study of thermal-pressure coupling effect in the evacuated tube transportation system on blocking ratio[J]. Journal of Engineering Thermophysics, 2013, 34(9): 1745-1748. (in Chinese) |
| [8] |
黄尊地, 梁习锋, 常宁. 真空管道交通列车气动阻力数值分析[J]. 机械工程学报, 2019, 55(8): 165-172. HUANG Z D, LIANG X F, CHANG N. Numerical analysis of train aerodynamic drag of vacuum tube traffic[J]. Journal of Mechanical Engineering, 2019, 55(8): 165-172. DOI:10.3901/JME.2019.08.165 (in Chinese) |
| [9] |
刘加利, 张继业, 张卫华. 真空管道高速列车气动特性分析[J]. 机械工程学报, 2013, 49(22): 137-143. LIU J L, ZHANG J Y, ZHANG W H. Analysis of aerodynamic characteristics of high-speed trains in the evacuated tube[J]. Journal of Mechanical Engineering, 2013, 49(22): 137-143. DOI:10.3901/JME.2013.22.137 (in Chinese) |
| [10] |
米百刚, 詹浩, 朱军. 基于动网格的真空管道高速列车阻力计算方法研究[J]. 真空科学与技术学报, 2013, 33(9): 877-882. MI B G, ZHAN H, ZHU J. Simulation of aerodynamic drag of high-speed train in evacuated tube transportation[J]. Chinese Journal of Vacuum Science and Technology, 2013, 33(9): 877-882. DOI:10.3969/j.issn.1672-7126.2013.09.07 (in Chinese) |
| [11] |
LI T, ZHANG X H, JIANG Y, et al. Aerodynamic design of a subsonic evacuated tube train system[J]. Fluid Dynamics & Materials Processing, 2020, 16(1): 121-130. DOI:10.32604/fdmp.2020.07976 |
| [12] |
刘加利, 张继业, 张卫华. 真空管道高速列车气动阻力及系统参数设计[J]. 真空科学与技术学报, 2014, 34(1): 10-15. LIU J L, ZHANG J Y, ZHANG W H. Impacts of pressure, blockage-ratio and speed on aerodynamic drag-force of high-speed trains[J]. Chinese Journal of Vacuum Science and Technology, 2014, 34(1): 10-15. DOI:10.3969/j.issn.1672-7126.2014.01.03 (in Chinese) |
| [13] |
周鹏, 李田, 张继业, 等. 真空管道超级列车激波簇结构研究[J]. 机械工程学报, 2020, 56(2): 86-97. ZHOU P, LI T, ZHANG J Y, et al. Research on shock wave trains generated by the hyper train in the evacuated tube[J]. Journal of Mechanical Engineering, 2020, 56(2): 86-97. DOI:10.3901/JME.2020.02.086 (in Chinese) |
| [14] |
周鹏, 李田, 张继业, 等. 真空管道超级列车气动热效应[J]. 机械工程学报, 2020, 56(8): 190-199. ZHOU P, LI T, ZHANG J Y, et al. Aerothermal effect generated by hyper train in the evacuated tube[J]. Journal of Mechanical Engineering, 2020, 56(8): 190-199. DOI:10.3901/JME.2020.08.190 (in Chinese) |
| [15] |
NIU J Q, SUI Y, YU Q J, et al. Numerical study on the impact of Mach number on the coupling effect of aerodynamic heating and aerodynamic pressure caused by a tube train[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 190: 100-111. DOI:10.1016/j.jweia.2019.04.001 |
| [16] |
ANDERSON J D. Fundamentals of aerodynamics[M]. 6th ed. New York: McGraw-Hill Education, 2017.
|
| [17] |
张晓涵, 李田, 张继业, 等. 亚音速真空管道列车气动壅塞及激波现象[J]. 机械工程学报, 2021, 57(4): 182-190. ZHANG X H, LI T, ZHANG J Y, et al. Aerodynamic choked flow and shock wave phenomena of subsonic evacuated tube train[J]. Journal of Mechanical Engineering, 2021, 57(4): 182-190. (in Chinese) |
| [18] |
SUI Y, NIU J Q, YUAN Y P, et al. An aerothermal study of influence of blockage ratio on a supersonic tube train system[J]. Journal of Thermal Science, 2020, 1-12. DOI:10.1007/s11630-020-1281-7 |
| [19] |
ZHOU P, ZHANG J Y. Aerothermal mechanisms induced by the super high-speed evacuated tube maglev train[J]. Vacuum, 2020, 173: 109142. DOI:10.1016/j.vacuum.2019.109142 |
| [20] |
张俊博, 李红梅, 王俊彪, 等. 低真空管道磁悬浮列车温度场数值计算[J]. 真空科学与技术学报, 2021, 41(5): 448-455. ZHANG J B, LI H M, WANG J B, et al. Numerical analysis of the temperature field of vacuum tube maglev train[J]. Chinese Journal of Vacuum Science and Technology, 2021, 41(5): 448-455. (in Chinese) |
| [21] |
SHEN C. Rarefied gas dynamics-fundamentals, simulations and micro flows[M]. Berlin, Germany: Springer-VerlagHeidelberg, 2005.
|
| [22] |
HIRSCHFELDER J, CURTISS C, BIRD R. Molecular theory of gases and liquids[M]. New York: John Wiley & Sons, 1954.
|
| [23] |
ANDERSON J D Jr. Hypersonic and high-temperature gas dynamics, second edition[M]. Reston, VA: AIAA, 2006. doi: 10.2514/4.861956
|
| [24] |
VERSTEEG H K, MALALASEKERA W. An introduction to computational fluid dynamics: the finite volume method [M]. 2nd ed. Pearson Education Limited, 2007.
|
| [25] |
SCHLICHTING H, GERSTEN K. Boundary-layer theory[M]. 9th ed. Berlin Heidelberg: Springer-Verlag, 2017.
|
| [26] |
MENTER F R, LANGTRY R, VÖLKER S. Transition modelling for general purpose CFD codes[J]. Flow, Turbulence and Combustion, 2006, 77(1/2/3/4): 277-303. DOI:10.1007/s10494-006-9047-1 |
| [27] |
BAO S J, HU X, WANG J K, et al. Numerical study on the influence of initial ambient temperature on the aerodynamic heating in the tube train system[J]. Advances in Aerodynamics, 2020, 2(1): 28. DOI:10.1186/s42774-020-00053-8 |
 2021, Vol. 39
2021, Vol. 39


