0 引　言

地铁列车因具有速度快、运量大、准点率高等特点已成为人们日常出行的主要交通工具^[1]。然而，在地铁列车实际运营过程中发现，地铁列车的客流量并非全天一直保持高位，早晚高峰潮汐式客流特征明显，即在人们上下班的早晚时间段客流量较大，而在平峰时间段客流量较小，这样的客流特征将会导致在高运量时间段车内易出现过热，低运量时间段车内易出现过冷现象，这将严重影响乘客乘车的热舒适性体验。

城轨列车客室热舒适性环境的研究方法主要有数值模拟^[2-3]、试验^[4-5]、问卷调查^[6-7]等，但是问卷调查易受主观因素的影响，试验会花费大量的时间与财力成本，数值模拟方法已在城轨列车客室热舒适性环境的研究中被广泛采用。Berlitz等认为数值模拟方法在轨道列车空调设计的初始阶段能够节省大量的优化时间成本，具有较强的参数设计及热舒适性预测能力^[8]。Yang等利用数值模拟方法对比了中国CRH2、CRH3、CRH5以及日本新干线四种不同类型出风口结构下的客室热舒适性以及污染物扩散，结果表明四种不同类型出风口结构下，客室内的热舒适性都能满足要求，但是气流和颗粒污染物的运动却截然不同^[9]。Tao等利用数值模拟中的多孔介质模型和多孔阶跃面模型来近似的替代地铁列车中的孔板模型，结果表明多孔介质模型与原始模型结果以及试验数据吻合较好^[10]。Aliahmadipour等利用数值模拟方法对一列火车客室内部环境进行分析，并对当前的客室结构进行修改以更好地满足乘客的热舒适性体验^[11]。Konstantinov等利用OpenFOAM和THESEUS-FE对德国下一代概念列车（NGT）客室内的热舒适性环境进行了耦合模拟，结果表明进风设计和客舱的能量利用效率与客室的热舒适性密切相关^[12]。

本文将数值模拟结果与实车试验结果进行对比，验证了所使用数值模拟方法的可靠性，并采用该方法对某型号地铁列车客室内的热舒适性环境展开研究，探讨了客流密度对地铁列车客室内热舒适性环境的影响规律，并结合地铁列车的载重信号，提出了一种基于客流密度的地铁列车空调夏季送风温度的控制模型。

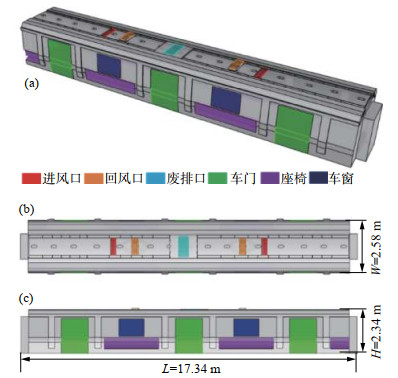
1 数值模拟方法 1.1 计算模型

本文根据某型号地铁列车的真实模型，建立了其中间车等比例的三维计算模型，如图1所示，车厢的长、宽、高分别用L、W、H表示。计算模型由中间车、两端连廊、风道等构成，未建立空调机组的实际模型，空调机组的送风口、废排口和回风口分别用速度和压力出口边界来近似替代。图中的红色部分为进风口，橙色为回风口，青色为废排口，绿色为车门，紫色为座椅，蓝色为车窗。车长为17.34 m，车宽为2.58 m，车高为2.34 m。

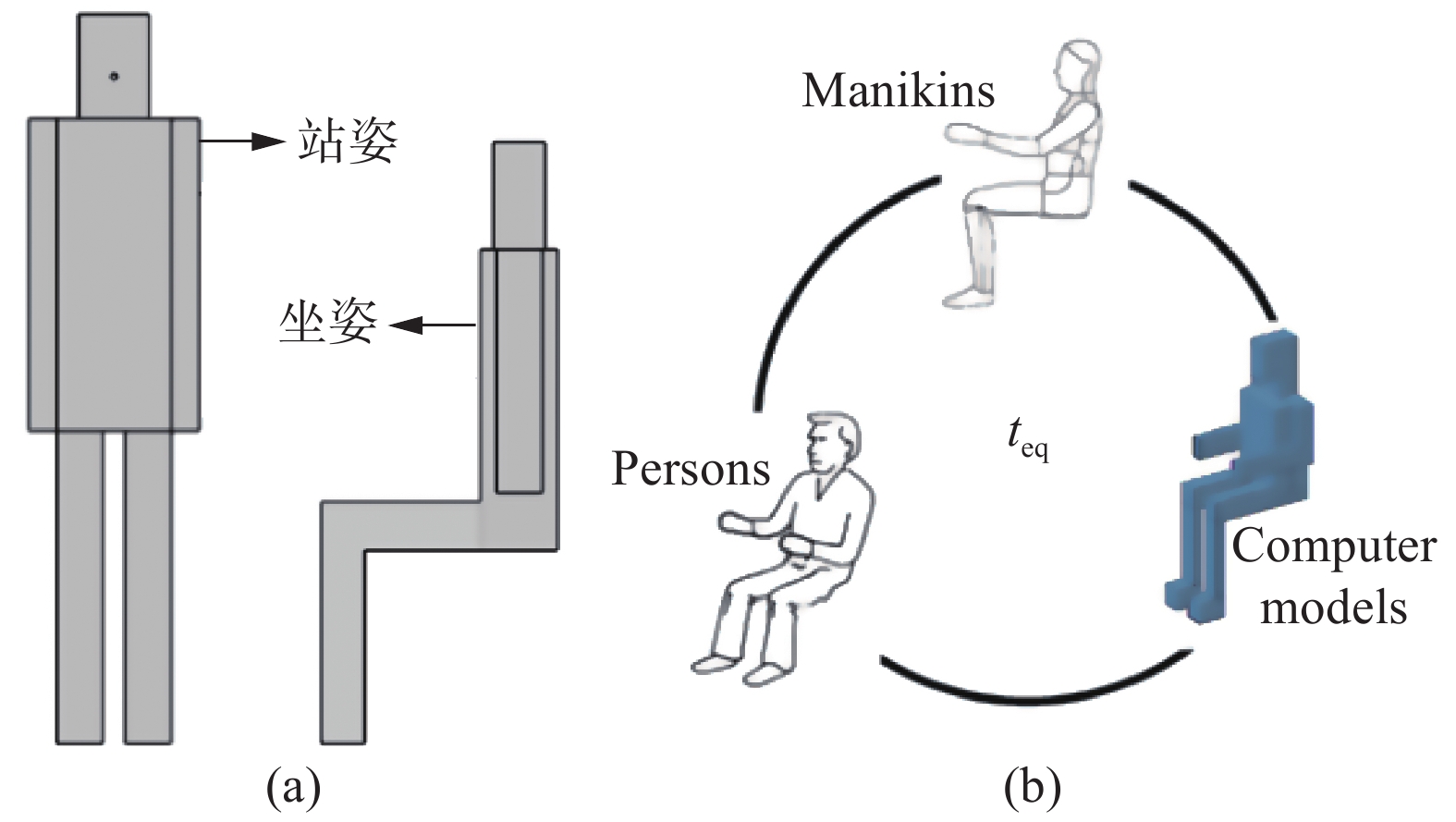
同时，本文根据中国成年人人体尺寸GB0000-88标准^[13]，建立单个乘客站姿及坐姿实体模型，如图2（a）所示，这种人体模型的近似简化，已在大量论文中使用^{[11, 14]}，如图2（b）所示。与此同时，在本文中还考虑了人体的呼吸，参考Ye等的研究^[15]，用一个点源来近似代替人体呼吸。

1.2 网格及边界条件

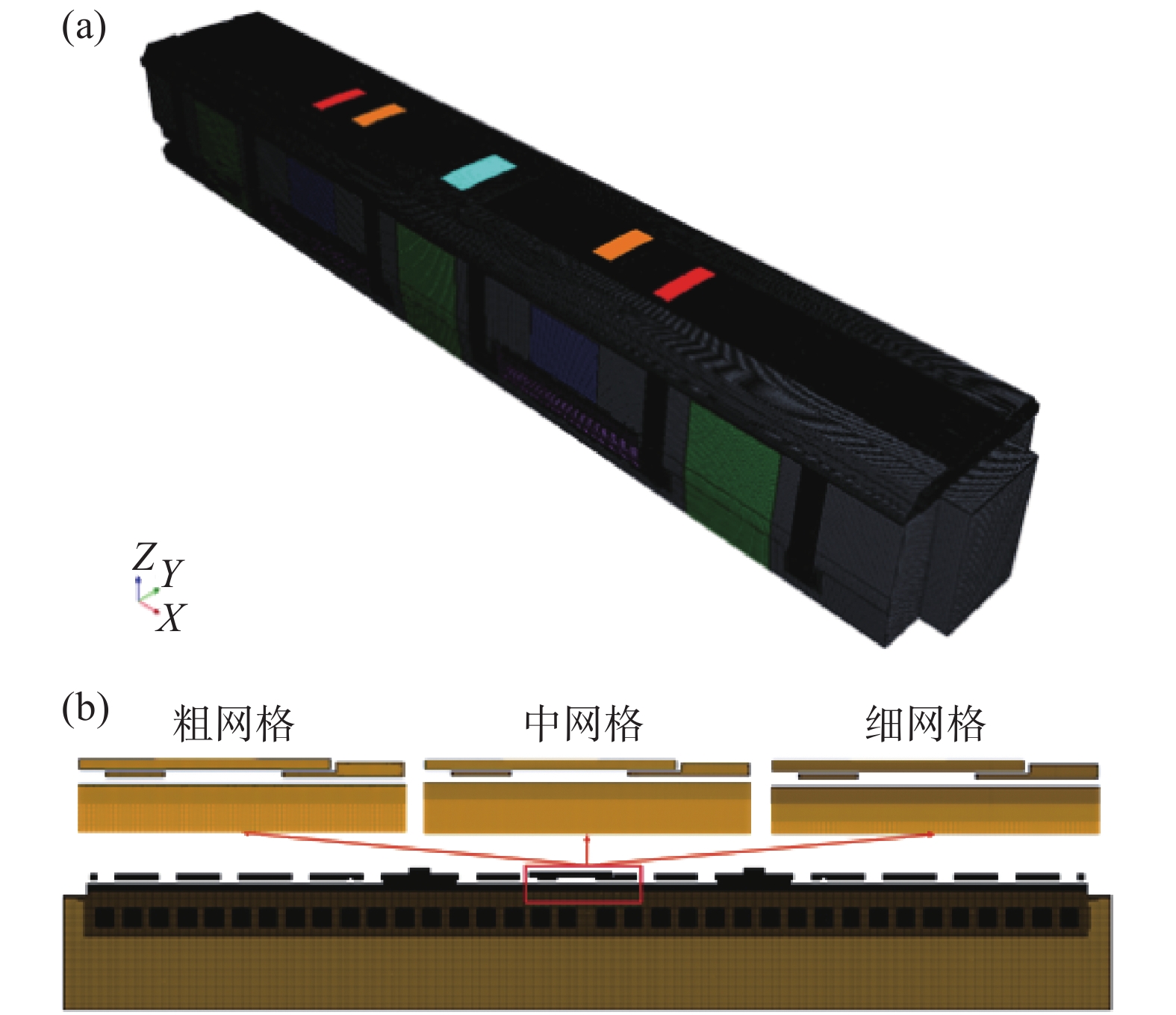
本文使用正交网格对计算模型进行网格划分。由于列车模型中的风道几何结构非常复杂，为了能够较为准确地捕捉气流在风道中的流动，对风道进行了局部加密，网格尺寸为10 mm，同时对风道壁面、客室壁面以及人体表面均设置了第一层厚度为1 mm的附面层。在客室内部流场的研究中，k-ε湍流模型被广泛应用^{[10, 16]}，且在模拟中要求y⁺在30～100的范围内。本文中所用网格的平均y⁺为34，符合其数值模拟要求。车厢体网格及局部放大网格如图3所示，图3（b）中的粗、中、细网格分别对应的网格数量为1.8×10⁶、4.2×10⁶、9.2×10⁶。

本文地铁列车采用的是车顶一体式空调，由两台独立的空调机组构成。在地铁列车内部流场的数值模拟研究中，空调机组送风口边界条件为流量入口，而废排风口为流量出口。每台空调机组总送风量为4250 m³/h，送风温度为20℃。其中，新风量为1300 m³/h，废排风量等于新风风量，因该型号列车废排口只有一个，所以废排风量为2600 m³/h，通过送风口和废排口的面积，换算得到送风口和废排口相应的速度边界为4.8281 m/s、−1.3604 m/s，负号表示流出。回风口为压力出口，环境温度为35 ℃，车体传热系数为2.5 W/ （m²· K）。人体面部的呼吸点源设置成质量流量出口，质量流量为0.03 g/s，温度为34℃^[15]。

1.3 计算设置及数据处理

在本文中，所有的数值计算均使用STAR-CCM+13.06进行隐式不定长求解，时间步长取0.01 s，总时间选取了该型号地铁列车运营过程中最长的跨站运行时间4 min。

在数值模拟中，参照EN-14750标准进行测点布置。对于本文中的数据处理，参考中华人民共和国铁道行业标准TB/T1675-2001《铁道客车空气调节试验方法》相关数据处理方法，客室中的温度用所有测点的平均温度来表示：

$ T=\frac{\displaystyle\sum {t}_{i}}{n} $

(1)

1.4 方法验证

为了验证本文所使用的数值模拟方法的可靠性，在某城市车辆段进行了该型号地铁列车的内部流场型式试验。

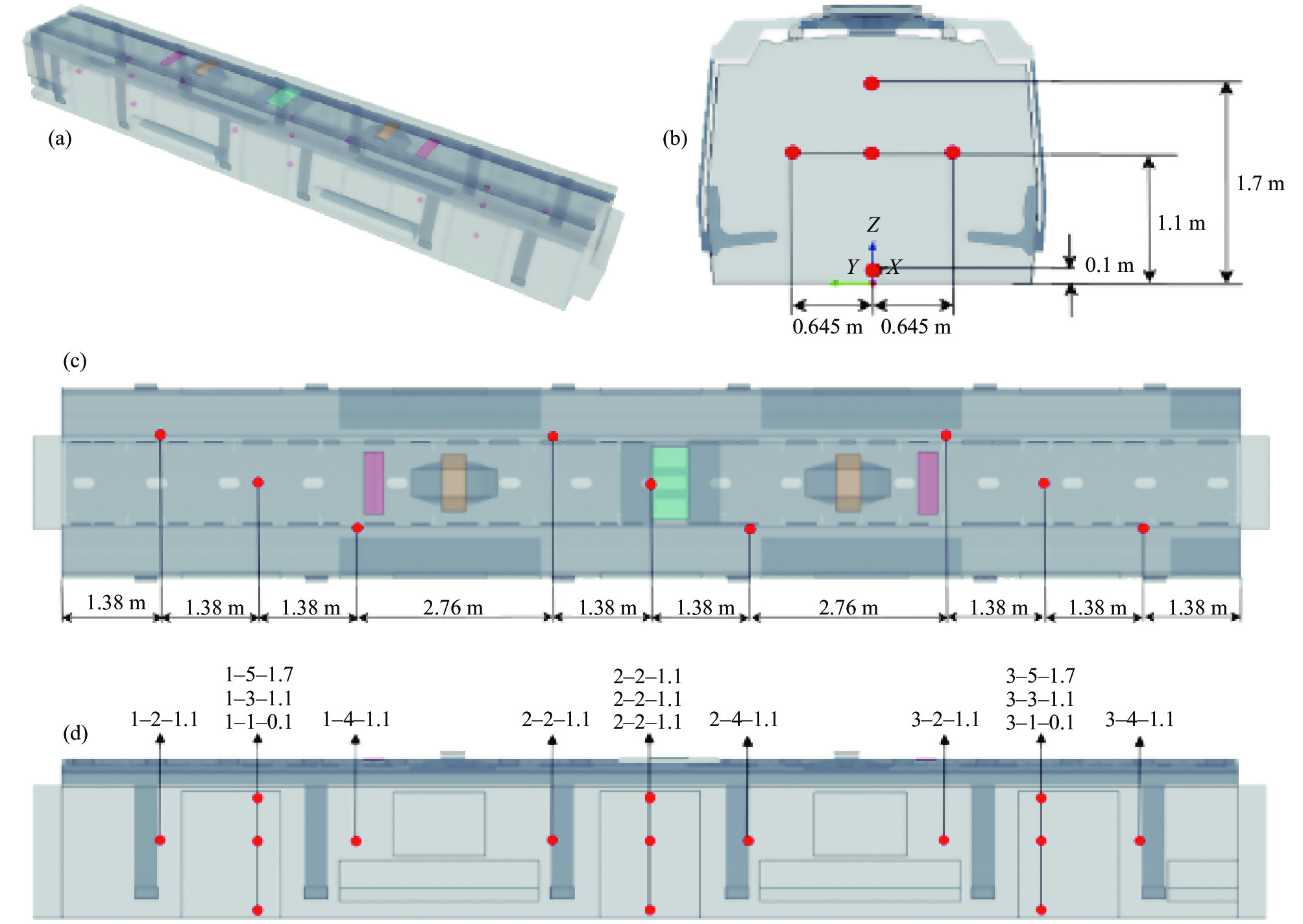
在本次试验中，参照欧洲标准EN 14750相关要求进行测点布置。测点在三维空间中的位置如图4（a）所示，测点Y/Z方向的位置如图4（b）所示，测点X方向的位置如图4（c）所示。为了对测点进行快速有效的区分识别，将每一个测点进行了单独的编号，如图4（d）所示。

地铁列车内部流场型式试验主要是测量客室内的温度以及风速。图5给出了现场试验照片以及试验中所使用的仪器设备，热线风速仪的探头固定在可伸缩的支撑架上，通过调节支撑架高度，便可实现不同高度测点温度以及风速的测量。

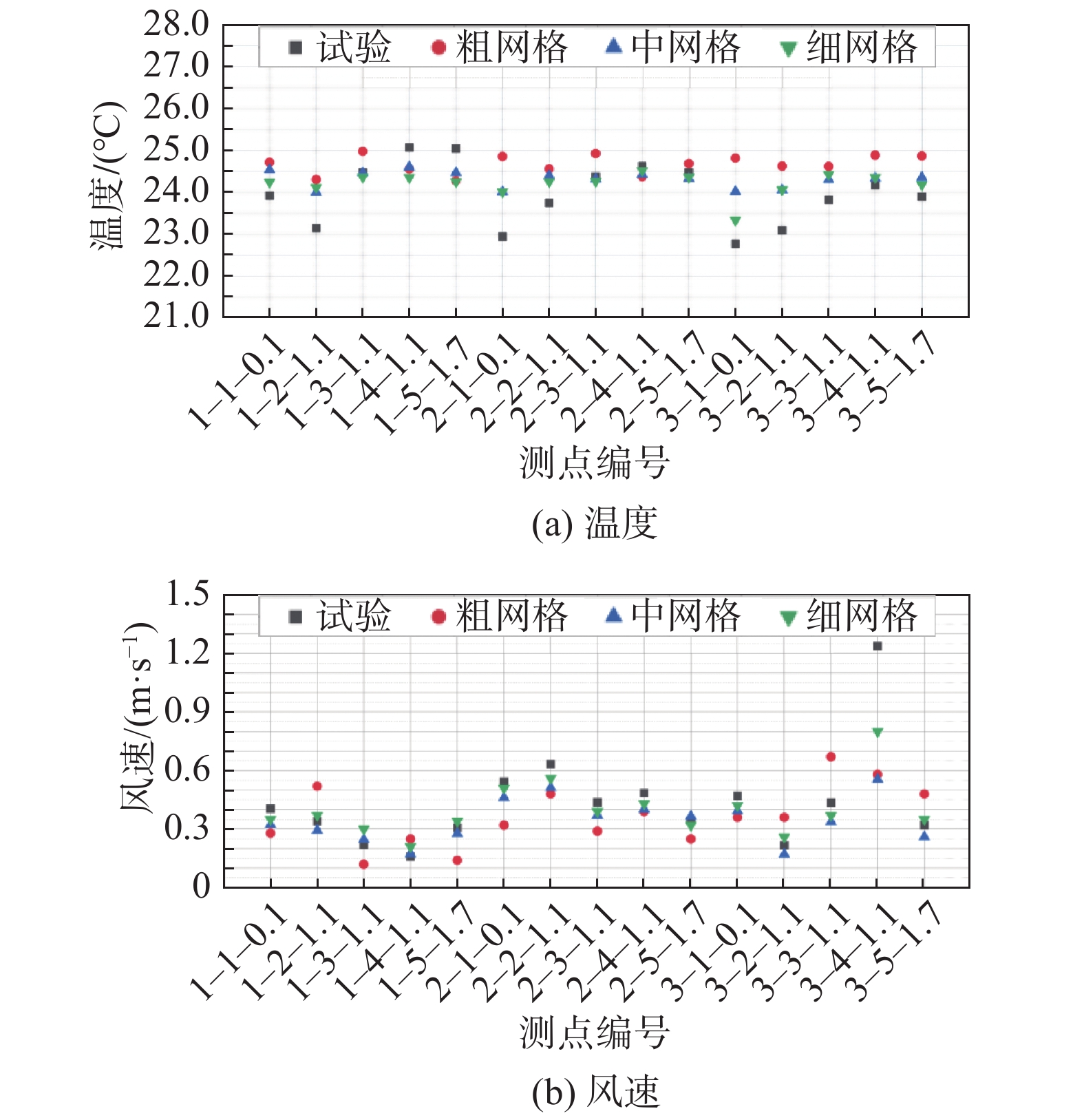
不同网格尺寸下数值模拟与实车试验的结果对比如图6所示。根据Pang等^[17]的研究，相对误差和平均相对误差分别定义如下：

$ {\delta }_{j}=\frac{\left|{\theta }_{\mathrm{Cal}}-{\theta }_{\mathrm{E}\mathrm{x}\mathrm{p}}\right|}{{\theta }_{\mathrm{E}\mathrm{x}\mathrm{p}}} $

(2)

$ \bar{{\delta }_{x}}=\frac{1}{15}\sum _{1}^{15}{\delta }_{j} $

(3)

式中： $ {\delta }_{j} $ 表示点j的温度或风速相对误差； ${\delta }_{\mathrm{Cal}}$ 表示数值模拟结果； $ {\delta }_{\mathrm{E}\mathrm{x}\mathrm{p}} $ 表示实车试验结果；j表示15个测点； $\bar{\delta }$ 表示平均相对误差；x表示温度（T）或风速（v）。

表1给出了不同网格尺寸数值模拟与实车试验结果的平均相对误差，可以看出：粗网格无论是温度还是风速，与实车试验结果的平均相对误差都较大。细网格与实车试验结果的平均相对误差最小，但网格量巨大，所需计算资源较多。兼顾结果误差以及计算资源，本文所有计算均基于中网格开展，由于客室内部风速较小，其数量级为10⁻²，一个小的干扰都会产生较大的相对误差，但风速的平均相对误差未超过30%，所以认为中网格下风速的误差在可接受范围内^[17]。

2 不同客流密度下客室目标温度探寻 2.1 不同客流密度下乘客位置分布

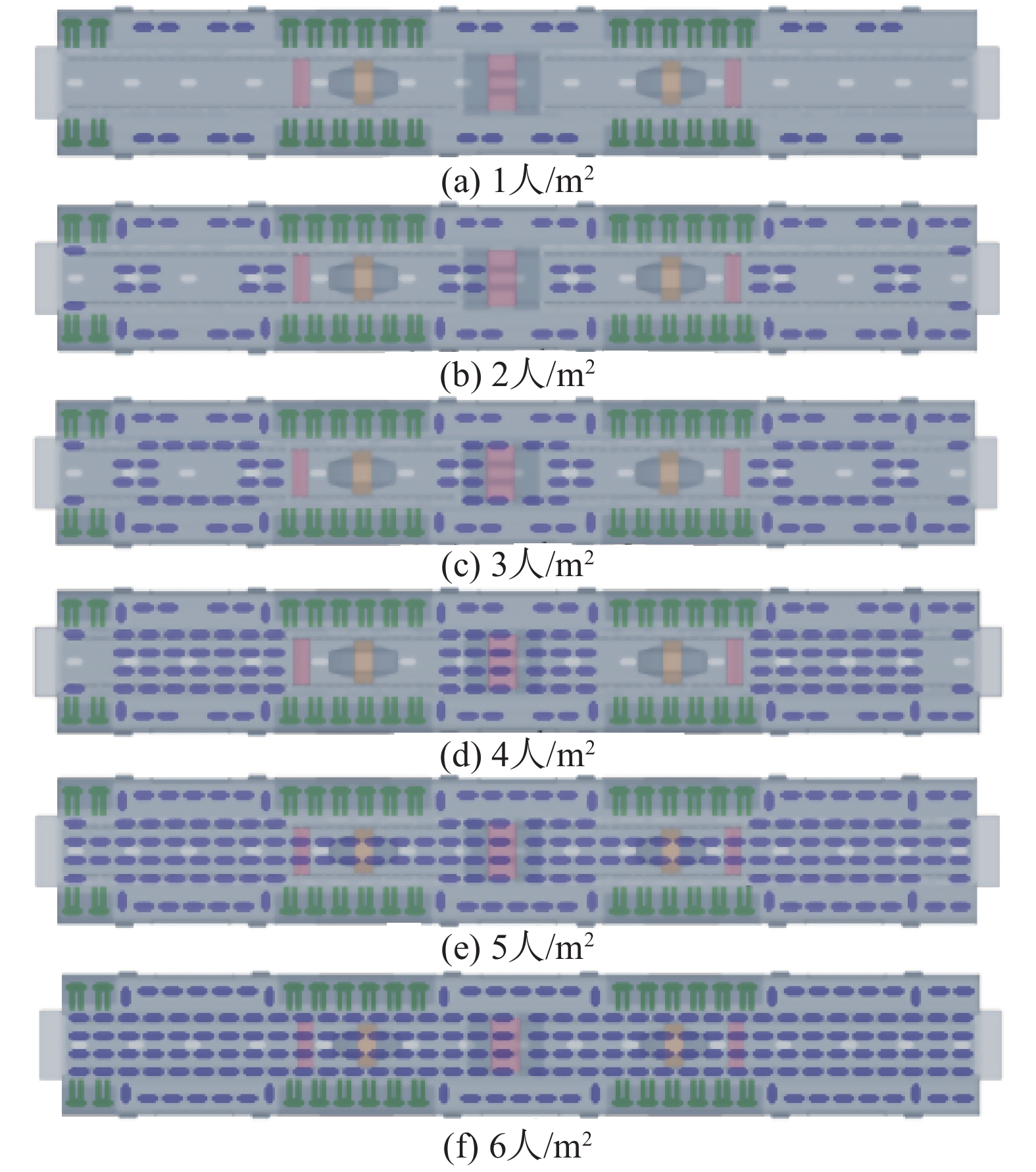
地铁列车相比于高铁列车而言，车厢内的座位较少，乘客分布较为离散，无法单一地由座位确定车内乘客分布，本文主要根据王哲^[18]对城轨列车车内乘客分布预测模型的建立及应用研究，确定了不同客流密度下乘客在车内的位置分布，如图7所示。

2.2 地铁车厢内目标温度的设定

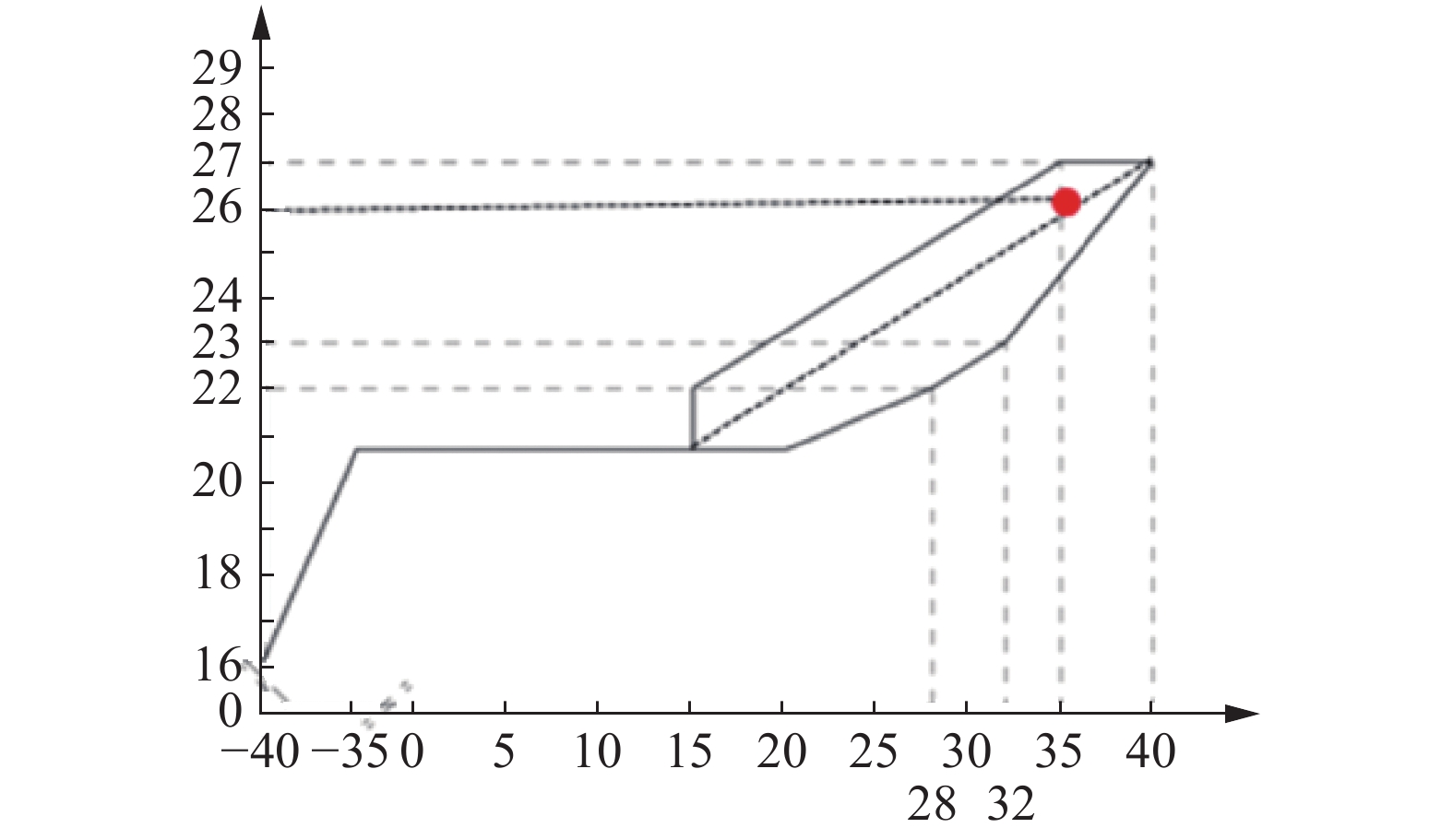
根据GB/T33193.1-2016《铁道车辆空调 第一部分：舒适度参数》中相关规定以及户晶荣等^[19]的研究：在夏季，地铁列车客室内的温度应该控制在26 ℃，如图8所示。26 ℃的室温既能保证乘客拥有良好的热舒适性体验，也能节约空调机组用电量，因此本文将26 ℃作为客室内的目标温度。

2.3 目标温度的探寻方法

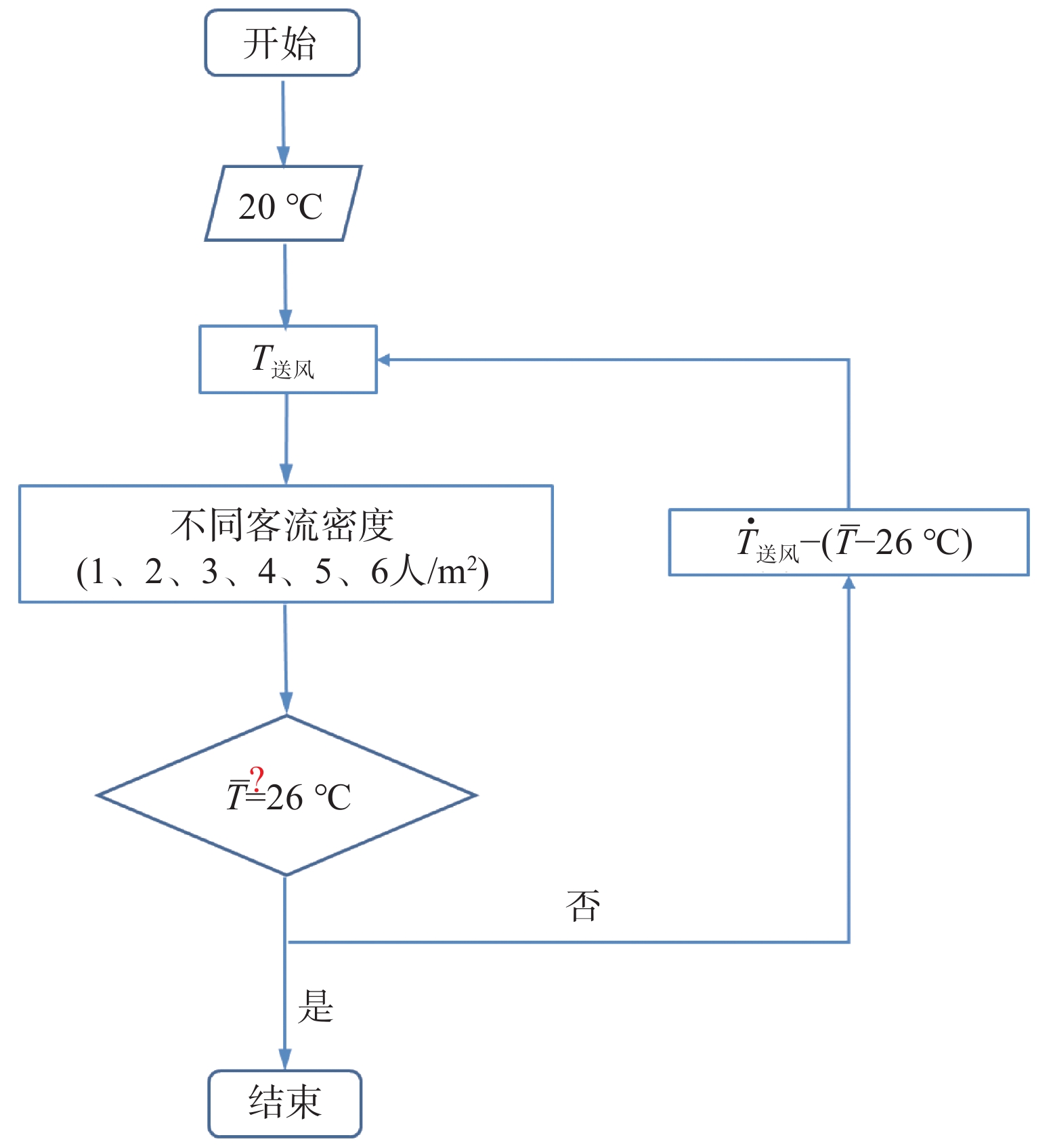
本文设计了一种方法来探究不同客流密度下当空调送风温度为多少时车内的平均温度为目标温度26℃，该方法的技术路线如图9所示，图中的 ${T}_{送风}$ 表示送风温度， $\bar {T}$ 表示客室内的平均温度， $\dot{{T}_{送风}}$ 表示上一次的送风温度。开始时以原始工况的20℃作为送风温度，然后判断不同客流密度下客室内部的平均温度是否为26℃，如果是，则结束，如果不是，则将进入循环。该循环的设计依据主要是：对于热源一定的场景，送风温度直接决定了客室温度，要抵消客室内平均温度高于或者低于26℃的量，必须通过调控送风温度来完成，近似认为 $ \dot{{T}_{送风}} $ − $ {T}_{送风} $ = $\bar {T}$ −26℃，即客室内平均温度与26 ℃之间的偏差等于前后送风温度的偏差，但是在地铁列车这样具有复杂结构的模型中，气流自上而下，再加上乘客对气流的阻碍作用，往往并非做一次循环就能得到想要的结果，与此同时，考虑到计算资源限制，当客室温度与目标温度的相对偏差较小时，循环可结束。

2.4 计算结果

根据2.3小节中设计的方法，不同客流密度下客室温度时程曲线如图10所示，从图中可以看出客室温度的时程曲线存在较小范围的波动，为了尽可能的减少数值模拟所带来的计算误差，本文取最后60 s（即180～240 s）的均值作为客室内的平均温度。

表2给出了不同客流密度下客室温度满足人体热舒适性体验（26℃）的空调送风温度。由于车辆空调主要是通过调节制冷功率来实现送风温度调控的，因此，在本文中还计算出了车辆空调送风温度在满足乘客热舒适性体验时所对应的制冷功率W，制冷功率W的计算公式如下：

$ W=C\rho V {\Delta }T $

(4)

式中： $ C $ 为空气的比热容，J/kg·℃； $\; \rho $ 为空气密度，kg/m³； $ V $ 为总送风量（新风量与回风量之和），m³/s； $ {\Delta }T $ 为空调机组所处理空气前后的温差，℃。

从表2中可以看出，不同客流密度下最后一次循环客室平均温度与目标温度（26℃）最大偏差为6人/m²时的2.49%，最小偏差为2人/m²时的0.24%。

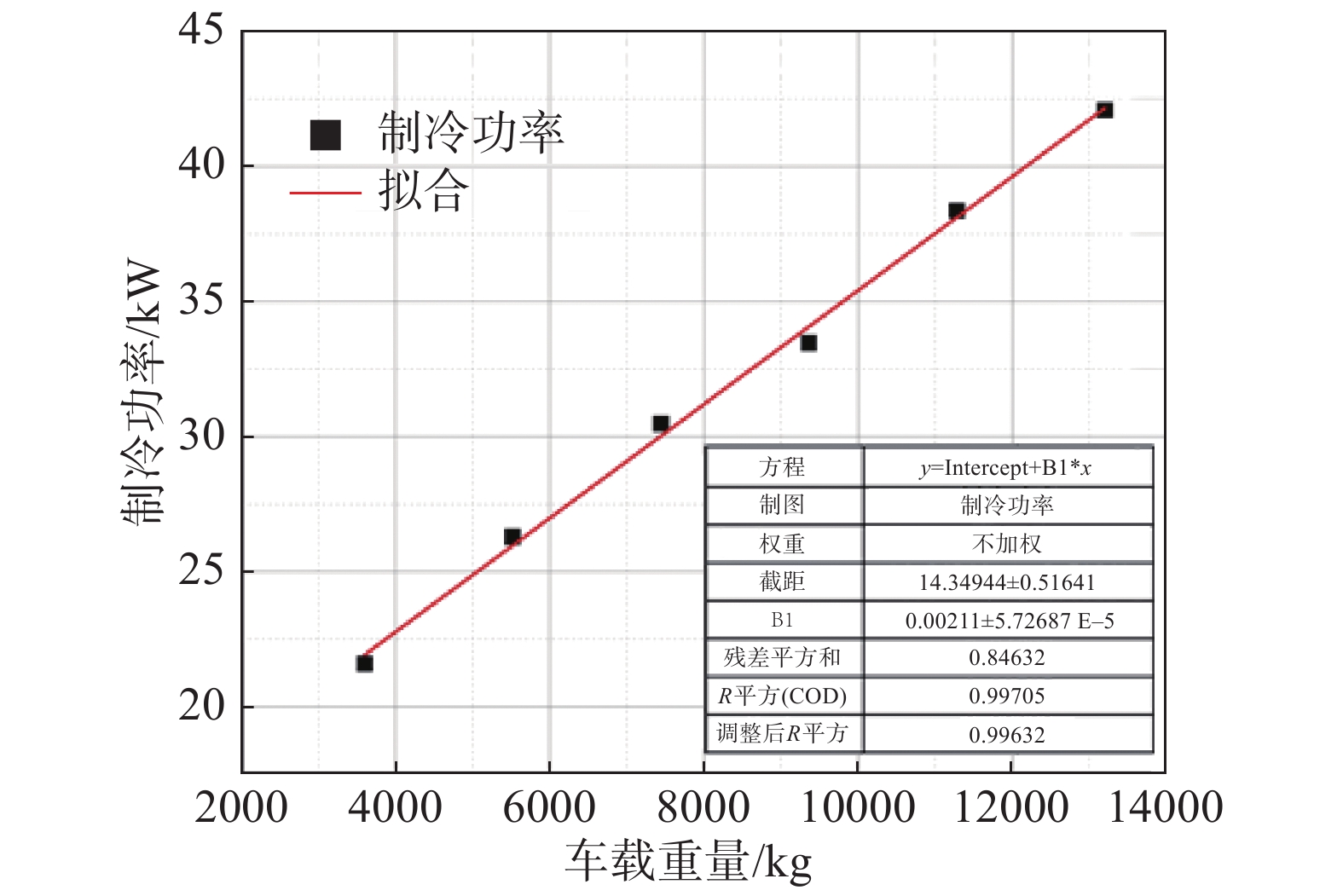
根据《GB/T7928-2003 地铁车辆通用技术条件》中车体的试验用垂直载荷人均体重按60 kg计算，将客流密度转换为车载重量，该车载重量即可以通过空气弹簧动态反应。图11给出了车载重量与空调机组在不同客流密度下满足乘客热舒适性体验时制冷功率的多项式拟合，可以得到车载重量与满足人体热舒适性体验的空调送风温度所对应的制冷功率存在如式（5）所表示的关系，其中拟合优度R²为0.997：

$ G=-0.002P+14.35 $

(5)

式中： $ G $ 为制冷功率， $ P $ 为车载重量。

3 温度控制模型 3.1 地铁车辆载重信号

图12是位于地铁列车转向架上的空气弹簧，空气弹簧最开始用于轨道列车中主要是缓冲减震，吸收和衰减列车在行驶过程中的冲击。后来，有学者研究可以利用空气弹簧进行称重既反映车辆的实际载重量^[20]。

空气弹簧的称重主要是根据其充/放气过程中腔体内气压变化的大小，再通过车辆所受纵向载荷和气压的关系，换算即可得到车辆的实际载重量。当前，空气弹簧的称重系统已被用于反映车内客流量，如长沙地铁就利用该系统做到了实时反映当前车厢的客流量。

3.2 温度控制模型的建立

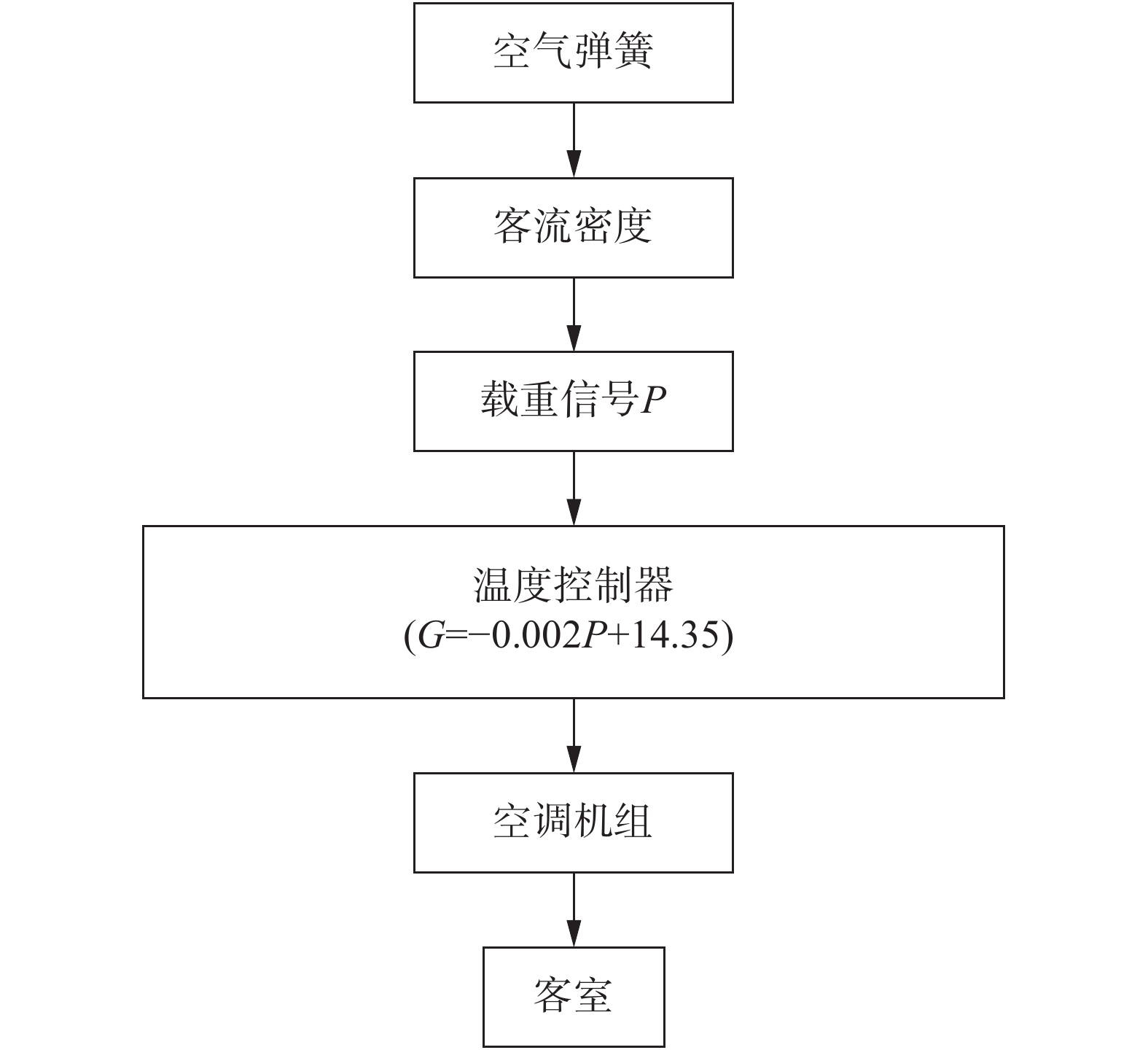
在本文中，将上面得出的车辆载重与空调机组制冷功率的拟合关系式和空气弹簧的载重信号相结合，便得到了如图13所示的基于客流密度的地铁列车空调送风温度控制模型。空气弹簧将客流密度转化为载重信号反馈给车载温度控制器，温度控制器已内置载重信号与制冷功率关系式，然后根据空气弹簧所反馈的载重信号调控空调机组的制冷功率，便可以使空调的送风温度能更好地满足乘客的热舒适性体验。

4 结　论

本文主要探究了客流密度对地铁列车客室热舒适性环境的影响规律，以及不同客流密度下客室温度与空调送风温度之间的关系，找到了不同客流密度下能满足乘客热舒适性体验的空调送风温度，最后提出了一种基于客流密度的地铁列车空调送风温度控制模型。主要有以下结论：

1）设计了一种方法来探究不同客流密度下送风温度为多少时车内的平均温度为26 ℃，结果表明该方法能够较为准确地得到不同客流密度下适合人体热舒适性的空调送风温度。将客流密度转化为车载重量，计算出车辆空调送风温度在满足乘客热舒适性体验时所对应的制冷功率，最后得到车载重量与满足人体热舒适性体验的空调送风温度所对应的制冷功率满足G = −0.002P + 14.35（G为制冷功率；P为车载重量）。

2）分析了现有的地铁列车空调温度控制的不足之处，提出了一种基于客流密度的地铁列车空调送风温度控制模型，该方法主要是将车载重量和满足人体热舒适性体验的空调送风温度所对应的制冷功率之间满足的关系式G = −0.002 P + 14.35与地铁列车空气弹簧的载重信号相结合，该方法能够做到根据客流密度动态调整空调送风温度，能更好的满足乘客乘车的热舒适性体验，同时节约电量的消耗。