2. 中国空气动力研究与发展中心 设备设计与测试技术研究所,绵阳 621000
2. Facility Design and Instrumentation Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China
风洞试验的雷诺数模拟不足,将会使边界层分离、旋涡流动、激波/边界层干扰、激波/旋涡干扰等黏性起支配作用的流动现象发生变化,使试验数据与真实飞行存在明显差异[1]。研究表明降低试验介质气流温度目前被认为是提高风洞试验雷诺数最有效的技术途径,低温风洞概念的发展极大拓展了亚跨声速风洞的试验能力。美欧建成的大型低温风洞NTF和ETW为波音和空客的创新发展发挥了不可替代的重要作用[2-6]。伴随我国低温高雷诺数风洞设计建设,相关技术研究成为热点 [7-12]。
低温风洞具有复杂的风洞控制问题,热力学是一个高度耦合、多变量和非线性过程。主要存在以下困难:一是大范围精确的流场模型难以获得;二是系统存在强烈非线性耦合;三是系统存在大时滞效应,特别是温度。兰利研究中心早期建设的NTF采用了非线性增益调度PI控制[13],欧洲ETW风洞采用一种具有自学习能力的控制算法不断自我优化[14]。国内祝汝松等探索了鲁棒自适应控制[15-16],刘为杰等开展了自抗扰控制研究[17],兰其龙等开展了基于神经网络预测控制[18],黄丽娟等开展了不协调目标信息系统多变量控制方法仿真[19]。结果表明现代控制理论以及智能控制由于其算法的复杂性,目前结果并不理想,调节时间较长,还不能够完全满足低温风洞运行控制需要。
风洞运行压比定义为风扇段出口截面和入口截面的总压比值,其与风扇转速、液氮喷射流量及排气流量深度耦合,是影响风洞控制的核心参数。本文以中国空气动力研究与发展中心新建成的0.3 m低温跨声速风洞测试数据为研究对象,探索建立了风洞运行压比与不同运行状态参数(压力、温度、马赫数)间统一的动态传递模型,可应用于风洞主控系统优化,通过有效前馈控制,缩短了运行参数调节和稳定时常。
1 研究设备简介0.3 m低温跨声速风洞是一座连续式单回流增压风洞,利用多级轴流低温风扇驱动。试验段截面尺寸325 mm(宽)× 275 mm(高),运行马赫数范围0.15~1.30,总温范围110~323 K,总压范围100~500 kPa。风扇由1.5 MW的外置电机和变频器驱动,转速范围为500~7200 r/min。洞体材料为不锈钢,表面覆盖绝热材料以减小与环境之间的热交换。通过向洞体内喷入液氮气化吸热平衡风扇运行功率和洞壁传热,液氮喷射流量范围0.6~6.5 kg/s。同时在风洞第三和第四拐角段之间配置排气系统将气化后的氮气排出实现洞体压力控制。风洞回路试验现场照片见图1。

|
图 1 0.3 m低温跨声速风洞 Fig.1 A photo of the 0.3 m cryogenic transonic wind tunnel |
风洞运行压比通过位于风扇段上下游截面周向均布的总压排架测量。入口截面为水平布置的两个5点总压排架,出口截面为周向均布的四个4点总压排架。压力传感器为PSI 9116扫描阀,量程为45 PSI,测量精度0.05%。并按环状面积积分计算得到压力的平均值。压力测量时,试验段内除了轴向静压探测管外为空风洞,同时试验段下游第二喉道完全拉开、支架段再入调节片开度5°。风洞运行状态参数则通过安装于试验段的皮托管获取总静压、总温探针测温度。压力测量采用Mensor CPT6180高精度绝压传感器,量程为70 PSI,测量精度优于0.02%。温度测量采用Lakeshore PT-102-14L传感器,测量精度2.49 mK。
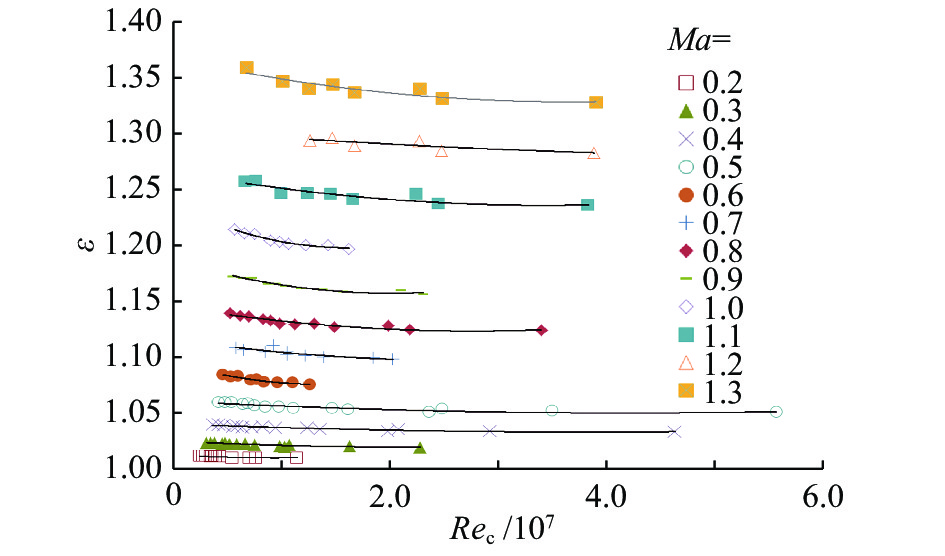
图2给出了风洞三个运行总压(115 kPa、200 kPa、450 kPa)、五个总温(110 K、150 K、200 K、280 K、323 K)和12个马赫数的组合状态校测点数据,共计119个组合,马赫数范围0.20~1.30,阶梯ΔMa = 0.10。其中,各孤立标示点的纵坐标为压比测量值,以变量 ε 表示;横坐标为基于风洞运行状态参数和试验段水力直径为特征尺寸的雷诺数,以Rec表示。每条曲线则为同一试验段马赫数下压比随特征雷诺数变化的多项式拟合曲线,所有测试状态雷诺数最小约为1.23×106,最大约55.3×106,变化范围达到45倍。
从图2中可以看出,对于所有给定的试验段马赫数,风洞运行压比总体上呈现出随着试验雷诺数增加而逐渐降低的趋势,且在雷诺数较低区域压比下降较快,而随着雷诺数的增加其变化率逐渐减小。笔者认为风洞运行压比的降低主要是由于雷诺数增大时回路内气体的黏性损失降低所致。且当雷诺数增大到一定程度后洞壁内附面层的气流流动全部发展为湍流附面层,管道黏性损失进一步降低则变得困难。各马赫数下测试数据随着雷诺数增加缓慢渐变还表明,导致这种结果最主要原因来自于气体黏性损失的降低,而不是由于风洞内部段局部气流流动状态的改善所致。
|
图 2 风洞运行压比与雷诺数关系 Fig.2 The variation of the running pressure ratio with Reynolds number at different Mach numbers |
另外需要指出虽然图中马赫数Ma = 1.1、1.2和1.3的测试结果也表现出与亚声速相似的变化趋势,但此时风洞试验段、支架段和第二喉道等部段气流已达到超声速,运行出现阻塞,进一步增加风扇转速和驱动功率并不会使试验段马赫数再增加。在这种情况下,风洞运行压比与雷诺数的关系则不再符合上述分析。
3 动态模型建立 3.1 数据拟合分析为了更全面的理解和预测低温风洞运行特性,为低温风洞运行参数的耦合自动控制方案优化提供技术支撑,需要以尽可能简洁的形式表达出风洞运行压比与试验参数的关系。为此对测试数据尝试进行拟合分析。
采用多项式拟合将风洞运行压比与风洞其它变量联系起来是一种最常用数据处理方法[20-21]。然而,由于低温风洞运行状态(温度、压力和马赫数)变化非常宽广,要将各参数之间的关系以方程的形式表示且达到理想精度,方程将变得非常复杂,实现起来也较为困难,因此需要探索新的解决途径。而现有的测试数据结果表明了风洞运行压比是试验段马赫数和特征雷诺数这两个变量的函数,能否构造出一个简单的函数表达式描述这三个变量之间的关系,就成为进一步分析的方向。
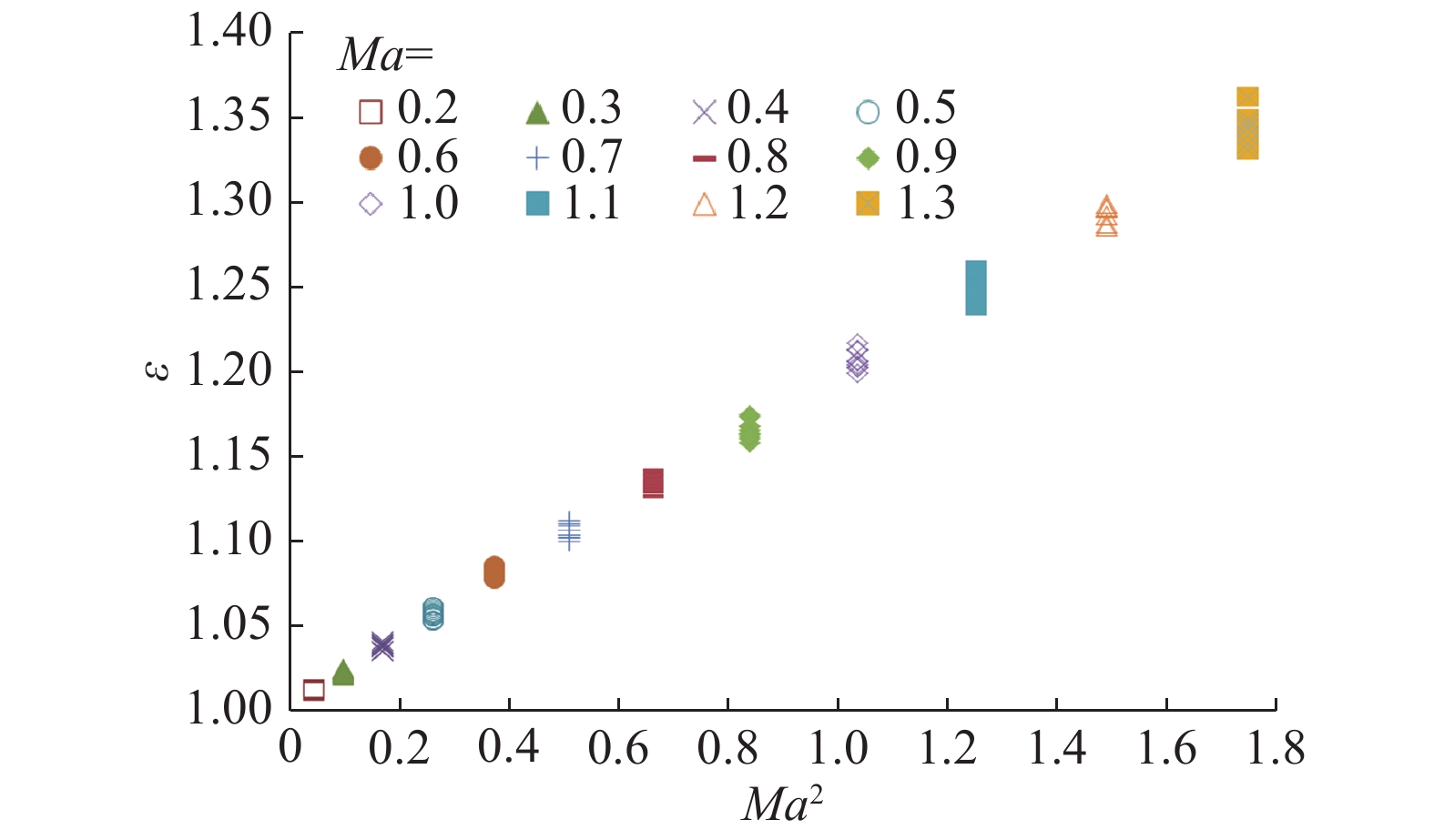
因为气流流动的压力损失与速压成正比,也就是与速度的平方成正比,因此可将测试数据进一步整理为运行压比与试验段马赫数平方的关系,见图3所示。其中横坐标为马赫数平方,纵坐标为运行压比。从图中可以看出风扇的压比与马赫数的平方成近似线性关系。假设压比与雷诺数为简单的幂函数,则可通过改变幂函数指数大小获得相对最佳数据拟合结果[22]。
|
图 3 风洞运行压比与马赫数平方关系 Fig.3 The variation of the running pressure ratio with the square of the Mach number |
基于上述分析,构造马赫数和雷诺数的组合函数
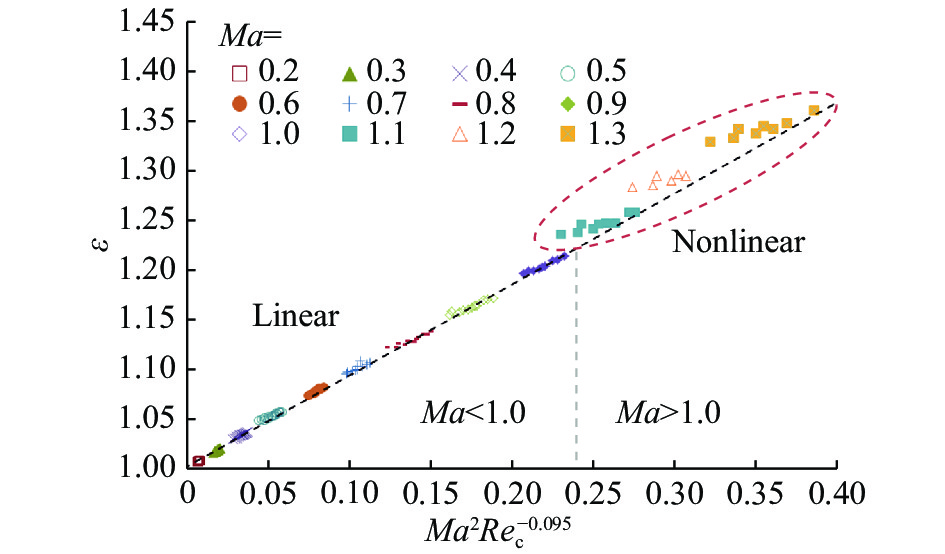
|
图 4 风洞运行压比与马赫数-雷诺数组合关系 Fig.4 The variation of the running pressure ration as a function of Ma2Rec−0.095 |
我们再针对上图中线性度较好的区域数据(Ma≤1.0),采用最小二乘法进行了线性拟合[23],见图5所示。直线斜率为0.9218,与纵坐标截距为1.0033。拟合优度可决系数R2为0.9987,表明拟合程度良好。因此,可给出风洞运行压比与组合函数的构造关系表达式如下:
| $\varepsilon = 0.9218 M{a^2} \cdot R{e_{\rm{c}}}^{ - 0.095} + 1.0033$ | (1) |
式中,Ma为试验段马赫数,Rec为特征雷诺数。

|
图 5 测试数据线性拟合 Fig.5 A linear fitting of test data |
依据风洞试验数据的不确定度评估理论,对上述测试马赫数和压比的不确定度进行分析。以风洞典型运行测试状态(总压pt = 115000 Pa,总温T0 = 110 K,马赫数Ma = 0.90)为例进行分析。主要运行参数包括:驻室参考静压pc= 67994 Pa,风扇段入口总压pFI = 99958 Pa,风扇段出口总压pFO = 116121 Pa。
自由流马赫数Ma是测量值总压pt和驻室参考静压pc的函数,通过状态方程式对各参数求导得到偏导数关系式,带入参数可得到偏导数值如下:
| $\begin{split}& \dfrac{{\partial Ma}}{{\partial {p_{\rm{t}}}}} = \dfrac{{0.31944}}{{{p_{\rm{c}}}{{\Bigg[\dfrac{{{p_{\rm{t}}}}}{{{p_{\rm{c}}}}}\Bigg]}^{\frac{5}{7}}}{{\Bigg[{{\Bigg(\dfrac{{{p_{\rm{t}}}}}{{{p_{\rm{c}}}}}\Bigg)}^{\frac{2}{7}}} - 1\Bigg]}^{\frac{1}{2}}}}} = 8.019 \times {10^{ - 6}}\;{\rm{ P}}{{\rm{a}}^{{\rm{ - 1}}}} \\& \dfrac{{\partial Ma}}{{\partial {p_{\rm{c}}}}} = \dfrac{{ - 0.31944{p_{\rm{t}}}}}{{{p_{\rm{c}}}^2{{\Bigg[\dfrac{{{p_{\rm{t}}}}}{{{p_{\rm{c}}}}}\Bigg]}^{\frac{5}{7}}}{{\Bigg[{{\Bigg(\dfrac{{{p_{\rm{t}}}}}{{{p_{\rm{c}}}}}\Bigg)}^{\frac{2}{7}}} - 1\Bigg]}^{\frac{1}{2}}}}} = - 1.356 \times {10^{ - 5}}\;{\rm{ P}}{{\rm{a}}^{{\rm{ - 1}}}} \\[-10pt] \end{split} $ | (2) |
因为测试pt和pc的传感器通过校准系统得到的校准不确定度是固定的,可作为测量值的偏差极限进行传递,pt和pc的相关偏差极限为:
| $ \begin{array}{*{20}{l}} {{B^\prime }_{{p_{\rm{t}}}} = \pm (4.79 + 0.00003{p_{\rm{t}}}) = \pm 8.24\;{\rm{Pa}}}\\ {{B^\prime }_{{p_{\rm{c}}}} = \pm (4.79 + 0.00003{p_{\rm{c}}}) = \pm 6.83\;{\rm{Pa}}} \end{array} $ | (3) |
马赫数的不确定度
| $\begin{split} {U_{Ma}} =& \pm \Bigg[{\Bigg(\dfrac{{\partial Ma}}{{\partial {p_{\rm{t}}}}}\Bigg)^2}({B^2_{{p_{\rm{t}}}}} + {P^2_{{p_{\rm{t}}}}}) + {\Bigg(\dfrac{{\partial Ma}}{{\partial {p_{\rm{c}}}}}\Bigg)^2}({B^2_{{p_{\rm{c}}}}} + {P^2_{{p_{\rm{c}}}}}) + \\&{\Bigg(\dfrac{{\partial Ma}}{{\partial {D_M}}}{B_{{D_M}}}\Bigg)^2} + 2\dfrac{{\partial Ma}}{{\partial {p_{\rm{t}}}}}\dfrac{{\partial Ma}}{{\partial {p_{\rm{c}}}}}{{B'}_{{p_{\rm{c}}}}}{{B'}_{{p_{\rm{t}}}}}{\Bigg]^{\frac{1}{2}}} \end{split} $ | (4) |
DM的校准不确定度也作为偏差极限传递,没有伴随产生的精度极限,根据校准结果
测试压比的不确定度
| $\begin{split} {U_\varepsilon } =& \pm \Bigg[{\Bigg(\dfrac{{\partial \varepsilon }}{{\partial {p_{{\rm{FI}}}}}}\Bigg)^2}({B^2_{{p_{{\rm{FI}}}}}} + {P^2_{{p_{{\rm{FI}}}}}}) + {\Bigg(\dfrac{{\partial \varepsilon }}{{\partial {p_{{\rm{FO}}}}}}\Bigg)^2}({B^2_{{p_{{\rm{FO}}}}}}+ {P^2_{{p_{{\rm{FO}}}}}}) +\\& 2\dfrac{{\partial \varepsilon}}{{\partial{p_{{\rm{FI}}}}}}\dfrac{{\partial \varepsilon}}{{\partial{p_{{\rm{FO}}}}}}{{B'}_{{p_{{\rm{FI}}}}}}{{B'}_{{p_{{\rm{FO}}}}}}{\Bigg]^{\frac{1}{2}}} \\[-15pt] \end{split} $ | (5) |
其中,
| $ \begin{split} \frac{\partial \varepsilon }{\partial {p}_{\rm{FO}}}=&\frac{1}{{p}_{\rm{FI}}}=1.001\times {10}^{-5}\;{\rm{ Pa}}^{\rm{-1}}\\ \frac{\partial \varepsilon }{\partial {p}_{\rm{FI}}}=&-\frac{{p}_{\rm{FO}}}{{p}_{\rm{FI}}{}^{2}}=-1.162\times {10}^{-5}\;{\rm{ Pa}}^{\rm{-1}}\\ {{B}^{\prime }}_{{p}_{\rm{FI}}}=&\pm (4.79+0.000\;03{p}_{\rm{FI}})=\pm 7.79\;\rm{Pa}\\ {{B}^{\prime }}_{{p}_{\rm{FO}}}=&\pm (4.79+0.000\;03{p}_{\rm{FO}})=\pm 8.27\;\rm{Pa}\end{split}$ | (6) |
将各参量值代入式(5),则可得到压比不确定度为:
虽然上文中风洞运行压比与马赫数和雷诺数组合函数的关系是通过风洞的实测数据归纳得出,但从传统的流体力学理论也同样可以推导出类似的方程式,下文进行简单阐述。
风洞管道流动压力的无因次损失系数k定义式如下:
| $k = \dfrac{{\Delta {p_0}}}{{\dfrac{1}{2}\rho {v^2}}} = \dfrac{{{p_{01}} - {p_{02}}}}{{\dfrac{1}{2}\rho {v_1}^2}}$ | (7) |
式中,v1为入口截面速度,p01为入口截面总压, p02为出口截面总压。
由于低温下的气体为不完全气体,需考虑真实气体效应,相关参数计算公式如下[2,24]:
气体密度:
| $\rho = \frac{p}{{RTZ}}$ | (8) |
速度:
| $v = Ma\sqrt {\gamma RTZ} $ | (9) |
动压:
| $q = \frac{1}{2}\gamma {p_{\rm{s}}}M{a^2}$ | (10) |
雷诺数:
| $R{e_{\rm{c}}} = \frac{{2qc}}{{\mu v}}$ | (11) |
式中,R为气体常数,γ为比热比,Z为压缩性因子,
利用连续性方程,并将式(10)带入式(7),则风扇段出口至入口的压力损失系数k的表达式为:
| $k = \frac{{2\left( {{p_2} - {p_1}} \right)}}{{\gamma {p_1}M{a^2}}} = \frac{2}{{\gamma M{a^2}}}\left( {\frac{{{p_2}}}{{{p_1}}} - 1} \right)$ | (12) |
式中,γ为比热比,p1为风扇入口截面静压,p2为风扇出口截面静压,Ma为试验段马赫数。
假设风扇段前后静压比值用变量
| $k = \frac{2}{{\gamma M{a^2}}}\left( {\varepsilon - 1} \right)$ | (13) |
上式可变形为:
| $\varepsilon = k\frac{{\gamma M{a^2}}}{2} + 1$ | (14) |
来流马赫数Ma < 1的无激波平板边界层流动阻力研究表明摩擦损失系数可表示为雷诺数的幂函数倒数和比例常数的乘积 [25],如下式:
| $k = ko \cdot R{e_{\rm{c}}}^{\left( { - \frac{1}{n}} \right)}$ | (15) |
式中,ko为比例常数(与风洞回路几何外形有关,而与雷诺数无关),指数n是雷诺数的函数。
将式(15)带入式(14),则得到风洞运行压比的理论表达式如下:
| $\varepsilon = \frac{\gamma }{2}ko \cdot M{a^2}R{e_{\rm{c}}}^{\left( { - \frac{1}{n}} \right)} + 1$ | (16) |
可以看出理论推导得到的关系式(16)和测试数据的拟合方程式(1)具有相同的表达型式。测试数据拟合得到的雷诺数指数(−1/n)值约为−0.095,介于−1/10和−1/11之间,基于平板附面层表面摩擦阻力得到的值介于−1/3到−1/9[25],两者存在差异可能是因为风洞回路流道的几何外形更为复杂,且包含了拐角导流片、开槽壁板和支架等流道内部件,需进行修正。另外,常数项偏差0.0033可能是由于液氮喷射所致或数据系统误差引起的,需要开展进一步精确测量研究解决,但该动态模型对于工程应用已有足够精度。
4 动态模型应用低温风洞运行控制多变量耦合关系示意见图6所示。最困难的是气流温度精确控制,它与压缩机转速、液氮喷射流量都是强耦合,动力学和热力学关系复杂。

|
图 6 运行控制多变量耦合关系 Fig.6 A schematic of the Multi-variable coupled control |
利用前文获得的压比与运行状态之间的传递函数(式(1))使得风洞运行的液氮需求和压缩机功率以相对简单的方式与试验运行状态相关联,表达式如下:
| ${P_f} = \dot m \cdot \frac{\gamma }{{\gamma - 1}} \cdot Z \cdot R \cdot {T_{t,i}} \cdot ({\varepsilon ^{\frac{{\gamma - 1}}{\gamma }}} - 1)$ | (17) |
| ${\dot m_{{\rm{LN2}}}} = \frac{{{P_f}}}{\beta }$ | (18) |
式中,
将该动态模型应用于0.3 m低温风洞控制方案,将使控制系统能够根据设定的风洞运行目标状态,提前获得风洞运行所需的精确液氮流量和压缩机转速,通过前馈控制则可提升控制系统效率,缩短运行状态参数稳定时长。
5 结 论利用0.3 m低温风洞的流场校测数据,成功构造马赫数和雷诺数的组合幂函数,并建立了马赫数小于1.0时风洞各运行工况条件下运行压比与马赫数-雷诺数的线性关联方程式,并利用传统的流体力学方程式推导获得了相同的数学表达型式。结果表明:风洞运行压比与马赫数-雷诺数组合函数存在简单线性关系,该研究成果作为动态模型应用于低温风洞多变量控制,可简化参数传递过程和优化方案,缩短状态参数的稳定时间。同时,由于马赫数大于1.0时风洞流道内存在激波、阻塞等流动状态,本文所得到压比关联式在超声速区域并不适用,对此还将进一步开展针对性研究。
| [1] |
廖达雄, 黄知龙, 陈振华, 等. 大型低温高雷诺数风洞及其关键技术综述[J]. 实验流体力学, 2014, 28(2): 1-6, 20. LIAO D X, HUANG Z L, CHEN Z H, et al. Review on large-scale cryogenic wind tunnel and key technologies[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(2): 1-6, 20. DOI:10.11729/syltlx20130102 (in Chinese) |
| [2] |
江雄, 牟斌, 王建涛, 等. 考虑低温增压真实气体效应的运输机气动特性数值模拟研究[J]. , 2016, 34(5): 652-658. JIANG X, MOU B, WANG J T, et al. Numerical simulation of transport aircraft under low temperature and high pressure real gas effect in wind tunnel[J]. Acta Aerodynamica Sinica, 2016, 34(5): 652-658. (in Chinese) |
| [3] |
WAHLS R. The National Transonic Facility - A research retrospective[C]//the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV. Reston, Virginia: AIAA, 2001. doi: 10.2514/6.2001-754.
|
| [4] |
KILGORE R A. The cryogenic wind tunnel concept for high Reynolds number testing[C]//Proceedings of the Ninth International Cryogenic Engineering Conference, Kobe, Japan, 1982. doi:https://doi.org/10.1016/B978-0-408-01252-2.50096-0
|
| [5] |
KILGORE R A, ADCOCK J B, RAY E J. The cryogenic transonic wind tunnel for high Reynolds number research: NTRS-19760018126[R]. NTRS - NASA Technical Reports Server, 1976. doi: https://ntrs.nasa.gov/citations/19760018126
|
| [6] |
ADCOCK J B, OGBURN M E. Power calculations for isentropic compressions of cryogenic nitrogen[R]. NTRS - NASA Technical Reports Server, 1977.
|
| [7] |
KILGORE R A, ADCOCK J B. Specific cooling capacity of liquid nitrogen: TM X-74015[R]. Washington DC: National Aeronautics and Space Administration, 1977.
|
| [8] |
宋远佳, 陈振华, 赖欢, 等. 低温风洞绝热系统的研究现状及其关键技术[J]. 哈尔滨工业大学学报, 2019, 51(7): 63-69. SONG Y J, CHEN Z H, LAI H, et al. Development and key technology of cryogenic wind tunnel insulation system[J]. Journal of Harbin Institute of Technology, 2019, 51(7): 63-69. DOI:10.11918/j.issn.0367-6234.201801115 (in Chinese) |
| [9] |
周廷波, 高超, 张正科, 等. NF-6风洞喷液氮降温系统研制[J]. 航空动力学报, 2018, 33(2): 327-337. ZHOU T B, GAO C, ZHANG Z K, et al. Development of liquid nitrogen injection cooling system of NF-6 wind tunnel[J]. Journal of Aerospace Power, 2018, 33(2): 327-337. (in Chinese) |
| [10] |
张蓓乐, 陈小砖, 薛绒, 等. 采用液氮喷雾技术的低温环路结构模拟系统研究[J]. 西安交通大学学报, 2019, 53(5): 109-114. ZHANG B L, CHEN X Z, XUE R, et al. Study on the low-temperature air loop simulation system based on liquid nitrogen spray technology[J]. Journal of Xi'an Jiaotong University, 2019, 53(5): 109-114. (in Chinese) |
| [11] |
廖达雄, 张海洋, 阮一逍, 等. 氮液滴在气流中的破碎和碰撞模拟[J]. 哈尔滨工业大学学报, 2018, 50(7): 185-191. LIAO D X, ZHANG H Y, RUAN Y X, et al. Numerical study on the breakup and collision of nitrogen droplets in high-speed gas flow[J]. Journal of Harbin Institute of Technology, 2018, 50(7): 185-191. DOI:10.11918/j.issn.0367-6234.201710038 (in Chinese) |
| [12] |
张伟, 高荣, 张双喜, 等. 0.3 m低温风洞液氮供给系统研制[J]. 航空动力学报, 2020, 35(5): 1009-1017. ZHANG W, GAO R, ZHANG S X, et al. Development of liquid nitrogen supplying system of 0.3 m cryogenic wind tunnel[J]. Journal of Aerospace Power, 2020, 35(5): 1009-1017. (in Chinese) |
| [13] |
BALAKRISHNA S, KILGORE W, THIBODEAUX J. Control of large cryogenic tunnels[C]//28th Joint Propulsion Conference and Exhibit, Nashville, TN. Reston, Virginia: AIAA, 1992. doi: 10.2514/6.1992-3930.
|
| [14] |
GOBERT J. ETW control system - Design and first results[C]//25th Plasmadynamics and Lasers Conference, Colorado Springs, CO. Reston, Virginia: AIAA, 1994. doi: 10.2514/6.1994-2514.
|
| [15] |
ZHU R S, YIN G F, TANG G S, et al. Temperature trajectory control of cryogenic wind tunnel with robust L1 adaptive control[J]. Transactions of the Institute of Measurement and Control, 2018, 40(13): 3675-3689. DOI:10.1177/0142331217728569 |
| [16] |
ZHU R S, YIN G F, CHEN Z H, et al. Temperature control of cryogenic wind tunnel with a modified L1 adaptive output feedback control[J]. Measurement and Control, 2018, 51(9-10): 498-513. DOI:10.1177/0020294018808672 |
| [17] |
刘为杰, 何帆, 杨国超. 低温风洞自抗扰控制研究[J]. 空气动力学学报, 2020, 38(5): 866-873. LIU W J, HE F, YANG G C. Active disturbance rejection control for cryogenic wind tunnels[J]. Acta Aerodynamica Sinica, 2020, 38(5): 866-873. (in Chinese) |
| [18] |
兰其龙. 基于神经网络预测控制的低温风洞多变量控制策略研究[D]. 绵阳: 中国空气动力研究与发展中心, 2016. LAN Q L. Research on multivariable control strategy based on neural network predictive control in cryogenic wind tunnel[D]. Mianyang: China Aerodynamics Research and Development Center, 2016. (in Chinese). |
| [19] |
黄丽娟, 邹文君, 吴凡. 不协调目标信息系统多变量控制方法仿真[J]. 计算机仿真, 2019, 36(7): 187-190, 212. HUANG L J, ZOU W J, WU F. Multi-variable control method simulation for uncoordinated target information system[J]. Computer Simulation, 2019, 36(7): 187-190, 212. (in Chinese) |
| [20] |
STOER J, BULIRSCH R. Error analysis[M]//Introduction to Numerical Analysis. New York, NY: Springer New York, 1993: 1-36. doi: 10.1007/978-1-4757-2272-7_1.
|
| [21] |
张善文, 刘建都, 韩小斌. 基于遗传算法的一种数据拟合方法[J]. 空军工程大学学报(自然科学版), 2007, 8(1): 66-68. ZHANG S W, LIU J D, HAN X B. A data fitness method based on genetic algorithm[J]. Journal of Air Force Engineering University (Natural Science Edition), 2007, 8(1): 66-68. (in Chinese) |
| [22] |
戚尔鹏, 叶鹰. 漂移幂函数的数值拟合与理论分析[J]. 情报学报, 2016, 35(12): 1285-1295. ERIC P. QI, FRED Y. YE. Data fitting and theoretical analysis of the shifted power function[J]. Journal of the China Society for Scientific AndTechnical Information, 2016, 35(12): 1285-1295. DOI:10.3772/j.issn.1000-0135.2016.012.006 (in Chinese) |
| [23] |
周浩. 线性数据拟合方法的误差分析及其改进应用[J]. 大学数学, 2013, 29(1): 70-76. ZHOU H. Error analysis and improved application of linear data fitting method[J]. College Mathematics, 2013, 29(1): 70-76. (in Chinese) |
| [24] |
AUNGIER R H. A fast, accurate real gas equation of state for fluid dynamic analysis applications[J]. Journal of Fluids Engineering, 1995, 117(2): 277-281. DOI:10.1115/1.2817141 |
| [25] |
BERTRAM, MITCHEL H. Calculations of compressible average turbulent skin friction: NASA report[R]. Washington DC: National Aeronautics and Space Administration, TR-R-123, 1962.
|
 2021, Vol. 39
2021, Vol. 39


