飞机在飞行中产生的尾涡流场是飞行安全的重要危害之一,近年来发生了多起飞机在高空巡航阶段飞行时遭遇前机尾流的不安全事件[1-2]。国外研究者[3-4]对尾涡安全间隔展开研究,评估了飞机起飞及着陆阶段所需最小安全间隔。在尾涡消散方面,国外研究者通过建立复杂的数学模型来描述尾涡消散机理。Holzäpfel等[5]建立两阶段尾涡消散模型来计算尾涡强度的衰减情况。Sarpkaya等[6-7]认为尾涡的消散主要取决于大气层结稳定性和大气湍流度,而与雷诺数关系不大。Proctor和Hamilton[8-9]等基于大涡模拟方法的终端区尾涡流场仿真系统平台建立了尾涡流场参数快速预测模型,并将常用的尾涡预测模型与几个机场的激光雷达探测数据进行吻合度分析。在巡航阶段尾涡遭遇方面,Pérez等[10]基于尾涡快速仿真计算模型分析在现行巡航阶段尾流间隔标准下长航时无人机RQ-4A及MQ-9遭遇前机尾流的风险。Hoogstraten等[11]研究发现当巡航阶段产生尾涡的飞机或遭遇尾涡的后机处于爬升或下降状态时,尾涡遭遇的概率会增加。Nelson[12]提出随着时间的推移,飞机的重量及尺寸上越来越大的差异会增加巡航阶段尾涡遭遇的概率及危害。
国内研究者主要致力于尾涡流场建模及尾涡参数计算方面的研究,而对巡航阶段尾涡特性鲜有论述。魏志强等[13-14]从理论上对民用飞机的尾涡消散机理进行研究,分析了不同侧风影响下的涡量衰减、涡心速度等参数的变化规律。谷润平等[15]提出一种基于垂直截面上尾涡诱导风场数据的尾涡特征参数计算方法。艾国远等[16]采用高精度大涡模拟方法,对不同雷诺数的翼型进行仿真,研究低雷诺数条件下翼型的气动特性。
近年来,日益繁忙的空中交通对空域利用效率提出了更高要求。2007年以来,我国在保证飞行安全的前提下,缩小了FL290~FL410之间的垂直间隔(Reduced Vertical Separation Minimum,RVSM)标准。美国和澳大利亚研究人员[17]于2017年开始研究在FL410以上高度实施RVSM的可行性。美澳研究者研究了RVSM空域上扩高度层随温度变化的可压缩特性,但未分析飞机尾流的消散及其对下层飞机的影响问题。国内外研究者在尾涡流场及安全间隔的建模方面开展的大量研究针对中低空及飞机的起飞、着陆阶段,未对12500 m以上高空巡航阶段尾涡流场特性进行分析。
为解决上述问题,本文首先分析了现有的尾涡流场快速仿真计算模型,给出不同飞行高度处尾涡危险区域计算方法;然后以某型飞机为例计算不同飞行高度处尾涡流场的运动规律及高空尾涡危险区域;最后分析高空尾涡危险区域的影响因素。研究结果为12500~15000 m之间的飞行高度层垂直间隔缩减可行性研究提供技术支持。
1 飞机尾涡的物理模型机翼在产生升力时,下翼面的压强高于上翼面,两个翼尖处的气流就会从下翼面绕到上翼面,形成两个反向旋转的翼尖涡流。由于涡流之间的相互诱导作用和重力、大气层结稳定性、大气湍流度等因素的影响,涡核以一定速度下降。尾涡向后运动的同时,其强度也在不断衰减。
1.1 尾涡的初始强度计算模型飞机尾涡一般使用涡旋环量
| ${\varGamma _0}{\rm{ = }}\frac{{mg}}{{{\rho _\infty }{V_\infty }{b_0}}}$ | (1) |
式中:
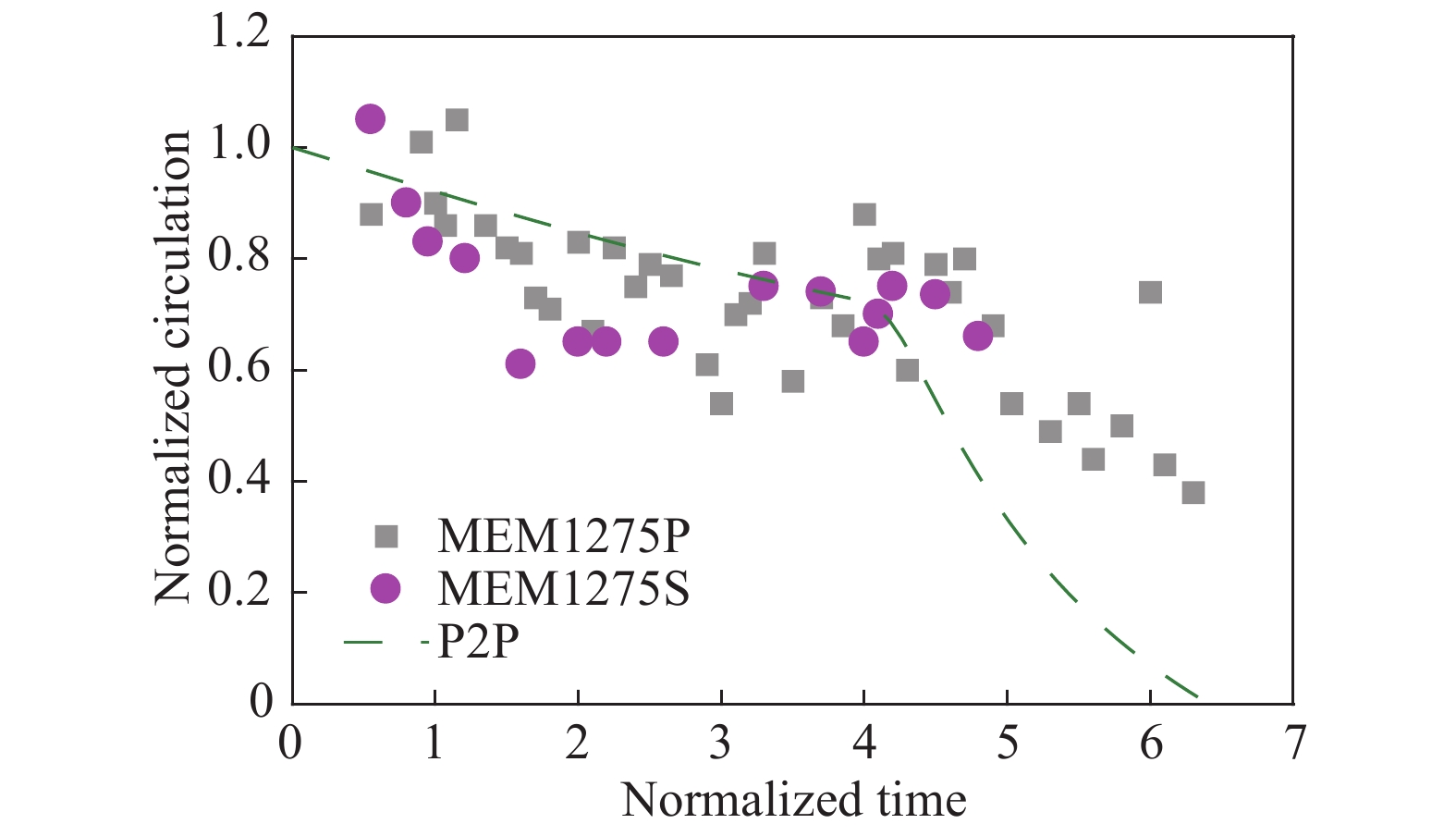
通过对尾涡基本演化机理的分析,结合大量实验数据(尾流直接探测、数值模拟)建立的计算模型能相对准确地对尾涡流场参数进行快速仿真计算。综合考虑尾涡消散的随机混沌特性及气象参数探测的不确定性,Robins和Holzäpfel[18-19]采用大涡模拟分析不同风条件下尾涡的变化规律,在两阶段消散模型的基础上加入随机扰动项,形成随机两阶段消散模型(Probabilistic Two-Phase Wake Vortex Decay,P2P),与激光雷达拟合度较高。依据P2P模型的仿真计算结果与文献[9]及文献[18]提供的孟菲斯(Memphis, MEM)机场测量结果MEM1275对比情况如图1所示。图中正方形和圆点分别代表连续波激光雷达测量出的左、右翼尖涡消散数据。
|
图 1 尾涡消散数据对比 Fig.1 The decay of wake vortices |
尾涡的消散主要受飞机特性及大气参数的影响,P2P模型可以较为准确的描述不同飞行高度处尾涡衰减情况。
1.3 尾涡消散过程P2P模型使用涡核半径5~15 m的环量均值作为该尾涡的环量,为了计算方便,通常使用相对于基准参数的无量纲标称参数。常用的基准参数包括尾涡参考时间
| ${t_0} = \frac{{{b_0}}}{{{w_0}}} = \frac{{2{\rm{{\text{π}} }}b_0^2}}{{{\varGamma _0}}}$ | (2) |
| ${w_0} = \frac{{2{\varGamma _0}}}{{{{\rm{{\text{π}} }}^2}B}}$ | (3) |
尾涡的消散分为扩散阶段和快速衰减阶段。在扩散阶段,尾涡消散的速度相对缓慢,其无因次尾涡环量计算公式如下:
| $ \varGamma _{5 - 15}^*\left( {{t^*}} \right) = \frac{1}{{11}}\sum\limits_{r = 5}^{15} {A - \exp \frac{{ - {r^{*2}}}}{{4\upsilon _1^*( {{t^*} - T_1^*} )}}} $ | (4) |
式中:
| $\varGamma _{5 - 15}^*( {{t^*}} ) = A - \exp [ { - {R^{*2}}/\upsilon _1^*( {{t^*} - T_1^*} )} ]$ | (5) |
式中:
尾涡消散的第二阶段为尾涡快速衰减阶段,环量
| $\begin{split} \varGamma _{5 - 15}^*( {{t^*}} ) =& A - \exp [ { - {R^{*2}}/\upsilon _1^*( {{t^*} - T_1^*} )} ] -\\& \exp [ { - {R^{*2}}/\upsilon _2^*( {{t^*} - T_2^*} )} ] \end{split} $ | (6) |
式中:
| ${\varepsilon ^*} = {( {\varepsilon {b_0}} )^{1/3}}/{w_0}$ | (7) |
大气层结稳定性用浮力频率
| ${N^*}{\rm{ = }}\frac{{2{\text{π}} Nb_0^2}}{{{\varGamma _0}}}$ | (8) |
在不同湍流水平下,
| $\left\{ \begin{array}{l} {T^*} = 0.804{\varepsilon ^{*\frac{3}{4}}},\;\;\;\;\;\;\;\;\;{\varepsilon ^*} > 0.2535 \\ {T^{*\frac{1}{4}}}\exp \left( { - 0.70{T^*}} \right) = {\varepsilon ^*},{\varepsilon ^*} > 0.0235 \end{array} \right.$ | (9) |
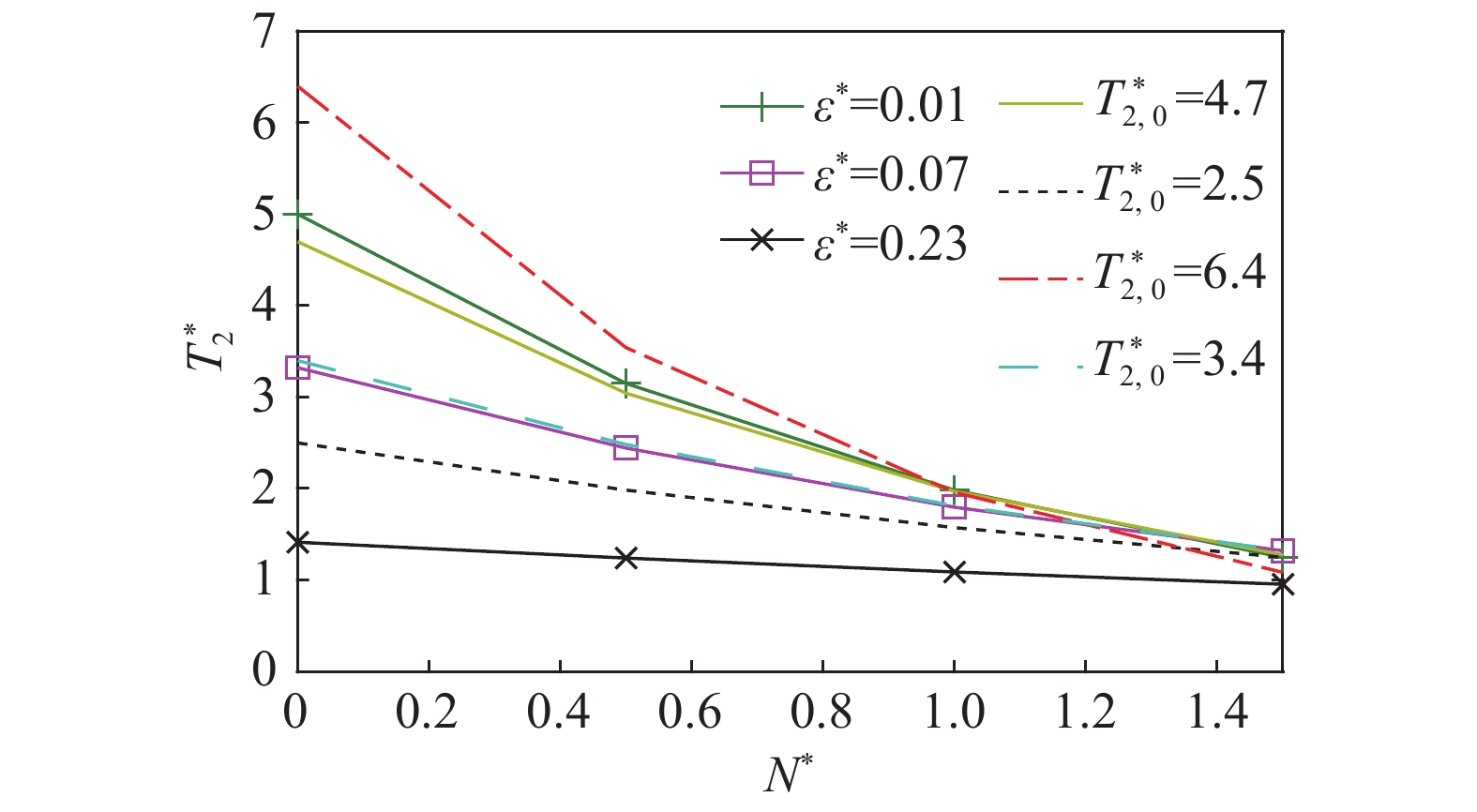
| $T_2^* = T_{2,0}^*\exp ( { - 0.185T_{2,0}^*{N^*}} )$ | (10) |
式中:
|
图 2 |
从图2可以看出,大气层结稳定性和大气湍流度的增加均会使
有效粘度因数
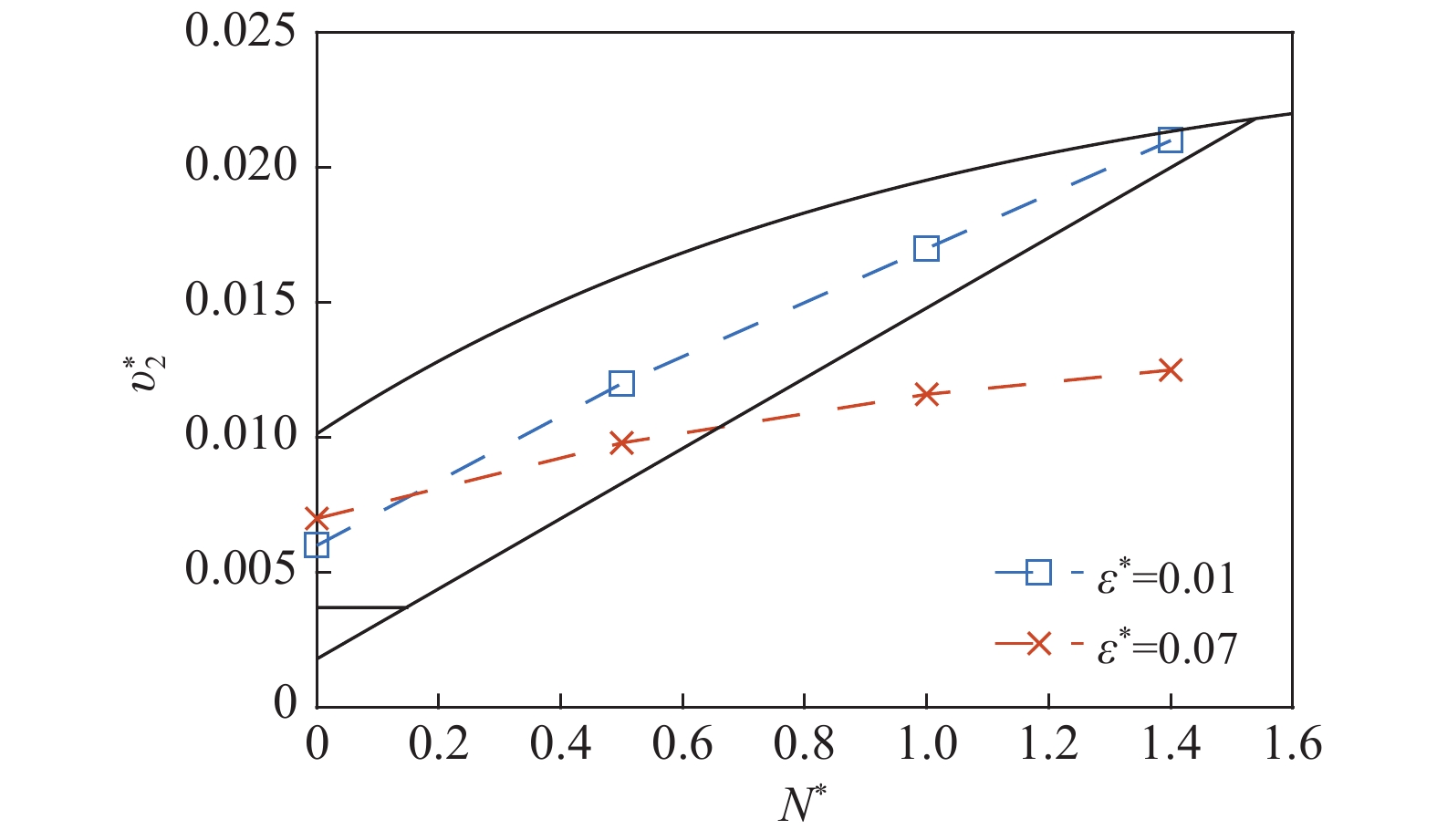
| $\left\{ \begin{array}{l} \upsilon _{2,u}^* = 0.025\left[ {1 - \exp \left( { - {N^*} - 0.52} \right)} \right] \\ \upsilon _{2,l}^* = 0.0018 + 0.013{N^*} \end{array} \right.$ | (11) |
式中:
|
图 3 不同湍流水平下 |
尾涡形成后,强度逐渐消散,同时尾涡向下运动,涡核位置发生变化。涡核下沉速度
| $w = \frac{{2{\varGamma _{5 - 15}}}}{{{{\rm{{\text{π}} }}^2}B}}$ | (12) |
经时间
| $h = \int {w{\rm{d}}t} $ | (13) |
尾涡在飞机后方的位置距离等效于经时间
| $s = {V_\infty } t$ | (14) |
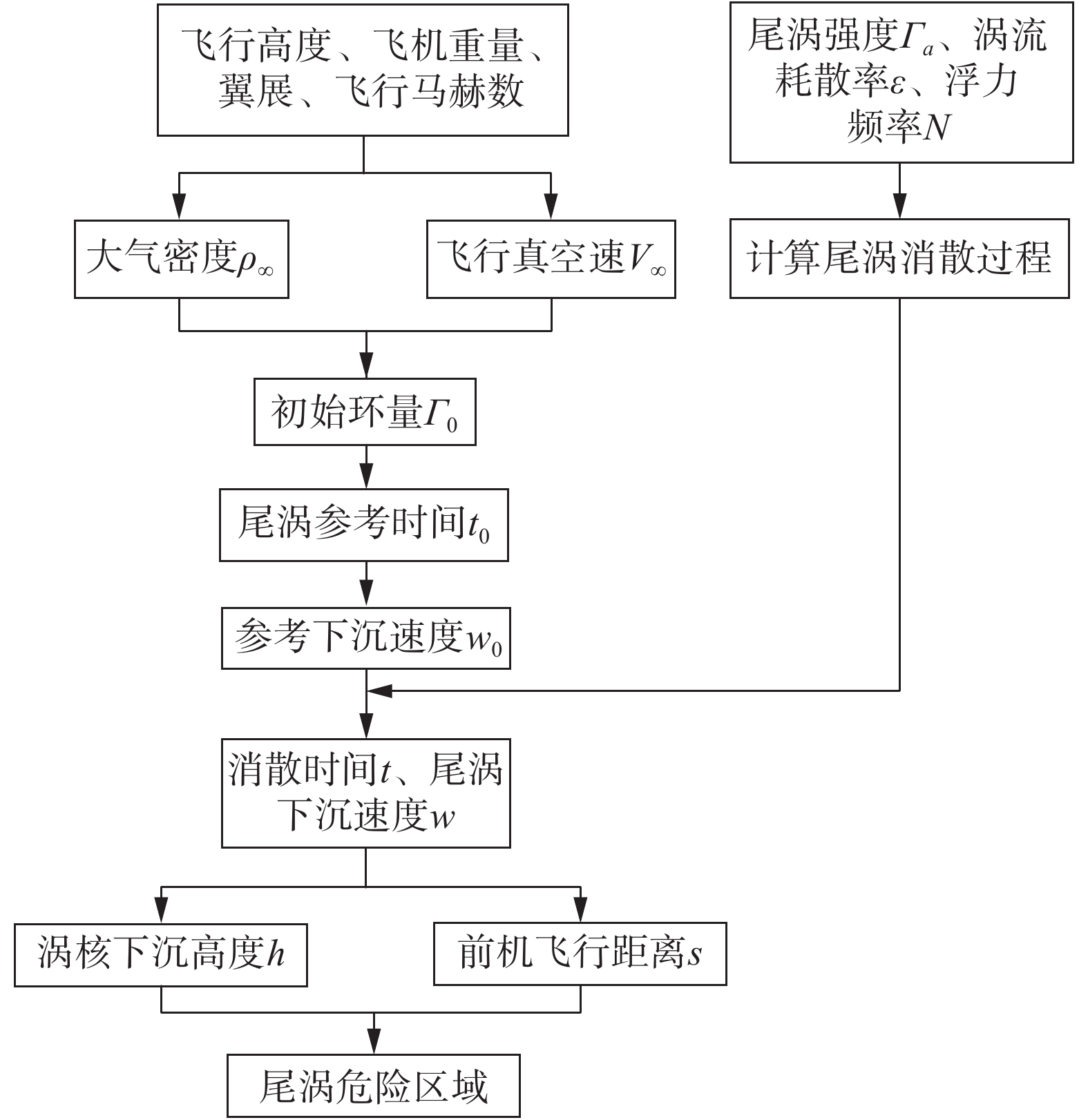
前机下后方形成的尾涡危险区域与后机所能承受的尾涡强度
|
图 4 尾涡危险区域计算流程 Fig.4 The flow chart for calculating the hazard areas of wake vortices |
本节以某型飞机为例,根据第1节中的尾涡物理模型,分析不同飞行高度处尾涡的形成及消散特性,计算高空尾涡危险区域。
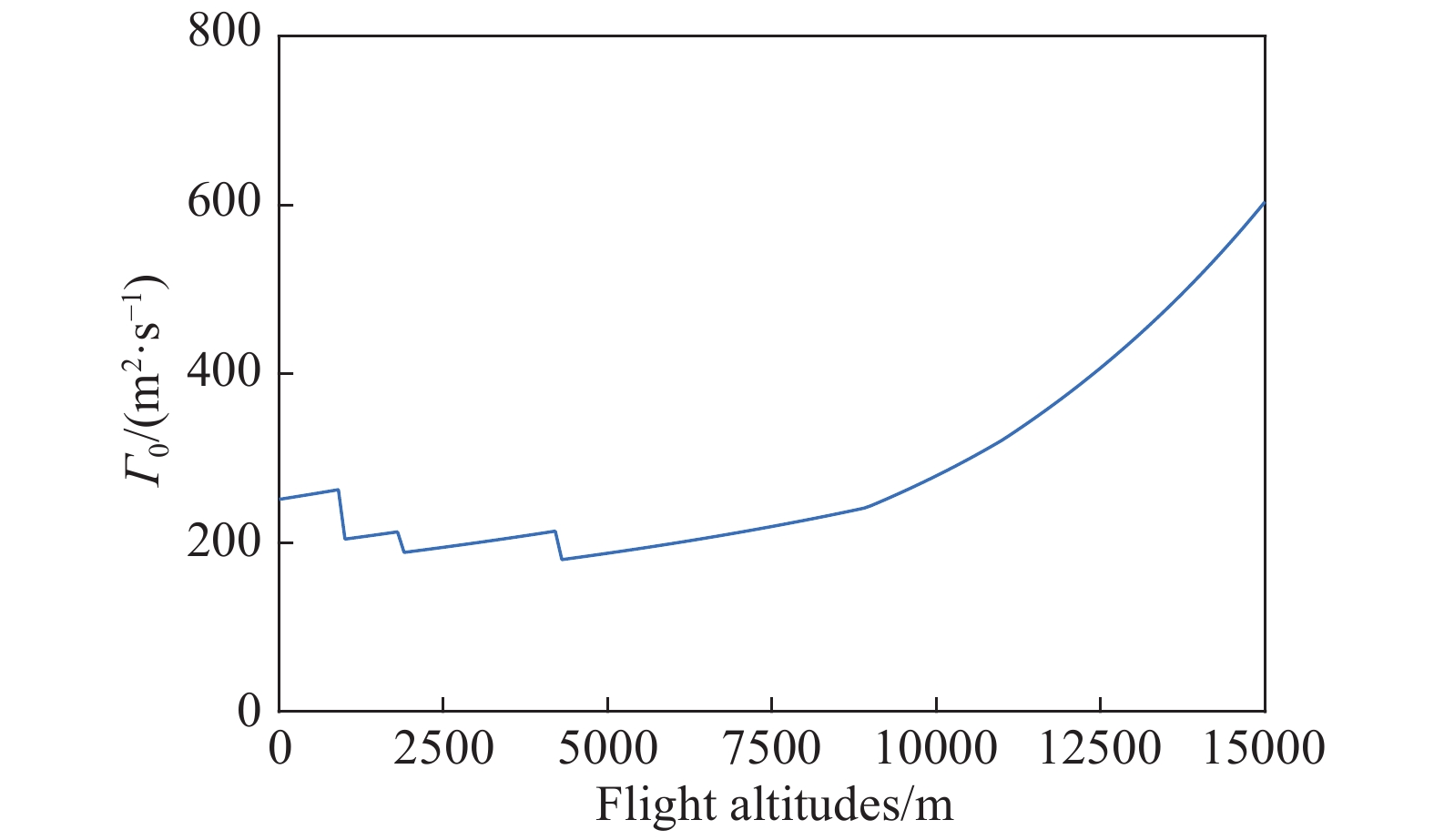
2.1 尾涡初始环量计算分析由公式(1)计算出该飞机在不同飞行高度处的尾涡初始环量
|
图 5 不同飞行高度处的尾涡初始环量 |
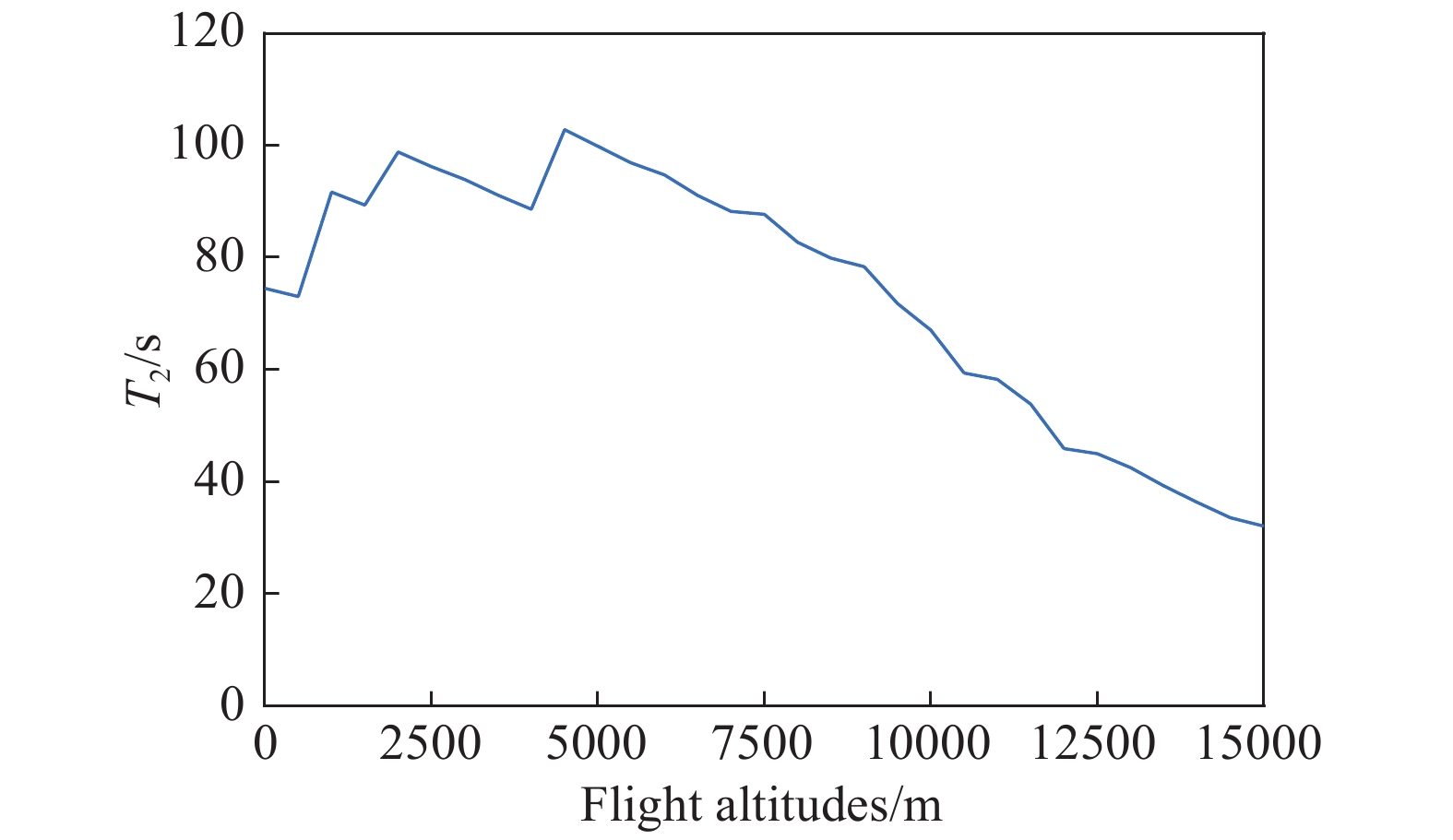
|
图 6 不同飞行高度处的 |
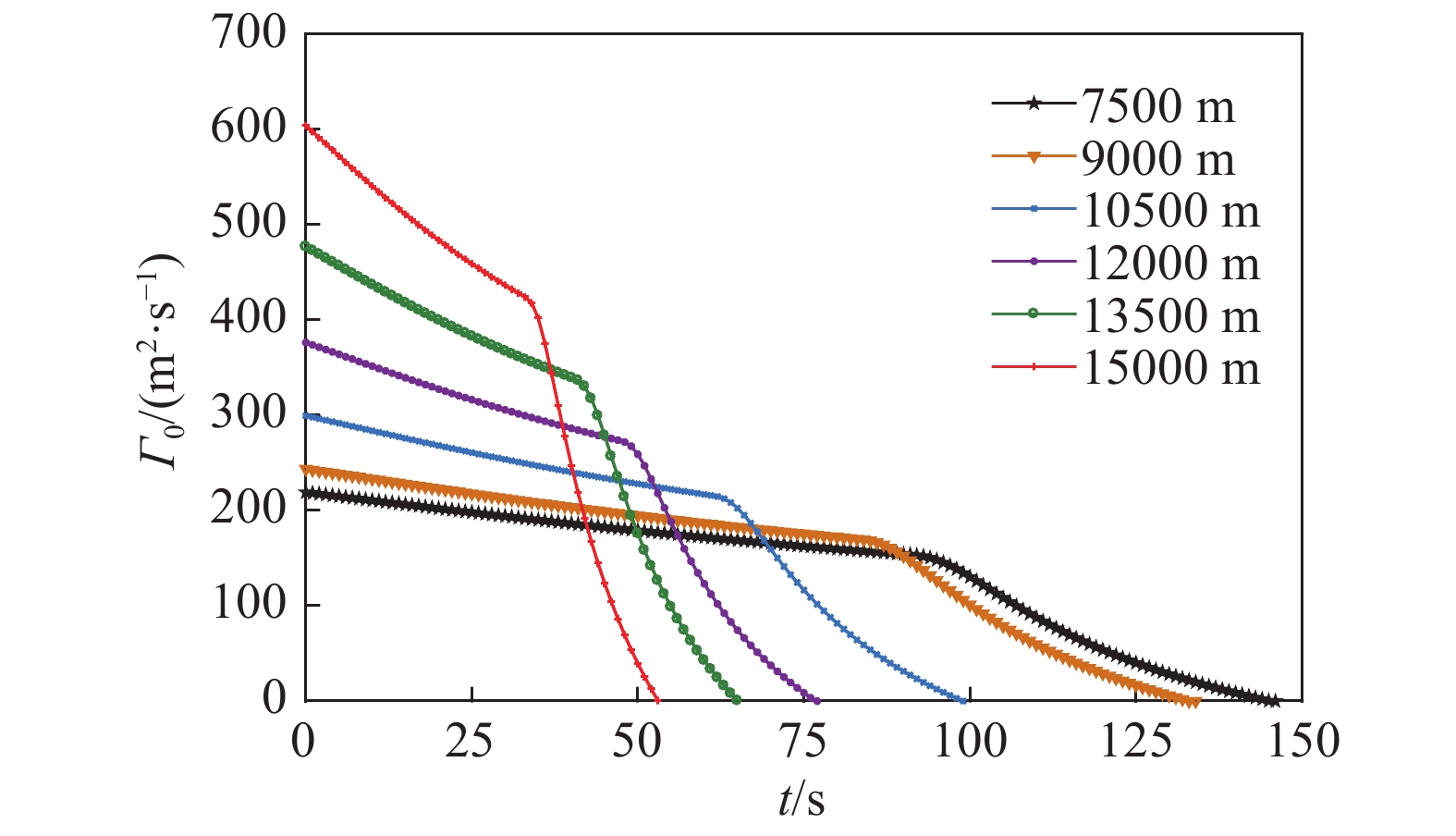
以7500~15000 m飞行高度为例,由公式(5)~公式(11)计算得到尾涡的消散过程见图7。从图7可以看出,直观上
|
图 7 不同飞行高度处的尾涡消散过程 Fig.7 The dissipation rates of wake vortices at different flight altitudes |
为了研究飞机下后方尾涡危险区域,需计算当尾涡环量消散到
不同飞行高度处的尾涡消散时间见图8。从图8可以看出,12500 m以上的高空中,飞行高度越高,尾涡环量消散到
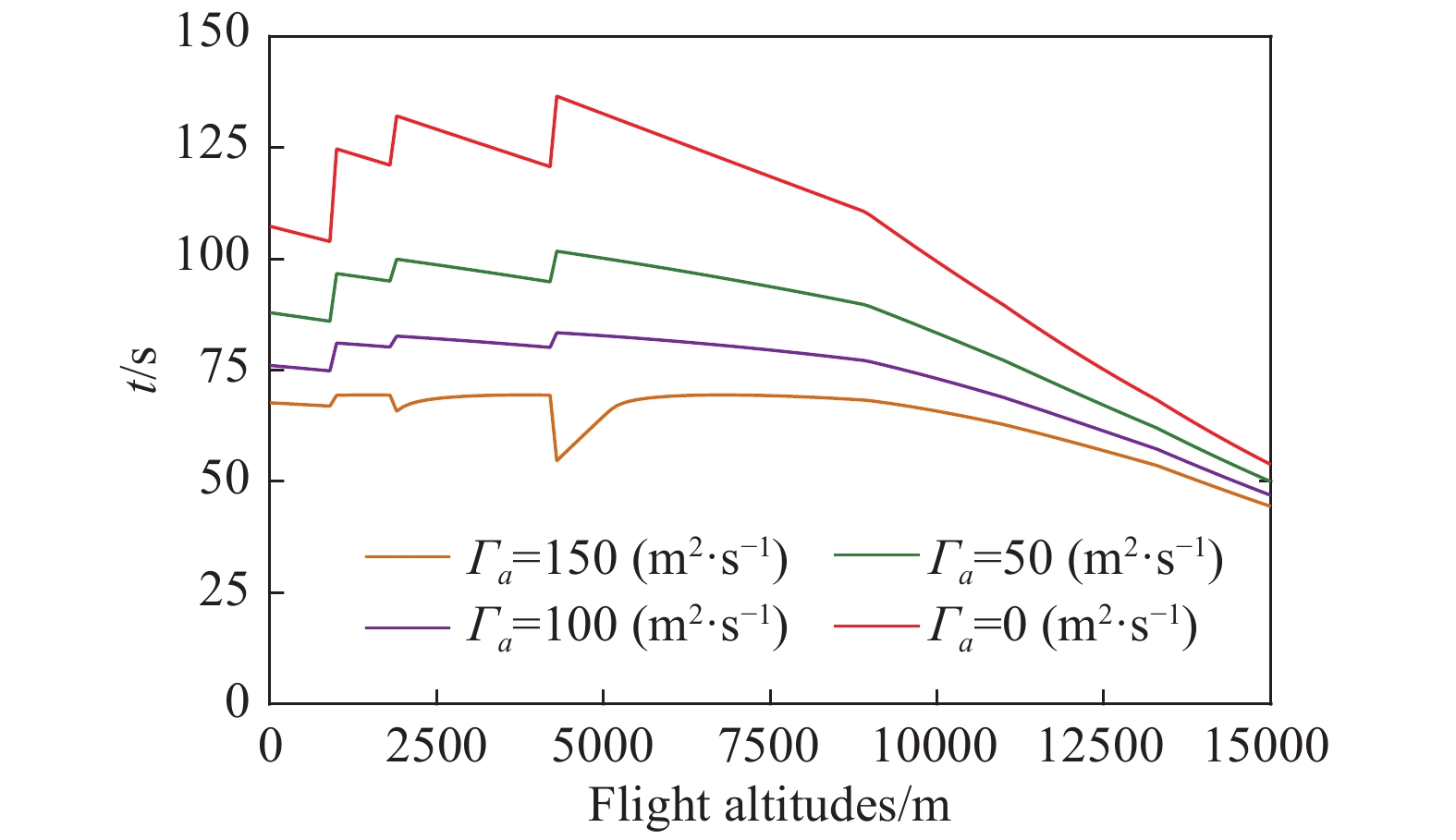
|
图 8 不同飞行高度处尾涡消散时间 Fig.8 The dissipation time of wake vortices at different flight altitudes |
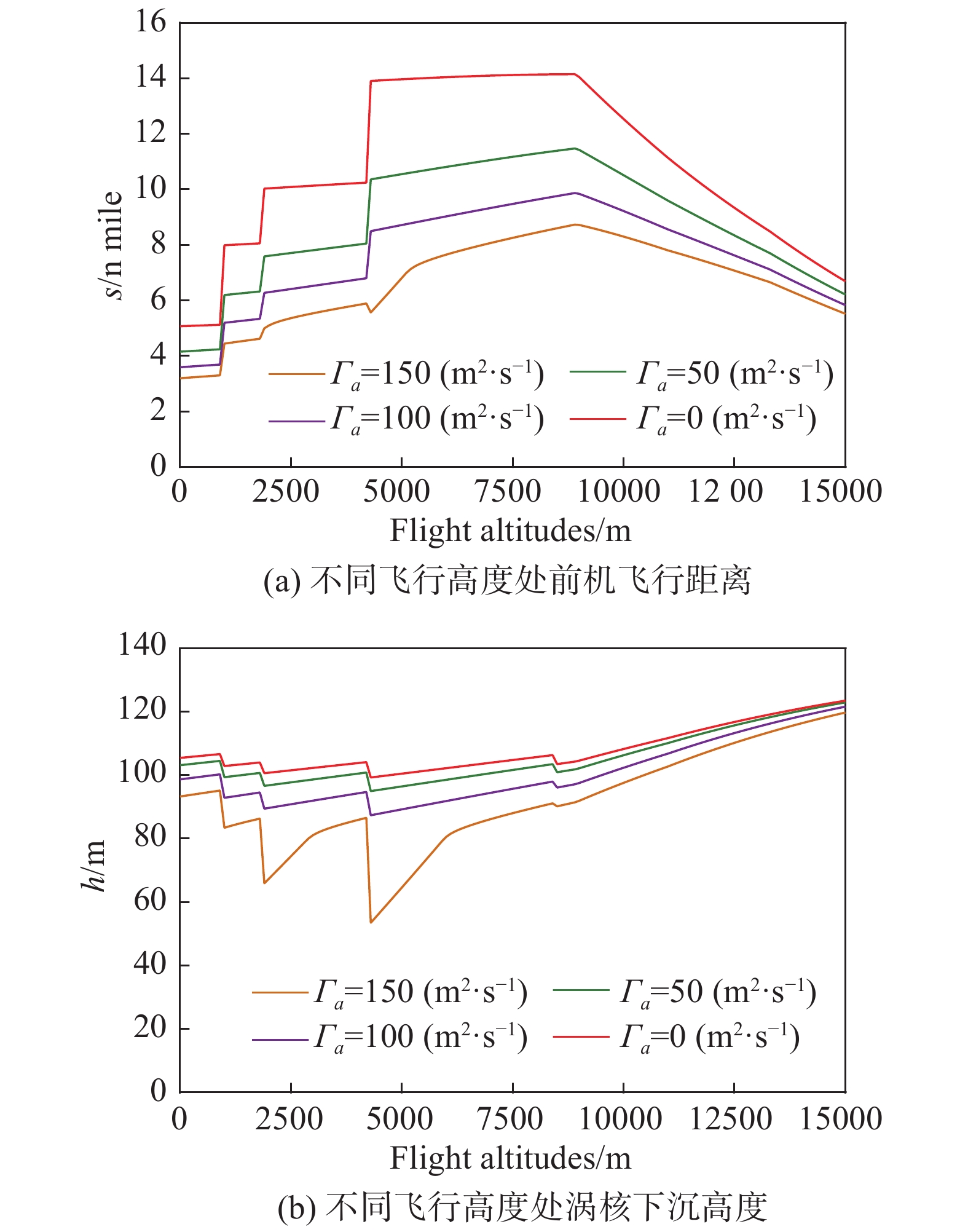
不同飞行高度处的尾涡危险区域见图9。从图9(a)可以看出,12500 m以上高空中,随着飞行高度的增加,尾涡环量消散到
从图9(b)可以看出,12500 m以上的高空中,尾涡环量消散到
与RVSM空域相比,高空尾涡危险区域在纵向范围减小,在垂直范围增大。为了计算垂直范围上高空尾涡涡核下沉高度增加的幅度,设尾涡环量消散到
|
图 9 不同飞行高度处尾涡危险区域 Fig.9 The hazard areas of wake vortices at different flight altitudes |
| 表 1 不同环量处涡核下沉高度差值 Table 1 The sinking height differences of wake vortices with different circulations |
|
|
产生尾涡的前机特性以及大气条件会影响尾涡的消散。此节分析飞机重量、大气湍流度、大气层结稳定性以及前机飞行速度对尾涡危险区域的影响。
3.1 飞机重量对尾涡危险区域的影响NASA的研究结果显示,飞机的重量和形状影响尾涡的初始强度,进而影响尾涡的消散,其中重量是主要影响因素。
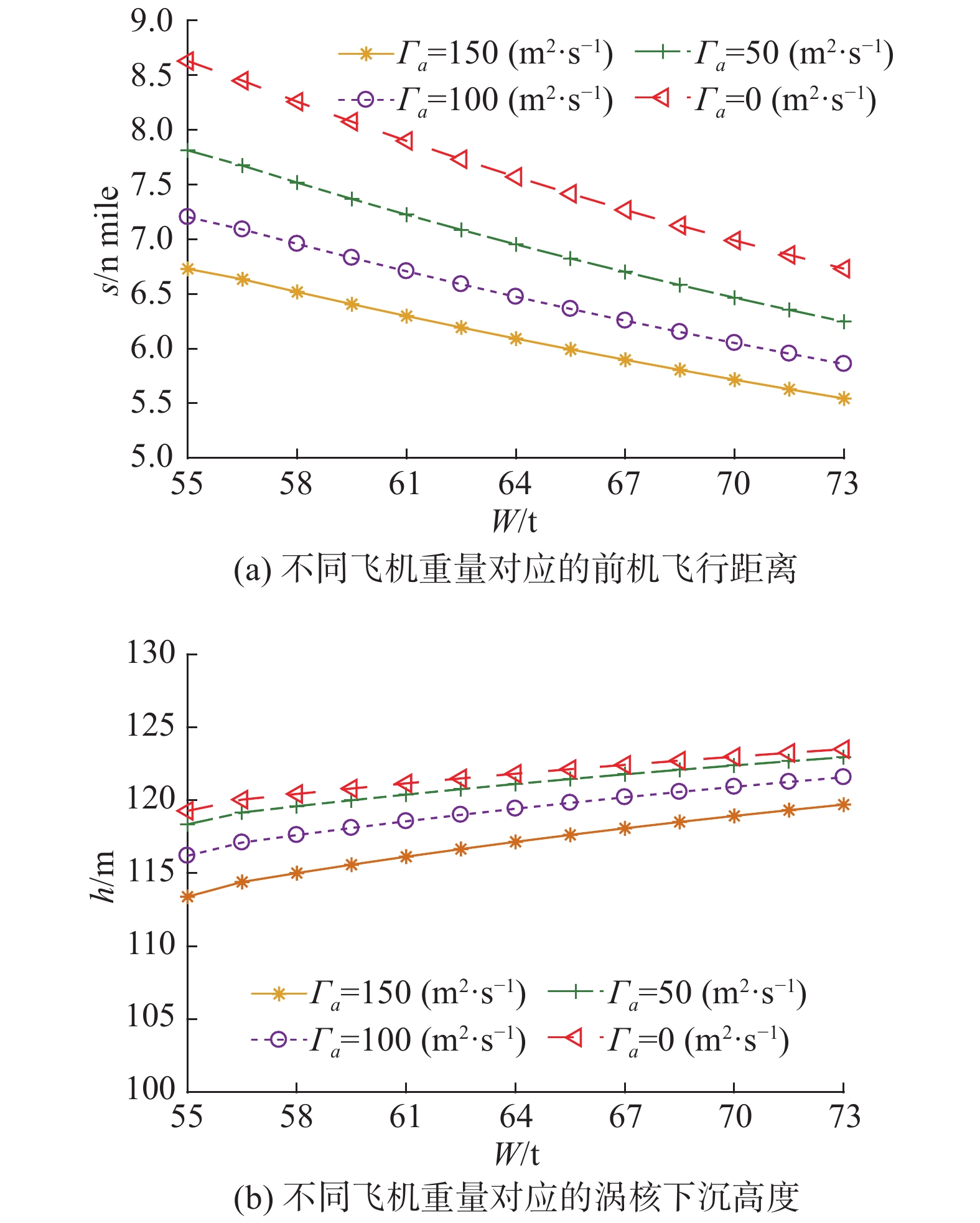
为了分析飞机重量对尾涡危险区域的影响,按照飞机重量55~73 t,涡流耗散率10−5 m2·s−3、浮力频率0.02 s−1、马赫数0.78的条件,由尾涡物理模型计算15000 m高空不同飞机重量对应的尾涡危险区域见图10。
从图10(a)可以看出,随飞机重量变化,尾涡危险区域在纵向范围减小。这是因为随着飞机重量增加,由公式(1)可知尾涡初始环量
|
图 10 不同飞机重量下尾涡危险区域变化趋势 Fig.10 The variation of hazard areas of wake vortices with aircraft weights |
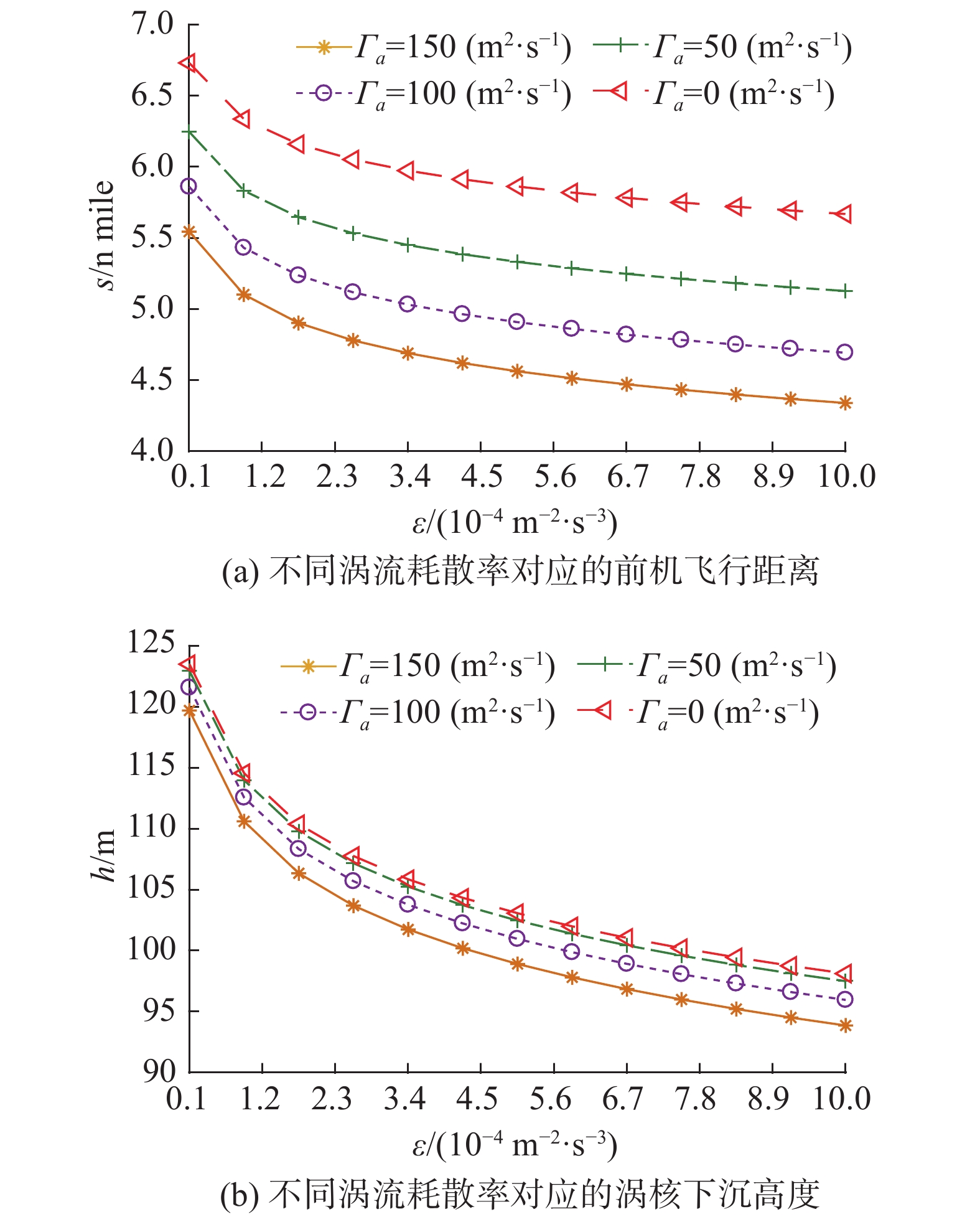
高空中大气湍流水平较低[20],为了分析大气湍流度对尾涡危险区域的影响,按照涡流耗散率1×10−5~1×10−3m2·s−3,飞机重量73 t,其余初始条件同3.1节的条件计算15000 m高空不同大气湍流度对应的尾涡危险区域见图11。
从图11可以看出,随着涡流耗散率增大,尾涡危险区域在纵向范围及垂直范围均减小。这是因为涡流耗散率大,意味着大气紊乱程度增加,从而加快尾涡消散速率。涡流耗散率超过1.8×10−4 m2·s−3后,尾涡危险区域随涡流耗散率变化缓慢。
|
图 11 不同大气湍流度下尾涡危险区域变化趋势 Fig.11 The hazard areas of wake vortices under the condition of different atmospheric turbulence intensities |
大气层结稳定性反映大气的稳定程度,为了分析大气层结稳定性对尾涡危险区域的影响,按照浮力频率0.02 ~0.06 s−1,飞机重量73 t,其余初始条件同3.1节的条件计算15000 m高空不同大气层结稳定性对应的尾涡危险区域见图12。
从图12可以看出,随着浮力频率增大,尾涡危险区域在纵向范围及垂直范围均减小。这是因为浮力频率越大,意味着大气分层越稳定,作用在尾涡上的浮力越大,从而加快尾涡消散速率。因此大气层结稳定性对尾涡危险区域的影响机理与大气湍流度的影响机理一致。
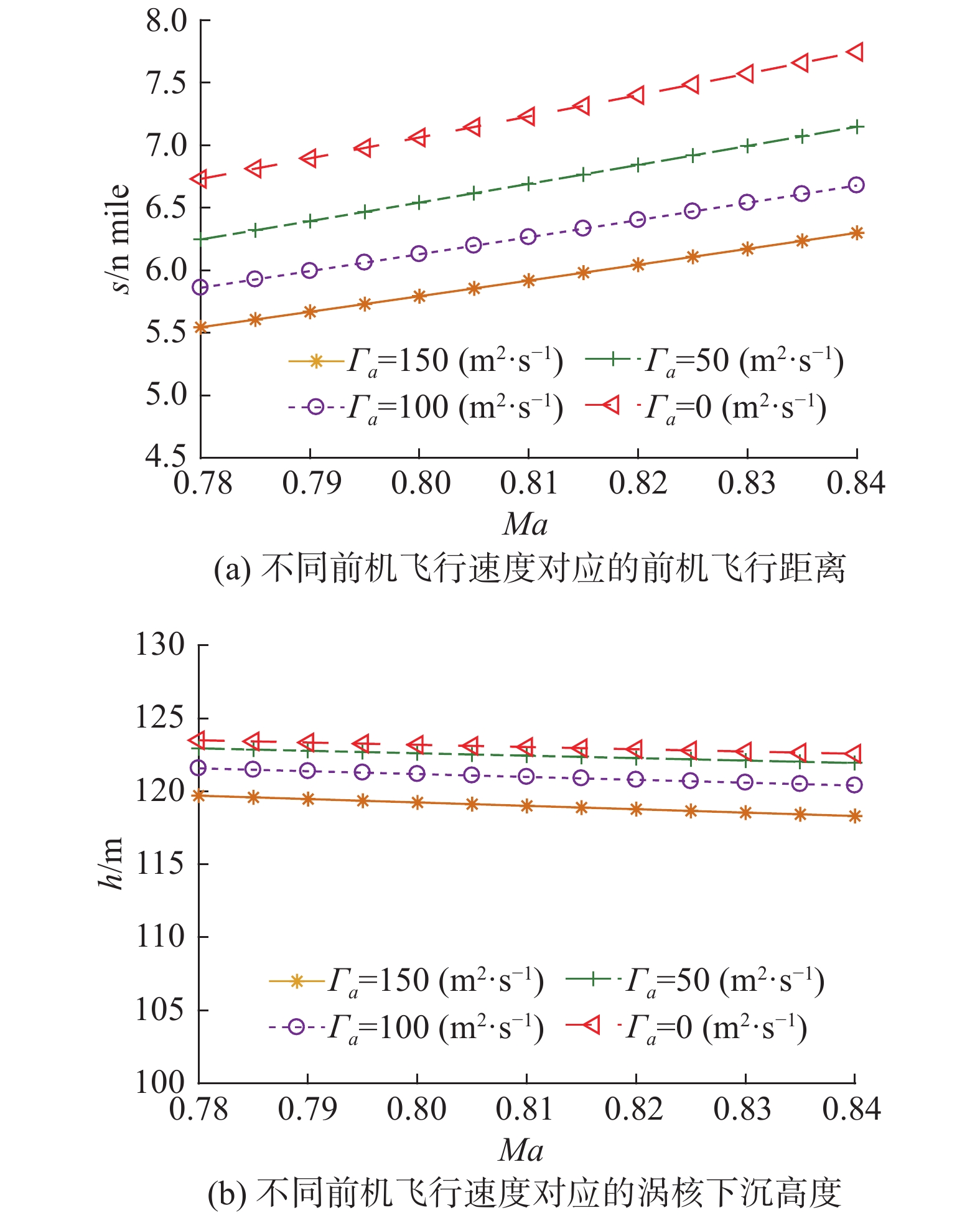
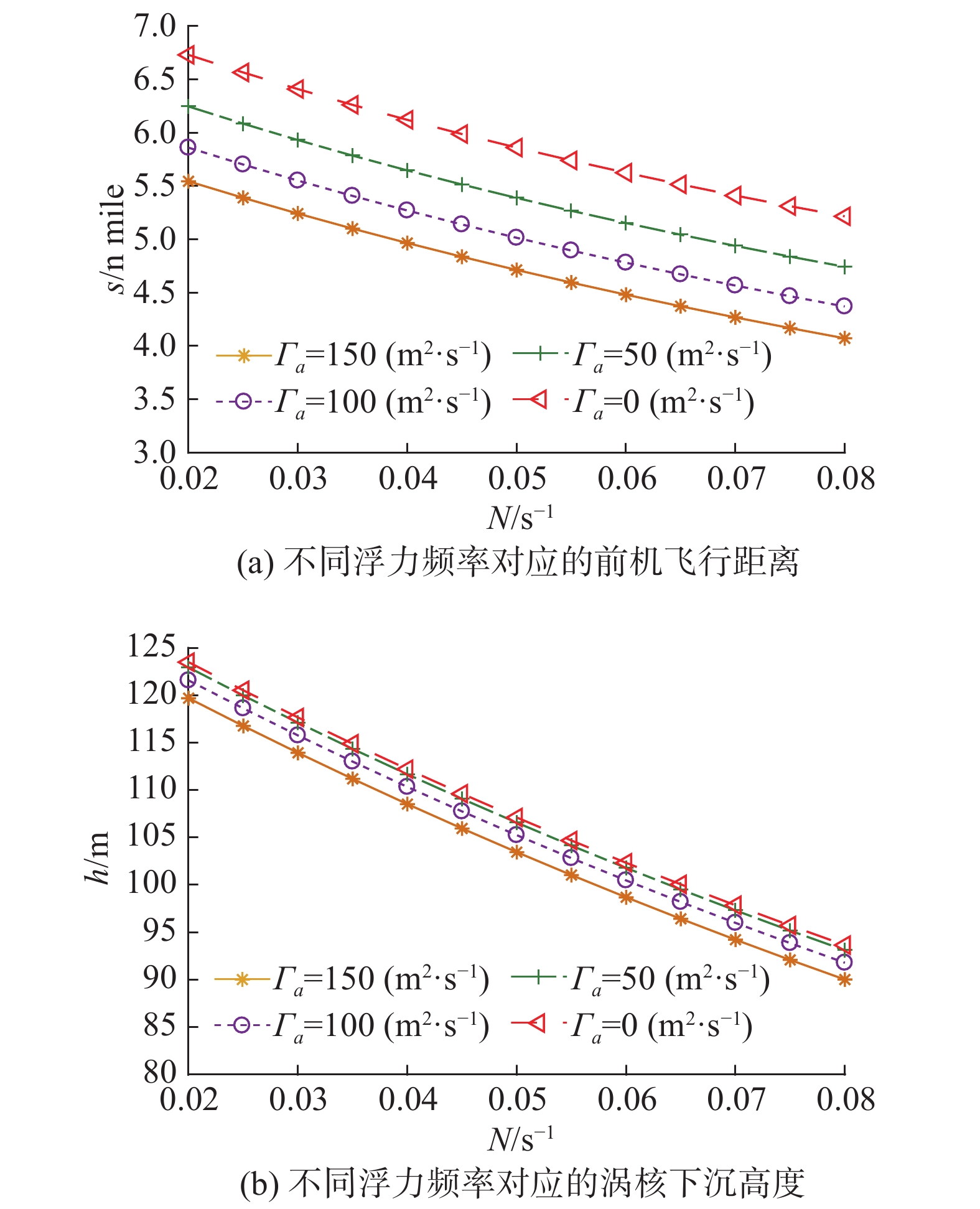
3.4 前机飞行速度对尾涡危险区域的影响为了分析前机飞行速度对尾涡危险区域的影响,按照前机飞行马赫数0.78~0.84,飞机重量73 t,其余初始条件同3.1节的条件计算15000 m高空不同前机飞行速度对应的尾涡危险区域见图13。
|
图 13 不同前机飞行速度下尾涡危险区域变化趋势 Fig.13 The hazard areas of wake vortices for airplanes with different flight speeds |
从图13(a)可以看出,随着马赫数的增加,尾涡危险区域在纵向范围增加,这是因为随着马赫数增大,前机飞行真空速
|
图 12 不同大气层结稳定性下尾涡危险区域变化趋势 Fig.12 The hazard areas of wake vortices under the condition of different atmospheric stratification stabilities |
从图13(b)可以看出,垂直范围上,马赫数从0.78增加到0.84的过程中,不同
本文在尾涡流场快速仿真计算模型基础上给出了不同飞行高度处尾涡危险区域计算方法,研究了高空巡航阶段飞机尾涡的形成及消散特性,计算并分析了高空尾涡危险区域及其影响因素,得到如下结论:
1)在高空中,大气密度较低,随着飞行高度的增加,尾涡初始环量增加显著,尾涡消散速率加快。
2)与中低空相比,高空巡航阶段尾涡环量消散到一定值时所对应的前机飞行距离在减小,尾涡涡核下沉高度在增加,其中涡核下沉高度的增量约为20.0~29.6 m。
3)飞机重量、大气湍流度、大气层结稳定性及前机飞行速度均会影响高空尾涡危险区域。飞机重量和前机飞行速度通过改变尾涡初始强度进而影响尾涡消散过程;大气湍流度及大气层结稳定性通过改变大气条件影响尾涡消散过程,其中涡流耗散率及浮力频率的增加均会使高空尾涡危险区域减小。
4)本文所使用的尾涡流场快速仿真计算模型为数据驱动的半经验模型。下一步需通过探测系统或流场数值模拟方法获得大量的尾涡消散与运动数据,进一步研究高空飞行中的尾涡消散特性。
| [1] |
FAN Z, SCHROEDER N, SWOL D, et al. Potential wake turbulence encounters analysis in current and NextGen flight operations[C]//Proc of the 2013 Integrated Communications, Navigation and Surveillance Conference (ICNS), Herndon, VA, USA. IEEE, 2013: 1-7. doi: 10.1109/ICNSurv.2013.6548576.
|
| [2] |
MELGOSA F M, PRATS M X, RUIZ N S, et al. A novel framework to assess the wake vortex hazards risk supported by aircraft in en-route operations[C]//Proc of the 7th SESAR Innovation Days. Belgrade: SESAR Innovation Days, 2017: 1-6.
|
| [3] |
HALLOCK J N, HOLZÄPFEL F. A review of recent wake vortex research for increasing airport capacity[J]. Progress in Aerospace Sciences, 2018, 98: 27-36. DOI:10.1016/j.paerosci.2018.03.003 |
| [4] |
WU S H, ZHAI X C, LIU B Y. Aircraft wake vortex and turbulence measurement under near-ground effect using coherent Doppler lidar[J]. Optics Express, 2019, 27(2): 1142-1163. DOI:10.1364/OE.27.001142 |
| [5] |
HOLZÄPFEL F. Probabilistic two-phase wake vortex decay and transport model[J]. Journal of Aircraft, 2003, 40(2): 323-331. DOI:10.2514/2.3096 |
| [6] |
SARPKAYA T. Decay of wake vortices of large aircraft[J]. AIAA Journal, 1998, 36: 1671-1679. DOI:10.2514/3.14021 |
| [7] |
SARPKAYA T, ROBINS R E, DELISI D P. Wake-vortex eddy-dissipation model predictions compared with observations[J]. Journal of Aircraft, 2001, 38(4): 687-692. DOI:10.2514/2.2820 |
| [8] |
PROCTOR F, HAMILTON D, SWITZER G. TASS driven algorithms for wake prediction[C]//Proc of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2006. doi: 10.2514/6.2006-1073.
|
| [9] |
PROCTOR F, HAMILTON D. Evaluation of fast-time wake vortex prediction models[C]//Proc of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, Florida. Reston, Virginia: AIAA, 2009. doi: 10.2514/6.2009-344
|
| [10] |
PÉREZ B M, MARCOS M, PASTOR L E. Effects of en-route wake vortex on RPAS operations[C]//6th SESAR Innovation Days-Book of Abstracts. Netherlands: SESAR Innovation Days, 2016: 1-7.
|
| [11] |
HOOGSTRATEN M, VISSER H G, HART D, et al. Improved understanding of en route wake-vortex encounters[J]. Journal of Aircraft, 2014, 52(3): 981-989. DOI:10.2514/1.C032858 |
| [12] |
NELSON R. Trailing vortex wake encounters at altitude - a potential flight safety issue?[C]//Proc of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Keystone, Colorado. Reston, Virigina: AIAA, 2006: 62-68. doi: 10.2514/6.2006-6268
|
| [13] |
魏志强, 屈秋林, 刘薇, 等. 飞机尾涡流场参数的仿真计算方法研究综述[J]. 空气动力学学报, 2019, 37(1): 33-42. WEI Z Q, QU Q L, LIU W, et al. Review on the artificial calculating methods for aircraft wake vortex flow field parameters[J]. Acta Aerodynamica Sinica, 2019, 37(1): 33-42. DOI:10.7638/kqdlxxb-2017.0160 (in Chinese) |
| [14] |
魏志强, 李志远, 刘薇. 侧风影响下的飞机尾流强度消散与涡核运动[J]. 空军工程大学学报(自然科学版), 2017, 18(6): 27-33. WEI Z Q, LI Z Y, LIU W. Research on aircraft wake vortex strength dissipation and vortex motion under crosswind impact[J]. Journal of Air Force Engineering University (Natural Science Edition), 2017, 18(6): 27-33. DOI:10.3969/j.issn.1009-3516.2017.06.005 (in Chinese) |
| [15] |
谷润平, 赵丽雅, 魏志强. 飞机尾涡流场特征参数估算方法研究[J]. 航空计算技术, 2017, 47(6): 14-17, 23. GU R P, ZHAO L Y, WEI Z Q. Study on estimation method of characteristic parameters of aircraft wake vortex[J]. Aeronautical Computing Technique, 2017, 47(6): 14-17, 23. DOI:10.3969/j.issn.1671-654X.2017.06.004 (in Chinese) |
| [16] |
艾国远, 叶建. 低雷诺数下翼型不同分离流态的大涡模拟[J]. 空气动力学学报, 2017, 35(2): 299-304. AI G Y, YE J. Large-eddy simulation of low Reynolds number airfoil with different separating flow regime[J]. Acta Aerodynamica Sinica, 2017, 35(2): 299-304. DOI:10.7638/kqdlxxb-2016.0159 (in Chinese) |
| [17] |
WALTON M, WARBURTON J. Compression of RVSM flight levels ICAO separation and airspace safety panel[R]. Washington, DC: 31st Meeting of the Working Group of the Whole, 2018.
|
| [18] |
HOLZÄPFEL F, ROBINS R E. Probabilistic two-phase aircraft wake vortex model: application and assessment[J]. Journal of Aircraft, 2004, 41(5): 1117-1126. DOI:10.2514/1.2280 |
| [19] |
HOLZÄPFEL F. Probabilistic two-phase aircraft wake-vortex model: further development and assessment[J]. Journal of Aircraft, 2006, 43(3): 700-708. DOI:10.2514/1.16798 |
| [20] |
ZARE-NOGHABI A, SHORTLE J F. Rare event simulation for potential wake encounters[C]//Proc of the 2017 Winter Simulation Conference (WSC), Las Vegas, NV, USA. IEEE, 2017: 2554-2565. doi: 10.1109/WSC.2017.8247983
|
 2021, Vol. 39
2021, Vol. 39


