直升机由于其独特的飞行能力受到各航空大国的普遍重视。旋翼系统是直升机的关键部件,是直升机主要的升力面、推力面和操纵面。旋翼桨叶是由翼型构成的,翼型和桨叶气动外形对旋翼性能有重要影响,高性能旋翼翼型可以提高旋翼悬停效率3%-5%,对直升机的前飞速度、等效升阻比和机动飞行能力、噪声水平等都有很大影响。高性能旋翼翼型设计技术也一直是直升机设计的核心技术,是衡量直升机技术水平的重要标志。
在不同的飞行状态和不同的桨叶半径位置上,旋翼桨叶翼型的运行环境是迥然不同的[1]。翼型的设计需要在较宽的马赫数范围内,有较高的静态和动态最大升力系数,以适应机动过载状态;在较高的马赫数及小迎角时,有较大的阻力发散马赫数,以推迟前行桨叶激波失速;在中等马赫数及中等迎角时,有较高的升阻比,以提高旋翼的悬停效率;在较低的马赫数及大迎角时,有较好的失速特性,以延缓后行桨叶的气流分离;在整个飞行包线内,有较小的俯仰力矩系数,以降低桨叶的操纵载荷,旋翼翼型设计需要综合考虑不同的飞行环境,具有明显的多点、多目标、强约束的特点。
旋翼翼型的设计方法主要分为反设计方法和数值优化设计方法两大类。反设计方法主要是根据给定的速度分布或压力分布设计翼型,缺点是理想的翼型速度分布、压力分布特性难以预先给定。随着CFD技术和计算机技术的不断进步,数值优化设计类方法逐渐成为翼型设计的主流方法,该类方法可以直接实现多目标气动性能的优化,降低了对人经验的依赖,符合旋翼翼型设计多点/多目标的应用环境。数值类方法又包含控制论方法[2-3]和进化算法[4-5]两大类,分别适用于不同的优化环境。
从20世纪70年代开始,直升机技术发达国家都开始致力于新型旋翼高性能翼型的研究,发展了一系列旋翼专用翼型,如美国Boeing-Vertol公司的VR翼型族、Sikorsky公司的SC翼型族,法国宇航院(ONERA)的OA翼型族,俄罗斯的TsAGI翼型族等[6-7]。这些翼型的成功应用,对改善直升机性能起到了重要作用。目前这些翼型族仍在继续发展中,但鲜有相关文献报道。国内也从20世纪90年代开始了对自主旋翼翼型的相关设计研究工作。尚克明等[8]基于Euler方程采用反设计的方法进行了旋翼翼型的设计研究。刘刚等[9]基于进化算法和Kriging模型开展了旋翼翼型多目标优化设计研究,优化结果经过风洞试验验证,满足了设计要求。杨旭东等[10]基于梯度信息改进的响应面方法建立了旋翼翼型多点多约束气动优化策略。韩忠华等[11]发展了基于Kriging模型与遗传算法的旋翼翼型多目标多约束气动优化设计方法,应用于OA209的设计取得了较好的效果。招启军等[12]开展了考虑旋翼翼型定常-非定常影响的综合优化设计研究,优化结果在设计状态下明显改善了翼型的动态失速特性。
近年来直升机工业得到了长足的发展,先进直升机对高性能旋翼翼型的需求愈发迫切。目前国内旋翼翼型的研究正处于探索性研究向旋翼翼型系列研制的起步发展阶段,自主翼型系列的研制还缺乏通用、高效、鲁棒的设计工具,还没有自主翼型应用于型号研究的先例。高性能旋翼翼型的设计,需要有先进的设计和优化框架作为支撑,以框架体系为基础消化吸纳各类先进技术,促进优化系统的不断迭代更新完善,才能更有效地促进旋翼翼型工程实际设计能力的不断提升。
本文通过综合采用基于进化算法的多目标优化设计方法、基于主成分分析的多目标降维技术、翼型参数化技术以及高精度CFD性能分析工具,自主开发了旋翼翼型气动设计与评估软件系统——HRADesign。本文主要介绍了系统的架构设计和工作流程,详细介绍了系统的多目标优化方法模块、多目标降维技术、几何管理模块以及CFD性能分析模块等功能模块。利用该系统对ADODG标准翼型优化算例、旋翼翼型的常规多目标优化设计以及考虑多目标降维的旋翼翼型优化设计进行了研究,验证了优化设计软件系统的有效性。最后部分对本文进行了总结。
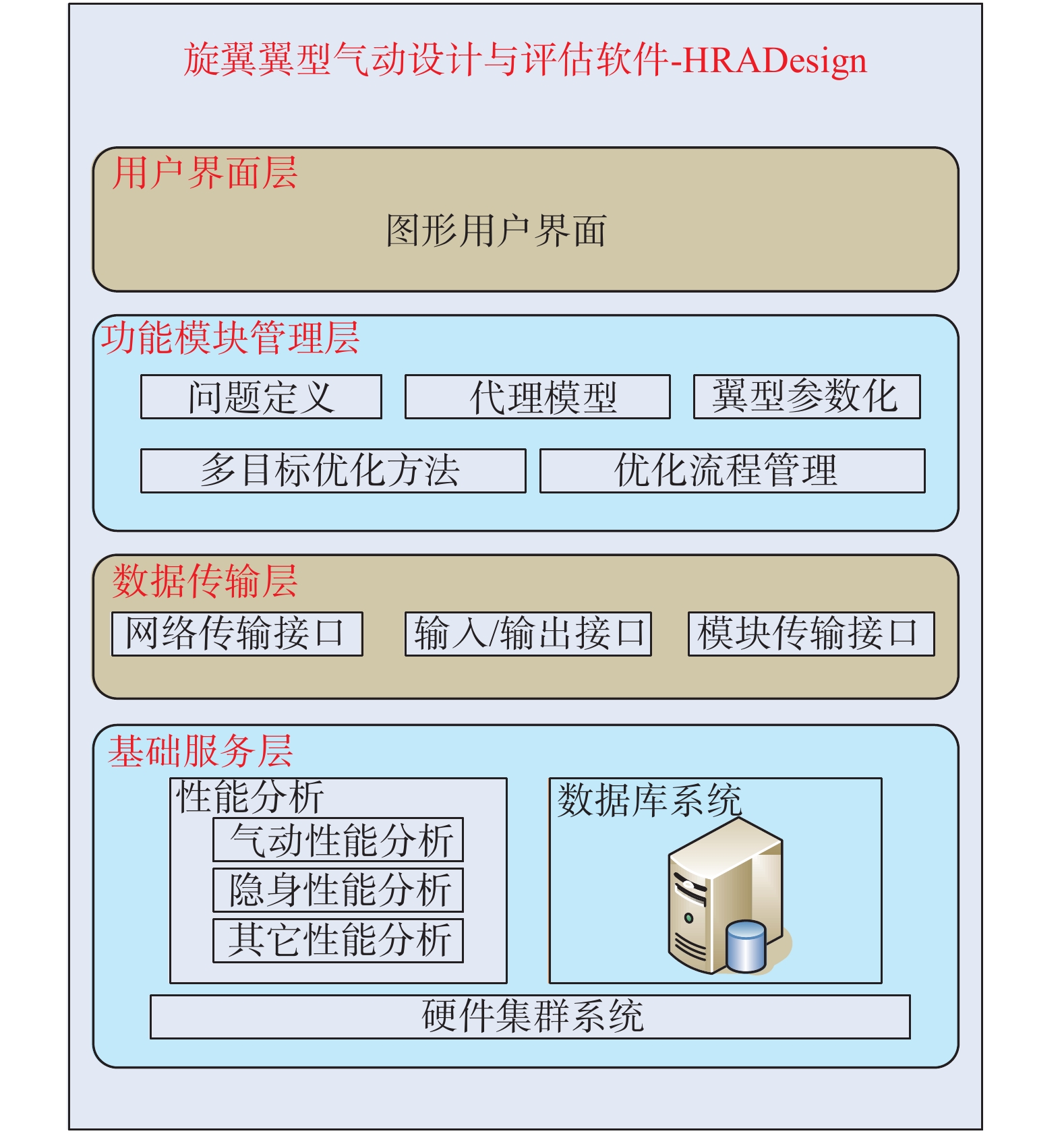
1 软件架构设计HRADesign作为一个综合的旋翼翼型设计和评估的软件系统,系统开发基于Eclipse集成环境,选用Python和C++语言作为开发工具,XML文件用于交换信息,采用wxWidgets软件包提供可视化支持。用户可以在PC机上完成优化问题的描述和参数的输入后,通过集群系统完成优化设计的流程。系统根据高内聚、低耦合的原则分成层次结构,包含用户界面层、功能模块管理层、数据传输层、以及基础服务层。图1给出了软件的体系结构示意图,各层的功能定位如下:
|
图 1 软件体系结构 Fig.1 A diagram of the software architecture |
1)用户界面层。界面层给用户提供了友好的人机交互接口来操作整个软件,借助该层功能,用户可实施优化设计问题建立、优化进度监控、优化结果查验等操作。
2)功能模块管理层。优化设计层集成了优化方法、代理模型、翼型参数化、优化目标处理、PCA降维技术、专家系统等模块,借助CFD或试验数据库的数据支撑,完成各种气动外形的优化设计功能。
3)数据传输层。该层主要负责为自适应优化设计层生产、收集和存储数据,提供目录管理、文件传输等基础功能。
4)基础服务层。该层提供整个软件运行所需要的基础服务,包括软件服务(CFD解算器、网格程序、数据库系统)和硬件服务(本地计算资源和大规模集群资源)。
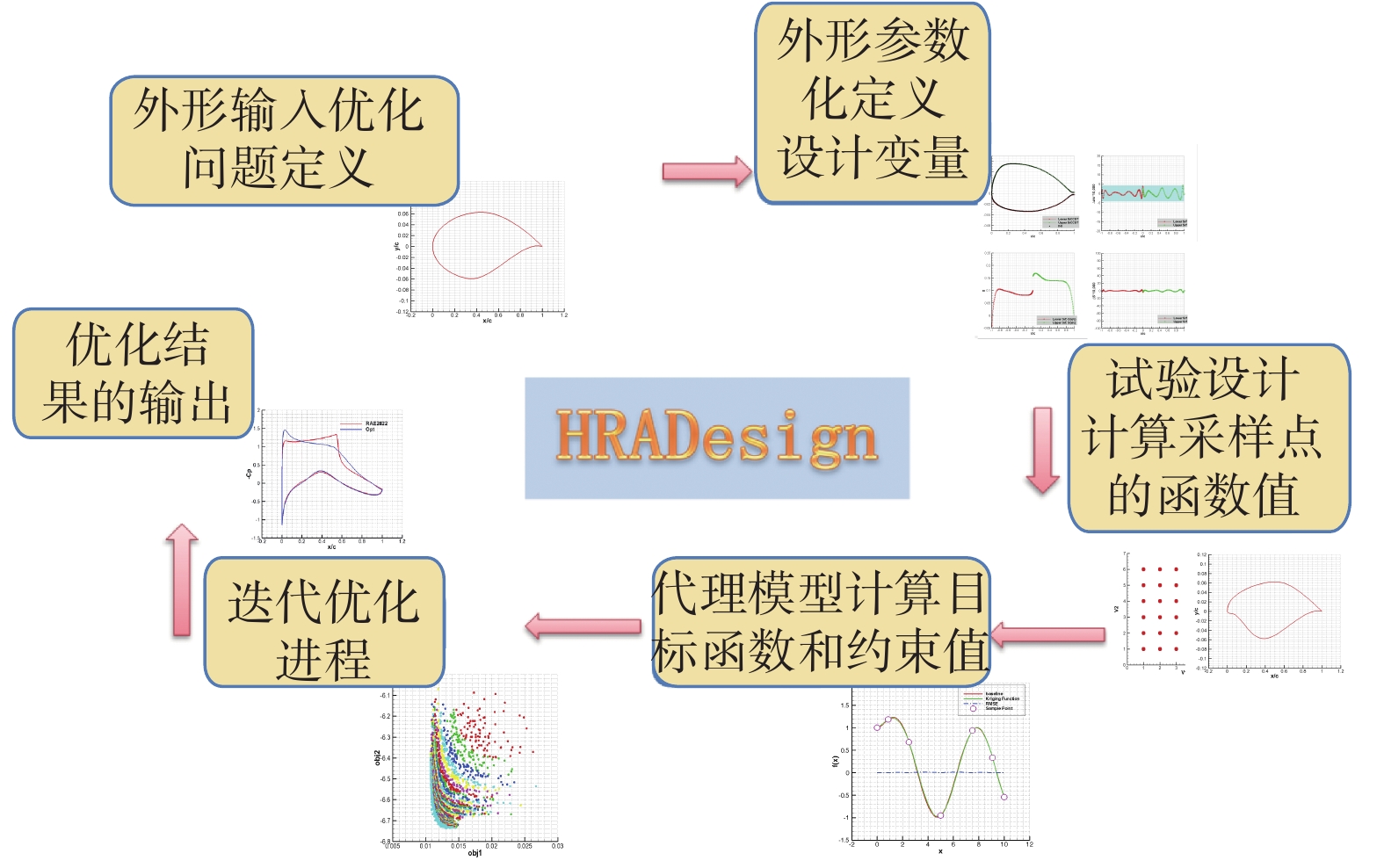
图2给出了HRADesign系统进行优化设计流程的示意图。初始翼型进入系统,进行参数化并提取设计变量;选择试验设计方法,对每个样本点进行网格生成和气动特性分析;用气动分析得到的数据来构建代理模型,利用该模型分析优化问题的优化目标和约束;最后进入优化迭代流程,直至获得最终的优化翼型外形。
|
图 2 系统优化设计流程示意图 Fig.2 A diagram of the optimization process |
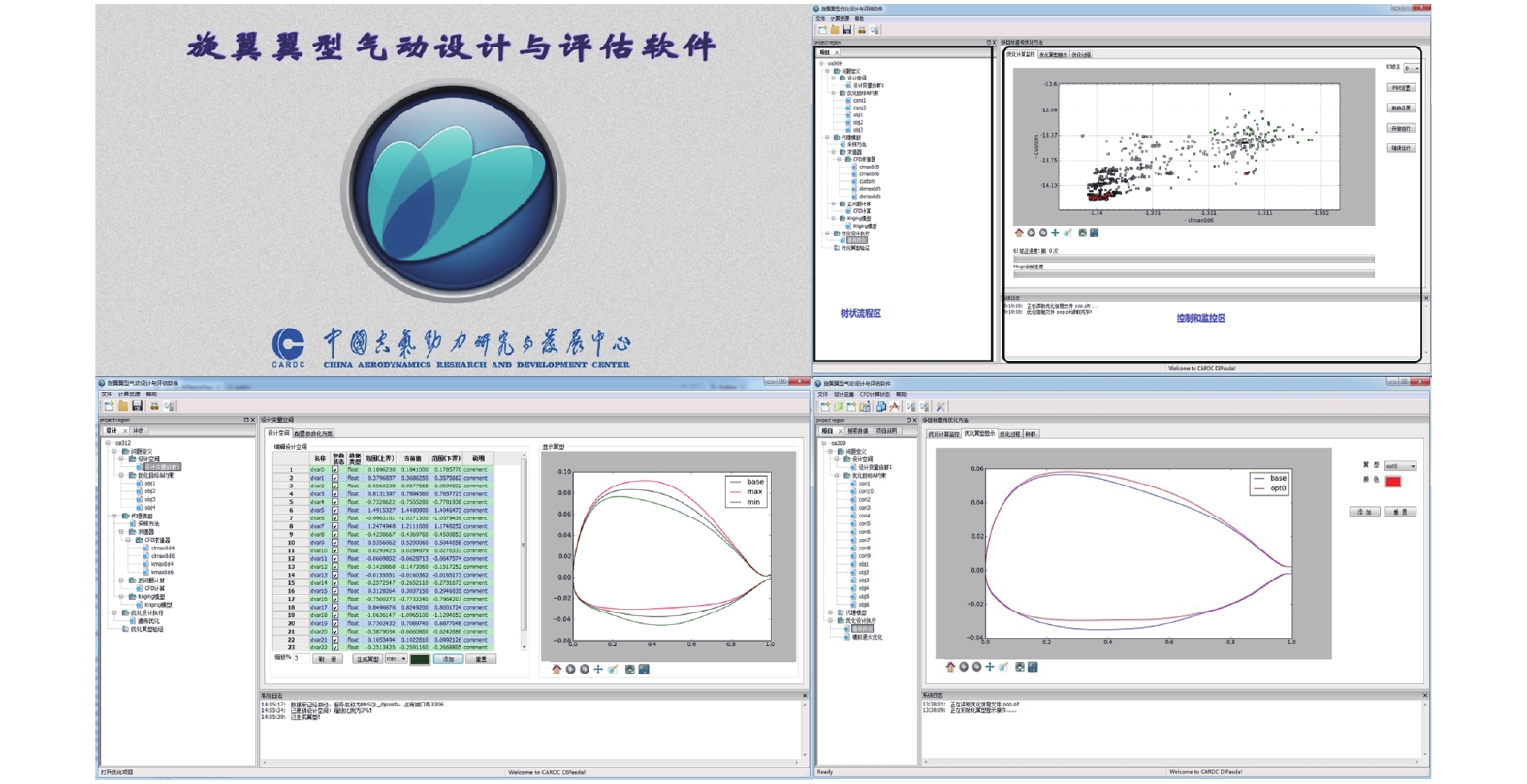
HRADesign系统由多目标优化方法模块、翼型参数化管理模块、代理模型模块、CFD性能分析模块等主要的功能模块构成,此外还包含问题定义,显示监控等辅助模块。系统提供了基于Windows的图形操作界面,用户在前台通过操作界面完成优化问题的定义以及各项参数的设置,系统底层封装了与后台集群系统的连接以及信息的交换,可以实现本地计算与集群系统计算的无缝切换,用户可以通过输入/输出系统监视优化进程,方便处理各类操作问题。图3给出了系统的主要应用界面示意图。
|
图 3 软件应用界面示意图 Fig.3 A diagram of the graphical user interface |
多目标优化方法模块主要完成各种全局和局部数值优化方法的封装,包含有进化算法和伴随方法等,用户通过应用界面可以选择不同的优化方法完成翼型的鲁棒设计、PCA降维分析等多目标设计功能。
HRADesign系统是以优化算法为核心,驱动整个优化流程的发展来进行翼型的优化设计。系统采用的多目标优化方法大多是以进化算法为基础,结合多目标Pareto解的概念以及约束处理机制发展起来的,进化类算法属于全局类优化方法,优化过程不依赖目标函数与设计变量的梯度信息,适合处理旋翼翼型复杂流动中的各类非线性问题。进化算法通过模拟生物种群的进化过程,利用选择、交叉、变异等进化算子来找到多目标问题的Pareto解,解决了传统优化设计中多目标加权的权重系数难以给定的难题,得到广泛应用。图4给出了利用该方法进行优化设计的流程图。

|
图 4 进化算法流程图 Fig.4 The flow chart of the optimization process based on the evolutionary algorithm |
主成分分析PCA的方法[13]是Deb在2005年提出的用于多目标降维的算法。算法首先对数据集进行标准化处理,求解目标函数的相关矩阵,得到相关矩阵的特征值及其特征向量,将特征值按从大到小的顺序排序并求出其贡献率,当贡献率的累积大于初始给定的参数阈值时停止累积。阈值的选取在很大程度上影响实验结果,如果阈值取太大,可能所有目标都会被选取,如果太小又容易丢失非冗余目标的信息。文献一般建议阈值取值为95%。算法简介如下[14]:
1) 设置阈值,非冗余目标集合Ⅰ为空。
2) 计算数据集。随机初始化种群,对种群中的个体计算目标集中的所有目标,得到个体目标的数据集合P。
3) 对数据集P进行PCA处理,选取非冗余目标Ⅰ:
(a) 对目标集进行归一化处理,计算相关矩阵,对相关矩阵计算特征值及对应的特征向量,依据特征向量来选取目标。
(b) 将特征值按照从大到小的顺序依次排序,计算每个特征值占总特征值的比率,则每个特征值对应的特征向量依次称为第一、第二、···、第n主成分。
(c) 依次分析每个主成分。如果主成分里的元素有正有负,选取最大和最小元素对应的目标加入非冗余目标集Ⅰ;如果所有元素均为正,选取最大元素值对应的目标加入非冗余目标集Ⅰ;如果所有元素均为负,将所有目标均加入到非冗余目标集Ⅰ。
(d) 如果主成分对应的特征值小于0.1,选取最大元素对应的目标加入到非冗余目标集Ⅰ。
(e) 考察特征值比率,如果大于阈值,停止分析过程,输出非冗余目标解集Ⅰ;否则转到(c)继续非冗余目标的选取。
在优化设计中通过PCA主成分分析得到各目标之间的关联关系后,提取决定问题本质的主要目标,将冗余目标剔除、或者转化为约束条件,将高维多目标优化转化为低维优化问题。可以解决多目标优化收敛慢甚至不收敛的问题,提高优化结果的可靠性。图5给出了基于PCA分析的优化设计流程图。

|
图 5 基于PCA分析的多目标优化设计流程图 Fig.5 The flow chart of PCA |
DTLZ测试函数[15]是由Deb提出的一组测试多目标优化算法性能的测试函数,共有9组函数,DTLZ测试函数有已知的Pareto最优解,其中DTLZ5(I,M)(M表示目标个数,I表示非冗余目标个数),用于测试算法处理包含冗余目标的能力。选取DTLZ5(2,10)函数用于测试,该函数有10个目标,其中2个为非冗余目标,函数公式见式(1):
| $ \begin{split}& {\rm{Min}} \;f\left( x \right)\; \\& {f_1}\left( x \right) = \left( {1 + g\left( {{x_M}} \right)} \right)\cos \left( {{\theta _1}} \right)\cos \left( {{\theta _2}} \right) \cdots \cos \left( {{\theta _{M - 2}}} \right)\cos \left( {{\theta _{M - 1}}} \right) \\& {f_2}\left( x \right) = \left( {1 + g\left( {{x_M}} \right)} \right)\cos \left( {{\theta _1}} \right)\cos \left( {{\theta _2}} \right) \cdots \cos \left( {{\theta _{M - 2}}} \right)\sin \left( {{\theta _{M - 1}}} \right) \\& {f_3}\left( x \right) = \left( {1 + g\left( {{x_M}} \right)} \right)\cos \left( {{\theta _1}} \right)\cos \left( {{\theta _2}} \right) \cdots \sin \left( {{\theta _{M - 2}}} \right) \\& \vdots \\& {f_{M - 1}}\left( x \right) = \left( {1 + g\left( {{x_M}} \right)} \right)\cos \left( {{\theta _1}} \right)\sin \left( {{\theta _2}} \right) \\& {f_M}\left( x \right) = \left( {1 + g\left( {{x_M}} \right)} \right)\sin \left( {{\theta _1}} \right) \\& {\rm{where}}\;g\left( {{x_M}} \right) = \sum\nolimits_{{x_i} \in {x_M}} {{{\left( {x - 0.5} \right)}^2}} \\& {\rm{ for}}\;i = 1, \cdots ,I - 1\;\;\;\;\;{\theta _i} = \frac{\pi }{2}{x_i} \\& {\rm{for}}\;i = I, \cdots ,M - 1\;\;\;{\theta _i} = \frac{\pi }{{4\left( {1 + g\left( {{x_M}} \right)} \right)}}\left( {1 + 2g\left( {{x_M}} \right){x_i}} \right) \\& {\rm{for}}\;i = 1, \cdots ,n\;\;\;\;\;\;\;\;\;\;\;0 \leqslant {x_i} \leqslant 1 \end{split} $ | (1) |
对该函数进行优化测试,经过PCA分析,得到目标9和目标10两个非冗余目标。首先对10个目标进行优化,得到优化结果对应的两个非冗余目标的Pareto前沿如图2(a)所示,去除冗余目标后再进行优化,得到优化结果如图2(b)所示。DTLZ5(2,10)函数的Pareto前沿收敛到圆弧曲线[16],通过图6可以看出,算法在处理冗余目标后,达到了最优Pareto前沿。

|
图 6 DTLZ5(2,10)测试函数收敛比较 Fig.6 Convergence of the test function DTLZ5(2,10) |
翼型参数化管理模块主要完成翼型的输入/输出,约束评估、翼型曲线参数化和网格自动重构、设计变量的选取和确定设计空间范围等功能。目前常用的参数化方法有解析函数线性叠加法,NURBS曲线[17]、CST[18]方法、FFD[19]方法等。本系统主要采用CST技术实现翼型的参数化表示。
CST方法是波音公司B.M.Kulfan等提出的一种通用几何参数化表示方法。可以用统一的解释函数表示钝前缘/尖后缘类翼型和双钝头翼型等新型翼型。用该方法描述翼型,容易控制前缘半径、弯度/厚度分布、后缘角以及后缘厚度等关键参数,而且设计参数数目容易控制,也具有局部修改控制的能力。
翼型上下表面均用以下公式描述:
| $ \varsigma = C_{N2}^{N1}(\psi )S(\psi ) + \psi \Delta \xi $ | (2) |
其中类型函数:
| $ C_{N2}^{N1}(\psi ) = {\psi ^{N1}}{(1 - \psi )^{N2}} $ | (3) |
形状函数:
| $ \begin{split} S(\psi ) = & \sum\limits_{i = 1}^n {{A_i}{S_i}(\psi )} \\ {S_i}(\psi ) = & {K_i}{\psi ^i}{(1 - \psi )^{n - i}}\; \\ {K_i} \equiv & \left( {\begin{array}{*{20}{c}} n \\ i \end{array}} \right) = \frac{{n!}}{{i!( {n - i )!} }} \\ \end{split} $ | (4) |
翼型表面形状改变后采用基于双曲方程[20]的网格生成方法完成计算网格重构,可以直接输出给CFD解算器使用。
2.4 Kriging代理模型优化设计过程中,采用高精度CFD分析工具进行翼型气动性能计算、优化目标函数和约束函数的评估,会带来计算资源成本过高、计算周期过长的问题。为了提高设计的效率,可以采用代理模型的方法构造目标函数和约束函数的近似函数,优化算法作用于近似目标函数和近似约束函数以寻找优化问题的最优解,通过近似函数的不断改进和优化算法的不断迭代,直至最终满足收敛条件。
HRADesign系统中,代理模型技术主要包括试验设计方法和代理模型方法两部分。试验设计方法决定了样本点的个数和样本点的空间分布情况,系统采用拉丁超立方采样[21]和均匀采样[22]的方法选取样本点,以保证样本点在设计空间的均匀分布。Kriging模型[23-24]则用来作为目标函数和约束函数的近似模型。
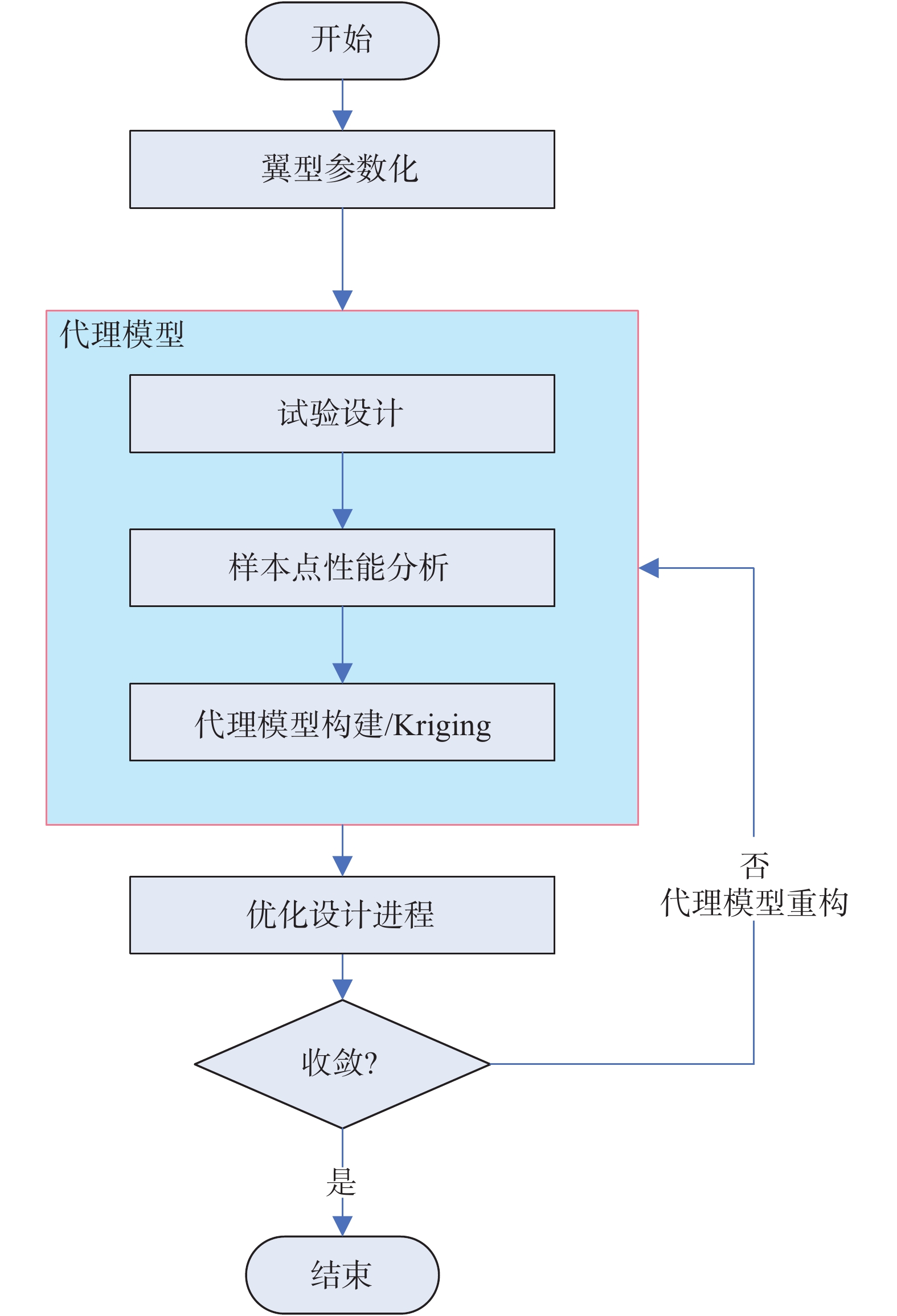
Kriging代理模型起源于地理空间统计学,是一种估计方差最小的无偏估计插值模型,具有全局近似和局部随机误差估计相结合的特点。通过Kriging模型可以得到未知点的函数值和不确定性,因而在优化过程中,Kriging模型需要根据优化进程自适应地更新,增加样本点在非线性区域的分布,提高模型的预测精度,系统采用EI方法或者最小值加点准则等方法,提高模型的精度和自适应能力。图7给出了基于代理模型的优化流程示意图。
|
图 7 基于代理模型的优化流程示意图 Fig.7 The flow chart of a surrogate-based multi-objective optimization |
第一步:试验设计。采用均匀设计等试验设计方法在设计空间中选取样本点。
第二步:样本点性能评估。对样本点分别生成计算网格,采用CFD工具进行气动性能评估。
第三步:构建Kriging模型。利用样本点的性能计算结果构建初始Kriging代理模型。
第四步:利用构建的Kriging代理模型,结合基于进化算法的多目标优化方法进行设计优化流程。
第五步:Kriging模型的重构。优化过程中评估种群个体的EI值,根据种群个体的EI值选定附加的样本点,对样本点进行计算网格的生成和CFD性能评估,在N = N + 1个样本点的基础上进行Kriging模型的重构。
第六步:返回第四步继续迭代循环。
第七步:直到系统收敛或达到设定的优化步数,返回优化结果。整个优化流程结束。
2.5 气动性能分析旋翼翼型CFD性能计算的精度和效率是进行气动设计优化的关键,对优化设计的结果有直接影响。
HRADesign系统中采用的CFD分析工具是自主开发的二维RANS解算器MBNS2D。MBNS2D采用格心型有限体积方法求解雷诺平均Navier-Stokes方程,空间离散采用Roe格式,湍流模型包含SA一方程模型和SST两方程模型,通过多重网格技术进行流场加速收敛,提高计算效率。
在旋翼翼型的计算中,转捩对翼型前缘流动影响很大,如果不考虑转捩的影响,阻力及零升阻力的计算结果会与试验差别很大,为了增强方法的适应性,HRADesign系统中采用了
为了提高优化设计软件的可信度,AIAA气动优化设计讨论组(ADODG)给出了一套优化设计的标准算例,用于优化设计软件的验证和确认。这些算例包含了翼型和机翼在气动和几何约束条件下阻力最小化优化设计问题。本文以其中跨声速条件下RAE2822翼型阻力最小化算例来考核优化设计系统的性能。
以RAE2822翼型作为初始翼型开始优化,翼型的跨声速设计条件为:
| $\left\{ \begin{array}{l} {\rm{Min}}\;{C_D} \\ {\rm{Subject\;to:}}\;{C_L} = 0.824 \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{C_m} \geqslant - 0.092 \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{S_{{\rm{area}}}} \geqslant { {S_{{\rm{area}}}}\;_{{\rm{initial}}}} \end{array} \right.$ |
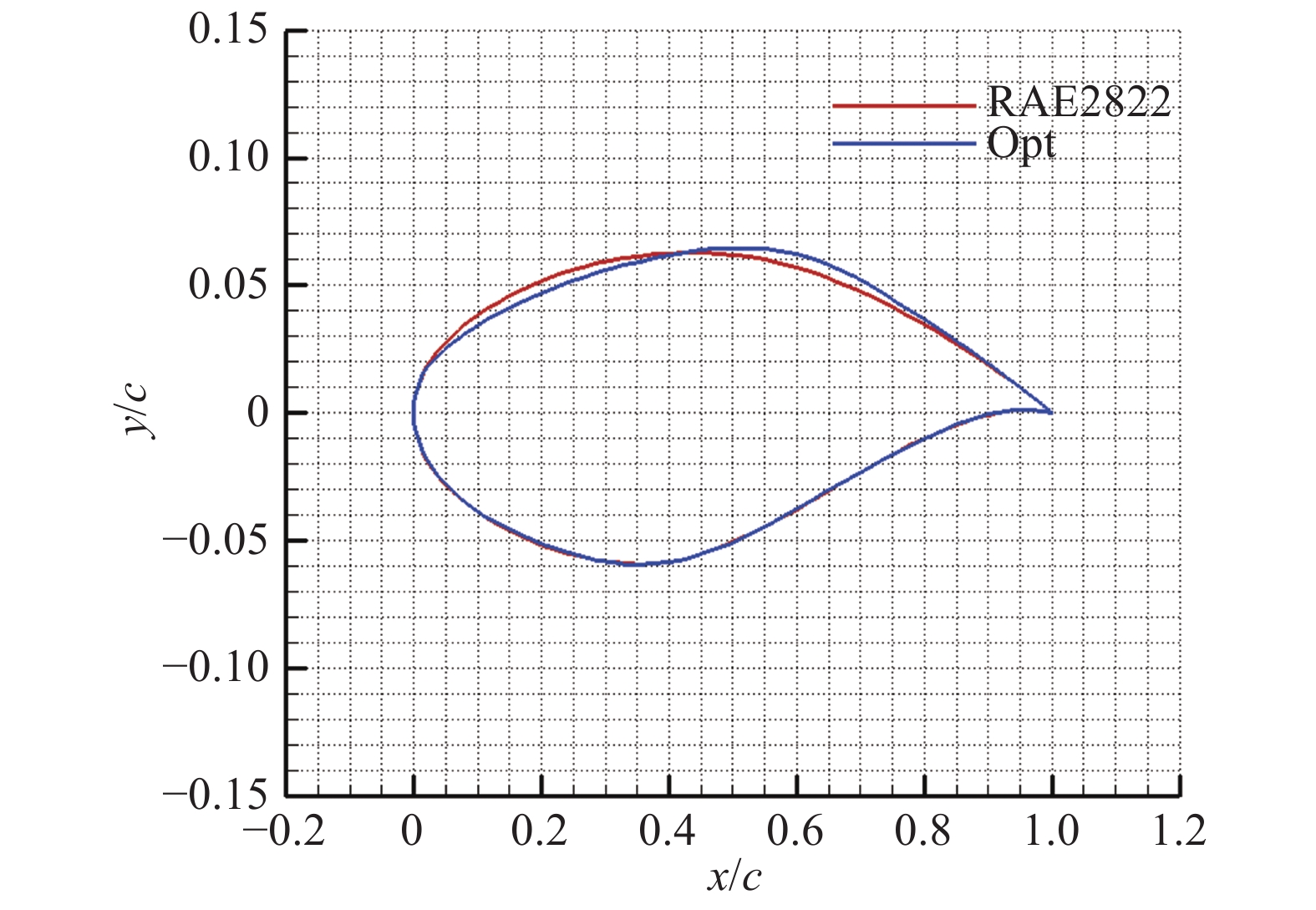
图8和图9分别给出了优化前后翼型的外形和表面压力分布的比较,图10给出了优化前后翼型压力云图的比较。可以看出,优化翼型前缘吸力峰增强,基本消除了初始翼型中段的强激波,等值线变得平顺光滑。表1给出了翼型在优化前后的气动特性比较,在保持升力和力矩的气动约束以及面积不减的几何约束条件下,优化翼型的阻力系数降低了约87 counts,优化翼型的阻力特性得到明显改善。文献[26]对该算例给出了进一步的分析。
|
图 8 优化前后翼型的形状比较 Fig.8 Configurations of the initial and optimized RAE2822 airfoils |

|
图 9 优化前后翼型表面压力分布比较 Fig.9 The comparison of airfoil pressure distributions between the initial and optimized airfoils |

|
图 10 优化前后翼型压力云图比较 Fig.10 The comparison of pressure contours between the initial and optimized airfoils |
| 表 1 优化前后翼型性能比较 Table 1 Performance of the original and optimized RAE2822 airfoils |
|
|
直升机旋翼翼型的设计,需要考虑多种飞行状态下的性能,一般要求:较高的最大升力系数;较高的阻力发散马赫数;在较大的马赫数范围内有较高的升阻比以及较小的俯仰力矩,属于典型的多目标设计优化问题。以某翼型为基本翼型,在保持厚度不减的条件下开展多点设计优化,使得前飞、机动、悬停条件下满足设计指标的要求。优化问题描述为:
| $ \left\{\begin{array}{l}(1){\text{提高前飞性能}}\\ {M}_{dd}\;\;{\rm{subject\;to}}:\left|{C}_{mdd}\right|\leqslant \left|{C}_{mdd0}\right|\\ (2){\text{提高机动性能}}\\ Ma=0.4,\;{C}_{L\mathrm{max}}\geqslant {C}_{L\mathrm{max}0},{K}_{\mathrm{max}}\geqslant {K}_{\mathrm{max}0}\;\\ Ma=0.6,\;{C}_{L\mathrm{max}}\geqslant {C}_{l\mathrm{max}0},{K}_{\mathrm{max}}\geqslant {K}_{\mathrm{max}0}\;\\ (3){\text{提高悬停性能}}\\ {\rm{Min}}\;{C}_{D},{\rm{when}}\; Ma=0.6,{C}_{L}=0.{6},\;\\ \;\;\;\;\;\;\;\;\;{\rm{subject\;to}}:{C}_{D}<{C}_{D0}\\ (4){\text{保持厚度不减}}\\ {\rm{subject\;to}}:{t}_{\mathrm{max}}\geqslant {t}_{\mathrm{max}0}\end{array}\right.$ |
其中
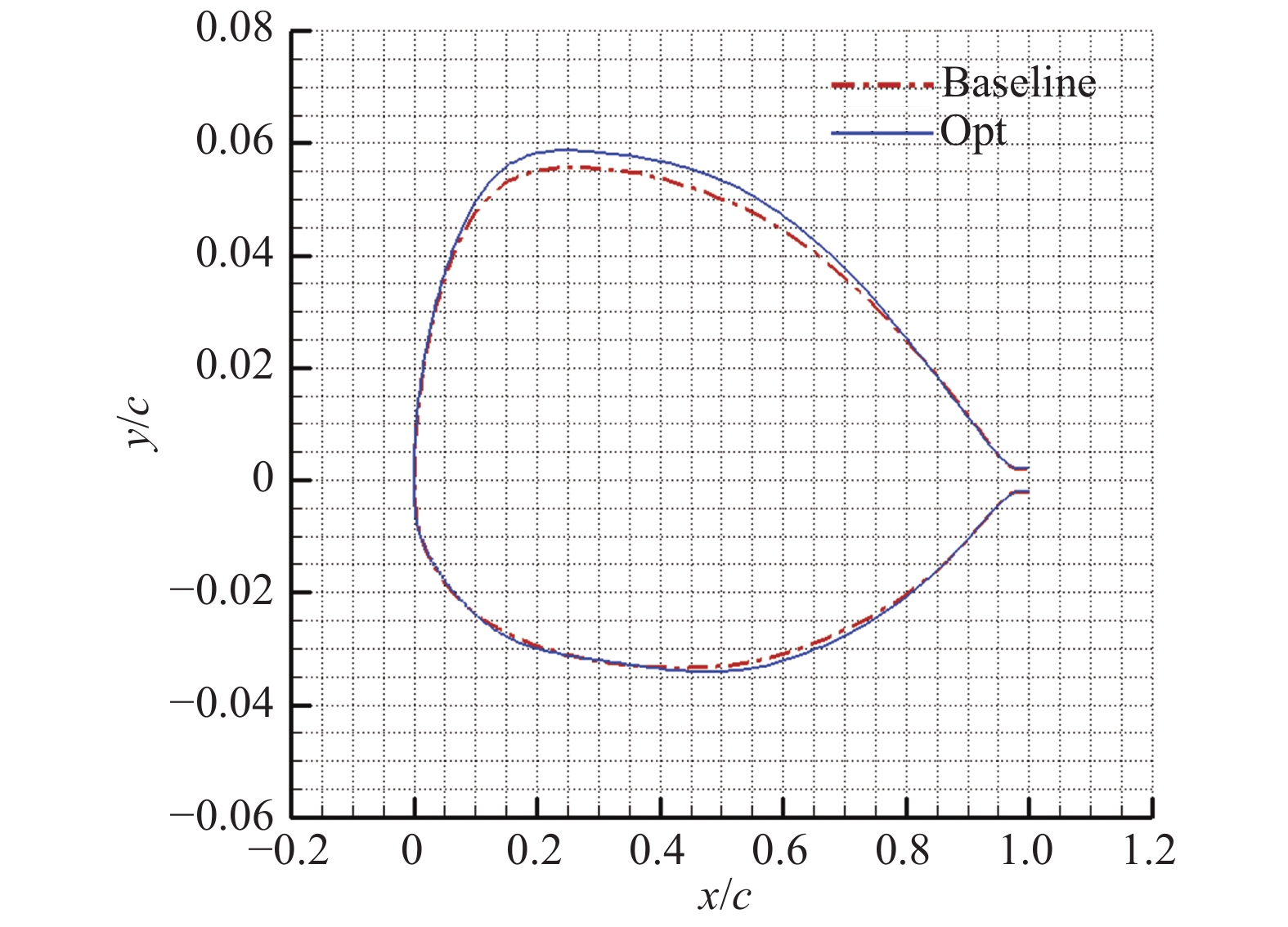
图11给出了优化翼型和基本翼型外形的比较,优化外形头部半径增大,上表面厚度增加。
|
图 11 优化前后翼型的形状比较 Fig.11 Configurations of the initial and optimized airfoils |
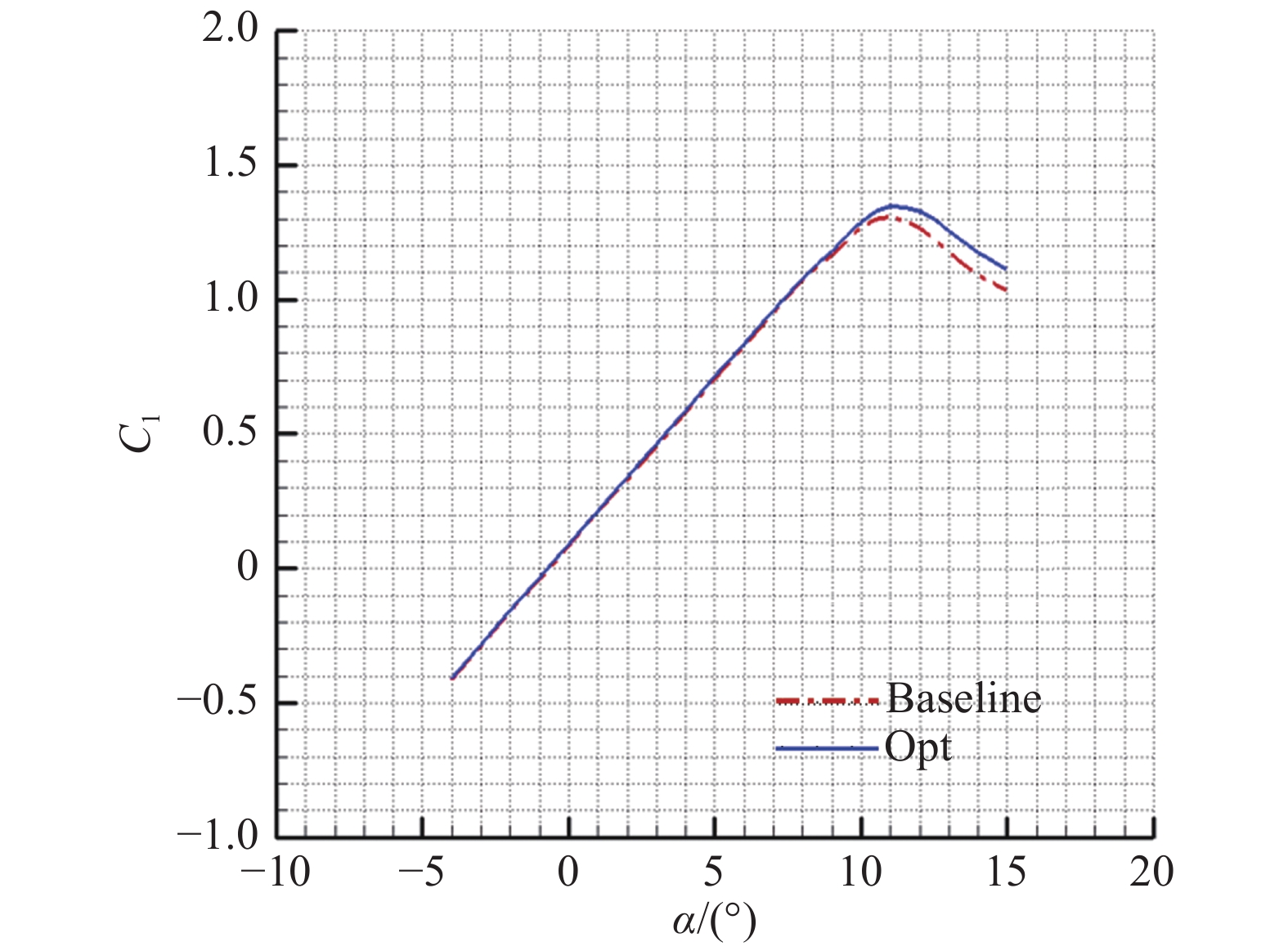
图12给出了机动状态
|
图 12 翼型升力特性比较( |

|
图 13 优化翼型与初始翼型极曲线特性比较( |
| 表 2 优化前后翼型性能比较 Table 2 Performance of the initial and optimized airfoils |
|
|
以某12%厚度翼型作为参考的基本翼型,综合利用本文发展的各项技术,开展多目标/多点设计优化,利用PCA方法实现多目标降维,验证了多目标降维技术的有效性。问题可描述为:
| $ \left\{\begin{array}{l}(1){\text{提高前飞性能}}\\ {M}_{dd}\;\;{\rm{subject\;to}}:\left|{C}_{mdd}\right|\leqslant \left|{C}_{mdd0}\right|\\ (2){\text{提高机动性能}}\\ Ma=0.3,\;{C}_{L\mathrm{max}}\geqslant {C}_{L\mathrm{max}0},{K}_{\mathrm{max}}\geqslant {K}_{\mathrm{max}0}\;\\ Ma=0.4,\;{C}_{L\mathrm{max}}\geqslant {C}_{L\mathrm{max}0},{K}_{\mathrm{max}}\geqslant {K}_{\mathrm{max}0}\;\\ Ma=0.5,\;{C}_{L\mathrm{max}}\geqslant {C}_{L\mathrm{max}0},{K}_{\mathrm{max}}\geqslant {K}_{\mathrm{max}0}\\ Ma=0.6,\;{C}_{L\mathrm{max}}\geqslant {C}_{L\mathrm{max}0},{K}_{\mathrm{max}}\geqslant {K}_{\mathrm{max}0}\;\\ (3){\text{提高悬停性能}}\\ \;\;\;\;\;\;K\geqslant {K}_{0},\;\;{\rm{subject\;to}}:Ma=0.5,{C}_{L}=0.{6}\\ \;\;\;\;\;\;K\geqslant {K}_{0},\;\;{\rm{subject\;to}}:Ma=0.6,{C}_{L}=0.{6}\\ (4){\text{保持厚度不减}}\\ {\rm{subject\;to}}:{t}_{\mathrm{max}}\geqslant {t}_{\mathrm{max}0}\end{array}\right. $ |
上述优化问题共有12个目标,其中前飞状态有2个目标,
利用拉丁超立方采样在设计空间中随机抽样,本文选取了480个样本点,利用CFD方法对样本点分别进行12个目标的气动性能计算,得到480个样本点的目标性能集,对性能集进行PCA分析。根据PCA的目标降维选取方法,对原始目标集进行降维后得到新的目标集为:
| $\left\{ \begin{array}{l} {M_{dd}}\;{\rm{subject\;to}}:\left| {{C_{mdd}}} \right| \leqslant \left| {{C_{mdd0}}} \right| \\ Ma = 0.4,\;{C_{L\max }} \geqslant {C_{L\max 0}}\; \\ Ma = 0.5,\;{K_{\max }} \geqslant {K_{\max 0}} \\ Ma = 0.6,\;{C_{L\max }} \geqslant {C_{L\max 0}}\; \\ K \geqslant {K_0},\;{\rm{subject\;to}}:Ma = 0.6,{C_L}{\rm{ = }}0.{\rm{6 }} \\ \;{\rm{subject\;to}}:{t_{\max }} \geqslant {t_{\max 0}} \\ \end{array} \right.$ |
经过PCA分析可以看出,原始优化问题含有7个冗余目标,非冗余优化目标剩下5个,简化了原始设计问题,针对经PCA降维分析后的问题开展研究。
图14给出了优化翼型和基本翼型的外形比较,表3给出了两者性能指标的比较。从结果可以看出,优化翼型略微变薄,最大厚度位置前移,优化翼型的前飞性能和悬停性能优于基准翼型,综合性能较基本翼型有所提高,可以有效提高旋翼的悬停和机动性能。

|
图 14 初始翼型和优化翼型外形比较 Fig.14 Configurations of the initial and optimized airfoils |
| 表 3 基准翼型和优化翼型性能比较 Table 3 The performance of the initial and optimized airfoils |
|
|
HRADesign软件系统主要提供通用、鲁棒、高效的直升机旋翼翼型工业设计能力。通过软件工程的设计方法,构建了通用的旋翼翼型气动设计和评估软件系统。
1)系统采用软件工程方法实现了架构设计和功能模块的集成,通过分层设计实现了功能模块的高内聚和低耦合,实现了功能模块的灵活扩充,提高了系统可扩展性和用户解决问题的灵活性,满足了设计目标要求。
2)系统集成了多目标进化算法、CFD性能分析工具、翼型参数化工具、网格自动重构、Kriging代理模型以及多目标降维等功能模块,可以满足旋翼翼型多目标优化设计的功能需求。
3)考核算例及应用验证了HRADesign集成系统功能模块的有效性和通用、鲁棒、高效的设计能力。PCA方法的应用展现了其在高维气动多目标优化问题中的应用潜力,对于分析问题的主要特征,降低设计的复杂程度有重要指导意义。
4)HRADesign系统平台目前主要集中于旋翼翼型静态气动特性多目标优化设计,下一步要发展完善静态/动态特性多目标优化设计方法,进一步提高旋翼翼型的综合设计能力。
| [1] |
LEISHMAN J G. Principle of helicopter aerodynamic[M]. Cambridge University Press, 2006.
|
| [2] |
JAMESON A, PIERCE N, MARTINELLI L, et al. Optimum aerodynamic design using the Navier-Stokes equations[C]//35th Aerospace Sciences Meeting and Exhibit, Reno, NV. Reston, Virginia: AIAA, 1997. doi: 10.2514/6.1997-101
|
| [3] |
NIELSEN E J, ANDERSON W K. Recent improvements in aerodynamic design optimization on unstructured meshes[J]. AIAA Journal, 2002, 40(6): 1155-1163. DOI:10.2514/2.1765 |
| [4] |
COELLO COELLO C A, LAMONT G B, Van VELDUIZEN D A. Evolutionary algorithms for solving multi-objective problems[M]. Kluwer Academic Publishers, New York, May 2002.
|
| [5] |
郑传宇, 黄江涛, 周铸, 等. 飞翼翼型高维目标空间多学科综合优化设计[J]. 空气动力学学报, 2017, 35(4): 587-597. ZHENG C Y, HUANG J T, ZHOU Z, et al. Multidisciplinary optimization design of high dimensional target space for flying wing airfoil[J]. Acta Aerodynamica Sinica, 2017, 35(4): 587-597. DOI:10.7638/kqdlxxb-2017.0079 (in Chinese) |
| [6] |
DADONE L U. Design and analytical study of a rotor airfoil[R]. NASA CR-2988, 1978.
|
| [7] |
THIBERT J J. The elaboration of a new family of helicopter blade profiles[R]. NASA TM-75907, 1981.
|
| [8] |
尚克明,招启军,王海. 基于Buler方程的直升机旋翼翼型反设计方法[J]. 直升机技术, 2008, 155(3): 92-97. SHANG K M, ZHAO Q J, WANG H. An inverse design method for the helicopter rotor airfoil based on Euler equation[J]. Helicopter Technique, 2008, 155(3): 92-97. (in Chinese) |
| [9] |
孙俊峰, 刘刚, 江雄, 等. 基于Kriging模型的旋翼翼型优化设计研究[J]. 空气动力学学报, 2013, 31(4): 437-441. SUN J F, LIU G, JIANG X, et al. Research of rotor airfoil design optimization based on the Kriging model[J]. Acta Aerodynamica Sinica, 2013, 31(4): 437-441. (in Chinese) |
| [10] |
丁存伟, 杨旭东. 一种旋翼翼型多点多约束气动优化设计策略[J]. 航空计算技术, 2013, 43(1): 52-57. DING C W, YANG X D. Multi-point aerodynamic optimization design strategy of rotor airfoil with multi-constrain conditions[J]. Aeronautical Computing Technique, 2013, 43(1): 52-57. DOI:10.3969/j.issn.1671-654X.2013.01.014 (in Chinese) |
| [11] |
杨慧, 宋文萍, 韩忠华, 等. 旋翼翼型多目标多约束气动优化设计[J]. 航空学报, 2012, 33(7): 1218-1226. YANG H, SONG W P, HAN Z H, et al. Multi-objective and multi-constrained optimization design for a helicopter rotor airfoil[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(7): 1218-1226. (in Chinese) |
| [12] |
招启军, 王清, 赵国庆. 旋翼翼型定常-非定常特性综合优化设计新方法[J]. 南京航空航天大学学报, 2014, 46(3): 355-363. ZHAO Q J, WANG Q, ZHAO G Q. New optimization design method for rotor airfoil considering steady-unsteady characteristics[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46(3): 355-363. DOI:10.16356/j.1005-2615.2014.03.006 (in Chinese) |
| [13] |
LÓPEZ JAIMES A, COELLO COELLO C A, CHAKRABORTY D. Objective reduction using a feature selection technique[C]//Proceedings of the 10th Annual Conference on Genetic and Evolutionary Computation - GECCO '08, Atlanta, GA, USA. New York: ACM Press, 2008: 673-680. doi: 10.1145/1389095.1389228
|
| [14] |
周草臣. 基于PCA的高维多目标优化算法研究[D]. 重庆: 重庆大学, 2014. ZHOU C C. The study on many-objective optimization algorithms based on PCA[D]. Chongqing: Chongqing University, 2014. (in Chinese) |
| [15] |
HUBAND S, HINGSTON P, BARONE L, et al. A review of multiobjective test problems and a scalable test problem toolkit[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(5): 477-506. DOI:10.1109/TEVC.2005.861417 |
| [16] |
SHANG R H, ZHANG K, JIAO L C, et al. A novel algorithm for many-objective dimension reductions: Pareto-PCA-NSGA-II[C]//Proc of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China. IEEE, 2014: 1974-1981. doi: 10.1109/CEC.2014.6900346
|
| [17] |
LES PIEGL, WAYNE TILLER. The NURBS book[M], Springer, 1997.
|
| [18] |
KULFAN B. Recent extensions and applications of the “CST” universal parametric geometry representation method[C]//Proc of the 7th AIAA ATIO Conf, 2nd CEIAT Int'l Conf on Innov and Integr in Aero Sciences, 17th LTA Systems Tech Conf; followed by 2nd TEOS Forum, Belfast, Northern Ireland. Reston, Virginia: AIAA, 2007. doi: 10.2514/6.2007-7709
|
| [19] |
SEDERBERG T W, PARRY S R. Free-form deformation of solid geometric models[J]. ACM SIGGRAPH Computer Graphics, 1986, 20(4): 151-160. DOI:10.1145/15886.15903 |
| [20] |
THOMPSON J F, SONI B K, WEATHERILL N P. Handbook of grid generation[M]. CRC Press, 1998. doi: 10.1201/9781420050349
|
| [21] |
MCKAY M D, BECKMAN R J, CONOVER W J. Comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J]. Technometrics, 1979, 21(2): 239-245. DOI:10.1080/00401706.1979.10489755 |
| [22] |
方开泰, 马长兴. 正交与均匀试验设计[M]. 北京: 科学与试验出版社, 1980. FANG K T, MA C X. Orthogonal and uniform experimental design[M]. Beiing: Science Press, 1980 (in Chinese). |
| [23] |
JEONG S, MURAYAMA M, YAMAMOTO K. Efficient optimization design method using kriging model[J]. Journal of Aircraft, 2005, 42(2): 413-420. DOI:10.2514/1.6386 |
| [24] |
韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225. HAN Z H. Kriging surrogate model and its application to design optimization: a review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225. (in Chinese) |
| [25] |
牟斌, 江雄, 肖中云, 等. γ-Reθ转捩模型的标定与应用
[J]. 空气动力学学报, 2013, 31(1): 103-109. MOU B, JIANG X, XIAO Z Y, et al. Implementation and caliberation of γ-Reθ transition model [J]. Acta Aerodynamica Sinica, 2013, 31(1): 103-109. (in Chinese) |
| [26] |
孙俊峰, 周铸, 黄勇, 等. 通用飞行器气动优化设计数字化集成平台——DIPasda[J]. 航空学报, 2020, 41(5): 623348. SUN J F, ZHOU Z, HUANG Y, et al. Digital inegrated platform for universal aircraft aerodynamic design optimization: DIPasda[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(5): 623348. DOI:10.7527/S1000-6893.2019.23348 (in Chinese) |
 2021, Vol. 39
2021, Vol. 39


