为满足现代战争对战斗飞行器高机动性的更高要求,国内外众多研究者致力于改进推进系统,将发动机推力矢量化,使其在提供前进动力的同时也提供侧向力[1-2],经过多年的研究发展,构建了较为完善的推力矢量控制技术体系。工程中已能够成熟应用机械式喷管改变出流方向从而实现推力矢量控制,海麻雀、战斧等型导弹和F35、SU-35等型战机均采用了此技术[3]。但因存在发动机结构复杂、可靠性差、推力损失严重、材料要求高等主要缺点,其进一步发展受到一定制约。20世纪90年代开始,人们对气动矢量喷管技术开展了广泛研究,发现其与机械式喷管相比,具有结构简单、质量较小、可靠性高、矢量效果更好等优点,已经发展演化出激波矢量控制型、喉道偏移型、同向流型、逆流型和双喉道型等五种基本类型。其中双喉道喷管(Dual Throat Nozzle,DTN)效果最为突出,近年来一直是研究的热点[4-8]。
美国NASA兰利中心Deere团队最早提出了双喉道喷管方案并阐述了其气动矢量机理[9]。随后国内外学者又围绕其矢量特性和构型优化展开了一系列研究,取得了丰硕成果[10-15]。其中南京航空航天大学徐惊雷团队提出的旁路式双喉道喷管(Bypass Dual Throat Nozzle, BDTN)方案[16]十分具有开创性:通过旁路通道直接从DTN的上游收敛部位引入喉部射流,以简化喷管的次流系统。经过Gu等[17-18]的实验与数值研究,验证了BDTN能够极大增强DTN的矢量性能。林泳辰等[19]基于BDTN提出了“单发倒V双喷管”布局,并通过飞行实验验证了其矢量性能。
本文基于这些基础,对BDTN构型进行了改进设计,通过在腔体扩张段引入额外的次流,以期改善BDTN因双喉道构型带来的内流壅塞及欠膨胀问题,同时进一步提升矢量性能。采用FLUENT软件对矩形截面矢量喷管在不同次流位置(扩张段在次流前长度与总长度在x轴投影之比,定义为Lx)和次流压比(次流总压与入口总压之比,Secondary Pressure Ratio,SPR)下的内流情况二维数值模拟,研究扩张段射流对BDTN气动矢量特性的影响。
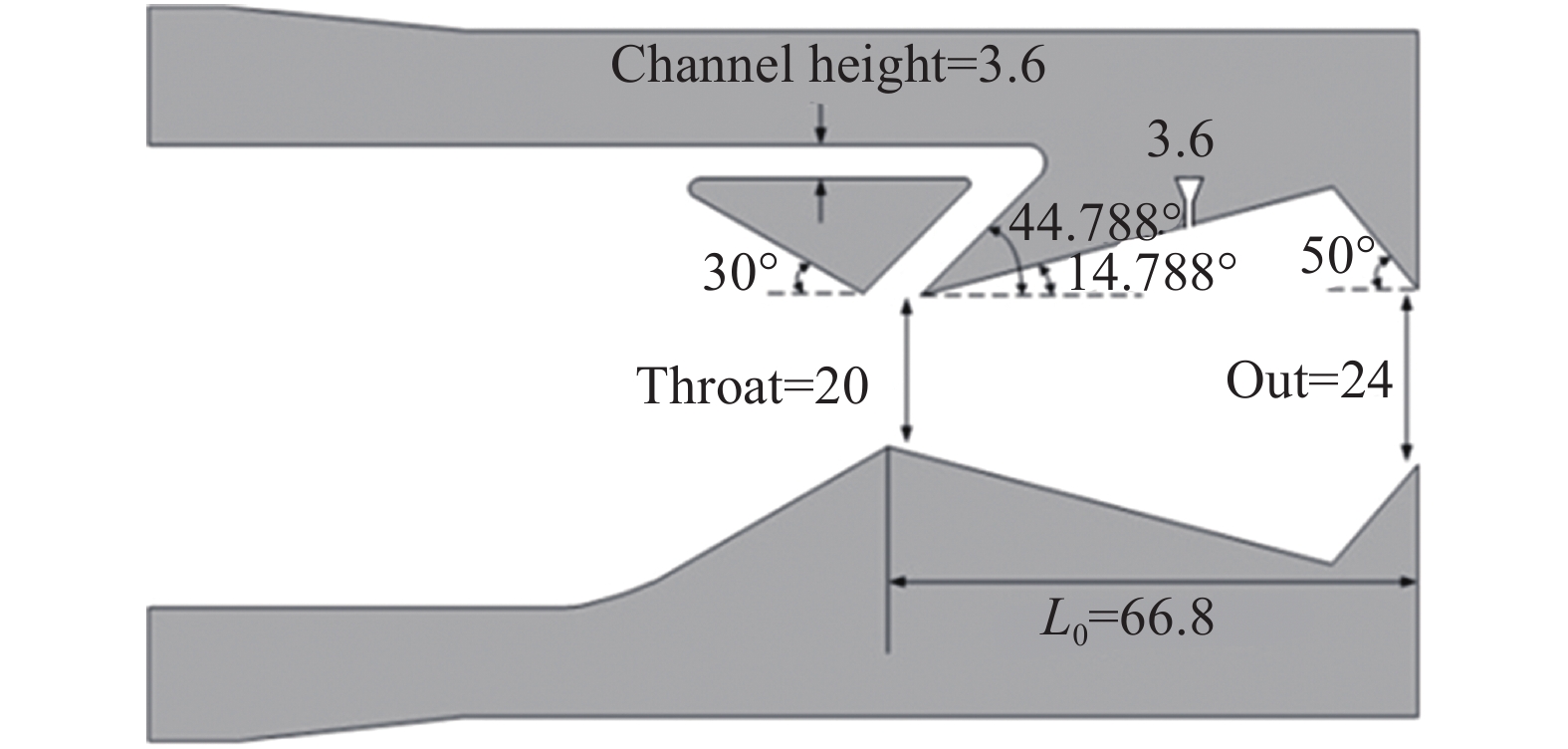
1 计算模型及数值方法 1.1 计算模型及数值方法基于Gu设计的BDTN模型[17],在旁路同一侧腔体扩张段增加收敛次流入口,入口宽度与旁路通道高度相同,出口宽度为1以使次流加速到声速,其位置Lx随算例不同而改变。模型其他各项参数如图1所示。
|
图 1 BDTN模型示意图 Fig.1 The configuration of a BDTN model |
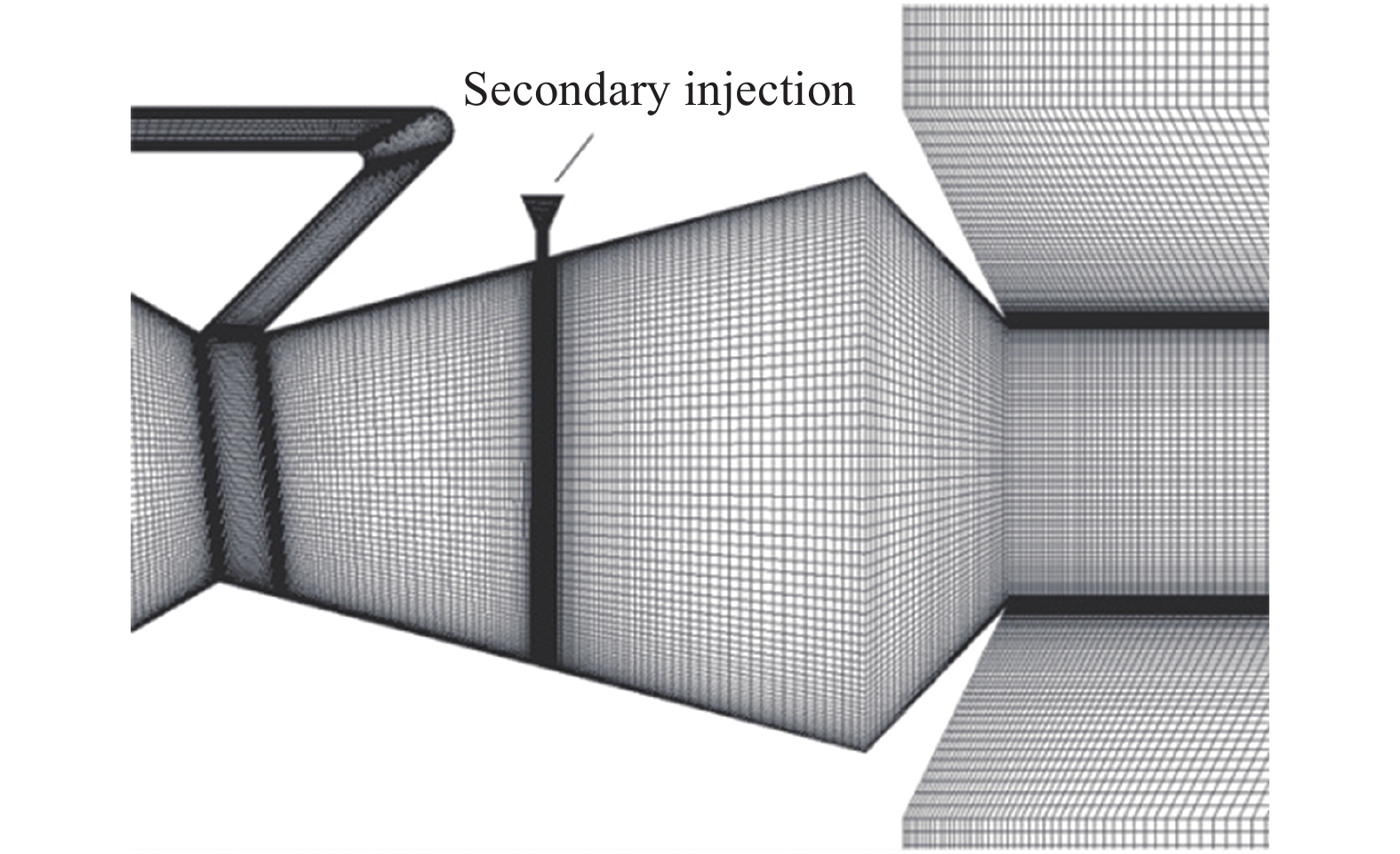
对整个喷管划分结构网格,在喉道、旁路通道和次流入口等参数梯度大的部位附近进行网格加密,第一层网格高度设置为0.01 mm,确保壁面处y+≤10,得到图2所示计算网格。
|
图 2 数值计算网格划分 Fig.2 The 2D computational mesh |
采用FLUENT软件进行数值模拟研究,计算方法为基于时间推进的有限体积法,控制方程为强守恒形式的Navier-Stokes(N-S)方程,离散格式为隐式二阶迎风格式以保证求解精度。湍流模型选用 RNG k-ε两方程模型,喷管近壁面采用标准壁面函数处理,燃气假定为理想可压缩气体,激活能量方程并考虑可压缩性的影响。所有壁面均设置为绝热无滑移壁面,喷管入口和次流入口均采用压力入口边界条件,入口总温(Tin*)与环境总温一致,设为300 K,落压比(入口总压与环境压力之比,Nozzle Pressure Ratio,NPR)为10。选用压力远场和压力出口边界条件,为避免计算中的刚性问题,外流场来流马赫数Ma设置为0.03,环境背压为0.1 MPa。当计算残差低于10−3,且进出质量流率基本保持恒定时,认为计算收敛。
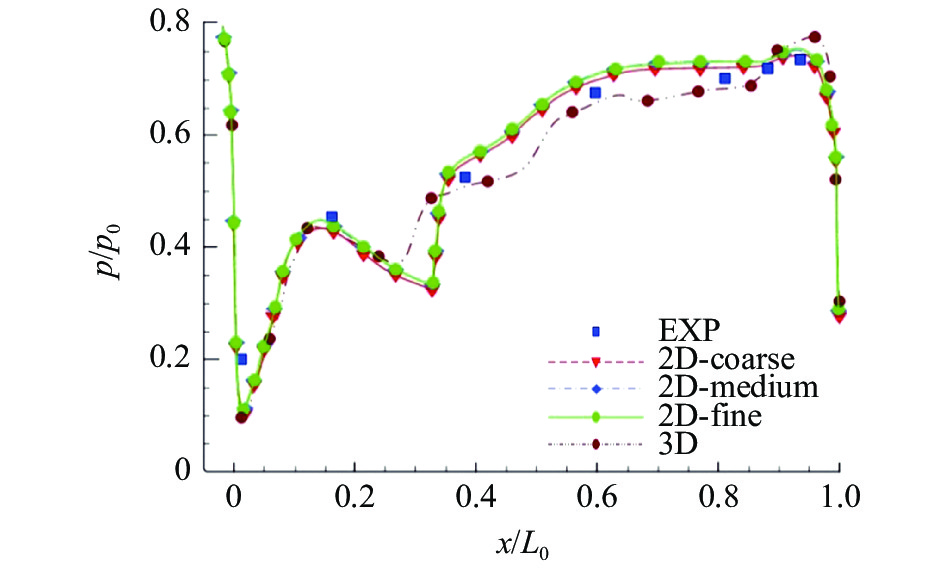
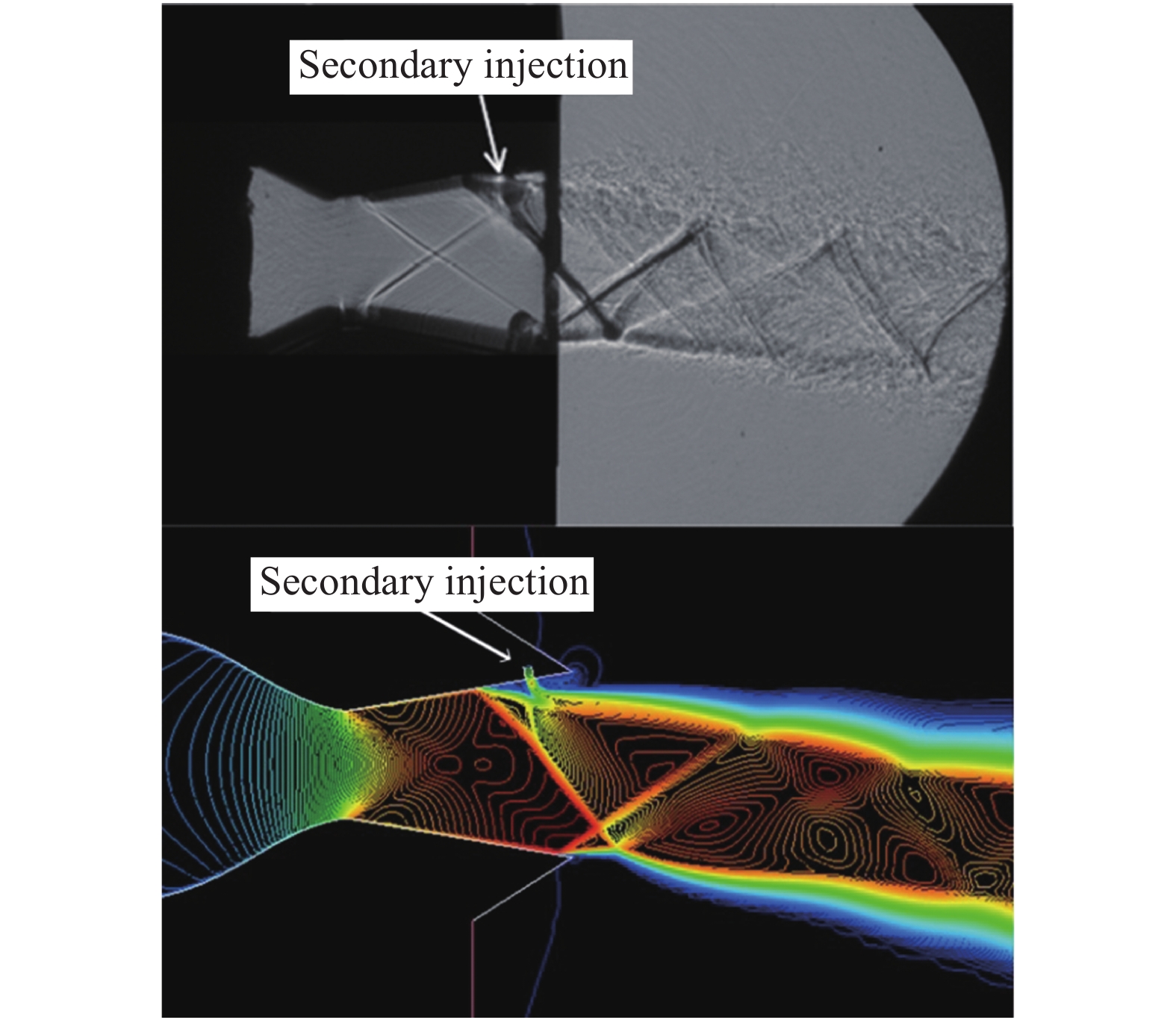
1.2 网格无关性及模型验证对喷管模型划分粗(coarse)、中等(medium)和细(fine)三种网格,网格总数分别为68820、102062、145548,同时设置z方向厚度为50 mm的三维算例进行数值计算,设置NPR为3、Tin*为300 K。计算时将次流入口关闭,以同现有的BDTN实验结果[16]进行比较分析。以喷管上游喉道为轴向起始位置,各算例下壁面(三维取z = 0平面与腔体下壁面交线)压力分布情况如图3所示,横纵坐标分别用上下游喉道之间腔体长度L0、入口压力p0进行无量纲化。另外,为验证数值方法对BDTN模拟的准确性,对文献[17]中的BDTN模型在NPR为3时的流动特性进行模拟计算,得到数值云图与实验纹影图对比如图4。综合图3、图4分析可知,三种不同密度的网格计算得到喷管下壁面压力差异很小,特别是中等网格和细网格几乎无差别,故采用中等网格以兼顾计算质量与效率;二维、三维计算结果基本都符合实验值,虽然三维模型模拟效果更好,但采用二维模拟已足以捕捉流动特性;BDTN模型的数值云图与实验纹影图吻合较好,表明数值方法能够很好地模拟BDTN流场情况。
|
图 3 不同算例下壁面压力分布 Fig.3 The pressure distributions on the lower-wall of numerical simulations and experiments |

|
图 4 喷管数值云图和实验纹影图对比(BDTN) Fig.4 The comparison between the numerical and experimental results for a BDTN nozzle |
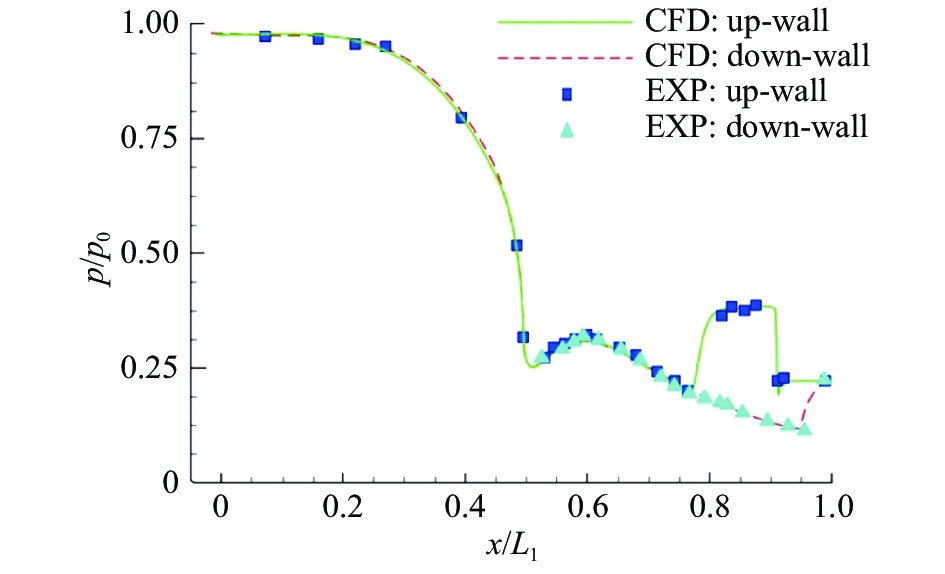
为验证数值方法对扩张段射流的适用性,对NASA兰利中心的激波矢量喷管(SVC)模型[20]进行相同条件下的模拟研究,其工况为:NPR = 4.6,SPR = 0.7,环境压强为0.1 MPa,外流为静止大气,总温为298 K。得到仿真结果与实验纹影照片对比如图5所示,喷管上下壁面静压分布曲线如图6所示,L1为喷管扩张段长度。可见数值云图较为准确地描绘了喷管内外流场形态,实验和仿真得到上下壁面静压分布呈现了良好的一致性,表明本文所采用的数值模拟方法具有较高的可信度。
|
图 5 喷管数值云图和实验纹影图对比(SVC) Fig.5 The comparison between the numerical and experimental results for a SVC nozzle |
|
图 6 喷管壁面压力分布数值及实验结果下对比 Fig.6 The comparison of wall-pressure distributions between computational and experimental ressults |
扩张段射流的旁路式双喉道喷管相关参数计算如下:
次流流量比:
| $\omega = {\dot m_s}/{\dot m_p}$ | (1) |
轴向(x方向)推力:
| $ {F}_{x}=\dot{m}{V}_{ex}+\left({p}_{e}-{p}_{b}\right) \cdot {A}_{e} $ | (2) |
俯仰方向(y方向)推力:
| ${F_y} = \dot m{V_{ey}}$ | (3) |
等熵推力:
| ${F_{i,p}} = {\dot m_p} \cdot \sqrt {\frac{{2\gamma }}{{\gamma - 1}}RT_{{\rm{in}}}^*\left( {1 - {{\rm{NPR}}^{\frac{{1 - \gamma }}{\gamma }}}} \right)} $ | (4) |
| ${F_{i,s}} = {\dot m_s} \cdot \sqrt {\frac{{2\gamma }}{{\gamma - 1}}RT_{{\rm{in}}}^*\left[ {1 - {{\left( {{\rm{NPR}} \cdot {\rm{SPR}}} \right)}^{\frac{{1 - \gamma }}{\gamma }}}} \right]} $ | (5) |
式中:
推力矢量角:
| $\delta = {\tan ^{ - 1}}({{{F_y}} / {{F_x}}})$ | (6) |
推力系数:
| ${C_f} = {{\sqrt {F_x^2 + F_y^2} } / {({F_{i,p}}}} + {F_{i,s}})$ | (7) |
矢量效率:
| $\eta = {{(\delta - {\delta _0})} / {\left( {\omega \times 100\% } \right)}}$ | (8) |
原始BDTN构型因不需要引入额外次流,故不用研究其矢量效率。此处的矢量效率主要表征扩张段射流构型中次流对整体矢量性能的作用,
图7为改进构型(Lx = 0.5,SPR = 0.9)与BDTN原始构型的部分流场马赫数及流线分布图。可知无次流时,旁路通道内高压气流经加速流动后,在喉部冲击剪切高速主流使气动喉道产生倾斜,在下部形成λ形斜激波,在上部产生剪切涡并聚集形成一个较大的低压分离区,而对侧腔体底部经高速主流冲击形成了封闭的高压回流区,从而在腔体内形成非对称流场结构,迫使主流以一定角度喷出以获得矢量推力。主流先在扩张段经历快速膨胀加速,后由于流道变窄流速又回落到声速附近,喷管内发生流动壅塞,气体欠膨胀现象较严重。次流入射后,λ形激波极大程度减弱,主流在下壁面扩张段贴壁流动距离更长,腔体下部回流区面积减小。射流将腔体上部分离区一分为二,并在其下游位置的分离区和主流之间充盈流动形成滑流层,主流被限制在整体平滑渐扩的流道内进行平稳加速流动,其马赫数始终保持在声速附近,上下回流区形状改变使流场非对称性更加明显,增强矢量性能的同时,双喉道喷管固有的内流壅塞及欠膨胀问题得到一定程度改善。

|
图 7 部分流场马赫数及流线分布云图 Fig.7 Mach number and streamlines for the (a) original and (b) modified BDTN |
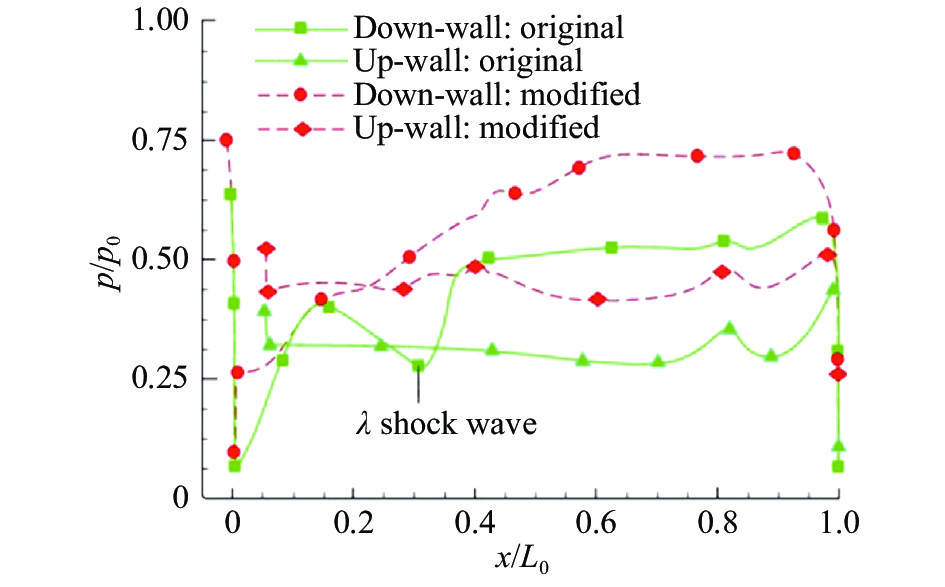
通过分析两型喷管腔体上下壁面压力曲线(见图8)可知,加入射流后喷管上下壁面压力均大幅增大,压差绝对值也相应增加,从而增大了矢量力;上壁面除在射流入口处上游位置有小幅的压力突升外,整体压力分布规律基本相同,而下壁面与原始构型相比激波位置后移(以x轴正向为前向)且强度大大减弱,避免了强激波系带来较大的推力损失。
|
图 8 喷管壁面压力分布对比图 Fig.8 The comparison of wall-pressure distributions between the original and modified BDTN |
取SPR = 0.8,Lx分别为0.25、0.375、0.5、0.675进行计算。图9为计算所得各算例喷管内流马赫数云图,可知Lx = 0.25时,入射位置距离主流较近,次流大部分被卷入旁路射流剪切主流形成的剪切涡中,小部分随着主流向下流动,主次流之间融合效果较差,在主流中激发了大量杂乱的低强度激波;随着Lx值增大,主流通道先是逐渐减小然后稍有扩张,在Lx = 0.5时为最小,产生流道壅塞导致欠膨胀现象加剧,Lx = 0.375时整体流道较为均匀,流动效果最好。次流入射点到主流之间距离随着入射位置后移而增加,次流对主流斜激波系的限制作用减弱,主流贴壁流动距离缩短并逐渐向腔体中线抬升,下部高压回流区面积增大而上部分离区面积减小,使出流喷射角度逐渐减小,从而影响推力矢量效果。当Lx = 0.625时,相比图7(b)相同工况下原始构型,主流脱离下壁面位置明显靠前,流场非对称性减弱,矢量效果不佳。

|
图 9 不同次流入射位置下马赫数分布云图 Fig.9 Mach number contours under the condition of different injection locations |
图10给出各算例喷管腔体上下壁面压力分布。可知,Lx = 0.25时主流近下壁面激波强度较大,且上壁面压力在入射口上游发生急剧变化。随着Lx增加,喷管下壁面高压区范围增加,而上壁面除在次流入口处有小幅上升外压力分布规律基本保持不变。而当Lx增大到0.625时腔体下部高压回流区压力减小,上部分离区压力减小幅度更大,使上下壁面压差减小。对比可发现Lx = 0.375时喷管上下壁面压差最大。

|
图 10 不同次流入射位置下壁面压力分布图 Fig.10 Wall-pressure distributions under the condition of different injection locations |
比较不同次流入射位置算例及其与原始BDTN(Case1)矢量性能参数(表1)可知:随着次流入射位置后移,喷管推力矢量角先增大随后逐步减小,推力系数逐渐增大且幅度渐缓。综合比较而言Lx = 0.375时其矢量效果最佳,与原始BDTN构型相比矢量角提高了6.38°,推力系数提高了0.01,矢量性能得到一定改善。此时次流流量比低至2.18%,次流矢量效率达到2.92°/1%次流流量。在工程实际中,可通过对相应构型喷管进行迭代优化,得到普适不同工况的最优次流入射位置。总体而言,通过在BDTN扩张段引入次流,其矢量效果明显强于仅在扩张段添加射流的激波矢量控制型喷管,也强于DTN和原始构型BDTN,对于扩充完善气动矢量技术体系具有一定研究价值。
| 表 1 不同次流入射位置算例矢量性能 Table 1 Thrust-vector performance under the condition of different injection locations |
|
|
取Lx = 0.375,SPR值分别为0.2、0.3~1进行计算。图11为SPR = 0.4、0.7、1时各算例喷管分离区马赫数云图及流线图。可见不同SPR下喷管的腔体上部分离区经历了不同的发展过程,SPR较小时,次流入射深度较浅,次流大部分被卷吸入上游分离区并发展出斜向错位分布的两个回流涡,其余次流融合进入主流边界滑流层,在下游分离区内形成后凸的回流区。SPR增加到0.7时,次流全部融入滑流层之中,对主流流道的限制作用明显增强,低速区域面积增大,喉道下部斜激波强度减弱,上游分离区两个回流涡变成前后分布。SPR继续增加,上游分离区中后回流涡主要由剪切涡发展而来,范围显著扩大,而靠近次流的前回流涡逐步向下部发展,最终与主流相联通。主流马赫数主要集中在0.8~1.2左右,低速区域起始位置向上游移动,而次流入射位置下游区域的主流马赫数几乎无变化。

|
图 11 不同次流压比下局部马赫数和流线云图 Fig.11 Mach number contours and streamlines under the condition of different SPRs |
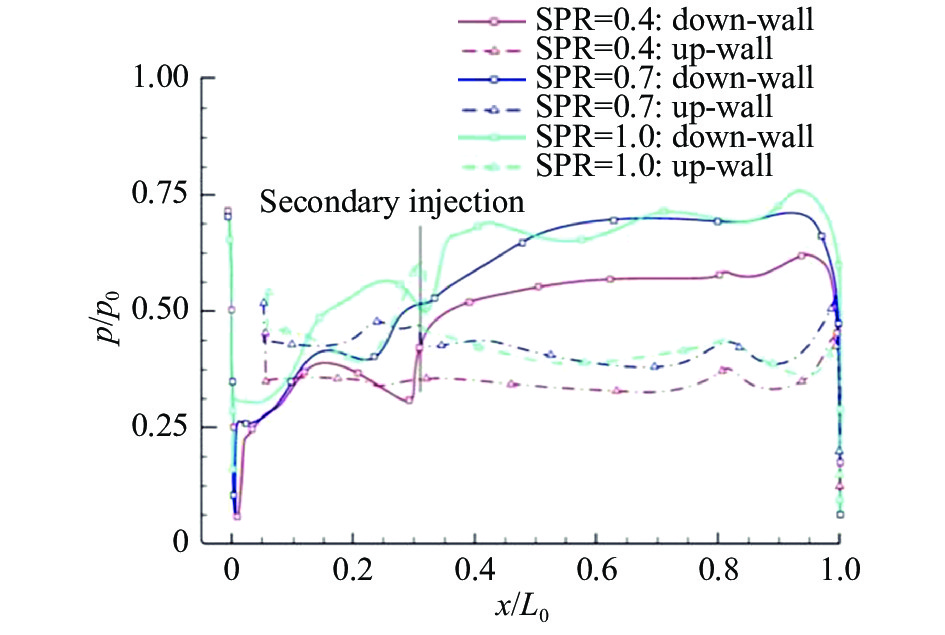
图12为喷管腔体上下壁面压力曲线图。由图可见,SPR从0.4增加到0.7时,喷管上下壁面压力均相应大幅增加,且壁面压差也增大,增加到1后次流下游喷管壁面沿程压力出现振荡,但大体分布无变化。结合图11分析可知,SPR增大过程中,次流的扰动作用加剧,对应次流上游流动区域的主流流速下降,导致x/L0在0.1~0.3左右下壁面动压降低静压上升。对于次流下游区域,SPR增加到0.7时,由于次流对流道限制作用增强,使喷管整体壁面压力明显提升。SPR增加到1后,下壁面压力随激波系变化而产生震荡,上壁面压力大体保持稳定,其中由于图11(c)中的前回流涡与壁面脱离并向主流方向发展,导致x/L0 = 0.3左右位置上壁面压力突升。
|
图 12 不同次流压比下壁面压力分布曲线 Fig.12 Wall-pressure distributions under the condition of different SPRs |
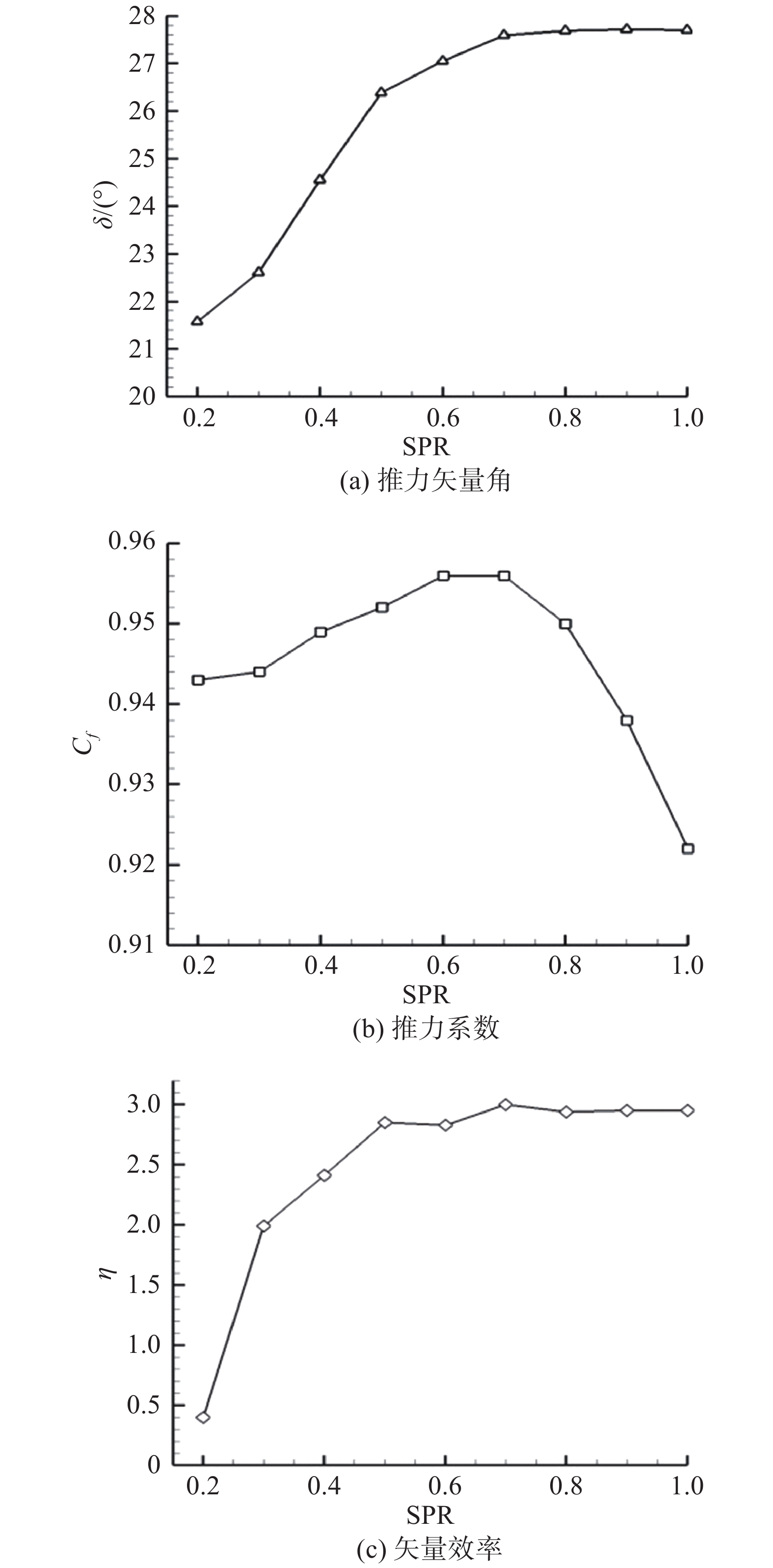
分析不同SPR下喷管各项性能参数变化情况(图13)可知,随着SPR增加,喷管推力矢量角逐渐增加,且在SPR增加到0.7后基本保持不变,而推力系数先增加后急剧下降;低SPR下矢量效率很低,在SPR增加到0.5过程中急剧上升,随后基本保持稳定。究其原因,在低SPR下次流对主流作用较弱,对矢量性能的改善作用不大。随着SPR在一定范围内逐渐增加,次流对主流流道限制作用增强,流场非对称性更加突出,主流膨胀渐趋平稳而出流偏转角度更大,使出流水平速度略有降低而垂直速度增加,同时喷管上下壁面压差增大而进出口压差变化较小,推力矢量角得以增大。因为激波系强度大大降低,且次流对主流的随流效果较好,弥补了部分推力损失,此种效果超过了出流水平速度轻微减小带来的负面影响,使推力系数也相应增加。大SPR下主流低速区面积显著增大,出流水平速度进一步减小,使推力系数急剧减小,甚至低于无次流的原始BDTN构型。此时腔体内的不对称流动已接近几何极限,主流几何流道几乎固定,次流质量流率受SPR影响减弱,而喷管入口质量流率和矢量角都保持稳定,从而使矢量效率趋于稳定。进行总体比较发现,SPR = 0.7时喷管推力矢量角达到27.59°,推力系数达到0.956,矢量效率为3°/1%次流流量,各项指标参数都在较高水平,综合矢量性能较为理想。
|
图 13 不同次流压比下的推力矢量性能 Fig.13 The thrust-vector performance under the condition of different SPRs |
本文采用CFD数值模拟方法对腔体扩张段射流的BDTN气动矢量特性进行研究,得到以下结论:
1)扩张段射流使喷管内流壅塞及欠膨胀问题得到一定程度改善,避免了强激波系带来的推力损失,增大壁面压差从而提高矢量角。
2)随着次流入射位置后移,推力矢量角先增大随后逐步减小,推力系数逐渐增大且幅度渐缓。
3)随着SPR增加,喷管推力矢量角逐渐增加后基本保持不变,而推力系数先增加后急剧下降,矢量效率很低先急剧上升随后基本保持稳定。总体比较而言,Lx = 0.375、SPR = 0.7时喷管推力矢量角达到27.59°,推力系数为0.956,矢量效率为3°/1%次流流量,各项矢量性能参数都较为理想。
| [1] |
晁祥林, 顾益龙. 推力矢量技术及其验证机试飞[J]. 飞行试验, 1996, 6: 2-7. ZHAO X L, GU Y L. Thrust-vectoring technology and its flying testing[J]. Flying Testing, 1996, 6: 2-7. (in Chinese) |
| [2] |
丛戎飞, 吴军强, 张长丰, 等. 扰流片式推力矢量喷管气动特性数值模拟研究[J]. 空气动力学学报, 2019, 37(2): 234-241. CONG R F, WU J Q, ZHANG C F, et al. Numerical research on jet tab thrust vector nozzle aerodynamic characteristic[J]. Acta Aerodynamica Sinica, 2019, 37(2): 234-241. DOI:10.7638/kqdlxxb-2016.0115 (in Chinese) |
| [3] |
周慧晨. 一种矢量增强型双喉道射流矢量喷管的数值模拟及实验验证研究[D]. 南京: 南京航空航天大学, 2009. ZHOU H C. Computational study of a vector-enhanced dual-throat thrust-vectoring nozzle and experimental validation[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009. (in Chinese) |
| [4] |
李克新, 额日其太, 韩景. 二元喉道倾斜矢量喷管调节方法[J]. 推进技术, 2012, 33(6): 946-950. LI K X, ERIQITAI, HAN J. Studies on control method of two dimensional fluidic throat skewing vectoring nozzle[J]. Journal of Propulsion Technology, 2012, 33(6): 946-950. DOI:10.13675/j.cnki.tjjs.2012.06.009 (in Chinese) |
| [5] |
范志鹏, 徐惊雷, 郭帅. 次流通道对双喉道气动矢量喷管的性能影响研究[J]. 推进技术, 2014, 35(9): 1174-1180. FAN Z P, XU J L, GUO S. Effects of secondary injection pipe on dual throat nozzle thrust-vectoring performances[J]. Journal of Propulsion Technology, 2014, 35(9): 1174-1180. DOI:10.13675/j.cnki.tjjs.2014.09.004 (in Chinese) |
| [6] |
GU R, XU J. Effects of cavity on the performance of dual throat nozzle during the thrust-vectoring starting transient process[J]. J Eng Gas Turbine Power, 2014, 136(1): 145021-145026. DOI:10.1115/1.4025243 |
| [7] |
李耀华, 李建强, 杨党国, 等. 二元双喉道射流推力矢量喷管流动参数影响的数值研究[J]. 空气动力学学报, 2015, 33(2): 211-217. LI Y H, LI J Q, YANG D G, et al. Numerical study of a dual-throat fluidic thrust-vectoring nozzle[J]. Acta Aerodynamica Sinica, 2015, 33(2): 211-217. DOI:10.7638/kqdlxxb-2012.0216 (in Chinese) |
| [8] |
夏雪峰, 高峰, 黄桂彬, 等. 双喉道推力矢量喷管研究进展[J]. 航空工程进展, 2017, 8(3): 249-255, 298. XIA X F, GAO F, HUANG G B, et al. Research progress of the dual-throat thrust-vectoring nozzle[J]. Advances in Aeronautical Science and Engineering, 2017, 8(3): 249-255, 298. DOI:10.16615/j.cnki.1674-8190.2017.03.001 (in Chinese) |
| [9] |
DEERE K. Summary of fluidic thrust vectoring research at NASA Langley Research Center[C]//21st AIAA Applied Aerodynamics Conference, Orlando, Florida. Reston, Virginia: AIAA, 2003. doi: 10.2514/6.2003-3800
|
| [10] |
FLAMM J, DEERE K, MASON M, et al. Experimental study of an axisymmetric dual throat fluidic thrust vectoring nozzle for supersonic aircraft application[C]//43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati, OH. Reston, Virginia: AIAA, 2007. doi: 10.2514/6.2007-5084
|
| [11] |
SHIN C S, KIM H D, SETOGUCHI T, et al. A computational study of thrust vectoring control using dual throat nozzle[J]. Journal of Thermal Science, 2010, 19(6): 486-490. DOI:10.1007/s11630-010-0413-x |
| [12] |
范志鹏, 徐惊雷, 汪阳生. 下游喉道对双喉道气动矢量喷管气动性能的影响[J]. 航空动力学报, 2015, 30(3): 580-587. FAN Z P, XU J L, WANG Y S. Effects of downstream throat on aerodynamic performance of dual throat nozzle[J]. Journal of Aerospace Power, 2015, 30(3): 580-587. DOI:10.13224/j.cnki.jasp.2015.03.008 (in Chinese) |
| [13] |
周慧晨, 谭慧俊, 孙姝, 等. 一种矢量增强型双喉道射流推力矢量喷管的数值模拟[J]. 航空动力学报, 2010, 25(9): 2070-2076. ZHOU H C, TAN H J, SUN S, et al. Numerical investigation of a vector-enhanced dual-throat thrust-vectoring nozzle[J]. Journal of Aerospace Power, 2010, 25(9): 2070-2076. DOI:10.13224/j.cnki.jasp.2010.09.026 (in Chinese) |
| [14] |
何敬玉, 陈强, 董金刚, 等. 双喉道推力矢量喷管的气动性能数值模拟[J]. 南京航空航天大学学报, 2017, 49(S1): 16-23. HE J Y, CHEN Q, DONG J G, et al. Numerical investigation of aerodynamic performance on dual throat thrust vectoring nozzle[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2017, 49(S1): 16-23. (in Chinese) |
| [15] |
顾瑞. 新型双喉道气动矢量喷管机理与关键技术研究[D]. 南京: 南京航空航天大学, 2013. GU R. Research on the key technology of new dual throat fluidic vectoring thrust nozzle[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013(in Chinese). |
| [16] |
李明, 徐惊雷, 黄顺洲, 等. 旁路式双喉道无源矢量喷管: CN102434315A[P]. 2012-05-02. LI M, XU J L, HUANG S Z, et al. Bypass type double-throat passive vectoring sprayer nozzle: CN102434315A[P]. 2012-05-02. (in Chinese) |
| [17] |
GU R, XU J L, GUO S. Experimental and numerical investigations of a bypass dual throat nozzle[J]. Journal of Engineering for Gas Turbines and Power, 2014, 136(8): 084501-1. DOI:10.1115/1.4026943 |
| [18] |
GU R, XU J L. Dynamic experimental investigations of a bypass dual throat nozzle[J]. Journal of Engineering for Gas Turbines and Power, 2015, 137(8): 72-79. DOI:10.1115/1.4029391 |
| [19] |
林泳辰, 徐惊雷, 韩杰星, 等. 气动推力矢量无舵面飞翼的飞行实验[J]. 航空动力学报, 2019, 34(3): 701-707. LIN Y C, XU J L, HAN J X, et al. Flight test of a fluidic thrust vectoring flying wing without rudder[J]. Journal of Aerospace Power, 2019, 34(3): 701-707. DOI:10.13224/j.cnki.jasp.2019.03.023 (in Chinese) |
| [20] |
WAITHE K, DEERE K. An experimental and computational investigation of multiple injection ports in a convergent-divergent nozzle for fluidic thrust vectoring[C]//21st AIAA Applied Aerodynamics Conference, Orlando, Florida. Reston, Virginia: AIAA, 2003. doi: 10.2514/6.2003-3802
|
 2021, Vol. 39
2021, Vol. 39

