相比多块结构化网格和笛卡尔网格,非结构网格因其便捷灵活的生成方式,近年来逐渐成为CFD研究与应用的热点[1-4],但伴随着非结构网格的广泛使用,一个涉及网格生成和模拟精度的矛盾开始变得愈发突出[5-6]。因此,学者们不断尝试改进基于非结构网格的离散算法,来实现自动化网格生成与精准化数值模拟的统一。
目前,针对非结构网格较常用的数值方法是具有二阶精度的有限体积方法[7-10],该方法因具有较好的数值表现而被应用于很多知名商业软件,如ANSYS公司开发的商业软件Fluent,以及NASA开发的In-house软件FUN3D等[11]。为了提高计算效率与流场分辨率,很多学者尝试将此数值方法向更高精度推广[12-16]。不同于二阶精度,高精度非结构有限体积方法的实现,除了需要引入更多的高斯积分点来实现高阶精度通量积分外,还需要重构控制体单元的高阶导数。有关高阶导数的重构,Barth与Jespersen[17-18]首先提出了k-exact重构算法,Ollivier-Gooch等[19-21]在此基础上发展了具有高阶精度的非结构有限体积离散方法,并系统研究了有关高阶精度非结构FV离散的对流、粘性通量与源项积分过程,以及曲线边界处理等一系列问题。
在高阶离散中,不同模板对实际计算(尤其是梯度与高阶导数重构过程)具有更直接的影响,因此部分学者也开展了相应的模板选择研究。文献[11]提出了一种“智能增加”(Smart Augmentation, SA)模板构造方法。在共面模板的基础上,从围绕中心单元每个节点的共点模板中寻找了一个距离中心单元最近的单元。该方法完全基于距离信息,可能导致流场出现非物理解。为了克服这一问题,在SA模板的基础上,Schwoppe等[11]继续从共点模板中选择单元,以改善最小二乘矩阵的条件数。Nishikawa在文献[22]研究指出,尽管该方法带来了一定程度的改进,但在高度变形网格上其计算稳定性较差。为克服这一问题,Nishikawa同样基于共面模板增加额外单元,其中一个是通过增加额外单元改进模板的对称性;另外一种以减小最小二乘矩阵系统Frobenius范数的倒数为目标,从而降低重构梯度的数值,以提高数值模拟的稳定性。但遗憾的是,这一模板构造方法在一定程度上降低了数值模拟的离散精度。
不同于上述模板选择方式,Xiong等[23- 24]针对二阶精度非结构有限离散,提出了一种基于局部方向的模板选择方式,使得模板选择沿着两个局部方向依次进行。这种模板选择方式在非结构网格上初步体现出类似结构网格的结构化特征,易于并行,并且在各向同性的三角形网格上,其中一个局部方向接近壁面法向,另一个方向沿着流向,比较有效地反映了例如边界层型流场的主要变化情况。但在高度各向异性三角形网格上,由于其中一个局部方向与偏离壁面法向间偏差相对较大,导致其稳定性下降[24]。
在局部方向模板的基础上,本文作者在前期工作中探索了一种基于计算域全局方向的模板选择方法[25]。例如边界层型流动,由于沿着壁面法向的变化相对剧烈,于是希望重构过程的模板单元能够尽可能多地体现壁面法向的流动信息。因此,其中一个全局方向可取当地壁面法向,同时为了使模板具有更好的空间延展性,并保留结构化特征,另一个方向可取流向。相比上述几种重构模板,全局方向的确定更加简便,摆脱了原始网格拓扑对模板构型的影响,并且能够准确反映流场特征。在二阶精度非结构有限体积方法中,其计算误差相比常用的共点与共面模板更低,并且所需的模板数量较少,在具有较高计算准确性的同时,有效节约了计算开销。
本文将全局方向模板推广至具有三阶精度非结构FV求解器,以测试其在高阶精度数值模拟中的计算效果。文章的总体结构如下:第1节给出了高阶精度非结构有限体积方法的控制方程离散以及k-exact重构的基本过程;第2节主要讨论了不同的模板选择方法,并叙述了全局方向模板选择方法的主要思想与基本过程,简要探讨了在相对复杂的外形上确定全局方向的基本思路;第3节分别测试了全局方向模板在两类数值算例中的表现情况,同时测试了局部方向模板在高阶精度非结构有限体积方法中的数值表现;第4节给出了本文结论与下一步工作展望。
1 非结构有限体积方法 1.1 控制方法与离散无粘流动的积分型控制方程如下:
| $\frac{\partial }{{\partial t}}\iiint\limits_V {{\boldsymbol{u}}{\rm{d}}V + \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_{\partial V} {{{\boldsymbol{F}}_c}({\boldsymbol{u}}) \cdot {\boldsymbol{n}}\;{\rm{d}}S} = 0}$ | (1) |
式中,u为守恒变量,Fc(u)为对流通量,n为控制体边界面外法向矢量,V与∂V分别代表积分域与积分域边界。在高阶精度FV离散过程中,方程(1)通常可被离散为:
| $\frac{\partial }{{\partial t}}{({\bar{\boldsymbol u}}V)_i} + {\left( {\sum\limits_{j = 1}^{{N_f}} {\sum\limits_{k = 1}^{{N_G}} {{\omega _k}{{\boldsymbol{\varPhi }}_{jk}} \cdot {{\boldsymbol{n}}_j}{S_j}} } } \right)_i} = 0$ | (2) |
式中
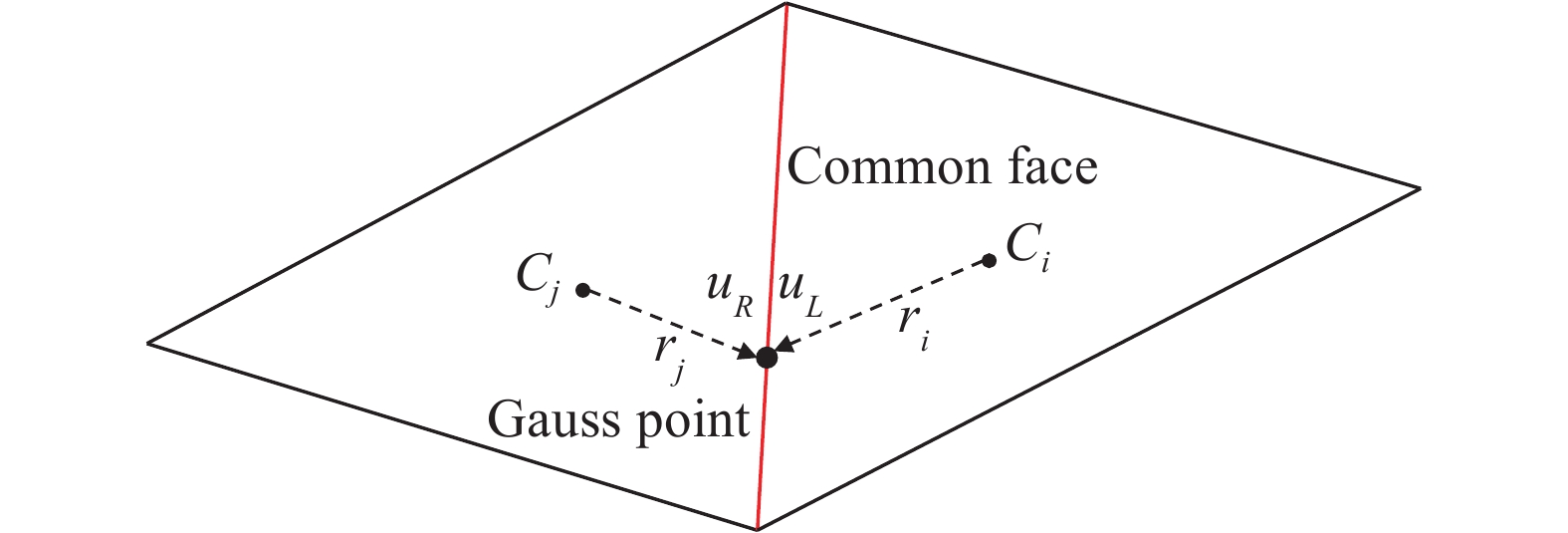
|
图 1 非结构有限体积高精度离散与通量构造示意图 Fig.1 Sketch of high-order unstructured finite volume discretization and flux construction |
| $\left. \begin{split} {\boldsymbol{u}}_L^n =& {{\boldsymbol{u}}_i} + {\left. {\dfrac{{\partial {\boldsymbol{u}}}}{{\partial x}}} \right|_i}\left( {{x_i} - {x_m}} \right) + {\left. {\dfrac{{\partial {\boldsymbol{u}}}}{{\partial y}}} \right|_i}\left( {{y_i} - {y_m}} \right) +\\&\;\;\;\;\;\;\;\;\; {\left. {\dfrac{{{\partial ^2}{\boldsymbol{u}}}}{{\partial {x^2}}}} \right|_i}\dfrac{{{{\left( {{x_i} - {x_m}} \right)}^2}}}{2} + {\left. {\dfrac{{{\partial ^2}{\boldsymbol{u}}}}{{\partial x\partial y}}} \right|_i}\left( {{x_i} - {x_m}} \right)\left( {{y_i} - {y_m}} \right) + \\&\;\;\;\;\;\;\;\;\;{\left. {\dfrac{{{\partial ^2}{\boldsymbol{u}}}}{{\partial {y^2}}}} \right|_i}\dfrac{{{{\left( {{y_i} - {y_m}} \right)}^2}}}{2} + \cdots \\ {\boldsymbol{u}}_R^n =&{{\boldsymbol{u}}_i} + {\left. {\dfrac{{\partial {\boldsymbol{u}}}}{{\partial x}}} \right|_j}\left( {{x_j} - {x_m}} \right) + {\left. {\dfrac{{\partial {\boldsymbol{u}}}}{{\partial y}}} \right|_j}\left( {{y_j} - {y_m}} \right) + \\&\;\;\;\;\;\;\;\;\; {\left. {\dfrac{{{\partial ^2}{\boldsymbol{u}}}}{{\partial {x^2}}}} \right|_j}\dfrac{{{{\left( {{x_j} - {x_m}} \right)}^2}}}{2} + {\left. {\dfrac{{{\partial ^2}{\boldsymbol{u}}}}{{\partial x\partial y}}} \right|_j}\left( {{x_j} - {x_m}} \right)\left( {{y_j} - {y_m}} \right) +\\&\;\;\;\;\;\;\;\;\; {\left. {\dfrac{{{\partial ^2}{\boldsymbol{u}}}}{{\partial {y^2}}}} \right|_j}\dfrac{{{{\left( {{y_j} - {y_m}} \right)}^2}}}{2} + \cdots \end{split} \right\}$ | (3) |
式中,
在二阶精度非结构有限体积方法中,通常采用最小二乘方法重构单元梯度,由于直接基于最小二乘方法进行泰勒级数展开无法达到二阶以上精度,因此本节采用k-exact方法来实现单元梯度与高阶导数重构。重构函数的形式如下:
| $\begin{split} {R_i}({\boldsymbol{x}} - {{\boldsymbol{x}}_i}) =& {\left. {\boldsymbol{u}} \right|_{{x_i}}} + {\left. {\frac{{\partial {\boldsymbol{u}}}}{{\partial x}}} \right|_{{{\boldsymbol{x}}_i}}}(x - {x_i}) + {\left. {\frac{{\partial {\boldsymbol{u}}}}{{\partial y}}} \right|_{{{\boldsymbol{x}}_i}}}(y - {y_i}) +\\& {\left. {\frac{{{\partial ^2}{\boldsymbol{u}}}}{{\partial {x^2}}}} \right|_{{{\boldsymbol{x}}_i}}}\frac{{{{(x - {x_i})}^2}}}{2} + {\left. {\frac{{{\partial ^2}{\boldsymbol{u}}}}{{\partial x\partial y}}} \right|_{{{\boldsymbol{x}}_i}}}(x - {x_i})(y - {y_i})+ \\& {\left. {\frac{{{\partial ^2}{\boldsymbol{u}}}}{{\partial {y^2}}}} \right|_{{{\boldsymbol{x}}_i}}}\frac{{{{(y - {y_i})}^2}}}{2} + \cdots \end{split} $ | (4) |
同时,其需要满足的约束为:
| $\frac{1}{{{A_i}}}\int_{{V_i}} {{R_i}({\boldsymbol{x}} - {{\boldsymbol{x}}_i}){\rm{d}}A = } \frac{1}{{{A_i}}}\int_{{V_i}} {{\boldsymbol{u}}({\boldsymbol{x}}){\rm{d}}A} \equiv {{\bar{\boldsymbol u}}_i}$ | (5) |
因此,将重构函数在单元j上积分可得:
| $\begin{split} {{{\bar{\boldsymbol u}}}_j} =& {\left. {\boldsymbol{u}} \right|_{{{\boldsymbol{x}}_i}}} + {\left. {\frac{{\partial {\boldsymbol{u}}}}{{\partial x}}} \right|_{{{\boldsymbol{x}}_i}}}{\widehat x_{ij}} + {\left. {\frac{{\partial {\boldsymbol{u}}}}{{\partial y}}} \right|_{{{\boldsymbol{x}}_i}}}{\widehat x_{ij}} + \frac{1}{2}{\left. {\frac{{{\partial ^2}{\boldsymbol{u}}}}{{\partial {x^2}}}} \right|_{{{\boldsymbol{x}}_i}}}{\widehat {{x^2}}_{ij}}+ \\& {\left. {\frac{{{\partial ^2}{\boldsymbol{u}}}}{{\partial x\partial y}}} \right|_{{{\boldsymbol{x}}_i}}}{\widehat {xy}_{ij}} + \frac{1}{2}{\left. {\frac{{{\partial ^2}{\boldsymbol{u}}}}{{\partial {y^2}}}} \right|_{{{\boldsymbol{x}}_i}}}{\widehat {{y^2}}_{ij}} + \cdots \end{split}$ | (6) |
式中
| $\left. \begin{split}& {\widehat {{x^n}{y^m}}_{ij}}\!\! \equiv\!\! \dfrac{1}{{{A_j}}}\!\!\displaystyle\int_{{V_j}} {{{\left[ {(x - {x_j}) + ({x_j} \!-\! {x_i})} \right]}^n}}\!\! \left[ {(y - {y_j})} \right. \!+\! {\left. {({y_j} \!-\! {y_i})} \right]^m}{\rm{d}}A \\&\;\;\;\;\;\;\;\;\;\;\;=\displaystyle\sum\limits_{l = 0}^m\displaystyle\sum\limits_{k = 0}^n {{\dfrac{{m!}}{{l!(m - l)!}}\dfrac{{n!}}{{k!(n - k)!}}} } {({x_j} - {x_i})^k}({y_j} - {y_i}{)^l} \\&\;\;\;\;\;\;\;\;\;\;\; {\overline {{x^{n - k}}{y^{m - l}}} _j} {\overline {{x^n}{y^m}} _j} = \dfrac{1}{{{A_j}}}\displaystyle\iint_{{V_j}} {{{\left( {x - {x_j}} \right)}^n}{{\left( {y - {y_j}} \right)}^m}} \end{split} \right\}$ | (7) |
其中
| $\overline {{x^n}{y^m}} = \frac{1}{{\left( {n + 1} \right){V_i}}}\oint_{\partial {V_i}} {{{\left( {x - {x_i}} \right)}^{n + 1}}{{\left( {y - {y_i}} \right)}^m}{n_x}\;{\rm{d}}S} $ | (8) |
式中
参照方程(6),针对任意模板单元均可构造一个重构多项式,并最终组建矩阵方程组:
| $\begin{split}& \left( {\begin{array}{*{20}{c}} 1\!\!\!&\!\!\!{\bar x}\!\!\!&\!\!\!{\bar y}\!\!\!&\!\!\!{\overline {{x^2}} }\!\!\!&\!\!\!{\overline {xy} }\!\!\!&\!\!\!{\overline {{y^2}} }\!\!\!&\!\!\! \cdots \\ {{\omega _{i1}}}\!\!\!&\!\!\!{{\omega _{i1}}{{\widehat x}_{i1}}}\!\!\!&\!\!\!{{\omega _{i1}}{{\widehat y}_{i1}}}\!\!\!&\!\!\!{{\omega _{i1}}{{\widehat {{x^2}}}_{i1}}}\!\!\!&\!\!\!{{\omega _{i1}}{{\widehat {xy}}_{i1}}}\!\!\!&\!\!\!{{\omega _{i1}}{{\widehat {{y^2}}}_{i1}}}\!\!\!&\!\!\! \cdots \\ {{\omega _{i2}}}\!\!\!&\!\!\!{{\omega _{i2}}{{\widehat x}_{i2}}}\!\!\!&\!\!\!{{\omega _{i2}}{{\widehat y}_{i2}}}\!\!\!&\!\!\!{{\omega _{i2}}{{\widehat {{x^2}}}_{i2}}}\!\!\!&\!\!\!{{\omega _{i2}}{{\widehat {xy}}_{i2}}}\!\!\!&\!\!\!{{\omega _{i2}}{{\widehat {{y^2}}}_{i2}}}\!\!\!&\!\!\! \cdots \\ {{\omega _{i3}}}\!\!\!&\!\!\!{{\omega _{i3}}{{\widehat x}_{i3}}}\!\!\!&\!\!\!{{\omega _{i3}}{{\widehat y}_{i3}}}\!\!\!&\!\!\!{{\omega _{i3}}{{\widehat {{x^2}}}_{i3}}}\!\!\!&\!\!\!{{\omega _{i3}}{{\widehat {xy}}_{i3}}}\!\!\!&\!\!\!{{\omega _{i3}}{{\widehat {{y^2}}}_{i3}}}\!\!\!&\!\!\! \cdots \\ \vdots \!\!\!&\!\!\! \vdots \!\!\!&\!\!\! \vdots \!\!\!&\!\!\! \vdots \!\!\!&\!\!\! \vdots \!\!\!&\!\!\! \vdots \!\!\!&\!\!\! \ddots \\ {{\omega _{iN}}}\!\!\!&\!\!\!{{\omega _{iN}}{{\widehat x}_{iN}}}\!\!\!&\!\!\!{{\omega _{iN}}{{\widehat y}_{iN}}}\!\!\!&\!\!\!{{\omega _{iN}}{{\widehat {{x^2}}}_{iN}}}\!\!\!&\!\!\!{{\omega _{iN}}{{\widehat {xy}}_{iN}}}\!\!\!&\!\!\!{{\omega _{iN}}{{\widehat {{y^2}}}_{iN}}}\!\!\!&\!\!\! \cdots \end{array}} \right) \times \\& {\left( {\begin{array}{*{20}{c}} {\boldsymbol{u}} \\ {{{\partial {\boldsymbol{u}}} / {\partial x}}} \\ {{{\partial {\boldsymbol{u}}} / {\partial y}}} \\ { {{{\partial ^2}{\boldsymbol{u}}} / {2\partial {x^2}}}} \\ {{{{\partial ^2}{\boldsymbol{u}}} / {\partial x\partial y}}} \\ {{{{\partial ^2}{\boldsymbol{u}}} / {2\partial {y^2}}}} \\ \vdots \end{array}} \right)_i} = \; \left( {\begin{array}{*{20}{c}} {{{{\bar{\boldsymbol u}}}_i}} \\ {{\omega _{i1}}{{{\bar{\boldsymbol u}}}_1}} \\ {{\omega _{i2}}{{{\bar{\boldsymbol u}}}_2}} \\ {{\omega _{i3}}{{{\bar{\boldsymbol u}}}_3}} \\ \vdots \\ {{\omega _{iN}}{{{\bar{\boldsymbol u}}}_N}} \end{array}} \right) \\[-10pt] \end{split} $ | (9) |
方程组的第一个方程是约束方程,除约束方程外,其余每个方程前均乘以权系数
| ${\omega _{ij}} = \frac{1}{{\left| {{{\boldsymbol{x}}_j} - {{\boldsymbol{x}}_i}} \right|}}$ | (10) |
该系数用来强调与中心控制体几何上邻近的模板单元对重构结果的影响。在得到单元梯度与高阶导数的基础上,可通过约束方程得到单元变量点值:
| $ {u}_{i}={\overline{u}}_{i}-\frac{\partial u}{\partial x}{\overline{x}}_{i}-\frac{\partial u}{\partial y}{\overline{y}}_{i}-\frac{1}{2}\frac{{\partial }^{2}u}{\partial {x}^{2}}{\overline{{x}^{2}}}_{i}-\frac{{\partial }^{2}u}{\partial x\partial y}{\overline{xy}}_{i}-\frac{1}{2}\frac{{\partial }^{2}u}{\partial {y}^{2}}{\overline{{y}^{2}}}_{i}$ | (11) |
该点值用来插值计算单元面高斯点处的左右状态矢量,以构造该点处的数值通量。
2 模板选择方法本节回顾了当前应用广泛的共点、共面模板以及局部方向模板选择方法的基本思路与存在的问题,并在此基础上,给出了全局方向模板选择方法的具体过程及其表现效果。
2.1 共点与共面模板共点模板以及共面模板的应用最为广泛,其依赖于网格拓扑,并通过相应的模板层数来控制模板单元数量使其满足重构方程的要求,如图2所示,共面模板由于网格单元面数量固定,因此随着模板层数的递增,模板单元数量增长平缓,而共点模板的数量较难控制,并且随着层数增加,单元数量快速上升。
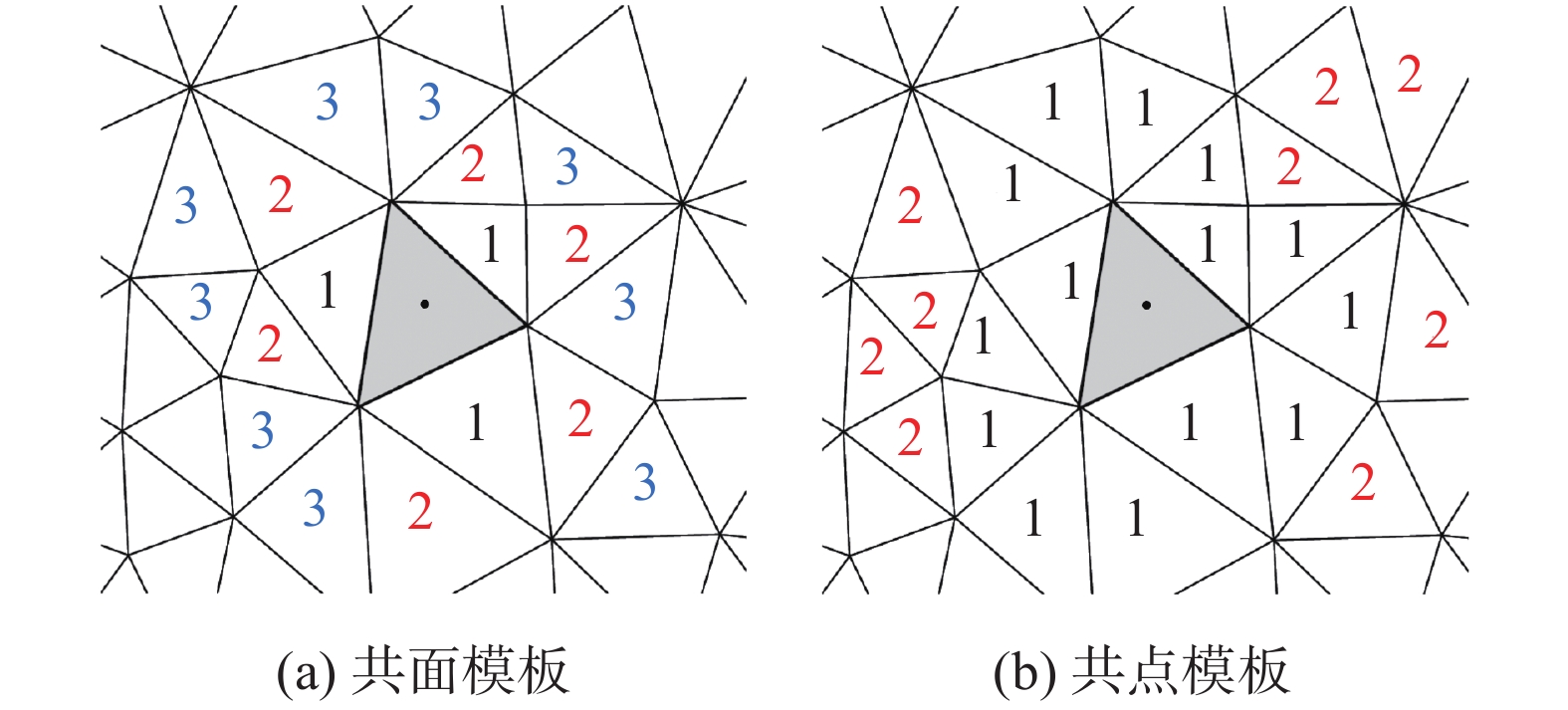
|
图 2 共面模板与共点模板 Fig.2 Face-neighbor and vertex-neighbor stencils |
此外,两种模板选择方式均依赖于固定的网格拓扑关系,针对不同流动无法有效捕捉到流场变化,并且两种模板在满足重构要求的基础上,包含过多冗余单元,尤其是进行高阶导数重构时,所需要的模板数量较多,因此随着层数的增加,冗余单元的数量也因此骤增,这将显著增大计算开销,降低求解效率。
2.2 局部方向模板针对上述两种模板存在的问题,Xiong等[23- 24]构建了基于两个局部方向的模板选择方法,这种模板选择方法有效减少了用于重构的模板单元数量,并且在各项同性或长宽比较小的三角形网格上,两个局部方向近似沿着壁面法向与流向,在二阶精度非结构有限体积求解器中取得了较好地数值表现。
如图3所示,对于四边形单元,局部方向就是网格单元两组对边中点的连线;在处理三角形单元时,可将三角形单元的一个顶点视作由四边形的一条边退化而成,并将其称为“退化点”,但由于存在三种可能的局部方向组合,因此需要采用阵面推进方法[26](Advancing Front Technique, AFT)来确定最终的局部方向组合方式。
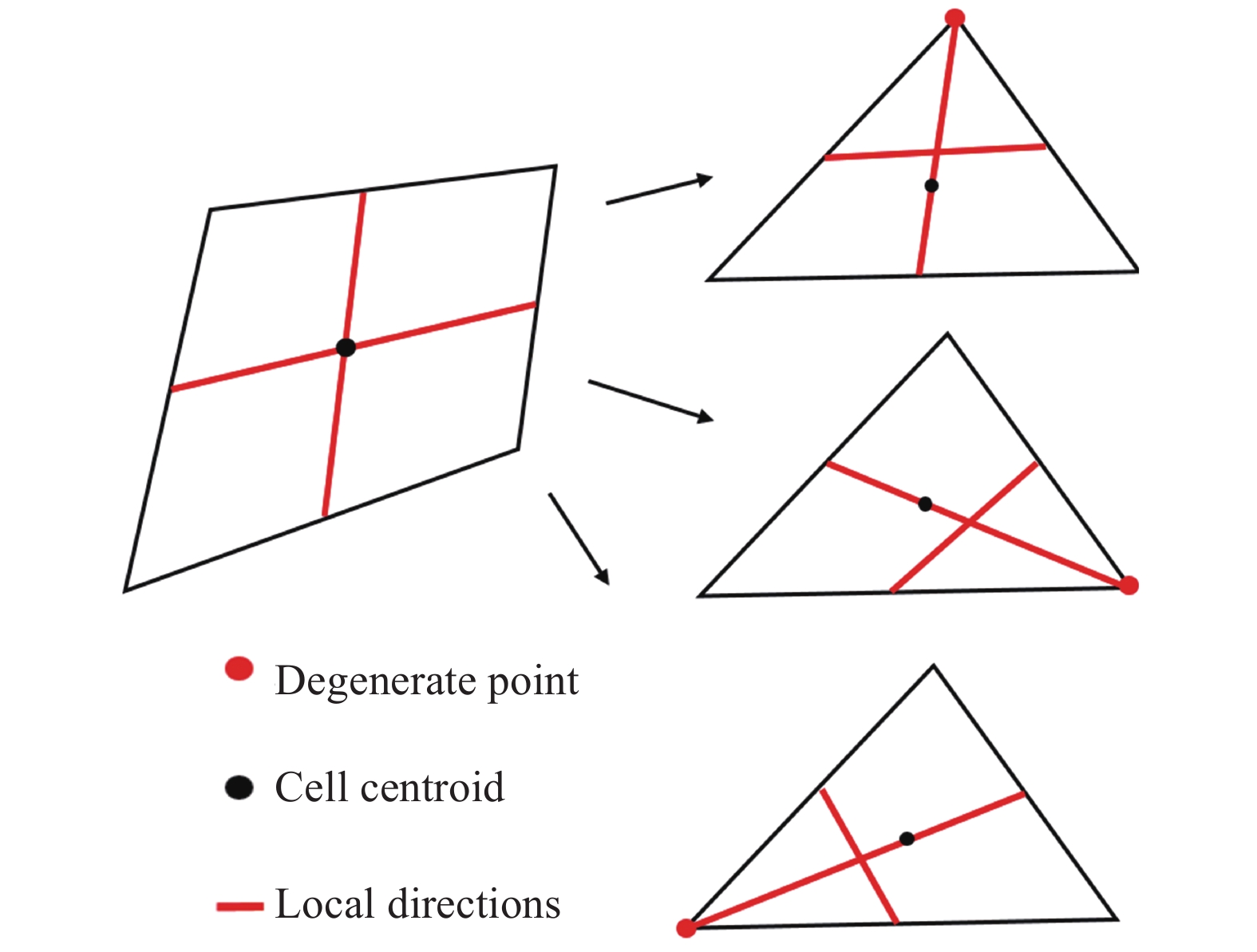
|
图 3 四边形与三角形单元的局部方向组合 Fig.3 Local directions of quadrilateral and triangular grids |
针对三角形网格,基于阵面推进方法找到的局部方向的组合结果如图4所示,从图中可以看出,当网格长宽比较大时,其第一局部方向已偏离壁面法向。
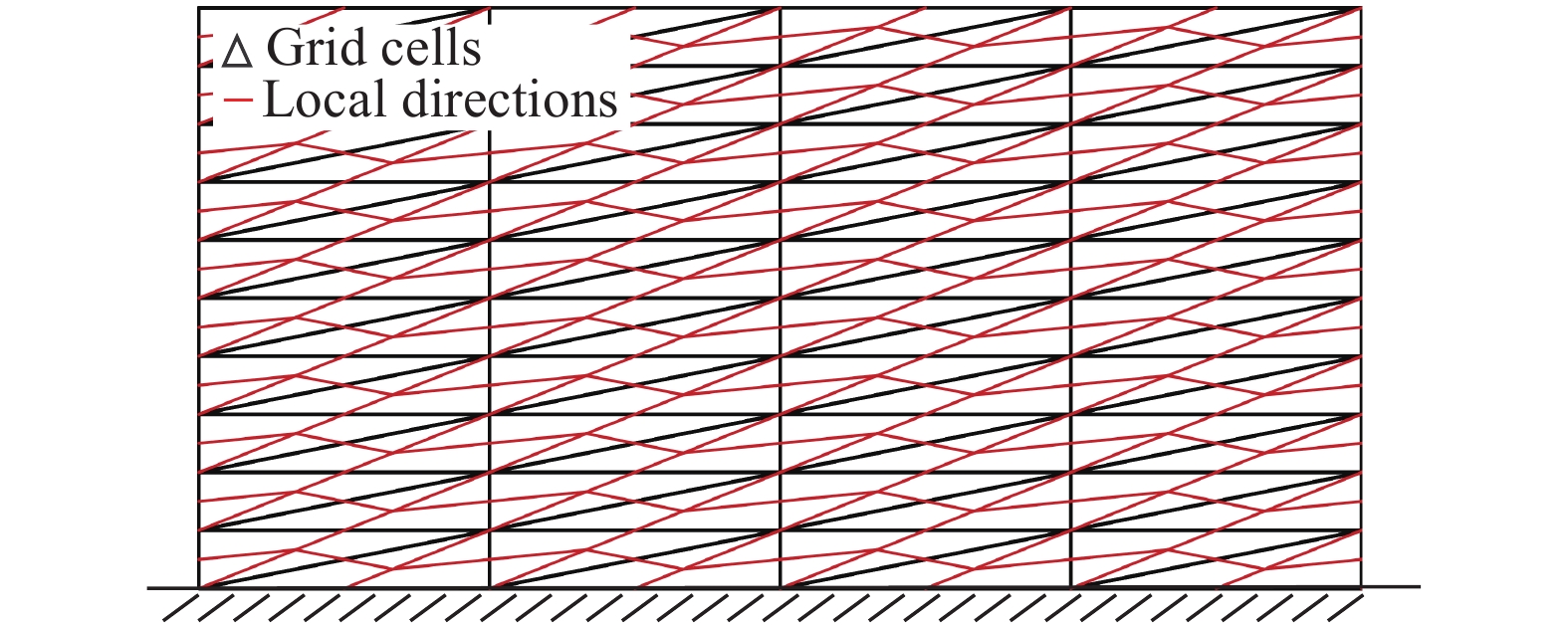
|
图 4 三角形网格单元的局部方向组合 Fig.4 Combination of local directions in a triangular grid |
在确定局部方向的基础上,可沿着两个方向扩充模板单元。如果中心单元为四边形,沿着局部方向选择的模板单元实际上是共面模板单元。
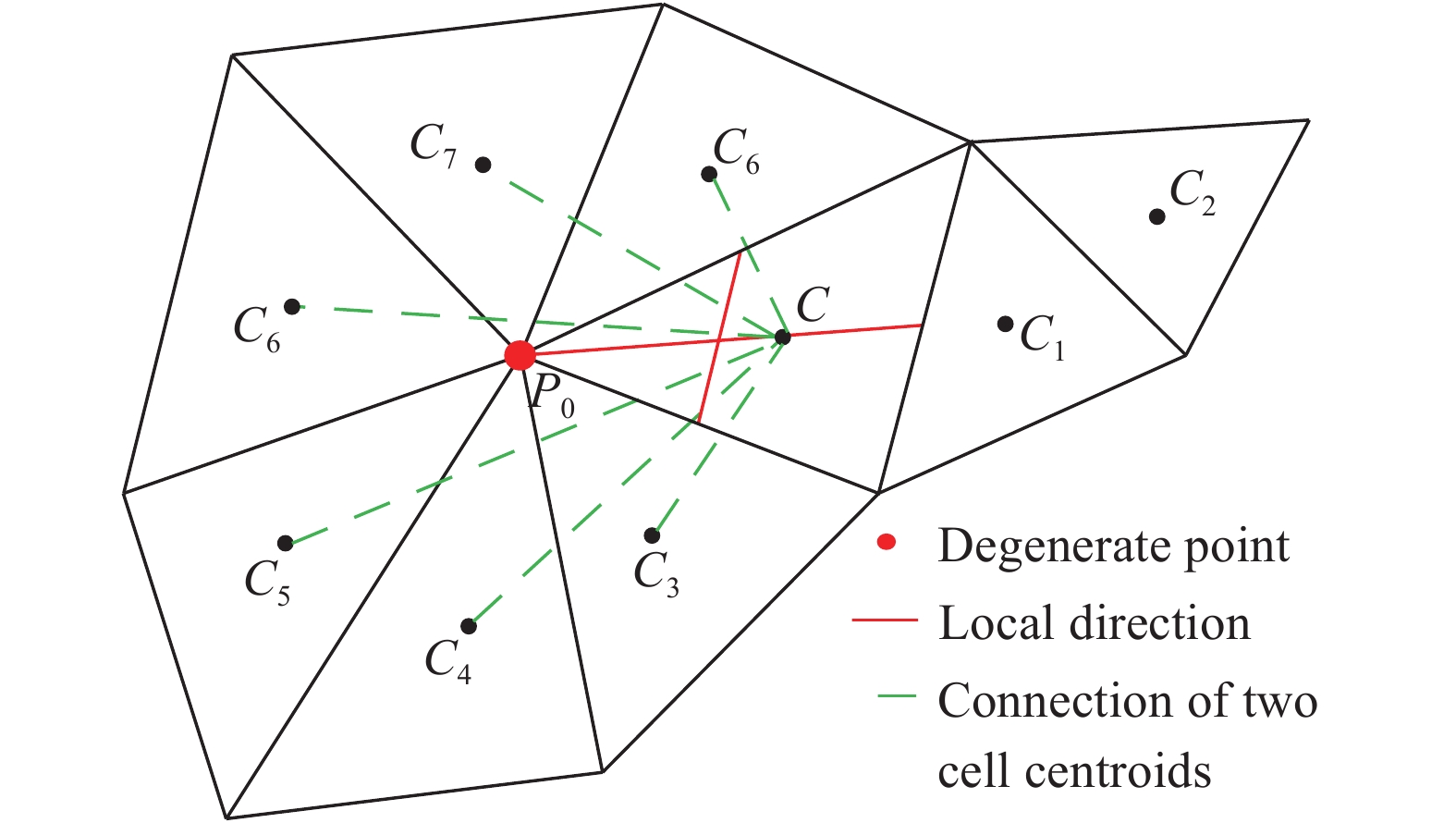
图5展示了三角形单元的模板构造方式。若局部方向通过“退化点”,例如图中的P0点,此时选择和局部方向夹角最大的单元;如果不通过“退化点”,则选择相应的共面模板。由于该模板选择方法涉及阵面推进与夹角判断过程,相对增加了前处理过程的处理开销。
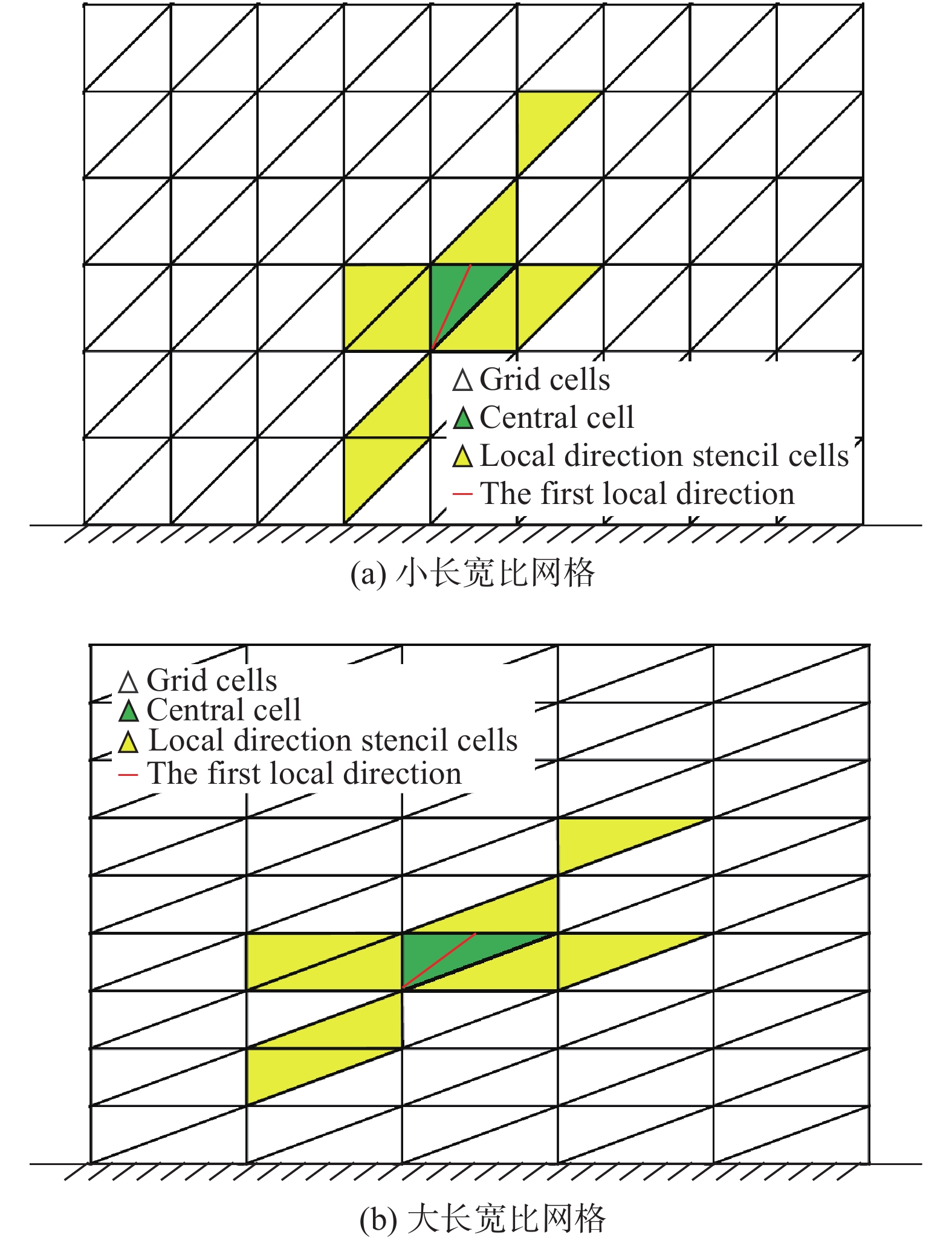
此外,如图6所示,当网格长宽比较小时,局部方向模板单元基本沿着壁面法向与流向,但在高度各向异性网格上,由于局部方向的偏离,导致沿两个方向找到的模板空间延展性下降。经测试,在此类网格上局部方向模板难以保证计算稳定性[24]。因此,针对这一问题,迫切需要发展一种新的模板构造方式,其能摆脱网格拓扑的约束,并准确捕捉流动的各向异性。
|
图 5 三角形网格的模板单元确定 Fig.5 Stencil selection on a triangular grid |
|
图 6 不同长宽比网格上的局部方向模板示意图 Fig.6 Diagram of local-direction stencils on grids with different aspect ratios |
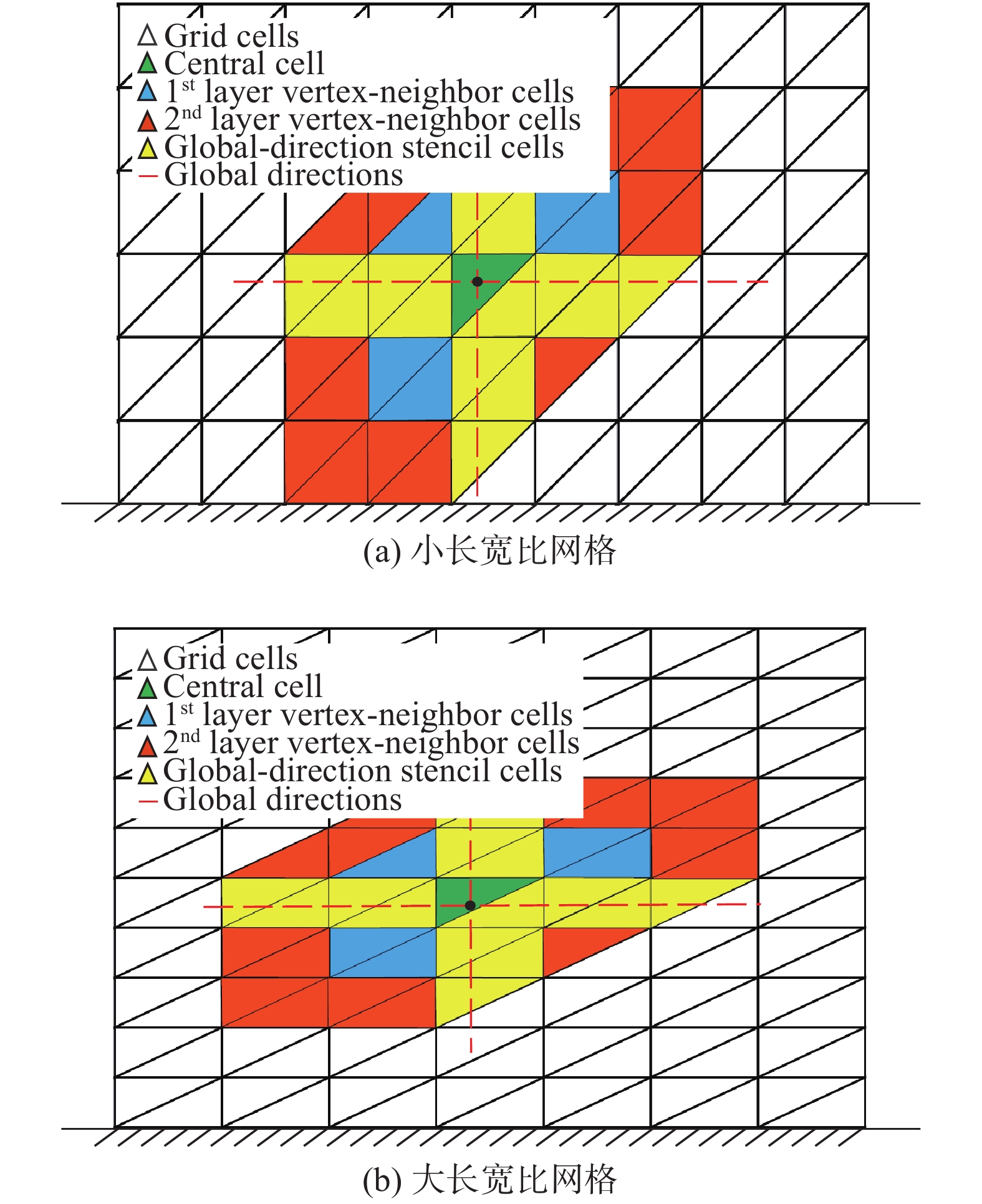
在局部方向模板的基础上,我们针对二阶精度非结构有限体积方法发展了一种全局方向模板选择方法,该方法不再依赖于每个网格单元内部的局部方向,而是计算域的全局方向。因此如图7所示,即使在大长宽比三角形网格上,全局方向模板始终沿着壁面法向与流向,能够准确捕捉到流场的各项异性特征。
具体而言,寻找全局方向模板单元可分为两个步骤,首先需要找到与中心单元共点的模板单元集合,在此基础上,过中心单元的几何中心做两条直线,找到集合中与两条直线相交的模板单元即可。因此,模板单元数量可得到较为准确地控制,并且整个过程并未引入任何复杂性。
|
图 7 不同长宽比网格上的全局方向模板示意图 Fig.7 Diagram of global-direction stencils on grids with different aspect ratios |
针对简单外形,确定壁面法向的过程相对简便,例如图7中给出的规则矩形计算域,其只包含一个壁面,确定全局方向时可直接取单元参考点处的壁面法向与切向。但对于更一般的外形,由于其物面不存在解析曲线,因此针对复杂外形确定计算域中单元参考点的全局方向时,可基于湍流模型中的壁函数计算首先获得单元壁面距离[27-29]。在此基础上,Jalali与Ollivier-Gooch[19]等提出了一种基于壁面距离来获得壁面法向的有效手段,可采用该方法得到计算域中每一单元参考点处的壁面法向。此外,为使模板具有更好的空间延展性,另一个全局方向可取与壁面法向垂直的方向。
但在网格划分好的前提下,对计算域中的每一个网格参考点计算一次壁面距离,并基于壁面距离确定壁面法向并不容易。这种处理方式会显著增加算法复杂度与实现的困难程度,尤其在并行计算中。更重要的是,针对凹腔[30]这类局部包含多个壁面的情况,若在整个计算域内均采用全局方向模板,会造成方向判断混乱,导致方法无法实施。
因此针对复杂外形,较好的处理方法是在对物面附近网格单元进行重构时,采用全局方向模板,来捕捉边界层内部的流场变化,但在远离边界层的各向同性区域仍采用依赖网格拓扑关系的共点或共面模板。这样做的好处在于,在边界层内部可以有效捕捉流动的各向异性特征,并减少重构过程使用的模板单元数量;此外,针对凹腔等外形,考虑局域性后可保证方法的正确实施;同时,仅对物面附近的网格单元确定全局方向,可有效简化算法的实现过程,并且在并行计算中的处理也会更加简便。
本文首先在一些简单外形上验证了全局方向模板在高阶精度非结构有限体积方法中的数值表现,为下一步将方法向复杂外形推广打下了基础。
3 数值验证为检验不同重构模板在高阶精度非结构有限体积求解器中的数值表现,本节通过基于制造解方法(Method of Manufactured Solutions, MMS)[31-33]的流动以及超声速涡流两类数值算例,分别对比了共点、共面模板以及全局方向模板在三阶精度求解器上的计算效果。由于2.2节分析了在各向异性的三角形网格上,基于局部方向找到的模板单元偏离壁面法向,导致其在二阶精度求解器上,计算稳定性下降[23]。本节为了进一步检验局部方向模模板在高阶精度非结构有限体积方法中应用的可行性,在测试上述三种模板计算效果的基础上,还测试了局部方向模板的数值表现。同时,为简化图表中对不同模板的描述,我们分别使用V-Stencil、F-Stencil、L-Stencil与G-Stencil来表示共点、共面、局部方向模板与全局方向模板。
3.1 基于制造解方法的流动本节针对欧拉方程构建了一个具有各向异性特征的MMS流动[34],并且解的形式如下:
| $\left. \begin{array}{l} \rho = 1.12 + 0.15\sin \left[ {{\text{π}} \left( {3.12x + 1895.92y} \right)} \right] \\ u = 1.32 + 0.06\sin \left[ {{\text{π}} \left( {2.09x + 2099.21y} \right)} \right] \\ v = 1.18 + 0.03\sin \left[ {{\text{π}} \left( {2.15x + 2001.32y} \right)} \right] \\ p = 1.62 + 0.31\sin \left[ {{\text{π}} \left( {3.79x + 1973.98y} \right)} \right] \\ \end{array} \right\}$ | (12) |
因此,可首先根据解的形式得到源项s为:
| ${\boldsymbol{s}} \!=\! {\rm{div}}{\boldsymbol{F}} \!=\! \left(\!\! \begin{array}{l} u\dfrac{{\partial \rho }}{{\partial x}} + \rho \dfrac{{\partial u}}{{\partial x}} + v\dfrac{{\partial \rho }}{{\partial y}} + \rho \dfrac{{\partial v}}{{\partial y}} \\ 2\rho u\dfrac{{\partial u}}{{\partial x}} + {u^2}\dfrac{{\partial \rho }}{{\partial x}} + \rho \left( {v\dfrac{{\partial u}}{{\partial y}} + u\dfrac{{\partial v}}{{\partial y}}} \right) + uv\dfrac{{\partial \rho }}{{\partial y}} + \dfrac{{\partial p}}{{\partial x}} \\ 2\rho v\dfrac{{\partial v}}{{\partial y}} + {v^2}\dfrac{{\partial \rho }}{{\partial y}} + \rho \left( {v\dfrac{{\partial u}}{{\partial x}} + u\dfrac{{\partial v}}{{\partial x}}} \right) + uv\dfrac{{\partial \rho }}{{\partial x}} + \dfrac{{\partial p}}{{\partial y}} \\ u\dfrac{{\partial \left( {\rho H} \right)}}{{\partial x}} + \rho H\dfrac{{\partial u}}{{\partial x}} + v\dfrac{{\partial \left( {\rho H} \right)}}{{\partial y}} + \rho H\dfrac{{\partial v}}{{\partial y}} \\ \end{array} \!\!\right)$ | (13) |
由于本文探讨三阶精度数值模拟中的不同模板选择方法,如果仅采用单元中心处的源项点值,无法达到二阶以上精度。因此需要对源项在控制体单元上进行数值积分,以保证其具有三阶精度:
| ${\boldsymbol{s}} = \sum\limits_{i = 1}^{{N_f}} {{w_i}{{\boldsymbol{s}}_i}} $ | (14) |
式中si与wi分别代表单元面中点处的源项与权系数,参照文献[20],wi可取

|
图 8 基于制造解的流场 Fig.8 Flow fields with manufactured solutions |
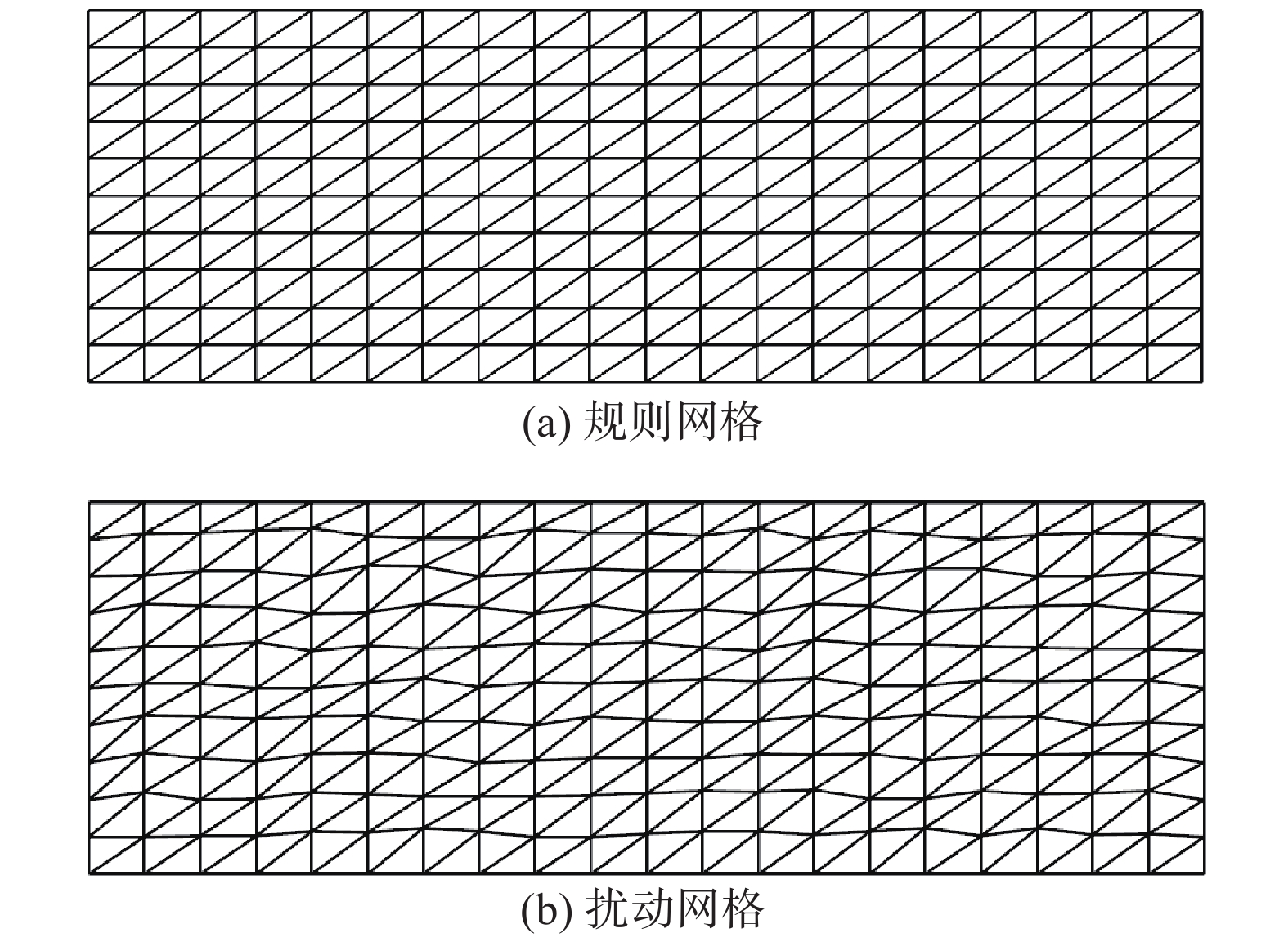
此外,我们分别测试了网格长宽比AR = 5×102、1×103的规则与扰动三角形网格,并且在每种长宽比下,分别设置了五套由疏到密的网格以测试不同模板的计算精度。网格示意图与背景四边形网格量分布如图9与表1所示。
|
图 9 规则与扰动三角形网格 Fig.9 Regular and randomly perturbed triangular grids |
| 表 1 不同长宽比下背景四边形网格的分布量 Table 1 The distribution of background quadrilateral grid cells with different aspect ratios |
|
|
为简化分析过程,并对比在高度各项异性网格上不同模板的表现,本节给出了长宽比AR = 1×103时的计算结果。但在测试过程中,我们发现局部方向模板在长宽比AR = 5×102与1×103的高度各向异性网格上计算发散。深入分析后发现,该方法在边界附近找到的模板单元数量不足。
如图10所示,对边界单元C扩充模板单元时,首先可沿第二局部方向,找到与单元C共面的模板单元C2,其次在沿第一局部方向寻找模板单元时,由于第一局部方向与CC2之间的夹角小于CC1,进而沿第一局部方向找到的模板单元仍为C2,导致在边界附近模板数量不足,需要不断扩充层数以保证正确求解边界单元的重构方程。因此后续的算例测试只给出了共点、共面模板与全局方向模板的计算结果。

|
图 10 边界附近的局部方向模板单元扩充 Fig.10 The stencil augmentation of boundary-adjacent cells |
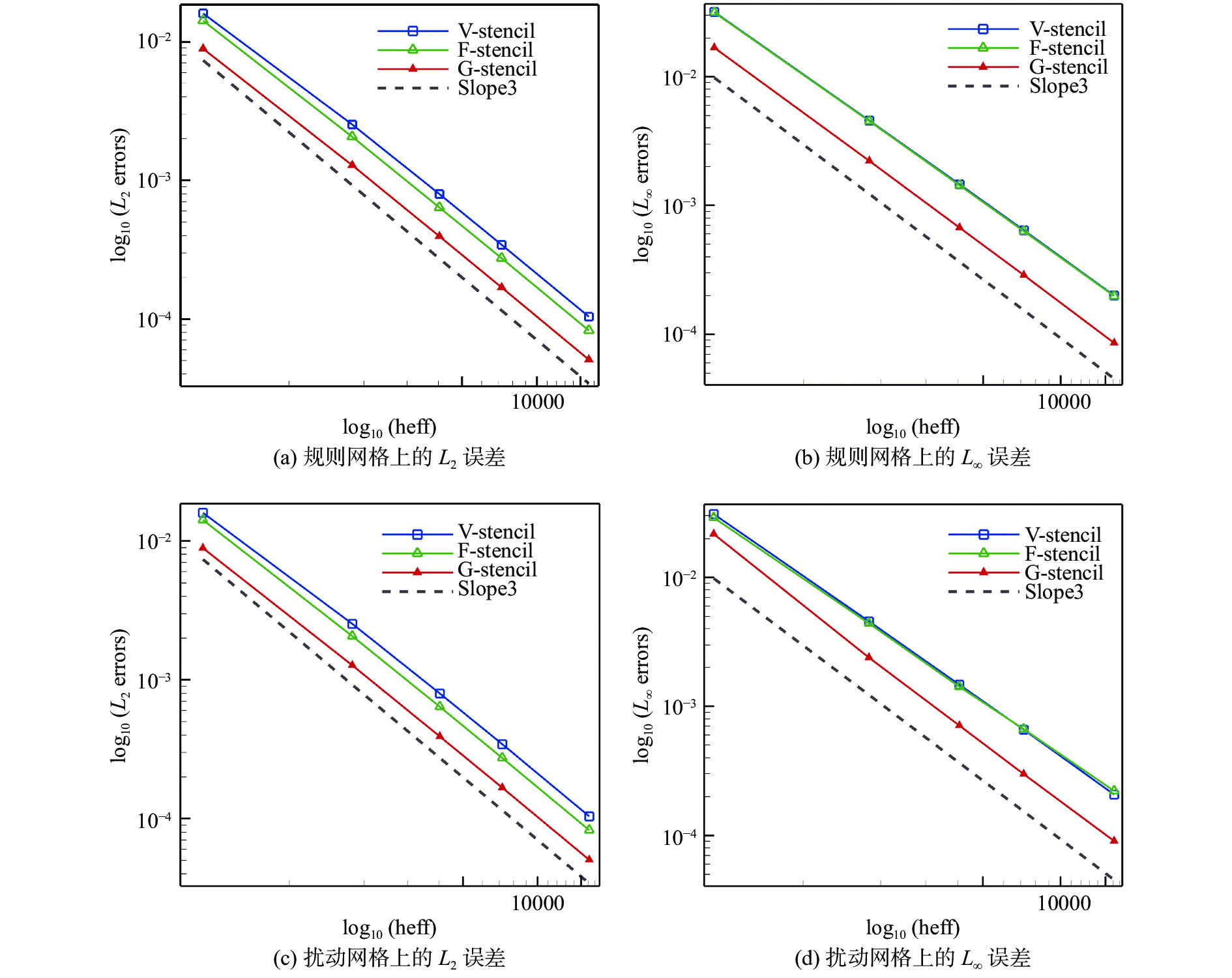
从图11与表2反映的计算结果来看,使用三种模板均能接近并达到求解器的设计精度,但在三种模板中,不论在规则网格还是添加随机节点扰动的网格上,全局方向模板得到的计算误差更低,因此,该模板的使用能够有效改善求解器的计算准确性。
| 表 2 规则密网格上的计算误差以及最后两套网格间的精度 Table 2 Errors on the finest regular grid and computational accuracy between the last two sets of grids |
|
|
|
图 11 规则网格与扰动网格上的计算误差 Fig.11 Computational errors on the regular and perturbed grids |
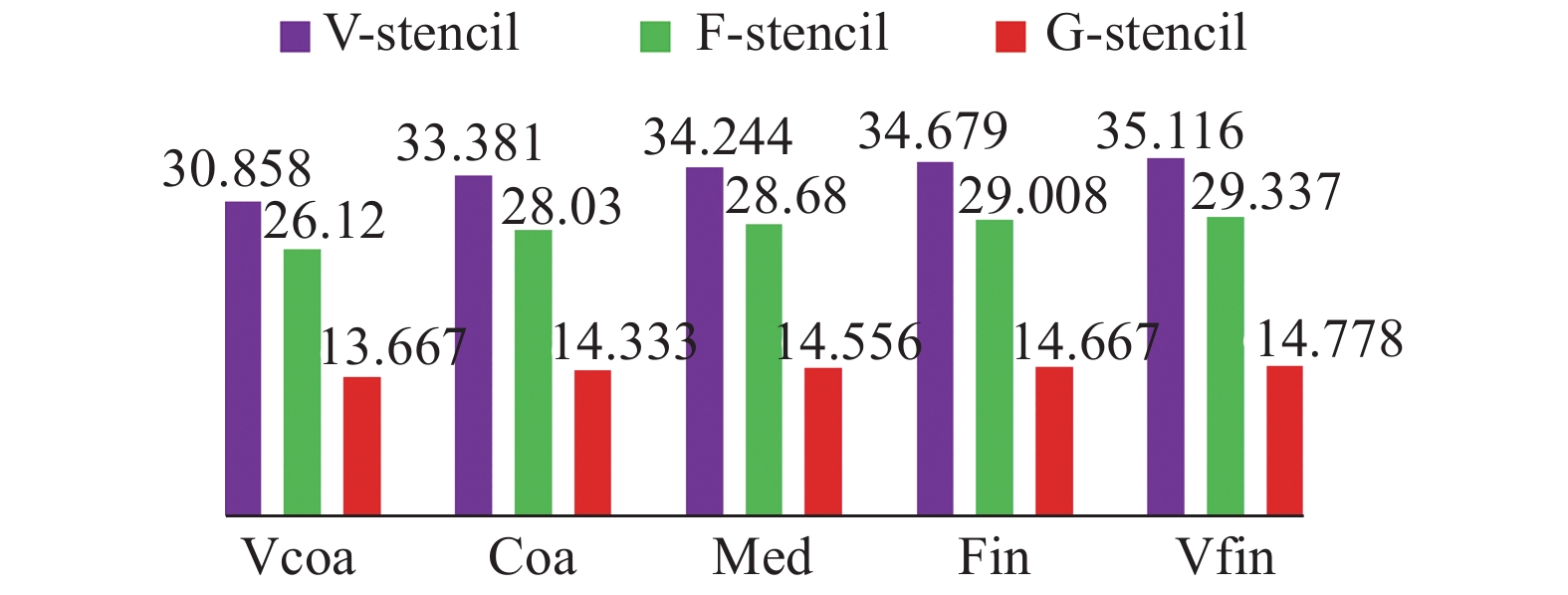
此外,由于三阶精度非结构FV方法的重构过程需要求解6个未知量,因此,至少需要6个模板单元。但共点模板当层数取1时,在边界单元上无法满足重构方程组的求解,因此,需要将层数扩充为2,而共面模板只有当层数增加至4层时才可进行流场计算。结合图12可以明显看出,相比这两种模板,全局方向模板所需要的模板单元数量更少,因此在具有更高计算准确性的同时,可相对降低重构过程的计算开销。
|
图 12 三种模板的平均模板单元数量 Fig.12 Average stencil sizes of three different stencils |
但在上述对比中,三种模板选择方式均是基于边界处的模板单元数量而给定整体的模板层数,从而造成共点与共面模板的单元数量在整个流场中明显增加。在此基础上,我们仅对边界单元扩充模板层数,而内部单元的层数保持最低,这样可有效缩减三种模板的规模。
在长宽比AR = 1×103的网格上,通过上述方案得到三种模板的模板单元数量如表3所示。
| 表 3 三种模板选择方式在不同网格上的平均模板单元数量 Table 3 Average stencil sizes of three stencil selection methods on five sets of triangular grids |
|
|
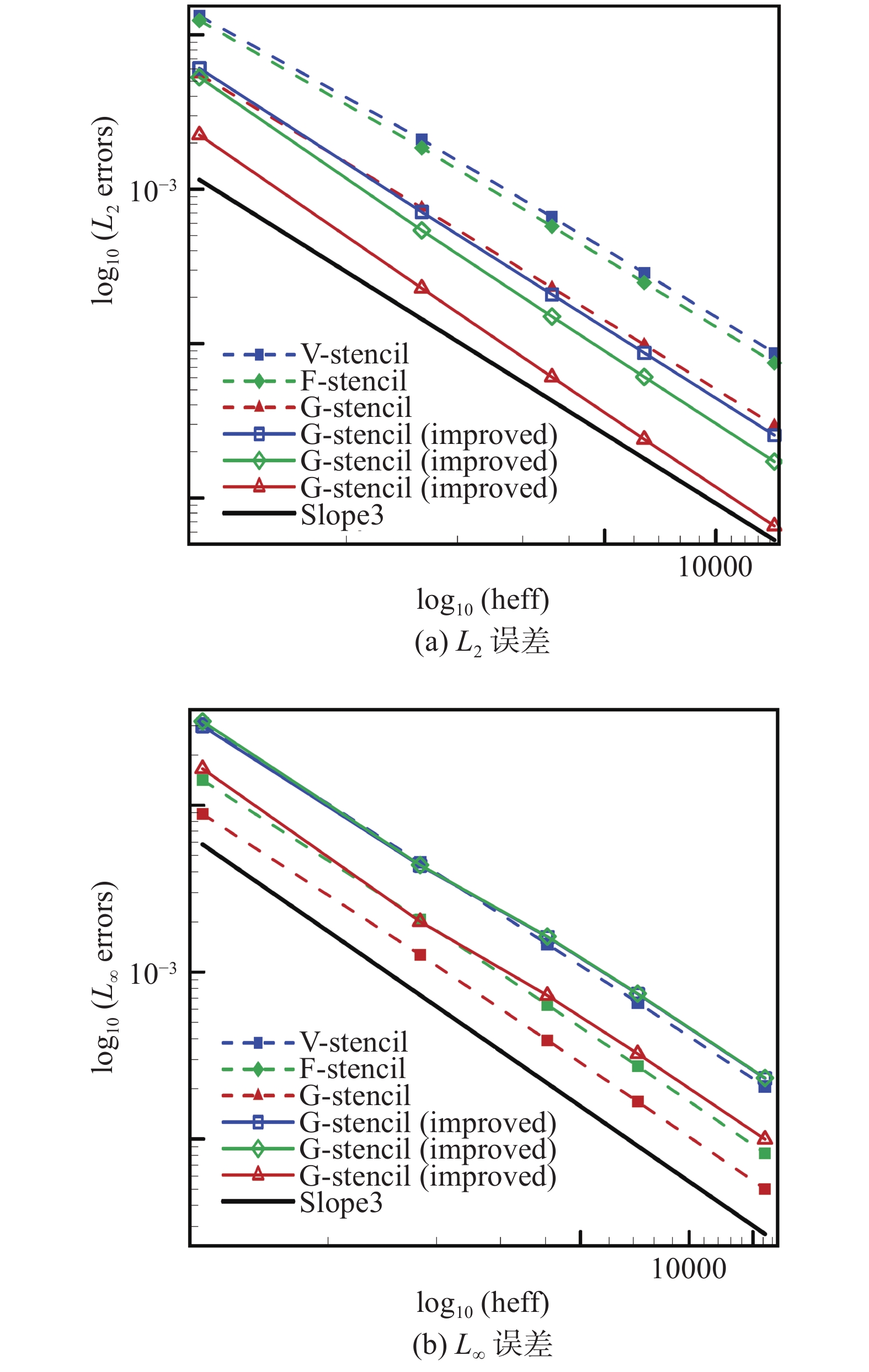
为对比控制模板层数前后的计算误差,两种情况的误差统计结果如图13所示,并且修改层数后的模板选择方法均添加标识“improved”。
|
图 13 修改模板层数前后的计算误差对比 Fig.13 The comparison of computational errors before and after altering stencil layers |
从图中可以明显看出,采用最小的模板层数后,三种模板的L2误差均明显降低,而L∞误差相比缩减模板层数之前有所上升。但不论是否缩减模板层数,全局方向模板的误差值在三种方法中均保持最低。同时结合表3中的数据可以看出,在对三种模板选择方式缩减模板层数后,共点、共面模板,以及全局方向模板的模板单元数量均有所减少,但全局方向模板单元数量仍保持最少。因此,在模板数量差距较小的情况下,全局方向模板的计算误差仍在三种方法中保持最低,有效证明了从完全多维的共点模板中提取具有分维特征的全局方向模板单元的必要性。
3.2 超声速涡流动本节采用含曲线边界的超声速涡流动,来进一步检验全局方向模板在真实流动中的数值表现。该流动具有解析解,其形式如下:
| $\left. \begin{array}{l} \rho = {\rho _i}{\left( {1 + \dfrac{{\gamma - 1}}{2}M_i^2\left( {1 - {{\left( {\dfrac{{{r_i}}}{r}} \right)}^2}} \right)} \right)^{\left( {1/\left( {\gamma - 1} \right)} \right)}} \\ P = \dfrac{{{\rho ^\gamma }}}{\gamma },\;\;\left\| {\boldsymbol{v}} \right\| = \dfrac{{{c_i}{M_i}}}{r} \end{array} \right\}$ | (15) |
式中
| ${c_i} = \sqrt {{\gamma} {{{P_i}} / {{{\rho} _i}}}} = 1$ | (16) |
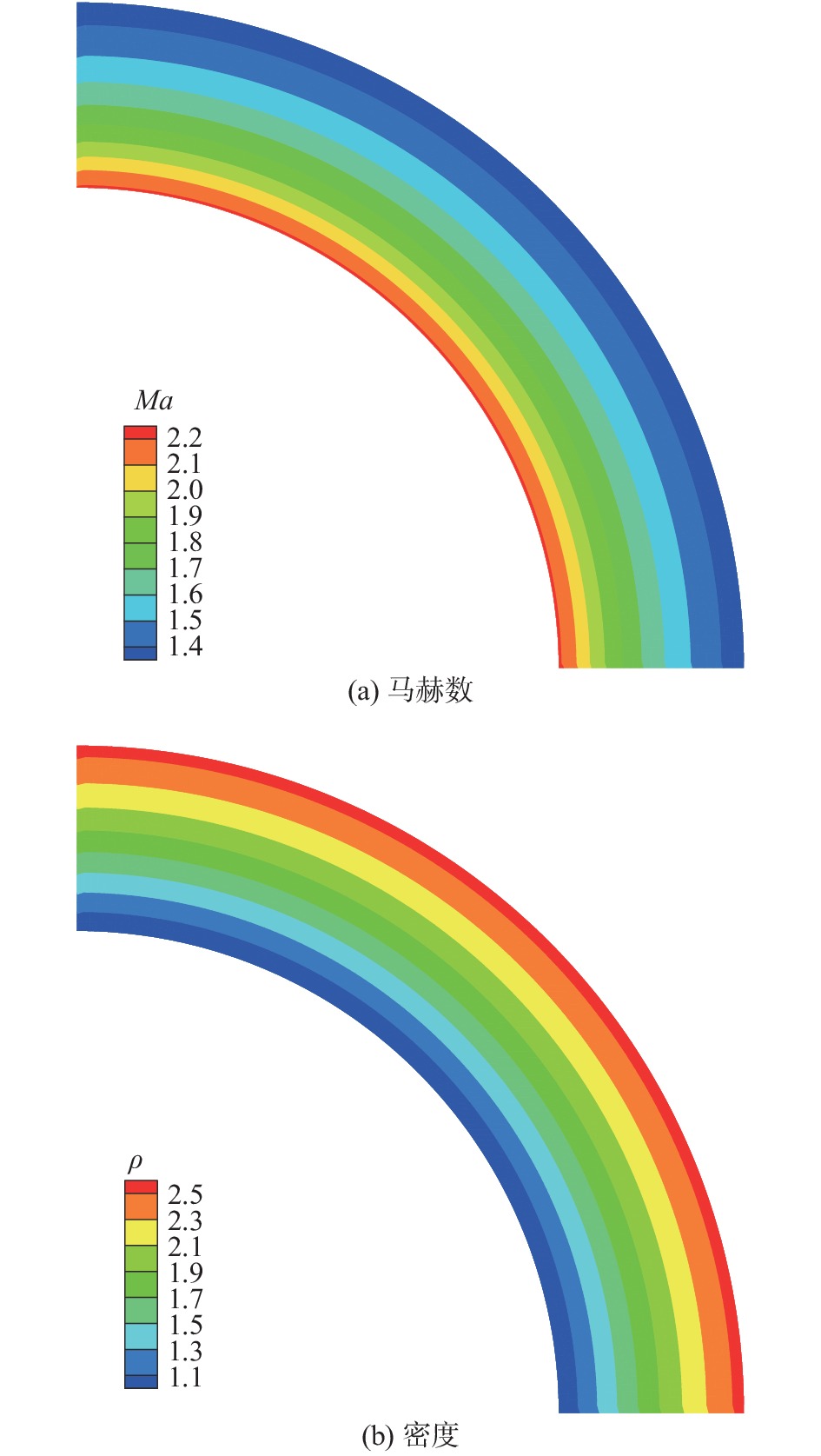
该流动的流场结构如图14所示。
|
图 14 超声速涡流场 Fig.14 Flow fields of the supersonic vortex flow |
同样,分别测试了两种不同长宽比网格下的计算结果,由于此算例包含曲线边界,网格长宽比不像直线边界网格在全场统一。因此采用壁面第一层网格的长宽比来近似代替。最疏一套网格示意图,以及背景四边形网格在径向、周向的分布量如图15与表4所示。该算例同样测试了局部方向模板的计算效果,但与3.1节所反映出的计算结果一致,局部方向模板在该数值算例中出现计算发散的现象。因此,在统计误差时只给出了共点、共面模板以及全局方向模板的计算结果。
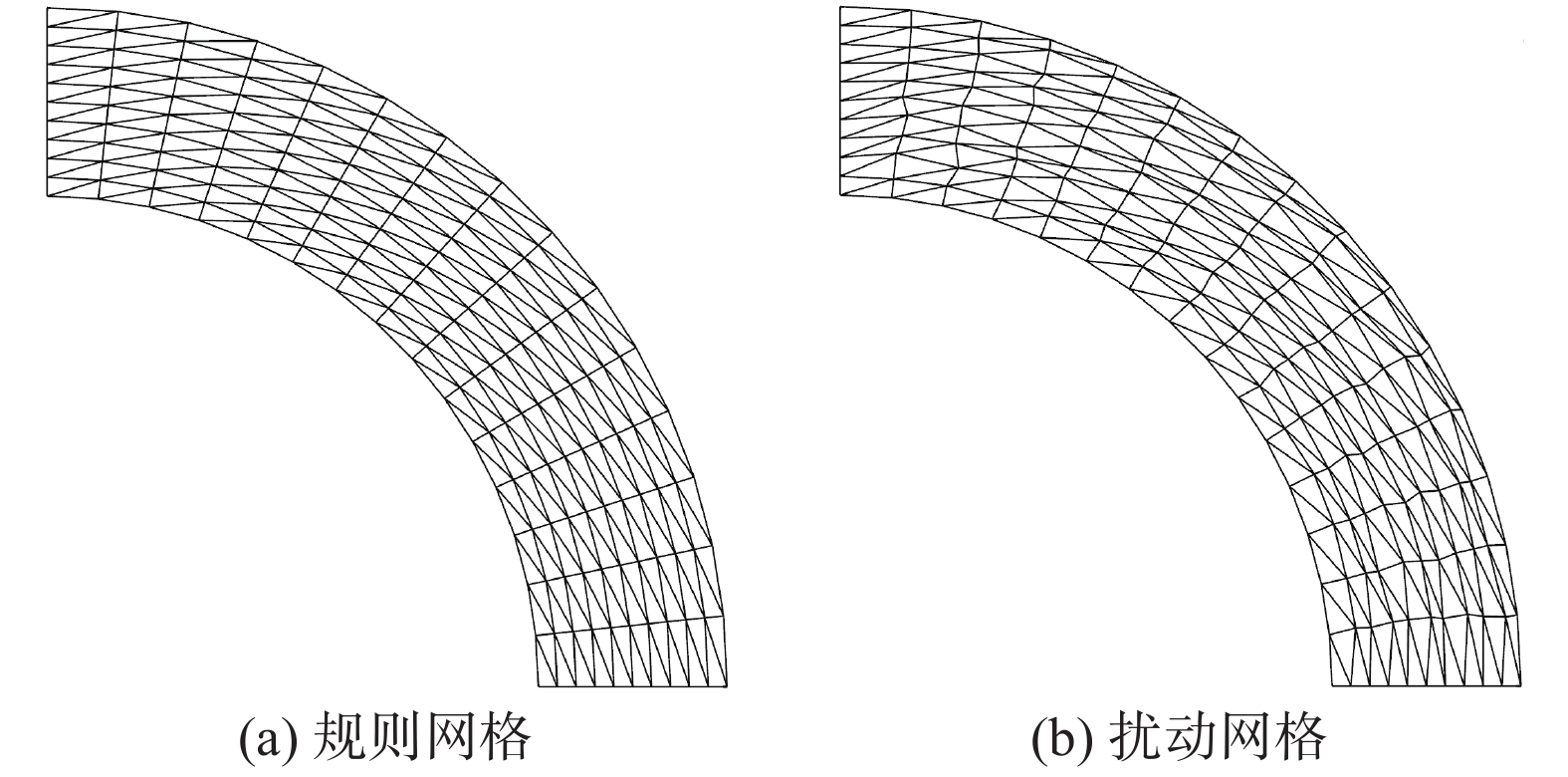
|
图 15 规则与扰动三角形网格 Fig.15 Regular and randomly perturbed triangular grids |
| 表 4 不同长宽比下的背景四边形网格在径向与周向的分布量 Table 4 The distribution of background quadrilateral grid cells in the radial and circumferential directions |
|
|
为简化结果分析,文中给出了长宽比AR ≈ 4.0时的计算结果。图16与图17分别为在规则网格和扰动网格上,三种模板在全场以及壁面附近的误差统计结果,表4中列举的数据为规则密网格上的具体误差值以及最后两套网格间的计算精度。
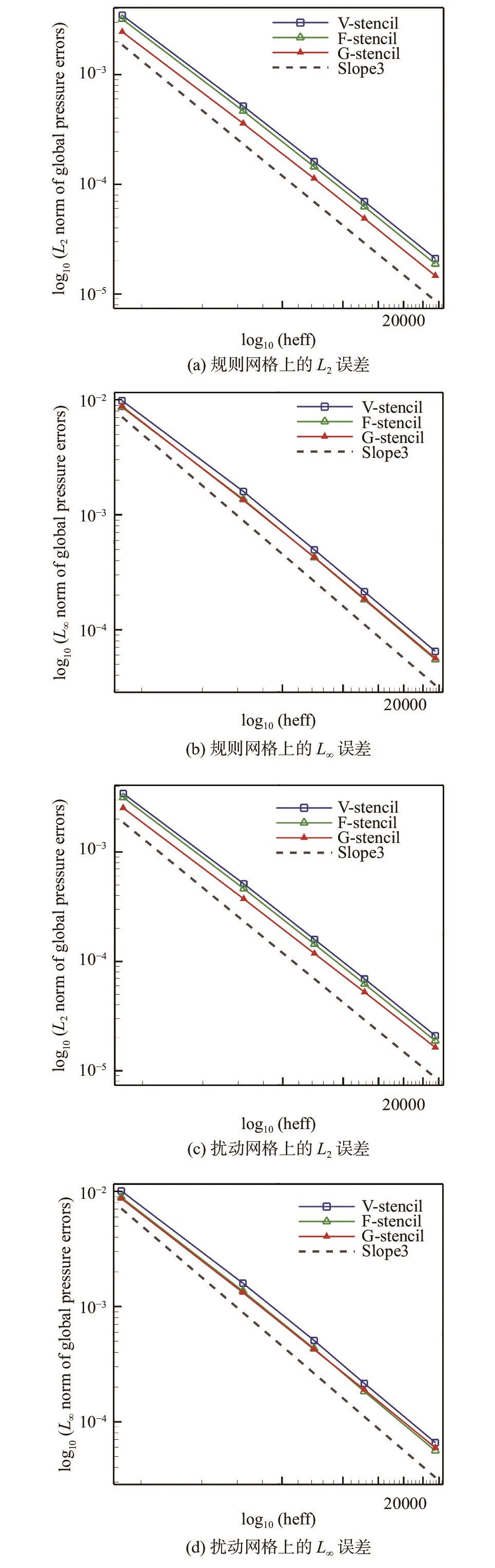
|
图 16 规则网格与扰动网格上的全场压力误差 Fig.16 Global pressure errors on the regular and perturbed grids |
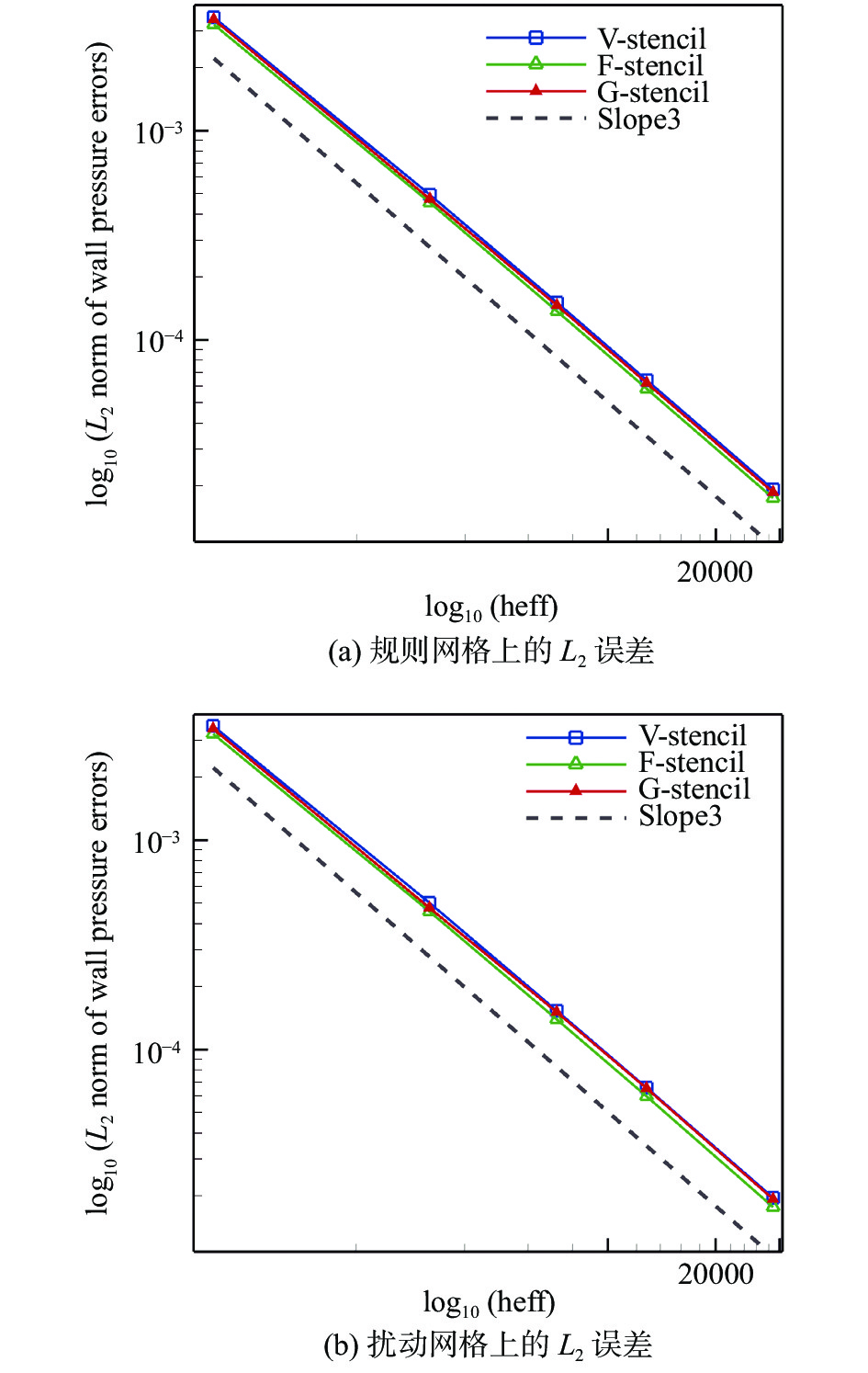
|
图 17 规则网格与扰动网格上的壁面压力误差 Fig.17 Wall pressure errors on the regular and perturbed grids |
从图16中可以看出,不论在规则网格还是扰动网格上,三种模板得到的计算结果均接近求解器的设计精度。从误差值来看,全局方向模板的L2误差在三种模板中最低,L∞误差与共面模板接近,并稍高于共面模板,但低于共点模板。在此基础上统计了壁面附近的误差值,其中最大误差通常位于壁面,而L∞误差曲线已在全场中统计,因此壁面附近只给出了L2误差曲线。
从图17可以看出,三种模板在壁面附近的误差接近,但结合表5的数据可以看出,其中共面模板的误差最低,全局方向模板的误差与共点模板接近并稍低于共点模板。
| 表 5 规则密网格上的计算误差以及最后两套网格间的精度 Table 5 Errors on the finest regular grid and computational accuracy between the last two sets of grids |
|
|
此外,从图18可以明显看出,全局方向模板所需要的模板单元数量更少,相比共点模板与共面模板,模板数量分别减少了57.9%与49.6%,在具备较高计算准确性的同时降低了重构过程的计算开销。

|
图 18 三种模板的平均模板单元数量 Fig.18 Average stencil sizes of three different stencils |
本文将全局方向模板推广至高阶精度非结构有限体积方法,并通过基于制造解的数值流动与真实超声速涡流分别检验了全局方向模板在具有三阶精度非结构有限体积求解器中的数值表现,得出以下结论:
1)首先从方法实现过程而言,全局方向模板选择方法的过程简便,相比局部方向模板,全局方向模板单元的确定有效避免了阵面推进与局部方向传递的繁琐;相比常用的共点模板,新方法只需要在确定共点单元的的基础上,找到与两个全局方向相交的网格单元即可,该过程并未引入任何复杂性。
2)其次从计算结果来看,相比两种常用的共点、共面模板,全局方向模板的使用可有效降低计算误差,在测试的两个数值算例中,全局方向模板均具有较好的数值表现。
3)此外,全局方向模板对不同长宽比的网格具有较强的适应性,摆脱了网格单元的拓扑约束,即使在大长宽比三角形网格上,模板单元始终能够保证沿着壁面法向与流向,具有较好的空间延展性。
4)最后,基于全局方向的模板选择方法从完全多维模板中提取了具有分维特征的模板单元,保证空间延展性的同时,可有效减少重构过程所需的模板单元数量。在具有三阶精度的非结构有限体积求解器中,相比共点与共面模板,分别减少模板总数的57.9%与49.6%,可节约计算开销。
综上,全局方向模板在高阶精度非结构有限体积方法中具有较好的数值表现,具备进一步推广与应用的可行性。接下来的工作将从两个方面分别开展:首先,从改善计算效率方面,针对计算域内的不同网格单元,进一步对比分析采用不同模板层数后几种模板的计算效果,以控制重构过程所需要的模板单元数量;其次,从方法推广与实际应用层面,应推广该重构模板在二维、三维复杂外形以及粘性流动中的使用。同时,粘性项的高精度离散同样也是下一步研究与关注的重点。
| [1] |
MAVRIPLIS D J. Unstructured grid techniques[J]. Annual Review of Fluid Mechanics, 1997, 29(1): 473-514. DOI:10.1146/annurev.fluid.29.1.473 |
| [2] |
LISEIKIN V. Grid generation methods[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 1999. doi: 10.1007/978-3-662-03949-6
|
| [3] |
DUFRESNE Y, MOUREAU V, LARTIGUE G, et al. A massively parallel CFD/DEM approach for reactive gas-solid flows in complex geometries using unstructured meshes[J]. Computers & Fluids, 2020, 198: 104402. DOI:10.1016/j.compfluid.2019.104402 |
| [4] |
陈建军, 黄争舸, 杨永健, 等. 复杂外形的非结构四面体网格生成算法[J]. 空气动力学学报, 2010, 28(04): 400-404. CHEN J J, HUANG Z G, YANG Y J, et al. Unstructured tetrahedral mesh generation for complex configurations[J]. Acta Aerodynamica Sinica, 2010, 28(04): 400-404. DOI:10.3969/j.issn.0258-1825.2010.04.006 (in Chinese) |
| [5] |
赵辉, 张耀冰, 陈江涛, 等. 非结构网格体心梯度求解方法的精度分析[J]. 空气动力学学报, 2019, 37(5): 844-854. ZHAO H, ZHANG Y B, CHEN J T, et al. The accuracy assessment of gradient computation methods on unstructured grids[J]. Acta Aerodynamica Sinica, 2019, 37(5): 844-854. DOI:10.7638/kqdlxxb-2018.0092 (in Chinese) |
| [6] |
唐静, 李彬, 周乃春, 等. 基于非结构网格流场超大规模并行计算[J]. 空气动力学学报, 2019, 37(1): 61-67. TANG J, LI B, ZHOU N C, et al. Large scale parallel computing for fluid dynamics on unstructured grid[J]. Acta Aerodynamica Sinica, 2019, 37(1): 61-67. DOI:10.7638/kqdlxxb-2016.0088 (in Chinese) |
| [7] |
DISKIN B, THOMAS J L, NIELSEN E J, et al. Comparison of node-centered and cell-centered unstructured finite-volume discretizations: viscous fluxes[J]. AIAA Journal, 2010, 48(7): 1326-1338. DOI:10.2514/1.44940 |
| [8] |
王年华, 李明, 张来平. 非结构网格二阶有限体积法中黏性通量离散格式精度分析与改进[J]. 力学学报, 2018, 50(03): 527-537. WANG N H, LI M, ZHANG L P. Accuracy analysis and improvement of viscous flux schemes in unstructured second-order finite-volume discretization[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(03): 527-537. DOI:10.6052/0459-1879-18-037 (in Chinese) |
| [9] |
DISKIN B, THOMAS J L. Comparison of node-centered and cell-centered unstructured finite-volume discretizations: inviscid fluxes[J]. AIAA Journal, 2011, 49(4): 836-854. DOI:10.2514/1.J051870 |
| [10] |
JAMESON A, MAVRIPLIS D. Finite volume solution of the two-dimensional Euler equations on a regular triangular mesh[J]. AIAA Journal, 1986, 24(4): 611-618. DOI:10.2514/3.9315 |
| [11] |
SCHWOPPE A, DISKIN B. Accuracy of the cell-centered grid metric in the DLR TAU-Code[J]. Notes on Numerical Fluid Mechanics and Multidisciplinary Design, 2013, 121: 429-437. DOI:10.1007/978-3-642-35680-3_51 |
| [12] |
李万爱. 非结构网格高精度数值方法的若干问题研究[D]. 北京: 清华大学, 2012. LI W A. Research on the high order accurate numerical methods on unstructured grids[D]. Beijing: Tsinghua University, 2012. (in Chinese) |
| [13] |
张来平, 李明, 刘伟, 等. 基于非结构/混合网格的高精度DG/FV混合方法研究进展[J]. 空气动力学学报, 2014, 32(06): 717-726. ZHANG L P, LI M, LIU W, et al. Recent development of high order DG/FV hybrid methods[J]. Acta Aerodynamica Sinica, 2014, 32(06): 717-726. DOI:10.7638/kqdlxxb-2014.0123 (in Chinese) |
| [14] |
XIE B, JIN P, XIAO F. 基于非结构网格的不可压N-S方程多矩有限体积法(英文)[J]. 空气动力学学报, 2016, 34(2):252-266. XIE B, JIN P, XIAO F. A multi-moment finite volume method for incompressible navier-stokes equations on unstructured grids[J]. Acta Aerodynamica Sinica, 2016, 34(2): 252-266.doi:10.7638/kqdlxxb-2016.0013 |
| [15] |
徐岚, 崔桂香, 许春晓, 等. 非均匀网格湍流大涡模拟高精度有限体积解法[J]. 空气动力学学报, 2006, 24(3): 275-284. XU L, CUI G X, XU C X, et al. High accurate finite volume method on non-uniform meshes for large eddy simulation of turbulent flows[J]. Acta Aerodynamica Sinica, 2006, 24(3): 275-284. DOI:10.3969/j.issn.0258-1825.2006.03.002 (in Chinese) |
| [16] |
郑华盛, 赵宁, 朱君. 二维非结构网格上的高精度有限体积WENO格式[J]. 空气动力学学报, 2010, 28(4): 446-451. ZHENG H S, ZHAO N, ZHU J. High order finite volume weighted essentially non-oscillatory schemes on two dimensional unstructured meshes[J]. Acta Aerodynamica Sinica, 2010, 28(4): 446-451. DOI:10.3969/j.issn.0258-1825.2010.04.015 (in Chinese) |
| [17] |
BARTH T, JESPERSEN D. The design and application of upwind schemes on unstructured meshes[C]// 27th Aerospace Sciences Meeting, Reno, NV. Reston, Virginia: AIAA, 1989. doi: 10.2514/6.1989-366
|
| [18] |
BARTH T. A 3-D upwind Euler solver for unstructured meshes[C]// 10th Computational Fluid Dynamics Conference, Honolulu, HI, USA. Reston, Virigina: AIAA, 1991. doi: 10.2514/6.1991-1548
|
| [19] |
JALALI A, OLLIVIER-GOOCH C. Higher-order unstructured finite volume RANS solution of turbulent compressible flows[J]. Computers & Fluids, 2017, 143: 32-47. DOI:10.1016/j.compfluid.2016.11.004 |
| [20] |
OLLIVIER-GOOCH C, NEJAT A, MICHALAK K. Obtaining and verifying high-order unstructured finite volume solutions to the Euler equations[J]. AIAA Journal, 2009, 47(9): 2105-2120. DOI:10.2514/1.40585 |
| [21] |
JALALI A, OLLIVIER GOOCH C F. Higher-order finite volume solution reconstruction on highly anisotropic meshes[C]// 21st AIAA Computational Fluid Dynamics Conference, San Diego, CA. Reston, Virginia: AIAA, 2013. doi: 10.2514/6.2013-2565
|
| [22] |
NISHIKAWA H. Efficient gradient stencils for robust implicit finite-volume solver convergence on distorted grids[J]. Journal of Computational Physics, 2019, 386: 486-501. DOI:10.1016/j.jcp.2019.02.026 |
| [23] |
XIONG M, DENG X G, GAO X, et al. A novel stencil selection method for the gradient reconstruction on unstructured grid based on OpenFOAM[J]. Computers & Fluids, 2018, 172: 426-442. DOI:10.1016/j.compfluid.2018.03.072 |
| [24] |
熊敏. 非结构有限体积梯度重构算法研究与应用[D]. 长沙: 国防科技大学, 2019. XIONG M. Research and application of unstructured finite volume gradient reconstruction algorithms[D]. Changsha: National University of Defense Technology, 2019. (in Chinese) |
| [25] |
KONG L F, DONG Y D, LIU W, et al. An improved global-direction stencil based on the face-area-weighted centroid for the gradient reconstruction of unstructured finite volume methods[J]. Chinese Physics B, 2020, 29(10): 100203. DOI:10.1088/1674-1056/aba2da |
| [26] |
MAVRIPLIS D J. An advancing front delaunay triangulation algorithm designed for robustness[J]. Journal of Computational Physics, 1995, 117(1): 90-101. DOI:10.1006/jcph.1995.1047 |
| [27] |
杨永国, 程兴华, 王万金. 大规模流畅模拟中壁面距离的并行计算方法研究[J]. 计算机工程与科学, 2016, 38(06): 1086-1090. YANG Y G, CHENG X H, WANG W J. A parallel computation method of wall distance for large-scale flow simulation[J]. Computer Engineering and Science, 2016, 38(06): 1086-1090. DOI:10.3969/j.issn.1007-130X.2016.06.003 (in Chinese) |
| [28] |
李广宁, 李凤蔚, 周志宏. 一种高效的壁面距离计算方法[J]. 航空工程进展, 2010, 1(2): 137-142. LI G N, LI F W, ZHOU Z H. An efficient method for calculating wall distance[J]. Advances in Aeronautical Science and Engineering, 2010, 1(2): 137-142. DOI:10.16615/j.cnki.1674-8190.2010.02.008 (in Chinese) |
| [29] |
赵慧勇, 贺旭照, 乐嘉陵. 一种新的壁面距离计算方法——循环盒子法[J]. 计算物理, 2008, 25(04): 427-430. ZHAO H Y, HE X Z, LE J L. Recursive box method for wall distance computation[J]. Chinese Journal of Computational Physics, 2008, 25(04): 427-430. DOI:10.3969/j.issn.1001-246X.2008.04.008 (in Chinese) |
| [30] |
KATZ A, WISSINK A M, SANKARAN V, et al. Application of strand meshes to complex aerodynamic flow fields[J]. Journal of Computational Physics, 2011, 230(17): 6512-6530. DOI:10.1016/j.jcp.2011.04.036 |
| [31] |
王年华, 张来平, 李明. 基于网格缩小的非结构网格梯度重构及制造解精度测试与验证[J]. 空气动力学学报, 2019, 37(5): 722-730. WANG N H, ZHANG L P, LI M. Investigation on accuracy of gradient reconstruction and flow simulation on general unstructured grids based on downscaling method[J]. Acta Aerodynamica Sinica, 2019, 37(5): 722-730. DOI:10.7638/kqdlxxb-2017.0106 (in Chinese) |
| [32] |
ROY C J. Review of code and solution verification procedures for computational simulation[J]. Journal of Computational Physics, 2005, 205(1): 131-156. DOI:10.1016/j.jcp.2004.10.036 |
| [33] |
ROACHE P J. Code verification by the method of manufactured solutions[J]. Journal of Fluids Engineering, 2002, 124(1): 4-10. DOI:10.1115/1.1436090 |
| [34] |
NISHIKAWA H. A face-area-weighted ‘centroid’ formula for finite-volume method that improves skewness and convergence on triangular grids[J]. Journal of Computational Physics, 2020, 401: 109001. DOI:10.1016/j.jcp.2019.109001 |
 2021, Vol. 39
2021, Vol. 39


