2. 南京航空航天大学 江苏省风力机设计高技术研究重点实验室,南京 210016
2. Jiangsu Key Laboratory of Hi-Tech Research for Wind Turbine Design, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
我国位于太平洋西岸并拥有绵长海岸线,是世界上遭受台风灾害最为严重的国家之一。准确掌握台风风参数对工程结构抗风安全具有重要指导意义。台风[1]是由复杂涡系组成的近似于圆形的大气涡旋系统,现行主要台风模型源于20世纪70年代Batts提出的第一代台风风场模型[2]和Meng提出的改进工程模型[3],可在满足基本精度的前提下实现大量台风样本的快速随机模拟。随后我国学者针对台风模拟参数的敏感性和台风模型在我国沿海地区极值风速预测的应用开展了许多研究[4-8],但台风模拟理论方法仍采用多个物理场不耦合的假定,预测结果过度依赖实测数据校准和关键参数取值经验,缺乏波浪、海流等海洋运动对台风过境全过程水平风速影响研究,一定程度限制了单个工程台风模型应用于土木工程结构设计风速的预测精度。
目前针对海洋运动与台风之间耦合作用的研究,主要集中于对风、浪、流模拟方法及海洋运动与台风之间相互影响的探讨[9-18]。关皓等[15]基于大气模型MM5-海洋模型、POM-海浪模型WW3的三元耦合模式系统,模拟研究了两种南海典型台风过程,结果表明波浪效应阻碍了台风系统的发展,增强了海表应力,加大了海面降温幅度和海流近惯性振荡的振幅。徐海波等[16]基于大气模型WRF-海洋模型ROMS-海浪模型SWAN耦合模拟了台风“Megi”过程中海洋与大气变化过程,研究表明海浪作用使得台风后部风速减小约3~5 m/s,加剧的海洋混合也导致了更大程度的降温。Liu等[17]基于耦合模式平台WRF-SWAN-POM对理想热带气旋进行数值模拟研究,结果表明海气耦合对热带气旋强度的总体影响是由与波浪相关的正反馈和海温冷却引起的负反馈之间的平衡决定的。Warner等[18]基于WRF-ROMS-SWAN-Sediment transport耦合模式对台风“Isabel”的海气交换及泥沙输移进行模拟,发现海洋与大气的耦合会导致边界层应力降低,而波浪与大气的耦合则会导致底部应力增加。已有研究为海上结构抗风安全设计与防护提供了一定参考依据,但均忽略了海洋运动对台风过境全过程时空水平风速特性的影响。
鉴于此,本文采用中尺度WRF模式、第三代海浪模式SWAN与有限体积海流模式FVCOM构建台风-波浪-海流实时耦合模拟平台,模拟分析了台风“莫兰蒂”过境全过程水平风速特性,同时与非耦合WRF模式的模拟结果进行对比,分析得到了海洋运动对于台风水平风速的影响,为海洋大气数值模型建立与海上风电场结构设计提供参考依据。
1 台风-波浪-海流耦合模拟 1.1 数值模拟方法 1.1.1 中尺度大气模式WRFWRF大气模型[19]是美国国家大气研究中心、美国国家海洋和大气管理局等联合开发的新一代中尺度天气预报系统。本文采用的WRF-ARW(研究模式)动力框架基于完全可压非静力平衡欧拉方程,水平方向上采用Arakawa C网格划分,垂直方向上采用静力气压地形追随坐标。
模式的近似通量形式欧拉控制动量方程组为:
| ${\partial _t}U + \left( {\nabla \cdot {\boldsymbol{V}}u} \right) - {\partial _x}\left( {p{\phi _n}} \right) + {\partial _x}\left( {p{\phi _x}} \right) = {F_U}$ | (1) |
| ${\partial _t}V + \left( {\nabla \cdot {\boldsymbol{V}}v} \right) - {\partial _v}\left( {p{\phi _n}} \right) + {\partial _v}\left( {p{\phi _v}} \right) = {F_V}$ | (2) |
| ${\partial _t}W + \left( {\nabla \cdot {\boldsymbol{V}}w} \right) - g\left( {{\partial _n}p - \mu } \right) = {F_W}$ | (3) |
式中:u、v、w分别为水平方向x向速度分量、水平方向y向速度分量、垂向速度分量;U、V、W分别为水平方向x向动量分量、水平方向y向动量分量、垂向动量分量;FU、FV、FW分别表示由物理过程、湍流混合、球面投影造成的力源项。
1.1.2 第三代海浪模式SWANSWAN海浪模型[20]是由荷兰Delft大学开发的第三代近岸海浪模型,具有模拟海洋风浪、涌浪及混合浪的能力。SWAN模式采用基于Euler近似的波作用动谱平衡方程作为描述海浪的控制方程,方程在笛卡尔坐标系下表达式为:
| $ \frac{\partial}{\partial t} N+\frac{\partial}{\partial x} C_{x} N+\frac{\partial}{\partial y} C_{y} N+\frac{\partial}{\partial \sigma} C_{\sigma} N+\frac{\partial}{\partial \theta} C_{\theta} N=\frac{S}{\sigma} $ | (4) |
式中:N为波浪作用谱密度;Cx、Cy、Cσ、Cθ分别为x、y、σ、θ四个方向上的波浪传播速度;S表示能量的源汇项,其中包括了风能的输入、能量的耗散以及波浪之间的非线性相互作用。
1.1.3 有限体积海流模式FVCOMFVCOM海洋模型[21]是由美国麻省理工大学和伍兹霍尔海洋研究所联合开发的适用于三维水动力模拟的有限体积海流模式。FVCOM模型在笛卡尔坐标下的三维动量方程为:
| $\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}} - fv{\rm{ = - }}\frac{{\rm{1}}}{{\rho_ {\rm{0}}}}\frac{{\partial p}}{{\partial x}} + \frac{\partial }{{\partial z}}\left( {K_m\frac{{\partial u}}{{\partial z}}} \right) + F_u$ | (5) |
| $\frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} + w\frac{{\partial v}}{{\partial z}} - fu{\rm{ = - }}\frac{{\rm{1}}}{{\rho_ {\rm{0}}}}\frac{{\partial p}}{{\partial y}} + \frac{\partial }{{\partial z}}\left( {K_m\frac{{\partial v}}{{\partial z}}} \right) + F_v$ | (6) |
| $\frac{{\partial w}}{{\partial t}} + u\frac{{\partial w}}{{\partial x}} + v\frac{{\partial w}}{{\partial y}} + w\frac{{\partial w}}{{\partial z}}{\rm{ = }}\frac{{\rm{1}}}{{\rho_ {\rm{0}}}}\frac{{\partial q}}{{\partial z}} + \frac{\partial }{{\partial z}}\left( {K_m\frac{{\partial w}}{{\partial z}}} \right) + F_w$ | (7) |
式中:x、y、z分别为笛卡尔坐标系三个方向上的坐标,u、v、w是三个方向上的速度分量,ρ为海水密度,ρ0为参考密度,f为科氏力参数,Km为垂向涡黏系数,Fu、Fv、Fw分别为三个方向上的动量。
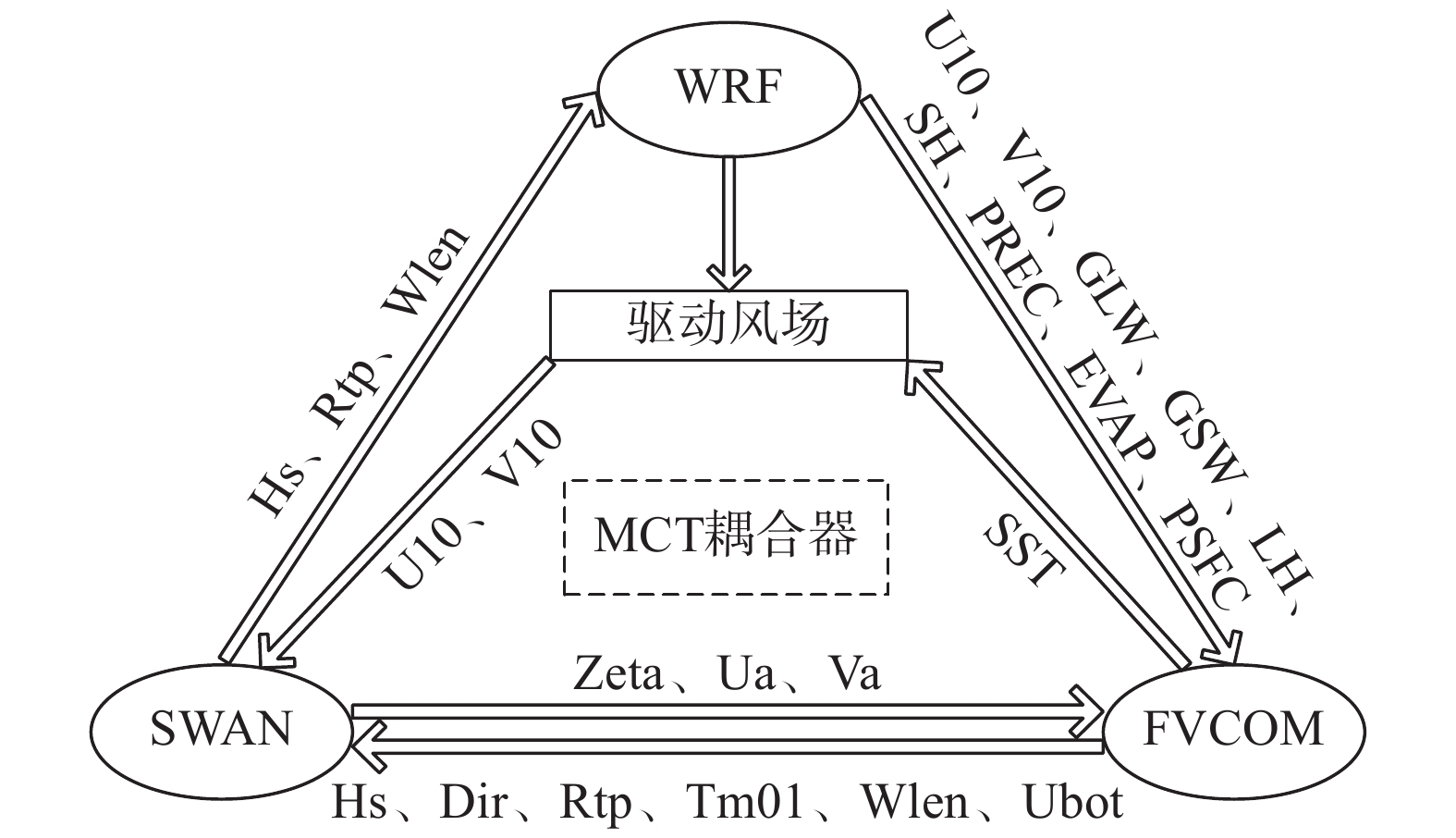
1.1.4 模型耦合机制W-S-F耦合模拟平台由主程序调用各子模型同时独立计算,各子模型调用MCT子程序进行数据的实时交换。模型耦合机制如图1所示。其中,WRF向SWAN和FVCOM传递风速驱动海洋运动;FVCOM向WRF传递海表温度,向SWAN传递海流潮位和流速;SWAN向FVCOM和WRF分别传递影响海流运动和台风发展的波形要素。
|
图 1 W-S-F模型耦合机制示意图 Fig.1 A diagram of the W-S-F coupling mechanism |
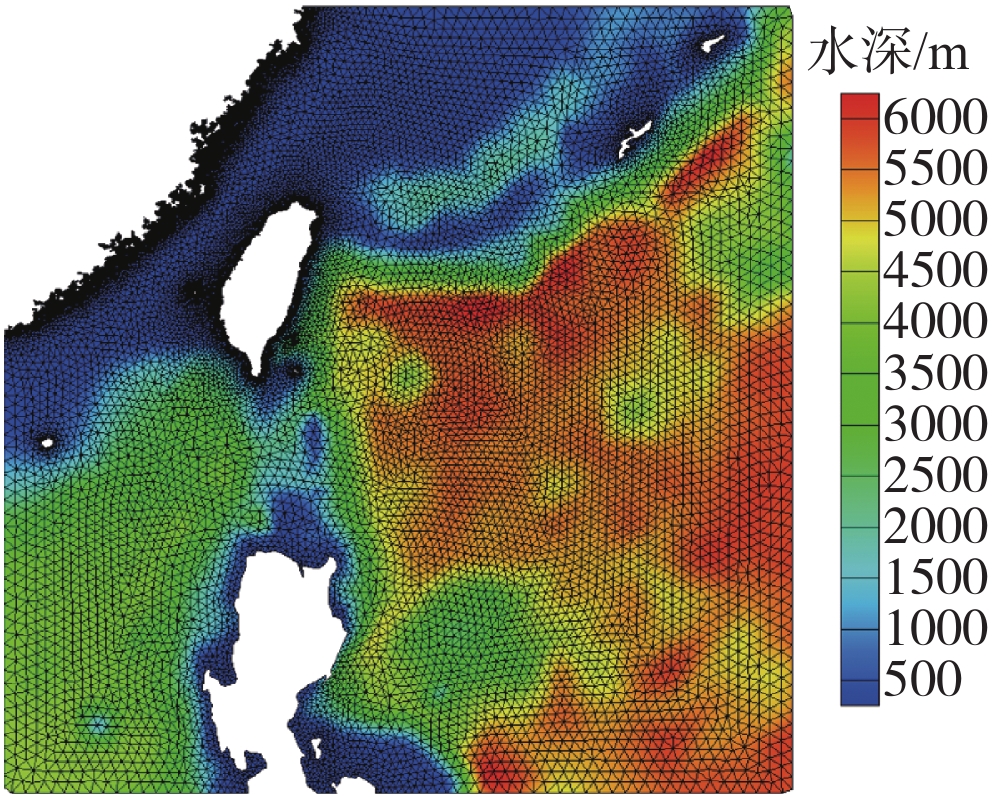
台风“莫兰蒂”(Meranti,国际编号:1614)于2016年9月10日14时在西北太平洋洋面上生成,11日14时加强为强热带风暴,12日11时继续加强为超强台风,13日晚间加强到顶峰(此时风速62 m/s)。此次台风于9月15日以强台风级在福建省厦门市登陆,登陆时中心最大风力35 m/s。为分析波浪与海流对台风过境全过程水平风速特性的影响,本文设计两组工况:1)非耦合WRF模式模拟未考虑海洋作用的台风运动;2)W-S-F耦合模拟海洋与大气实时传递作用的台风运动。控制两组工况下的模拟计算区域及WRF的设计参数完全一致,WRF的物理化参数方案及模拟计算域内波浪、海流网格划分如表1所示。模拟计算时间为2016年9月11日16时~2016年9月15日12时共92 h。WRF、SWAN、FVCOM三种模型的部分参数设置见表2。
| 表 1 WRF物理化参数方案及模拟计算域设置 Table 1 Physical parameterization schemes of WRF and the setting of simulation computing region |
|
|
| 表 2 W-S-F耦合模拟平台参数设置 Table 2 Parameters of the W-S-F coupling simulation |
|
|
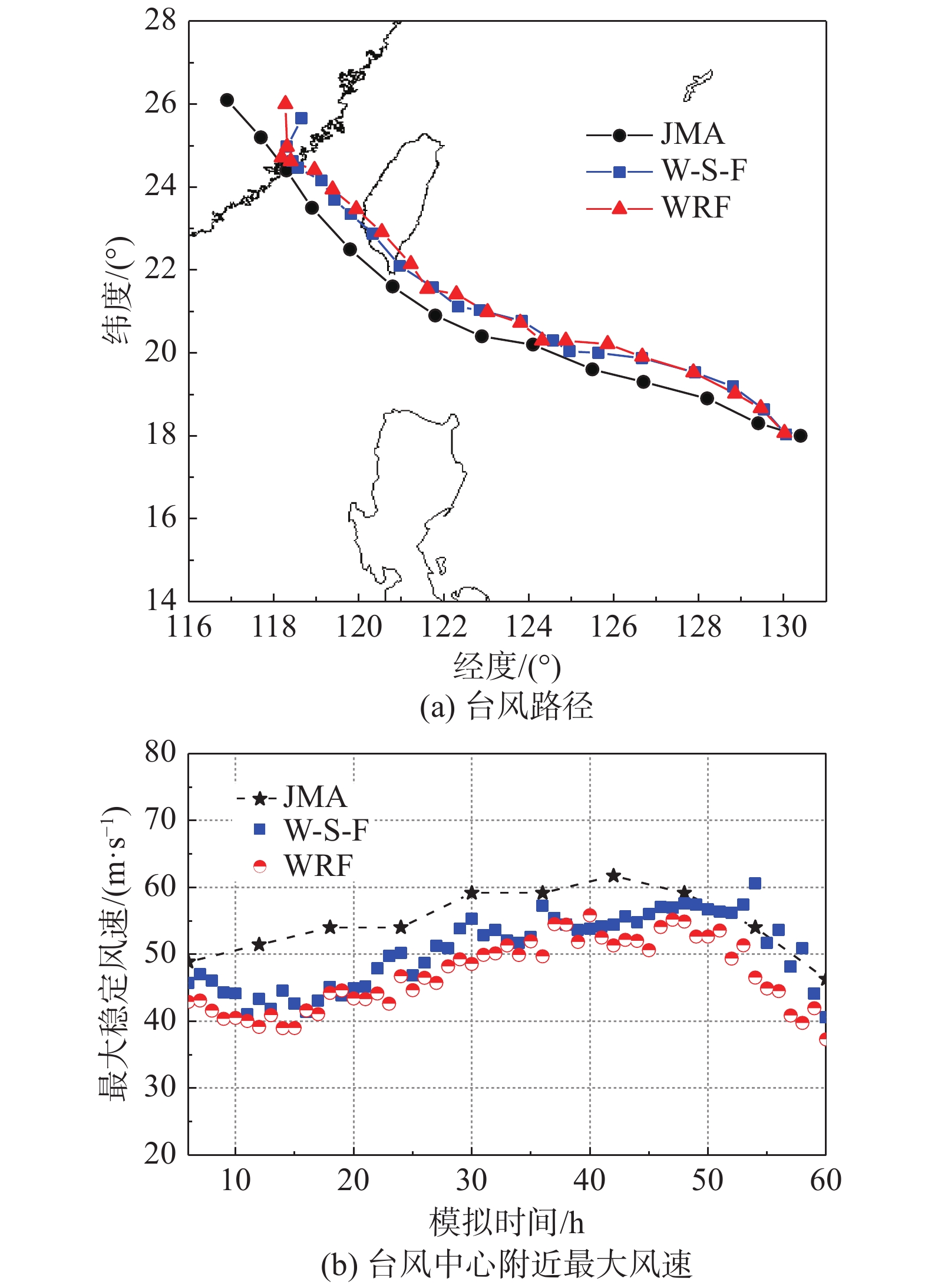
为验证W-S-F耦合平台数值模拟的有效性,以日本气象厅东京区域专业气候中心JMA提供的台风最佳路径数据集[22]为参考,图2给出了W-S-F耦合模式与WRF非耦合模式模拟的台风路径以及台风中心附近最大稳定风速误差对比结果。由图可知,整个模拟时间范围内,非耦合WRF模式与W-S-F模式模拟的台风移动路径比JMA最佳路径均略偏北,W-S-F耦合模拟的台风路径比WRF非耦合模拟更接近JMA最佳路径;两种模式模拟的台风中心附近最大稳定风速在模拟期间先增大再减小,与JMA实测数据变化趋势一致,W-S-F模式模拟效果全程优于非耦合WRF模式。
|
图 2 W-S-F耦合模式模拟结果有效性验证 Fig.2 The validity of simulationresults obtained by the W-S-F coupling model |
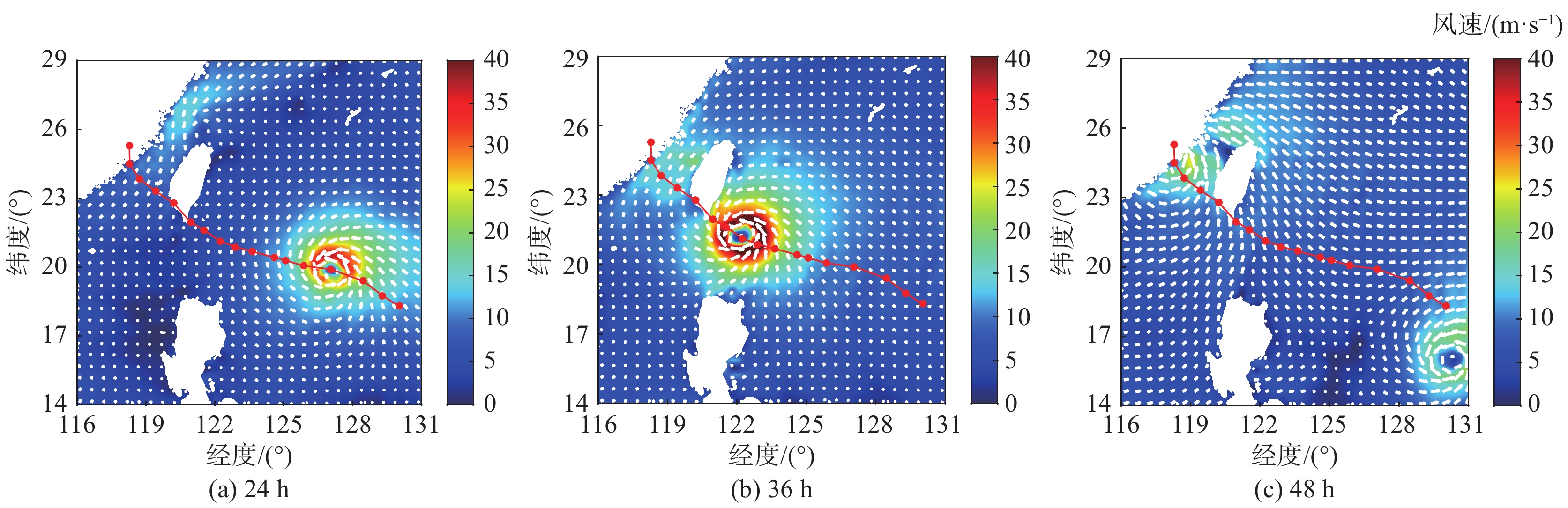
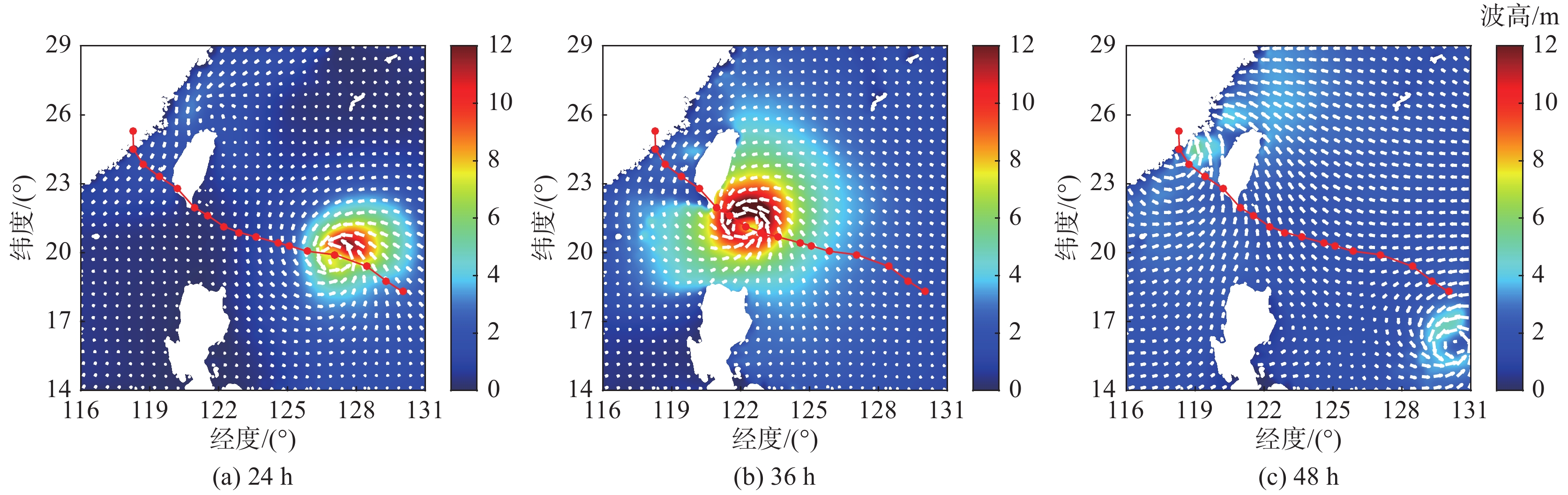
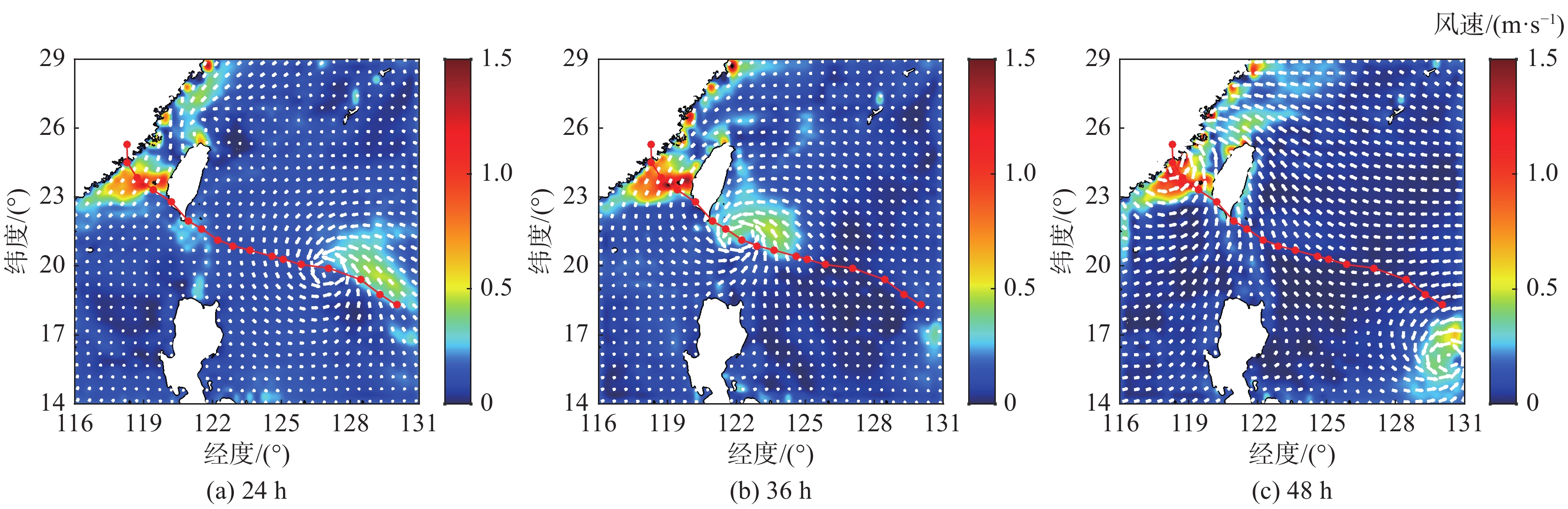
图3~图5分别给出了在台风“莫兰蒂”10 m高度处风速矢量、有效波高以及表层流场云图。
|
图 3 不同时刻风场模拟结果 Fig.3 Numerical results of the wind fields at different time instants |
|
图 4 不同时刻有效波高模拟结果 Fig.4 Numerical results of the significant wave heights at different time instants |
|
图 5 不同时刻表层流场模拟结果 Fig.5 Numerical results of the surface flow at different time instants |
由图可知:1)台风移动过程风速呈现非对称分布,其中心右侧风速明显大于左侧,台风浪以及表层流场在空间上同样呈现出“右偏性”的不对称性分布特征;2)台风作用下海域形成了明显的旋转波浪场,波浪场的旋转中心位于台风移动路径的左侧小浪区,其与表层流场对于台风具有一定的滞后性,表层流场的滞后性较为明显;3)台风“莫兰蒂”10 m高度处风速最高可达45 m/s以上,台风中心附近形成有效波高10 m以上的狂涛区,表层流速在远海区域达到1 m/s。
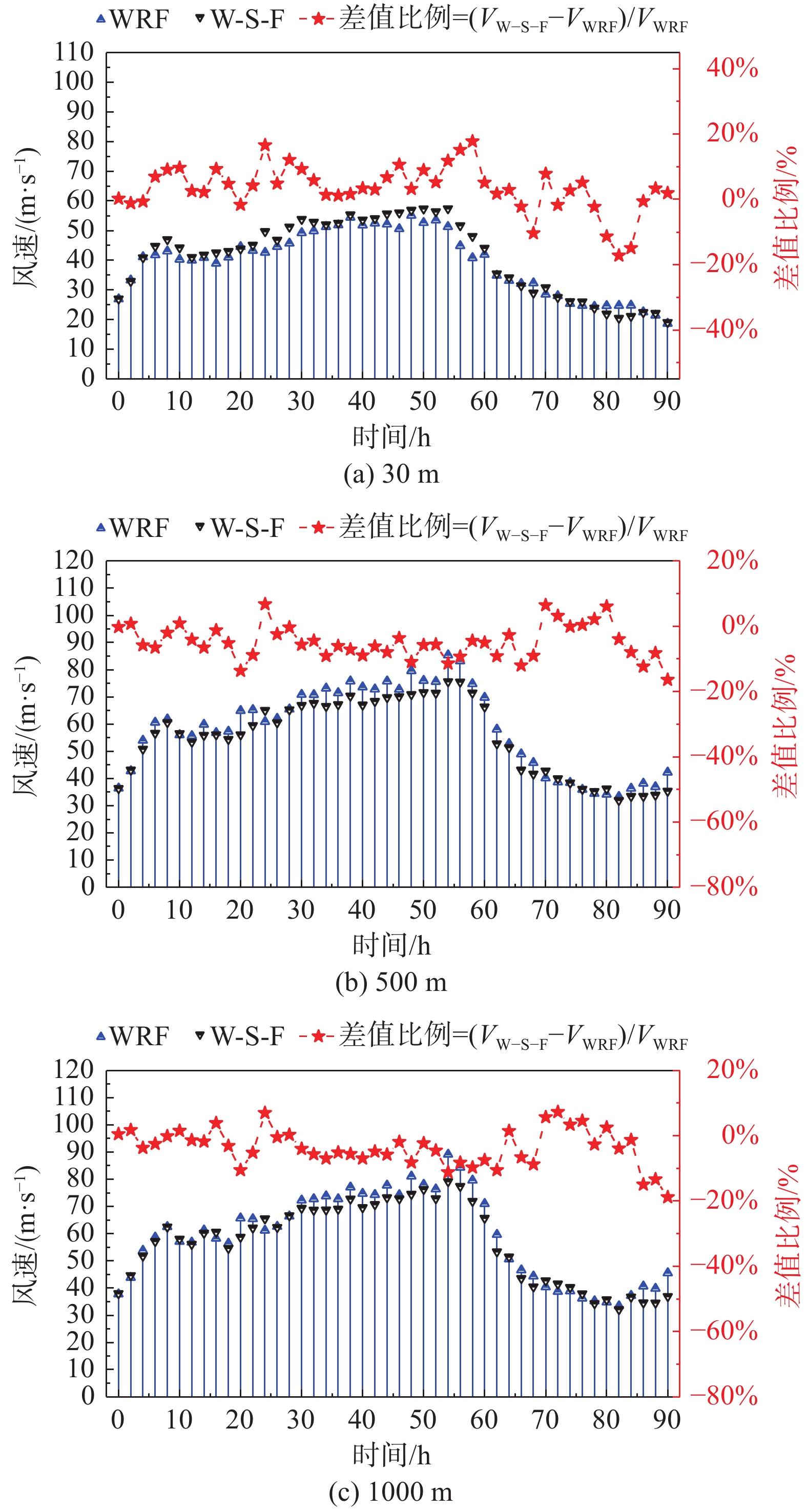
2 海洋运动对台风水平风速影响 2.1 台风典型高度风速时程图6给出了台风典型高度最大风速时程对比曲线,由图可知,不同高度处台风“莫兰蒂”最大风速呈现先增大后减小的趋势。海洋运动作用对于台风在不同高度处的最大风速变化存在不同影响。
|
图 6 台风典型高度最大风速时程对比曲线 Fig.6 Time histories of the maximum wind speedsat typical heights of typhoon |
在风速上升阶段(0~45 h),海洋运动促进了低空台风风速的发展,对高空台风风速发展具有抑制作用。在强风阶段(45~55 h),海洋运动对于高空处台风发展的抑制作用更为显著。在近海登陆过程中(55~92 h),海洋运动对大气的影响随着风速减小逐渐减弱。
产生这种差异结果的原因可能为:耦合模式考虑了复杂的大气、海浪、洋流的相互作用与能量传递,在风速上升阶段,风应力的增加使上层海洋发生湍流混合,海气热量交换强烈。波浪破碎与能量耗散的升温作用促进低空风速的发展;而随着高度的增加,热量耗散不断累积,大气能量减小,因而海洋运动对高空台风风速产生一定的削弱。而在风速下降阶段,海气能量交换作用随台风强度降低而逐渐减小,海洋运动对大气的影响也随之减弱。
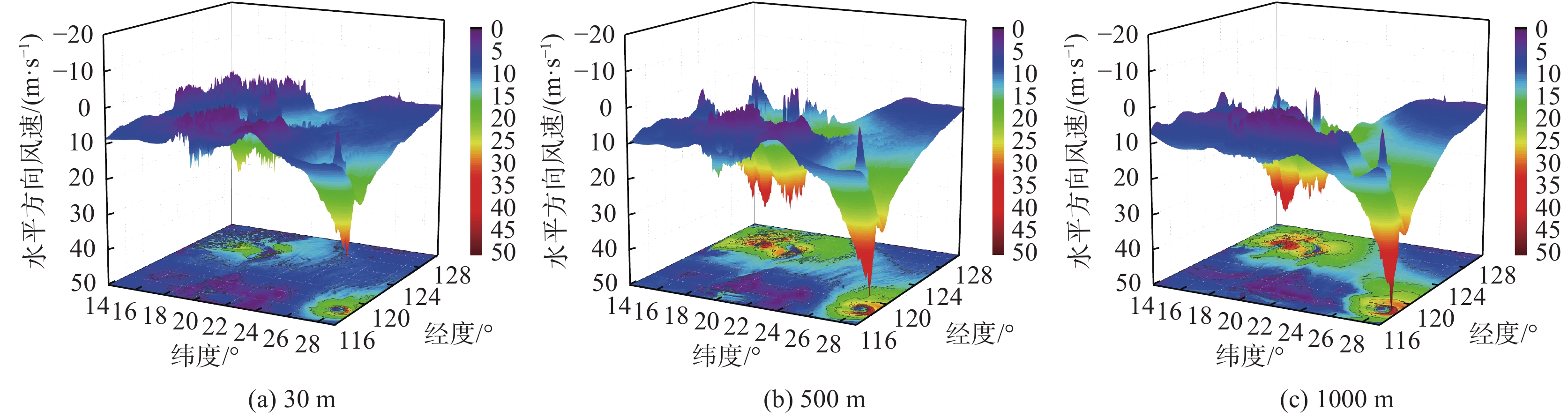
2.2 台风三维风速分布图7和8分别给出了两组工况下台风登陆时刻典型高度截面水平方向风速随经度及纬度的三维分布图。从图中可以看出:在不同高度处,两种工况下的三维风速分布情况基本一致,且均具有明显的台风眼结构。登陆期台风强度不断削弱,海洋运动使得台风登陆期发展较快,以致台风水平向风速较小且起伏更为平缓。
|
图 7 W-S-F耦合模式台风风速分布三维云图 Fig.7 Three-dimensional nephograms of the wind speed distribution obtained by the W-S-F coupling model |
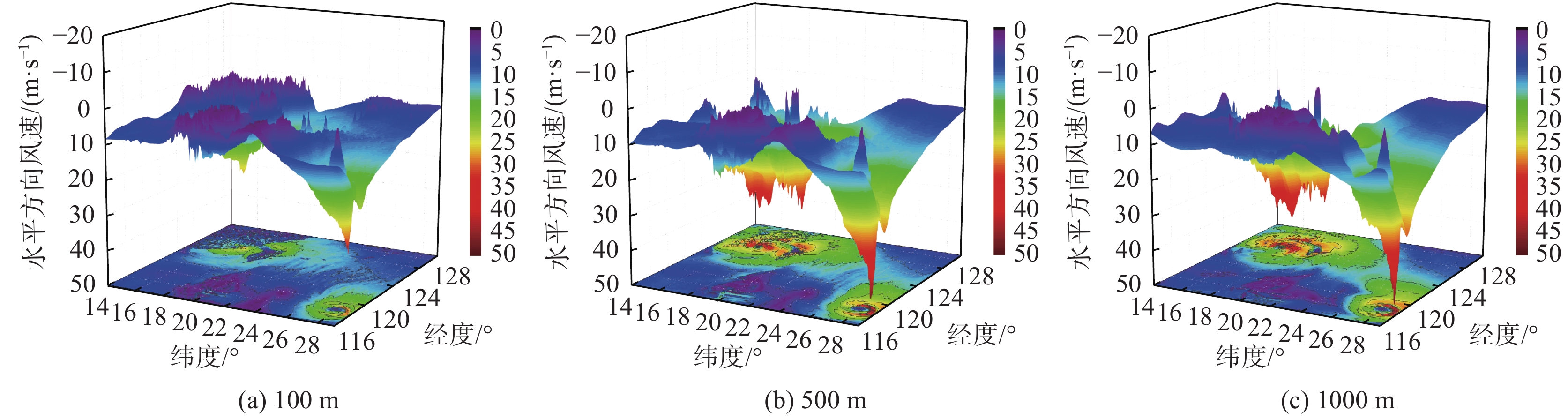
|
图 8 WRF非耦合模式台风风速分布三维云图 Fig.8 Three-dimensional nephograms of the wind speed distribution obtained by the uncoupled WRF model |
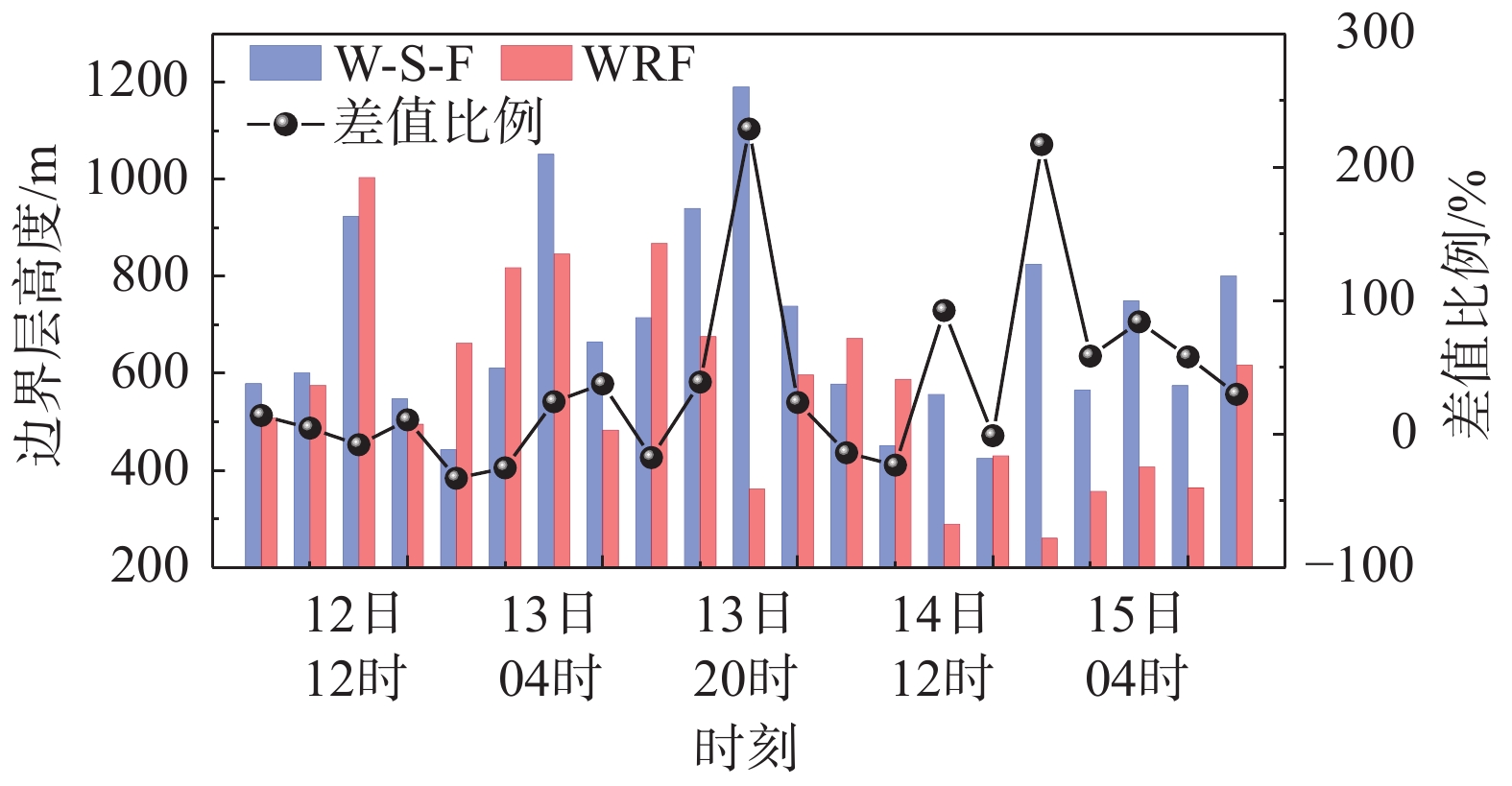
图9给出了台风过境全过程的边界层高度对比。由图可知,WRF模式模拟的台风影响全过程的边界层高度平均值为566 m,耦合模式为692 m,海洋运动使得边界层高度增大到约1.2倍。基于WRF模式台风过境三个时期边界层高度平均值分别为698 m、657 m和412 m,耦合模式下边界层高度分别为755 m、943 m和619 m。
|
图 9 台风过境全过程边界层高度对比图 Fig.9 A comparison of boundary layer thickness throughout the typhoon landing process |
与建筑结构荷载规范(GB 50009—2012)[23]中A类地形的取值300 m相比,两种工况下台风各边界层高度计算值普遍偏大,耦合模式下的边界层高度最大值达到了规范值的3.4倍,非耦合模式最大值达到了规范值的2.9倍。
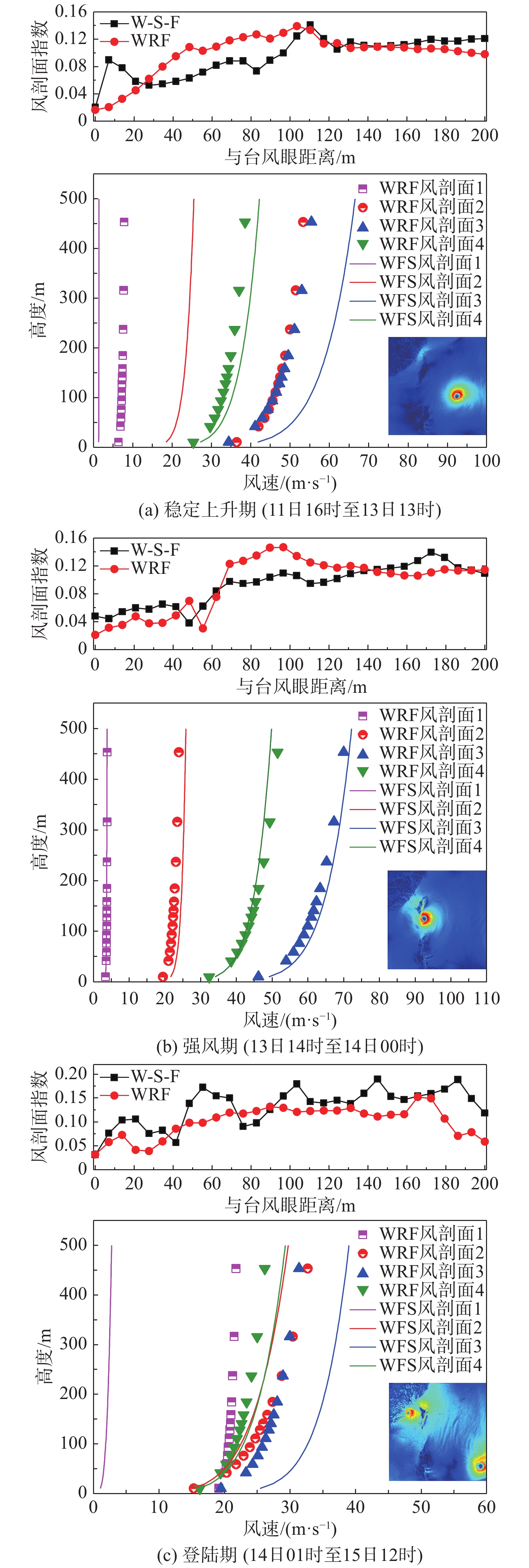
2.4 风剖面及指数时序规律考虑台风发展经历的稳定上升期、强风期和登陆期三个阶段,图10给出了不同时期两种工况下台风结构不同位置处的风剖面结果对比。其中,风剖面1~4分别位于台风中心至台风眼壁区域(风剖面1和2)、台风眼壁区域(风剖面3)、台风外围区域(风剖面4)。风剖面指数与台风眼距离的变化关系选取距台风眼相同距离的所有模拟结果的均值。由图可知,台风风剖面拟合指数在各时期皆呈现随着与台风眼距离的增大而逐渐上升的趋势,登陆期风剖面指数均值较登陆前明显增大,海洋运动对台风各个生命周期、同一位置处的风剖面均存在一定影响。风速稳定上升期台风眼区不考虑海洋运动的风速及风剖面幂指数更高,且靠近台风眼壁区域差异较大,而台风眼壁及以外产生相反的情况。台风发展至强风期,海洋运动对台风眼壁处风剖面拟合指数影响较大,较不考虑海洋运动情况下的差异最高可达0.04。在台风登陆时期,海洋运动使得风剖面拟合指数随着与台风眼距离的增大变化更为强烈。
|
图 10 台风不同时期两种工况下风剖面模拟结果对比 Fig.10 The comparison of numerical results of wind profiles under two working conditions at different stages of typhoon |
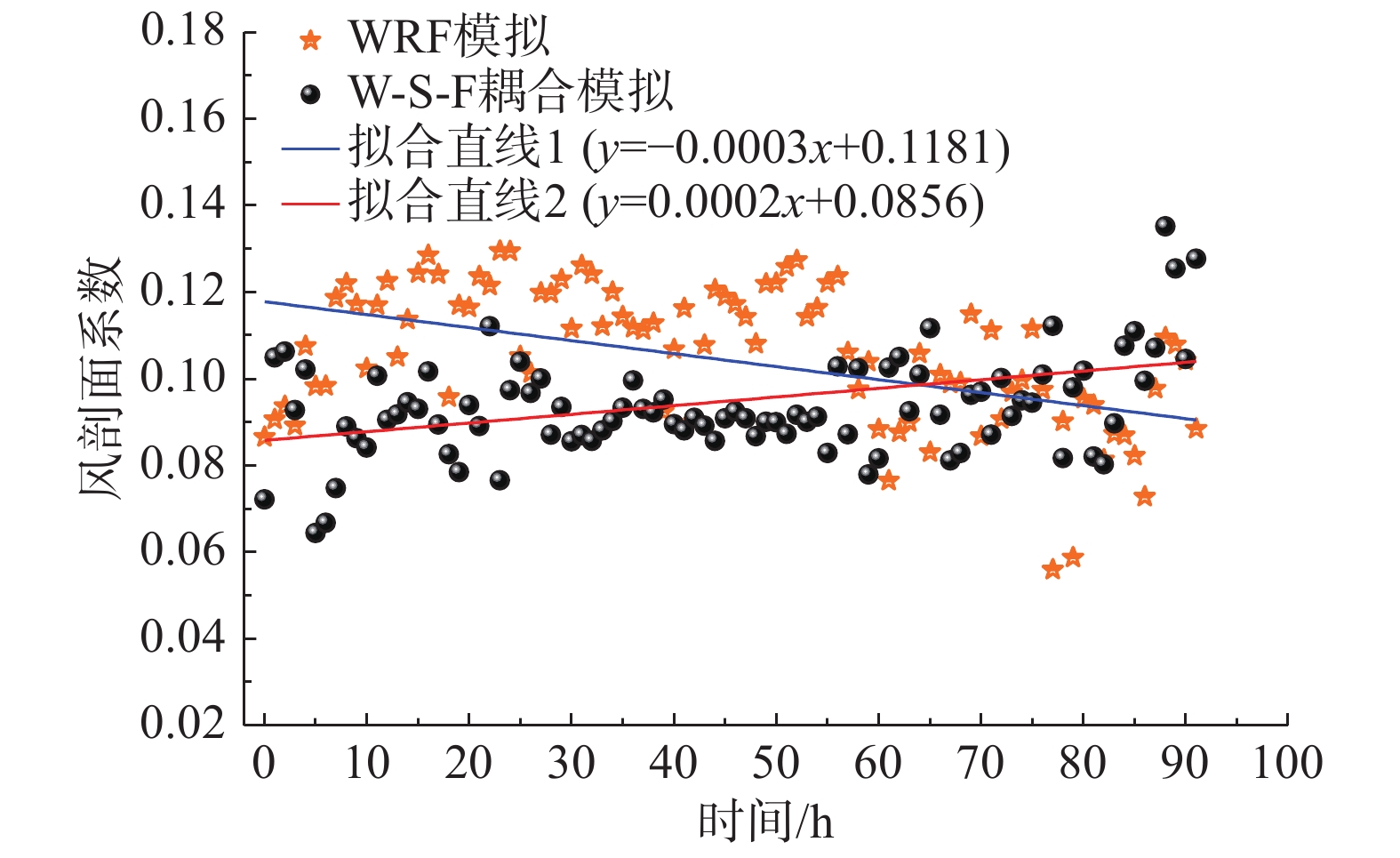
图11给出了台风眼壁处风剖面幂指数时序图,由图可知,两种工况下台风眼壁处风剖面幂指数α随时间的变化呈相反的趋势,分别随时间在拟合直线1(WRF)及拟合直线2(W-S-F)的上下波动,台风登陆前海洋运动对风剖面指数影响较大,并随着台风濒临陆地逐渐减小。台风登陆后两种模式下的风剖面指数基本位于0.1左右,海洋运动对其影响较为微弱。
|
图 11 风剖面指数时序图 Fig.11 Time series of the power exponents of wind profiles |
图12以最大水平风速作为判定依据,给出海洋运动对台风水平风速的影响随高度与时间变化示意图。其中,影响系数定义为海洋运动影响下台风最大水平风速与不考虑海洋运动的台风最大水平风速的比值。
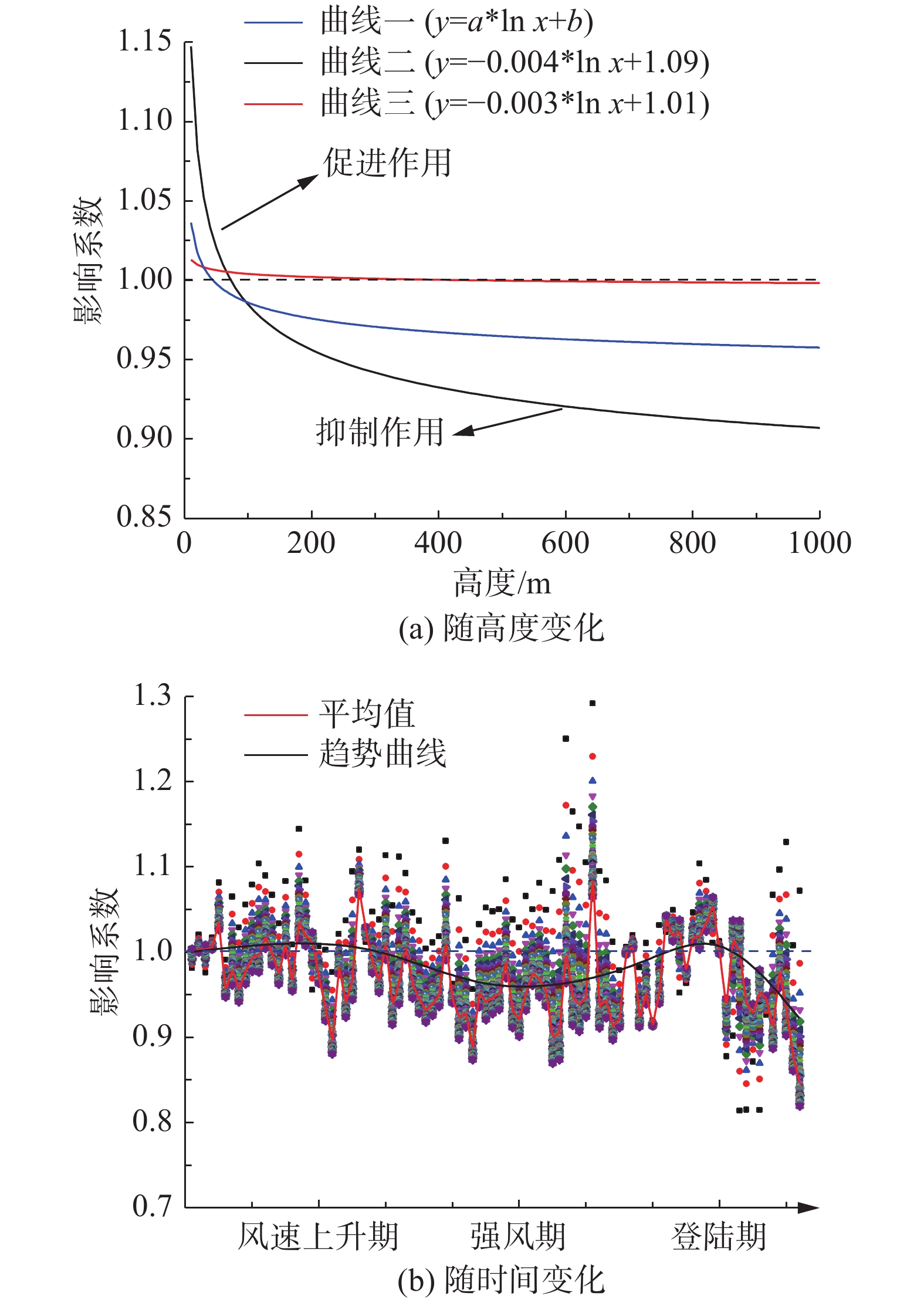
|
图 12 海洋运动对台风强度影响随高度与时间的变化 Fig.12 Variations of the influences of ocean movement on the typhoon intensity with height and time |
对比分析得到:
1)台风发展过程中海洋运动对台风强度的影响系数随高度增大呈对数率减小。低空处海洋运动促进台风强度,并随高度增加影响逐渐减小。到达一定高度时,海洋运动对台风强度产生抑制作用,且这种消耗随高度增大而加强。
2)台风不同生命周期其高度影响特性呈现不同程度的增减。风速上升期,海洋运动影响对于高度的敏感性逐渐增强,即随高度变化影响程度逐渐增大。而登陆期,海洋运动的高度影响曲线随风速减小而趋于平缓。基于此给出了海洋运动影响系数随高度变化的对数模型:
| $ y = a\ln x + b, - 0.004 \leqslant a \leqslant - 0.003,1.01 \leqslant b \leqslant 1.09$ | (8) |
式中:a代表海洋运动的高度影响程度,与风速值呈负相关;b代表海洋运动影响系数截距,与风速值呈正相关。
3)海洋运动对于台风1000 m高度范围内强度均值的影响随台风发展呈先促进后消耗,随后消耗作用逐渐减弱后又不断增强。结合海洋运动对于不同高度台风的影响大小,可得到台风发展过程中各个时刻与高度受海洋运动的作用程度。
4 结 论本文基于MCT耦合器,通过中尺度WRF大气模型、三维水动力FVCOM模型以及第三代浅海海浪SWAN模型建立了大气-海洋-海浪的实时耦合平台,分析了海洋运动对台风过境全过程水平风速特性的影响规律。研究表明,本文提出的W-S-F耦合平台可以准确模拟考虑海洋运动的台风过境全过程风速场,且海洋运动对台风过境全过程水平风速的影响不可忽略。
两者相互作用和影响机理阐述如下:海洋与大气通过热量传递、摩擦阻力、气压变化等能量交换过程相互促进、相互消耗。低空处海洋运动能促进台风强度,随高度增加影响逐渐减小;高空处海洋运动对台风强度产生抑制作用,且这种消耗随高度增大而加强。在台风整个发展周期,海洋运动对低空台风强度的影响呈现先促进后抑制规律,随着高度增加逐渐形成相反特点。海洋运动使得边界层高度显著增大,可使边界层高度平均值最大放大到1.2倍。
| [1] |
陈联寿, 丁一汇. 西太平洋台风概论[M]. 北京: 科学出版社, 1979.
|
| [2] |
BATTS M E, SIMIU E, RUSSELL L R. Hurricane wind speeds in the United States[J]. Journal of the Structural Division, 1980, 106(10): 2001-2016. DOI:10.1061/jsdeag.0005541 |
| [3] |
MENG Y, MATSUI M, HIBI K. An analytical model for simulation of the wind field in a typhoon boundary layer[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 56(2-3): 291-310. DOI:10.1016/0167-6105(94)00014-5 |
| [4] |
ZHAO L, YANG X N, FANG G S, et al. Observation-based study for the evolution of vertical wind profiles in the boundary layer during super typhoon Mangkhut[J]. Acta Aerodynamica Sinica, 2019, 37(1): 43-54. DOI:10.7638/kqdlxxb-2018.0297 |
| [5] |
王叶红, 赵玉春. 边界层参数化方案对“莫兰蒂”台风(1614)登陆阶段影响的数值模拟研究[J]. 大气科学, 2020, 44(5): 935-959. WANG Y H, ZHAO Y C. Numerical investigation of the effects of boundary layer parameterization schemes on typhoon Meranti (1614) landing process[J]. Chinese Journal of Atmospheric Sciences, 2020, 44(5): 935-959. (in Chinese) |
| [6] |
柯清派, 史训涛, 雷金勇, 等. 大气层结和海气交换作用影响的海面风剖面研究[J]. 热带气象学报, 2020, 36(3): 370-376. KE Q P, SHI X T, LEI J Y, et al. Influence of atmospheric stratification and air-sea interaction on sea surface wind profile[J]. Journal of Tropical Meteorology, 2020, 36(3): 370-376. (in Chinese) |
| [7] |
FANG G S, ZHAO L, CAO S Y, et al. A novel analytical model for wind field simulation under typhoon boundary layer considering multi-field correlation and height-dependency[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 175: 77-89. DOI:10.1016/j.jweia.2018.01.019 |
| [8] |
FANG G S, PANG W, ZHAO L, et al. Toward a refined estimation of typhoon wind hazards: parametric modeling and upstream terrain effects[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2021, 209: 104460. DOI:10.1016/j.jweia.2020.104460 |
| [9] |
LI L X, XIAO Y Q, KAREEM A, et al. Modeling typhoon wind power spectra near sea surface based on measurements in the South China sea[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 104-106: 565-576. DOI:10.1016/j.jweia.2012.04.005 |
| [10] |
YANG Z H, SHAO W Z, DING Y, et al. Wave simulation by the SWAN model and FVCOM considering the sea-water level around the Zhoushan Islands[J]. Journal of Marine Science and Engineering, 2020, 8(10): 783. DOI:10.3390/jmse8100783 |
| [11] |
TAKEMI T. The evolution and intensification of Cyclone Pam (2015) and resulting strong winds over the southern Pacific Islands[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 182: 27-36. DOI:10.1016/j.jweia.2018.09.007 |
| [12] |
HUANG M F, WANG Y F, LOU W J. Examination of typhoon-wind profiles reaching 1, 000-m height over the Southeast China sea based on reanalysis data set and mesoscale simulation[J]. Journal of Structural Engineering, 2020, 146(9): 04020192. DOI:10.1061/(asce)st.1943-541x.0002744 |
| [13] |
WALKER N D, LEBEN R R, BALASUBRAMANIAN S. Hurricane-forced upwelling and chlorophyll a enhancement within cold-core cyclones in the Gulf of Mexico[J]. Geophysical Research Letters, 2005, 32(18): L18610. DOI:10.1029/2005GL023716 |
| [14] |
HE Y C, LI Q S, CHAN P W, et al. Toward modeling the spatial pressure field of tropical cyclones: insights from Typhoon Hato (1713)[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 184: 378-390. DOI:10.1016/j.jweia.2018.12.001 |
| [15] |
关皓, 周林, 薛彦广, 等. 南海中尺度大气-海流-海浪耦合模式的建立及应用[J]. 热带气象学报, 2012, 28(2): 211-218. GUAN H, ZHOU L, XUE Y G, et al. An applied study on the atmosphere-ocean-wave coupled model in the South China sea[J]. Journal of Tropical Meteorology, 2012, 28(2): 211-218. DOI:10.3969/j.issn.1004-4965.2012.02.008 (in Chinese) |
| [16] |
徐海波, 杜华栋, 项杰, 等. 台风“Megi”(2010)过程中海浪的特征及其对大气海洋的影响研究[J]. 海洋预报, 2020, 37(3): 6-17. XU H B, DU H D, XIANG J, et al. The characteristics of ocean wave induced by typhoon “Megi” (2010) and its influence on the ocean and atmosphere[J]. Marine Forecasts, 2020, 37(3): 6-17. DOI:10.11737/j.issn.1003-0239.2020.03.002 (in Chinese) |
| [17] |
LIU B, LIU H Q, XIE L, et al. A coupled atmosphere-wave-ocean modeling system: simulation of the intensity of an idealized tropical cyclone[J]. Monthly Weather Review, 2011, 139(1): 132-152. DOI:10.1175/2010mwr3396.1 |
| [18] |
WARNER J C, ARMSTRONG B, HE R Y, et al. Development of a coupled ocean-atmosphere-wave-sediment transport (COAWST) modeling system[J]. Ocean Modelling, 2010, 35(3): 230-244. DOI:10.1016/j.ocemod.2010.07.010 |
| [19] |
LAPRISE R. The Euler equations of motion with hydrostatic pressure as an independent variable[J]. Monthly Weather Review, 1992, 120(1): 197-207. DOI:10.1175/1520-0493(1992)120<0197:teeomw>2.0.co;2 |
| [20] |
BOOIJ N, HAAGSMA I J G, HILTHUIJSEN LH, et al. SWAN user manuals, SWAN cycle Ⅲ version 40.81[R]. Delft University of Technolog, 2011.
|
| [21] |
郑沛楠, 宋军, 张芳苒, 等. 常用海洋数值模式简介[J]. 海洋预报, 2008, 25(4): 108-120. ZHENG P N, SONG J, ZHANG F R, et al. Common instruction of some OGCM[J]. Marine Forecasts, 2008, 25(4): 108-120. DOI:10.3969/j.issn.1003-0239.2008.04.016 (in Chinese) |
| [22] |
Japan Meteorological Agency. RSMC best track data (Text)[DB/OL]. http://www.jma.go.jp/jma/jma-eng/jma-center/rsmc-hp-pub-eg/besttrack.html
|
| [23] |
中华人民共和国住房和城乡建设部. 中华人民共和国国家标准: 建筑结构荷载规范 GB 50009—2012[S]. 北京: 中国建筑工业出版社, 2012.
|
 2021, Vol. 39
2021, Vol. 39