2. 中国空气动力研究与发展中心 计算空气动力研究所,绵阳 621000
2. Computational Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China
计算流体力学(CFD)在航空航天领域展现出巨大的发展潜力和工程应用价值,被广泛地应用于飞行器气动布局设计、气动性能评估和复杂流动模拟等方面[1-2]。CFD不确定度量化已经成为当前CFD发展的研究重点与难点。一方面,CFD数值方法中采用的模型及假设会对数值模拟结果产生影响,因此需要发展CFD不确定度量化方法,定量描述预测结果的不确定范围,评估CFD结果的可信度。另一方面,确定性的CFD计算无法考虑飞行器工作环境的随机变化对其性能的影响,不确定度量化方法能够给出关注变量的不确定随机解,从而支撑飞行器外形、结构及飞行控制系统的精细化设计。
不确定性的概念源自验证与确认工作。国外的专家学者很早就开展了CFD不确定度量化研究工作。1998年,美国航空航天协会(AIAA)在CFD验证与确认指南[3]中初步给出不确定性的定义。Oberkampf等[4]对不确定性的基础理论进行了补充和完善。美国机械工程协会(ASME)[5-7]进行了大量验证与确认方面的工作,进一步意识到不确定度量化工作的重要性,制定并完善了验证与确认标准。验证与确认工作的展开是为了检验计算模型是否真实反映物理模型。大多数CFD模拟所采用的数学模型都是确定性的,物性参数、几何模型和边界条件等也都是确定性的,并以寻求确定性解为目标。然而现实的物理环境中存在着大量的不确定性因素,如果研究对象的性能参数对某些不确定性因素较为敏感,采用确定性方法将会带来较大的风险。不确定性CFD技术的发展为工业设计提供了新的思路。欧盟实施NODESIM-CFD[8]项目,旨在辨识不确定性来源,发展不确定度量化方法,对CFD典型算例进行不确定性模拟。NASA在《CFD2030愿景》报告[9]中将不确定度量化作为未来研究的重点之一。空客在欧洲流动、湍流和燃烧研究共同体(ERCOFTAC)2015研讨会[10]中强调了CFD不确定度量化在工程实践中的需求及挑战,指出不确定度量化在飞行器设计各个环节发挥的重要作用。
随着国内对CFD验证与确认工作的逐渐重视,不确定度量化工作逐步展开。张涵信[11]等参照试验不确定度估算的做法,提出了CFD不确定度估算方法,用计算数据有效位数可以达到真值的前n位来表示计算结果的准确度。王瑞利等[12]结合爆轰流体力学多物理耦合的非线性偏微分方程和数值求解,介绍多物理耦合数学建模与模拟中的不确定度量化方法,开展大量的爆轰流体力学不确定度量化工作[13-14]。中国空气动力研究与发展中心组织召开了第一届航空CFD可信度研讨会[15],采用自主设计的单通道运输机模型(CHN-T1)开展CFD验证与确认工作,评估国内CFD当前技术状态,探索CFD进一步发展的研究方向,为不确定度量化提供了标准模型及数据库。国家数值风洞工程(NNW)设置不确定度量化研究专题,发展了一整套完整的参数不确定度量化方法[16]。
本文主要回顾国内外已经开展的诸多不确定度量化工作,总结不确定度量化工作的基本内容和方法,并结合CFD系统包含的典型环节介绍不确定度量化方法在CFD领域中的应用,最后给出进一步开展不确定度量化工作的思考与建议。
1 不确定度量化的基本内容及方法不确定度量化的目标是定量地分析不确定因素对计算结果的影响。不确定度量化工作围绕以下四个方面展开[5, 17-18]:(1)识别。明确不确定性产生的来源。(2)表征。探究不确定性的表现形式,并用恰当的数学表达对其进行表征。(3)传播与融合。采用不确定度量化方法研究不同种类不确定性变量在CFD系统中的传播,并给出数值模拟结果的整体不确定度。(4)分析。分析变量的不确定性对于CFD系统的影响。
1.1 识别与表征对不确定性来源的辨识是CFD不确定度量化的前提。Schaefer等[19]对数值模拟中的不确定性来源进行了归纳总结。CFD系统的不确定性主要产生于以下几个方面:(1)模型形式的不确定性。例如,几何建模过程中的简化处理使得计算采用的几何模型不能完全反应真实的物理模型,从而影响最终的计算结果;采用不同的假设构造湍流模型会对数值模拟结果有较大的影响。(2)模型参数的不确定性。例如湍流模型系数,湍流模型中的系数通常根据基础流动标定,改变参数设置将会对计算结果带来影响。(3)数值求解方法的不确定性。采用不同的时间、空间离散方法以及数值格式将会对CFD计算结果有较大的影响。(4)输入量的不确定性。风洞试验洞壁干扰等因素导致数值计算设置的来流边界条件不能完全反应真实情况,从而引入此类不确定性。(5)结果后处理的不确定性。流场分析需要采用插值、积分等方法对CFD计算结果进行后处理,从而导致此类不确定性。
用恰当的数学表达描述不确定变量是CFD不确定度量化工作的基础。不确定性按照表现形式的不同可以分为随机不确定性和认知不确定性[20]。随机不确定性是一类客观存在的不确定性,无法消除。随机不确定变量易于用概率表征,此类不确定性通常可以采用概率学的方法进行量化分析。认知不确定性是一类主观的不确定性,因为对问题的认识不足而造成。认知不确定变量通常难以给出具体的概率分布,此类不确定性通常采用非概率方法来进行量化和分析。
1.2 传播与分析不确定性的传播与分析是CFD不确定度量化工作的重点。依据不确定性表现形式的不同,人们发展了多种不确定度量化方法。
1.2.1 随机不确定度量化方法随机不确定度量化通常采用概率相关的方法。其中,基于抽样的方法是最为简单有效的。多种多样的抽样方法为此类不确定度量化方法提供了不同的研究思路。蒙特卡洛方法(MC)[21]是一种简单通用的抽样方法,通过构造随机过程并从已知的空间中进行抽样,得到大量的抽样结果,对抽样结果进行计算分析从而获取随机变量的统计信息。
对于随机变量
| $ \mu =\frac{1}{N}\sum\nolimits_{i=1}^{N}\varphi \left({\theta }_{i}\right) $ | (1) |
方差的计算公式为:
| $ {\sigma }^{2}=\frac{1}{N-1}\sum\nolimits_{i=1}^{N}{\left[\varphi \left({\theta }_{i}\right)-\mu \right]}^{2} $ | (2) |
其误差精度可表示为:
| $ \varepsilon =\frac{{\lambda }_{\alpha }\sigma }{\sqrt{N}} $ | (3) |
其中,
根据变量特点抽样可以有效减少样本点数量,从而提高抽样方法的效率,典型的方法有:分层抽样、拉丁超立方抽样[23-26]等。上述加速算法能够在一定程度上提高计算效率,但是并没有改变抽样方法本质上对样本数量的高需求,仍然需要进行大量的计算。为了进一步提高效率,科研工作者们开始将多项式混沌方法应用于不确定度量化。
取
| $ \varphi \left({\boldsymbol{X}},t,\theta \right)=\sum\nolimits_{k=0}^{\infty }{a}_{k}\left({\boldsymbol{X}},t\right){\varPsi }_{k}\left({\boldsymbol{\xi }}\right)\approx \sum\nolimits_{k=0}^{{N}_{PC}}{a}_{k}\left({\boldsymbol{X}},t\right){\varPsi }_{k}\left({\boldsymbol{\xi }}\right) $ | (4) |
式中,
| $ {N}_{PC}=\frac{\left(p+n\right)!}{p!n!}-1 $ | (5) |
其中,
| $ \begin{split}&\!\!\!\!\!\! \left\langle {\varPsi }_{i},{\varPsi }_{j}\right\rangle \\& = \int {\varPsi }_{i}\left({\xi }_{1},{\xi }_{2},\cdots ,{\xi }_{n}\right){\varPsi }_{j}\left({\xi }_{1},{\xi }_{2},\cdots ,{\xi }_{n}\right)d{\xi }_{1}d{\xi }_{2},\cdots ,d{\xi }_{n} \\& ={\varPsi }_{i}^{2}{\delta }_{ij}\\[-10pt]\end{split} $ | (6) |
式中,
按照与求解器耦合方式的不同,多项式混沌方法可以分为嵌入式与非嵌入式两种。嵌入式方法将流动变量展开为多项式混沌形式,在求解流体力学方程的同时可以直接得到变量的统计特性,计算量相对较小。Dinescu等[28]成功地将多项式混沌方法耦合到NUMECA的结构求解器FINE™/Turbo以及非结构求解器FINE™/Hexa中,并对NASA rotor37模型进行不确定度量化分析。然而嵌入式方法需要对求解器进行修改,大大增加了程序编写的工作量,实用性受到很大的限制。
非嵌入式方法将求解器看成“黑箱”,以确定性解为基础计算关注变量的统计特性。非嵌入式多项式混沌方法的核心是展开式系数的求解,其实现方式主要有两种:谱投影方法以及线性回归方法(又称为配置点法或随机响应面法[29])。谱投影法利用内积对每个基函数的响应进行投影,根据正交性计算展开式系数。线性回归方法通过线性最小二乘拟合求解展开式系数。非嵌入式概率配置点法[30-31]结合了多项式混沌与配置点思想,利用概率分布函数的特性得到混沌多项式系数的近似值,可以进一步减少计算量,提高效率。当随机输入变量服从标准正态分布时,对应的多项式系数可以通过Askey方法求得[32]。对于任意分布的不确定变量,相应的正交多项式系数可以通过Gram-Schmidt方法求得[33]。
为了实现对多个不确定变量的综合不确定度量化,需要将非嵌入式概率配置点方法扩展到多维。目前主要的思路是通过张量积实现多维求积,然而扩展到多维后其维度的增加将会导致配置点的数量呈几何级数增长,从而引发“维度灾难”。稀疏网格[34]以及降阶模型[35]的引入可以在一定程度上克服“维度灾难”的问题,提高非嵌入式概率配置点方法在不确定变量较多情况下的分析效率。
1.2.2 认知不确定度量化方法由于对输入变量概率分布的认识不足,很难用概率类方法对认知不确定性进行量化分析。传统的认知不确定度量化方法有区间法[36]、模糊逻辑法[37]等。区间法将变量以区间的形式表达,区间包含变量所有可能的取值,经过CFD计算后得到关注变量的不确定带,该不确定度带包含关注变量的所有取值。模糊逻辑法可以用来表达界限不清晰的定性知识与经验,采用隶属函数描述模糊性,运用无穷连续值的模糊集合去研究模糊性对象。
1.2.3 混合不确定度量化方法实际的物理问题十分复杂,既包含随机不确定性,也包含认知不确定性。混合不确定度量化方法针对两种不确性来源分别进行处理,实现对复杂物理过程的不确定度量化。混合不确定度量化方法主要有两种。
一种是嵌套迭代的方法:在外循环中处理认知变量而在内循环中处理随机变量[38]。根据外层循环中对认知不确定变量处理方式的不同可以分为区间值概率方法(IVP,也被称为概率范围分析PBA)、二阶概率方法(SOP)以及DS证据理论(DSTE)。IVP方法[39]将不确定性变量转化为区间的形式,通过嵌套迭代的方式得到关注变量的累积分布函数(CDF)或互补累计分布函数(CCDF)。SOP方法与IVP方法类似,也采用嵌套迭代的方式,有所不同的是,SOP方法[40]通过主观概率分布描述不确定性变量。DSTE方法[41]证据理论以两种互补的不确定性度量方式(信任测度和似然测度)描述不确定变量。在计算统计量时采用随机展开法并且在计算上下界限时采用区间优化算法将会大大提高上述三种方法的精度和效率[42]。
另一种混合不确定度量化方法是P-box方法[43-45]。P-box方法通过上下界的方式给出变量的CDF,按照上下界计算方式的不同通常可以分为参数化P-box和非参数化P-box。参数化P-box可以由一组参数位于同一区间的分布函数表示,而非参数化P-box由CDF的包络线产生。
以上内容介绍了不确定度量化工作涉及的基本内容以及不同表现形式不确定变量的量化分析方法。下面将根据CFD计算中的不确定性来源介绍不确定度量化方法在CFD计算中的应用情况。
2 计算网格的不确定度量化网格的拓扑关系、黏性网格的第一层高度、增长率以及网格的空间分布等因素决定了网格的质量,也影响了CFD计算的收敛以及数值模拟的最终结果。开展计算网格的不确定度量化工作对于CFD可信度评估具有重要意义。
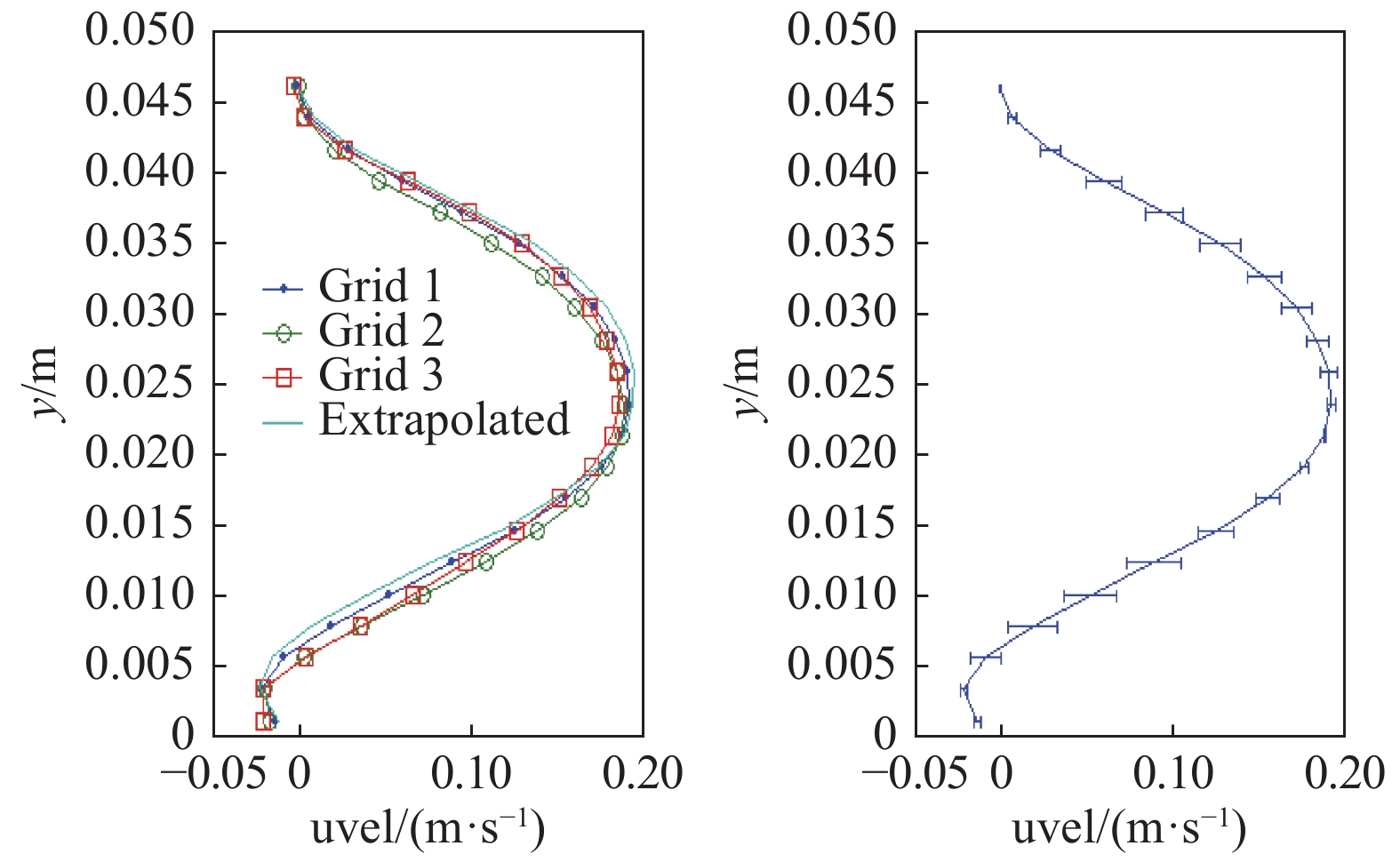
Richardson外推方法[46-47]可以估算离散误差,研究人员将其应用于CFD网格的不确定度量化。如图1所示,Celik等[48]在Richardson外推方法的基础上提出了网格收敛性指标(GCI),并以此研究了网格数量对二维后台阶流动计算结果的影响,结果表明,在速度接近0时轴向速度对网格的敏感度最大。赵训友等[49]对现有的GCI离散不确定度估算法进行了改进,用加权平均的数值解代替细网格数值解来估算离散误差及不确定度,使得结果具有更高的置信度。Schaefer等[50]研究了网格以及湍流模型系数的不确定性对于RAE2822翼型气动特性的影响。按照网格的疏密分布、第一层网格高度以及拓扑关系的不同,Schaefer等生成了6套计算网格,并采用非嵌入式多项式混沌方法对SA、Wilcox k-ω以及SST湍流模型系数的不确定度进行量化分析,并通过sobol灵敏度分析了各个湍流模型系数对于总不确定性的贡献。结果表明,少部分的湍流模型系数对CFD数值模拟结果有较大影响,例如SA模型中的σ和κ等。该研究为湍流建模以及后续的三维构型不确定度量化工作打下了基础。
|
图 1 二维后台阶流动轴向速度分布[48] Fig.1 Wall-normal profiles of axial velocities for a two-dimensional backward-facing-step laminar flow simulated by different grids[48] |
由于制造公差的存在以及对真实模型的简化处理,用于计算的几何模型与真实情况不可避免地存在着一些误差,从而引入几何外形的不确定性。对几何外形的不确定度量化对于飞行器气动设计有着重要的意义。
Loeven等[51]为了减少不确定性因素的数量,采用参数化方法对NACA 4系列翼型进行建模,并利用概率配置点法研究了翼型的最大弯度、最大弯度位置以及厚度等关键设计变量的不确定性对翼型气动特性的影响。图2给出了NACA5412翼型最大弯度、最大弯度位置以及厚度等不确定性因素影响下的升力系数不确定带。对于升力系数而言,最大弯度带来的不确定性最大,大迎角下厚度带来的不确定性较大。Parussini等[52]将张量展开混沌配置法与虚拟域方法结合,对几种基本流动问题的几何不确定性进行量化分析。Liu等[53]采用梯度增强的径向基函数方法(GERBF)、多项式混沌方法等研究了RAE2822翼型几何随机扰动对跨声速条件下气动特性的影响,研究表明,梯度增强的降阶模型方法较之直接积分方法效率更高。Liu等[54]采用非嵌入式概率配置点方法考察了风速的不确定性对风力机气动特性的影响,探究了不确定性在流场中的传播,实现了不确定CFD技术对传统验证与确认工作的补充。Trojak等[55]研究了非均匀网格对多维通量重构的影响,归纳总结了波角和网格变形对通量重构的影响规律。Liu等[56]等基于RBF插值对翼型进行参数化,通过Kriging响应面法建立翼型流场的代理模型,并采用蒙特卡洛方法研究了压敏材料厚度分布不确定性对自然层流机翼气动力的影响。
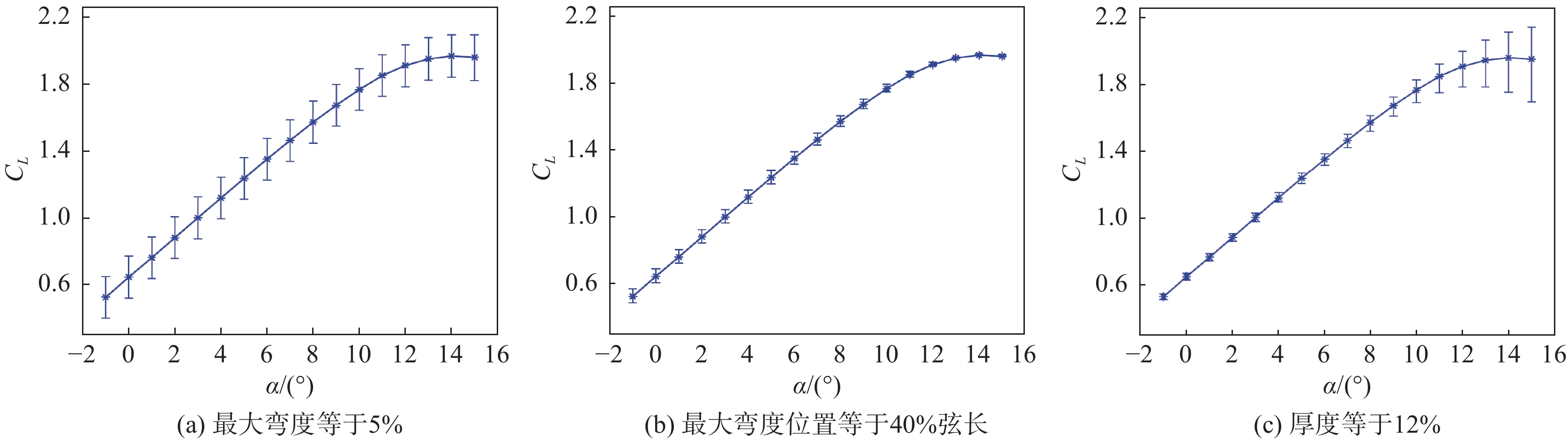
|
图 2 NACA5412翼型升力系数不确定带[51] Fig.2 The uncertainty bounds of lift coefficient for NACA5412 airfoil[51] |
CFD流场求解过程涵盖了湍流模型、离散方法和数值格式等核心要素。这些模型代表了对物理问题的近似,然而不同的方法依据不同的假设,其近似的程度也有所不同,对这些要素的不确定性进行量化分析是CFD计算和可信度评估的核心环节。目前在流场计算这一层级的工作主要集中在湍流模型以及来流边界条件这两个方面。
Xiu等[57]提出了广义多项式混沌方法(GPC),理论证明了不同的概率分布存在不同的最优多项式混沌与之对应,多项式展开可以按照指数收敛,并用此方法研究了不可压槽道流动和方柱绕流的不确定度量化问题。Loeven等[58]发展了用拉格朗日插值多项式(LIP)构造随机变量的非嵌入式概率配置点法,可以在保证计算精度一定的情况下减小确定性计算的数量,并且将该方法应用于NACA0012翼型的不确定性分析中。Mariotti等[59]运用概率配置点法对二维矩形柱体的来流不确定性进行了研究,考察了入射角、来流纵向湍流强度以及湍流积分尺度的不确定性对其空气动力学特性的影响。Avdonin等[60]采用多项式混沌展开方法研究了预混合层流火焰传递函数的工况不确定性,考察了入口速度、燃烧器板温度和等效比等因素的影响。研究表明,非嵌入式多项式混沌方法能够高效地处理热声学不确定性问题,不确定变量概率分布函数的方差对结果的影响较大。
如图3所示,Zhu等[61]采用概率配置点方法考察了来流条件不确定性对NASA0714翼型跨声速抖振状态气动特性的影响。研究表明,激波运动区域对于来流条件十分敏感。刘智益等[62]采用非嵌入式概率配置点法研究了转子叶顶间隙尺寸不确定性对某轴流压气机流量、效率、压比以及马赫数变化量的影响。邬晓敬等[63]采用非嵌入式概率配置点法研究了迎角及马赫数不确定性对NACA0012翼型跨声速条件下气动特性的影响。王言金等[64]采用非嵌入式多项式混沌方法考察了不可压圆柱绕流的不确定性问题。邓小兵等[65]通过在自由来流中引入随机脉动的方式开展了复杂构型细长体飞行器大迎角横侧向气动力不确定性的数值模拟研究。研究表明,大迎角气动力出现不确定性的原因是头部分离涡的结构不稳定性。徐林程等[66]发展了基于自动微分方法的不确定度量化方法,研究了来流参数不确定性对风洞试验结果精确度的影响。结果显示,在亚声速来流条件下,迎角是影响风洞试验精度的主要因素;在跨声速来流条件下,影响风洞试验精度的主要因素转变为马赫数。
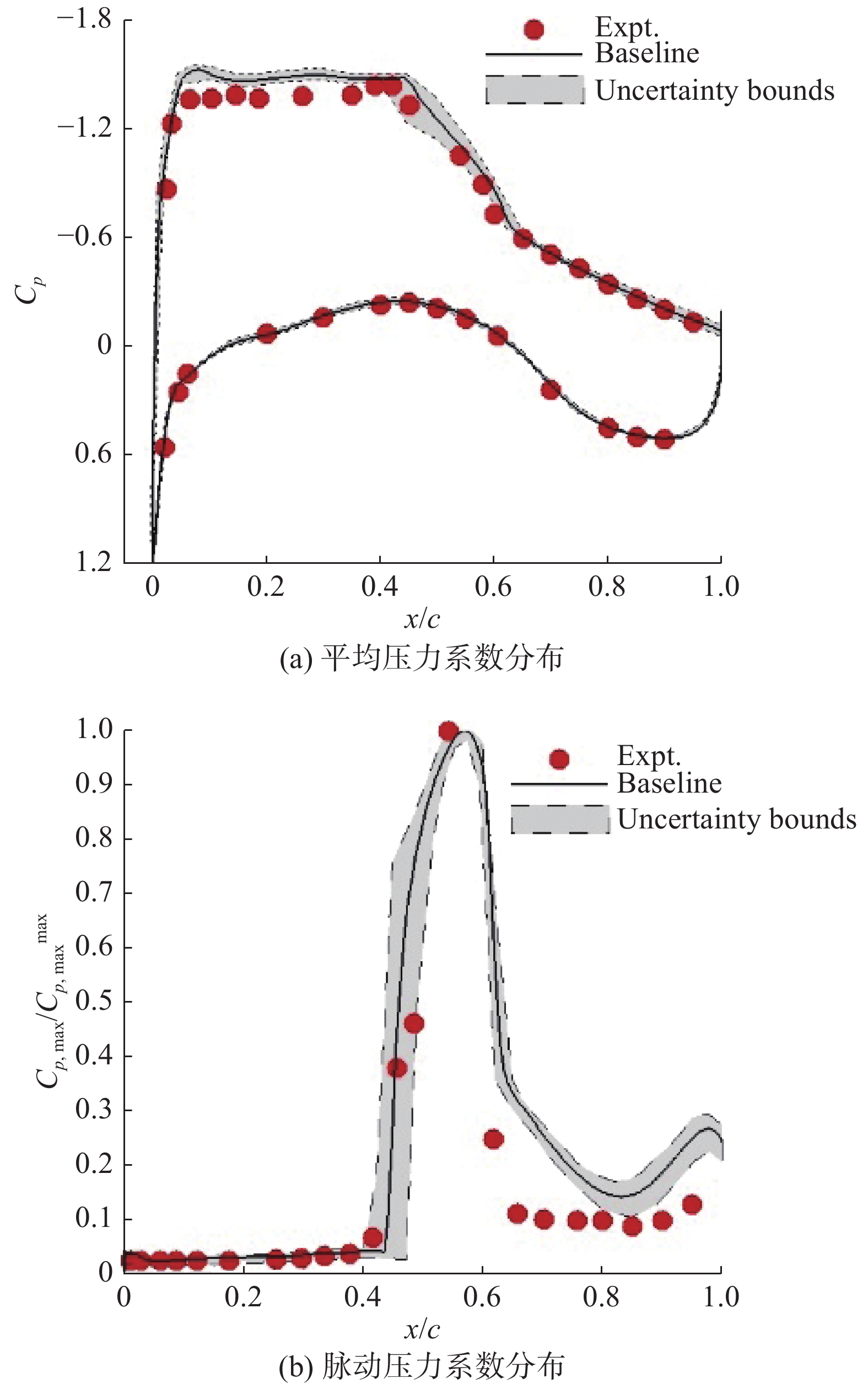
|
图 3 NASA SC(2)-0714翼型表面压力系数及脉动压力系数不确定带[61] Fig.3 The mean and root-means-square of the pressure coefficient with uncertainty bounds[61] |
以湍流模式理论为基础建立的湍流模拟方法是目前CFD最常使用的计算湍流的手段,在精度和效率方面取得较好的平衡,满足绝大多数的工程需求。湍流模式理论以雷诺平均运动方程与随机脉动运动方程为基础,通过一系列的假设,建立描述湍流脉动量的封闭方程。在进行雷诺平均的过程中,将会进行多个层次的假设,引入潜在误差,从而限制模拟结果的可信度。
Duraisamy等[67]将RANS湍流模型中的不确定性来源归纳为以下四个方面:系综平均导致的不确定性、雷诺应力函数和运算表达的不确定性、模型中函数形式的不确定性以及模型系数的不确定性。图4中以雷诺应力输运模型和线性涡黏模型为例,标注出湍流模型中可能存在的不确定性来源。
Xiao等[68]对RANS模拟中湍流模型的不确定度量化方法进行了归纳和总结。根据二阶对称张量有三个不变量:迹、平方以及立方迹。进而可以利用雷诺偏应力张量和主应力的物理含义分析出雷诺偏应力的约束条件,即Lumley曲边三角形[69]。如图5所示,Banerjee等[70]用线性关系式的方式建立了雷诺偏应力张量特征值和坐标之间的关系,从而将Lumley曲边三角形这一限制条件转换到重心坐标系统下的直边三角形。Emory等[71-72]在雷诺应力张量中引入物理约束并对雷诺应力进行摄动,从而对湍流模型的不确定性进行量化。该方法建立在雷诺应力特征值分解的基础之上,着重考虑了对特征值的限制,忽视了对湍动能以及特征向量的约束。Iaccarino等[73]探究了给定约束条件下雷诺应力的变化范围,对已有考虑特征值约束的方法进行了补充。采用极限状态的特征值给出湍动能的最大值和最小值,通过五次RANS计算就能得到流动演化过程中特征空间的摄动范围,从而给出CFD计算结果的不确定度带。Iaccarino等采用该方法研究了湍流射流模拟中湍流模型不确定性对流动的影响。
如图6所示,Mishra等[74]同时考虑了对特征值及特征向量的约束,以摄动法雷诺应力椭球极值状态的形式形象地阐释了该方法的物理含义。如图7所示,Mishra等将这种方法应用于MD30P30N多段翼型,得到该翼型在湍流模型涡黏假设不确定条件下的压力系数及摩擦力系数不确定带。
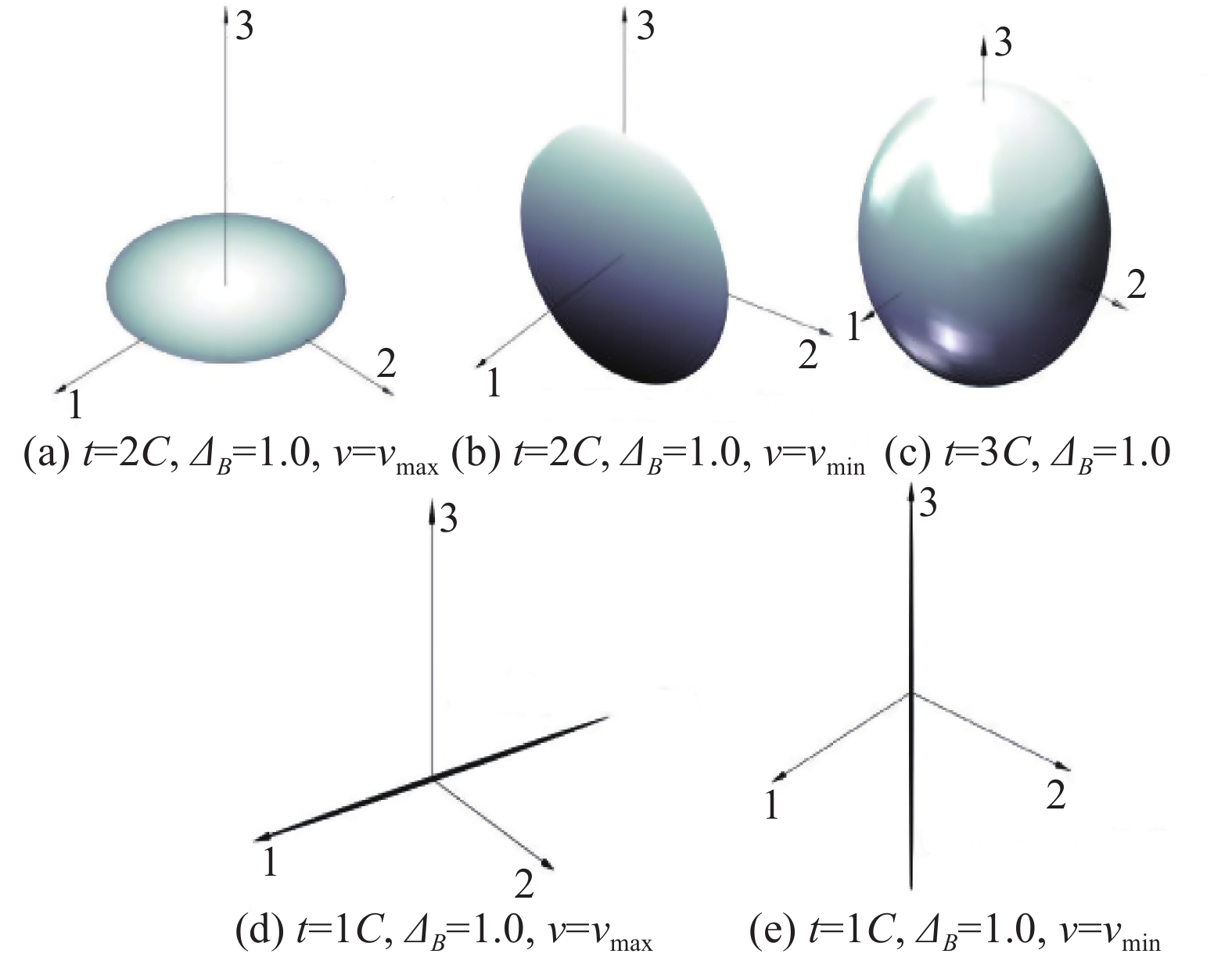
|
图 6 摄动法雷诺应力椭球极值状态可视化显示[74] Fig.6 Schematic visualization of the extremal states as Reynolds stress ellipsoids in the eigenspace perturbation methodology [74] |
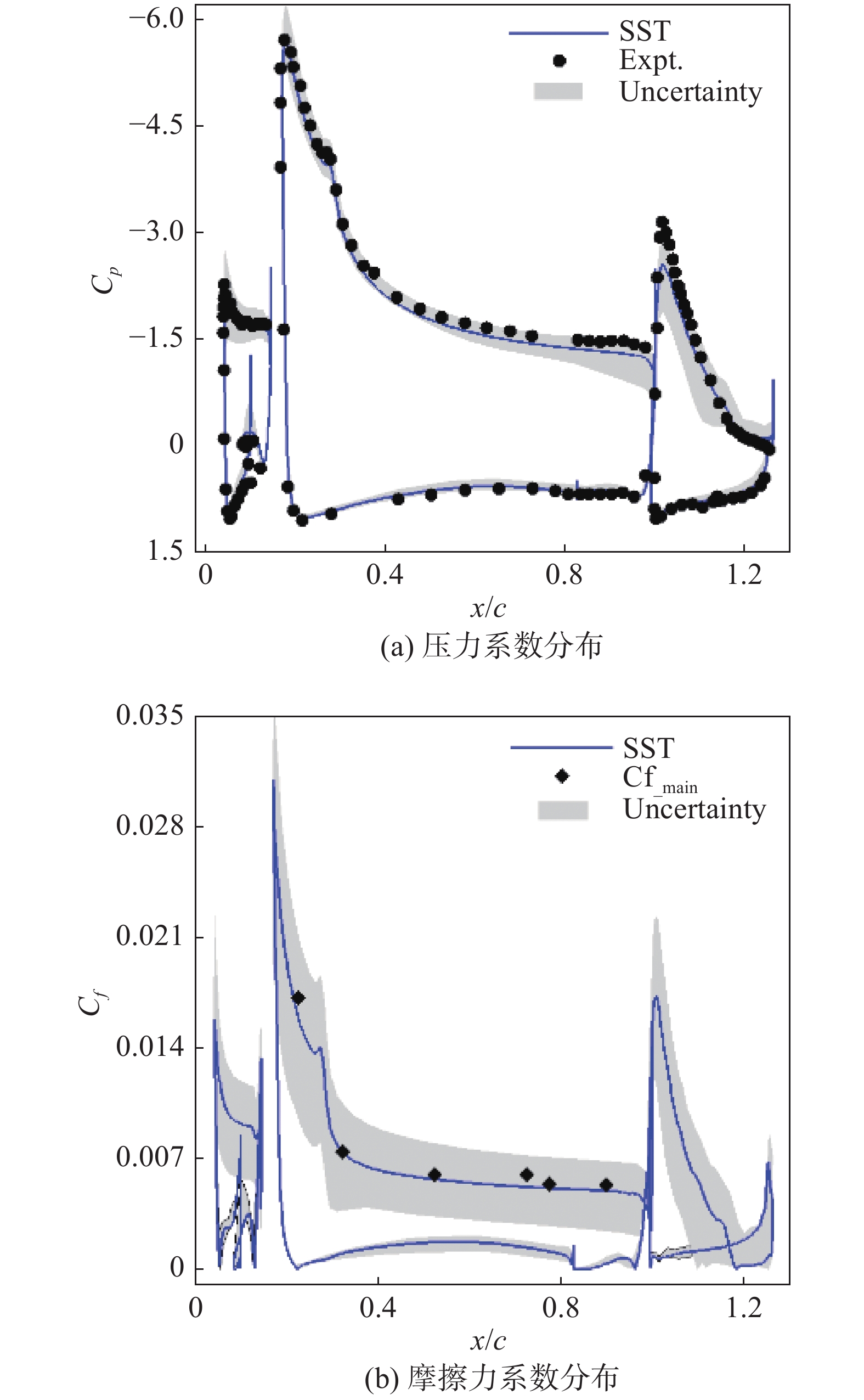
|
图 7 MD30P30N多段翼型采用雷诺应力摄动法表面压力系数及摩擦力系数不确定带 Fig.7 The mean and root-mean-square of (a) pressure and (b) friction coefficients on MD30P30N with uncertainty bounds |
作为对基于特征值分解的物理方法的替代,Xiao等[75]给出了雷诺应力不确定性的概率描述。将雷诺应力用一个半正定的随机矩阵来表示,期望为RANS模型的雷诺应力,并且定义了雷诺应力张量的最大熵分布,通过对其采样来表征雷诺应力的不确定性。随机矩阵法和基于特征值分解的方法类似,无论是对雷诺应力张量进行摄动还是对雷诺应力张量的分布进行抽样都能保证其可实现性。Wang等[76]采用随机矩阵法研究了特征值和特征向量的不确定性空间,并且通过定义在随机矩阵上的最大熵分布,说明了他们之间存在的关联性。与特征值分解方法相比,这种方法不能从物理的角度对极限状态做出明确的解释。这两种方法都侧重于单点的雷诺应力误差带研究,忽视了雷诺应力随空间变化导致的不确定性。Edeling等[77]提出了“回归涡黏模型”,对雷诺应力张量进行摄动,采用该方法对亚声速射流进行数值模拟,分析了湍流模型不确定性的影响。
湍流模型中的模型参数通常是通过一些基本流动进行校准的(例如,均匀各向同性湍流、平板流动、槽道流动等)。然而这些参数并不是普适的,需要根据流动的特性进行调整,例如,Pope[78]以及Eisfeld[79]列举了几种典型自由剪切流的最优参数(平板射流、圆形射流以及尾流等)。在复杂湍流流动的数值模拟中,如果模型参数仍然采用基本流动的默认值,会引入不确定性。采用经典的不确定度量化方法可以简单地考察湍流模型中系数的选择对于仿真结果的影响。这些方法基本都依赖于对湍流模型中相关系数的描述。Dunn等[80]采用拉丁超立方抽样方法研究了k-ε模型系数不确定性对二维后台阶流动的影响。研究表明,模型系数对再附点附近回流区的流向速度以及自由剪切层湍流强度影响较大。Platteeuw等[81]采用概率配置点法研究了带有壁函数的k-ε模型系数不确定性对平板流动的影响。研究表明,壁函数参数的波动对平板流动有着显著的影响。
6 混合不确定度量化CFD系统非常复杂,涉及到大量的不确定性因素,将这些因素割裂分析将会忽略他们之间的联系,需要对CFD系统进行整体不确定度量化。混合不确定度量化方法被广泛地应用于CFD整体不确定度量化中。Shah等[82]将DS证据理论与非嵌入式概率配置点方法结合,研究了迎角、来流马赫数以及SA模型系数等不确定性因素对RAE2822翼型跨声速条件下气动特性的影响。高超声速再入流动模拟中存在着大量的不确定性因素,采用传统方法计算量过大,针对这种情况,West等[83]发展了多步不确定度量化方法。多步不确定度量化方法首先采用局部敏感性分析对不确定性变量降维,最终采用改进的非嵌入式概率配置点方法进行不确定度量化。Quagliarella等[84]将五种基于元模型的蒙特卡洛方法、多级蒙特卡洛方法以及非嵌入式概率配置点法分别应用于NACA2412翼型的不确定度量化中,研究了来流马赫数以及几何外形不确定性对其气动特性的影响。
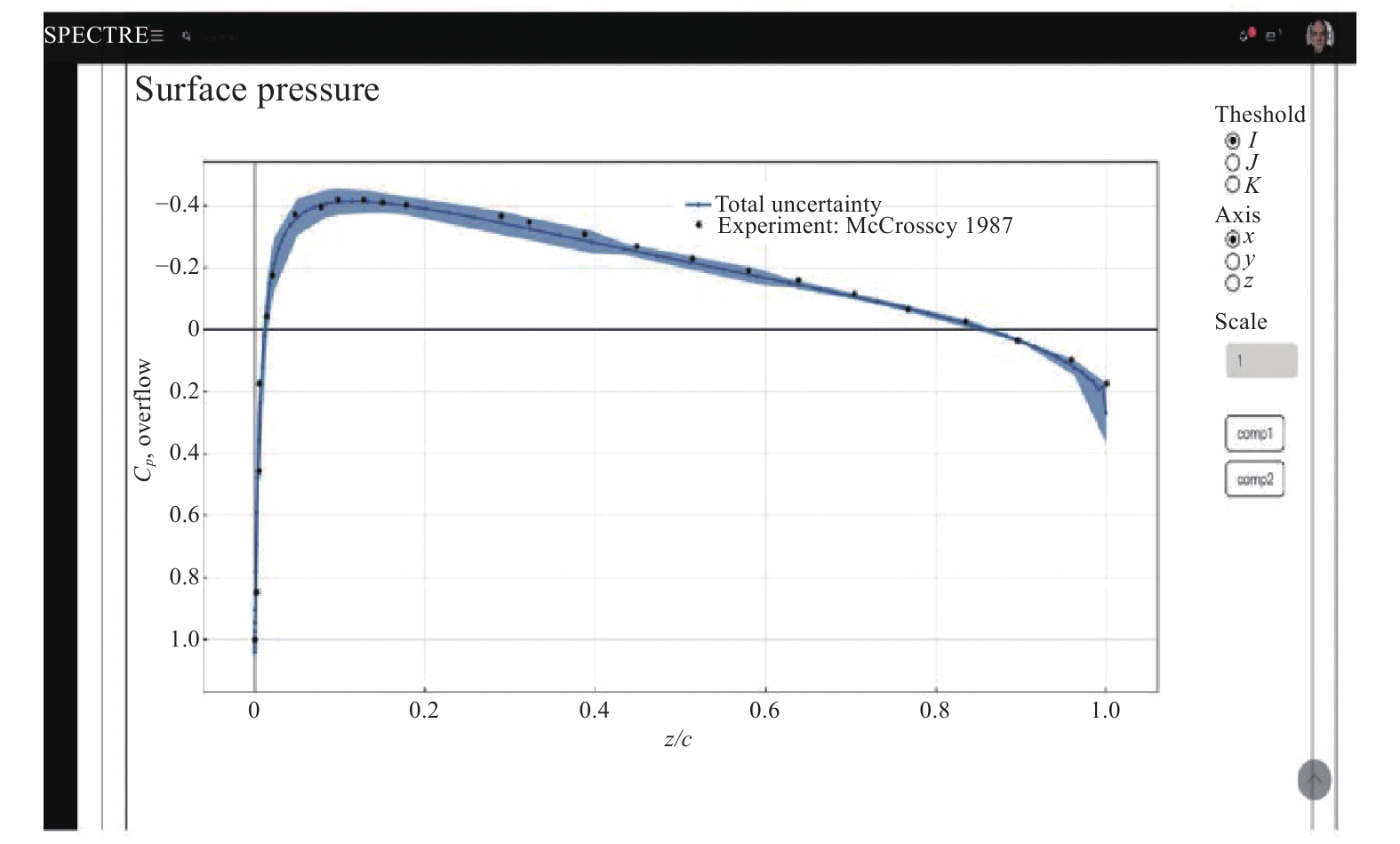
Duque等[85]开发了“Spectre”平台,该平台能够根据用户的自定义进行网格以及来流参数(马赫数、迎角、雷诺数等)的不确定度量化,实现CFD整体不确定度量化的商业化。图8、图9展示了利用该平台对NACA0012翼型进行不确定度量化获取的升力系数及表面压力系数的统计信息。该平台能够根据用户需求给出关注变量的统计信息以及整体不确定度。Schaefer等[86]采用了SOP方法实现了对网格、来流参数以及SA湍流模型系数的整体不确定度量化,并成功应用于NASA高升力CRM构型,验证了集成不确定度量化方法在工程应用上的可行性。Wignall等[87]结合数据融合和降阶模型技术研究了模型以及风洞试验数据转化的不确定性对火箭气动载荷的影响。
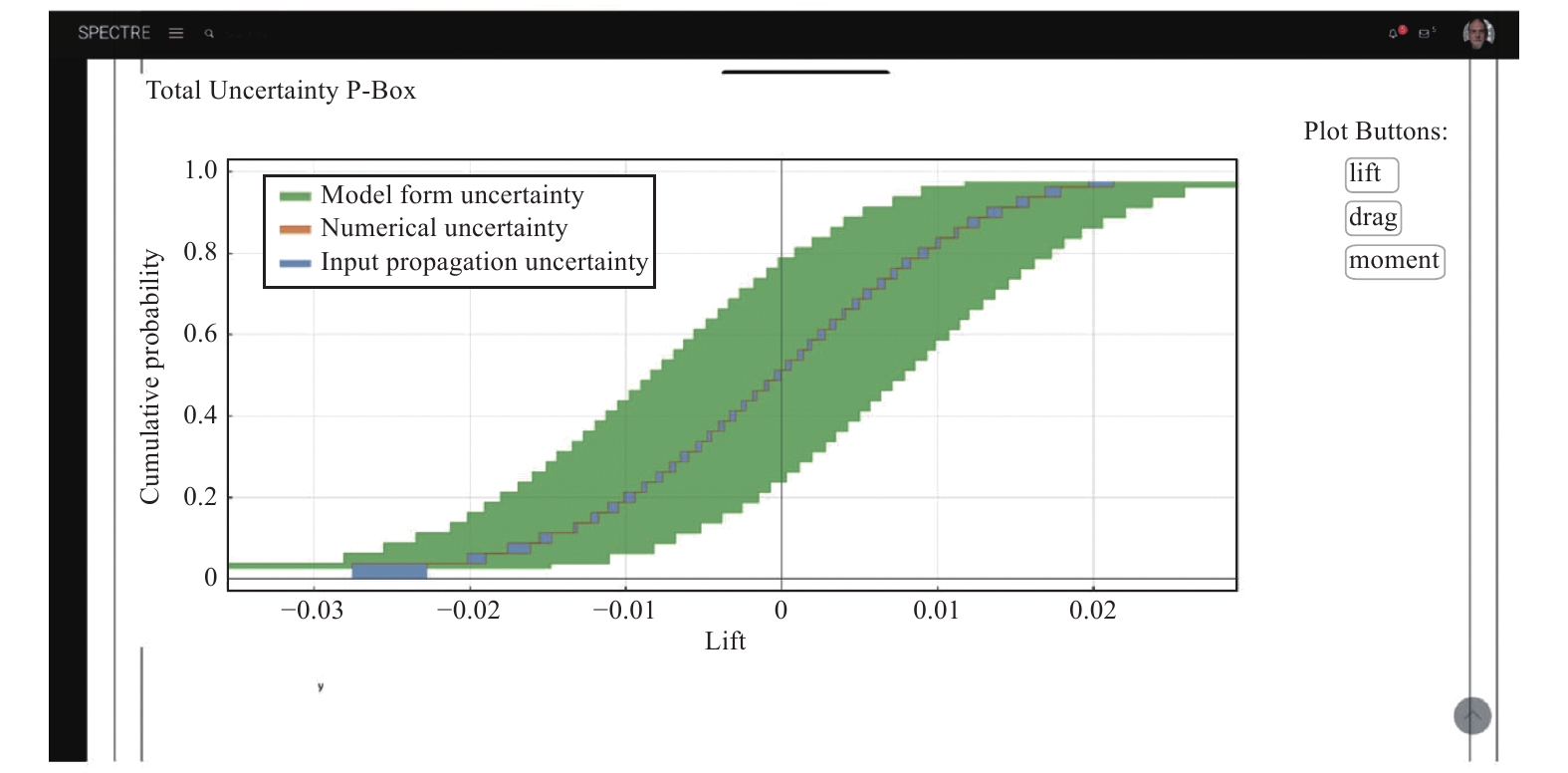
|
图 8 NACA0012翼型升力系数累积密度分布函数[86] Fig.8 The cumulative probability distribution of lift coefficient for NACA0012[86] |
7 不确定性因素的敏感性分析
对不确定度量化结果的分析也是不确定性研究中不可或缺的内容。一旦明确了CFD数值模拟中的各种不确定性来源和表现形式,并且对这些不确定性在CFD系统中的传递进行了量化,研究各类不确定性因素对总不确定性的贡献就显得尤为关键。敏感性分析常常被用来研究不确定性因素对CFD计算结果的影响大小。目前对敏感性分析的研究主要集中在提升效率和精度上。
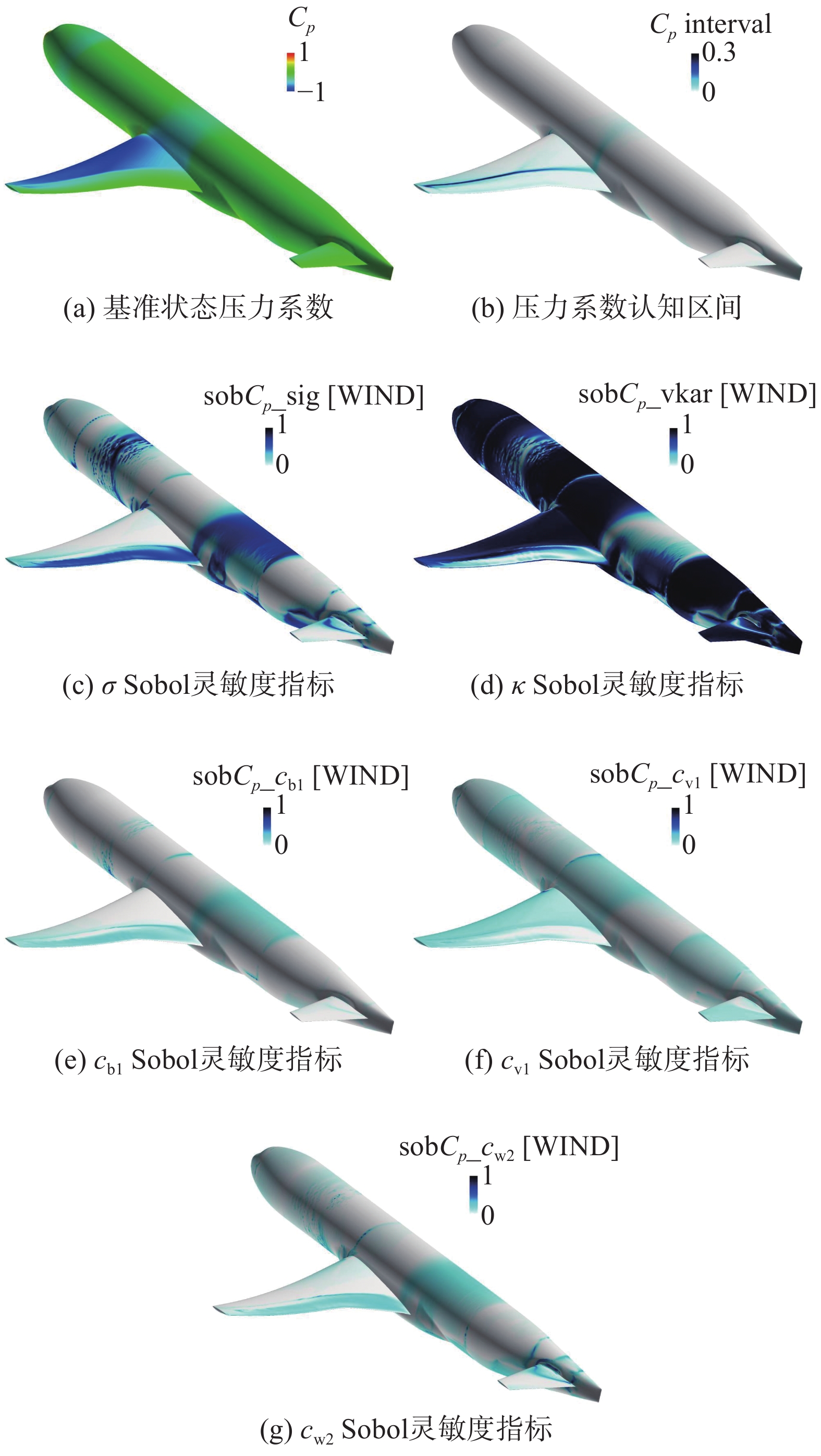
如图10所示,Schaefer等[88]采用非嵌入式概率配置点方法研究了SA湍流模型系数不确定性对NASA CRM构型气动特性的影响,借助sobol灵敏度指标分析了SA模型各个系数的不确定度在总体不确定度中所占的比重。研究表明,SA湍流模型中系数σ和κ对于跨声速近壁面流动的影响最大。肖思男等[89]对基于概率描述的不确定性结构全局灵敏度分析方法进行了概述。传统灵敏度指标分析方法在输入变量很多时效率较低且准确性得不到保证。针对这种情况,Storlie等[90]提出了一种基于元模型和引导置信区间的敏感性分析方法,在提高敏感性分析效率的同时也保证了方法的准确性。Saltelli等[91]采用基于方差的敏感性分析方法对模型的全局输出进行了敏感度的考察。Sudret等[92]引入广义多项式混沌展开方法构建降阶模型,实现高效的全局敏感性分析。与基于蒙特卡洛方法的敏感性分析方法相比,该方法可以应用于不确定变量很多的情况,并且大大提高计算效率。Duvigneau等[93]采用连续灵敏度方程方法(CSEM)实现了对翼型形状参数的快速不确定度量化。Fiorini等[94]推导了管道流问题的敏感性方程,利用敏感性方程方法给出入口速度不确定条件下管道内流动变量的不确定带。将定常流动模拟结果与蒙特卡洛方法进行了对比,验证了该方法的准确性。针对非定常流动模拟敏感性随时间增加的情况,对敏感性导数进行滤波,依据滤波后的敏感性导数计算出流动变量的不确定带。
8 CFD不确定度量化工作的总结与展望随着CFD技术在工程实践中的广泛应用以及对CFD算法认识的不断加深,CFD不确定度量化已经成为当前的研究热点,国内外针对CFD系统各个关键环节开展了大量的不确定度量化工作。CFD不确定度量化首先需要辨识不确定性因素的来源,按照形式的不同选择恰当的方法考察不确定性在CFD计算过程中的传播,最终根据结果的统计特性分析不确定性因素对于CFD系统的影响。
目前针对几何外形、来流条件、湍流模型等因素的不确定度量化方法已经较为成熟,然而针对数值格式的不确定度量化工作开展较少,对计算网格的不确定度量化也仅仅是针对网格量这一因素。发展对这些不确定性因素的量化分析方法对于完善CFD系统的不确定度量化体系有着重要的作用。
CFD系统中存在大量的不确定性因素,为了探究不确定性来源之间的关联性,从而更好地指导CFD方法的工程应用,需要对CFD系统进行全局不确定度量化分析。然而,随着待考察变量的增加,不确定度量化的计算量急剧增加,为了实现对物理问题的快速不确定度量化,需要进一步提升不确定度量化方法的效率。
当前不确定度量化工作大多针对简单构型以及一些较为简单的流动问题。随着CFD数值模拟对象的逐渐复杂化,需要扩展不确定度量化的应用范围,对更为复杂的构型以及流动进行不确定度量化。
现代飞行器需要面临复杂的飞行环境,其性能参数对某些不确定性因素非常敏感,确定性CFD计算已经不足以满足工程实际的需求,利用不确定性CFD技术进行飞行器外形、结构及飞行控制系统的精细化设计已经成为未来不断探索的研究方向。
| [1] |
JAMESON A. Computational aerodynamics for aircraft design[J]. Science, 1989, 245(4916): 361-371. DOI:10.1126/science.245.4916.361 |
| [2] |
AGARWAL R. Computational fluid dynamics of whole-body aircraft[J]. Annual Review of Fluid Mechanics, 1999, 31(1): 125-169. DOI:10.1146/annurev.fluid.31.1.125 |
| [3] |
OBERKAMPF W L, SINDIR M N, CONLISK A T. Guide: Guide for the verification and validation of computational fluid dynamics simulations(AIAA G-077-1998(2002))[M]. American Institute of Aeronautics and Astronautics, 1998.
|
| [4] |
OBERKAMPF W L, DELAND S M, RUTHERFORD B M, et al. Estimation of total uncertainty in modeling and simulation[R]. Sandia National Laboratories, SAND 2000-0824, 2000.
|
| [5] |
SCHWER L E. Guide for verification and validation in computational solid mechanics: an overview of the PTC 60/V&V 10[M]. The American Society of Mechanical Engineers, 2006.https://cstools.asme.org/csconnect/FileUpload.cfm?View=yes&ID=24816
|
| [6] |
ASME V&V 20-2009. Standard for verification and validation in computational fluid dynamics and heat transfer[S]. The American Society of Mechanical Engineers, 2009. https://files.asme.org/Catalog/Codes/PrintBook/21356.pdf
|
| [7] |
ASME V&V 10.1-2012. An illustration of the concepts of verification and validation in computational solid mechanics[S]. The American Society of Mechanical Engineers, 2012. https://www.asme.org/getmedia/ae188d7f-e6ad-483f-bf6f-194d1049d17a/31917.pdf
|
| [8] |
HIRSCH C. NODESIM-CFD: Non-deterministic simulation for CFD based design methodologies[R]. AST5-CT-2006-030959, 2006. https://trimis.ec.europa.eu/sites/default/files/project/documents/20121026_100225_36867_Aerodays-2011.pdf
|
| [9] |
SLOTNICK J, KHODADOUST A, ALONSO J, et al. CFD vision 2030 study: a path to revolutionary computational aerosciences[R]. NASA Langley Research Center, Hampton, Virginia, NASA CR-2014-218178. https://core.ac.uk/download/pdf/42732819.pdf
|
| [10] |
Airbus Group Innovations. Current engineering practices in UQ&M in aeronautics and associated challenges[Z/OL]. 2016.https://reseau-mexico.fr/sites/mexicoD8/files/Mangeant_2.pdf
|
| [11] |
张涵信. 关于CFD计算结果的不确定度问题[J]. 空气动力学学报, 2008, 26(1): 47-49, 90. ZHANG H X. On the uncertainty about CFD results[J]. Acta Aerodynamica Sinica, 2008, 26(1): 47-49, 90. DOI:10.3969/j.issn.0258-1825.2008.01.009 (in Chinese) |
| [12] |
王瑞利, 江松. 多物理耦合非线性偏微分方程与数值解不确定度量化数学方法[J]. 中国科学: 数学, 2015, 45(6): 723-738. WANG R L, JIANG S. Mathematical methods for uncertainty quantification in nonlinear multi-physics systems and their numerical simulations[J]. SCIENTIA SINICA Mathematica, 2015, 45(6): 723-738. DOI:10.1360/N012014-00115 (in Chinese) |
| [13] |
梁霄, 王瑞利. 爆炸波问题中偶然不确定度的量化[J]. 高压物理学报, 2016, 30(6): 531-536. LIANG X, WANG R L. Quantification of aleatory uncertainty in blast wave problem[J]. Chinese Journal of High Pressure Physics, 2016, 30(6): 531-536. (in Chinese) |
| [14] |
梁霄, 王瑞利. 爆炸波中的混合不确定度量化方法[J]. 计算物理, 2017, 34(5): 574-582. LIANG X, WANG R L. Mixed uncertainty quantification of blast wave problem[J]. Chinese Journal of Computational Physics, 2017, 34(5): 574-582. DOI:10.3969/j.issn.1001-246X.2017.05.006 (in Chinese) |
| [15] |
王运涛, 刘刚, 陈作斌. 第一届航空CFD可信度研讨会总结[J]. 空气动力学学报, 2019, 37(2): 247-261, 246. WANG Y T, LIU G, CHEN Z B. Summary of the first aeronautical computational fluid dynamics credibility workshop[J]. Acta Aerodynamica Sinica, 2019, 37(2): 247-261, 246. DOI:10.7638/kqdlxxb-2018.0219 (in Chinese) |
| [16] |
陈坚强. 国家数值风洞(NNW)工程关键技术研究进展[J]. 中国科学: 技术科学, 2020(在线发表). CHEN J Q. Advances in the key technologies of Chinese national numerical windtunnel project[J]. SCIENTIA SINICA Technologica, 2020(online). (in Chinese) doi: 10.1360/SST-2020-0334 |
| [17] |
LEE H B, GHIA U, BAYYUK S, et al. Development and use of engineering standards for computational fluid dynamics for complex aerospace systems[C]//46th AIAA Fluid Dynamics Conference, Washington D C, Reston, Virginia: AIAA, 2016. doi: 10.2514/6.2016-3811
|
| [18] |
NASA-STD-7009. Standard for Models and Simulations[S]. National Aeronautics and Space Administration, 2008. https://standards.nasa.gov/sites/default/files/nasa-std-7009.pdf
|
| [19] |
SCHAEFER J A, ROMERO V J, SCHAFER S R, et al. Approaches for quantifying uncertainties in computational modeling for aerospace applications[C]//AIAA Scitech 2020 Forum, Orlando, FL. Reston, Virginia: AIAA, 2020. doi: 10.2514/6.2020-1520
|
| [20] |
CULLEN A, FREY H C. Probabilistic techniques in exposure assessment: A handbook for dealing with variability and uncertainty in models and inputs[M]. Plenum Press, New York, 1999.
|
| [21] |
SÁNDOR Z, ANDRÁS P. Alternative sampling methods for estimating multivariate normal probabilities[J]. Journal of Econometrics, 2004, 120(2): 207-234. DOI:10.1016/S0304-4076(03)00212-4 |
| [22] |
LE MAÎTRE O P, KNIO O M. Spectral methods for uncertainty quantification: with applications to computational fluid dynamics[M]. Springer, 2010. doi: 10.1007/978-90-481-3520-2
|
| [23] |
MCKAY M D, BECKMAN R J, CONOVER W J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J]. Technometrics, 1979, 21(2): 239. DOI:10.2307/1268522 |
| [24] |
SANTNER T J, WILLIAMS B J, NOTZ W I. The design and analysis of computer experiments[M]. New York, NY: Springer New York, 2003. doi: 10.1007/978-1-4757-3799-8
|
| [25] |
HELTON J C, DAVIS F J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems[J]. Reliability Engineering & System Safety, 2003, 81(1): 23-69. DOI:10.1016/S0951-8320(03)00058-9 |
| [26] |
HELTON J C, JOHNSON J D, SALLABERRY C J P, et al. Survey of sampling-based methods for uncertainty and sensitivity analysis.[R]. Sandia National Laboratories, SAND 2006-2901, 2006. https://digital.library.unt.edu/ark:/67531/metadc891681/m2/1/high_res_d/886897.pdf
|
| [27] |
GHANEM R G, SPANOS P D. Stochastic finite elements: A spectral approach[M]. New York, NY: Springer New York, 1991. doi: 10.1007/978-1-4612-3094-6
|
| [28] |
DINESCU C, SMIRNOV S, HIRSCH C, et al. Assessment of intrusive and non-intrusive non-deterministic CFD methodologies based on polynomial chaos expansions[J]. International Journal of Engineering Systems Modelling and Simulation, 2010, 2(1/2): 87-98. DOI:10.1504/ijesms.2010.031874 |
| [29] |
MYERS R H, MONTGOMERY D C. Response surface methodology[J]. IIE Transactions, 1996, 28(12): 1031-1032. DOI:10.1080/15458830.1996.11770760 |
| [30] |
HOSDER S, WALTERS R W, BALCH M. Point-collocation nonintrusive polynomial chaos method for stochastic computational fluid dynamics[J]. AIAA Journal, 2010, 48(12): 2721-2730. DOI:10.2514/1.39389 |
| [31] |
ELDRED M. Recent advances in non-intrusive polynomial chaos and stochastic collocation methods for uncertainty analysis and design[C]//50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Palm Springs, California. Reston, Virginia: AIAA, 2009. doi: 10.2514/6.2009-2274
|
| [32] |
XIU D B, LUCOR D, SU C H, et al. Stochastic modeling of flow-structure interactions using generalized polynomial chaos[J]. Journal of Fluids Engineering, 2002, 124(1): 51-59. DOI:10.1115/1.1436089 |
| [33] |
WITTEVEEN J A S, BIJL H. Modeling arbitrary uncertainties using gram-Schmidt polynomial chaos[C]//44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2006. doi: 10.2514/6.2006-896
|
| [34] |
RESMINI A, PETER J, LUCOR D. Sparse grids-based stochastic approximations with applications to aerodynamics sensitivity analysis[J]. International Journal for Numerical Methods in Engineering, 2016, 106(1): 32-57. DOI:10.1002/nme.5005 |
| [35] |
BOMPARD M, PETER J, DÉSIDÉRI J S. Surrogate models based on function and derivative values for aerodynamic global optimization[C]//V European Conference on Computational, 2010, Lisbonne, Portugal. INRIA-00537120. https://hal.inria.fr/inria-00537120/document
|
| [36] |
HANSEN E, WALSTER G W. Global optimization using interval analysis[M]. New York: Marcel Dekker, 1992.
|
| [37] |
TABER R. The fuzzy systems handbook: a practitioner's guide to building, using, and maintaining fuzzy systems (earl cox)[J]. SIAM Review, 1995, 37(2): 281-282. DOI:10.1137/1037078 |
| [38] |
TUCKER W T, FERSON S. Sensitivity in risk analyses with uncertain numbers[R]. Sandia Report, SAND 2006-2801, 2006. https://digital.library.unt.edu/ark:/67531/metadc874250/m2/1/high_res_d/886899.pdfdoi:10.2172/886899
|
| [39] |
FERSON S, TUCKER W T. Sensitivity analysis using probability bounding[J]. Reliability Engineering & System Safety, 2006, 91(10-11): 1435-1442. DOI:10.1016/j.ress.2005.11.052 |
| [40] |
GOODMAN I R, NGUYEN H T. Probability updating using second order probabilities and conditional event algebra[J]. Information Sciences, 1999, 121(3-4): 295-347. DOI:10.1016/S0020-0255(99)00089-4 |
| [41] |
SWILER L P, PAEZ T L, MAYES R L. Epistemic uncertainty quantification tutorial[C]//IMAC XXVII conference and exposition on structural dynamics, Orlando, FL, 2009. https://cfwebprod.sandia.gov/cfdocs/CompResearch/docs/294_swi.pdf
|
| [42] |
ELDRED M S, SWILER L P, TANG G. Mixed aleatory-epistemic uncertainty quantification with stochastic expansions and optimization-based interval estimation[J]. Reliability Engineering & System Safety, 2011, 96(9): 1092-1113. DOI:10.1016/j.ress.2010.11.010 |
| [43] |
WILLIAMSON R C, DOWNS T. Probabilistic arithmetic. I. Numerical methods for calculating convolutions and dependency bounds[J]. International Journal of Approximate Reasoning, 1990, 4(2): 89-158. DOI:10.1016/0888-613X(90)90022-T |
| [44] |
FERSON S, KREINOVICK V, GINZBURG L, et al. Constructing probability boxes and dempster-shafer structures[R]. Sandia Report, SAND 2002-4015, 2003. https://www.researchgate.net/publication/2898381_Constructing_Probability_Boxes_and_Dempster-Shafer_Structures doi: 10.2172/809606
|
| [45] |
ROMERO V. Approximate probability boxes and other shortcuts in a broad-before-deep approach to balanced UQ[C]//ASME 2015 V&V Symposium, Las Vegas, NV. SAND 2015-3605C. https://www.osti.gov/servlets/purl/1252925
|
| [46] |
RICHARDSON L F. The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam[J]. Philosophical Transactions of the Royal Society A, 1911, 210(1): 459-470. DOI:10.1098/rsta.1911.0009 |
| [47] |
CELIK I, KARATEKIN O. Numerical experiments on application of Richardson extrapolation with nonuniform grids[J]. Journal of Fluids Engineering, 1997, 119(3): 584-590. DOI:10.1115/1.2819284 |
| [48] |
CELIK I B, GHIA U,. ROACHE P J, et al. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications[J]. Journal of Fluids Engineering, 2008, 130(7): 078001. DOI:10.1115/1.2960953 |
| [49] |
赵训友, 林景松, 童晓艳. 基于Richardson外推法的CFD中离散不确定度估计[J]. 系统仿真学报, 2014, 26(10): 2315-2320. ZHAO X Y, LIN J S, TONG X Y. Discretization uncertainty estimation in CFD based on Richardson extrapolation method[J]. Journal of System Simulation, 2014, 26(10): 2315-2320. (in Chinese) |
| [50] |
SCHAEFER J A, HOSDER S, MANI M, et al. The effect of grid topology and flow solver on turbulence model closure coefficient uncertainties for a transonic airfoil[C]//46th AIAA Fluid Dynamics Conference, Washington D C. Reston, Virginia: AIAA, 2016. doi: 10.2514/6.2016-4400
|
| [51] |
LOEVEN A, BIJL H. Airfoil analysis with uncertain geometry using the probabilistic collocation method[C]// 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Schaumburg, IL, 2008. AIAA 2008-2070. doi: 10.2514/6.2008-2070
|
| [52] |
PARUSSINI L, PEDIRODA V, POLONI C. Prediction of geometric uncertainty effects on fluid dynamics by polynomial Chaos and fictitious domain method[J]. Computers & Fluids, 2010, 39(1): 137-151. DOI:10.1016/j.compfluid.2009.07.008 |
| [53] |
LIU D S, LITVINENKO A, SCHILLINGS C, et al. Quantification of airfoil geometry-induced aerodynamic uncertainties---comparison of approaches[J]. SIAM/ASA Journal on Uncertainty Quantification, 2017, 5(1): 334-352. DOI:10.1137/15m1050239 |
| [54] |
LIU Z Y, WANG X D, KANG S. Stochastic performance evaluation of horizontal axis wind turbine blades using non-deterministic CFD simulations[J]. Energy, 2014, 73: 126-136. DOI:10.1016/j.energy.2014.05.107 |
| [55] |
TROJAK W, WATSON R, SCILLITOE A, et al. Effect of mesh quality on flux reconstruction in multi-dimensions[J]. Journal of Scientific Computing, 2020, 82(3): 1-36. DOI:10.1007/s10915-020-01184-2 |
| [56] |
LIU S Y, WANG Y B, QIN N, et al.. Quantification of airfoil aerodynamic uncertainty due to pressure-sensitive paint thickness[J]. AIAA Journal, 2020, 58(4): 1432-1440. DOI:10.2514/1.J058801 |
| [57] |
XIU D B, KARNIADAKIS G E. The Wiener: askey polynomial chaos for stochastic differential equations[J]. SIAM Journal on Scientific Computing, 2002, 24(2): 619-644. DOI:10.1137/s1064827501387826 |
| [58] |
LOEVEN G J A, BIJL H. Probabilistic Collocation used in a two-step approach for efficient uncertainty quantification in computational fluid dynamics[J]. Computer Modeling in Engineering and Sciences, 2008, 36(3): 193-212. DOI:10.3970/cmes.2008.036.193 |
| [59] |
MARIOTTI A, SALVETTI M V, SHOEIBI OMRANI P, et al. Stochastic analysis of the impact of freestream conditions on the aerodynamics of a rectangular 5:1 cylinder[J]. Computers & Fluids, 2016, 136: 170-192. DOI:10.1016/j.compfluid.2016.06.008 |
| [60] |
AVDONIN A, POLIFKE W. Quantification of the impact of uncertainties in operating conditions on the flame transfer function with nonintrusive polynomial chaos expansion[J]. Journal of Engineering for Gas Turbines and Power, 2019, 141(1): 011020. DOI:10.1115/1.4040745 |
| [61] |
ZHU H Y, WANG G, LIU Y, et al. Numerical investigation of transonic buffet on supercritical airfoil considering uncertainties in wind tunnel testing[J]. International Journal of Modern Physics B, 2020, 34(14n16): 2040083. DOI:10.1142/s0217979220400834 |
| [62] |
刘智益, 王晓东, 康顺. 叶顶间隙尺度的不确定性对压气机性能影响的CFD模拟[J]. 工程热物理学报, 2013, 34(4): 628-631. LIU Z Y, WANG X D, KANG S. CFD simulations of uncertain tip clearance effect on compressor performance[J]. Journal of Engineering Thermophysics, 2013, 34(4): 628-631. (in Chinese) |
| [63] |
邬晓敬, 张伟伟, 宋述芳, 等. 翼型跨声速气动特性的不确定性及全局灵敏度分析[J]. 力学学报, 2015, 47(4): 587-595. WU X J, ZHANG W W, SONG S F, et al. Uncertainty quantification and global sensitivity analysis of transonic aerodynamics about airfoil[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(4): 587-595. DOI:10.6052/0459-1879-14-372 (in Chinese) |
| [64] |
WANG Y J, ZHANG S D. Uncertainty quantification of numerical simulation of flows around a cylinder using non-intrusive polynomial chaos[J]. Chinese Physics Letters, 2016, 33(9): 090501. DOI:10.1088/0256-307x/33/9/090501 |
| [65] |
邓小兵, 陈琦, 袁先旭, 等. 复杂构型细长体飞行器大迎角气动不确定性机理研究[J]. 中国科学: 技术科学, 2016, 46(5): 493-499. DENG X B, CHEN Q, YUAN X X, et al. Study of aerodynamic uncertainty on the complex slender vehicle at high angle of attack[J]. SCIENTIA SINICA Technologica, 2016, 46(5): 493-499. DOI:10.1360/N092015-00053 (in Chinese) |
| [66] |
徐林程, 王刚, 武洁, 等. 翼型风洞试验中不确定性分析的自动微分方法[J]. 航空学报, 2014, 35(8): 2102-2111. XU L C, WANG G, WU J, et al. Uncertainty analysis of airfoil wind tunnel tests with automatic differentiation[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(8): 2102-2111. (in Chinese) |
| [67] |
DURAISAMY K, IACCARINO G, XIAO H. Turbulence modeling in the age of data[J]. Annual Review of Fluid Mechanics, 2019, 51(1): 357-377. DOI:10.1146/annurev-fluid-010518-040547 |
| [68] |
XIAO H, CINNELLA P. Quantification of model uncertainty in RANS simulations: a review[J]. Progress in Aerospace Sciences, 2019, 108: 1-31. DOI:10.1016/j.paerosci.2018.10.001 |
| [69] |
LUMLEY J L, NEWMAN G R. The return to isotropy of homogeneous turbulence[J]. Journal of Fluid Mechanics, 1977, 82(1): 161-178. DOI:10.1017/s0022112077000585 |
| [70] |
BANERJEE S, KRAHL R, DURST F, et al. Presentation of anisotropy properties of turbulence, invariants versus eigenvalue approaches[J]. Journal of Turbulence, 2007, 8: N32. DOI:10.1080/14685240701506896 |
| [71] |
EMORY M, PECNIK R, IACCARINO G. Modeling structural uncertainties in Reynolds-averaged computations of shock/boundary layer interactions[C]//49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, Florida. Reston, Virginia: AIAA, 2011. doi: 10.2514/6.2011-479
|
| [72] |
EMORY M, LARSSON J, IACCARINO G. Modeling of structural uncertainties in Reynolds-averaged Navier-Stokes closures[J]. Physics of Fluids, 2013, 25(11): 110822. DOI:10.1063/1.4824659 |
| [73] |
IACCARINO G, MISHRA A A, GHILI S. Eigenspace perturbations for uncertainty estimation of single-point turbulence closures[J]. Physical Review Fluids, 2017, 2(2): 024605. DOI:10.1103/PhysRevFluids.2.024605 |
| [74] |
MISHRA A A, MUKHOPADHAYA J, IACCARINO G, et al. Uncertainty estimation module for turbulence model predictions in SU2[J]. AIAA Journal, 2018, 57(3): 1066-1077. DOI:10.2514/1.J057187 |
| [75] |
XIAO H, WANG J X, GHANEM R G. A random matrix approach for quantifying model-form uncertainties in turbulence modeling[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 313: 941-965. DOI:10.1016/j.cma.2016.10.025 |
| [76] |
WANG J X, SUN R, XIAO H. Quantification of uncertainties in turbulence modeling: a comparison of physics-based and random matrix theoretic approaches[J]. International Journal of Heat and Fluid Flow, 2016, 62: 577-592. DOI:10.1016/j.ijheatfluidflow.2016.07.005 |
| [77] |
EDELING W N, IACCARINO G, CINNELLA P. Data-free and data-driven RANS predictions with quantified uncertainty[J]. Flow, Turbulence and Combustion, 2018, 100(3): 593-616. DOI:10.1007/s10494-017-9870-6 |
| [78] |
POPE S B. Turbulent flows[M]. Cambridge, UK: Cambridge Univ. Press, 2000.
|
| [79] |
EISFELD B. Reynolds stress anisotropy in self-preserving turbulent shear flows[R]. DLR-Interner Bericht. DLR-IB-AS-BS-2017-106, 158 S. https://elib.dlr.de/113887/
|
| [80] |
DUNN M C, SHOTORBAN B, FRENDI A. Uncertainty quantification of turbulence model coefficients via Latin hypercube sampling method[J]. Journal of Fluids Engineering, 2011, 133(4): 041402. DOI:10.1115/1.4003762 |
| [81] |
PLATTEEUW P D A, LOEVEN G J A, BIJL H. Uncertainty quantification applied to the k-epsilon model of turbulence using the probabilistic collocation method[C]//49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Schaumburg, IL. Reston, Virginia: AIAA, 2008. doi: 10.2514/6.2008-2150
|
| [82] |
SHAH H R, HOSDER S, WINTER T. A mixed uncertainty quantification approach with evidence theory and stochastic expansions[C]//16th AIAA Non-Deterministic Approaches Conference, National Harbor, Maryland. Reston, Virginia: AIAA, 2014. doi: 10.2514/6.2014-0298
|
| [83] |
WEST T K, HOSDER S, JOHNSTON C O. Multistep uncertainty quantification approach applied to hypersonic reentry flows[J]. Journal of Spacecraft and Rockets, 2013, 51(1): 296-310. DOI:10.2514/1.A32592 |
| [84] |
QUAGLIARELLA D, SERANI A, DIEZ M, et al. Benchmarking uncertainty quantification methods using the NACA2412 airfoil with geometrical and operational uncertainties[C]//AIAA Aviation 2019 Forum, Dallas, Texas. Reston, Virginia: AIAA, 2019. doi: 10.2514/6.2019-3555
|
| [85] |
DUQUE E P, LAWRENCE S. Spectre: a computational environment for managing total uncertainty quantification of CFD studies[C]//AIAA Scitech 2019 Forum, San Diego, California. Reston, Virginia: AIAA, 2019. doi: 10.2514/6.2019-2221
|
| [86] |
SCHAEFER J A, CARY A W, DUQUE E P, et al. Application of a CFD uncertainty quantification framework for industrial-scale aerodynamic analysis[C]//AIAA Scitech 2019 Forum, San Diego, California. Reston, Virginia: AIAA, 2019. doi: 10.2514/6.2019-1492
|
| [87] |
WIGNALL T J, HOULDEN H. Uncertainty quantification for launch vehicle aerodynamic lineloads[C]//AIAA Scitech 2020 Forum, Orlando, FL. Reston, Virginia: AIAA, 2020. doi: 10.2514/6.2020-1521
|
| [88] |
SCHAEFER J A, CARY A W, MANI M, et al. Uncertainty quantification and sensitivity analysis of SA turbulence model coefficients in two and three dimensions[C]//55th AIAA Aerospace Sciences Meeting, Grapevine, Texas. Reston, Virginia: AIAA, 2017. doi: 10.2514/6.2017-1710
|
| [89] |
肖思男, 吕震宙, 王薇. 不确定性结构全局灵敏度分析方法概述[J]. 中国科学: 物理学 力学 天文学, 2018, 48(1): 8-25. XIAO S N, LV Z Z, WANG W. A review of global sensitivity analysis for uncertainty structure[J]. SCIENTIA SINICA (Physica, Mechanica & Astronomica), 2018, 48(1): 8-25. (in Chinese) |
| [90] |
STORLIE C B, SWILER L P, HELTON J C, et al. Implementation and evaluation of nonparametric regression procedures for sensitivity analysis of computationally demanding models[J]. Reliability Engineering & System Safety, 2009, 94(11): 1735-1763. DOI:10.1016/j.ress.2009.05.007 |
| [91] |
SALTELLI A, ANNONI P, AZZINI I, et al. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index[J]. Computer Physics Communications, 2010, 181(2): 259-270. DOI:10.1016/j.cpc.2009.09.018 |
| [92] |
SUDRET B. Global sensitivity analysis using polynomial chaos expansions[J]. Reliability Engineering & System Safety, 2008, 93(7): 964-979. DOI:10.1016/j.ress.2007.04.002 |
| [93] |
DUVIGNEAU R, PELLETIER D. A sensitivity equation method for fast evaluation of nearby flows and uncertainty analysis for shape parameters[J]. International Journal of Computational Fluid Dynamics, 2006, 20(7): 497-512. DOI:10.1080/10618560600910059 |
| [94] |
FIORINI C, DESPRÉS B, PUSCAS M A. Sensitivity equation method for the Navier-Stokes equations applied to uncertainty propagation[J]. International Journal for Numerical Methods in Fluids, 2021, 93(1): 71-92. DOI:10.1002/fld.4875 |
 2021, Vol. 39
2021, Vol. 39