复杂流动中的颗粒运动在自然环境和工业生产等领域中普遍存在,比如云层冰晶以及雨雪的形成[1]、浮游生物的运动与聚集现象[2]、纸浆纤维与造纸过程[3-4]、化学制药过程[5]等。同时,颗粒的形状通常是各向异性的。但是过去大部分的研究用等效的球形点颗粒模型对颗粒运动进行描述,开展颗粒的沉积、聚集以及与湍流相互作用等问题的研究[6–10]。然而,颗粒的非球形的形状特征在一定程度上会对颗粒的输运产生影响。与此同时,在一些特定的自然与工程问题中,颗粒的形状特征不可忽略。因此由颗粒形状各向异性引起的取向行为就具有十分重要的研究意义,比如造纸过程中细长的纸纤维的取向影响纸张的力学性能[3-4];纤维增强材料中纤维的排列决定了材料的微结构,进而影响材料的力学性能;在减阻控制中,纤维的取向行为影响纤维与湍流之间的相互作用[11];浮游生物的取向行为会影响生物的聚集与迁移过程[12]等。
Fan 和 Ahmadi[13-14]、Zhang等[15]较早采用欧拉-拉格朗日方法对杆状颗粒在壁湍流中的运动问题进行数值模拟。随后,Mortensen 等[16-17]、Marchioli等[6,18-19]、Marchioli & Soldati [20] 和Challabotla等[21-23]对非球形颗粒在壁湍流中的输运过程开展了大量相关研究工作。其中,欧拉-拉格朗日方法是背景流场在欧拉的观点下进行求解,而颗粒则通过拉格朗日追踪的方法进行求解。壁湍流是一类在壁面附近存在强剪切与丰富的拟序结构的湍流,比如槽道、圆管以及边界层湍流等[24]。因此,壁湍流中的非球形颗粒两相流研究主要关注以下几类问题:1)非球形颗粒在壁湍流中的统计行为(平动、转动以及取向);2)非球形颗粒与湍流中的相干结构之间的相互作用;3)非球形颗粒对湍流的减阻控制的作用。
本文主要综述了近些年关于微小非球形颗粒在壁湍流中取向行为的研究工作进展,具体结构如下:第1节介绍相关工作使用的理论与数值模拟方法,第2节讨论非球形颗粒在槽道湍流中的取向行为,第3节介绍颗粒倾向性取向行为的机理,第4节讨论颗粒的取向行为会在近壁区呈现“形状敏感性”的现象,最后对本文的内容进行总结和展望。
1 数值方法前期的壁湍流颗粒数值研究主要方法为欧拉-拉格朗日耦合的直接数值模拟。这里对流场及颗粒求解方法做简单的介绍。
1.1 流体相直接数值模拟对不可压缩的纳维-斯托克斯方程进行求解,求解的连续方程与动量方程分别为:
| $ \frac{\partial {u}_{i}}{\partial {x}_{i}}=0 $ | (1) |
| $ \frac{\partial {u}_{i}}{\partial t}+{u}_{j}\frac{\partial {u}_{i}}{\partial {x}_{j}}=-\frac{1}{{\rho }_{f}}\frac{\partial p}{\partial {x}_{i}}+\nu \frac{{\partial }^{2}{u}_{i}}{\partial {x}_{j}\partial {x}_{j}} $ | (2) |
其中
主要算例的计算域大多为
本文主要介绍的颗粒尺寸远小于流体的Kolmogorov尺度,且颗粒相为稀疏悬浮,因此不考虑颗粒对流体的反作用以及颗粒与颗粒之间的碰撞作用。同时,颗粒的尺寸非常小(考虑的微粒弛豫时间与流体弛豫时间小于0.1,但颗粒与流体的密度比可以达到1 000左右),颗粒惯性与流体惯性对颗粒运动学的影响可以被忽略[25]。此时,颗粒可近似认为跟随流体的轨迹线,即
| $ \frac{{\rm{d}}{x}_{p,i}}{{\rm{d}}t}={u}_{p,i} $ | (3) |
其中
| $ \frac{{\rm{d}}{p}_{i}}{{\rm{d}}t}={O}_{ij}{p}_{j}+\frac{{{\lambda }}^{2}-1}{{\lambda }^{2}+1}\left({S}_{ij}{p}_{j}-{p}_{j}{S}_{jk}{p}_{k}{p}_{i}\right) $ | (4) |
其中
本文中颗粒相的时间推进格式与流体相的时间推进格式保持一致,而颗粒处的流体信息通过二阶三维拉格朗日插值格式从颗粒附近的流体网格中插值得到。同时,颗粒与壁面之间采用完全弹性碰撞模型。取向随机的颗粒在初始时刻被均匀地以当地流场速度放入充分发展的槽道湍流中,待颗粒在流场中充分发展后进行统计与分析。
2 颗粒在壁面附近的取向行为在槽道湍流中,因为槽道内部湍流非均匀且各向异性,非球形颗粒的取向与转动行为受颗粒形状的影响较大,尤其对于极细长的杆状颗粒和极扁平的碟状颗粒。而且,颗粒的行为在槽道中的不同位置处会呈现出不同的行为特征。
Challabotla等[22]针对非球形颗粒在槽道中的取向行为展开了研究。图1展示了瞬时细长颗粒与扁平颗粒在近壁面处的分布,可以明显看到颗粒具有倾向性的取向,同时这种取向分布与颗粒形状有关。图2展示了非球形颗粒回转轴与流向、展向与法向方向的夹角余弦绝对值的统计平均值。在槽道中部,因为中部的流动状态趋近于均匀各向同性湍流[27],所以非球形颗粒的运动行为与其在均匀各向同性湍流中的结果基本一致,即杆状颗粒倾向性地朝着涡量方向而碟状颗粒垂直于涡量方向。在惯性参考系中看,颗粒的回转轴方向与惯性参考系各个轴的夹角余弦的绝对值的统计值均趋于0.5,这意味着非球形颗粒在槽道中部的取向在空间上是趋于一种随机分布的状态。然而,从槽道的黏性底层区(
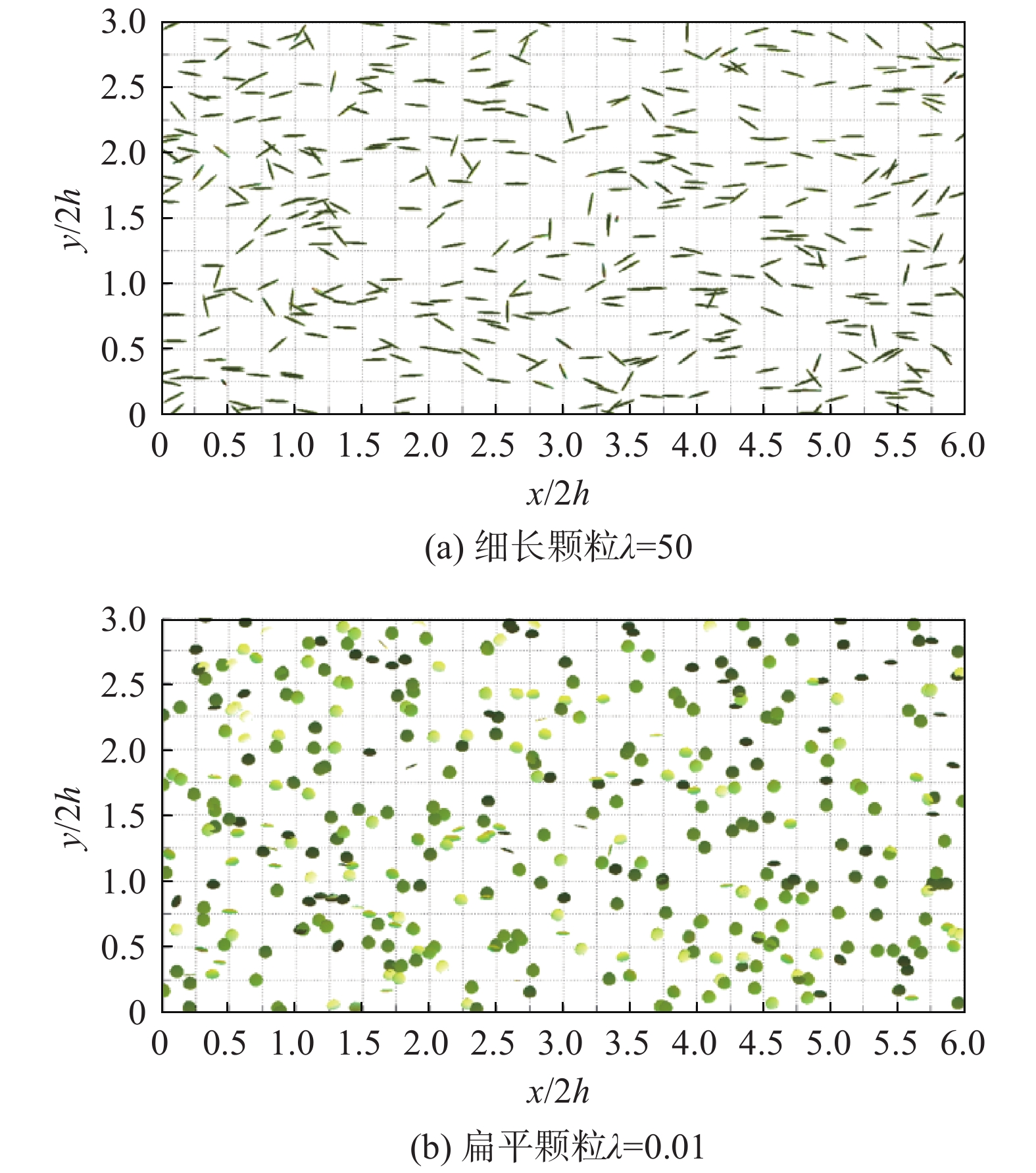
|
图 1 非球形颗粒在平行壁面平面上的瞬时分布图(z+≈10) Fig.1 Instantaneous distribution of non-spherical particles in a wall-parallel plane at z+≈10 |
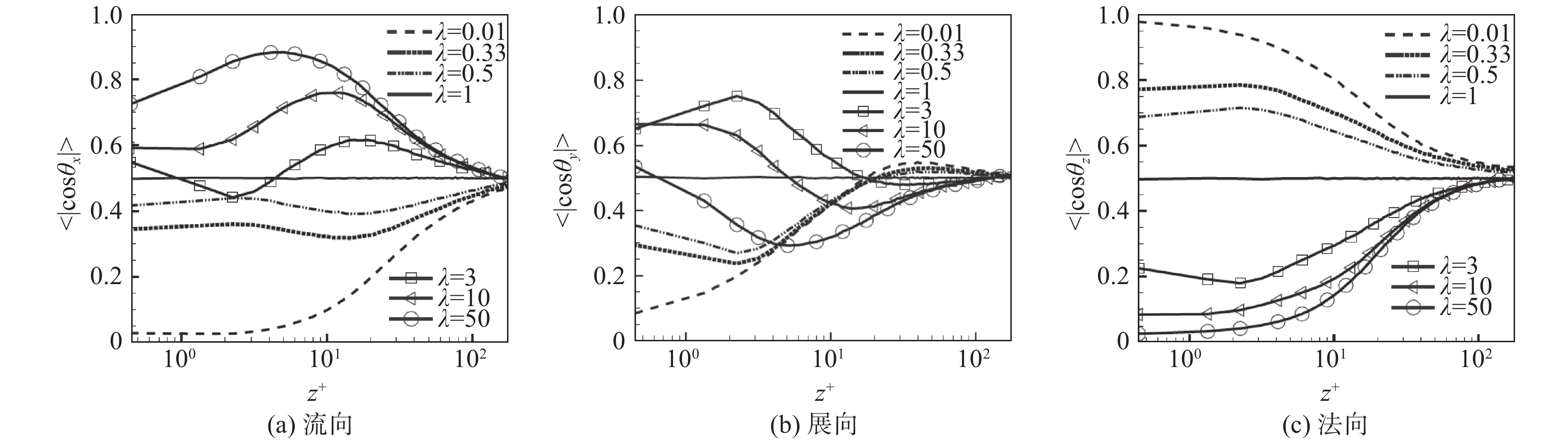
|
图 2 非球形颗粒回转轴与流向、展向与法向方向的夹角余弦绝对值的统计平均值[22] Fig.2 Average absolute cosine values between particle symmetry axis and the streamwise, the spanwise and the wall-normal direction[22] |
通过Jeffery方程[26]可知,非球形颗粒的转动行为与取向行为是一种相互影响的关系,即颗粒取向的时间导数
颗粒取向行为的机理一直以来都是关注的热点问题。在均匀各向同性湍流的研究中,目前普遍接受的观点主要有两种:1)非球形颗粒的取向与流体的涡量以及变形率张量的第二特征值方向相关[30-32];2)非球形颗粒的取向与流体的拉格朗日拉伸与压缩方向相关[33-34]。前者主要是基于欧拉的观点去讨论颗粒与流场物理量之间的关系,其中涡量随时间演化的拉格朗日控制方程与杆状颗粒退化的演化方程相似,唯一的不同点在于涡量方程多出了黏性扩散项[30,32]。同时,由于涡量与变形率张量之间的关联,颗粒的取向同样与变形率张量的第二特征值方向具有较强的相关性。然而,颗粒与涡量相关的解释仅在各向同性湍流或远离壁面区域的湍流有效,但是在具有较强剪切的壁面附近并不成立。因为壁面的存在,流场在壁面会存在较强的展向涡量,但是杆状颗粒与碟状颗粒均不会倾向性地朝着展向[22],所以杆状颗粒与碟状颗粒被观察到垂直于涡量方向。同时,在二维流场中,涡量方向永远垂直于流场的平面。因此,第一种解释具有一定的局限性。对于第二种观点,极细长的杆状颗粒可以看成无限小的物质线段,而该物质线段与流体的拉格朗日拉伸方向渐近一致[30,35-36],当时间足够长时,杆状颗粒与拉格朗日拉伸方向一致。Ni 等[34]发现在均匀各向同性湍流中形状参数
流体的拉格朗日拉伸与压缩方向是指初始时刻为球形的流体微团沿着拉格朗日轨迹线发生拉伸与压缩变形的方向[34]。因此,为了得到流体的拉格朗日拉伸与压缩方向,首先需要沿着流体迹线积分得到对应的变形梯度张量
| $ \frac{{\rm{d}}{F}_{ij}}{{\rm{d}}t}={A}_{jk}{F}_{kj} $ | (5) |
其中
| $ {M}_{ij}={F}_{ik}{F}_{jk} $ | (6) |
通常设定初始时刻的
图4展示了颗粒回转轴方向
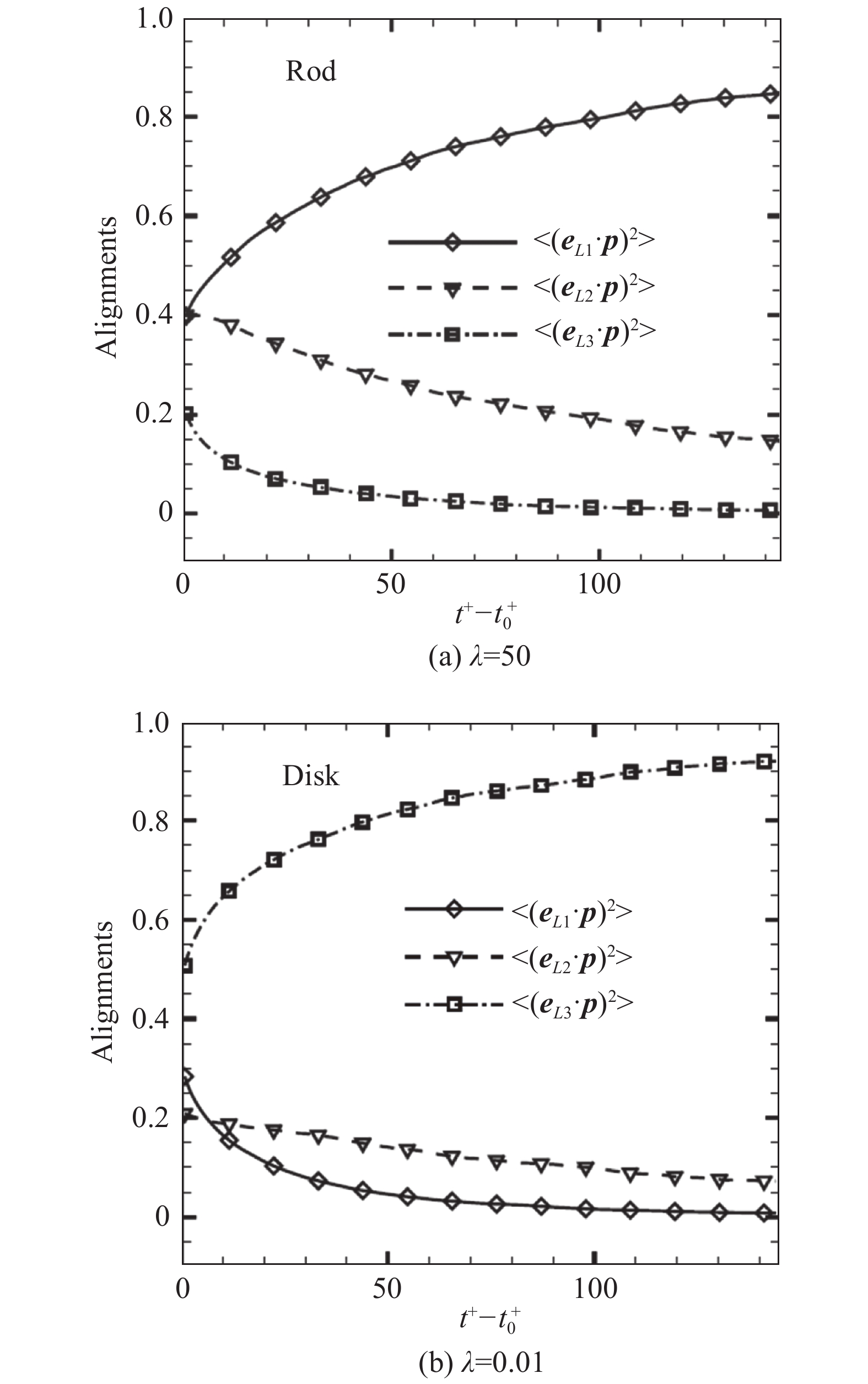
|
图 4 颗粒回转轴的方向与左柯西格林张量的三个主轴方向的夹角随时间演化的关系[37] Fig.4 Time evolution of the alignment of the orientation vector p of spheroidal particles with aspect ratio relative to the three eigenvectors of left Cauchy-Green tensor[37] |
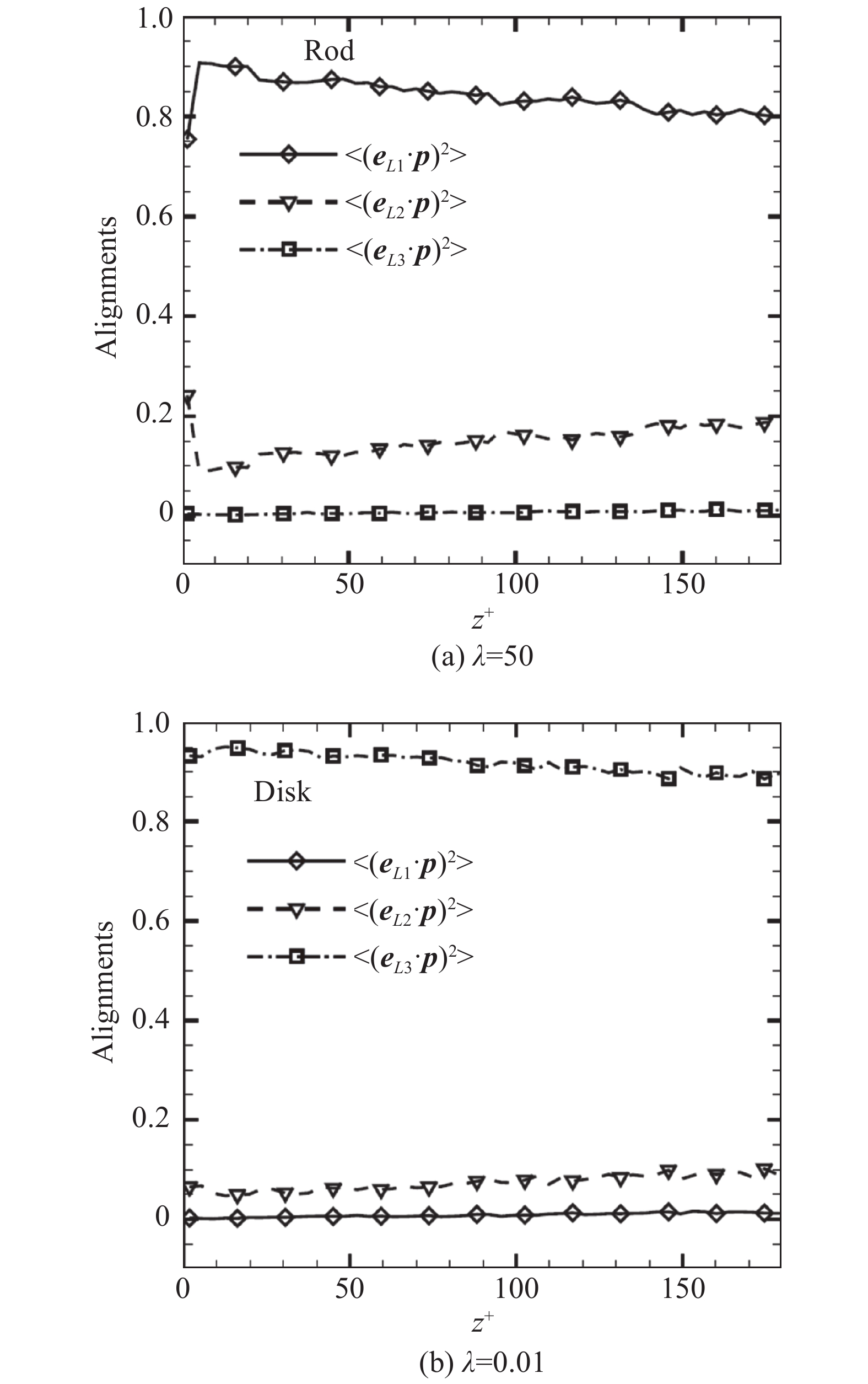
|
图 5 颗粒回转轴的方向与柯西格林张量的三个主轴方向的夹角的空间分布图[37] Fig.5 Variation of the alignment of the orientation vector p of spheroidal particles with aspect ratio relative to the three eigenvectors of left Cauchy-Green tensor with different aspect ratio[37] |
在第3节中,本文介绍到杆状颗粒与拉格朗日拉伸方向以及碟状颗粒与拉格朗日的压缩方向具有较强的相关性。但是,颗粒与拉格朗日拉伸与压缩方向的差异随颗粒形状参数
首先,在崔智文等[38]的工作中,他们选取一条轨迹线,并截取颗粒已经充分发展且在壁面附近有较长时间停留但与壁面无碰撞过程的轨迹段,如图6所示。图6展示了同一条轨迹线上形状参数
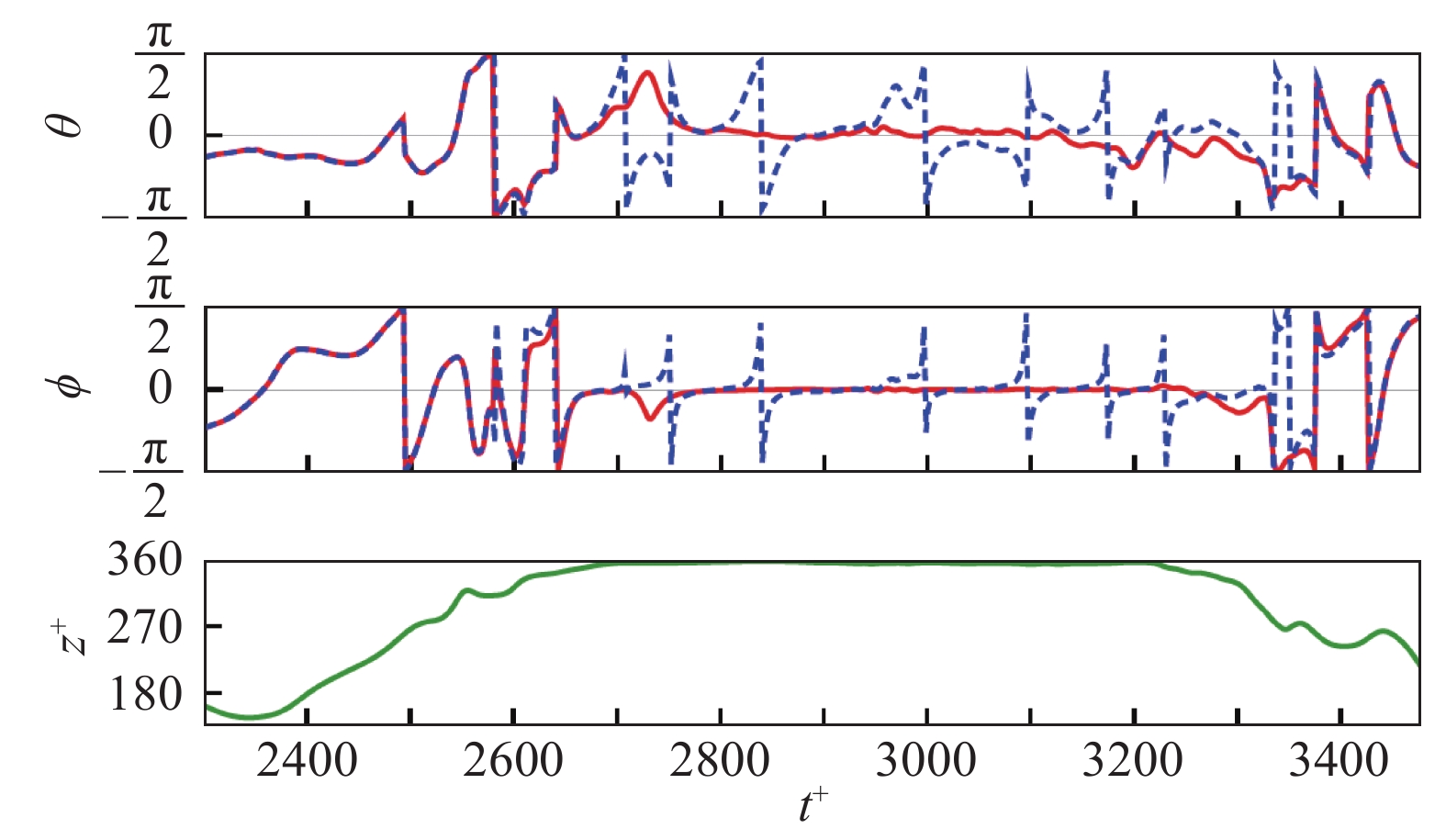
|
图 6 |
为进一步分析,崔智文等[38]对细长杆状颗粒在拉格朗日坐标系(由柯西格林张量三个主轴方向组成,即
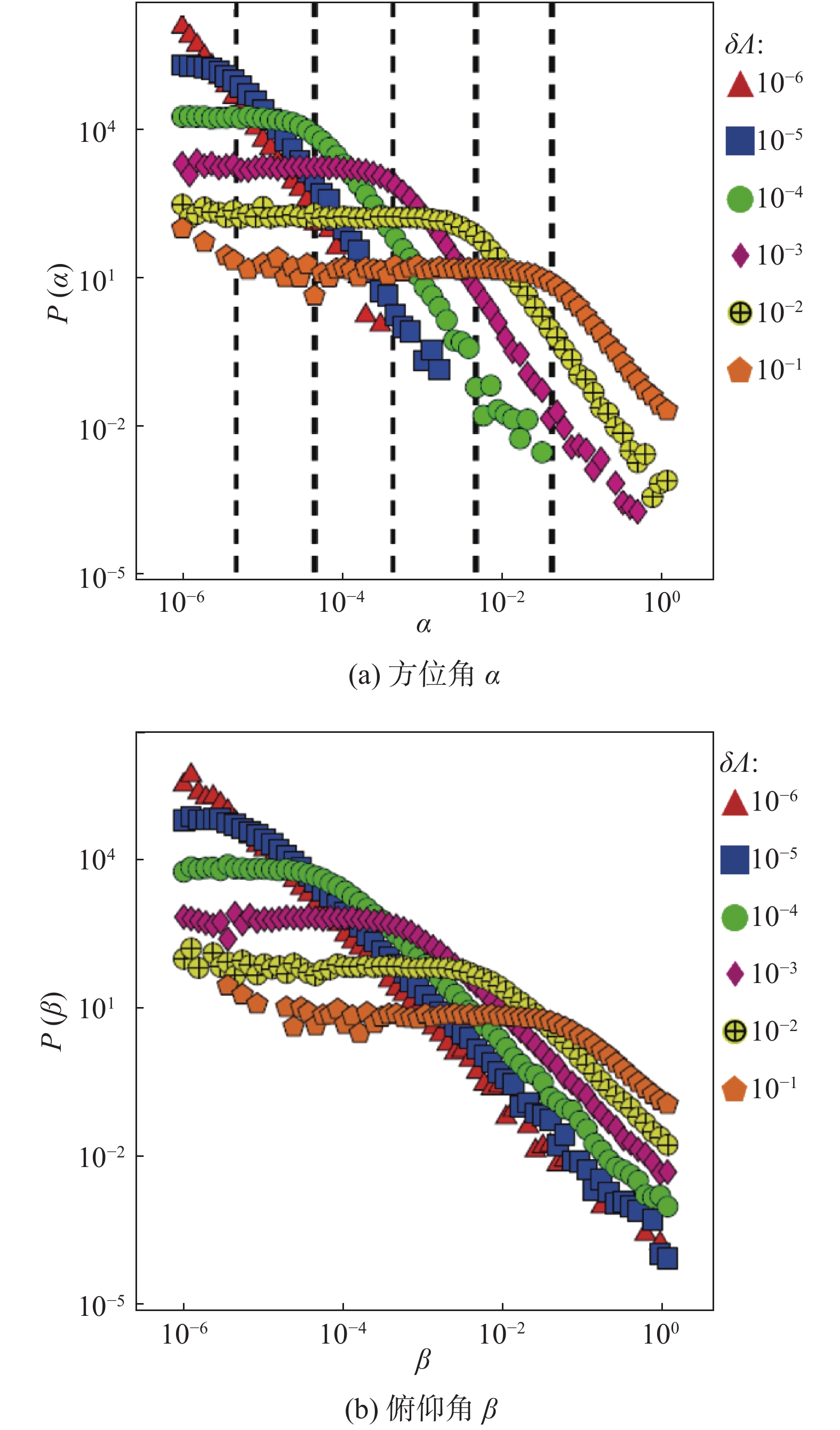
|
图 7 槽道中部( |
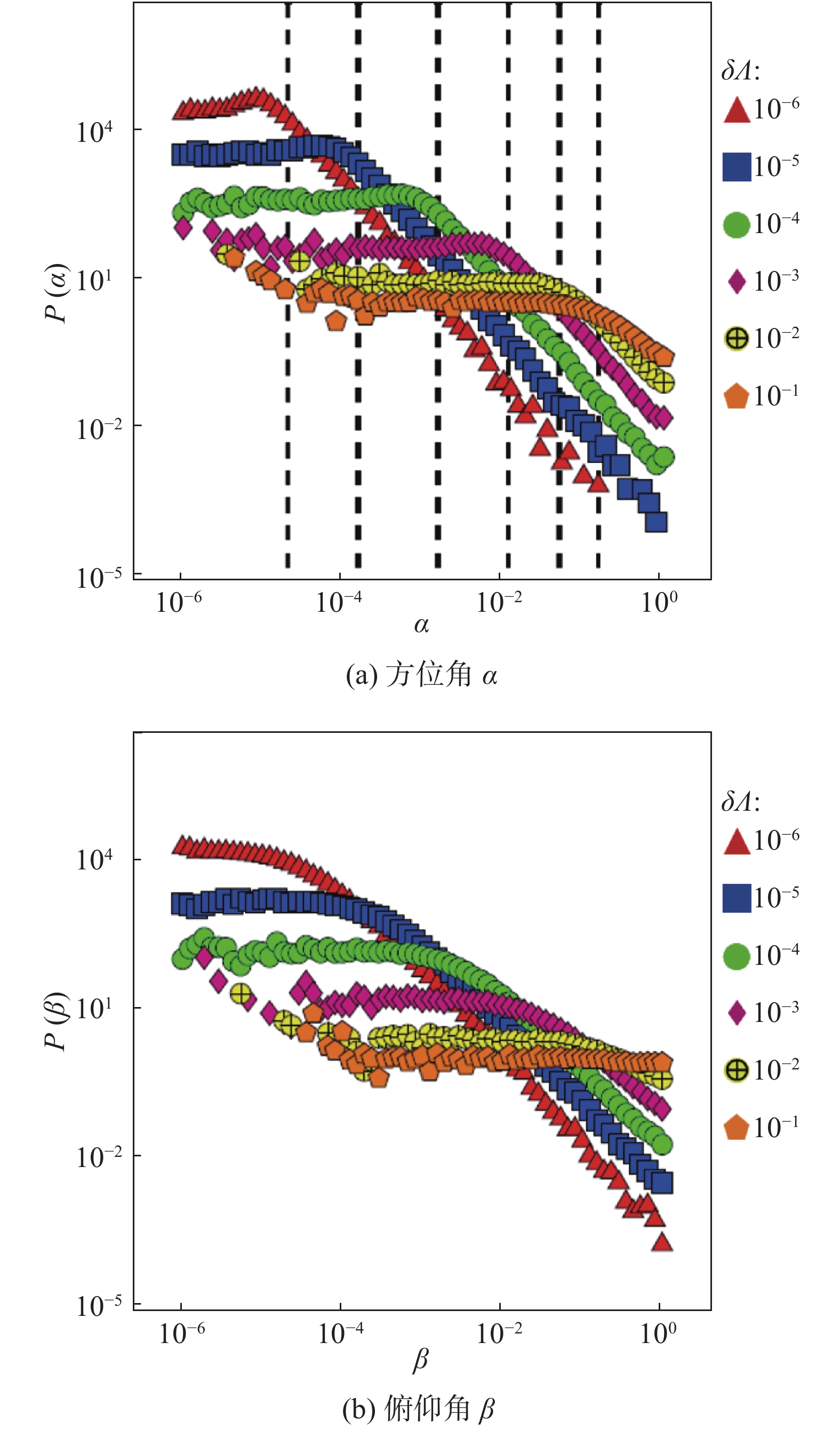
|
图 8 黏性底层( |

|
图 9 临界方位角 |
4.1节与4.2节分别讨论了
为了进一步验证该想法,崔智文等[38]基于Jeffery方程建立了二维简化的颗粒取向模型,并从方程角度出发分析在存在强剪切与速度梯度脉动下颗粒转动周期随形状的变化,即:
| $ \frac{\mathrm{d}\mathrm{\phi }}{\mathrm{d}{t}}=-\frac{s}{2}\left(1-\mathrm{cos}2\phi \right)+{\eta }_{\phi } $ | (7) |
其中,
| $\begin{split}& \left\langle \tau \right\rangle s = \\&\qquad \sqrt {\text{π}} {12^{\frac{1}{6}}}{\left( {\frac{s}{D}} \right)^{\frac{1}{3}}}{{\rm{\varLambda }}^{ - \frac{2}{3}}}\mathop \int \nolimits_0^\infty \frac{1}{{\sqrt y }}{{{\rm{e}}}^{ - {{\left( {\frac{3}{2}} \right)}^{\frac{1}{3}}}{{\left( {\frac{s}{D}} \right)}^{\frac{2}{3}}}\delta {\rm{\varLambda }}{{\rm{\varLambda }}^{ - \frac{1}{3}}}y - {y^3}}}{\rm{d}}y\end{split}$ | (8) |
图10为颗粒平均翻转时间
| $ \left\langle \tau \right\rangle s=\sqrt{{\text{π}} }{2}^{\frac{4}{3}}{3}^{\frac{1}{6}}\mathrm{\varGamma }\left(\frac{7}{6}\right){\left(\frac{s}{D}\right)}^{\frac{1}{3}} $ | (9) |
当
| $ \left\langle \tau \right\rangle s=\sqrt{2}{\text{π}} \delta {\varLambda }^{-\frac{1}{2}} $ | (10) |
图10展示了颗粒的转动周期随形状变化
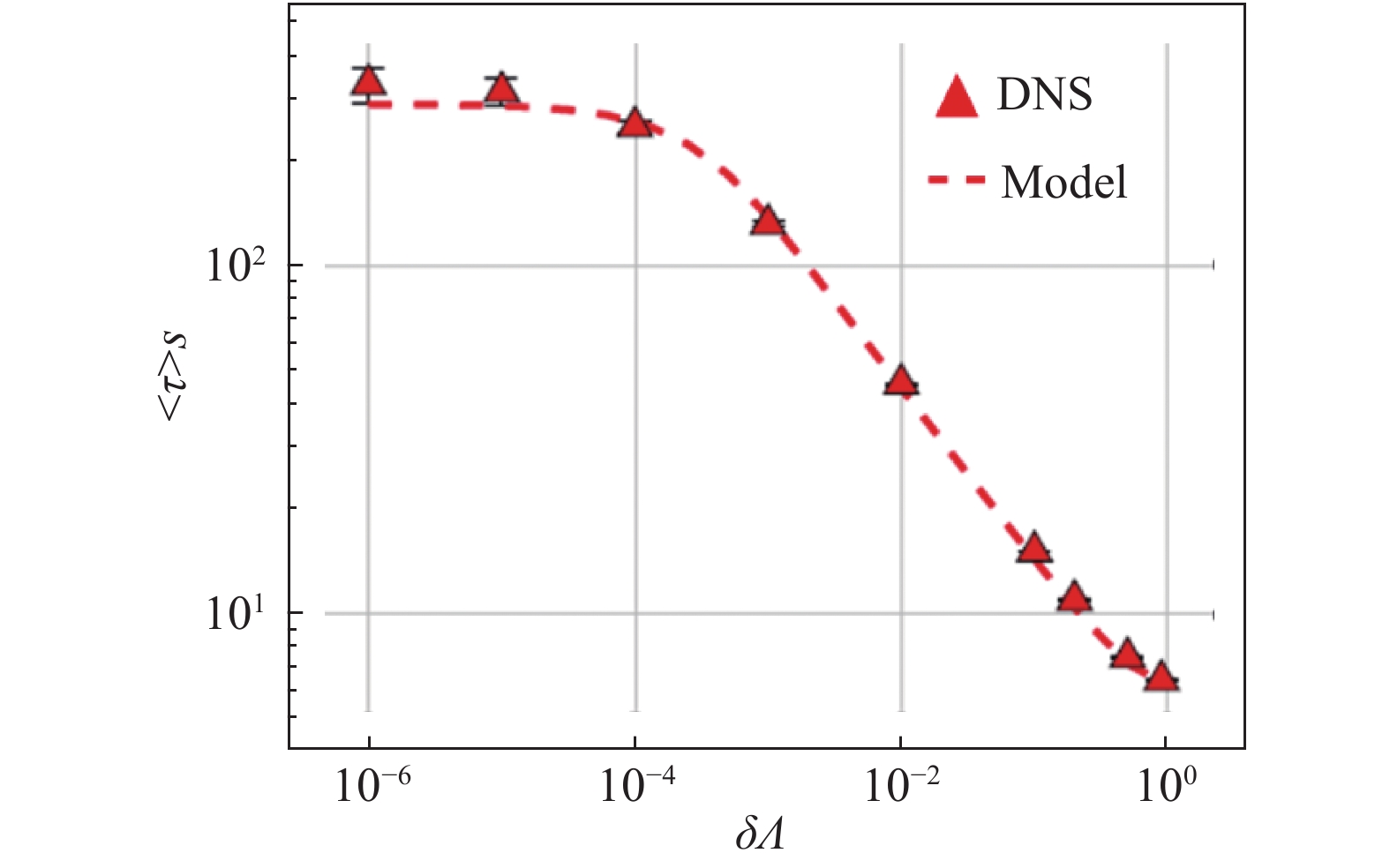
|
图 10 颗粒平均翻转时间 |
本文回顾了非球形颗粒在壁湍流中的取向行为的直接数值模拟研究。在忽略颗粒惯性的作用下,近壁区的杆状颗粒倾向性地朝着流向方向而碟状颗粒则倾向性地朝着壁面法向方向,且颗粒的倾向性取向行为的程度随颗粒偏离球形的程度的增加而增强。而非球形颗粒之所以会在壁面具有倾向性取向,是因为偏离球形程度越大的颗粒与流体的拉格朗日拉伸与压缩方向具有非常强的相关性。同时,研究工作也发现即使非球形颗粒的形状因子
在未来的研究工作中,可以考虑非球形颗粒取向行为与湍流中的相干结构之间的相互作用关系,并将其应用在纤维减阻控制的研究之中,进而加深对湍流减阻控制作用的理解。此外,真实流动中非球形颗粒随着形状的不规则性增强,易变形特性会逐渐体现出来,而此时模拟计算中颗粒的柔性需要考虑,所以关于柔性颗粒在湍流中的行为研究也是该领域可以进一步探索的问题之一。
致谢:本文涉及到工作是作者赵立豪在挪威科技大学以及回国后在清华大学的研究内容,全部已公开发表。本工作得到了挪威研究理事会、国家自然科学基金以及清华大学国强研究院项目的支持。
| [1] |
HEYMSFIELD A J. Precipitation development in stratiform ice clouds: a microphysical and dynamical study[J]. Journal of the Atmospheric Sciences, 1977, 34(2): 367-381. DOI:10.1175/1520-0469(1977)034<0367:pdisic>2.0.co;2 |
| [2] |
PEDLEY T J, KESSLER J O. Hydrodynamic phenomena in suspensions of swimming microorganisms[J]. Annual Review of Fluid Mechanics, 1992, 24(1): 313-358. DOI:10.1146/annurev.fl.24.010192.001525 |
| [3] |
LUNDELL F, SÖDERBERG L D, ALFREDSSON P H. Fluid mechanics of papermaking[J]. Annual Review of Fluid Mechanics, 2011, 43(1): 195-217. DOI:10.1146/annurev-fluid-122109-160700 |
| [4] |
HÅKANSSON K M, FALL A B, LUNDELL F, et al. Hydrodynamic alignment and assembly of nanofibrils resulting in strong cellulose filaments[J]. Nat Commun, 2014, 5: 4018. DOI:10.1038/ncomms5018 |
| [5] |
ERNI P, CRAMER C, MARTI I, et al. Continuous flow structuring of anisotropic biopolymer particles[J]. Advances in Colloid and Interface Science, 2009, 150(1): 16-26. DOI:10.1016/j.cis.2009.05.005 |
| [6] |
MARCHIOLI C, SOLDATI A, KUERTEN J G M, et al. Statistics of particle dispersion in direct numerical simulations of wall-bounded turbulence: Results of an international collaborative benchmark test[J]. International Journal of Multiphase Flow, 2008, 34(9): 879-893. DOI:10.1016/j.ijmultiphaseflow.2008.01.009 |
| [7] |
MARCHIOLI C, SOLDATI A. Mechanisms for particle transfer and segregation in a turbulent boundary layer[J]. Journal of Fluid Mechanics, 2002, 468: 283-315. DOI:10.1017/s0022112002001738 |
| [8] |
MILICI B, DE MARCHIS M, SARDINA G, et al. Effects of roughness on particle dynamics in turbulent channel flows: a DNS analysis[J]. Journal of Fluid Mechanics, 2014, 739: 465-478. DOI:10.1017/jfm.2013.633 |
| [9] |
ZHAO L H, MARCHIOLI C, ANDERSSON H I. Stokes number effects on particle slip velocity in wall-bounded turbulence and implications for dispersion models[J]. Physics of Fluids, 2012, 24(2): 021705. DOI:10.1063/1.3690071 |
| [10] |
ZHAO L H, ANDERSSON H I, GILLISSEN J J J. Turbulence modulation and drag reduction by spherical particles[J]. Physics of Fluids, 2010, 22(8): 081702. DOI:10.1063/1.3478308 |
| [11] |
SHARDT O, DERKSEN J J. Direct simulations of dense suspensions of non-spherical particles[J]. International Journal of Multiphase Flow, 2012, 47: 25-36. DOI:10.1016/j.ijmultiphaseflow.2012.06.007 |
| [12] |
QIU J R, MARCHIOLI C, ANDERSSON H I, et al. Settling tracer spheroids in vertical turbulent channel flows[J]. International Journal of Multiphase Flow, 2019, 118: 173-182. DOI:10.1016/j.ijmultiphaseflow.2019.06.012 |
| [13] |
FAN F G, AHMADI G. A sublayer model for wall deposition of ellipsoidal particles in turbulent streams[J]. Journal of Aerosol Science, 1995, 26(5): 813-840. DOI:10.1016/0021-8502(95)00021-4 |
| [14] |
FAN F G, AHMADI G. A sublayer model for turbulent deposition of particles in vertical ducts with smooth and rough surfaces[J]. Journal of Aerosol Science, 1993, 24(1): 45-64. DOI:10.1016/0021-8502(93)90084-M |
| [15] |
ZHANG H F, AHMADI G, FAN F G, et al. Ellipsoidal particles transport and deposition in turbulent channel flows[J]. International Journal of Multiphase Flow, 2001, 27(6): 971-1009. DOI:10.1016/S0301-9322(00)00064-1 |
| [16] |
MORTENSEN P H, ANDERSSON H I, GILLISSEN J J J, et al. Dynamics of prolate ellipsoidal particles in a turbulent channel flow[J]. Physics of Fluids, 2008, 20(9): 093302. DOI:10.1063/1.2975209 |
| [17] |
MORTENSEN P H, ANDERSSON H I, GILLISSEN J J J, et al. On the orientation of ellipsoidal particles in a turbulent shear flow[J]. International Journal of Multiphase Flow, 2008, 34(7): 678-683. DOI:10.1016/j.ijmultiphaseflow.2007.12.007 |
| [18] |
MARCHIOLI C, ZHAO L, ANDERSSON H I. On the relative rotational motion between rigid fibers and fluid in turbulent channel flow[J]. Physics of Fluids, 2016, 28(1): 013301. DOI:10.1063/1.4937757 |
| [19] |
MARCHIOLI C, FANTONI M, SOLDATI A. Orientation, distribution, and deposition of elongated, inertial fibers in turbulent channel flow[J]. Physics of Fluids, 2010, 22(3): 033301. DOI:10.1063/1.3328874 |
| [20] |
MARCHIOLI C, SOLDATI A. Rotation statistics of fibers in wall shear turbulence[J]. Acta Mechanica, 2013, 224(10): 2311-2329. DOI:10.1007/s00707-013-0933-z |
| [21] |
CHALLABOTLA N R, ZHAO L H, ANDERSSON H I. Orientation and rotation of inertial disk particles in wall turbulence[J]. Journal of Fluid Mechanics, 2015, 766: R2. DOI:10.1017/jfm.2015.38 |
| [22] |
CHALLABOTLA N R, ZHAO L H, ANDERSSON H I. Shape effects on dynamics of inertia-free spheroids in wall turbulence[J]. Physics of Fluids, 2015, 27(6): 061703. DOI:10.1063/1.4922864 |
| [23] |
CHALLABOTLA N R, ZHAO L H, ANDERSSON H I. Orientation and rotation dynamics of triaxial ellipsoidal tracers in wall turbulence[J]. Physics of Fluids, 2016, 28(12): 123304. DOI:10.1063/1.4971318 |
| [24] |
张兆顺, 崔桂香, 许春晓, 等. 湍流理论与模拟[M]. 北京: 清华大学出版社, 2017. ZHANG Z Z, CUI G X, XU C X, et al. Theory and modeling of turbulence[M]. Beijing: Tsinghua University Press, 2017(in Chinese). |
| [25] |
VOTH G A, SOLDATI A. Anisotropic particles in turbulence[J]. Annual Review of Fluid Mechanics, 2017, 49(1): 249-276. DOI:10.1146/annurev-fluid-010816-060135 |
| [26] |
JEFFERY G B. The motion of ellipsoidal particles immersed in a viscous fluid[J]. Proceedings of the Royal Society of London Series A, Containing Papers of a Mathematical and Physical Character, 1922, 102(715): 161-179. DOI:10.1098/rspa.1922.0078 |
| [27] |
ANDERSSON H I, ZHAO L H, VARIANO E A. On the anisotropic vorticity in turbulent channel flows[J]. Journal of Fluids Engineering, 2015, 137(8): 084503. DOI:10.1115/1.4030003 |
| [28] |
JIE Y C, XU C X, DAWSON J R, et al. Influence of the quiescent core on tracer spheroidal particle dynamics in turbulent channel flow[J]. Journal of Turbulence, 2019, 20(7): 424-438. DOI:10.1080/14685248.2019.1664747 |
| [29] |
JIE Y C, ZHAO L H, XU C X, et al. Preferential orientation of tracer spheroids in turbulent channel flow[J]. Theoretical and Applied Mechanics Letters, 2019, 9(3): 212-214. DOI:10.1016/j.taml.2019.03.010 |
| [30] |
PUMIR A, WILKINSON M. Orientation statistics of small particles in turbulence[J]. New Journal of Physics, 2011, 13(9): 093030. DOI:10.1088/1367-2630/13/9/093030 |
| [31] |
BYRON M, EINARSSON J, GUSTAVSSON K, et al. Shape-dependence of particle rotation in isotropic turbulence[J]. Physics of Fluids, 2015, 27(3): 035101. DOI:10.1063/1.491350 |
| [32] |
PARSA S, CALZAVARINI E, TOSCHI F, et al. Rotation rate of rods in turbulent fluid flow[J]. Physical Review Letters, 2012, 109(13): 134501. DOI:10.1103/physrevlett.109.134501 |
| [33] |
PARSA S, GUASTO J S, KISHORE M, et al. Rotation and alignment of rods in two-dimensional chaotic flow[J]. Physics of Fluids, 2011, 23(4): 043302. DOI:10.1063/1.3570526 |
| [34] |
NI R, OUELLETTE N T, VOTH G A. Alignment of vorticity and rods with Lagrangian fluid stretching in turbulence[J]. Journal of Fluid Mechanics, 2014, 743: R3. DOI:10.1017/jfm.2014.32 |
| [35] |
BATCHELOR G K. . The effect of homogeneous turbulence on material lines and surfaces[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1952, 213(1114): 349-366. DOI:10.1098/rspa.1952.0130 |
| [36] |
JOHNSON P L, BASSENNE M, MOIN P. Turbophoresis of small inertial particles: theoretical considerations and application to wall-modelled large-eddy simulations[J]. Journal of Fluid Mechanics, 2020, 883: A27. DOI:10.1017/jfm.2019.865 |
| [37] |
ZHAO L H, ANDERSSON H I. Why spheroids orient preferentially in near-wall turbulence[J]. Journal of Fluid Mechanics, 2016, 807: 221-234. DOI:10.1017/jfm.2016.619 |
| [38] |
CUI Z, DUBEY A, ZHAO L, et al. Alignment statistics of rods with the Lagrangian stretching direction in a channel flow[J]. Journal of Fluid Mechanics, 2020, 901: A16. DOI:10.1017/jfm.2020.547 |
| [39] |
TURITSYN K S. Polymer dynamics in chaotic flows with a strong shear component[J]. Journal of Experimental and Theoretical Physics, 2007, 105(3): 655-664. DOI:10.1134/S1063776107090245 |




