2. 中国空气动力研究与发展中心,绵阳 621000
2. China Aerodynamics Research and Development Center, Mianyang 621000, China
分布式推进和电推进技术[1-3]在航空领域的应用越来越广泛。纯电动或油电混合动力的分布式螺旋桨推进不仅具有较高的推进效率,更重要的是能充分利用螺旋桨滑流实现螺旋桨动力系统和机翼气动布局的有利气动耦合,大幅提高飞行器气动性能,满足短距起降和长航时飞行需求,降低燃油消耗,减少排放[4],从而成为当今国内外航空领域研究的新热点。
2014年起,NASA开展了系统性的分布式电动螺旋桨相关技术研究[5-6],主要包括两大试验平台—螺旋桨电推进试验台和混合电力系统平台(HEIST),以及两大分布式电动螺旋桨应用技术—前缘异步螺旋桨技术(LEAPTech)及可扩展电推进技术和运营(SCEPTOR)。Stoll等[7]采用等效盘模型近似代替分布式螺旋桨,用数值模拟方法对前缘布置了18个高升力螺旋桨(High-Lift Propeller, HLP)的分布式电推进技术验证机X-57开展研究,结果表明飞机最大升力系数可达5.2;并进一步指出分布式螺旋桨飞机机翼面积减小为原来的1/3就能获得相同的升力;同时由于机翼面积减小,有效地降低了飞行阻力,巡航升阻比可达20。Stoll[8]进一步基于NASA混合电力系统平台(HEIST)对X-57验证机进行了试验研究,结果表明分布式推进不仅能大幅提升机翼升力系数,还能改善飞机操纵性能。Patterson等[9-10]针对验证机X-57低速状态设计了保形高升力螺旋桨,在起飞降落时,分布式高升力螺旋桨能大幅提高滑流动压从而有效提高机翼升力;在高速巡航状态下,分布式高升力停止工作,桨叶折叠与整流罩和短舱保形,最大限度减小巡航阻力。Litherland等[11]对X-57的分布式高升力折叠螺旋桨方案进行了验证,采用数值模拟方法分析了高升力和翼尖螺旋桨系统的散热性能。Massey等[12]对X-57大展弦比机翼的气动弹性进行了分析。Borer等[13-14]采用多学科优化方法对分布式推进螺旋桨叶型进行了优化设计,得到了既能在巡航状态保持较高推进效率,又能在起降状态提供较大推力的螺旋桨。Murphy等[15]对基于分布式混合电推进技术的倾转动力验证机GL-10进行了系列试验,验证了倾转动力飞机的气动特性和飞行控制的可行性。
国内关于分布式螺旋桨推进技术的相关研究比较少。王科雷[16]、王红波等[17]分别研究了分布式螺旋桨滑流对太阳能无人机的气动影响,认为螺旋桨滑流使机翼升阻力都增大、升阻比减小,还能抑制流动分离。杨小川等[18-19]研究了分布式螺旋桨在多种旋转方向组合条件下,滑流效应对机翼及整机气动特性的影响。
大多数关于分布式螺旋桨推进技术的研究主要集中在滑流对机翼或其他部件的气动影响和作用机理上,而在考虑分布式螺旋桨滑流对机翼气动性能影响下,针对分布式螺旋桨动力布局进行优化设计方面的研究却非常少。
以分布式电动螺旋桨为动力的飞机,多个小型电动螺旋桨工作时产生的滑流彻底改变了整个机翼周围的流场性质,螺旋桨滑流对飞机机翼等关键气动部件的干扰作用特别显著,造成机翼和整个飞机的气动特性也发生巨大变化[20-21]。而传统的螺旋桨飞机设计中,由于螺旋桨滑流对机翼流场影响范围有限,因此很少考虑动力安装位置对飞机气动特性的影响,这对分布式螺旋桨飞机的动力布局设计是存在很大缺陷的。所以建立一套考虑螺旋桨滑流对机翼气动特性影响的分布式动力布局优化设计方法,最大限度提高螺旋桨布局对飞机气动特性的有利作用,对分布式螺旋桨飞机研究与应用是非常有意义的。选取起飞状态为设计状态,该方法也同样适用于巡航状态的设计研究。
1 数值模拟方法 1.1 控制方程在惯性笛卡尔坐标系中,忽略彻体力,Navier-Stokes方程可表达为:
| $\frac{{\partial {{Q}}}}{{\partial t}} + \frac{{\partial {{E}}}}{{\partial x}} + \frac{{\partial {{F}}}}{{\partial y}} + \frac{{\partial {{G}}}}{{\partial z}} = \frac{{\partial {{{E}}_v}}}{{\partial x}} + \frac{{\partial {{{F}}_v}}}{{\partial y}} + \frac{{\partial {{{G}}_v}}}{{\partial z}}$ | (1) |
其中,
| $ \begin{array}{l} {{F}} = \left( {\begin{array}{*{20}{c}} {v\rho } \\ {v\rho u} \\ {v\rho v + p} \\ {v\rho w} \\ {v\rho h} \end{array}} \right),\;\;{{G}} = \left( {\begin{array}{*{20}{c}} {w\rho } \\ {w\rho u} \\ {w\rho v} \\ {w\rho w + p} \\ {w\rho h} \end{array}} \right),\\ {{{E}}_v} = \left( {\begin{array}{*{20}{c}} 0 \\ {{\tau _{xx}}} \\ {{\tau _{xy}}} \\ {{\tau _{xz}}} \\ {k{T_x} + u{\tau _{xx}} + v{\tau _{xy}} + w{\tau _{xz}}} \end{array}} \right),\\ {{{F}}_v} = \left( {\begin{array}{*{20}{c}} 0 \\ {{\tau _{yx}}} \\ {{\tau _{yy}}} \\ {{\tau _{yz}}} \\ {k{T_y} + u{\tau _{yx}} + v{\tau _{yy}} + w{\tau _{yz}}} \end{array}} \right),\\ {{{G}}_v} = \left( {\begin{array}{*{20}{c}} 0 \\ {{\tau _{zx}}} \\ {{\tau _{zy}}} \\ {{\tau _{zz}}} \\ {k{T_z} + u{\tau _{zx}} + v{\tau _{zy}} + w{\tau _{zz}}} \end{array}} \right) \end{array} $ |
其中,ρ表示气体质量密度;u、v、w分别表示x、y、z方向的速度分量;p表示压力;e、h分别表示单位质量的总能及总焓。
1.2 等效盘模型与验证在优化设计过程中,需要对分布式螺旋桨滑流进行多次数值模拟。为了提高流场解算效率,达到快速优化设计的目的,用等效盘代替真实螺旋桨,采用定常数值模拟方法快速求解分布式螺旋桨飞机流场,获得相应的气动力。
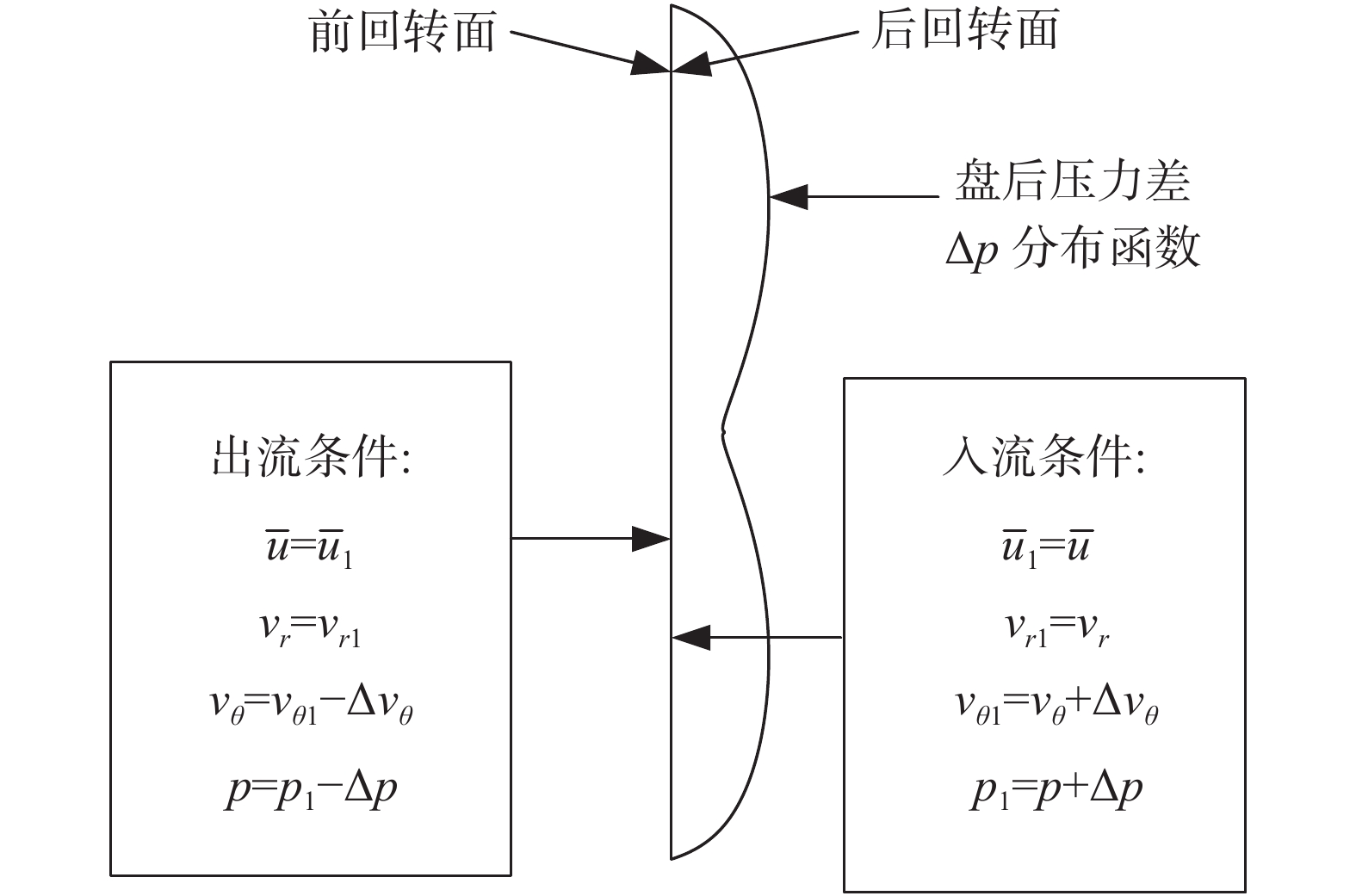
等效盘方法将三维螺旋桨叶片旋转区域简化为无厚度的圆盘,采用时间平均和稳态近似的方法处理从圆盘上游流入及下游流出的气流[22],并且保持圆盘前后与螺旋桨前后流过的气流具有相同的参数,使得等效盘对气流的加速加旋作用效果与螺旋桨叶片类似[23]。等效盘前后气流压力增量和旋向动量增量分别产生拉力和扭矩;等效盘不同位置的前后压差及周向速度差也不同。距螺旋桨中心半径r处,长度dr的微元某时刻受到拉力、扭矩的表达式为[24]:
| ${\rm{d}}T = \frac{1}{2}\rho {W^2}c{\rm{d}}r({C_L}\cos{\alpha _i} - {C_D}\sin {\alpha _i})$ | (2) |
| ${\rm{d}}Q = \frac{1}{2}\rho {W^2}c{\rm{d}}r({C_L}\sin {\alpha _i} + {C_D}\cos {\alpha _i})$ | (3) |
其中,c、CL和CD分别为r处叶型弦长、升力系数和阻力系数;
| $\Delta p = {K_p}\frac{N}{{4{\text{π}} r}}\rho {W^2}c({C_L}\cos{\alpha _i} - {C_D}\sin {\alpha _i})$ | (4) |
| $\Delta {v_\theta } = {K_{{v_\theta }}}\frac{{N{W^2}c}}{{4{\text{π}} r\bar u}}({C_L}\sin {\alpha _i} + {C_D}\cos{\alpha _i})$ | (5) |
其中,
本文将等效盘前设为出流边界,盘后设为入流边界,如图1所示。圆盘前后
|
图 1 等效盘边界条件示意图 Fig.1 Schematic of the boundary conditions of an actuator disk |
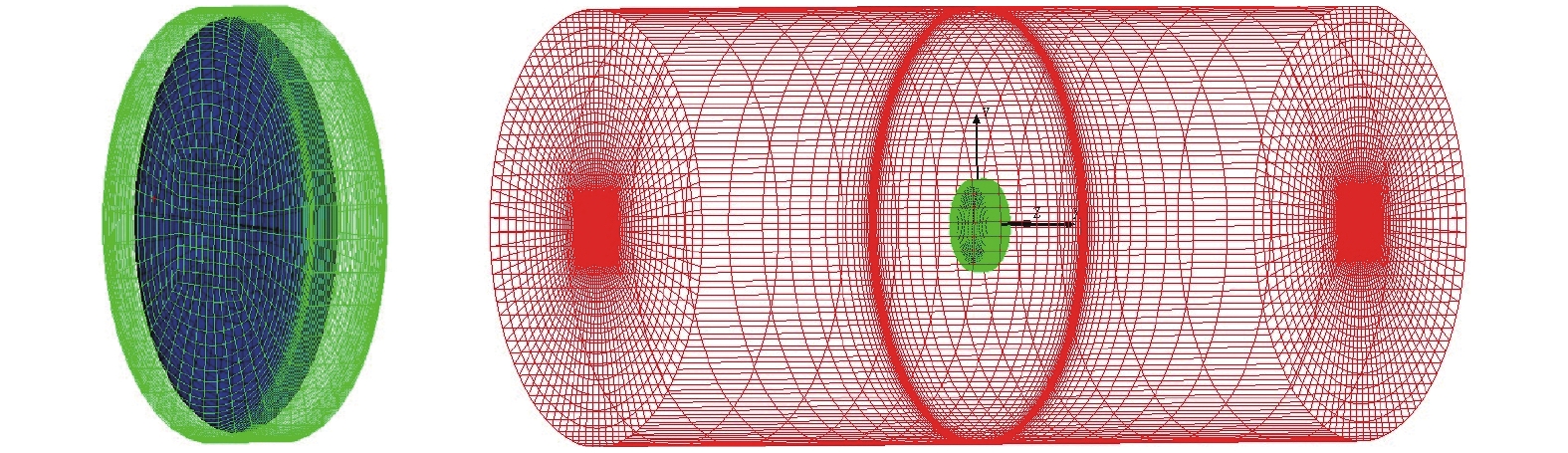
为了验证计算程序的准确性,对某单独双叶螺旋桨进行模拟。该螺旋桨直径为0.76 m,桨叶剖面采用Clark Y翼型,可变桨距[23]。选取一个试验工况:自由来流速度为30 m/s,螺旋桨转速为3200 r/min,螺旋桨0.75R处安装角为16°。数值模拟中采用低速预处理技术,湍流模型选择非线k-ε性模型。为了便于后文优化过程中改变等效盘位置时自动生成计算网格,运用重叠网格技术生成全流场计算网格:将包含等效盘圆盘的一个较小的扁平柱状区域作为一个流场子域单独生成结构网格,将包含远场的区域作为另一个流场子域单独生成结构网格作为背景网格,然后将等效盘子域网格以嵌入的方式与背景网格结合,得到最终的等效盘滑流流场计算网格,如图2所示。通过盘面法向、径向及周向加密的方法生成了粗、中、细三套不同密度的网格,第一层网格高度均为1.2×10−5 m,总网格量分别约为40万、80万、160万。
|
图 2 等效盘子域网格和滑流流场整体计算网格(中网格) Fig.2 Computational grids in the subarea of an actuator disk and the integrated propeller flow field (medium grid) |
将本文采用等效盘方法对螺旋桨进行模拟的计算结果与试验数据及文献[23-24]的计算结果进行比较,如表1所示。
| 表 1 螺旋桨计算结果与试验数据比较 Table 1 Comparison of the computational and test results of the propeller |
|
|
从表1中可以看出:本文使用粗、中、细三套网格分别采用等效盘模型对螺旋桨进行模拟,得到的拉力和扭矩分别相差都是极小的,说明网格密度增加对计算结果影响很小。本文采用的等效盘模型推力计算值误差约1%,扭矩计算值误差约8%;与文献[23]的计算结果相比,文献[24]和本文计算得到的拉力值与试验值更接近,而扭矩值误差相对较大,这可能是等效盘模型中三维效应的修正系数不同造成的。
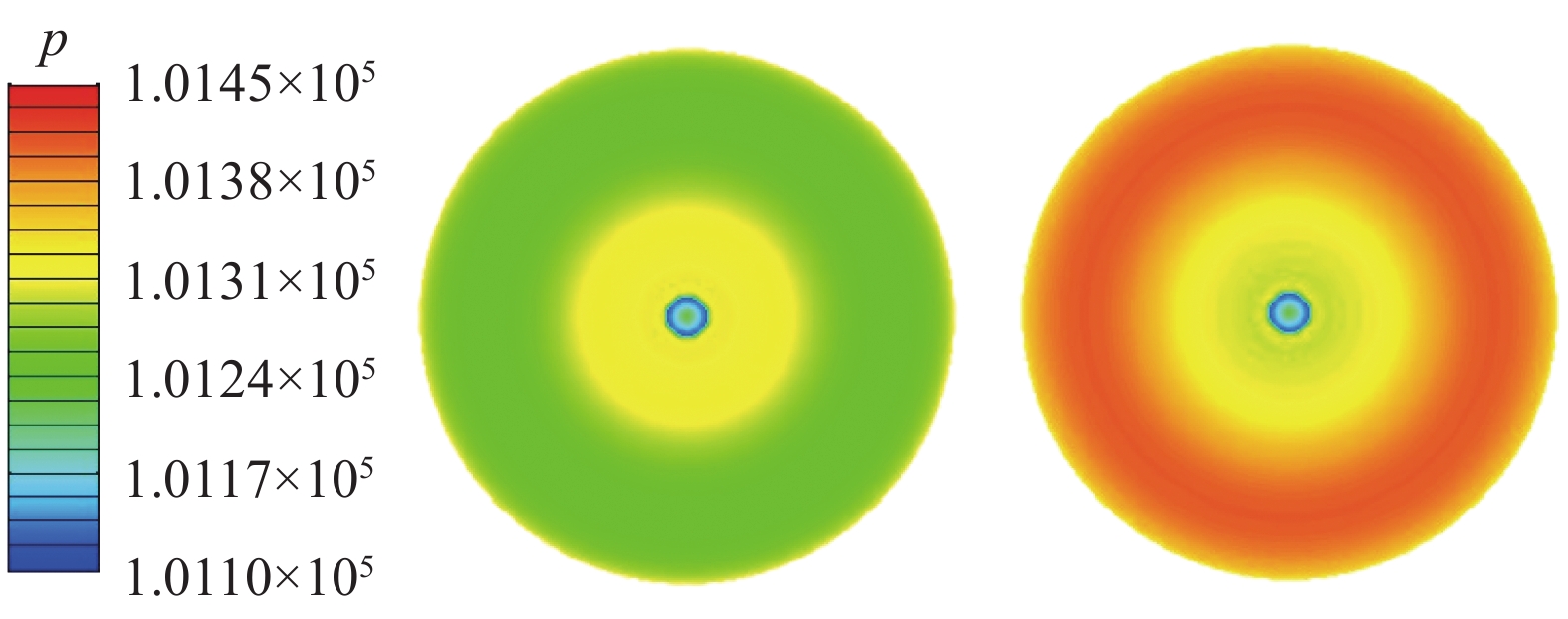
图3给出了使用中等网格计算得到的等效盘前(图左)、后(图右)的压力云图,可以看出,盘前、后压力均沿桨盘径向变化,盘后0.75R附近区域压力最大;流管收缩使得盘前压力变小,而气流经过桨盘后,压力突然跃升。
|
图 3 等效盘前后压力图 Fig.3 Pressure contour in the front and back surfaces of the actuator disk |
图4是流场纵向截面(y = 0)速度云图,桨盘后面形成显著的滑流区,滑流区内的气流速度比滑流区外的明显增大;越往下游,滑流边界越模糊。

|
图 4 y= 0截面速度云图 Fig.4 Velocity contour in the plane at y= 0 |
可见本文的等效盘模型能在一定程度上模拟螺旋桨的真实气动效应,能够满足分布式螺旋桨布局优化设计工程应用需求。
2 量子粒子群优化算法量子粒子群优化算法(Quantum-behaved Particle Swarm Optimization, QPSO)最早由SUN等[25-26]提出,他们将量子力学的思想引入粒子群优化算法(Particle Swarm Optimization, PSO),认为量子粒子处于
设QPSO中有M个个体,每个个体看做N维空间中的无体积粒子,粒子i的当前位置为
| $X_{i,n + 1}^j = p_{i,n}^j \pm \alpha \left| {X_{i,n}^j - C_n^j} \right|\ln (1/u_{i,n + 1}^j)$ | (6) |
其中:n为当前迭代次数;i = 1,2,···,M;j = 1,2,···,N;
QPSO算法过程如下:
第1步:初始化全部粒子的当前位置
第2步:计算粒子的平均最优位置,
第3步:求出每个粒子的适应度响应值,与历史最优值进行比较,如果当前值优于历史最优值,则粒子的当前位置记为个体最优位置,即:若
第4步:求解当前全局最优位置,
第5步:比较粒子群当前的全体最优位置和全体历史最优位置,如果当前的全体最优位置优于全体历史最优位置,则将粒子群当前的全体最优位置记为全体历史最优位置;
第6步:计算每个粒子的吸引子,
第7步:更新下一代粒子位置,
第8步:重复第2~7步,直到满足停机条件或达到最大迭代步。
相对于PSO算法,QPSO算法不需要粒子的速度信息,进化方程更简单、控制参数更少。SUN等对上述QPSO算法进行了理论分析和数值实验,指出量子粒子群优化算法具有以概率1的全局收敛性和较好的搜索精度[26]。
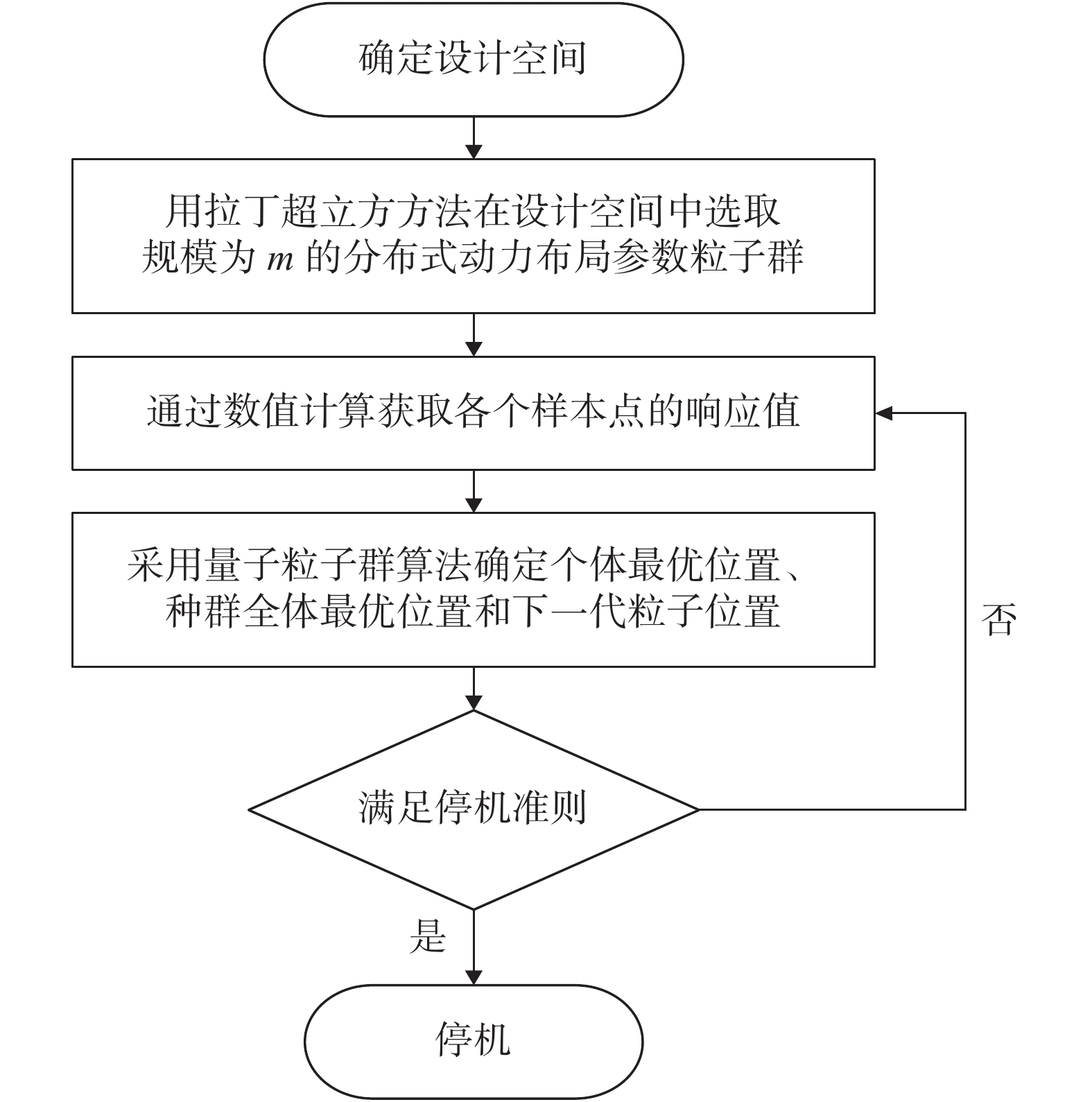
建立考虑分布式螺旋桨滑流对飞机机翼气动特性影响的分布式动力布局优化设计系统如图5所示。该系统采用拉丁超立方(Latin Hypercube Sample, LHS)方法从设计空间中抽样,基于等效盘模型、重叠网格技术和定常流动数值模拟方法,对每个样本点的流场进行快速解算,从而得到相应样本点机翼的气动数据,结合QPSO搜索算法不断更新粒子并且找到全局最优解。
|
图 5 分布式动力布局优化设计系统 Fig.5 Optimal design system for the distributed propeller layout |
分布式螺旋桨主要通过滑流提高机翼表面动压来提高升力,因此,沿机翼展向除了保持螺旋桨之间必要的间距以外,螺旋桨应当尽量布满机翼前缘,使得分布式螺旋桨滑流尽可能覆盖机翼翼展。
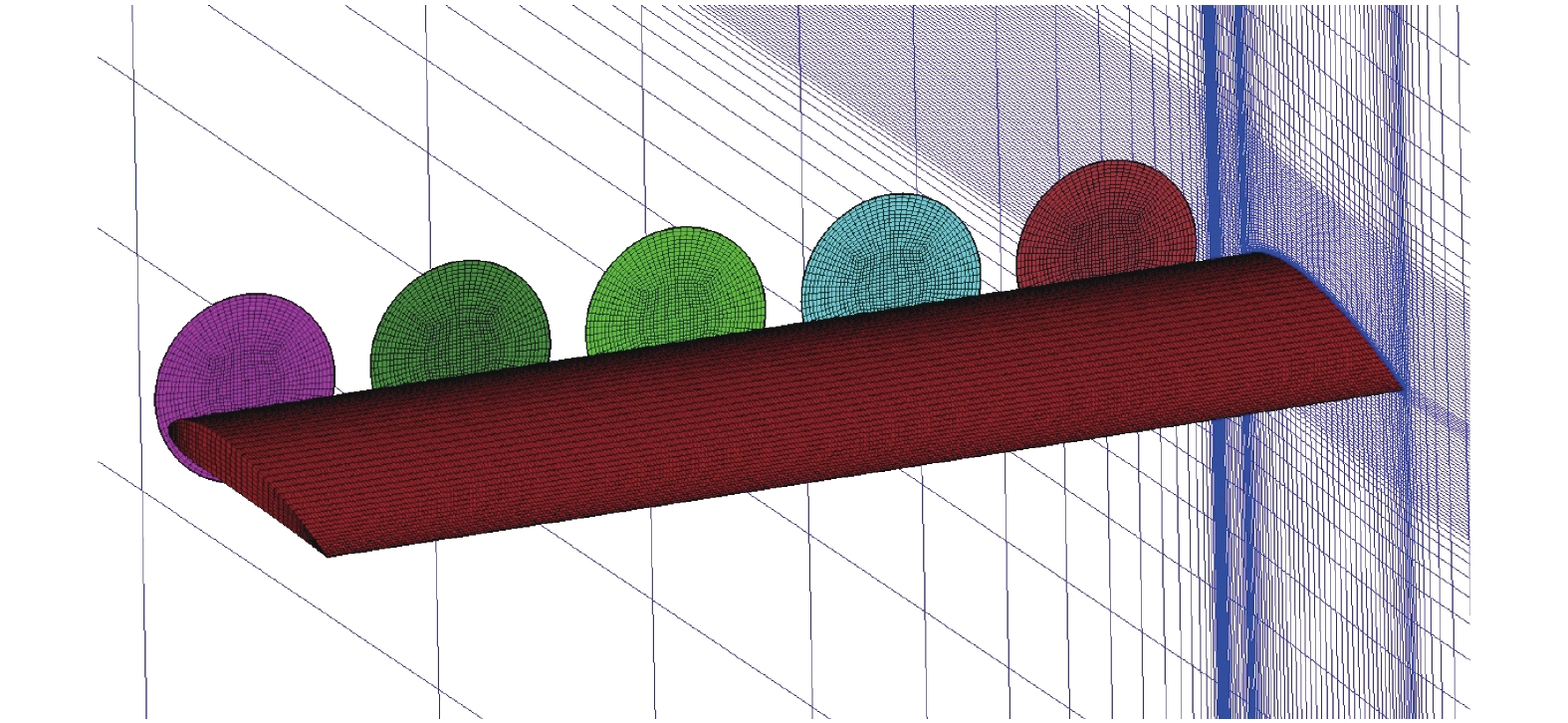
选取以前沿分布式电动螺旋桨为动力的小型低速固定翼无人机为研究对象,设计起飞速度为30 m/s。为减小优化过程的计算量,将分布式螺旋桨飞机半模简化成分布式螺旋桨-机翼构型(如图6所示)。机翼为采用NACA4412翼型的平直机翼,展长b = 3.0 m,机翼弦长c = 1.0 m,参考面积为3.0 m2,安装角为3°;机翼前缘点0.2 m处沿展向均匀布置5个相同的电动螺旋桨,桨叶半径R = 0.25 m,单个螺旋桨包含4片桨叶,螺旋桨转速均为N = 6000 r/min,螺旋桨从下游看为逆时针方向旋转,来流方向与桨叶旋转平面垂直。
|
图 6 分布式螺旋桨-机翼构型计算网格 Fig.6 Computational grids of the distributed propeller-wing configuration |
再考虑设计起飞状态、分布式螺旋桨滑流对机翼绕流影响下,对分布式螺旋桨飞机的动力位置布局进行优化设计。用等效盘代替真实螺旋桨,由于分布式螺旋桨布局由5个等效盘中心位置确定,结合已有研究,忽略对滑流影响很小的流向x坐标,选取对滑流影响大的法向y坐标和展向z坐标,共10个设计参数。设翼根处前缘点为坐标原点,从翼梢到翼根5个等效盘依次记为disk i(i = 1,···,5),中心坐标为(−0.2, yi, zi)。考虑到分布式螺旋桨滑流对机翼绕流的作用,yi的变化范围在螺旋桨半径的值;disk1的z坐标不超过翼梢,每个等效盘盘面相互之间、disk5和对称面之间间隔不小于0.05 m。CFD计算网格采用结构对接网格技术,网格单元总量约为700万。
优化设计目标为在设计起飞状态下,通过优化分布式螺旋桨布局,提高在滑流影响下机翼的升力系数,改善起飞性能。该优化设计问题可以表述为:
| $\begin{array}{*{20}{l}} {{\rm{Objective}}\;{\rm{function}}:{\rm{min}}({\rm{ - }}{{{C}}_L})}\\ {{\rm{s}}.{\rm{t}}.\left\{ {\begin{array}{*{20}{l}} { - 0.25 \leqslant {y_i} \leqslant 0.25,(1 \leqslant i \leqslant 5)}\\ {z_1} \leqslant 3.0\\ {z_i} - {z_j} \geqslant 0.55,(1 \leqslant i < j \leqslant 5) \\ {{z_5} \geqslant 0.30} \end{array}} \right.} \end{array}$ |
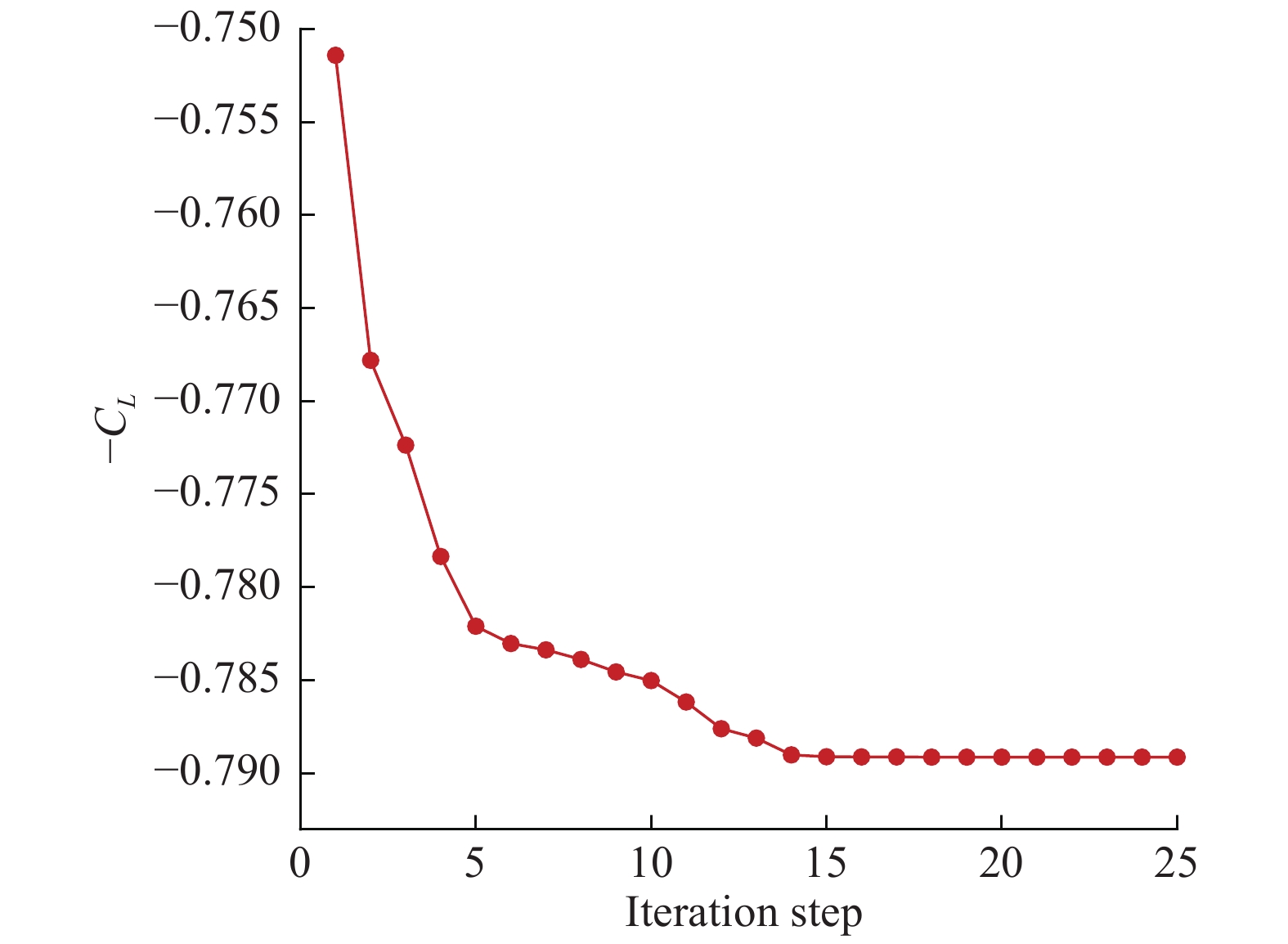
根据建立的优化设计系统对起飞状态下分布式螺旋桨的安装位置进行优化设计,采用拉丁超立方方法选取初始粒子,粒子群体规模为10。采用QPSO算法进行寻优搜索,迭代步数为25步。粒子寻优迭代历程如图7所示,可以看出,QPSO算法能够快速地得到全局范围内较为满意的样本点。
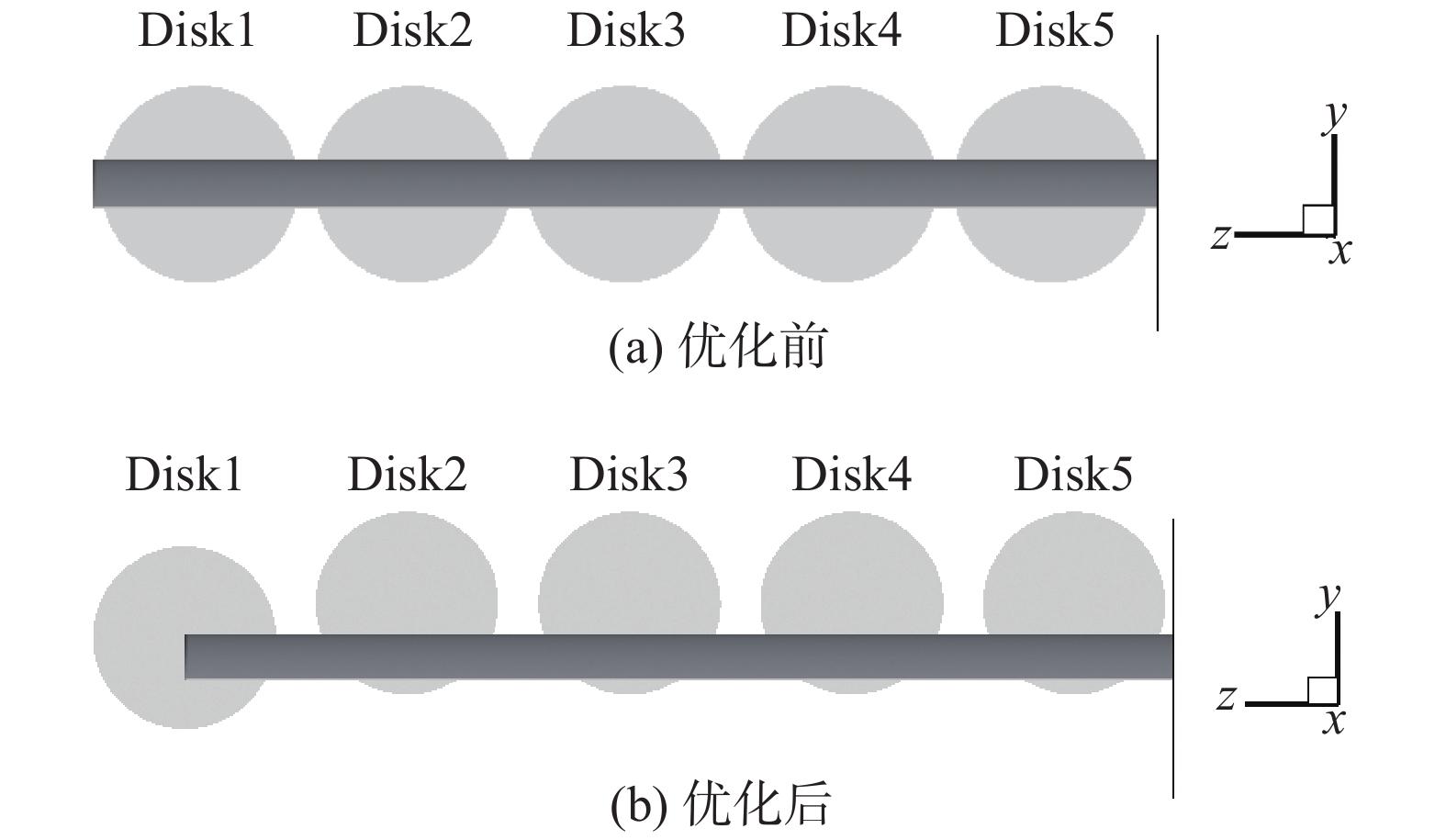
优化后分布式螺旋桨中心位置的空间坐标如表2所示(坐标单位:m,精确到小数点后三位)。相应的分布式螺旋桨/机翼构型如图8所示,图中视角为从下游向正上游方向(−x方向)看,机翼根部竖线表示对称面,浅灰色圆盘表示等效盘。相比优化前,优化后靠近翼梢的螺旋桨disk1中心几乎沿机翼展向(z方向)移动到了最远端,沿法向(y方向)也略有移动;其余4个螺旋桨disk2~disk5,沿法向移动的距离比较明显,而且移动的距离都相等;总体上看,5个螺旋桨沿展向分布仍然比较均匀,相邻的螺旋桨之间的间隔都比较接近。
|
图 7 QPSO优化搜索迭代过程 Fig.7 Iteration history of the optimization search by QPSO |
| 表 2 优化后分布式螺旋桨中心点的坐标 Table 2 Center coordinates of distributed disks after optimization |
|
|
|
图 8 优化前后的分布式螺旋桨/机翼构型 Fig.8 Configuration of distributed propellers and wingbefore and after optimization |
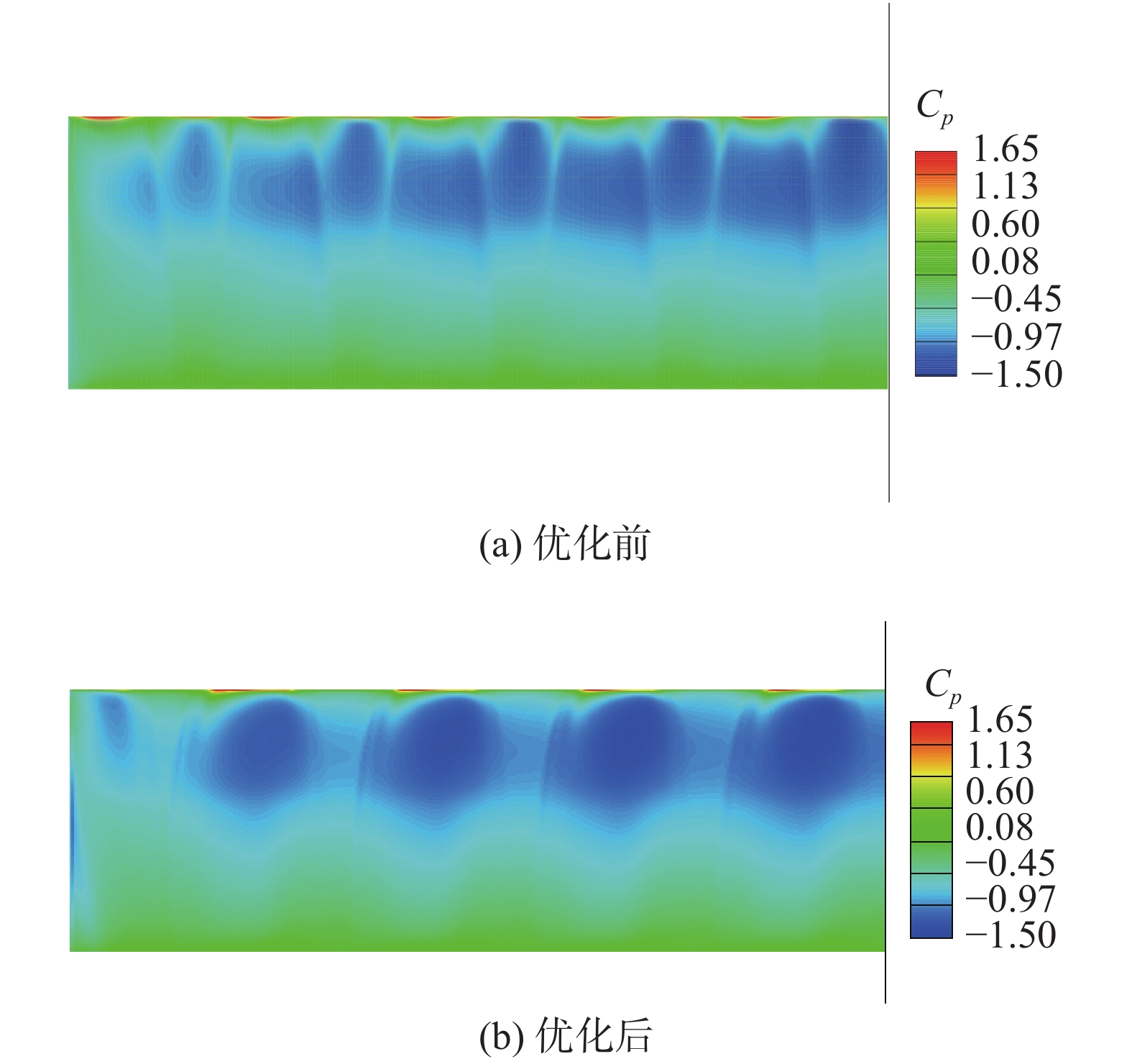
对比动力位置优化前后的流场计算结果,两种布局构型的机翼上表面压力系数云图分别对应图9(a)和图9(b),可以看出,分布式螺旋桨滑流对机翼前缘至2c/3之间的大部分区域影响较大,负压增强比较明显,对2c/3与尾缘之间的区域影响相对较弱,负压增强不明显。翼根附近负压增强效果最显著,从翼根到翼梢,螺旋桨滑流对机翼表面流动的作用强度逐渐减弱,这是机翼的三维效应造成的。分布式螺旋桨布局不同,产生的滑流对机翼的作用区域、面积和强度等都发生了非常明显的变化。优化前,所有螺旋桨都是中间部分正对机翼,对每个螺旋桨,滑流最强位置在0.7r附近的环形区域,使得对应的下游机翼表面受到明显的上洗和下洗作用,上洗和下洗区滑流有明显的分界面,上洗区域负压略强于下洗区域,滑流上洗和下洗及旋转效应使得从机翼前缘往下游,最大负压位置向翼根方向偏斜,下洗区域变宽,上洗区域变窄。优化后,除最靠近翼梢的螺旋桨外,其余4个螺旋桨位置都明显上移,使得原本每个螺旋桨滑流对机翼的上洗和下洗区的界限消失,滑流对机翼表面负压增强效果更加显著,负压增强区域连为一片且范围变得更宽;相邻两个螺旋桨之间的滑流作用区域之间的间隔变大;机翼表面滑流作用下负压增强区域随气流往下游流动而向翼梢有所偏斜,这主要是机翼绕流的三维效应引起的;翼梢处螺旋桨位置优化后,滑流对机翼表面的影响区域更加接近翼梢,也更加靠近当地机翼前缘,负压增强效果也有所增强。
|
图 9 优化前后机翼表面压力系数云图 Fig.9 Surface pressure coefficient contour on the wingbefore and after optimization |
反映到气动数据上,如表3所示。相比优化前的原构型,优化后机翼升力系数CL得到明显提升,增加了5.6%,与预期一致。同时,机翼阻力系数CD大幅减小88.7 counts (1 count = 1×10−4),减小约13.9%,升阻比提高22.2%。进一步,从机翼阻力构成上看,压差阻力是摩擦阻力的2倍多。分布式螺旋桨布局优化后,机翼摩擦阻力系数CDF减小12.9 counts,减幅约6.9%,压差阻力系数CDP则大幅减小75.8 counts,减幅达16.8%,占总阻力系数减小量的85.5%。可见,采用本文的分布式螺旋桨布局优化设计方法得到的结果,不仅能够显著提高机翼升力,还能起到大幅减小阻力的效果,从而有效地提升分布式螺旋桨飞机的气动性能。
| 表 3 优化设计前后机翼气动特性对比 Table 3 Comparison of aerodynamic characteristics of thewing before and after optimization |
|
|
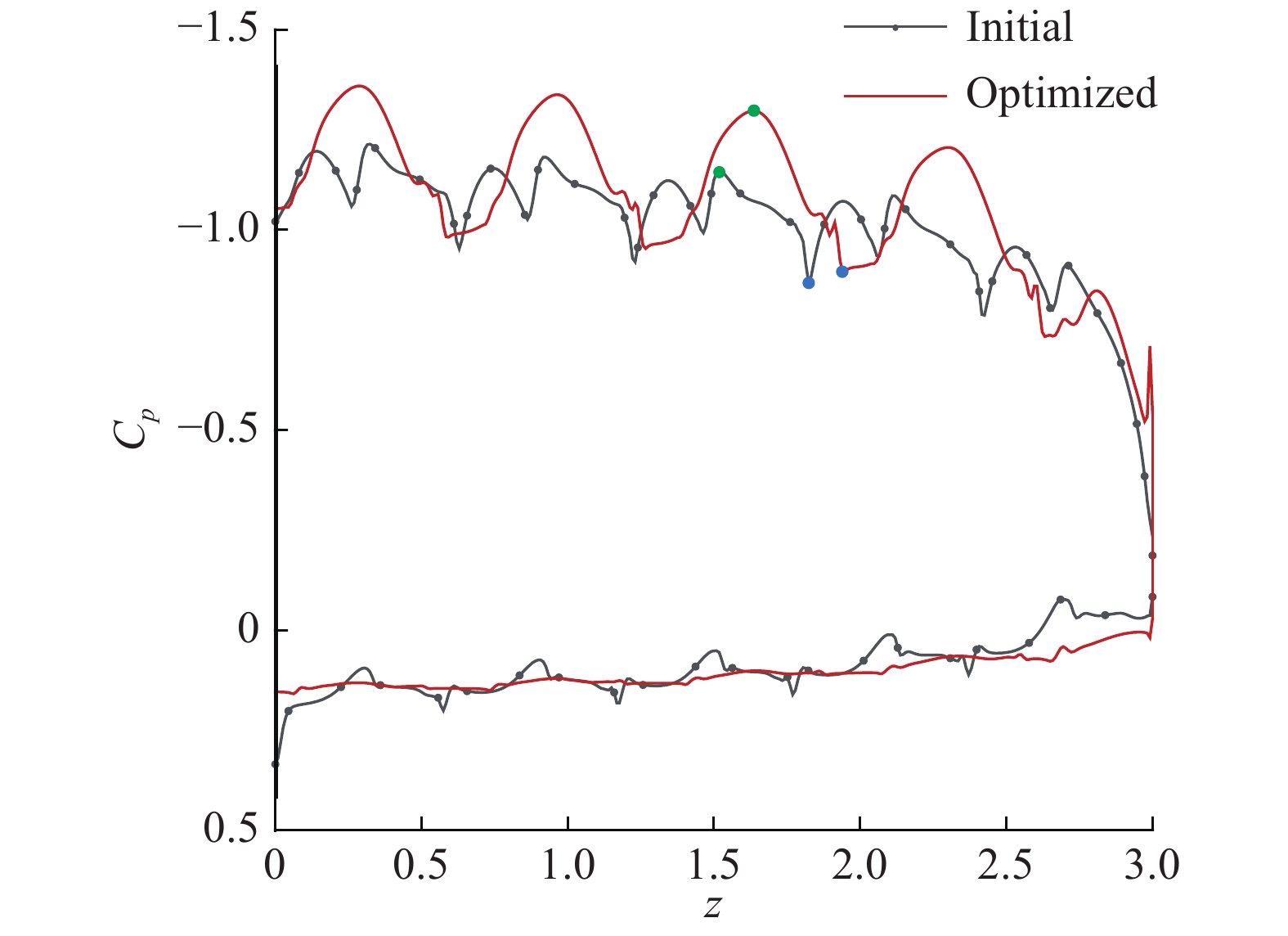
分布式螺旋桨布局优化前后,机翼1/4c处展向的压力分布系数对比如图10所示。分布式螺旋桨布局优化前,滑流使得机翼前缘上、下表面都受到了明显的上洗和下洗作用,因此每个螺旋桨的滑流所对应的下游机翼上表面区域都出现两个负压吸力峰,整个机翼上表面出现了10个吸力峰。优化后,滑流引起的机翼气流上洗和下洗效应分界线基本消失。螺旋桨disk2~disk5滑流区的机翼前缘上表面对应地出现了4个更加强烈的吸力峰,上表面压力系数分布更加饱满,压力系数局部最低点上移,这是机翼升力增加的主要原因;下表面压力系数分布更加光滑和均匀。优化后,翼梢处螺旋桨disk1沿机翼展向外移,使得翼梢附近下表面压力明显变大且更加平顺,上表面压力系数分布在翼梢处更加饱满,表明翼尖涡流得到更大程度的抑制,也有利于提高机翼升力。
|
图 10 优化前后机翼1/4弦长处压力系数分布对比 Fig.10 Comparison of pressure coefficient distributions at 1/4 chord length of the wing before and after optimization |
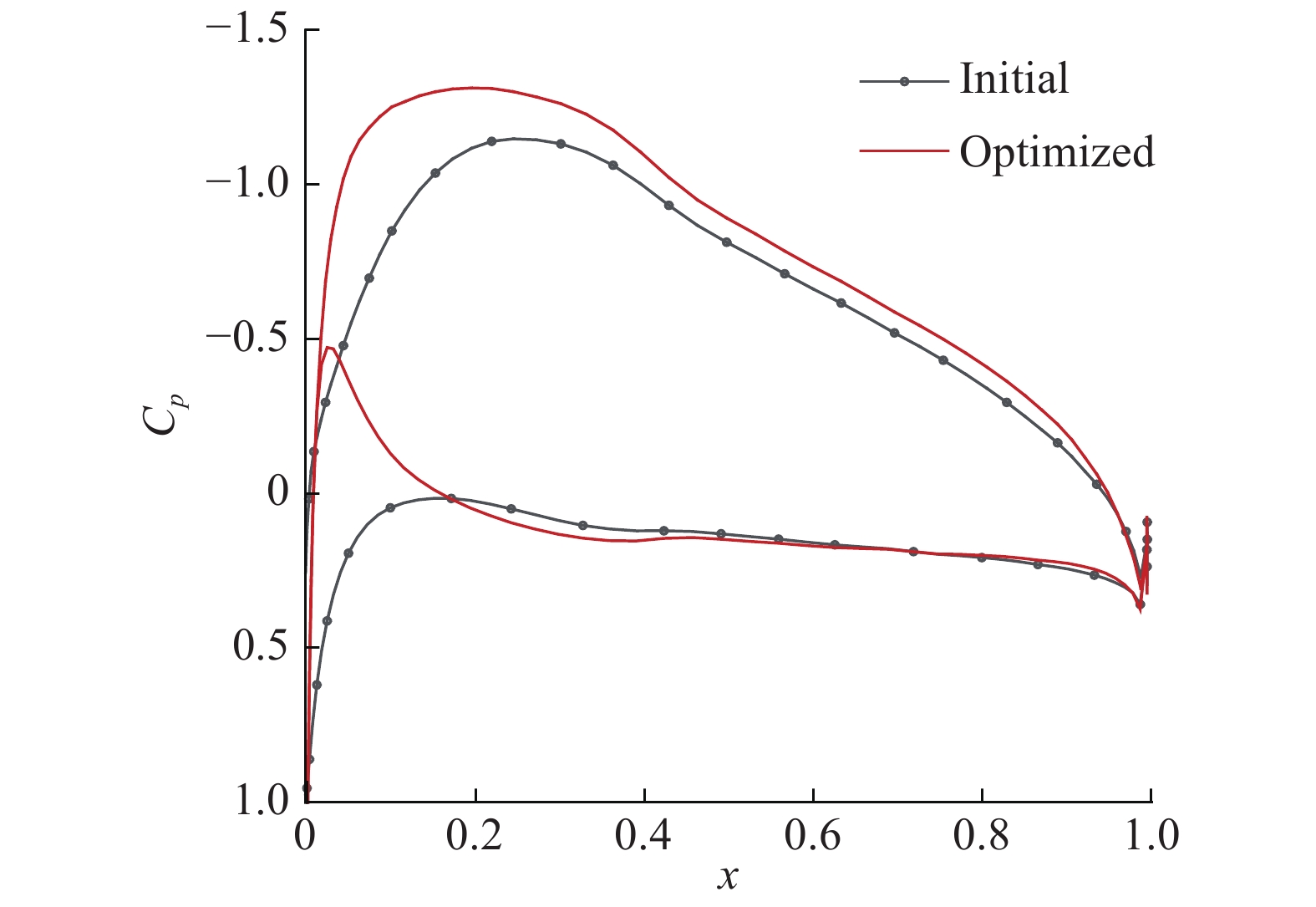
进一步对比机翼展向不同站位翼型的压力系数分布,以优化前后中间位置等效盘(disk3)对应的机翼上表面负压最高点(图10中绿点)和最低点(图10中蓝点)处为例,分别称作“峰点”和“谷点”,截面翼型的压力系数分布对比分别如图11和图12所示。
|
图 11 优化前后机翼“峰点”处型面压力系数分布对比 Fig.11 Comparison of pressure coefficient distributions at the "peak" section location of the wing before and after optimization |
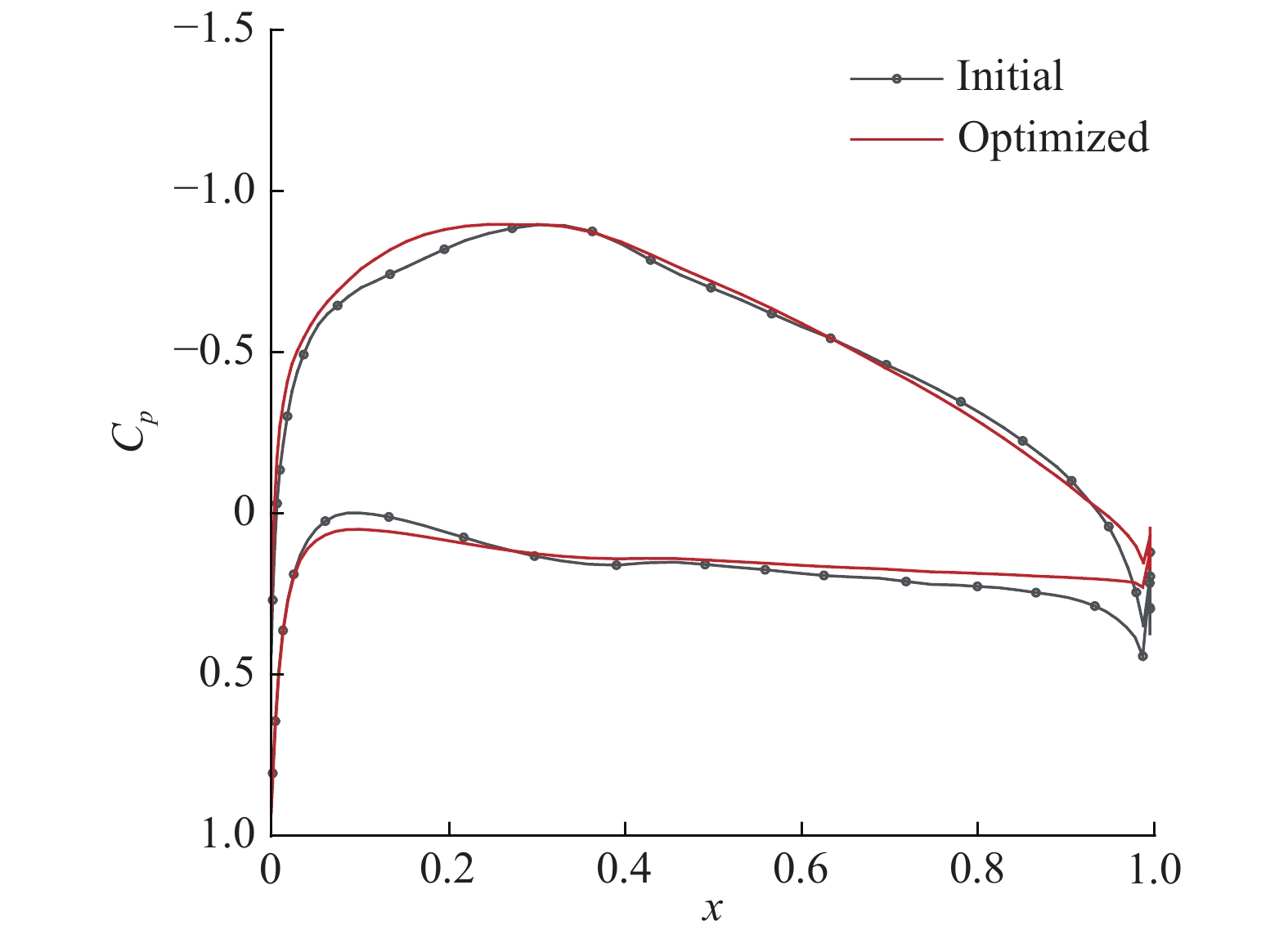
|
图 12 优化前后机翼“谷点”处型面压力系数分布对比 Fig.12 Comparison of pressure coefficient distributions at the "trough" section lociation of the wing before and after optimization |
从图11可见,分布式螺旋桨布局优化后,机翼上表面负压显著增强,这是由于滑流作用使得气流速度更快,动压更大。翼型上表面前缘附近,负压吸力在x方向的分量与阻力方向相反,分布式螺旋桨布局优化后,此区域负压显著增强,使得机翼阻力明显减小。另一方面,下表面前缘附近,分布式螺旋桨布局优化前,高压很显著,且压力在x方向的分量与阻力相同,使得阻力也较大;优化后,此区域高压区范围显著减小,甚至部分区域变成了负压吸力区,这使得机翼前缘受到的阻力显著减小。这表明,优化后“峰点”截面附近的机翼升力显著提高,阻力显著降低。
从图12可见,分布式螺旋桨布局优化后,“谷点”截面翼型压力系数分布在前缘附近更加饱满,使得升力系数有所增大;压力系数分布在后缘附近更加平滑,且压力变小,有利于减小摩擦阻力系数。这表明,优化后“谷点”截面附近的机翼升力显著提高,阻力显著降低。
4 结 论本文考虑分布式螺旋桨飞机滑流作用对机翼的气动影响,建立了分布式螺旋桨布局优化设计方法,并对简化的分布式螺旋桨/机翼构型进行了动力布局优化设计。结果表明:
1) 等效盘能较好地代替螺旋桨对滑流流场进行数值模拟,能够满足滑流气动效应下的分布式螺旋桨优化设计需求。
2) 分布式螺旋桨布局优化后,起飞状态下,机翼的升力系数提高了5.6%,阻力系数减小了13.9%。因此,建立的分布式螺旋桨布局优化设计是合理的,能够有效改善分布式螺旋桨飞机的气动特性,该方法也适用于巡航状态。
3) 分布式螺旋桨布局优化后,滑流区气流速度更快,动压更大,使得机翼上表面负压显著增强,是机翼升力增加的主要原因;下表面前缘附近,高压区范围显著减小,甚至部分区域变为负压吸力区,是机翼阻力显著减小的主要原因。
考虑滑流作用对飞机机翼气动影响的分布式螺旋桨布局优化设计方法,对促进螺旋桨飞机动力/气动布局一体化设计理念的发展具有重要意义。考虑螺旋桨滑流影响下,对分布式螺旋桨飞机动力布局和气动外形进行一体化优化设计,更大地提升分布式推进飞机气动特性是后续研究的重要方向。
| [1] |
黄俊, 杨凤田. 新能源电动飞机发展与挑战[J]. 航空学报, 2016, 37(1): 57-68. HUANG J, YANG F T. Development and challenges of electric aircraft with new energies[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(1): 57-68. DOI:10.7527/S1000-6893.2015.0274 (in Chinese) |
| [2] |
GOHARDANI A S, DOULGERIS G, SINGH R. Challenges of future aircraft propulsion: a review of distributed propulsion technology and its potential application for the all electric commercial aircraft[J]. Progress in Aerospace Sciences, 2011, 47(5): 369-391. DOI:10.1016/j.paerosci.2010.09.001 |
| [3] |
孔祥浩, 张卓然, 陆嘉伟, 等. 分布式电推进飞机电力系统研究综述[J]. 航空学报, 2018, 39(1): 46-62. KONG X H, ZHANG Z R, LU J W, et al. Review of electric power system of distributed electric propulsion aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(1): 46-62. DOI:10.7527/S1000-6893.2017.21651 (in Chinese) |
| [4] |
PATTERSON M D, GERMAN B. Conceptual design of electric aircraft with distributed propellers: multidisciplinary analysis needs and aerodynamic modeling development[C]//Proc of the 52nd Aerospace Sciences Meeting, National Harbor, Maryland. Reston, Virginia: AIAA, 2014.doi: 10.2514/6.2014-0534
|
| [5] |
MOORE M D, FREDERICKS B. Misconceptions of electric aircraft and their emergent aviation markets[C]//52nd Aerospace Sciences Meeting, National Harbor, Maryland. Reston, Virginia: AIAA, 2014. doi: 10.2514/6.2014-0535
|
| [6] |
徐德康. NASA重构航空研究计划[J]. 国际航空, 2015(3): 69-71. XU D K. NASA restructures aeronautic research programs[J]. International Aviation, 2015(3): 69-71. (in Chinese) |
| [7] |
STOLL A M, BEVIRT J, MOORE M D, et al. Drag reduction through distributed electric propulsion[C]// 14th AIAA Aviation Technology, Integration, and Operations Conference, Atlanta, GA. Reston, Virginia: AIAA, 2014.doi: 10.2514/6.2014-2851
|
| [8] |
STOLL A M. Comparison of CFD and experimental results of the LEAPTech distributed electric propulsion blown wing[C]//15th AIAA Aviation Technology, Integration, and Operations Conference, Dallas, TX. Reston, Virginia: AIAA, 2015. doi: 10.2514/6.2015-3188
|
| [9] |
PATTERSON M D, DERLAGA J M, BORER N K. High-lift propeller system configuration selection for NASA's SCEPTOR distributed electric propulsion flight demonstrator[C]//16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, D.C.. Reston, Virginia: AIAA, 2016.doi: 10.2514/6.2016-39223
|
| [10] |
PATTERSON M D, BORER N K. Approach considerations in aircraft with high-lift propeller systems[C]//17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, Colorado. Reston, Virginia: AIAA, 2017.doi: 10.2514/6.2017-3782
|
| [11] |
LITHERLAND B L, PATTERSON M D, DERLAGA J M, et al. A method for designing conforming folding propellers[C]//17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, Colorado. Reston, Virginia: AIAA, 2017.doi: 10.2514/6.2017-3781
|
| [12] |
MASSEY S J, WIESEMAN C D, STANFORD B, et al. Aeroelastic analysis of a distributed electric propulsion wing[C]// 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Grapevine, Texas. Reston, Virginia: AIAA, 2017.doi: 10.2514/6.2017-0413
|
| [13] |
BORER N K, MOORE M D, TURNBULL A. Tradespace exploration of distributed propulsors for advanced on-demand mobility concepts[C]//14th AIAA Aviation Technology, Integration, and Operations Conference, Atlanta, GA. Reston, Virginia: AIAA, 2014.doi: 10.2514/6.2014-2850
|
| [14] |
BORER N K, MOORE M D. Integrated propeller-wing design exploration for distributed propulsion concepts[C]//53rd AIAA Aerospace Sciences Meeting, Kissimmee, Florida. Reston, Virginia: AIAA, 2015. doi: 10.2514/6.2015-1672
|
| [15] |
MURPHY P C, LANDMAN D. Experiment design for complex VTOL aircraft with distributed propulsion and tilt wing[C]//AIAA Atmospheric Flight Mechanics Conference, Kissimmee, Florida. Reston, Virginia: AIAA, 2015.doi: 10.2514/6.2015-0017
|
| [16] |
王科雷, 祝小平, 周洲, 等. 低雷诺数分布式螺旋桨滑流气动影响[J]. 航空学报, 2016, 37(9): 2669-2678. WANG K L, ZHU X P, ZHOU Z, et al. Distributed electric propulsion slipstream aerodynamic effects at low Reynolds number[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(9): 2669-2678. DOI:10.7527/S1000-6893.2016.0032 (in Chinese) |
| [17] |
王红波, 祝小平, 周洲, 等. 太阳能无人机螺旋桨滑流气动特性分析[J]. 西北工业大学学报, 2015, 33(6): 913-920. WANG H B, ZHU X P, ZHOU Z, et al. Aerodynamic investigation on propeller slipstream flows for solar powered airplanes[J]. Journal of Northwestern Polytechnical University, 2015, 33(6): 913-920. DOI:10.3969/j.issn.1000-2758.2015.06.008 (in Chinese) |
| [18] |
杨小川, 王运涛, 孟德虹, 等. 不同分布式螺旋桨转向组合下的机翼滑流效应研究[J]. 空气动力学学报, 2019, 37(1): 89-98. YANG X C, WANG Y T, MENG D H, et al. Study on wing slipstream effects of distributed propellers with different rotating directions[J]. Acta Aerodynamica Sinica, 2019, 37(1): 89-98. DOI:10.7638/kqdlxxb-2018.0168 (in Chinese) |
| [19] |
杨小川, 李伟, 王运涛, 等. 一种分布式螺旋桨运输机方案及其滑流效应研究[J]. 西北工业大学学报, 2019, 37(2): 361-368. YANG X C, LI W, WANG Y T, et al. Research on aerodynamic shape design scheme of a distributed propeller transport aircraft and its slipstream effect[J]. Journal of Northwestern Polytechnical University, 2019, 37(2): 361-368. DOI:10.3969/j.issn.1000-2758.2019.02.020 (in Chinese) |
| [20] |
张小莉, 张一帆. 螺旋桨滑流对增升装置气动特性影响研究[J]. 航空计算技术, 2011, 41(4): 1-3, 7. ZHANG X L, ZHANG Y F. Research on interaction of propeller and high- lift system[J]. Aeronautical Computing Technique, 2011, 41(4): 1-3, 7. DOI:10.3969/j.issn.1671-654X.2011.04.001 (in Chinese) |
| [21] |
王伟, 段卓毅, 耿建中, 等. 考虑螺旋桨滑流影响的双发涡桨飞机气动特性研究[J]. 西北工业大学学报, 2017, 35(6): 1105-1111. WANG W, DUAN Z Y, GENG J Z, et al. Aerodynamics analysis of Twin?Turboprop aircraft with propeller slipstream effects considered[J]. Journal of Northwestern Polytechnical University, 2017, 35(6): 1105-1111. DOI:10.3969/j.issn.1000-2758.2017.06.026 (in Chinese) |
| [22] |
STRASH D, LEDNICER D, RUBIN T. Analysis of propeller-induced aerodynamic effects[C]//16th AIAA Applied Aerodynamics Conference, Albuquerque, NM. Reston, Virginia: AIAA, 1998.doi: 10.2514/6.1998-2414
|
| [23] |
李博, 梁德旺, 黄国平. 基于等效盘模型的滑流对涡桨飞机气动性能的影响[J]. 航空学报, 2008, 29(4): 845-852. LI B, LIANG D W, HUANG G P. Propeller slipstream effects on aerodynamic performance of turbo-prop airplane based on equivalent actuator disk model[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(4): 845-852. DOI:10.3321/j.issn:1000-6893.2008.04.013 (in Chinese) |
| [24] |
杨小川, 王运涛, 王光学. 基于等效盘的螺旋桨飞机数值模拟[J]. 气体物理-理论与应用, 2012, 7(3): 40-47. YANG X C, WANG Y T, WANG G X. Numerical Simulation of Propeller Slipstream Based on Equivalent Actuator Disk Model[J]. Physics of Gases Theory and Application, 2012, 7(3): 40-47. (in Chinese) |
| [25] |
SUN J, XU W B, FENG B. A global search strategy of quantum-behaved particle swarm optimization[C]//IEEE Conference on Cybernetics and Intelligent Systems, 2004, Singapore, Singapore. IEEE, 2004: 111-116. doi: 10.1109/ICCIS.2004.1460396
|
| [26] |
SUN J, FANG W, WU X J, et al. Quantum-behaved particle swarm optimization: analysis of individual particle behavior and parameter selection[J]. Evolutionary Computation, 2012, 20(3): 349-393. DOI:10.1162/EVCO_a_00049 |



