2. 中国空气动力研究与发展中心,绵阳 621000
2. China Aerodynamics Research and Development Center, Mianyang 621000, China
乘波前体/进气道设计技术[1-2]能最大程度地提高吸气式高超声速飞行器前体压缩效率并减少进气道溢流,对冲压发动机燃烧室进气量匹配、进气品质以及飞行器整机气动性能等都起着至关重要的作用。但是现阶段单纯基于流线追踪的乘波体设计方法在实际应用时会存在一定的误差。一般的乘波体设计流程是在给定的基准流场中进行流线追踪得到相应的乘波构型。乘波体基准流场的求解主要包括斜激波关系式方法、Taylor-Maccoll流动方程求解法[3-6]、高超声速一阶小扰动理论[7-8]、特征线方法(MOC)[9-11]、CFD方法[12-13]等。在现有求解方法基础上,通过流线追踪生成的是无黏条件下理想的乘波构型,而在实际黏性情况下,虽然总体趋势上符合设计预期,但是由于黏性边界层的影响,进气道入口大约有5%~7%左右的流量损失。尤其在前体/进气道/隔离段一体化乘波构型中,黏性边界层会造成隔离段内的多次反射激波,严重降低隔离段流场品质。因此针对包含有内流型面的乘波前体/进气道/隔离段耦合构型,进行边界层黏性修正非常有必要。
黏性修正的关键是边界层位移厚度的修正,可分为经验方法和精确方法。边界层位移厚度的粗略值可以直接通过求解与雷诺数相关的工程经验公式获得,虽然简单方便,但是工程经验公式的粗略值在精度上误差太大。位移厚度精确值可以通过全N-S方程对边界层速度型的求解以及对位移厚度方程的积分求得,或者通过Euler方程求解外缘流场参数作为简化后的边界层方程[14]初值解,进一步通过有限差分求得速度型并且积分获得位移厚度。基于Euler或者N-S方程的位移厚度精确值求解方法,需要生成网格,过程复杂且较为费时,不方便与乘波体设计程序耦合,且在激波附近容易出现不光滑的求解值,不适合多级波系的乘波构型。
针对以上问题,本文在基于特征线法的多级前体与截短Busemann进气道一体化乘波布局设计方法基础上,发展了一种适用于多级波系锥导[15-16]或吻切锥乘波体[17-18]尤其是包含消波隔离段构型的边界层黏性修正方法。基于特征线法求解的乘波压缩面参数相当于外缘流场参数,通过耦合可压缩的动量方程积分方法来求解边界层位移厚度,最终生成黏性修正后的前体/进气道一体化乘波构型,并达到隔离段消波的目的。该方法属于结合工程方法的数值积分方法,不需要额外生成基准流场网格,计算量较小,且在求解边界层位移厚度方面有较高的精度,避免了Euler方程或N-S方程计算量大和纯经验公式精度较低的缺点,同时能直接与乘波体设计程序耦合。对修正前后一体化乘波构型进行了设计状态下的流场对比验证以及非设计状态下给定马赫数和迎角范围下的气动性能影响分析。数值结果验证了黏性边界层修正方法的正确性,及与前体/进气道/消波隔离段一体化乘波布局设计方法耦合的优异性和必要性。
1 前体/进气道黏性边界层修正方法采用的边界层位移厚度求解方法是Sivells和Payne[19]提出的适用于高超声速可压缩轴对称流动的冯•卡门动量方程积分方法。该黏性修正方法非常适合应用到锥导或吻切锥乘波体上,即在单个吻切面内基准流场同样是高超声速可压缩轴对称流动。本文后续基于吻切流场理论和特征线法的前体/进气道乘波验证构型符合该条件。
由于黏性的影响,垂直物面边界附近流场存在速度型。相对于过流场中某点无黏时的流线,有黏时流线被外推的距离被称为位移厚度
| $ {\delta }^{\rm{*}}={\displaystyle {\int }_{0}^{{{{y}}}_{1}}\left[1-\left(\rho u\right)/\left({\rho }_{{\rm{e}}}{u}_{{\rm{e}}}\right)\right]}{{\rm{d}}}y,\; \delta \leqslant {y}_{1}\to \infty $ | (1) |
| $ \phi ={\displaystyle {\int }_{0}^{{y}_{1}}\left[\left(\rho u\right)/\left({\rho }_{{\rm{e}}}{u}_{{\rm{e}}}\right)\right]\left(1-u/{u}_{{\rm{e}}}\right)}{{\rm{d}}}y,\;\delta \leqslant {y}_{1}\to \infty $ | (2) |
| $H = {\delta ^ * }/\phi $ | (3) |
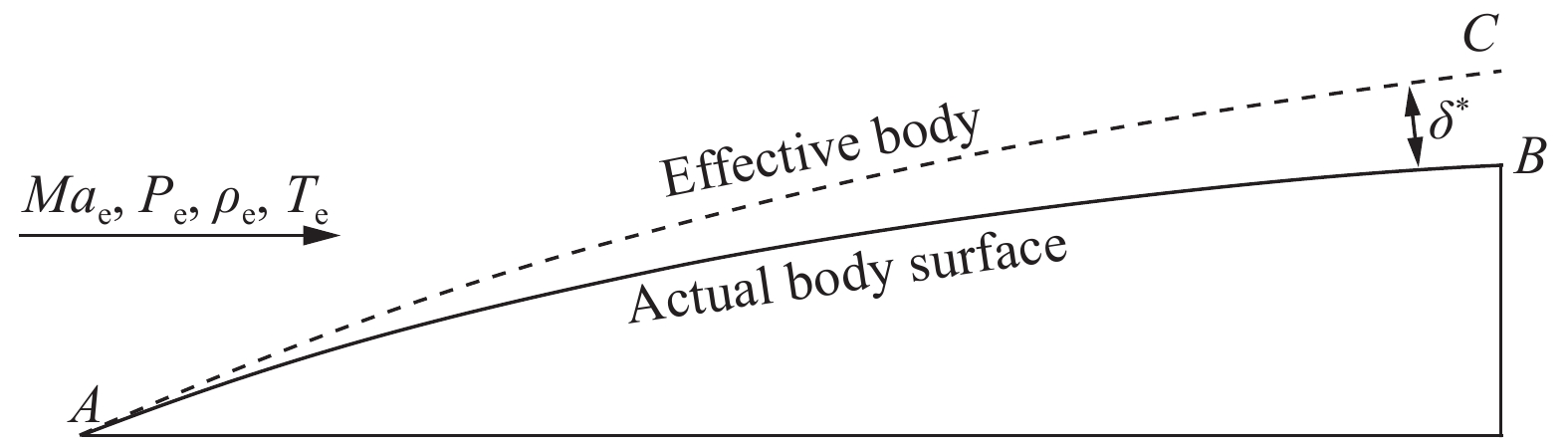
由位移厚度引出了等效壁面的概念如图1所示。实际物面AB上的流场参数与自由来流并不一致,由于边界层的原因,自由来流的流线被外推了相当于位移厚度的距离,流场中过实际物面前缘,第一条与外部流场参数一致的流线被称为等效壁面(图1虚线AC)。本文基于特征线法的黏性修正按照等效壁面的定义反向进行,如图2,特征线法生成的无黏物面流线相当于黏性流场中的等效壁面流线,特征线法求解的物面无黏流场参数相当于黏性流场中等效壁面外缘流场参数,修正后的实际物面为等效壁面减去相应的位移厚度。因此实际壁面黏性修正的关键是求解边界层位移厚度。
|
图 1 等效壁面定义 Fig.1 Definition of the equivalent wall |

|
图 2 乘波体壁面黏性修正原理 Fig.2 Principle of viscous correction |
采用适用于高超声速可压缩轴对称流动的冯•卡门动量方程积分方法求解边界层位移厚度。动量方程如下,式中
| $ \frac{{{\rm{d}}\phi }}{{{\rm{d}}x}} + \phi \left[ {\frac{{2 - {Ma^2} + H}}{{Ma\left( {1 + \dfrac{{\gamma - 1}}{2}{Ma^2}} \right)}}\frac{{{\rm{d}}Ma}}{{{\rm{d}}x}}{\rm{ + }}\sigma \frac{1}{r}\frac{{{\rm{d}}r}}{{{\rm{d}}x}}} \right] = \frac{{{C_f}}}{2}\sec \omega $ | (4) |
利用特征线法求得的壁面几何参数和无黏流场参数(
求解可压缩流动边界层动量方程的关键是求解边界层形状因子H和表面摩擦系数
| $ \phi {\rm{ = }}{\phi _{{\rm{tr}}}}{\left( {1 + \frac{{\gamma - 1}}{2}{Ma^2}} \right)^{\frac{{\gamma + 1}}{{2\left( {\gamma - 1} \right)}}}} = {\phi _{{\rm{tr}}}}{\left( {\frac{{{T_0}}}{{{T_{\rm{e}}}}}} \right)^{\frac{{\gamma + 1}}{{2\left( {\gamma - 1} \right)}}}} $ | (5) |
| $ H = {H_{{\rm{tr}}}}\left( {1 + \frac{{\gamma - 1}}{2}{Ma^2}} \right) + \frac{{\gamma - 1}}{2}{Ma^2} = \left( {{H_{{\rm{tr}}}} + 1} \right)\frac{{{T_0}}}{{{T_{\rm{e}}}}} - 1 $ | (6) |
式(6)中下标e代表边界层外缘流场参数,下标0代表滞止流场参数,下标tr代表Stewartson转换后参数。边界层动量方程进一步变换为:
| $ \frac{{{\rm{d}}{\phi _{{\rm{tr}}}}}}{{{\rm{d}}x}} + \frac{{{\phi _{{\rm{tr}}}}}}{Ma}\frac{{{\rm{d}}Ma}}{{{\rm{d}}x}}\left( {2 + {H_{{\rm{tr}}}}} \right) + \sigma \frac{{{\phi _{{\rm{tr}}}}}}{r}\frac{{{\rm{d}}r}}{{{\rm{d}}x}} = \frac{{{C_f}}}{2}\sec \omega {\left( {\frac{{{T_{\rm{e}}}}}{{{T_0}}}} \right)^{\frac{{\gamma {\rm{ + }}1}}{{2\left( {\gamma - 1} \right)}}}} $ | (7) |
当普朗特数为1且边界层没有热交换时,转换后的形状因子
| ${H_{{\rm{tr}}}} = {H_i}\frac{{{T_{\rm{w}}}}}{{{T_0}}} + \frac{{{T_{{\rm{aw}}}}}}{{{T_0}}} - 1$ | (8) |
| $ \begin{split}& {T}_{\rm{w}}={T}_{\rm{aw}}={T}_{{\rm{e}}}\left(1+\lambda \frac{\gamma -1}{2}{Ma}_{{\rm{e}}}{}^{2}\right)\\& \quad\qquad\qquad\lambda = P{r}^{\frac{1}{3}}\\& \qquad{T}_{0}={T}_{{\rm{e}}}\left(1+\frac{\gamma -1}{2}{Ma}_{{\rm{e}}}{}^{2}\right)\end{split} $ | (9) |
物面边界为绝热壁面条件,取壁面温度
不可压缩形状因子
| ${H_i} = \frac{1}{{1 - 7\sqrt {\dfrac{C_{fi}}2} }}$ | (10) |
不可压缩表面摩擦系数
| ${C_{fi}} = \frac{{0.088\left( {\lg R{e_X} - 2.3686} \right)}}{{{{\left( {\lg R{e_X} - 1.5} \right)}^3}}}$ | (11) |
式(11)中
| ${C_f} = \frac{{{T_{\rm{e}}}}}{{{T^ * }}}\frac{{0.088\left( {\lg Re_x^ * - 2.3686} \right)}}{{{{\left( {\lg Re_x^ * - 1.5} \right)}^3}}}$ | (12) |
相对应的Stewartson变换等价雷诺数
| $ R{e_x} = \frac{{{\rho _{\rm{e}}}{u_{\rm{e}}}x}}{{{\mu _{\rm{e}}}}} = \frac{{{P_{\rm{e}}}{Ma_{\rm{e}}}x}}{{{\mu _{\rm{e}}}}}\sqrt {\frac{\gamma }{{R{T_{\rm{e}}}}}} $ | (13) |
| $Re_x^ * = \frac{{{\rho ^ * }{u_{\rm{e}}}x}}{{{\mu ^ * }}} = \frac{{{T_{\rm{e}}}{\mu _{\rm{e}}}}}{{{T^ * }{\mu ^ * }}}R{e_x}$ | (14) |
| $\begin{split} R{e_x} =& \dfrac{{\dfrac{{{\mu ^*}Re_x^*}}{{{\mu _0}}}}}{{\lg \left( {\dfrac{{{\mu ^*}Re_x^*}}{{{\mu _0}}}} \right) - 2.3686}} \!{\text{·}}\! \\& \left\{ {\dfrac{{{{\left[ {\lg \left( {\dfrac{{{\mu ^*}Re_x^*}}{{{\mu _0}}}} \right){\rm{ - }}1.5} \right]}^3}}}{{{{\left( {\lg Re_x^* - 1.5} \right)}^2}}} - 0.8686} \right\} \end{split}$ | (15) |
式(15)中参考温度
| ${T^ * } = 0.5{T_{\rm{w}}} + 0.22{T_{{\rm{aw}}}} + 0.28{T_{\rm{e}}}$ | (16) |
| ${\mu ^ * }{\rm{ = }}1.4580 \times {10^{ - 6}}\frac{{{T^ * }}}{{{T^*} + 110.4}}$ | (17) |
| ${\mu _0}{\rm{ = }}1.4580 \times {10^{ - 6}}\frac{{{T_0}}}{{{T_0} + 110.4}}$ | (18) |
求解可压缩表面摩擦系数
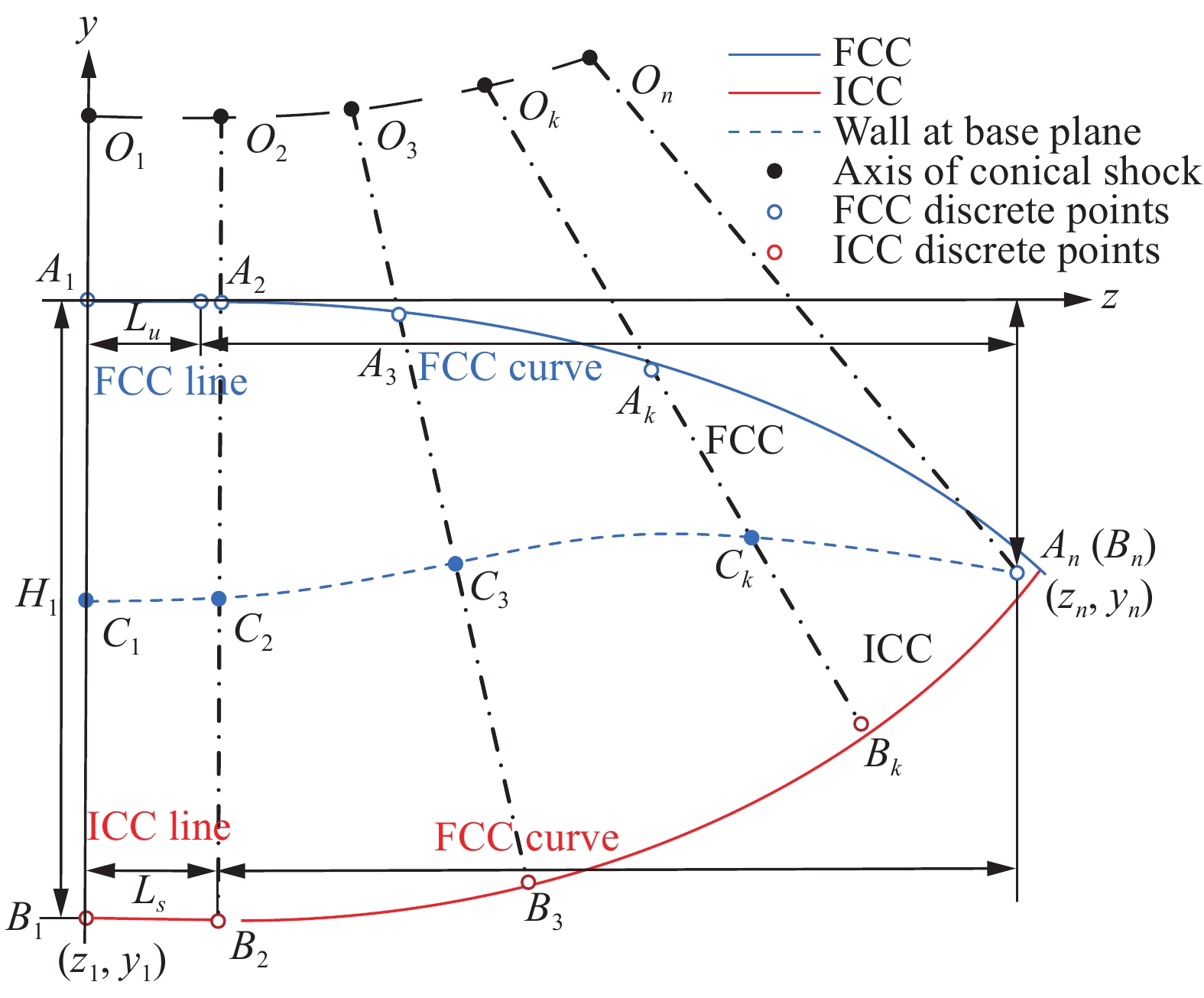
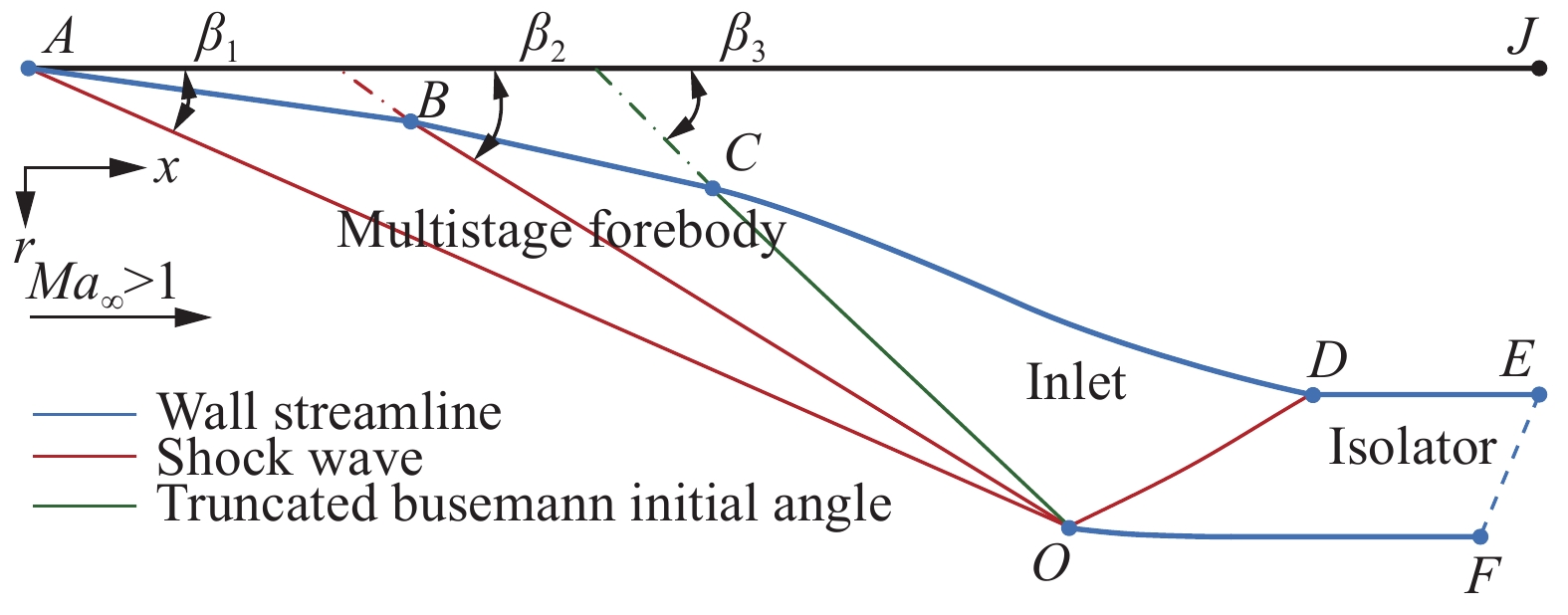
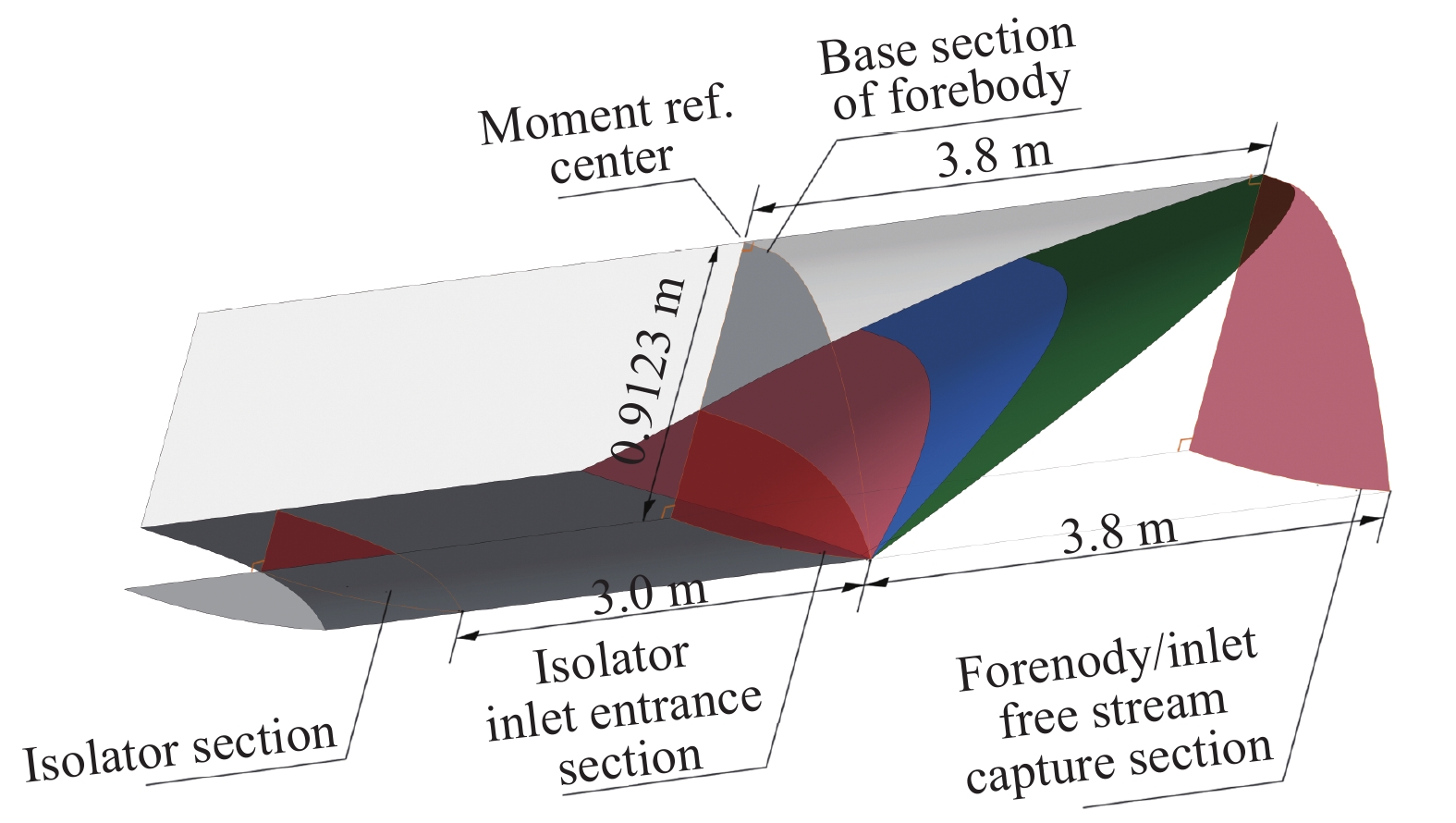
为验证边界层黏性修正方法在前体/进气道一体化乘波布局设计上的正确性以及方便后续气动性能对比分析,首先生成了具有隔离段消波设计的乘波前体/进气道耦合构型。采用吻切理论并且按照图3和式(19)构造FCC和ICC曲线,相关设计参数如表1所示。如图4所示,一体化乘波体构型包括多级压缩乘波前体、截短Busemann进气道和消波隔离段。本算例中前体压缩激波取两级且形状取直线,设计状态取(
|
图 3 吻切锥理论原理图 Fig.3 Schematic of the osculating cone |
| 表 1 吻切锥乘波体FCC和ICC设计参数 Table 1 Design parameters for FCC and ICC of the osculating-cone waverider |
|
|
|
图 4 吻切面内基准流场示意 Fig.4 Schematic of the generated flow field in an osculating plane |
| 表 2 前体/进气道构型来流与激波参数 Table 2 Parameters of the inflow and shock waves for the integrated airframe-inlet configuration |
|
|
|
图 5 乘波前体/进气道耦合构型示意 Fig.5 Schematic of the integrated airframe-inlet configuration |
限于篇幅,基于特征线法的多级乘波前体与截短Busemann进气道一体化乘波体设计方法将在另外文章中详述,本文仅生成乘波耦合构型作为黏性修正方法的验证算例。
| $\begin{array}{l} {\rm{FCC:}} \\ \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} y = 0,\;{\rm{ 0}} \leqslant z \leqslant L_u \\ y = A{\left( {z - L_u} \right)^m} + B{\left( {z - L_u} \right)^n},\;z \geqslant L_u \\ \end{array} \\ \quad {{\rm{when }}\;B \ne 0,\;{\rm{ }}AB < 0\;{\rm{ and }}\;m > n \geqslant 2} \end{array}} \right. \end{array} $ | (19) |
| $ \begin{array}{l}{\rm{ICC:}}\\ \left\{ \begin{array}{l} y = \operatorname{sign} ({y_1}){\rm{ }} \cdot H_1,\;{\rm{ 0}} \leqslant z \leqslant L_s \\ y = C{\left( {z - L_s} \right)^k}{\rm{ + }}\operatorname{sign} ({y_1}){\rm{ }} \cdot H_1,\;z \geqslant L_s \end{array} \right. \end{array} $ | (20) |
将边界层黏性修正方法应用到本文前体/进气道一体化乘波构型,生成修正位移厚度后的耦合构型,设计状态同样为(
|
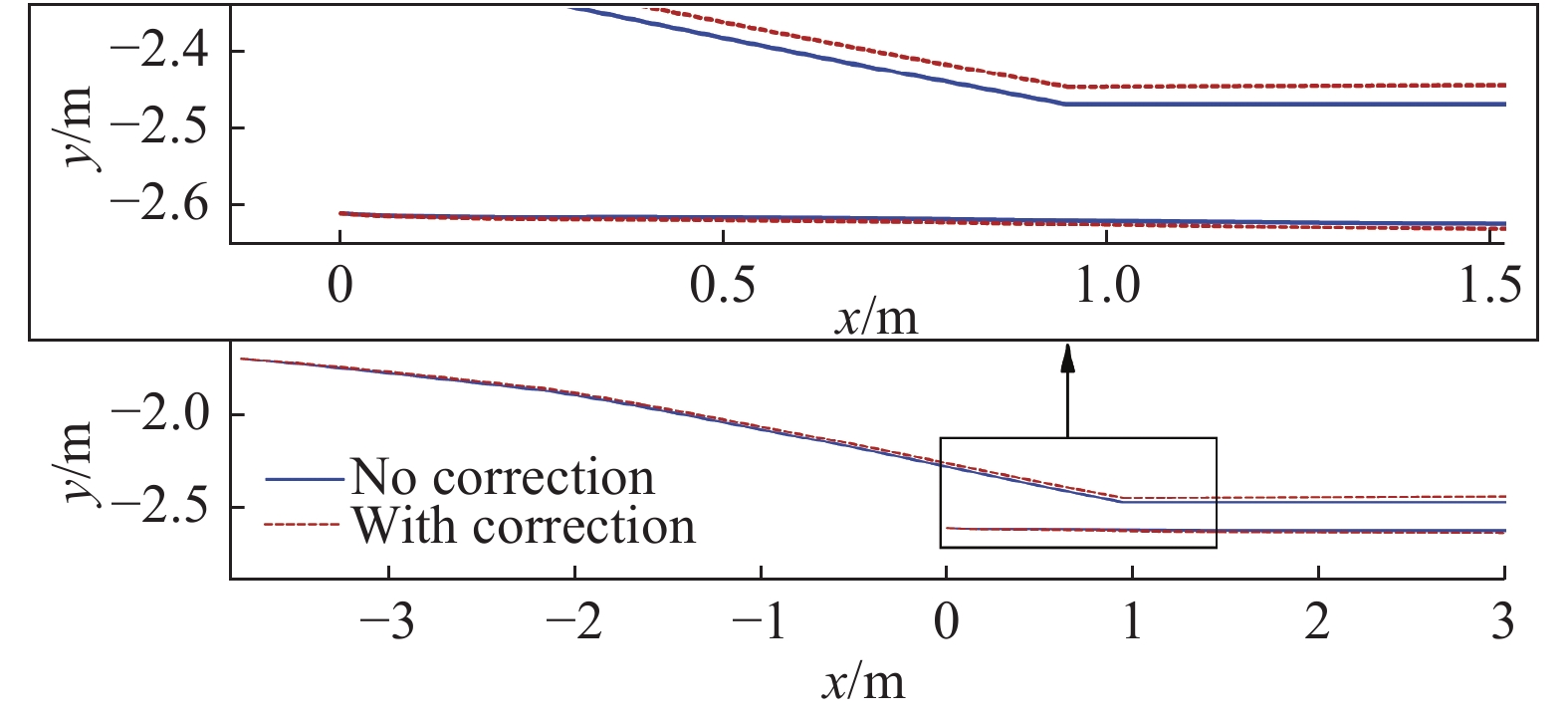
图 6 修正前后对称面型线及进气道入口局部放大 Fig.6 Comparison between outlines of the inlet in the symmetric plane before and after the correction, and its zoomed-in view |
修正前后对称面型线对比结果显示,前体/进气道上壁面相对下壁面较长,受黏性影响较为严重,修正的位移厚度明显大于下壁面的。如图5,隔离段出口截面距进气道入口截面为3 m,前体长度3.8 m,修正后构型对称面隔离段出口上壁面位移厚度最大为30.01 mm,下壁面位移厚度最大为14.69 mm,相对于上下壁面长度分别占比0.44%和0.45%。
修正前后两种构型在对称面来流捕获高度是相同的,都为912.3 mm。修正前构型在对称面隔离段出口高度为155.57 mm,修正后为200.26 mm,边界层位移厚度占比为22.32%。总压缩比由5.86变为4.56,总压缩比变化幅度同样为22.32%左右。黏性修正对隔离段几何形状以及总压缩比的影响非常巨大。
2.3 黏性修正前后流场对比验证取计算条件为设计状态(
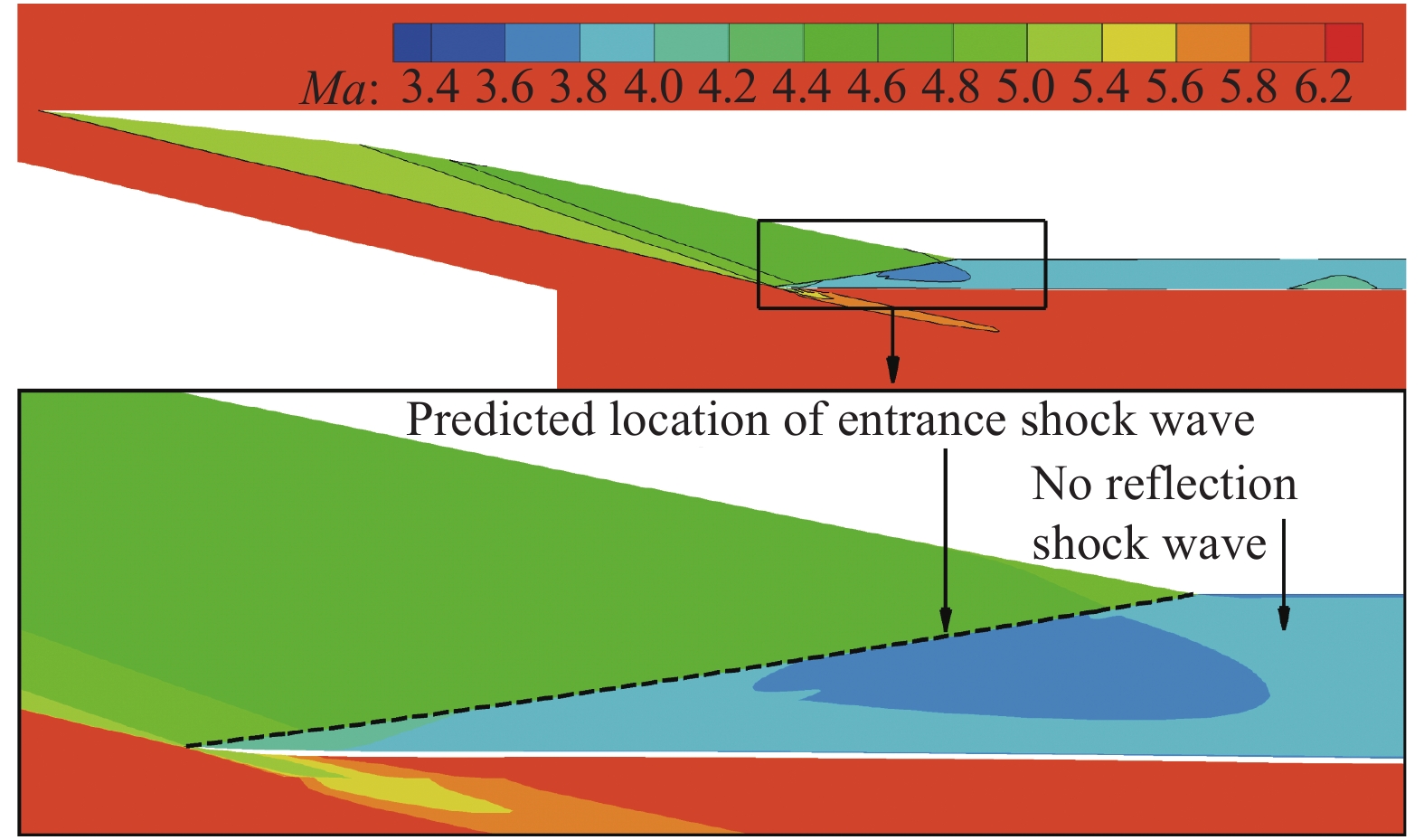
基于MOC方法生成的前体/进气道一体化乘波构型是无黏的。如图7所示,无黏性修正构型的无黏CFD数值模拟结果显示,对称面马赫数云图中进气道入口激波位置与MOC设计方法激波位置完全一致,且基本交于隔离段上壁面转折点处,隔离段内无任何反射激波且马赫数较为均匀。即在不考虑黏性的前提下,验证构型在设计状态下能够高精度地满足隔离段消波的设计目的,大大改善了隔离段流场品质,对提高隔离段出口总压及流场均匀度有极大的效果,更加有利于后续燃烧室及喷管流场性能的提升。
|
图 7 无黏性修正构型对称面无黏马赫数云图(Euler) Fig.7 Inviscid Mach number contour in the symmetric plane for the configuration without viscous correction (Euler) |
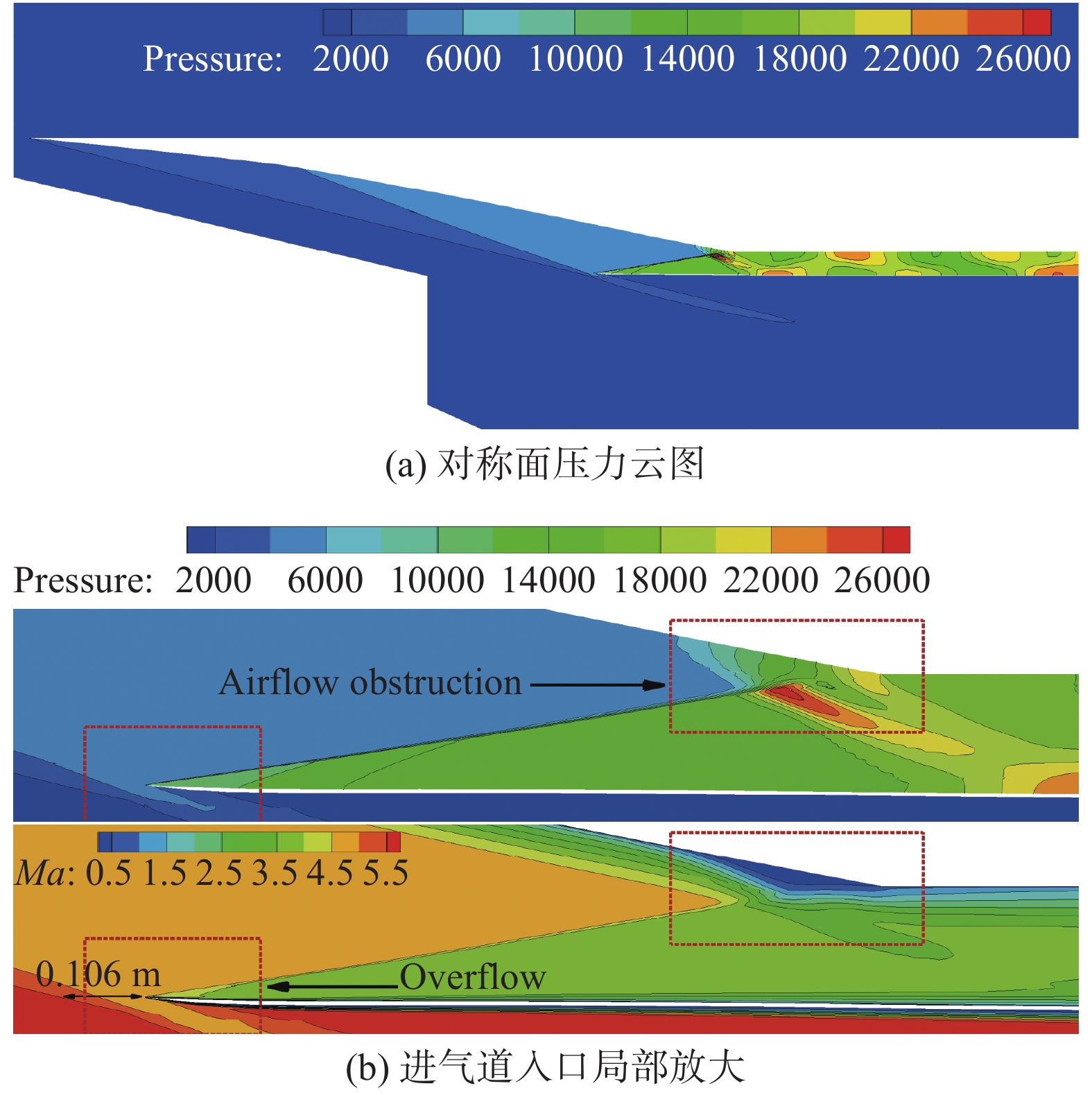
无黏性修正构型N-S方程数值模拟流场在对称面的云图如图8所示。计算结果得出:1)无黏性修正构型的两级前体激波未交于设计位置ICC处,对称面唇口处存在长度约为0.106 m的溢流区;2)通过对隔离段截面(位置参考图5,距入口截面3 m)流量积分得出前后流量比为93.38%,相对于无黏设计状态将近100%流量比,有小部分的损失;3)压强云图显示隔离段入口上壁面存在一个高压低速的气流堵塞区,马赫数云图显示该堵塞区域在对称面入口上壁面高度大约为22 mm左右,高度大致与边界层厚度相同;4)图8(a)压力云图显示,堵塞区进而导致隔离段较强的压力脉动,效果类似于多次反射的激波串,对流场均匀度以及总压造成较大的损失,隔离段截面处流场参数积分得出总压恢复系数为38.24%。
|
图 8 无黏性修正构型对称面流场云图(N-S) Fig.8 Flow field in the symmetric plane for the configuration without viscous correction (N-S) |
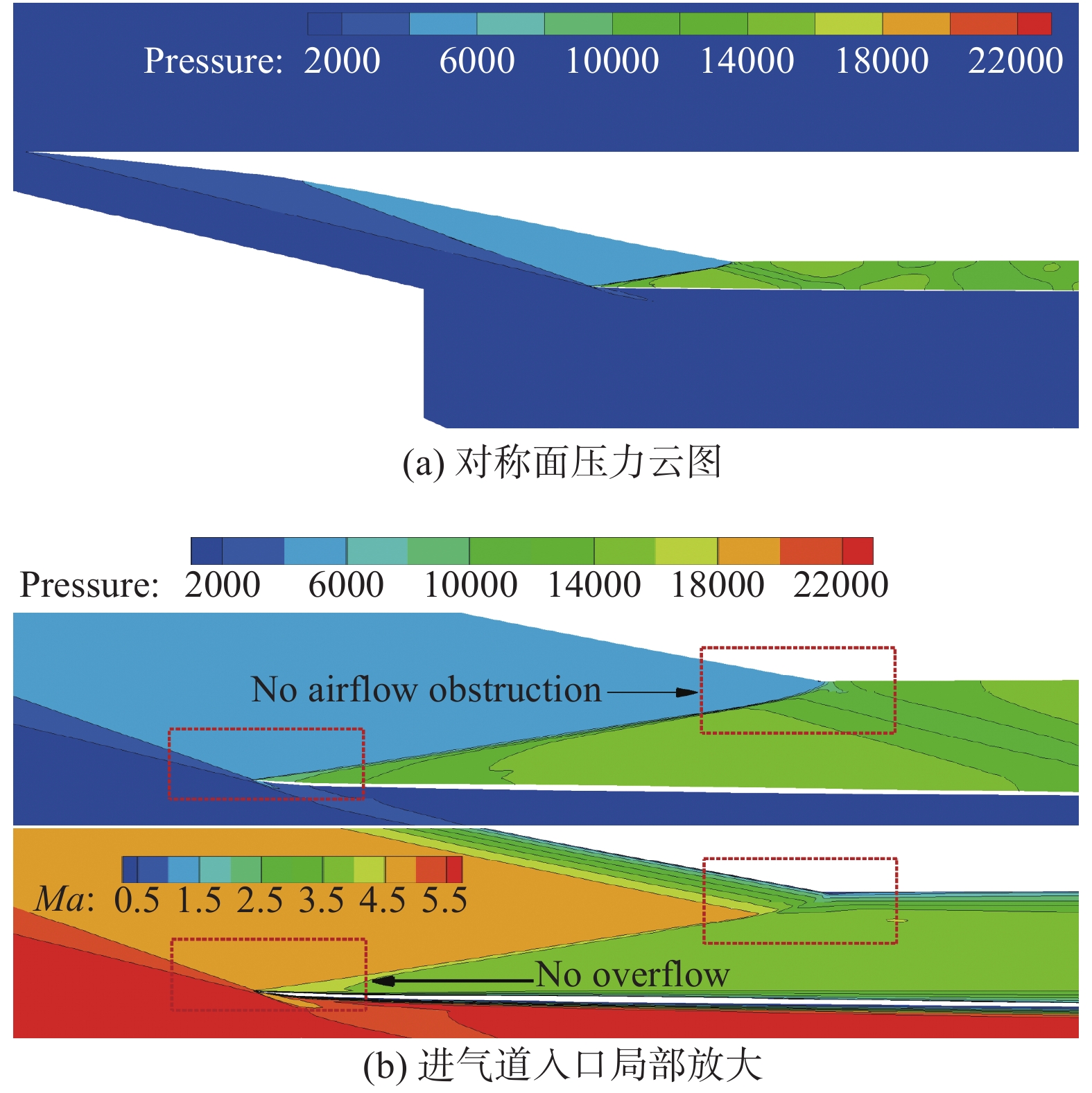
黏性修正构型N-S方程数值模拟流场在对称面的云图如图9所示。计算结果得出:1)黏性修正构型的前体两级激波基本汇交于设计位置ICC曲线处;2)通过对隔离段截面流量积分得出黏性修正后设计状态流量比为97.89%,溢流损失基本可以忽略,相对修正前提升了4.51%;3)图9(b)进气道入口局部放大图显示,入口激波吻合设计位置且交于隔离段上壁面转折点处,基本达到隔离段消波的设计目标,改善了未修正前入口气流堵塞的现象;4)隔离段截面处总压恢复系数为46.47%,相对未修正前提升了8.23%;5)马赫数云图显示除了边界层以外整个隔离段马赫数较为均匀,流场品质大为改善,有利于后续燃烧室及喷管性能的提升。黏性修正对进气道和隔离段流场品质及部分关键参数提升较为明显。
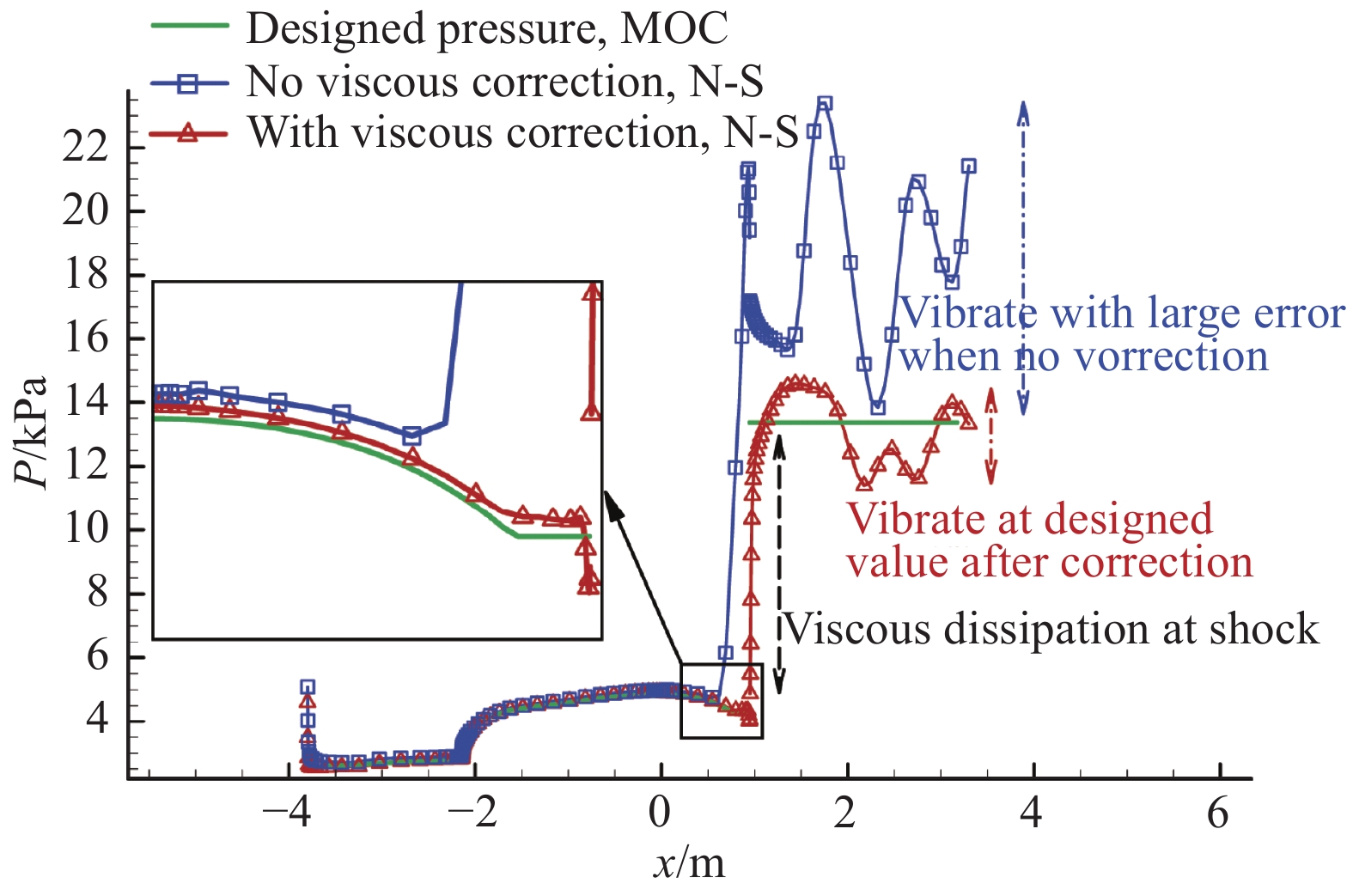
提取黏性修正前后两种构型在对称面上壁面的N-S方程数值模拟压强与特征线法设计状态压强对比如图10所示,图中红色曲线为黏性修正构型对称面物面压强,蓝色曲线为未修正构型物面压强。结果显示:1)由于黏性耗散的影响,激波前后物面的气动参数是连续的,在激波处物面压强与设计值有一定误差,但是激波厚度较小,对整体性能影响有限;2)无论黏性边界层是否修正,在前体两级压缩面和截短Busemann压缩面,两种构型有黏压强与设计值都比较吻合,但是黏性修正构型相比于未修正构型压强吻合度更加精确;3)无黏性修正构型在靠近入口反射激波位置误差较为明显,严重偏离设计值,而黏性修正构型在靠近入口反射激波的进气道物面压强仍然与设计值高度吻合;4)由于网格相关性以及黏性影响,隔离段物面压强数值模拟结果不可避免呈波动状态。黏性边界层未修正构型在隔离段的压强波动范围较大且无规律可循,与设计值存在较大误差,但是修正后构型隔离段物面压强波动幅度明显减小,最为重要的是波动范围稳定在设计值附近,验证了可压缩冯•卡门动量方程黏性边界层修正方法的适用性。
|
图 9 黏性修正构型对称面流场云图(N-S) Fig.9 Flow field in the symmetric plane for the configuration with viscous correction (N-S) |
|
图 10 黏性修正前后N-S及MOC在对称面的压强对比 Fig.10 Pressure in the symmetric plane compared among uncorrected, corrected and MOC cases |
综上,在多级压缩乘波体前体与截短Busemann进气道部分,即入口反射激波前的单纯外流乘波构型部分,黏性边界层修正前后,两构型外流部分流场参数都与设计值较为吻合,但是黏性修正能进一步大幅提升外流乘波构型的精度。在入口反射激波后的隔离段内流部分,尤其是有隔离段消波设计的乘波耦合构型内流部分,无黏性修正构型内流流场品质较差且大幅偏离设计值,隔离段内存在多次反射激波,而黏性修正构型内流部分基本与设计值吻合,达到隔离段消波目的,流场品质较高。因此,对包含进气道和隔离段的内外流一体化乘波构型进行边界层黏性修正是非常有必要的。
3 黏性修正前后气动性能对比对本文中多级乘波前体与截短Busemann进气道耦合构型进行边界层黏性修正前后的两种构型进行有黏的CFD数值模拟和部分气动性能参数的对比,计算状态包括马赫数范围(5、6、7)和迎角范围(0°、2°、4°、6°),来流参数为海拔30 km大气条件。计算分析的气动性能参数包括隔离段截面(距进气道入口截面3 m)的流量比
| $\boldsymbol{F} = \int_0^S {\left( {P - {P_\infty }} \right)} {\rm{ d}}\boldsymbol{S}$ | (21) |
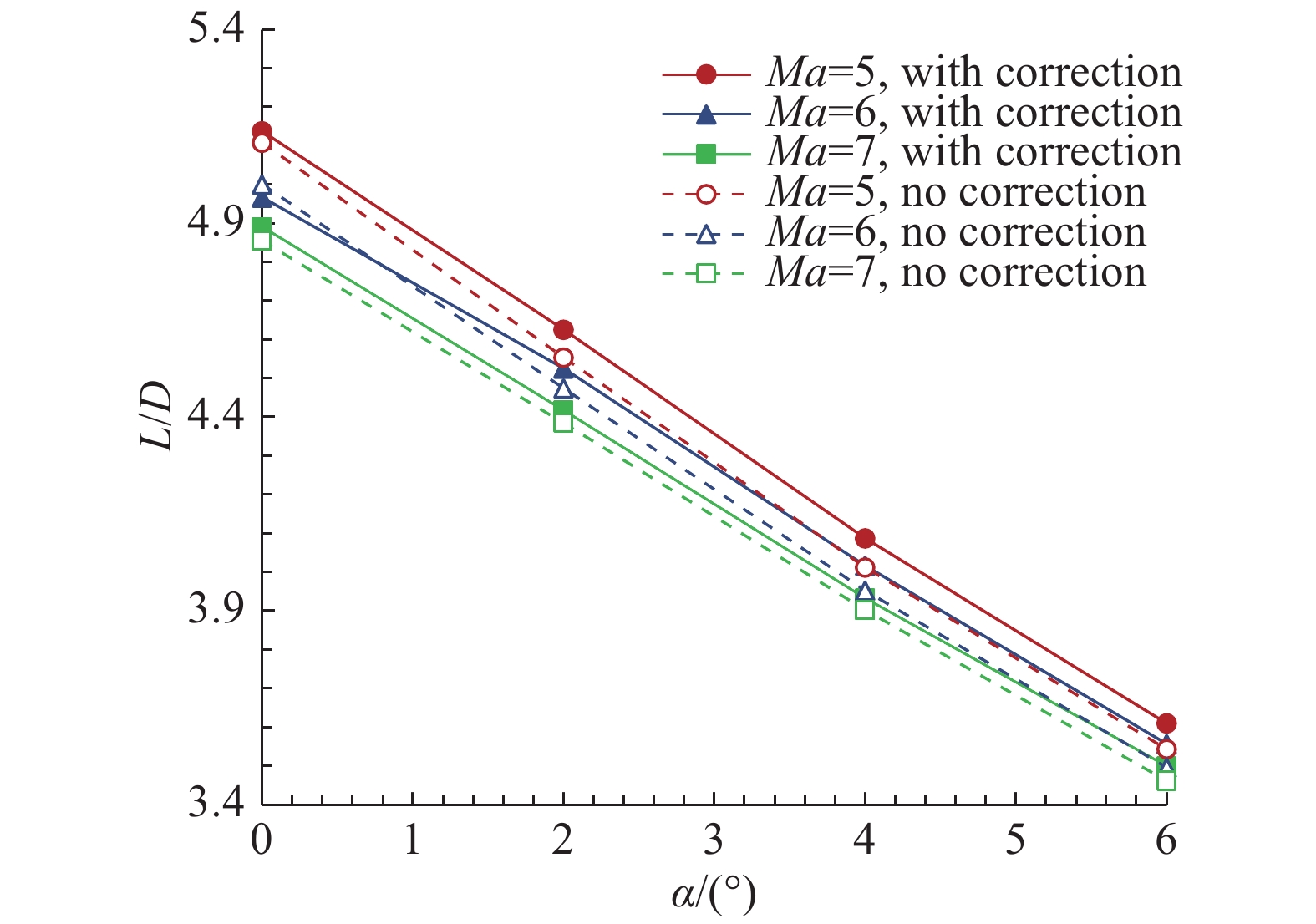
如图11所示,N-S方程数值模拟结果显示,边界层黏性修正前后,两种构型前体/进气道升阻比基本一致。在设计状态下(
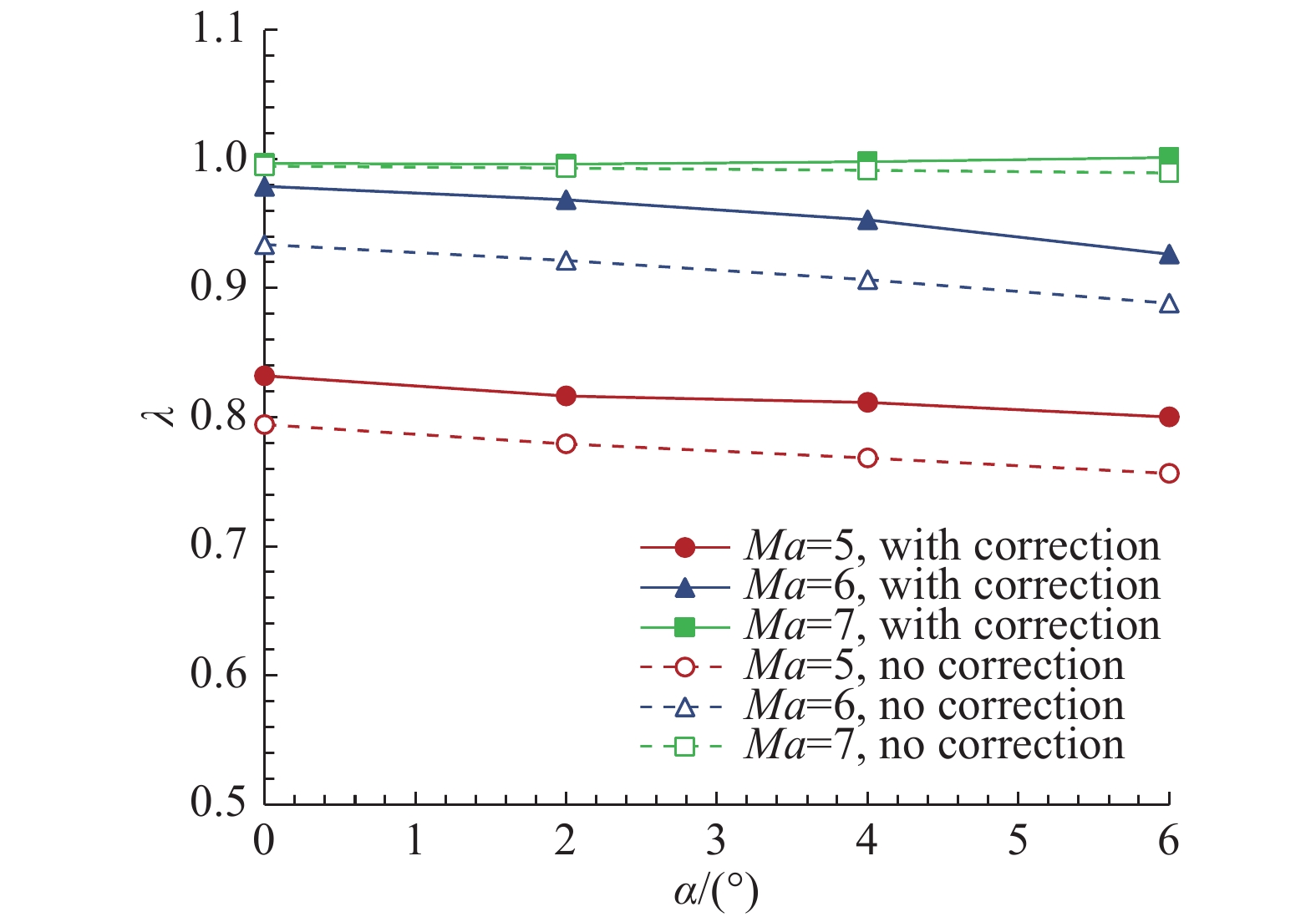
图12显示,在大于设计马赫数时,因为前体激波汇交到进气道入口内部,两种构型流量比都接近100%,即基本无溢流;在等于和小于设计马赫数时,黏性修正后构型流量比明显大于未修正构型,提升幅度在4%~5%之间。
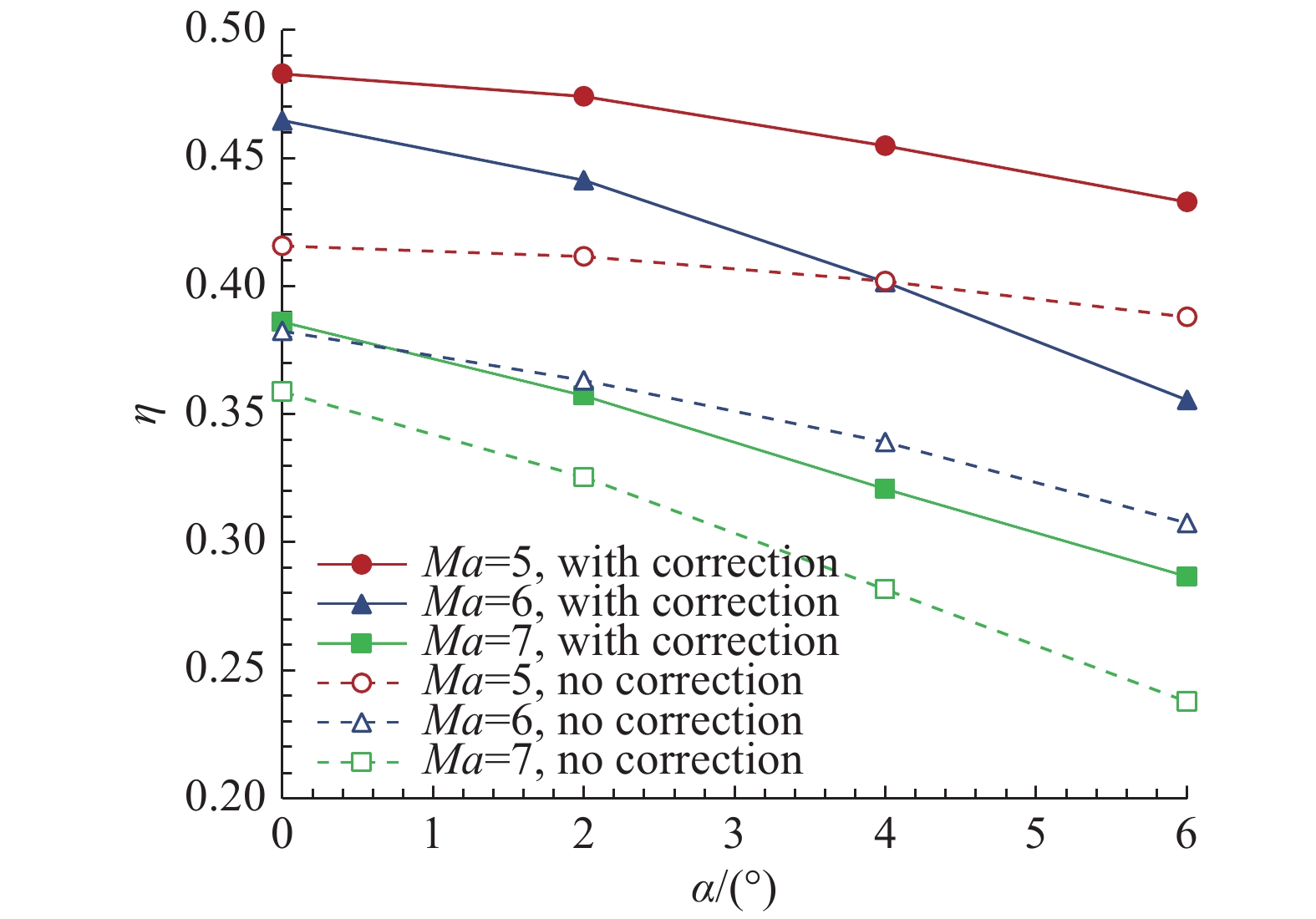
图13显示,由于黏性和激波的影响,吸气式高超声速飞行器在隔离段出口总压一般会有较大损失,以设计状态为例,未修正构型距入口3 m处隔离段截面的总压恢复系数为38.24%,黏性修正构型通过消除(设计状态)和减弱(非设计状态)隔离段反射激波串大幅降低了隔离段内的总压损失,边界层厚度修正后,设计状态对应总压恢复系数为46.465%,其他非设计状态同样有较大的总压提升。
|
图 11 黏性修正前后两构型升阻比对比(N-S) Fig.11 Lift-to-drag ratio compared before and after viscous correction (N-S) |
|
图 12 黏性修正前后两构型流量比对比(N-S) Fig.12 Flowrate ratio compared before and after viscous correction (N-S) |
|
图 13 黏性修正前后两构型总压恢复系数对比(N-S) Fig.13 Total pressure recovery coefficient compared before and after viscous correction (N-S) |
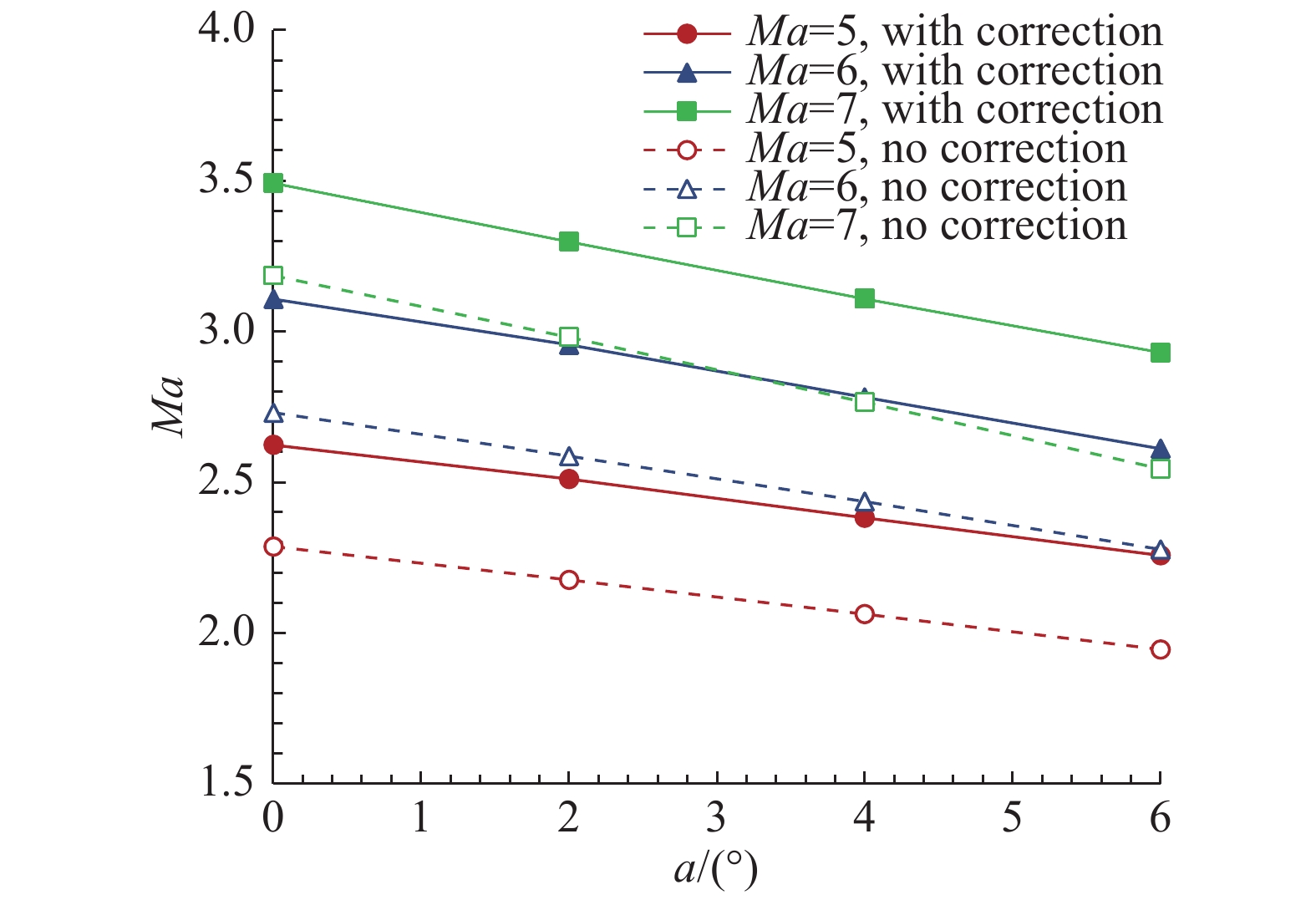
图14显示,黏性修正构型隔离段截面平均马赫数大于未修正构型,这是因为减去边界层位移厚度后,总体压缩比减小,压缩能力有一定的下降。但是总体趋势上,修正后构型仍然有较强的压缩能力,设计来流马赫数为6时,0°迎角隔离段截面上平均马赫数为3.1,6°迎角时平均马赫数可压缩至2.6。
|
图 14 黏性修正前后两构型平均马赫数对比(N-S) Fig.14 Mean Mach number comparised before and after viscous correction (N-S) |
综上,边界层黏性修正后,前体/进气道耦合构型压缩能力小幅下降,但是升阻比有小幅提升,流量比大幅提升,对来流捕获能力更强,隔离段出口总压损失更小。修正后乘波构型气动性能一定程度上得到提升。
4 结 论针对单纯流线追踪得到的前体/进气道一体化乘波布局在黏性状态下隔离段内存在较大误差的问题,发展了一种适用于多级波系锥导或吻切锥乘波体的边界层黏性修正方法。对修正前后的前体/进气道一体化构型进行了设计状态下的流场对比验证以及非设计状态下给定马赫数和迎角范围下的气动性能对比分析。相关结论如下:
1)在基于特征线法的多级前体与截短Busemann进气道一体化乘波布局设计方法基础上,耦合了高超声速可压缩轴对称流动的冯•卡门动量方程积分方法,进行多级波系乘波布局的边界层黏性修正。设计状态下,修正后乘波构型流场中多道激波位置和物面压强与设计预期基本一致,数值模拟结果验证了修正方法的精确性。
2)设计状态下,相对于黏性修正前的一体化乘波构型,修正后构型进一步提升了外流部分流场与设计值的吻合度,减少了进气道溢流,进气道入口流量比提升了4.51%;在内流部分流场,大幅减小了物面压强相对于设计值的误差,达到了消除隔离段多次反射激波的目的,隔离段出口总压恢复系数提升了8.23%。发展的边界层黏性修正方法对包含进气道尤其是消波隔离段的内外流一体化乘波构型具有一定的优异性和必要性。
3)非设计状态下在给定的马赫数和迎角范围内,相对于未修正构型,黏性修正后的前体/进气道耦合构型压缩能力小幅下降,但是升阻比有小幅提升,流量比大幅提升,来流捕获能力更强,隔离段出口总压损失更小。黏性修正后乘波构型气动性能一定程度上得到提升。
| [1] |
王江峰, 王旭东, 李佳伟, 等. 高超声速巡航飞行器乘波布局气动设计综述[J]. 空气动力学学报, 2018, 36(5): 705-728. WANG J F, WANG X D, LI J W, et al. Overview on aerodynamic design of cruising waverider configuration for hypersonic vehicles[J]. Acta Aerodynamica Sinica, 2018, 36(5): 705-728. DOI:10.7638/kqdlxxb-2017.0117 (in Chinese) |
| [2] |
张华军, 郭荣伟, 李博. TBCC进气道研究现状及其关键技术[J]. 空气动力学学报, 2010, 28(5): 613-620. ZHANG H J, GUO R W, LI B. Research status of TBCC inlet and its key technologies[J]. Acta Aerodynamica Sinica, 2010, 28(5): 613-620. DOI:10.3969/j.issn.0258-1825.2010.05.022 (in Chinese) |
| [3] |
WANG X D, WANG J F, LYU Z J. A new integration method based on the coupling of mutistage osculating cones waverider and Busemann inlet for hypersonic airbreathing vehicles[J]. Acta Astronautica, 2016, 126: 424-438. DOI:10.1016/j.actaastro.2016.06.022 |
| [4] |
朱旭程, 侯志强, 李日华. 基于样条曲线的乘波体外形优化方法[J]. 空气动力学学报, 2007, 25(3): 396-399. ZHU X C, HOU Z Q, LI R H. Spline-based waverider configuration optimization method[J]. Acta Aerodynamica Sinica, 2007, 25(3): 396-399. DOI:10.3969/j.issn.0258-1825.2007.03.022 (in Chinese) |
| [5] |
吕侦军, 王旭东, 季卫栋, 等. 三级压缩锥导乘波体设计技术与实验分析[J]. 实验流体力学, 2015(5): 38-44. LYU Z J, WANG X D, JI W D, et al. Design and experimental analysis of three-stage compression cone-derived waverider[J]. Journal of Experiments in Fluid Mechanics, 2015(5): 38-44. DOI:10.11729/syltlx20150003 (in Chinese) |
| [6] |
吕侦军, 王江峰. 多级压缩锥导/吻切锥乘波体设计与对比分析[J]. 北京航空航天大学学报, 2015, 41(11): 2103-2109. LYU Z J, WANG J F. Design and comparative analysis of multistage compression cone-derived waverider and osculating cone waverider[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(11): 2103-2109. DOI:10.13700/j.bh.1001-5965.2014.0740 (in Chinese) |
| [7] |
RASMUSSEN M L. Waverider configurations derived from inclined circular and elliptic cones[J]. Journal of Spacecraft and Rockets, 1980, 17(6): 537-545. DOI:10.2514/3.57771 |
| [8] |
LIN S C, RASMUSSEN M L. Cone-derived waveriders with combined transverse and longitudinal curvature[C]//26th Aerospace Sciences Meeting, Reno, NV. Reston, Virginia: AIAA, 1988. AIAA 88-0371.doi: 10.2514/6.1988-371
|
| [9] |
尤延铖, 梁德旺. 内乘波式进气道内收缩基本流场研究[J]. 空气动力学学报, 2008, 26(2): 203-207. YOU Y C, LIANG D W. Investigation of internal compression flowfield for internal waverider-derived inlet[J]. Acta Aerodynamica Sinica, 2008, 26(2): 203-207. DOI:10.3969/j.issn.0258-1825.2008.02.012 (in Chinese) |
| [10] |
吴颖川, 贺元元, 贺伟, 等. 基于密切曲锥的乘波构型一体化飞行器设计方法研究[J]. 空气动力学学报, 2014, 32(1): 8-13. WU Y C, HE Y Y, HE W, et al. The design of osculating curved cone waverider based hypersonic vehicle[J]. Acta Aerodynamica Sinica, 2014, 32(1): 8-13. DOI:10.7638/kqdlxxb-2012.0054 (in Chinese) |
| [11] |
DING F, LIU J, SHEN C B, et al. Novel approach for design of a waverider vehicle generated from axisymmetric supersonic flows past a pointed von Karman ogive[J]. Aerospace Science and Technology, 2015, 42: 297-308. DOI:10.1016/j.ast.2015.01.025 |
| [12] |
李博, 梁德旺. 一种基于三维黏性流场的乘波体生成方法[J]. 空气动力学学报, 2005, 23(4): 464-469. LI B, LIANG D W. A design method of waveriders derived from 3D viscous flow[J]. Acta Aerodynamica Sinica, 2005, 23(4): 464-469. DOI:10.3969/j.issn.0258-1825.2005.04.013 (in Chinese) |
| [13] |
陈冰雁, 刘传振, 纪楚群. 基于激波装配法的乘波体设计与分析[J]. 空气动力学学报, 2017, 35(3): 421-428. CHEN B Y, LIU C Z, JI C Q. Waverider design and analysis based on shock-fitting method[J]. Acta Aerodynamica Sinica, 2017, 35(3): 421-428. DOI:10.7638/kqdlxxb-2017.0039 (in Chinese) |
| [14] |
ANDERSON J D JR. Fundamentals of Aerodynamics[M]. Fourth Edition. New York: McGraw Hill Companies, Inc., 2006: 878-879.
|
| [15] |
YU K K, XU J L, GONG H, et al. Inverse design methodology of cone-derived waverider based on pre-defined shock wave under strong geometric constraints[J]. Acta Astronautica, 2019, 159: 527-539. DOI:10.1016/j.actaastro.2019.02.011 |
| [16] |
CHEN S H, LIU J, DING F, et al. Novel design methodology of integrated waverider with drip-like intake based on planform leading-edge definition method[J]. Acta Astronautica, 2020, 167: 314-330. DOI:10.1016/j.actaastro.2019.11.007 |
| [17] |
LIU J, LIU Z, WEN X, et al. Novel osculating flowfield methodology for wide-speed range waverider vehicles across variable Mach number[J]. Acta Astronautica, 2019, 162: 160-167. DOI:10.1016/j.actaastro.2019.05.056 |
| [18] |
CHEN L L, DENG X L, GUO Z, et al. A novel approach for design and analysis of volume-improved osculating-cone waveriders[J]. Acta Astronautica, 2019, 161: 430-445. DOI:10.1016/j.actaastro.2019.02.033 |
| [19] |
SIVELLS J C, PAYNE R. A method of calculating turbulent-boundary-layer growth at hypersonic Mach numbers[R]. AEDC-TR-59-3, 1959.doi: 10.21236/ad0208774
|



