2. 清华大学,北京 100084;
3. 中国船舶科学研究中心,无锡 214082
2. Tsinghua University, Beijing 10084, China;
3. China Ship Scientific Research Center, Wuxi 214082, China
格子Boltzmann方法(Lattice Boltzmann Method, LBM)[1]是计算流体力学中一种重要的数值方法。不同于传统的宏观方法和微观模型方法,LBM结合了介观动理学以及微观模型的特点,拥有很多独特的优势,如编程简单、具有天生的并行性、物理背景清晰等。近年来,LBM在很多领域都得到了广泛应用,如多孔介质流[2-3]、多相流[4]、燃烧[5]、湍流[6]问题等。LBM计算的模型也从方腔、圆柱等简单几何体变为飞机机翼、汽车、动车等形状十分复杂的几何体,而精确快速的几何前处理是实现LBM计算工程应用的前提条件。
目前,CAD(Computational Aided Design)软件在汽车、轮船等领域得到了广泛应用,在此基础上,人们制定了很多通用的数据格式。流体计算中模型生成的文件是立体光刻(Stereolithographic, STL)数据类型,该通用数据文件格式是为了在不同的软件、不同的用途之间进行模型数据交换。这种文件格式在快速成型(Rapid Prototyping, RP)技术中有着广泛的应用,尤其是3D打印中。基于哈希表的拓扑重构算法能够快速的重建拓扑结构[7]、基于分层的优化算法[8-9]能够提高STL文件分层效率。文献[10]主要对在3D打印过程中模型支撑架的设计提出算法,使得模型重建易于实现。文献[11]对模型的表面进行了拟合,使其更加平滑。文献[12]基于自适应层深度法向图像针对模型重建问题提出了一个有效的方法。文献[13]能够很好地识别模型的轮廓,以及判定外轮廓以及内轮廓。Michael等[14]以八叉树为基本数据结构,对GPU的特点提出了并行算法。文献[15]对三维多边形网格的26-邻接体素模型提出了快速算法。
在利用LBM方法进行流体力学计算的过程中,物面边界的处理通常有三种方法:浸没边界法、插值曲面边界、阶梯状近似的直接反弹法。三种方法中前两种精度较高,但处理相对复杂,后一种精度稍低但处理简单,数值稳定性好,非常适合超大规模并行计算,在网格数量足够的情况下同样可以获得准确的结果。本文主要针对直接反弹法设计LBM的前处理算法。直接反弹法中需要用到流体计算区域内的格点相对模型的位置关系,判断计算流体点是在物体内部、表面或者外部。LBM计算过程中物体外部点为流场点实施正常的碰撞迁移操作,内部点为固体点不参与计算,表面点为物面边界点实施反弹操作。
为了能够根据STL几何文件得到LBM计算所需的格点类型信息,完成LBM计算的前处理,本文提出了一种快速、高效、准确的方法。该算法主要目标是精简计算量,提高计算效率,并能保证计算流体模型能够很好地还原原始物体几何特征。关键点包括:
(1) 读取通用的物体模型文件即STL文件,利用STL文件存储的信息生成物体原始模型;
(2)通过任意视角(视角指x、y、z三个方向)得到物体的边界点,此边界点是计算区域的格点,根据边界点重构几何计算模型;
(3) 通过优化判别方法,减少计算量,提高边界点判定的效率;
(4)算法本身具有良好的并行性,为以后程序的并行提供了基础。
1 STL文件格式STL文件格式是由3D SYSTEMS公司在1988年制定的一个标准接口协议,是大多数CAD软件通用的文件格式。STL文件由多个三角形面组合而成。其类型可以进一步分为文本文件(ASCII格式)和二进制文件(BINARY)。
(1)二进制文件格式。二进制文件利用固定的字符长度来给出三角面片的几何信息。前80个字节存储几何相关的注释信息。随后存储三角形的总数目,之后存储每个三角形的法向量坐标、根据右手法则排列的三角形顶点信息,两两三角形信息之间由两个空格分开。该格式相对于文本文件格式更加简洁,占用磁盘空间更少,后期对文件的操作相对更方便。
(2)文本文件格式。文本格式第一行以solid开始,最后一行以endsolid标识。中间部分每7行存储一个三角形的信息。首先存储三角形法向量的三个坐标,然后按照右手法则依次存储三角形三个顶点的坐标信息。这种格式存储直观,程序读取方便。本文方法主要基于文本文件格式开展。
2 快速生成流体计算模型算法计算模型重建的主要目的是得到计算区域内各网格点的类型。格点类型可分为几何体内部点、几何体外部点、几何体边界点。目前比较常用的方法有:
(1)数学表达式法。主要针对规则的几何形状,如球、立方体、椭球等能用数学表达式直接表示的几何外形。这种方法可以根据表达式直接得到格点的类型,效率最高。但是它适用范围很窄,无法较好解决现实中的复杂问题。
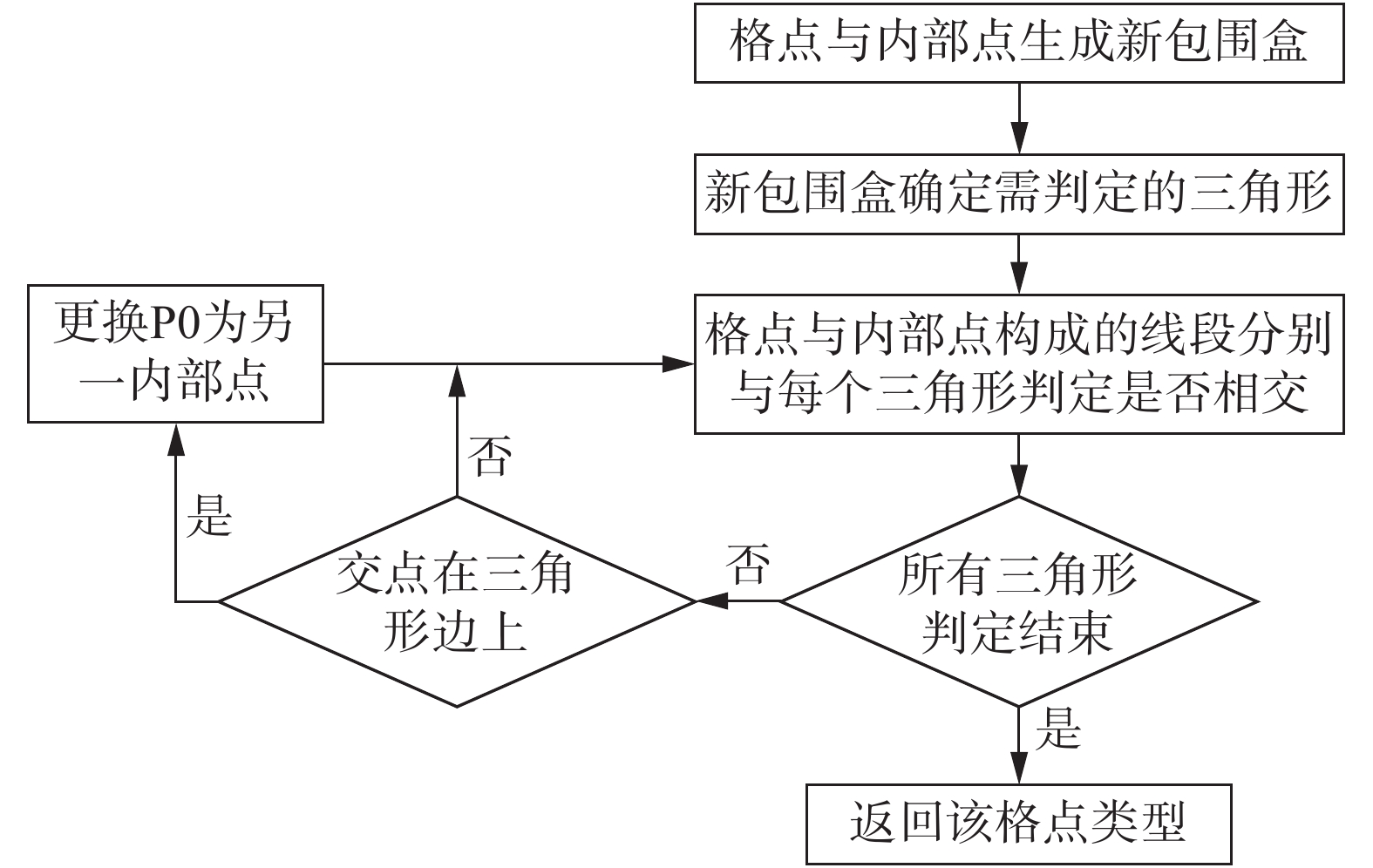
(2)直接法。例如文献[16]中实现模型的重建过程都是利用的直接法。它首先找到一个比几何体要大的包围盒把几何体包住,然后在这个包围盒中遍历所有的格点并对这些格点进行判断,包围盒外部所有的格点都是几何体外部点。在对包围盒中格点的遍历中,需要根据格点与所有的STL文件中三角形的位置关系来判断这个格点是几何内部点或者是几何外部点。遍历完所有格点后,就可以得到计算区域内几何体的模型。
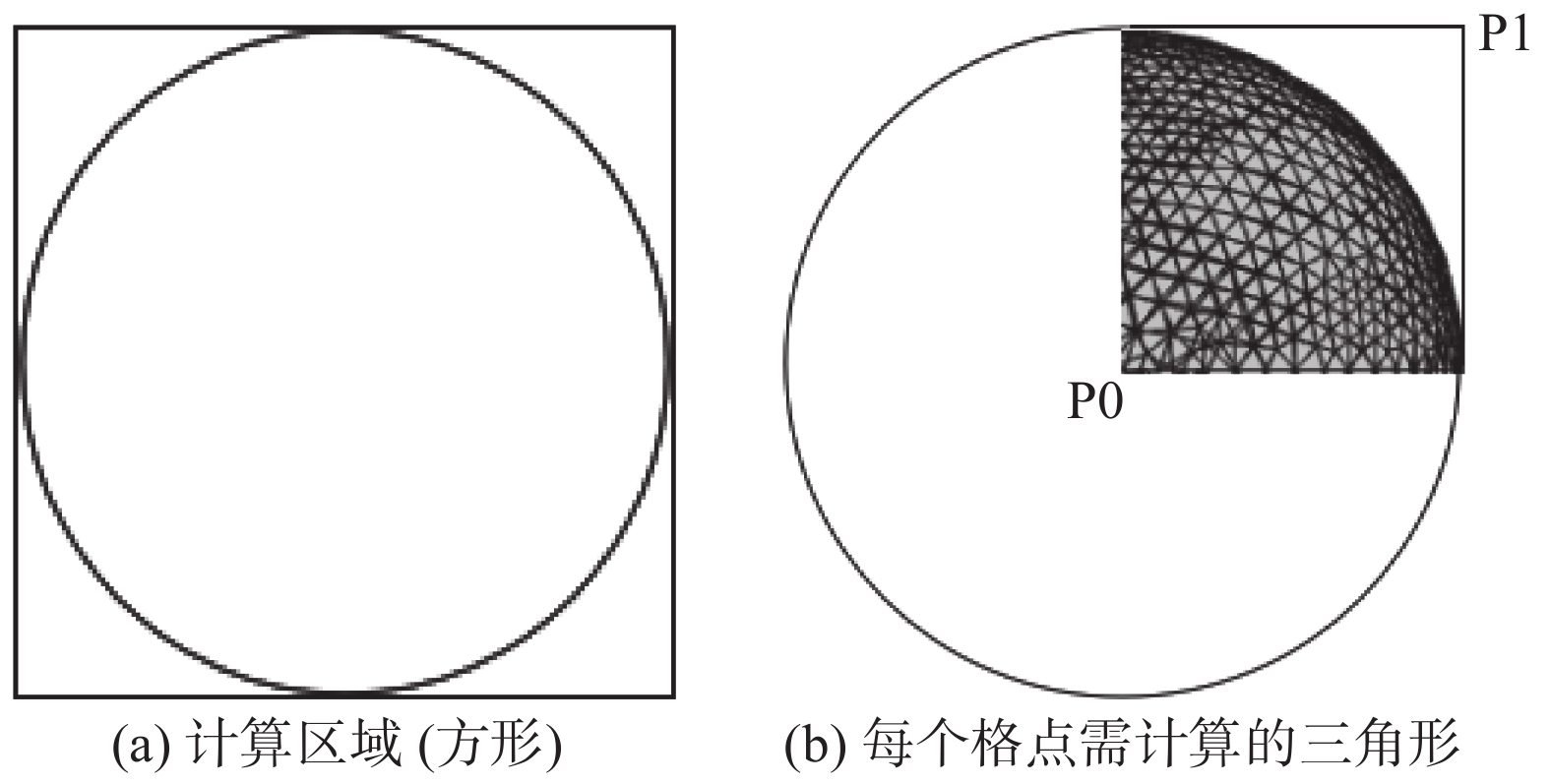
图1(a)中,方形区域内的格点为需要计算的格点范围,图1(b)展示的是圆球模型中对一个格点P1位置判定过程所有需要计算的三角形。为了显示的直观性,图中给出的是圆球的一个投影面。其中,图1(b)中P1点是需判定的格点,P0是模型内部任意一点,因为圆球的对称性,因此P0点选为球心。图2是直接法判定格点类型的流程图。
|
图 1 直接法示意图 Fig.1 Schematic of the direct method |
|
图 2 格点类型判断流程图 Fig.2 Flowchart for the grid type identification |
直接法可以直接得到流场内所有网格点的类型,但由于其遍历次数的影响,在几何体面网格复杂和计算区域较大的情况下,该方法的时间消耗很大,会占用流体计算过程的很大部分,影响了整个程序的效率。
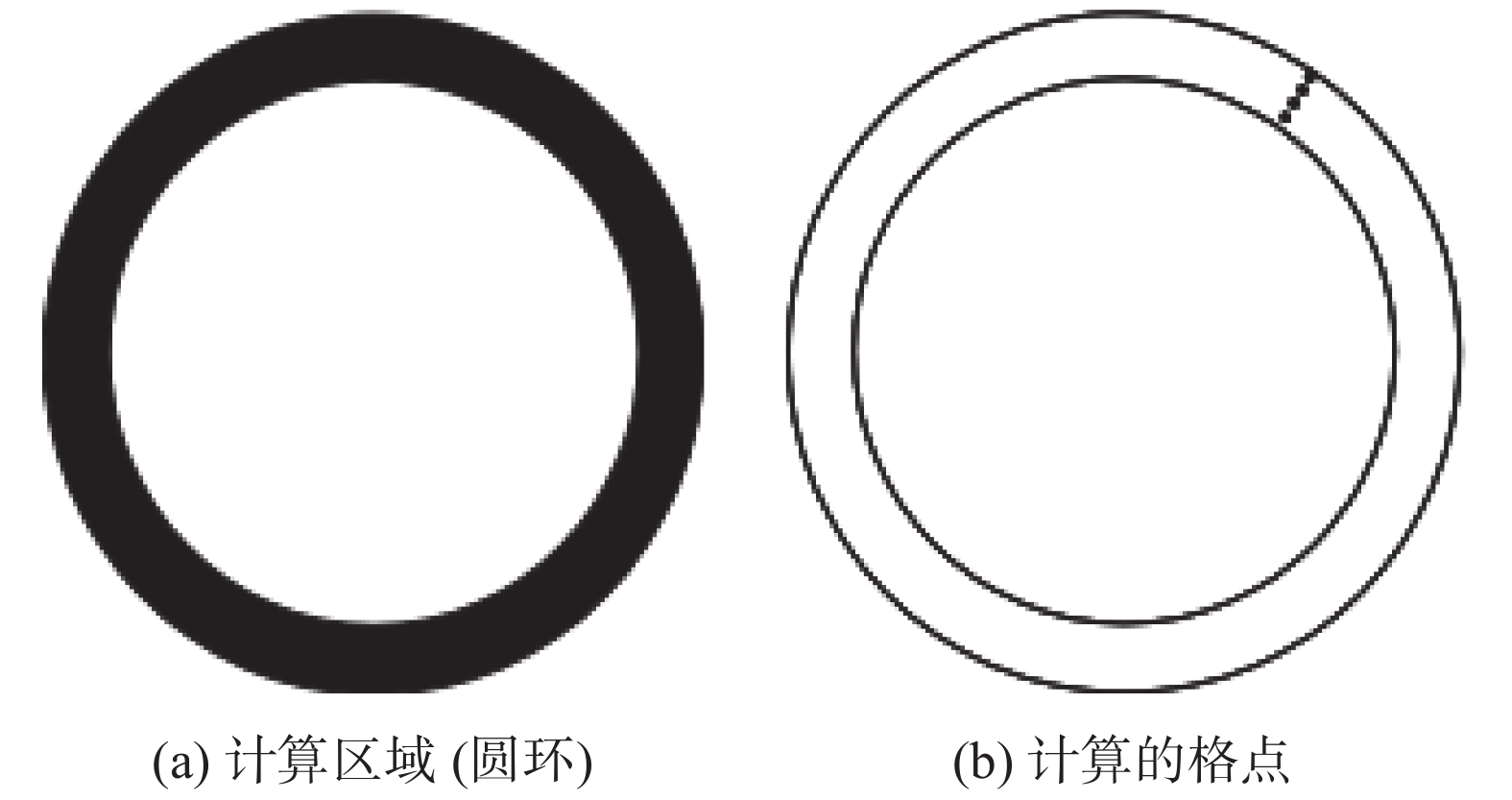
(3)本文方法。本文提出了一种快速生成流体计算模型的算法。图3(a)中阴影区域是计算格点区域。图3(b)圆环中格点是需要计算的格点。只需要计算格点距离模型(内圆)的距离,最近的格点即为所求边界点。图3(a)中,需要计算的格点均位于黑色圆环区域,该区域远小于直接法的方形区域。图3(b)中的黑点是需要计算的格点,其在数量上也小于直接法的面三角形数。
|
图 3 本文提出的算法示意图 Fig.3 Schematic of the algorithm proposed in this study |
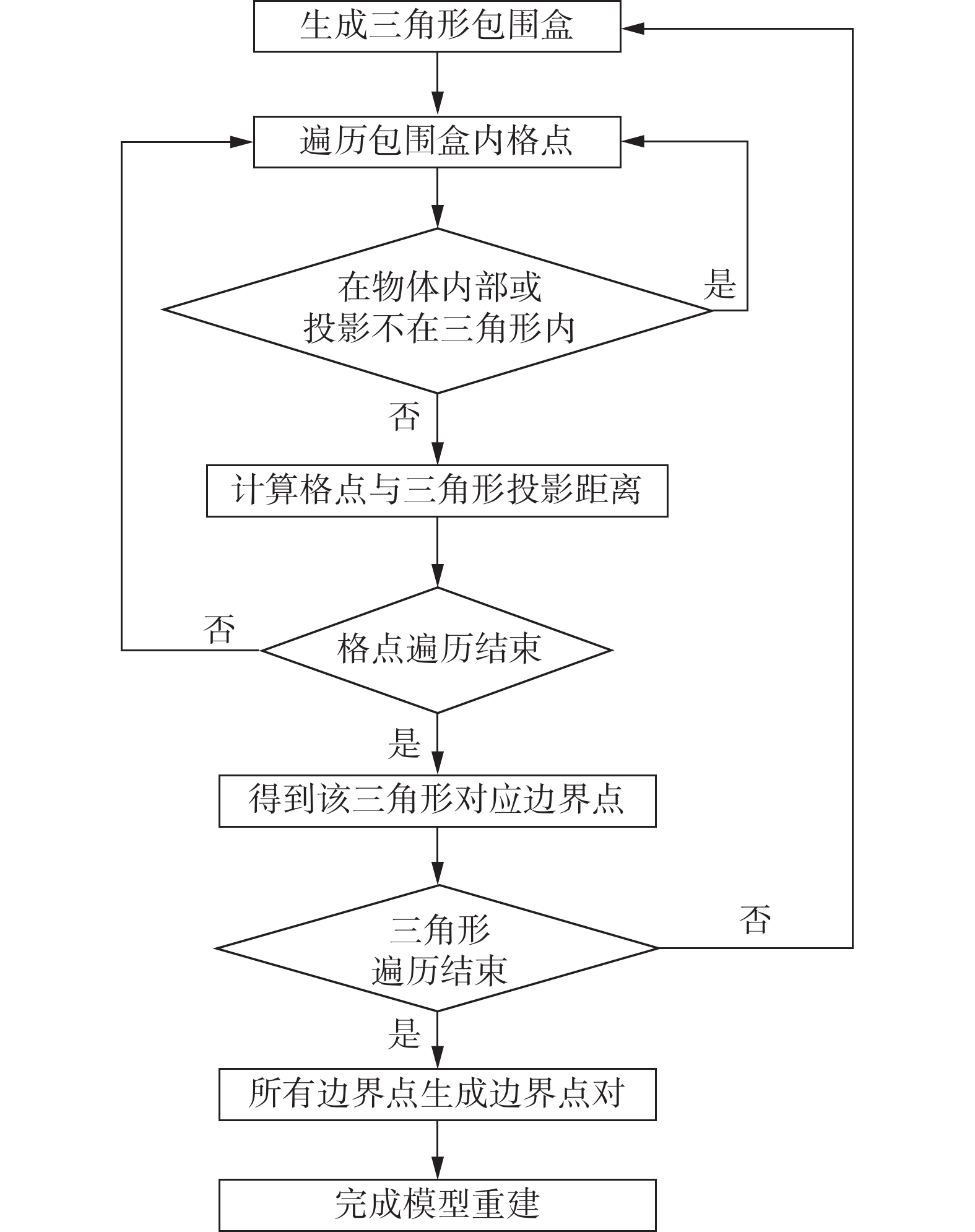
算法主要过程如图4所示。算法主要步骤如下:
(1)为了缩小计算量,只计算由三角形生成包围盒内部的点(三角形包围盒是指边平行于坐标轴的体积最小的长方体,长方体的顶点是计算格点,且三角形的三个顶点都在长方体的内部)。为了进一步减少计算量,继续排除不满足条件的格点,采取了以下处理方法:1)去除三角形对应在物体内部的格点:这里判断的方法是,以靠近物体内部的格点为终点,以三角形顶点为起点,构成的向量与三角形的法向量方向相反;2)去除不是该三角形对应的点:同时将格点和三角形沿着某一坐标轴投影,如果格点的投影不在三角形的投影内部,那么这个格点不是三角形对应的格点。
(2)在筛选后的格点中,对于某个坐标轴选取距离三角形最近的格点,例如选取x轴,则对于一个(y,z)坐标选取距离x轴最近的格点,该距离可以直接用格点到三角形的投影距离,然后即可得到该三角形对应的所有物体边界点。
(3)对于每个三角形重复前面两步,得到物体所有的边界点。
(4)进一步生成边界点对,边界点对是两个边界点构成的点对,且这两个点所确定的直线平行于坐标轴。边界点对中间的格点是物体内部点。
(5)根据边界点对可以确定所有的内部点,即可完成物体模型的重建。
|
图 4 本文算法流程图 Fig.4 Flowchat of the algorithm proposed in this study |
通过测试,该算法能够用于大部分模型文件读取,并快速进行模型重建。具体特点包括:
(1)不严格要求物体几何封闭。对于模型STL文件中存在的平行于某一坐标轴的三角形,该算法不需要这些三角形便可以完成模型的重建,即对STL文件的要求不是十分严格。
(2)能够处理部分不规范网格文件。正常情况下网格文件只包含物体表面三角形,但是部分模型网格文件存在物体内部三角形。而直接法有一个重要的假定就是网格三角形是模型内部与外部的分界点,此时冗余的内部三角形信息将会导致直接法无法正常判断网格类型。而本文算法能够较好地解决这类问题。
(3)能够快速处理标准模型的重建。该算法是根据物体的面网格来确定物体的边界格点,然后根据边界格点重建物体模型。所以运行时间只与物体STL文件中三角形个数有关,在相同数量的面网格三角形下,运行时间基本不受物体几何复杂度影响。
4 测试与结果比较 4.1 测试环境测试使用“神威•太湖之光”计算机集群系统进行测试,以“申威 26010”异构众核处理器为核心,访存带宽136.51 GB/s,主存容量32 GB,网络接口双向带宽16 GB/s。采用sw5CC进行程序编译。
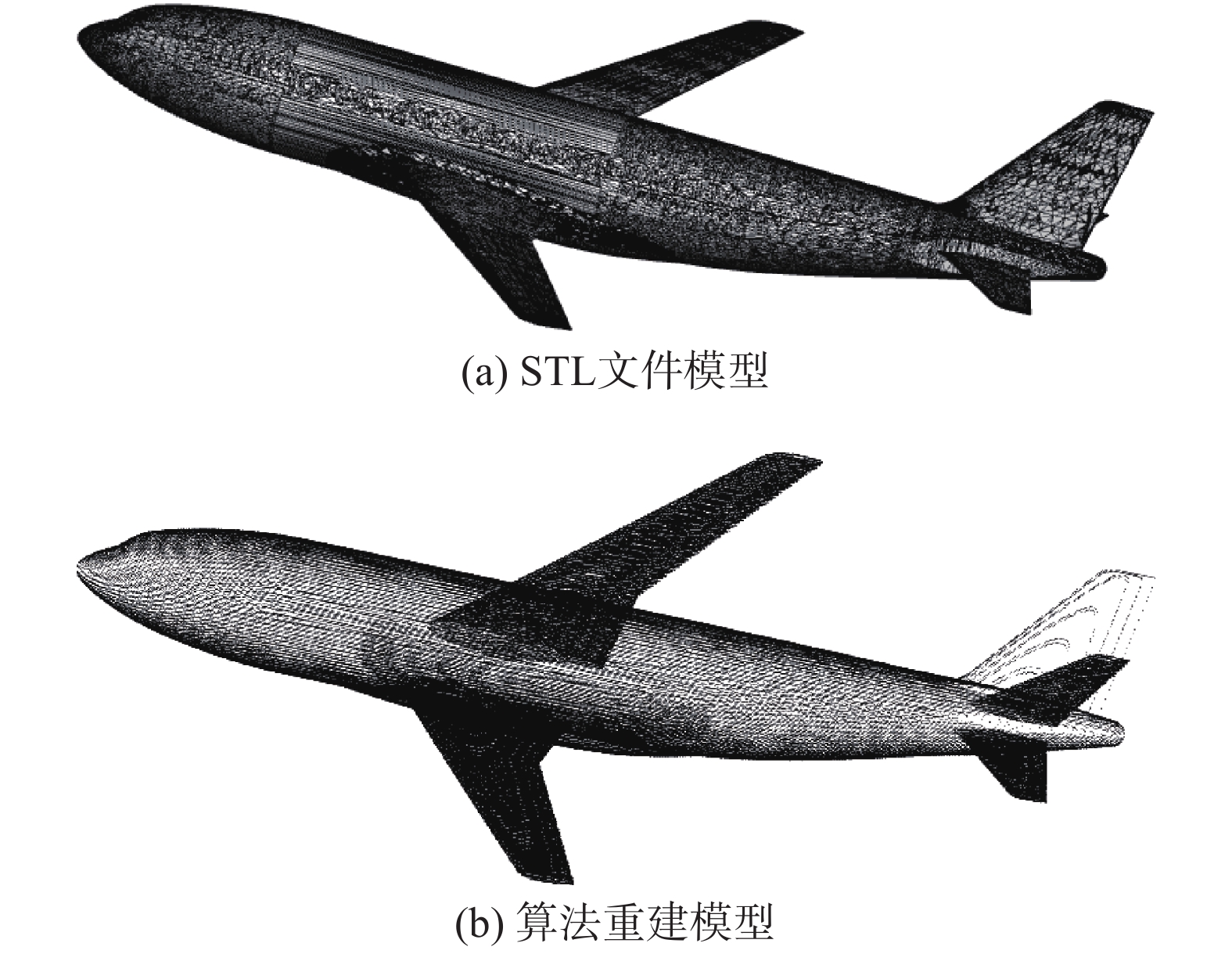
4.2 测试案例测试中选取了3种比较有代表性的物体模型对直接法和本文算法进行比较。三种模型分别为:圆球、NACA0012翼型、CHN-T1飞机标模。圆球模型是一种简单的模型,其形状分布均匀、对称、形状简单,网格量少。NACA0012翼型代表了形状分布不均匀、表面三角形密集、网格量较大的模型,本文用到的是一种更为特殊的不封闭的NACA0012翼型模型,该模型只有型线面上有网格,侧面为空。CHN-T1飞机标模属于复杂的模型,它结构复杂、不同的部位的三角形有不同大小、网格量巨大。程序测试结果分别如下图。图5(a)、5(b)是圆球的面网格和经过算法重建的模型,图6(a)、6(b)是NACA0012的面网格和重建模型结果,图7(a)、7(b)是CHN-T1飞机标模的面网格和重建模型。由图5、图6、图7中的结果可以看出,本文算法有很好的整体重建能力,能够反应原模型的复杂度,保留原有模型几何特征。

|
图 5 圆球模型 Fig.5 Sphere model |

|
图 6 NACA0012翼型 Fig.6 NACA0012 airfoil |
|
图 7 CHN-T1飞机标模 Fig.7 CHN-T1 aircraft model |
在神威平台上的测试结果如表1所示。两个算法除了判断处理部分步骤不同,其他都相同。从表1中可以看出,本文算法相对于直接法有着明显的速度提升。在圆球、NACA0012翼型测试中,直接法和本文算法均采用单核测试,判断时间由525.4 s和5895.5 s降到了0.17 s和0.4 s。从结果可以看出直接法随着几何复杂度增加,计算耗时急剧增加,而本文方法耗时并未显著增加。在对CHN-T1模型建模过程中直接法采用单核已无法完成,通过120核的并行生成判断花了40056 s(11.13 h),而采用本文算法即使采用1核计算判断过程也只耗时4.5 s,加文件读写,前处理总耗时约20 s。测试结果表明本文算法极大提高了LBM针对复杂几何的前处理效率。
| 表 1 本文算法和直接法的测试结果 Table 1 Testing results for the present algorithm and the direct method |
|
|
针对不同算例,基于本文的前处理算法开展网格生成,并采用SWLBM[17]软件开展了相应流场计算。图8为针对圆球模型开展以直径为特征长度Re = 3.3×106工况下计算获得的Q涡结构与轴向切面速度场,可以发现基于本文方法构建的网格可以获得圆球绕流的复杂涡系结构。

|
图 8 圆球绕流Q涡结构与速度云图 Fig.8 Vortical structures based on Q-criterion and the velocity contour for flow around a sphere |
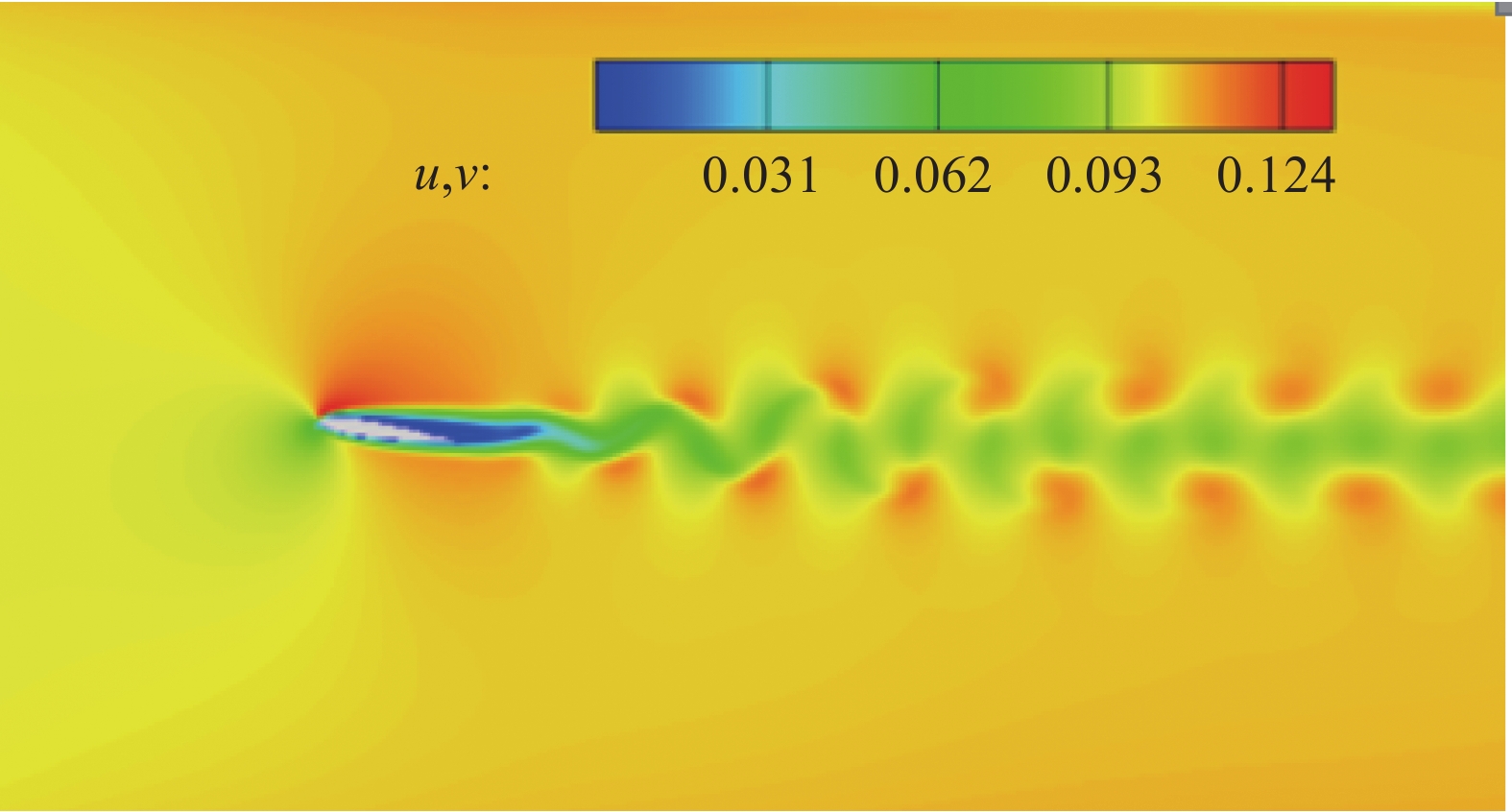
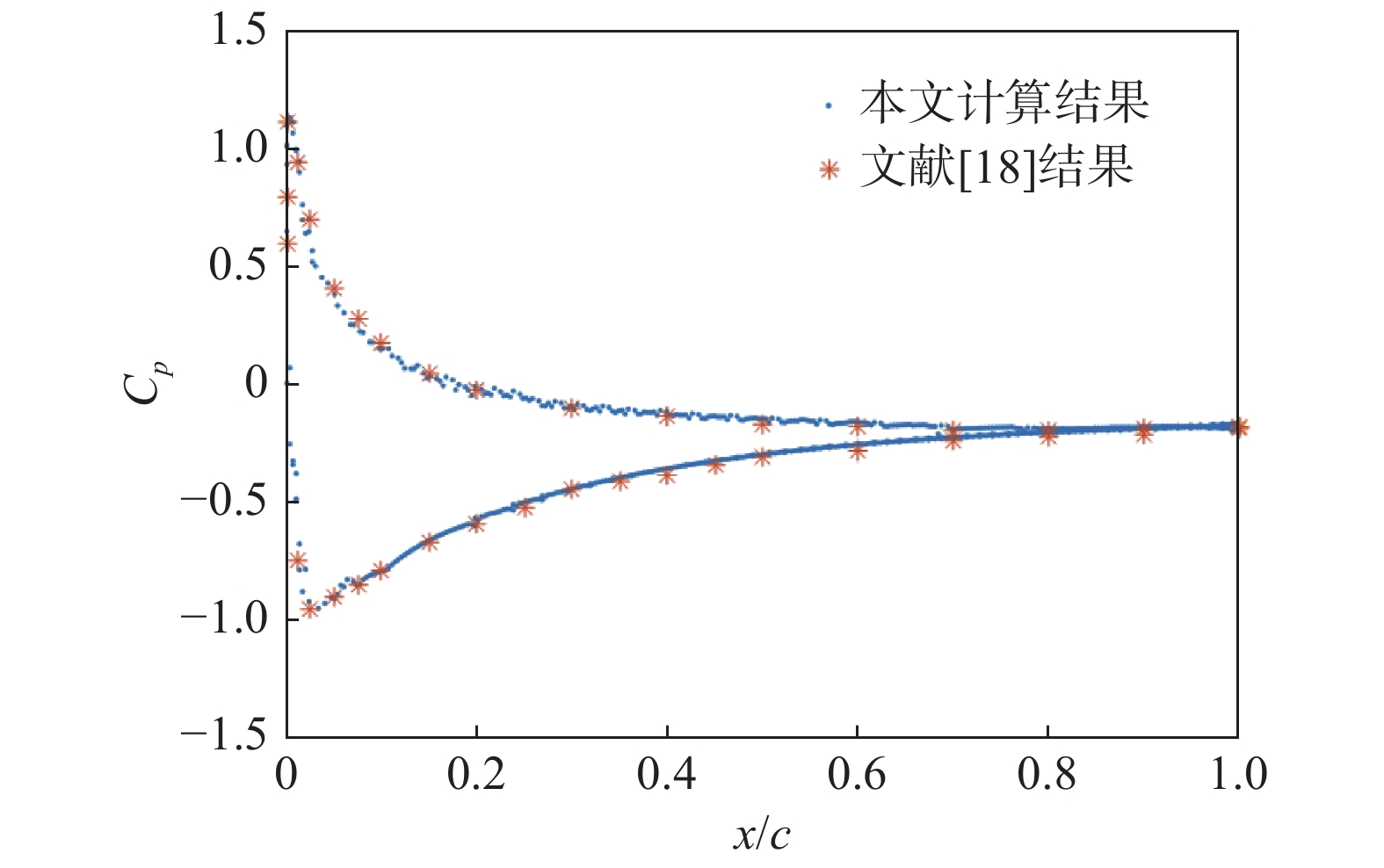
图9为本文算法所建模型计算获得的在8°攻角下NACA0012翼型Re = 1000工况下的绕流场速度云图。图10为本文计算所得翼型表面压力系数与文献[18]的结果对比,由图可见两者基本一致,表明基于本文所建立的前处理算法获得的网格模拟,可以获得同样准确的结果。
|
图 9 NACA0012翼型绕流速度云图 Fig.9 Velocity contour for flow around the NACA0012 airfoil |
|
图 10 NACA0012表面压力系数 Fig.10 Pressure coefficient along NACA0012 airfoil |
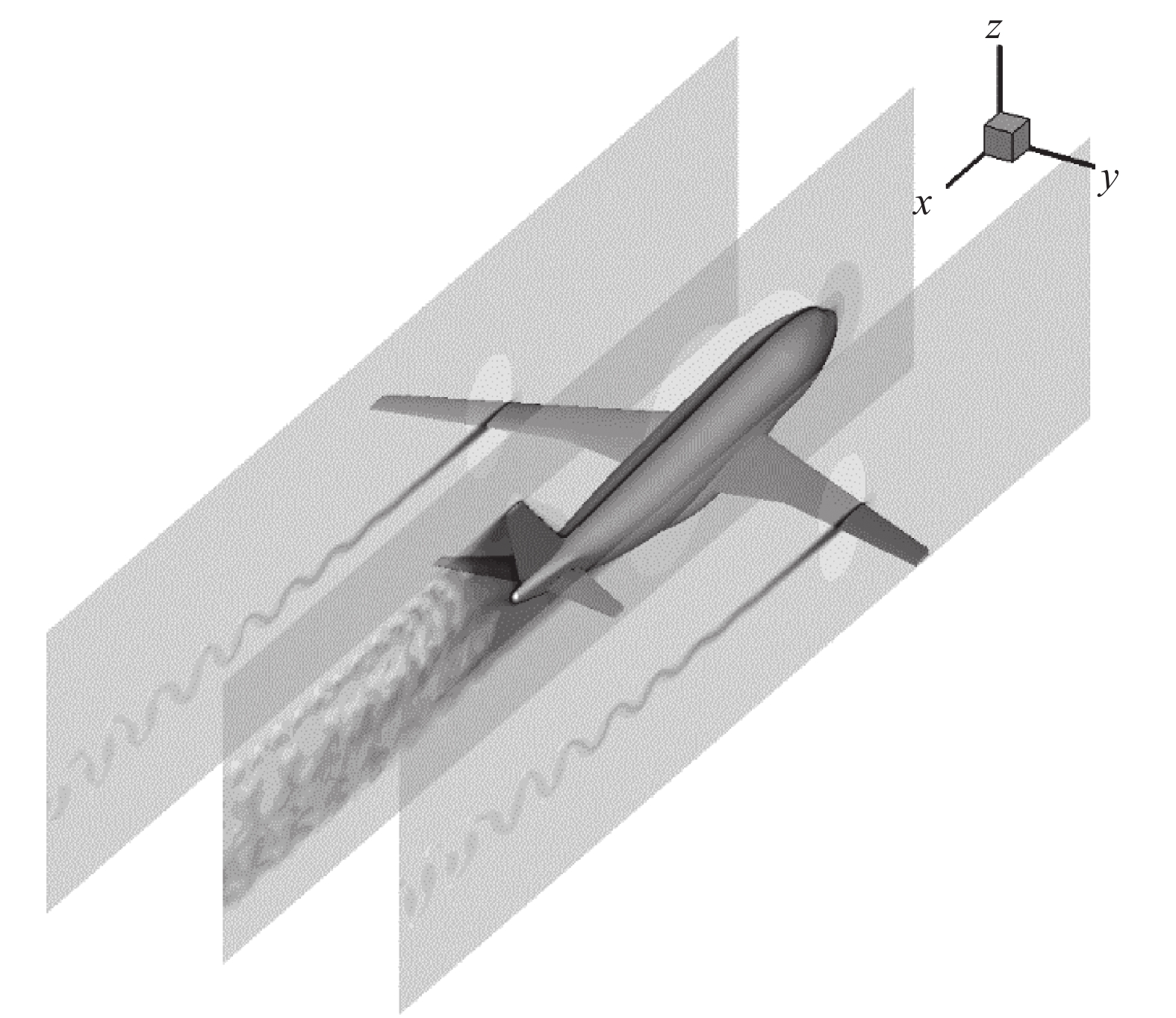
图11为基于本文算法前处理获得CHN-T1标模2 mm分辨率笛卡尔网格开展4°攻角Re = 3.3×106、Ma = 0.2工况下,流场计算获得的不同视角瞬态Q涡结构。图12为同状态下不同特征截面上的速度场云图。可以看到基于本文前处理方法获得的网格开展的流场计算,可以获得从机翼脱落的涡结构,垂尾形成的卡门涡街也清晰可见。

|
图 11 CHN-T1模型不同视角的Q涡结构 Fig.11 Vortical structures based on Q-criterion for flow around the CHN-T1 model from different perspectives |
|
图 12 CHN-T1模型不同特征面速度场 Fig.12 Velocity contours in different characteristic planes of the CHN-T1 model |
以上三个算例结果,验证了本文前处理方法在LBM计算中的适用性。
6 结束语本文针对LBM计算中流场网格类型判断需求,建立了一套基于STL几何文件的快速前处理方法。与常用的直接法比较,克服了其随着几何复杂度增加耗时急剧增加问题,并且对复杂几何具有同样高效。该算法从模型的面网格三角形出发,找出面网格对应的边界格点,进一步由边界格点完成对模型的重构。基于本算法的LBM前处理技术已经在SWLBM软件中获得很好的应用。在之后的工作中,还将从并行以及针对更为特殊的模型等方面考虑,进一步扩大算法的适用性,提高算法的模型重建效率。
| [1] |
CHEN S Y, DOOLEN G D. Lattice Boltzmann method for fluid flows[J]. Annual Review of Fluid Mechanics, 1998, 30(1): 329-364. DOI:10.1146/annurev.fluid.30.1.329 |
| [2] |
AGARWAL U, ALPAK F O, KOELMAN J M V A. Permeability from 3D porous media images: a fast two-step approach[J]. Transport in Porous Media, 2018, 124(3): 1017-1033. DOI:10.1007/s11242-018-1108-0 |
| [3] |
TANG G H, TAO W Q, HE Y L. Gas slippage effect on microscale porous flow using the lattice Boltzmann method[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2005, 72(5 Pt 2): 056301. DOI:10.1103/PhysRevE.72.056301 |
| [4] |
SARITHA G, BANERJEE R. Development and application of a high density ratio pseudopotential based two-phase LBM solver to study cavitating bubble dynamics in pressure driven channel flow at low Reynolds number[J]. European Journal of Mechanics - B, 2019, 75: 83-96. DOI:10.1016/j.euromechflu.2018.12.004 |
| [5] |
YU H D, LUO L S, GIRIMAJI S S. Scalar mixing and chemical reaction simulations using lattice Boltzmann method[J]. International Journal of Computational Engineering Science, 2002, 3(1): 73-87. DOI:10.1142/s1465876302000551 |
| [6] |
CHEN H D, KANDASAMY S, ORSZAG S, et al. Extended Boltzmann kinetic equation for turbulent flows[J]. Science, 2003, 301(5633): 633-636. DOI:10.1126/science.1085048 |
| [7] |
王增波. STL格式文件的快速拓扑重建算法[J]. 计算机应用, 2014, 34(9): 2720-2724. WANG Z B. Fast topological reconstruction algorithm for a STL file[J]. Journal of Computer Applications, 2014, 34(9): 2720-2724. DOI:10.11772/j.issn.1001-9081.2014.09.2720 (in Chinese) |
| [8] |
王春香, 李振华. STL模型分层算法的优化及应用[J]. 机械设计与制造, 2013(3): 87-90. WANG C X, LI Z H. The optimization and application of the STL model layer algorithm[J]. Machinery Design & Manufacture, 2013(3): 87-90. DOI:10.19356/j.cnki.1001-3997.2013.03.027 (in Chinese) |
| [9] |
林洁琼, 王一博, 靖贤, 等. 增材制造中STL模型的自适应分层算法研究[J]. 机械设计与制造, 2018(2): 51-53, 57. LIN J Q, WANG Y B, JING X, et al. Research on adaptive slicing algorithm of STL model in additive manufacturing[J]. Machinery Design & Manufacture, 2018(2): 51-53, 57. DOI:10.19356/j.cnki.1001-3997.2018.02.015 (in Chinese) |
| [10] |
宋廷强, 张敏, 刘亚林. 基于STL文件的树形支撑结构自动生成算法[J]. 计算机应用, 2018, 26(9): 277-282. SONG T Q, ZHANG M, LIU Y L. Tree-based support structure automatic generation algorithm based on STL file[J]. Journal of Computer Applications, 2018, 26(9): 277-282. (in Chinese) |
| [11] |
陈博, 李骁健, 李春芳, 等. 基于STL切片数据截面轮廓的高质量分段拟合算法[J]. 机械制造与自动化, 2017, 46(5): 149-151. CHEN B, LI X J, LI C F, et al. High quality segmentation fitting algorithm based on STL slice data[J]. Machine Building & Automation, 2017, 46(5): 149-151. DOI:10.19344/j.cnki.issn1671-5276.2017.05.038 (in Chinese) |
| [12] |
ZENG L, LAI L M L, QI D, et al. Efficient slicing procedure based on adaptive layer depth normal image[J]. Computer-Aided Design, 2011, 43(12): 1577-1586. DOI:10.1016/j.cad.2011.06.007 |
| [13] |
ZHANG Z Y, JOSHI S. An improved slicing algorithm with efficient contour construction using STL files[J]. The International Journal of Advanced Manufacturing Technology, 2015, 80(5-8): 1347-1362. DOI:10.1007/s00170-015-7071-9 |
| [14] |
SCHWARZ M, SEIDEL H P. Fast parallel surface and solid voxelization on GPUs[J] ACM Transactions on Graphics, 2010, 29(6): 1-9.doi: 10.1145/1882262.1866201.
|
| [15] |
吴晓军, 刘伟军, 王天然. 基于八叉树的三维网格模型体素化方法[J]. 工程图学学报, 2005, 26(4): 1-7. WU X J, LIU W J, WANG T R. Octree structure based voxelization of polygonal meshes[J]. Journal of Engineering Graphics, 2005, 26(4): 1-7. DOI:10.3969/j.issn.1003-0158.2005.04.001 (in Chinese) |
| [16] |
刘智翔. 改进的格子Boltzmann方法研究及大规模并行计算[D]. 上海: 上海大学, 2014. LIU Z X. The research on modified lattice Boltzmann method and large-scale parallel computing[D]. Shanghai: Shanghai University, 2014. (in Chinese. |
| [17] |
褚学森, 刘钊, 石树鹏, 等. 基于神威架构的SWLBM计算流体软件研发进展[C]//第十届全国流体力学学术会议论文集. 杭州, 2018: 352-353.
|
| [18] |
KURTULUS D F. On the unsteady behavior of the flow around NACA 0012 airfoil with steady external conditions at Re=1000
[J]. International Journal of Micro Air Vehicles, 2015, 7(3): 301-326. DOI:10.1260/1756-8293.7.3.301 |



