相比结构化网格和笛卡尔网格,非结构网格因其对复杂外形的适应性、网格生成的自动化程度[1-3]以及对运动边界、多体分离、流场自适应等问题的模拟能力,逐渐成为学术研究和应用的重点[4]。
基于非结构网格的数值格式通常包含有限元(Finite Element, FE)[5]、间断伽辽金(Discontinuous Galerkin, DG)[6-7]和有限体积(Finite Volume, FV)[8-13] 等方法,其中,具有二阶精度的FV方法因其在鲁棒性和计算开销较小等方面的优势而被广泛应用于当前主流的CFD商业与开源软件。这也一定程度上极大促进了二阶FV格式的发展,使其趋于成熟。
在二阶精度的基础上,近年来具有高阶精度的FV离散格式同样得到了较快发展,以满足高效计算与高保真数值模拟的需求[12-15]。Ollivier-Gooch与Jalali等[16-18]系统研究了高阶非结构FV格式中的k-exact重构[19,20]、曲边界处理与通量、源项积分等一系列问题。Li[21]在高阶非结构数值格式的框架内探索了新的限制器构造策略,以及考虑黏性边界条件的约束k-exact重构。Kong等基于k-exact方法,在二阶与高阶FV离散格式的框架内提出了一种新的重构模板[22]与单元参考点选择策略[23],有效改善了原有格式在各向异性网格上的数值表现。
相比重构与离散算法研究,在非结构FV算法,尤其是高阶精度算法框架内,针对边界条件的细致研究相对较少,然而实践表明,采用不同的边界条件设置方法可导致流场求解效果的差异[24]。如果边界条件设置恰当,求解过程的鲁棒性以及计算效果能够得到明显改善;反之,若边界条件设置不当,则有可能收敛至错误的流场,甚至导致计算发散。
对于真实流动,通常可将边界条件的施加分为强施加与弱施加两类。强施加是一种变量施加方法,即通过边界条件得到边界位置的变量;而弱施加是一种通量施加方法,即通过边界条件得到边界位置的数值通量。强施加方法一般基于特征理论,认为双曲守恒律方程代表特征波的传播,在对应的边界位置存在传入或者传出计算域的特征波[25-26]。其中,外传波的特征一般取决于内部流场;而内传波需要基于无黏关系式,在界面构造演化方程[27]。
对基于非结构网格的数值格式,当前较为常用的强施加边界条件是引入虚拟单元来设置特征边界条件[28-29],该方法能够准确反映边界附近特征波传播情况,但此过程需要人为判断特征波传播方向以得到时变幅值,对于多维效应明显的流动,通常还需要引入横向修正[29]。此外,对边界面处特征虚拟单元的变量赋值过程引入了一阶误差,严重破坏了流场求解精度[30-31]。而本文的研究目标是探讨边界条件在高阶精度有限体积方法中的表现效果,因此不再考虑这种强施加边界条件在高阶精度求解器上的应用。
不同于强施加方法,弱施加边界条件旨在得到边界面的数值通量。对于内部单元面,可根据单元面处的变量左右值采用近似黎曼解构造数值通量,而对于边界面的通量构造同样可采用此方法。Kopriva等[32-33]指出,FUN3D的边界条件处理也采用了这种方法。但当前对亚声速入口、出口以及远场这类边界条件的主要处理方式是基于一维黎曼不变量来得到边界面处的右状态矢量,这种方法仍需采用特征关系式,并基于黎曼不变量进行繁冗推导。为简化这类弱施加边界条件的处理方法,Atkins和Casper[34]针对结构网格上的高精度格式,提出了一种基于有限波模型的精度保持边界条件施加方法来统一处理包括亚声速入口、出口以及远场等边界,该方法基于有限波模型得到的精确解,将内部流场与外部瞬态条件有效联系起来,得到了高阶收敛精度。Dong等[30-31]将这种边界条件由基于结构网格的有限差分方法推广至二阶精度非结构有限体积方法,并将其与常用的特征虚拟单元边界条件对比后发现,采用黎曼边界条件能够得到较高的计算精度与收敛效率,同时也可显著提高求解器的计算稳定性。
在此基础上,本文将这种弱施加边界条件推广至高阶精度非结构有限体积方法,以检验其在高阶精度求解器中的表现效果。此外,在高阶有限体积方法的框架内将这种边界条件推广至基于制造解方法(MMS)[35-38]的流动。这种特殊的数值流动当前被广泛用来检验算法的有效性,但通常在基于MMS流动研究某些问题时,一般未考虑对其施加边界条件。较常见的处理方式是所有边界面处的变量左值由内部流场插值得到,而右值均赋值为当前位置的精确解。Folkner和Katz[35]以及Wang等[36]在二阶精度非结构有限体积方法的框架内验证了施加边界条件的MMS流动的数值表现,经检验,对MMS流动施加边界条件后可达到二阶精度。但在高精度数值方法中,对此类流动施加边界条件,尤其是黎曼边界条件的相关研究还未开展。因此,本文计划在高阶精度非结构有限体积方法的框架内,验证对MMS流动和部分真实流动施加黎曼边界条件的合理性,并对比其与常用无反射边界条件[35]间的差异,以进一步推广此类弱施加边界条件在非结构网格数值格式中的应用。
1 非结构有限体积格式 1.1 控制方程对无黏流动探讨弱施加黎曼边界条件,需要求解的控制方程为:
| $\frac{\partial }{{\partial t}}\iint_V {{{u}}{\rm{d}}V} + \iint_V {\nabla \cdot {{{F}}_c}\;{\rm{d}}V} = 0$ | (1) |
其中,u为待求解变量,
| $\frac{\partial }{{\partial t}}{({{\bar u}}V)_i} + {\left( {\sum\limits_{j = 1}^{{N_f}} {\sum\limits_{k = 1}^{{N_G}} {{\omega _k}{{{\varPhi }}_{jk}} \cdot {{{n}}_j}{S_j}} } } \right)_i} = 0$ | (2) |
式中
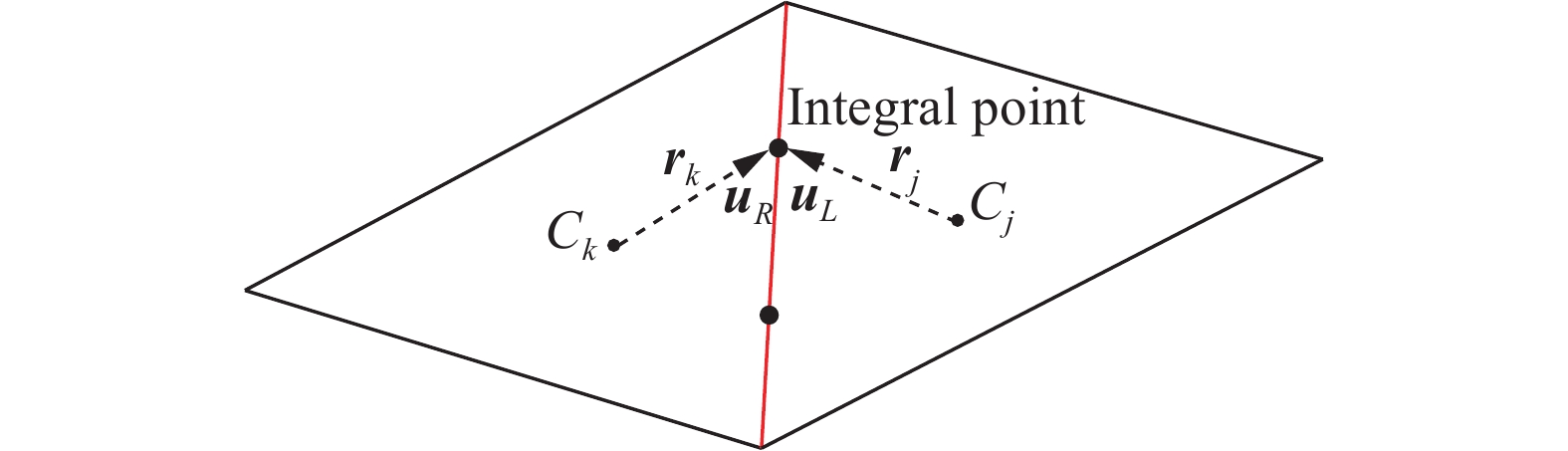
对于高阶方法,一个通量点无法满足积分精度要求,因此需要多个通量点(如图1所示)。对应不同精度下的通量点的数目可参考文献[23]。在基于Roe格式构造通量点数值通量时,需要知道该点的变量左右值,并且变量左右值的获取依赖于从单元参考点到面通量点的泰勒展开,因此需重构控制体单元的变量梯度及其高阶导数。
|
图 1 数值通量构造示意图 Fig.1 Schematic diagram of the numerical flux evaluation |
对于二阶格式,常采用最小二乘(Least Square, LSQ)法与格林高斯(Green Gauss, GG)方法来获得变量梯度。但对基于积分型控制方程的高阶FV格式而言,传统的LSQ或GG方法均无法满足高于二阶的重构精度要求,因此本文采用k-exact方法[16-18]计算变量的梯度与高阶导数。该方法的详细过程本文不再重述,最终需要求解的方程组形式如下:
| $\begin{split} \left( {\begin{array}{*{20}{c}} 1&{\bar x}&{\bar y}&{\overline {{x^2}} }&{\overline {xy} }&{\overline {{y^2}} }& \cdots \\ {{\omega _{i1}}}&{{\omega _{i1}}{{\widehat x}_{i1}}}&{{\omega _{i1}}{{\widehat y}_{i1}}}&{{\omega _{i1}}{{\widehat {{x^2}}}_{i1}}}&{{\omega _{i1}}{{\widehat {xy}}_{i1}}}&{{\omega _{i1}}{{\widehat {{y^2}}}_{i1}}}& \cdots \\ {{\omega _{i2}}}&{{\omega _{i2}}{{\widehat x}_{i2}}}&{{\omega _{i2}}{{\widehat y}_{i2}}}&{{\omega _{i2}}{{\widehat {{x^2}}}_{i2}}}&{{\omega _{i2}}{{\widehat {xy}}_{i2}}}&{{\omega _{i2}}{{\widehat {{y^2}}}_{i2}}}& \cdots \\ {{\omega _{i3}}}&{{\omega _{i3}}{{\widehat x}_{i3}}}&{{\omega _{i3}}{{\widehat y}_{i3}}}&{{\omega _{i3}}{{\widehat {{x^2}}}_{i3}}}&{{\omega _{i3}}{{\widehat {xy}}_{i3}}}&{{\omega _{i3}}{{\widehat {{y^2}}}_{i3}}}& \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \\ {{\omega _{iN}}}&{{\omega _{iN}}{{\widehat x}_{iN}}}&{{\omega _{iN}}{{\widehat y}_{iN}}}&{{\omega _{iN}}{{\widehat {{x^2}}}_{iN}}}&{{\omega _{iN}}{{\widehat {xy}}_{iN}}}&{{\omega _{iN}}{{\widehat {{y^2}}}_{iN}}}& \cdots \end{array}} \right) \;\; \times {\left( {\begin{array}{*{20}{c}} {{u}} \\ {{\dfrac{\partial {{u}}} {\partial x}}} \\ {{\dfrac{\partial {{u}}} {\partial y}}} \\ \dfrac{1}{2}\dfrac{{{\partial ^2}{{u}}}}{{\partial {x^2}}} \\ \dfrac{{{\partial ^2}{{u}}}}{{\partial x\partial y}} \\ \dfrac{1}{2}\dfrac{{{\partial ^2}{{u}}}}{{\partial {y^2}}} \\ \vdots \end{array}} \right)_i} = \;{\kern 1pt} \left( {\begin{array}{*{20}{c}} {{{{{\bar u}}}_i}} \\ {{\omega _{i1}}{{{{\bar u}}}_1}} \\ {{\omega _{i2}}{{{{\bar u}}}_2}} \\ {{\omega _{i3}}{{{{\bar u}}}_3}} \\ \vdots \\ {{\omega _{iN}}{{{{\bar u}}}_N}} \end{array}} \right) \\[-10pt] \end{split} $ | (3) |
式中,
| $ \begin{array}{l} {\widehat {{x^n}{y^m}}_{ij}}\! = \!\dfrac{1}{{{A_j}}}\displaystyle\int_{{V_j}} {{{\left[ {(x \!-\! {x_j})\! +\! ({x_j} \!-\! {x_i})} \right]}^n}} \left[ {(y - {y_j})} \right. \!+\! {\left. {({y_j} \!-\! {y_i})} \right]^m}{\rm{d}}A \\ {\overline {{x^n}{y^m}} _j} = \dfrac{1}{{{A_j}}}\displaystyle\iint_{{V_j}} {{{\left( {x - {x_j}} \right)}^n}{{\left( {y - {y_j}} \right)}^m}}{\rm{d}}A \\[-15pt] \end{array} $ | (4) |
同时,权系数
由于强施加方法多依赖于特征虚拟单元来处理相应的边界条件,该方法在对无黏边界处的虚拟单元赋值过程引入了一阶误差。因此,本文不再讨论这种边界条件强施加方式。
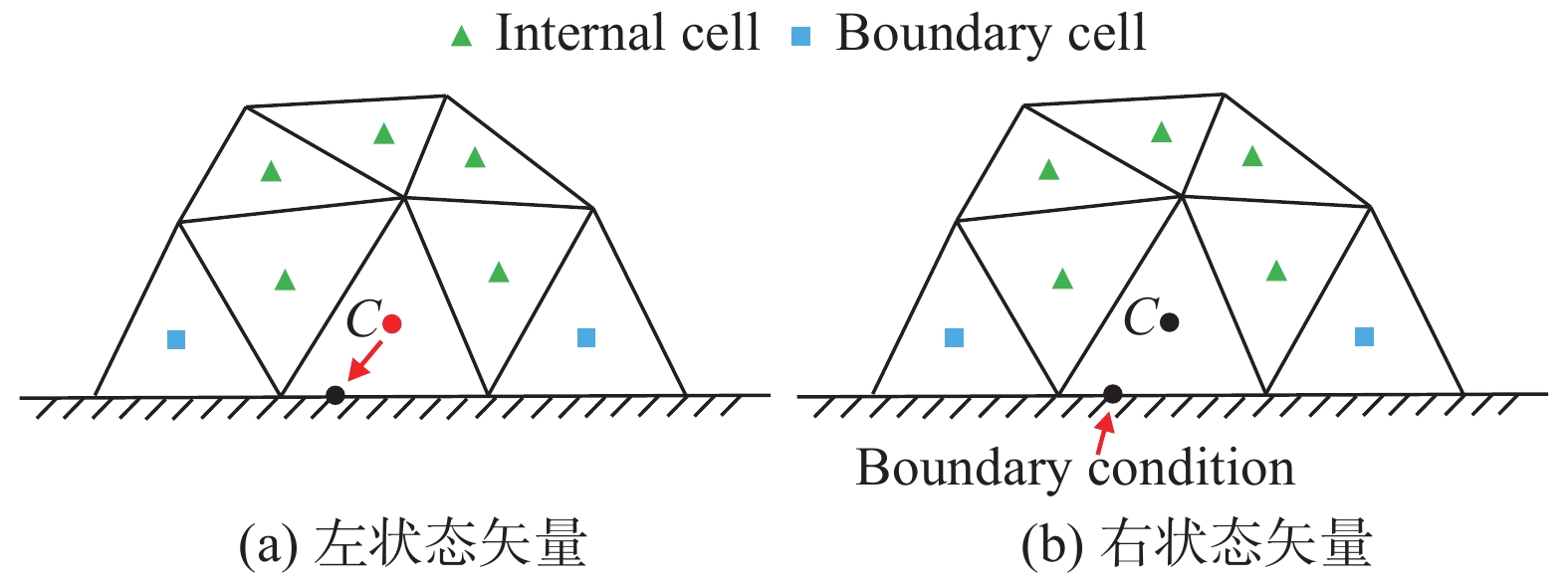
为了在边界面施加弱边界条件,根据近似黎曼公式,需要给定边界面处的两个状态,如图2所示,其中左状态由内部流场插值得到,右状态依赖于相应的边界条件。
|
图 2 重构模板与边界条件弱施加示意图 Fig.2 Schematic diagram for the reconstruction stencil and weak-imposition boundary condition |
在基于内部流场插值时需要注意避免引入一阶误差。本文研究具有三阶精度的有限体积方法,因此首先可通过内部流场信息得到边界面左值,即:
| $\begin{split} {{{W}}_L} =& {{{W}}_C} + {\left. {\frac{{\partial {{W}}}}{{\partial x}}} \right|_C}\left( {{x_C} - {x_b}} \right) + {\left. {\frac{{\partial {{W}}}}{{\partial y}}} \right|_C}\left( {{y_C} - {y_b}} \right) + \\ & {\left. {\frac{1}{2}\frac{{{\partial ^2}{{W}}}}{{\partial {x^2}}}} \right|_C}{\left( {{x_C} - {x_b}} \right)^2} + \frac{{{\partial ^2}{{W}}}}{{\partial x\partial y}}\left( {{x_C} - {x_b}} \right)\left( {{y_C} - {y_b}} \right) + \\ & {\left. {\frac{1}{2}\frac{{{\partial ^2}{{W}}}}{{\partial {y^2}}}} \right|_C}{\left( {{y_C} - {y_b}} \right)^2} \\ \end{split}$ | (5) |
式中WC为边界单元参考点处的变量值,b为边界面通量点。因此,通过方程(5)可得到边界面高斯积分点处的左状态矢量。边界面右值需要根据相应的边界条件获得。下面将针对亚声速入口、出口以及远场等不同边界,给出其边界条件的具体施加方式。
2.1 无黏壁面边界对于无黏壁面,不同弱施加方法的处理过程基本一致。在施加边界条件时,需要保证速度的左右状态关于壁面边界对称。为满足这个条件,右状态矢量可定义为:
| $ \begin{array}{l} {{{u}}_R} = {{{u}}_L} - 2{u_{{{n}},L}} {{{n}}} \\ \end{array} $ | (6) |
其中逆变速度由左值计算得到:
| ${{{u}}_{n,L}} = {{{u}}_L} \cdot {{{n}}}$ | (7) |
压力和温度满足零梯度条件,即:
| ${T_R} = {T_L},\;\;\;\;\;{p_R} = {p_L}$ | (8) |
由于在超声速条件下特征波传播方向唯一,因此超声速入口、出口的处理相对简单。其中超声速入口右值直接取来流值,即:
| ${{{u}}_R} = {{{u}}_{{\rm{inf}}}},\;\;\;\;{T_R} = {T_{{\rm{inf}}}},\;\;\;\;{p_R} = {p_{{\rm{inf}}}}$ | (9) |
超声速出口右值与左值相等:
| ${{{u}}_R} = {{{u}}_L},\;\;\;\;{T_R} = {T_L},\;\;\;\;{p_R} = {p_L}$ | (10) |
与壁面、超声速入口和出口的处理方式不同,在处理亚声速入口、出口以及远场时,本文采用黎曼边界条件。该方法通过求解对应的黎曼问题,在边界面位置可得到物理上相容的左右状态,因此避免了采用特征关系式与黎曼不变量对这类边界条件的判断与推导[35]。
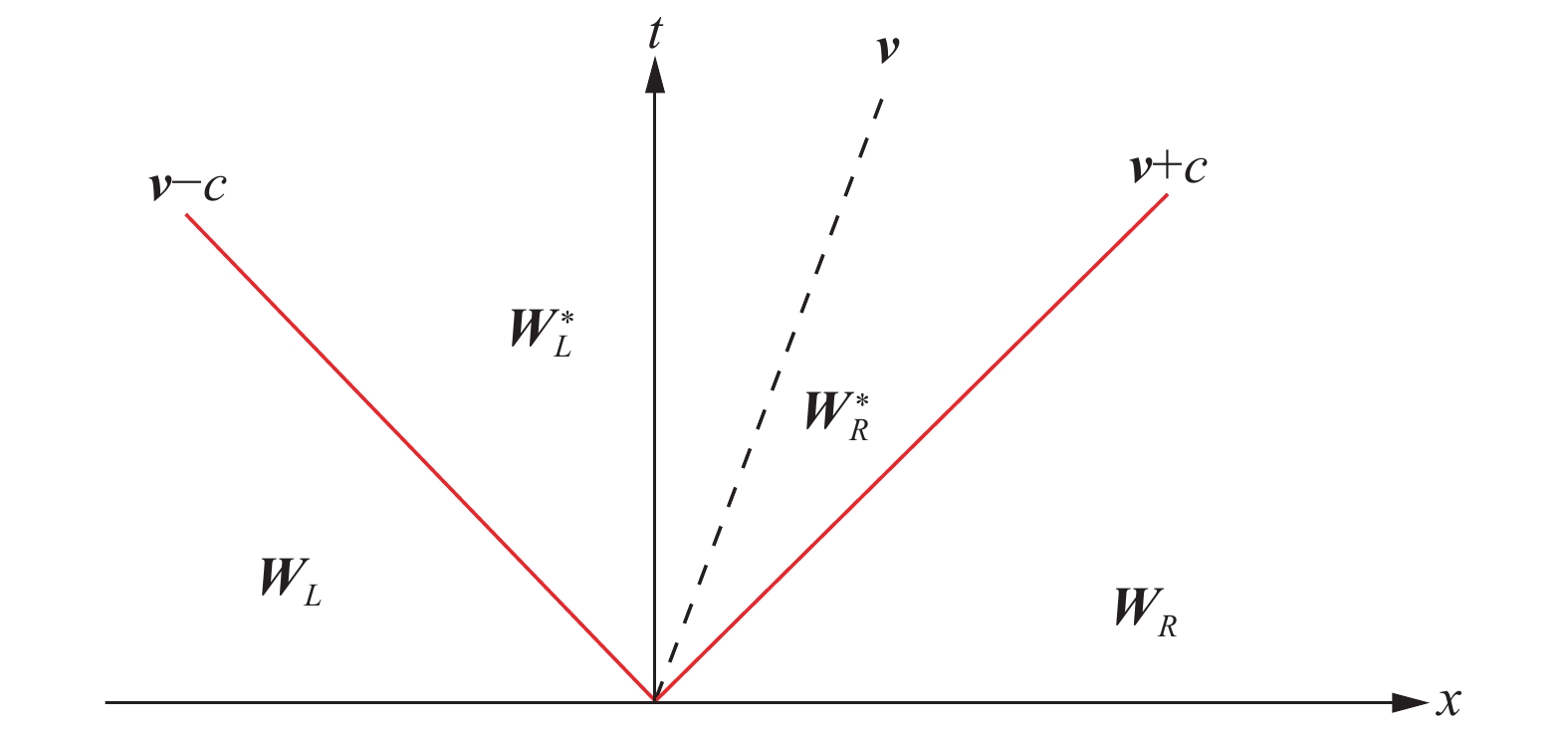
如图3所示,有限波模型假设内部流场与外部瞬态状态通过两道由接触间断分隔的膨胀波进行过渡,图中标有u的虚线代表接触间断,另外两条红色直线对应膨胀波,膨胀波之间的区域将其称为星区。
现构造如下黎曼问题,无穷远处的自由来流参数作为右状态矢量,记为WR,而左状态矢量WL由内部流场插值得到。通过精确求解此黎曼问题,可以获得星区的左右状态矢量,分别记为
| ${p^*} = \left[ {\frac{{{c_L} + {c_R} - 0.5\left( {\gamma - 1} \right)\left( {{u_{n,R}} - {u_{n,L}}} \right)}}{{\dfrac{c_L}{p_L^{2\gamma \left( {\gamma - 1} \right)}} + \dfrac{c_R}{p_R^{2\gamma \left( {\gamma - 1} \right)}}}}} \right]$ | (11) |
其中,c为局部声速,γ为比热比。逆变速度的定义为:
| $\rho _L^ * {\rm{ = }}{\rho _L}{\left( {\frac{{{p^ * }}}{{{p_L}}}} \right)^{\tfrac{1}{ \gamma }}},\;\;\;\;\;\rho _R^ * {\rm{ = }}{\rho _R}{\left( {\frac{{{p^ * }}}{{{p_R}}}} \right)^{\tfrac{1}{ \gamma }}}$ | (12) |
以及星区的逆变速度:
| $u_n^* = \dfrac{{\dfrac{{{p_{LR}}{u_{n,L}}}}{{{c_L}}} + \dfrac{{{u_{n,R}}}}{{{c_R}}} + \dfrac{{2\left( {{p_{LR}} - 1} \right)}}{{\gamma - 1}}}}{{\dfrac{{{p_{LR}}}}{{{c_L}}} + \dfrac{1}{{{c_R}}}}}$ | (13) |
其中
| $ \begin{array}{l} {{{u}}^ * } = {{{u}}_R} + \left( {u_n^ * - {u_{n,R}}} \right){{{n}}} \\ \end{array} $ | (14) |
在此基础上,边界右状态可通过星区状态矢量即
|
图 3 有限波模型示意图 Fig.3 Schematic diagram of the finite wave model |
相比常用的无反射边界条件[35],采用黎曼边界条件处理亚声速入口、出口与远场边界时,均可通过精确求解对应的黎曼问题来给定边界右值,无需再基于法向速度与特征关系来判断不同边界,并单独处理。因此,这种边界条件施加方式可有效简化对亚声速入口、出口以及远场边界的处理过程。
3 MMS流动中的精度验证当前,MMS方法广泛应用于对算法计算精度的检验,但在基于该方法验证精度时,一般未对其施加任何物理边界条件,即边界面的右状态均以参考点处的精确解赋值。本节将对MMS流动采用黎曼方法处理亚声速入口、出口边界,以验证对MMS流动施加黎曼边界条件的合理性。同时为了验证工作的完整性,还测试了对MMS流动施加无黏壁面以及超声速入口、出口这类具有真实物理意义边界条件后的数值表现,以期在高阶精度非结构有限体积框架内,为MMS流动提供一种便捷合理的边界处理方式。
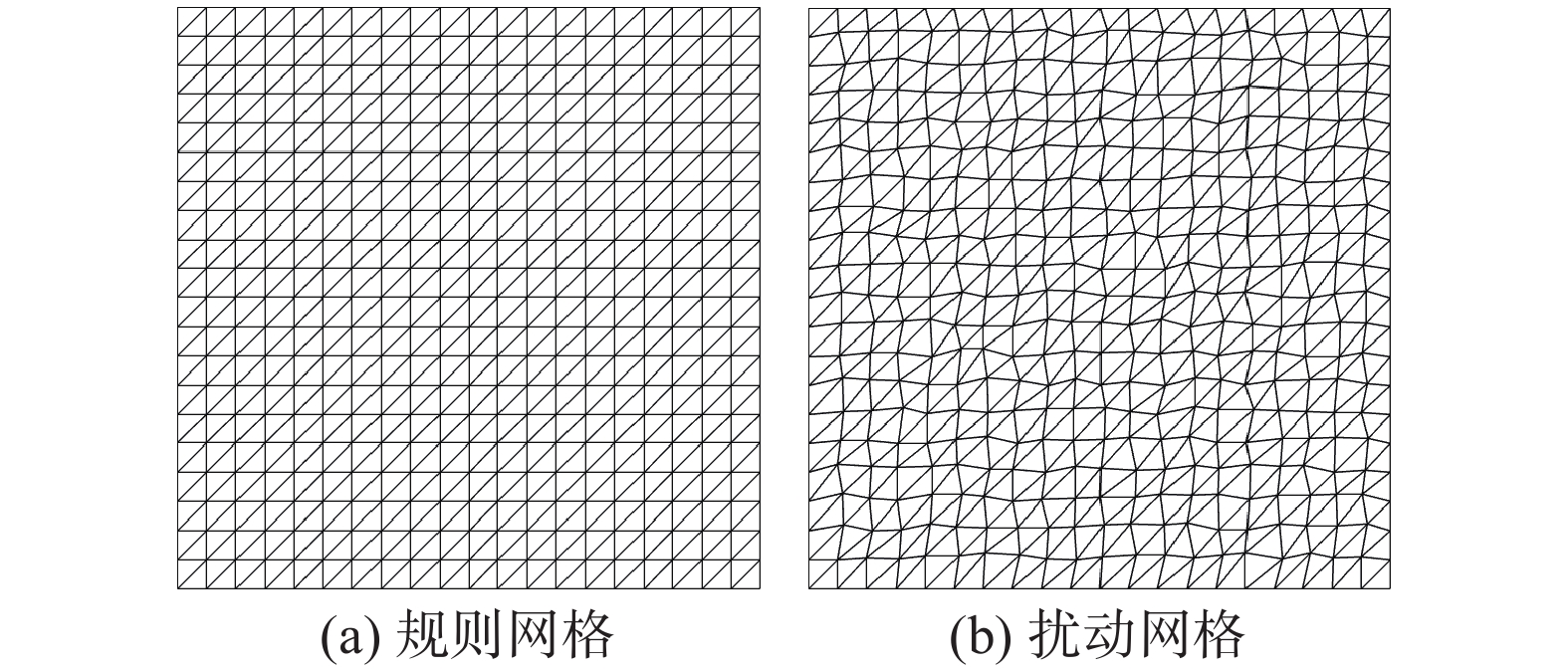
测试网格分别采用了六套由疏到密的规则三角形网格与扰动三角形网格。网格示意图与网格点分布情况见图4与表1。
|
图 4 规则与扰动三角形网格示意图 Fig.4 Schematics of regular and randomly perturbed grids |
| 表 1 背景四边形网格在x与y方向的分布量 Table 1 Distribution of background quadrilateralgrid in x- and y-directions |
|
|
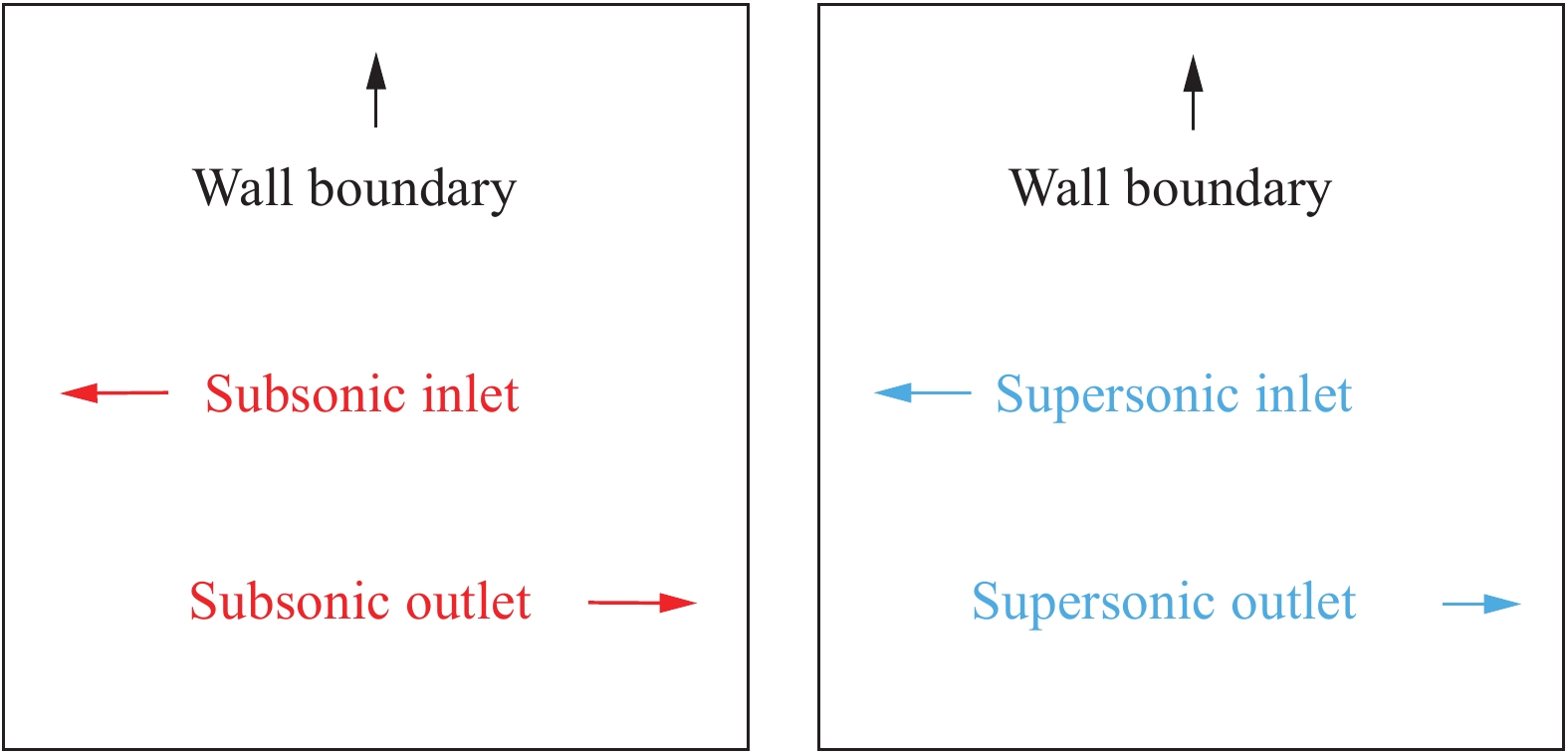
当来流速度为亚声速时,计算域的左右边界分别设置为亚声速入口与出口;对于超声速流动,左右边界分别对应超声速入口和出口。此外,设置壁面边界时,考虑到特征波的传播方向,统一将计算域上边界设置为壁面,示意图见图5。
|
图 5 边界条件设置示意图 Fig.5 Schematic diagram of the correspondingboundary conditions |
在研究不同边界条件的影响之前,为了验证求解器的求解精度,首先测试了不添加边界条件的MMS流动计算效果。在相应的边界高斯积分点处,左值均由内部流场插值得到,而右值由MMS制造解给定。其形式如下:
| $ \begin{array}{l} \rho{_{\rm{MMS}}} = 1.12 + 0.15\sin \left[ {{\rm{{\text{π}} }}\left( {3.12x + 1.92y} \right)} \right] \\ u {_{\rm{MMS}}}= 1.32 + 0.06\sin \left[ {{\rm{{\text{π}} }}\left( {2.09x + 2.21y} \right)} \right] \\ v{_{\rm{MMS}}} = 1.18 + 0.03\sin \left[ {{\rm{{\text{π}} }}\left( {2.15x + 2.32y} \right)} \right] \\ p{_{\rm{MMS}}} = 1.62 + 0.31\sin \left[ {{\rm{{\text{π}} }}\left( {3.79x + 1.98y} \right)} \right] \end{array} $ | (15) |
流动控制方程如式(1),因此可首先根据控制方程推导出源项s的统一表达式为:
| ${{s}} = \left( \begin{array}{l} u{_{\rm{MMS}}}\dfrac{{\partial \rho{_{\rm{MMS}}} }}{{\partial x}} + \rho{_{\rm{MMS}}} \dfrac{{\partial u{_{\rm{MMS}}}}}{{\partial x}} + v{_{\rm{MMS}}}\dfrac{{\partial \rho{_{\rm{MMS}}} }}{{\partial y}} + \rho{_{\rm{MMS}}} \dfrac{{\partial v{_{\rm{MMS}}}}}{{\partial y}} \\ 2\rho{_{\rm{MMS}}} u{_{\rm{MMS}}}\dfrac{{\partial u{_{\rm{MMS}}}}}{{\partial x}} + {u{_{\rm{MMS}}}^2}\dfrac{{\partial \rho{_{\rm{MMS}}} }}{{\partial x}} + \rho{_{\rm{MMS}}} \left( {v{_{\rm{MMS}}}\dfrac{{\partial u{_{\rm{MMS}}}}}{{\partial y}} + u{_{\rm{MMS}}}\dfrac{{\partial v{_{\rm{MMS}}}}}{{\partial y}}} \right) + u{_{\rm{MMS}}}v{_{\rm{MMS}}}\dfrac{{\partial \rho{_{\rm{MMS}}} }}{{\partial y}} + \dfrac{{\partial p{_{\rm{MMS}}}}}{{\partial x}} \\ 2\rho{_{\rm{MMS}}} v{_{\rm{MMS}}}\dfrac{{\partial v{_{\rm{MMS}}}}}{{\partial y}} + {v{_{\rm{MMS}}}^2}\dfrac{{\partial \rho{_{\rm{MMS}}} }}{{\partial y}} + \rho{_{\rm{MMS}}} \left( {v{_{\rm{MMS}}}\dfrac{{\partial u{_{\rm{MMS}}}}}{{\partial x}} + u{_{\rm{MMS}}}\dfrac{{\partial v{_{\rm{MMS}}}}}{{\partial x}}} \right) + u{_{\rm{MMS}}}v{_{\rm{MMS}}}\dfrac{{\partial \rho{_{\rm{MMS}}} }}{{\partial x}} + \dfrac{{\partial p}}{{\partial y}} \\ u{_{\rm{MMS}}}\dfrac{{\partial \left( {\rho{_{\rm{MMS}}} H{_{\rm{MMS}}}} \right)}}{{\partial x}} + \rho{_{\rm{MMS}}} H{_{\rm{MMS}}}\dfrac{{\partial u{_{\rm{MMS}}}}}{{\partial x}} + v{_{\rm{MMS}}}\dfrac{{\partial \left( {\rho{_{\rm{MMS}}} H{_{\rm{MMS}}}} \right)}}{{\partial y}} + \rho{_{\rm{MMS}}} H{_{\rm{MMS}}}\dfrac{{\partial v{_{\rm{MMS}}}}}{{\partial y}} \end{array} \right)$ | (16) |
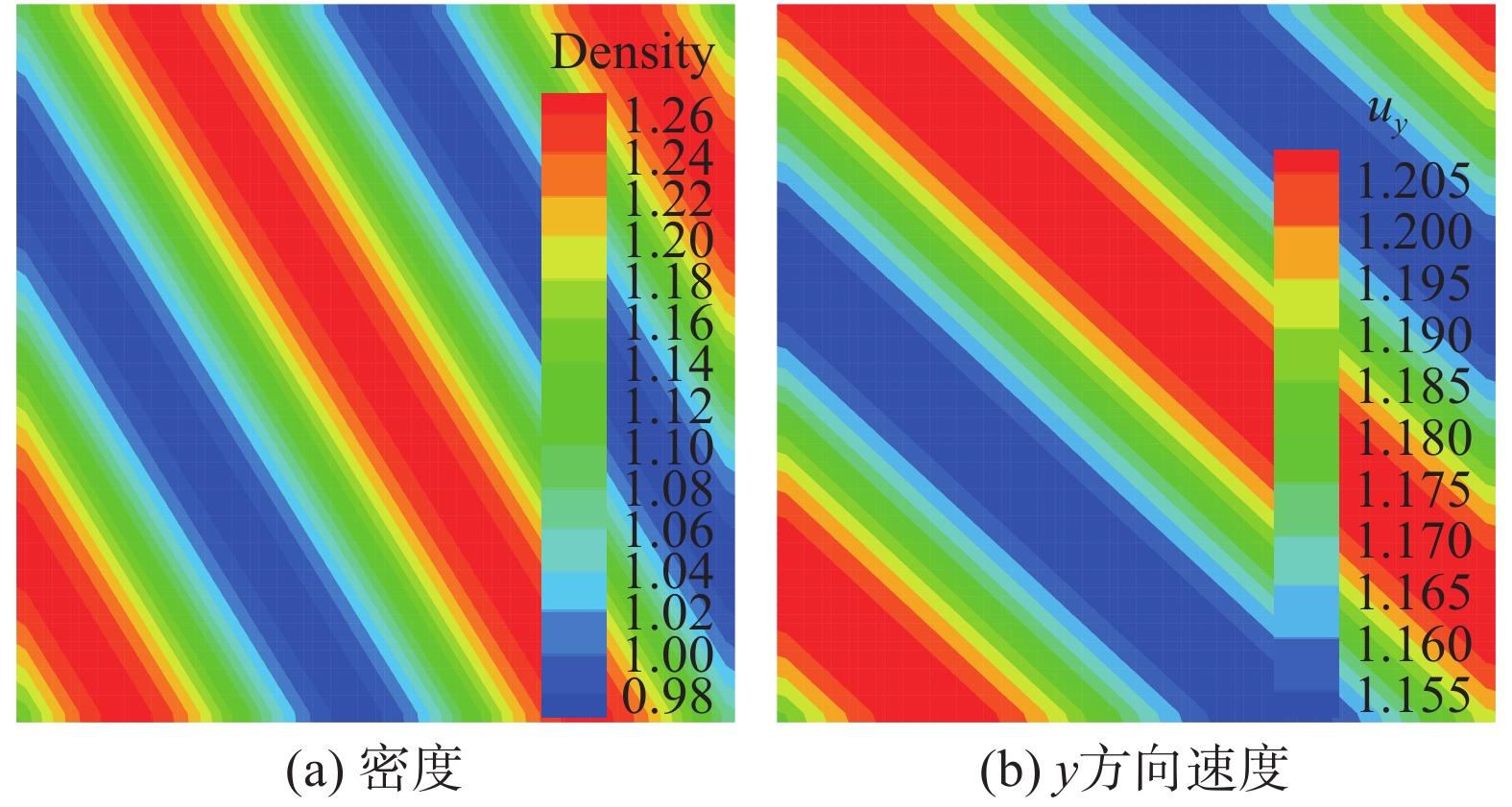
基于该解析解,得到的流场如图6所示。
|
图 6 当前制造解流场 Fig.6 Flow fields of current manufactured solutions |
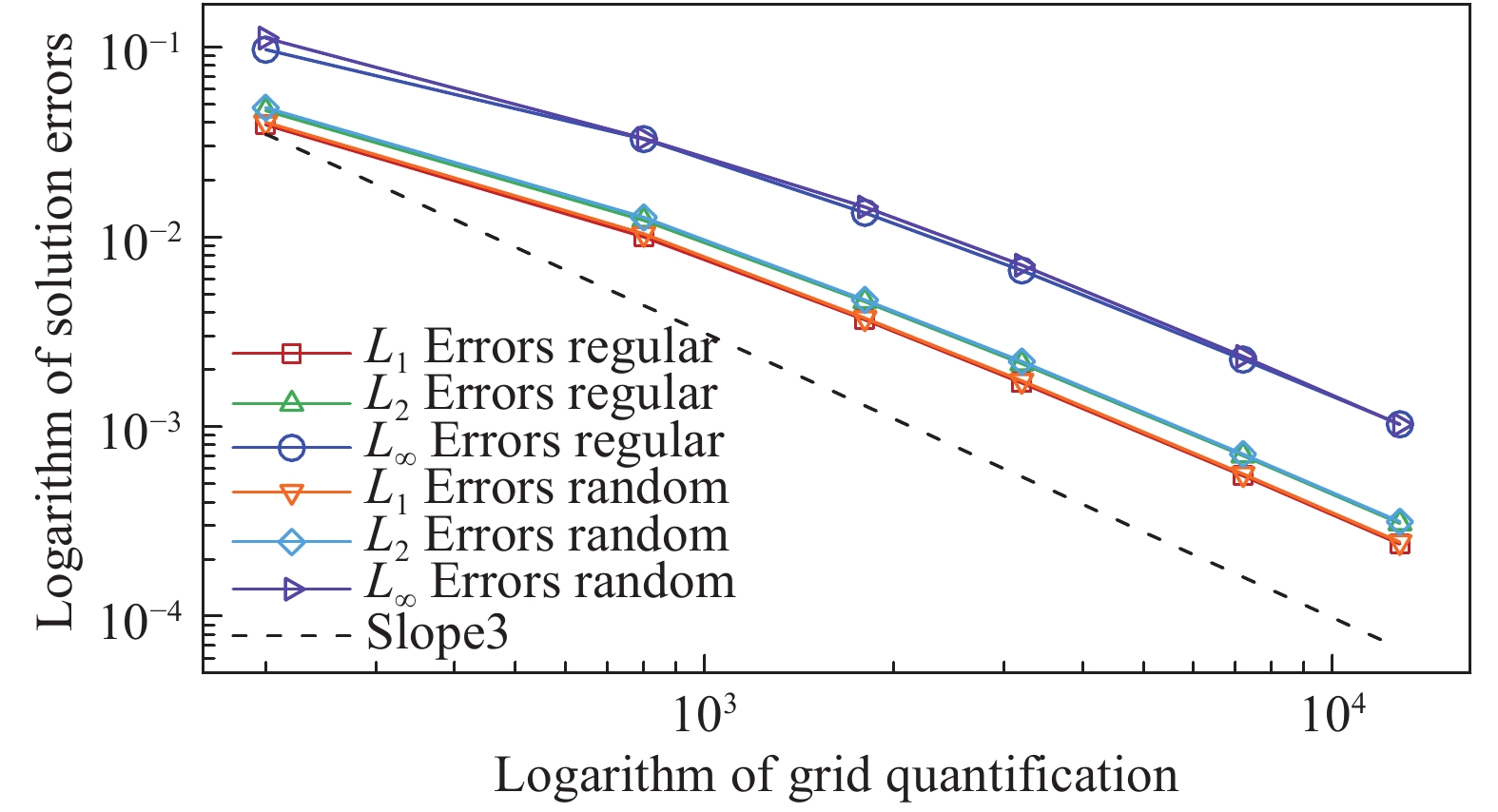
计算收敛后,统计了每套网格误差的 L1、L2以及 L∞范数来充分测试高阶求解器的计算精度。图7中Slope3表示三阶精度标准线。从图7中可以看出,不添加边界条件时,在疏网格上精度一开始并未达到三阶,但随着网格加密,计算结果逐渐趋于设计精度。因此,在不施加边界条件的情况下,首先验证了求解器具有三阶精度。接下来对计算域的不同位置单独施加黎曼边界条件,来验证在高阶方法中对此类流动施加边界条件的合理性。
|
图 7 无边界条件的误差曲线 Fig.7 Error curves without any boundary condition |
对于真实流动的亚声速入口与出口,可通过精确求解黎曼问题来获得对应的边界条件。在求解黎曼问题时,WR通常用无穷远处的来流参数赋值。而MMS流动与真实流动不同,一般不包含无穷远处的参数信息。因此尝试在MMS流动中,WR统一用边界处的制造解提供,并在得到右状态的基础上,通过求解黎曼问题来得到星区状态矢量
验证这两种边界条件时,需要保证在对应的入口与出口位置速度为亚声速,因此给定解的形式如下:
| $ \begin{array}{l} {\rho}_{\rm{MMS}} = 0.32 + 0.15\sin \left[ {{\rm{{\text{π}} }}\left( {0.79x + 0.21y} \right)} \right] \\ u_{\rm{MMS}} = 0.59 + 0.06\sin \left[ {{\rm{{\text{π}} }}\left( {0.47x + 0.53y} \right)} \right] \\ v_{\rm{MMS}} = 0.48 + 0.03\sin \left[ {{\rm{{\text{π}} }}\left( {0.49x + 0.51y} \right)} \right] \\ p_{\rm{MMS}} = 0.53 + 0.31\sin \left[ {{\rm{{\text{π}} }}\left( {0.82x + 0.18y} \right)} \right] \end{array} $ | (17) |
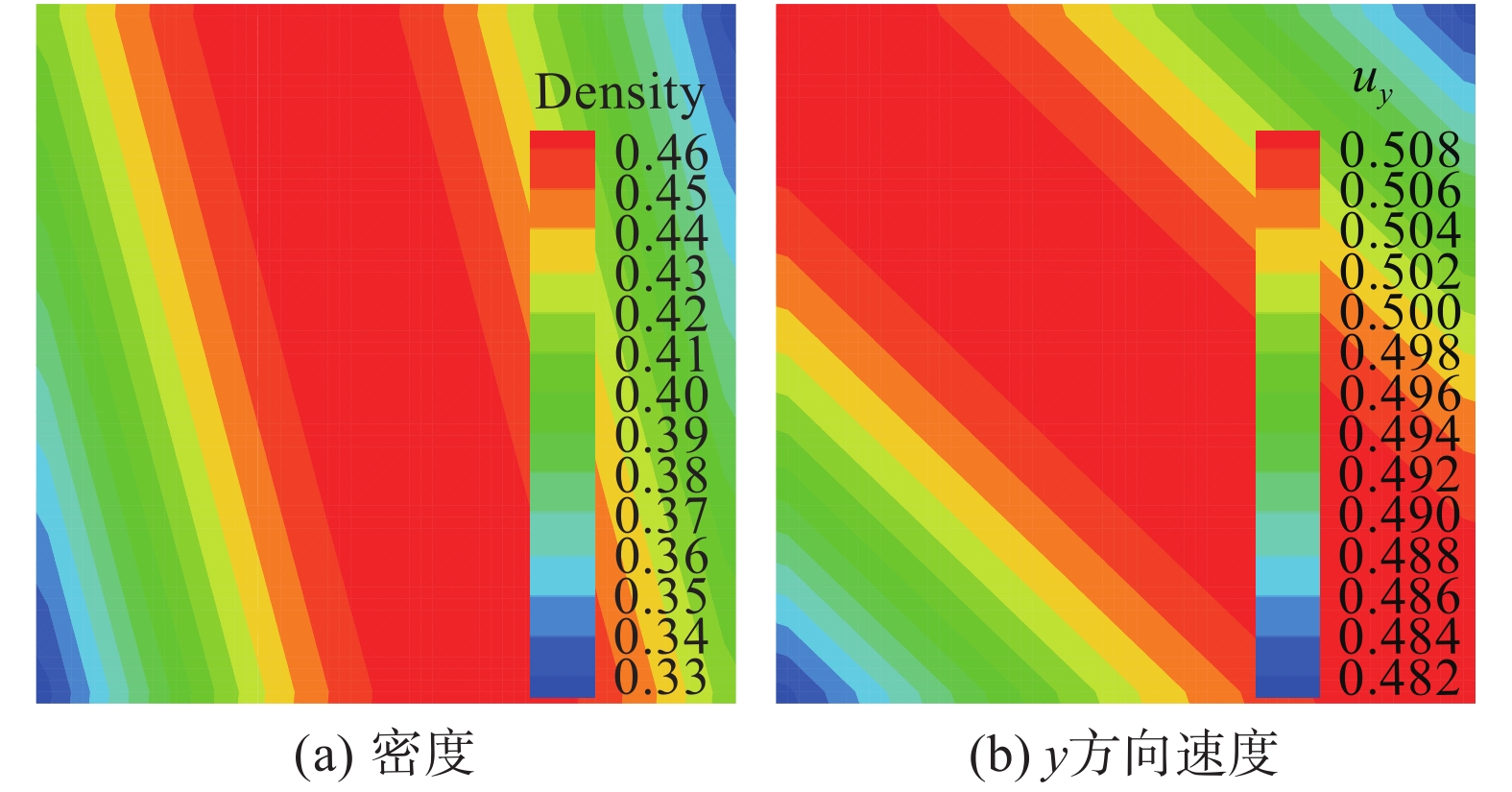
对应该制造解,得到的流场如图8所示。
|
图 8 当前制造解流场 Fig.8 Flow fields of current manufactured solutions |
对入口与出口条件单独验证,在验证其中一个边界条件时,其余边界右值均使用MMS精确解赋值,这样有利于研究不同边界对流动求解精度的直接影响。统计误差如图9与图10所示。
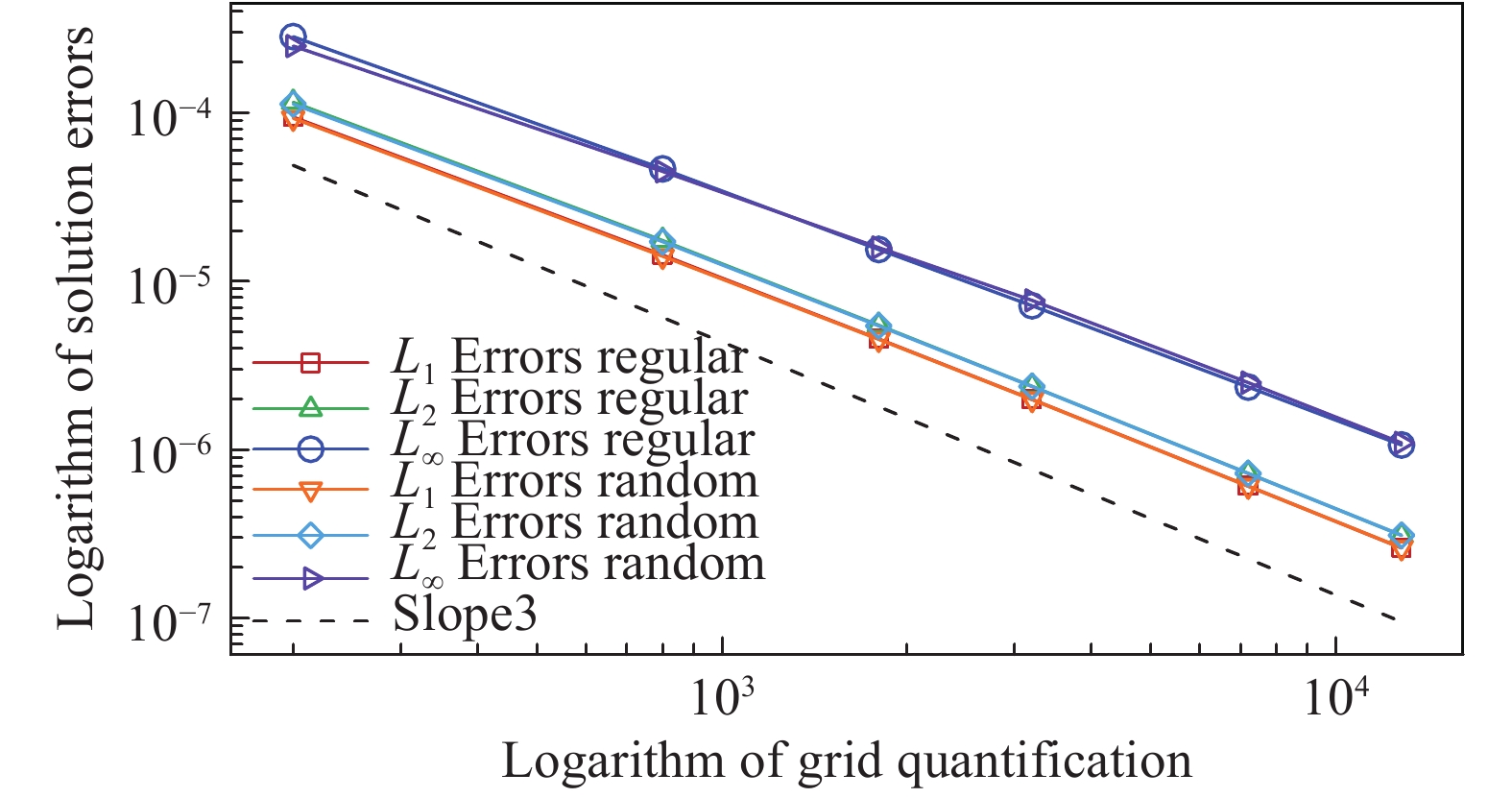
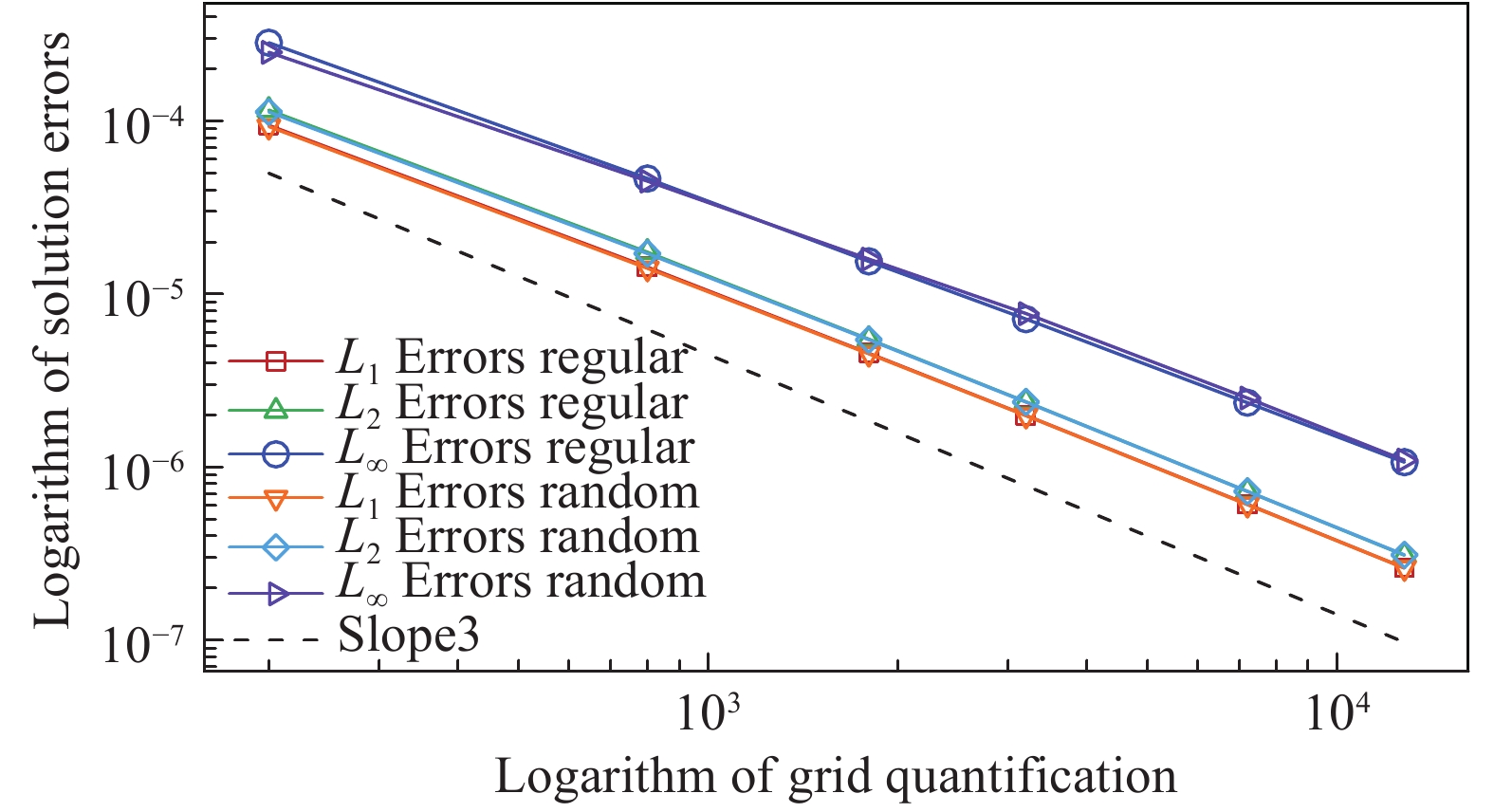
从图9与图10反映的结果可以看出,对MMS流动单独施加亚声速入口、出口边界条件时,不论是在规则网格还是扰动网格上,均达到了三阶精度。因此,对MMS流动的亚声速入口与出口施加黎曼边界条件不会影响流动的求解精度。
|
图 9 施加亚声速入口边界条件的误差曲线 Fig.9 Error curves with the subsonic inlet boundary condition |
|
图 10 施加亚声速出口边界条件的误差曲线 Fig.10 Error curves with the subsonic outlet boundary condition |
不同的弱施加边界条件对无黏壁面的处理方式基本一致。壁面法向速度为0,压力和温度的右值与左值相等。为保证速度的法向分量为0,验证壁面时给定解的形式为:
| $ \begin{array}{l} \rho_{\rm{MMS}} = 0.32 + 0.15\sin \left[ {{\rm{{\text{π}} }}\left( {0.79x + 0.21y} \right)} \right] \\ u _{\rm{MMS}} = 0.36 + 0.06\sin \left[ {{\rm{{\text{π}} }}\left( {0.47x + 0.53y} \right)} \right] \\ v_{\rm{MMS}} = 0.11\left( {1 - y} \right)\sin \left[ {{\rm{{\text{π}} }}\left( {0.49x + 0.51y} \right)} \right] \\ p _{\rm{MMS}} = 0.43 + 0.31\sin \left[ {{\rm{{\text{π}} }}\left( {0.82x + 0.18y} \right)} \right] \end{array} $ | (18) |
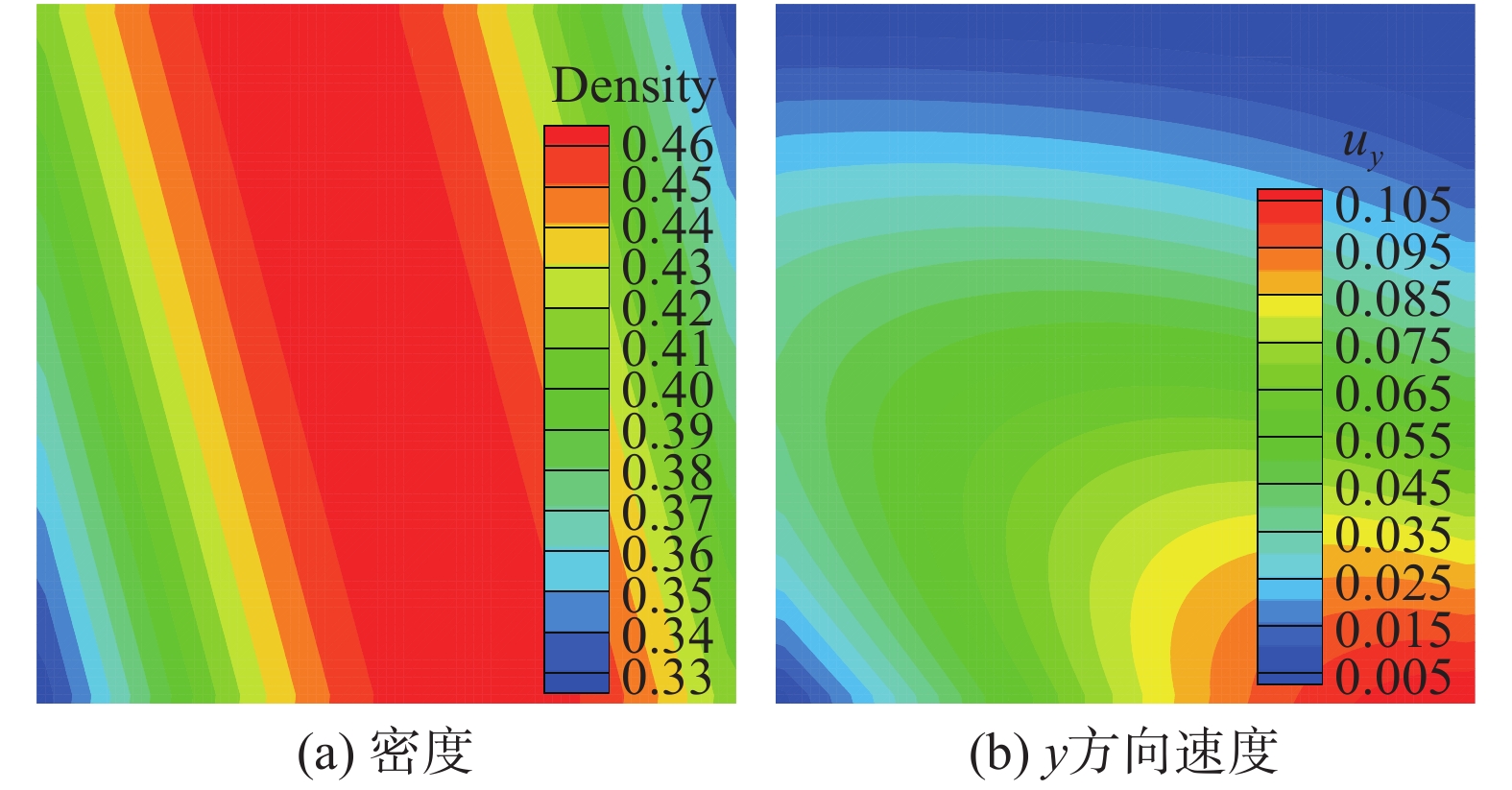
Folkner和Katz等[35]在二阶精度有限体积方法中验证了对MMS流动施加此类含有真实物理意义边界条件的可行性。本节将其推广至高阶精度非结构有限体积方法,以检验在高阶方法中对MMS流动施加此类边界的合理性。基于方程(27)得到的流场如图11所示。
|
图 11 MMS流场信息 Fig.11 Flow fields of the MMS flow |
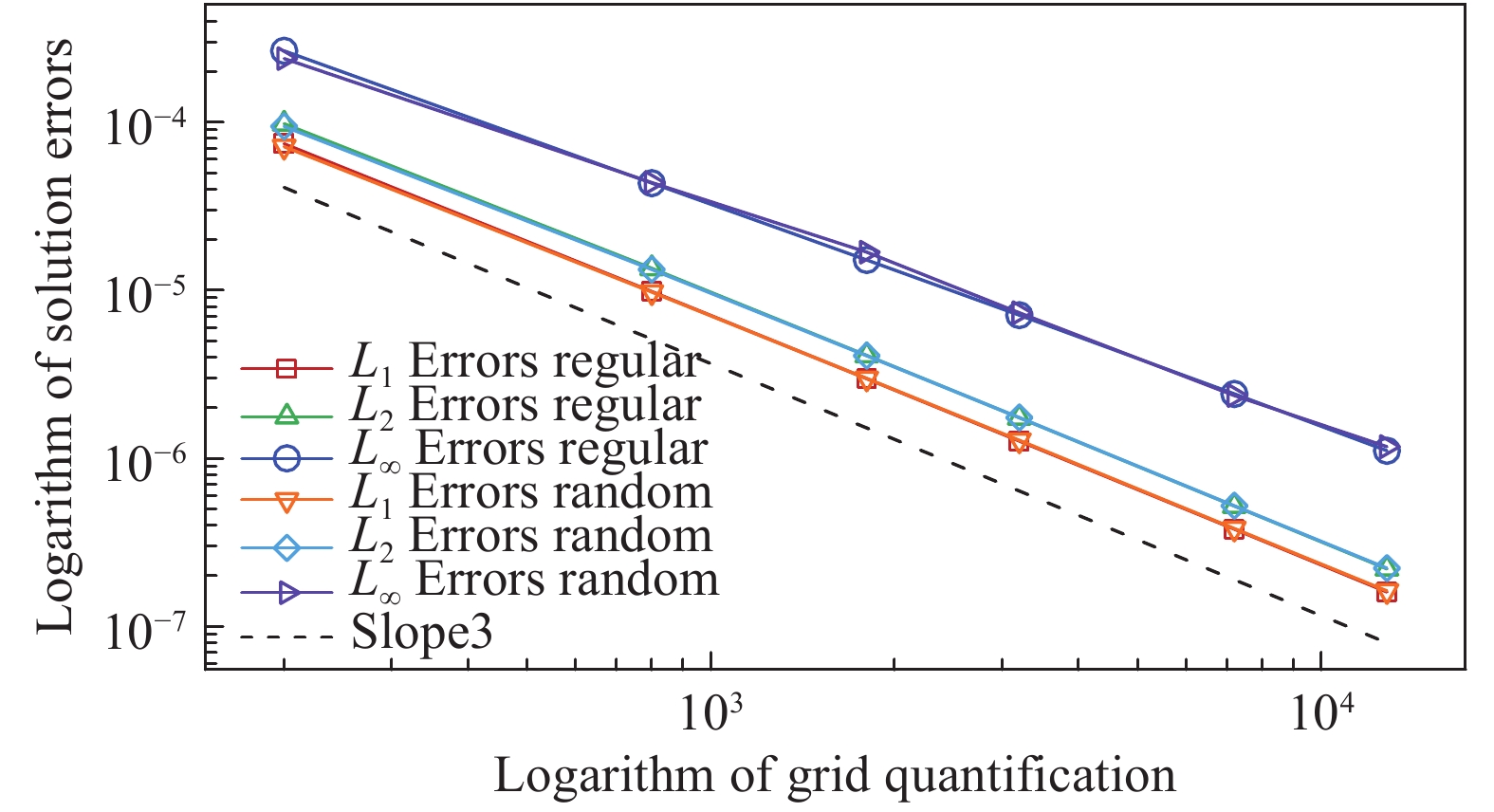
在验证壁面边界时,除壁面外其余边界右值均由MMS精确解赋值。在规则与扰动网格下的统计误差如图12所示。由图12可以看出,对MMS流动施加相应的壁面边界条件后,不论在规则网格还是扰动网格上,计算结果仍可达到三阶精度。由此验证了对MMS流动施加壁面边界条件的可行性,同时也将文献[35]中提出的壁面边界验证方式有效推广至高阶精度非结构有限体积算法。
|
图 12 施加无黏壁面边界条件的误差曲线 Fig.12 Error curves with the inviscid wall boundary condition |
相比亚声速入口、出口的边界条件施加方式,超声速入口与出口的边界条件施加相对简便—入口采用MMS精确解赋值,出口的右值等于左值。为保证入口、出口处为超声速,给定解的形式为:
| $ \begin{array}{l} \rho_{\rm{MMS}} = 2.12 + 0.15\sin \left[ {{\rm{{\text{π}} }}\left( {0.79x + 0.21y} \right)} \right] \\ u_{\rm{MMS}} = 2.62 + 0.06\sin \left[ {{\rm{{\text{π}} }}\left( {0.47x + 0.53y} \right)} \right] \\ v _{\rm{MMS}} = 2.18 + 0.03\sin \left[ {{\rm{{\text{π}} }}\left( {0.49x + 0.51y} \right)} \right] \\ p_{\rm{MMS}} = 2.62 + 0.31\sin \left[ {{\rm{{\text{π}} }}\left( {0.82x + 0.18y} \right)} \right] \end{array} $ | (19) |
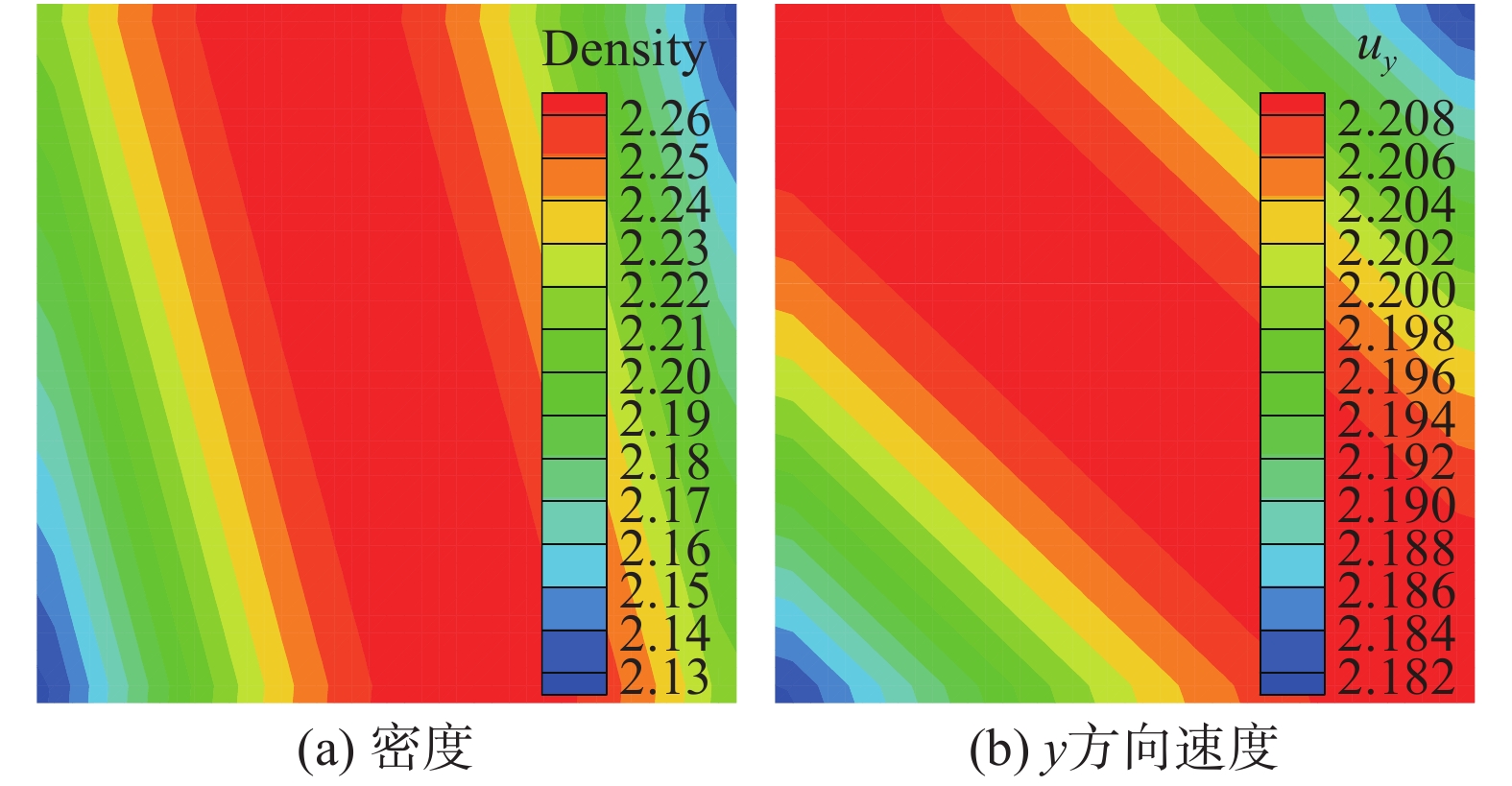
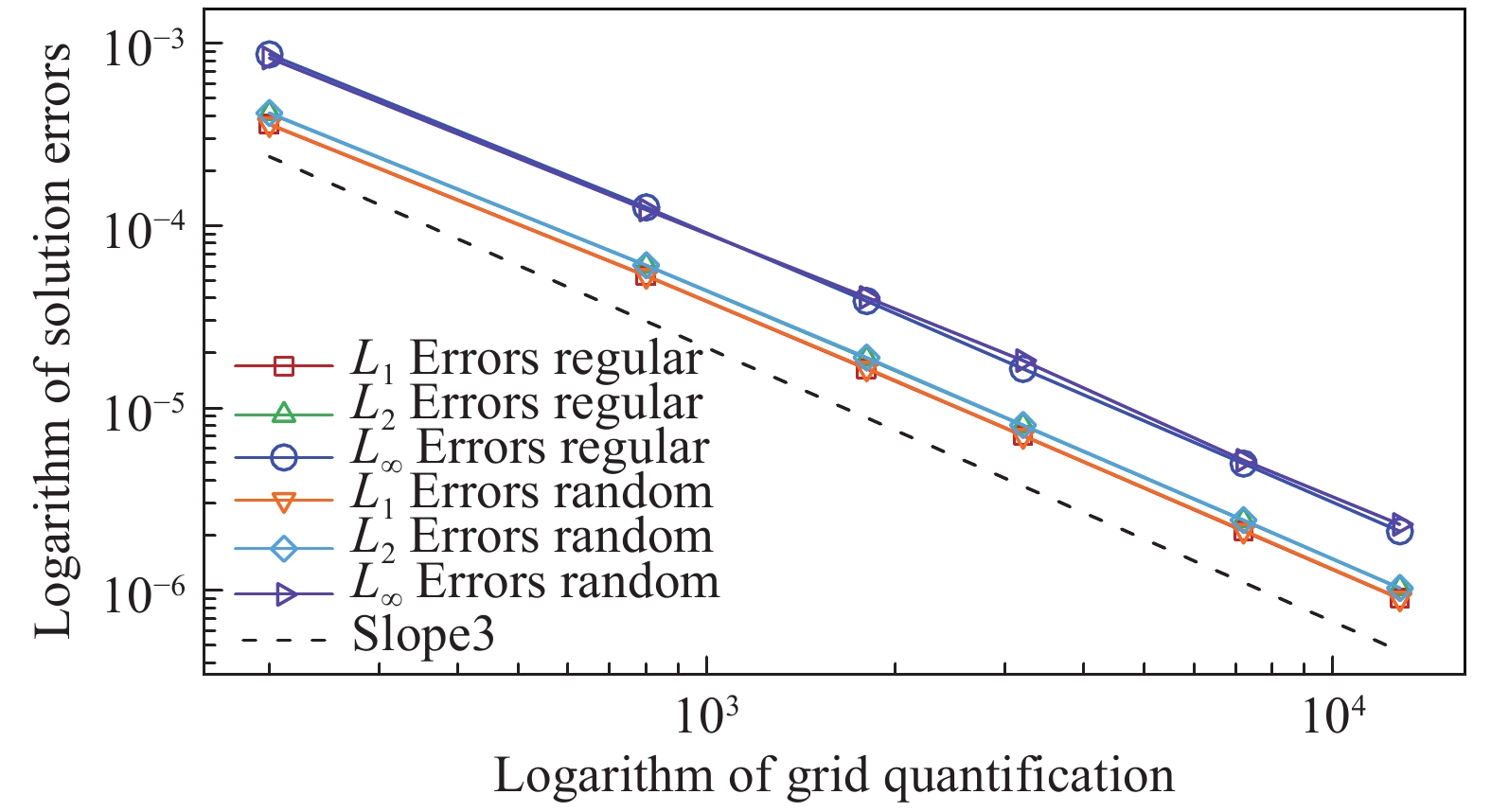
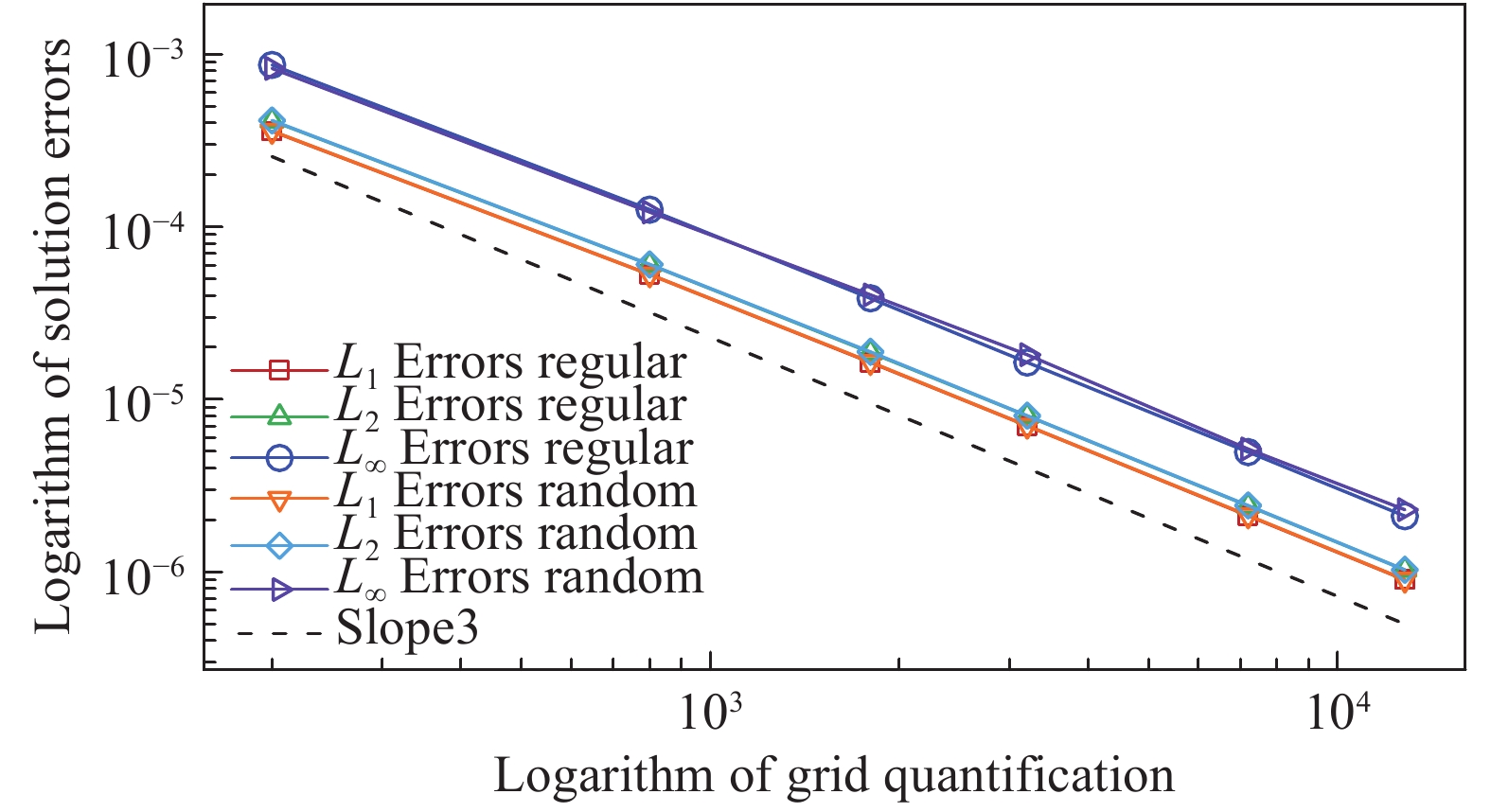
图13为该制造解对应的流场云图。与3.2和3.3节的验证方式相同,对入口与出口条件单独验证。图14与15分别给出了施加超声速入口与出口条件得到的误差。从图14与图15反映的结果来看,单独对MMS流动施加超声速入口或出口条件,并未破坏计算精度,L1、L2与L∞误差均达到了三阶精度。我们将三类边界条件在规则密网格上得到的计算精度汇总,结果如表2所示。
|
图 13 MMS流场信息 Fig.13 Flow fields of the MMS flow |
|
图 14 施加超声速入口边界条件的误差曲线 Fig.14 Error curves with the supersonic inlet boundary condition |
|
图 15 施加超声速出口边界条件的误差曲线 Fig.15 Error curves with the supersonic outlet boundary condition |
| 表 2 不同弱施加边界条件在密网格之间的计算精度 Table 2 Accuracy of different weak boundary conditions between vfin and vvfin grids |
|
|
从表2可以看出,对MMS流动的不同边界单独施加相应的边界条件后,在密网格上L1与L2误差均达到了三阶精度,L∞误差略低于但接近三阶精度。此外,从误差统计曲线可以明显看出,对MMS流动施加合理的边界条件后,随着网格加密,求解精度的变化较小,即使在稀疏网格上结果同样接近三阶精度,并趋于一致收敛。因此,这也从一个层面论证了在高阶方法中对MMS流动施加具有真实物理意义边界条件的合理性。
综上,黎曼边界条件在MMS流动中具有较好的数值表现,尤其在处理亚声速入口、出口时,为MMS流动的高精度数值模拟提供了一种简单有效的边界条件施加方式。
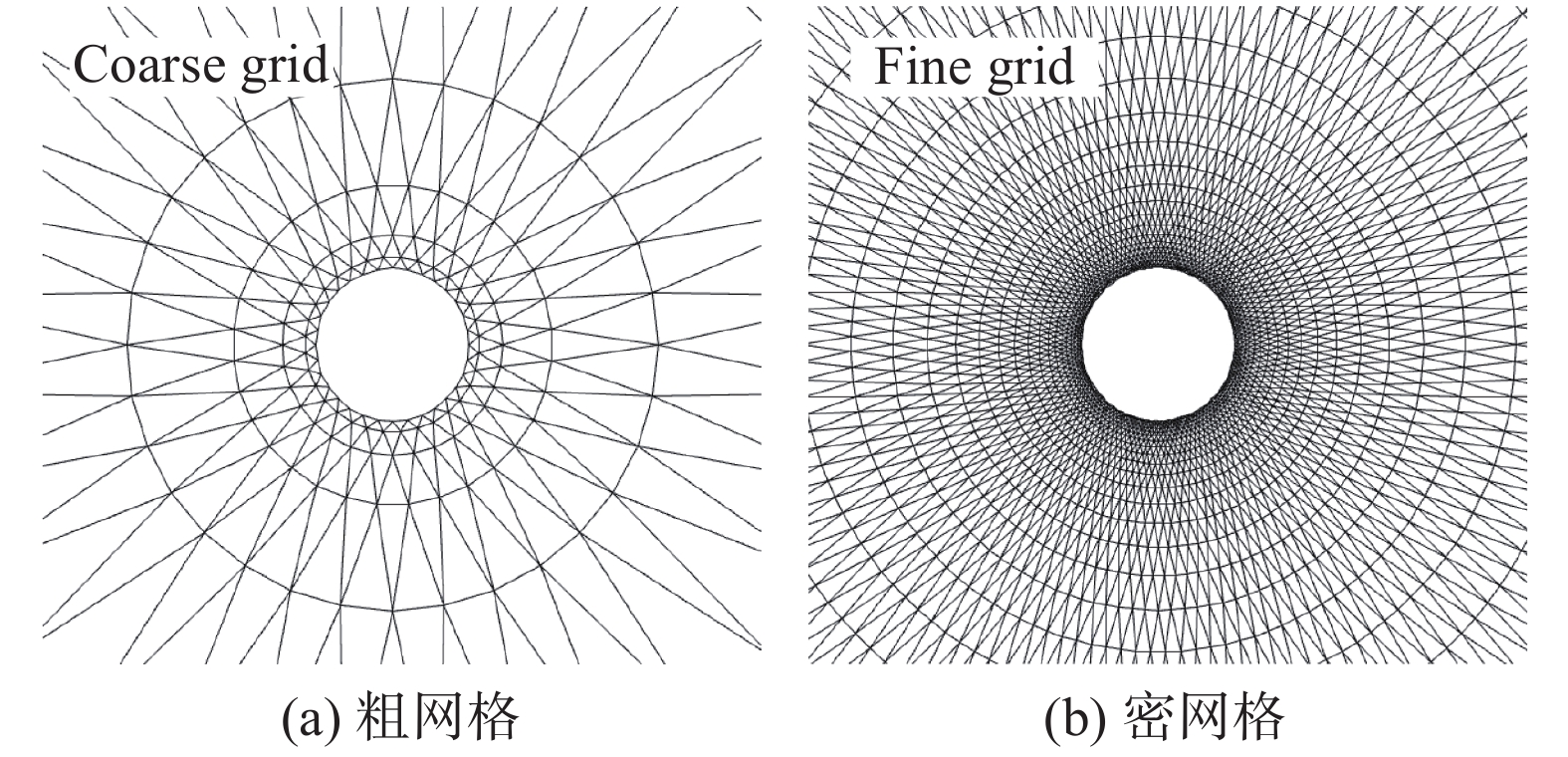
4 亚声速无黏圆柱绕流验证为了测试上述边界条件在真实流动中的表现,在亚声速无黏圆柱绕流上检验其数值效果。该流动是典型的亚声速算例,边界条件包括亚声速远场和无黏壁面。由之前的分析可以知,黎曼边界可有效简化对亚声速远场的处理过程。为对比黎曼边界条件在高阶求解器中的数值表现,在处理远场边界时,还测试了常用的基于一维黎曼不变量的无反射边界条件[35]。网格采用O型拓扑,壁面附近的局部放大图如图16所示。主要来流参数
| ${r_i} = {r_0} + \left( {1 + \frac{{2{\rm{{\text{π}} }}}}{{512}}\sum\limits_{k = 0}^{i - 1} {{\alpha ^k}} } \right),\;i = 1,\;2,\;...,\;32$ | (20) |
其中
|
图 16 圆柱绕流计算网格示意图 Fig.16 Schematic diagram of grids for the cylinder flow simulation |
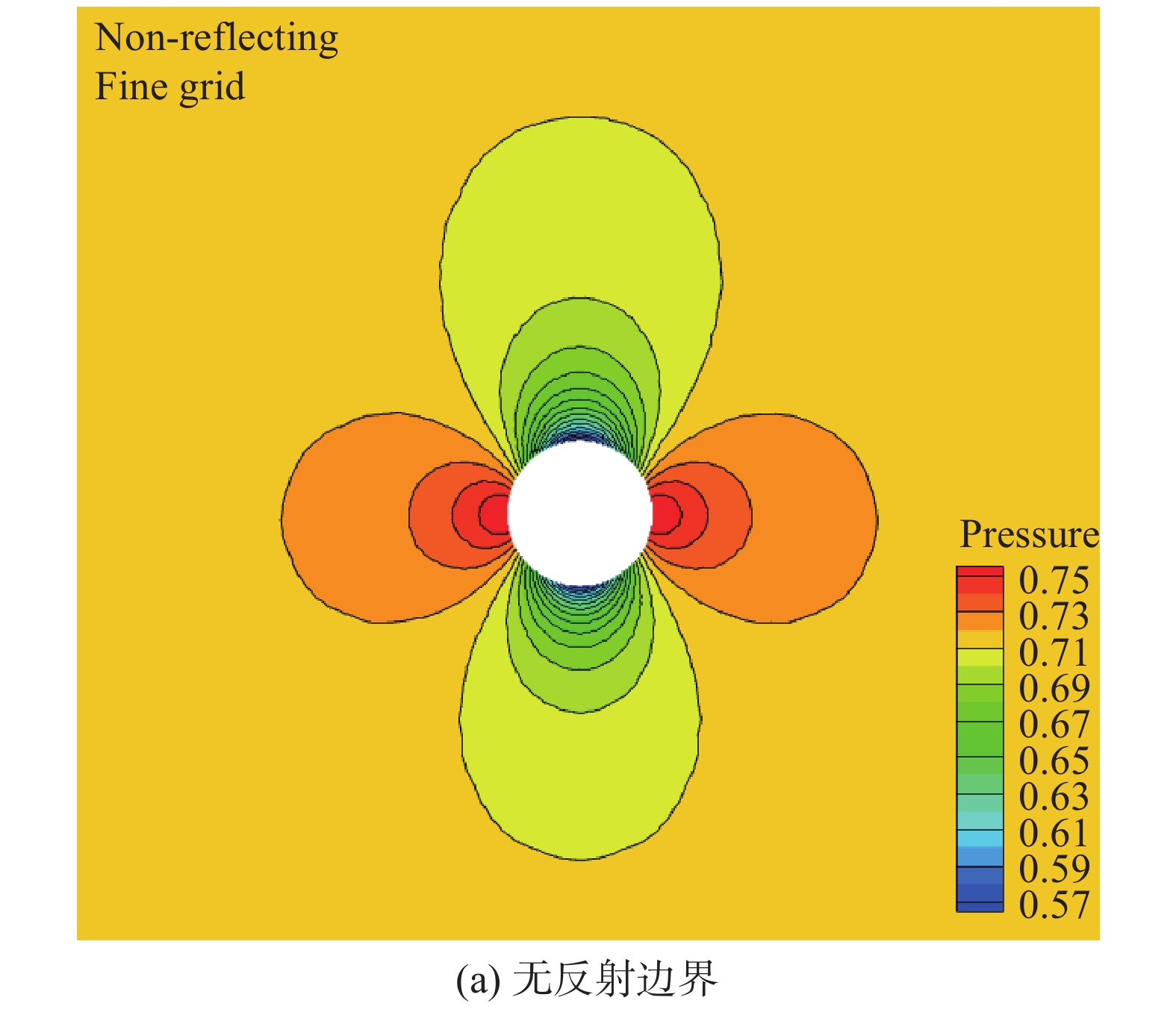
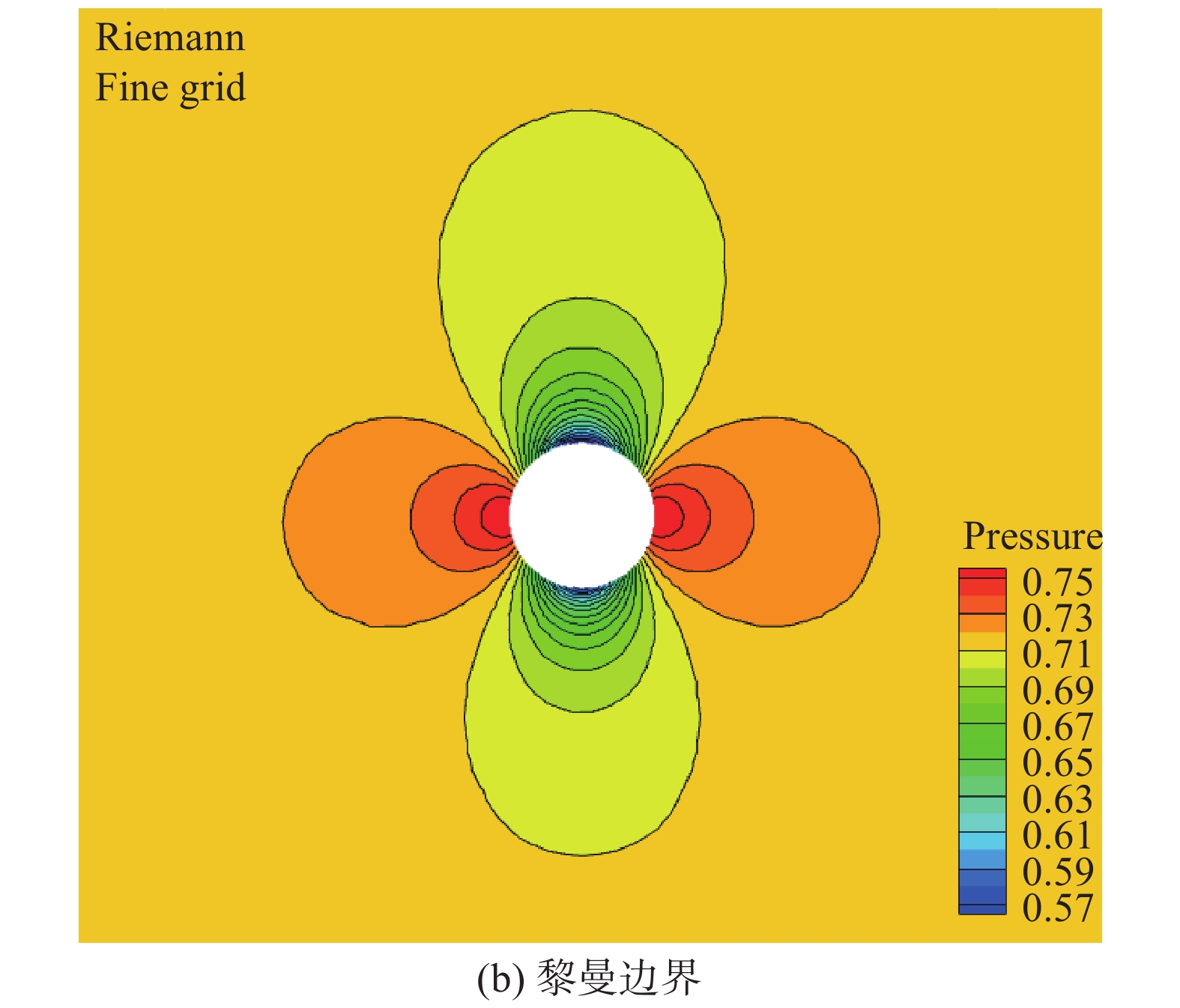
基于两种不同的弱施加边界条件,首先测试了由两种边界条件得到的流场压力云图,如图17所示。从流场云图可以看出,由两种边界条件得到的流场均具有较好的对称性。
|
图 17 |
|
图 17 不同边界条件下的圆柱绕流流场 Fig.17 Flow fields of the cylinder flow with differentboundary conditions |
为进一步量化对比两种边界条件之间的差异,统计了沿圆柱表面的总压恢复系数与熵误差。总压恢复系数的定义如下:
| $r = \frac{{{p_t}}}{{{p_{t,\infty }}}}$ | (21) |
根据等熵关系式可得到总压
| ${p_t} = p{\left( {1 + \frac{{\gamma + 1}}{2}M{a^2}} \right)^{\tfrac{\gamma }{{\left( {\gamma - 1} \right)}}}}$ | (22) |
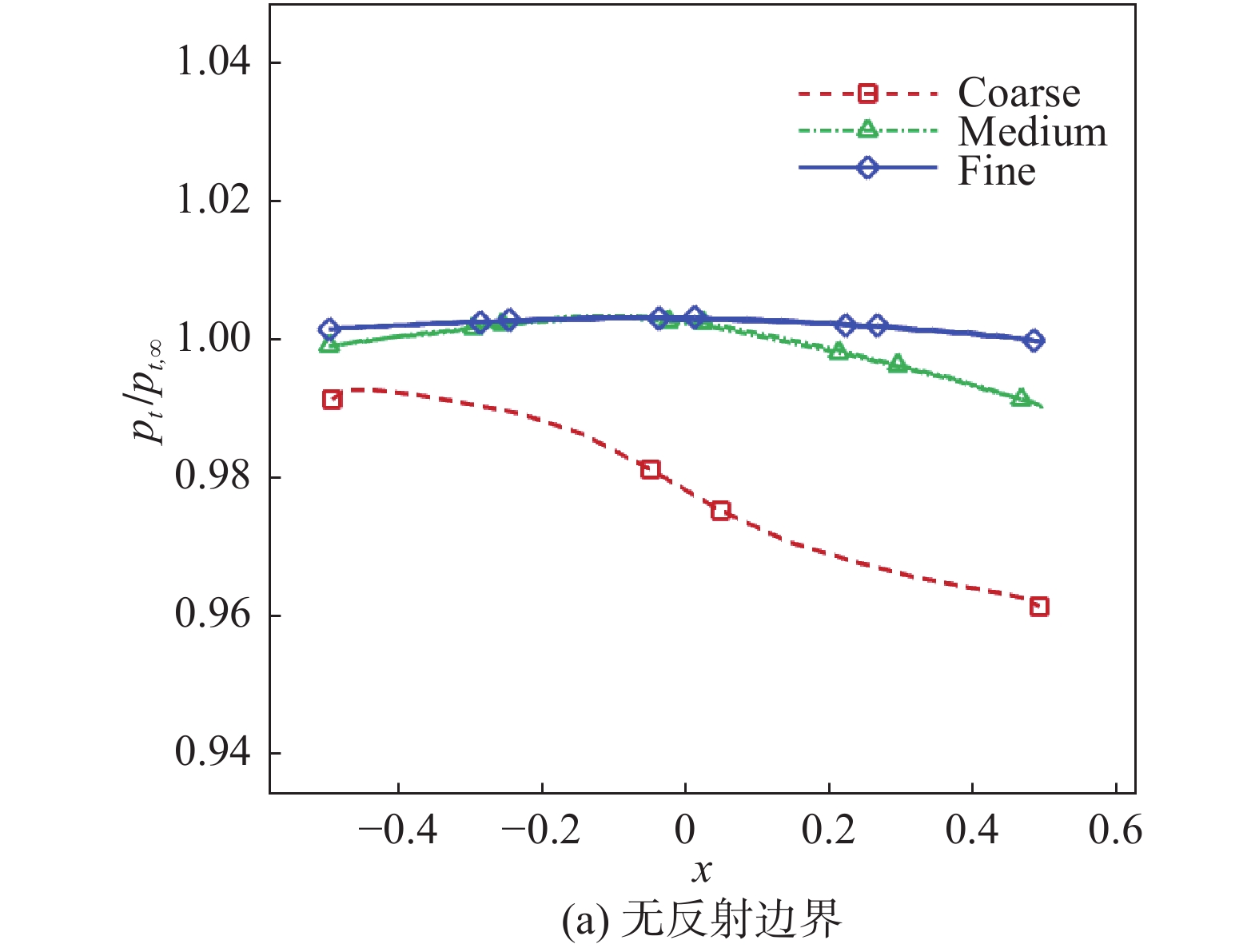
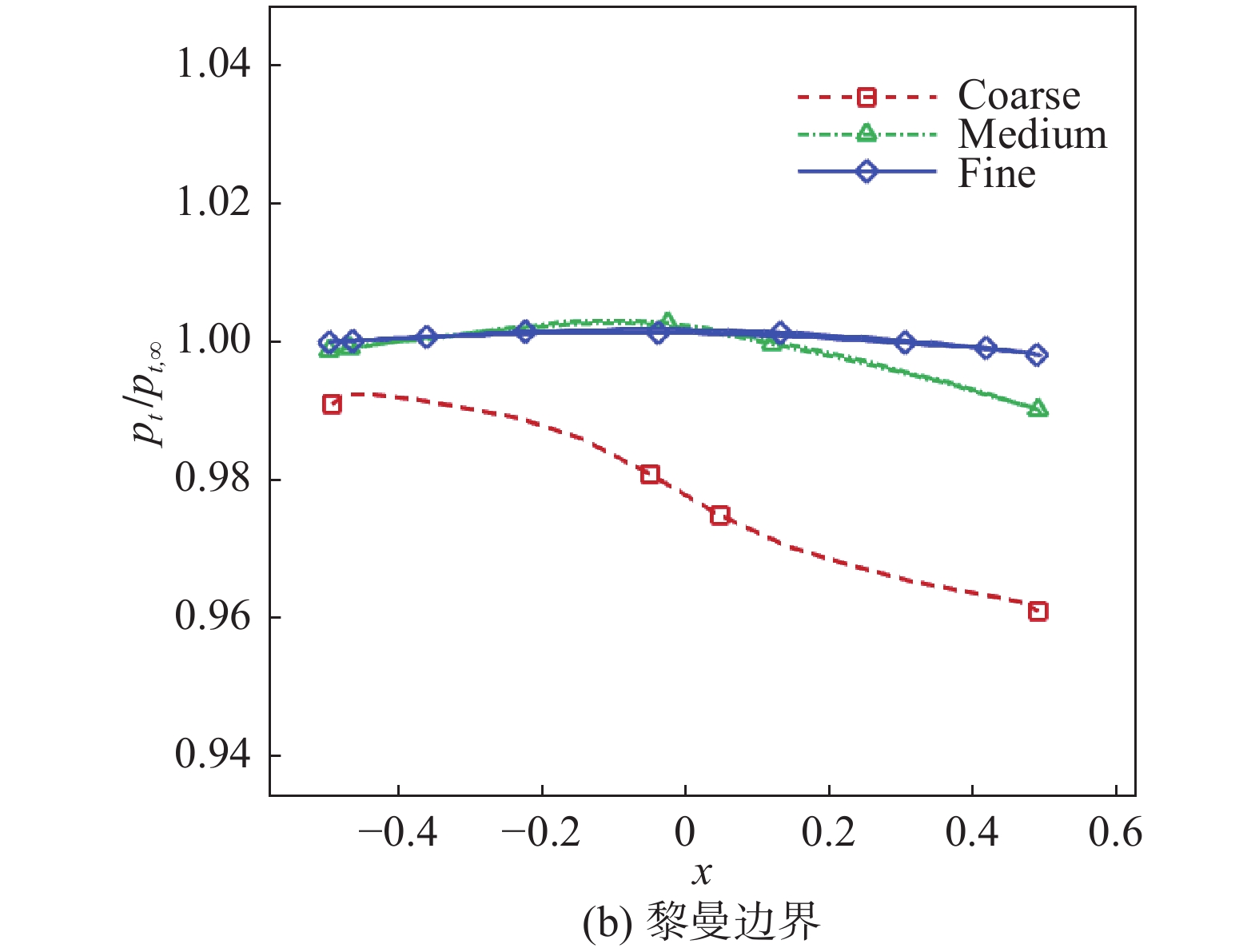
由于该算例为无黏亚声速流动,因此理想情况下总压恢复系数应当精确等于1.0。图18给出了总压恢复系数沿壁面的分布情况。从图中可明显看出,在梳网格上,总压损失较大,而随着网格的不断加密,数值耗散逐渐降低,总压恢复系数接近理想值。
|
图 18 |
|
图 18 圆柱绕流总压恢复系数分布曲线 Fig.18 Total pressure recovery coefficients of the cylinder flow |
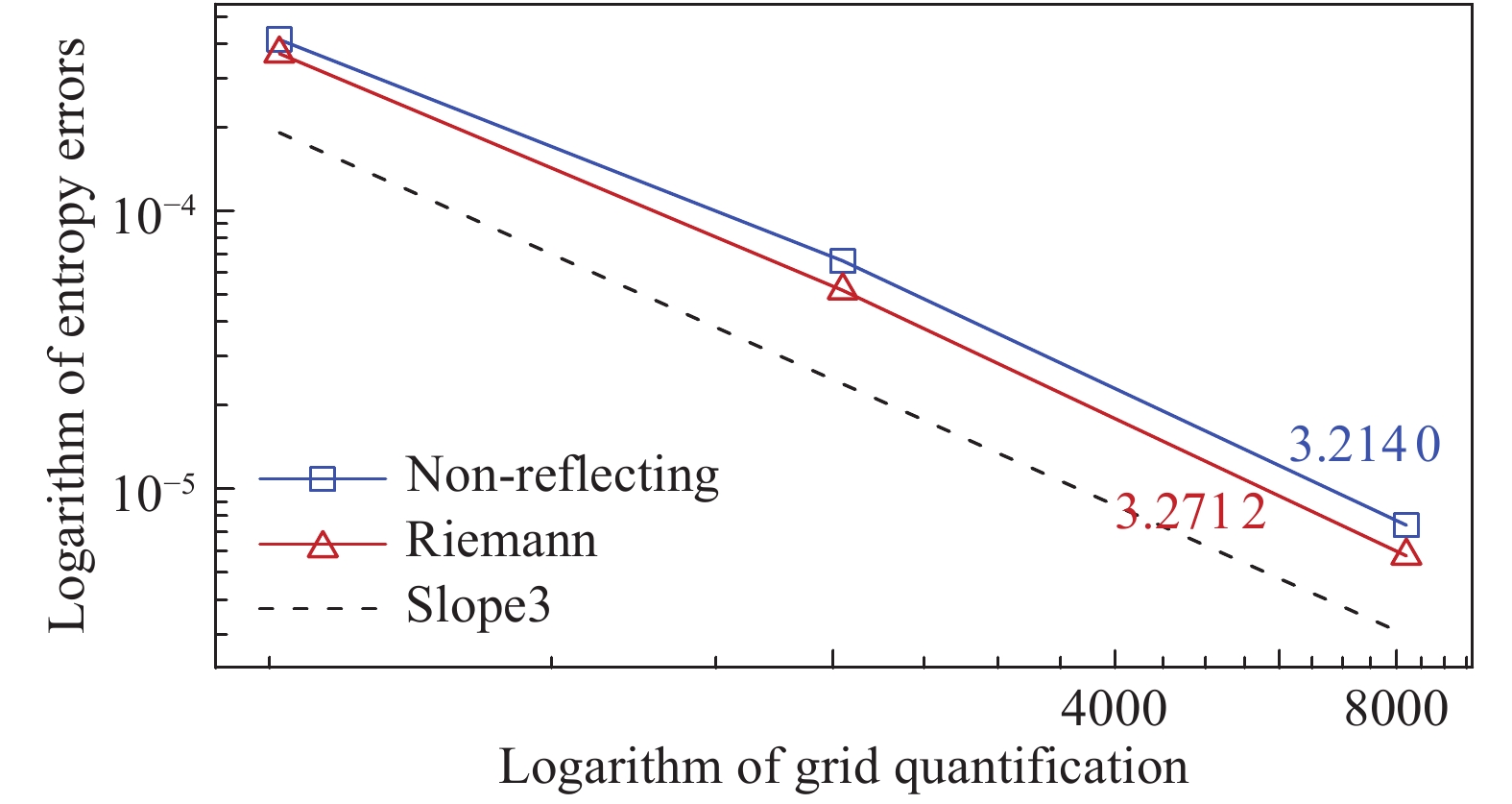
此外,统计了由不同边界条件得到的熵误差,结果如图19所示。从图19可以看出,采用两种远场边界条件得到的计算精度基本一致,但由黎曼边界得到的误差值略低于常用的无反射边界,更利于计算结果的准确性。综上,在亚声速圆柱绕流中,黎曼边界条件的数值表现优于无反射边界条件。
|
图 19 熵误差统计 Fig.19 Entropy errors |
本节引入添加初始高斯脉冲(Gaussian Pulse)的非定常熵波传播算例,来测试黎曼边界条件在出口处的无反射特性。初始扰动函数如下[40]:
| ${\rho _0} = 1 + 0.1{{\rm{e}}^{ - 400{{\left( {x - {x_c}} \right)}^2}}}$ | (23) |
式中xc取0.5,计算域为
| $\left( {{u_0},\;{v_0},\;{p_0}} \right) = \left( {0.5,\;0,\;1} \right)$ | (24) |
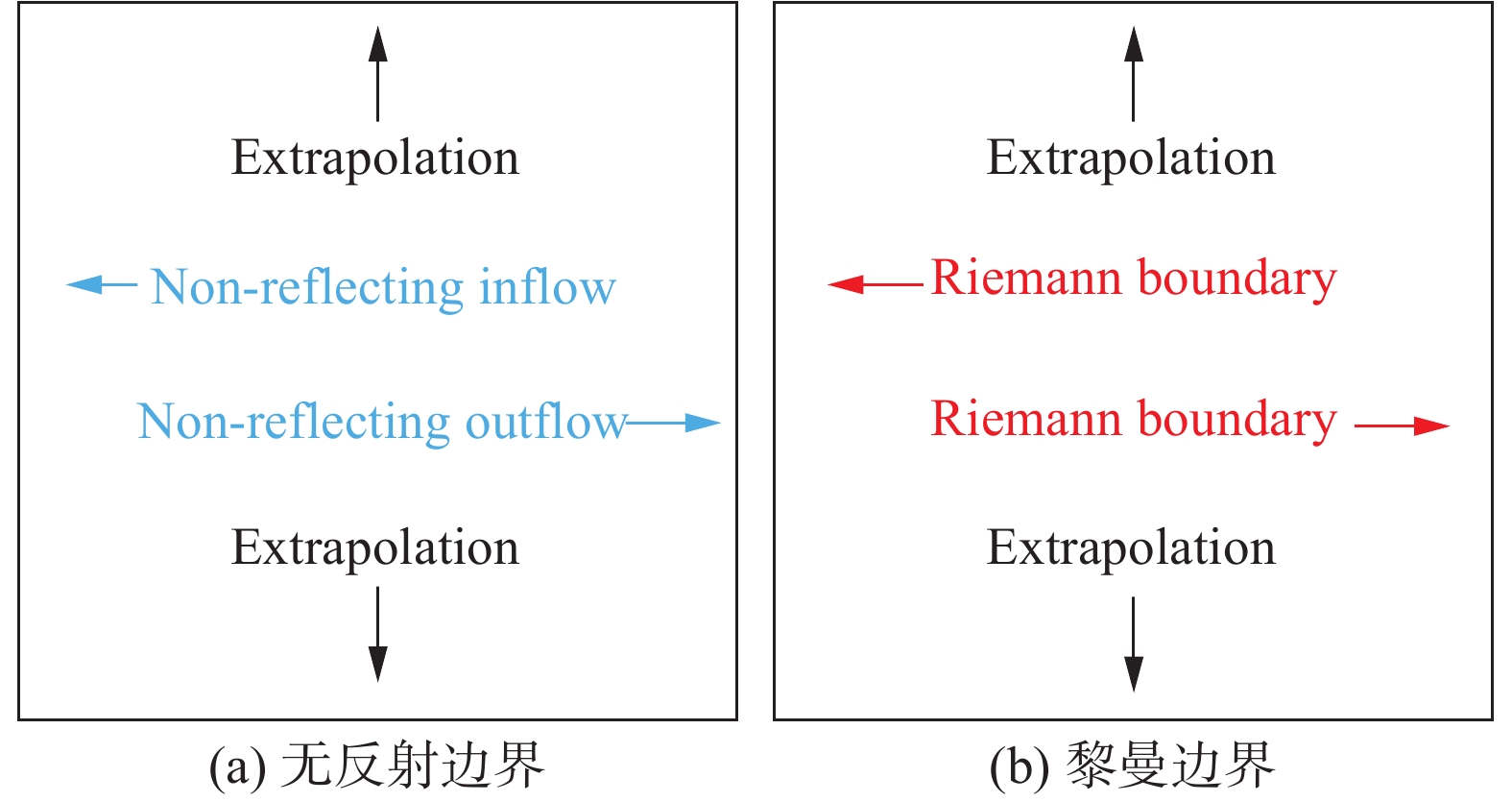
计算过程中,分别对比了由黎曼边界条件与无反射边界条件得到的出口特性。在施加相应的边界条件时,为防止y方向边界条件对计算结果的影响,计算域的上下边界均采用外推边界。具体的边界条件施加示意图如图20。从图20可以看出,黎曼边界条件针对亚声速入口与出口可通过精确求解对应的黎曼问题来统一处理,相比无反射边界条件更加简便。
|
图 20 两种边界条件的施加示意图 Fig.20 Schematic diagram for the imposition of two boundary conditions |
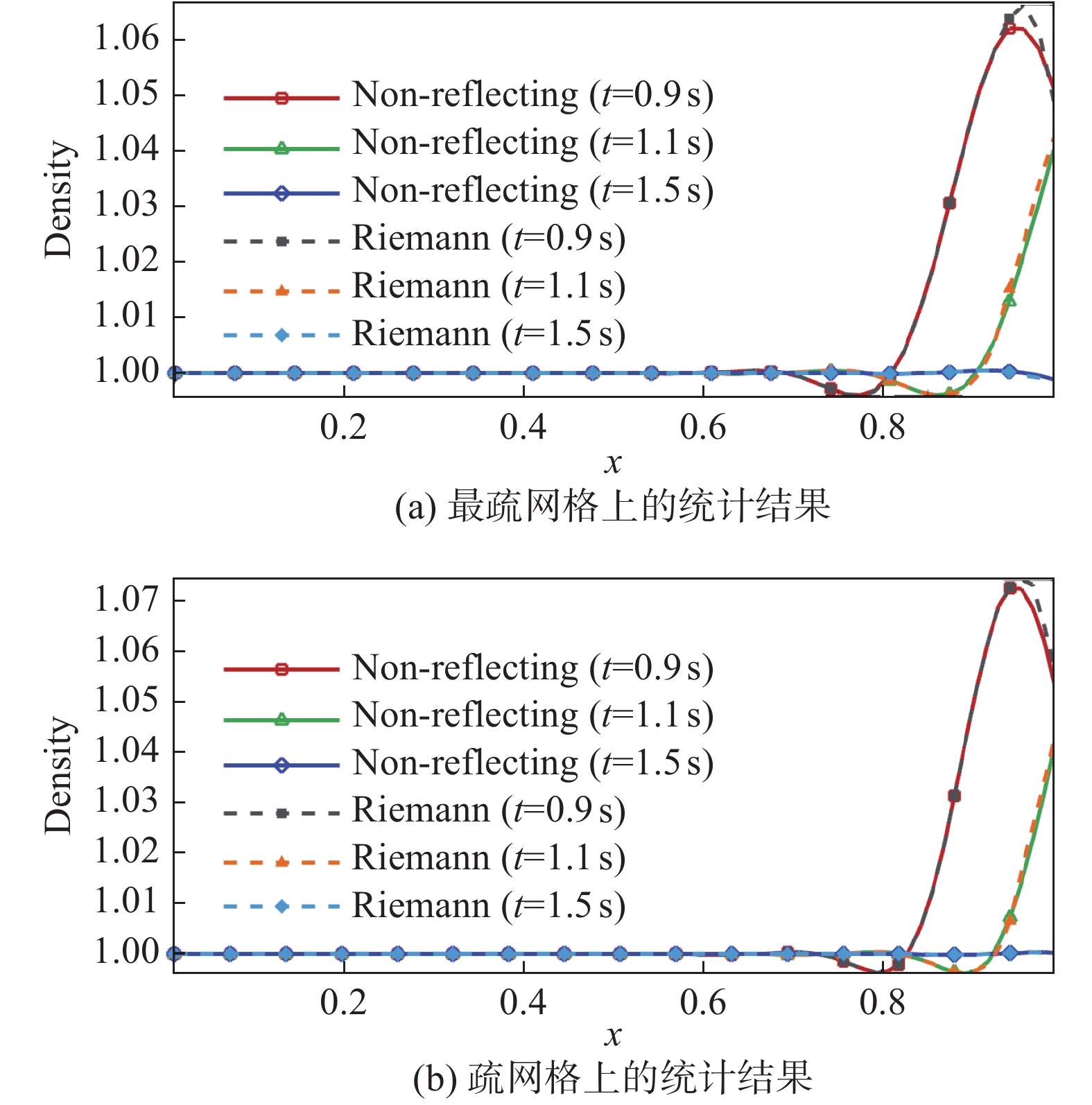
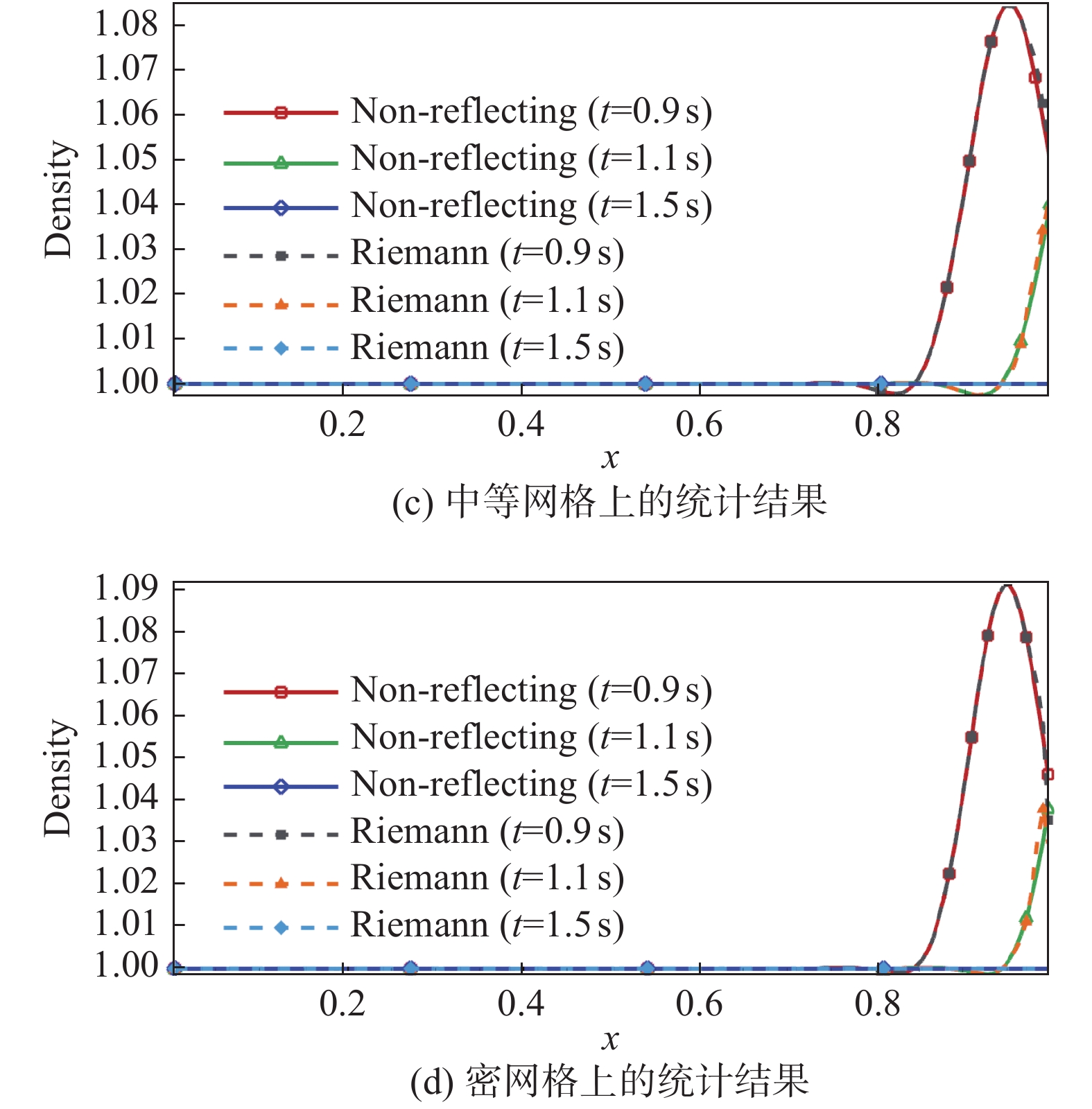
为对比两种边界在出口处的无反射特性,分别设置了四套由疏到密的均匀四边形网格,分布量从60×60至160×160(图21)。在四套网格下,统计了添加初始高斯扰动的ρ沿x方向的变化情况,同时参考文献[40],分别给出了时间t = 0.9 s、1.1 s以及1.5 s时的结果。统计结果如图22所示。表3、表4为不同时刻两种边界条件得到的L2误差的具体数值。

|
图 21 疏网格与密网格 Fig.21 Coarse and fine grids |
|
图 22 |
|
图 22 不同网格上密度在三个时刻的统计结果 Fig.22 Density on different grids at three moments |
| 表 3 无反射边界条件在不同时刻的L2误差统计 Table 3 L2 errors of the non-reflective boundary conditionat different moments |
|
|
从图22中可以看出,随着网格的不断加密,两种边界条件的密度变化曲线接近,在出口边界均具有较好的无反射特性。因此说明了对亚声速非定常扰流施加黎曼边界条件具有一定的合理性。此外,结合表3的数据可以看出,黎曼边界条件与无反射边界条件在四套网格上,不同时刻的L2误差接近,并在t = 0.9 s与t =1.5 s时误差均低于无反射边界条件。
| 表 4 黎曼边界条件在不同时刻的L2误差统计 Table 4 L2 errors of the Riemann boundary condition at different moments |
|
|
最后,相比无反射边界条件,黎曼边界条件针对亚声速入口与出口,可通过精确求解黎曼问题来统一处理,有效简化了边界条件的处理过程。
6 结 论本文对黎曼边界条件展开了细致讨论,并将其推广至高精度非结构有限体积方法。现将这种弱施加边界条件在高阶精度数值方法中的表现情况总结如下:
1)从方法实现层面而言,相比传统无反射边界条件,黎曼边界在处理亚声边界时,均可通过精确求解黎曼问题来统一施加,无需判断特征方向。
2)从数值结果来看,在高阶精度框架内对MMS流动单独施加黎曼边界条件,以及壁面、超声速入口与出口边界条件后,计算结果均可达到设计精度,并趋于一致收敛。
3)在真实流动中,基于黎曼边界条件和无反射边界条件得到的流场及总压恢复系数效果接近,并且其熵误差更低。
4)在添加初始高斯脉冲扰动的非定常流动中,新的边界条件在出口处维持了较好的无反射特性。因此,在非定常扰流中施加黎曼边界条件合理可行。
综上,黎曼边界条件在高阶精度非结构有限体积方法中的有效性得到了较好地验证,为非结构高精度数值格式提供了一种便捷有效的亚声速边界处理途径。在接下来的工作中,将进一步验证推广黎曼边界在黏性流动和实际工程问题中的应用。
| [1] |
MAVRIPLIS D J. Unstructured grid techniques[J]. Annual Review of Fluid Mechanics, 1997, 29: 473-547. DOI:10.1146/annurev.fluid.29.1.473 |
| [2] |
王年华, 李明, 张来平. 非结构网格二阶有限体积法中黏性通量离散格式精度分析与改进[J]. 力学学报, 2018, 50(3): 527-537. WANG N H, LI M, ZHANG L P. Accuracy analysis and improvement of viscous flux schemes in unstructured second-order finite-volume discretization[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(3): 527-537. DOI:10.6052/0459-1879-18-037 (in Chinese) |
| [3] |
LISEIKIN V D. Grid generation methods[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 1999.doi: 10.1007/978-3-662-03949-6.
|
| [4] |
赵辉, 张耀冰, 陈江涛, 等. 非结构网格体心梯度求解方法的精度分析[J]. 空气动力学学报, 2019, 37(5): 844-854. ZHAO H, ZHANG Y B, CHEN J T, et al. The accuracy assessment of gradient computation methods on unstructured grids[J]. Acta Aerodynamica Sinica, 2019, 37(5): 844-854. DOI:10.7638/kqdlxxb-2018.0092 (in Chinese) |
| [5] |
XIA Y D, WANG C J, LUO H, et al. Assessment of a hybrid finite element and finite volume code for turbulent incompressible flows[J]. Journal of Computational Physics, 2016, 307: 653-669. DOI:10.1016/j.jcp.2015.12.022 |
| [6] |
PANDARE A K, LUO H. A hybrid reconstructed discontinuous Galerkin and continuous Galerkin finite element method for incompressible flows on unstructured grids[J]. Journal of Computational Physics, 2016, 322: 491-510. DOI:10.1016/j.jcp.2016.07.002 |
| [7] |
党亚斌, 刘凯礼, 孙一峰, 等. 用隐式高精度间断伽辽金方法模拟可压层流和湍流[J]. 空气动力学学报, 2018, 36(3): 535-541. DANG Y B, LIU K L, SUN Y F, et al. Implicit high order discontinuous Galerkin method for compressible laminar and turbulent flow simulation[J]. Acta Aerodynamica Sinica, 2018, 36(3): 535-541. DOI:10.7638/kqdlxxb-2017.0183 (in Chinese) |
| [8] |
DISKIN B, THOMAS J L, NIELSEN E J, et al. Comparison of node-centered and cell-centered unstructured finite-volume discretizations: viscous fluxes[J]. AIAA Journal, 2010, 48(7): 1326-1338. DOI:10.2514/1.44940 |
| [9] |
DISKIN B, THOMAS J L. Comparison of node-centered and cell-centered unstructured finite-volume discretizations: inviscid fluxes[J]. AIAA Journal, 2011, 49(4): 836-854. DOI:10.2514/1.J050897 |
| [10] |
JAMESON A, MAVRIPLIS D J. Finite volume solution of the two-dimensional Euler equations on a regular triangular mesh[J]. AIAA Journal, 1986, 24(4): 611-618. DOI:10.2514/3.9315 |
| [11] |
XIE B, JIN P, XIAO F. 基于非结构网格的不可压N-S方程多矩有限体积法[J]. 空气动力学学报, 2016, 34(2): 252-266. BIN X, PENG J, FENG X. A multi-moment finite volume method for incompressible Navier-Stokes equations on unstructured grids[J]. Acta Aerodynamica Sinica, 2016, 34(2): 252-266. DOI:10.7638/kqdlxxb-2016.0013 (in Chinese) |
| [12] |
徐岚, 崔桂香, 许春晓, 等. 非均匀网格湍流大涡模拟高精度有限体积解法[J]. 空气动力学学报, 2006, 24(3): 275-284. XU L, CUI G X, XU C X, et al. High accurate finite volume method on non-uniform meshes for large eddy simulation of turbulent flows[J]. Acta Aerodynamica Sinica, 2006, 24(3): 275-284. DOI:10.3969/j.issn.0258-1825.2006.03.002 (in Chinese) |
| [13] |
郑华盛, 赵宁, 朱君. 二维非结构网格上的高精度有限体积WENO格式[J]. 空气动力学学报, 2010, 28(4): 446-451. ZHENG H S, ZHAO N, ZHU J. High order finite volume weighted essentially non-oscillatory schemes on two dimensional unstructured meshes[J]. Acta Aerodynamica Sinica, 2010, 28(4): 446-451. DOI:10.3969/j.issn.0258-1825.2010.04.015 (in Chinese) |
| [14] |
ZHANG L P, LIU W, HE L X, et al. A class of hybrid DG/FV methods for conservation laws Ⅰ: Basic formulation and one-dimensional systems[J]. Journal of Computational Physics, 2012, 231(4): 1081-1103. DOI:10.1016/j.jcp.2011.06.010 |
| [15] |
ZHANG L P, LIU W, HE L X, et al. A class of hybrid DG/FV methods for conservation laws II: Two-dimensional cases[J]. Journal of Computational Physics, 2012, 231(4): 1104-1120. DOI:10.1016/j.jcp.2011.03.032 |
| [16] |
JALALI A, OLLIVIER-GOOCH C. Higher-order unstructured finite volume RANS solution of turbulent compressible flows[J]. Computers & Fluids, 2017, 143: 32-47. DOI:10.1016/j.compfluid.2016.11.004 |
| [17] |
OLLIVIER-GOOCH C F, NEJAT A, MICHALAK K. Obtaining and verifying high-order unstructured finite volume solutions to the Euler equations[J]. AIAA Journal, 2009, 47(9): 2105-2120. DOI:10.2514/1.40585 |
| [18] |
JALALI A, OLLIVIER GOOCH C F. Higher-order finite volume solution reconstruction on highly anisotropic meshes[C]//21st AIAA Computational Fluid Dynamics Conference, San Diego, CA. Reston, Virginia: AIAA, 2013.doi: 10.2514/6.2013-2565.
|
| [19] |
BARTH T, JESPERSEN D. The design and application of upwind schemes on unstructured meshes[C]// 27th Aerospace Sciences Meeting, Reno, NV. Reston, Virginia: AIAA, 1989.doi: 10.2514/6.1989-366.
|
| [20] |
BARTH T J. A 3-D upwind Euler solvers for unstructured meshes[C]//10th Computational Fluid Dynamics Conference, Honolulu, HI, USA, 1991.doi: 10.2514/6.1991-1548.
|
| [21] |
李万爱. 非结构网格高精度数值方法的若干问题研究[D]. 北京: 清华大学, 2012. LI W A. Research on the high order accurate numerical methods on unstructured grids[D]. Beijing: Tsinghua University, 2012. (in Chinese). |
| [22] |
孔令发, 董义道, 刘伟. 全局方向模板对非结构有限体积梯度与高阶导数重构的影响[J]. 力学学报, 2020, 52(5): 1334-1349. KONG L F, DONG Y D, LIU W. The influence of global-direction stencil on gradient and high-order derivatives reconstruction of unstructured finite volume methods[J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(5): 1334-1349. DOI:10.6052/0459-1879-20-093 (in Chinese) |
| [23] |
KONG L F, DONG Y D, LIU W, et al. Extending the global-direction stencil with “face-area-weighted centroid” to unstructured finite volume discretization from integral form[J]. Advances in Aerodynamics, 2020, 2(1): 1-43. DOI:10.1186/s42774-020-00048-5 |
| [24] |
MORETTI G. Importance of boundary conditions in the numerical treatment of hyperbolic equations[J]. The Physics of Fluids, 1969, 12: 11-13. DOI:10.1063/1.1692426 |
| [25] |
THOMPSON K W. Time-dependent boundary conditions for hyperbolic systems[J]. Journal of Computational Physics, 1987, 68(1): 1-24. DOI:10.1016/0021-9991(87)90041-6 |
| [26] |
THOMPSON K W. Time-dependent boundary conditions for hyperbolic systems II[J]. Journal of Computational Physics, 1990, 89(2): 439-461. DOI:10.1016/0021-9991(90)90152-Q |
| [27] |
POINSOT T J, LELEF S K. Boundary conditions for direct simulations of compressible viscous flows[J]. Journal of Computational Physics, 1992, 101(1): 104-129. DOI:10.1016/0021-9991(92)90046-2 |
| [28] |
GROSS A, FASEL H F. Characteristic ghost-cell boundary condition[J]. AIAA Journal, 2007, 45(1): 302-306. DOI:10.2514/1.23130 |
| [29] |
MOTHEAU E, ALMGREN A, BELL J B. Navier-Stokes characteristic boundary conditions using ghost cells[J]. AIAA Journal, 2017, 55(10): 3399-3408. DOI:10.2514/1.J055885 |
| [30] |
DONG Y D, DENG X G, GAO X, et al. A comparative study of boundary conditions for the density-based solvers in the framework of OpenFOAM[J]. Computers & Fluids, 2018, 172: 284-300. DOI:10.1016/j.compfluid.2018.04.031 |
| [31] |
董义道. 非结构有限体积算法边界条件研究及其在分离涡模拟中的应用[D]. 长沙: 国防科技大学, 2018. DONG Y D. Boundary condition treatments of unstructured finite volume algorithms and its application in detached eddy simulation[D]. Changsha: National University of Defense Technology, 2018. |
| [32] |
KOPRIVA D A, KOLIAS J H. A conservative staggered-grid Chebyshev multidomain method for compressible flows[J]. Journal of Computational Physics, 1996, 125(1): 244-261. DOI:10.1006/jcph.1996.0091 |
| [33] |
KOPRIVA D A. A staggered-grid multidomain spectral method for the compressible Navier-Stokes equations[J]. Journal of Computational Physics, 1998, 143(1): 125-158. DOI:10.1006/jcph.1998.5956 |
| [34] |
ATKINS H, CASPER J. Nonreflective boundary conditions for high-order methods[J]. AIAA Journal, 1994, 32(3): 512-518. DOI:10.2514/3.12015 |
| [35] |
FOLKNER D, KATZ A, SANKARAN V. Design and verification methodology of boundary conditions for finite volume schemes[J]. Computers & Fluids, 2014, 96: 264-275. DOI:10.1016/j.compfluid.2014.03.028 |
| [36] |
王年华, 张来平, 李明. 基于网格缩小的非结构网格梯度重构及制造解精度测试与验证[J]. 空气动力学学报, 2019, 37(5): 722-730. WANG N H, ZHANG L P, LI M. Investigation on accuracy of gradient reconstruction and flow simulation on general unstructured grids based on downscaling method[J]. Acta Aerodynamica Sinica, 2019, 37(5): 722-730. DOI:10.7638/kqdlxxb-2017.0106 (in Chinese) |
| [37] |
ROACHE P J. Code verification by the method of manufactured solutions[J]. Journal of Fluids Engineering, 2002, 124: 4-10. DOI:10.2172/759450 |
| [38] |
KRIVODONOVA L, BERGER M. High-order accurate implementation of solid wall boundary conditions in curved geometries[J]. Journal of Computational Physics, 2006, 211(2): 492-512. DOI:10.1016/j.jcp.2005.05.029 |
| [39] |
ROE P L. Characteristic-based schemes for the Euler equations[J]. Annual Review of Fluid Mechanics, 1986, 18: 337-365. DOI:10.1146/annurev.fl.18.010186.002005 |
| [40] |
SUBRAMANIAM A, WONG M L, LELE S K. A high-order weighted compact high resolution scheme with boundary closures for compressible turbulent flows with shocks[J]. Journal of Computational Physics, 2019, 397: 108822. DOI:10.1016/j.jcp.2019.07.021 |



