2. 中国空气动力研究与发展中心 计算空气动力研究所,绵阳 621000
2. Computational Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China
颗粒流体两相流广泛存在于化工及航空航天等领域,如流态化反应器、航空发动机和大推力火箭燃烧室等。在这些实际问题中,对于弥散相,一般颗粒数目
在工程应用中,如页岩气开采,通过把带颗粒的非牛顿流体垂直向下注入地表层中,液体压力会使得岩石破裂,而悬浮颗粒会占据岩石裂缝的空间,使得岩石无法闭合。这样,水压力就可以进一步破裂岩石,从而为开采地下的天然气提供条件。因此近年来基于工程需求的推动,驻点流中的颗粒动力学蓬勃发展。例如 Vigolo[3]用点颗粒模型耦合直接数值模拟和物理实验研究T管流中的大密度比颗粒群运动(图1);Li[4-5]用颗粒解析的直接数值模拟PR-DNS研究一个中性颗粒在三维轴对称驻点流对称轴上的运动;Manoorkar[6-7]通过物理实验和直接数值模拟,研究T管流中有限尺寸中性颗粒群的输运特征;Rallabandi[8]用理论解研究在低雷诺数条件下,一个颗粒在驻点流中的运动。Vigolo[3] 发现,颗粒反弹系数和颗粒惯性高度相关,而且由于三维涡效应,颗粒反弹系数分布是弥散状的。Manoorkar[6-7]也同样发现T管流的三维涡效应,还发现颗粒输运惯性分选的特征。Wang[9]通过物理实验研究了驻点流的三维涡效应,他们通过在远离壁面的距离施加不同的扰动,得到了一个类似于卡门涡的脱离涡对,这个涡对在靠近壁面时始终不撞击对称中心(图2)。工业问题中的驻点流非常容易出现三维涡效应,抑或是流场本身出现三维涡结构(Vigolo[3]),抑或是来流扰动导致(Wang[9])。鉴于此,Li[4-5]采用三维轴对称的数值控制域,考虑中性颗粒只在对称轴上运动的情况,移除了驻点流三维不对称效应带来的复杂性,得出了相似结论—颗粒惯性主导驻点流中的颗粒动力学,并且得出了更多的进一步细节。

|
图 1 T型管流运动的示意图 Fig.1 Particles clustering in a T junction |
除了Vigolo[3]的大密度比颗粒群课题,大多数研究的共同点都是:颗粒惯性与流体惯性相当
|
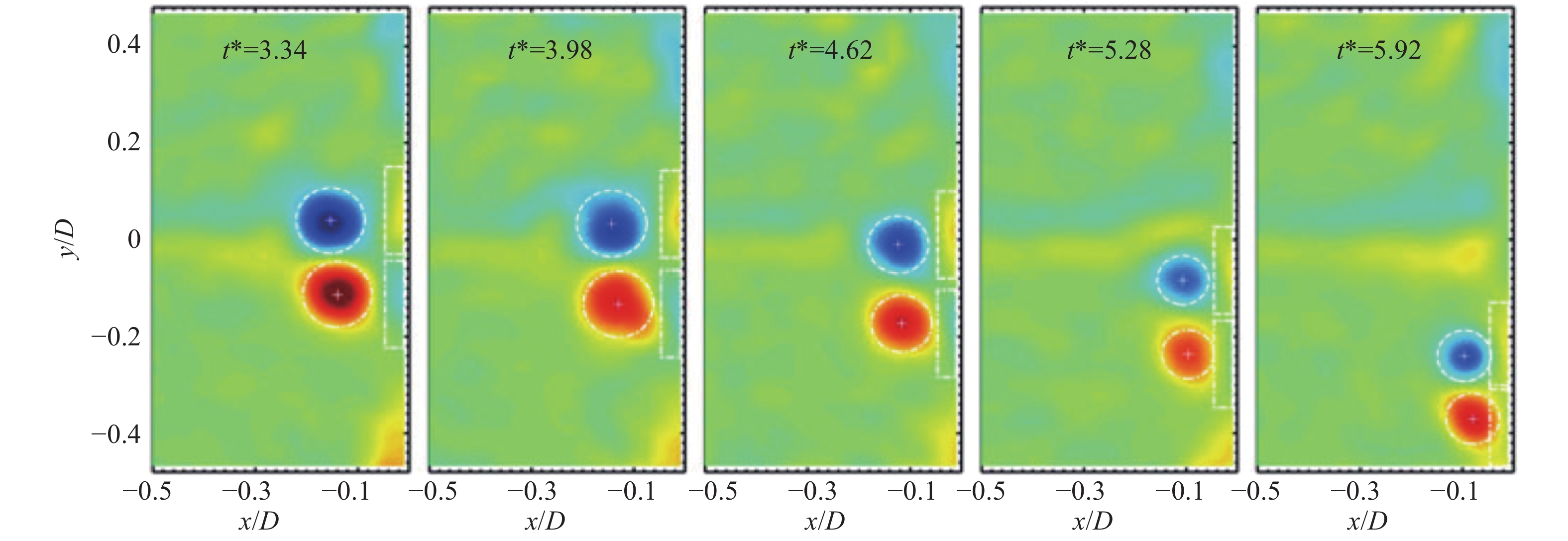
图 2 驻点流来流扰动涡对在近壁面的非对称特性[9] Fig.2 The non-axisymmetric characteristic of a perturbed vortex pair in a stagnation point flow[9] |
|
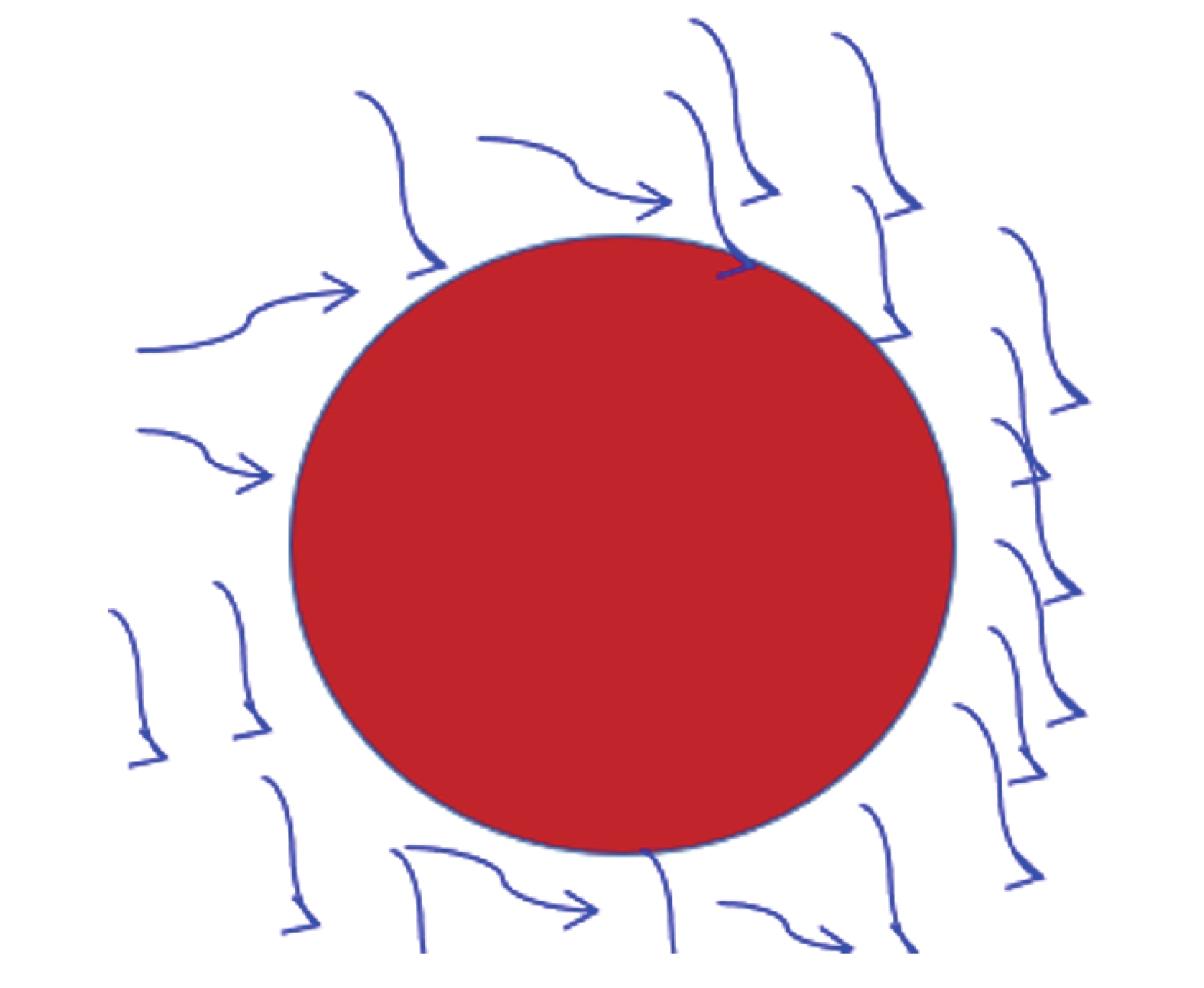
图 3 有限尺寸悬浮颗粒尺度与流体微团最小运动尺度量级相当情况下的示意图 Fig.3 A schematic of a suspended particle with the same order of characteristic length scale as that of the flow |
接下来,简要介绍和回顾Li[4-5]的核心工作。Li特别关注驻点流中的颗粒动力学机制问题,这个领域还罕有研究,但是却很重要。在实际工业问题中,颗粒悬浮的装置往往是复杂几何外形,包括驻点流情况。开发颗粒两相流的欧拉-欧拉连续模型则首先需要对复杂几何外形下的颗粒悬浮机理有清晰的认识。驻点流颗粒悬浮问题是一类特殊和典型的问题,比如常见的化工T型管道。
1 颗粒解析的直接数值模拟方法:浸没式边界方法IBM| $\frac{{{\rm{D}}{u}}}{{{\rm{D}}t}} = {g} + {\mu }\Delta {u} + {{f}_{{\rm{IBM}}}}$ | (1) |
| $\frac{{{\rm{d}}{{V}_{{p}}}}}{{{\rm{d}}t}} = \left( {1 - \frac{{{\rho _f}}}{{{\rho _p}}}} \right){g} + \frac{{{\rho _f}}}{{{\rho _p}\varOmega}}\left( {\frac{{\rm{d}}}{{{\rm{d}}t}}\int {{u}\rm{d}\varOmega} + \int {{{f}_{{\rm{IBM}}}}{{\rm{d}}{\varOmega}}} } \right)$ | (2) |
方程(1)和方程(2)概括描述了颗粒解析的直接数值模拟方法IBM。式中
在湍流问题中,随着
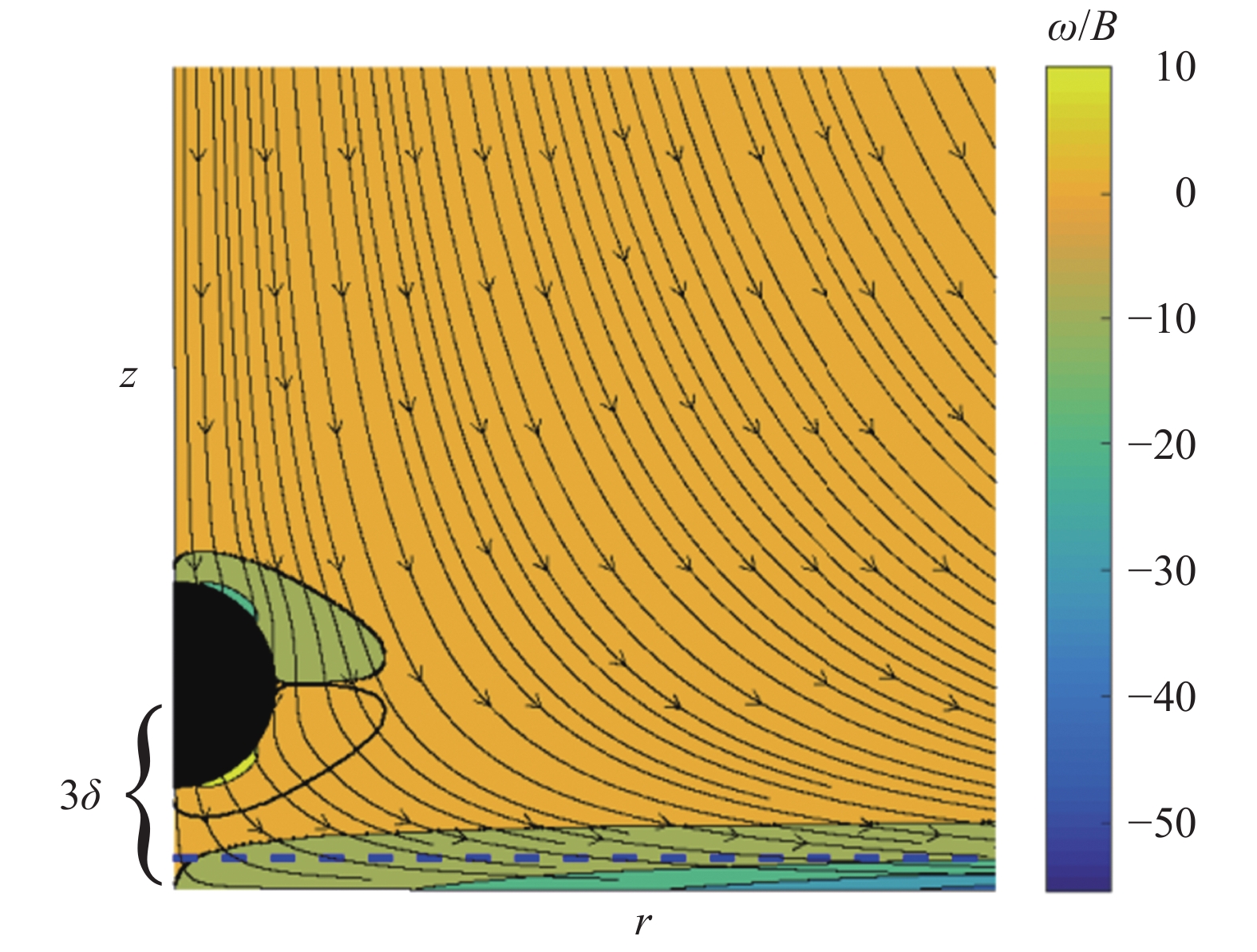
驻点流的理论模型Hiemenz 流动可以在三维或者三维轴对称的条件下,通过自相似解求得[18]。Hiemenz 流动是全场非均匀的,远场速度大,近壁面速度小,压力则是远场小,近壁面大,这是因为流体动能转化为压力的缘故。远离壁面,壁面法向距离大于大约三个Hiemenz 特征长度
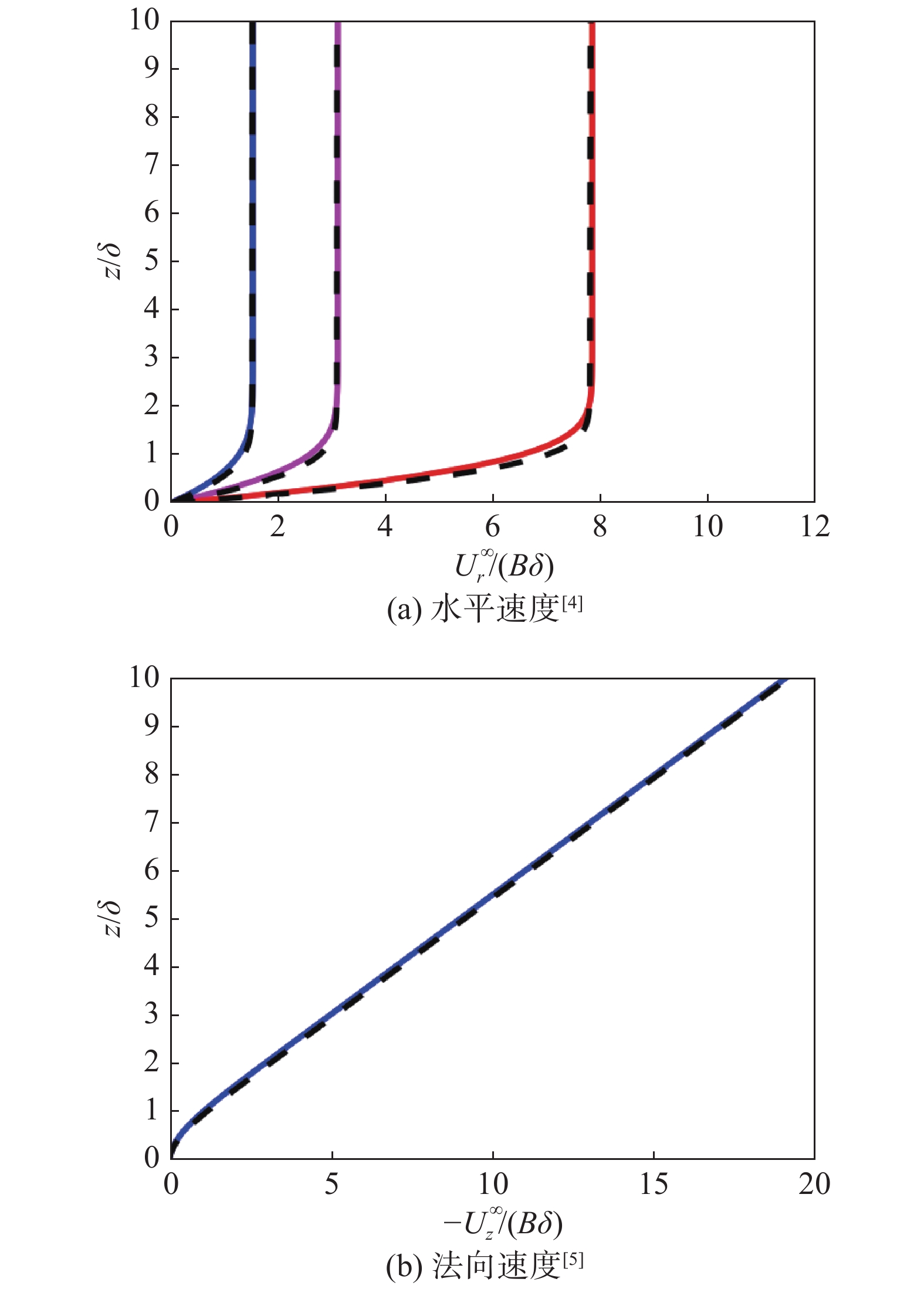
图4表明,Li[4-5]的数值方法能很好地重构一个Hiemenz流场并与理论解吻合。图4 的横轴分别表示归一水平速度和法向速度,竖轴表示归一化的壁面距离,黑色虚线表示Hiemenz流动的理论解,从左到右不同彩色实线表示不同径向位置切面
|
图 4 DNS流场归一化速度与驻点流理论解验证 Fig.4 Comparisons of dimensionless velocities between DNS and the theoretical solution |
|
图 5 一个有限尺寸中性悬浮颗粒在三维轴对称驻点流中的动力学的颗粒解析的直接数值模拟PR-DNS示意图[5]( |
| ${\rho _p}V\frac{{{\rm{d}}{{V}_{{p}}}}}{{{\rm{d}}t}} = {\rho _f}\left( {\frac{{\rm{d}}}{{{\rm{d}}t}}\int {{u}{\rm{d}}{{V}}} } \right)$ | (3) |
| ${\rho _p}V\frac{{{\rm{d}}{{V}_{{p}}}}}{{{\rm{d}}t}} = {\rho _f}V\frac{{{\rm{D}}{u}}}{{{\rm{D}}t}}$ | (4) |
| $\frac{{{\rm{d}}{{V}_{{p}}}}}{{{\rm{d}}t}} = \frac{{{\rm{D}}{u}}}{{{\rm{D}}t}}$ | (5) |
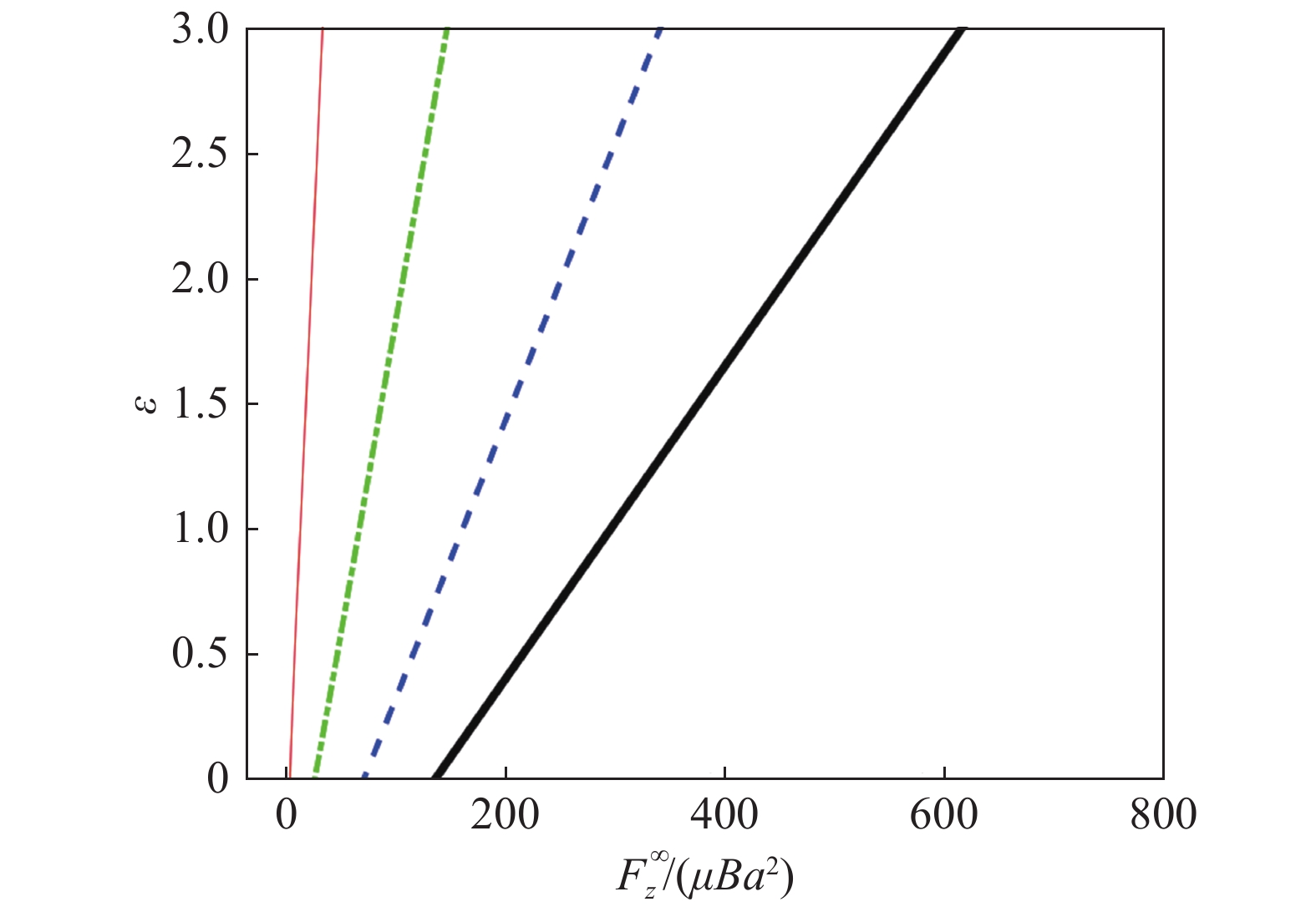
图6 显示了不同有限尺寸颗粒受到的无黏环境压力的理论解,
|
图 6 不同有限尺寸颗粒受到的无黏环境压力的理论解[4] Fig.6 The dimensionless theoretical ambient pressure force excerted on different finite size neutrally-buoyant particle[4] |
图7(a)显示了不同有限尺寸颗粒沿法向对称轴受到的总水动力。远离壁面,总水动力线性递减,只受到无黏环境压力,呈示踪粒子行为。靠近壁面,由于壁面黏性边界层与颗粒相互作用,颗粒受到的总水动力不再是无黏环境压力,示踪粒子行为不再成立,见图7(b)。

|
图 7 在不同壁面距离条件下,不同惯性颗粒受到的总水动力以及速度与流体微团速度的比较[4] Fig.7 The hydrodynamic force on inertial particles at different gaps between the bottom of particles and the wall , and the velocities of inertial particles as a function of the distances between the center of particles and the wall [4] |
图7(a)的横轴表示不同有限尺寸颗粒在驻点流中受到的归一化总水动力,竖轴表示归一化的壁面距离,从左到右不同的彩色线表示从小到大的有限尺寸中性悬浮颗粒
当弹性碰撞发生后,方程(6)描述了颗粒动力学,方程(1)描述了有颗粒扰动的流体力学场。理论上是,求解一个考虑颗粒相动量注入的流体力学偏微分方程,同时求解一个颗粒动力学方程.之前的难点在于如何给出
| ${m_p}\frac{{{\rm{d}}{{V}_{{p}}}}}{{{\rm{d}}t}} = {{F}_{{\rm{IBM}}}} + {{F}_{c}}$ | (6) |
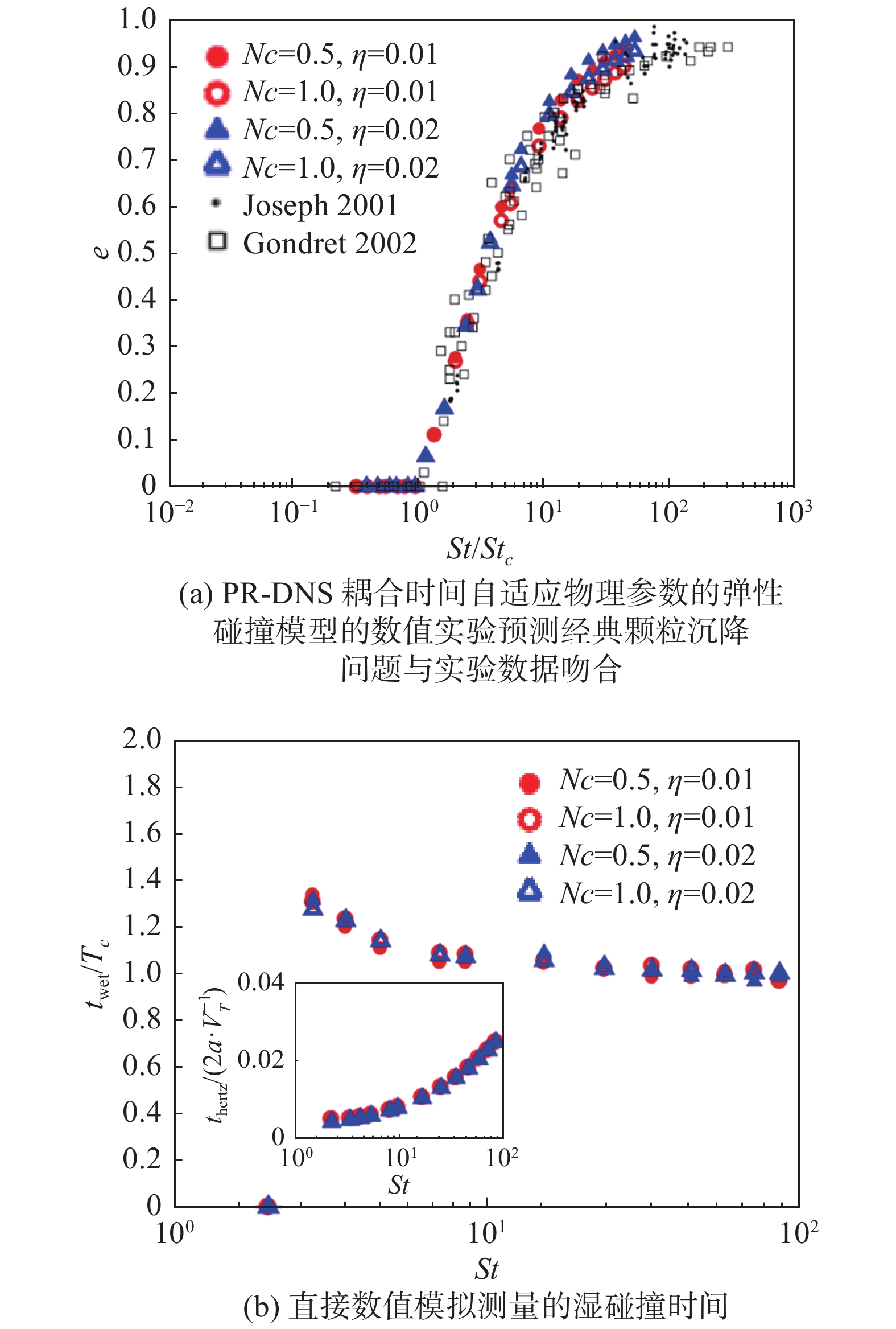
图8表明,Li[5]的数值方法能很好地重构湿润碰撞的物理场景,准确预测了湿润碰撞的反弹系数,并且反应湿润碰撞的不同惯性颗粒的不同碰撞时间,湿润碰撞时间不取决于任意的数值光滑参数,数值上具有鲁棒性。图8(a)的横轴表示归一化的不同颗粒惯性,竖轴表示归一化的反弹速度,黑白符号代表实验数据(Joseph[21] 和 Gondret[22]),彩色符号代表不同数值参数下的直接数值模拟DNS结果。图8(b)的横轴表示归一化的不同颗粒惯性,竖轴表示归一化的颗粒湿润碰撞时间,插图的竖轴表示归一化的干碰撞时间,彩色符号代表不同数值参数下的直接数值模拟DNS结果。Nc表示数值光滑参数,
|
图 8 PR-DNS数值模拟的重力沉降问题的反弹系数和湿碰撞时间[5] Fig.8 PR-DNS results of rebound coefficients and wet collision time for settling problem[5] |
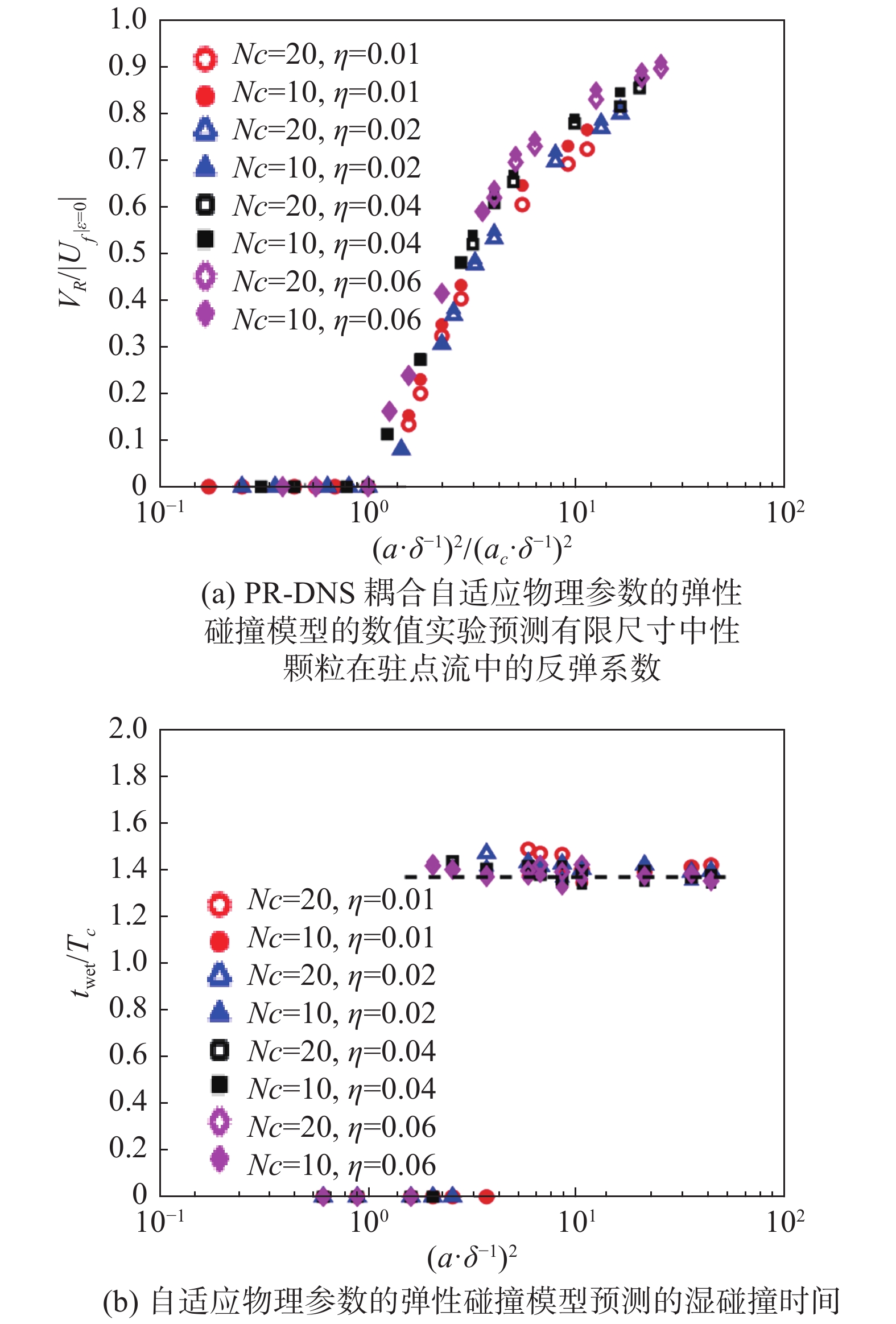
Li[5]给出了不同惯性的有限尺寸中性颗粒的反弹系数,数值实验表明,中性颗粒在驻点流中的动力学与沉降颗粒类似,都是依赖于颗粒惯性;数值方法上,湿润碰撞时间反应湿润碰撞的不同惯性颗粒的不同碰撞时间,湿润碰撞时间不取决于任意的数值光滑参数,数值上具有鲁棒性,见图9。这里Nc表示数值光滑参数,
|
图 9 PR-DNS数值模拟的中性颗粒在驻点流中的反弹系数和湿碰撞时间[5] Fig.9 PR-DNS results of rebound coefficients and wet collision time for a neutrally-buoyant particle in a stagnation point flow[5] |

|
图 10 不同有限尺寸中性颗粒与黏性边界层厚度对比示意图,a)和b)分别表示不同的有限尺寸中性悬浮颗粒在三维轴对称驻点流近壁面对流场的影响[4] Fig.10 A schematic of surrounding flow fields around neutrally-buoyant particles with different sizes. Dashed lines represent the boundary layer edge [4] |
实际问题中,颗粒往往是一群的,它们聚集或者分散,因此研究一对中性颗粒的行为将为我们研究大量弥散颗粒在驻点流中的动力学打下研究基础(见图11(a))。在确保网格无关和时间步无关的前提下,我们测试了不同的惯性颗粒和不同的初始颗粒间距,确保图11(b)的结果是可重复的[5]。图11(b)的横轴表示归一化的时间,竖轴表示不同颗粒的归一化壁面距离,蓝色虚线代表单个中性颗粒,蓝色实线代表两倍于蓝色虚线的颗粒半径的中性颗粒,红黑线代表分别代表一对颗粒中的低位和高位颗粒,红色实线代表与蓝色虚线半径相同的低位颗粒,黑色实线代表与蓝色虚线半径相同的高位颗粒,绿色符号表示低位颗粒的无壁面接触的反弹点。我们发现,一对颗粒中的低位颗粒(红色轨迹)可以不接触壁面发生反弹,见图11(b)和插图里的绿色符号,而单个颗粒却没有这种行为(蓝色虚线轨迹)。这很反常,仅凭借水动力效应就能把一个惯性颗粒弹起吗?

|
图 11 驻点流中的颗粒非接触碰撞反弹现象[5] Fig.11 Contactless bouncing phenomenon of particle in a stagnation point flow[5] |
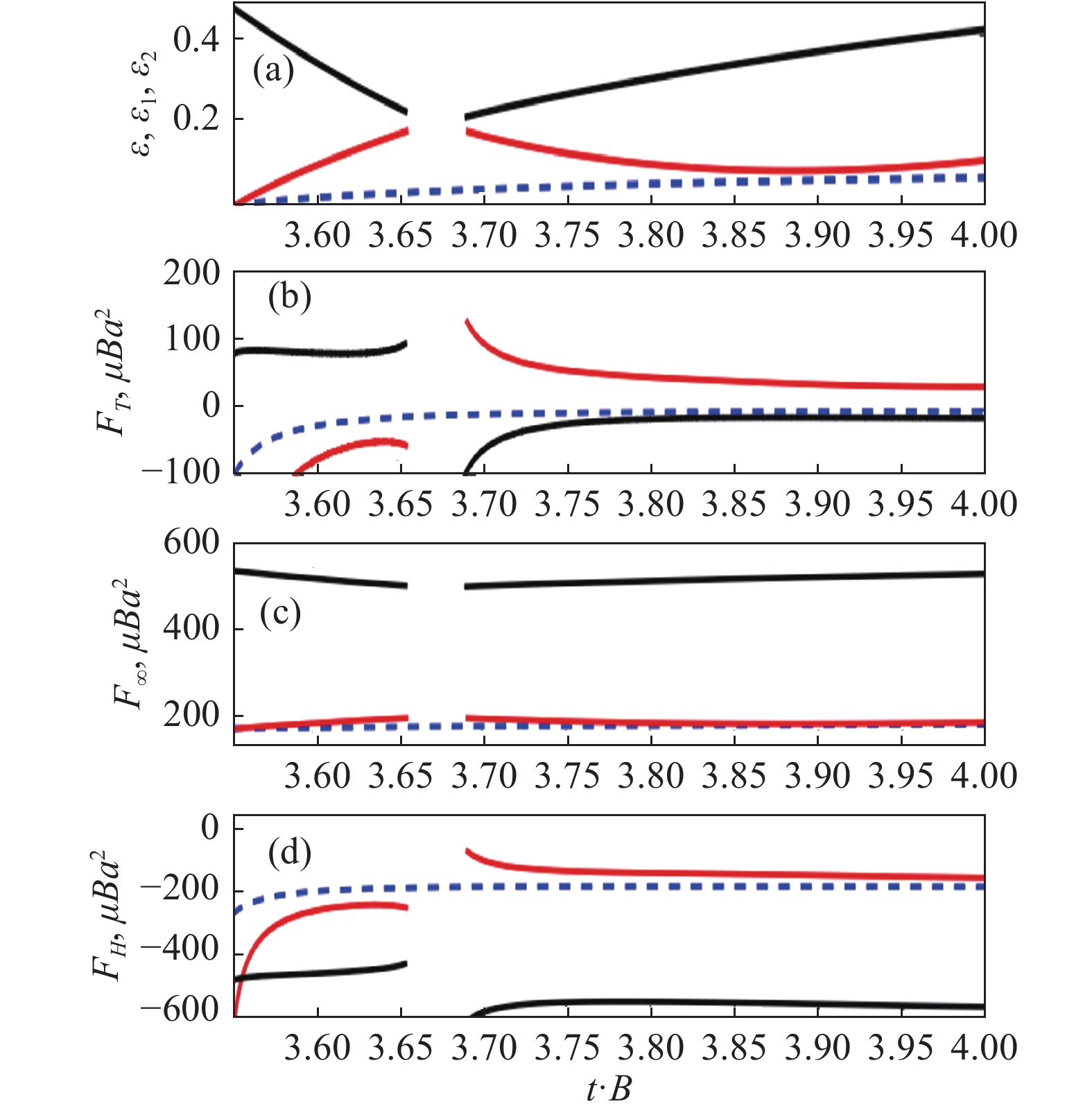
图12解释了这种反常的反弹。图12的水平轴表示归一化时间。图12(a)的竖轴表示不同颗粒的归一化壁面距离,图12(b)的竖轴表示不同颗粒受到的总水动力,图12(c)的竖轴表示不同颗粒受到的无黏环境压力,图12(d)的竖轴表示不同颗粒受到的总水动力减去无黏环境压力的净效应。蓝色虚线代表单个中性颗粒,红黑线代表分别代表一对颗粒中的低位和高位颗粒,红色实线代表与蓝色虚线半径相同的低位颗粒,黑色实线代表与蓝色虚线半径相同的高位颗粒。简单来说,就是一对颗粒的情况下,高位颗粒替低位颗粒阻挡了来自上方的驻点流向下挤压效应 [26], 而低位颗粒没有物体替它阻挡。驻点流的非均匀性会产生一个向上托举的无黏环境压力[19],见方程(3),见图6。图12也通过颗粒解析的直接数值模拟的结果表明,低位颗粒的总水动力是向上的,而单个颗粒则是向下的。无黏环境压力始终存在于驻点流,由于一对颗粒的高位颗粒的庇护作用,使得低位颗粒可以被无黏环境压力托举起来[5]。
Li[26]还发现惯性小的颗粒会抱团撞击壁面,惯性大的则无法抱团,见图13,水平轴表示归一化的颗粒惯性;左,右竖轴分别表示单个颗粒和一对颗粒中的低位颗粒的归一化反弹系数。Li[26]认为这是驻点流的挤压效应与颗粒惯性竞争的结果,当颗粒惯性小的时候,挤压效应大于颗粒惯性,颗粒间相互碰撞后无法弹开,被挤压流牢牢抱紧在一起;惯性大则不会。Li[26]归一化了抱团颗粒对的惯性后发现,抱团颗粒对的归一化反弹系数曲线和单个颗粒的反弹系数曲线是重合。这再一次印证了Li[4]的结论,驻点流中的颗粒动力学由颗粒惯性控制。
|
图 12 单个和一对有限尺寸中性颗粒在驻点流中的受力以及各力分量比较示意图[5] Fig.12 A illustration of the dynamics of a single and a pair of neutrally-buoyant particles in a stagnation point flow[5] |
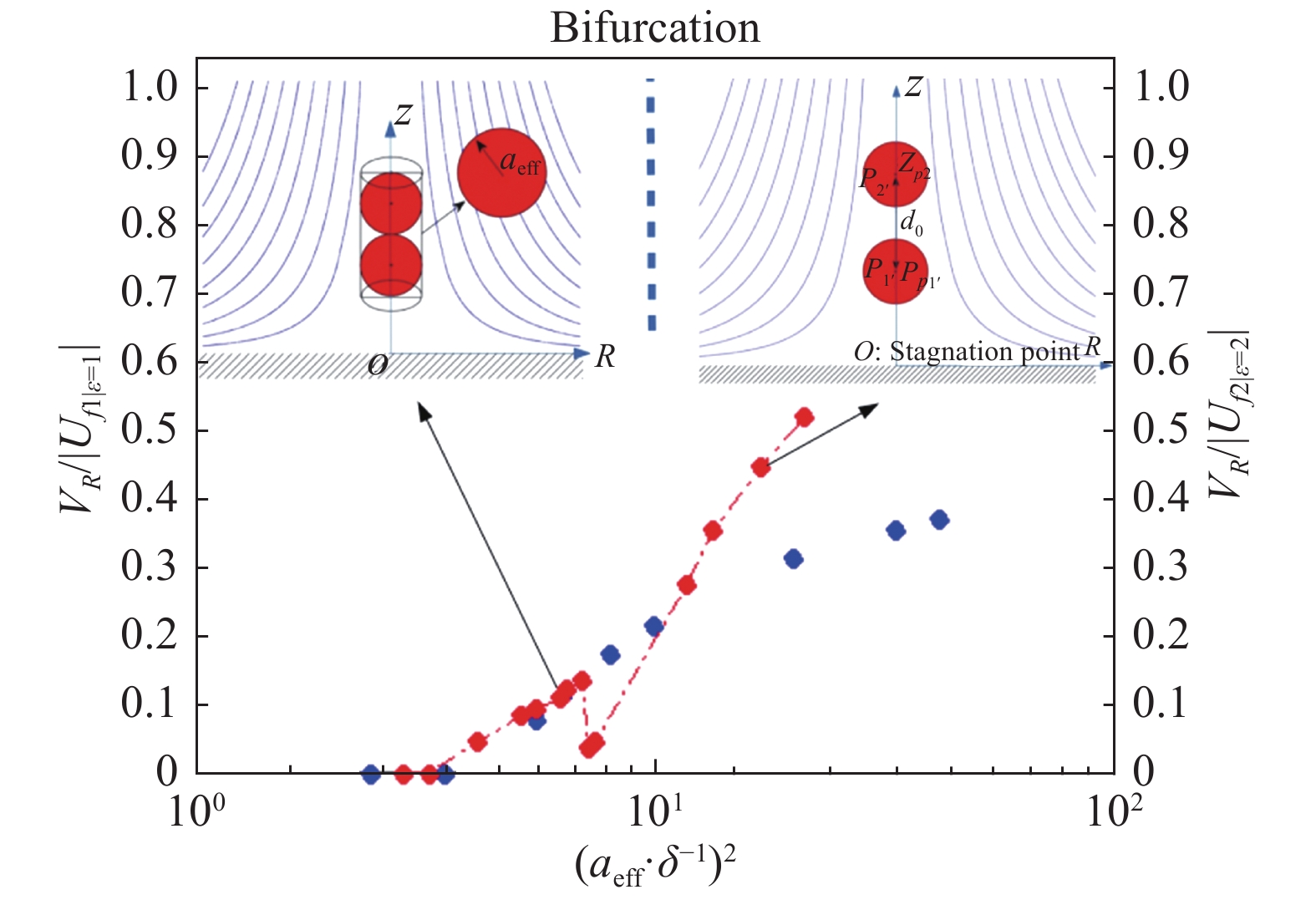
|
图 13 单个(蓝色)和一对有限尺寸中性颗粒(红色)在驻点流中的反弹系数比较示意图[26] Fig.13 The dimensionless rebound velocities of a single (blue) and a pair of (red) isolated neutrally-buoyant particles[26] |
驻点流中的颗粒动力学与非驻点流颗粒动力学非常不同。研究通过选取有限尺寸中性悬浮颗粒在三维轴对称驻点流对称轴上运动这个基本模型,移除了真实来流扰动或者数值扰动的影响,移除了密度比对颗粒惯性的影响,这样颗粒惯性完全来自于颗粒有限尺寸,颗粒动力学将局限于法向,颗粒与环境流体和壁面的相互作用,不需要考虑来流扰动导致的非定常效应,不需要考虑颗粒不在对称轴上导致的剪切诱导升力。
远离壁面,中性颗粒会像示踪流体微团一样运动。通过数学推导,研究得出,颗粒动力方程的牛顿惯性项等于流体微团的随体导数。这在数学上解释了:为什么有限尺寸惯性颗粒与数学上无穷小的流体微团示踪粒子的运动轨迹重合。
靠近壁面,颗粒惯性的不同将导致颗粒偏移流体示踪颗粒轨迹的幅值不同: 惯性大的颗粒,将会诱导出大的润滑力,反之亦然。但是润滑力是数学理想模型。当颗粒惯性小,黏性润滑力足以耗散掉所有的颗粒动能,颗粒将会减速至零并停留在壁面;当颗粒惯性大,在撞击有限尺度的粗糙度壁面前,润滑力不足以耗散掉颗粒动能,颗粒将会以有限速度撞击壁面,弹性碰撞将会发生,这个有限速度与颗粒惯性成正比。当弹性碰撞发生后,流体力学问题变成了流固耦合问题。因此我们耦合一个固体弹性力学的解析表达式到碰撞模型里,与流体求解器耦合求解,与经典沉降实验数据吻合。
研究发现,单个中性颗粒在驻点流中的反弹系数与沉降颗粒类似,与颗粒惯性相关。但是当研究到一对中性颗粒的时候,反常的现象发生了。首先,根据颗粒惯性不同,颗粒对有可能会抱团,这是驻点流挤压效应与颗粒惯性相互竞争的结果;其次,当颗粒对以抱团撞击壁面的时候,颗粒的反弹系数与单个颗粒反弹系数是重合的;最后,当颗粒对不抱团的时候,低位颗粒可以不撞击壁面发生反弹。
研究阐明了驻点流中的有限尺寸中性颗粒动力学完全由颗粒惯性/有限尺寸控制的机理,为进一步研究驻点流中的颗粒动力学铺垫了基础。对于某些工业应用中的驻点流中的颗粒动力学问题,颗粒运动轨迹往往不是在对称轴上的,那么随之而来的平行加速流带来的剪切诱导升力就必须要考虑;此外,颗粒与携带流体的密度比也不总是1,颗粒的惯性将不再由有限尺寸单独控制,颗粒相对流体的密度比效应也需要考虑。未来我们将针对这些真实问题带来的复杂效应,进行更深入的基础研究。
致谢 感谢国家重点研发计划(2019YFA0405200)经费的支持,感谢图卢兹大学Abbas 教授、Climent教授、Magnaudet教授和纽约城市大学Morris教授在作者博士工作期间给予的帮助和支持。
| [1] |
LI J H, KWAUK M. Particle-fluid two-phase flow: the energy-minimization multi-scale method[M]. Metallurgical Industry Press, 1994.
|
| [2] |
MORRIS J F, BOULAY F. Curvilinear flows of noncolloidal suspensions: The role of normal stresses[J]. Journal of Rheology, 1999, 43(5): 1213-1237. DOI:10.1122/1.551021 |
| [3] |
VIGOLO D, GRIFFITHS I M, RADL S, et al. An experimental and theoretical investigation of particle–wall impacts in a T-junction[J]. Journal of Fluid Mechanics, 2013, 727: 236-255. DOI:10.1017/jfm.2013.200 |
| [4] |
LI Q, ABBAS M, MORRIS J, et al. Near-wall dynamics of a neutrally buoyant spherical particle in an axisymmetric stagnation point flow[J]. Journal of Fluid Mechanics, 2020, 892:A32.
|
| [5] |
LI Q, ABBAS M, MORRIS J F. Particle approach to a stagnation point at a wall: Viscous damping and collision dynamics[J]. Physical Review Fluids, 2020, 5(10): 104301. DOI:10.1103/physrevfluids.5.104301 |
| [6] |
MANOORKAR S, SEDES O, MORRIS J F. Particle transport in laboratory models of bifurcating fractures[J]. Journal of Natural Gas Science and Engineering, 2016, 33: 1169-1180. DOI:10.1016/j.jngse.2016.04.008 |
| [7] |
MANOORKAR S, KRISHNAN S, SEDES O, et al. Suspension flow through an asymmetric T-junction[J]. Journal of Fluid Mechanics, 2018, 844: 247-273. DOI:10.1017/jfm.2018.183 |
| [8] |
RALLABANDI B, HILGENFELDT S, STONE H A. Hydrodynamic force on a sphere normal to an obstacle due to a non-uniform flow[J]. Journal of Fluid Mechanics, 2017, 818: 407-434. DOI:10.1017/jfm.2017.135 |
| [9] |
WANG J J, PAN C, CHOI K S, et al. Formation, growth and instability of vortex pairs in an axisymmetric stagnation flow[J]. Journal of Fluid Mechanics, 2013, 725: 681-708. DOI:10.1017/jfm.2013.205 |
| [10] |
BALACHANDAR S, EATON J K. Turbulent dispersed multiphase flow[J]. Annual Review of Fluid Mechanics, 2010, 42(1): 111-133. DOI:10.1146/annurev.fluid.010908.165243 |
| [11] |
WANG L , ZHOU G, WANG X , et al. Direct numerical simulation of particle–fluid systems by combining time-driven hard-sphere model and lattice Boltzmann method[J]. Particuology, 2010, 8(4):379–328.
|
| [12] |
ZHANG J, MERCIER M J, MAGNAUDET J. Core mechanisms of drag enhancement on bodies settling in a stratified fluid[J]. Journal of Fluid Mechanics, 2019, 875: 622-656. DOI:10.1017/jfm.2019.524 |
| [13] |
YU Z S, SHAO X M. A direct-forcing fictitious domain method for particulate flows[J]. Journal of Computational Physics, 2007, 227(1): 292-314. DOI:10.1016/j.jcp.2007.07.027 |
| [14] |
PIERSON J L, MAGNAUDET J. Inertial settling of a sphere through an interface. Part 2. Sphere and tail dynamics[J]. Journal of Fluid Mechanics, 2018, 835: 808-851. DOI:10.1017/jfm.2017.748 |
| [15] |
TANAKA T, EATON J. Classification of turbulence modification by dispersed spheres using a novel dimensionless number[J]. Phys Rev Lett, 2008, 101: 114502. DOI:10.1103/PhysRevLett.101.114502 |
| [16] |
MITTAL R, IACCARINO G. Immersed boundary methods[J]. Annual Review of Fluid Mechanics, 2005, 37(1): 239-261. DOI:10.1146/annurev.fluid.37.061903.175743 |
| [17] |
POPE S B. Turbulent Flows[M]. Cambridge University Press, 2001.
|
| [18] |
WHITE F. Viscous fluid flow[M]. McGraw-Hill, 2006.
|
| [19] |
AUTON T, HUNT J, PRUD’HOMME M. The force exerted on a body in inviscid unsteady non-uniform rotational flow[J]. Journal of Fluid Mechanics, 1988, 197: 241-257. |
| [20] |
WU W. Fluid Mechanics[M]. Peking University Press, 1983.
|
| [21] |
JOSEPH G, ZENIT R, HUNT M, et al. Particle-wall collisions in a viscous fluid[J]. Journal of Fluid Mechanics, 2001,433: 329.
|
| [22] |
GONDRET P, LANCE M, PETIT L. Bouncing motion of spherical particles in fluids[J]. Physics of Fluids, 2002, 14(2): 643-652. DOI:10.1063/1.1427920 |
| [23] |
ZENIT R, HUNT M L, BRENNEN C E. Collisional particle pressure measurements in solid–liquid flows[J]. Journal of Fluid Mechanics, 1997, 353: 261-283. DOI:10.1017/s0022112097007647 |
| [24] |
BIRWA S K, RAJALAKSHMI G, GOVINDARAJAN R, et al. Solid-on-solid contact in a sphere-wall collision in a viscous fluid[J]. Physical Review Fluids, 2018, 3(4): 044302. DOI:10.1103/physrevfluids.3.044302 |
| [25] |
GOLDSMITH W. The theory and physical behaviour of colliding solids[M]. Dover Publ, 1999.
|
| [26] |
LI Q. Near-wall dynamics of neutrally buoyant particles in a wall-normal flow: From viscous damping to collision[D]. INP Toulouse, France, 2019.
|



