2. 兰州大学 土木工程与力学学院,兰州 730000;
3. 兰州大学 大气科学学院,兰州 730000;
4. 洛桑联邦理工学院 建筑、土木与环境工程学院,瑞士 洛桑 1015
2. School of Civil Engineering and Mechanics, Lanzhou University, Lanzhou 730000, China;
3. College of Atmospheric Science, Lanzhou University, Lanzhou 730000, China;
4. School of Architecture, Civil and Environmental Engineering, École Polytechnique Fédérale de Lausanne, Lausanne 1015, Switzerland
积雪是自然界最活跃的地表元素之一,在地球广泛分布,最大覆盖面积可占地球表面积的四分之一,因其高反照率、低热传导性等特性,对全球辐射平衡具有重要的影响[1]。由于积雪对温度十分敏感,积雪分布及其时空演化对全球气候变化具有重要的指示和反馈作用[2]。同时,融雪水是地球重要的淡水资源,对区域全球水文循环、生态系统乃至人类的生活生产具有重要的作用[3]。Barnett等研究表明,北纬40°以上的河流径流主要由融雪主导[4]。雪山山脉可以称为天然的“水塔”,因为它们是许多河流和其他淡水源的重要源头。在严寒的冬季,山区逐日降雪在地表形成积雪层,在春季至初夏逐渐融化,顺流而下的融雪水在地表形成了小溪、河流、湖泊,最终汇合进入海洋。从亚洲的喜马拉雅山脉到欧洲的阿尔卑斯山脉再到北美的落基山脉,高海拔的山区的融雪水滋养着数十亿人的生命。
积雪分布受多个因素的影响,而风吹雪是改变积雪分布的重要过程之一[5]。风吹雪是风夹带颗粒向前运动的一种典型多相流运动,会极大地改变积雪的分布形态。在高海拔山区,风速高、地表植被覆盖稀少,风吹雪现象频发,由此产生的积雪重分布对融雪径流有着重要的影响[6]。极地风吹雪是冰盖质能平衡的重要物质来源,例如在北极苔原地带,估计有18%的降雪由于高风速而重新分配到低洼地带[7]。而在南极部分地区,年均累计风吹雪时间能占全年总时间的三分之一[8]。同时,风吹雪还伴随着雪粒的升华过程,造成积雪质量的巨大损失。以北美地区为例,Pomeroy等认为在草原环境下,冬季风吹雪升华可占到年降水量的10%~50%[9]。风吹雪升华还是海盐气溶胶生成的主要机制之一,对极地大气化学过程(比如臭氧的生成)具有重要的影响[10-12]。
除此之外,风吹雪还会导致多种灾害,影响人们的出行和生产安全,甚至危及人类生命。最常见的风吹雪灾害是降低能见度,掩埋公路、铁路,引发严重的交通事故,例如2008年,我国南方发生大面积雪灾,多处铁路、公路、民航交通中断,为救灾工作带来极大的困难,因灾损失高达上千亿元人民币[13]。在山区,风吹雪会在山脊处生成雪檐,或者在背风坡处形成局部积雪堆积,成为雪崩的诱发因素。而雪崩是导致山区积雪再分布的另一个重要原因[14]。以北极为例,在挪威Svalbard地区,超过45%的雪崩由雪檐崩塌造成[15]。
目前,已有不少学者进行了风吹雪研究综述研究。早期的学者主要从研究方法的角度去描述风吹雪的研究进展[16-18],比如模拟手段或者实验观测。而近年来,学者们主要从物理过程描述风吹雪在不同尺度上的大气和水文效应[19-21]。
本文从积雪质能平衡方程出发,针对风对积雪分布的影响,回顾了降雪的优先沉降、风吹雪对积雪的再分布以及风吹雪升华对积雪的质量损耗等三个物理过程的研究现状与进展,阐明风在雪水文过程中的重要地位,并就我国雪水文学存在的问题展开讨论,提出我国未来雪水文学的发展趋势,供读者参考借鉴。
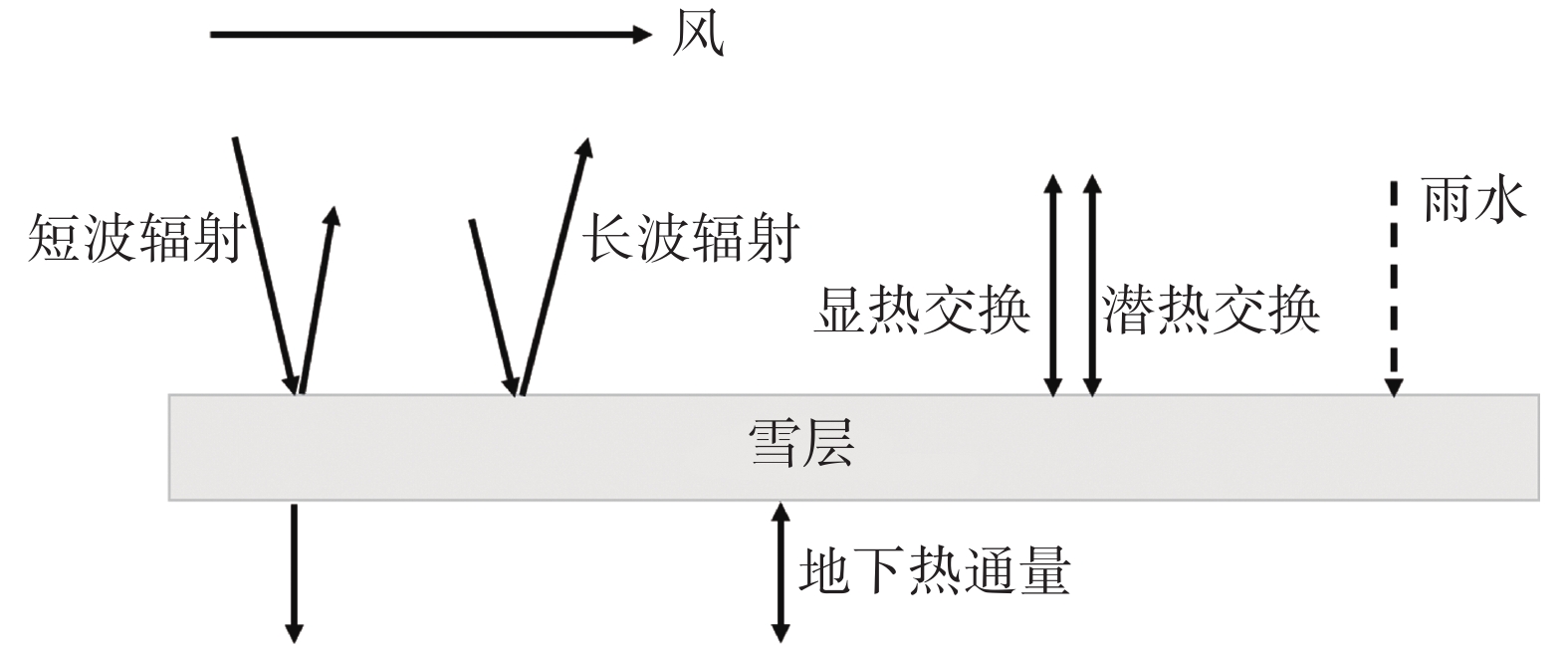
1 积雪层的质能平衡积雪对地球系统的作用主要体现在能量和质量平衡两部分[2]。作用在雪层表面的短波辐射和长波辐射能是雪层与大气最初发生能量交换的地方,之后的过程还包括由于湍流与水汽蒸发或者升华相变过程产生的潜热对流交换、由于空气和雪表面的温度差引起的显热交换,以及降雨和土地热传导向雪层表面或者基底提供相对较少的热量等。这一能量交换总过程如图1所示。
|
图 1 雪层能量平衡过程示意图 Fig.1 Schematic diagram of snow energy balance process |
雪层内的能量是获得和损失能量的代数和:
| $ \frac{{{\rm{d}}Q}}{{{\rm{d}}t}} = {Q_{ns}} + {Q_{nl}} + {Q_h} + {Q_e} + {Q_a} + {Q_g} $ | (1) |
其中:
积雪和环境的能量交换最终表现在雪层内由于融雪、蒸发或者升华产生的水分损失率。包含了风雪流动力学过程的雪层质量平衡方程可以表示为:
| $ \frac{{{\rm{d}}m}}{{{\rm{d}}t}} = P - \nabla \cdot {D_{bs}} - {E_{bs}} \pm E - R $ | (2) |
其中
风在积雪的质能平衡过程中起到了重要的作用。首先,风会改变降雪的沉降分布,尤其在山区,使得最初的降雪不是均匀地降落;其次,当风足够大时,风吹雪使得地表积雪开始迁移,进一步加深积雪的不均匀分布;同时,在风吹雪的过程中,由于风会加速雪颗粒与空气之间的潜热对流交换,即风吹雪升华过程,增强了积雪的损失率,影响最终的融雪径流生成。
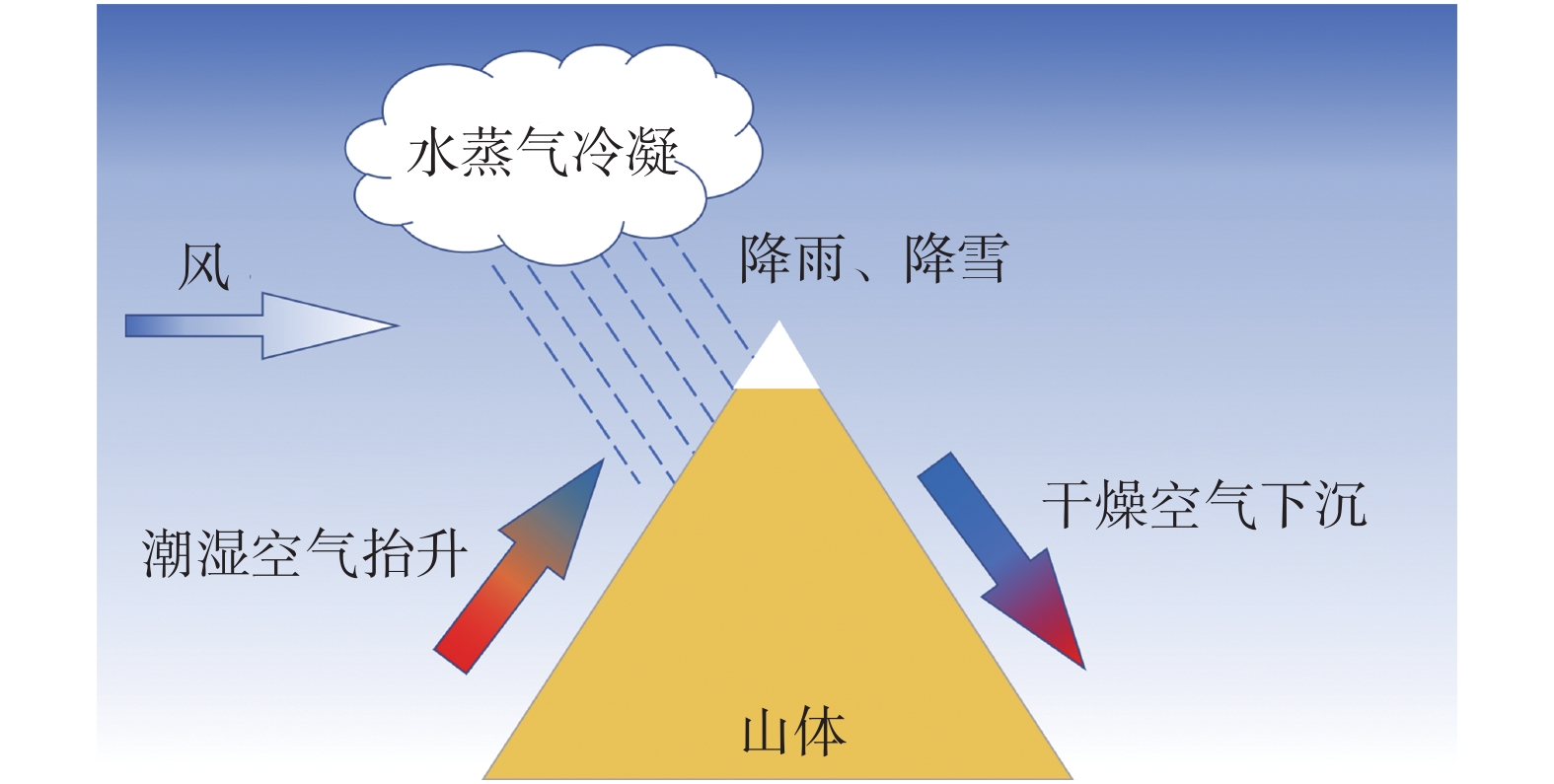
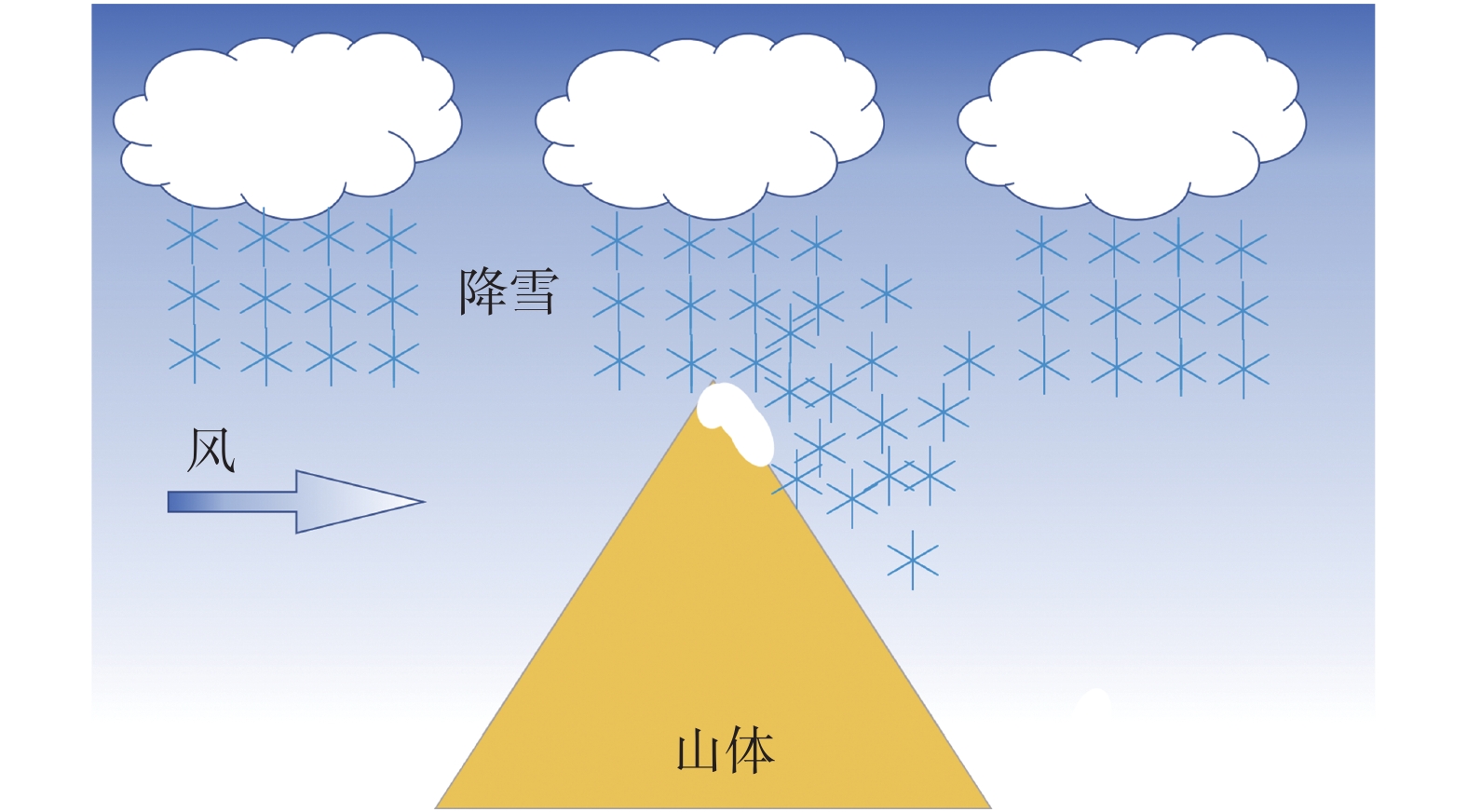
2 风雪流动力过程对雪层质能平衡的影响 2.1 降雪沉积地表的积雪首先来自降雪。降雪导致的不均匀分布一共有两种情况:一是降雪本身在空间上的不均匀性。例如,由于地形抬升引起的地形降水非常普遍。在地形抬升降水中,种子补给机制。发挥了重要的作用。如图2所示,种子补给机制是指在特殊地形下潮湿空气的运动在某个位置形成过饱和的补给云,雪粒在通过该区域时吸收水汽从而体积增大,导致该区域对应的积雪沉积量增大[22-24]。二是降雪在湍流和地形的共同作用下,在地形的局部地区发生更多沉积的现象,瑞士科学家Lehning等称之为优先沉降[25],如图3所示。这一机理已在野外雷达观测中被证明[26]。然而,在模型预测和野外观测中,不同的研究获得的积雪在地形周围的沉积差异很大。例如一些研究表明水平对流使得降雪颗粒向下风向漂移从而引起背风坡积雪沉积增强[27];而另一些研究表明雪粒可能在迎风坡或坡顶聚集[28]。
|
图 2 种子补给机制原理示意图 Fig.2 Schematic diagram of seeder-feeder principle |
|
图 3 优先沉降原理示意图 Fig.3 Schematic diagram of preferential deposition principle |
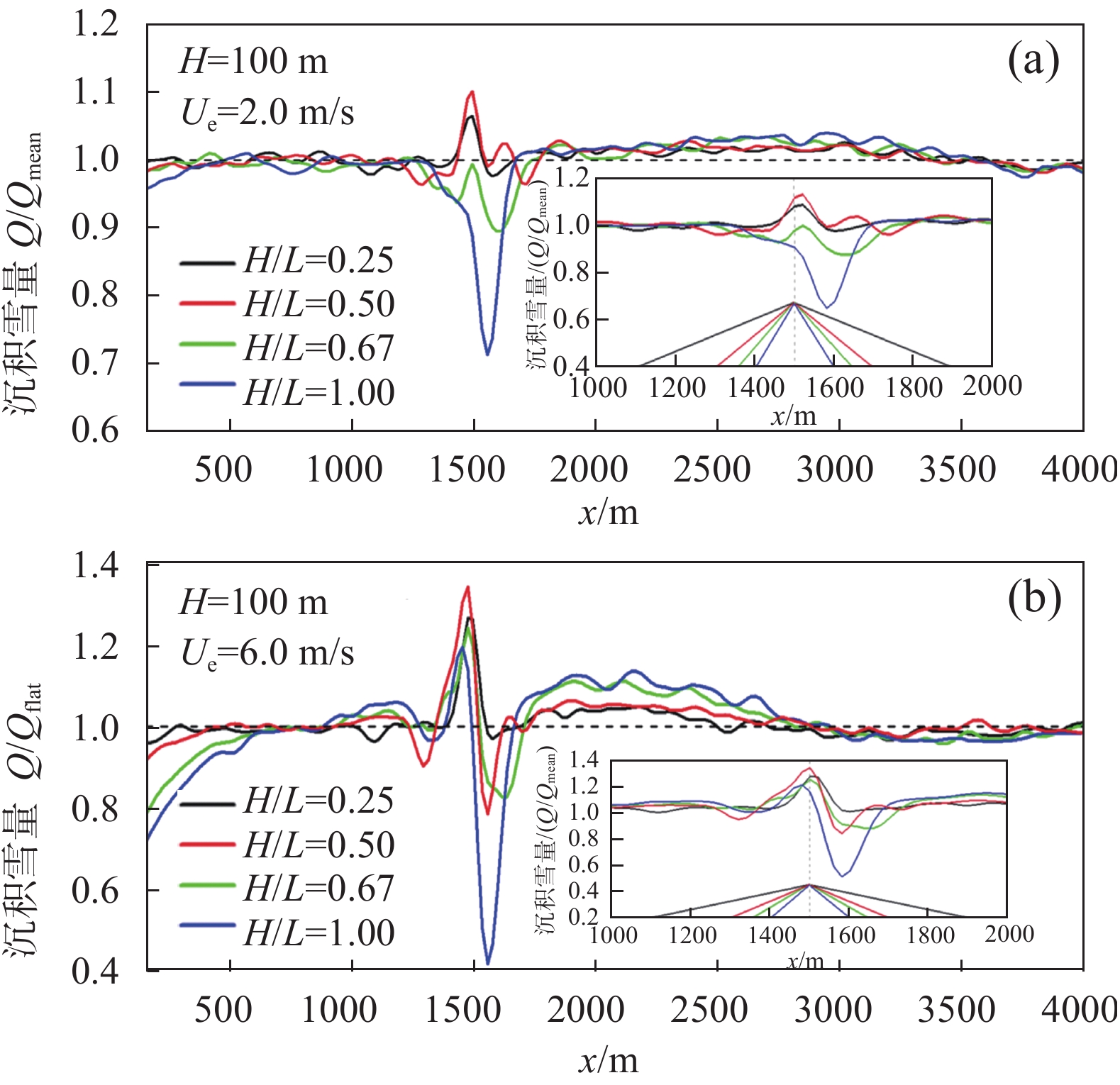
Wang和Huang[29-30]在美国奥克拉荷马大学开发的ARPS(Advanced Regional Prediction System)大涡模拟源代码的基础上进行改进,采用四阶精度的高阶差分格式提高对流向的空间离散精度,并引入适用于复杂地形的Lagrangian动态亚格子湍流模型,同时加入拉格朗日颗粒追踪模型,与流场、温度场和湿度场进行有效的耦合,建立了一套湍流流场下考虑固相颗粒相变过程的气-固两相流耦合模式。在此基础上,开展了典型地形下的降雪沉积规律的研究。采用拉格朗日粒子追踪法追踪每一颗降雪颗粒的下落轨迹,分析不同风速和不同形状地形周围的降雪沉积情况的成因及影响因素。得到的主要结论有:复杂地形湍流对空中雪粒运动轨迹的影响是导致降雪不均匀沉积分布的直接原因。小风速下,迎风坡沉积量和背风坡沉积量比值接近1,并且与地形形状无关。在大风速下,迎风坡降雪沉积量增大而背风坡沉积量减小。对于地形高宽比大的山体,迎风坡和背风坡的沉积量随风速的增大而增大,且迎风坡的增长效应大于背风坡,迎风坡和背风坡的降雪沉积机制不同,较大的迎风面积和抬升气流导致的雪通量汇聚是迎风坡和坡顶附近降雪沉积的主要机制,而背风坡后的回流涡是背风坡上沉积的主要原因。如图4(a)所示,在大风速下,陡峭的地形会加剧降雪沉积的不均匀程度。在相同的地形下,在小风速下,优先沉降的位置是背风坡;在大风速(4~6 m/s)下,优先沉降的位置转移到了迎风坡上,如图4(b)所示。
Geber等[31]通过野外观测,证实了Wang和Huang的研究结果,即优先沉降在复杂地形上呈现复杂的沉降规律,并通过WRF大涡模拟发现优先沉降增强了背风坡10%左右的降雪,其效应受气温和大气稳定度影响[32]。Comola等[33]则通过结合大涡模拟、拉格朗日随机模型计算颗粒轨迹以及浸没边界法发展了一个综合模型,用于研究连续理想山区的优先沉降问题。通过控制无量纲参数,Comola等发现了与Wang和Huang统一的结论,即存在不同的优先沉积模式,最大沉积区域既可能出现在迎风坡,也可能出现在背风坡。
|
图 4 不同风速和地形下降雪沉积量沿流向的分布[29] Fig.4 Falling snow deposition mass per unit area along the streamwise for different terrains and wind velocities (triangle terrain)[29] |
地表有积雪时,当风速到达一定阈值,就会发生风吹雪现象。风吹雪涉及湍流和颗粒的相互作用、物理相变过程及其对大气温湿度的反馈作用等复杂物理过程,时空尺度跨度大,从颗粒碰撞的微秒、微米尺度到积雪分布的季节、公里尺度,跨越8~9量级,是一个多尺度、多场耦合、多相变化的多相流动力学问题。
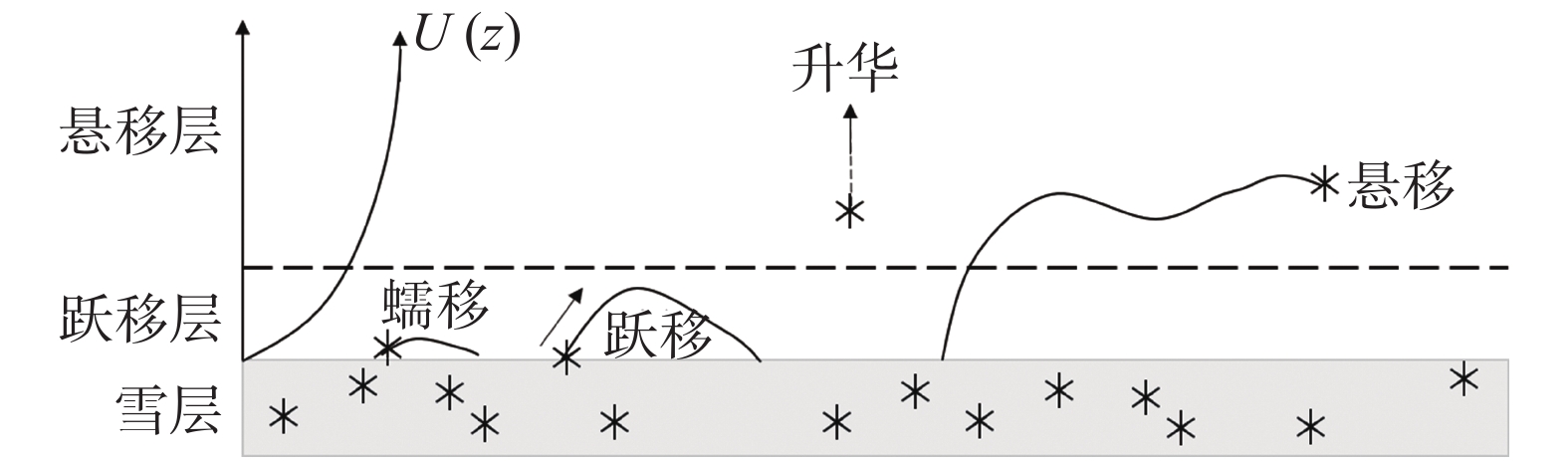
风吹雪过程中,雪粒的运动状态分为三类:大的颗粒由于惯性强,很难被吹起来,只能在地表滚动或者滑动,我们称之为蠕移;中等颗粒在风力的作用下向前跳跃,冲击地表,反弹并溅起其他颗粒,我们称之为跃移;小颗粒被吹起或者溅起,跟随湍流在空中悬浮着前进,我们称之为悬移,如图5所示。
|
图 5 风吹雪动力学过程示意图 Fig.5 Schematic diagram of wind and snow dynamics process |
由于较难区分蠕移和跃移颗粒,很多学者把风吹雪颗粒归为跃移和悬移两类。典型的风吹雪跃移模型包括雪粒的起动、雪粒与粒床的相互作用、雪粒在风场中的运动以及雪粒对风场的修正四个过程。而对雪粒悬移过程的描述则主要通过扩散方程和升华公式来表征。
早期的风吹雪研究以野外观测为主,偏向于点尺度的经验性的描述。例如,国际学者们自20世纪60年代起开展的南极观测[33-41],得出了一些关于吹雪通量、粒径分布形态与摩阻风速的经验性公式,对于雪粒起动的临界条件、风吹雪中雪粒升华的影响条件得到了初步的结论;从高海拔山区的积雪分布的野外观测中得到山脊吹雪运输机制和积雪在山区的分布形态规律及其影响因素[42]。近年来,野外观测实验偏向于更大尺度的研究,通过雷达或卫星系统观测地区风吹雪事件发生频率及环境对其的作用[43-44]。
随着研究的深入,定量化的风洞实验成为风吹雪运动机理研究的重要手段。例如:有些学者利用激光或高速摄影相机追踪运动的雪粒轨迹,分析雪粒的速度和受力等信息,总结雪粒的运动规律[45-50]。有的学者则关注雪波纹结构及其迁移过程[51]、雪壳形成物理机制[52-53]等微地貌过程,还有一些学者从工程的角度研究屋顶积雪情况[54]和路基周围积雪覆盖情况[55]。
20世纪80年代以后,随着计算机技术和计算流体力学的快速发展,数值模拟方法成为风吹雪运动机理研究的主要方式之一[56-59]。风吹雪的数值模拟主要分为两大类:一类是将颗粒作为一种特殊的流体而建立的风吹雪运动欧拉-欧拉双流体模型,适用于颗粒较小且计算区域较大研究;另一类是将雪粒作为固体颗粒,在流场内进行追踪从而分析其运动轨迹,称为欧拉-拉格朗日模型,目前大多数风吹雪计算都基于此类模型。
前期大多数数值模拟计算中简化了计算模型,例如把雪粒视作均匀粒径分布的同等大小的球形颗粒,只考虑在平坦床面上的风雪流运动,忽略空气的湍流脉动、地形等对风雪流运动的影响以及雪粒对风的反作用力等[60]。
后期的数值模拟研究热点以细化模型、精确描述雪粒运动规律为主。例如,2008年Zhang和Huang在Nemoto和Nishimura稳态模型的基础上建立了风场和颗粒相互作用的耦合发展跃移模型,总结了颗粒的平均跃移高度和长度随着摩阻风速指数增加,反弹雪颗粒数目和流向雪运输速率随着摩阻风速的增大而增加等物理规律[61]。
随着模拟技术的不断提高,风吹雪模型从最初基于平均流的、以稳态跃移层为前提的一维和二维模型逐渐转变为考虑湍流、风场-雪粒耦合、非稳态跃移层、复杂地形等因素的三维计算模型[62-67]。例如,Huang和Wang开展了在湍流风场作用下风吹雪引起的积雪再分布、风吹雪的形成、风雪流发展过程、雪粒的运动机理的研究[68],研究首次再现了与野外实际风雪流吻合的风雪流条带,并揭示出条带(图6所示)的形成主要是空中运动雪粒在高速旋转的旋涡作用下的一种自组织现象,随机的粒-床相互作用很大程度上决定了风雪流条带的形状。Comola等考虑了跃移雪粒的破碎过程[69],使得风吹雪模型趋于完善。

|
图 6 湍流边界层内的风雪流条带结构[68] Fig.6 Streamer structures of wind and snow flow in turbulent boundary layer[69] |
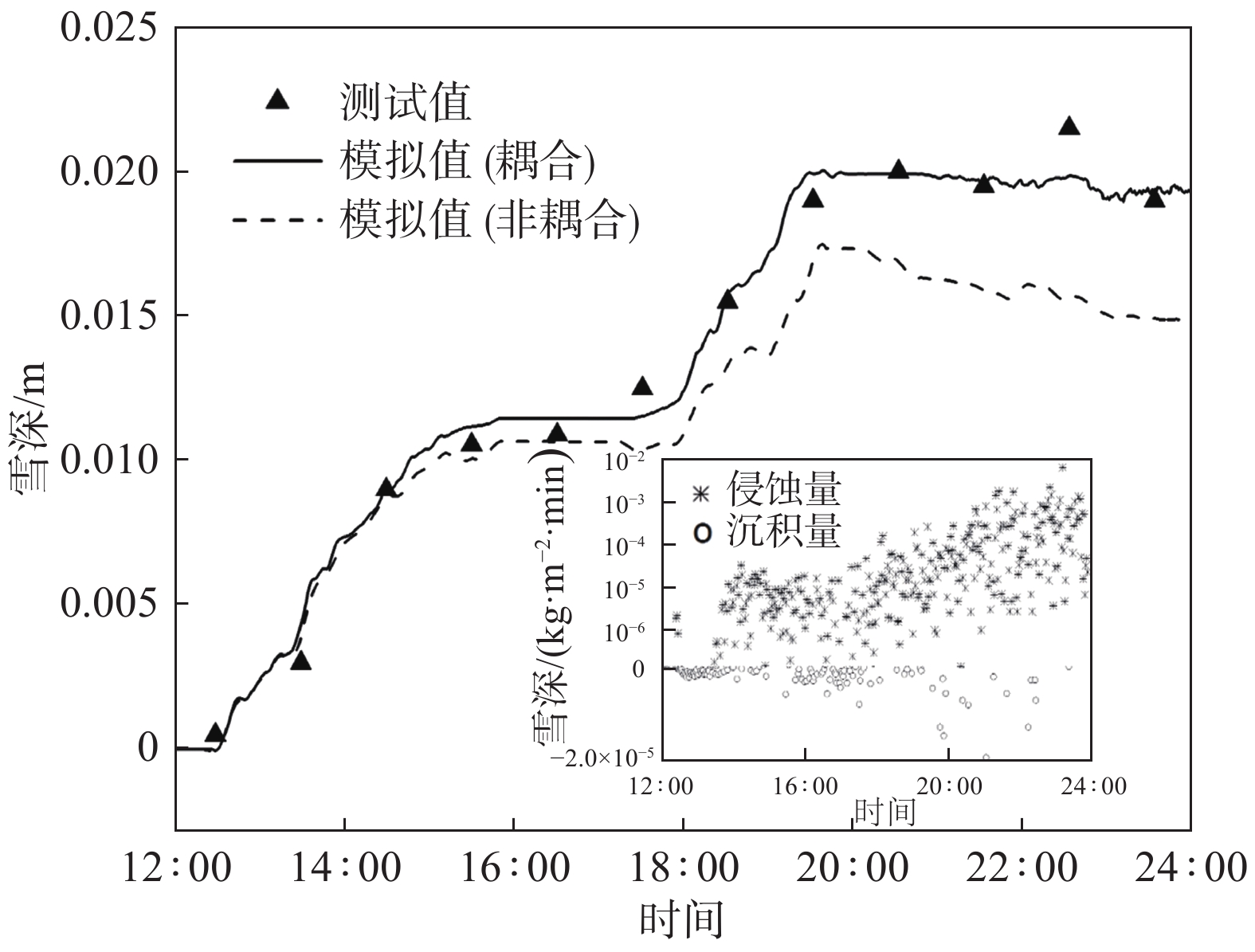
Li等基于前人的实验结果结合理论推导,发展了坡面地形的风吹雪参数化方案,开展了真实区域降雪沉积规律以及由降雪和风吹雪共同导致的复杂地形积雪分布和演变过程的研究[70],如图7所示,图中实线和虚线分别代表考虑和不考虑雪粒与风场耦合作用的结果,散点代表实验观测值。从结果可以看出,考虑雪粒对风场的反作用力比忽略雪粒与风场之间的耦合作用,模拟得到的雪深随时间的变化与实验结果更加吻合。
|
图 7 野外测量积雪深度与模拟雪深度随时间的演变(插图为模拟计算侵蚀与沉积值)[70] Fig.7 Field measurement of snow depth and the evolution of simulated snow depth over time (the illustration shows the simulated calculation of erosion and sedimentation values)[70] |
国际上,越来越多的学者关注到积雪再分布的重要性。一些学者基于地形参数预测山区积雪再分布[71-72]。Freudier等指出—考虑积雪再分布能大大提高对世界各地山区流域的积雪和雪水当量分布模式以及融雪径流的预测精度,但是目前积雪再分布模型仍然存在限制,仍然没有可以广泛使用的统计水文模型和精确描述物理细节的积雪模型[21]。
2.3 吹雪升华在风吹雪过程中,还会伴随雪粒的升华现象。在空气流体中运动的雪颗粒系统中至少有三相组成,从固态雪粒相变为气态的过程称为升华,雪粒的升华受到温度、相对湿度和辐射量的影响[73-74]。风吹雪引起的雪粒升华对于积雪时空演变、升华对于雪层质能平衡有不可忽略的影响,因此许多雪水文模型中考虑了升华效应[75-78]。近年研究表明,风吹雪模型中跃移层的升华过程的忽略会导致低估风吹雪升华总量[79-82]。
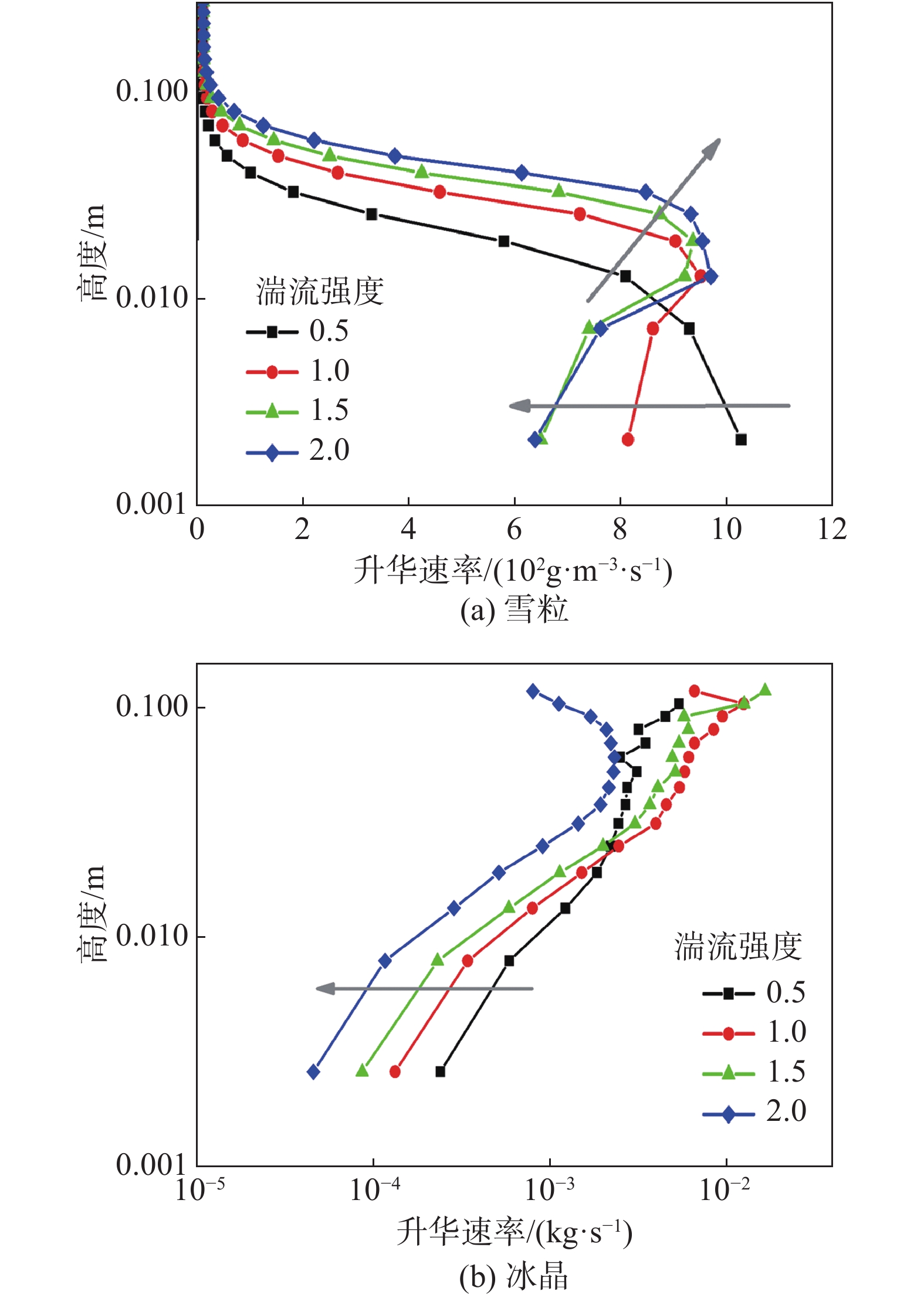
之前的研究认为近地表跃移层水汽会随着风吹雪升华的发生很快达到饱和,从而使吹雪跃移层升华受到抑制,因而在研究中普遍认为跃移层的风吹雪升华可以被忽略。Wang等通过对风吹雪过程中升华的研究发现,在湍流存在的情况下,近地表跃移雪粒和悬移雪粒均可持续发生升华[83],并且通过数值模拟发现,相同风速下,雪粒升华速率随湍流强度的增大而增大,冰晶升华速率随湍流强度的增大而减小(如图8所示)。Sharma等通过直接数值求解雪粒的质量和热量平衡方程,对比它的稳定解TM模型,发现稳定解模型会大大低估跃移颗粒的升华速率[84]。这些工作对人们深刻认识风吹雪动力过程与区域水文过程的关联提供了重要的理论基础。
|
图 8 风吹雪中雪粒和冰晶升华速率随高度变化[83] Fig.8 Snow particles and ice crystal sublimation rate varies with height in windblown snow[83] |
风雪流的动力过程的研究目的是最终将之植入雪水文模型中,应用于预测寒区水文过程。
流域水文模型能够统一模拟降水/蒸发、产流、河网汇流、土壤水运动、地下水运动等水文过程,使人们可以站在流域整体视角研究各种水文过程的综合影响。水文模型一般可以分为概念性和分布式物理模型两类。概念性模型有Stanford模型[85]、水箱模型[86]以及新安江模型[87]等,用经验、概化的方法表达流域的水文过程,结构简单,被广泛使用。而分布式水文模型则通过连续性方程和动力学方程来描述水文循环中的各个子过程,大部分模型参数具有明确的物理意义,充分考虑各变量的空间变异性,具有很强的适应性,如SHE模型[88]、TOPMODEL[89]、WEP[90]等。寒区水文模型侧重表达融雪径流在水文过程中的作用,对融雪过程的描述是其重点。
与水文模型类似,融雪模型也可以分为概念性模型和分布式物理模型两类。最常用的概念型模型为度-日模型[91-93],它是基于冰雪消融与气温尤其是冰雪表面的正积温之间的线性关系而建立的,目前广泛应用于高山冰川的冰雪消融研究中。而分布式物理模型则通过求解积雪质能平衡方程,来获得各个网格点上的融雪量,如ISNOBAL[94]、Alpine3D[95]、SnowModel[96]等,它们具有分布式、详尽、复杂和高时空分辨率的特征,但应用时需要庞大的气象观测数据和计算资源的支持,因此只适用于小流域短时间的模拟,而对于中尺度和全球尺度模拟无法适用。相比之下,简单的统计水文模型应用更广泛,但它们往往需要大量的气温指标拟合公式来简化计算,并不具备普适性,尤其是不同地区可能需要不同的参数来修正,但是实际上包括极地、祁连山等山区是人迹罕至的地方,很难获得需要的观测数据去支持这样的修正。
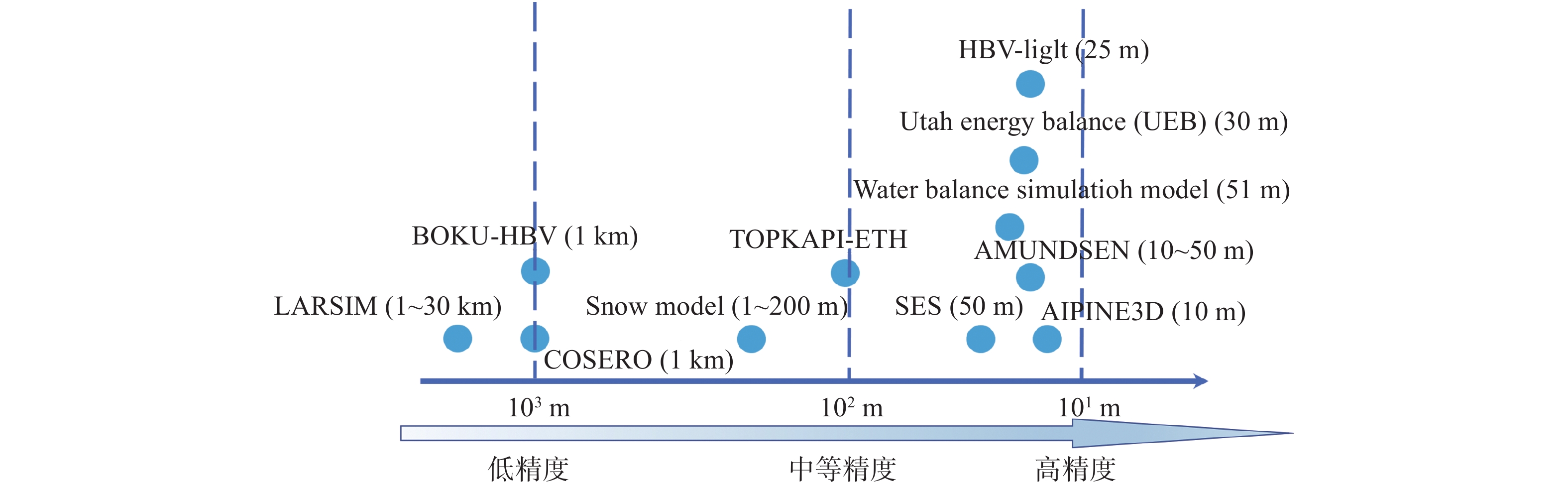
在实际中,季节性积雪经常以斑状积雪的形式存在,这种不均匀的积雪覆盖大大提高了对于模型中网格分辨率的要求。在模型中不同分辨率的网格会造成计算结果差异显著[20]。近年来,国际上针对模拟全球气候和相应对融雪水文学的影响开发出很多融雪模型,取得了快速的科学研究进展。从分辨率角度考虑可以划分为以千米单位的低分辨率模型、以百米为单位的中分辨率模型和以米作单位的高分辨率模型,如图9所示。但是,目前几乎所有模型采用的风吹雪方案如SPBM[7]、PIEKTUK-B[97]等都大同小异,很少有能体现尺度差异的模型。
风吹雪和降雪沉降对于积雪再分布有重要的影响。因此,从模型中是否考虑风雪动力学问题可将水文模型划分为三类:第一类模型认为积雪只与降雪有关,不考虑风对积雪的作用,或者用简单的统计方法来考虑风的效应[98-100];第二类是在雪水文模型中考虑到风吹雪对积雪再分布影响的模型,而降雪只是一个简单的输入条件,例如AMUNDSEN[101]、Water balance Simulation Mode[102-103]和SnowModel[104];第三类则是在模型中同时考虑了降雪沉降和分吹雪对积雪分布影响的模型,有OEZ[105]、SES[106]、Utah Energy Balance (UEB)[107]等。Li等将风吹雪模型与降雪沉降模型结合起来,建立了一个适用于复杂地形的中尺度积雪分布预测模式来研究地形和风速等因素对复杂地形积雪分布的影响。结合2013年到2015年的降雪季节对研究区域进行了多次野外观测,测量结果验证了预测模式的可靠性,同时,分析了影响复杂地形积雪分布的主要影响因素,如图10所示。
|
图 9 不同水文模型的分辨率比较 Fig.9 Resolution comparison of different hydrological models |

|
图 10 不同风速下风吹雪导致的侵蚀与沉积[69] Fig.10 Erosion and deposition caused by wind and snow at different wind speeds[69] |
然而,这些模型中对降雪的优先沉降、风吹雪、风吹雪升华过程的研究在很大程度上依赖于经验系数和个体案例研究,其中的吹雪方案对不同尺度的适应性还值得继续研究,远未达到能够准确预测区域积雪分布及其时空演化的程度。
纵观目前存在的水文模型,本文提出以下仍待解决的问题:
1)积雪分布时空演化是一个十分复杂的问题。目前对不同下垫面的积雪过程在不同时空尺度上的物理机制还不明晰。降雪和积雪在不同下垫面的沉积特性受地表特征、大气湍流和地形的相互作用影响,而在不同的时空尺度上,积雪过程的主导物理机制不同,影响因子也不同,这些内容都需要在高寒地区雪水文模型中加以体现。然而大部分雪水文模型只是考虑降雪和融雪过程,而忽略风吹雪及其升华对其的影响,或者采用简单的参数化方案对其进行描述,无法反应下垫面特征、大气条件、地形和时空尺度对积雪过程表征的影响,不能准确描述不同时空尺度的积雪过程物理特征,因而难以准确预测实际的积雪分布时空变化。在自然中实际地形较为复杂,很难用一个统一的优先沉降模式来描述降雪导致的不均匀分布。
2)风吹雪升华在水文模型中发挥着重要的作用。例如近年来关于极地的研究表明,风吹雪升华导致的质量损失占总雪水资源损失量的主要部分[108]。然而,目前通用的Thorpe和Mason模型只适用于稳态情形,对于非稳态情形下雪粒的升华估计会产生很大的误差。因此,如何准确描述雪粒在湍流边界层中的升华速率的问题,以及如何准确评估雪层表面升华和风吹雪升华产生的质量损失,还有待未来的研究。这对于雪水文学模型的改进有重要的意义。
3)我国积雪主要分布在西北干旱地区,降水稀少,积雪往往呈现斑状分布,时空异质性极强。斑状分布积雪情况下,采用传统的二值法会高估雪深或雪水当量[109]。同时,由于斑状分布,风吹雪较难达到饱和,现有的风吹雪模型无法满足准确模拟其动力学过程的要求。而目前对于模型中使用高分辨率模拟斑状雪演化过程的动力学的研究还很缺乏。
4)遥感反演是近年来发展最快的积雪研究方法,是我国积雪分布应用最广泛的技术手段,在中大尺度的积雪面积分布研究中具有很大的优势,但是在积雪深度和雪水当量方面仍有所局限,在对山区和复杂下垫面的积雪信息提取方面也还存在困难。遥感手段的时空分辨率受到遥感卫星探测器的测量频率和精度的限制,无法满足风吹雪频繁发生、积雪分布迅速变化的高寒地区雪水文过程的模拟要求。而室内实验和野外观测往往都是局限在点尺度的观测实验,很难突破尺度限制,而积雪动力学在各个尺度上的体现往往是不同的动力学机制在起主导作用。因此,发展三者的融合方法,突破尺度限制,是积雪监测研究的重点和难点。
以上提出的亟待解决的前沿科学问题本质上都是多相流理论在积雪水文领域的实际应用。未来的研究中需要通过将多相流理论更多地应用于实际观测或数值模拟中,来解释或分析实际风雪流中的自然规律。
4 结 论研究风雪多相流过程对于水文学中精确估计高山积雪分布和径流量估计有重要的意义。本文回顾了目前关于风吹雪动力学过程的研究,指出了降雪沉积、风吹雪再分布和风吹雪升华对雪层质能变化的原理,并分析了其对于准确描述高山或极地雪水资源的重要性。对于目前现存的水文模型从不同角度进行分类和比较,指出目前模型中存在的问题和未来的重点研究方向。迄今为止,关于吹/积雪动力过程的研究工作依然相对独立,但是将吹/积雪动力过程导致的雪盖时空演化与气象、水文模式及气候参数相互耦合并建立起综合的水文模型还需要进一步研究开发。未来面临的主要的挑战是将风吹雪模型及雪水文模型应用于更大的时空尺度,从而实现适用于中国高寒极地地区的雪水资源分布的准确预测和评估。
| [1] |
WARREN S G. Optical properties of snow[J]. Reviews of Geophysics, 1982, 20(1): 67-89. DOI:10.1029/RG020i001p00067 |
| [2] |
ARMSTRON R L, BRUN E. Snow and climate: physical processes, surface energy exchange and modeling[M]. Cambridge University Press, 2008.
|
| [3] |
OKI T, KANAE S. Global hydrological cycles and world water resources[J]. Science, 2006, 313(5790): 1068-1072. DOI:10.1126/science.1128845 |
| [4] |
BARNETT T P, ADAM J C, LETTENMAIER D P. Potential impacts of a warming climate on water availability in snow-dominated regions[J]. Nature, 2005, 438(7066): 303-309. DOI:10.1038/nature04141 |
| [5] |
DEEMS J S, FASSNACHT S R, ELDER K J. Fractal distribution of snow depth from lidar data[J]. Journal of Hydrometeorology, 2006, 7(2): 285-297. DOI:10.1175/jhm487.1 |
| [6] |
BUTTLE J M. Using a temperature-based model of snow accumulation and melt to assess the long-term hydrologic behaviour of forested headwater basins in south-central Ontario[C]//66th Eastern Snow Conference. Ontario: 2009.
|
| [7] |
POMEROY J W, MARSH P, GRAY D M. Application of a distributed blowing snow model to the Arctic[J]. Hydrological Processes, 1997, 11(11): 1451-1464. DOI:10.1002/(SICI)1099-1085(199709)11:11<1451:AID-HYP449>3.0.CO;2-Q |
| [8] |
NISHIMURA K, NEMOTO M. Blowing snow at Mizuho station, Antarctica[J]. Philosophical Transactions Series A, Mathematical, Physical, and Engineering Sciences, 2005, 363(1832): 1647-1662. DOI:10.1098/rsta.2005.1599 |
| [9] |
POMEROY J W, ESSERY R L H. Turbulent fluxes during blowing snow: field tests of model sublimation predictions[J]. Hydrological Processes, 1999, 13(18): 2963-2975. DOI:10.1002/(SICI)1099-1085(19991230)13:18<2963:AID-HYP11>3.0.CO;2-9 |
| [10] |
YANG X, PYLE J A, COX R A. Sea salt aerosol production and bromine release: Role of snow on sea ice[J]. Geophysical Research Letters, 2008, 35(16): L16815. DOI:10.1029/2008GL034536 |
| [11] |
FREY M M, NORRIS S J, BROOKS I M, et al. First direct observation of sea salt aerosol production from blowing snow above sea ice[J]. Atmospheric Chemistry and Physics, 2020, 20(4): 2549-2578. DOI:10.5194/acp-20-2549-2020 |
| [12] |
YANG X, BLECHSCHMIDT A M, BOGNAR K, et al. Pan-Arctic surface ozone: modelling vs. measurements[J]. Atmospheric Chemistry and Physics, 2020, 20(24): 15937-15967. DOI:10.5194/acp-20-15937-2020 |
| [13] |
王慧彦, 李志伟. 2008年雪灾的原因及日本应急制度给我国的启发[J]. 防灾科技学院学报, 2008, 10(2): 47-50. WANG H Y, LI Z W. Causes of 2008 snow disaster in China and enlightenment from Japanese emergency system[J]. Journal of Institute of Disaster-Prevention Science and Technology, 2008, 10(2): 47-50. DOI:10.3969/j.issn.1673-8047.2008.02.013 (in Chinese) |
| [14] |
LUETSCHG M, STOECKLI V, LEHNING M, et al. Temperatures in two boreholes at Flüela Pass, Eastern Swiss Alps: the effect of snow redistribution on permafrost distribution patterns in high mountain areas[J]. Permafrost and Periglacial Processes, 2004, 15(3): 283-297. DOI:10.1002/ppp.500 |
| [15] |
ECKERSTORFER M, CHRISTIANSEN H H. Topographical and meteorological control on snow avalanching in the Longyearbyen area, central Svalbard 2006-2009[J]. Geomorphology, 2011, 134(3-4): 186-196. DOI:10.1016/j.geomorph.2011.07.001 |
| [16] |
MELLOR M. A brief review of snow drifting research[J]. Snow Removal and Ice Control Research, 1970(115): 196-209. |
| [17] |
KIND R J. Snowdrifting: a review of modelling methods[J]. Cold Regions Science and Technology, 1986, 12(3): 217-228. DOI:10.1016/0165-232X(86)90036-4 |
| [18] |
NAAIM M, NAAIM-BOUVET F, MARTINEZ H. Numerical simulation of drifting snow: erosion and deposition models[J]. Annals of glaciology, 1998, 26: 191-196. DOI:10.3189/1998AoG26-1-191-196 |
| [19] |
CLARK M P, HENDRIKX J, SLATER A G, et al. Representing spatial variability of snow water equivalent in hydrologic and land-surface models: a review[J]. Water Resources Research, 2011, 47(7): W07539. DOI:10.1029/2011WR010745 |
| [20] |
MOTT R, VIONNET V, GRÜNEWALD T. The seasonal snow cover dynamics: review on wind-driven coupling processes[J]. Frontiers in Earth Science, 2018, 6: 197. DOI:10.3389/feart.2018.00197 |
| [21] |
FREUDIGER D, KOHN I, SEIBERT J, et al. Snow redistribution for the hydrological modeling of alpine catchments[J]. Wiley Interdisciplinary Reviews: Water, 2017, 4(5): e1232. DOI:10.1002/wat2.1232 |
| [22] |
BERGERON T. On the low-level redistribution of atmospheric water caused by orography[C]//Conference of Cloud Physics. Tokyo: 1965.
|
| [23] |
COLLE B A, SMITH R B, WESLEY D A. Theory, observations, and predictions of orographic precipitation[M]//Springer Atmospheric Sciences. Dordrecht: Springer Netherlands, 2012: 291-344. doi: 10.1007/978-94-007-4098-3_6
|
| [24] |
STOELINGA M T, STEWART R E, THOMPSON G, et al. Microphysical processes within winter orographic cloud and precipitation systems[M]// CHOW F K, DE WEKKER S, SNYDER B J, eds. Mountain Weather Research and Forecasting. Springer Atmospheric Sciences. Dordrecht: Springer Netherlands, 2012: 345-408. doi: 10.1007/978-94-007-4098-3_7
|
| [25] |
LEHNING M, LÖWE H, RYSER M, et al. Inhomogeneous precipitation distribution and snow transport in steep terrain[J]. Water Resources Research, 2008, 44(7): W07404. DOI:10.1029/2007WR006545 |
| [26] |
MOTT R, SCIPIÓN D, SCHNEEBELI M, et al. Orographic effects on snow deposition patterns in mountainous terrain[J]. Journal of Geophysical Research: Atmospheres, 2014, 119(3): 1419-1439. DOI:10.1002/2013JD019880 |
| [27] |
DORE A J, CHOULARTON T W, FOWLER D, et al. Orographic enhancement of snowfall[J]. Environmental Pollution, 1992, 75(2): 175-179. DOI:10.1016/0269-7491(92)90037-B |
| [28] |
HOUZE R A Jr. Orographic effects on precipitating clouds[J]. Reviews of Geophysics, 2012, 50(1): RG1001. DOI:10.1029/2011RG000365 |
| [29] |
王正师. 复杂地形积雪分布及其演化的大涡模拟研究[D]. 兰州: 兰州大学, 2016. WANG Z S. Large eddy simulation of the distribution and evolution of snow over complex terrain[D]. Lanzhou: Lanzhou University, 2016. (in Chinese) |
| [30] |
WANG Z S, HUANG N. Numerical simulation of the falling snow deposition over complex terrain[J]. Journal of Geophysical Research: Atmospheres, 2017, 122(2): 980-1000. DOI:10.1002/2016JD025316 |
| [31] |
GERBER F, LEHNING M, HOCH S W, et al. A close-ridge small-scale atmospheric flow field and its influence on snow accumulation[J]. Journal of Geophysical Research: Atmospheres, 2017, 122(15): 7737-7754. DOI:10.1002/2016JD026258 |
| [32] |
GERBER F, MOTT R, LEHNING M. The importance of near-surface winter precipitation processes in complex alpine terrain[J]. Journal of Hydrometeorology, 2019, 20(2): 177-196. DOI:10.1175/JHM-D-18-0055.1 |
| [33] |
COMOLA F, GIOMETTO M G, SALESKY S T, et al. Preferential deposition of snow and dust over hills: governing processes and relevant scales[J]. Journal of Geophysical Research: Atmospheres, 2019, 124(14): 7951-7974. DOI:10.1029/2018JD029614 |
| [34] |
DINGLE W R, RADOK U W. Antarctic snow drift and mass transport[M]. IASH Publ, 1961.
|
| [35] |
BUDD W F. The drifting of nonuniform snow Particles[M]. Studies in Antarctic Meteorology. Washington, D. C. : American Geophysical Union, 2013: 59-70. doi: 10.1029/ar009p0059
|
| [36] |
KOBAYASHI S. Snow transport by katabatic winds in mizuho camp area, east Antarctica[J]. Journal of the Meteorological Society of Japan Ser II, 1978, 56(2): 130-139. DOI:10.2151/jmsj1965.56.2_130 |
| [37] |
TAKAHASHI S. Characteristics of drifting snow at mizuho station, Antarctica[J]. Annals of Glaciology, 1985, 6: 71-75. DOI:10.1017/s0260305500010028 |
| [38] |
DOVER S E. Numerical modelling of blowing snow[D]. United Kingdom: University of Leeds, 1993.
|
| [39] |
VAUGHAN D G, MARSHALL G J, CONNOLLEY W M, et al. Recent rapid regional climate warming on the Antarctic peninsula[J]. Climatic Change, 2003, 60(3): 243-274. DOI:10.1023/A:1026021217991 |
| [40] |
MANN G W, ANDERSON P S, MOBBS S D. Profile measurements of blowing snow at Halley, Antarctica[J]. Journal of Geophysical Research: Atmospheres, 2000, 105(D19): 24491-24508. DOI:10.1029/2000JD900247 |
| [41] |
BINTANJA R. Surface heat budget of Antarctic snow and blue ice: Interpretation of spatial and temporal variability[J]. Journal of Geophysical Research: Atmospheres, 2000, 105(D19): 24387-24407. DOI:10.1029/2000JD900356 |
| [42] |
FÖHN P M B. Snow transport over mountain crests[J]. Journal of Glaciology, 1980, 26(94): 469-480. DOI:10.3189/s0022143000010984 |
| [43] |
PALM S P, YANG Y, SPINHIRNE J D, et al. Satellite remote sensing of blowing snow properties over Antarctica[J]. Journal of Geophysical Research: Atmospheres, 2011, 116(D16): D16123. DOI:10.1029/2011JD015828 |
| [44] |
WALTER B, HUWALD H, GEHRING, et al. Radar measurements of blowing snow off a mountain ridge[J]. The Cryosphere, 2020, 14(6): 1779-1794. DOI:10.5194/tc-14-1779-2020 |
| [45] |
NISHIMURA K, YOKOYAMA C, ITO Y, et al. Snow particle speeds in drifting snow[J]. Journal of Geophysical Research: Atmospheres, 2014, 119(16): 9901-9913. DOI:10.1002/2014JD021686 |
| [46] |
KIKUCHI T. A wind tunnel study of the aerodynamic roughness associated with drifting snow[J]. Cold Regions Science and Technology, 1981, 5(2): 107-118. DOI:10.1016/0165-232X(81)90045-8 |
| [47] |
ARAOKA K, MAENO N. Dynamical behaviors of snow particles in the saltation layer[J]. Memoirs of National Institute of Polar Research, 1981, 19(10): 253-263.
|
| [48] |
SCHMIDT D S, SCHMIDT R A, DENT J D. Electrostatic force in blowing snow[J]. Boundary-Layer Meteorology, 1999, 93(1): 29-45. DOI:10.1023/A:1002045818907 |
| [49] |
SUGIURA K, MAENO N. Wind-tunnel measurements of restitution coefficients and ejection number of snow particles in drifting snow: determination of splash functions[J]. Boundary-Layer Meteorology, 2000, 95(1): 123-143. DOI:10.1023/A:1002681026929 |
| [50] |
CLIFTON A, RÜEDI J D, LEHNING M. Snow saltation threshold measurements in a drifting-snow wind tunnel[J]. Journal of Glaciology, 2006, 52(179): 585-596. DOI:10.3189/172756506781828430 |
| [51] |
SUGIURA K, NISHIMURA K, MAENO N, et al. Measurements of snow mass flux and transport rate at different particle diameters in drifting snow[J]. Cold Regions Science and Technology, 1998, 27(2): 83-89. DOI:10.1016/S0165-232X(98)00002-0 |
| [52] |
SOMMER C G, LEHNING M, FIERZ C. Wind tunnel experiments: saltation is necessary for wind-packing[J]. Journal of Glaciology, 2017, 63(242): 950-958. DOI:10.1017/jog.2017.53 |
| [53] |
SOMMER C G, WEVER N, FIERZ C, et al. Investigation of a wind-packing event in Queen Maud Land, Antarctica[J]. The Cryosphere, 2018, 12(9): 2923-2939. DOI:10.5194/tc-12-2923-2018 |
| [54] |
ZHOU X Y, HU J H, GU M. Wind tunnel test of snow loads on a stepped flat roof using different granular materials[J]. Natural Hazards, 2014, 74(3): 1629-1648. DOI:10.1007/s11069-014-1296-z |
| [55] |
LÜ X, HUANG N, TONG D. Wind tunnel experiments on natural snow drift[J]. Science China Technological Sciences, 2012, 55(4): 927-938. DOI:10.1007/s11431-011-4731-3 |
| [56] |
KIND R J. A critical examination of the requirements for model simulation of wind-induced erosion/deposition phenomena such as snow drifting[J]. Atmospheric Environment (1967), 1976, 10(3): 219-227. DOI:10.1016/0004-6981(76)90094-9 |
| [57] |
DYUNIN A K, KOTLYAKOV V M. Redistribution of snow in the mountains under the effect of heavy snow-storms[J]. Cold Regions Science and Technology, 1980, 3(4): 287-294. DOI:10.1016/0165-232X(80)90035-X |
| [58] |
SCHMIDT R A. Transport rate of drifting snow and the mean wind speed profile[J]. Boundary-Layer Meteorology, 1986, 34(3): 213-241. DOI:10.1007/BF00122380 |
| [59] |
POMEROY J W, PARVIAINEN J, HEDSTROM N, et al. Coupled modelling of forest snow interception and sublimation[J]. Hydrological Processes, 1998, 12(15): 2317-2337. DOI:10.1002/(SICI)1099-1085(199812)12:15<2317:AID-HYP799>3.0.CO;2-X |
| [60] |
NEMOTO M, NISHIMURA K. Numerical simulation of snow saltation and suspension in a turbulent boundary layer[J]. Journal of Geophysical Research: Atmospheres, 2004, 109(D18): D18206. DOI:10.1029/2004JD004657 |
| [61] |
ZHANG J, HUANG N. Simulation of snow drift and the effects of snow particles on wind[J]. Modelling and Simulation in Engineering, 2008, 2008: 1-6. DOI:10.1155/2008/408075 |
| [62] |
LISTON G E, STURM M. A snow-transport model for complex terrain[J]. Journal of Glaciology, 1998, 44(148): 498-516. DOI:10.3189/s0022143000002021 |
| [63] |
NAAIM M, NAAIM-BOUVET F, MARTINEZ H. Numerical simulation of drifting snow: erosion and deposition models[J]. Annals of Glaciology, 1998, 26: 191-196. DOI:10.1017/s0260305500014798 |
| [64] |
GROOT ZWAAFTINK C D, DIEBOLD M, HORENDER S, et al. Modelling small-scale drifting snow with a Lagrangian stochastic model based on large-eddy simulations[J]. Boundary-Layer Meteorology, 2014, 153(1): 117-139. DOI:10.1007/s10546-014-9934-2 |
| [65] |
GAUER P. Blowing and drifting snow in Alpine terrain: numerical simulation and related field measurements[J]. Annals of Glaciology, 1998, 26: 174-178. DOI:10.1017/s0260305500014762 |
| [66] |
NEMOTO M, NISHIMURA K, KOBAYASHI S, et al. Numerical study of the time development of drifting snow and its relation to the spatial development[J]. Annals of Glaciology, 2004, 38: 343-350. DOI:10.3189/172756404781815202 |
| [67] |
DOORSCHOT J J J, LEHNING M. Equilibrium saltation: mass fluxes, aerodynamic entrainment, and dependence on grain properties[J]. Boundary-Layer Meteorology, 2002, 104(1): 111-130. DOI:10.1023/A:1015516420286 |
| [68] |
HUANG N, WANG Z S. The formation of snow streamers in the turbulent atmosphere boundary layer[J]. Aeolian Research, 2016, 23: 1-10. DOI:10.1016/j.aeolia.2016.09.002 |
| [69] |
COMOLA F, KOK J F, GAUME J, et al. Fragmentation of wind-blown snow crystals[J]. Geophysical Research Letters, 2017, 44(9): 4195-4203. DOI:10.1002/2017GL073039 |
| [70] |
LI G, WANG Z S, HUANG N. A snow distribution model based on snowfall and snow drifting simulations in mountain area[J]. Journal of Geophysical Research: Atmospheres, 2018, 123(14): 7193-7203. DOI:10.1029/2018JD028434 |
| [71] |
WINSTRAL, A, MARKS D. Simulating wind fields and snow redistribution using terrain-based parameters to model snow accumulation and melt over a semi-arid mountain catchment[J]. Hydrological Processes, 2002, 16(18): 3585-3603. DOI:10.1002/hyp.1238 |
| [72] |
SCHÖN, P., NAAIM-BOUVET, F., VIONNET, V., et al. Merging a terrain-based parameter with blowing snow fluxes for assessing snow redistribution in alpine terrain[J]. Cold Regions Science and Technology, 2018, 155: 161-173. DOI:10.1016/j.coldregions.2018.08.002 |
| [73] |
DYUNIN A K. Fundamentals of the mechanics of snow storms[C]// International Conference on Low Temperature Science, I: Conference on Physics of Snow and Ice. Japan: Sapporo, 1967.
|
| [74] |
SCHMIDT R A. Sublimation of wind-transported snow: A model[Z]. United States: USDA Forest Service, 1972.
|
| [75] |
POMEROY J W, SCHMIDT R A. The use of fractal geometry in modelling intercepted snow accumulation and sublimation[C]// Proceedings of the Eastern Snow Conference. Quebec: Honor Paper Award, 1993.
|
| [76] |
DÉRY S J, YAU M K. Large-scale mass balance effects of blowing snow and surface sublimation[J]. Journal of Geophysical Research: Atmospheres, 2002, 107(D23): ACL8-1-ACL8-17. DOI:10.1029/2001jd001251 |
| [77] |
DURAND Y, GUYOMARC'H G, MÉRINDOL L, et al. Improvement of a numerical snow drift model and field validation[J]. Cold Regions Science and Technology, 2005, 43(1-2): 93-103. DOI:10.1016/j.coldregions.2005.05.008 |
| [78] |
GROOT ZWAAFTINK C D, LÖWE H, MOTT R, et al. Drifting snow sublimation: a high-resolution 3-D model with temperature and moisture feedbacks[J]. Journal of Geophysical Research: Atmospheres, 2011, 116(D16): D16107. DOI:10.1029/2011JD015754 |
| [79] |
DAI X, HUANG N. Numerical simulation of drifting snow sublimation in the saltation layer[J]. Scientific Reports, 2014, 4: 6611. DOI:10.1038/srep06611 |
| [80] |
HUANG N, DAI X Q, ZHANG J. The impacts of moisture transport on drifting snow sublimation in the saltation layer[J]. Atmospheric Chemistry and Physics, 2016, 16(12): 7523-7529. DOI:10.5194/acp-16-7523-2016 |
| [81] |
HUANG N, SHI G L. The significance of vertical moisture diffusion on drifting snow sublimation near snow surface[J]. The Cryosphere, 2017, 11(6): 3011-3021. DOI:10.5194/tc-11-3011-2017 |
| [82] |
LI G, HUANG N, WANG Z S. Drifting snow and its sublimation in turbulent boundary layer[J]. Journal of Physics: Conference Series, 2017, 822: 012045. DOI:10.1088/1742-6596/822/1/012045 |
| [83] |
WANG Z S, HUANG N, PÄHTZ T. The effect of turbulence on drifting snow sublimation[J]. Geophysical Research Letters, 2019, 46(20): 11568-11575. DOI:10.1029/2019GL083636 |
| [84] |
SHARMA V, COMOLA F, LEHNING M. On the suitability of the Thorpe-Mason model for calculating sublimation of saltating snow[J]. The Cryosphere, 2018, 12(11): 3499-3509. DOI:10.5194/tc-12-3499-2018 |
| [85] |
CRAWFORD N H, LINSLEY R K. Digital Simulation in Hydrology' Stanford Watershed Model 4[R]. United States: The National Academies of Sciences, 1966.
|
| [86] |
KITANIDIS P K, BRAS R L. Real‐time forecasting with a conceptual hydrologic model: 2. Applications and results[J]. Water Resources Research, 1980, 16(6): 1034-1044. DOI:10.1029/WR016i006p01034 |
| [87] |
刘金涛, 宋慧卿, 张行南, 等. 新安江模型理论研究的进展与探讨[J]. 水文, 2014, 34(1): 1-6. LIU J T, SONG H Q, ZHANG X N, et al. A discussion on advances in theories of Xinanjiang Model[J]. Journal of China Hydrology, 2014, 34(1): 1-6. DOI:10.3969/j.issn.1000-0852.2014.01.001 (in Chinese) |
| [88] |
JABER F H, SHUKLA S. MIKE SHE: Model use, calibration, and validation[J]. Transactions of the ASABE, 2012, 55(4): 1479-1489. DOI:10.13031/2013.42255 |
| [89] |
BEVEN K, FREER J. A dynamic TOPMODEL[J]. Hydrological Processes, 2001, 15(10): 1993-2011. DOI:10.1002/hyp.252 |
| [90] |
JIA Y W, NI G H, KAWAHARA Y, et al. Development of WEP model and its application to an urban watershed[J]. Hydrological Processes, 2001, 15(11): 2175-2194. DOI:10.1002/hyp.275 |
| [91] |
BRAITHWAITE R J, ZHANG Y. Sensitivity of mass balance of five Swiss glaciers to temperature changes assessed by tuning a degree-day model[J]. Journal of Glaciology, 2000, 46(152): 7-14. DOI:10.3189/172756500781833511 |
| [92] |
CESARACCIO C, SPANO D, DUCE P, et al. An improved model for determining degree-day values from daily temperature data[J]. International Journal of Biometeorology, 2001, 45(4): 161-169. DOI:10.1007/s004840100104 |
| [93] |
ZHANG Y, LIU S Y, DING Y J. Observed degree-day factors and their spatial variation on glaciers in Western China[J]. Annals of Glaciology, 2006, 43: 301-306. DOI:10.3189/172756406781811952 |
| [94] |
MARKS D, DOMINGO J, SUSONG D, et al. A spatially distributed energy balance snowmelt model for application in mountain basins[J]. Hydrological Processes, 1999, 13(12-13): 1935-1959. DOI:10.1002/(SICI)1099-1085(199909)13:12/13<1935:AID-HYP868>3.0.CO;2-C |
| [95] |
LEHNING M, VÖLKSCH I, GUSTAFSSON D, et al. ALPINE3D: a detailed model of mountain surface processes and its application to snow hydrology[J]. Hydrological Processes, 2006, 20(10): 2111-2128. DOI:10.1002/hyp.6204 |
| [96] |
LISTON G E, ELDER K. A distributed snow-evolution modeling system (SnowModel)[J]. Journal of Hydrometeorology, 2006, 7(6): 1259-1276. DOI:10.1175/jhm548.1 |
| [97] |
DÉRY S J, YAU M K. A bulk blowing snow model[J]. Boundary-Layer Meteorology, 1999, 93(2): 237-251. DOI:10.1023/A:1002065615856 |
| [98] |
ANDERSON E A. A point energy and mass balance model of a snow cover[D]. United States: National Weather Service, 1976.
|
| [99] |
YAMAZAKI T, KONDO J, SAKURAOKA T, et al. A one-dimensional model of the evolution of snow-cover characteristics[J]. Annals of Glaciology, 1993, 18: 22-26. DOI:10.1017/s0260305500011204 |
| [100] |
MARTINEC J, RANGO A, MAJOR E. Snowmelt-runoff model (SRM) user's manual[Z]. United States: NASA Reference Publication, 1983.
|
| [101] |
STRASSER U, CORRIPIO J, PELLICCIOTTI F, et al. Spatial and temporal variability of meteorological variables at Haut Glacier d'Arolla (Switzerland) during the ablation season 2001: Measurements and simulations[J]. Journal of Geophysical Research: Atmospheres, 2004, 109(D3). DOI:10.1029/2003jd003973 |
| [102] |
MIDDELKOOP H, DAAMEN K, GELLENS D, et al. Impact of climate change on hydrological regimes and water resources management in the Rhine basin[J]. Climatic Change, 2001, 49(1-2): 105-128. DOI:10.1023/A:1010784727448 |
| [103] |
WARSCHER M, STRASSER U, KRALLER G, et al. Performance of complex snow cover descriptions in a distributed hydrological model system: a case study for the high Alpine terrain of the Berchtesgaden Alps[J]. Water Resources Research, 2013, 49(5): 2619-2637. DOI:10.1002/wrcr.20219 |
| [104] |
RANDIN C F, DEDIEU J P, ZAPPA M, et al. Validation of and comparison between a semidistributed rainfall-runoff hydrological model (PREVAH) and a spatially distributed snow-evolution model (SnowModel) for snow cover prediction in mountain ecosystems[J]. Ecohydrology, 2015, 8(7): 1181-1193. DOI:10.1002/eco.1570 |
| [105] |
KUHN M. Redistribution of snow and glacier mass balance from a hydrometeorological model[J]. Journal of Hydrology, 2003, 282(1-4): 95-103. DOI:10.1016/S0022-1694(03)00256-7 |
| [106] |
ASZTALOS J, KIRNBAUER R, ESCHER-VETTER H, et al. A distributed energy balance snow melt model as a component of a flood forecasting system for the Inn river[C]//Munich: Proceedings of the Alpine Snow Workshop, 2006: 9-17.
|
| [107] |
TARBOTON D G, LUCE C H. Utah energy balance snow accumulation and melt model (UEB)[R]. Utah Water Research Laboratory, Utah State University & USDA Forest Service, Intermountain Research Station, 1996. https://www.fs.fed.us/rm/boise/publications/watershed/rmrs_1996_tarbotond001.pdf
|
| [108] |
AMORY C, KITTEL C. Brief communication: Rare ambient saturation during drifting snow occurrences at a coastal location of East Antarctica[J]. The Cryosphere, 2019, 13(12): 3405-3412. DOI:10.5194/tc-13-3405-2019 |
| [109] |
车涛, 郝晓华, 戴礼云, 等. 青藏高原积雪变化及其影响[J]. 中国科学院院刊, 2019, 34(11): 1247-1253. CHE T, HAO X H, DAI L Y, et al. Snow cover variation and its impacts over the Qinghai-Tibet plateau[J]. Bulletin of Chinese Academy of Sciences, 2019, 34(11): 1247-1253. DOI:10.16418/j.issn.1000-3045.2019.11.007 (in Chinese) |



