2. 上海核工程研究设计院有限公司,上海 200233
2. Shanghai Nuclear Engineering Research & Design Institute, Shanghai 200233, China
气液两相流广泛存在于核电、石油化工、海洋工程等工业领域的管道中,如饱和蒸汽管道、油气混输管道和海洋立管等[1-2]。这些管道大多为薄壁结构,气液两相流与薄壁管道之间的相互耦合作用,可引发管道流致振动,引起管道疲劳损伤甚至导致管道爆裂,酿成重大安全事故[3-4]。
气液两相流引起的管道振动包含了复杂的流固耦合机理,国内外很多学者对此问题开展了实验研究。Hara等[5]通过研究发现当段塞流峰值频率与管道自振频率比为2/3、1和2时,水平管道振动响应最为剧烈。Rodriguez等[6]通过实验研究了不同流型下水平管道的振动响应,发现其取决于流动和结构参数,如混合速度、相体积分数和流型。Thorpe等[7]通过实验研究发现,长泡状流下水平管道的振动为窄带随机振动,而弹状流和环状流下则表现为周期性振动。Hashimy等[8]研究了两端固支的柔性立管的振动响应,研究发现段塞流速是决定柔性立管振动的关键因素,振动位移随液相表观流速的增大而增大。Zhu等[9]研究了气液两相内流引起的柔性立管振动,发现气液比和气液两相流速是影响柔性立管振动的主要因素。Lannes等[10]通过研究发现,水平管道的振动加速度随两相流体积流量和含气率的增大而增大。Liu等[11]通过实验研究发现,当液相流速一定时,90°弯管的振动幅值随气相流量增加而增大,并在环状流下达到最大值;田茂诚等[12]研究了不同流型下垂直U型管的振动,发现U型管主要发生面内振动,表现为两相流流体激振力主频与管道固有频率相近时引发的共振现象。
目前针对气液两相流管道流致振动开展的研究主要集中在直管、弯管及倾斜管中,针对T型管的两相流振动实验非常有限,主要研究分支位置气液相分配及流体激励力。Wang等[13]研究了搅拌流下T型管内两相流流动特性,发现入口气相和液相表观流速的增加均会导致分支位置流体脉动压力的剧烈波动。王栋等[14]对异径水平T型管进行实验研究,发现流体所受惯性力是影响分支位置相分离特性的主要原因。Azzi等[15]研究发现弹状流流型与管道尺寸无关,得出T型管道内弹状流的相分离与管道内径无关的结论。王来顺等[16]对水平T型管内泡状流气液分离情况进行数值模拟,发现泡状流具有明显的气液分离现象,并得到了相分布图、压力图及速度场图。Riverin等[17]对内径为20.6 mm的U型和T型管进行了实验研究,认为管内气液两相流诱导的振动不能忽略,并用韦伯数对作用力均方根值进行关联,关联式在较宽的几何结构和水力条件下取得较好的一致性。
综上,国内外针对两相流引起的管道振动研究主要集中在直管、弯管和倾斜管道,而T型管的研究主要集中在三通相分离特性及流体激励特性,涉及T型管两相流流固耦合问题的研究相对较少,且大多局限于数值计算。因此我们搭建了水平T型管气液两相流流致振动实验系统,通过实验揭示了段塞流下气液表观流速对管内流体流动及结构振动响应的影响机制,以期为两相流管道设计和振动控制提供参考依据。
1 实验方法 1.1 实验回路如图1所示,搭建的水平T型管气液两相流流致振动实验台架主要包括气相供给系统、液相供给系统、主管路系统、液相循环系统以及数据采集系统五部分。气相供给系统包括压气机、储气罐、电动调节阀和质量流量计,其中气相质量流量计量程分别为0~200 kg/h和0~500 kg/h。液相供给系统包括:水箱、离心泵、电动调节阀和电磁流量计,其中电磁流量计量程分别为0~80 m3/h和0~150 m3/h。气相和液相流量计前均设有电动调节阀和球阀,通过控制调节阀和球阀开度来调节空气和水的流量。空气和水经流量计后进入静态混合器充分混合,进而流入主管路系统。实验段前设有充分发展段以确保两相流形成特定流型。实验段出入口均接有橡胶管道以减少环境振动及流体脉动对实验结果的影响。实验采用高速摄像机拍摄T型管三通部分两相流流动图像,并利用高频脉动压力传感器和加速度传感器分别监测管内两相流体的压力变化及管道的振动响应。空气和水通过实验段后通过液相循环系统流入水箱循环使用。

|
图 1 实验系统示意图 Fig.1 Schematic of experimental setup |
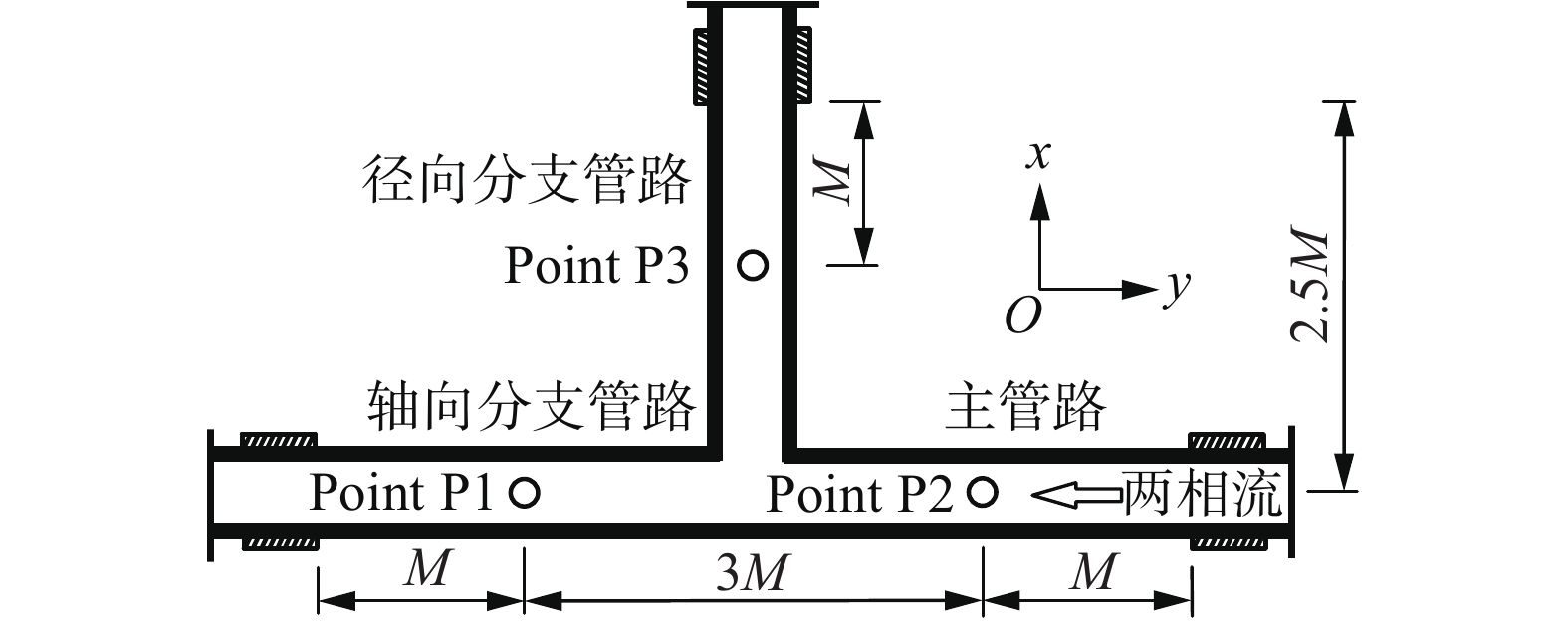
实验段采用的T型管为内径51 mm、壁厚3 mm的304不锈钢管,管内流体介质为常温下的空气和去离子水,相关参数见表1。为隔绝环境振动的影响,确保T型管的固定约束条件,T型管主管及支管端部均安装有刚性支撑以夹紧管道。为了采集管道的振动响应,在主管及各分支管均布置有1个三向加速度传感器(精度为0.1%),如图1所示。3个动态压力传感器(精度为0.1%)布置位置如图2所示,用于同步监测管内流体的压力脉动。为了拍摄三通位置两相流的流动图像,实验加工了尺寸形状相同的有机玻璃管以替换不锈钢管,实验中采用的高速摄像机最大像素为640×480,最高拍摄频率为500 fps。
| 表 1 结构及流体物理参数 Table 1 Physical properties of fluid and structure |
|
|
|
图 2 实验段结构模型 Fig.2 Schematic of test section |
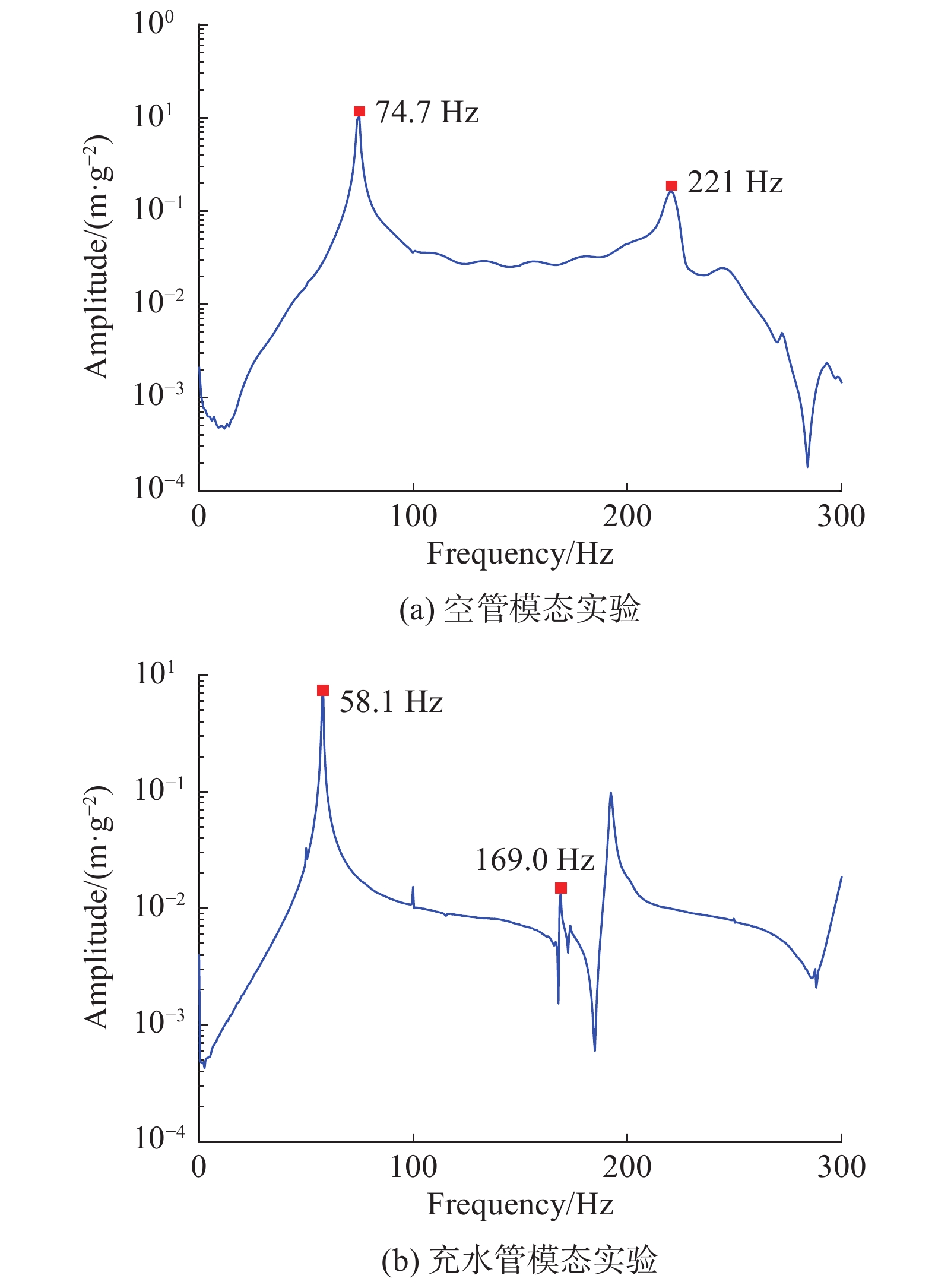
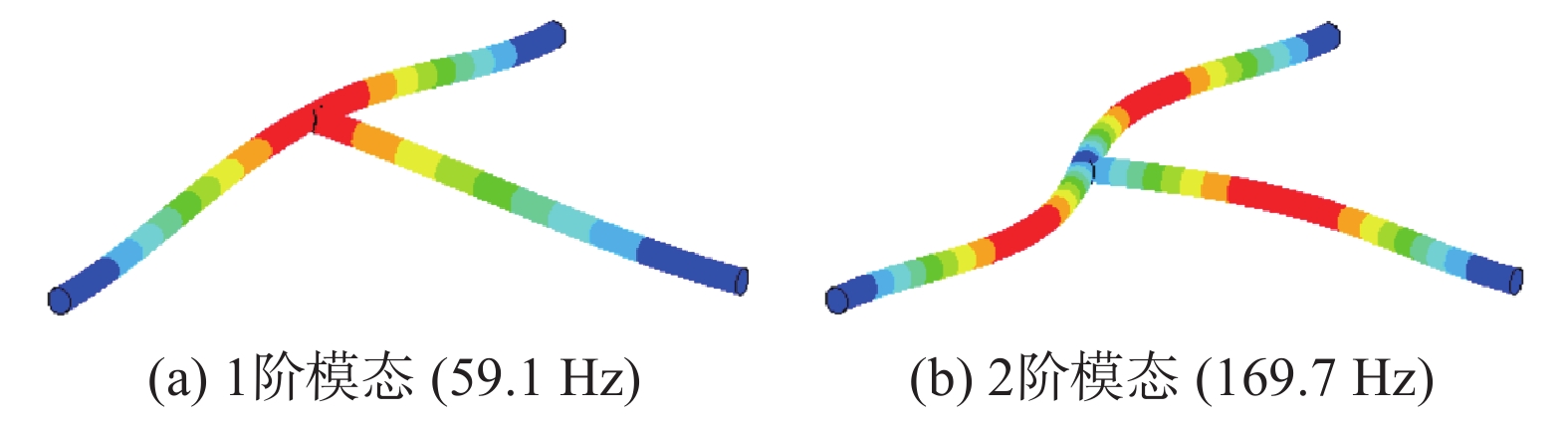
实验测试前,采用锤击法分别测试空管及充水状态下T型管的固有频率。测试采用多点激励三点响应方法,移动力锤对管道的不同位置进行激励,采集T型管3个加速度测点的响应信号,将加速度衰减曲线进行傅里叶变换后,得到其前二阶固有频率,如图3所示。其中,空管前二阶固有频率分别为74.7 Hz和221 Hz,充水管道前二阶固有频率分别为58.1 Hz和169.0 Hz。此外,建立了空管有限元数值计算模型,管道尺寸及材料参数分别如图2和表1所示。其中,结构采用六面体八节点实体单元进行离散,结构单元数为36000,管道主管路及分支管路端部单元节点自由度完全约束。采用分块Lanczos法求得空管前二阶固有频率为76.1 Hz及215.1 Hz,与实验结果相对误差分别为1.84%和2.67%。基于声固耦合法建立充水管道流固耦合有限元数值计算模型,分析了管内静水对T型管模态特征的影响,结构及流体物性参数如表1所示。其中,采用八节点可压缩无黏声学流体单元对流体进行离散,结构则由六面体八节点实体单元进行离散,流体单元数为264600,结构单元数为25200,管道主管路及分支管路端部结构单元节点自由度完全约束。考虑线性小扰动情况,采用非对称法求得充水管前二阶模态数值解为59.1 Hz和169.7 Hz,相对误差分别为1.64%和0.4%。充水管道前二阶模态主要为弯曲模态,振型如图4所示。由此可见,实验中采用的刚性支撑满足固定约束条件。
|
图 3 模态实验结果 Fig.3 The results of modal tests |
|
图 4 仿真所得振型图 Fig.4 Numerical results of vibration modes |
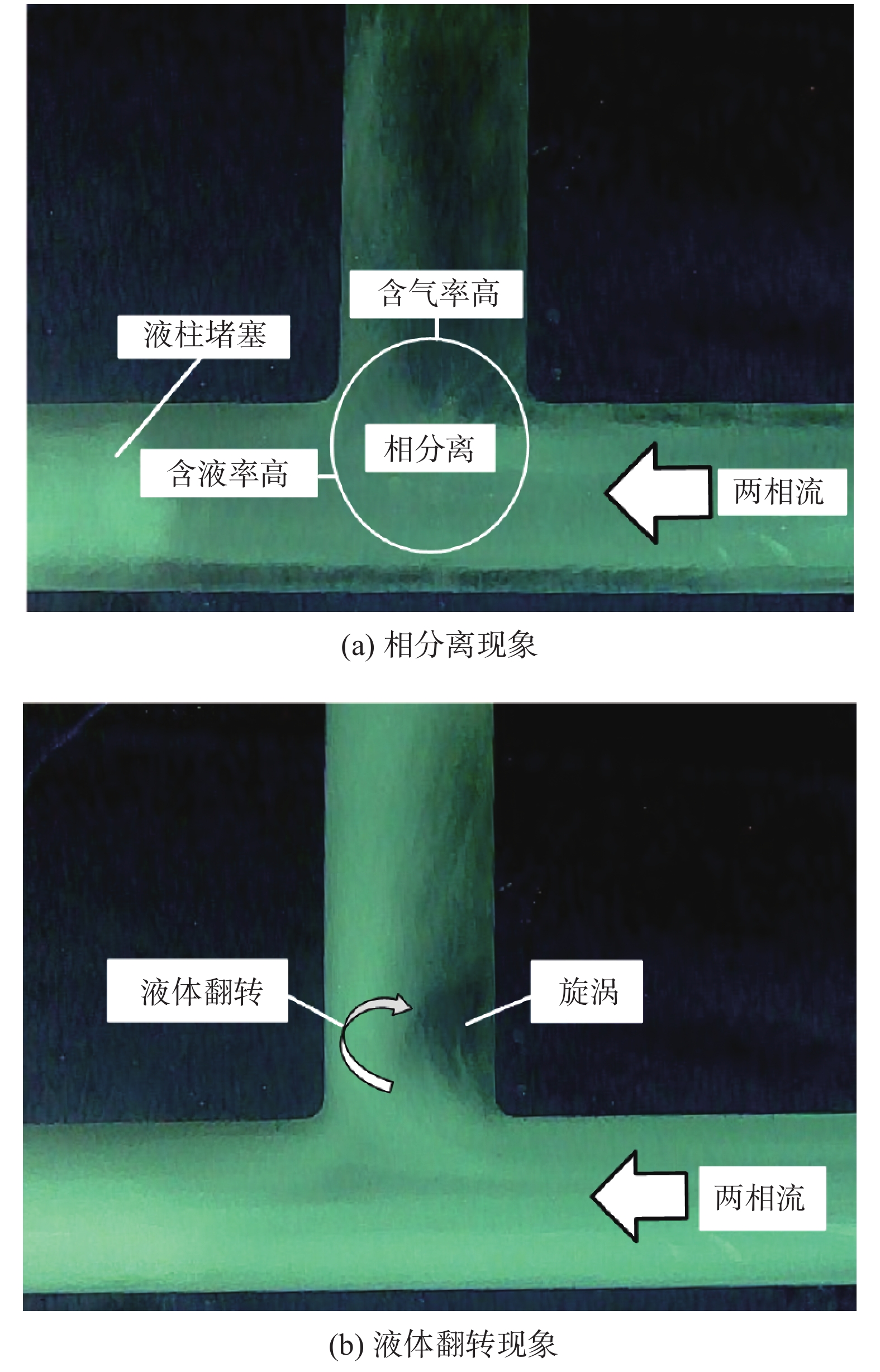
图5给出了气相表观流速Usg = 9.65 m/s、液相表观流速Usl = 2.05 m/s时,三通部位的两相流流动图像。由图5可知,轴向和径向分支管路的液塞流速慢于主管路。这是由于液相的密度远高于空气,液相惯性大,会优先进入轴向分支管路,主管路的两相流经过分流后,分支管路流量减小,流速减慢,低密度的空气受轴向分支管中液柱阻挡后流入径向分支管路,出现气液相分离现象。与弯管类似,当液塞流经三通时,由于液体流动方向发生改变,径向分支管中出现液体翻转现象,随后管道顶部的水膜在重力作用下回落到管道底部。
|
图 5 三通部位流动图像 Fig.5 Flow visualization of slug flow in tee-junction |
图6(a)给出了液相表观流速Usl = 3.03 m/s时,两种气相表观流速下T型管主管及分支管内三个测点的压力脉动曲线。从时域曲线中可以看出,管内压力脉动主要源于气塞和液塞的交替流动。当液塞通过时,测点压力增大,当气塞通过时,测点压力减小。其中,轴向分支管压力脉动幅值最大,径向分支管压力脉动最小。这是由于轴向分支管液相占比大,两相流平均流速慢,来自主管的高速流体冲击轴向支管中的低速水柱,造成轴向支管流体压力脉动量增大;径向分支管空气占比大,流体具有的动量小,压力脉动量小。
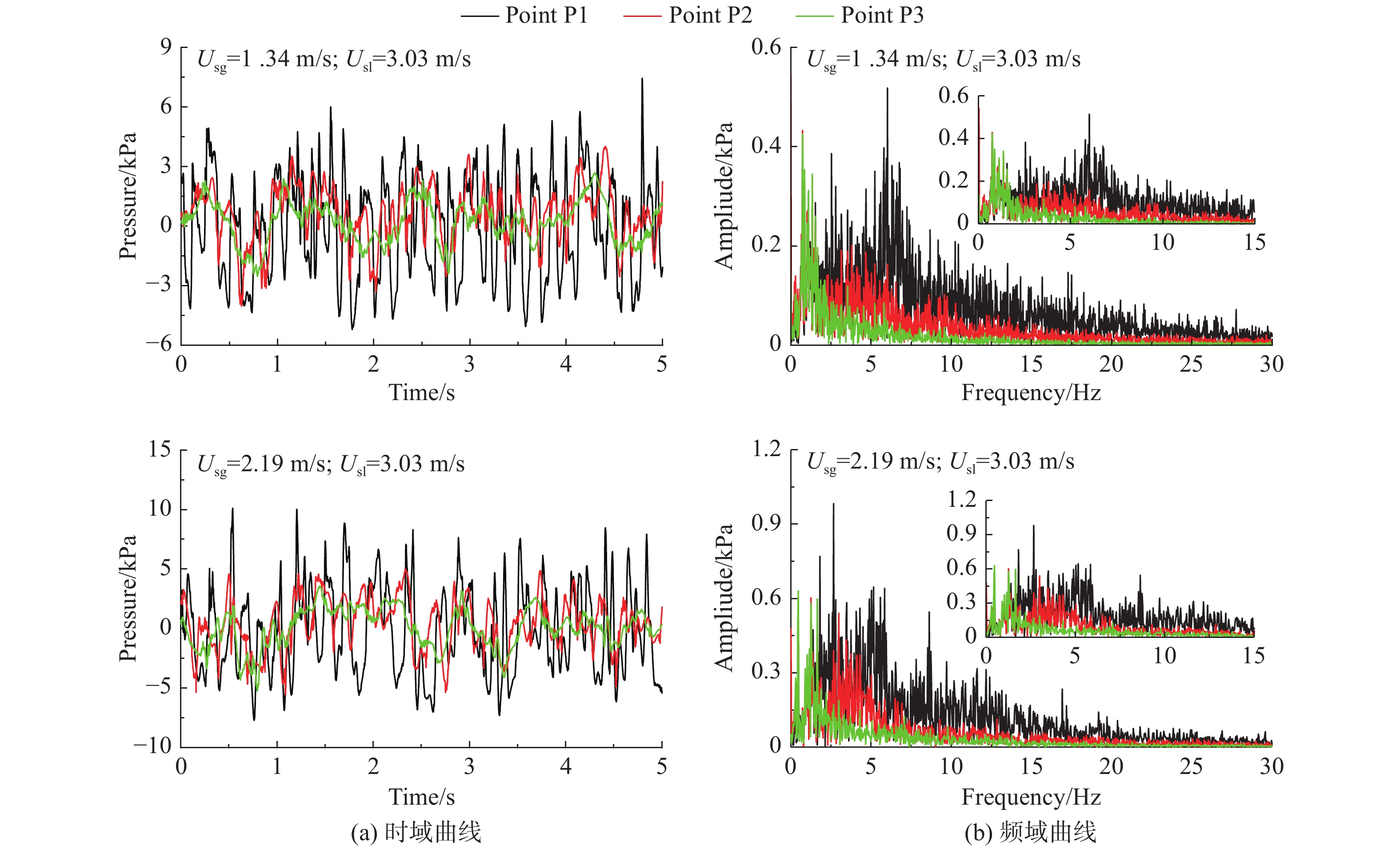
|
图 6 低气相流率下不同测点压力脉动曲线 Fig.6 Pressure fluctuations at different points for low gas flow rate |
由图6(b)频域曲线可知,T型管内流体压力脉动频率集中分布在0~15 Hz之间。其中,主管路和轴向分支管路在0~2.5 Hz及4~10 Hz之间均出现了较高的峰值频率,径向分支管路则集中分布在0~2.5 Hz之间。与直管相似,4~10 Hz内的峰值频率主要由气塞和液塞的交替时间决定,随着气相表观流速的增加,气塞长度增大,相邻两个液塞通过测点的时间增长,脉动压力峰值频率减小。轴向分支管路存在水堵现象,来自主管路的气塞撞击堵塞的液柱,少量的气相进入液柱,形成较大的气泡,导致轴向分支管路频带范围更宽。径向分支管路液相占比小,气液塞交替引起的压力脉动减弱,其4~10 Hz频段内的频率幅值远小于主管路及轴向分支管路。0~2.5 Hz内的峰值频率与三通部位气液分流现象有关,随着气相流速的升高,三通部位的气液分流现象减弱,该频段内的峰值频率升高。
图7给出了液相表观流速Usl = 2.05 m/s时,不同气相表观流速下管道压力脉动曲线。结果表明,气相表观流速较小时,管内液塞主要由大气泡分割液相形成。随着气相表观流速增加,液塞转变为由波状分层流形成,此时压力脉动频率会随气相表观流速的增大而逐渐增大。随着气相表观流速增加,两个分支管的气液相分配渐趋均匀,压力脉动频谱图中有一个较高的尖峰,其他频率处峰值较低,此时压力脉动主要与气液塞的交替有关。因此,气相表观流速是影响水平T型管内液塞速度的主要因素,改变气相流速会明显影响分支管路内的流动情况。
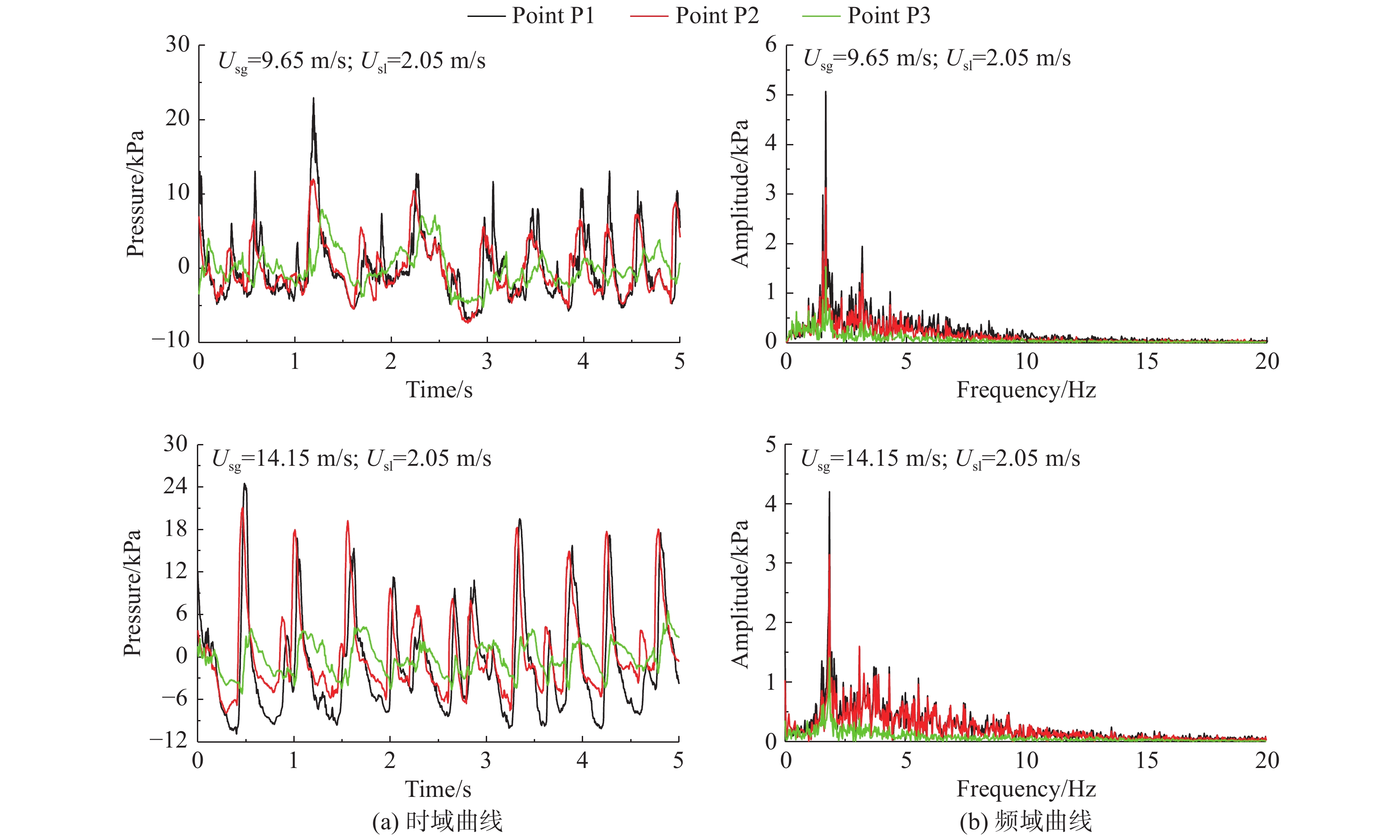
|
图 7 大气相流率下不同测点压力脉动曲线 Fig.7 Pressure fluctuations at different points for high gas flow rate |
图8给出了Usg = 1.34 m/s、Usl = 3.03 m/s时,测点A1三个方向的加速度曲线。从时域曲线中可以看出,T型管在两相流的激励作用下主要表现为垂向振动,主管及分支管由于轴向刚度大,管道轴向振动幅值最小;与直管不同,T型管主管及分支管横向刚度大,其横向振动幅值远小于垂向振动。结合图6压力脉动时域曲线可知,管道振动与气塞和液塞的交替运动有关,当液塞经过时,管道受到冲击振动幅值增大,加速度曲线出现波峰,随后在阻尼的作用下逐渐衰减直到下一个液塞通过。与直管类似,段塞流主要激起管道的运行模态,受三通部位气液分流的影响,T型管振动幅值明显高于直管且其二阶振动模态幅值远小于一阶振动模态。
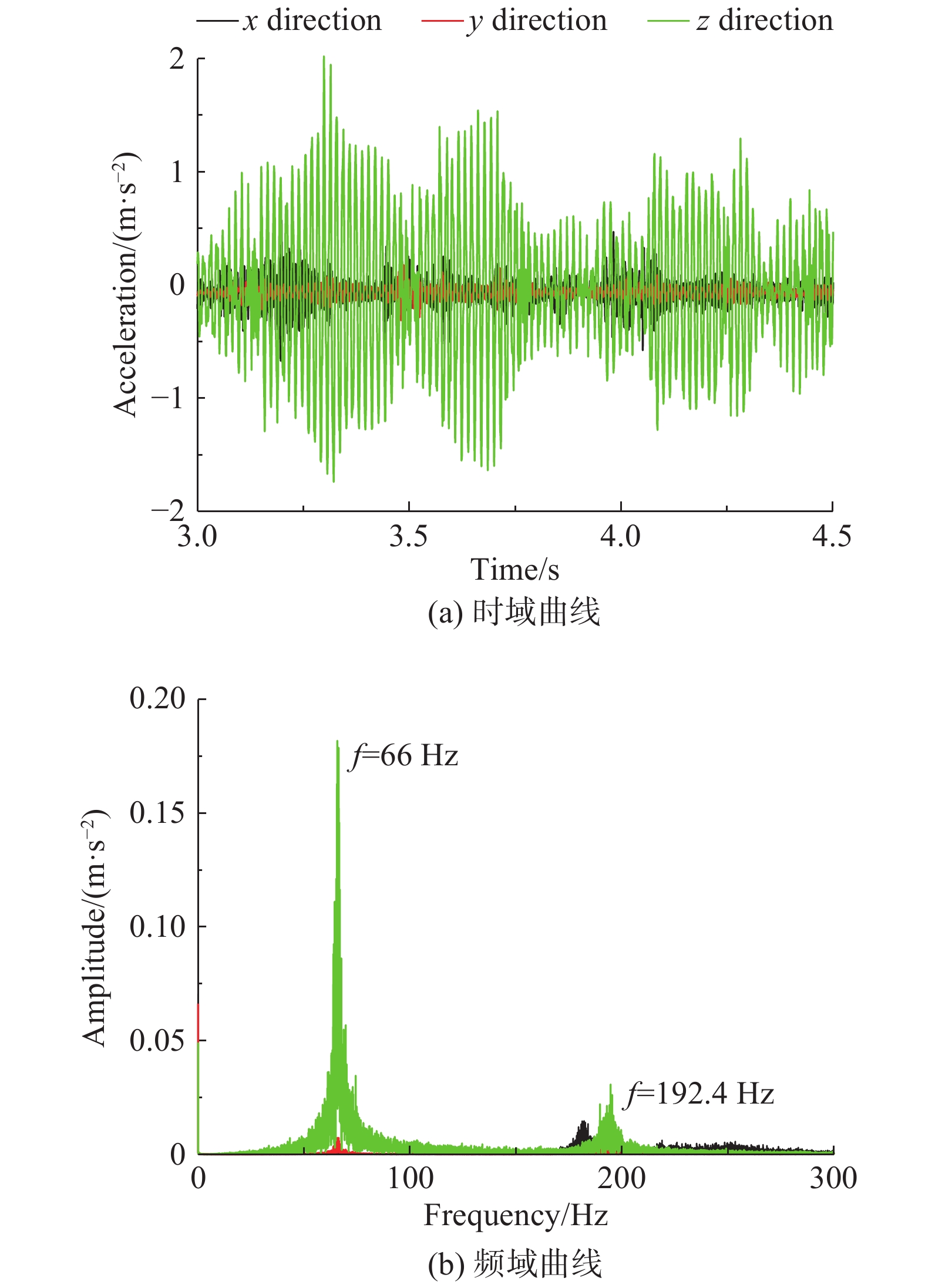
|
图 8 测点A1三方向加速度曲线 Fig.8 Vibration responses at point A1 |
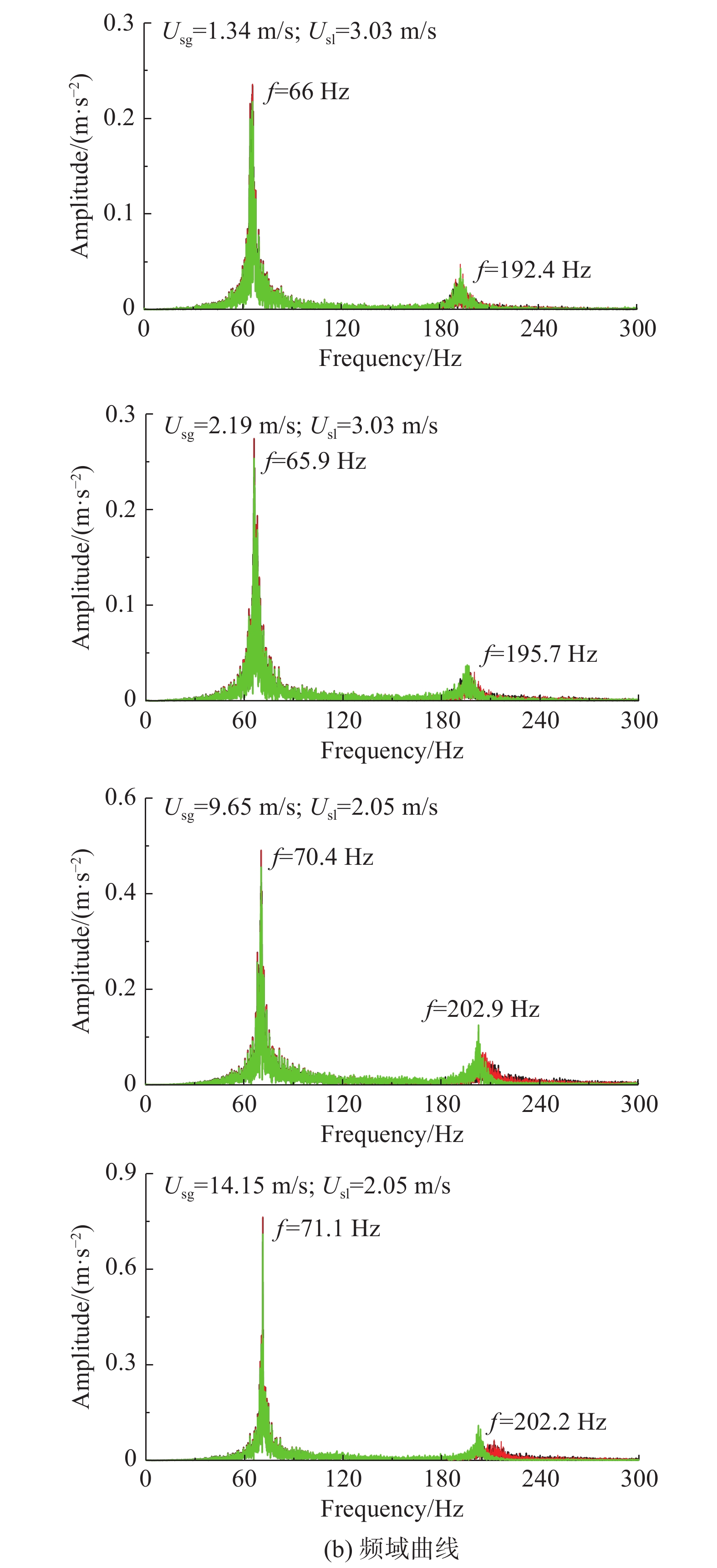
图9给出了液相表观流速为3.03 m/s和2.05 m/s时,四种不同工况下3个加速度测点沿z方向的加速度曲线。从频域曲线中可以看出,振动谱线主要分布在64~68 Hz之间,介于空管及充水管道一阶固有频率之间。由于充水管道的一阶固有频率为59.11 Hz,远高于段塞流压力脉动的主频带0~20 Hz,段塞流的冲击激励为宽频带载荷,主要激起管道的运行模态并以一阶振动模态为主。由于主管路两相流流量大,平均速度高于分支管路,导致主管路振动响应幅值最高,峰值频率最小。轴向分支管路由于液相占比大,平均密度高,且存在液柱堵塞引起的流体冲击现象,导致轴向分支管路振动响应幅值高于径向分支管路,峰值频率低于径向分支管路。
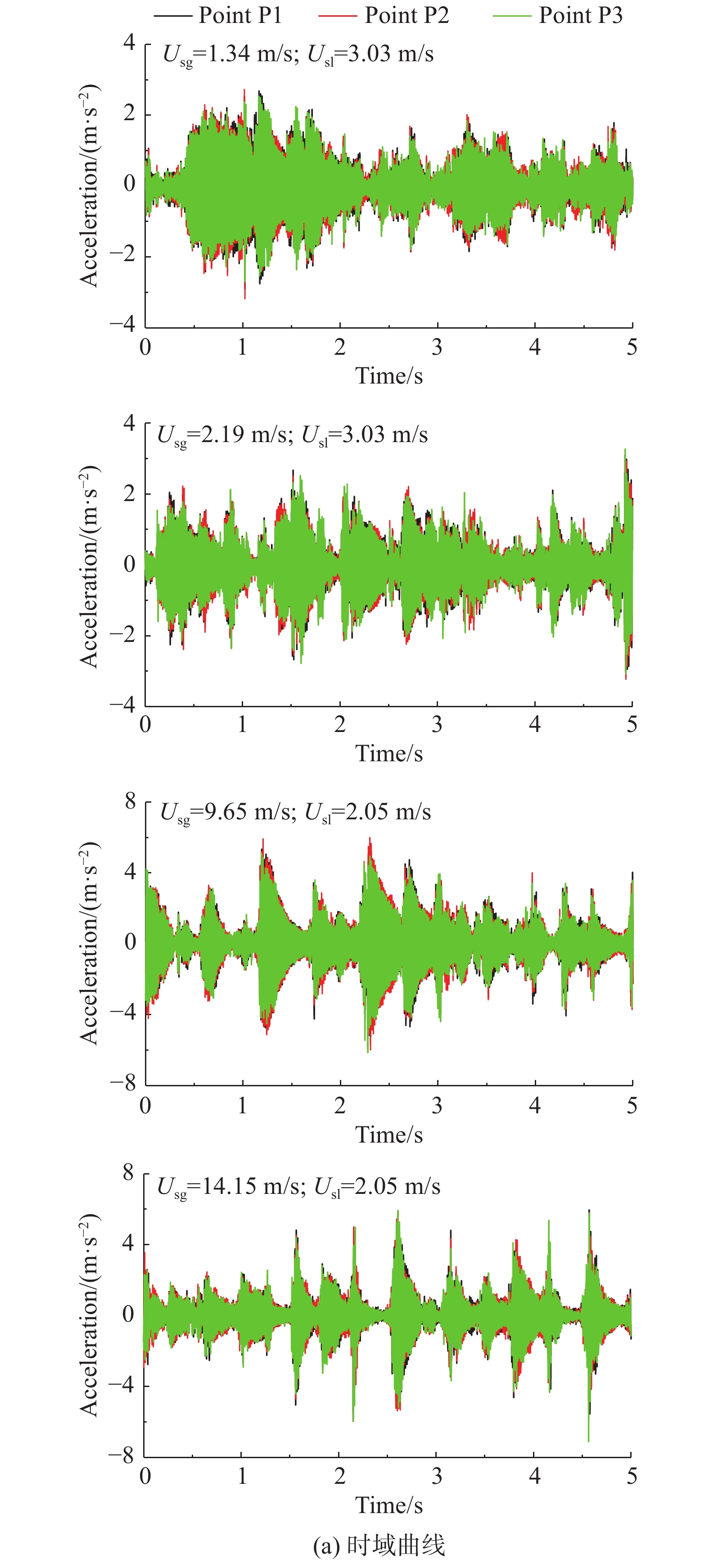
|
图 9 |
|
图 9 z方向振动响应曲线 Fig.9 Vibration responses in z direction |
由图9(a)中的加速度时域曲线可知,随着气相表观流速增加,流体平均流速增加,气塞和液塞动能增大,气塞和液塞交替时作用于壁面上的激励力增大,导致T型管振动响应幅值增大。由图9(b)中的频域曲线可知,随着气相表观流速的增加,空气和水质量比增大,单位截面两相流平均密度降低,主管及分支管一阶振动模态频率升高。
3 结 论本文建立了气液两相流水平T型管道流致振动实验系统,研究了水平T型管内两相流压力脉动特性及结构振动响应的影响因素,为今后的工程实际提供参考依据。研究得出的主要结论如下:
1)T型管支管处相分流现象与流体惯性力有关,轴向及径向分支管相分配随气相表观流速增加逐渐趋于均匀化;T型管内段塞流的压力脉动频率主要集中在0~15 Hz;随着气相表观流速的增大,压力脉动频率呈现先减小后增大的趋势。
2)段塞流冲击激励产生的宽带载荷主要激起管道的运行模态且以一阶振动模态为主;管道振动响应主频及振动幅值随气相表观流速增加而增大。
3)水平T型管内段塞流诱导振动机理为:气塞和液塞交替运动导致两相流动量剧烈波动,结构振动响应接近于周期性冲击振动;相分离造成主支管气液两相分配不均,径向分支管气相占比大,流体平均动量波动小,振动幅值最小。
| [1] |
CHENG L X, RIBATSKI G, THOME J R. Two-phase flow patterns and flow-pattern maps: fundamentals and applications[J]. Applied Mechanics Reviews, 2008, 61(5): 050802. DOI:10.1115/1.2955990 |
| [2] |
席红敏, 张伟, 姚明辉. 变流速输液管的周期和混沌振动[J]. 动力学与控制学报, 2008, 6(3): 243-248. XI H M, ZHANG W, YAO M H. Periodic and chaotic vibration of an infusion tube with variable velocity[J]. Journal of Dynamics and Control, 2008, 6(3): 243-248. DOI:10.3969/j.issn.1672-6553.2008.03.011 (in Chinese) |
| [3] |
JAEGER J, SANTOS C M, ROSA L M, et al. Experimental and numerical evaluation of slugs in a vertical air-water flow[J]. International Journal of Multiphase Flow, 2018, 101: 152-166. DOI:10.1016/j.ijmultiphaseflow.2018.01.009 |
| [4] |
DAUDE F, GALON P A. Finite-Volume approach for compressible single- and two-phase flows in flexible pipelines with fluid-structure interaction[J]. Journal of Computational Physics, 2018, 362: 375-408. DOI:10.1016/j.jcp.2018.01.055 |
| [5] |
HARA F, YAMASHITA T. Parallel two-phase-flow-induced vibrations in fuel pin model[J]. Journal of Nuclear Science and Technology, 1978, 15(5): 346-354. DOI:10.1080/18811248.1978.9735520 |
| [6] |
ORTIZ-VIDAL L E, MUREITHI N W, RODRIGUEZ O M H. Vibration response of a pipe subjected to two-phase flow: Analytical formulations and experiments[J]. Nuclear Engineering and Design, 2017, 313: 214-224. DOI:10.1016/j.nucengdes.2016.12.020 |
| [7] |
TAY B L, THORPE R B. Hydrodynamic forces acting on pipe bends in gas-liquid slug flow[J]. Chemical Engineering Research and Design, 2014, 92(5): 812-825. DOI:10.1016/j.cherd.2013.08.012 |
| [8] |
AL-HASHIMY Z I, AL-KAYIEM H H, TIME R W. Experimental investigation on the vibration induced by slug flow in horizontal pipe[J]. Journal of Engineering and Applied Sciences, 2016, 11(20): 12134-12139. |
| [9] |
ZHU H J, GAO Y, ZHAO H L. Experimental investigation of slug flow-induced vibration of a flexible riser[J]. Ocean Engineering, 2019, 189: 106370. DOI:10.1016/j.oceaneng.2019.106370 |
| [10] |
LANNES D P, GAMA A L. On the relationship between pipe accelerance and the void fraction of internal two-phase flow[J]. Journal of Fluids and Structures, 2018, 80: 350-369. DOI:10.1016/j.jfluidstructs.2018.04.005 |
| [11] |
LIU Y, MIWA S, HIBIKI T, et al. Experimental study of internal two-phase flow induced fluctuating force on a 90° elbow[J]. Chemical Engineering Science, 2012, 76: 173-187. DOI:10.1016/j.ces.2012.04.021 |
| [12] |
马晓旭, 田茂诚, 张冠敏, 等. 垂直U形管内气液两相流诱导振动模拟[J]. 工程热物理学报, 2015, 36(10): 2221-2225. MA X X, TIAN M C, ZHANG G M, et al. Numerical simulation of gas-liquid two-phase flow induced vibration in a vertical U-tube[J]. Journal of Engineering Thermophysics, 2015, 36(10): 2221-2225. (in Chinese) |
| [13] |
WANG S F, SHOJI M. Fluctuation characteristics of two-phase flow splitting at a vertical impacting T-junction[J]. International Journal of Multiphase Flow, 2002, 28(12): 2007-2016. DOI:10.1016/S0301-9322(02)00104-0 |
| [14] |
王栋, 张修刚, 林益, 等. 不等径水平三通的相分离特性研究[J]. 工程热物理学报, 2003, 24(2): 259-261. WANG D, ZHANG X G, LIN Y, et al. The split of two-phase flow at horizontal t-junctions of unequal diameters[J]. Journal of Engineering Thermophysics, 2003, 24(2): 259-261. DOI:10.3321/j.issn:0253-231X.2003.02.022 (in Chinese) |
| [15] |
AZZI A, AL-ATTIYAH A, QI L, et al. Gas-liquid two-phase flow division at a micro-T-junction[J]. Chemical Engineering Science, 2010, 65(13): 3986-3993. DOI:10.1016/j.ces.2010.03.037 |
| [16] |
王来顺, 刘丽芳, 田文喜, 等. T型管内泡状流相分离特性研究[J]. 核动力工程, 2014, 35(2): 53-57. WANG L S, LIU L F, TIAN W X, et al. Research of phase separation phenomenon in two-phase bubbly flow in T-junction[J]. Nuclear Power Engineering, 2014, 35(2): 53-57. (in Chinese) |
| [17] |
RIVERIN J L, DE LANGRE E, PETTIGREW M J. Fluctuating forces caused by internal two-phase flow on bends and Tees[J]. Journal of Sound and Vibration, 2006, 298(4-5): 1088-1098. DOI:10.1016/j.jsv.2006.06.039 |



