2. 中国科学院大学 工程科学学院,北京 100049;
3. 中国科学院力学研究所 高温气体动力学国家重点实验室,北京 100190;
4. 西安交通大学 动力工程多相流国家重点实验室,西安 710049
2. School of Engineering Science, University of the Chinese Academy of Sciences, Beijing 100049, China;
3. State Key Laboratory of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China;
4. State Key Laboratory of Multiphase Flow in Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China
液气相变引起的潜热传递导致沸腾现象具有高效传热性能,在地面常重力和空间不同重力环境都有着重要而广泛的应用前景。气、液两相介质密度间的巨大差异,使得重力可以通过驱动运动、改变界面等强烈影响着沸腾现象。因此,掌握和预测不同的重力环境中沸腾传热特性是其空间应用所面临的关键挑战。然而,目前关于沸腾现象的知识往往充斥着大量的经验关联式和半经验的机制模型,它们又往往强烈依赖着大量精心设计的地面实验数据。尽管在诸多经验关联式和半经验机制模型包含了重力参数,但在其经验基础之外应用时往往失败,甚至连基本变化趋势都可能预测错误。
一般来说,沸腾现象中,热流密度q可以表示为加热面过热度ΔTw、重力g和加热器特征长度Lh的指数函数的乘积形式,即
| $q = a\Delta T_{\rm{w}}^n{g^m}L_{\rm{h}}^s$ | (1) |
其中指数n、m和s是与过热度、重力和加热器特征长度相关的无量纲标度指数,比例常数a反映了其他材料和环境参数的影响[1]。核态池沸腾传热中广为应用的Rohsenow模型[2]表明,在恒定过热度下,重力标度指数m = 0.5。然而,目前文献中关于重力标度指数的结果极为分散,一般在−0.35到0.5之间[3],甚至高达1[4]。
基于失重飞机进出失重阶段的短时(3~5 s)重力过渡状态实验数据,Raj等[5–8]提出了一个核态池沸腾传热重力标度模型,即Raj-Kim-McQuillen重力标度定律(简称为RKM模型):存在浮力主导的沸腾区(BDB)和表面张力主导的沸腾区(SDB)2种模式,二者间的边界重力gtrans与加热器特征长度Lh有关,对应于基于Laplace长度Lc= {σ/[g(ρl−ρv)]}0.5(这里,σ、ρ分别代表表面张力系数和密度,下标l、v分别代表液相和气相)的无量纲加热器特征长度Lh/Lc = 2.1;在BDB区,热流密度随重力指数增加,重力标度指数mBDB与过热度有关,其数值由核态沸腾起始时的0单调增加到临界热流(CHF)时的1/4;而在SDB区,重力对热流密度没有影响,即mSDB等于0。BDB和SDB间存在热流跳变,其幅度随过冷度减小而增大[9-10]。
杜王芳和赵建福[1]指出,RKM模型存在两个缺乏理论和/或经验依据的隐含假设,即不同重力条件下核态沸腾起始温度和CHF温度恒定。最近关于池沸腾传热的格子Boltzmann方法数值研究结果表明,CHF温度随着重力减弱而明显减小[11-12]。此外,该模型关于沸腾起始点和CHF附近的渐近行为(mBDB分别趋于0和1/4)的假设,事实上混淆了过热度恒定、热流密度恒定和基于临界热流的无量纲热流密度恒定等不同限制条件下的重力标度指数间的物理意义。
经验数据的匮乏及局限性也是RKM模型缺陷存在的客观原因之一。随着计算机技术和计算科学的迅速发展,数值模拟已经被诸多研究者用来揭示沸腾过程细观特征和内在机理。例如,Stephan和Hammer[13]、Son等[14]、Zhao等[15]和Yi等[16]在忽略加热固壁热容影响的情况下对单气泡沸腾进行了数值研究。Fuchs等[17]、Aktinol和Dhir[18]、Zhang等[19、20]和Li等[21]对有限厚度加热固壁上的单气泡沸腾进行了数值研究,揭示了加热固壁热响应对局部温度分布、气泡行为及相应的传热性能均有显著影响。Dhruv等[22]发展了一个计入多气泡相互作用的池沸腾传热模拟方法,得到了与RKM模型预测相符的预测结果,但计算中未考虑加热固壁热响应的影响。
本文在Zhang等[19-20]和Li等[21]常重力单气泡沸腾研究基础上,对不同重力条件下饱和FC-72单泡池沸腾过程中的气泡动力学和传热性能开展数值模拟研究,重点关注在不同重力条件下热流密度的重力标度行为。
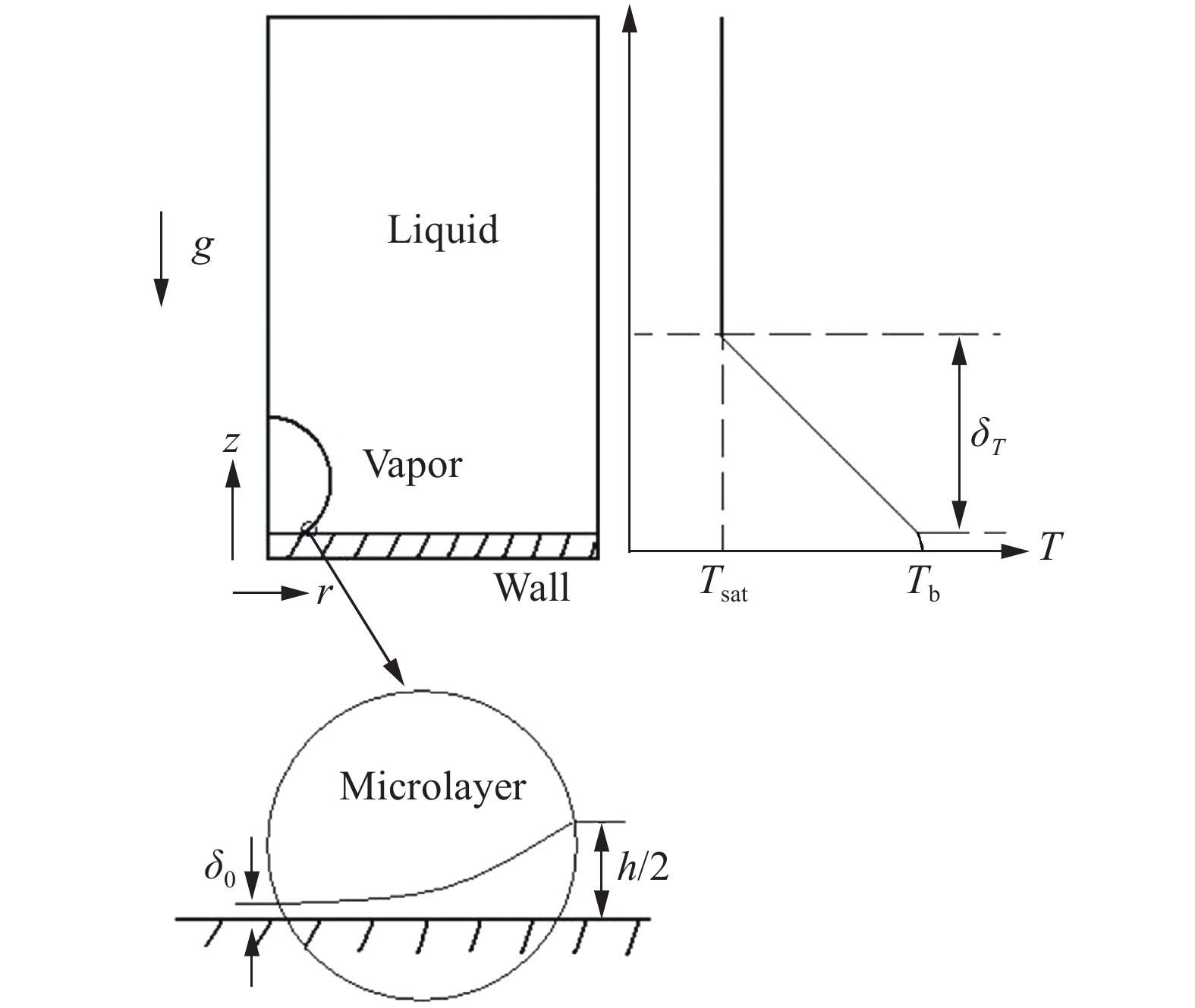
1 数值模型本文采用最初由Stephan和Hammer[13]提出的接触线模型描述生长气泡底部液-气-固三相线附近的相互作用,采用虚拟流体方法(Ghost Fluid方法)刻画液气界面突变。沸腾过程中的单气泡生长简化为轴对称流动与传热,计算域划分为微观区和宏观区(图1),其中,微观区(即生长气泡底部三相接触线附近的超薄液膜区,也称为微液层)采用Son等[14]的模型,宏观区(包括微观区之外的液、气区域及生长气泡底部加热固壁)采用连续介质模型,数值求解描述其质量、动量和能量守恒规律的封闭方程组。
|
图 1 数值模拟中的计算区域 Fig.1 Computational domain used in numerical simulation |
模型中采用了以下假设:1)液、气两相均为黏性不可压牛顿流体;2)材料物性参数恒定,不受温度和压力的影响;3)流体运动是层流;4)表观接触角恒定,忽略动态接触角效应;5)加热固壁底面温度恒定。
1.1 宏观区宏观区速度u、压力p、温度T的演化由如下质量、动量和能量守恒方程予以描述:
| $\begin{array}{*{20}{c}} {\nabla \cdot {{u}} = 0},\;\;{\varOmega = \left\{ {{\varOmega _{\rm{v}}}\;{\rm{or}}\;{\varOmega _{\rm{l}}}} \right\}} \end{array} $ | (2) |
| $\begin{split}&\rho \left( {\frac{{\partial {{u}}}}{{\partial t}} + {{u}} \cdot \nabla {{u}}} \right) = \\&\qquad - \nabla p + \nabla \cdot \mu (\nabla {{u}} + \nabla {{{u}}^{\rm{T}}}) + \rho \left[ {1 - {\beta _T}\left( {T - {T_{{\rm{sat}}}}} \right)} \right]{{g}}\;\;,\\&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\;\;\; \varOmega = \left\{ {{\varOmega _{\rm{v}}}\;{\rm{or}}\;{\varOmega _{\rm{l}}}} \right\}\end{split}$ | (3) |
| $\begin{split}\left\{ {\begin{array}{*{20}{l}} {\dfrac{{\partial T}}{{\partial t}} + {{u}} \cdot \nabla T = \dfrac{1}{{\rho {C_p}}}\nabla \cdot k\left( {\nabla T} \right)}&,{\varOmega = \left\{ {{\varOmega _{\rm{l}}} \cup {\varOmega _{\rm{s}}}} \right\}} \\ {T = {T_{{\rm{sat}}}}\left( {{p_{\rm{v}}}} \right)}&,{{\varOmega _{\rm{v}}}\;} \end{array}} \right.\end{split}$ | (4) |
式中,Ω表示连续域,下标s、sat分别代表固相和饱和状态,μ、βT、Cp、k分别代表动力黏性系数、热膨胀系数、定压比热和热传导系数。
相间界面∂Ω处物理量间断关系如下:
| ${\left[ {{u}} \right]_\varGamma } = \left\{ {\begin{array}{*{20}{l}} { - {{\left[ {1/\rho } \right]}_\varGamma }\dot m{{n}}}&,{\partial {\varOmega _{{\rm{lv}}}}}\\ 0&,{\partial {\varOmega _{{\rm{fs}}}}} \end{array}} \right.$ | (5) |
| $\begin{array}{*{20}{c}} {{{\left[ {\mu \left( {\nabla {{u}} \cdot {{n}},\nabla {{v}} \cdot {{n}}} \right) \cdot {{t}} + \mu \left( {\nabla {{u}} \cdot {{t}},\nabla {{v}} \cdot {{t}}} \right) \cdot {{n}}} \right]}_\varGamma } = 0}\;\;\;\;\;\;\;\;,{\partial {\varOmega _{{\rm{lv}}}}} \end{array} $ | (6) |
| $\begin{array}{*{20}{c}} {{{\left[ p \right]}_\varGamma } = 2{{\left[ {\mu \left( {\nabla {{u}} \cdot {{n}},\nabla {{v}} \cdot {{n}}} \right) \cdot {{n}}} \right]}_\varGamma } - \sigma \kappa - {{\left[ {{1 / \rho }} \right]}_\varGamma }{{\dot m}^2}}\;\;\;\;,{\partial {\varOmega _{{\rm{lv}}}}} \end{array} $ | (7) |
| $\begin{array}{*{20}{c}} {{{\left[ T \right]}_\varGamma } = 0}\;\;\;,{\partial {\varOmega _{{\rm{lv}}}}} \end{array} $ | (8) |
| ${\left[ {k\nabla T \cdot {{n}}} \right]_\varGamma } = \left\{ {\begin{array}{*{20}{l}} {\dot m{h_{{\rm{fg}}}}}&,{\partial {\varOmega _{{\rm{lv}}}}}\\ 0&,{\partial {\varOmega _{{\rm{fs}}}}} \end{array}} \right.$ | (9) |
式中,[Λ]Γ = Λl–Λv表示参数Λ在界面两侧的间断,质量通量
假设微观区液气界面斜率恒定[23],相应的微液层可视作轴对称的锥台侧面,基于润滑理论近似之下的质量、动量和能量方程,得到了如下显式的微观区热流密度qmic和相变质量流率mmic:
| $\begin{split} {q_{{\rm{mic}}}} =& \frac{{2{\text{π}} {k_{\rm{l}}}\left( {{T_{\rm{w}}} - {T_{{\rm{sat}}}}} \right)}}{{\Delta {A_{{\rm{mic}}}}}}\left[ {\left( {{R_1} - \frac{h}{{2\tan \gamma }}} \right)\frac{1}{{\tan \gamma }}\ln \left( {\frac{h}{2}\frac{{{h_{{\rm{ev}}}}}}{{{k_{\rm{l}}}}} + 1} \right) + } \right.\\& \left. {\frac{h}{{2{{\tan }^2}\gamma }} - \frac{{{k_{\rm{l}}}}}{{{h_{{\rm{ev}}}}}}\frac{1}{{{{\tan }^2}\gamma }}\ln \left( {\frac{h}{2}\frac{{{h_{{\rm{ev}}}}}}{{{k_{\rm{l}}}}} + 1} \right)} \right] \end{split}$ | (10) |
| ${\dot m_{{\rm{mic}}}} = \frac{{{q_{{\rm{mic}}}}}}{{{h_{{\rm{fg}}}}}}$ | (11) |
式中,ΔAmic、h、R1分别微液区的面积、边缘厚度与半径,γ代表表观接触角。
1.3 Level-set方程在宏观区,采用Level-set方法跟踪液-气、流(液或气)-固界面,后者将不同物质相态区分开来。
液-气界面的Level-set函数φ被定义为到液气界面的距离,其中液相为正,气相为负,界面位置对应φ = 0。液气界面的运动受下述方程控制:
| $\frac{{\partial \varphi }}{{\partial t}} = - {{{u}}_{\rm{int} }} \cdot \nabla \varphi $ | (12) |
其中,
| ${{{u}}_{\rm{int} }} = \frac{{\dot m{{n}}}}{\rho } + {{u}}$ | (13) |
另一个Level-set函数ψ用于处理流(液或气)-固体界面,其定义为到固定的流-固界面(即加热固壁顶面)的符号距离,负值表示固体区,正值表示流体区,界面固定不动。
利用Heaviside函数
| $H = \left\{ {\begin{array}{*{20}{c}} 1&,{{\rm{if }}\;\varphi \;{\rm{ or }}\;\psi > 0} \\ 0&,{{\rm{if }}\;\varphi \;{\rm{ or }}\;\psi \leqslant 0} \end{array}} \right.$ | (14) |
可将不同区域物性参数表示为如下形式:
| $\rho = {\rho _{\rm{s}}} + \left[ {{\rho _{\rm{v}}} + \left( {{\rho _{\rm{l}}} - {\rho _{\rm{v}}}} \right)H\left( \varphi \right) - {\rho _{\rm{s}}}} \right]H\left( \psi \right)$ | (15) |
| $\mu = {\mu _{\rm{s}}} + \left[{{\mu _{\rm{v}}} + \left( {{\mu _{\rm{l}}} - {\mu _{\rm{v}}}} \right)H\left( \varphi \right) - {\mu _{\rm{s}}}} \right]H\left( \psi \right)$ | (16) |
| ${k^{ - 1}} = k_{\rm{s}}^{ - 1} + \left[ {k_{\rm{l}}^{ - 1}H\left( \varphi \right) - k_{\rm{s}}^{ - 1}} \right]H\left( \psi \right)$ | (17) |
为了避免有限的计算区域边界对气泡生长过程的影响,同时节省计算资源,流体所在的计算域尺寸选择为(1Lc×2Lc),固壁厚度固定为5 mm。
边界条件如下:
1)对称轴:
2)外侧:
3)加热固壁底部:
4)顶部:
此外,还须考虑另外2个条件,描述加热固壁顶面三相区附近的微液层相变与接触线运动行为:
| ${\left( {k\frac{{\partial T}}{{\partial z}}} \right)_{{\rm{mic}}}} = - {q_{{\rm{mic}}}}$ | (18) |
| $\frac{{\partial \varphi }}{{\partial z}} = - \cos \gamma $ | (19) |
后者对应于表观接触角恒定假设。
流体初始静止,即:
| $u = v = 0$ | (20) |
初始温度设置如图1所示,加热固壁内部温度均匀分布,近壁过热液层厚度δT由下式给出[24]:
| ${\delta _T} = 7.14{\left( {\frac{{{\nu _{\rm{l}}}{\alpha _{\rm{l}}}}}{{g{\beta _T}\Delta T}}} \right)^{{1 / 3}}}$ | (21) |
式中,ν、α分别代表运动黏性系数和热扩散系数。
鉴于连续介质模型不能自动模拟核化的发生,在一个新的气泡周期开始,须在核化点(即加热固壁顶面对称轴位置)设置一个初始半径0.05Lc的截球状小气泡,随后计算其生长、脱落与运动;气泡脱落后,加热固壁顶面温度将持续恢复,一旦核化点温度达到由Hsu核化模型[25]确定的、与1 μm空穴直径对应的、恒定的核化过热度,则开始后继新的一个气泡周期。有关数值方法的更多细节,请参见Zhang等[20]和Li等[21]。为了消除初始条件对物理真实的偏离的影响,需进行多个气泡周期模拟才能得到准稳态的单气泡沸腾。
1.5 离散方法与数值验证宏观区流体空间离散化采用100×200标准MAC网格对进行,Navier-Stokes方程的数值求解采用投影法,动量方程和能量方程中对流项的离散采用二阶ENO格式,扩散项则采用中心差分格式。在常重力条件下本文模型预测结果与Siegel和Keshock[24]实验结果以及Son[26]、Son等[14]数值结果符合甚好,详细的数值验证情况可参考Zhao等[15]、Zhang等[19]和张良[23],这里不再赘述。
2 结果与讨论本文关注于不同重力条件下的单气泡沸腾现象,具体研究了饱和FC-72在1g0(即地面常重力状态)、0.3g0、0.1g0、0.03g0和0.01g0等重力条件下单气泡池沸腾过程中的气泡动力学和传热性能(表1)。加热固壁材质为石英玻璃,底面过热度固定为10 K。考虑到蒸气反冲效应,沸腾现象中生长气泡的表观接触角往往远大于其静态接触角,计算中表观接触角取为γ = 42°。
| 表 1 不同重力条件下的主要结果 Table 1 Main results at different gravity levels |
|
|
表1中列出了5个算例的主要结果,其中,由于加热固壁内部热容影响,与工质直接接触的加热固壁顶面上的时空平均热流密度和过热度,将不再是预先给定的,而成为计算的输出结果。显然,气泡生长周期tc和脱落直径Db随着重力的降低而增大,传热性能则明显恶化:加热固壁表面的时空平均的热流密度qave随着重力的降低而显著下降,而相应的时空平均的壁面过热度ΔTw,ave略有增加。这里所谓的“时空平均”,是指在一个准稳态的气泡周期(相邻2个核化时刻之间的时段)内整个加热面上相应物理量的时间和空间双重平均结果。表中,ΔTw,ave、qave为原始输出结果,基于1Lc×2Lc计算域对应的半径为1Lc的加热器表面面积平均得到的。鉴于Laplace长度与重力的平方根成反比,加热器的物理尺寸将随着重力的减小而增大,从而导致不同重力条件下加热器的物理尺寸不同,传热性能原始输出结果间的直接比较显然不尽合理。考虑到计算域外侧边界条件隐含的外侧流动和计算域内气泡生长过程间无影响假设,本文采用“加热固壁表面人为扩展”的办法,将不同重力条件下加热器均扩大为最小重力(即0.01g0)条件下1Lc所对应的数值,扩展的加热表面上的局部温度和热流密度与相应重力条件下计算域外侧加热表面相应数值相等,基于扩展的加热器表面面积计算得到修正的传热性能时空平均结果ΔT*w,ave、q*ave,保证了不同重力条件下加热器物理尺寸的一致,使得传热性能间的比较合理性增强。
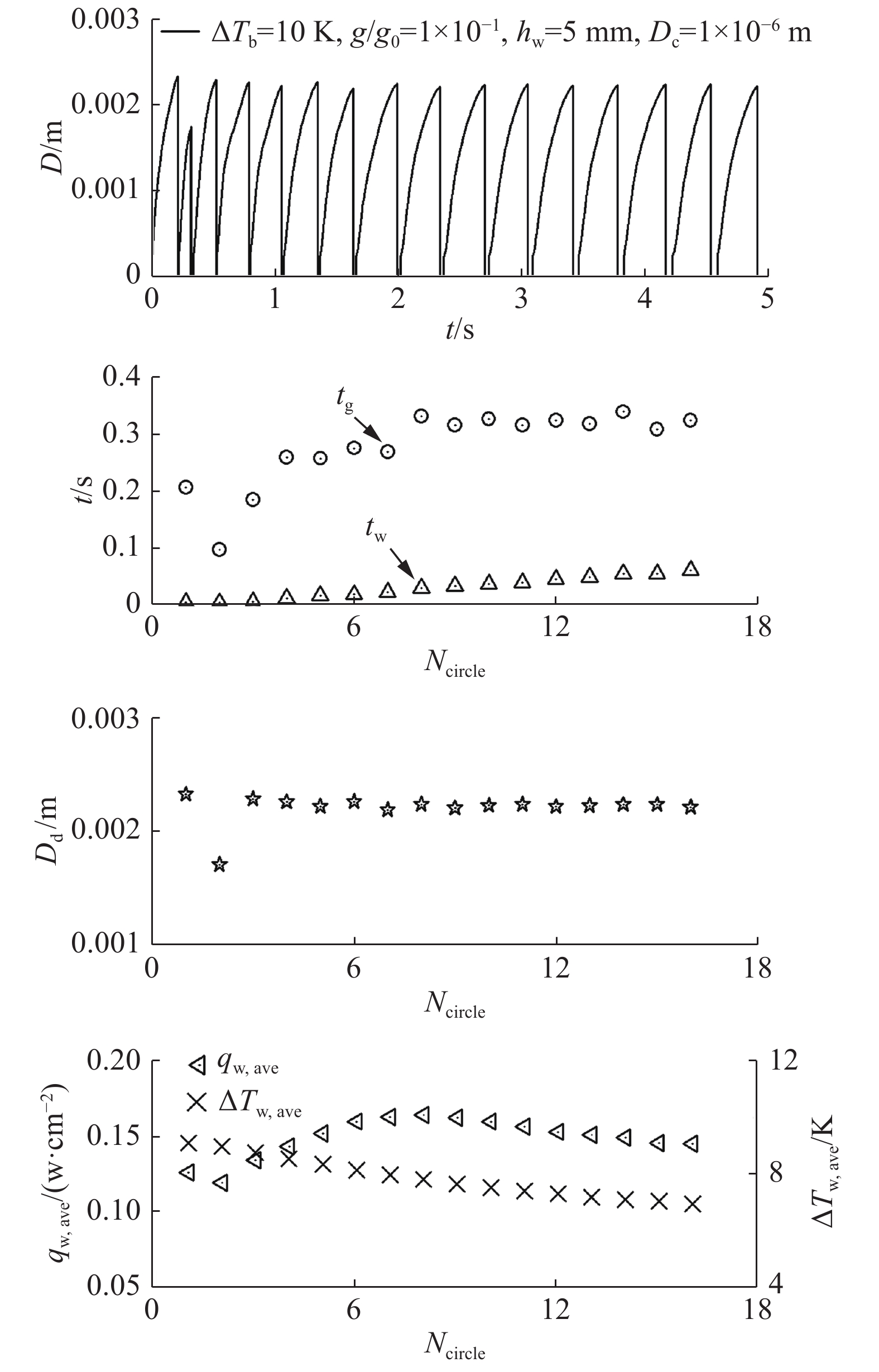
图2~图4显示了不同重力条件下标称过热度10 K时单气泡沸腾多周期生长过程模拟结果,包括气泡直径D随时间的变化和每个气泡生长周期内的生长时间tg、等待时间tw、脱落直径Dd以及时空平均的热流密度qw,ave和壁面过热度ΔTw,ave,其中,气泡生长时间tg和等待时间tw之和即气泡周期tc。

|
图 2 1g0(常重力)时多气泡周期的气泡生长过程 Fig.2 Multi-cycle process of bubble growth at 1g0 |
|
图 3 0.1g0时多气泡周期的生长过程 Fig.3 Multi-cycle process of bubble growth at 0.1g0 |
|
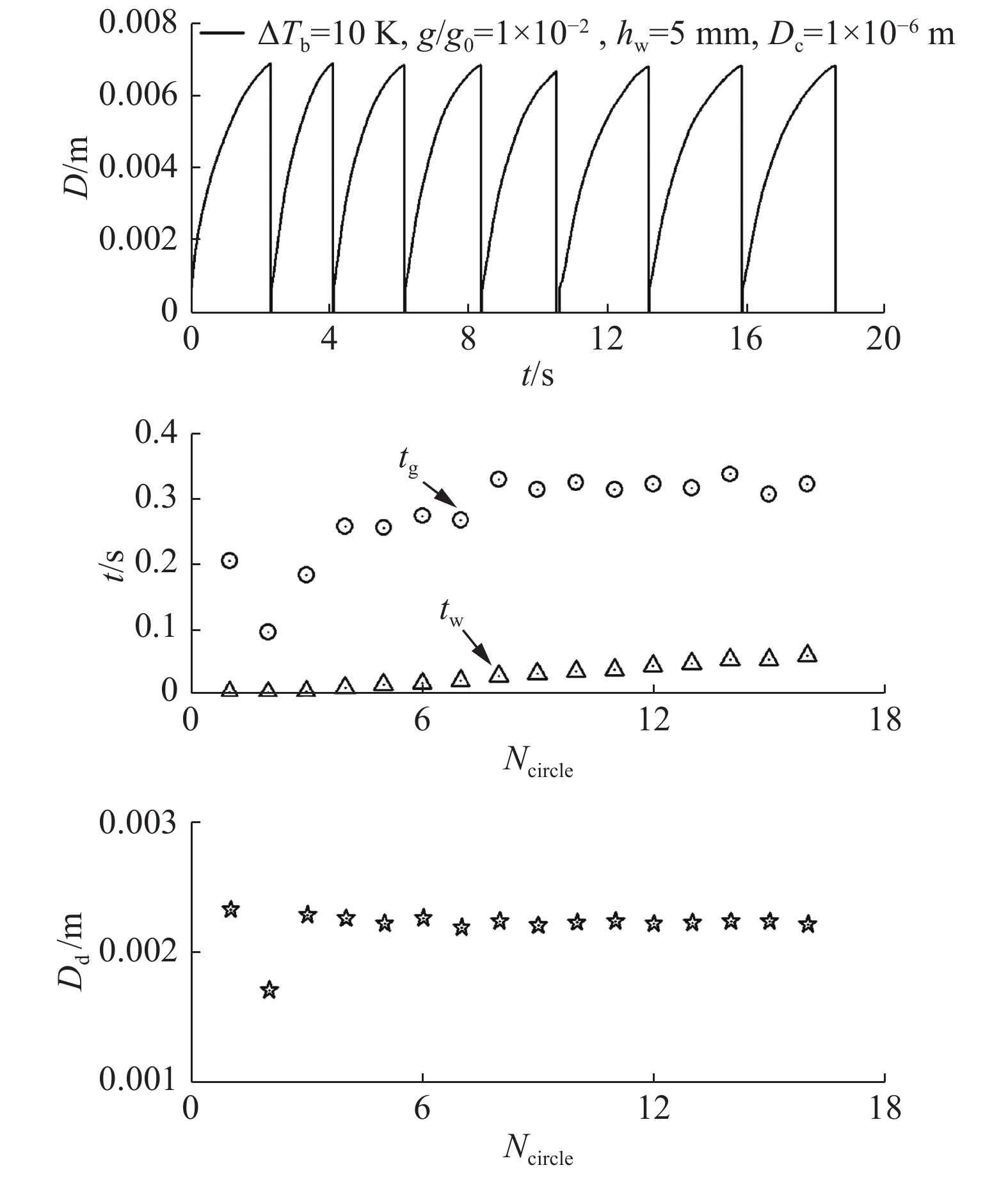
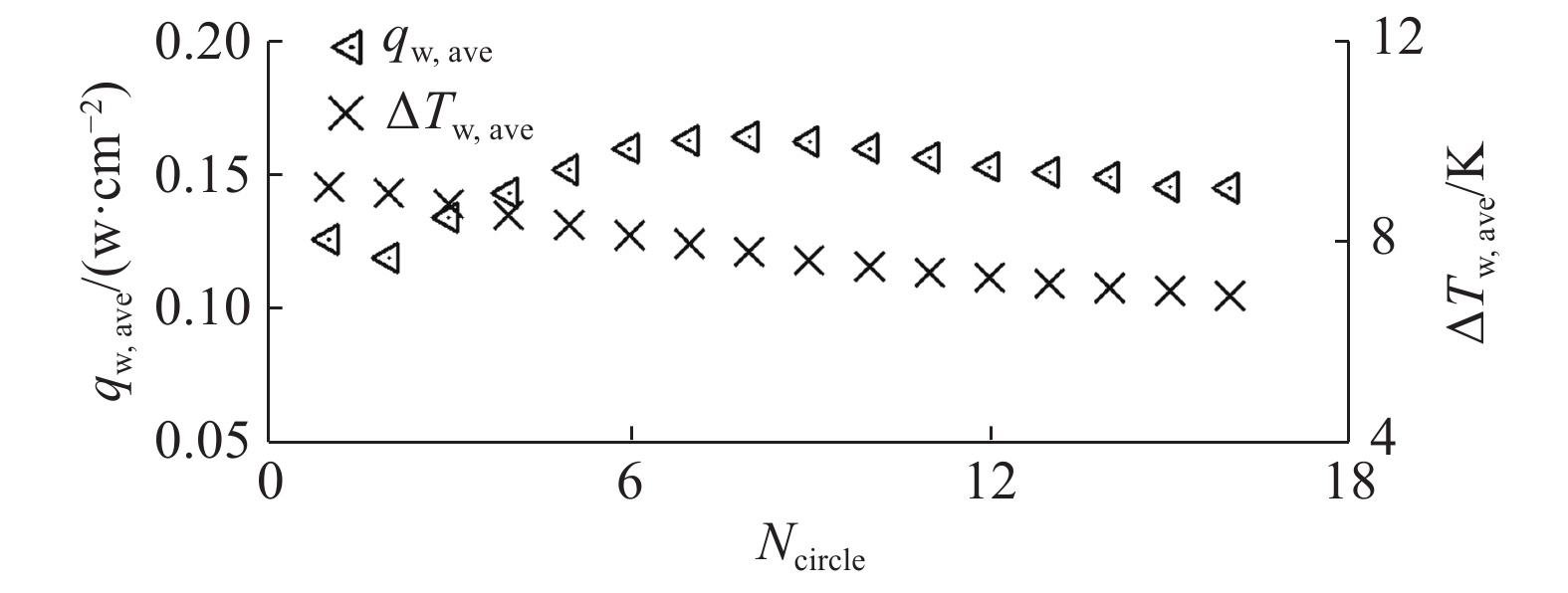
图 4 |
|
图 4 0.01g0时多气泡周期的生长过程 Fig.4 Multi-cycle process of bubble growth at 0.01g0 |
图中可以清楚地观察到,气泡生长过程随周期不同有明显差异,特别是在计算的初期。其主要原因在于理想化的初始条件。因此,为了消除初始条件对气泡生长过程及相应传热特性的影响,多周期模拟是必须的,甚至数十个气泡周期的计算依然只是达到某种准稳定状态(也许这正反映了相邻脱落气泡间的某种非稳态的相互影响)。
图5和6显示了工况2和4最后一个气泡周期内若干典型时刻加热固壁表面局部温度和热流分布的演变,与之相对应的气泡形态和温度场演变如图7所示。为了便于比较,温度场的描述采用无量纲温度,即0对应饱和温度,1对应标称过热度ΔTw = 10 K。

|
图 5 0.3g0时典型气泡生长周期内加热表面局部温度和热流密度的分布 Fig.5 The distribution of temperature and heat flux on the heater surface at different time in a typical bubble circle at 0.3g0 |

|
图 6 0.03g0时典型气泡生长周期内加热表面局部温度和热流密度的分布 Fig.6 The distribution of temperature and heat flux on the heater surface at different time in a typical abubble circle at 0.03g0 |

|
图 7 0.3g0和0.03g0时气泡形态及其周围温度场的演化 Fig.7 The evolutions of bubble topology and temperature field isotherm at 0.3g0and at 0.03g0 |
气泡生长过程中,在接触线附近可以观察到因剧烈蒸发引起的明显温度下降与热流密度的尖峰,这有助于热量向流体的传递。温降区域受接触线运动的推动而往复移动,导致生长气泡下方加热器表面(特别是在移动接触线来回扫掠的区域)局部温度和热流密度的剧烈波动。远离核化点处相变影响较弱,传热仅依赖自然对流,热流密度很小,而壁温往往会高于核化起始温度。重力越低,壁温与核化起始温度的差值越大,对应于低重力时液相自然对流的减弱。
气泡脱落后,回流的新鲜液体抑制了液气相变,气泡底部加热面温度随之开始上升,直到核化点温度再次达到核化起始温度,新的气泡周期再次启动。在气泡附近液体中也可以清楚地观察到过热液层的周期性变化,以及固壁内的瞬时热吸收和释放。这些局部对流在沸腾传热中起着重要的作用。
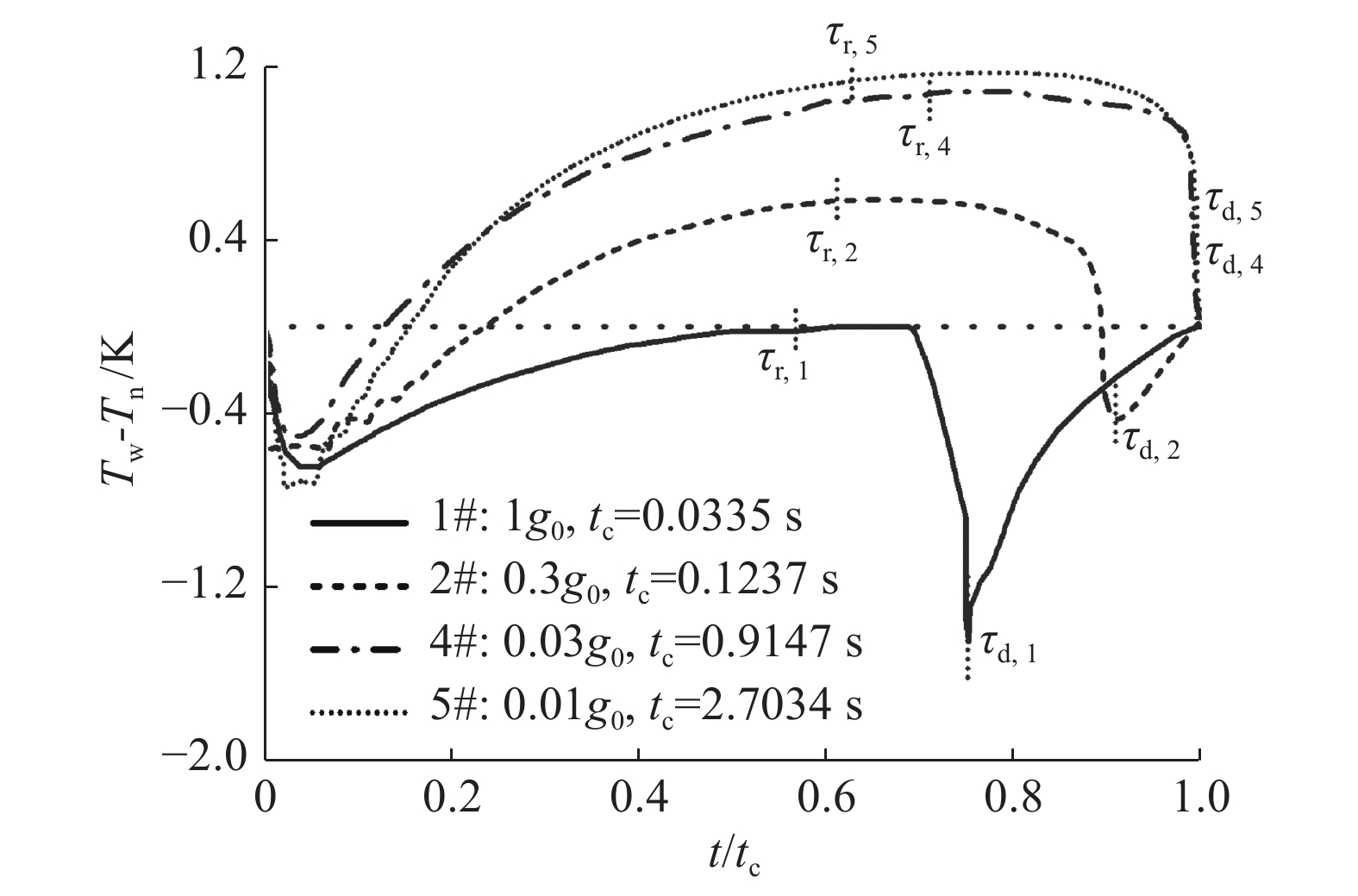
图8显示了不同重力条件下准稳态气泡生长周期内核化点处壁温的演变特征,并标明了气泡底部接触线无量纲回退时间(即τr = tr/tc)和脱落时间(即τd = td/tc)。为清楚起见,图中略去了工况3。核化点活化(这里表现为截球状小气泡的人工置入)后,气泡先是浸没在过热液层内,液体在气泡表面蒸发相变使得气泡尺寸及其与加热表面接触的底部在早期迅速向外膨胀,相变所需热量不仅来自过热液层的显热,也包括加热固壁存储的热量,后者导致核化点处壁温的快速下降。该温降过程持续的相对时间与重力关联较弱,但温降幅度随着重力的降低先减后增,临界重力约为0.03g0。随着气泡长大,气泡底部扩张使得接触线远离核化点,核化点附近为气体覆盖,局部传热恶化使得其温度持续回升,甚至超过核化起始温度;同时,气泡体积的增大,也使得作用在气泡上的浮力作用逐渐增强,抬升气泡质心,当抬升效应超过扩张效应时,气泡底部转而向核化点方向收缩(即接触线回退),直至脱离壁面。接触线相对回退时间随重力的变化是非单调的,即先增后减,临界重力同样约为0.03g0。
|
图 8 不同重力条件下典型气泡生长周期内核化点温度的演化情况 Fig.8 The evolution of wall temperature at the nucleation site in a bubble cycle at different gravity levels |
而邻近气泡脱落时,接触线附近的微对流和强蒸发使壁温再次快速下降,其幅度往往超过核化起始时,尤其是常重力条件下。气泡脱落后,加热面附近过热液层逐渐恢复,直至核化点温度达到相应核化起始条件,开始后续新的一个气泡周期。气泡脱落后的等待时间随重力下降快速减小,超过0.03g0后几乎完全消失。
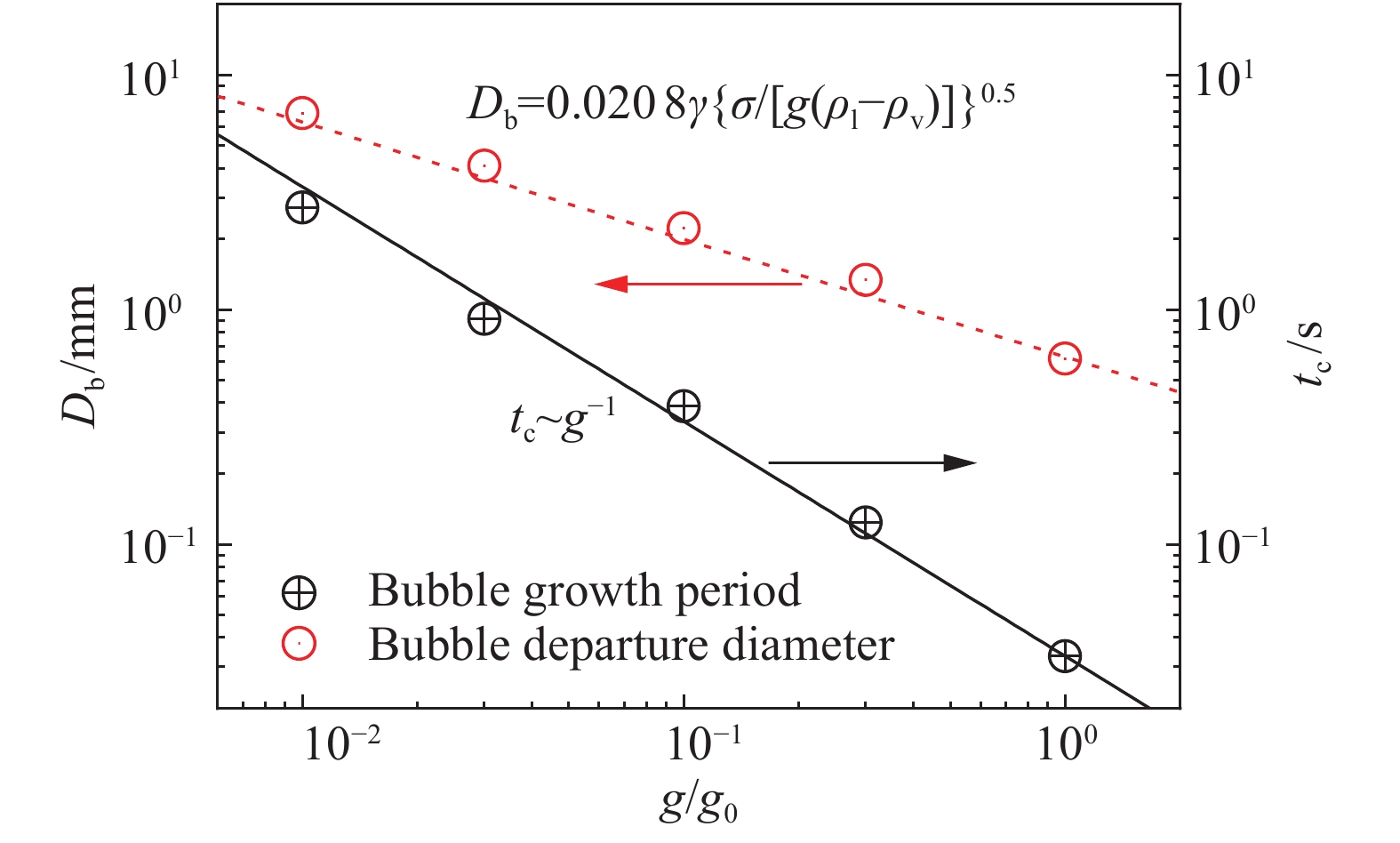
图9显示了气泡脱落直径和生长周期随重力的变化。可以发现,气泡脱落直径与Fritz模型(即Db = 0.0208γLc)[27]预测相符,反比于重力的1/2次方;而气泡脱生长周期反比于重力。这样,不同重力条件下Db f 1/2 = 常数,其中气泡脱落频率f = 1/tc。
|
图 9 气泡生长周期和气泡脱落直径随重力的变化 Fig.9 The variations of bubble growth period and bubble departure diameter with the gravity |
图10显示了热流密度相对于重力的标度行为。鉴于本文计算中加热固壁表面温度并非预先给定,而是最后输出结果,不同工况下时空平均的壁面过热度随重力有微弱变化,这里采用5个工况壁面过热度的平均值7.6 K(最大偏差不超过1 K)来表征壁面热状态。可以看到,无论是否对输出结果进行面积校正,0.01g0时传热特性均明显偏离了较高重力条件下热流密度与重力呈指数函数关系的变化趋势,反映出2个区域内有着明显不同的沸腾机制。较高重力区传热特性变化趋势与RKM模型[5-8]中浮力主导沸腾区(BDB)相似,热流密度与重力相关。较小重力时,RKM模型称之为表面张力主导区(SDB),传热特性与重力无关。这样,通过两条趋势线的交点可以得到重力相关区和重力无关区的分界位置,确定过渡(或临界)重力的数值,或者对应的无量纲加热器尺寸Lh/Lc的临界值:对未校正结果Lh/Lc = 2.9,而对校正结果Lh/Lc = 3.2,均接近RKM模型建议的数值Lh/Lc = 2.1。此外,加热面积校正使得重力相关区传热性能的重力标度指数从未校正时的0.475到校正后的0.425,变化不大。但在重力无关区,加热面积校正会引起无量纲热流密度的明显提升,这实际上源于常重力沸腾时加热面积校正引入的扩展加热面上较低的单相传热,导致校正后的热流密度大幅减小。

|
图 10 单气泡沸腾传热中的重力标度行为 Fig.10 Gravity scaling of heat transfer in single bubble boiling |
Zhao等[15]不考虑加热固壁热效应的数值模拟结果及加热面积校正结果同样示于图10,明显存在与本文模拟结果相同的特征。重力相关区和重力无关区分界位置所对应的无量纲加热器尺寸Lh/Lc的临界值与壁面过热度存在微弱的相关:5 K过热度时约2.3,10 K过热度约2.6,15 K过热度约2.8,均与RKM模型建议的2.1值相近。而重力相关区传热性能的重力标度指数则随过热度增加而有明显的单调增大的趋势:5 K过热度时约0.36,10 K过热度时约0.44,15 K过热度时约0.5(与经典的Rohsenow关联式预测值相同)。这种单调的增长趋势与RKM模型定性一致,只是具体数值增大约2倍。此外,与本文模拟结果相比可以发现,重力相关区加热固壁热响应对热流密度的重力标度指数影响不大,但在重力无关区则有着明显的影响。因此,加热器热响应对微重力沸腾传热的影响尤其值得重视。
3 结 论本文研究了不同重力条件下饱和FC-72单气泡池沸腾过程中的气泡动力学和传热特性,其中考虑了5 mm厚SiO2加热固壁的瞬态热响应。计算中对加热固壁底面给定恒定、均匀的10 K过热度,这样,与流体工质相接触的加热表面上的时空平均热流密度和过热度都不再是预先给定的变量,而是模拟的结果。为了消除初始条件对气泡生长过程及相应传热特性的影响,需要进行多气泡周期模拟,来实现准稳态的沸腾过程。
气泡生长周期内,气泡底部加热面会经历局部干斑的扩展、回退和表面再润湿等过程。虽然气泡周期随重力的减小而增大,但相对回退时间却非单调变化,最大值约发生在0.03g0,两侧的不同表现预示着沸腾机制的改变。生长气泡底部加热表面温度在接触线附近存在明显温降和相应的热流峰值,其位置随接触线运动而变。在接触线来回扫掠区域内,壁温和热流密度均有剧烈的波动,而远离核化点处属于单相液体传热,传递给工质的热流密度较小且近似恒定。当气泡从加热面上脱落时,液体对气泡底部干斑的再润湿会抑制核化点处的局部高温,形成等待期;等待期内壁温回升,当再次达到核化起始条件后,新的气泡出现,开始下一个气泡周期。在气泡附近可以清楚地观察到过热液层的周期性变化,以及固壁内热的瞬态吸收和释放。这些局部对流换热在沸腾现象中起着重要的作用。此外,本文模拟结果表明,气泡脱落直径与重力的1/2次方成反比,且与Fritz[27]模型预测一致;而气泡频率则与重力成正比。
本文提出了一个热流密度的面积校正方法,以便在相同的加热器物理尺寸下比较不同重力条件下的沸腾传热性能。观察到与RKM模型[5-8]相似的热流密度在不同重力区间的标度行为差异:当重力不小于0.03
| [1] |
杜王芳, 赵建福. 核态池沸腾传热现象中的重力标度规律[J]. 科学通报, 2020, 65(17): 1629-1637. DU W F, ZHAO J F. Gravity scaling law of heat transfer in nucleate pool boiling[J]. Chinese Science Bulletin, 2020, 65(17): 1629-1637. DOI:10.1360/TB-2019-0337 (in Chinese) |
| [2] |
ROHSENOW W M. A method of correlating heat transfer data for surface boiling of liquids[J]. Transactions of the ASME, 1962, 84: 969-976. |
| [3] |
STRAUB J. Boiling heat transfer and bubble dynamics in microgravity[J]. Advances in Heat Transfer, 2001, 35: 57-172. DOI:10.1016/S0065-2717(01)80020-4 |
| [4] |
RAJ R. Development of a boiling regime map and gravity scaling parameter for pool boiling heat transfer[D]. College Park: University of Maryland , 2010.
|
| [5] |
RAJ R, KIM J, MCQUILLEN J. Subcooled pool boiling in variable gravity environments[J]. Journal of Heat Transfer, 2009, 131(9): 091502. DOI:10.1115/1.3122782 |
| [6] |
RAJ R, KIM J, MCQUILLEN J. Gravity scaling parameter for pool boiling heat transfer[J]. Journal of Heat Transfer, 2010, 132(9): 091502. DOI:10.1115/1.4001632 |
| [7] |
RAJ R, KIM J, MCQUILLEN J. On the scaling of pool boiling heat flux with gravity and heater size[J]. Journal of Heat Transfer, 2012, 134(1): 011502. DOI:10.1115/1.4004370 |
| [8] |
RAJ R, KIM J, MCQUILLEN J. Pool boiling heat transfer on the international space station: experimental results and model verification[J]. Journal of Heat Transfer, 2012, 134(10): 101504. DOI:10.1115/1.4006846 |
| [9] |
WANG L, ZHU K, XIE F S, et al. Prediction of pool boiling heat transfer for hydrogen in microgravity[J]. International Journal of Heat and Mass Transfer, 2016, 94: 465-473. DOI:10.1016/j.ijheatmasstransfer.2015.11.049 |
| [10] |
WANG X L, ZHANG Y H, QI B J, et al. Experimental study of the heater size effect on subcooled pool boiling heat transfer of FC-72 in microgravity[J]. Experimental Thermal and Fluid Science, 2016, 76: 275-286. DOI:10.1016/j.expthermflusci.2016.03.031 |
| [11] |
MA X J, CHENG P, GONG S, et al. Mesoscale simulations of saturated pool boiling heat transfer under microgravity conditions[J]. International Journal of Heat and Mass Transfer, 2017, 114: 453-457. DOI:10.1016/j.ijheatmasstransfer.2017.06.019 |
| [12] |
FENG Y, LI H X, GUO K K, et al. Numerical study on saturated pool boiling heat transfer in presence of a uniform electric field using lattice Boltzmann method[J]. International Journal of Heat and Mass Transfer, 2019, 135: 885-896. DOI:10.1016/j.ijheatmasstransfer.2019.01.119 |
| [13] |
STEPHAN P, HAMMER J. A new model for nucleate boiling heat transfer[J]. Heat and Mass Transfer, 1994, 30(2): 119-125. DOI:10.1007/BF00715018 |
| [14] |
SON G, DHIR V K, RAMANUJAPU N. Dynamics and heat transfer associated with a single bubble during nucleate boiling on a horizontal surface[J]. Journal of Heat Transfer, 1999, 121(3): 623-631. DOI:10.1115/1.2826025 |
| [15] |
ZHAO J F, LI Z D, ZHANG L, et al. Numerical simulation of single bubble pool boiling in different gravity conditions[C]// New Trends in Fluid Mechanics Research. Proc. 6th Int. Conf. Fluid Mech., Guangzhou, China, 2011. doi: 10.1063/1.3651978.
|
| [16] |
YI T H, LEI Z S, ZHAO J F. Numerical investigation of bubble dynamics and heat transfer in subcooling pool boiling under low gravity[J]. International Journal of Heat and Mass Transfer, 2019, 132: 1176-1186. DOI:10.1016/j.ijheatmasstransfer.2018.12.096 |
| [17] |
FUCHS T, KERN J, STEPHAN P. A transient nucleate boiling model including microscale effects and wall heat transfer[J]. Journal of Heat Transfer, 2006, 128(12): 1257-1265. DOI:10.1115/1.2349502 |
| [18] |
AKTINOL E, DHIR V K. Numerical simulation of nucleate boiling phenomenon coupled with thermal response of the solid[J]. Microgravity Science and Technology, 2012, 24(4): 255-265. DOI:10.1007/s12217-012-9308-7 |
| [19] |
ZHANG L, LI Z D, LI K, et al. Influence of heater thermal capacity on pool boiling heat transfer[J]. Journal of Computational Multiphase Flows, 2014, 6: 361-375. DOI:10.1260/1757-482X.6.4.361 |
| [20] |
ZHANG L, LI Z D, LI K, et al. Influence of heater thermal capacity on bubble dynamics and heat transfer in nucleate pool boiling[J]. Applied Thermal Engineering, 2015, 88: 118-126. DOI:10.1016/j.applthermaleng.2014.11.080 |
| [21] |
LI Z D, ZHANG L, ZHAO J F, et al. Numerical simulation of bubble dynamics and heat transfer with transient thermal response of solid wall during pool boiling of FC-72[J]. International Journal of Heat and Mass Transfer, 2015, 84: 409-418. DOI:10.1016/j.ijheatmasstransfer.2014.12.061 |
| [22] |
DHRUV A, BALARAS E, RIAZ A, et al. A formulation for high-fidelity simulations of pool boiling in low gravity[J]. International Journal of Multiphase Flow, 2019, 120: 103099. DOI:10.1016/j.ijmultiphaseflow.2019.103099 |
| [23] |
张良. 单气泡池沸腾现象中的流动与传热特性数值模拟[D]. 北京: 中国科学院大学, 2014. ZHANG L. Study on the thermal dynamical characteristics of fluid particles in microgravity[D]. Beijing: Institute of Mechanics, Chinese Academy of Sciences, 2014. |
| [24] |
SIEGEL R, KESHOCK E G. Effects of reduced gravity on nucleate boiling bubble dynamics in saturated water[J]. AIChE Journal, 1964, 10(4): 509-517. DOI:10.1002/aic.690100419 |
| [25] |
HSU Y Y. On the size range of active nucleation cavities on a heating surface[J]. J. Heat Transfer, 1962, 84(3): 207-213. DOI:10.1115/1.3684339 |
| [26] |
SON G. Numerical study on a sliding bubble during nucleate boiling[J]. KSME International Journal, 2001, 15(7): 931-940. DOI:10.1007/BF03185271 |
| [27] |
FRITZ W, ENDE W. Berechnungen des Maximalvolumens von Dampfblasen[J]. Physik, Zeitschr, 1935, 36: 379-384. |


