0 引　言

近年来，临近空间因其重要的战略价值受到重视，临近空间超声速飞行器成为各国研究的热点^[1-2]。依照飞行任务不同，临近空间飞行器主要分为飞船返回舱、临近空间高超声速飞行器和天地往返运输系统等几类；依照气动外形不同，主要有升力体、乘波体、轴对称锥形体等，代表性的验证飞行器有X-43A^[3]、HTV2^[4]、X-37B等。目前，高超飞行器的飞行高度已覆盖了临近空间（20～100 km）整个范围，这一范围内空气密度随高度变化很大，环境密度的变化导致气体流动呈现从连续到稀薄的不同状态。

Breguet方程指出，巡航条件下飞行器的巡航距离与整机升阻比正相关，提高飞行器的升阻比可以有效提高巡航距离。然而，在高超声速飞行条件下，激波阻力和摩擦阻力急剧增加，飞行器升阻比受到严重制约，飞行器遭到“升阻比屏障”^[5]。目前，乘波体^[6]是一种公认的气动性能较好的高速飞行器设计方案。其特点是高速飞行时激波附着在机体前缘，机体将激波后的高压区完全包裹在机身下方；为减小作用在机身上表面的压力，上表面一般设置为平行于来流，这样可以实现较大的升阻比。然而，乘波体的设计思路决定了其厚度相对较薄，容积率小。为提高容积，一方面，可以将绝对尺寸增加，但这会导致迎风面积和浸润面积增大，阻力急剧增大；另一方面，可以将上表面适当隆起，但气流在上表面的压缩会削弱升力。

高速飞行器的基本功能是实现远程快速运输，因而容积与巡航距离是两项重要的设计指标。由上述分析可知，飞行器的升阻比与容积存在严重的相互制约关系。目前各类飞行器气动设计的本质是依据飞行任务不同，在各项设计指标间进行权衡和折中。国内外已有学者对各类高超声速飞行器进行了大量的计算，详细分析了各类气动布局的优缺点^[7-9]。近年来，针对高速飞行器的高容积、高升力、高升阻比的设计需求，崔凯等^[10-12]提出了一种新型气动构型，称为高压捕获翼（High-pressure Capturing Wing，以下简称HCW）。其基本设计思路是在机体上方合理位置设置增升翼，充分利用机体上表面压缩产生的高压区，实现大容积飞行器的升力补偿。文献[12]针对一种乘波体耦合HCW的飞行器进行数值模拟，结果显示，引入HCW后，在给定工况下飞行器的升力提高32.8%，升阻比提高26.3%。

对高超声速飞行器而言，稀薄过渡流域内的气动性能同样重要，此时环境密度小，因而空气阻力小，可以实现更高速度的飞行，但稀薄效应会严重影响升力与升阻比等气动性能。流场的稀薄程度通常可用无量纲参数Knudsen数（Kn）,即气体分子的平均自由程 $\lambda $ 和流场特征长度l的比值，进行衡量。钱学森^[13]在1946年发表的论文中强调了稀薄效应在空气动力学中的重要性。依照Kn的大小，通常可将流动分为连续流（ $Kn \leqslant 0.001$ ）、滑移流（ $0.001 < Kn \leqslant 0.1$ ）、过渡流（ $0.1 < Kn \leqslant10$ ）和自由分子流（ $Kn > 10$ ）。例如，对于特征长度为0.1 m的系统，在海拔70 km的高空，空气平均自由程约为1×10⁻³ m， $Kn = 0.01$ ，属于滑移流域，稀薄效应有一定的影响；而在100 km的高空，空气平均自由程可达0.14 m， $Kn = 1.4$ ，此时流动处于过渡流区。在该情况下，气体分子的平均碰撞时间与流动特征时间相当，分子碰撞不足以将分子速度分布维持在平衡态附近，一旦出现扰动，分子的速度分布便将远离平衡态分布，稀薄效应十分显著^[14]。另一方面，空气稀薄意味着飞行器容易实现更高的速度。在高超声速条件下，由于激波压缩和边界层内的黏性耗散导致温度升高，气体分子的振动能被高温激发，导致气体离解、电离甚至发生化学反应。这种现象通常称为高温真实气体效应，会对高超声速飞行器的升力、阻力和力矩带来较大影响^[6]。

由上可知，同类飞行器在做跨大气层飞行时其气动特性需要重新进行评估。孙泉华^[15]总结了一些飞行器在不同Kn下的升阻比数据，涉及的飞行器包括乘波体、航天飞机、NACA机翼等，结果表明各种气动外形的升阻比均随着稀薄程度的增加而明显下降，稀薄效应会严重影响飞行器的气动性能。因此，学者们希望设计一种从连续区到稀薄过渡区均有良好气动性能的新型气动布局。目前，关于HCW构型的数值模拟与风洞实验主要集中在连续流域^{[12, 16-17]}，对于稀薄领域的研究还很缺乏。稀薄气体效应会导致激波脱体、激波层变厚甚至没有明显的激波结构^[18-19]，同时由于HCW设计为平行于来流的薄翼结构，阻力主要是摩擦阻力，稀薄过渡区摩擦阻力占比迅速上升^[20]，HCW带来的额外阻力不可忽视。因此，研究HCW构型的跨流域气动性能十分重要。

对于具有稀薄效应的流动模拟，传统的计算流体力学（CFD）方法存在一定的局限性。在滑移流域，稀薄效应体现在固体壁面边界上出现速度滑移和温度跳跃，此时可以采用Navier-Stokes (N-S)方程加上滑移边界条件进行处理。对于过渡区的流动，此时N-S方程内描述应力和热流的线性本构关系失效。目前模拟稀薄流动最为可靠的数值模拟方法是直接模拟Monte Carlo (DSMC)方法^{[14, 21]}。DSMC方法以分子动理论为基础，通过追踪分子的运动和碰撞过程对气体进行建模。分子的运动是确定性的，在一个时间步长内，根据分子的速度更新分子的位置；分子的碰撞是随机性的，通过在一个碰撞网格内随机选取分子对进行。流场的宏观信息，如密度、速度和温度等，是通过对网格中所有分子进行统计平均得到的。原理上，DSMC方法可以应用在从连续流到自由分子流的整个流动领域，但需要注意的是，为了保证计算的精度，DSMC方法要求碰撞网格小于分子的平均自由程，时间步长小于分子的平均碰撞时间^[22]。因此，DSMC方法对于稀薄流的计算是十分高效的，但对于连续流的计算相对较慢。近年来，DSMC方法及其改进的多尺度粒子方法^[23-24]已在航天器再入^{[18, 20]}、临近空间高超声速飞行器^[25-26]的气动特性以及流动机理^[27-28]等方面得到了广泛应用。

本文针对一种简单的HCW原理性构型，以马赫数20、飞行高度在70～100 km为条件，采用DSMC方法进行数值模拟。重点研究不同飞行高度下的流场结构、HCW下表面的气动力/气动热分布以及壁面反射模型对气动力/气动热分布的影响规律，探讨HCW构型的跨流域气动特性，并为后续跨流域飞行器外形优化等工作奠定基础。

1 高压捕获翼设计原理与计算模型

高压捕获翼（HCW）的基本设计原理如图1所示^[12]，其中二维的楔形代表机体，平行于来流的极薄平板代表HCW。自由来流被机体上表面压缩后，产生第一道斜激波S₁，波后压力上升，气流偏折后与机体上表面平行，之后这部分气流被HCW再次压缩形成激波S₂，波后压力进一步上升。由于机体尾部气体膨胀，气流经过膨胀波系后压力逐渐下降。根据激波与膨胀波的相对位置将流场划分为5个区域，其中，1区域为自由来流，2区域内来流被机体上表面压缩，并在3区域内被HCW再次压缩，压力达到最大，之后经过一系列膨胀波进入区域4，压力逐渐下降；由于HCW平行与来流，区域5内的压力与自由来流基本相等。经过两次压缩，HCW下表面的压力明显高于上表面，因此HCW可以为飞行器提供较大的额外升力。

本文研究的重点是不同稀薄程度下，机体与HCW之间的流场特征以及HCW下表面的气动力/气动热分布，未考虑机体前缘与HCW的热防护设计以及机体与HCW之间的支撑结构。根据上述设计思路，本文以二维楔形为概念机体，其上方布置HCW，HCW外形为极薄的二维矩形。机体长度为1 m，高度为0.2 m，并以机体高度作为飞行器的特征长度。HCW的长度和厚度分别为0.4 m、0.002 m，与机体的相对位置依据文献[29]中的思路给定。

2 计算方法与可靠性验证

为了准确模拟简化模型在稀薄过渡流域的流场结构和气动特性，选择DSMC方法作为计算工具，该方法被认为是模拟稀薄流动最成功的方法之一^[21]。计算程序使用开源DSMC模拟软件SPARTA^[30]，分子碰撞过程采用变径软球（VSS）模型处理，内能松弛使用Larsen-Borgnakke统计模型处理，化学反应模型为TCE模型。计算网格采用笛卡尔网格，并采用网格自适应技术，保证网格尺度小于当地自由程，且每个网格中粒子数目大于30。

为方便比较不同高度壁面物理量变化规律，对气动力、气动热进行无量纲处理，壁面压力系数、摩擦系数与热流系数的定义为：

$ {C_p} = ({p_w} - {p_\infty })/({\rho _\infty }u_\infty ^2/2) $

(1)

$ {C_f} = {\tau _w}/({\rho _\infty }u_\infty ^2/2) $

(2)

$ {C_h} = {q_w}/({\rho _\infty }u_\infty ^3/2) $

(3)

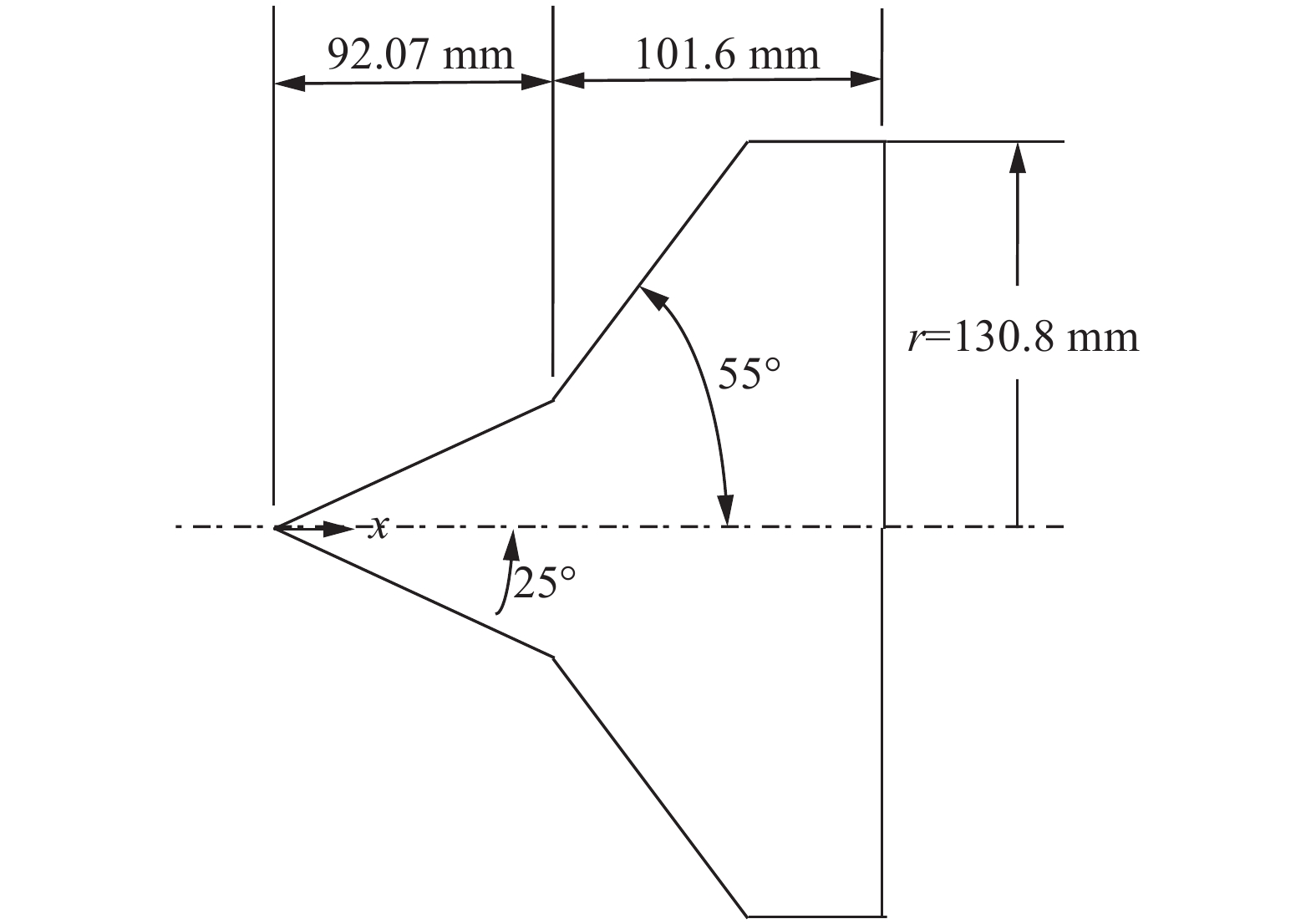
首先采用SPARTA软件对双锥模型进行模拟，并将结果与实验测量得到的气动力和气动热数据进行对照，以验证计算方法的可靠性。双锥的几何外形如图2所示。来流气体为N₂，密度为1.757×10⁻⁴ kg/m³，温度为42.6 K，速度为2073 m/s，锥体壁面温度297.2 K。计算中采用了网格自适应技术，以保证碰撞对的选取网格尺度小于当地分子平均自由程。

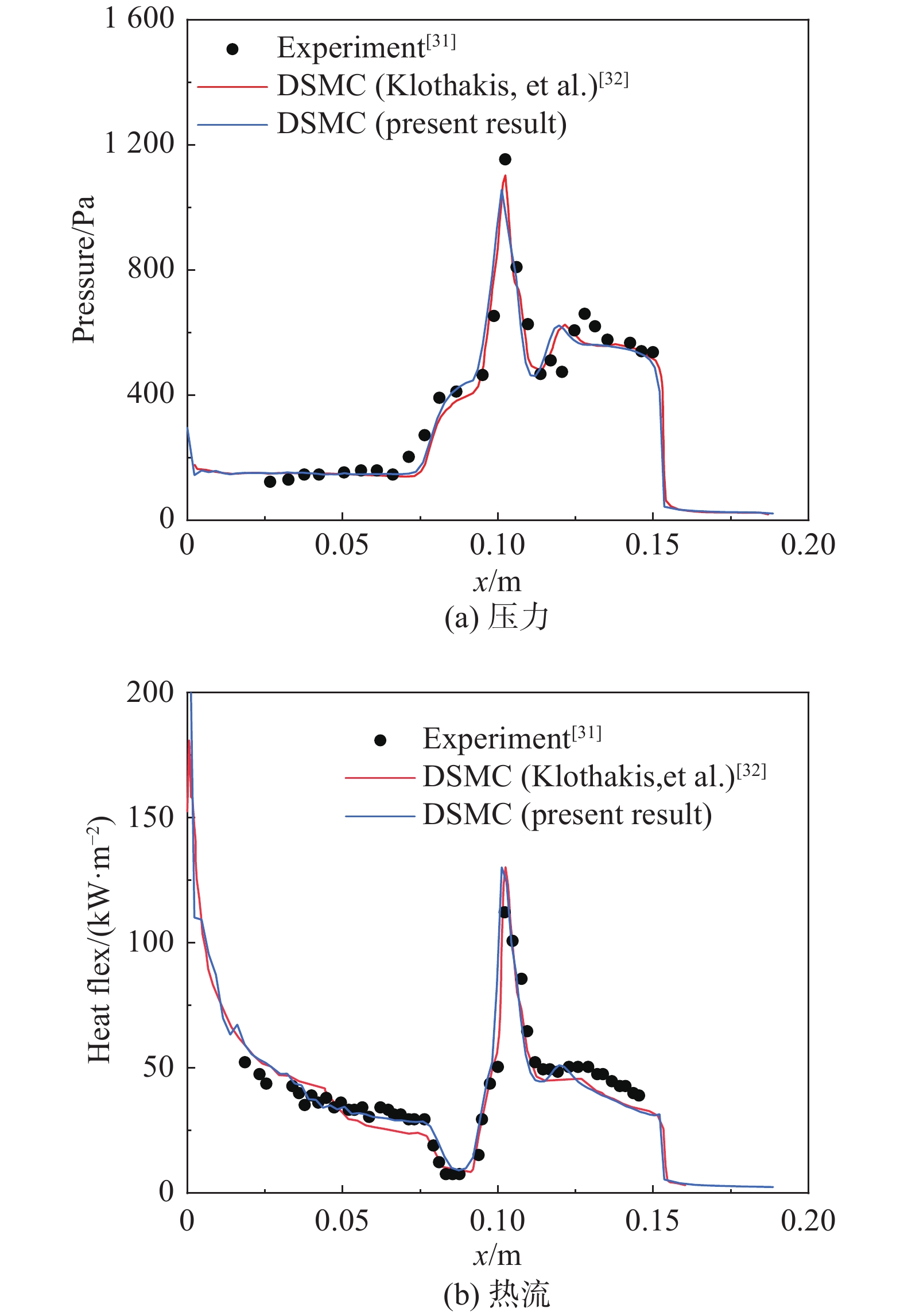
图3给出了表面压力与热流分布，图中三组数据分别为实验结果^[31]、Klothakis等的DSMC计算结果^[32]及本文的DSMC计算结果。结果表明本文的数值结果与已有实验值以及文献中的数值模拟结果较为吻合，SPARTA能够准确地预测再附点的位置。以实验结果作为基准，本文DSMC结果在再附点处压力差异约8.4%，热流差异约13.8%，SPARTA程序的结果具有较高的可信度。

3 计算结果及分析

为比较HCW构型在不同稀薄程度大气中的流场结构以及气动性能，选取了四个典型的飞行高度，来流马赫数Ma = 20，来流基本参数由美国标准大气(USSA-76)模型^[33]确定，具体数据见表1。机体与HCW表面均采用Maxwell反射模型，若无特殊说明，适应系数取为 ${\alpha _M} = 0.8$ ，即有80%的分子在壁面为漫反射，其余20%的分子为镜面反射。壁面温度设置为300 K。

为确保计算结果不受网格密度影响，对飞行高度为90 km的工况，依据整个流场中网格尺度与当地平均自由程之比最大值 ${({L_{{\rm{cell}}}}/{\lambda _{{\rm{local}}}})_{\max }}$ 的不同，使用三套不同的网格进行网格独立性验证。由于SPARTA程序可以在挑选碰撞对时优先选择距离较近的分子，计算中可适当放宽对网格的要求。初步选定的粗网格满足 ${({L_{{\rm{cell}}}}/{\lambda _{{\rm{local}}}})_{\max }} < 2$ ，中网格满足 ${({L_{{\rm{cell}}}}/{\lambda _{{\rm{local}}}})_{\max }} < 1$ ，细网格满足 ${({L_{{\rm{cell}}}}/{\lambda _{{\rm{local}}}})_{\max }} < 0.5$ 。时间步长取为 $\vartriangle t = $ $ \tau /3$ ，其中 $\tau $ 为分子平均碰撞时间。

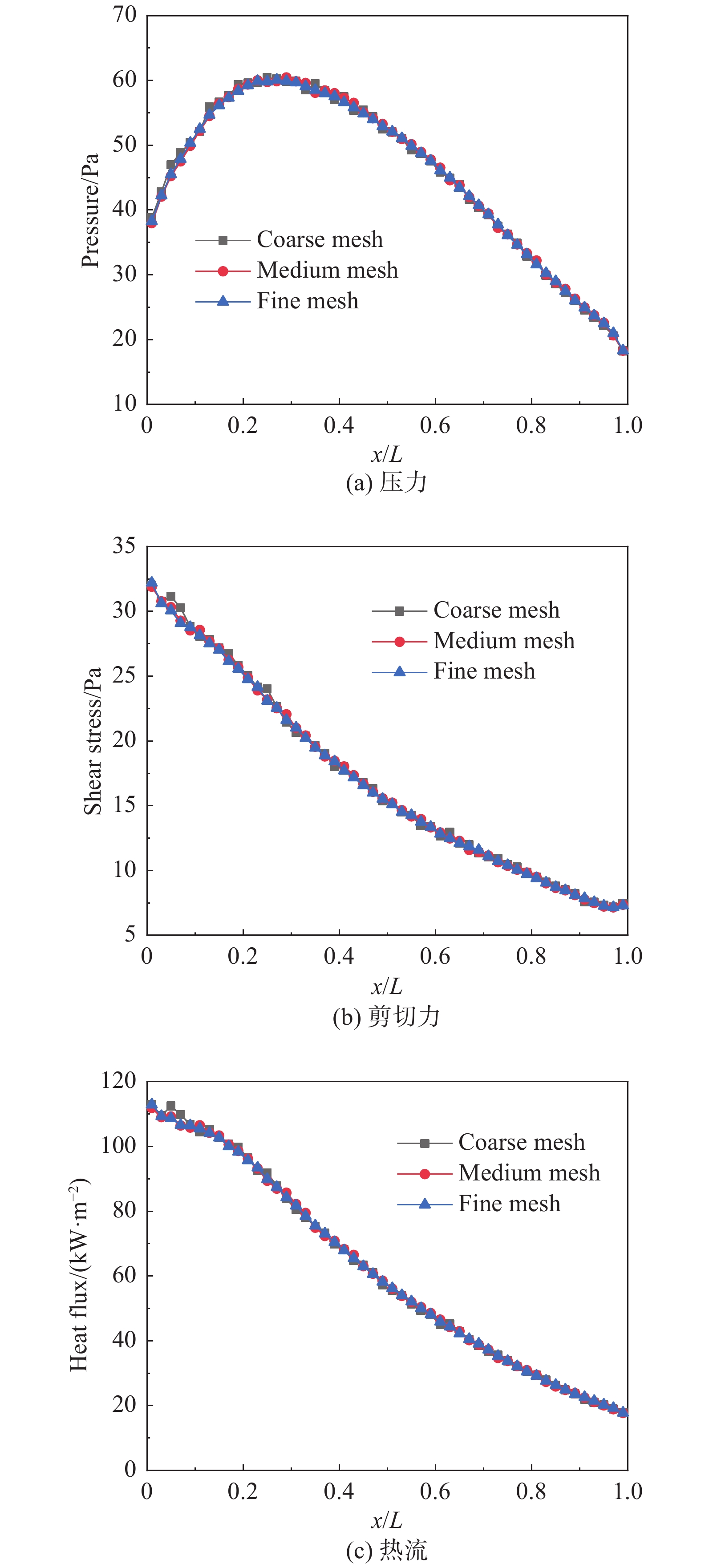
如图4所示，三套网格计算得到的HCW下表面压力分布差别很小；粗网格与中网格得到的HCW下表面剪切力和热流存在微小差距，而中网格与细网格得到的剪切力与热流几乎相同，这表明中网格与细网格模拟精度非常好。基于此，后续计算均使用满足 ${({L_{{\rm{cell}}}}/{\lambda _{{\rm{local}}}})_{\max }} < 1$ 的网格（对于较为连续的工况，为提高计算效率，使用满足 ${({L_{{\rm{cell}}}}/{\lambda _{{\rm{local}}}})_{\max }} < 2$ 的网格）。

精确预测激波位置等流场特征对HCW外形设计十分重要，但随着飞行高度增加，稀薄效应会导致激波层变厚，激波边缘变模糊；表面气动量（压力、剪切力、热流等）的分布是高超声速流动中备受关注的物理量，因为表面量的分布直接影响飞行器的气动性能。在验证网格独立性的基础上，本节针对HCW的二维简化外形，分析稀薄效应对流场特征和HCW下表面气动量的影响。考虑到稀薄条件下分子在固体壁面的反射方式对流场结构和表面气动量有重要影响^[34]，进一步研究了不同高度下气固作用模型对HCW表面剪切力分布的影响，为实现高压捕获翼构型在稀薄流域减阻提供一种思路。

3.1 流场特征分析

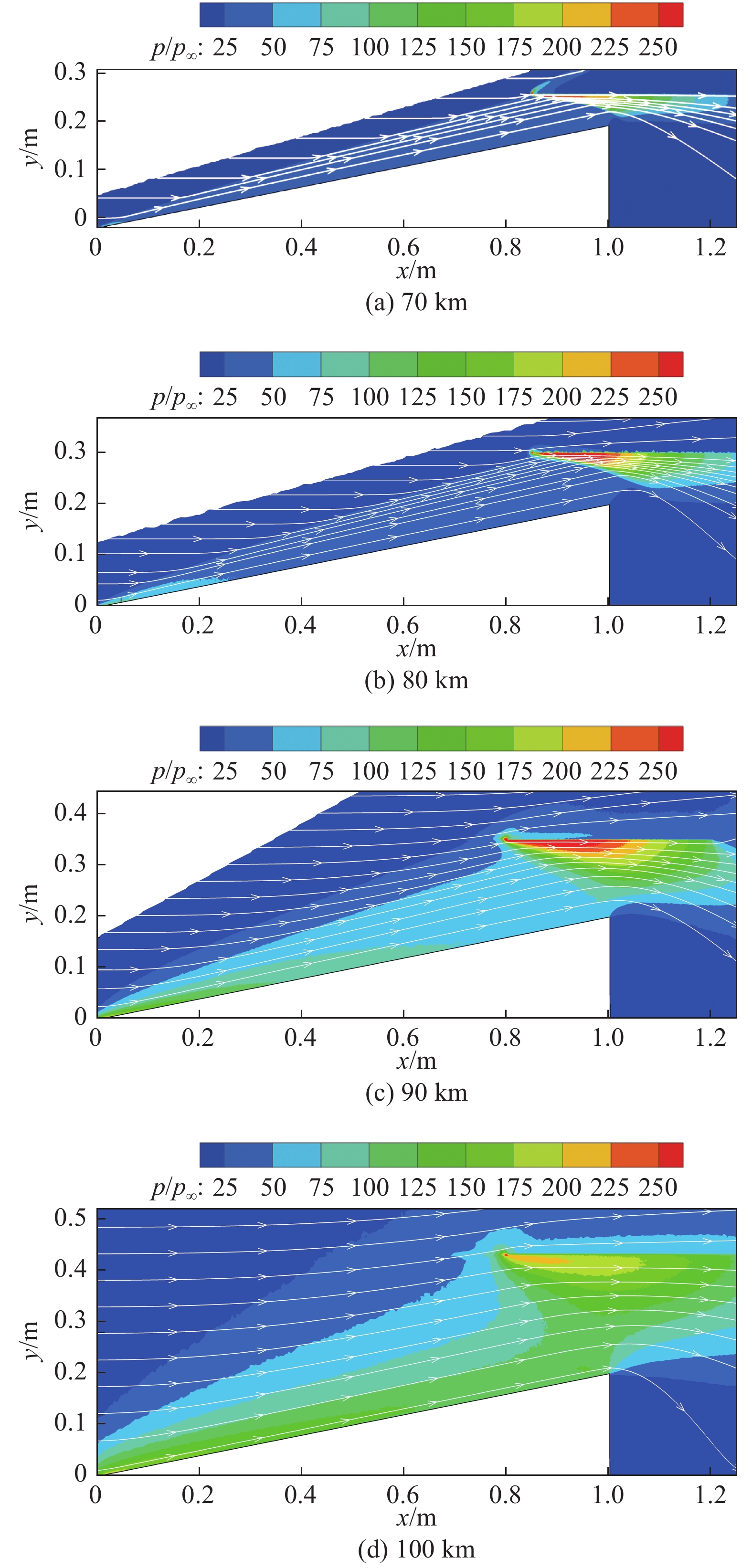
图5给出了不同高度下无量纲压力云图和流线图，以自由来流压强对当地压强进行无量纲化（ $p/{p_\infty }$ ）。不同高度对应的结果显示，高速来流在被楔形机体压缩之后方向偏折，并被HCW再次压缩，HCW下方压力显著升高，上、下表面存在明显压力差，即通过增加HCW可以实现额外的增升效果。需要说明的是，随着高度增加，激波层变厚，机体诱导的波后高压区边缘逐渐远离物面。由文献[29]提出的HCW位置设计方法，激波S₂需要掠过机体尾部最高点，因此HCW与机体之间的距离随高度增加也需要逐渐增大。

对于飞行高度为70 km、80 km的工况，Kn分别为4.91×10⁻³与2.20×10⁻²，由于来流速度较大，此时壁面已经出现速度滑移现象，流动属于滑移流域。此时流场结构与连续流区得到的计算结果^[10]类似，HCW压缩产生的激波S₂能掠过机体最高点，而不直接作用在机体上表面；飞行高度为90 km时， $Kn = 0.119$ ，流动已进入过渡流域，此时激波边缘比较模糊，激波S₂与机体最高点产生相互干扰，但总体而言影响较小；当飞行高度为100 km时， $Kn = 0.71$ ，此时稀薄效应更加突出，已经无法观察到清晰的激波S₂，机体与HCW之间的开放通道内出现严重的相互干扰，加入HCW对机体升力造成较大损失。

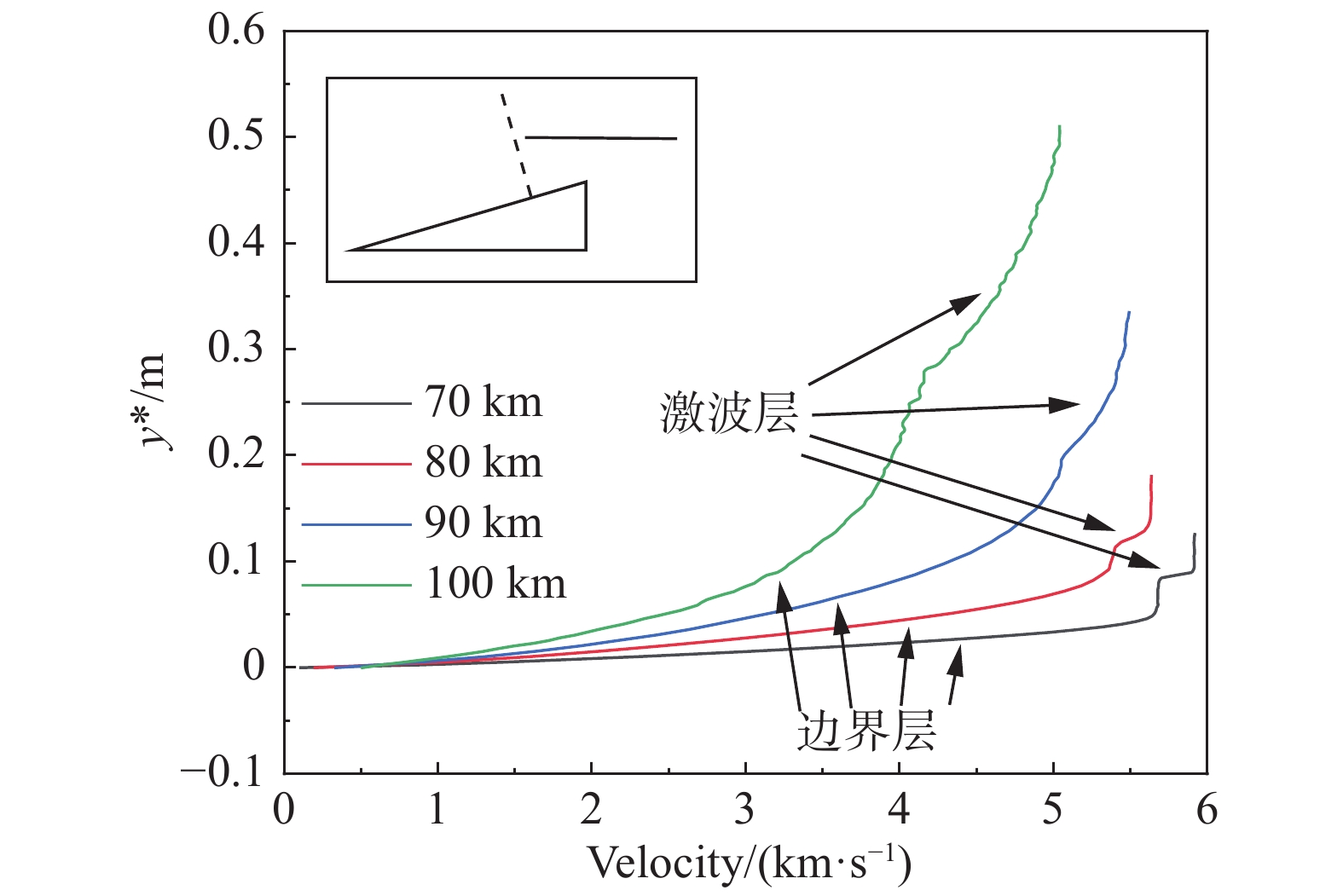
为了进一步研究激波S₁后流场分布情况，比较了机体上方（距离机体头部0.816 m处，见图6中的小图）速度沿壁面法向的分布，图中y*为距壁面高度。从图6可以看出，70 km工况下，流场中存在清晰的激波层和边界层结构；80～90 km工况下，激波层和边界层逐渐变厚，二者间的过渡变得模糊；100 km以上，激波层和边界层已经融合在一起，流动演变为渐进压缩过程。综合以上分析，对本文考虑的原理性构型而言，飞行高度在100 km及以上时，HCW的优势不再明显。因此后文仅对70～90 km工况展开分析。

3.2 壁面气动力和气动热分布特性

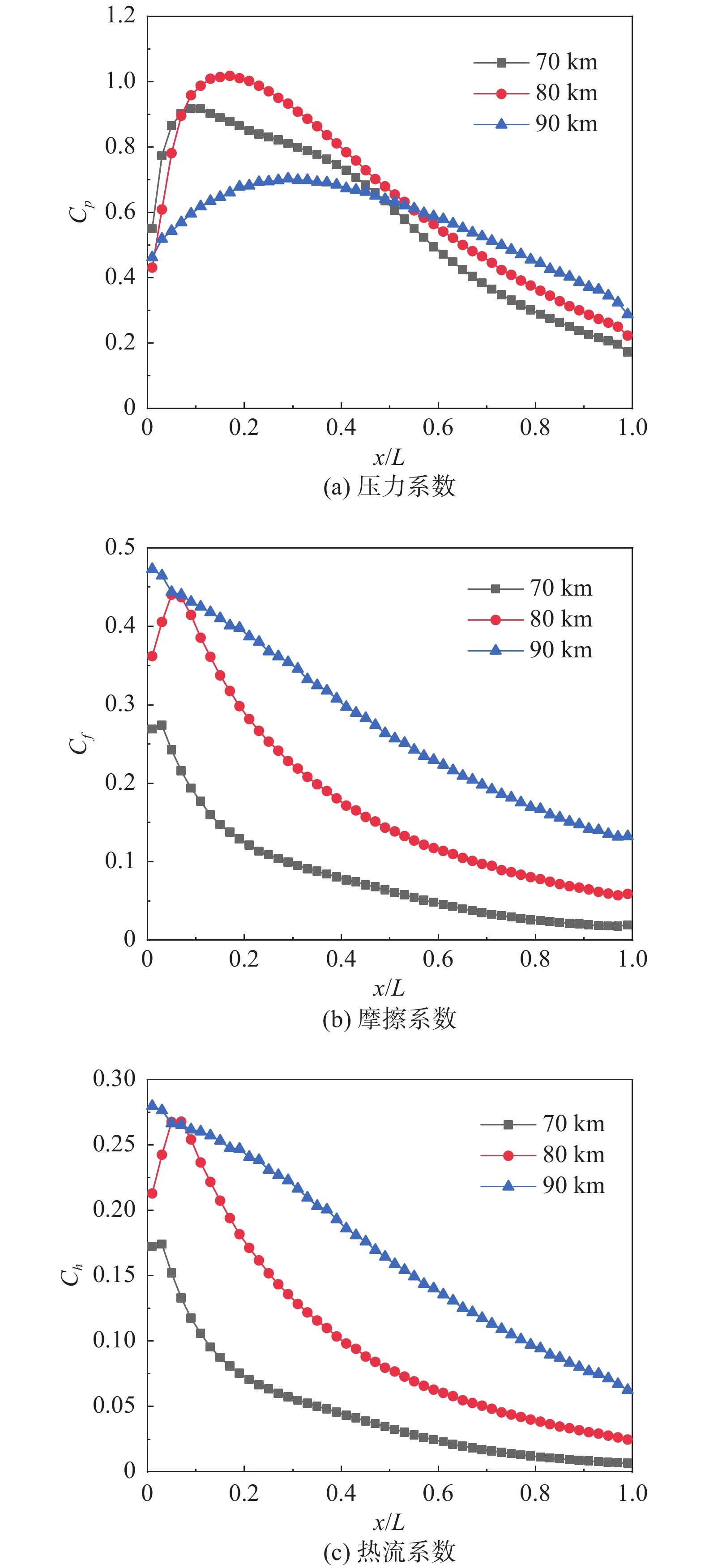
当飞行高度增加，稀薄效应会改变飞行器周围的流场结构，表面压力、剪切力与热流也会呈现不同的变化规律。图7（a）给出了HCW下表面压力系数分布。不同高度下HCW下表面压力最大值均出现在前端。沿着流向发展，压力逐渐下降。从图5的无量纲压力云图可以看出，激波S₂之后气体压力进一步上升，流场中压力值达到最大，相应地，作用在HCW下表面的压力也为最大。当气流通过机体最高点之后，流道拓宽，气体膨胀，作用在HCW下表面的压力逐渐下降。随着高度增加，通道内沿流动方向压力梯度逐渐减小，沿HCW下表面压力系数变化变得相对平缓，这表明稀薄效应会降低气体相对膨胀的速度。

一般而言，由于气体密度下降，飞行器表面的剪切力和热流都会下降。但无量纲后的剪切力和热流随Kn增大而明显增大^[15]。如图7（b）和7（c）所示，HCW下表面剪切力和热流峰值出现在激波S₁撞击HCW的位置。同时在HCW的大部分区域，无量纲后的剪切力与热流均随飞行高度增加而增大，可见稀薄气体效应增加了飞行器壁面的相对摩擦与相对传热率。

对本文所考虑的原理性构型，HCW非常薄且平行于自由来流，因而其升力主要来源为下壁面压力，阻力主要来源为下壁面的摩擦。在70～90 km飞行高度范围内，随稀薄程度增加，HCW下表面压力系数的变化幅度相对较小，但摩擦系数迅速增加，HCW引入的摩擦阻力占飞行器总阻力比重迅速上升，成为制约飞行器整体气动性能的重要因素。

3.3 气固作用方式对壁面气动量影响分析

由于HCW设计为平行于来流的薄翼结构，气动摩擦是阻力的主要组成部分，同时，过渡流域气体稀薄，气体分子在壁面的反射方式对流场结构与表面气动力有较大影响。为研究稀薄条件下高压捕获翼构型的气动性能，特别是壁面摩擦与气固作用的相关程度，本节针对HCW的不同壁面反射模型展开研究。

一般认为，气体分子与壁面相互作用可以由Maxwell反射模型表征^[35]，该模型由镜面反射模型与漫反射模型按一定比例组合而成，并将漫反射所占比例定义为Maxwell适应系数 ${\alpha _M}$ 。其中发生镜面反射时，气体分子撞击壁面后，切向速度不发生改变，只有法向速度改变方向，这种状态下分子与壁面不交换切向动量与能量，只有法向动量的交换，宏观上体现为壁面没有黏性。发生完全漫反射时，粒子反射速度与入射速度无关，是壁面温度下的Maxwell平衡态分布，这时气体分子与壁面在切向动量、法向动量与能量各方面均存在剧烈交换，宏观上体现为壁面黏性最大。大量分子束实验与分子动力学模拟结果表明，适应系数受壁面材料种类、粗糙程度、分子入射速度、分子入射角度等因素影响，大部分情况下适应系数分布在0.3～1.0之间^[36-37]。

本节以飞行高度90 km为例，假定机体表面适应系数不变，均为0.8，分析HCW壁面适应系数分别为0.8、0.6、0.4三种情况下表面气动力、气动热以及流场结构的差异。

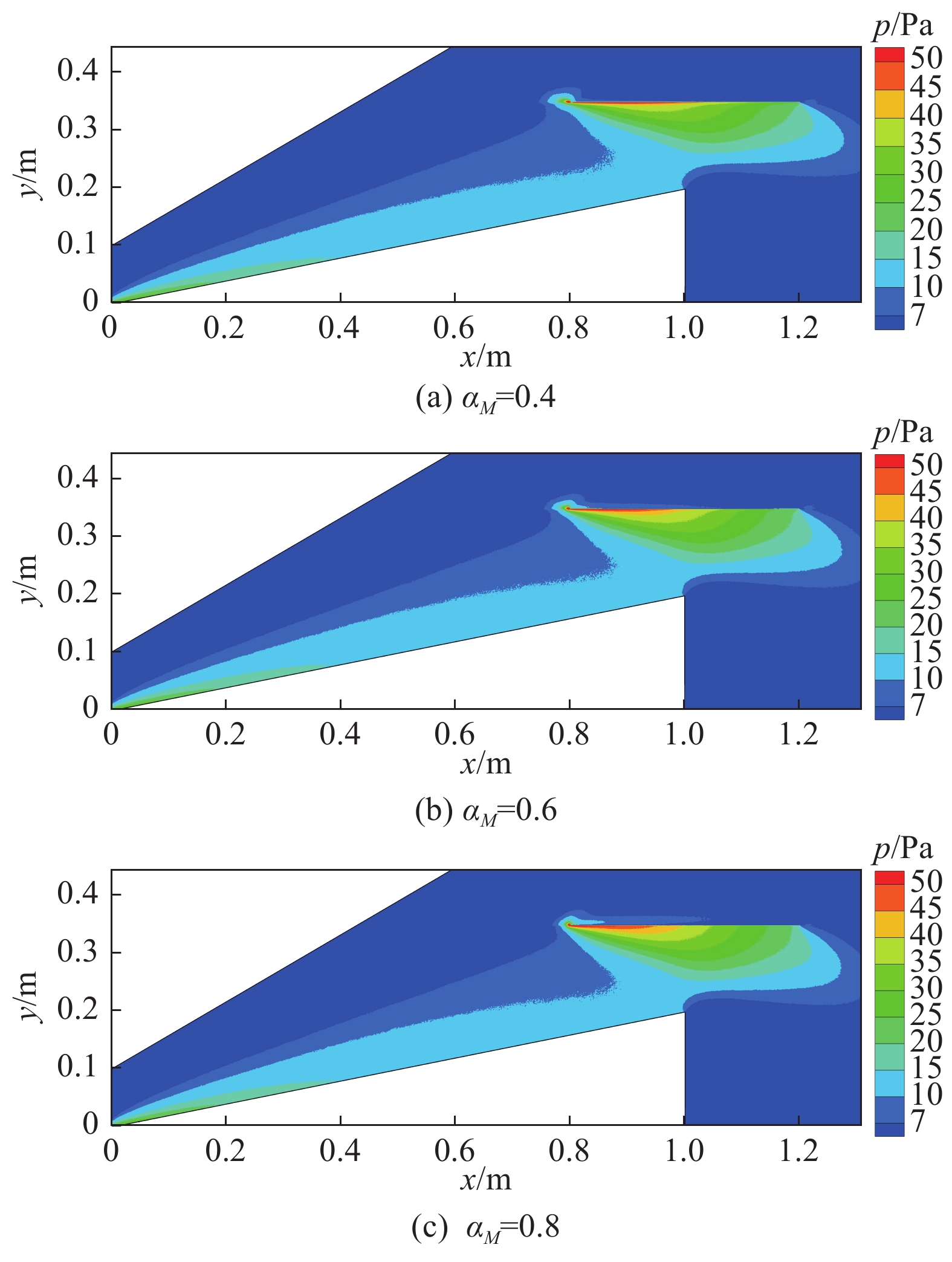
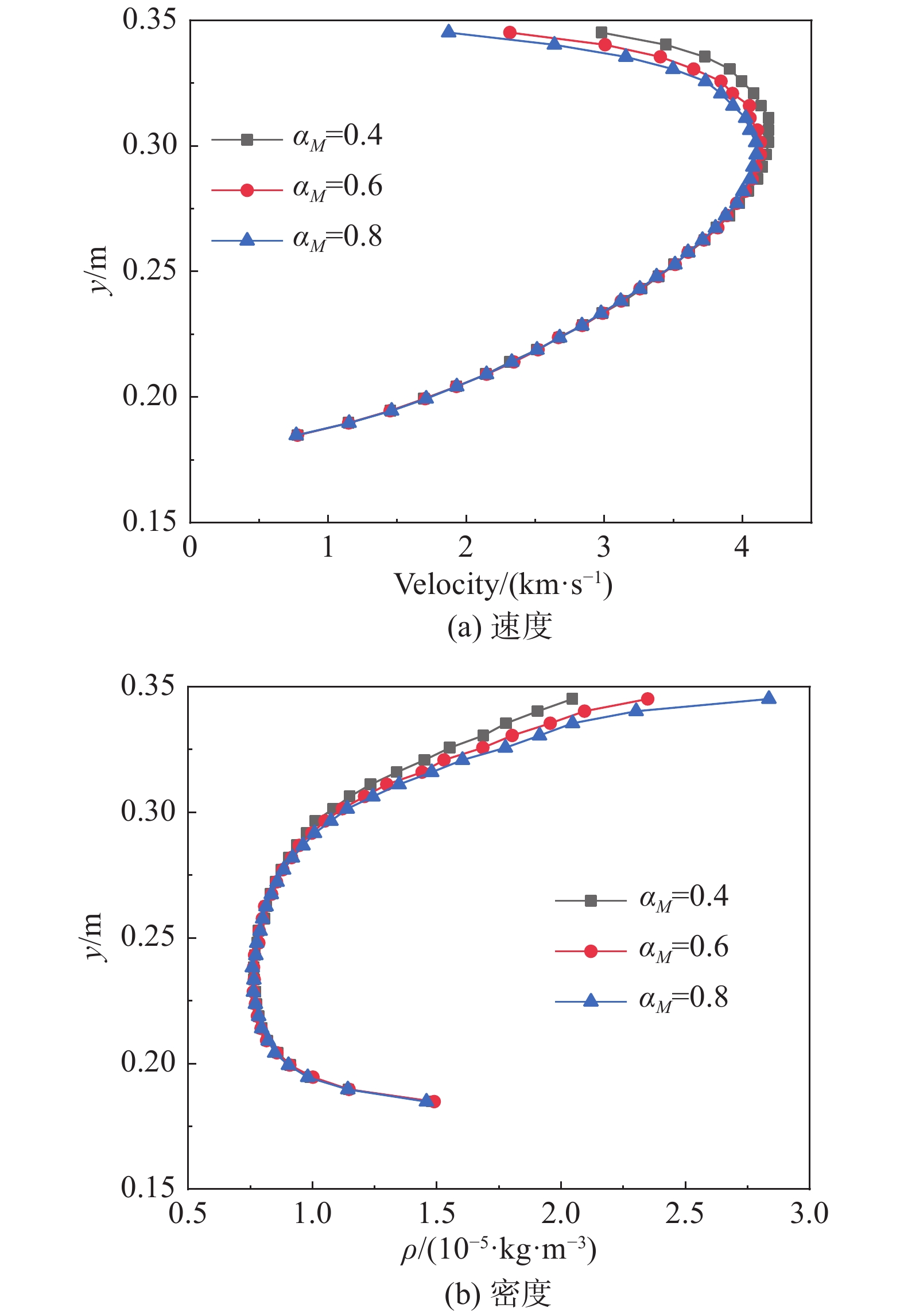
图8给出了上述三种工况下的压力云图。各工况对应结果的差异只存在于HCW附近，对机体几乎没有额外干扰。图9展示了流场中速度和密度沿 $x=0.9\;\mathrm{m}$ 的分布，结果表明，随着适应系数下降，壁面阻碍流动的效果削弱，HCW近壁面气流流速增加，边界层内气体密度下降。

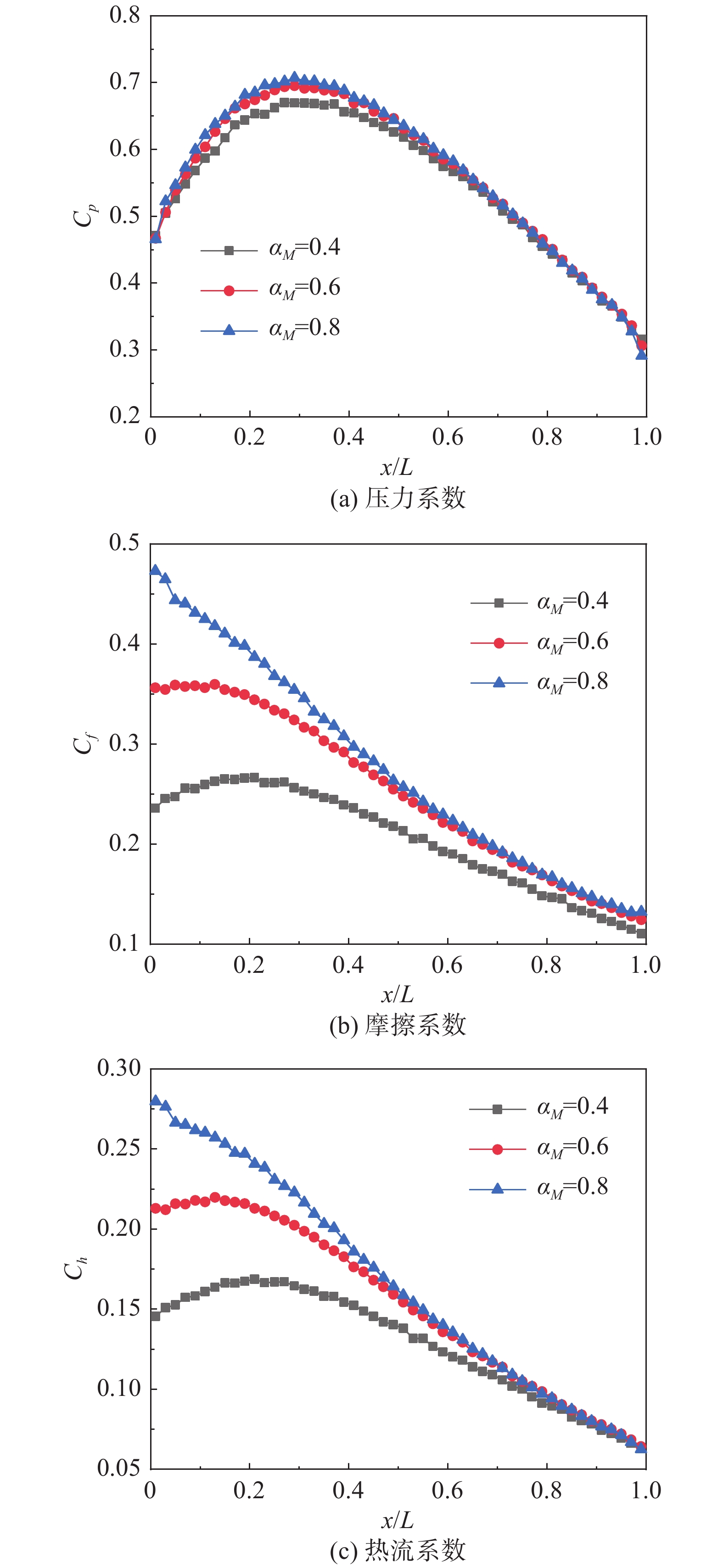
图10给出了不同适应系数对应的HCW下表面气动力、气动热系数分布。随着适应系数下降，HCW下表面的压力、剪切力和热流均呈现下降趋势。其中，压力的下降幅度最小，剪切力和热流下降幅度较大。这是由于Maxwell适应系数对气体法向动量的调节较小，HCW壁面压力值的小幅下降主要是由于边界层内空气流速增加，导致气流“拥堵”程度下降，近壁面密度下降，气体分子与壁面碰撞频率下降。壁面剪切力与热流值大幅下降，是由于Maxwell适应系数与气体与壁面的切向动量适应程度以及能量适应程度相关性大，适应系数下降导致气体分子与壁面的切向动量交换、能量交换被削弱。宏观上表现为HCW头部的剪切力和热流存在较大差别，随着气体向后流动，气流逐渐被减速，HCW下表面剪切力、热流逐渐下降，不同适应系数对应结果的差异也逐渐减小。

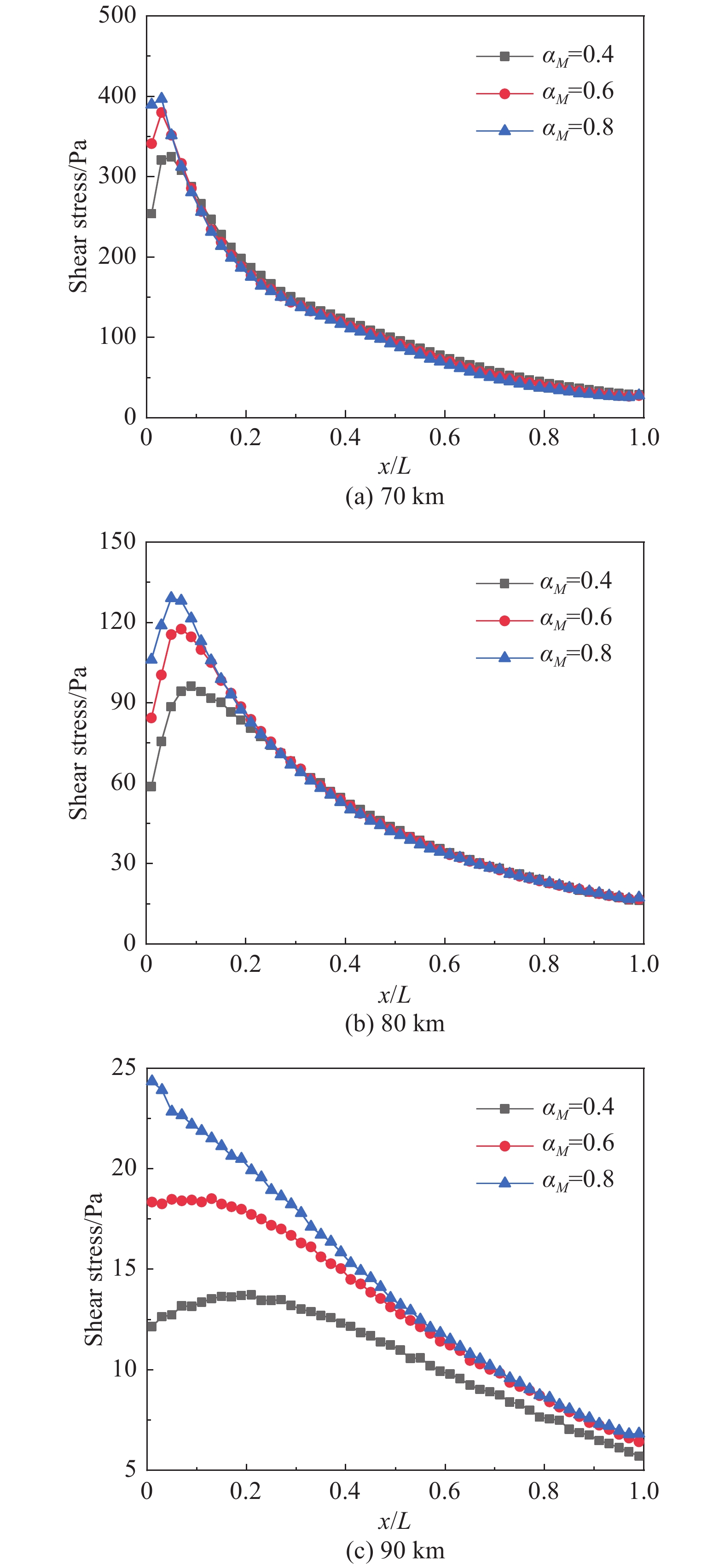
图11给出了70～90 km不同飞行高度下，HCW下表面剪切力分布对比。由图可知，在激波S₁撞击HCW下表面处，高速气流未经边界层减速直接冲击壁面，气体与壁面进行剧烈的动量交换，剪切力出现峰值。沿着流向的发展，气流在HCW近壁面被逐渐减速，气体分子撞击壁面时入射速度下降，在气固相互作用过程中气体损失的切向动量也逐渐下降，气体分子与壁面之间的动量交换减弱，在HCW下表面体现为气动剪切沿流向逐渐下降。

不同适应系数的HCW表面，剪切力的差异仅存在于头部一段区间内，在本节所考虑的适应系数范围内（0.4 ≤ α_M ≤ 0.8），随着壁面适应系数下降，气动摩擦明显下降。但沿着流向发展，这种差异逐渐减小。当飞行高度增加，适应系数对壁面气动力影响的范围增加。例如，在70 km工况下，不同适应系数对壁面剪切的影响只存在头部约10%范围内，之后不同适应系数对应的壁面剪切没有明显差别；在80 km工况下，HCW下表面约前20%范围内剪切力有明显区别；在90 km工况下，整个HCW下表面的剪切力都存在差异。可见，稀薄气体效应增大了壁面适应系数对气动力与气动热的影响范围。

4 结　论

本文基于一种简化的二维楔-板HCW原理性构型，通过模拟其在高度70～100 km范围内的非平衡流动，分析了HCW的流场结构与壁面气动力和气动热数据，获得了这种气动布局在连续-稀薄流域中的基本特性。得到以下基本结论：

1） HCW构型主要原理是利用机身上表面压缩后形成的高压区。随着飞行高度上升，机体诱导的激波结构逐渐模糊，这使得HCW利用高压区增升的效果减弱。同时HCW与机体之间的通道内容易出现相互干扰，因此需要扩大二者之间的间距。掠过机体最高点后，捕获翼下方气体膨胀的速度下降，HCW下表面压力变化变得相对平缓。

2） 稀薄程度增加，HCW表面的气动力、气动热下降，但对应的无量纲后的气动力与气动热呈现出不同的变化趋势。其中压力系数随飞行高度变化幅度相对最小，稀薄效应主要影响HCW下开放通道内气体膨胀速率；摩擦系数和热流系数与稀薄程度有很强的相关性，稀薄效应显著增大了飞行器表面相对摩擦与相对传热率。对实际飞行器而言，这种变化使得摩擦阻力相对于升力增大，HCW引入的阻力将会成为飞行器阻力的重要组成部分。

3） 壁面适应系数对HCW头部的气动力、气动热分布有很大影响，并且随着稀薄程度增加，适应系数的影响的范围逐渐扩大，这表明在稀薄流域飞行器气动力对壁面适应系数更为敏感。对于飞行在稀薄过渡流域的飞行器，壁面适应系数将是影响飞行器气动性能的重要因素。对于实际问题而言，气体分子与壁面的作用过程较为复杂，Maxwell反射模型作为一种较为简单的模型，描述实际问题的能力可能有所欠缺，对于具体实例，特别是极高马赫数下的气固作用方式，仍需开展细致的研究。

本文着眼于探究HCW气动布局的跨流域气动性能，因此主要针对一种二维原理性构型展开分析。从结果来看，该构型在过渡流区可以提高飞行器升力，但相对摩擦过大导致气动效率逐渐下降，这个问题可以通过更换HCW表面材料得到缓解。此外，为尽快探索该构型的跨流域流动特征，现有工作仅分析了特定马赫数下的结果，尚未考虑来流马赫数范围、机体长高比、捕获翼长度选择等因素的影响，这些问题都是我们正在或即将开展的工作。