0 引　言

在自然界和工程实际应用的气固两相流中，固相的颗粒如粉、尘、烟、霾等不仅受到流体相的输运作用，其自身还往往出现由物理或化学作用导致的生长、凝并（颗粒碰撞后形成一个颗粒）、破碎等现象。颗粒一般动力学方程（General dynamic equation, GDE），又称颗粒数平衡方程（Population balance equation, PBE），可用来描述颗粒相数密度在流体输运下出现以上现象后的演变过程^[1]。

在大多数情况下，两相流处于湍流状态，湍流导致的流动无序性与多尺度特性，使得两相湍流变得很复杂，因而更具有研究价值。流场物理量的脉动是湍流场的一个重要特征，对于湍流脉动特性的研究，其科学意义不仅局限于湍流或多相流领域^[2]。本文关注微纳颗粒两相湍流中的湍流脉动效应，在微纳颗粒两相湍流中，颗粒的形成与生长受到环境因素如流场速度、流场剪切率、化学组分浓度、温度、压力等的影响，而这些环境因素会受到湍流脉动的影响变化，所以颗粒的形成和生长速率会受到湍流脉动的影响。于是，若不考虑湍流的脉动而仅仅用平均后的环境因素来计算颗粒的形成和生长就会与实际情形产生偏差。例如，在云层凝结的过程中，湍流导致的温度脉动会使水蒸气饱和度发生变化，从而使得用平均参数给出的云雾颗粒形成率与生长率与实际不符^[3-8]。在实验室条件下，湍流造成的温度脉动、物质组分脉动也不可忽略^[9-11]，否则会使实验测量结果产生偏差^[12-13]。在数值模拟方面，已有一些探讨湍流脉动影响的研究，例如将DNS得到的结果与用平均场求得的结果进行对比^[14-18]，将LES得到的结果与用雷诺平均方法得到的结果进行对比^[19-24]，将用和不用脉动量概率密度函数进行修正的结果进行对比^[25-27]。除了颗粒的形成与生长受湍流脉动的影响外，颗粒的凝并与破碎也受湍流脉动的影响，因为颗粒的布朗凝并、湍流凝并、湍流破碎都与颗粒的浓度有关，而颗粒浓度在湍流场中也存在脉动^{[2, 10, 28-34]}。湍流脉动对颗粒凝并影响的研究虽然较少，但这种影响是存在的^{[25, 35-38]}。

1 颗粒相方程 1.1 颗粒一般动力学方程

颗粒一般动力学方程是描述颗粒数密度函数（Number density function, NDF）的控制方程。假设颗粒尺度小于最小流动尺度且颗粒雷诺数远小于1，颗粒数密度分布 $n\left(\xi ;{{x}},t\right)$ 表示颗粒在不同尺度 $ \xi $ 、时间 $ t $ 与空间 ${{x}}$ 上的数量分布。根据需要， $ \xi $ 可以选取颗粒体积 $ v $ 或颗粒直径 $ {d}_{p} $ ，本文选颗粒体积，简写作 $ n\left(v\right) $ 或 $n$ ，则一般动力学方程为^[1]：

$ \frac{\partial n}{\partial t}+\nabla \cdot n{{u}}-\nabla \cdot {D}_{p}\nabla n={S}_{n}+{S}_{g}+{S}_{c}+{S}_{b} $

(1)

式中 ${{{u}}}$ 为流场速度， $ {D}_{p} $ 为颗粒扩散系数，方程左边依次为非定常项、对流项和扩散项，方程右边表示导致颗粒数密度变化的因素，依次为成核项、凝积生长项（小颗粒沉积在大颗粒上使大颗粒尺度增大）、碰撞凝并项和破碎项。方程（1）是通过对颗粒数密度建立守恒方程而得到，具有合理性，适用于数密度连续且可微的情形。

（1）成核项。成核是指通过结晶或其他化学作用形成初始体积为 $ {v}_{0} $ 的颗粒的过程：

$ {S}_{n}=B\left({Y}\right)\cdot \delta \left(v-{v}_{0}\right) $

(2)

式中 $ B\left({Y}\right) $ 为颗粒生成核函数， $ {Y} $ 为各类环境参数的向量，根据颗粒的性质不同，环境参数向量包含的变量也不一样，例如水蒸气中液滴核的生成核函数中包括温度、压力、表面张力和饱和度等变量，而一些化学变化中则包含各类化学组分的变量。

（2）生长项。颗粒的凝积生长是指其他物质凝结、沉积在颗粒上，使颗粒尺度增长的过程：

$ {S}_{g}=\frac{\partial }{\partial v}\left(G\left({Y},v\right)\cdot n\left(v\right)\right) $

(3)

式中 $ G\left({Y},v\right) $ 为颗粒生长核函数，也具有多种形式。此外，一些颗粒尺度减小的过程如蒸发、升华，也可用生长项描述，只是其值为负数。

（3）凝并项。凝并是指颗粒间相互碰撞聚集导致颗粒整体尺度增大、数密度减少的过程：

$ \begin{split} {S}_{c}=&\frac{1}{2}{\int }_{0}^{v}\beta \left(v-{v}_{1},{v}_{1}\right)n\left(v-{v}_{1}\right)n\left({v}_{1}\right){\rm{d}}{v}_{1}-\\& {\int }_{0}^{\mathrm{\infty }}\beta \left(v,{v}_{1}\right)n\left(v\right)n\left({v}_{1}\right){\rm{d}}{v}_{1} \end{split}$

(4)

式中 $\; \beta \left(v,{v}_{1}\right)$ 为凝并核函数，描述体积为 $ v $ 和 $ {v}_{1} $ 两种颗粒的碰撞概率。

（4）破碎项。破碎是指颗粒因无法支撑团聚状态而导致裂解，使得颗粒整体尺度减小、数密度增加的过程：

$ {S}_{b}={\int }_{0}^{\mathrm{\infty }}a\left({v}_{1}\right)b\left(v|{v}_{1}\right)n\left({v}_{1}\right){\rm{d}}{v}_{1}-a\left(v\right)n\left(v\right) $

(5)

式中 $ a\left(v\right) $ 是破碎核函数，描述体积为 $ v $ 的颗粒的破碎概率， $ b\left(v|{v}_{1}\right) $ 是破碎子函数，描述体积为 $ {v}_{1} $ 的颗粒在发生破碎时其子颗粒体积为 $ v $ 的条件概率。

对方程（1）的求解难点在于对源项的处理，当对每个源项给出相应的表示方式后，便可对方程（1）进行求解。除了极少数情况能得到方程（1）的相似解^[1]，大多数情况需要采用数值方法求解。在数值求解方法中，分区法和节点法是在将颗粒尺度离散化的基础上得到离散的尺度分布，然后通过计算大量离散尺度下的颗粒数密度得到收敛的数密度分布^[39-40]。矩方法则是将颗粒数密度分布对颗粒尺度 $ {\xi }^{k} $ 进行积分，经过近似假设和数学处理得到 $ k $ 阶矩方程后进行求解，该方法大大简化了求解的方程，且不同阶的矩具有特定的物理意义，因而被大量使用^[41-46]。此外，还有运用统计学方法，将颗粒的尺度分布处理成联合PDF方程进行求解^{[25-27, 47-50]}，也有对颗粒的虚拟拉格朗日粒子进行蒙特卡洛模拟的方法^[51-55]。前者的优点是能利用比较成熟的微积分方程数值求解方法进行求解，缺点是联合概率密度函数的确定具有一定的复杂性。后者的优点是不必进行离散化处理，缺点是往往需要较大的计算量。

1.2 湍流场的颗粒一般动力学方程

采用雷诺平均方法，将流场速度和颗粒数密度表示成平均量和脉动量之和：

${{u}}={{{\bar u}}}+{{{u}}}' ,\;\;n=\bar{n}+{n}'$

将其代入方程(1)后进行平均得：

$ \begin{split}& \frac{\partial \bar{n}}{\partial t}+\nabla \left({{{\bar u}}}\cdot \bar{n}\right)+\nabla \left( \overline{{{{u}}}'\cdot {n}'}\right)-{D}_{p}{\nabla }^{2}\bar{n}=\\&\qquad {\bar{S}}_{n}+{\bar{S}}_{g}+{\bar{S}}_{c}+{\bar{S}}_{b} \end{split} $

(6)

左边第三项为脉动对流项，通常采用梯度扩散假说进行封闭，引入湍流扩散系数 $ {D}_{t} $ ，使

$ \overline{{{{u}}}'\cdot {n}'}=-{D}_{t}\nabla \bar{n} $

(7)

将其与左边第四项合并得：

$ \frac{\partial \bar{n}}{\partial t}+\nabla \left({{{\bar u}}}\cdot \bar{n}\right)-\left({D}_{p}+{D}_{t}\right){\nabla }^{2}\bar{n}={\bar{S}}_{n}+{\bar{S}}_{g}+{\bar{S}}_{c}+{\bar{S}}_{b} $

(8)

则方程左边完全封闭，接下来处理右边。

(1) 成核项。经平均后的成核项为：

$ {\bar{S}}_{n}=\bar{B}\left({Y}\right)\cdot \delta \left(v-{v}_{0}\right) $

(9)

$ \bar{B}\left({Y}\right) $ 为平均成核率。有些研究采取简化方案，通过平均环境参数 $ {{\bar Y}} $ 求出表观成核率 $ B({{\bar Y}}) $ 来代替 $ \bar{B}\left({Y}\right) $ ，但通常 $ B({{\bar Y}})\ne \bar{B}\left({Y}\right) $ 。

(2)生长项。生长项的雷诺平均有几种情况：

①最简单的情况是生长核函数与环境参数无关，用 $ G\left(v\right) $ 表示，则生长项的雷诺平均为：

$ {\bar{S}}_{g}=\bar{n}\left(v\right)\frac{\partial G\left(v\right)}{\partial v}+G\left(v\right)\frac{\partial \bar{n}\left(v\right)}{\partial v} $

(10)

该情况的生长项无需封闭，当温度、化学组分等环境参数对颗粒生长的影响很小时，可直接使用。

②若生长核函数与环境参数相关，但与颗粒尺度无关，核函数会受到环境参数脉动的影响，则生长核函数可写成 $ G({Y}) $ 的形式，对 $G({{\bar Y}}+{{Y}}')\cdot [\bar{n}(v)+{n}'(v)]$ 求平均后，通常生长核函数为环境变量的非线性函数，即 $ G({{\bar Y}}+{{Y}}')\ne G({{\bar Y}})+G({{Y}}') $ ，因此有

$ {\bar{S}}_{g}=\bar{G}\left({Y}\right)\frac{\partial \bar{n}\left(v\right)}{\partial v}+\overline{G\left({{\bar Y}}+{{Y}}'\right)\frac{\partial {n}'\left(v\right)}{\partial v}} $

(11)

式中的实际平均生长率 $ \bar{G}({Y}) $ 与表观生长率不同，即 $ G({{\bar Y}})\ne \bar{G}({Y}) $ ，需要模化。当颗粒尺度的演变局限在某一范围内且生长核函数可近似视为与颗粒尺度无关时，可用上式。

③若生长核函数与环境参数以及颗粒尺度 $ v $ 相关，则：

$\begin{split} {\bar{S}}_{g}=& \bar{G}\left({Y},v\right)\frac{\partial \bar{n}\left(v\right)}{\partial v}+\overline{G\left({Y},v\right)\frac{\partial {n}'\left(v\right)}{\partial v}}+\\& \bar{n}\left(v\right)\frac{\partial \bar{G}\left({Y},v\right)}{\partial v}+\overline{{n}'\left(v\right)\frac{\partial G\left({Y},v\right)}{\partial v}} \end{split}$

(12)

式中的 $ \bar{G}\left({Y},v\right) $ 和 $ \overline{G\left({Y},v\right){n}'\left(v\right)} $ 需要模化。

(3) 凝并项。该项的雷诺平均也分有几种情况：

①凝并核函数 $\; \beta \left(v,{v}_{1}\right) $ 与环境参数无关或对环境参数变化不敏感，则：

$ \begin{split} {\bar{S}}_{c}=&\frac{1}{2}{\int }_{0}^{v}\beta \left(v-{v}_{1},{v}_{1}\right)\bar{n}\left(v-{v}_{1}\right)\bar{n}\left({v}_{1}\right){\rm{d}}{v}_{1}-\\& {\int }_{0}^{\mathrm{\infty }}\beta \left(v,{v}_{1}\right)\bar{n}\left(v\right)\bar{n}\left({v}_{1}\right){\rm{d}}{v}_{1}+\\& \frac{1}{2}{\int }_{0}^{v}\beta \left(v-{v}_{1},{v}_{1}\right)\overline{{n}'\left(v-{v}_{1}\right){n}'\left({v}_{1}\right)}{\rm{d}}{v}_{1}-\\& {\int }_{0}^{\mathrm{\infty }}\beta \left(v,{v}_{1}\right)\overline{{n}'\left(v\right){n}'\left({v}_{1}\right)}{\rm{d}}{v}_{1} \end{split}$

(13)

方程中的脉动凝并项 $ \overline{{n}'\left(v\right){n}'\left({v}_{1}\right)} $ 需要模化。

②凝并核函数 $ \; \beta \left(v,{v}_{1}\right) $ 与环境参数有关，则环境参数的脉动对 $ \; \beta \left(v,{v}_{1}\right) $ 有影响， $ \overline{\beta \left(v,{v}_{1}\right)n\left(v\right)n\left({v}_{1}\right)} $ 需要模化，此时要根据具体情况对

$ \begin{split} {\bar{S}}_{{c}}=&\frac{1}{2}{\int }_{0}^{v}\overline{\beta \left(v-{v}_{1},{v}_{1}\right)n\left(v-{v}_{1}\right)n\left({v}_{1}\right)}{\rm{d}}{v}_{1}-\\& {\int }_{0}^{\mathrm{\infty }}\overline{\beta \left(v,{v}_{1}\right)n\left(v\right)n\left({v}_{1}\right)}{\rm{d}}{v}_{1} \end{split} $

(14)

进行展开，例如湍流凝并核函数为^[56]:

$ \beta \left(v,{v}_{1}\right)=\alpha \varGamma _{\eta }\left({v}^\frac{1}{3}+{v}_{1}^\frac{1}{3}\right) $

(15)

式中 $ \alpha $ 为常数，剪切率 $\varGamma _{\eta }$ 与湍流耗散率 $ \varepsilon $ 和流体黏度 $ \nu $ 相关，在Kolmogorov尺度上 $\varGamma _{\eta }={\left(\varepsilon /\nu \right)}^{1/2}$ 。

(4) 破碎项。

①当破碎核函数不含任何湍流脉动量时，平均后的破碎项为：

$ {\bar{S}}_{{b}}={\int }_{0}^{\mathrm{\infty }}a\left({v}_{1}\right)b\left(v|{v}_{1}\right)\bar{n}\left({v}_{1}\right){\rm{d}}{v}_{1}-a\left(v\right)\bar{n}\left(v\right) $

(16)

②当破碎核函数含湍流脉变量时，平均后的破碎项为：

$ {\bar{S}}_{{b}}={\int }_{0}^{\mathrm{\infty }}b\left(v|{v}_{1}\right)\overline{a\left({v}_{1}\right)n\left({v}_{1}\right)}{\rm{d}}{v}_{1}-\overline{a\left(v\right)n\left(v\right)} $

(17)

如湍流破碎核为：

$ a\left(v\right)={k}_{b}{\left(\frac{\mu \varGamma _{\eta }}{\varGamma ^{\mathrm{*}}}\right)}^{q}{v}^\frac{1}{3} $

(18)

式中： $ {k}_{b} $ 为玻尔兹曼常数； $\; \mu $ 为流体动力黏度； $\varGamma ^{*}$ 是特征切应力；指数 $ q $ 为正实数，由实验确定。

湍流脉动引起颗粒的成核、生长、凝并与破碎项使方程(1)变得不封闭，目前尚无对这些项模化的公认模型，大部分数值模拟中只能直接忽略这些项，而已有研究表明，有些情况下这些项并不可忽略，例如湍流微尺度与颗粒尺度相当的情形^[1]。

2 湍流脉动导致的颗粒成核与生长

随着对湍流研究的不断深入，湍流场中脉动压力、脉动温度对颗粒成核与生长的影响逐渐引起人们的关注。最早开始研究湍流脉动对颗粒生成与生长影响的是Levin和Sedunov^[57]，他们认为湍流场中压力的脉动影响饱和度的稳定，从而改变雨滴的生长率，使雨滴的尺度分布变宽。然而，他们没有给出颗粒浓度和粒径分布的最终信息。随着对概率密度函数(PDF)方程求解技术的提高，有关湍流脉动对颗粒生成与生长影响的研究有了比较有效的手段。Lesniewski和Friedlander^[12]计算了圆湍射流场蒸汽冷凝过程中颗粒成核的速率，并对比了用温度PDF和平均温度场计算得出的结果。经典理论表明，在过饱和点的位置附近，颗粒成核速率会急剧增加，而在该位置之外成核速率几乎为零。采用温度PDF研究的结果表明，所有情况下都存在蒸汽冷凝成核，只是最大成核速率没有经典理论给出的那么大。在考虑温度脉动的情况下，得到的颗粒浓度分布较均匀且更宽。后来，Lesniewski和他的同事^{[13, 58]}继续用二丁基邻苯二甲酸与氮气在圆湍射流中进行颗粒成核实验，以说明脉动温度与脉动组分浓度对成核的影响，结果表明湍流导致的脉动对颗粒生成与生长的影响不可忽略，这一结果引起了人们的重视，后续的数值模拟研究^{[15-17, 19-22, 26-27, 37]}中都采用了与该实验相同的条件。

2.1 颗粒成核率、生长率的数值模拟结果

采用不同的数值模拟方法，得到的颗粒成核率、生长率的结果也不同。以下采取统一的表达方式来描述瞬时、表观和各类平均的数值结果。以经典的蒸汽凝结均质成核速率表达式为例：

$ B=\frac{{P}_{v}{N}_{v}{v}_{m}}{kT}{\left(\frac{2\sigma }{{\text{π}} m}\right)}^ \frac{1}{2}\mathrm{exp}\left[-\frac{16{\text{π}} {\sigma }^{3}{m}^{2}}{3{\left(kT\right)}^{3}{\rho }_{p}^{2}{\left(\mathrm{ln}S\right)}^{2}}\right] $

(19)

式中 $ {P}_{v} $ 、 $ {N}_{v} $ 表示蒸汽压力和浓度， $ {v}_{m} $ 为摩尔体积， $ m $ 为分子质量， $ k $ 为玻尔兹曼常数， $ T $ 为绝对温度， $ S $ 为饱和度， $ \sigma $ 表示液滴的表面张力。将各种环境参数表示为向量 $ {Y} $ ，则 $ {Y} $ 在湍流场中存在脉动。如果将用DNS得到的瞬时环境参数代入，得到的是瞬时成核速率 $ B\left({Y}\right) $ 。将DNS给出的实时成核速率进行时间平均或系综平均，可得到真实平均值 $ \bar{B}\left({Y}\right) $ 。若将各类环境参数的平均值代入，得到的是表观值 $B({{\bar Y}})$ 。

要考虑环境参数脉动对成核的影响，一种方法是引入脉动环境参数已知的PDF，然后计算PDF的平均值。例如，考虑温度和蒸汽浓度的脉动时，PDF平均成核速率为^{[13, 19]}：

$\begin{split} & B\left(\mathrm{p}\mathrm{d}\mathrm{f}\left\langle T,{N}_{v}\right\rangle \right)=\\ &\qquad \int_0^1 {\int_0^1 I } \left({\theta }_{N},{\theta }_{T},{N}_{0},{N}_{\mathrm{\infty }},{T}_{0},{T}_{\mathrm{\infty }}\right)P\left({\theta }_{N},{\theta }_{T}\right){\rm{d}}{\theta }_{N}{\rm{d}}{\theta }_{T} \end{split} $

(20)

式中 ${\rm{pdf} \left\langle \; \right\rangle}$ 是温度 $T $ 和蒸汽浓度 $N_v $ 的概率平均值，由其概率分布函数PDF得出。

Fager等^[20]将用LES得到的环境参数代入成核速率式，得到空间滤波的成核速率，还以前面的成核率为例：

$ B\left(\left\langle {Y}\right\rangle \right)=\frac{\left\langle {P}_{v}\right\rangle \left\langle {N}_{v}\right\rangle {v}_{m}}{k\left\langle T\right\rangle }{\left(\frac{2\sigma }{{\text{π}} m}\right)}^\frac{1}{2}\mathrm{exp}\left[-\frac{16{\text{π}} {\sigma }^{3}{m}^{2}}{3{\left(k\left\langle T\right\rangle \right)}^{3}{\rho }_{p}^{2}{\left(\mathrm{ln}\left\langle S\right\rangle \right)}^{2}}\right] $

(21)

对生长核函数 $ G\left({Y},v\right) $ 而言，可以用上述的方法定义表观值 $ G({{\bar Y}},v) $ 、PDF平均值 $ G\left(\mathrm{p}\mathrm{d}\mathrm{f}\left\langle {Y}\right\rangle ,v\right) $ 、空间滤波值 $ G\left(\left\langle {Y}\right\rangle ,v\right) $ 和真实平均值 $ \bar{G}\left({Y},v\right) $ 。

Veroli和Rigopoulos^[27]采用蒙特卡洛方法计算了二丁基邻苯二甲酸蒸汽在圆湍射流中的凝结成核，并对用平均温度场和温度场PDF得到的表观饱和度 $ S(\bar{T}) $ 和PDF平均饱和度 $ S(\mathrm{p}\mathrm{d}\mathrm{f}\langle T\rangle ) $ 进行了比较，发现在射流出口附近， $ S(\bar{T}) $ 的值更高，分布更加集中，而 $ S(\mathrm{p}\mathrm{d}\mathrm{f}\langle T\rangle ) $ 的值较低，分布较为分散，这一结果与Lesniewski和Friedlander的实验结果^[13]相符。

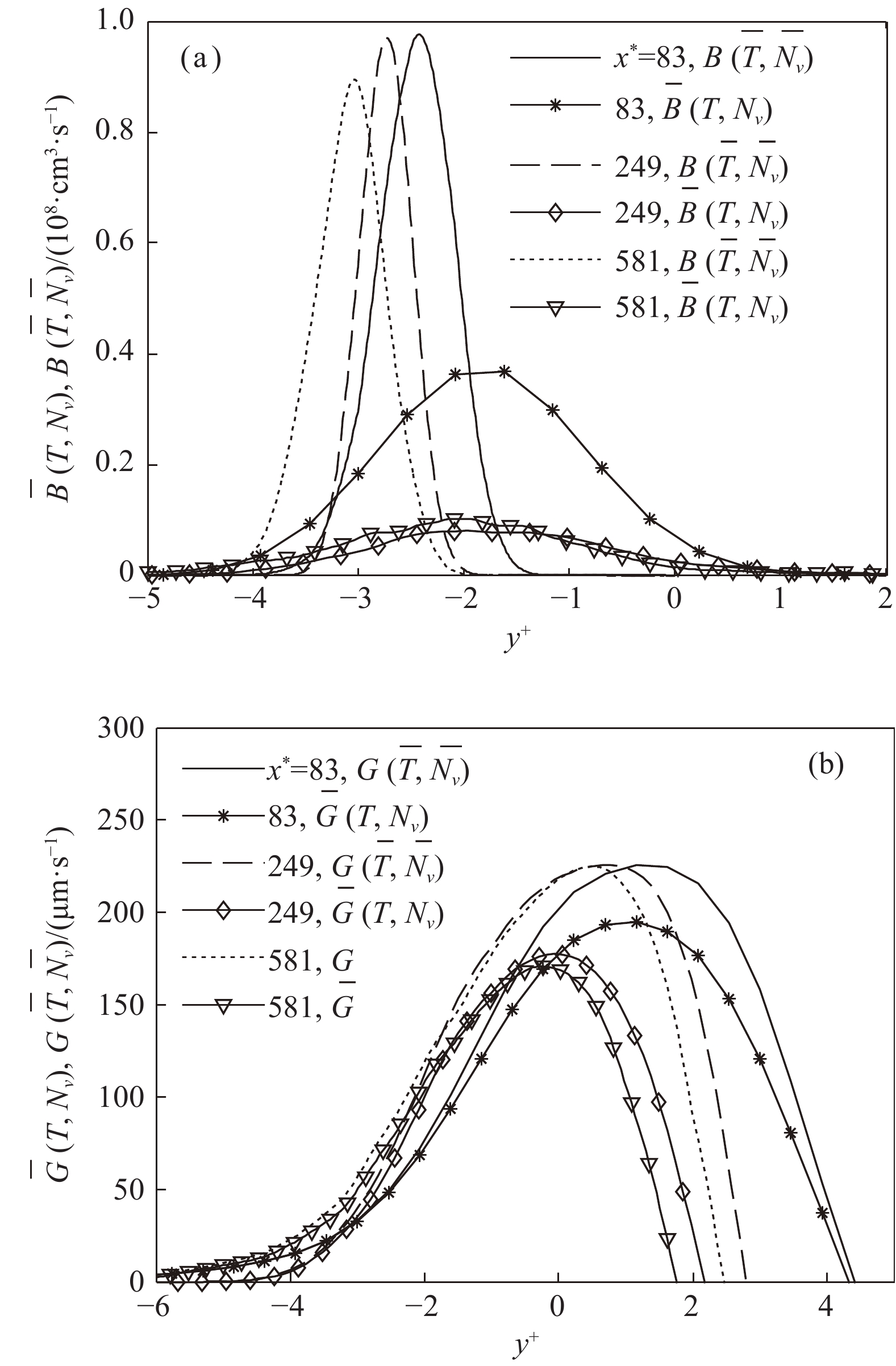
Zhou等^[17]用DNS方法模拟流场、积分矩方法(Quadrature Method of Moment, QMOM)求解颗粒相的源项，计算了二丁基邻苯二甲酸蒸汽在混合剪切层中的冷凝成核与凝积生长，并将成核速率和生长速率的真实平均值 $ \bar{B}(T,{N}_{v}) $ 、 $ \bar{G}(T,{N}_{v}) $ 与表观平均值 $ B(\bar{T},{\bar{N}}_{v}) $ 、 $ G(\bar{T},{\bar{N}}_{v}) $ 进行了比较，结果如图1所示。可见在考虑湍流脉动的情况下，成核速率在空间的分布更分散，最大值更小，而生长速率在空间的分布趋势没有明显变化，只是总体数值降低。

Pesmazoglou等^[22]用LES数值模拟了圆湍射流中二丁基邻苯二甲酸蒸汽的凝结成核，并将由LES和RANS方法得到的空间滤波成核速率 $ B(\langle {Y}\rangle ) $ 和表观成核速率 $ B({{\bar Y}}) $ 进行了比较，得到了类似图1（a）的结果，说明用两种方法得到的结果存在差异。

2.2 湍流脉动对颗粒成核率、生长率的影响程度

在对受湍流脉动影响的颗粒成核项和生长项进行模化时，首先需确定湍流脉动在特定条件下对这两项的影响程度。例如，在蒸汽凝结成核过程中，颗粒成核率对温度的变化很敏感，Garrick等对二丁基邻苯二甲酸蒸汽的凝结成核进行了数值模拟^{[15-16, 20-21]}，发现湍流场中的颗粒成核率主要受温度、饱和度、组分浓度这三者脉动的影响。

用 $ {{\left(*\right)}_{L}}^{F} $ 表示变量 $ * $ 经大尺度滤波后的结果，Murfield和Garrick^[15]研究了二丁基邻苯二甲酸蒸汽在平面湍射流中的凝结成核过程，在考虑温度和组分浓度脉动情况下，分别用DNS和LES计算了湍流场，给出了滤波饱和度 $ {S}_{L}^{F} $ 与瞬时饱和度 $ S $ 之间的关系（图2（a））以及滤波成核率 $ {B}_{L}^{F} $ 与瞬时成核率 $ B $ 之间的关系（图2（b））。如果亚格子尺度的温度脉动和组分浓度脉动对成核率没有影响，那么 ${B}^{{\rm{SGS}}}\equiv B-{B}_{L}^{F}$ 应该等于零，其散点图应该成为一条对角的直线。由图可见，温度脉动和组分脉动对成核率均有影响，其中成核率的亚格子脉动范围很大，其幅值高达 $1 \times {10}^{15}$ ～ $ 1 \times {10}^{16} $ m³/s，数量级上接近瞬时成核率，成核率的亚格子尺度负脉动比正脉动的幅度要大。

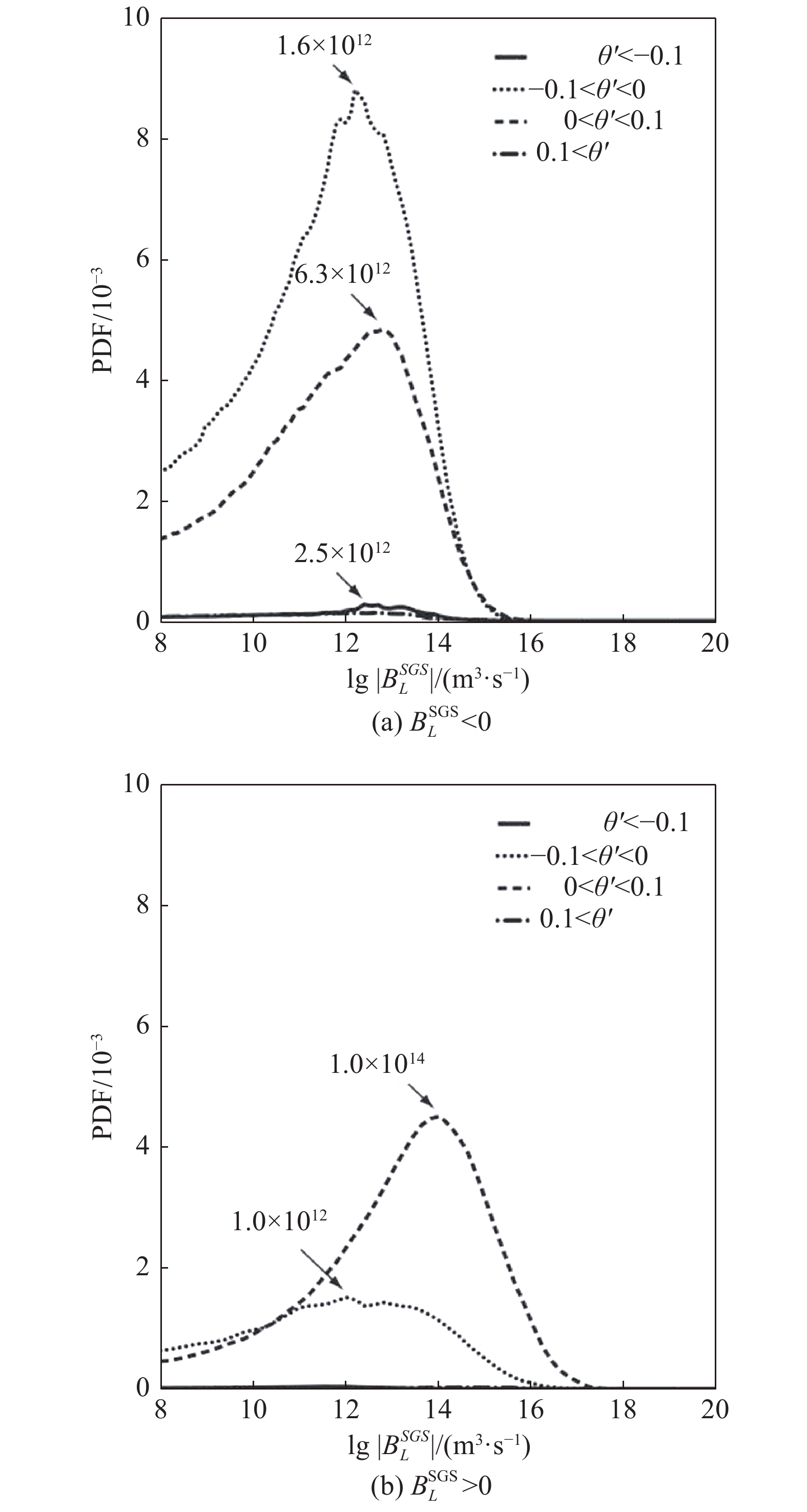
进一步对数据进行处理和研究，可以得到不同温度脉动情况下的成核率亚格子尺度脉动，结果如图3所示。对比图3（a）和图3（b）可知，成核率的负脉动比正脉动的幅值大，温度的负脉动和正脉动对成核率的负脉动和正脉动的影响最大，成核率约为 $1 \times{10}^{12}$ m³/s时对温度脉动最敏感。

3 湍流脉动导致的颗粒凝并与破碎

在颗粒凝并项方程(13)中，包含了 $ \overline{{n}'\left(v\right){n}'\left({v}_{1}\right)} $ ，该项是颗粒脉动数密度的二阶关联，是个未知项，需要模化^[59-60]。由方程(13)可知，由湍流脉动引起的颗粒凝并与颗粒的数密度脉动有关。Becker等^{[28, 61-62]}由实验证明了颗粒浓度在湍流场中确实存在脉动，并测量给出了颗粒浓度脉动均方根、脉动强度、脉动谱在圆管湍射流场中的分布。文献[63]对相关的实验研究进行了总结，在此不赘述。

$ \overline{{n}'\left(v\right){n}'\left({v}_{1}\right)} $ 与雷诺应力的表达式有相似之处，只是后者为脉动速度，于是人们寻找 $ \overline{{n}'\left(v\right){n}'\left({v}_{1}\right)} $ 与湍动能和湍流耗散的关系。Spalding^[29]曾提出关于颗粒浓度脉动的预测方程，该方程将颗粒浓度脉动的均根方值与湍动能的生成与耗散相联系，最终经过修正得到 k-ε-g方程^[64]。

随着空间滤波方法的出现以及LES方法的发展，人们提出了颗粒数密度脉动的空间自关联形式 $\left\langle {n}'\left({{x}}\right){n}'\left({{x}}+{{r}}\right)\right\rangle$ ，引入颗粒径向分布函数 $g\left({{r}}\right)$ 将脉动项与平均项联系起来，并对 $g\left({{r}}\right)$ 的性质进行了研究^{[30-31, 65-67]}。Eaton和Fessler^[32]认为在小的时间尺度内，湍流涡的离心作用将颗粒甩到流场的高应变区域，形成了颗粒数密度聚集区，该区的范围与颗粒Stokes数有关。Stokes数定义为颗粒松弛时间和流体特征时间之比：

$ St\equiv \dfrac{{\tau }_{p}}{{\tau }_{\eta }}=\dfrac{\dfrac{1}{18}\left(\dfrac{{\rho }_{p}}{{\rho }_{f}}\right)\dfrac{{d}_{p}^{2}}{\nu }}{{\left( \dfrac{\nu}{\varepsilon} \right)}^ \frac{1}{2}}=\dfrac{1}{18}\left(\dfrac{{\rho }_{p}}{{\rho }_{f}}\right){\left(\dfrac{{d}_{p}}{\eta }\right)}^{2} $

(22)

式中 $ {\tau }_{p} $ 和 $ {\tau }_{\eta } $ 分别为颗粒松弛时间和流体特征时间， $ {\tau }_{\eta }={\left(\nu /\varepsilon \right)}^{1/2} $ 为Kolmogorov时间尺度， $\eta ={({\nu }^{3}/\varepsilon )}^{1/4}$ 为Kolmogorov空间尺度， $ {\rho }_{p} $ 和 $ {\rho }_{f} $ 分别为颗粒密度和流体密度。

3.1 颗粒聚集效应与凝并核函数的修正

为了体现湍流脉动对颗粒凝并的影响，一种思路是对颗粒凝并率进行湍流脉动的修正，即给出湍流凝并核函数 $ \beta $ 。基于这种思路，可以将颗粒径向分布函数 $g\left({{r}}\right)$ 引入作为增强系数^[67-73]，从而得到聚集效应下的凝并核函数。Reade和Collins^[69]在DNS方法中引入体现颗粒数密度脉动对颗粒凝并影响的增强因子，并用函数 $ {G}_{11} $ 和 $ {G}_{12} $ 来分别描述单分散和双分散颗粒的情形。Zhou等^[71]则从欧拉方法和统计方法出发提出增强因子：

$ {G}_{11}\left(R\right)\approx \frac{\overline{{N}^{2}}}{{\overline{N}}^{2}},\; \;{G}_{12}\left(R\right)\approx \frac{\overline{{N}_{1}{N}_{2}}}{\overline{{N}_{1}}\cdot \overline{{N}_{2}}}$

(23)

式中 $ {N}_{1} $ 和 $ {N}_{2} $ 分别代表半径为 $ {a}_{1} $ 和 $ {a}_{2} $ 颗粒的数密度。通过DNS可计算出增强因子，从而得到适用于高颗粒数密度条件下的修正凝并核函数。

Sundaram^[67]提出颗粒聚集时单分散颗粒的凝并核函数：

$ \beta =4{\text{π}} {{d}_{p}}^{2}g\left({d}_{p}\right){\int }_{-\mathrm{\infty }}^{0}-{w}_{r}P\left({w}_{r}|{d}_{p}\right){\rm{d}}{w}_{r} $

(24)

式中 $ {w}_{r} $ 为两个颗粒的径向相对速度， $ P\left({w}_{r}|r\right) $ 为两个颗粒在距离为 $ r $ 时其径向相对速度为 $ {w}_{r} $ 的条件概率。

基于上述凝并核函数的形式，Reade和Collins^[69]得到颗粒径向分布函数为 $g(r)=g(\hat{r}=r/\eta > 1,{\hat{d}}_{p}= {d}_{p}/\eta , $ $ St)$ ，该函数与粒径、Stokes数相关，当 $ St\to 0 $ 或 $ St\to \infty $ 时，增强因子趋近于1，意味着湍流脉动导致的颗粒聚集效应不存在，只有在Stokes数达到1的量级时，增强因子达到最大。

Wang等^[70]进一步得到新的凝并核函数 $ \; \beta = $ $ 2{\text{π}} {d}_{p}^{2}g\;({d}_{p})\;\langle \;|{w}_{r}|\;\rangle $ 。这里的 $ {w}_{r} $ 假设为高斯分布，并给出径向分布函数 $ g\;(r)\;=g\;(r,R{e}_{\lambda },St)\; $ ，这里的 $ g(r) $ 不仅包含Stokes数，还包含了以泰勒微尺度为特征尺度的雷诺数 $ R{e}_{\lambda }\equiv {{U}'}^{2}\sqrt{15\;/\;(\nu \varepsilon )} $ （ $ {U}' $ 为湍流强度）。当 $ St=1 $ 时，增强因子最大，当 $ St\to 0 $ 或 $ St\to \infty $ 时，增强因子趋近于1。此外，雷诺数 $ R{e}_{\lambda } $ 越大，增强因子越大。

Zhou等^[71]得到双分散颗粒情况下任意两种尺度颗粒的凝并核函数：

$ {\beta }_{ij}=2{\text{π}} {\left({r}_{i}+{r}_{j}\right)}^{2}{g}_{ij}\left({r}_{i}+{r}_{j}\right)\left\langle \left|{w}_{r}\right|\right\rangle $

(25)

双分散颗粒的径向分布函数 ${g}_{12}({r}_{1}+{r}_{2})=1+ $ $ \;{\rho }_{12}^{n} {[{g}_{11}(r)-1]}^{1/2}{[{g}_{22}(r)-1]}^{1/2}$ ， $ \;{\rho }_{12}^{n} $ 是两种颗粒速度的相关系数，受 $ \mathrm{max}({\tau }_{p1}/{\tau }_{p2},{\tau }_{p2}/{\tau }_{p1}) $ 制约，而单分散颗粒的径向分布函数依然满足 $ {g}_{ii}(r)={g}_{ii}(r,R{e}_{\lambda },S{t}_{i}\equiv {\tau }_{pi}/{\tau }_{\eta }) $ ，其中包含雷诺数 $ R{e}_{\lambda } $ 和两种颗粒的Stokes数。

Saffman和Turner^[56]提出适用于剪切条件下的湍流凝并核，Chun等^[74]基于该凝并核，得到在 $ St\to 0 $ 情况下具有颗粒聚集效应的湍流凝并核：

$ {\beta }_{ij}=\gamma \alpha \varGamma _{\eta }{\left({d}_{i}+{d}_{j}\right)}^{3}{c}_{0}{\left(\frac{\eta }{{d}_{i}+{d}_{j}}\right)}^{{c}_{1}} $

(26)

式中 $ {c}_{1}\propto S{t}^{2} $ ， $ \gamma \approx 1 $ ，在 $ St\to 0 $ 且 $ \eta /{d}_{ij}\ll 1 $ 的情况下，颗粒聚集的增强效应接近于 $ {c}_{0} $ （一个待定的匹配系数）。

上述研究都是基于颗粒的拉格朗日描述用DNS来求解流场，这在惯性颗粒系统中有效^[75-76]，但对零惯性颗粒（忽略颗粒质量）而言则无效。从物理机制看，零惯性颗粒有良好的跟随性，颗粒与流体的速度几乎一致，湍流场的涡运动无法因离心效应而导致颗粒的聚集。因此，需要采用其他方法描述零惯性颗粒的浓度脉动。

3.2 湍流脉动对凝并生长效应的影响

颗粒的生长除了凝积外，还可以通过凝并。凝并使颗粒粒径增大、浓度减少。定义粒径增长率为：

$ \varOmega =\frac{\partial \left({d}_{g}\right)}{\partial t},\;\;\varOmega ={\left(\frac{2}{9{\text{π}} }\right)}^\frac{1}{3}{v}_{g}^{-\frac{2}{3}}\frac{\partial {v}_{g}}{\partial t} $

(27)

式中 $ {d}_{g} $ 和 $ {v}_{g} $ 是颗粒的几何平均直径和几何平均体积。粒径增长率可用来综合衡量颗粒成核、凝积生长和凝并导致颗粒粒径增长的效果，在单独考虑凝并作用时，也可以衡量凝并对颗粒粒径的增长作用。

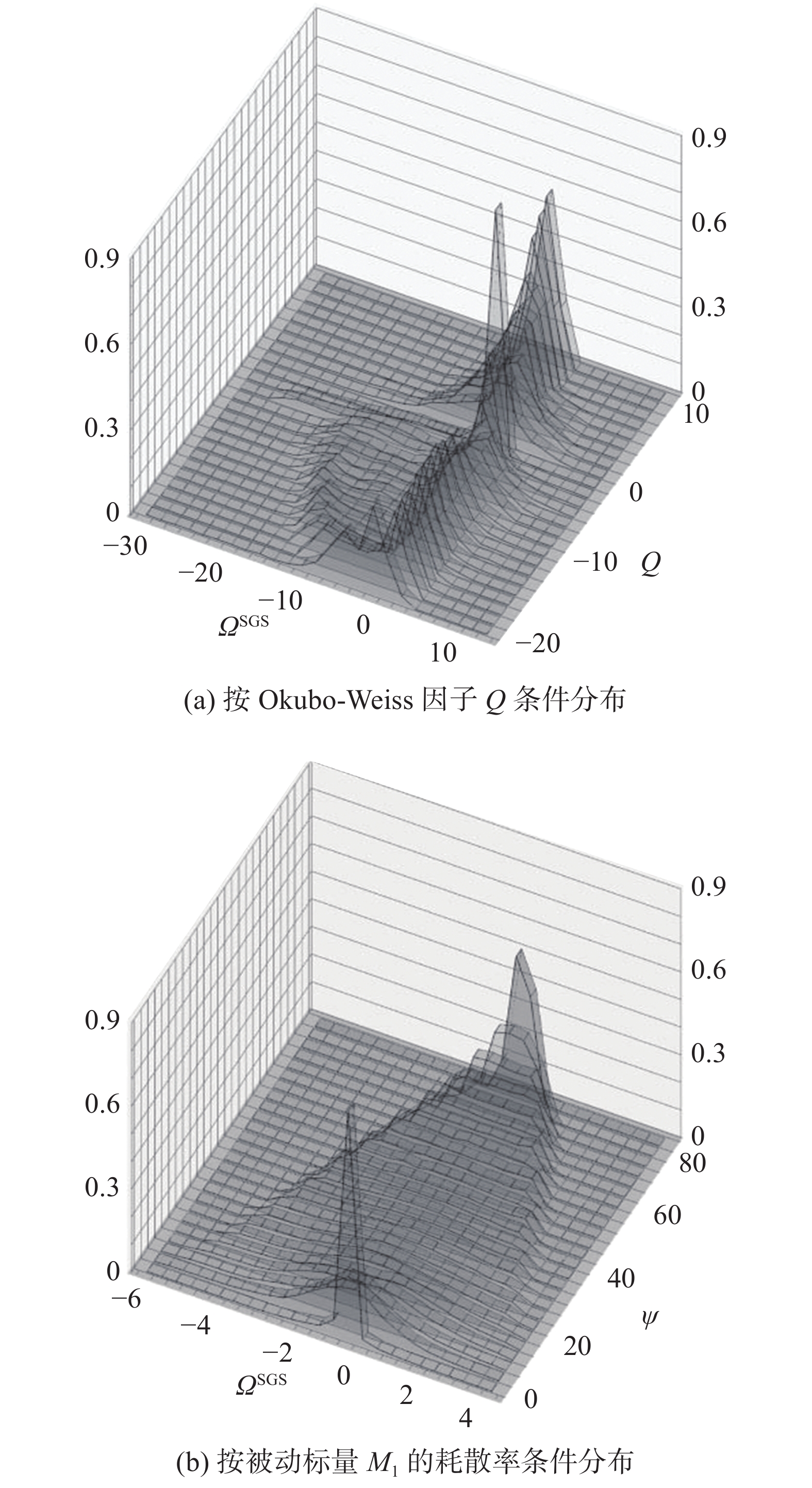
在直接数值模拟方法中，对包含完整脉动信息的颗粒数密度场 $ n $ 的模拟，可以得到粒径的瞬时增长率 $\varOmega$ 。对采用大尺度滤波的数密度场 $ \left\langle n\right\rangle $ 模拟，得到的时滤波增长率 ${\varOmega }_{F}$ ，则亚网格尺度（SGS）作用增长率为 ${\varOmega }^{{\rm{SGS}}}=\varOmega -{\varOmega }_{L}^{F}$ 。Garrick^[36]采用DNS和LES方法研究混合层湍流，通过矩方法使包含颗粒凝并源项的方程得以封闭后求解，得到了瞬时增长率 $\varOmega$ 和SGS尺度作用增长率 ${\varOmega }^{{\rm{SGS}}}$ ，并建立SGS尺度作用增长率与流场剪切旋转效应和湍流场的标量耗散率之间的关系（如图4所示）。

不可压缩流场中，定义Okubo-Weiss因子 $Q={\sigma }_{f}^{2}- $ $ {\omega }_{f}^{2}$ ，式中 ${\sigma }_{f}^{2}$ 为应变率的平方， $ {\omega }_{f}^{2} $ 为涡量的平方。根据 $ Q $ 大于、等于或小于零，可以将流场划分为应变主导区域、应变旋转平衡区（或完全静止区域）以及旋涡主导区域。由图4（a）可知，在 $ Q=0 $ 的区域 ${\varOmega }^{{\rm{SGS}}}$ =0，即粒径增长率不存在SGS尺度的脉动。在 $ Q>0 $ 的区域， ${\varOmega }^{{\rm{SGS}}}$ 的PDF分布比较对称，说明湍流脉动导致的颗粒凝并增强作用和减弱作用基本抵消。在 $ Q<0 $ 的区域， ${\varOmega }^{{\rm{SGS}}}$ 的PDF分布偏向小于0的区域，意味着湍流在小空间尺度上将抑制颗粒的凝并。

在湍流场中，被动标量 $ {M}_{1} $ 的耗散率定义为：

$ \varPsi =\frac{1}{ReS{c}_{M}}\left(\frac{\partial {M}_{1}}{\partial {x}_{i}}\frac{\partial {M}_{1}}{\partial {x}_{i}}\right) $

(28)

式中 $ {M}_{1} $ 是 $ n\left(v\right) $ 的内部一阶矩，与颗粒的总质量浓度相关，不受颗粒凝并作用的影响。由图4（b）可知，在质量浓度耗散率为零和最大值处， ${\varOmega }^{{\rm{SGS}}}$ 的PDF分布比较对称，且集中分布在 $ Q=0 $ 附近的区域。在零和最大值处之间， ${\varOmega }^{{\rm{SGS}}}$ 的PDF分布非常分散且偏向负值。可见，由湍流脉动导致的颗粒浓度脉动抑制了颗粒的凝并，这与Rigopoulos^[25]的研究结论相符。综合颗粒的成核、凝积生长和凝并这几个因素，湍流脉动会抑制颗粒的增长^{[14, 18, 37]}。

3.3 颗粒凝并项与破碎项增强因子的重新定义

考虑到 $ \overline{{n}'\left(v\right){n}'\left({v}_{1}\right)} $ 的形式与统计学里的协方差相似，且根据增强因子的定义：

$ {g}_{nn}=\frac{\overline{{n}'\left(v\right){n}'\left({v}_{1}\right)}}{\bar{n}\left(v\right)\bar{n}\left({v}_{1}\right)} $

(29)

于是，可用 $ {g}_{nn} $ 来对颗粒凝并项进行描述，即：

$\begin{split} {\bar{S}}_{{c}}=&\frac{1}{2}{\int }_{0}^{v}\left(1+{g}_{nn}\right)\beta \left(v-{v}_{1},{v}_{1}\right)\bar{n}\left(v-{v}_{1}\right)\bar{n}\left({v}_{1}\right){\rm{d}}{v}_{1}-\\& {\int }_{0}^{\mathrm{\infty }}\left(1+{g}_{nn}\right)\beta \left(v,{v}_{1}\right)\bar{n}\left(v\right)\bar{n}\left({v}_{1}\right){\rm{d}}{v}_{1} \\[-14pt]\end{split}$

(30)

该式中还需确定 $ {g}_{nn} $ 。Yang等^[77]认为对零惯性颗粒而言， $ {g}_{nn} $ 可表示为流场湍动能与总动能之比：

$ {g}_{nn}=\frac{k}{k+\frac{{\bar{u}}_{i}^{2}}{2}} $

(31)

式中 $ k $ 是湍动能，他们基于该式对圆管湍流场进行了数值模拟，得到的结果与实验结果吻合。

除了 $ \overline{{n}'\left(v\right){n}'\left({v}_{1}\right)} $ ，当湍流凝并核函数的剪切率也存在湍流脉动时，会有新的未知项：

$ \overline{\beta \left(v,{v}_{1}\right)n\left(v\right)n\left({v}_{1}\right)}=\alpha \left({v}^\frac{1}{3}+{v}_{1}^\frac{1}{3}\right)\overline{\varGamma _{\eta }n\left(v\right)n\left({v}_{1}\right)} $

(32)

对 $\overline{\varGamma _{\eta }n\left(v\right)n\left({v}_{1}\right)}$ 进一步展开可得：

$\begin{split}& \overline{\varGamma _{\eta }n\left(v\right)n\left({v}_{1}\right)}=\varGamma _{\eta }\bar{n}\left(v\right)\bar{n}\left({v}_{1}\right)+{\bar\varGamma }_{\eta }\overline{{n}'\left(v\right){n}'\left({v}_{1}\right)}+\\&\qquad \bar{n}\left(v\right)\overline{\varGamma _{\eta }'{n}'\left({v}_{1}\right)}+\bar{n}\left({v}_{1}\right)\overline{\varGamma _{\eta }'{n}'\left(v\right)}+\overline{\varGamma _{\eta }'{n}'\left(v\right){n}'\left({v}_{1}\right)} \end{split}$

(33)

定义新的增强因子：

$ {g}_{\mathrm{\varGamma }n}=\frac{\overline{\varGamma _{\eta }'{n}'\left(v\right)}}{{\overline\varGamma }_{\eta }\bar{n}\left(v\right)} ,\;\;{g}_{\mathrm{\varGamma }nn}=\frac{\overline{\varGamma _{\eta }'{n}'\left(v\right){n}'\left({v}_{1}\right)}}{{\bar\varGamma }_{\eta }\bar{n}\left(v\right)\bar{n}\left({v}_{1}\right)}$

(34)

令 ${g}_{3}={g}_{nn}+2{g}_{{\varGamma }n}+{g}_{{\varGamma }nn}$ ，则 $\overline{\varGamma _{\eta }n\left(v\right)n\left({v}_{1}\right)}=\left(1+{g}_{3}\right) {\bar\varGamma }_{\eta }\bar{n} \left(v\right) \cdot $ $ \bar{n}\left({v}_{1}\right)$ ，再代入凝并项后得^[78]：

$ {g}_{3}=\frac{2k}{{\bar{u}}_{i}^{2}} $

(35)

对于破碎项中的 $ \overline{a\left(v\right)n\left(v\right)} $ ，可将湍流破碎核函数代入破碎项中进行平均，再应用二项式定理得：

$\begin{split} \overline{\varGamma _{\eta }^{q}n\left(v\right)}=&{\bar\varGamma }_{\eta }^{q}\bar{n}\left(v\right)+\sum _{i=1}^{\mathrm{\infty }}\frac{q!}{i!\left(q-i\right)!}{\bar\varGamma }_{\eta }^{q-i}\overline{{\varGamma '}_{\eta }^{i}{n}'\left(v\right)}+\\& \sum _{i=2}^{\mathrm{\infty }}\frac{q!}{i!\left(q-i\right)!}\varGamma _{\eta }^{q-i}\bar{n}\left(v\right)\overline{{\varGamma '}_{\eta }^{i}} \end{split}$

(36)

则新的增强因子定义为 $ {g}_{q} $

$ \overline{{\tau }_{\eta }^{q}n\left(v\right)}=\left(1+{g}_{q}\right){\bar{\tau }}_{\eta }^{q}\bar{n}\left(v\right) $

(37)

此处沿用并定义 $ {g}_{nn} $ 、 $ {g}_{3} $ 和 $ {g}_{q} $ 等增强因子出于两方面考虑，一是基于颗粒聚集效应的研究^{[73-74, 79]}，在极低颗粒惯性情况下，颗粒凝并的增强受颗粒多分散性的作用很小，则 $ {v}_{1}=v $ ， ${g_{nn}} = \dfrac{{\overline {n'} {{\left( v \right)}^2}}}{{\bar n{{\left( v \right)}^2}}}$ 。二是若忽略颗粒多分散性的作用，则 $ {g}_{nn} $ 近似于颗粒数密度脉动的均方根，这便于对湍流脉动凝并项方程的封闭求解，甚至可采用Elghobashi^[64]提出的k-ε-g方程求解。关于 $ {g}_{3} $ 增强因子中出现的 ${g}_{{\varGamma }n}$ 、 ${g}_{{\varGamma }nn}$ ，已有前人进行过研究^[35]。

4 结束语

微纳米颗粒两相湍流存在于自然现象和大量的实际应用中，研究其规律具有重要的实际意义。微纳米颗粒两相流与大颗粒两相流相比具有其特殊性和复杂性，对其研究具有重要的科学意义。

在微纳米颗粒两相湍流中，湍流导致的流场速度脉动、颗粒浓度脉动、温度脉动以及饱和度脉动会对颗粒相的成核、凝积生长、碰撞凝并、破碎产生影响。本文在给出颗粒一般动力学方程的基础上，分析了方程中因湍流脉动导致的与颗粒成核、生长、凝并、破碎相关的脉动量关联项，介绍了对这些关联项进行模化从而使方程得以封闭的研究途径和相关的研究结果。

湍流脉动对颗粒成核、凝积生长、碰撞凝并、破碎的影响已受到人们的重视并开展了研究，但仍有一些方面的问题有待将来进一步探讨。

1）颗粒聚集使颗粒碰撞的几率增加，从而导致颗粒凝并的增强。而在第3.3节的研究结论中，湍流脉动会抑制颗粒的凝并，这与颗粒聚集导致颗粒凝并增强的结论似乎存在矛盾，因为湍流脉动使得颗粒数密度脉动，而数密度脉动的结果也有可能导致颗粒聚集。所以有必要对湍流脉动对颗粒凝并的影响进行深入的研究。

2）微纳颗粒两相湍流场的实验研究具有一定的难度。湍流场尤其是充分发展的湍流场具有空间和时间多尺度的特征。受多尺度的影响，在测量颗粒的取样频率还很低的情况下，难以全面获得微纳尺度颗粒在流场中的运动信息^[80]，有必要在实验仪器和实验技术方面做进一步的研究。

3）在纳颗粒两相湍流场中，对颗粒一般动力学方程进行雷诺平均后会出现与颗粒成核、生长、凝并、破碎相关的脉动量关联项，这些项使得平均后的方程不封闭，要使方程封闭，就要对这些项进行模化。目前，由模化后得到的数值模拟结果与实验结果如颗粒燃烧^[81-83]、成核^[13]、凝并^[84]、破碎弥散^[85-86]还存在一定的差异，原因是数值模拟中可以有针对性地对成核、生长、凝并、破碎中的某一项进行，而实验的结果往往是这几项中若干项的综合结果。所以有必要进一步对颗粒一般动力学方程中未知项的模化开展有针对性的实验研究。