近年来,微型飞行器(Micro Aerial Vehicle, MAV)因其潜在的军用和民用前景,成为航空领域研究的热门[1-2]。MAV的雷诺数很小,通常在100~10 000之间。低雷诺数下流体的黏性效应十分显著,导致MAV的阻力大幅增加。然而,在相近的雷诺数下,自然界中的鸟类、昆虫和鱼类依赖其特有的扑翼飞行或游动方式实现自主推进[3]。为优化MAV设计,人们围绕扑翼的推力特性及其背后的流动机理开展了大量研究。
目前已开展的大部分工作基于大展弦比假设对绕扑翼流动进行了二维近似。Koochesfahani[4]利用激光多普勒测速(Laser Doppler Velocimetry, LDV)技术对NACA0012翼型作小幅度俯仰运动的尾迹流场进行了测量,发现缩减频率较小时,尾迹形态为卡门涡街,其中顺时针旋转的涡处于逆时针旋转的涡上方;随着缩减频率的增大,顺时针涡与逆时针涡的纵向位置交换,前者位于后者下方,该尾迹形态称为反卡门涡街。Jones等[5]及Von Ellenrieder和Pothos[6]对NACA0012翼型作浮沉运动的实验研究表明,当斯特劳哈尔数大于某一临界值时,出现尾迹不对称现象,即反卡门涡偏离水平线向上方或向下方倾斜。Godoy-Diana等[7]实验研究了俯仰翼型尾迹不对称性机制,建立了反卡门涡对称性破坏准则。Andersen团队[8-9]对俯仰翼型和浮沉翼型的实验及数值研究发现,在改变振荡频率和幅度时,除观察到卡门涡街(2S BvK)和反卡门涡街(2S RBvK)外,还出现2P型、2P+2S型、4P型、4P+2S型等更复杂的尾迹形态,其中“S”表示孤立涡,“P”表示由两个旋转方向相反的涡组成的涡对,“2”和“4”为每个振荡周期内从翼型后缘脱落到尾迹中的孤立涡或涡对的数目。
尾迹形态随扑翼运动学、动力学的演变是扑翼流场的主要特征,其与推力产生的关系是研究的重点。Von Karman和Burgers[10]在对平板横向振荡的研究中发现,反卡门涡街的“喷流”现象能够产生推力。Koochesfahani[4]的研究表明,当俯仰翼型尾迹形态由卡门涡街转变为反卡门涡街时,对应的尾迹流场由速度损失型变为速度增加型或“喷流”。他进一步基于积分动量定理证实,反卡门涡街是一种推力产生型尾迹。Jones等[5]在对浮沉翼型的研究中也发现,随着无量纲浮沉速度的增大,发生阻力型尾迹(卡门涡街)到推力型尾迹(反卡门涡街)的转变。Lai和Platzer[11]在此基础上研究了浮沉翼型尾迹的“喷流”特性,指出最大喷流速度是无量纲浮沉速度的线性函数。
尽管反卡门涡街的“喷流”理论揭示了扑翼产生推力的流动机制,但随着研究的深入,人们发现反卡门涡街的出现与推力产生并不是完全对应的。Godoy-Diana等[12]采用粒子图像测速(Particle Image Velocimetry, PIV)技术观察了俯仰翼型的尾迹形态(
目前对扑翼推力特性的研究取得了一些重要结论。Sarkar和Venkatraman[17]研究发现,俯仰翼型的时均推力随缩减频率的增大而增大,随平均迎角的增大而减小。Mackowski和Williamson[18]的研究表明俯仰翼型阻力-推力转变对应的临界缩减频率随雷诺数的增大而减小。Das等[14]进一步指出,俯仰翼型阻力-推力转变对应的临界斯特劳哈尔数
尽管上述工作对扑翼的流场特征和推力特性的认识已相对深入,但目前还没有相关文献针对在低雷诺数下,随着斯特劳哈尔数增大,俯仰振荡翼型的推力产生滞后于反卡门涡街形成的现象进行系统性研究,尤其对其背后的流动机制的认识存在不足。为此,本文采用CFD方法对NACA0012翼型在1 000雷诺数下作简谐俯仰运动的非定常流场进行了数值模拟,考察了阻力-推力转变临界点附近的尾迹形态特征和推力特性。采用翼型表面积分方法和基于有限控制体的气动力估计方法分别研究翼面分布力特性和尾迹流场特性变化对推力产生的影响,以探究阻力-推力转变滞后于卡门涡街-反卡门涡街转变的物理机制。
1 数值计算和验证 1.1 控制参数考虑NACA0012翼型以正弦规律绕1/4弦长位置作纯俯仰运动:
| ${\alpha} ={\alpha _0}\sin{ (2 {\text{π}} ft)}$ | (1) |
其中,
| ${A_D}{\rm{ = }}A{\rm{/}}D{\rm{ = 1}}{\rm{.5}}c\sin {\alpha _0}{\rm{/}}D$) | (2) |
| $S\!t{\rm{ = }}fD{\rm{/}}{U_\infty }\;\;{\rm{ or }}\;\;S\!{t_A}{\rm{ = }}fA{\rm{/}}{U_\infty }{\rm{ }}$ | (3) |
其中,D为翼型厚度,A为在一个俯仰周期内翼型后缘通过的垂直距离。
本文选取俯仰幅度(
计算域为足够大的圆形区域,直径为100倍翼型弦长,圆心位于1/4弦长位置,如图1所示。采用481(周向)×241(径向)的O型结构网格对计算域进行离散,第一层网格高度为0.001c,满足y+ < 1。对直径为10倍弦长的内部圆形区域加密(径向),使其具有较高的流场分辨率;该圆形区域之外为较粗化的网格。两块网格的周向节点数一致,且在交界面上的节点一一对应。
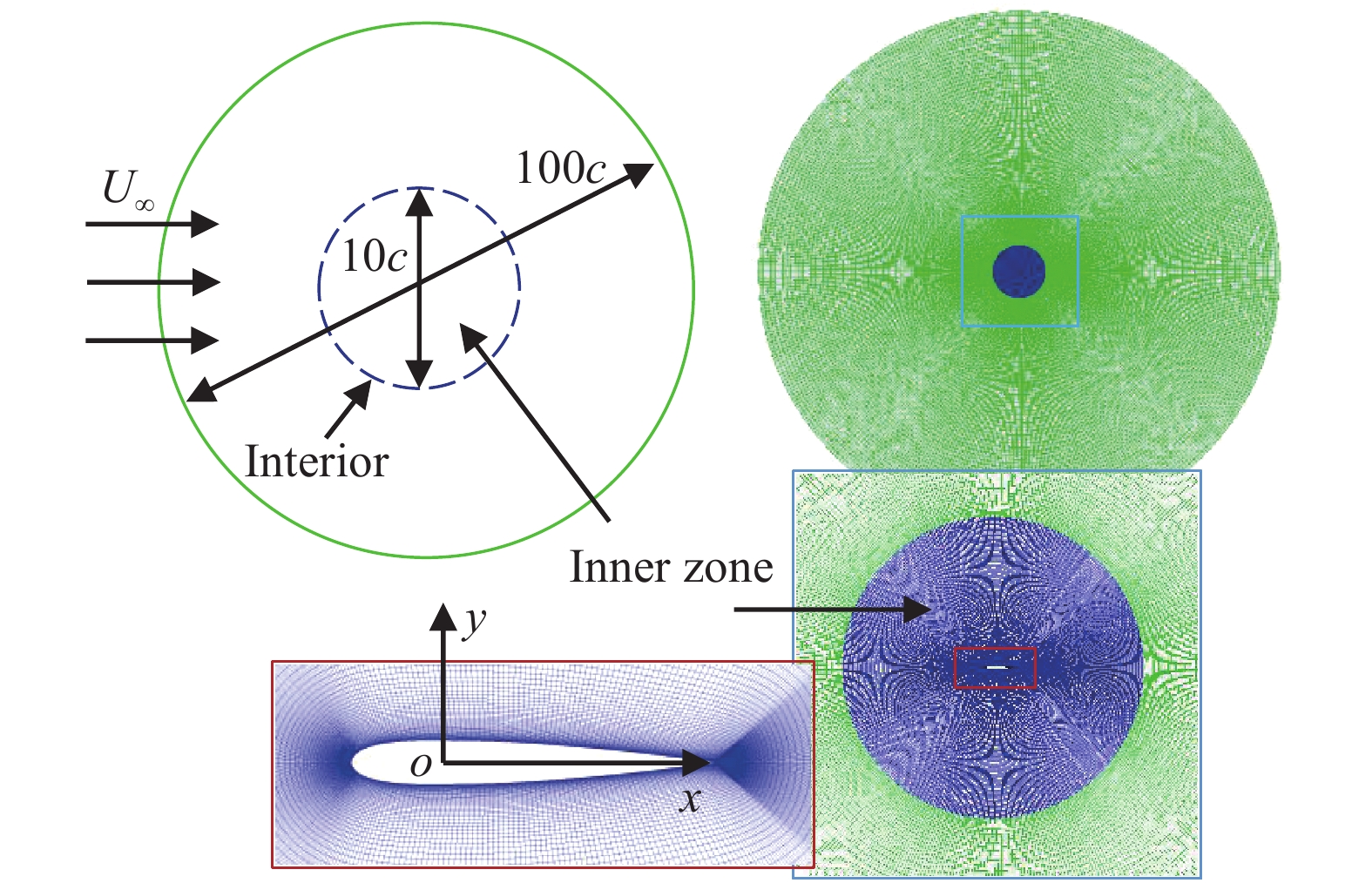
|
图 1 计算模型及网格 Fig.1 Computational model and the corresponding grid used |
采用Fluent 17.2压力基求解器数值求解二维不可压N-S方程。远场设置为速度入口边界条件,来流速度为0.146 m/s,相应的雷诺数为1 000。选择该雷诺数的原因是,一方面
压力-速度耦合求解采用SIMPLEC算法,空间离散中对流项和黏性项分别采用二阶迎风格式和二阶中心格式,时间项采用二阶隐式双步法,对每个俯仰周期分N个时间步进行时间推进,每个时间步内进行25次内迭代。为获得周期性稳定解,每个算例均至少计算60个俯仰周期。
1.3 相关验证采用四套疏密程度不同的网格验证网格无关性,网格信息见表1。验证算例中选取α0 = 10°,
为进一步验证求解器的可靠性,将计算结果与文献中的结果进行对比。Deng等[20]的CFD计算中
| 表 1 网格信息 Table 1 Information of the grids |
|
|
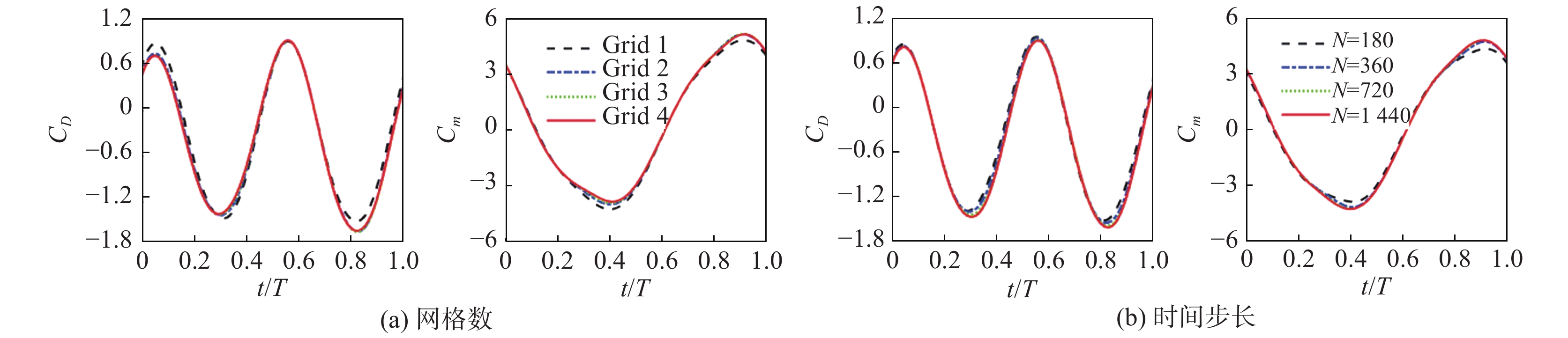
|
图 2 网格和时间步长无关性检查 Fig.2 Grid and time step independence test results |

|
图 3 阻力/力矩系数与文献结果[20]对比 Fig.3 Drag and momentum coefficients compared with the Ref. [20] |
为分析俯仰翼型诱导形成的非定常尾迹对推力产生的影响,采用基于有限控制体的气动力估计方法建立局部尾迹与推力产生的联系。对不可压黏性流动,由动量定理,作用在翼型上的气动力为:
| ${{F}} = - \mathop{{\int\!\!\!\!\!\int}\mkern-18mu \bigcirc}\nolimits_{\partial B} {( - p{{n}} + {{\tau }}){\rm{d}}S}$ | (4) |
| ${{F}} = - \rho \iiint_{{V_{\rm{f}}}} {{{a}}{\rm{d}}V}{\rm{ + }}\mathop{{\int\!\!\!\!\!\int}\mkern-18mu \bigcirc}\nolimits_{\varSigma} {( - p{{n}} + {{\tau}} ){\rm{d}}S} $ | (5) |
其中,
| $ \begin{split} { F}\!=\! &\underbrace{\rho \iiint_{{{V}_{\rm{f}}}}{{ u}\times { \omega }{\rm{d}}V}}_{(1){\text{涡力}}({\rm{V}})}\underbrace{\!-\! \rho \iiint_{{{V}_{\rm{f}}}}{\frac{\partial { u}}{\partial t}{\rm{d}}V}}_{(2){\text{局部流体加速}}({\rm{A}})}\underbrace{-\mathop{{\int\!\!\!\!\!\int}\mkern-18mu \bigcirc}\nolimits_{\partial B } {\frac{1}{2}\rho |{{u}}|^2}{ n}{\rm{d}}S }_{(3){\text{固体占据的虚拟流体}}({\rm{B}})}\!\!\!+\! \\ & \underbrace{-\mathop{{\int\!\!\!\!\!\int}\mkern-18mu \bigcirc}\nolimits_{{\varSigma}} {\frac{1}{2}\rho |{{u}}|^2}{ n}{\rm{d}}S }_{(4){\text{动量诱导}}({\rm{M}})}\underbrace{- \mathop{{\int\!\!\!\!\!\int}\mkern-18mu \bigcirc}\nolimits_{{\varSigma}} p{ n}{\rm{d}}S }_{(5){\text{压力诱导}}({\rm{P}})}\underbrace{+ \mathop{{\int\!\!\!\!\!\int}\mkern-18mu \bigcirc}\nolimits_{{\varSigma}} { \tau }{\rm{d}}S }_{(6){\text{粘性剪切}}({\rm{S}})} \\[-18pt] \end{split} $ | (6) |
其中,
通过实验方法得到压力场的空间分布并不方便,而对速度场的测量相对容易且测量技术较为成熟[25]。Wang等结合不可压N-S方程进一步将压力场转化为速度场,同时选取特殊的矩形控制体以消除方程(6)中的压力项。在CFD计算中容易得到压力场,因此本文直接应用方程(6)进行气动力分解且不对控制体的选取作任何限制。为避免后处理中的数值插值和积分误差,将方程(4)和方程(6)写入UDF文件,基于原始网格在CFD求解计算的过程中同时完成对各气动力分量的计算。为减小由涡量耗散引入的积分误差和不确定性,控制体与图1中计算网格的加密区一致,该范围内涡量耗散程度较小。
3 结果和讨论 3.1 推力产生滞后于反卡门涡街出现图4给出了零推力点附近不同俯仰幅度下周期平均推力系数随斯特劳哈尔数的变化,图中曲线为对各离散点的二次函数拟合,零推力点由拟合函数近似给出,并经计算验证满足推力系数在

|
图 4 不同俯仰幅度下的周期平均推力系数 Fig.4 Cycle averaged thrust coefficients for different pitching amplitudes |
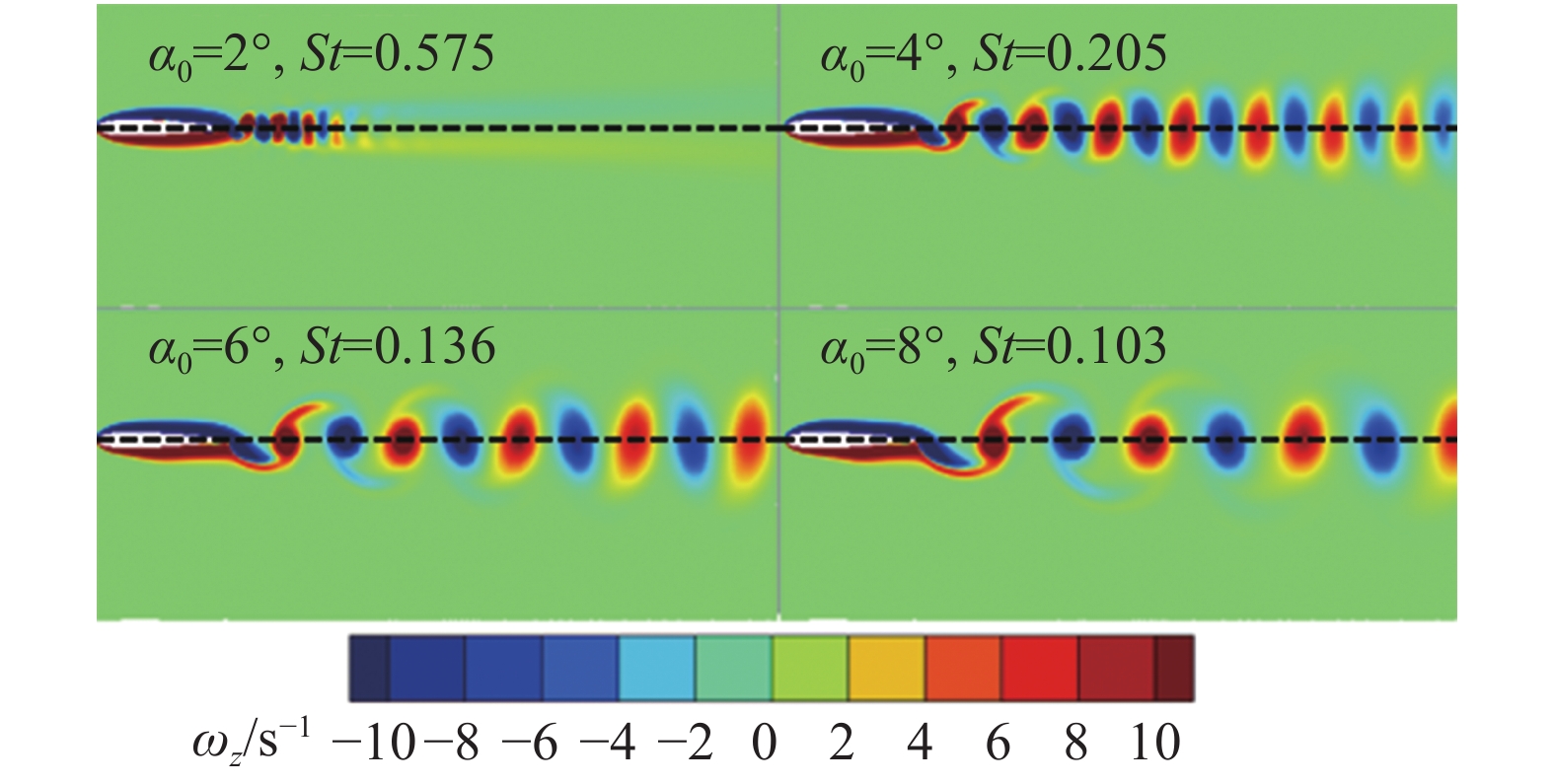
图5对比了俯仰幅度为10°时不同斯特劳哈尔数下的尾迹形态。

|
图 5 |
为较准确判断卡门涡街-反卡门涡街转变临界点,根据涡量极值点确定了后缘下游0.25~3.25倍弦长范围内所有尾迹涡的涡核位置
| $ {\left|\: {{\overline y_{\rm{c}}}}\: \right|} {\rm{ = }}\frac{1}{M}\sum\limits_{i = 1}^{i = M} {\left| {{y_{{\rm{c,}}i}}} \right|} $ | (7) |
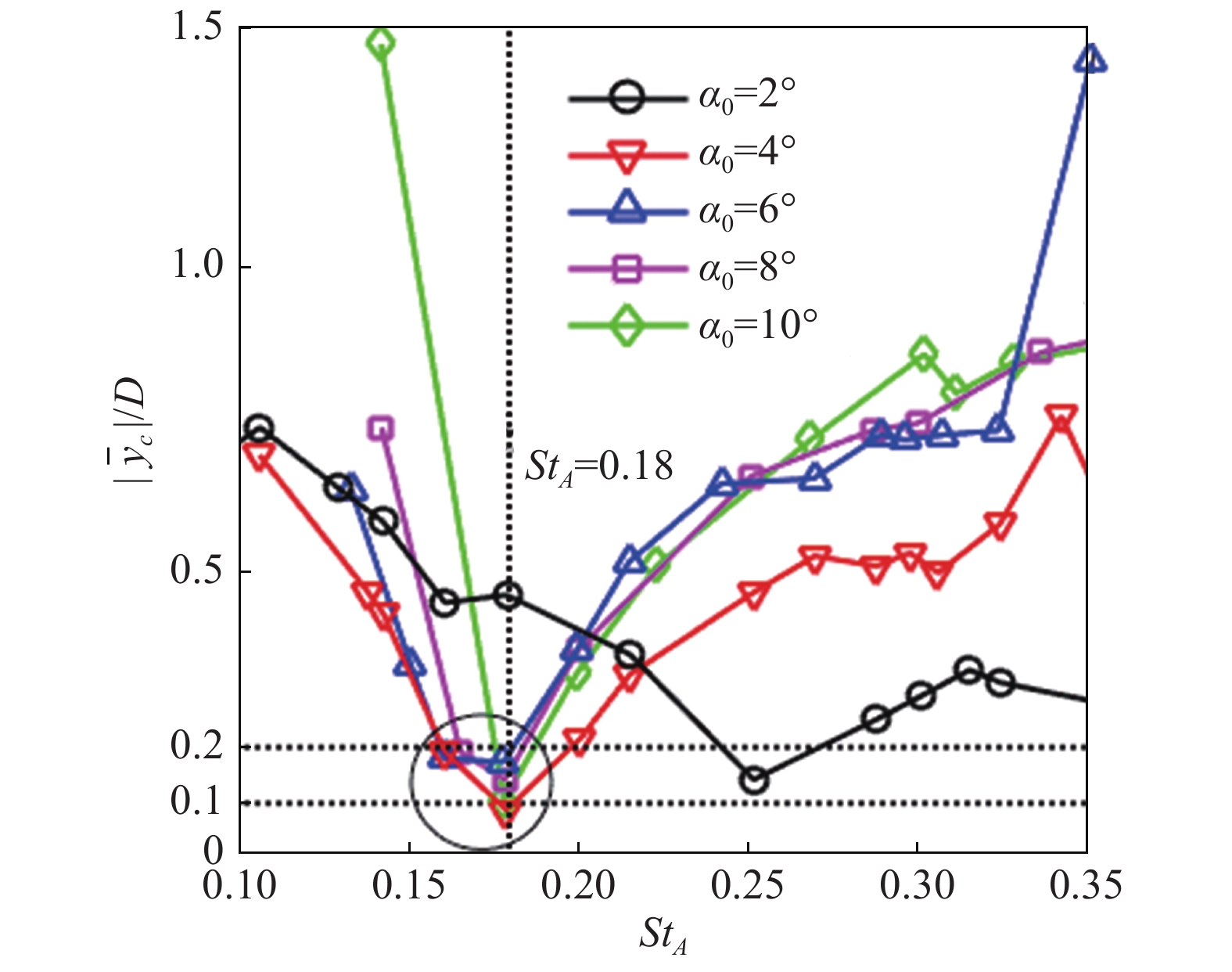
|
图 6 涡核纵向平均偏离量随 |
|
图 7 不同俯仰幅度下的临界尾迹 Fig.7 Neutral wakes for various pitching amplitudes |
基于以上分析,图8绘制了尾迹形态随无量纲幅度
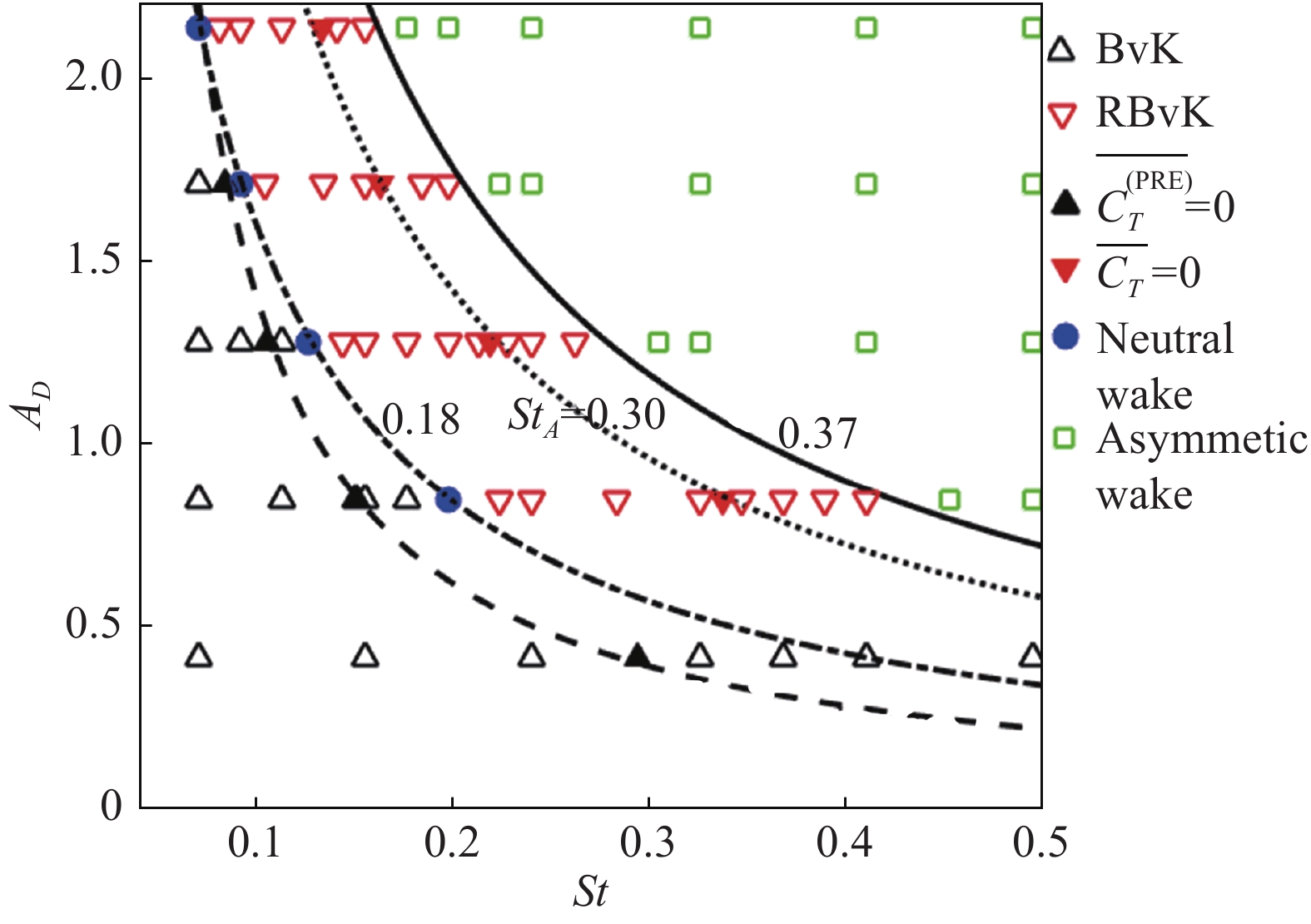
|
图 8 尾迹形态在 |
图8显示,在每个俯仰幅度取值下(α0 = 2°~10°或
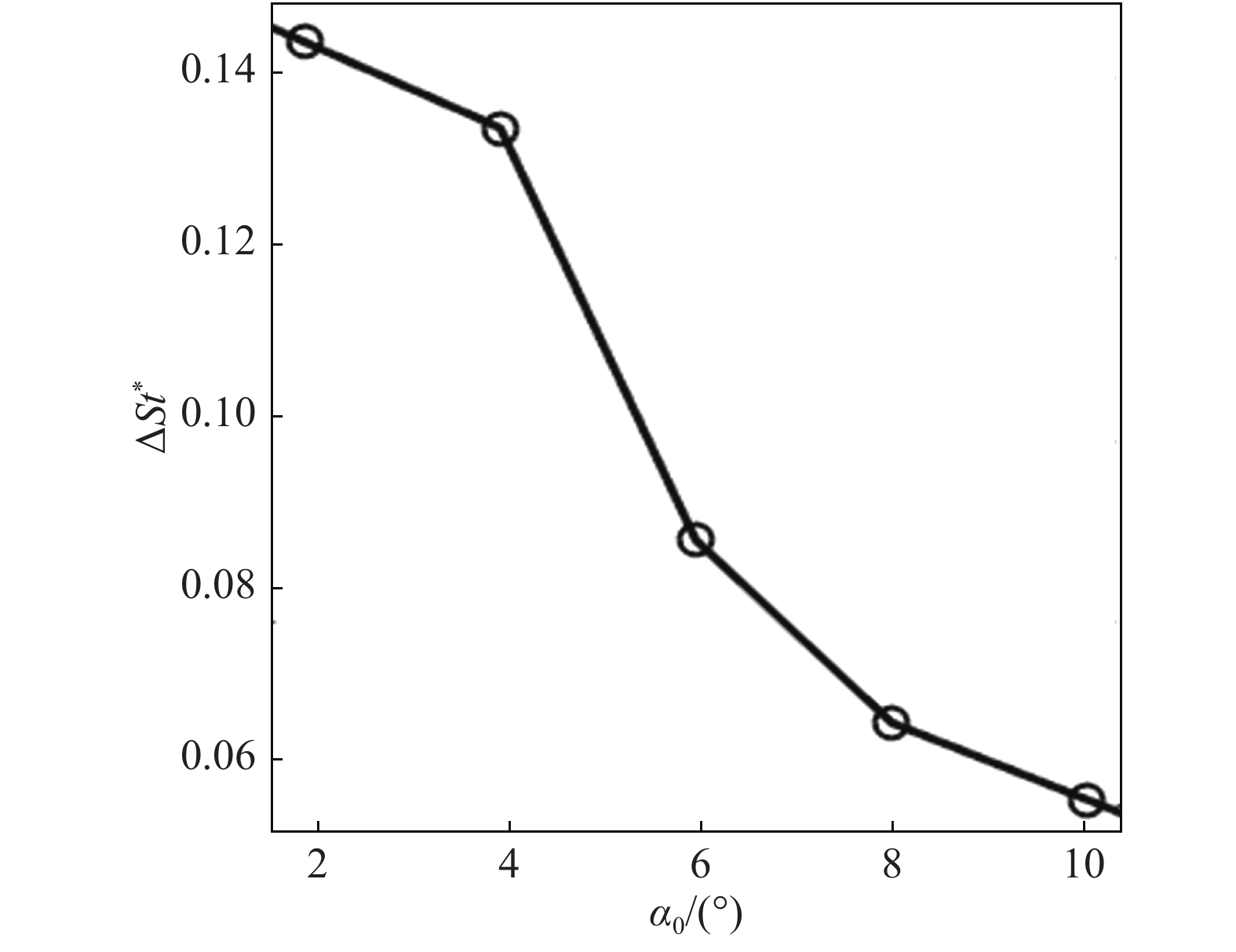
|
图 9 |
不可压黏性流动中气动力的主要来源是翼型表面的压力和黏性应力分布,当压力分布不均产生的推力与剪切层的黏滞阻力相平衡时出现零推力点。为分析造成俯仰翼型推力产生滞后于反卡门涡街出现的主要因素,首先利用方程(4)考察翼型表面非定常压力和黏性应力分布对推力产生的贡献。图10给出了俯仰幅度为6°和10°时周期平均推力系数及其分量随斯特劳哈尔数的变化。发现基于方程(4)计算的总推力系数随
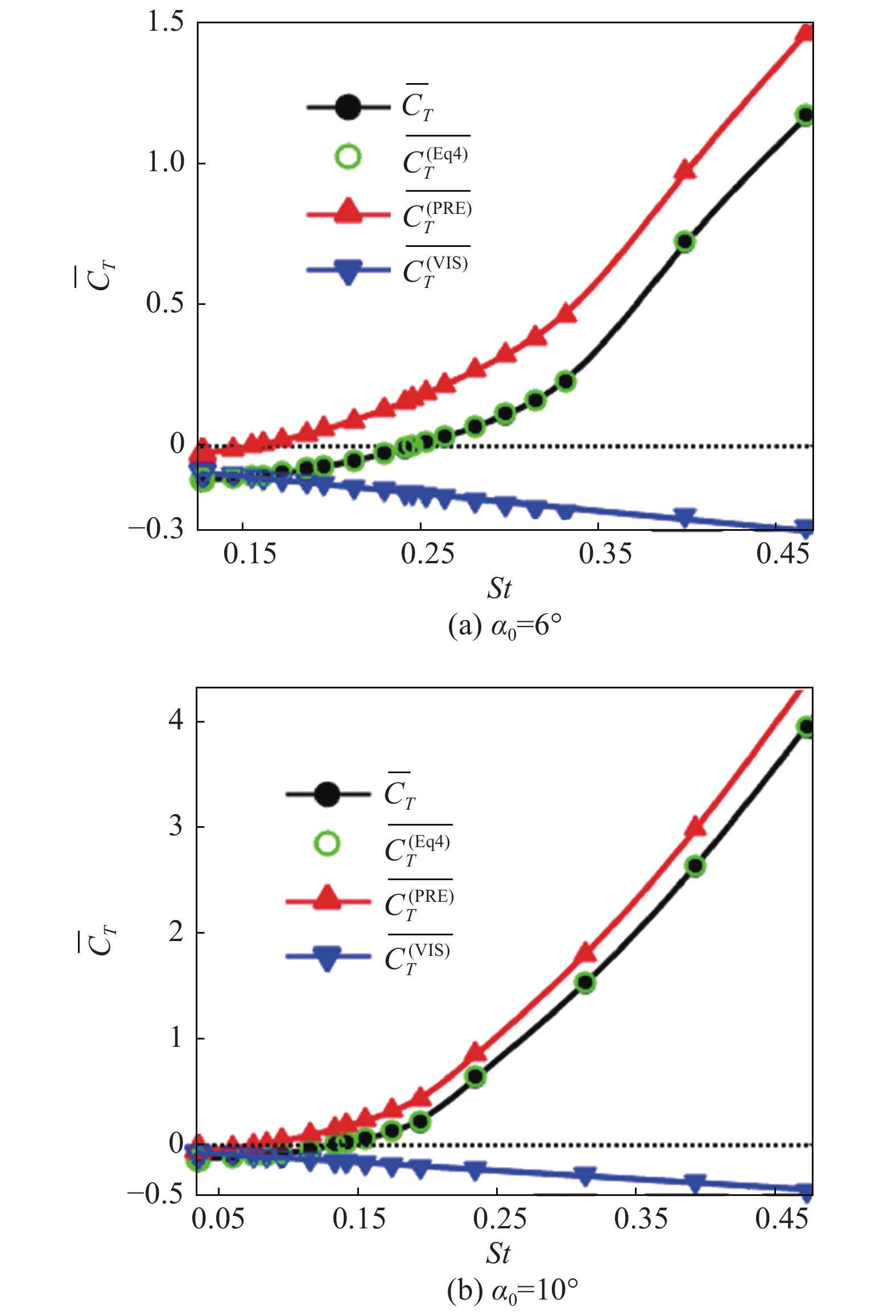
|
图 10 不同俯仰幅度下的周期平均推力系数及其分量 Fig.10 Cycle averaged thrust coefficient and the corresponding components for different pitching amplitudes |
图10显示,在两个俯仰幅度下,翼面压力分布产生的推力分量仅在
为更直观地显示,图11将图10中零推力点附近进行了放大,对黏滞阻力加了负号。图中阴影区为反卡门涡街对应的斯特劳哈尔数范围,其左侧为卡门涡街区域,右侧为不对称尾迹区域。俯仰幅度为6°时,推力的压力分量在卡门涡街-反卡门涡街转变临界点之前就变为正值,但无法克服黏性剪切层产生的阻力;之后在反卡门涡街区域中间靠左部分,压力诱导推力随
图8中绘制了推力的压力分量为零时对应的临界斯特劳哈尔数
对给定的俯仰幅度,在推力为零和其压力分量为零时可以分别唯一确定一个临界斯特劳哈尔数StT=0和StTP=0,对应一个数对(StT=0,StTP=0);通过改变俯仰幅度就可以确定一系列数对。图12反映了由这些数对确定的点在StT=0- StTP=0参数空间中的分布。发现这些点全部落在了StT=0- StTP=0空间中的一条直线上(实线),拟合的相关系数几乎为1。在雷诺数为无穷大或忽略黏性效应影响时,推力全部由翼面压力分布产生,因此StT=0=StTP=0,对应图12中的虚线。这表明低雷诺数的黏性效应将无黏时的零推力临界斯特劳哈尔数StTP=0按照线性比例规律放大为StT=0,且当俯仰幅度在2°~10°范围内时放大因子(系数)不依赖于俯仰幅度大小。对低雷诺数流动,翼型表面的压力分布可以通过实验测量,而对黏性应力分布的测量比较困难。因此根据StT=0和StTP=0的线性依赖性可以直接由压力分量临界点确定总推力的临界点,从而忽略对黏滞阻力的测量。StT=0和StTP=0之间的线性相关规律仅是针对NACA0012翼型在1 000雷诺数下作较小幅度(α0 = 2°~10°)俯仰运动得到的,对不同雷诺数、不同翼型形状及更大的俯仰幅度是否成立还需要进一步探究。
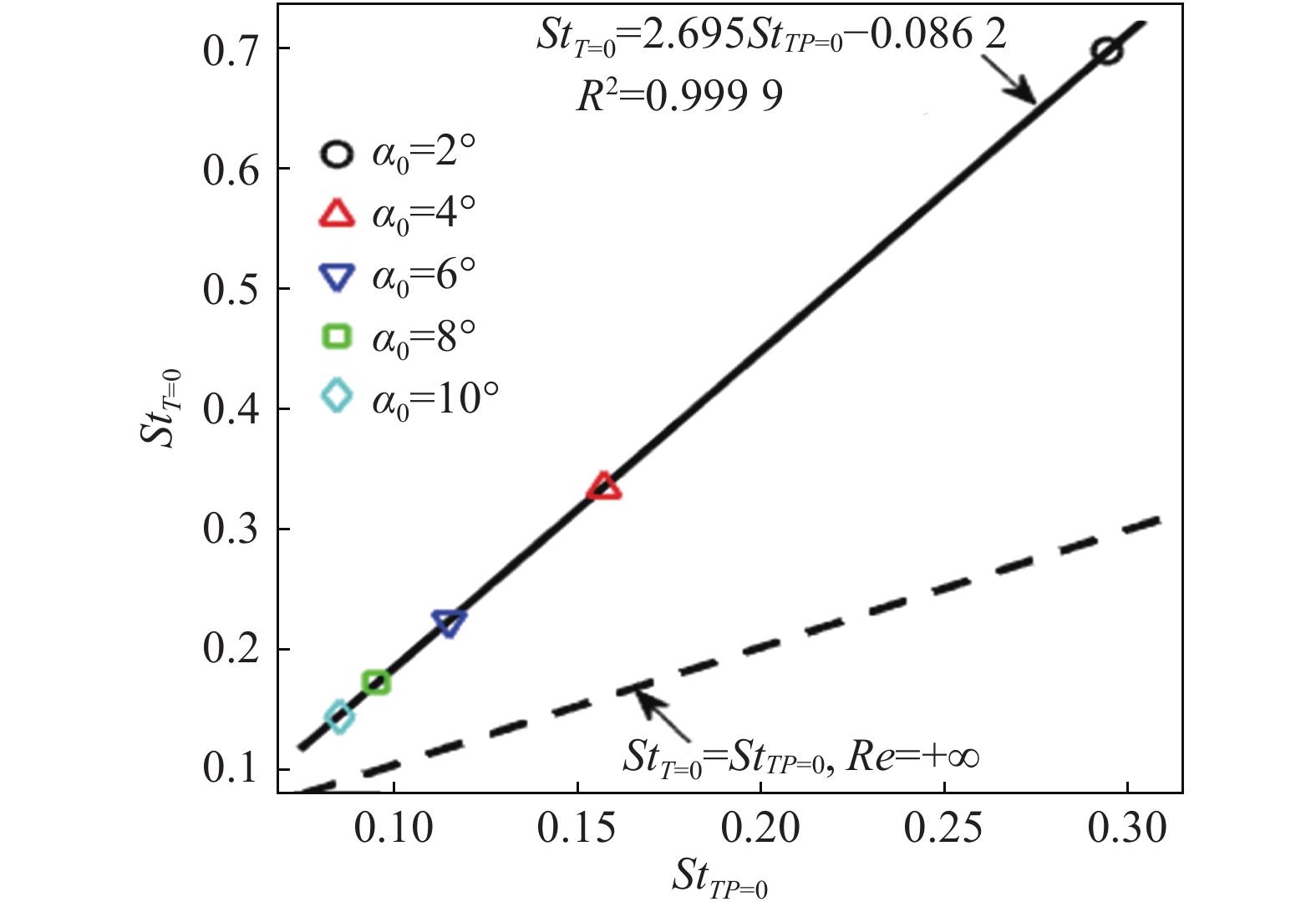
|
图 12 推力与其压力分量的临界斯特劳哈尔数的关系 Fig.12 Correlation between the critical Strouhal numbers of the thrust and its pressure component |
尾迹形态随斯特劳哈尔数的演变是扑翼流场的主要特征,为分析其对推力产生的影响,基于方程(6)定量估计非定常尾迹对推力的贡献。关于该方程中各分量的物理意义及控制体的选取已在第2节说明。图13对比了俯仰幅度为10°时由CFD直接计算的各瞬时气动力系数和基于有限控制体的尾迹流场积分结果。发现对不同的
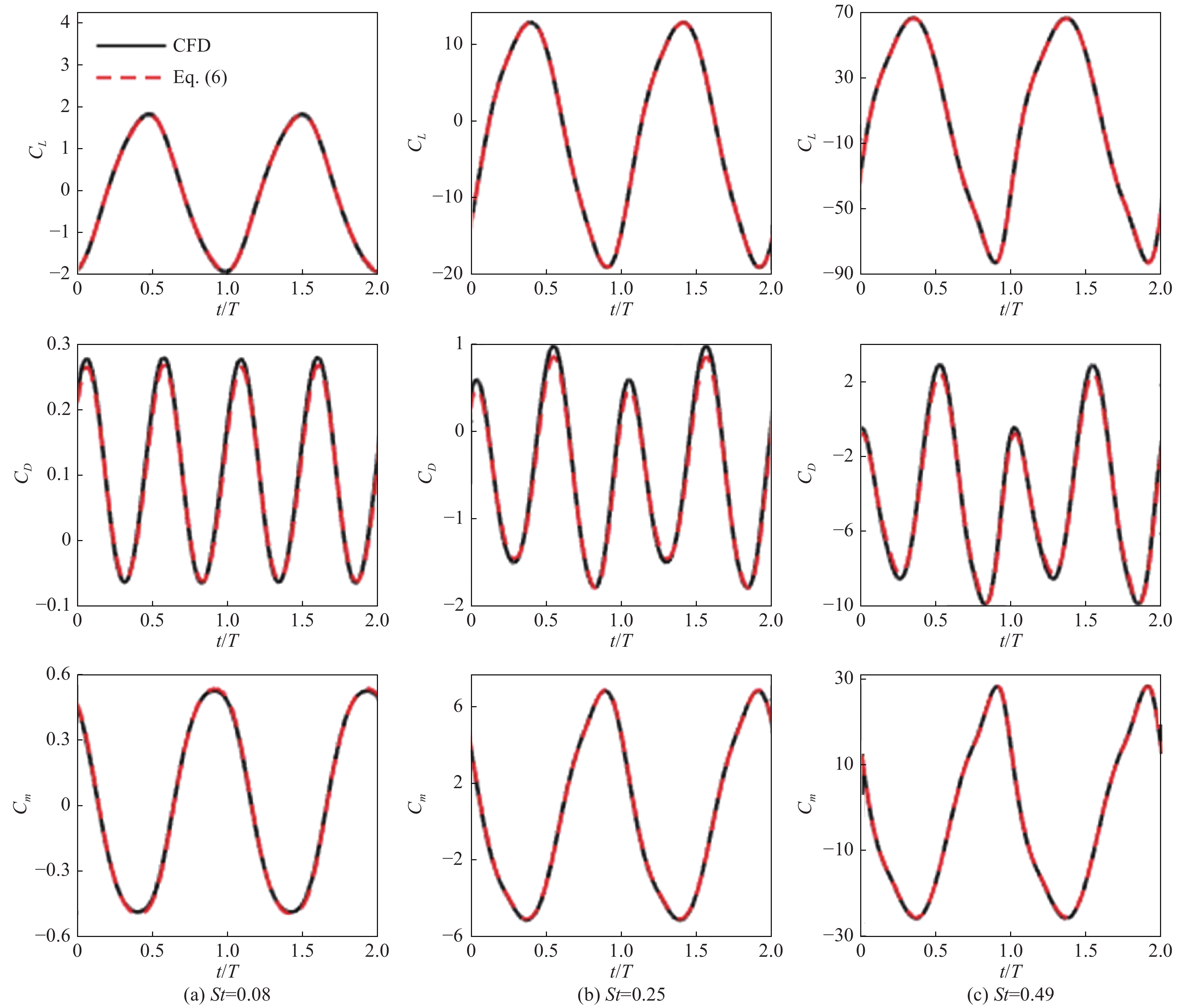
|
图 13 各气动力系数的时间历程曲线, |
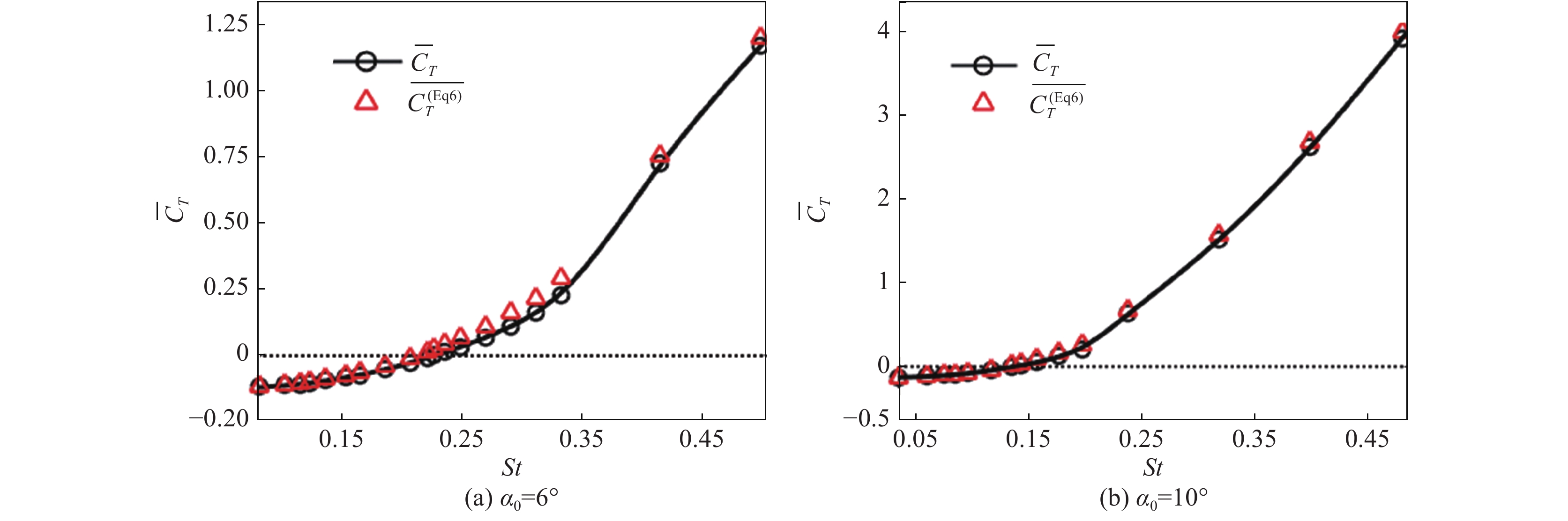
|
图 14 CFD得到的周期平均推力系数与尾迹积分结果对比 Fig.14 Comparison of the cycle averaged thrust coefficient computed by CFD with that by the wake integration |
图15对比了俯仰幅度为10°时不同斯特劳哈尔数下各推力系数分量的时间历程曲线,图中推力系数上标V表示涡推力,A和B分别为翼型运动的非定常惯性效应引起的局部流体加速和翼型占据的虚拟流体对推力的贡献,M、P、S分别代表动量诱导推力、压力诱导推力和黏性剪切力。

|
图 15 各推力系数分量的时间历程曲线, |
图15显示,外控制面上的黏性应力分布对推力的贡献(
基于以上分析,非定常尾迹对推力的贡献主要包括三部分,即涡推力(

|
图 16 时均流场随 |
图15显示,St = 0.041~0.164范围内,
综上分析,在零推力点
图17显示了
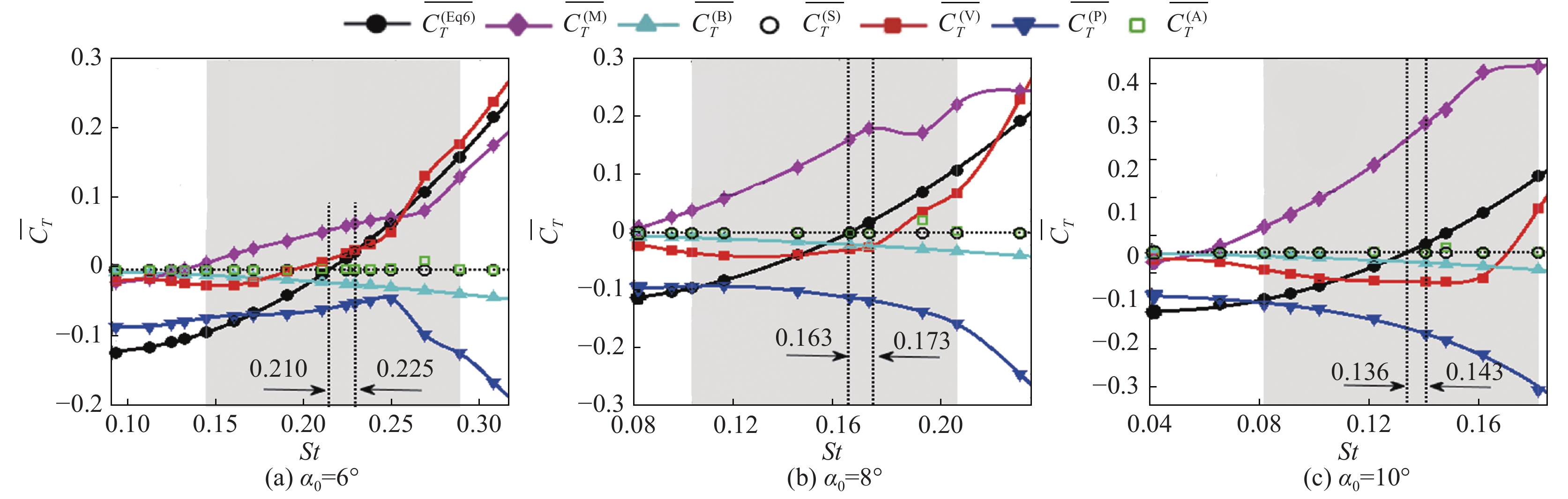
|
图 17 各周期平均推力系数分量随 |
图17(c)显示,对α = 10°,St < 0.164时,
本文针对在低雷诺数下(
1) 俯仰幅度在2°~10°范围内时,随 St增大,卡门涡街-反卡门涡街转变临界点与阻力-推力转变临界点均不重合,且前者先于后者出现;二者之间的相对滞后程度随俯仰幅度的增大而减小。
2) 俯仰翼型的推力主要由翼型表面压力分布产生,黏性应力分布对推力大小的影响有限。不同俯仰幅度下,翼面压力分布积分得到的推力分量在卡门涡街-反卡门涡街转变临界点之前或附近就由负值变为正值,因此零推力点后移不是由翼面的压差阻力造成的。
3) 当翼型振荡参数进入对应反卡门涡街尾迹形态区域时,翼面压力分布产生的推力分量无法克服剪切层的黏滞阻力,是导致推力产生滞后于反卡门涡街出现的主要原因。
4) 基于控制体的气动力分析表明,尽管反卡门涡街会产生“喷流效应”,但在
本文系统地讨论了俯仰翼型推力产生与反卡门涡街形成的相对滞后特征,较深入地探究了该滞后现象的发生机制,但也存在其局限性,如暂未考虑来流速度及雷诺数的影响。此外,翼型形状、俯仰轴位置的影响还需进一步探究。尾迹形态演变是扑翼流场的主要特征,深入认知反卡门涡街与推力产生的关系有利于揭示扑翼推力产生机理,在扑翼式MAV设计方面具有潜在的应用价值。
| [1] |
昆虫飞行的高升力机理[J]. 力学进展, 2002, 32(3): 425-434. SUN M. Unsteady lift mechanisms in insect flight[J]. Advances in Mechanics, 2002, 32(3): 425-434. DOI:10.6052/1000-0992-2002-3-J2001-051 (in Chinese) |
| [2] |
机械蜻蜓悬停时的气动力实验研究[J]. 实验流体力学, 2011, 25(1): 69-75. YAO D P, SHEN G X, ZHU B L, et al. Force measurement of hovering dragonfly via an electromechanical model[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(1): 69-75. DOI:10.3969/j.issn.1672-9897.2011.01.014 (in Chinese) |
| [3] |
SHI X, HUANG X W, ZHENG Y, et al. Effects of cambers on gliding and hovering performance of corrugated dragonfly airfoils[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2016, 26(3/4): 1092-1120. DOI:10.1108/HFF-10-2015-0414 |
| [4] |
KOOCHESFAHANI M M. Vortical patterns in the wake of an oscillating airfoil[J]. AIAA Journal, 1989, 27(9): 1200-1205. DOI:10.2514/3.10246 |
| [5] |
JONES K D, DOHRING C M, PLATZER M F. Experimental and computational investigation of the Knoller-Betz effect[J]. AIAA Journal, 1998, 36(7): 1240-1246. DOI:10.2514/2.505 |
| [6] |
VON ELLENRIEDER K D, POTHOS S. PIV measurements of the asymmetric wake of a two dimensional heaving hydrofoil[J]. Experiments in Fluids, 2008, 44(5): 733-745. DOI:10.1007/s00348-007-0430-z |
| [7] |
GODOY-DIANA R, MARAIS C, AIDER J L, et al. A model for the symmetry breaking of the reverse Bénard–von Kármán vortex street produced by a flapping foil[J]. Journal of Fluid Mechanics, 2009, 622: 23-32. DOI:10.1017/s0022112008005727 |
| [8] |
SCHNIPPER T, ANDERSEN A, BOHR T. Vortex wakes of a flapping foil[J]. Journal of Fluid Mechanics, 2009, 633: 411-423. DOI:10.1017/s0022112009007964 |
| [9] |
ANDERSEN A, BOHR T, SCHNIPPER T, et al. Wake structure and thrust generation of a flapping foil in two-dimensional flow[J]. Journal of Fluid Mechanics, 2017, 812: R4. DOI:10.1017/jfm.2016.808 |
| [10] |
VON KARMAN T, BURGERS J M. General aerodynamic theory- perfect fluids[M]. Division E, Vol. II, Aerodynamic Theory, Ed. Durand, W. F., 1943.308.
|
| [11] |
LAI J C S, PLATZER M F. Jet characteristics of a plunging airfoil[J]. AIAA Journal, 1999, 37: 1529-1537. DOI:10.2514/3.14353 |
| [12] |
GODOY-DIANA R, AIDER J L, WESFREID J E. Transitions in the wake of a flapping foil[J]. Physical Review E, 2008, 77: 016308. DOI:10.1103/physreve.77.016308 |
| [13] |
DENG J, SUN L P, SHAO X M. Dynamical features of the wake behind a pitching foil[J]. Physical Review E, 2015, 92(6): 063013. DOI:10.1103/physreve.92.063013 |
| [14] |
DAS A, SHUKLA R K, GOVARDHAN R N. Existence of a sharp transition in the peak propulsive efficiency of a low-Re pitching foil[J]. Journal of Fluid Mechanics, 2016, 800: 307-326. DOI:10.1017/jfm.2016.399 |
| [15] |
BOHL D G, KOOCHESFAHANI M M. MTV measurements of the vortical field in the wake of an airfoil oscillating at high reduced frequency[J]. Journal of Fluid Mechanics, 2009, 620: 63-88. DOI:10.1017/s0022112008004734 |
| [16] |
ASHRAF I, AGRAWAL A, KHAN M H, et al. Thrust generation and wake structure for flow across a pitching airfoil at low Reynolds number[J]. Sadhana, 2015, 40(8): 2367-2379. DOI:10.1007/s12046-015-0449-4 |
| [17] |
SARKAR S, VENKATRAMAN K. Numerical simulation of thrust generating flow past a pitching airfoil[J]. Computers & Fluids, 2006, 35(1): 16-42. DOI:10.1016/j.compfluid.2004.10.002 |
| [18] |
MACKOWSKI A W, WILLIAMSON C H K. Direct measurement of thrust and efficiency of an airfoil undergoing pure pitching[J]. Journal of Fluid Mechanics, 2015, 765: 524-543. DOI:10.1017/jfm.2014.748 |
| [19] |
DENG J, CAULFIELD C P. Three-dimensional transition after wake deflection behind a flapping foil[J]. Physical Review E, 2015, 91(4): 043017. DOI:10.1103/physreve.91.043017 |
| [20] |
DENG J, SUN L P, TENG L B, et al. The correlation between wake transition and propulsive efficiency of a flapping foil: a numerical study[J]. Physics of Fluids, 2016, 28(9): 094101. DOI:10.1063/1.4961566 |
| [21] |
TIAN W, BODLING A, LIU H, et al. An experimental study of the effects of pitch-pivot-point location on the propulsion performance of a pitching airfoil[J]. Journal of Fluids and Structures, 2016, 60: 130-142. DOI:10.1016/j.jfluidstructs.2015.10.014 |
| [22] |
间歇式俯仰转动扑翼的自主推进[J]. 空气动力学学报, 2018, 36(1): 151-155. DAI L Z, ZHANG X. Self-propulsion of a flapping foil powered by intermettent pitching motion[J]. Acta Aerodynamica Sinica, 2018, 36(1): 151-155. DOI:10.7638/kqdlxxb-2017.0198 (in Chinese) |
| [23] |
WANG S Z, ZHANG X, HE G W, et al. A lift formula applied to low-Reynolds-number unsteady flows[J]. Physics of Fluids, 2013, 25(9): 093605. DOI:10.1063/1.4821520 |
| [24] |
定常黏性外流气动力分量的同源性及流场断层扫描诊断原理[J]. 空气动力学学报, 2019, 37(06): 871-882. ZOU S F, WU J Z. Homology of aerodynamic force components and principle of aerodynamic computed topography in steady viscous external flow[J]. Acta Aerodynamica Sinica, 2019, 37(06): 871-882. DOI:10.7638/kqdlxxb-2019.0099 (in Chinese) |
| [25] |
基于PIV速度场测量重构压强场的研究进展[J]. 实验流体力学, 2014, 28(4): 1-8, 24. WANG Y, CHEN P, GENG Z H, et al. Bevelopment of PIV-based instantaneous pressure determination[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(4): 1-8, 24. DOI:10.11729/syltlx20140012 (in Chinese) |
 2021, Vol. 39
2021, Vol. 39



