20世纪80年代,美国、欧洲等发达国家和地区已对数值模拟可信度开展了大规模、有组织、有计划的研究工作[1],在研究过程中提出了验证与确认的概念作为数值模拟可信度研究的重要内容。1998年美国航空航天学会(AIAA)发布了CFD验证与确认研究的指南[2],提出了该领域的一些基本问题和基本概念。在此基础上,CFD验证与确认工作不断深入,国内外机构通过发布基准模型构建研究和比较平台,系统性地开展了一系列试验与计算工作。
可信度研究可以分为验证与确认两个过程。根据文献[2]的定义,验证过程是评估计算模型的求解精度,确认过程则是评估计算模型反映实际物理问题的精度,即本文对计算精度的研究属于验证过程。
目前CFD验证工作主要集中在定常问题,主要内容是空间离散以及网格尺度带来的影响,其中一项重要手段是网格收敛性研究,通过Richardson外插方法来获得网格无关解、分析计算空间精度和不确定度。但是对于非定常问题,时间离散带来的影响同样需要考虑。时间离散精度目前得到的关注较少,一般使用算法的理论分析精度来替代实际计算精度,没有进行相关的不确定度分析。对于气动弹性问题的时域求解,涉及到流场和结构的耦合计算,相较于单纯CFD问题更为复杂,其精度不仅取决于CFD以及CSD求解精度还和耦合算法有关,实际计算精度与理论分析精度难免有所差异。同时作为一种更为精细的气动弹性问题预测方法,时域模拟需要耗费大量计算资源,对其结果进行可信度分析,不仅能够得到可靠的计算结果,而且能够选取更为经济的时间离散步长,提高计算效率。
由于非定常问题的时间离散在数学上与空间离散并无本质上的差别,因此可以把时间离散看作一维空间离散问题,把空间离散问题的验证方法加以推广进行时间离散验证。本文参照网格收敛性分析方法,对颤振问题的时域模拟进行了时间步长收敛性分析,采用广义Richardson外插分析计算时间精度并获得时间步长无关解,采用网格收敛指数IGC(Grid Convergence index,GCI)估计时间离散不确定度。建立了颤振问题时域分析时间精度的验证过程,并检验了该方法的可行性。
1 Richardson外插方法及验证方法 1.1 Richardson外插方法Richardson外插方法又称“h2外插法”、“迭代外插法”,于1910年[3]由Richardson首次使用,并于1927年[4]加以完善。该方法使用离散步长h将离散解f与精确解fexact的关系表示为级数的形式:
| $ f = {f_{{\rm{exact}}}} + {g_1}h + {g_2}{h^2} + {g_3}{h^3} + O({h^4}) $ | (1) |
其中g1、g2等参数与离散过程无关。
对于二阶精度方法g1 = 0,此时只需离散步长分别为h1和h2时的离散解f1、f2即可求得离散无关解
| $ {f_{{\rm{exact}}}} = \frac{{h_2^2{f_1} - h_1^2{f_2}}}{{h_2^2 - h_1^2}} $ | (2) |
根据离散解f1、f2计算方法的不同,外插
采用Roache[5]的方法Richardson外插可推广至p阶方法,可称之为广义 Richardson外插方法。此时离散解与精确解之间的关系可以表示为:
| $ f = {f_{{\rm{exact}}}} + {g_p}h_{}^p + O({h^{p + 1}}) $ | (3) |
对于非定常问题时间离散,选取时间步长h3>h2>h1及其对应计算结果f1、f2、f3,代入公式(3)可得:
| $ \begin{split} &{f_1} = {f_{{\rm{exact}}}} + {g_p}h_1^p + O({h^{p + 1}_1})\\ &{f_2} = {f_{{\rm{exact}}}} + {g_p}h_2^p + O({h^{p + 1}_2})\\ &{f_3} = {f_{{\rm{exact}}}} + {g_p}h_3^p + O({h^{p + 1}_3}) \end{split} $ | (4) |
由式(4)可得精度p:
| $ p = \frac{1}{{\ln ({r_{21}})}}\left| {\ln \left| {\left. {\frac{{{\varepsilon _{32}}}}{{{\varepsilon _{21}}}}} \right| + q(p)} \right.} \right| $ | (5) |
| $ q(p) = \ln \left( {\frac{{r_{21}^p - s}}{{r_{32}^p - s}}} \right) $ | (6) |
| $ s = 1 \cdot {\rm{sgn}} \left(\dfrac{\varepsilon _{32}}{\varepsilon _{21}}\right) $ | (7) |
其中:
| $ \begin{split}& {r_{21}} = {h_2}/{h_1},\;{r_{32}} = {h_3}/{h_2}\\ &{\varepsilon _{21}} = {f_2} - {f_1},\;{\varepsilon _{32}} = {f_3} - {f_2} \end{split} $ |
为保证分析结果准确性,时间步长选取时需要保证
外插得到“精确解”:
| $ \tilde f_{{\rm{exact}}}^{21} = (r_{21}^p{f_1} - {f_2})/(r_{21}^p - 1) $ | (8) |
需要说明的是,此处“精确解”
在使用Richardson外插方法进行分析的过程中,需要注意所选结果离散步长不能够太大,此时计算过程没有充分收敛,分析过程中忽略的高阶项会对分析结果产生影响,使分析结果具有很强的不确定性。
1.3 验证方法采用上述结果可继续进行误差及不确定度估计。
近似相对误差:
| $ e_a^{21} = \left| {\frac{{{f_1} - {f_2}}}{{{f_1}}}} \right| \times 100\% $ | (9) |
外插相对误差:
| $ e_{{\rm{exact}}}^{21} = \left| {\frac{{\tilde f_{{\rm{exact}}}^{21} - {f_1}}}{{\tilde f_{{\rm{exact}}}^{21}}}} \right| \times 100\% $ | (10) |
网格收敛指数[7]:
| $ I_{{\rm{GC}}}^{21} = \frac{{e_a^{21}}}{{r_{21}^p - 1}}{F_s} \times 100\% $ | (11) |
本文选取安全系数
本文研究工作基于TRIP软件气动弹性模块[8-9]开展。该模块主要包括流场计算、结构计算、耦合界面插值和动网格四个主要功能部分,依照耦合计算方法的流程依次调用。
2.1 计算方法流场求解器采用课题组自主开发的亚跨超声速CFD软件平台TRIP。经过课题组多年的发展,TRIP已经成为一个非常成熟的数值模拟软件平台,大量验证工作[10-11]表明TRIP软件具有较高的计算精度和效率。
结构求解模块采用基于模态坐标的气动弹性运动方程,可使用龙格库塔法、线性多步法、双时间步方法等多种方法求解。为避免CFD/CSD耦合求解中的质量不相似问题,本文采用变刚度方法[12-13]确定颤振边界。
动网格模块集成了目前工程应用中常用的TFI、Delaunay以及RBF插值方法,以及基于这些基础方法开发的一些复合型动态网格变形方法,如RBF_TFI、RBF_Delaunay等。界面插值模块集成了无限平板样条IPS、薄板样条TPS和径向基函数插值RBF三种插值方式。本文二维算例Isogai Wing模型为二元翼型,满足刚体运动假设,动网格方法采用刚性旋转法。为简化计算,该算例中结构求解部分与流场求解采用相同网格,无需使用界面插值技术。
2.2 耦合方法目前实际应用中的耦合计算方法主要分为松耦合和紧耦合两类。松耦合方法通过交替求解流场和结构方程进行时间推进,不在单场求解过程中进行流场与结构的数据交换。该方法能够充分利用现有的流场和结构求解器,实现过程简单,应用广泛。但是松耦合方法为了计算简便往往造成流场和结构的时间不同步,耦合精度只有一阶。为提高松耦合方法计算精度,部分学者采用预估校正思想对松耦合方法进行改进,提出了具有二阶精度的改进的松耦合方法[14-16]。紧耦合方法则是将流场和结构方程均构造为子迭代形式[17-18],在每个物理时间步内,对流场和结构进行多次数据交换,来消除流场与结构信息交换不同步的问题,时间精度能够达到二阶。
为充分验证所建立精度分析方法的可靠性,本文分别选取松耦合方法、改进的松耦合方法和紧耦合方法的结果进行分析。松耦合方法采用冻结气动力的龙格库塔方法[14],即在松耦合流程中结构求解使用简化的龙格库塔方法。作为对照,使用相同耦合流程,使用双时间步方法作为结构求解方法,构造了使用双时间步方法的松耦合方法,两种松耦合方法理论时间精度均为一阶。改进的松耦合方法采用二阶杂交的线性多步法[15],理论精度为二阶。本文所使用紧耦合方法根据文献[17]构造,理论精度为二阶。同时作为对照,本文将龙格库塔方法作为结构求解嵌入流场求解子迭代过程中,自行构造了一种一阶精度的紧耦合方法。本文选取上述多种精度的共五种耦合方法进行计算,并对计算结果进行精度分析。五种耦合方法的对比如表1所示。
| 表 1 耦合方法对比 Table 1 Comparison of coupling methods |
|
|
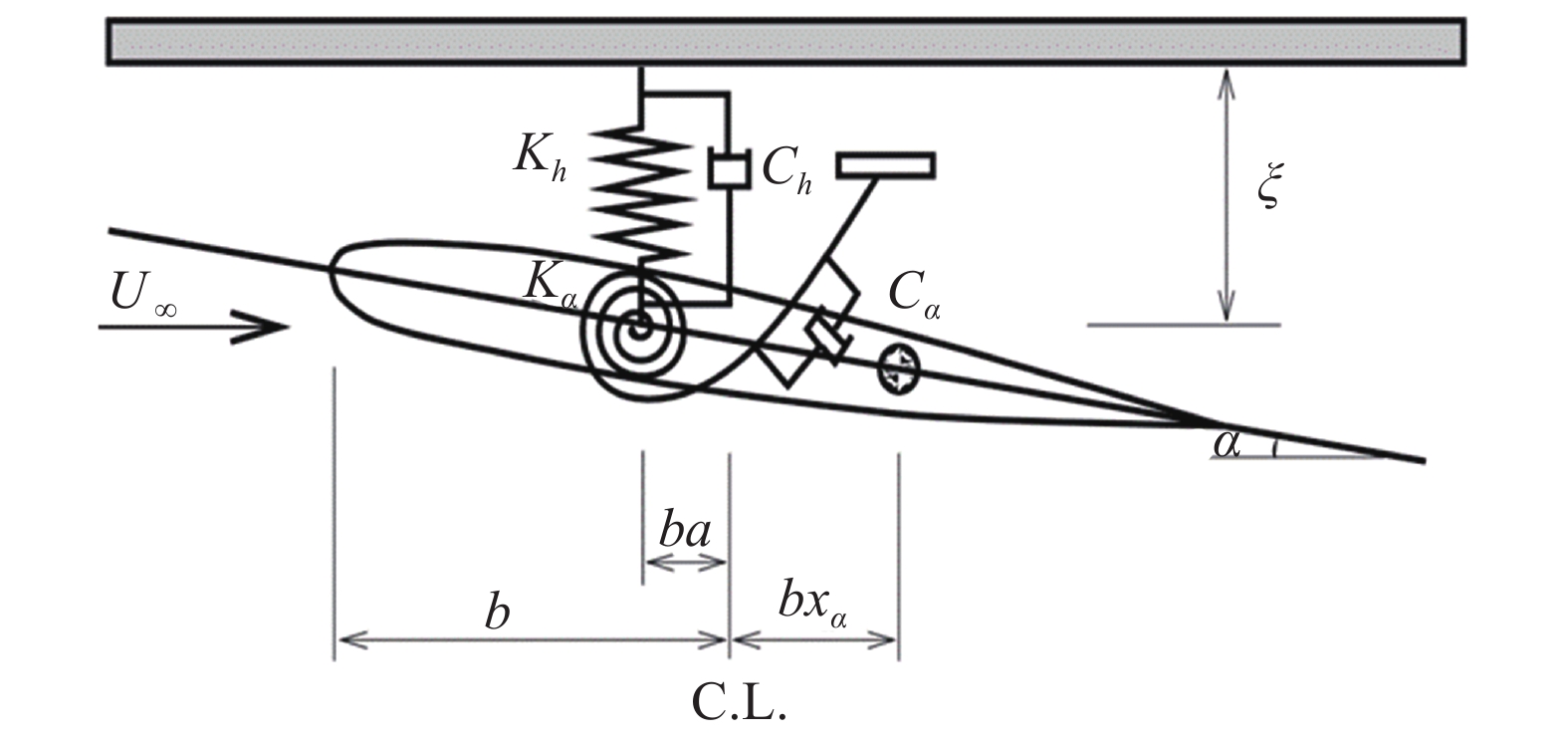
Isogai Wing[19-21]是由Isogai提出的后掠机翼颤振问题的典型截面,是检验气弹不稳定性预测方法的二维标准算例。翼型截面采用NACA010翼型,属于二元机翼,翼型结构如图1所示。图中来流速度为U∞ ,机翼半弦长b = 0.5 m,在弹性轴(对应于刚心)处固定一个垂直方向的线弹簧以及一个扭转弹簧,弹簧刚度分别为Kn和Kα,弹簧阻尼分别为Ch和Cα。选取机翼后缘一侧为正方向,弹性轴在距翼弦中点(C.L.)ab
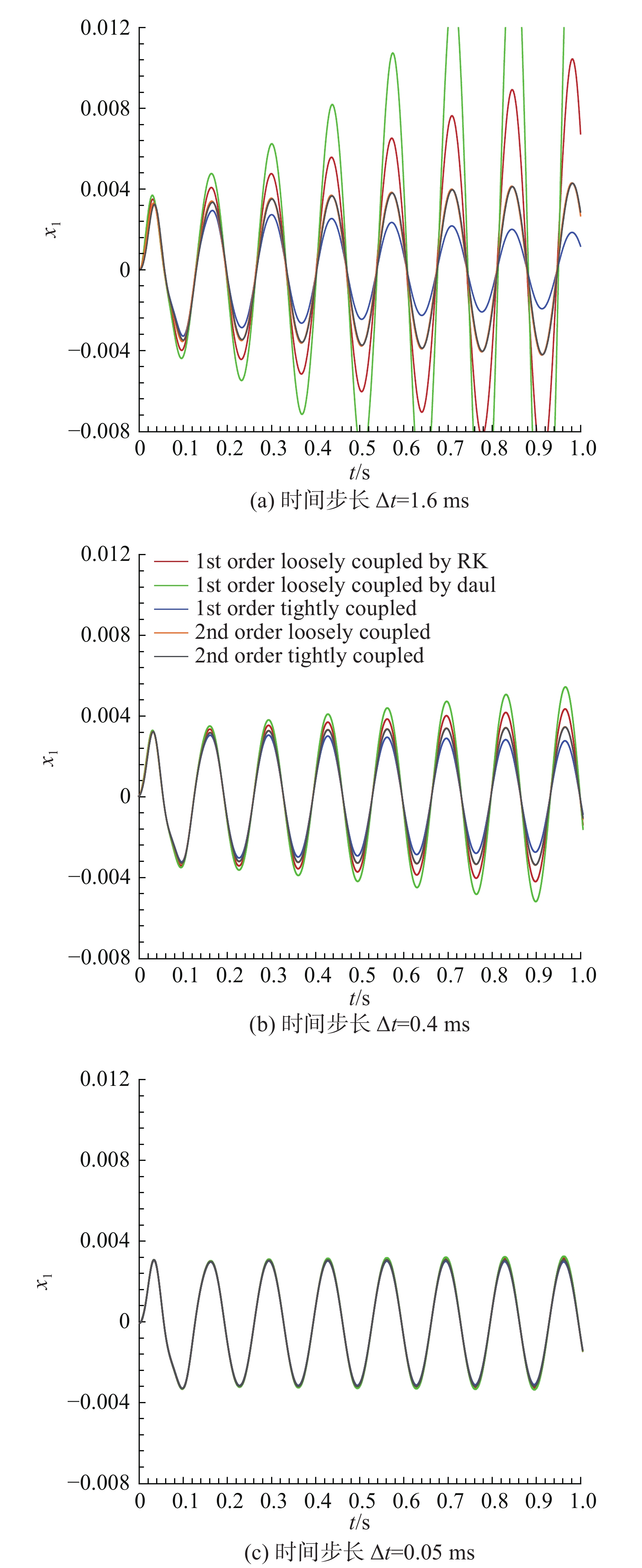
选取Ma = 0.6,颤振临界状态下无量纲来流速度vf = 1.710,不同时间步长下五种耦合方法的结构响应对比如图2所示,横轴为时间t,纵轴为结构一阶广义位移x1。
|
图 2 不同时间步长下机翼时域结构响应对比 Fig.2 Comparison of time domain structural response with different time step sizes |
由结果对比可知,时间离散步长对计算结果具有显著影响。由图2(a)可知,时间步长较大时,五种耦合方法的结构响应存在较大差异,表明此时不同耦合方法的颤振边界存在较大差异;随着时间步长的减小(图2(b)),结果趋向一致,颤振边界趋向收敛;时间步长进一步减小(图2(c))五种方法所得结果基本重合,此时五种方法所得颤振边界基本一致,即可推断随着时间步长减小各耦合方法计算颤振边界均趋向收敛,时间步长足够小时五种耦合方法均能够得到正确结果。
通过图2可以对五种耦合方法进行初步精度分析:两种二阶精度耦合方法计算所得结构响应曲线基本重合,并且不受时间步长的影响,即两种二阶精度方法在计算中表现出的精度基本一致;三种一阶精度耦合方法结构响应存在一定差异,即实际计算精度存在差异,结构求解采用双时间步方法的松耦合方法精度略小于冻结气动力的龙格库塔方法、一阶精度的紧耦合方法计算精度小于两种二阶精度方法。由于随时间步长减小结构响应曲线趋向收敛的方向不同,这种定性分析方法并不能够直接对比一阶精度的松耦合方法与二阶精度方法的计算精度,这也说明了本文所建立的精度分析方法的必要性。
4 Isogai Wing模型数值精度分析为系统地研究时间离散对计算结果的影响,在Ma= 0.6条件下选取一系列时间离散步长计算模型的颤振边界。颤振边界的确定采用对数减幅法,选取颤振临界速度和颤振临界频率作为目标变量进行分析。
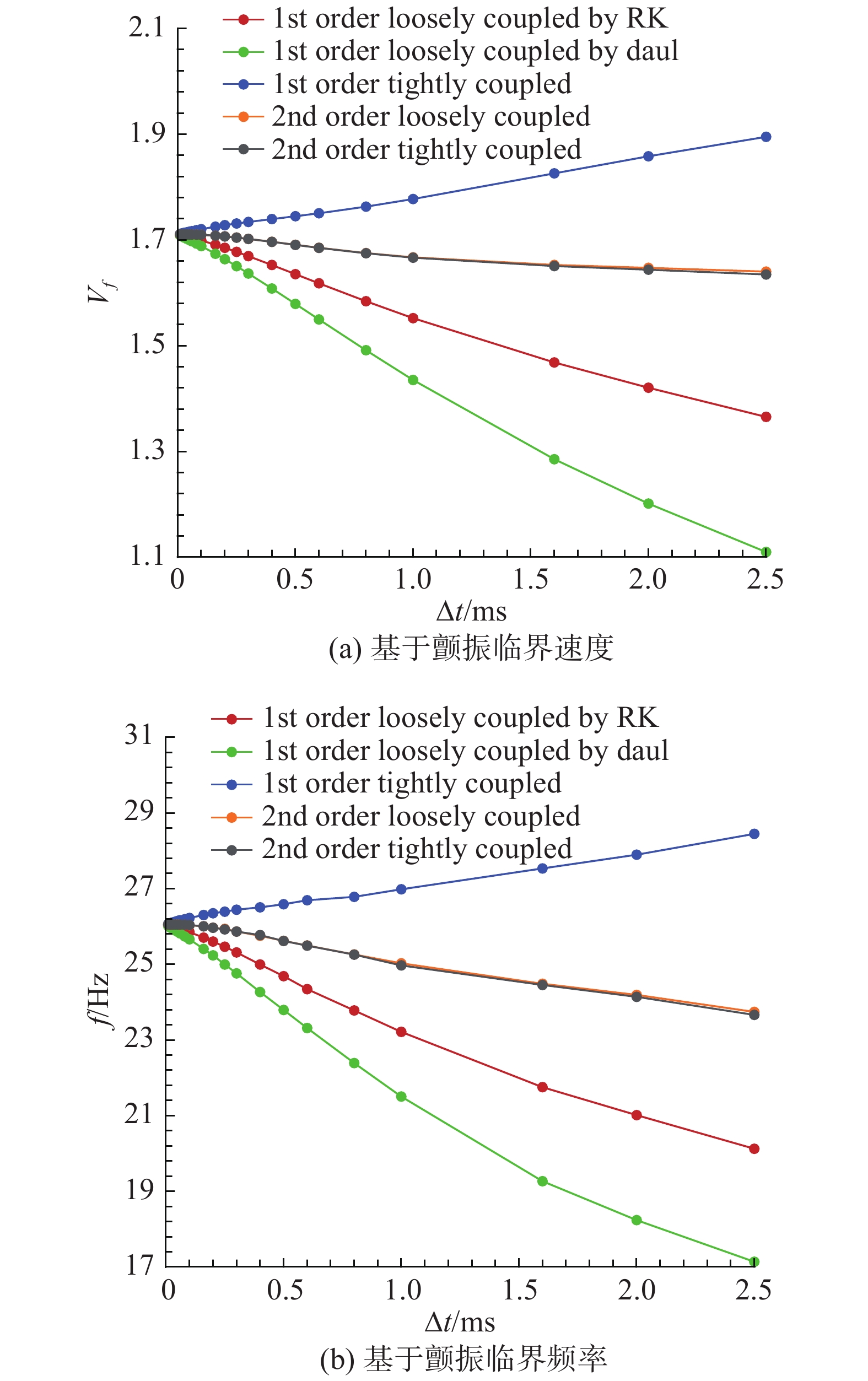
4.1 时间收敛性为确定计算结果的时间收敛性,如图3所示,对比五种方法在不同时间步长下的颤振临界速度和颤振频率。五种方法颤振临界速度和颤振频率均随时间步长的减小而单调变化,最终收敛于同一点。即五种方法均具有良好的时间收敛性,可以使用Richardson外插方法进行分析。
|
图 3 不同时间步长下Isogai Wing模型颤振边界计算结果 Fig.3 Flutter boundary simulation results of Isogai Wing with different time step sizes |
首先选取合适时间步长及其计算结果。根据1.2节分析,所选取时间步长不应过大,同时应使r大于1.3,另考虑对数减幅法判断颤振临界状态带来的误差,同样需要避免选取过小的时间步长,最终选取时间步长0.05 、0.1、0.2 ms,即每周期约800、400、200个时间步。
使用广义Richardson外插方法分析所选计算结果实际精度,并计算不确定度。基于颤振临界速度分析可得表2。结果表明,分析所得精度p与理论精度基本相符。两种松耦合方法和两种二阶精度耦合方法实际精度均略高于理论精度,一阶精度紧耦合方法精度略低于理论精度。冻结气动力的龙格库塔方法精度略高于采用双时间步方法的松耦合方法,改进的松耦合方法和传统紧耦合方法精度均高于一阶精度紧耦合方法,改进的松耦合方法和传统紧耦合方法精度及误差基本相同,与3.2节的定性分析结果一致,说明该方法得到了可信的分析结果。五种方法插值所得时间离散无关解
| 表 2 基于颤振临界速度的时间精度分析结果 Table 2 Time accuracy analysis results based on the flutter critical velocity |
|
|
如表3所示,基于颤振临界频率与颤振临界速度的分析结果基本一致。但是一阶精度紧耦合方法、改进的松耦合方法和传统紧耦合方法精度与颤振临界速度分析结果均有一定差异,表明使用广义Richardson外插方法进行精度分析时,所选取目标量对分析结果有一定影响。
| 表 3 基于颤振临界频率的时间精度分析结果 Table 3 Time accuracy analysis results based on the flutter critical frequency |
|
|
若计算要求颤振临界速度误差小于1%,各耦合方法能够取的最大时间步长如表4所示。二阶精度耦合方法能够大幅提高计算效率,体现了进行精度分析的重要意义。
|
表 4 外插相对误差小于1%时的最大时间步长
Table 4 Maximum time step for
|
|
|
基于广义Richardson外插方法进行时间精度分析需要选取三个计算时间步长的计算结果,因此需要考虑特定时间步长是否对分析结果产生影响。为避免所选时间步长结果带来的偶然性,对4.1节使用的计算结果进行进一步处理,以确定该方法进行时间精度分析的可行性。
以上述计算结果为基础,将外插所得时间离散无关值

|
图 4 Isogai Wing模型颤振边界计算结果时间精度曲线 Fig.4 Time domain accuracy results for Isogai Wing with flutter boundaries |
如1.2节所述,在时间步长较大时,分析结果具有很强的不确定性,不适用于采用广义Richardson外插方法进行精度分析,因此图4中时间步长大于0.6 ms(每周期约60个时间步)时曲线线性度较差。在时间步长较小时,计算误差相对较小,使用对数减幅法判断颤振边界引入的误差对精度分析带来较大干扰,因此图4中时间步长小于0.04 ms (每周期约1 000个时间步)时,曲线线性度相对较差。若去除时间步长过大和过小的部分,曲线则具有良好的线性度。为更直观地说明剩余点拟合曲线良好的线性度,对时间步长在0.04~0.6 ms之间的点进行线性回归分析。线性回归所拟合直线如图5所示,直线斜率k和可决系数R2在表5和表6中给出。

|
图 5 Isogai Wing模型颤振边界计算结果线性回归拟合直线 Fig.5 Linear regression fitting for Isogai Wing with flutter boundaries |
| 表 5 基于颤振临界速度的线性回归分析结果 Table 5 Linear regression analysis results based on the flutter critical velocity |
|
|
| 表 6 基于颤振临界频率的线性回归分析结果 Table 6 Linear regression analysis results based on the flutter critical frequency |
|
|
拟合直线斜率k即耦合计算精度,可决系数R2则反映了拟合直线与选取数据点的接近程度。线性回归分析所得计算精度与4.2节分析结果基本一致,R2非常接近于1,数据点与拟合直线相当接近,即所选取数据点具有良好的线性度。线性回归结果表明在恰当的时间步长区间内,使用广义Richardson外插方法分析所得结果与具体时间步长选取无关,也进一步验证了本文所提出时间精度分析方法的可行性。
5 AGARD 445.6 Wing颤振计算及精度分析 5.1 计算模型AGARD 445.6 Wing [23-24]被广泛应用于颤振计算程序的验证工作。机翼材质为均匀的桃花心木薄板,1/4弦长处后掠角为45°,机翼截面为NACA65A004对称翼型。本文计算网格单元数为321万,结构计算选取前四阶模态,模态频率为试验所得频率,计算马赫数0.499。
5.2 时间精度分析选取颤振临界速度和颤振临界频率为分析变量,分析三维颤振标模AGARD 445.6的计算精度。由于计算量的限制,相较于二维算例,所选计算时间步长及耦合方法较少。
如图6所示,该算例具有良好的时间收敛性,可以使用Richardson外插方法进行精度分析。根据1.2节及4.2节所述时间步长选取原则,考虑一阶精度与二阶精度耦合方法收敛性的差异,一阶精度松耦合方法选取时间步长为0.05、0.1、0.2 ms (每周期约900、450、225个时间步),改进的松耦合方法选取时间步长为0.2、0.4、0.8 ms (每周期约225、113、57个时间步)。

|
图 6 不同时间步长下AGARD 445.6 Wing模型颤振边界计算结果 Fig.6 Flutter boundary simulation results of AGARD 445.6 Wing with different time step sizes |
采用上述时间步长结果进行精度分析,结果如表7、表8所示。改进的松耦合方法基于颤振临界速度的精度与理论精度差异稍大,其余分析精度与理论精度基本一致。由于三维问题更为复杂,相较于二维算例分析结果,两种耦合方法实际计算精度均有所下降。对于两个目标变量,两种耦合方法得到的时间离散无关解误差分别为0.07%、0.18%,均得到了一致的“精确解”。由以上分析结果可知,该精度分析方法在该三维算例中得到了合理的分析结果。
| 表 7 基于颤振临界速度的时间精度分析结果 Table 7 Time accuracy analysis results based on the flutter critical velocity |
|
|
| 表 8 基于颤振临界频率的时间精度分析结果 Table 8 Time accuracy analysis results based on theflutter critical frequency |
|
|
为进一步研究三维算例中时间步长选取对分析结果的影响。采用4.3节所述方法,得到如图7所示精度曲线。由于计算结果已经收敛,计算误差相对较小,改进的松耦合方法精度曲线在小时间步长处线性度较差。由于精度较低,松耦合方法精度曲线在较大时间步长处线性度较差。两种耦合方法结果分别去除较小时间步长或较大时间步长的点进行线性回归分析,分析结果如表9、表10所示,拟合直线如图7虚线所示。

|
图 7 AGARD 445.6 Wing模型颤振边界计算结果时间精度曲线 Fig.7 Time domain accuracy results for AGARD 445.6 Wing with flutter boundaries |
| 表 9 基于颤振临界速度的线性回归分析结果 Table 9 Linear regression analysis results based on the fluttercritical velocity |
|
|
| 表 10 基于颤振临界频率的线性回归分析结果 Table 10 Linear regression analysis results based onthe flutter critical frequency |
|
|
线性回归分析所得计算精度k与表7、表8分析结果基本一致;R2均大于0.99,即数据点与拟合直线相当接近,具有良好的线性度。线性回归结果表明,在恰当的时间步长区间内,使用广义Richardson外插方法分析所得结果与具体时间步长选取无关,进一步验证了本文所提出时间精度分析方法针对三维颤振问题的可行性。
6 结 论本文参照网格收敛性分析方法,对颤振问题的时域模拟结果进行了时间收敛性和计算精度分析,建立了基于广义Richardson外插方法的时间精度分析方法,并对该分析方法进行了验证。
分析结果表明:
1)本文建立的颤振问题模拟时间精度的分析方法,相较于传统的定性分析方法,能够更为准确地反映颤振问题时域模拟中的计算精度和误差,为耦合方法及时间步长的选取提供依据;
2)相比于一阶精度方法,二阶精度耦合方法实际计算中表现精度更高,具有明显的精度优势,能够减小颤振计算所需时间步长,提高计算效率;
3)基于广义Richardson外插方法分析所得精度与理论分析基本一致,分析结果可靠。线性回归分析证明,在合适的时间步长区间内,分析所得结果与具体时间步长选取无关。因此,本文提出的时间精度分析方法能够应用于颤振问题时域模拟的时间精度分析。
致谢:本文得到了课题组洪俊武、孙岩、李伟和杨小川等人的帮助,在此表示衷心的感谢。
| [1] |
计算流体力学中的验证与确认[J]. 力学进展, 2007, 37(2): 279-288. DENG X G, ZONG W G, ZHANG L P, et al. Verification and validation in computational fluid dynamics[J]. Advances in Mechanics, 2007, 37(2): 279-288. DOI:10.3321/j.issn:1000-0992.2007.02.011 (in Chinese) |
| [2] |
AIAA. Guide for the verification and validation of computational fluid dynamics simulations: AIAA G-077-1998[S]. Reston: American Institute of Aeronautics and Astronautics Strandards Department, 1998: 1-29.
|
| [3] |
RICHARDSON L F. IX. The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam[J]. Philosophical Transactions of the Royal Society of London Series A, Containing Papers of a Mathematical or Physical Character, 1911, 210(459-470): 307-357. DOI:10.1098/rsta.1911.0009 |
| [4] |
RICHARDSON L F, ARTHUR GAUNT J. VIII. The deferred approach to the limit[J]. Philosophical Transactions of the Royal Society of London Series A, Containing Papers of a Mathematical or Physical Character, 1927, 226(636-646): 299-361. DOI:10.1098/rsta.1927.0008 |
| [5] |
ROACHE P J, KNUPP P M. Completed Richardson extrapolation[J]. Communications in Numerical Methods in Engineering, 1993, 9(5): 365-374. DOI:10.1002/cnm.1640090502 |
| [6] |
CELIK I, GHIA U, ROACHE P J, et al. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications[J]. Journal of Fluids Engineering, 2008, 130(7): 078001. DOI:10.1115/1.2960953 |
| [7] |
ROACHE P J. Perspective: a method for uniform reporting of grid refinement studies[J]. Journal of Fluids Engineering, 1994, 116(3): 405-413. DOI:10.1115/1.2910291 |
| [8] |
TRIP软件的静气动弹性计算模块开发及精度验证[J]. 空气动力学学报, 2017, 35(5): 620-624. SUN Y, HUANG Y, WANG Y T, et al. Development and precision validation of static aeroelastic computational module on flow solver TRIP[J]. Acta Aerodynamica Sinica, 2017, 35(5): 620-624. DOI:10.7638/kqdlxxb-2015.0154 (in Chinese) |
| [9] |
超大规模气动弹性数值模拟软件研制(2017)[J]. 空气动力学学报, 2018, 36(6): 1019-1026. WANG Y T, MENG D H, SUN Y, et al. Software development of ultra-scale numerical simulaiton for aero-elastic problem(2017)[J]. Acta Aerodynamica Sinica, 2018, 36(6): 1019-1026. DOI:10.7638/kqdlxxb-2018.0030 (in Chinese) |
| [10] |
DPWⅢ机翼和翼身组合体构型数值模拟[J]. 空气动力学学报, 2011, 29(3): 264-269. WANG Y T, WANG G X, ZHANG Y L. Numerical simulation of DPW Ⅲ wing and wing-body configurations[J]. Acta Aerodynamica Sinica, 2011, 29(3): 264-269. DOI:10.3969/j.issn.0258-1825.2011.03.002 (in Chinese) |
| [11] |
DPW4翼/身/平尾组合体的数值模拟[J]. 空气动力学学报, 2013, 31(6): 739-744. WANG Y T, ZHANG S J, MENG D H. Numerical simulation and study for DPW4 wing/body/tail[J]. Acta Aerodynamica Sinica, 2013, 31(6): 739-744. (in Chinese) |
| [12] |
跨音速颤振计算方法研究[J]. 航空学报, 2004, 25(3): 214-217. LU Z L, GUO T Q, GUAN D. A study of calculation method for transonic flutter[J]. Acta Aeronautica et Astronautica Sinica, 2004, 25(3): 214-217. DOI:10.3321/j.issn:1000-6893.2004.03.002 (in Chinese) |
| [13] |
郭同庆. 复杂组合体跨音速非定常气动力和颤振计算[D]. 南京: 南京航空航天大学, 2006. GUO T Q. Transonic unsteady aerodynamics and flutter computations for complex assemblies[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2006 (in Chinese). |
| [14] |
一种改进的气动弹性时域推进方法[J]. 振动与冲击, 2005, 24(5): 118-120. ZHANG W W, LYU L L, YE Z Y. Improved time-marching technique for solving aeroelastic equations[J]. Journal of Vibration and Shock, 2005, 24(5): 118-120. DOI:10.3969/j.issn.1000-3835.2005.05.036 (in Chinese) |
| [15] |
基于CFD技术的流场/结构时域耦合求解方法研究[J]. 振动工程学报, 2007, 20(4): 396-400. JIANG Y W, ZHANG W W, YE Z Y. Study of time-marching method for fluid/structure coupling solution based on CFD technique[J]. Journal of Vibration Engineering, 2007, 20(4): 396-400. DOI:10.16385/j.cnki.issn.1004-4523.2007.04.012 (in Chinese) |
| [16] |
二阶时间精度的CFD/CSD耦合算法研究[J]. 空气动力学学报, 2009, 27(5): 547-552. AN X M, XU M, CHEN S L. Analysis for second order time accurate CFD/CSD coupled algorithms[J]. Acta Aerodynamica Sinica, 2009, 27(5): 547-552. DOI:10.3969/j.issn.0258-1825.2009.05.008 (in Chinese) |
| [17] |
飞行器跨声速气动弹性数值分析[J]. 力学学报, 2005, 37(6): 769-776. YANG G W, QIAN W. Numerical analyses of transonic flutter on an aircraft[J]. Acta Mechanica Sinica, 2005, 37(6): 769-776. DOI:10.3321/j.issn:0459-1879.2005.06.014 (in Chinese) |
| [18] |
计算气动弹性若干研究进展[J]. 力学进展, 2009, 39(4): 406-420. YANG G W. Recent progress on computational aeroelasticity[J]. Advances in Mechanics, 2009, 39(4): 406-420. DOI:10.3321/j.issn:1000-0992.2009.04.004 (in Chinese) |
| [19] |
ISOGAI K. On the transonic-dip mechanism of flutter of a sweptback wing[J]. AIAA Journal, 1979, 17(7): 793-795. DOI:10.2514/3.61226 |
| [20] |
ISOGAI K. Transonic dip mechanism of flutter of a sweptback wing. II[J]. AIAA Journal, 1981, 19(9): 1240-1242. DOI:10.2514/3.7853 |
| [21] |
ALONSO J, JAMESON A. Fully-implicit time-marching aeroelastic solutions[C]//32nd Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 1994: 1-12.doi: 10.2514/6.1994-56.
|
| [22] |
MARQUES S, TIMME S, BADCOCK K J, et al. ECERTA Project [EB/OL]. (2012-05-02)[2019-05-05]. http://www.cfd4aircraft.com/research_ecerta_isogai.html
|
| [23] |
YATES Jr E C. AGARD standard aeroelastic configuration for dynamic response, candidate configuration I.– Wing 445.6: NASA-TM-100492 [R]. NASA, 1987: 1-73.
|
| [24] |
SILVA W A, CHWALOWSKI P, PERRY B. Evaluation of linear, inviscid, viscous, and reduced-order modelling aeroelastic solutions of the AGARD 445.6 wing using root locus analysis[J]. International Journal of Computational Fluid Dynamics, 2014, 28(3-4): 122-139. DOI:10.1080/10618562.2014.922179 |
 2021, Vol. 39
2021, Vol. 39