飞机结冰广泛存在于飞行实践中,并严重威胁飞行安全[1-2]。民用航空适航规章要求制造商通过结冰防护等手段,确保飞机在结冰气象条件下的飞行安全。结冰风洞试验[3],即利用结冰风洞在地面模拟飞机结冰过程验证飞机防除冰系统性能,是目前重要的飞机结冰适航审定手段,已经广泛应用于飞机适航审定实践中。为满足结冰风洞适航应用要求[4],结冰风洞必须开展全面的流场品质评估,以验证其适航符合性,其中气流场品质是重要的评估验证内容。
美国NASA Glenn IRT结冰风洞在该领域最早开展研究[5],建立了系统的气流场校测方法,该风洞围绕1999年和2011年开展的两次大型设备升级改造[6-11],相继开展了多期气流场校测,采用风洞试验和数值计算两种手段,全面评估了改造后的风洞稳定段和试验段内流场品质,支撑了该风洞流场的适航符合性验证。意大利CIRA IWT结冰风洞作为目前国际上尺寸最大、性能最完善的结冰风洞之一[12],同样发展了配套的气流场校测设备和方法,开展了全面的气流场校测,为该风洞适航应用奠定了基础[13]。此外,美国Cox结冰风洞于2007年也开展了气流场校测[14],评估了气流场品质,进而为风洞升级改造提供了数据支撑。但是,我国在大型结冰风洞气流场适航符合性验证方面缺乏系统的研究,仅针对小尺寸风洞,开展了部分仪器应用研究[15]。近年来,随着国内大型结冰风洞3 m × 2 m结冰风洞的建成,其适航符合性亟待得到验证,其中气流场是符合性验证的关键一环。
因此,鉴于目前国内研究现状以及急迫的型号试验需求,本文首先发展结冰风洞气流场适航符合性验证方法,然后针对3 m × 2 m结冰风洞主试验段构型,开展气流场适航符合性验证试验,考察试验段气流速度和喷嘴干空气射流对流场特征参数(气流速度、气流偏角和气流湍流度)的影响,最后评估试验段内气流场空间均匀性和时间稳定性,获得试验段气流总压、静压和马赫数修正关系,形成结冰风洞气流场控制包线,为3 m × 2 m结冰风洞适航应用奠定基础。
1 3 m × 2 m结冰风洞简介中国空气动力研究与发展中心3 m × 2 m结冰风洞是一座闭口回流式高亚声速风洞(图1),主要包括结冰喷雾系统、制冷系统、高度模拟系统和风机动力系统。结冰喷雾系统利用喷雾耙和喷嘴产生结冰云雾,其中喷雾耙安装于稳定段蜂窝器下游、收缩段入口位置,共有20排,每排设置了50个喷嘴安装位置,共计1 000个喷嘴。该风洞拥有三个可更换的试验段:主试验段、次试验段和高速试验段,三个试验段收缩比分别为14.67、5.73和29.33。本文仅针对主试验段构型开展研究,主试验段尺寸为6.5 m(长) × 3 m (宽) × 2 m(高)。

|
图 1 3 m × 2 m结冰风洞 Fig.1 Configuration of the icing wind tunnel at CARDC |
结冰风洞总压和静压探针如图2所示。总静压探针为自研设备,均具有加热功能,用于结冰风洞动力系统气流速度控制,其中总压探针位于喷雾耙与蜂窝器之间,共计4根,分别安装于各洞壁水平中心线处,静压探针位于试验段入口,在左右洞壁各布置2根探针。

|
图 2 结冰风洞总压和静压探针 Fig.2 Total and static pressure probes inthe icing wind tunnel of CARDC |
结冰风洞气流场适航符合性验证方法流程图如图3所示,该方法主要包括试验标准、试验内容、试验仪器、试验方法和数据处理五部分内容,本节将分别进行详细论述。

|
图 3 结冰风洞气流场适航符合性验证方法流程图 Fig.3 Flow diagram of the airworthiness compliance verification method for the aerodynamic flowfield of icing wind tunnels |
《Calibration and Acceptance of Icing Wind Tunnels》(SAE ARP5905)为国际结冰适航领域公认的结冰风洞流场校测和符合性标准[16],是结冰风洞气流场适航符合性验证的基础。该标准给出了结冰风洞气流场品质指标,如表1所示。表中针对气流速度、气流偏角和湍流度三个流场特征参数,分别给出了测试设备最大不确定度、空间均匀性、风洞中心线时间稳定性和最大限制范围四个典型参数的符合性指标。因此,本文依据SAE ARP5905标准,以气流速度、气流偏角和湍流度三个流场特征参数为试验对象,考察试验段气流速度和喷嘴干空气射流对流场参数的影响,评估其空间均匀性和时间稳定性,进而验证气流场适航符合性。
| 表 1 结冰风洞气流场品质指标 Table 1 Quality indexes of the air flowfield of icing wind tunnels |
|
|
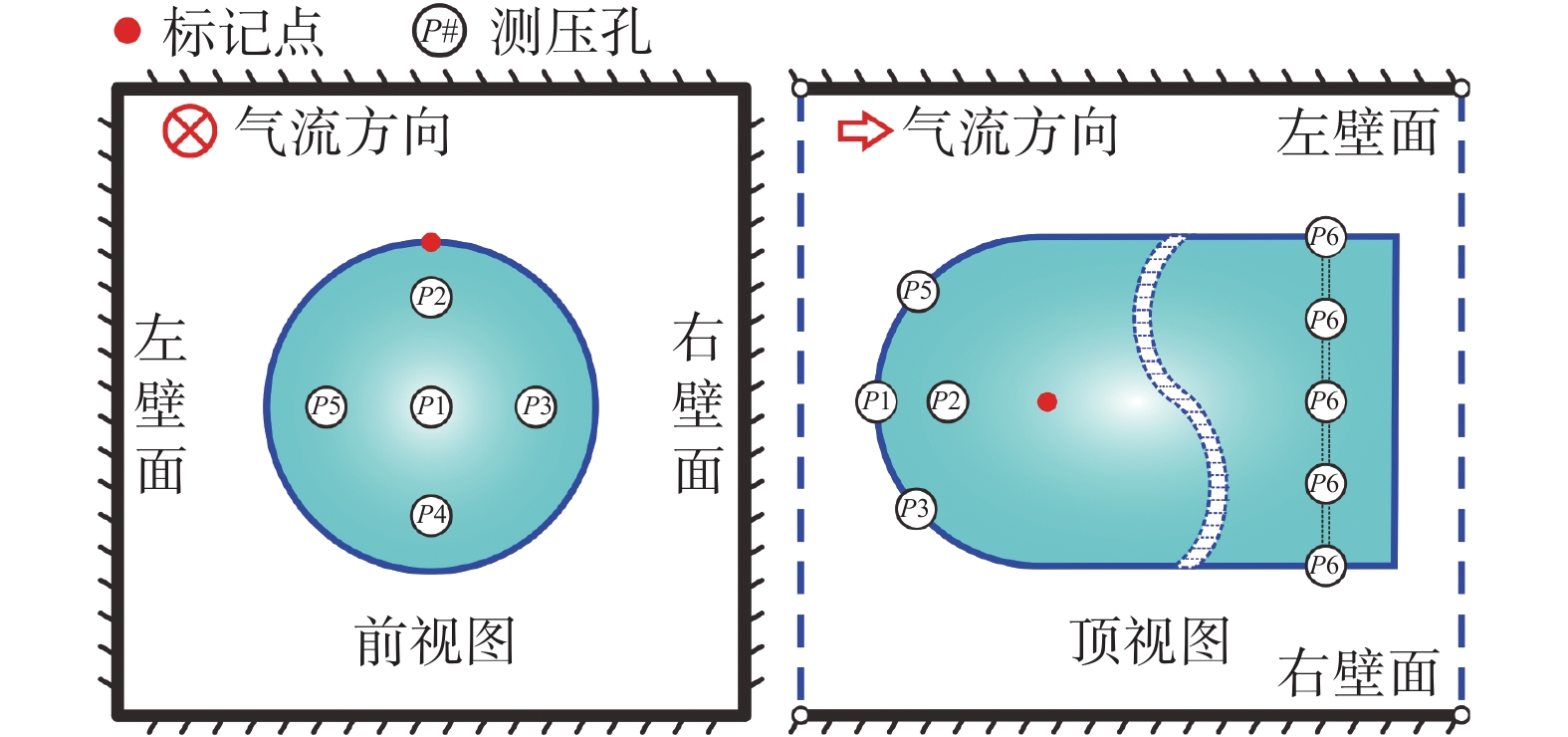
五孔气流方向探针和五孔探针排管架装置用于测量试验段内气流总静压和方向角,如图4所示。

|
图 4 五孔气流方向探针和五孔探针排管架 Fig.4 Five-hole flow angle probe and five-hole vertical rake |
五孔气流方向探针前端为半球形,总长370 mm,外径Φ

|
图 5 热线风速仪和热线排管架 Fig.5 Hot wire anemometer and hot wire vertical rake |
|
图 7 五孔气流方向探针测压孔位置示意图 Fig.7 Schematics of pressure tap positions of the five-hole probe |
五孔探针排管架装置尺寸为厚25 mm、宽200 mm、高2000 mm,其前缘设置9个探针安装孔,安装孔间距为200 mm。排管架竖直安装于试验段内,上下洞壁处设置了11个横向安装位置,位置间隔为230 mm。
热线风速仪和热线排管架装置用于测量试验段内气流湍流度,如图6所示。

|
图 6 五孔探针排管架测量点位置矩阵 Fig.6 Location matrix of measuring points of thefive-hole vertical rake |
热线风速仪由热线探针和数据分析机组成,其中热线探针外径Φ4 mm、长250 mm,其前部安装热线探头,尾部通过BNC线连接至数据分析机。试验前对热线风速仪进行了校准,校准结果显示其速度测量精度和湍流度测量精度分别为1%和0.1%。应该指出的是,热线探头可以实现多维度速度矢量的测量,本期试验仅采用一维气流速度测量探头。
热线探针排管架装置尺寸为厚21 mm、宽250 mm、高2 000 mm,其前缘设置7个探针安装孔,安装孔间距为250 mm。排管架竖直安装于试验段内,上下洞壁处设置11个横向安装位置(与五孔探针排管架装置共用安装板),位置间隔为230 mm。
2.3 试验方法及数据处理 2.3.1 气流速度和气流偏角表2给出了气流速度和气流偏角试验工况,其中排管架测点位置如图7所示。试验段名义气流速度(VTS)选取40、80、100、120、140、160 m/s,覆盖主试验段主要试验速度范围。喷嘴喷气压力(pa)选取0、0.4、0.9 MPa,其中0 MPa和0.9 MPa分别对应喷嘴喷气关闭工况和喷嘴最大喷气压力工况。
| 表 2 气流速度和气流偏角试验工况 Table 2 Test conditions for airspeeds and airflow angularities |
|
|
图7所示的排管架测量点位置矩阵,其中x-y平面为风洞试验段测试截面,CP为试验段中心位置,x轴从试验段左壁(沿流向左侧为左壁)指向右壁,y轴从试验段下壁面指向上壁面。试验段内共设置11列测量位置(C1~C11),每列包括9个测量点,共计99个测量位置,测量点横向(x方向)和纵向(y方向)间距分别为230 mm和200 mm,分别覆盖77%横向和80%纵向试验段区域。
试验时,首先测量试验段中心处测量点(位置对应图7中C6列),然后沿x轴依次测量其余10个位置测量点(位置对应图7中C1~C5 和 C7 ~C11列),各测量点压力参数采样时间为60 s,采样频率为1 Hz。应该指出的是,在每个横向位置(x轴方向)压力测量前,应先测量排管架的安装俯仰角和偏航角,获得气流偏角修正参数。
试验后利用测量的压力参数,采用五孔探针计算公式,计算当地气流总静压、马赫数和气流偏角。根据五孔探针测压孔位置示意图(见图5),当地气流总压(pt,Local)、静压(ps,Local)和马赫数(MaLocal)计算式表示为:
| $\begin{split}& \begin{array}{*{20}{c}} {{p_{t,{\rm{Local}}}} = {p_1}\;,}&{{p_{s,{\rm{Local}}}} = {p_6}} \end{array}, \\& M{a_{{\rm{probe}}}} = \sqrt {\frac{2}{{\gamma - 1}}\left[ {{{\left( {\frac{{{p_1}}}{{{p_6}}}} \right)}^{\frac{{\gamma - 1}}{\gamma }}} - 1} \right]}\;, \\& M{a_{{\rm{Local}}}} = C\left( {M{a_{{\rm{probe}}}}} \right)M{a_{{\rm{probe}}}} \end{split} $ | (1) |
式中,Maprobe为探针计算马赫数,该参数经过修正获得当地气流马赫数;C(Ma)为马赫数修正系数,通过探针标定获得。
当地气流偏角包括俯仰角(α)和偏航角(β),计算公式为:
| $\begin{split} &{\alpha} = {K_{0,{\alpha }}}\left( {M{a_{{\rm{probe}}}}} \right) + {K_{1,{\alpha} }}\left( {M{a_{{\rm{probe}}}}} \right){C_{\alpha} } + {{\Delta} _{\alpha} }\;,\\& {\beta} = {K_{0,{\beta} }}\left( {M{a_{{\rm{probe}}}}} \right) + {K_{2,{\beta} }}\left( {M{a_{{\rm{probe}}}}} \right){C_{\beta }} + {{\Delta} _{\beta }}\;,\\& {\theta} = \sqrt {{{\alpha} ^2}{\rm{ + }}{{\beta }^2}} \;,\;{C_{\alpha} } = \frac{{{p_4} - {p_2}}}{{{p_1} - {p_6}}}\;,\;{C_{\beta }} = \frac{{{p_5} - {p_3}}}{{{p_1} - {p_6}}}\end{split}$ | (2) |
式中,θ、Cα和Cβ分别为当地气流偏角绝对角度、俯仰角压力系数和偏航角压力系数;K0, α、K1, α、K0,β和K2, β分别为俯仰角和偏航角系数,由探针标定获得;
气流速度和气流偏角空间分布以试验段中心线处流场参数为基准,采用马赫数比空间偏差(
| $\begin{split} \Delta M{{a}_{\rm{R}}} =& M{{a}_{\rm{R}}} - M{{a}_{{\rm{R,C}}}}\;,\;M{{a}_{\rm{R}}} = Ma{_{{\rm{TS}}}}/M{a_{{\rm{WT}}}}\;, \\ \Delta \alpha = &\alpha - {\alpha _{\rm{C}}}\;,\;\Delta \beta = \beta - {\beta _{\rm{C}}} \end{split} $ | (3) |
其中下标C表示试验段中心线参数,MaR、MaTS和MaWT分别为马赫数比、试验段马赫数和风洞马赫数。进而采用马赫数比空间偏差标准差(σ(∆MaR))和最大绝对值(|∆MaR|max)评估试验段内气流速度均匀性;同理,采用气流偏角空间偏差标准差(σ(∆α),σ(∆β))和最大绝对值(|∆α|max,|∆β|max)评估气流偏角均匀性。
气流速度时间分布以试验段中心线处马赫数时间平均值((MaC)mt)为基准,采用马赫数时间偏差(∆MaT)表征,表示为:
| $\Delta M{a_{\rm{T}}} = \frac{{M{{a}_{\rm{C}}}{\rm{ - }}{{\left( {M{{a}_{\rm{C}}}} \right)}_{{\rm{mt}}}}}}{{{{\left( {M{{a}_{\rm{C}}}} \right)}_{{\rm{mt}}}}}} \times 100\% $ | (4) |
式中下标mt表示时间平均。进而采用马赫数时间偏差标准差(σ(∆MaT))和最大绝对值(|∆MaT|max)评估试验段中心线处气流速度时间稳定性。
最后,利用试验段气流总压(pt,TS)、静压(ps,TS)和马赫数(MaTS)与风洞测量的气流总压(pt,WT)、静压(ps,WT)和马赫数(MaWT),获得试验段中心线处总压、静压和马赫数修正关系,表示为:
| $\begin{split}& {{p_{t,{\rm{TS}}}} =}{ {K_{p_{t}}}\left( {{p_{t,{\rm{WT}}}}} \right)\;,}\;{{p_{{s},{\rm{TS}}}} = {K_{p_{s}}}\left( {{p_{{s},{\rm{WT}}}}} \right)\;,} \\& M{a_{{\rm{TS}}}} = {K_{Ma}}\left( {{Ma_{{\rm{WT}}}}} \right) \end{split} $ | (5) |
式中,
气流湍流度试验工况如表3所示,其中测量点位置如图8所示;试验段名义气流速度选取40、60、80、100、120、140 m/s,其中120 m/s和140 m/s工况仅测量试验段中心线处(P5位置)的气流湍流度;喷嘴喷气压力(pa)选取0 MPa和0.4 MPa,其中0.4 MPa为常用试验条件下喷嘴最大喷气压力。
| 表 3 气流湍流度评估工况 Table 3 Test conditions for the turbulence intensity |
|
|

|
图 8 热线排管架测量点位置矩阵 Fig.8 Location matrix of measuring points of the hot wire probe rake |
热线探针排管架测量点位置矩阵如图8所示,图中坐标系统与图6相同。试验段内共设置11列测量位置,每列包括7个测量位置(对应探针安装位置),共计77个测量位置(如图灰色点所示),测量点间横向(x方向)和纵向(y方向)间距分别为230 mm和250 mm。实际试验中,考虑到热线探头易损坏等因素,仅测量试验段模型区内P1~P9九个位置的气流湍流度(如图红色点所示),其中P5为测试截面中心点位置。
试验前,应在试验段内对热线风速仪进行标定,标定风速范围覆盖试验范围(见表3)。试验时,为降低热线探头损坏的风险,仅进行单点测试,首先测量截面中心位置测量点(位置对应图8中P5点),然后依次测量其余8个位置(P1~P4 和 P6~P9),各测量点参数采样时间为5 s,采样频率为3 000 Hz。
试验后利用测量的风速参数,计算当地气流湍流度(TI),表达式为
| $\begin{split}& T\!I = \frac{1}{{{U_{{\rm{rms}}}}}}\sqrt {\frac{1}{{N{\rm{ - }}1}}\sum\limits_{i = 1}^N {{{\left( {{U_i} - {U_{{\rm{rms}}}}} \right)}^2}} } \times 100\% \\& {U_{{\rm{rms}}}} = \frac{1}{N}\sum\limits_{i = 1}^N {{U_i}} \end{split} $ | (6) |
式中,Ui、Urms和N分别为气流速度(沿流向一维速度)、平均速度和速度采样个数。
气流湍流度空间分布和时间分布以试验段中心线处气流湍流度(TITS,C)为基准,采用湍流度空间偏差(
| $\begin{split} \Delta {T\!I_{\rm{S}}} =& {\left( {{T\!I_{{\rm{TS}}}}} \right)_{{\rm{mt}}}} - {\left( {{T\!I_{{\rm{TS,C}}}}} \right)_{{\rm{mt}}}} \\ \Delta {T\!I_{\rm{T}}} =& {T\!I_{{\rm{TS,C}}}} - {\left( {{T\!I_{{\rm{TS,C}}}}} \right)_{{\rm{mt}}}} \end{split} $ | (7) |
式中TITS为试验段气流湍流度。进而采用湍流度空间偏差和时间偏差标准差(σ(
首先,为评估试验段气流速度空间均匀性,图9给出了试验段内马赫数空间分布云图,图中包括0 MPa和0.4 MPa两种喷嘴气压条件下40 m/s、80 m/s和160 m/s三个典型速度对应的试验结果,红色虚线框表示模型区,模型区范围为−920 mm≤x≤920 mm,−600 mm≤y≤600 mm。从图中可以看出:80 m/s和160 m/s工况下,马赫数分布一致性较好,其中模型区内马赫数比均在±1%范围内;但是在40 m/s工况下,马赫数空间分布差异较大,试验段内存在偏差超过2%的非均匀峰值区域,并且这些非均匀区域主要集中在C3(−670 mm)和C9(670 mm)位置,对应喷雾耙竖直支撑排架位置(见图1(b))。由此可见,喷雾耙结构会影响试验段内马赫数空间分布形态,进而导致40 m/s工况下形成了非均匀的气流速度峰值区。

|
图 9 试验段马赫数空间分布云图 Fig.9 Spatial distribution of the Mach number contour in the test section |
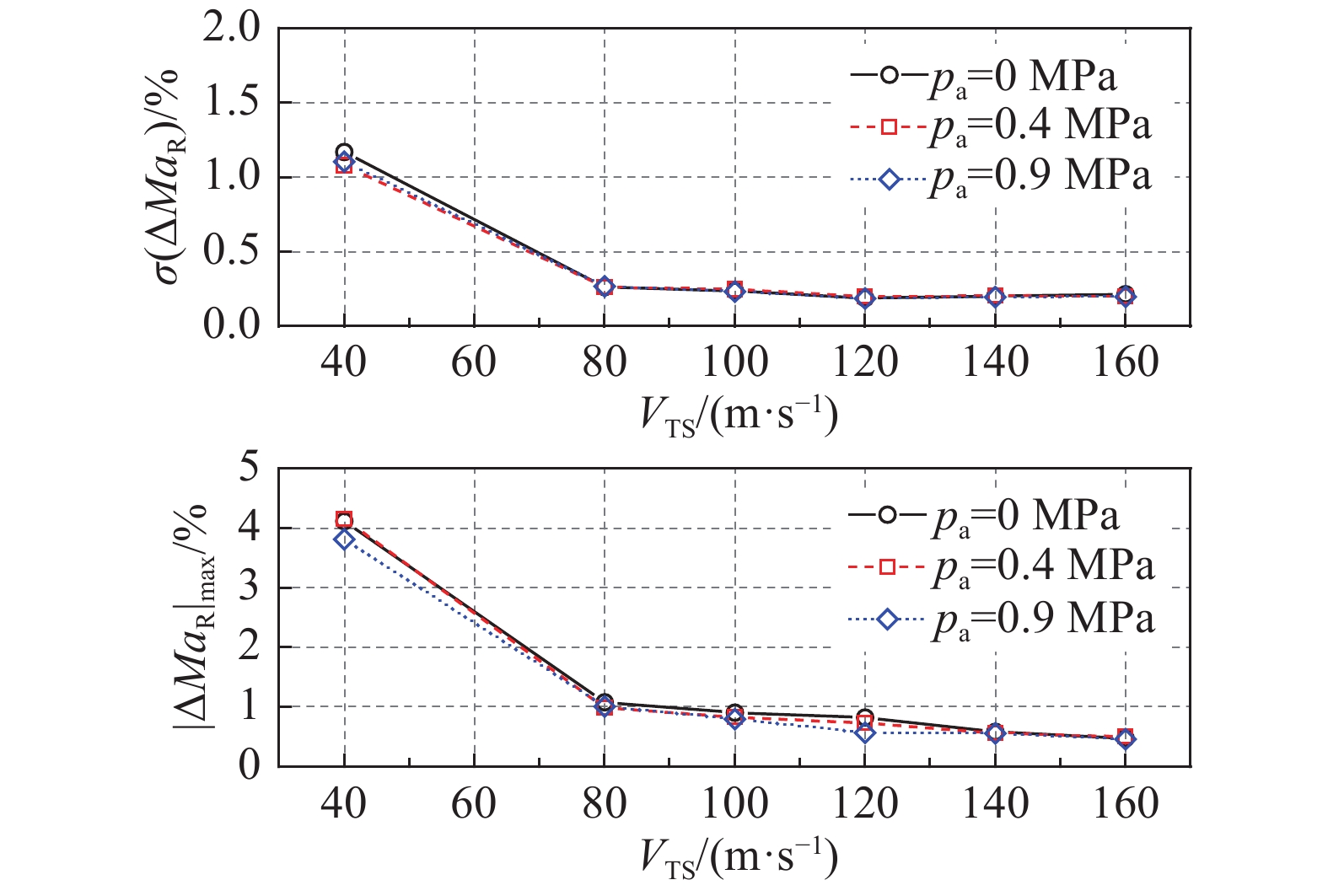
进一步,为定量评估试验段气流速度空间均匀性,图10给出了试验段模型区内马赫数比空间标准差和最大绝对值。从图中可以看出:随着气流速度的增加,马赫数比空间偏差标准差和最大绝对值不断减小,气流速度空间均匀性不断增强,尤其当气流速度超过80 m/s后,标准差和最大绝对值分布近似为0.25%和1%,但在40 m/s工况下分别近似为1.2%和4%,此时模型区内出现超过2%的非均匀峰值区;喷嘴干空气射流对气流速度均匀性并无显著影响,参数变化幅度小于0.5%。
|
图 10 试验段模型区内马赫数空间比偏差标准差和最大绝对值 Fig.10 Standard deviation and maximum absolute value of the Mach number ratio spatial deviation in the model area of the test section |
然后,为评估试验段中心线处气流速度时间稳定性,图11给出了试验段中心线处马赫数时间偏差变化曲线,图中包括0 MPa、0.4 MPa和0.9 MPa三种喷气状态下20 m/s、40 m/s、80 m/s和160 m/s四个速度对应的试验结果,从图中可以看出:各试验工况下,试验段中心线处马赫数时间偏差均在±2%范围内,其中20 m/s和40 m/s条件下气流马赫数出现显著的脉动,喷嘴气压越高,脉动越强烈,气流稳定性越弱,而80 m/s以上时,气流马赫数较稳定,偏差在±0.2%范围内。

|
图 11 试验段中心线处马赫数时间偏差变化曲线 Fig.11 Time variation of the Mach number time deviation in the centerline of the test section |
进一步,图12给出了试验段中心线处马赫数时间偏差标准差和最大绝对值,从图中可以看出:随着气流速度的增加,马赫数时间偏差标准差和最大绝对值不断减小,气流速度时间稳定性不断增强,整体而言,标准差和最大绝对值分别均小于0.8%和2%,尤其当气流速度超过60 m/s后,标准差和最大绝对值分别均小于0.2%和0.4%;增大喷嘴气压会增大马赫数时间偏差标准差和最大绝对值,但增大幅度会随着气流速度的增加而不断减小,其中对于20 m/s工况,标准差和最大绝对值的最大变化幅度约为0.4%和1%,但当气流速度超过60 m/s后,变化幅度均小于0.2%,由此可见喷嘴干空气射流仅对60 m/s以下试验工况的气流速度时间稳定性产生较显著影响,并且随着喷嘴气压的增大,气流速度时间稳定性不断减弱。

|
图 12 试验段中心线处马赫数时间偏差标准差和最大绝对值 Fig.12 Standard deviation and maximum absolute value of the Mach number time deviation in thecenterline of the test section |
最后,试验段中心线处总压、静压和马赫数修正关系如图13所示,图中包括喷嘴气压为0 MPa、0.4 MPa和0.9 MPa对应的试验结果、拟合曲线和拟合曲线公式。从图中可以看出,风洞测量的气流总压、静压和马赫数与试验段中心线处气流总压、静压和马赫数具有显著的线性关系,拟合公式表示为:

|
图 13 试验段中心线处气流总压、静压和马赫数修正关系 Fig.13 Correction relationships of the total pressure, the static pressure and the Mach number in the centerline of the test section |
| $\begin{split}& {p_{t,{\rm{TS}}}} = 1.023\;03{p_{t{\rm{,WT}}}} - 1.906\;35 \;\;\& \;\;{R^2} = 0.999\;88 \\& {p_{s{\rm{,TS}}}} = 0.993\;82{p_{s,{\rm{WT}}}} + 0.974\;49 \;\;\& \;\;{R^2} = 0.999\;98 \\& M{a_{{\rm{TS}}}} = 1{\rm{.002\;24}}M{a_{{\rm{WT}}}}{\rm{ - 0}}{\rm{.002\;35 \;\;\&\;\; }}{R^2}{\rm{ = 0}}{\rm{.999\;95}} \end{split} $ | (10) |
进一步,图14给出了各工况下试验段中心线处气流马赫数比,从图中可以看出:随着气流速度的增加,马赫数比逐渐增大,但是随着喷嘴气压的增大,马赫数比的增大趋势不断减弱,尤其当气压为0.9 MPa时,各气流速度下马赫数比近似为0.995;增大喷嘴气压,会增大马赫数比,但增大幅度会随着气流速度的增加而不断减小,其中在20 m/s工况下马赫数比最大偏差(对应0.9 MPa与0 MPa马赫数比之差)接近7%,但当气流速度超过60 m/s后,马赫数比最大偏差将小于1%。这主要是因为喷嘴会向试验气流中注入高速空气射流,这些高速空气射流会将自身携带的动能传递给试验气流,进而增大试验段气流速度,并且气压越大,则射流流量和动能越大,试验段气流速度增大幅度越大;但是随着试验段气流速度的增加,试验气流流量和动能不断增大,此时喷嘴干空气射流对试验气流的影响不断减弱,速度增加幅度则不断减小。

|
图 14 试验段中心线处马赫数比 Fig.14 Mach number ratio in the centerlineof the test section |
为评估试验段内气流偏角空间均匀性,图15给出了试验段气流偏角空间分布云图,图中包括喷嘴不喷气条件下40 m/s、80 m/s和160 m/s三个典型速度对应的试验结果,分布结果以气流偏角绝对角度θ表示,图中箭头方向表示当地气流偏角在测量平面内的投影,红色虚线框表示模型区,范围为−920 mm≤x≤920 mm,−600 mm≤y≤600 mm。从图中可以看出:各工况下气流偏角方向分布形态相似,呈现上下区域向中心收缩、左右区域向外侧发散的形态;各工况下普遍存在偏角超过1°的气流偏角非均匀峰值区,并且这些区域主要集中在C3(−670 mm)和C9(670 mm)位置,对应喷雾耙竖直支撑排架位置(见图1(b)),这与气流速度空间分布特征相一致。由此可见,喷雾耙结构同样会影响气流偏角空间分布形态,进而导致试验段内出现非均匀的气流偏角峰值区。

|
图 15 试验段气流偏角空间分布云图 Fig.15 Spatial distribution of the airflow angularity in the test section |
进一步,为定量评估试验段内气流偏角空间均匀性,图16给出了试验段模型区内气流偏角(俯仰角和偏航角)最大绝对值、空间偏差标准差和空间偏差最大绝对值。从图中可以看出:试验段气流速度对俯仰角和偏航角最大绝对值并无显著影响,其中俯仰角最大绝对值均小于1.5°,而偏航角最大绝对值在气流速度80 m/s以上均小于1.5°,但在40 m/s工况下,由于受到喷嘴干空气射流的显著影响,偏航角最大绝对值会随着喷嘴气压不断增大,最大值约为3°;试验段气流速度对俯仰角和偏航角空间偏差标准差也无显著影响,表明气流速度对气流偏角空间均匀性的影响不显著,其中俯仰角空间偏差标准差均小于0.5°,而偏航角空间偏差标准差在80 m/s以上小于0.6°,但对于40 m/s工况,由于受到喷嘴干空气射流的显著影响,标准差会随着喷嘴气压不断增大,最大值约为1.1°;俯仰角空间偏差最大绝对值均小于1.2°,而偏航角空间偏差最大绝对值在80 m/s以上小于2°,但对于40 m/s工况,在喷嘴干空气射流的显著影响下,最大绝对值会随着喷嘴气压不断增大,进而导致模型区内出现气流偏角超过2°的非均匀峰值区。

|
图 16 试验段模型区内气流偏角(俯仰角和偏航角)最大绝对值、空间偏差标准差和最大绝对值 Fig.16 The maximum absolute value, standard deviation and its maximum absolute value of the airflow angularities (pitch angle and yaw angle) in the model area of the test section |
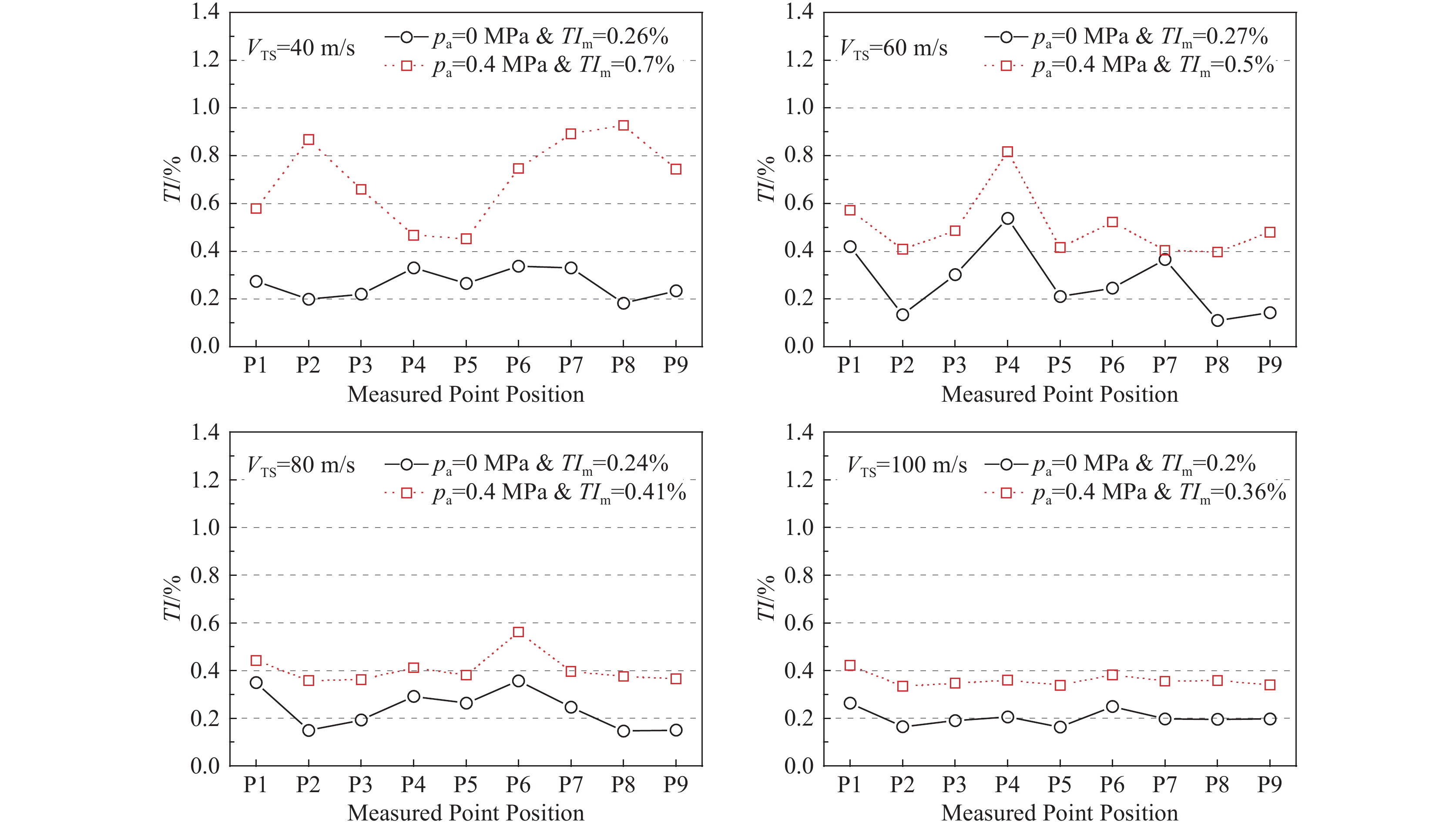
为评估试验段内气流湍流度空间均匀性,图17给出了试验段气流湍流度空间分布曲线,图中横轴P1~P9位置如图8所示,其中P5对应试验段中心线位置,图中包括0 MPa和0.4 MPa两种喷气状态下40 、60、80、100 m/s四个速度对应的试验结果,同时给出了平均气流湍流度(TIm)。从图中可以看出:各试验工况下,试验段气流湍流度均小于1%;喷嘴干空气射流会显著提高气流湍流度,尤其对于40 m/s工况,平均气流湍流度增大幅度约0.44%。
|
图 17 试验段气流湍流度空间分布曲线 Fig.17 Spatial distribution of the airflow turbulence intensity in the test section |
进一步,为定量评估试验段湍流度空间均匀性,图18给出了试验段内湍流度空间偏差标准差和最大绝对值,从图中可以看出:湍流度空间偏差标准差和最大绝对值随试验段气流速度并无明显变化,表明试验段气流速度对气流湍流度空间均匀性影响不显著,整体而言,湍流度空间偏差标准差和最大绝对值分别小于0.2%和0.5%;喷嘴干空气射流对40 m/s工况下气流湍流度均匀性影响较大,其中标准差和最大绝对值增幅接近0.15%和0.5%。

|
图 18 试验段湍流度空间偏差标准差和最大绝对值 Fig.18 The standard deviation and maximum absolute value of the turbulence intensity spatial deviation in the test section |
为评估试验段中心线处气流湍流度时间稳定性,图19给出了试验段中心线处湍流度时间偏差变化曲线,图中包括0 MPa和0.4 MPa两种喷气状态下60 m/s、80 m/s、100 m/s和140 m/s四个速度对应的试验结果,从图中可以看出:各试验工况下,试验段中心线处湍流度时间偏差均在±0.2%范围内;喷嘴气压对湍流度时间偏差影响不显著,影响幅度小于0.1%。

|
图 19 试验段中心线处湍流度时间偏差变化曲线 Fig.19 Time variation of the turbulence intensity time deviation in the centerline of the test section |
图20给出了试验段中心线处湍流度时间偏差标准差和最大绝对值,从图中可以看出:湍流度时间偏差标准差和最大绝对值随试验段气流速度并无明显变化,表明试验段气流速度对气流湍流度时间均匀性影响不显著,整体而言,湍流度时间偏差标准差和最大绝对值分别小于0.1%和0.2%;喷嘴干空气射流会增大标准差和最大绝对值,进而减弱气流湍流度时间稳定性,其中标准差和最大绝对值最大增幅接近0.08%和0.15%。

|
图 20 试验段中心线处湍流度时间偏差标准差和最大绝对值 Fig.20 Standard deviation and maximum absolute value of the turbulence intensity time deviation in thecenterline of the test section |
根据3 m×2 m结冰风洞主试验段气流场品质评估结果,图21给出了3 m×2 m结冰风洞主试验段气流场控制包线,图中黑色点为试验工况点,红线区域为控制包线,该包线针对气流速度、气流偏角和气流湍流度三个流场特征参数,综合考虑流场空间均匀性和时间稳定性品质,给出了满足适航审定要求的试验气流速度范围。从图中可以看出,3 m×2 m结冰风洞主试验段气流场品质在主要试验速度范围内均满足适航审定要求,其中试验速度在80 m/s至140 m/s间的气流场品质最优(如图蓝色线所示)。

|
图 21 3 m×2 m结冰风洞主试验段气流场控制包线 Fig.21 Operating envelop of the aerodynamic flowfield in the main test section of the icing wind tunnel at CARDC |
本文发展了结冰风洞气流场适航符合性验证方法,开展了3 m × 2 m结冰风洞主试验段气流场适航符合性验证试验,评估了其气流场品质,主要得到以下结论:
1)喷雾耙结构会影响试验段内气流速度和气流偏角空间分布形态,进而导致了非均匀峰值区的形成。
2)增大试验段气流速度会增强试验段气流速度空间均匀性和时间稳定性,但喷嘴干空气射流会减弱气流偏角和气流湍流度空间均匀性,同时降低气流速度和气流湍流度时间稳定性,尤其对试验段气流速度低于60 m/s的气流场品质影响最为显著。
3) 3 m × 2 m结冰风洞主试验段气流场品质在主要试验速度范围内满足适航审定要求,其中80 m/s至140 m/s范围内的气流场品质最优。
致谢:感谢中国商飞上海飞机设计研究院李海星博士对本文试验方法和数据处理部分提出的宝贵建议。
| [1] |
飞机结冰热力学行为研究综述[J]. 航空学报, 2017, 38(2): 25-36. DU Y X, LI M, GUI Y W, et al. Review of thermodynamic behaviors in aircraft icing process[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(2): 25-36. DOI:10.7527/S1000-6893.2016.0277 (in Chinese) |
| [2] |
飞机结冰冰形测量方法研究进展[J]. 航空学报, 2017, 38(2): 13-24. YI X, WANG B, LI W B, et al. Research progress on ice shape measurement approaches for aircraft icing[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(2): 13-24. DOI:10.7527/S1000-6893.2016.0276 (in Chinese) |
| [3] |
结冰风洞中液滴过冷特性数值研究[J]. 航空学报, 2017, 38(10): 121254. GUO X D, WANG Z X, LI M, et al. Numerical study of super-cooling characteristics of droplet in icing wind tunnel[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(10): 121254. DOI:10.7527/S1000-6893.2017.121254 (in Chinese) |
| [4] |
3m×2m结冰风洞云雾参数校测方法[J]. 实验流体力学, 2018, 32(2): 61-67. WANG Z X, SHEN H, GUO L, et al. Cloud calibration method of 3m×2m icing wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2018, 32(2): 61-67. DOI:10.11729/syltlx20170163 (in Chinese) |
| [5] |
IRVINE T, KEVDZIJA S, SHELDON D, et al. Overview of the icing and flow quality improvements program for the NASA-Glenn Icing Research Tunnel[C]// 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 2001. doi: 10.2514/6.2001-229
|
| [6] |
GONSALEZ J, ARRINGTON E, CURRY M. Quality surveys of the NASA Glenn icing research tunnel (2000 tests)[C]// 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 2001. doi: 10.2514/6.2001-232
|
| [7] |
GONSALEZ J, ARRINGTON E, CURRY M. Thermal calibration of the NASA Glenn icing research tunnel (2000 tests)[C]// 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 2001. doi: 10.2514/6.2001-233
|
| [8] |
BHARGAVA C, LOTH E, POTAPCZUK M. Aerodynamic simulations of the NASA Glenn icing research tunnel[C]// 41st Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2003. doi: 10.2514/6.2003-566
|
| [9] |
PASTOR-BARSI C, ARRINGTON A. Aero-thermal calibration of the NASA Glenn icing research tunnel (2012 test)[C]// 4th AIAA Atmospheric and Space Environments Conference, New Orleans, Louisiana. Reston, Virigina: AIAA, 2012. doi: 10.2514/6.2012-2934
|
| [10] |
STEEN L C, VAN ZANTE J, BROEREN A, et al. Flow quality surveys in the settling chamber of the NASA Glenn icing research tunnel (2011 tests)[C]// 4th AIAA Atmospheric and Space Environments Conference, New Orleans, Louisiana. Reston, Virigina: AIAA, 2012. doi: 10.2514/6.2012-2935
|
| [11] |
CLARK K, MALINOWSKI M, LOTH E, et al. Air flow and liquid water concentration simulations of the 2012 NASA Glenn icing research tunnel[C]// 4th AIAA Atmospheric and Space Environments Conference, New Orleans, Louisiana. Reston, Virginia: AIAA, 2012. doi: 10.2514/6.2012-2936
|
| [12] |
VECCHIONE L, DE MATTEIS P. An overview of the CIRA icing wind tunnel[C]// 41st Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2003. doi: 10.2514/6.2003-900
|
| [13] |
ESPOSITO B M, RAGNI A, FERRIGNO F, et al. Cloud calibration update of the CIRA icing wind tunne: 2003-01-2132[R].SAE Technical Paper, 2003.
|
| [14] |
IRANI E, AL-KHALIL K. Calibration and recent upgrades to the Cox icing wind tunnel[C]// 46th AIAA Aerospace Sciences Meeting and Exhibit, 2008.
|
| [15] |
亚声速气流中五孔探针的校准及应用[J]. 实验流体力学, 2011, 25(3): 88-90. FU C, PENG Q, LI X F, et al. Five-hole flow angle probe calibration and measurement in subsonic flow[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(3): 88-90. (in Chinese) |
| [16] |
Ac-9c Aircraft Icing Technology Committee. Calibration and acceptance of icing wind tunnels: SAE ARP-5905 [S]. 2009.
|
| [17] |
GONSALEZ J C, ARRINGTON E A. Five-hole flow angle probe calibration for the NASA Glenn Icing Research Tunnel[C]//19th AIAA Advanced Measurement and Ground Testing Technology Conference, 1996.
|
 2021, Vol. 39
2021, Vol. 39

