飞机结冰是飞行安全的主要威胁之一[1],为了评估结冰对飞行性能的影响,需要对飞机进行结冰风洞试验。若结冰风洞受试验段尺寸限制无法进行全尺寸模型试验,或参考工况超过结冰风洞的模拟能力范围,需要对试验工况进行相似转换。相似参数是描述结冰过程的重要无量纲数,相似转换是指利用相似参数计算合适的试验工况,使试验可在风洞能力范围内进行,并获得与参考工况相同的冰形。但是在实际试验过程中发现,现有相似转换方法的结果很多时候超出风洞的实际能力范围:在参考工况速度较高或液态水含量较小时,往往转换结果的风速更高或液态水含量更小,导致转换后的参数在风洞中难以实现。因此需要开展更具实用性的相似转换方法研究。
国外的相似转换研究始于20世纪50年代,对相似参数的研究已经相对完备,通过不同相似参数的组合形成了多种相似转换方法。目前常用的转换方法为Ruff方法[2](或称AEDC方法),以及Ruff与Anderson提出的改进Ruff方法[3]。法国宇航局的Charpin等提出了ONERA方法[4]。还有LWC×Time方法[5]和Olsen方法[6],可以有效对液态水含量(LWC)进行转换。单独对温度、速度和压力进行的转换方法[7-9]由于没有试验验证很少被采用。国内对相似转换的研究多在已有方法上拓展现应用场景,如针对过冷大水滴[10-11]转部件[12-13]的相似转换方法,对转换方法的优化和改进较少。
国外现有的相似转换方法对霜冰条件的转换已经成熟,明冰条件的结冰机理还缺乏理解[14],转换效果有限。对于转换速度如何确定还存在一些讨论,主要集中在韦伯数We特征长度的定义上,可能作为特征长度的有:翼型前缘半径[15]、水滴直径[16]、水膜厚度[17]等,对于如何合理确定转换速度仍未得到合理解释。其中Kind[17]和Feo[18]等从表面水膜流动和水滴表面张力等方面对Ruff方法进行了修正。在实际应用上国外以Ruff方法为主,近年关于ONERA方法的改进和验证的文献相对较少。
国外对结冰相似准则的研究随应用需求转入过冷大水滴[19]、后掠翼[20-21]、发动机冰晶结冰[22]和防冰试验相似转换[23]等研究领域,对传统的相似转换理论研究逐渐降温。
为拓展相似转换方法的适用范围,提高其工程实用价值,发展适合我国大型结冰风洞的相似转换方法,本文对相似参数及其变化规律进行了深入分析,根据相似参数和来流条件的关联性,提出了一种混合相似转换方法。该方法根据满足的相似参数不同分为四种模式,每种模式的转换参数选择范围不同。使用混合转换方法对某机翼结冰试验的工况进行了相似转换,并通过数值模拟[24]计算了试验工况、参考工况以及被普遍使用的Ruff方法转换工况的冰形,并对试验和计算结果进行了对比。
1 结冰试验相似转换理论 1.1 相似参数为保证水收集系数相似,需要满足水滴运动轨迹相似。在流场相似的前提下满足水滴惯性系数
| ${K_0} = \frac{1}{8} + \frac{\lambda }{{{\lambda _{{\rm{stokes}}}}}}\Bigg(K - \frac{1}{8}\Bigg)$ | (1) |
其中,
模型表面水收集总量受水收集系数、LWC和结冰时间影响,用积聚系数
| ${A_{\rm{c}}} = \frac{{{\rm{LWC}} \cdot V\tau }}{{{\rho _{\rm{i}}}D}}$ | (2) |
其中,
根据Messinger模型[27]的能量守恒方程,可以推导出模型表面冻结系数:
| $n = \Bigg(\frac{{{c_{p,{\rm{ws}}}}}}{{{\varLambda _{\rm{f}}}}}\Bigg)\Bigg(\phi + \frac{\theta }{b}\Bigg)$ | (3) |
其中,
| $b = \frac{{{\rm{LWC}} \cdot V{\beta _0}{c_{p,{\rm{ws}}}}}}{{{h_{\rm{c}}}}}$ | (4) |
| $\phi = {t_{\rm{f}}} - {t_{{\rm{st}}}} - \frac{{{V^2}}}{{2{c_{p,{\rm{ws}}}}}}$ | (5) |
| $\theta = \Bigg({t_{\rm{s}}} - {t_{{\rm{st}}}} - \frac{{{V^2}}}{{2{c_{p{\rm{,ws}}}}}}\Bigg) + \frac{{{h_{\rm{G}}}}}{{{h_{\rm{c}}}}}\Bigg(\frac{{{p_{{\rm{ww}}}} - {p_{\rm{w}}}}}{{{p_{{\rm{st}}}}}}\Bigg){\varLambda _{\rm{v}}}$ | (6) |
其中,
翼型驻点位置冻结系数
常见的相似转换方法有ONERA方法、Ruff方法和Olsen方法。以上方法均有一定试验数据进行支撑,但每种方法均有一定局限性。其中ONERA方法根据Modane风洞的硬件条件设计,没有将压力作为可调整变量[28]纳入转换方法中。Ruff方法建议使用
| $ {We}_{L}=\frac{{\rho }_{\rm{w}}{V}^{2}L}{{\rm{\sigma }}_{{\rm{w}}{\rm{a}}}} $ | (7) |
LWC×Time方法仅适用于温度较低的霜冰工况,Olsen方法的部分试验结果显示其转换结果欠佳[29]。
2 相似参数的变化规律 2.1 相似参数的影响因素通过上节中相似参数定义分析,可以定性的得出以下推论:1)
由以上推论可将相似参数分为三组:一是
惯性系数
| ${K_0} = \left[ {\frac{{{\rho _{\rm{w}}}R_{\rm{a}}^k}}{{18{k_l}(1 - k)\mu _{\rm{a}}^{1 - k}}}} \right]\frac{{{\delta ^{2 - k}}{V^{1 - k}}{T^k}}}{{d{P^k}}}$ | (8) |
其中,
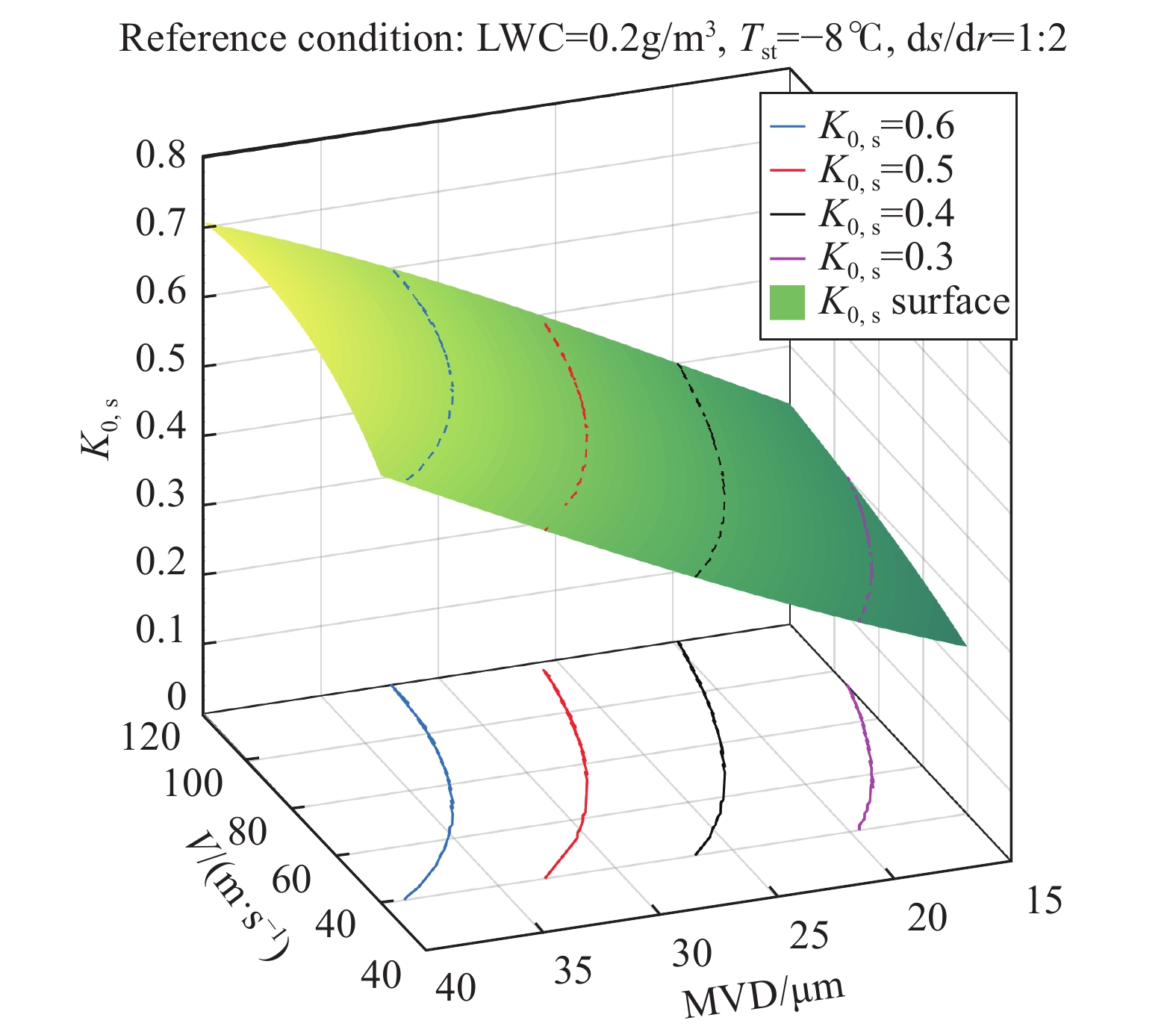
|
图 1 |
根据3.1节的推论(2)可知,
| ${n_0} = {{{A}}_1}\Bigg( - {T_{{\rm{st}}}} + \frac{{{{{A}}_2}{T_{{\rm{st}}}}}}{{{\rm{LWC}}}} + \frac{{{{{A}}_3}}}{{{\rm{LWC}}}}\Bigg)$ | (9) |
由于计算
根据公式(9)绘制在满足
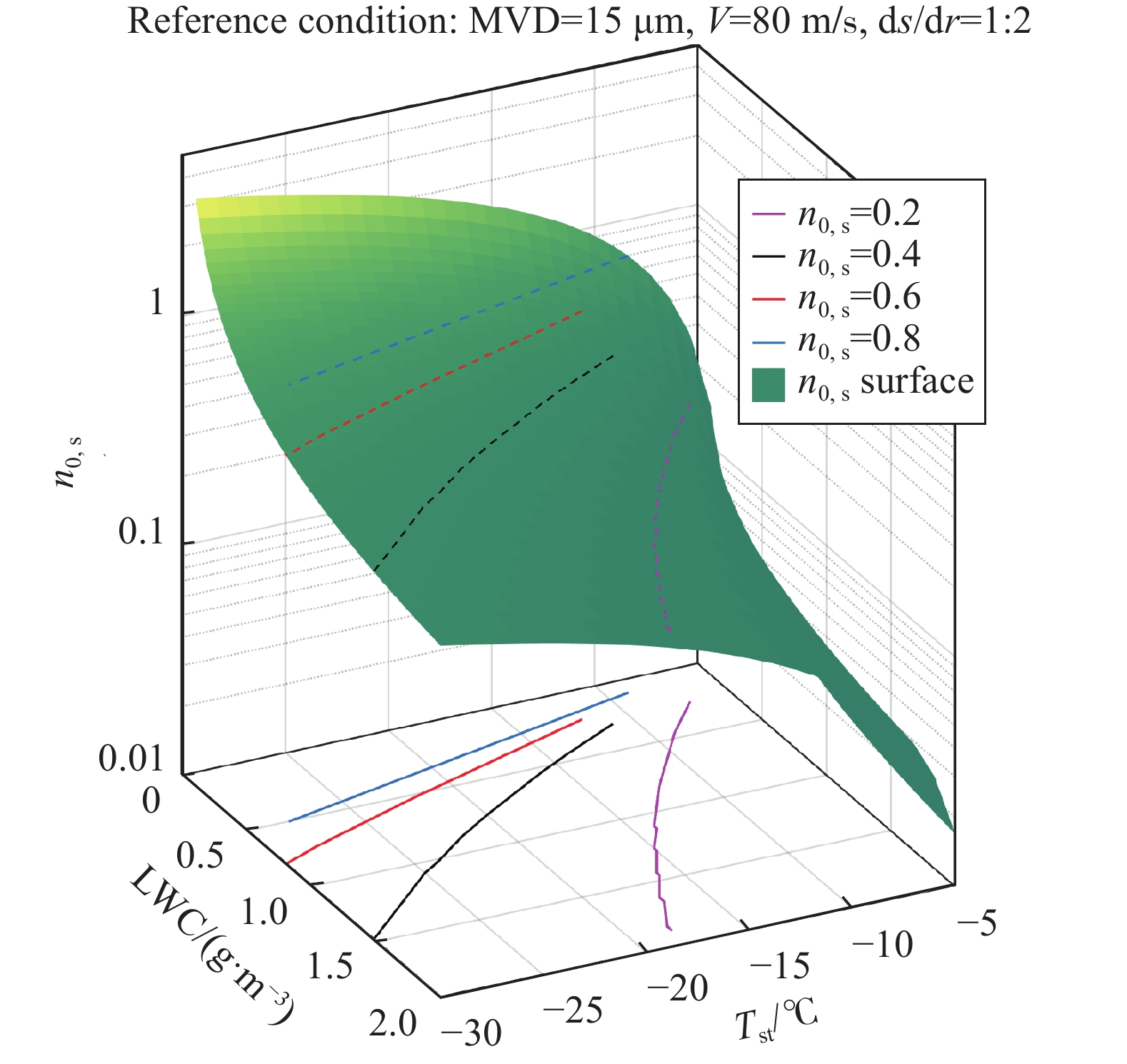
|
图 2 |
为了保证相似转换前后的冰形尽可能相似,Ruff方法和ONERA方法均在
相对热系数
| $ b=\frac{{\beta }_{0}{C}_{p,{\rm{ws}}}{d}^{0.5}{\mu }_{{\rm{a}}}^{0\cdot 5}}{1.14·{k}_{{\rm{a}}}{\rho }_{{\rm{a}}}^{0.5}{Pr}^{0.4}}\cdot {\rm{LWC}}\cdot {V}^{0.5} $ | (10) |
其中,
依据公式(10)绘制在满足
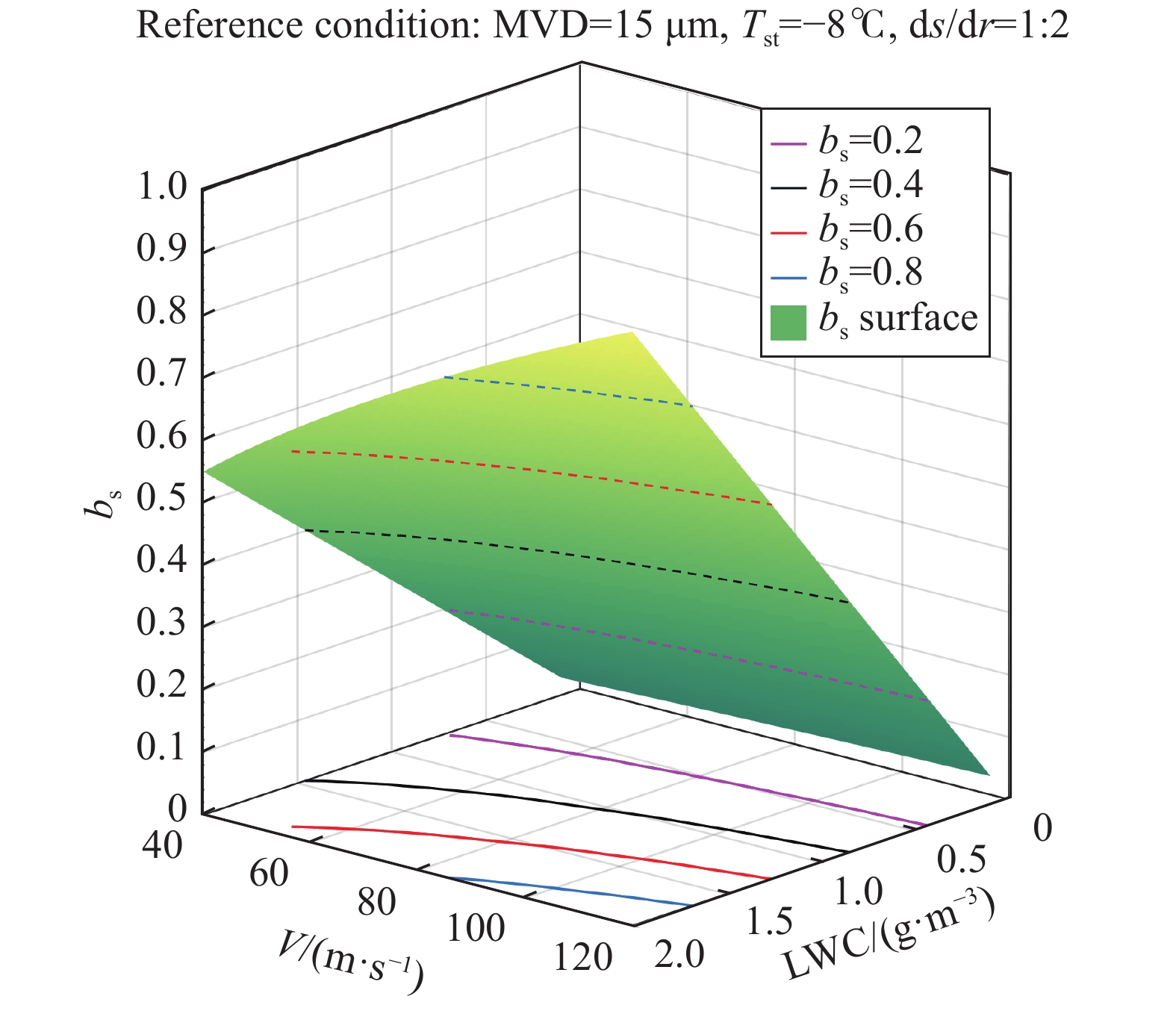
|
图 3 |
同理根据公式(5)做出
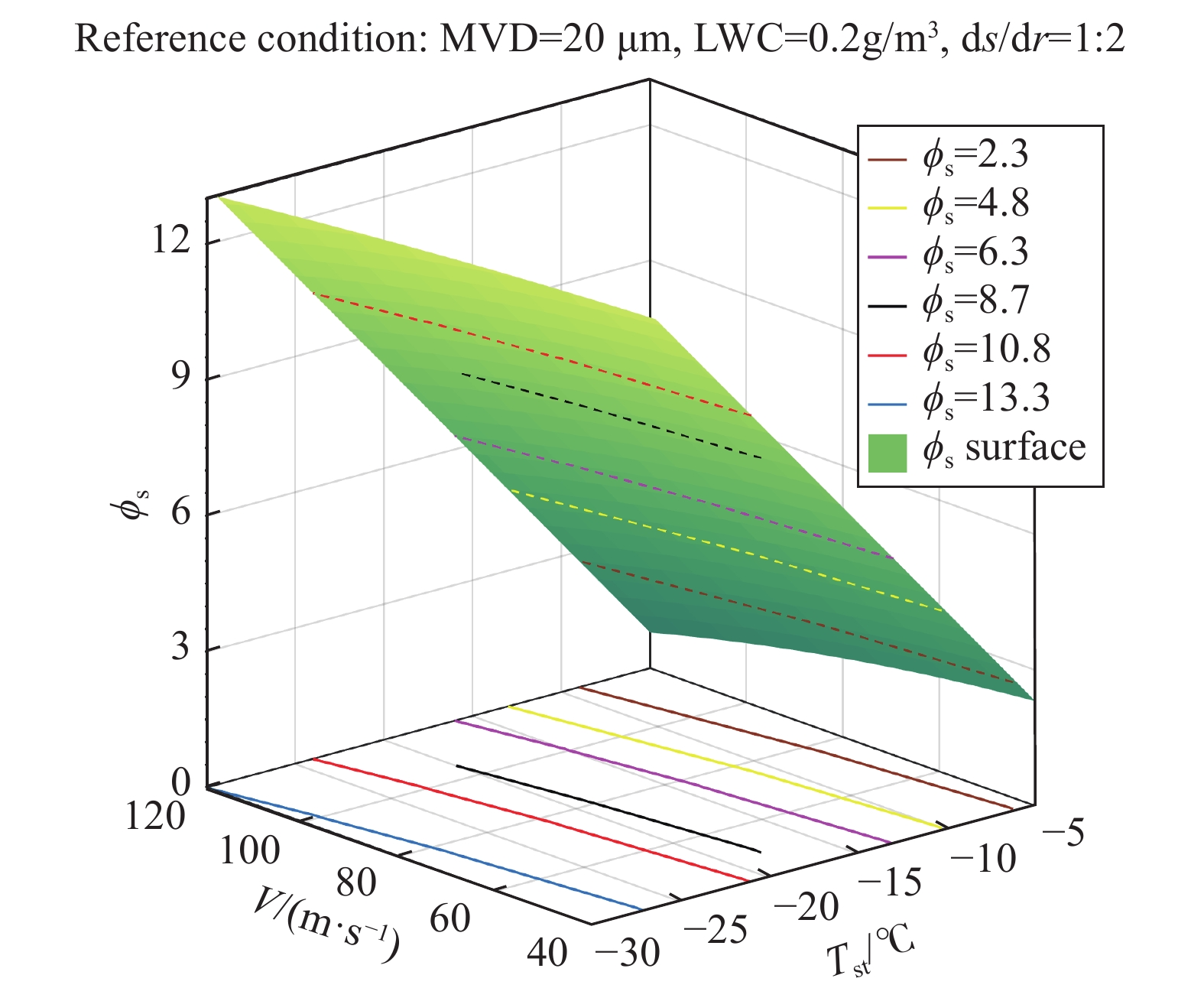
|
图 4 |
由以上分析可以知道,在相似转换方法仅满足
在没有其他约束条件作为前提时,
根据公式(6),当其余来流条件确定时,
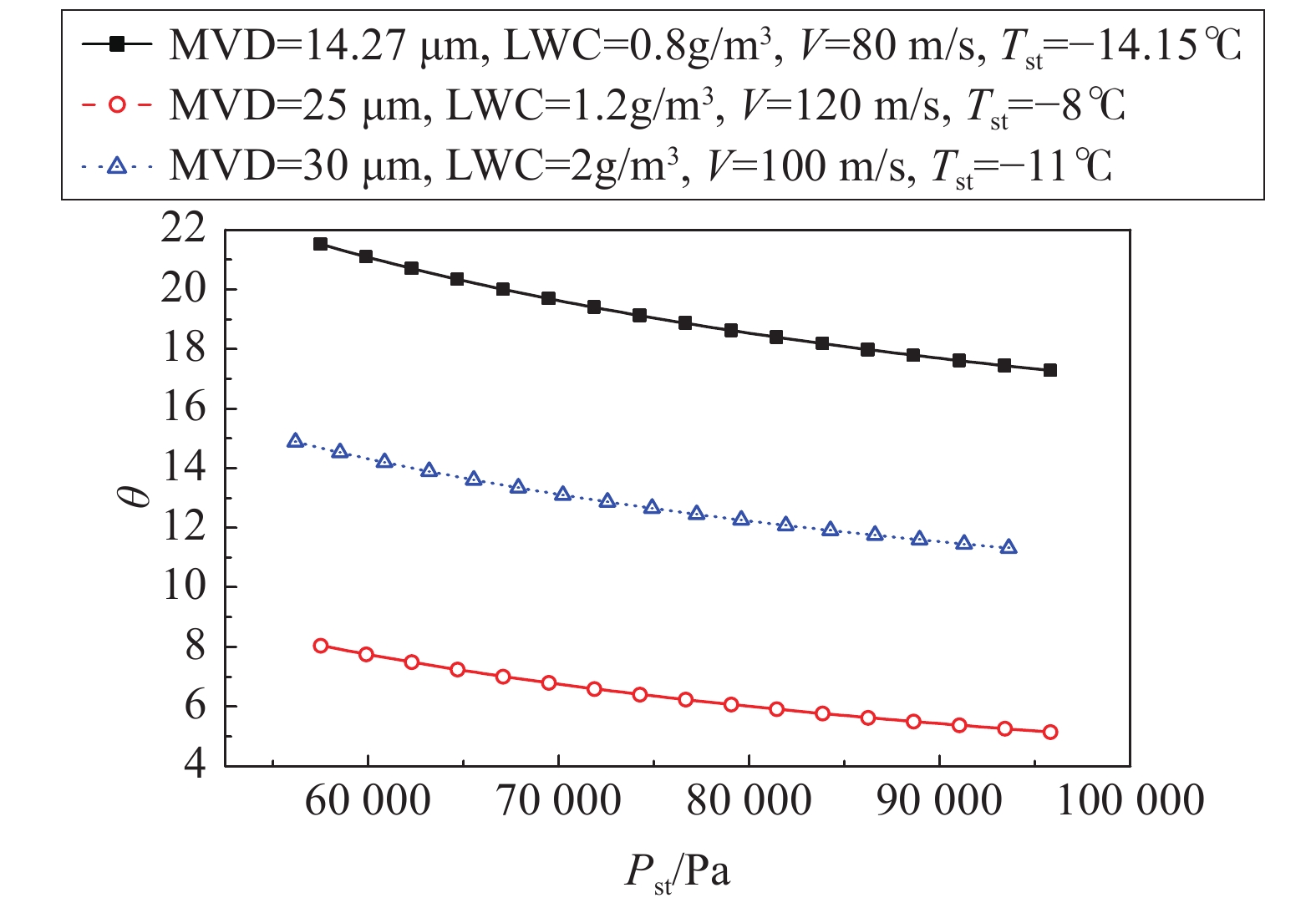
|
图 5 不同条件下 |
经过对水滴惯性系数、冻结系数以及三个热平衡参数的分析,已经确定了来流的主要参数,仅剩结冰时间。根据
相似参数可分为三组:约束
一种混合相似转换方法的流程如图6所示,具体实施流程为:
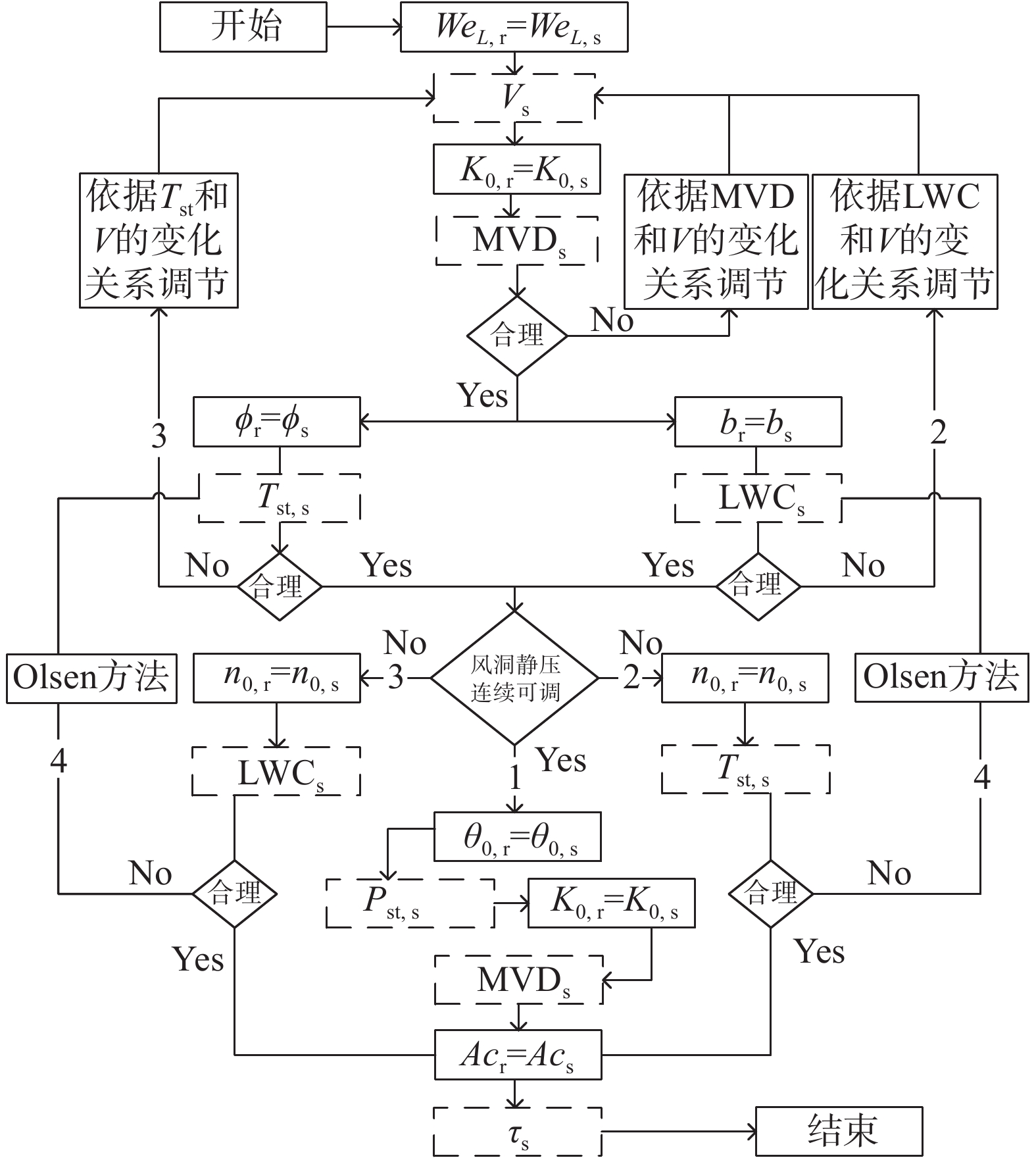
|
图 6 混合转换方法流程图 Fig.6 Flow chart for hybrid scaling method |
1)指定速度
2)根据
3)a. 如果风洞具备连续调节压力的能力,可根据公式(7)计算
b. 如果风洞无法连续调节压力,则在
c. 当模式2或模式3所计算的参数超出风洞能力范围时改用Olsen方法,指定LWCs或
d. 根据
根据满足的相似参数不同,混合相似转换方法又区分为四种模式。混合相似转换方法与常见方法的对比见表1。
模式1同时满足了
根据需要转换的参考工况和试验设备的能力在四种模式中进行选择:试验设备具有高度模拟的能力可以考虑使用模式1;使用模式2或模式3的参数选择范围相对自由,同时也有大量的文献和试验结果支撑其转换效果,可信度最高;模式4最具泛用性,考虑到有公开文献验证Olsen方法的转换结果并不总是令人满意,特定情况下模式4下转换效果可能较差。
| 表 1 相似转换方法满足相似参数表 Table 1 Scaling parameters fitted by different scaling method |
|
|
分别使用混合相似转换方法的四种模式,对文献[30]中的试验工况进行了相似转换,使用数值模拟方法计算了转换工况的冰形,并与文献中的试验结果进行了对比。参考状态使用弦长0.533 4 m的NACA0012翼型,转换状态的试验和计算均使用0.2667 m的缩比模型。算例如表2所示。
| 表 2 混合相似转换方法验证算例 Table 2 Validation cases by hybrid scaling method |
|
|
图7展示了两组不同速度的计算结果与试验的对比结果,试验与计算结果基本吻合,主要差异在于:转换工况的驻点冰厚较试验更低;下冰角角度和厚度基本一致,但上冰角吻合程度稍差;结冰极限相对试验更靠近前缘。考虑到数值模拟采用单粒径水滴和单步法计算结冰,与试验结果的误差在可接受范围内。
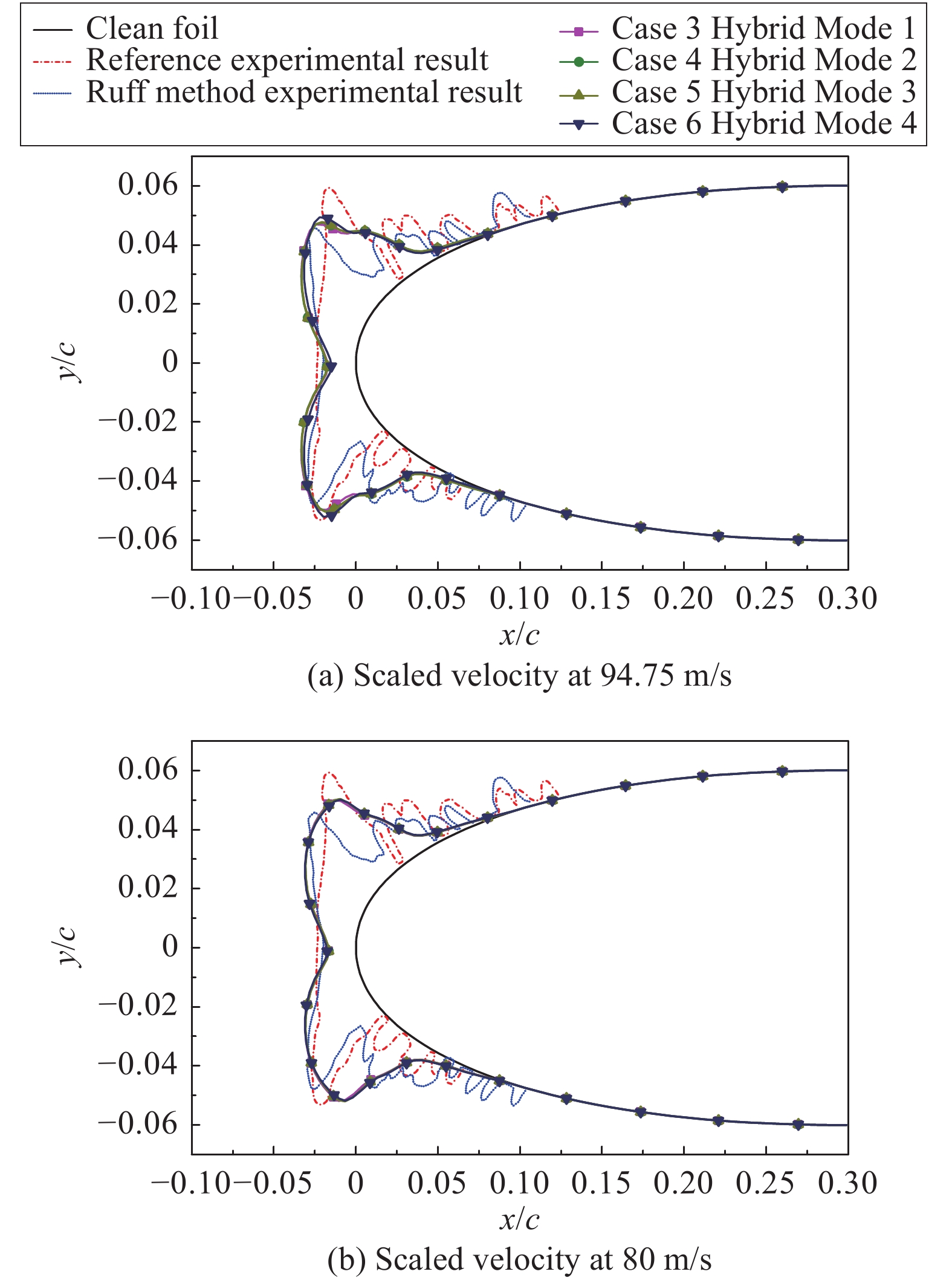
|
图 7 混合相似转换方法计算验证结果图 Fig.7 Ice shape results comparison with validation cases by hybrid scaling method |
从验证结果来看,混合相似转换方法的四种模式均能有效获得与参考工况相近的转换结果。速度不同时转换结果的冰形存在一定差异,但区别并不明显。
4.2 试验验证试验在中国空气动力研究与发展中心(CARDC)的3 m×2 m结冰风洞进行。该风洞试验能力覆盖液态水含量0.2~2.0 g/m3,水滴中值体积直径15~50 μm的云雾参数范围,主试验段最大风速210 m/s。
使用混合转换方法,对某型飞机的结冰试验工况进行了相似转换,具体工况见表3至表5。其中工况1是因模型存在缩比而进行相似转换;工况2和工况3是因原定试验参数超出结冰风洞试验能力而进行相似转换。试验工况均采用混合转换方法所得,在表中以#号标出。通过热刀法截取的翼型中截面冰形。对试验工况、原始工况和其他相似转换工况进行了数值模拟,并对比了试验结果和计算结果。
| 表 3 工况1参数表 Table 3 Reference and scaled conditions for test 1 |
|
|
| 表 5 工况3参数表 Table 5 Reference and scaled conditions for test 3 |
|
|
工况1中对比了Ruff方法和混合相似准换方法,如图8所示。从计算所得冰形结果分析,Ruff方法和混合转换方法均能获得与参考冰形类似的结果,且均与试验结果对比较好。但Ruff方法的转换结果风速高,液态水含量小,超过了试验设备的能力范围。
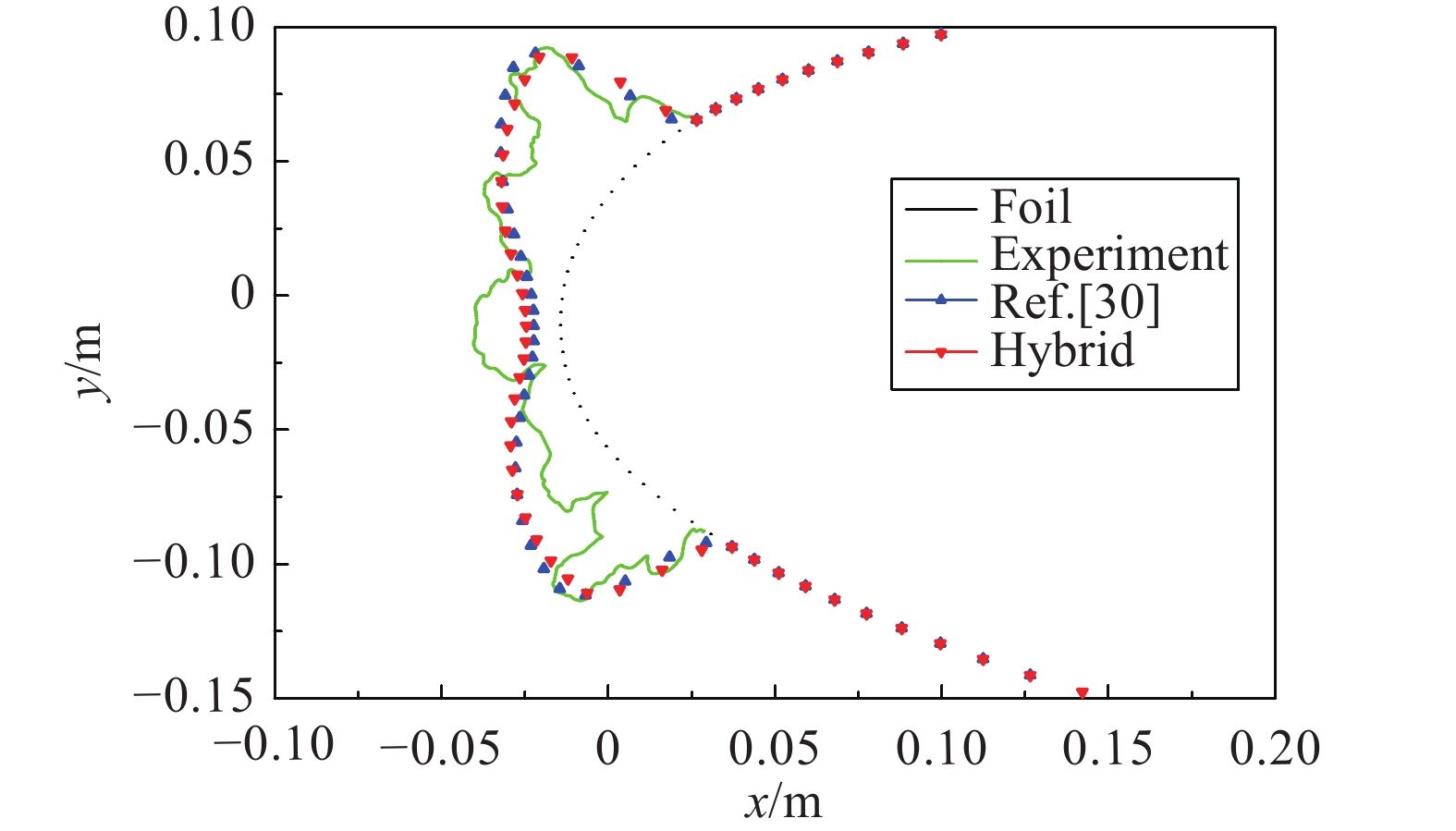
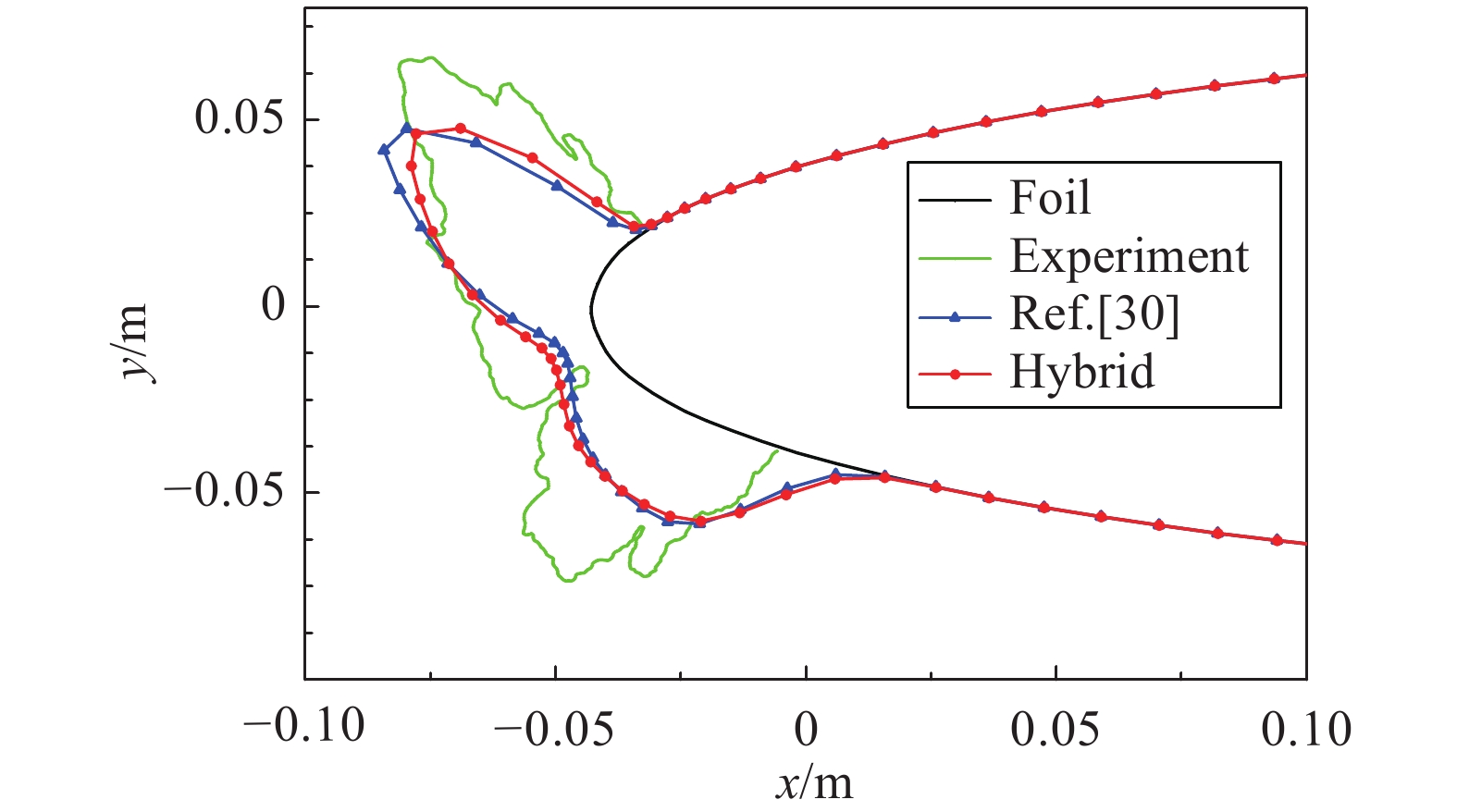
工况2和工况3来流条件相同,但所用翼型不同,对比结果分别如图9、图10所示。转换前后的冰形基本相同,与试验结果对比,冰形特征基本吻合。其中工况3计算冰形的冰角角度和下冰角厚度与试验结果有表明显的差异,其来源可能是没有对冰增长过程进行多步法求解。
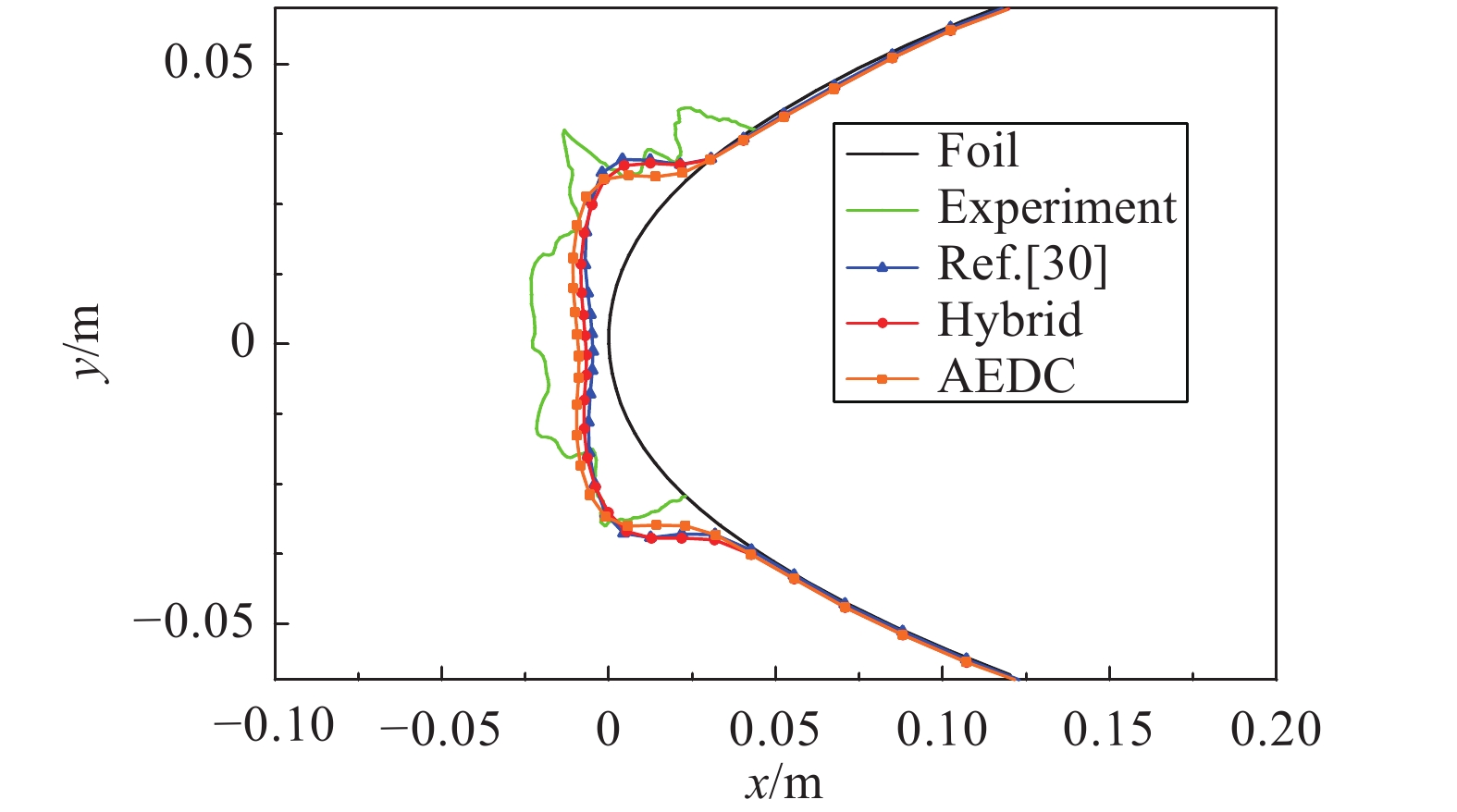
|
图 8 工况1试验与计算结果冰形对比 Fig.8 Ice shape results comparison with validation cases for test 1 |
|
图 9 工况2试验与计算结果冰形对比 Fig.9 Ice shape results comparison with validation cases for test 2 |
|
图 10 工况3试验与计算结果冰形对比 Fig.10 Ice shape results comparison with validation cases for test 3 |
| 表 4 工况2参数表 Table 4 The reference and scaled conditions for test 2 |
|
|
本文分析了相似参数随试验参数的变化规律,提出了一种混合相似转换方法,通过试验和数值模拟进行了对比验证,得到以下结论:
1)使用数值模拟方法验证了混合相似转换方法的四种模式,对比文献试验结果,四种模式均与试验吻合良好,验证了本文方法的有效性。又以混合相似转换方法对某机翼的结冰试验进行了相似转换,对比了试验结果和计算结果,初步验证了本方法的实用性;
2)混合相似转换方法相比传统的相似转换方法,提供了更宽的适用范围,并根据参考状态的需求确定不同的初始转换条件,选择对应的转换模式,能够更好的解决实际工程问题;
3)混合相似转换方法的四种模式中,模式1创新的提出了一种使三个热平衡参数同时满足相等的转换方法,相比经典的Ruff方法和ONERA方法只能满足三个热平衡参数中的一个,其转换结果在理论上更接近参考状态的结冰热力学过程;
4)后续工作一方面会继续在理论上拓展相似转换方法,通过考虑水膜流动对结冰过程的影响,对来流风速的选择缺乏有力的理论约束;另一方面将积极开展结冰风洞标模试验,进一步验证混合相似转换方法的有效性。
| [1] |
APPIAH-KUBBI P, MARTOS B, ATUAHENE I, et al. U. S. inflight icing accidents and incidents, 2006 to 2010[C]// Industrial and Systems Engineering Research Conference, USA, 2013.
|
| [2] |
RUFF G A. Analysis and verification of the icing scaling equations. volume 1[R]. Defense Technical Information Center, 1985. doi: 10.21236/ada162226
|
| [3] |
RUFF G, ANDERSON D. Quantification of ice accretions for icing scaling evaluations[C]// 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV. Reston, Virginia: AIAA, 1998. doi: 10.2514/6.1998-195
|
| [4] |
FRANCOIS C, GUY F. Icing testing in the large Modane wind tunnel on full scale and reduced scale models: NASA-TM-75373[R]. United States: NASA Center for Aerospace Information, 1979.
|
| [5] |
ANDERSON D N, RUFF G A. Scaling methods for simulating aircraft in-flight icing encounters[C]// 2nd International Symposium on Scale Modeling. Lexington, Kentuchy, USA: 1997.
|
| [6] |
OLSEN W, WALKER E. Experimental evidence for modifying the current physical model for ice accretion on aircraft surfaces: NASA-TM-87184[R]. United States: NASA Lewis Research Center Cleveland, 1986. https://ntrs.nasa.gov/citations/19880003091
|
| [7] |
BARLETT C S. An analytical study of icing similitude for aircraft engine testing: AEDC-TR-86-26[R]. Arnold Engineering Development Center, 1986.
|
| [8] |
BARTLETT C S. Icing scaling considerations for aircraft engine testing[C]// 26th Aerospace Sciences Meeting, Reno, NV, USA. Reston, Virigina: AIAA, 1988. doi:10.2514/6.1988-202
|
| [9] |
OLESKIW M M, GREGORIO F D, ESPOSITO B. The effect of altitude on icing tunnel airfoil icing simulation[C]// FAA International Conference on Aircraft Icing. Washington, DC, USA: 1996.
|
| [10] |
考虑水滴动力学效应的结冰试验相似准则[J]. 实验流体力学, 2016, 30(2): 20-25. ZHOU Z H, YI X, GUI Y W, et al. Icing scaling law with the dynamic effects of water droplets[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(2): 20-25. (in Chinese) |
| [11] |
过冷大水滴条件下结冰相似准则[J]. 航空动力学报, 2019, 34(5): 1101-1110. SHI H, WANG J Y, CHEN J M, et al. Icing scaling law at supercooled large droplet conditions[J]. Journal of Aerospace Power, 2019, 34(5): 1101-1110. DOI:10.13224/j.cnki.jasp.2019.05.016 (in Chinese) |
| [12] |
旋转帽罩结冰相似准则的研究[J]. 推进技术, 2015, 36(8): 1164-1169. ZHANG L F, ZHANG M H, WU D Y, et al. Research on icing scaling law for rotating cone[J]. Journal of Propulsion Technology, 2015, 36(8): 1164-1169. DOI:10.13675/j.cnki.tjjs.2015.08.007 (in Chinese) |
| [13] |
涡扇发动机短舱结冰试验相似方法[J]. 航空动力学报, 2019, 34(9): 1988-2000. YANG Q, DONG W, GUO Z Q, et al. Scaling method of turbofan engine nacelle under icing test[J]. Journal of Aerospace Power, 2019, 34(9): 1988-2000. DOI:10.13224/j.cnki.jasp.2019.09.016 (in Chinese) |
| [14] |
KIND R J. Scaling of icing tests: a review of recent progress[J]. AIAA Journal, 2003, 41(8): 1421-1428. DOI:10.2514/2.2120 |
| [15] |
BILANIN A, ANDERSON D. Ice accretion with varying surface tension[C]// 33rd Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 1995. doi:10.2514/6.1995-538
|
| [16] |
ANDERSON D N. Evaluation of constant-Weber-number scaling for icing tests[C]// 34th Aerospace Sciences Meeting and Exhibit, Reno, NV. Reston, Virginia: AIAA, 1996. doi:10.2514/6.1996-636
|
| [17] |
KIND R, OLESKIW M M. Recent developments in scaling methods for icing wind tunnel testing at reduced scale[C]// ICAS Congress Conference, 2002.
|
| [18] |
ANDERSON D, FEO A. Ice-accretion scaling using water-film thickness parameters[C]// 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 2002. doi:10.2514/6.2002-522
|
| [19] |
ANDERSON D, TSAO J C. Additional results of ice-accretion scaling at SLD conditions[C]// 41st Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2003.doi: 10.2514/6.2003-390
|
| [20] |
VARGAS M, RESHOTKO E. Physical mechanisms of glaze ice scallop formations on swept wings[C]// 36th AIAA Aerospace Scie nces Meeting and Exhibit, Reno, NV. Reston, Virginia: AIAA, 1998. doi: 10.2514/6.1998-491
|
| [21] |
TSAO J C. Further evaluation of swept wing icing scaling with maximum combined cross section ice shape profiles[C]// 2018 Atmospheric and Space Environments Conference, Atlanta, Georgia. Reston, Virginia: AIAA, 2018. doi: 10.2514/6.2018-3183
|
| [22] |
STRUK P M, BENCIC T, TSAO J C, et al. Preparation for scaling studies of ice-crystal icing at the NRC research altitude test facility[C]// 5th AIAA Atmospheric and Space Environments Conference, San Diego, CA. Reston, Virginia: AIAA, 2013. doi: 10.2514/6.2013-2675
|
| [23] |
LEE S, ADDY H E, BROEREN A P, et al. Evaluation of alternative altitude scaling methods for thermal ice protection system in NASA icing research tunnel[C]// 9th AIAA Atmospheric and Space Environments Conference, Denver, Colorado. Reston, Virginia: AIAA, 2017. doi: 10.2514/6.2017-3927
|
| [24] |
翼型积冰的数值模拟[J]. 空气动力学学报, 2002, 20(4): 428-433. YI X, ZHU G L, WANG K C, et al. Numerically simulating of ice accretion on airfoil[J]. Acta Aerodynamica Sinica, 2002, 20(4): 428-433. DOI:10.3969/j.issn.0258-1825.2002.04.009 (in Chinese) |
| [25] |
BRAGG M B. A similarity analysis of the droplet trajectory equation[J]. AIAA Journal, 1982, 20(12): 1681-1686. DOI:10.2514/3.8004 |
| [26] |
LANGMUIR I, BLODGETT K B. A mathematical investigation of water droplet trajectories[R]. Army Air Forces Technical Report No. 5418, February 1946.
|
| [27] |
MESSINGER B L. Equilibrium temperature of an unheated icing surface as a function of air speed[J]. Journal of the Aeronautical Sciences, 1953, 20(1): 29-42. DOI:10.2514/8.2520 |
| [28] |
ANDERSON D. Effect of velocity in icing scaling tests[C]// 38th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 2000. doi: 10.2514/6.2000-236
|
| [29] |
BILANIN A J. Proposed modifications to ice accretion/icing scaling theory[J]. Journal of Aircraft, 1991, 28(6): 353-359. DOI:10.2514/3.46034 |
| [30] |
BOND T H, ANDERSON D N. Manual of scaling method: NASA/CR-2004-212875 [R]. United States: NASA Glenn Research Center Cleveland, OH, 2004.
|
 2021, Vol. 39
2021, Vol. 39


