0 引　言

冰晶积冰是飞行安全的重要威胁。传统观点认为发动机结冰是由于过冷水滴撞击到发动机进气道前缘、整流罩、支板以及导流叶片表面进而引起外部结冰现象^[1]。然而自从上世纪90年代以来，在超过海拔7000 m且不存在过冷水滴的高空发生了多起大涵道比涡扇发动机功率损失事件，研究表明事故原因是由发动机所吸入冰晶在内涵道部件表面发生部分融化，进而结冰所导致的^[2-3]。

当飞机为躲避低空中发生降雨的区域而在其上空巡航时，发动机会吸入大量冰晶。冰晶在发动机高温内流的作用下，会部分融化而形成冰水混合相。冰水混合相粒子会进一步在压气机叶片等发动机内部结构表面形成液态水膜，后续吸入的冰晶依附在这些润湿表面并将表面温度冷却至冰点以下。伴随着冰晶的持续吸入，最终会在内部结构表面累积成冰。与过冷水滴撞击所引发的发动机外部结冰不同，在发动机整个低压压气机至高压压气机一级静子叶片区域均可能发生冰晶结冰现象^[2-4]。冰晶积冰会导致发动机喘振、熄火、功率损失，甚至会由于冰脱落而造成内部结构损伤^[3]。

国内外学者分别采用地面试验和数值模拟方法对冰晶结冰机理进行深入研究。在试验研究方面，Struck^[5]、Currie^[6]等认为可以用湿球温度T_wb作为结冰是否稳固的判断依据，即当T_wb < 0℃时，润湿表面可以形成稳固的积冰。Currie ^[7]用黏附效率描述积冰过程，并探讨了融化率（Melt Ratio, MR）和撞击角度对黏附效率的影响。Al-Khalil等^[8]分别对霜冰和明冰条件下的冰晶结冰进行了实验，并发现冰晶撞击会对冰晶结冰起到削弱作用。Knezevici等^[9]则进一步发现由于冰晶侵蚀效应，大尺寸冰晶较小尺寸冰晶结冰量有所降低。Hauk等^[10-11]研究了球形及不规则外形冰晶的撞击特性和影响因素。

然而，模拟航空发动机冰晶结冰试验具有成本高、周期长、结果不具备普适性等特点。因此数值模拟方法也成为了研究冰晶结冰的重要手段。Villedieu等^[12]采用Lagrange方法对冰晶形状、传热传质、相变以及冰晶撞击过程中的黏附、破碎、反弹、飞溅等现象建立数学模型。Trontin等^[13]在此基础上，考虑冰晶侵蚀效应影响，对冰晶黏附效率模型加以改进，并根据试验数据校正数值模型中经验参数；随后对过冷大液滴、冰晶及混合相等条件下结冰情况进行了数值仿真^[14]。Norde等^[15]采用欧拉法计算粒子轨迹，建立了冰晶撞击和侵蚀模型，并针对混合相传热传质过程的特点，改良了经典Messinger结冰热力学模型。Currie^[16]、Bartkus^[17]、Baumert^[18]等分别根据冰风洞试验数据的校准并完善了其冰晶结冰数值计算软件。

而国内对冰晶结冰研究仍处于起步阶段。Zhang等^[19]综合考虑液滴的飞溅以及冰晶的破碎和反弹等现象，建立了冰晶撞击模型，并在此基础上提出了混合相态结冰热力学模型。姜飞飞等^[20]对冰晶的传热传质过程进行离散化处理，计算分析了冰晶的粒子半径、冰晶温度、冰晶速度等参数变化，获得了冰晶在低压压气机内涵通道内的运动轨迹及与碰撞特性。卜雪琴等^[21]考虑了冰晶黏附效应，分别对霜冰与明冰条件下二维NACA0012翼型表面结冰情况进行了数值研究，结果表明冰晶黏附效应对混合相下结冰量及冰形均有较大影响。

本文分析了混合相态下结冰表面的传热传质过程，通过改进的Messinger结冰热力学模型，建立了混合相态冰晶积冰热力学数值模型。通过与Cox冰风洞NACA0012翼型冰晶积冰实验对比，验证了本文数值模型的正确性，并在此基础上分析了融化率对冰晶积冰过程的影响机制，以及环境温度、马赫数等参数对积冰形态和积冰生长率的影响。

1 混合相态下积冰模型 1.1 混合相态下结冰热力学模型 1.1.1 质量守恒

混合相态下结冰热力学行为需要对经典Messinger模型进行扩展，忽略冰层内部、冰层与壁面之间的热传导，基于控制体积法建立如下所示的质量和能量平衡方程^[21]。

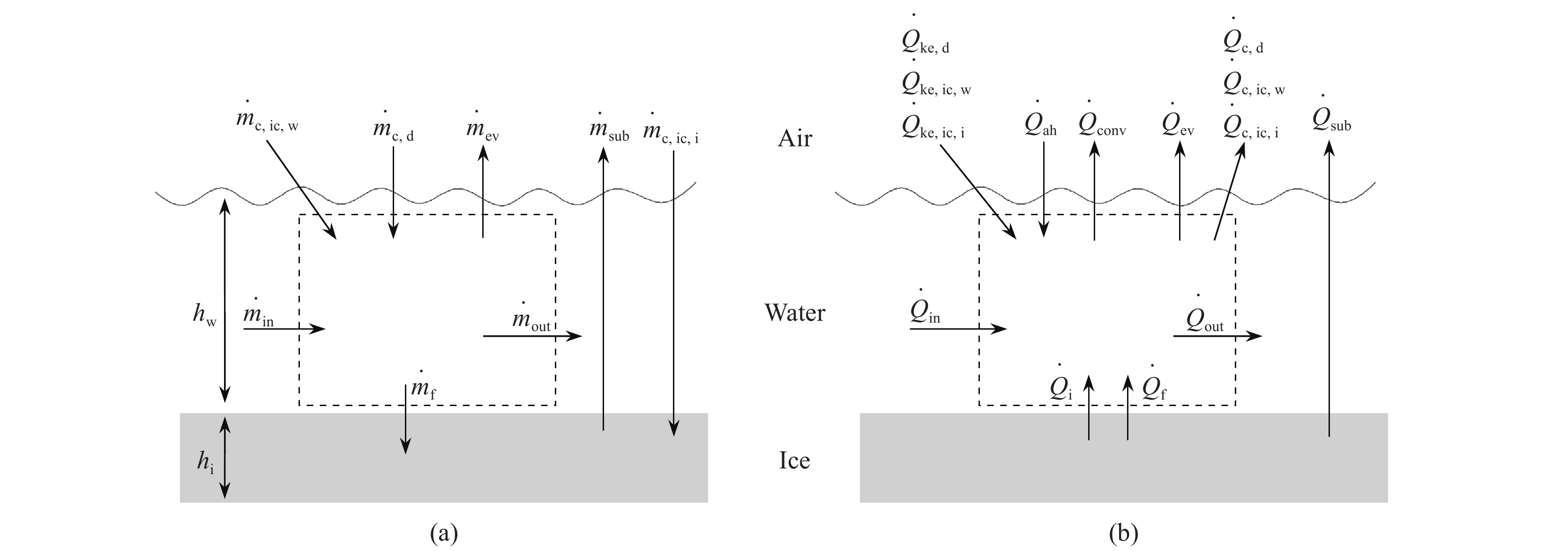
控制体内液态水质量传递如图1(a)所示，流入控制体的质量流量有：撞击到翼面的液滴 $ {\dot {m}}_{\rm{c},\rm{d}}$ 和冰晶已融化部分的质量流量 $ {\dot {m}}_{\rm{c,}\rm{ic,}\rm{w}}$ ，流入控制体的溢流水质量流量 $ {\dot {m}}_{\rm{in}}$ 。而流出控制体的质量流量为：冻结成冰的质量流量 $ {\dot {m}}_{\rm{f}}$ （为负时表示冰融化为水进入控制体），蒸发的质量流量 $ {\dot {m}}_{\rm{ev}}$ ，以及流出控制体的溢流水质量流量 $ {\dot {m}}_{\rm{out}}$ 。因此可建立控制体内质量平衡方程：

$ {\dot {m}}_{\rm{c,}\rm{ic,}\rm{w}}+{\dot {m}}_{\rm{c}，\rm{d}}+{\dot {m}}_{\rm{in}}={\dot {m}}_{\rm{f}}+{\dot {m}}_{\rm{ev}}+{\dot {m}}_{\rm{out}}$

(1)

控制体内结冰的质量流量 $ {\dot {m}}_{\rm{i}}$ 应包含以下三部分：控制体内冻结成冰的质量流量 $ {\dot {m}}_{\rm{f}}$ ，撞击并依附在壁面上的冰晶尚未融化的质量流量 $ {\dot {m}}_{\rm{c,}\rm{ic,}\rm{i}}$ ，及由于升华现象而损失的质量流量 $ {\dot {m}}_{\rm{sub}}$ ，即

$ {\dot {m}}_{\rm{i}}={\dot {m}}_{\rm{f}}+{\dot {m}}_{\rm{c,}\rm{ic,}\rm{i}}-{\dot {m}}_{\rm{sub}}$

(2)

上述式（1-2）中，

$ {\dot {m}}_{{{\rm{c}},}{{\rm{ic}},}{{\rm{w}}}}={{\rm{IWC}}}\cdot {V}_{\infty ,{{\rm{ic}}}}\cdot {\beta }_{\rm{ic}}\cdot {\eta }_{\rm{ic}}\cdot {S_{\rm{w}}}$

(3)

$ {\dot {m}}_{\rm{c,ic,i}}{={\rm{IWC}}}\cdot {V}_{\infty ,{{\rm{ic}}}}\cdot {\beta }_{\rm{ic}}\cdot (1-{\eta }_{\rm{ic}})\cdot {S}_{\rm{w}}$

(4)

$ {\dot {m}}_{\rm{c,d}}{={\rm{LWC}}}\cdot {V}_{\infty ,{{\rm{d}}}}\cdot {\beta }_{\rm{d}}\cdot {S}_{\rm{w}}$

(5)

式中，LWC、IWC分别为流场中过冷液滴的液态水含量与冰晶含量， ${V_{\infty ,{\rm{d}}}}$ 与 ${V_{\infty ,{\rm{ic}}}}$ 分别为自由来流的水滴速度和冰晶速度， $\;{\beta _{\rm{d}}}$ 、 $\;{\beta _{{\rm{ic}}}}$ 分别为过冷水滴和冰晶的收集系数， ${S_{\rm{w}}}$ 为控制体的底面积， ${\eta _{{\rm{ic}}}}$ 为冰晶融化比， ${\eta _{{\rm{ic}}}}= $ $ {\rm{ LW}}{{\rm{C}}_{{\rm{ic}}}}/{\rm{IWC}}$ ， ${\rm{LW}}{{\rm{C}}_{{\rm{ic}}}}$ 为部分融化冰晶中液态水含量。

式（1）中当前控制体流入的溢流水质量流量为上一个控制体流出的溢流水质量流量，即 $ {\dot {m}}_{\rm{in}}= $ $ {\dot {m}}_{{\text{上一个控制体}},{\rm{out}}}$ ；而当前控制体流出的溢流水质量流量为：

$ {\dot {m}}_{\rm{out}}={\rho }_{\rm{w}}\cdot h{}_{\rm{f}}\cdot {U}_{\rm{f}}\cdot {Z}_{\rm{w}}$

(6)

式中， ${\rho _{\rm{w}}}$ 为水的密度， $h{{\kern 1pt} _{\rm{f}}}$ 为控制体内液膜高度， ${U_{\rm{f}}}$ 为控制体内液态水溢流速度， ${Z_{\rm{w}}}$ 为沿翼型展向控制体宽度。

最后，质量平衡方程中蒸发的质量流量 $ {\dot {m}}_{\rm{ev}}$ 为：

$ {\dot {m}}_{\rm{ev}}=\frac{0.7\cdot {h}_{\rm{c}}\cdot {S}_{\rm{w}}}{{c}_{\rm{p,air}}}\cdot \left[\frac{{P}_{\rm{vap,w}}-{{\rm{HR}}}\cdot {{{P}}}_{\rm{vap},\infty }}{{P}_{\rm{s,w}}}\right]$

(7)

式中， ${h_{\rm{c}}}$ 为对流换热系数， ${c_{{\rm{p,air}}}}$ 为空气比热容， ${P_{{\rm{vap,w}}}}$ 为壁面处饱和蒸气压， ${P_{{\rm{vap}},\infty }}$ 为环境空气饱和蒸气压， ${P_{{\rm{s,w}}}}$ 为控制体外静压， ${\rm{HR}}$ 为相对湿度。

1.1.2 能量守恒

控制体内能量传递机理如图1(b)所示。控制体内热量损失项有：因对流损失的热量 $ {\dot {Q}}_{\rm{conv}}$ ，蒸发散热 $ {\dot {Q}}_{\rm{ev}}$ ，壁面收集液滴显热 $ {\dot {Q}}_{\rm{c,d}}$ ，壁面收集的冰晶显热 $ {\dot {Q}}_{\rm{c,ic}}$ （由冰晶未融化部分的固态显热 $ {\dot {Q}}_{\rm{c,ic,i}}$ 和已融化部分的液态显热 $ {\dot {Q}}_{\rm{c,ic,w}}$ 两部分组成），及流出控制体溢流水的显热 $ {\dot {Q}}_{\rm{out}}$ 。而控制体内热量增加项有：壁面收集液滴动能 $ {\dot {Q}}_{\rm{ke,d}}$ ，壁面收集冰晶动能 $ {\dot {Q}}_{\rm{ke,ic}}$ （同样由冰晶未融化部分的固态动能 $ {\dot {Q}}_{\rm{ke,ic,i}}$ 和已融化部分的液态动能 $ {\dot {Q}}_{\rm{ke,ic,w}}$ 组成），结冰热 $ {\dot {Q}}_{\rm{f}}$ ，水膜与冰层间温差引起的显热 $ {\dot {Q}}_{\rm{i}}$ ，以及流入控制体溢流水的显热 $ {\dot {Q}}_{\rm{in}}$ 。因此可建立控制体内能量平衡方程：

$\begin{split}& {\dot {Q}}_{\rm{ke,d}}+{\dot {Q}}_{\rm{ke,ic,w}}+{\dot {Q}}_{\rm{ke,ic,i}}+{\dot {Q}}_{\rm{f}}+{\dot {Q}}_{\rm{i}}+{\dot {Q}}_{\rm{in}} \\& ={\dot {Q}}_{\rm{conv}}+{\dot {Q}}_{\rm{ev}}+{\dot {Q}}_{\rm{c,d}}+{\dot {Q}}_{\rm{c,ic,i}}+{\dot {Q}}_{\rm{c,ic,w}}+{\dot {Q}}_{\rm{out}}\end{split}$

(8)

上式中进入控制体的质量项动能分别为：

$ {\dot {Q}}_{\rm{ke,d}}=\frac{1}{2}{\dot {m}}_{\rm{c,d}}{U}_{\rm{imp,d}}^{2}$

(9)

$ {\dot {Q}}_{\rm{ke,ic}}=\frac{1}{2}{\dot {m}}_{\rm{c,ic}}{U}_{\rm{imp,ic}}^{2}$

(10)

式中， ${U_{{\rm{imp,d}}}}$ 与 ${U_{{\rm{imp,ic}}}}$ 分别为水滴和冰晶粒子撞击到结冰表面时的撞击速度。

控制体内存在液态水的冻结与蒸发，以及冰的升华三种相变过程，式（8）中相变潜热项为：

$ {\dot {Q}}_{\rm{f}}=\dot {{m}_{\rm{f}}}{L}_{\rm{f}}$

(11)

$ {\dot {Q}}_{\rm{ev}}=\dot {{m}_{\rm{ev}}}{L}_{\rm{ev}}$

(12)

$ {\dot {Q}}_{\rm{sub}}=\dot {{m}_{\rm{sub}}}{L}_{\rm{sub}}$

(13)

式中， ${L_{\rm{f}}}$ 为结冰潜热， ${L_{{\rm{ev}}}}$ 为蒸发潜热， ${L_{{\rm{sub}}}}$ 为升华潜热。

能量守恒方程(8)中对流换热项为：

$ {\dot {Q}}_{\rm{conv}}={h}_{\rm{c}}{S}_{\rm{w}}\left({T}_{\rm{s}}-{T}_{\mathrm{inf}}\right)$

(14)

式中， ${T_{\rm{s}}}$ 为壁面温度， ${T_{\inf }}$ 为自由来流温度。

控制体内显热传递，主要有水滴和冰晶粒子温度变化引起的显热传递和流入/流出控制体的水引起的显热传递。能量守恒方程中所有温差引起的显热传递可以表示为：

$ {\dot {Q}}_{\rm{c,d}}={\dot {m}}_{\rm{c,d}}{c}_{\rm{p,w}}\left({T}_{\rm{m}}-{T}_{\mathrm{inf}}\right)$

(15)

$ {\dot {Q}}_{\rm{c,ic,w}}={\dot {m}}_{\rm{c,ic,w}}{c}_{\rm{p,w}}\left({T}_{\rm{m}}-{T}_{\mathrm{inf}}\right)$

(16)

$ {\dot {Q}}_{\rm{c,ic,i}}={\dot {m}}_{\rm{c,ic,i}}{c}_{\rm{p,i}}\left({T}_{\rm{m}}-{T}_{\mathrm{inf}}\right)$

(17)

$ {\dot {Q}}_{\rm{in}}={\dot {m}}_{\rm{in}}{c}_{\rm{p,w}}\left({T}_{{\text{上一个控制体}}}-{T}_{\mathrm{inf}}\right)$

(18)

$ \begin{array}{l}{\dot {Q}}_{\rm{i}}=({\dot {m}}_{\rm{c,d}}+{\dot {m}}_{\rm{c,ic,w}}+{\dot {m}}_{\rm{c,ic,i}}+{\dot {m}}_{\rm{in}}) \cdot {{{c}}}_{\rm{p,ic}}\left({T}_{\rm{m}}-{T}_{\rm{s}}\right)\end{array}$

(19)

式中， ${T_{\rm{m}}}$ 为融化温度， ${c_{{\rm{p,w}}}}$ 和 ${c_{{\rm{p,ic}}}}$ 分别为水和冰的比热容。

1.2 结冰热力学模型求解

对于二维翼型，驻点所在控制体流入的溢流水质量流量为零，且此控制体内的液态水等分为两部分，分别沿翼型表面向上下游溢流。值得注意的是，前一个控制体的溢流水流出质量流量等于下一个控制体的流入质量流量，即 $ {\dot {m}}_{\rm{out,}\rm{i}}={\dot {m}}_{\rm{in,}\rm{i+1}}$ 。

首先假定壁面温度等于融化温度，即 ${T_{\rm{s}}} = {T_{\rm{m}}}$ 。根据能量守恒方程可得冻结成冰的质量流量 $ {\dot {m}}_{\rm{f}}$ ，进而根据 $ {\dot {m}}_{\rm{f}}$ 判断结冰状态^[15]：

1) 当 $ {\dot {m}}_{\rm{f}}\geqslant{\dot {m}}_{\rm{c,ic,w}}+{\dot {m}}_{\rm{c,d}}+{\dot {m}}_{\rm{in}}$ 时，即冻结成冰质量流量大/等于当前控制体内所有液态水含量。控制体内液态水全部冻结，积冰为霜冰（ $ {\dot {m}}_{\rm{out}}=0$ , $ {\dot {Q}}_{\rm{out}}=0$ ）。此时表面没有液态水存在，则蒸发引起的质量损失为零( $ {\dot {m}}_{\rm{ev}}=0$ )，蒸发潜热 $ {\dot {Q}}_{\rm{ev}}$ 由升华潜热 $ {\dot {Q}}_{\rm{sub}}$ 代替。因此，质量和能量守恒方程分别做如下调整

$\begin{split}& {\dot {m}}_{\rm{i}}={\dot {m}}_{\rm{f}}+{\dot {m}}_{\rm{c,ic,i}}-{\dot {m}}_{\rm{sub}} \\&= ({\dot {m}}_{\rm{c,ic,w}}+{\dot {m}}_{\rm{c,d}}+{\dot {m}}_{\rm{in}})+{\dot {m}}_{\rm{c,ic,i}}-{\dot {m}}_{\rm{sub}}\end{split}$

(20)

$ \begin{split}& {\dot {Q}}_{\rm{ah}}+{\dot {Q}}_{\rm{ke,d}}+{\dot {Q}}_{\rm{ke,ic,w}}+{\dot {Q}}_{\rm{ke,ic,i}}+{\dot {Q}}_{\rm{f}}+{\dot {Q}}_{\rm{i}}+{\dot {Q}}_{\rm{in}} \\& = {\dot {Q}}_{\rm{conv}}+{\dot {Q}}_{\rm{sub}}+{\dot {Q}}_{\rm{c,d}}+{\dot {Q}}_{\rm{c,ic,i}}+{\dot {Q}}_{\rm{c,ic,w}}+{\dot {Q}}_{\rm{out}}\end{split}$

(21)

其中， $ {\dot {Q}}_{\rm{f}}={\dot {m}}_{\rm{f}}{L}_{\rm{m}}$ ， $ {\dot {Q}}_{\rm{i}}={c}_{\rm{p,i}}({\dot {m}}_{\rm{i}}+{\dot {m}}_{\rm{sub}})({T}_{\rm{m}}-{T}_{\rm{s}})$ 。

2) 当 ${\dot {m}}_{\rm{f}}\leqslant -{\dot {m}}_{\rm{c,ic,i}}$ 时，说明撞击到控制体内固态冰晶全部融化，此时没有发生结冰，表面为润湿状态( $ {\dot {m}}_{\rm{i}}=0$ , $ {\dot {Q}}_{\rm{i}}=0$ )。此时动量和能量平衡方程为

$ {\dot {m}}_{\rm{c,ic,w}}+{\dot {m}}_{\rm{c,ic,i}}+{\dot {m}}_{\rm{c,d}}+{\dot {m}}_{\rm{in}}-{\dot {m}}_{\rm{ev}}={\dot {m}}_{\rm{out}}$

(22)

$ \begin{split}& {\dot {Q}}_{\rm{ah}}+{\dot {Q}}_{\rm{ke,d}}+{\dot {Q}}_{\rm{ke,ic,w}}+{\dot {Q}}_{\rm{ke,ic,i}}+{\dot {Q}}_{\rm{f}}+{\dot {Q}}_{\rm{in}}\\& ={\dot {Q}}_{\rm{conv}}+{\dot {Q}}_{\rm{ev}}+{\dot {Q}}_{\rm{c,d}}+{\dot {Q}}_{\rm{c,ic,i}}+{\dot {Q}}_{\rm{c,ic,w}}+{\dot {Q}}_{\rm{out}}\end{split}$

(23)

其中， $ {\dot {Q}}_{\rm{f}}={\dot {m}}_{\rm{f}}{L}_{\rm{m}}$ , $ {\dot {Q}}_{\rm{out}}={c}_{\rm{p,w}}({\dot {m}}_{\rm{out}}+{\dot {m}}_{\rm{ev}})({T}_{\rm{m}}-{T}_{\rm{s}})$ 。

3) 当 $-{\dot {m}}_{\rm{c,ic,i}} < {\dot {m}}_{\rm{f}}<{\dot {m}}_{\rm{c,ic,w}}+{\dot {m}}_{\rm{c,d}}+{\dot {m}}_{\rm{in}}$ 时，说明此时液滴和冰晶并没有完全冻结，而是部分冻结、部分形成水膜，此时积冰为明冰（ $ {\dot {Q}}_{\rm{i}}=0$ , $ {\dot {Q}}_{\rm{out}}=0$ ）。质量平衡方程形如式（1）、（2），而能量平衡方程可简化为如下形式：

$ \begin{split}& {\dot {Q}}_{\rm{ah}}+{\dot {Q}}_{\rm{ke,d}}+{\dot {Q}}_{\rm{ke,ic,w}}+{\dot {Q}}_{\rm{ke,ic,i}}+{\dot {Q}}_{\rm{f}}+{\dot {Q}}_{\rm{in}}\\& ={\dot {Q}}_{\rm{conv}}+{\dot {Q}}_{\rm{ev}}+{\dot {Q}}_{\rm{c,d}}+{\dot {Q}}_{\rm{c,ic,i}}+{\dot {Q}}_{\rm{c,ic,w}}+{\dot {Q}}_{\rm{out}}\end{split}$

(24)

其中， $ {\dot {Q}}_{\rm{f}}={\dot {m}}_{\rm{f}}{L}_{\rm{m}}$ 。

1.3 冰晶黏附模型

通常情况下认为过冷水滴在撞击结冰表面后会全部发生黏附参与结冰过程。而冰晶与过冷水滴存在很大不同，冰晶撞击表面后可能发生破碎、反弹和黏附等结果。Nilamdeen等^[22]基于Euler方法定义了黏附系数，并指出冰晶撞击动力学行为受冰晶粒径尺寸、撞击速度以及液膜厚度等参数影响。文献[22]假定在霜冰区域冰晶全部反弹，在液膜区域冰晶全部黏附，即黏附系数分别为 ${\varepsilon _{{\rm{st}}}}=0$ 和 ${\varepsilon _{{\rm{st}}}}={\rm{ 1}}$ ；而在明冰区域内，冰晶黏附系数 ${\varepsilon _{{\rm{st}}}}$ 则与冰晶撞击速度和液膜厚度等参数有关，遵循以下关系式：

${\varepsilon _{{\rm{st}}}}{\rm{ = }}\frac{{{h_{\rm{f}}}}}{{{h_{{\rm{f,}}{\kern 1pt} {\rm{max}}}}}}\frac{1}{{\exp \left( {\chi {{\left\| {{v_n}} \right\|}^2}} \right)}}$

(25)

式中， ${h_{\rm{f}}}$ 为液膜高度， $ {h}_{\rm{f},\mathrm{max}}$ 为计算最大液膜厚度， ${v_n}$ 为冰晶的法向速度分量。参数 $\chi $ 用于控制撞击速度阈值 ${v_c}$ ，即当所有冰晶粒子法向速度分量大于速度阈值时（ ${v_n} > {v_c}$ ），冰晶全部发生反弹而不发生黏附，即黏附系数 ${\varepsilon _{{\rm{st}}}}{\rm{ = }}0$ 。假定 $ {h}_{\rm{f}}={h}_{\rm{f},\mathrm{max}}$ 、 ${\varepsilon _{{\rm{st}}}}{\rm{ = }}\varPsi$ ， $\chi $ 可由式（25）推得，具体表达式如下所示。

$\chi {\rm{ = }}\frac{1}{{{v_c}^2}}\ln \left( {\frac{1}{\varPsi }} \right)$

(26)

其中， $\varPsi$ 为极小正值， ${v_c}$ 为定义反弹边界的撞击速度阈值， ${v_c} = \sqrt {\dfrac{2}{{{d_{\rm{p}}}}}}$ ， ${d_{\rm{p}}}$ 为冰晶直径。

2 数值结果与分析 2.1 数值模型验证

本文基于FENSAP-ICE结冰数值计算软件，湍流模型采用Spalart–Allmaras一方程模型，采用欧拉法计算液滴和冰晶撞击特性。冰晶粘附模型采用NTI Bouncing Model^[22-23]，通过改进的Messinger结冰热力学模型，采用单步法对积冰增长及结冰表面水膜流动进行求解。

根据文献[8]中Cox冰风洞实验结果进行数值模型验证工作。该实验以NACA0012翼型为研究对象，弦长为0.9144 m，攻角为0°。液滴当量直径为20 μm，冰晶当量直径为150或200 μm，结冰时间均为600 s，详细结冰条件参见表1。

网格划分采用结构化网格，翼型附近网格划分如图2所示，全局网格数量为321600，展向分布5层网格，且近壁处网格划分满足y⁺≈1原则，由文献[15]可知，本文所采用的结构化网格满足收敛性要求。计算域高度与文献[8]中Cox冰风洞试验段尺寸保持一致。

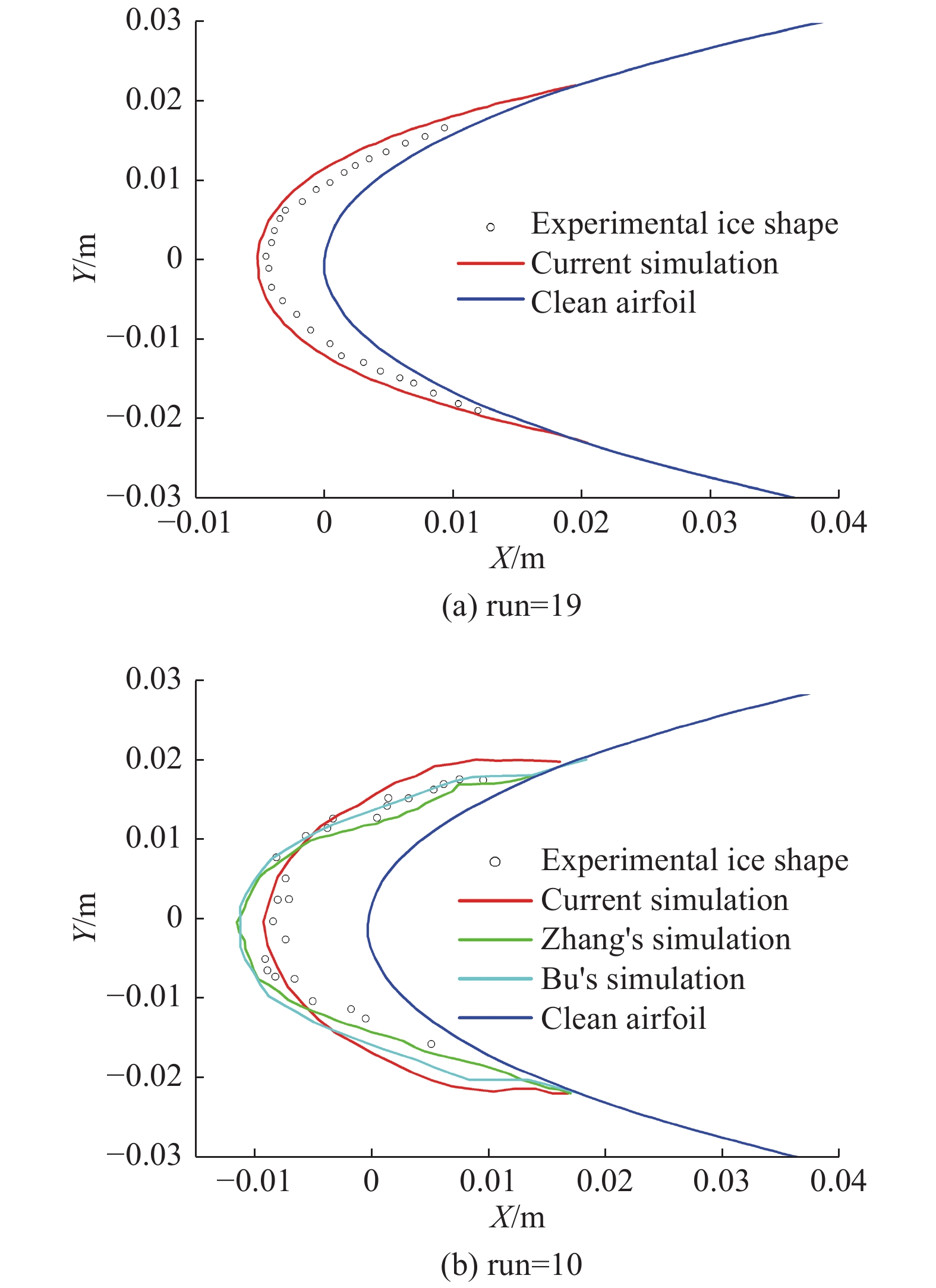
如图3所示，取本文数值模型计算的冰形与文献[8]中实验结果进行对比。可以看出，无论是工况run19中霜冰结冰条件，还是工况run 10中明冰结冰条件，本文数值结果与实验所得冰形均较为一致，进而验证了本文数值方法的正确性。混合相态积冰问题中冰晶侵蚀作用主要受冰晶粒径和撞击速度以及黏附效率影响响^[23]，图3（b）中在考虑冰晶侵蚀作用后，虽然结冰范围较实验结果略大，却明显抑制了翼型前缘处冰形生长，可以更好地吻合试验结果。

2.2 参数分析 2.2.1 融化率

为研究融化率(MR = LWC/TWC)对冰晶结冰过程的影响，在保证总水含量TWC = 1.4 g/m³前提下，本文分别选取IWC/LWC = 0.1/1.3、0.4/1.0、0.7/0.7、1.0/0.4、1.3/0.1共五组工况进行对比研究，其余结冰参数与表1中run 10所示参数保持一致。

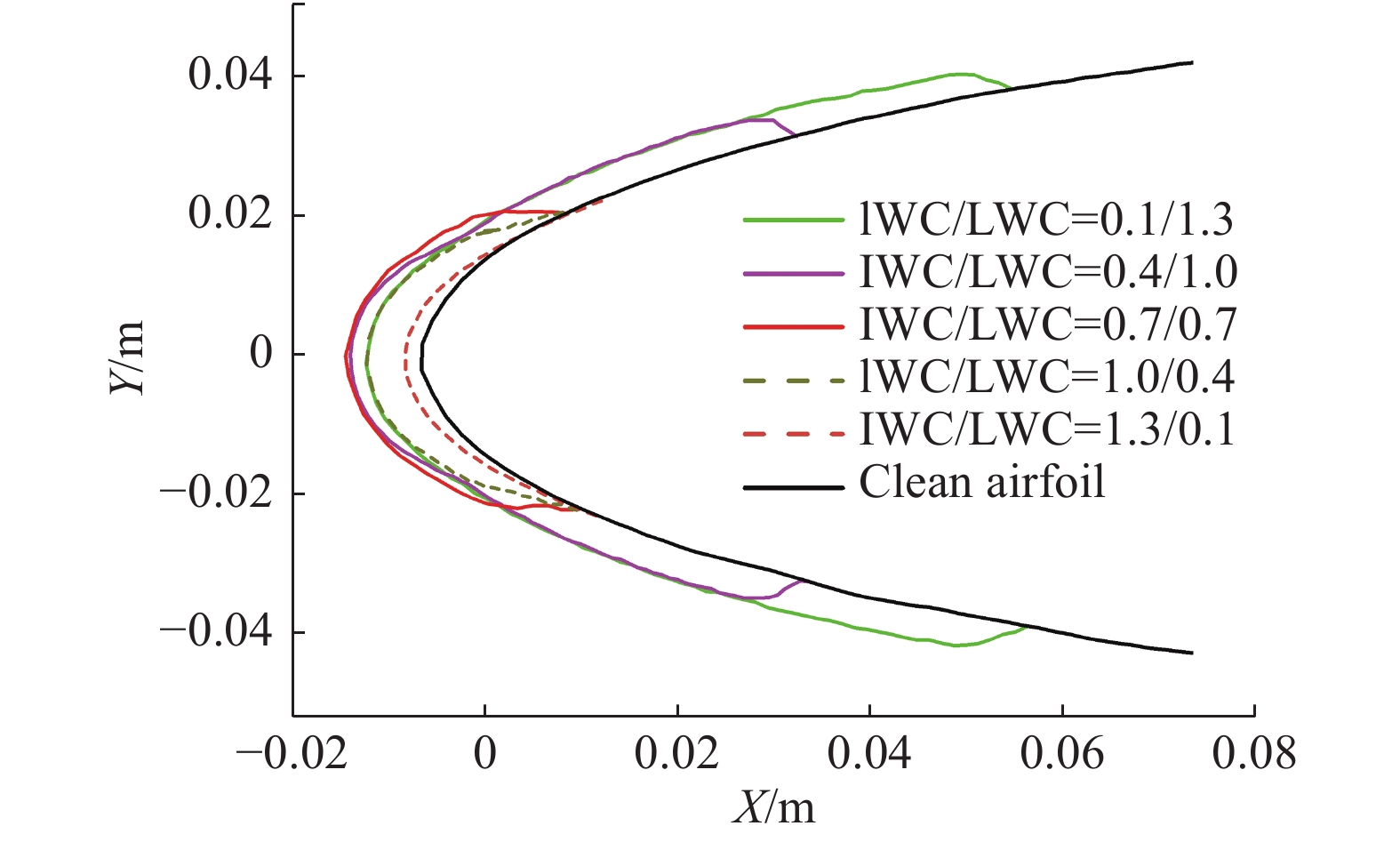
图4为不同融化率下冰形对比。可知当液态水含量LWC占主导时，结冰范围较大，且结冰范围随LWC下降而不断缩小。这是由于此时壁面所收集到的液态水在气动力作用下，从前缘驻点沿翼型上下表面向下游溢流，最终全部冻结；而冰晶粒径尺度相对较大，其运动轨迹不易受到气动力影响，更加集中地收集于翼型前缘。当冰水含量IWC占主导时，结冰范围基本保持不变，但结冰厚度显著降低。

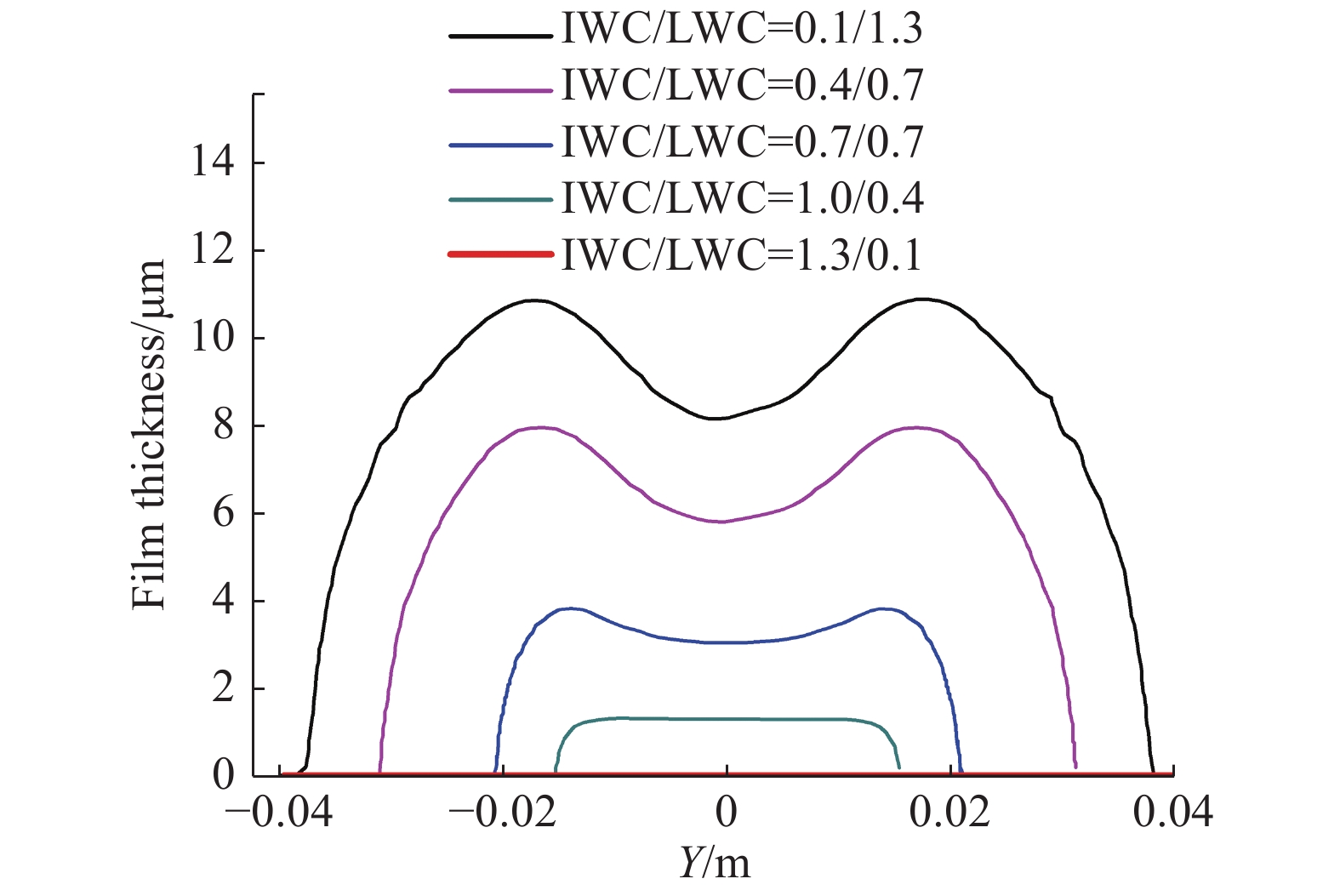
图5为不同融化率下翼型前缘液膜厚度。当IWC/LWC = 1.3/0.1时，由于液态水含量过小，液滴撞击到翼型表面后会在低温作用下即刻结冰，故此时水膜厚度为0 μm。随着LWC不断增大，液膜的厚度和润湿范围均随之增大，可以黏附更多的冰晶在结冰表面换热积冰。当IWC/LWC = 0.1/1.3时，液膜厚度和润湿范围均达到最大值，其中液膜厚度峰值约为10.7 μm，此时润湿范围对应图5中的积冰极限。此外由图4、图5可知，随着LWC不断降低，虽然冰晶的侵蚀效应随之减弱^[14]，但与此同时结冰表面液膜厚度变小，不足以黏附更多的冰晶，导致总体结冰量逐渐减小。

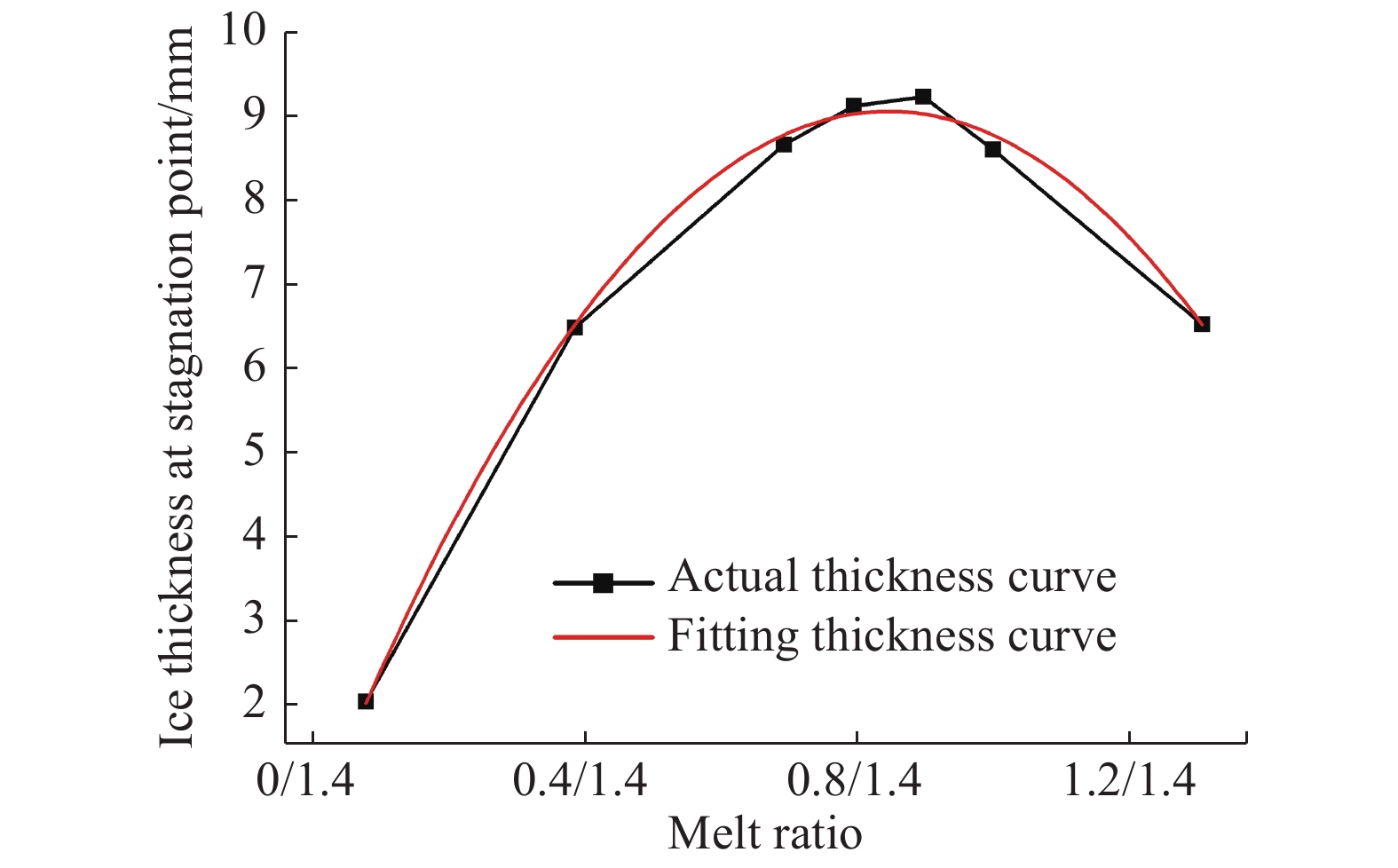
图6为不同融化率下翼型前缘驻点处结冰厚度。为确定翼型前缘驻点处达到最大结冰厚度时的融化率，增加了IWC/LWC = 0.5/0.9、0.6/0.8两组工况。由图6可知，在run 10结冰条件下，当IWC/LWC = 0.5/0.9时前缘驻点结冰厚度达到最大值，约为9.3 mm。综上所述，混合相冰晶积冰若达到最大结冰厚度，不仅要有足够的冰晶含量，以保证冰晶经过相变换热使结冰表面温度降至冰点以下，也需要有足够的液态水含量，足以黏附冰晶在结冰表面进行换热。

2.2.2 环境温度

为探究环境温度对于冰晶结冰过程影响，本文分别选取环境温度T为−4℃、−7℃、−10℃。由表2可知，在保证相对湿度（Relative Humidity，RH）一定情况下，不同温度下翼型表面粒子收集质量差异较小，随温度逐渐升高，粒子收集质量略有增加。

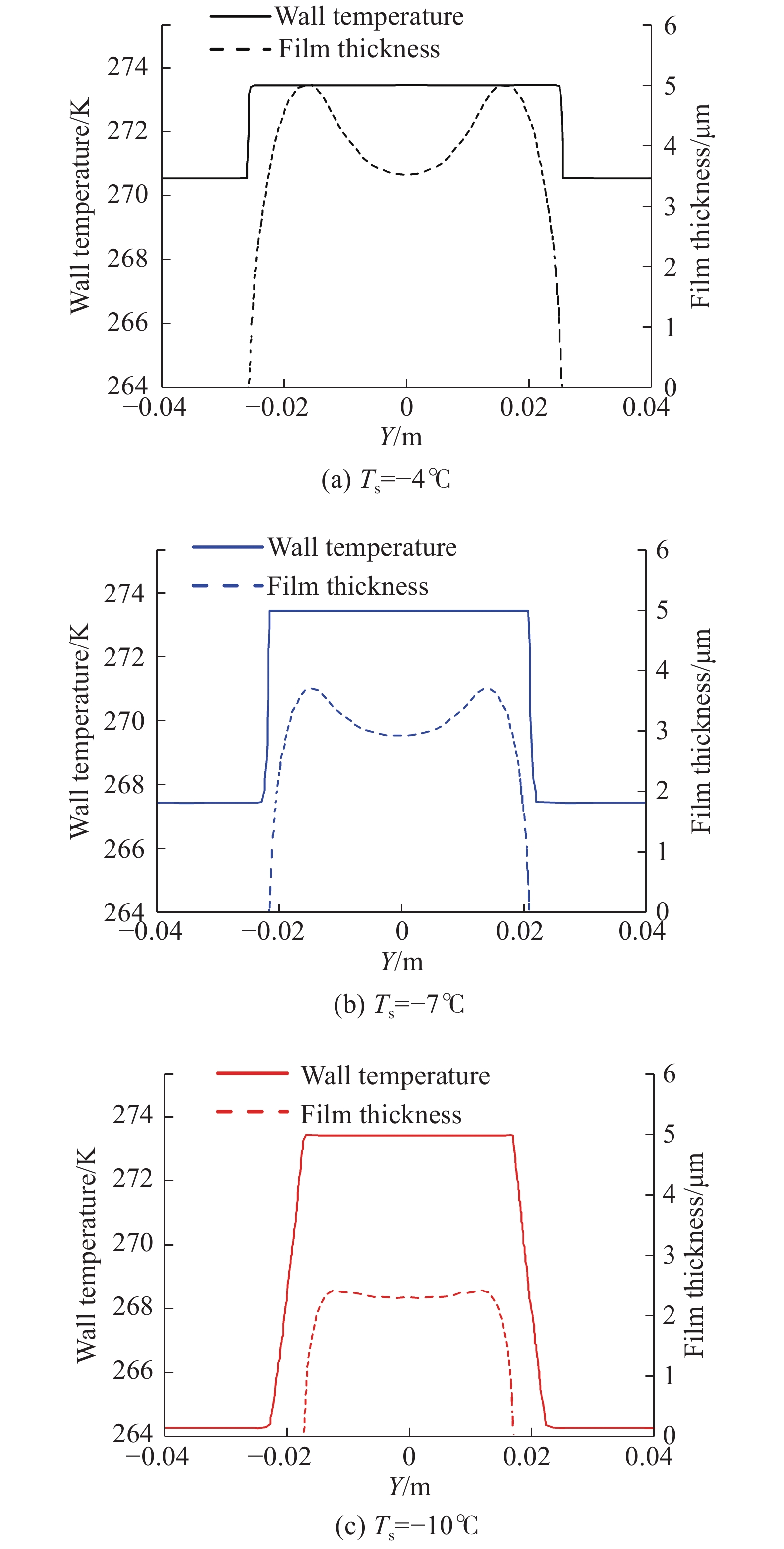
环境温度的变化也直接影响了湿球温度T_wb变化，三种情况下湿球温度T_wb与环境温度近似，同样为−4℃、−7℃、−10℃。湿球温度变化会影响粒子的相变传热过程，进而影响结冰过程。如图7所示，翼型表面所收集的液态水并未在撞击处完全冻结，而是在驻点附近（约−0.03 < Y < 0.03）形成溢流水且壁面温度约为0℃，从而形成混合态积冰条件。同时可以发现，随着环境温度升高，液膜的厚度和润湿范围均随之增大。

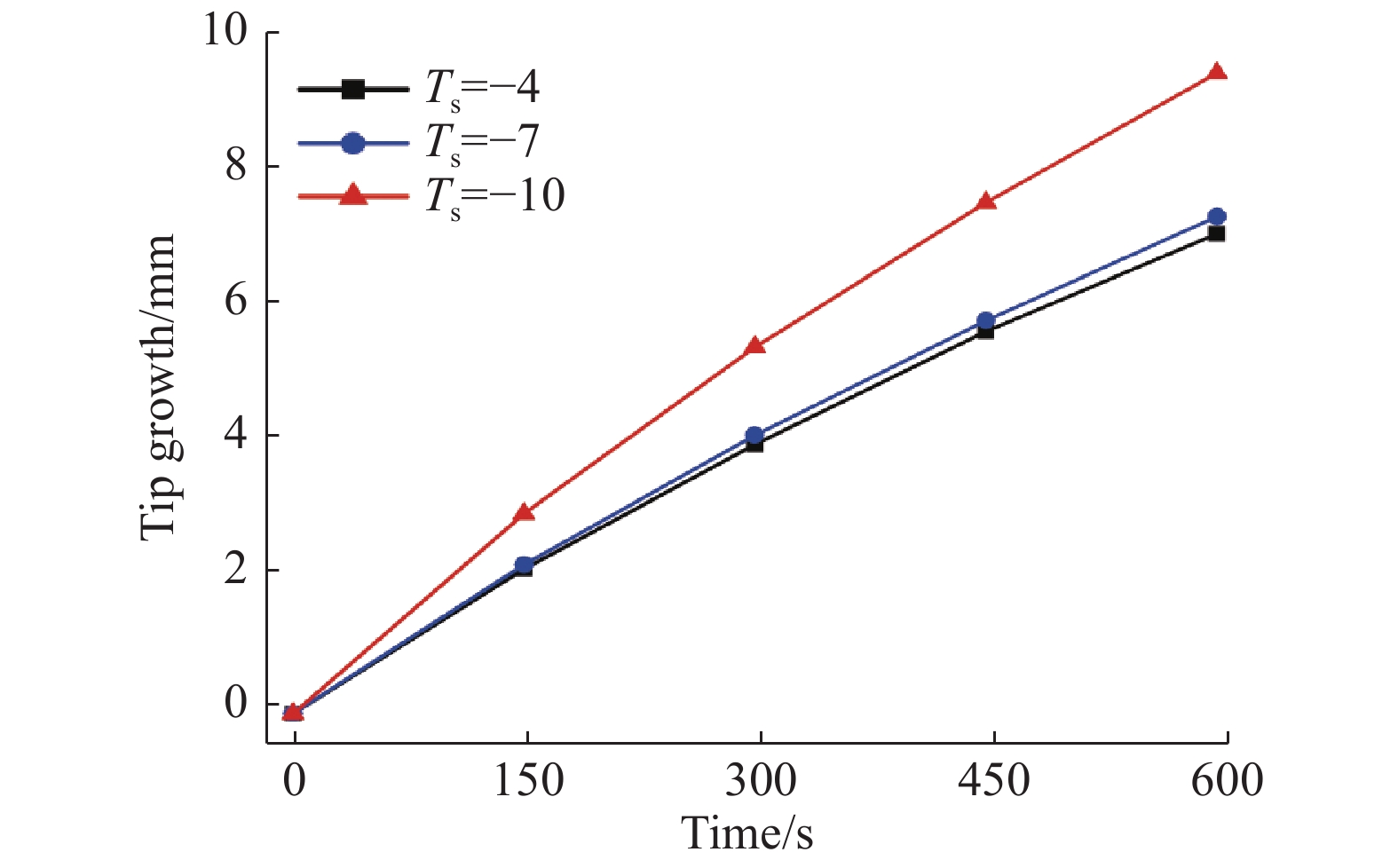
图8为不同温度下翼型前缘驻点积冰生长量对比。可以看出随着温度降低，翼型前缘驻点处结冰量和积冰速率均有明显增加。此外，可知在结冰初期积冰速率均较快，相对应的增长量曲线较为陡峭；而随着积冰的生长，积冰速度逐渐稳定，积冰增长量曲线也趋于平缓。

2.2.3 马赫数

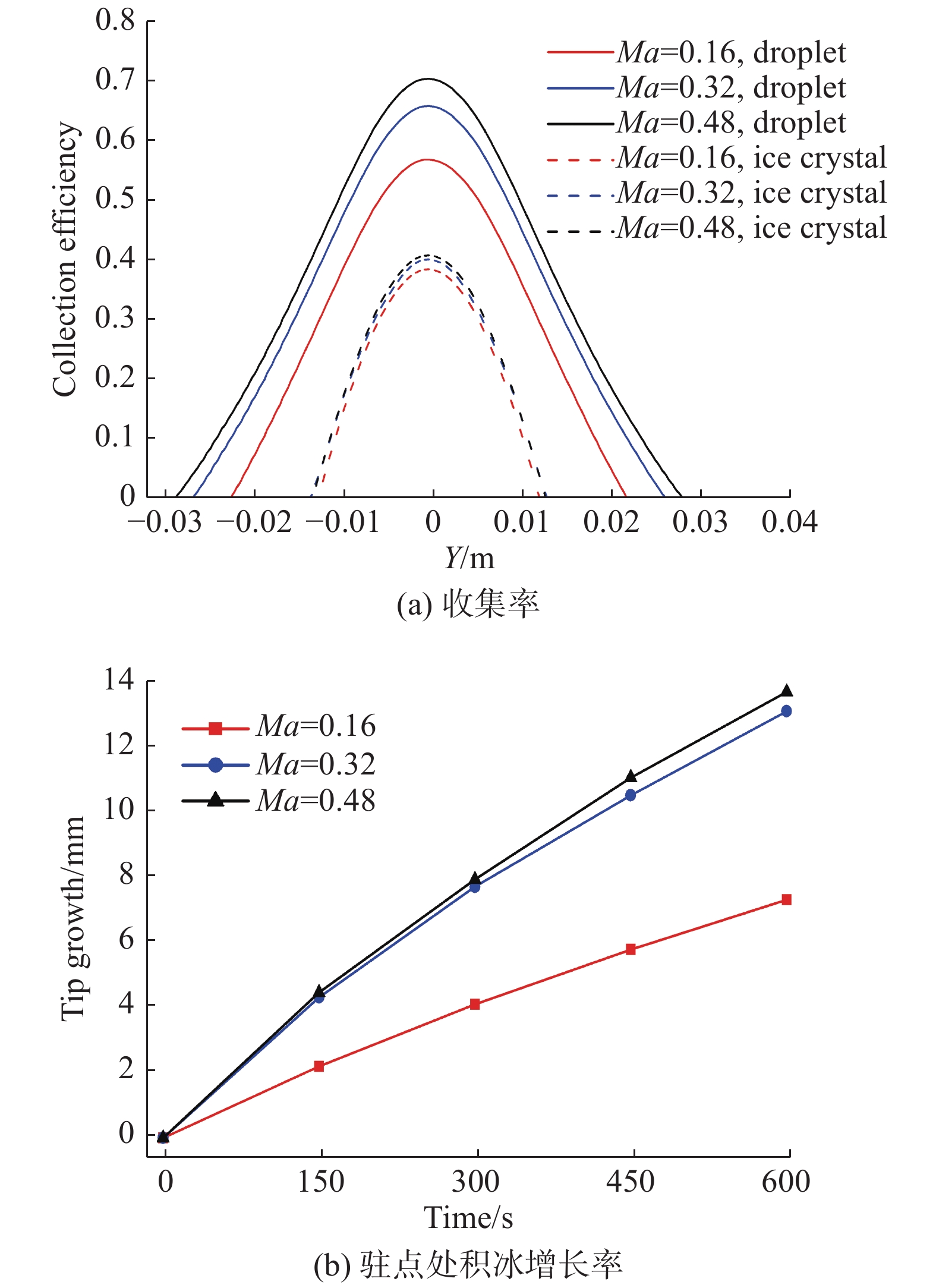
本文取马赫数Ma = 0.16、0.24、0.48，以研究其对混合相态结冰过程影响，相对应的液滴与冰晶收集系数和驻点积冰生长率分别如图9（a）、（b）所示。由图9（a）可知，随着马赫数增大，翼型表面液滴收集系数与润湿极限均随之增大，其中前缘驻点处液滴收集系数从0.575增加至0.711；而冰晶收集系数虽略有增加但变化并不显著，前缘驻点处冰晶收集系数仅从0.391增加至0.415。发生该现象的原因是液滴质量相较于冰晶更小，因而在高气动力作用下更容易改变其运动轨迹。

而从图9（b）中可得知，当马赫数较小（如Ma = 0.16）时，前缘驻点处积冰生长量随Ma数增大而显著增大；当马赫数较大（如Ma= 0.32）时，继续增大马赫数，前缘驻点积冰生长量并没有明显增长。此外，由图9（b）可知，在经历初期较快结冰速率后，随着积冰生长，结冰表面的积冰速度同样表现出逐渐平缓的趋势。

3 结　论

本文分析了混合相态下结冰表面的传热传质过程，通过改进的Messinger结冰热力学模型，建立了混合相态冰晶积冰热力学数值模型。通过与文献中Cox冰风洞下NACA0012翼型积冰实验结果对比，验证了本文数值模型的正确性，并在此基础上分析和研究了融化率对冰晶积冰过程的影响机制，以及环境温度、马赫数等参数对积冰形态和积冰生长率的影响。具体结论如下：

1）混合相冰晶积冰若达到最大结冰厚度，不仅要有足够的冰晶含量，以保证冰晶经过相变换热使结冰表面温度降到冰点以下，也需要有足够的液态水含量，足以黏附冰晶在结冰表面进行换热。因此针对不同结冰环境，存在最严酷结冰融化率；

2）环境温度直接影响了粒子湿球温度变化，进而影响粒子传热传质和相变过程。随环境温度升高，液膜的厚度和润湿范围也随之增大；

3）当环境温度降低或马赫数增大，翼型前缘驻点处结冰量和积冰速率均有明显增加；随着积冰的生长，积冰速度逐渐稳定，积冰增长量曲线也趋于平缓。