架空输电线路导线在表面覆冰后会形成非圆形的截面形状,其风致气动力可诱发导线舞动,严重威胁输电线路的安全 [1-2]。
李万平[3-4]、楼文娟[5]、阎东[6]、李新民[7]等对新月形、D形覆冰导线进行风洞试验研究全风攻角下气动力系数。Hisato[8]等对不同厚度的三角覆冰和圆角三角覆冰导线进行表面测压试验和天平测力试验,验证两种试验结果的一致性,并获得了覆冰导线气动力数据。
基于计算流体力学(CFD)的数值模拟方法能够展现完备的流场信息,可与风洞试验互补,便于更深层次地研究流场结构的演化。李新民[9]用SA湍流模型对23 mm厚新月形覆冰导线进行数值模拟,发现在风攻角15°附近存在回流涡现象。Ishihara[10]利用大涡模拟(LES)对圆角三角形覆冰导线进行模拟,模拟结果与风洞试验数据相吻合。林巍[11]、吕翼[12]分别用k-ω SST湍流模型和SA湍流模型对覆冰6.7 mm (导线直径26.82 mm)和覆冰18 mm (导线直径32.76 mm)的新月形覆冰导线进行数值模拟,并得到了较好的模拟结果。符玉珊[13]运用格子玻尔兹曼方法对18 mm覆冰的新月形覆冰导线(导线直径32.76 mm)进行大涡模拟,在较低耗时情况下得到了较高精度的模拟结果。
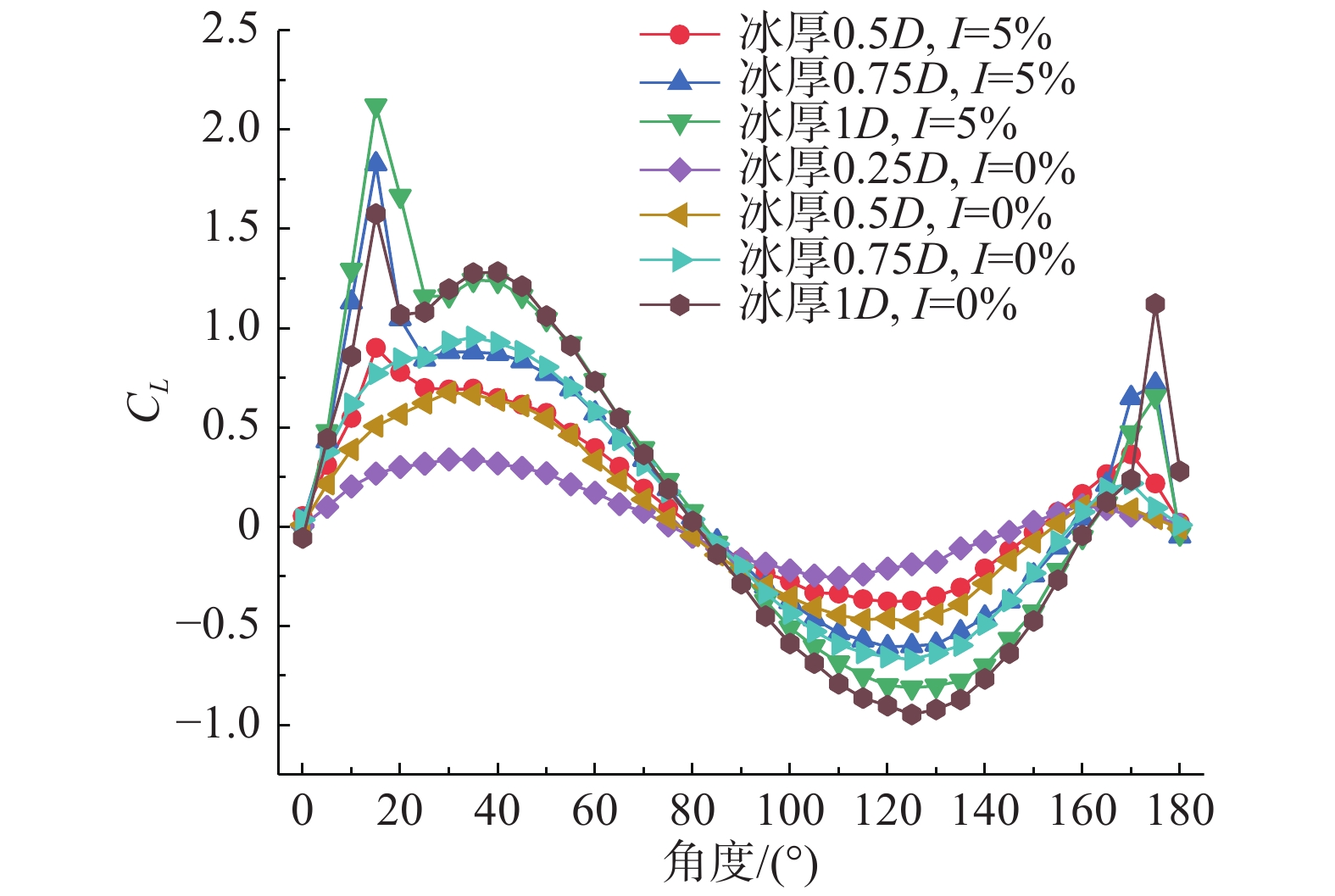
现有对覆冰导线气动力特性的数值模拟研究中,覆冰厚度多数小于1D (D为导线直径),而根据历史观测数据,覆冰厚度达到1D及以上的情况在覆冰严重地区经常出现[14-15]。图1根据文献[5-6]的风洞试验数据绘制,为不同厚度覆冰导线升力系数随风攻角变化情况的示意图。当覆冰厚度较大时,覆冰导线的升力系数曲线在风攻角15°附近区间出现“尖峰”,并且随着冰厚的增大更加明显。升力系数的突变使得在该风攻角区间易出现覆冰导线的风致舞动现象[6,16-17],准确模拟和理解这一升力系数的“尖峰”,对于覆冰导线风致舞动的验算和防治具有特别意义。
|
图 1 不同厚度新月形覆冰升力系数(I为湍流度) Fig.1 Lift coefficients of the crescent-shape ice with different thickness (I indicates the turbulence intensity) |
目前覆冰导线气动力系数的CFD模拟大多局限于无升力“尖峰”的较薄覆冰,通常选用雷诺时均法进行气动力模拟。但对于厚覆冰导线的模拟结果并不理想,尤其是风攻角15°附近升力系数“尖峰”模拟较为困难;另外,对于厚覆冰导线升力系数在风攻角15°附近出现极大值的原因也尚不明确,鲜有讨论。本文分别采用ANSYS Fluent软件内基于k-ω SST湍流模型的雷诺时均法和大涡模拟的数值方法,通过网格和时间步长的优化提高模拟精度,得到风攻角10°~20°范围内1D新月形厚覆冰导线气动力参数和绕流风场结果,并利用风洞试验结果验证数值方法的适用性。通过对覆冰导线表面压力分布和绕流风场结构分析,进一步探究厚覆冰导线升力系数在风攻角15°附近出现“尖峰”的原因。
1 数值方法和计算模型 1.1 大涡模拟大涡模拟通过空间滤波将湍流分成大尺度涡和小尺度涡。其中,大尺度涡对湍流输运的动量、质量、能量等物理量起到决定性作用,因此对大尺度的涡进行了不可压缩Navier-Stokes方程直接模拟。小尺度的涡趋于各向同性,其对大尺度涡的影响通过亚格子模型模拟。
本文的大涡模拟选用局部涡黏度壁面自适应(WALE)亚格子模型。WALE亚格子模型是在Smagorinsky-Lilly亚格子模型的基础上发展过来的,它修正了Smagorinsky-Lilly亚格子模型在近壁面涡黏系数不为0的缺陷[18]。其亚格子应力张量具体形式如下:
| ${\tau _{ij}} - \frac{1}{3}{\tau _{kk}}{\delta _{ij}}{\rm{ = - 2}}{\mu _{\rm{t}}}\overline {{S_{ij}}} $ | (1) |
| $ \overline {{S_{ij}}} = \frac{1}{2}\left(\frac{{\partial {{\overline u }_i}}}{{\partial {x_j}}} + \frac{{\partial {{\overline u }_j}}}{{\partial {x_i}}}\right) $ | (2) |
其中,μt为亚格子黏度系数,其定义式如下:
| ${\mu _{\rm{t}}} = \rho L_{\rm{s}}^2\frac{{{{(S_{ij}^{\rm{d}}S_{ij}^{\rm{d}})}^{3/2}}}}{{{{({{\overline S }_{ij}}{{\overline S }_{ij}})}^{5/2}} + {{(S_{ij}^{\rm{d}}S_{ij}^{\rm{d}})}^{5/4}}}}$ | (3) |
其中,
| $ {L_{\rm{s}}} = \min (\kappa d,{C_{\rm{w}}}\Delta ) $ | (4) |
| $S_{ij}^{\rm{d}} = \frac{1}{2}({\overline {{g_{ij}}} ^2} + {\overline {{g_{ji}}} ^2}) - \frac{1}{3}{\delta _{ij}}{\overline {{g_{kk}}} ^2}$ | (5) |
| ${\overline g _{ij}} = \frac{{\partial {{\overline u }_i}}}{{\partial {x_j}}}$ | (6) |
式中,Cw为WALE常数,取0.325;Δ为过滤之后的尺寸,
雷诺时均法(RANS)将流场分为系综平均量和湍流脉动量,并通过湍流模型来封闭N-S方程。其中,基于湍流动能k和比耗散率ω的k-ω模型[19]是一种较为常用的湍流模型。k-ω模型在湍流黏度的定义中考虑了湍流剪切应力的传递,并通过设定混合函数将标准k-ε模型和k-ω模型进行结合,在近壁面区域内使用k-ω湍流模型求解,在边界层外则使用k-ε模型。既能充分发挥k-ε模型在模拟远离壁面的充分发展湍流的优势,又能适应于各种压力梯度下的边界层模拟,在模拟压力梯度和分离流上具有较大优势,常被用于模拟钝体绕流。
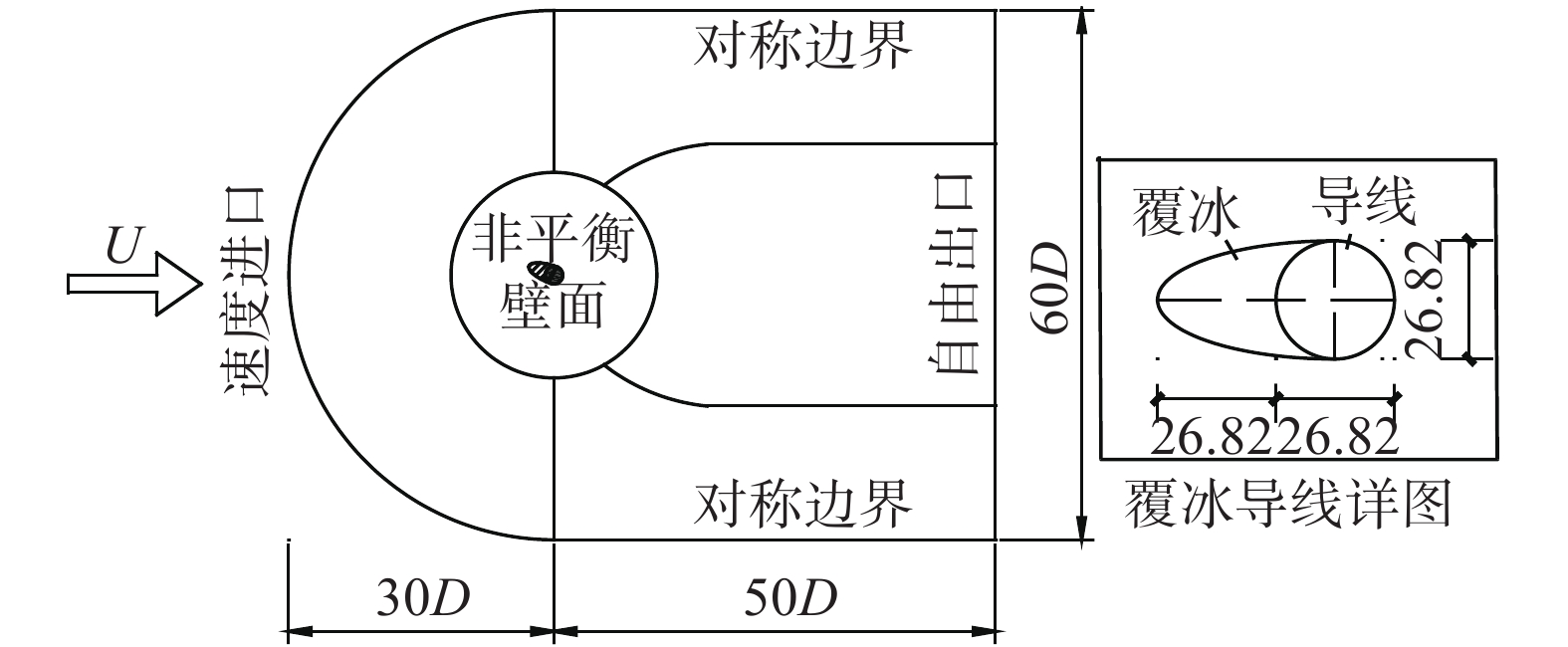
1.3 计算模型本文研究对象为1D新月形覆冰导线,裸导线直径D为26.82 mm。计算域入口边界至导线中心距离为30D,出口边界距导线中心50D;计算域的横风向宽度为60D,展向高度为2D,最大阻塞率为2.0%。计算域入口设为速度入口(入口风速U = 10 m/s),出口为自由出流,覆冰导线表面为光滑无滑移壁面,展向边界为周期性边界,其余为对称边界。几何模型和计算域如图2所示。计算网格为使用Pointwise生成的结构网格,近壁面第一层网格高度设为0.001D,以满足LES计算时y+≈1要求,网格增长率为1.05。图3为计算网格局部示意图。
|
图 2 几何模型和计算域 Fig.2 Schematic of the model and the computational domain |

|
图 3 近壁面网格 Fig.3 Near-wall grid |
大涡模拟采用SIMPLEC算法求解压力-速度耦合方程,压强项为二阶格式,动量项为有界中心差分格式,时间离散方式为二阶隐式格式。在使用基于k-ω SST模型的雷诺平均法在求解黏性子层时同样需要满足y+≈1的网格要求,选用与LES相同的计算网格。k-ω SST模型计算时湍动能和耗散率项均设置为二阶迎风格式,其余和LES设置相同。
1.4 网格与时间步长无关性验证为分析网格数和时间步长对大涡模拟计算结果的影响,分别计算了风攻角15°下的4个算例,结果列于表1。
| 表 1 不同计算工况设置 Table 1 Parameters for different computation conditions |
|
|
由表1可得,周向节点数对气动力模拟结果有较大影响。随覆冰厚度增大,需要更多节点来捕捉覆冰导线壁面弧度细节。针对本文工况,600个周向节点能较好表现覆冰导线截面形状特性。综合考虑计算精度与耗时,本文LES选用Case2的网格与时间步长设置;k-ω SST湍流模型选取同样的网格,但由于本文算例中k-ω SST湍流模型对时间步设置不敏感,因此参考文献[10]中的取值,无量纲时间步设置为0.186。
2 结果对比及分析 2.1 气动力系数覆冰导线升力系数、阻力系数以及扭矩系数定义为:
| $ {C_L} = \dfrac{{2{F_L}}}{{\rho {U^{\rm{2}}}DH}};\;\;{C_D} = \dfrac{{2{F_D}}}{{\rho {U^{\rm{2}}}DH}};\;\; {C_m} = \dfrac{{2M}}{{\rho {U^2}D{H^2}}} $ | (7) |
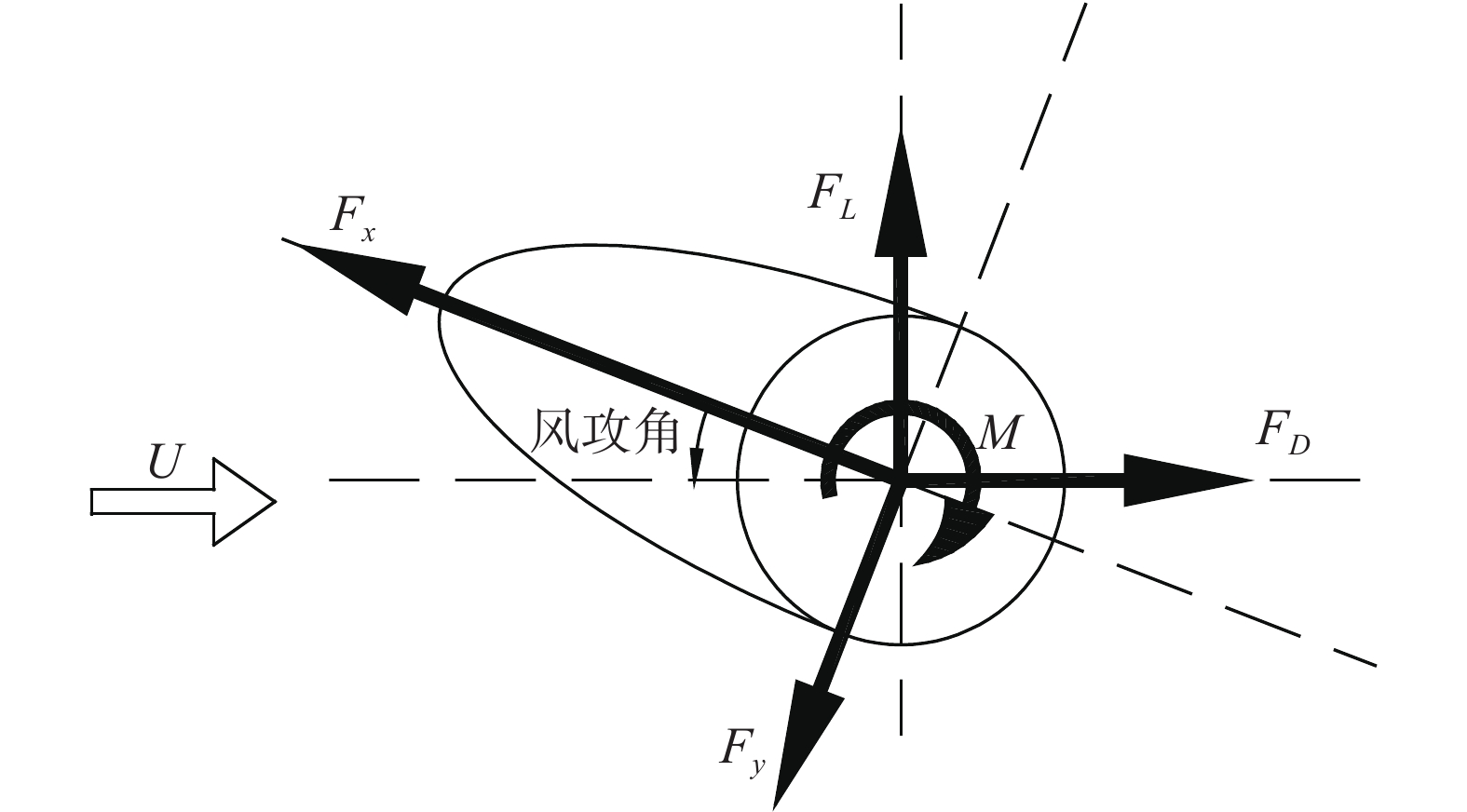
式中,空气密度ρ为1.225 kg/m3,导线外径D为26.82 mm,展向长度H为2D,U为试验风速。升力FL、阻力FD、扭矩M的方向如图4所示。
|
图 4 气动力方向及风攻角定义 Fig.4 Definition of the aerodynamic force directions and wind attack angles |
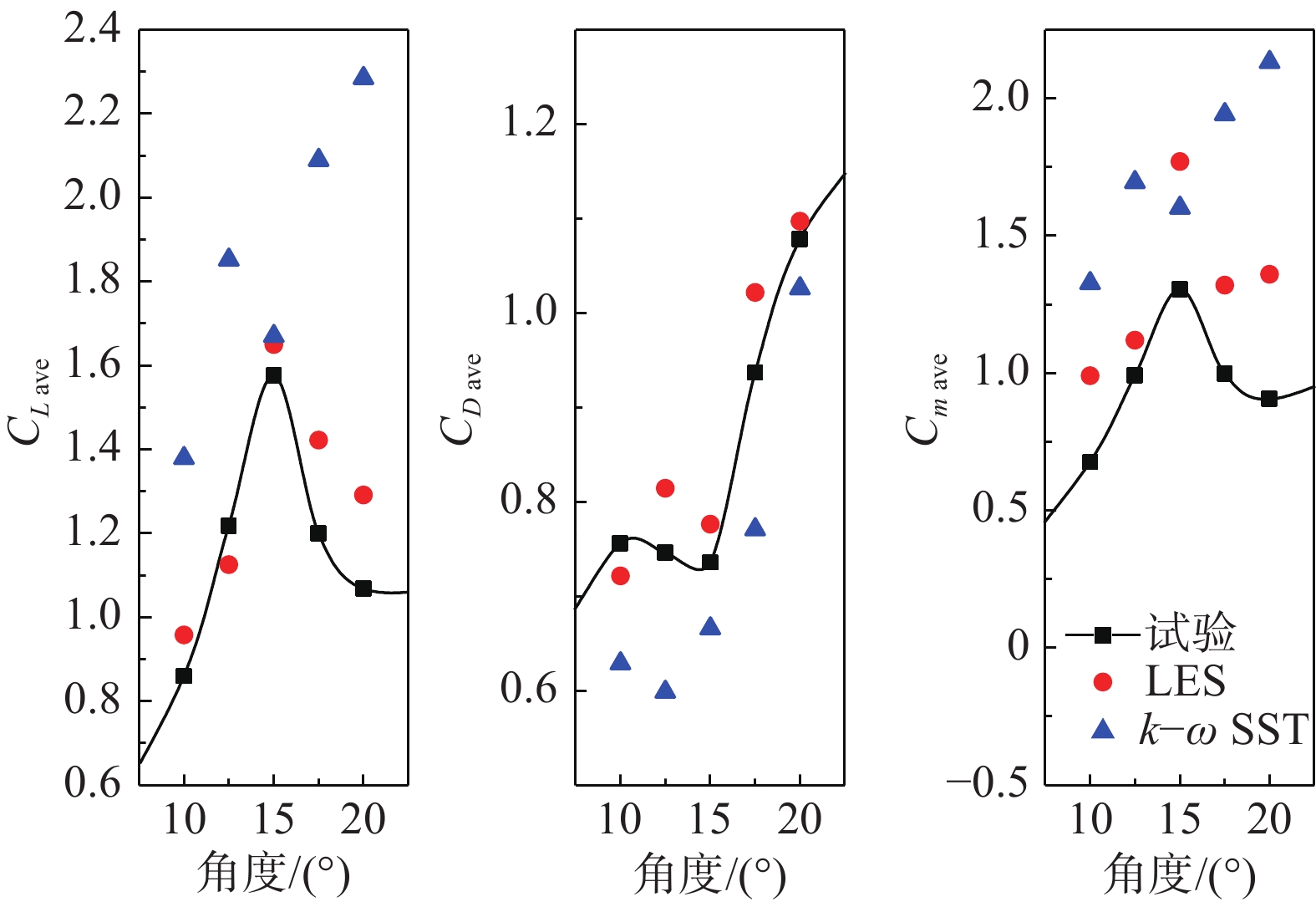
图5为风攻角10°~20°范围内1D新月形覆冰导线的气动力系数。对比k-ω SST和LES的计算气动力系数可以发现,LES模拟结果与试验结果非常接近,在风攻角15°下,升力系数、扭转系数均出现“尖峰”,并且对角度一阶求导后得到的Den Hartog系数和Nigol系数(图6)在负斜率部分也和试验值非常接近;而k-ω SST模拟结果在风攻角15°~20°范围内升力系数没有降低,没有出现明显的“尖峰”。因此,LES模型比k-ω SST模型更能准确模拟覆冰导线的气动力,能满足覆冰导线舞动分析的需求。
|
图 5 各风攻角下1D新月形覆冰导线气动力系数 Fig.5 Aerodynamic coefficients of a 1D crescent-shape iced conductor at various wind attack angles |
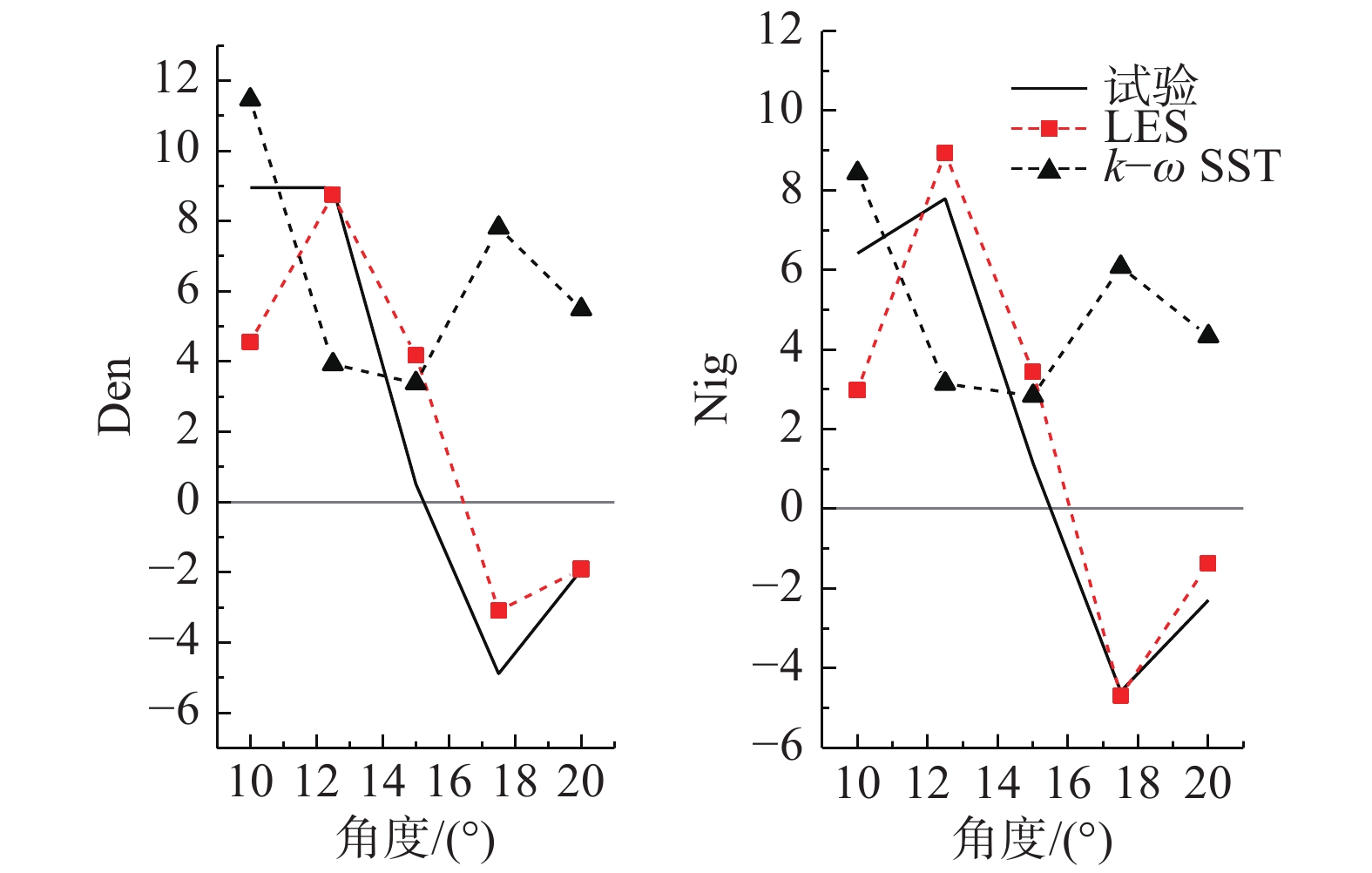
|
图 6 1D新月形覆冰导线Den Hartog系数和Nigol系数 Fig.6 Den Hartog and Nigol coefficients of a 1D crescent-shape iced conductor |
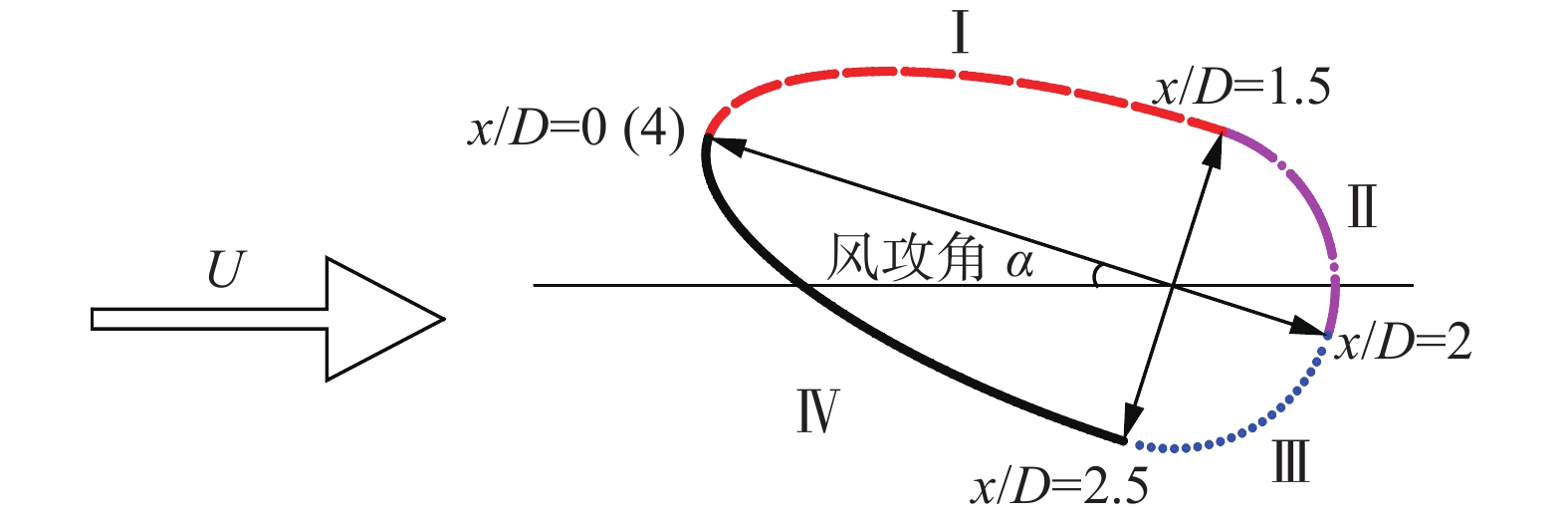
根据1D新月形覆冰导线表面的压力分布特征,将其分为四个区域:覆冰端上侧(0 < x/D < 1.5)、导线端上侧(1.5 < x/D < 2)、导线端下侧(2 < x/D < 2.5)和覆冰端下侧(2.5 < x/D < 4),并分别将其记为Ⅰ区、Ⅱ区、Ⅲ区、Ⅳ区,如 图7所示。
|
图 7 覆冰导线分区及周向坐标定义 Fig.7 Partitions of the iced conductor with the circumferential coordinates |
图8为两种数值方法计算得到的平均流线图。整体而言,两种算法的平均流场在Ⅱ区和Ⅲ区均有较大尺度的回流,Ⅱ区逆时针大尺度涡紧贴着导线壁面,Ⅲ区涡为上侧流体绕过Ⅱ区涡后再次附着在导线表面的二次涡,且Ⅱ区回流区域面积大于Ⅲ区回流区域面积。

|
图 8 不同风攻角下平均流线图 Fig.8 Averaged streamline patterns under various wind attack angles |
k-ω SST模型计算的平均回流区长度在风攻角10°与12.5°较为接近,在15°附近最大,并在15°至20°范围内随风攻角增大而减小。LES计算得到的平均回流区长度则在10°~15°下没有明显变化,在15°~20°下随风攻角增大而明显增大。
相比较k-ω SST模型而言,LES能够模拟出Ⅰ、Ⅱ区紧贴壁面逆时针的分离泡。随着风攻角的增大,这些分离泡的位置逐渐前移靠近导线覆冰端顶点,覆冰导线上侧分离点也向覆冰顶端靠近,且在Ⅲ区存在小尺度涡结构。Ⅲ区壁面附近涡结构仅在15°风攻角下为一对方向相反的小尺度涡,其余风攻角下仅存在一个顺时针涡。
2.3 表面风压系数从图5可看到,k-ω SST模型和LES模拟的升力系数在15°~20°有明显区别,图9为该范围覆冰导线壁面平均风压系数分布图。由图9可得,1D新月形覆冰导线表面平均风压系数在Ⅱ、Ⅲ区均保持在0附近,靠近导线覆冰端顶点的平均压力系数存在大幅度突变。平均压力系数均在覆冰顶端的上表面和下表面附近(约x/D = 0.1与x/D = 3.9处)达到最小值和最大值。k-ω SST模型和LES计算结果差异主要体现在Ⅰ区。
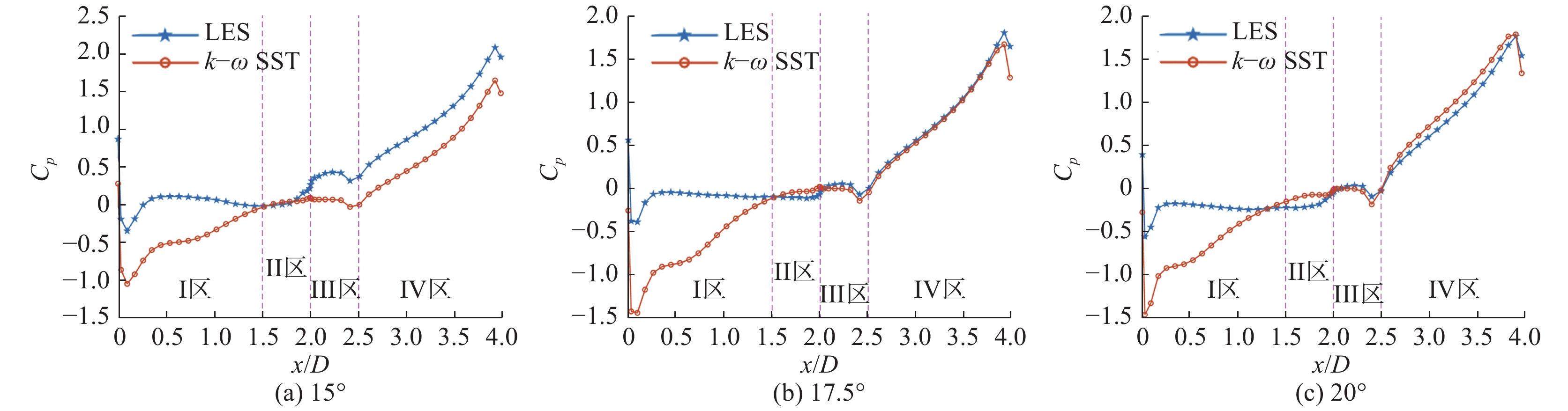
|
图 9 风攻角15° ~ 20°下的平均风压系数 Fig.9 Averaged wind pressure coefficient at wind attack angles ranging from 15° to 20° |
图10为各风攻角的平均速度和压力云图。可以看到,LES结果中最大平均速度都在15 m/s左右,k-ω SST模型计算得到的最大平均速度和LES基本一致,仅在20°风攻角下突然增大至17 m/s。在各风攻角下均存在两个高流速区域(x/D = 0.1和x/D = 2.5附近),此处流场对覆冰导线的吸力最大,对应压力曲线上的两个极小值。

|
图 10 各风攻角下的平均速度云图和平均压力系数 Fig.10 Averaged velocity contours and averaged wind pressure coefficients at various wind attack angles |
在覆冰端高速区域内,k-ω SST模型的高速区域面积更大,呈半圆形;LES模型的高速区域呈长条状,对应于图9所示的LES模型在覆冰端上侧的平均压力分布明显小于k-ω SST模型。LES方法捕捉到的小尺度涡脱引起覆冰导线上侧出现风速介于最大速度和0之间的中速区,高速区向上抬升,减小了导线在此范围内的吸力。
k-ω SST和LES模拟结果存在区别,其主要原因是LES能够模拟出紧贴覆冰导线上侧壁面的多个小尺度涡,而这些小尺度涡对覆冰导线壁面压力有着不可忽视的影响;k-ω SST模型仅模拟出了Ⅰ区和Ⅱ区的大尺度回流涡,无法模拟出Ⅰ区壁面上的小尺度涡,夸大了Ⅰ区壁面的风吸力。并且随着覆冰厚度的增大,覆冰端上侧的小尺度涡结构会更复杂,对覆冰导线的影响更大。因此对于较厚覆冰导线,LES是数值模拟的首选。
3 升力系数突变原因由图8可知,风攻角10°至20°是覆冰导线尾流处的涡不断扩大并附着于覆冰导线上壁面的过程;并随着覆冰厚度增大,Ⅰ、Ⅱ区的小尺度涡结构更加复杂。在该过程中,覆冰导线周围流场变化致使导线气动力出现较大变化。由图5可知,LES方法能更有效地模拟1D新月形覆冰导线气动力系数随风攻角的变化情况,其表面压力分布结果更准确。下面根据LES方法模拟所得平均流场结果,分析升力系数在风攻角15°出现“尖峰”的流体动力学机制。
表2为各风攻角下壁面四个区域的升力系数分量,从中可以看到覆冰导线升力主要来源于Ⅳ区正压以及Ⅰ区负压。对Ⅳ区,在10°至20°范围内随着风攻角的增大,Ⅳ区前沿驻点的位置远离覆冰顶点,驻点处的壁面曲率减小,来流与壁面夹角增大,根据动量定律,壁面压力增大;同时,随着风攻角的增大,Ⅳ区正压沿升力方向的分量减小,沿阻力方向的分量增大。如表2所示,Ⅳ区正压提供的升力在15°风攻角下达到最大值。对Ⅰ区,在10°~20°范围,随着风攻角增大,分离点向来流方向前移,并出现紧贴壁面的小尺度涡,其与尾流区域涡旋结构的相互作用致使Ⅰ区壁面吸力先减后增。同时,在风攻角15°下,覆冰导线Ⅲ区附近的一对方向相反的小尺度涡增大了沿壁面法向的压力梯度,使Ⅲ区出现较大的正压。综合覆冰导线上侧吸力略微减小、下侧(Ⅲ、Ⅳ区)的壁面压力因驻点所在处的壁面曲率、来流夹角和壁面切线方向等因素影响达到最大值,致使导线上下表面压力差明显大于其余风攻角,1D厚覆冰导线的升力系数曲线在15°风攻角附近出现“尖峰”。
| 表 2 各风向角下各壁面分区的升力系数分量 Table 2 Components of the lift coefficient in each surface partition under various wind attack angles |
|
|
本文分别采用基于k-ω SST湍流模型的雷诺时均法和大涡模拟的数值方法模拟1D新月形覆冰导线在风攻角10°~20°范围内的气动力特性和绕流风场,并结合风洞试验数据对结果进行对比分析。主要结论如下:
1)相比于覆冰导线气动力模拟中广泛应用的雷诺时均法,大涡模拟能够准确捕捉壁面附近的小尺度涡结构,有较准确的模拟结果。对于较厚覆冰导线的气动力数值模拟,应首选LES。
2)1D新月形覆冰导线在上侧壁面处的涡结构影响整体流场,并在下侧壁面曲率、来流夹角和壁面切线方向共同作用下导致风攻角15°时的升力系数突变。
根据本文的模拟结果以及出现升力“尖峰”的原因阐释,得到了较厚新月形覆冰的流场特征,但具体的防舞措施还需进一步探究尝试。
| [1] |
郭应龙, 李国兴, 尤传永. 输电线路舞动[M]. 北京: 中国电力出版社, 2003. GUO Y L, LI G X, YOU C Y. Galloping of transmission conductor[M]. Beijing: China Electric Power Press, 2002. (in Chinese). |
| [2] |
刘和云. 架空导线覆冰防冰的理论与应用[M]. 北京: 中国铁道出版社, 2001. LIU H Y. Theories and applications of ice accretion and anti-icing on overhead transmission lines[M]. Beijing: China Railway Publishing House, 2001. (in Chinese). |
| [3] |
覆冰导线群的动态气动力特性[J]. 空气动力学学报, 2000(4): 31-38. LI W P. Dynamic aerodynamic characteristics of the galloping of bundled iced power transmission lines[J]. Acta Aerodynamica Sinica, 2000(4): 31-38. DOI:10.3969/j.issn.0258-1825.2000.04.006 (in Chinese) |
| [4] |
特大覆冰导线气动力特性测试[J]. 华中科技大学学报, 2001, 29(8): 84-86. LI W P, HUANG H, HE Z. Aerodynamic characteristics of heavily iced conductors[J]. Huazhong Univ. of Sci. & Tech., 2001, 29(8): 84-86. DOI:10.3321/j.issn:1671-4512.2001.08.029 (in Chinese) |
| [5] |
不同厚度新月形覆冰对导线气动力特性的影响[J]. 空气动力学学报, 2013, 31(5): 616-622. LOU W J, LIN W, HUANG M F, et al. The impact of ice thickness on the aerodynamic characteristics crescent shape iced conductors[J]. Acta Aerodynamica Sinica, 2013, 31(5): 616-622. (in Chinese) |
| [6] |
湍流度对覆冰导线气动力特性影响的试验研究[J]. 高电压技术, 2014, 40(2): 450-457. YAN D, LYU Z B, et al. Experimental study on effect of turbulence intensity on the aerodynamic characteristics of iced conductors[J]. High Voltage Engineering, 2014, 40(2): 450-457. DOI:10.13336/j.1003-6520.hve.2014.02.017 (in Chinese) |
| [7] |
1520mm2大截面两分裂新月形覆冰导线空气动力特性试验研究
[J]. 科学技术与工程, 2017, 17(27): 53-58. LI X M, NIE X C, YAN Z T, et al. Experimental study on aerodynamic characteristics of 1520mm2 2-bundled large cross-section crescent shape iced conductors [J]. Science Technology and Engineering, 2017, 17(27): 53-58. DOI:10.3969/j.issn.1671-1815.2017.27.008 (in Chinese) |
| [8] |
MATSUMIYA H, SHIMIZU M, NISHIHARA T. Steady aerodynamic characteristics of single and four-bundled conductors of overhead transmission lines under ice and snow accretion[J]. Journal of Structural Engineering, 2010, 588-601. |
| [9] |
典型覆冰导线空气动力学特性数值和试验模拟[J]. 高电压技术, 2014, 40(2): 427-433. LI X M, ZHU K J, LIU B. Numerical and experimental simulation of aerodynamic characteristics of typical iced conductor[J]. High Voltage Engineering, 2014, 40(2): 427-433. DOI:10.13336/j.1003-6520.hve.2014.02.014 (in Chinese) |
| [10] |
ISHIHARA T, OKA S. A numerical study of the aerodynamic characteristics of ice-accreted transmission lines[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2018, 177: 60-68. |
| [11] |
林巍. 覆冰输电导线气动力特性风洞试验及数值模拟研究[D]. 浙江大学, 2012. LIN W. Wind tunnel and numerical study on aerodynamic characteristics of ice accreted transmission lines[D]. Hangzhou: Zhejiang University, 2012. (In Chinese). |
| [12] |
吕翼. 覆冰导线气动力特性的数值模拟研究[D]. 浙江大学, 2008. LYU Y. Numerical simulations of aerodynamic characteristics of iced conductors[D]. Hangzhou: Zhejiang University, 2008. |
| [13] |
新月形覆冰单导线静气动力特性的无网格数值模拟研究[J]. 贵州大学学报(自然科学版), 2016, 33(6): 38-42. FU Y S, QIAN J. Mesh-free numerical simulation of static aerodynamic characteristics on crescent-shape iced power transmission line[J]. Journal of Guizhou University(Natural Sciences), 2016, 33(6): 38-42. DOI:10.15958/j.cnki.gdxbzrb.2016.06.10 (in Chinese) |
| [14] |
六盘水地区的导线覆冰[J]. 气象, 1985(2): 22-23,2. XU J Y. Icing of conductors in Liupanshui area[J]. Meteorological Monthly, 1985(2): 22-23,2. DOI:10.7519/j.issn.1000-0526.1985.02.006 (in Chinese) |
| [15] |
天津地区导线覆冰舞动的现场观测和起因分析[J]. 电网技术, 1988(1): 64-65. CHANG Y. Field observation and cause analysis of the galloping of iced conductors in Tianjin area[J]. Power System Technology, 1988(1): 64-65. (in Chinese) |
| [16] |
临界雷诺数区准椭圆形覆冰导线风压特性研究[J]. 实验流体力学, 2014(5): 53-58. MA W Y, ZHANG X B, LI L Z, et al. Study on wind pressure characteristics on quasi-oval shaped iced conductor at critical Reynolds numbers regime[J]. Journal of Experiments in Fluid Mechanics, 2014(5): 53-58. DOI:10.11729/syltlx20130090 (in Chinese) |
| [17] |
薄覆冰导线气动力特性风洞试验研究[J]. 电力建设, 2013, 34(3): 12-16. LI H R, GUO H C, XIE Q. Wind tunnel test on aerodynamic characteristic of conductor with thin ice accretions[J]. Electric Power Construction, 2013, 34(3): 12-16. DOI:10.3969/j.issn.1000-7229.2013.03.003 (in Chinese) |
| [18] |
NICOUD F, DUCROS F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor[J]. Flow, Turbulence and Combustion, 1999, 62(3): 183-200. DOI:10.1023/A:1009995426001 |
| [19] |
MENTER F R. Zonal two equation k-ω turbulence models for aerodynamic flows: AIAA-93-2906[R]. Reston: AIAA, 1993.
|
 2021, Vol. 39
2021, Vol. 39

