2. 国家计算流体力学实验室,北京 100191
2. National Laboratory for Computational Fluid Dynamics, Beijing 100191, China
近年来,飞行高度在40~70 km、马赫数在5~20的近空间飞行器的研发受到重视[1]。在此环境下飞行普遍面临着局部稀薄效应导致的连续介质假设失效的问题。因此,考虑气体分子输运统计分布函数演化特性的介观方法获得了广泛的关注。Boltzmann方程是介观方法的理论基础[2]。在研究应用中,为了定量化表征处理Boltzmann方程复杂的碰撞项,很多简化的模型方程被提出,包括BGK模型方程[3]、Shakhov模型方程[4]、ES-BGK模型方程[5]、Rykov模型方程[6]等,所能模拟的气体流动介质也从最初的单原子理想气体发展到多原子、多组分,考虑转动、振动激发及热化学非平衡效应的跨流域空气动力学模拟体系日趋完善[7-17]。
模型方程是描述气体分子速度分布函数关于时间、空间及速度相空间七个维度的偏微分方程。由于方程的数值求解涉及到对七个维度的离散,提高计算效率一直是亟待解决的难题。针对BGK模型、ES-BGK模型方程,Mieusses[18]通过构造具有保守恒特性的离散平衡分布函数解析表达形式,建立了严格守恒的数值方法,使得该方法能以较少的离散速度点实现方程求解。Chen、Huang等[19-20]同样立足于减少离散速度空间的大小,采用叉树数据结构对UGKS的离散速度空间进行优化以提高计算效率。进一步地,2016年,江定武[21]针对显式UGKS计算效率低下的问题,利用CFD领域的经典数值方法构造了隐式格式,并采用MPI+OpenMP并行计算策略以改善UGKS的计算效率及收敛速度。在耦合方法方面,2012年Alessandro等[22]采用DSMC方法对单原子ES-BGK方程进行数值求解,并通过区域剖分实现了与Euler方程的耦合求解,并将其应用到一维间断问题分析模拟。2014年Rovenskaya等[23]采用有限差分法与离散速度坐标法结合,开展了Shakhov模型方程与NS模型方程的耦合求解,并将其应用于低速稀薄气体流动分析,实现了任意压比下的薄板稀薄绕流模拟。最近,基于多重网格技术及采用宏观方程预测平衡分布函数的全隐UGKS成功应用于跨流域稀薄流模拟,大幅提升了传统UGKS的计算效率[24]。
在气体动理学理论框架下,N-S方程可以通过Boltzmann方程或模型方程的Chapman-Enskog展开一阶近似。这体现了N-S方程与模型方程的理论可衔接性,也体现出N-S方程的质量、动量及能量守恒的基本特性即使在稀薄非平衡效应加重的近连续流区依旧成立,而对于稀薄效应更为严重、气体分子速度分布函数呈现显著非平衡特征的流动,N-S方程所遵从的本构关系难以正确表征模拟时,通常采用滑移边界可解决边界条件失效问题,但针对本构关系失效却是难以修正。这也是二阶滑移边界条件,如Cercignan模型[25-26]、Deissler模型[27]等的模拟精度相较于一阶滑移边界条件的提升有限的根本原因[28-29]。为了描述更复杂的本构关系,肖洪[30]在广义流体力学方程(GHE)的基础上提出了非线性耦合本构关系(NCCR),并在激波结构、二维高超声速稀薄绕流等问题模拟中获得成功。Burnett方程、Grad矩方程同样立足于通过理论建模的方式获得非守恒量—应力张量及热流的输运关系,也取得了成功的应用[31]。
为了从数值层面构建本构关系,拓宽N-S方程在稀薄气体动力学方面的模拟能力,规避复杂的宏观非守恒量输运方程带来的求解难题,本研究以多原子气体ES-BGK模型方程为基础,采用气体动理论统一算法(GKUA)[7-17]描述非线性本构关系及壁面速度滑移、温度跳跃,修正N-S方程的线性本构关系及滑移边界条件,拓展其在过渡流、滑移流域的应用能力。在后续内容中,本文首先通过Chapman-Enskog基于Maxwell平衡态分布渐近展开给出ES-BGK方程当地平衡态分布函数、本构关系的一阶近似,其次,构造基于N-S方程本构关系修正及滑移边界耦合的数值求解方法,并通过可压缩平板边界层流动、圆柱绕流经典案例来进行验证。
1 理论模型经典热力学理论认为分子内能可以通过分子的自由度及温度来表征。基于该理论,Brull等[5, 16]在单原子ES-BGK模型的基础上通过引入内能自由度
| $\frac{{\partial f}}{{\partial t}} + {{\xi }} \cdot \frac{{\partial f}}{{\partial {{x}}}} = \upsilon \left( {G - f} \right)$ | (1) |
式中,
| $ \begin{split} G = &\frac{{n{\varLambda _\delta }}}{{\sqrt {{\rm{det}}(2{\text {π}}{{\varGamma }})} {{\left( {R{T_{{\rm{rel}}}}} \right)}^{\delta /2}}}} \; {\rm{exp}}\left( { - \frac{1}{2}{{C}} \cdot {{\varGamma }}_{}^{ - 1} \cdot {{C}} - \frac{{e_{{\rm{int}}}^{2/\delta }}}{{R{T_{{\rm{rel}}}}}}} \right) \end{split} $ | (2) |
| ${\varLambda _\delta } = 1\Bigg/\int_0^{ + \infty } {\exp \left( { - {e_{\rm{int} }}^{2/\delta }} \right)} {\rm{d}} {e_{\rm{int} }}$ | (3) |
| ${T_{{\rm{tr}}}} = \frac{1}{{3nR}}\int_0^{ + \infty } {\int_{ - \infty }^{ + \infty } {{{{C}}^2}f{\rm{d}} {{\xi }}{\rm{d}} {e_{\rm{int} }}} } $ | (4) |
| ${T_{\rm{int} }} = \frac{2}{{\delta nR}}\int_0^{ + \infty } {\int_{ - \infty }^{ + \infty } {{e^{2/\delta }}f{\rm{d}} {{\xi }}{\rm{d}} {e_{\rm{int} }}} } $ | (5) |
| ${{\varTheta }} = m\int_0^{ + \infty } {\int_{ - \infty }^{ + \infty } {{{C}} \otimes {{C}} \cdot f{\rm{d}} {{\xi }}{\rm{d}} {e_{\rm{int} }}} } $ | (6) |
| $ \begin{split} {{\varGamma }} =& \left( {1 - {Z^{ - 1}}} \right)\left[ {\left( {1 - b} \right)R{T_{{\rm{tr}}}}{{I}} + b{{\varTheta }}/\left( {mn} \right)} \right] +{Z^{ - 1}}R{T_{{\rm{eq}}}}{{I}} \end{split} $ | (7) |
| $ {T_{{\rm{eq}}}} = \frac{{3{T_{{\rm{tr}}}} + \delta {T_{\rm{int} }}}}{{3 + \delta }},\;{T_{{\rm{rel}}}} = {Z^{ - 1}}{T_{{\rm{eq}}}} + \left( {1 - {Z^{ - 1}}} \right){T_{\rm{int} }} $ | (8) |
| $ \begin{split} \upsilon = &{Pr}\frac{{n{k_B}t}}{\mu },\;{Pr} = \frac{1}{{1 - b + b{Z^{ - 1}}}} = \frac{\mu }{\kappa }{C_p},\;b = \frac{{1 - {{P}}{{{r}}^{ - 1}}}}{{1 - {Z^{ - 1}}}} \end{split} $ | (9) |
其中,
| $ \begin{split}& {f_M} = \frac{{n{\varLambda _\delta }}}{{{{\left( {2{\rm{{\text{π}} }}R{T_{{\rm{eq}}}}} \right)}^{3/2}}{{\left( {R{T_{{\rm{eq}}}}} \right)}^{\delta /2}}}}\exp \left( { - \frac{{{{{C}}^2}}}{{2R{T_{{\rm{eq}}}}}} - \frac{{{e_{\rm{int} }}^{2/\delta }}}{{R{T_{{\rm{eq}}}}}}} \right) \end{split} $ | (10) |
对式(1)求碰撞不变量
| $\begin{split}& \frac{\partial }{{\partial t}}\left( {\begin{array}{*{20}{c}} \rho \\ {\rho {{{u}}_i}} \\ E \end{array}} \right) + \frac{\partial }{{\partial {{{x}}_j}}} \cdot \left( {\begin{array}{*{20}{c}} {\rho {{{u}}_j}} \\ {\rho {{{u}}_i}{{{u}}_j} + p{{{I}}_{ij}}} \\ {E{{{u}}_j} + p{{{u}}_j}} \end{array}} \right) = \frac{\partial }{{\partial {{{x}}_j}}}\left( {\begin{array}{*{20}{c}} 0 \\ {{{{\sigma }}_{ij}}} \\ {{{{u}}_i}{{{\sigma }}_{ij}} - {{{q}}_j}} \end{array}} \right)\end{split}$ | (11) |
式中,
| ${{\sigma }} = m\int_0^{ + \infty } {\int_{ - \infty }^{ + \infty } {f\left( {{{C}} \otimes {{C}} - \frac{1}{3}{{{C}}^2}{{{I}}_{}}} \right)} } {\rm{d}} {{\xi d}}{e_{\rm{int} }}$ | (12) |
| ${{q}} = {{{q}}_{\rm{int} }} + {{{q}}_{{\rm{tr}}}}$ | (13) |
| $E = \frac{1}{2}\rho {{{u}}^2} + \rho {C_v}{T_{{\rm{eq}}}}$ | (14) |
| ${{{q}}_{tr}} = \frac{m}{2}\int_0^{ + \infty } {\int_{ - \infty }^{ + \infty } f {{{C}}^2}{{C}}{\rm{d}} {{\xi }}{\rm{d}} {e_{\rm{int} }}} $ | (15) |
| ${{{q}}_{\rm{int} }} = m\int_0^{ + \infty } {\int_{ - \infty }^{ + \infty } f e_{\rm{int} }^{2/\delta }{{C}}{\rm{d}} {{\xi }}{\rm{d}} {e_{\rm{int} }}} $ | (16) |
对ES-BGK模型方程进行基于Maxwell平衡态分布的Chapman-Enskog渐近分析。基于量纲原理将式(1)改写为如下形式[26, 32]:
| $\frac{{\partial f}}{{\partial t}} + {{\xi }} \cdot \frac{{\partial f}}{{\partial {{x}}}} = \frac{\upsilon }{\varepsilon }\left( {G - f} \right)$ | (17) |
式中,无量纲参数
对分布函数及当地平衡态分布函数进行渐近展开,具有如下形式:
| ${\left. f\;\right|_{{\rm{CE}}}} = {f^{(0)}} + \varepsilon {f^{(1)}} + {\varepsilon ^2}{f^{(2)}} + \cdots $ | (18) |
| ${\left. G\; \right|_{{\rm{CE}}}} = {G^{(0)}} + \varepsilon {G^{(1)}} + {\varepsilon ^2}{G^{(2)}} + \cdots $ | (19) |
由Chapman-Enskog渐近分析需要遵循的约束条件:
| $ \int_0^{ + \infty } {\int_{ - \infty }^{ + \infty } {\varphi {f^{(\alpha )}}} } {\rm{d}} {{\xi }}{\rm{d}} {e_{\rm{int} }} = 0,\;\alpha \geqslant 1 $ | (20) |
可知
| ${T_{{\rm{tr}}}} = {T_{{\rm{eq}}}} + O\left( \varepsilon \right)\Delta {T_{\rm{tr}}}$ | (21) |
| ${T_{\rm{int} }} = {T_{\rm{eq}}} + O\left( \varepsilon \right)\Delta {T_{\rm{int} }}$ | (22) |
式中,
| $3\Delta {T_{{\rm{tr}}}} + \delta \Delta {T_{\rm{int} }} = 0$ | (23) |
对于非守恒量—应力张量及热流进行多尺度展开:
| ${{\sigma }} = \varepsilon {{\sigma }}_{}^{(1)} + {\varepsilon ^2}{{\sigma }}_{}^{(2)} + {\varepsilon ^3}{{\sigma }}_{}^{(3)} + \cdots $ | (24) |
| ${{q}} = \varepsilon {{q}}_{}^{(1)} + {\varepsilon ^2}{{q}}_{}^{(2)} + {\varepsilon ^3}{{q}}_{}^{(3)} + \cdots $ | (25) |
式中,
| $ \begin{split} {{\sigma }}_{}^{(\alpha )} = m\int_0^{ + \infty } {\int_{ - \infty }^{ + \infty } {{f^{(\alpha )}}\left( {{{C}} \otimes {{C}} - \frac{1}{3}{{C}}_{}^2{{I}}} \right)} }& {\rm{d}} {{\xi }}{\rm{d}} {e_{\rm{int} }},\\& \alpha \geqslant 1 \end{split} $ | (26) |
| $ \begin{split} {{q}}_{}^{(\alpha )} =& \frac{m}{2}\int_0^{ + \infty } {\int_{ - \infty }^{ + \infty } {{f^{(\alpha )}}} {{{C}}^2}{{C}}{\rm{d}} {{\xi }}{\rm{d}} {e_{\rm{int} }}}+ \\ m & \int_0^{ + \infty } {\int_{ - \infty }^{ + \infty } {{f^{(\alpha )}}} e_{\rm{int} }^{2/\delta }{{{{{C}}}}}{\rm{d}} {{\xi }}{\rm{d}} {e_{\rm{int} }}} , \\& \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \alpha \geqslant 1 \end{split} $ | (27) |
| $ {{\sigma }}_{}^{(0)} = 0\;,\;\;{{q}}_{}^{(0)} = 0 $ | (28) |
为了获得当地平衡分布函数
| ${{\varGamma }} = \theta {{I}} + \frac{{\hat b}}{\rho }{{\sigma }} + O\left( \varepsilon \right)\lambda \delta {{I}}$ | (29) |
式中:
| $\begin{split} \theta =& R{T_{{\rm{eq}}}},\;\overset\frown{b} = b\left( {1 - {Z^{ - 1}}} \right), \lambda = \left( {1 - {Z^{ - 1}}} \right)\left( {1 - b} \right)R\Delta {T_{{\rm{tr}}}} \end{split}$ | (30) |
将式(24)带入式(29),并保留
| $\det \left( {{\varGamma }} \right) = {\theta ^3} + 3\varepsilon {\theta ^2}\lambda $ | (31) |
| ${{{\varGamma }}^{ - 1}} = \frac{{{I}}}{\theta } - \varepsilon \frac{{\overset\frown{b} }}{{p\theta }}{{\sigma }}_{}^{(1)} - \varepsilon \frac{\lambda }{{{\theta ^2}}}{{I}}$ | (32) |
针对量热完全气体不考虑
| $ {G^{(0)}} = {f_M},\;{G^{(1)}} = {f_M}\frac{{\overset\frown{b} }}{{2\rho {\theta ^2}}}{{\sigma }}_{ij}^{(1)}{{{C}}_{ < i}}{{{C}}_{j > }} $ | (33) |
进一步地,将
| $\frac{{\partial {f_M}}}{{\partial t}} + {{\xi }} \cdot \frac{{\partial {f_M}}}{{\partial {{x}}}} = \upsilon \left( {{G^{(1)}} - {f^{(1)}}} \right)$ | (34) |
等式左端等于[5]:
| $\begin{split}& {\frac{{\partial {f_M}}}{{\partial t}} + {{\xi }} \cdot \frac{{\partial {f_M}}}{{\partial {{x}}}} = \left\{ {{{C}}\frac{1}{{{T_{{\rm{eq}}}}}}\frac{{\partial {T_{{\rm{eq}}}}}}{{\partial {{x}}}}\left( {\frac{{{C^2} + 2{e_{\rm{int} }}^{2/\delta }}}{{2R{T_{{\rm{eq}}}}}} - \frac{{5 + \delta }}{2}} \right)} \right.} +\\& {\left. { \frac{1}{{R{T_{{\rm{eq}}}}}}\left\{ {\left[ {{{C}} \otimes {{C}} - \frac{1}{{3 + \delta }}\left( {{{{C}}^2} + 2{e_{\rm{int} }}^{2/\delta }} \right)} \right] \cdot {{I}}} \right\} \cdot {{D}}\left( u \right)} \right\} \; {f_M}} \end{split}$ | (35) |
式中,
| ${{D}}{\left( u \right)_{ij}} = \frac{1}{2}\left( {\frac{{\partial {{{u}}_i}}}{{\partial {{{x}}_j}}} + \frac{{\partial {{{u}}_j}}}{{\partial {{{x}}_i}}}} \right) - \frac{1}{3}{\rm{div}}\left( {{u}} \right) \cdot {{{I}}_{ij}}$ | (36) |
可得:
| $\begin{split}& {{f^{(1)}} = {G^{(1)}} - \frac{1}{\upsilon }\left\{ {{{C}} \cdot \frac{1}{{{T_{{\rm{eq}}}}}}\frac{{\partial {T_{{\rm{eq}}}}}}{{\partial {{{x}}_{}}}}\left( {\frac{{{{{C}}^2} + 2{e_{\rm{int} }}^{2/\delta }}}{{2R{T_{{\rm{eq}}}}}} - \frac{{5 + \delta }}{2}} \right)} \right.}+ \\& \;\;\;{\left. { \frac{1}{{R{T_{{\rm{eq}}}}}}\left[ {{{C}} \otimes {{C}} - \frac{1}{{3 + \delta }}\left( {{{{C}}^2} + 2{e_{\rm{int} }}^{2/\delta }} \right){{I}}} \right] \cdot {{D}}\left( {{u}} \right)} \right\}{f_M}} \end{split}$ | (37) |
因此,利用式(9)可知分布函数的Chapman-Enskog渐近展开一阶近似表达式为:
| $\begin{split} {f^{{\rm{CE}}}} =&{ \left[ {1 + \frac{{\left( {\gamma - 1} \right){{C}}{{{q}}^{(1)}}}}{{\gamma \rho {{\left( {R{T_{{\rm{eq}}}}} \right)}^2}}}\left( {\frac{{{{{C}}^2} + 2e_{\rm{int} }^{2/\delta }}}{{2R{T_{{\rm{eq}}}}}} - \frac{{5 + \delta }}{2}} \right)} \right]{f_M}} +\\ & \;\;{ \frac{1}{2}\frac{{{{{\sigma }}^{(1)}}\left[ {{{C}} \otimes {{C}} - \dfrac{1}{{3 + \delta }}\left( {{{{C}}^2} + 2e_{\rm{int} }^{2/\delta }} \right){{I}}} \right]}}{{\rho {{\left( {R{T_{{\rm{eq}}}}} \right)}^2}}}{f_M}} \end{split}$ | (38) |
式中,
| $ {{\sigma }}_{ij}^{(1)} = - 2\mu \left[ {\frac{1}{2}\left( {\frac{{\partial {{{u}}_i}}}{{\partial {{{x}}_j}}} + \frac{{\partial {{{u}}_j}}}{{\partial {{{x}}_i}}}} \right) - \frac{1}{3}{\rm{div}}\left( {{u}} \right){{{I}}_{ij}}} \right] $ | (39) |
| ${{q}}_i^{(1)} = - \kappa \frac{{\partial {T_{{\rm{eq}}}}}}{{\partial {{{x}}_i}}}$ | (40) |
可见,ES-BGK模型的应力张量
本耦合方法基于课题组气体动理论统一算法 (GKUA)及开源代码OpenCFD-EC2D的NS有限体积求解器构建。作为原理验证研究,本文中耦合区域通过计算调整给定。其中,GKUA求解需要进行N-S方程本构关系修正的区域—壁面附近与平均分子自由程相当的区域,N-S求解器对全流区进行守恒方程求解,如图1所示。
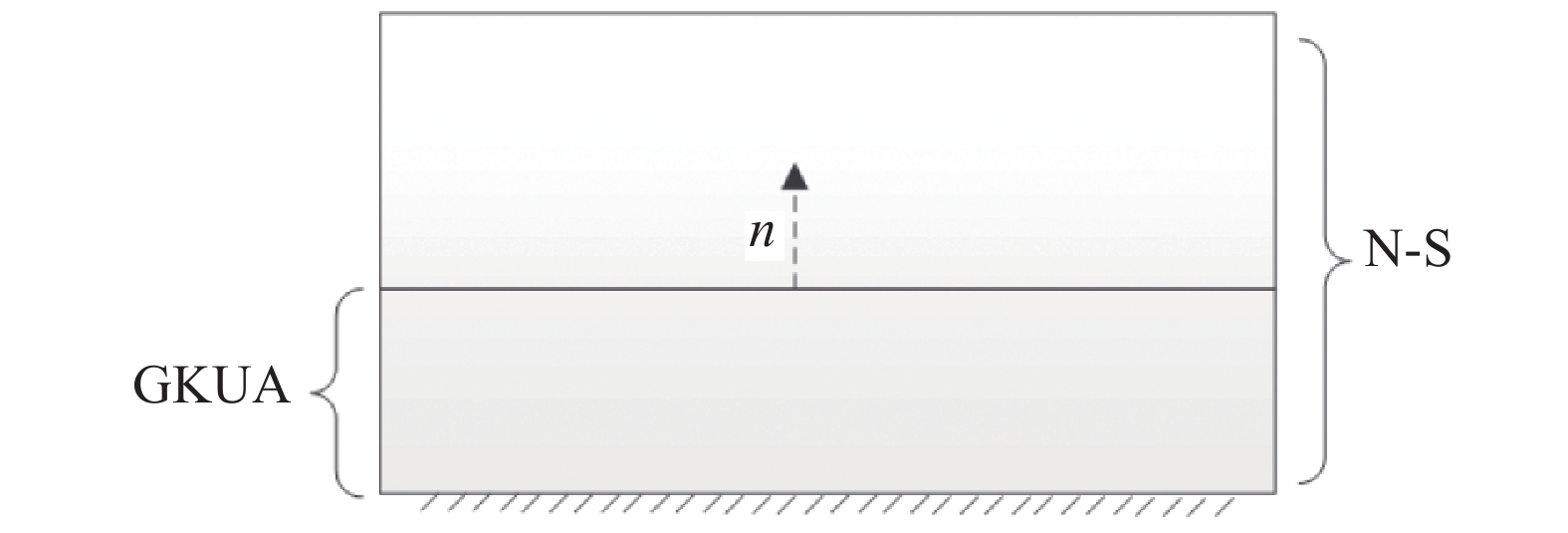
|
图 1 求解域分区示意图 Fig.1 Schematic view of the computational domain decomposition |
气体动理论耦合策略大致可分如下几步:
1)通过有限体积法全流域求解N-S方程;
2)通过GKUA方法求解壁面区域,耦合边界处的分布函数根据特征线
3)求解GKUA计算域的应力张量
4)利用获得的
5)以修正后的本构关系及壁面边界进行下一时间步N-S方程及GKUA求解。
为了降低对计算资源的需求,采用离散速度坐标法直接数值求解Boltzmann模型方程通常对分布函数的自变量进行约化[7-8],引入变量:
| $ {f_1} = \int_0^{ + \infty } {f{\rm{d}} {e_{\rm{int} }}},{f_2} = \int_0^{ + \infty } {fe_{\rm{int} }^{2/\delta }} {\rm{d}} {e_{\rm{int} }} $ | (41) |
对于二维流动问题,引入下式对ES-BGK模型方程进行进一步的约化:
| $\begin{split}& {g_1} = \int_{ - \infty }^{ + \infty } {{f_1}{\rm{d}} {{{\xi }}_z}},\;{g_2} = \int_{ - \infty }^{ + \infty } {{{{\xi }}_z}^2{f_1}{\rm{d}} {{{\xi }}_z}} ,\; {g_3} = \int_{ - \infty }^{ + \infty } {{f_2}{\rm{d}} {{{\xi }}_z}} \end{split} $ | (42) |
在空间格式构造方面,本文采用二阶NND格式对N-S方程及ES-BGK模型方程进行界面重构[7-9],采用Steger-Warming格式进行界面通量计算,并且采用LU-SGS隐式格式对时间项进行离散以提高效率。
3 算例验证为了验证构建的基于修正本构关系的气体动理论耦合方法,本文分别进行了可压缩平板边界层流动模拟及稀薄圆柱绕流模拟。其中,DSMC计算结果由DS2V软件[33]计算得到。
3.1 可压缩平板边界层本研究首先模拟了连续流域不同马赫数可压缩平板边界层流动,以验证介观方法及传统CFD在连续流域模拟的一致性。计算域x×y = [0,1 m]×[0,0.5 m],网格量:100×100,壁面第一层网格高度:0.0001 m。来流状态为:高度H = 55 km,静压p = 42.5 Pa,静温T = 206.7 K,密度ρ = 5.68×10−4 kg/m3,马赫数Ma = 2、4、8,各状态的雷诺数Re分别为:2.22×104、4.45×104、8.89×104。壁面温度等于来流静温。分别采用N-S及GKUA进行了Ma = 2、4、8流场的数值模拟,并将其速度场和温度场结果与文献[34]给出的可压缩层流边界层方程的理论结果进行了对比,见图2。根据边界层相似理论,其横坐标

|
图 2 不同马赫数下平板边界层模拟结果 Fig.2 Simulation results of a flat-plate boundary layer at different Mach numbers |
| $\eta = y\sqrt {\frac{{Re}}{{x{L_{{\rm{ref}}}}}}} $ | (43) |
对比可知,采用单一方法计算连续流域可压缩平板边界层流动给出的速度场及温度场结果与文献吻合良好,验证了本文的GKUA及N-S的可靠性。
随着高度的增加,稀薄效应将逐渐显现,壁面附近将出现速度滑移及温度跳跃。本文对来流条件:高度H= 80 km,静压p= 1.05 Pa,静温T= 198.6 K,密度ρ= 1.8458×10−5 kg/m3,马赫数Ma= 2,雷诺数Re= 7.9×102的可压缩平板边界层流动进行了模拟,壁面温度等于来流静温。数值方法包括GKUA方法、无滑移NS方法、DSMC方法及采用前文所述理论构建的耦合方法—“Kinetic Boundary”。其中,耦合方法的本构关系修正区域给定为壁面附近2倍平均分子自由程高度范围内的区域。由图3所示壁面物理量对比可以看出,构建的耦合方法的壁面压力计算结果与GKUA、N-S计算结果吻合良好,略大于DSMC结果;耦合方法计算的温度跳跃结果和GKUA吻合良好,并和DSMC基本吻合;滑移速度及壁面剪切应力与GKUA、DSMC计算结果吻合良好。并且,由于平板前缘的速度滑移现象较平板后部严重,采用耦合方法、GKUA及DSMC方法计算的壁面剪切应力在平板前缘较N-S小;在平板后缘,各种结果相互吻合良好。

|
图 3 Ma= 2平板边界层壁面物理量 Fig.3 Distributions of physical quantities along the streamwise direction on the surface of a flat-plate boundary layer at Ma= 2 |
为了进一步验证采用气体动理论耦合方法的有效性,本文以高度H = 90 km,静压p = 0.183 Pa,静温T = 186.8 K,密度ρ = 3.41631×10−6 kg/m3,马赫数Ma= 2、4,其雷诺数 Re分别为150、300作为来流条件,模拟了圆柱超声速稀薄绕流,并对流场及壁面物理量进行了对比分析。壁面温度等于来流静温。其中,耦合方法的N-S方程本构关系修正区域给定为壁面附近2倍平均分子自由程高度范围内的区域。圆柱半径1 m,远场半径10 m,网格量:周向60×径向80,壁面第一层网格高度0.0005 m。
图4给出了气体动理论耦合方法计算的流场马赫数、静压、密度云图的与DSMC计算结果的对比情况。图5给出了圆柱壁面物理量计算结果对比,其中,横坐标θ = 180°对应于圆柱迎风面驻点。从图4可以看出,本文构建的耦合方法获得的流场与DSMC获得的流场在圆柱迎风侧吻合良好,在圆柱背风回流区存在一定的差异。结合图5的壁面剪切应力及滑移速度对比图可看出,本文构建的耦合方法获得的回流区小于DSMC获得的分离区,是导致圆柱背风区流场云图存在差异的主要原因。

|
图 4 Ma = 2圆柱稀薄绕流流场 Fig.4 Rarefied flow fields around a circular cylinder at Ma= 2 |
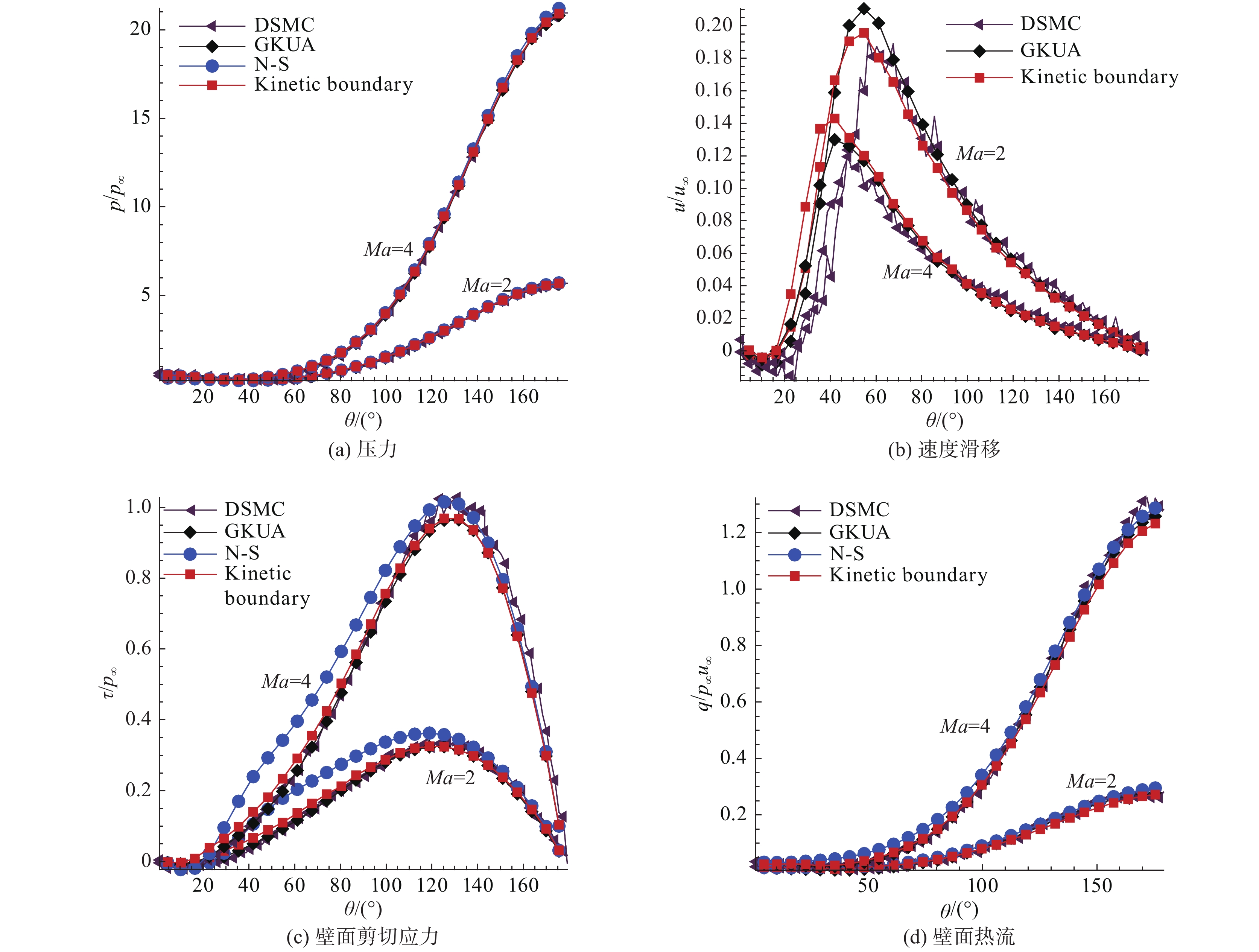
|
图 5 圆柱稀薄绕流壁面物理量 Fig.5 Distributions of physical quantities along the circumferential direction on the surface of a circular cylinder in rarefied flow |
从图5可知,各方法获得的壁面压力吻合良好。壁面速度滑移结果显示:DSMC、GKUA及气体动理论耦合方法在圆柱迎风一侧(θ∈[90°,180°])吻合良好;在背风区,由于计算的分离区的大小差异导致结果存在一定偏差,但总体规律基本吻合。进一步地,虽然图中给出的Ma = 4流动无量纲壁面速度滑移小于Ma = 2流动,但其有量纲的绝对量是大于Ma2流动的壁面速度滑移。壁面剪切应力对比结果显示,DSMC、GKUA及气体动理论耦合方法计算结果基本吻合,而无滑移NS计算结果和其他结果存在一定差异。并且,该差异整体上随壁面滑移速度的增大而增加,流动分离点(θ≈ 40°)附近的流动较复杂,其差异最大。壁面热流计算结果显示无滑移N-S结果略大于其他方法计算结果,但各方法计算结果总体吻合。
4 结 论本研究通过对多原子气体ES-BGK方程进行Chapman-Enskog渐近分析,构建了分布函数、应力张量、热流矢量的渐近一阶表达式,证明了ES-BGK方程与NS方程在连续流域的物理描述上具有理论一致性。在此基础上,提出通过对稀薄效应明显的流动区域进行应力张量及热流矢量修正,构造了气体动理论耦合方法,避免了离散速度坐标法引入的质量、动量及能量守恒型误差对耦合方法计算结果的影响。
进一步地,本研究通过引入约化变量,构造了分布函数一阶表达式的二维约化形式,并通过有限体积法对二维耦合方程进行数值求解。通过二维可压缩平板边界层及圆柱绕流算例的数值模拟及结果对比,初步验证了本研究提出气体动理论耦合方法的有效性,预期进一步研究发展,可得到一套适于近连续滑移过渡流区高效可靠的气体动理论耦合方法。
致谢:感谢中国科学院力学研究所李新亮研究员团队提供的帮助。
| [1] |
空气动力学的新问题[J]. 中国科学(物理学 力学 天文学), 2015, 45(10): 104709. ZHOU H, ZHANG H X. New problems of aerodynamics[J]. Scientia Sinica (Physica, Mechanica & Astronomica), 2015, 45(10): 104709. (in Chinese) |
| [2] |
CHAPMAN S, COWLING T G. The mathematical theory of non-uniform gases[M]. London: Cambridge Univ. Press, 1990.
|
| [3] |
BHATNAGAR P L, GROSS E P, KROOK M. A model for collision processes in gases. I. small amplitude processes in charged and neutral one-component systems[J]. Physical Review, 1954, 94(3): 511. DOI:10.1103/physrev.94.511 |
| [4] |
SHAKHOV E M. Generalization of the Krook kinetic relaxation equation[J]. Fluid Dynamics, 1968, 3(5): 95-96. DOI:10.1007/bf01029546 |
| [5] |
BRULL S, SCHNEIDER J. On the ellipsoidal statistical model for polyatomic gases[J]. Continuum Mechanics and Thermodynamics, 2009, 20(8): 489-508. DOI:10.1007/s00161-009-0095-3 |
| [6] |
RYKOV V A. A model kinetic equation for a gas with rotational degrees of freedom[J]. Fluid Dynamics, 1975, 10(6): 959-966. DOI:10.1007/bf01023275 |
| [7] |
李志辉. 从稀薄流到连续流的气体运动论统一数值算法研究[D]. 绵阳: 中国空气动力研究与发展中心, 2001. LI Z H. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[D]. Mianyang: China Aerodynamics Research and Development Center, 2001( in Chinese). |
| [8] |
LI Z H, ZHANG H X. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[J]. Journal of Computational Physics, 2004, 193(2): 708-738. DOI:10.1016/j.jcp.2003.08.022 |
| [9] |
求解Boltzmann模型方程的气体运动论大规模并行算法[J]. 计算物理, 2008, 25(1): 65-74. LI Z H, ZHANG H X. Massive parallelization of gas-kinetic algorithm for boltzmann model equation[J]. Chinese Journal of Computational Physics, 2008, 25(1): 65-74. DOI:10.3969/j.issn.1001-246X.2008.01.010 (in Chinese) |
| [10] |
LI Z H, ZHANG H X. Gas-kinetic numerical studies of three-dimensional complex flows on spacecraft re-entry[J]. Journal of Computational Physics, 2009, 228(4): 1116-1138. DOI:10.1016/j.jcp.2008.10.013 |
| [11] |
含转动非平衡效应Boltzmann模型方程统一算法与跨流域绕流问题模拟研究[J]. 空气动力学学报, 2014, 32(2): 137-145. LI Z H, WU J L, JIANG X Y, et al. The unified algorithm for various flow regimes solving Boltzmann model equation in rotational non-equilibrium[J]. Acta Aerodynamica Sinica, 2014, 32(2): 137-145. (in Chinese) |
| [12] |
LI Z H, PENG A P, ZHANG H X, et al. Rarefied gas flow simulations using high-order gas-kinetic unified algorithms for Boltzmann model equations[J]. Progress in Aerospace Sciences, 2015, 74: 81-113. DOI:10.1016/j.paerosci.2014.12.002 |
| [13] |
求解Boltzmann模型方程高性能并行算法在航天跨流域空气动力学应用研究[J]. 计算机学报, 2016, 39(9): 1801-1811. LI Z H, JIANG X Y, WU J L, et al. Study on high performance parallel algorithm for spacecraft Re-entry aerodynamics in the whole of flow regimes using boltzmann model equation[J]. Chinese Journal of Computers, 2016, 39(9): 1801-1811. (in Chinese) |
| [14] |
含振动能激发Boltzmann模型方程气体动理论统一算法验证与分析[J]. 物理学报, 2017, 66(20): 204703. PENG A P, LI Z H, WU J L, et al. Validation and analysis of gas-kinetic unified algorithm for solving Boltzmann model equation with vibrational energy excitation[J]. Acta Physica Sinica, 2017, 66(20): 204703. DOI:10.7498/aps.66.204703 (in Chinese) |
| [15] |
跨流域空气动力学模拟方法与返回舱再入气动研究[J]. 空气动力学学报, 2018, 36(5): 826-847. LI Z H, LIANG J, LI Z H, et al. Simulation methods of aerodynamics covering various flow regimes and applications to aerodynamic characteristics of re-entry spacecraft module[J]. Acta Aerodynamica Sinica, 2018, 36(5): 826-847. DOI:10.7638/kqdlxxb-2018.0121 (in Chinese) |
| [16] |
彭傲平. 大型航天器跨流域非平衡玻尔兹曼模型方程统一算法应用研究[D]. 绵阳: 中国空气动力研究与发展中心, 2017. PENG A P. Application and study of gas kinetic unified algorithm based on non-equilibrium Boltzmann model equation for large scale spacecraft covering all flow regimes[D]. Mianyang: China Aerodynamics Research and Development Center, 2017( in Chinese). |
| [17] |
吴俊林. 热化学非平衡Boltzmann模型方程统一算法与返回舱再入跨流域应用研究[D]. 绵阳: 中国空气动力研究与发展中心, 2018. WU J L. Study of gas-kinetic unified algorithm based on thermochemical non- equilibrium Boltzmann model equation and application for re-entry flows of spacecraft capsule covering various flow regimes[D]. Mianyang: China Aerodynamics Research and Development Center, 2018. |
| [18] |
MIEUSSENS L. Discrete-velocity models and numerical schemes for the Boltzmann-BGK equation in plane and axisymmetric geometries[J]. Journal of Computational Physics, 2000, 162(2): 429-466. DOI:10.1006/jcph.2000.6548 |
| [19] |
CHEN S Z, XU K, LEE C, et al. A unified gas kinetic scheme with moving mesh and velocity space adaptation[J]. Journal of Computational Physics, 2012, 231(20): 6643-6664. DOI:10.1016/j.jcp.2012.05.019 |
| [20] |
HUANG J C, XU K, YU P B. A unified gas-kinetic scheme for continuum and rarefied flows Ⅱ: multi-dimensional cases[J]. Communications in Computational Physics, 2012, 12(3): 662-690. DOI:10.4208/cicp.030511.220911a |
| [21] |
江定武.基于模型方程解析解的气体动理学算法研究[D]. 中国空气动力研究与发展中心, 2016. JIANG D W. Study of the gas kinetic scheme based on the analytic solution of model equations[D]. Mianyang: China Aerodynamics Research and Development Center, 2016( in Chinese). |
| [22] |
ALAIA A, PUPPO G. A hybrid method for hydrodynamic-kinetic flow – Part Ⅱ – Coupling of hydrodynamic and kinetic models[J]. Journal of Computational Physics, 2012, 231(16): 5217-5242. DOI:10.1016/j.jcp.2012.02.022 |
| [23] |
ROVENSKAYA O, CROCE G. Application a hybrid solver to gas flow through a slit at arbitrary pressure ratio[J]. Vacuum, 2014, 109: 266-274. DOI:10.1016/j.vacuum.2014.04.018 |
| [24] |
ZHU Y J, ZHONG C W, XU K. Unified gas-kinetic scheme with multigrid convergence for rarefied flow study[J]. Physics of Fluids, 2017, 29(9): 096102. DOI:10.1063/1.4994020 |
| [25] |
CERCIGNANI C. Higher order slip according to the linearized Boltzmann equation[R]. Institute of Engineering Research Report AS-64-19, 1964.
|
| [26] |
CERCIGNANI C. The Boltzmann equation[M]//The Boltzmann Equation and Its Applications. New York, NY: Springer, 1988: 40-103. doi: 10.1007/978-1-4612-1039-9_2
|
| [27] |
DEISSLER R G. An analysis of second-order slip flow and temperature-jump boundary conditions for rarefied gases[J]. International Journal of Heat and Mass Transfer, 1964, 7(6): 681-694. DOI:10.1016/0017-9310(64)90161-9 |
| [28] |
BAILEY C L. A critical review of the drag force on a sphere in the transition flow regime[C]// the AIP Conference Proceedings, Bari (Italy). AIP, 2005. doi: 10.1063/1.1941624
|
| [29] |
LOCKERBY D A, REESE J M, GALLIS M A. Capturing the Knudsen layer in continuum-fluid models of nonequilibrium gas flows[J]. AIAA Journal, 2005, 43(6): 1391-1393. DOI:10.2514/1.13530 |
| [30] |
NCCR方程在近平衡气体流动区域的验证[J]. 载人航天, 2015, 21(3): 303-308, 314. XIAO H, SHI Y Y, SHANG Y H, et al. Validation of nonlinear coupled constitutive relations in near-equilibrium gas flows[J]. Manned Spaceflight, 2015, 21(3): 303-308, 314. DOI:10.3969/j.issn.1674-5825.2015.03.015 (in Chinese) |
| [31] |
陈伟芳, 赵文文. 稀薄气体动力学矩方法及数值模拟[M]. 北京: 科学出版社, 2017. CHEN W F, ZHAO W W. Momentum method and its numerical simulation for rarefied gas dynamics[M]. Beijing: Science Press, 2017(in Chinese). |
| [32] |
应纯同. 气体输运理论及应用[M]. 北京: 清华大学出版社, 1990. YING C T. Theory of gas transportation and application[M]. Beijing: Tsinghua University Press, 1990(in Chinese). |
| [33] |
BIRD G A. The DS2V/3V program for DSMC calculation[C]// 24th International Symposium on Rarefied Gas Dynamics. Melville, NY, 2005: 541- 546.
|
| [34] |
VAN DRIEST E R. Investigation of laminar boundary layer in compressible fluids using the Crocco method: NACA-TN-2597[R]. NTRS - NASA Technical Reports Server, 1952.
|
 2021, Vol. 39
2021, Vol. 39


