2. 上海交通大学 机械与动力工程学院 叶轮机械研究所,上海 200240;
3. 上海汽轮机有限公司,上海 200240
2. Institute of Turbomachinery, School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;
3. Shanghai Turbine Co., Ltd., Shanghai 200240, China
蒸汽调节阀是蒸汽动力系统的重要控制部件。通过调整调节阀的开度,可以控制动力系统的蒸汽输入,使系统实现能量平衡。准确掌握蒸汽调节阀通流特性对蒸汽动力系统设计和运行至关重要,既有助于工程设计人员在系统的设计阶段完成阀门选型,优化系统构造,又能方便系统运行控制人员快速、准确地完成动力系统的调节,保证动力系统的稳定高效运行。目前主流的调节阀通流特性研究方法大都采用雷诺时均(Reynolds Averaged Navier-Stokes, RANS)计算流体力学(Computational Fluid Dynamics, CFD)模拟,使用湍流模型封闭方程。然而,湍流模型计算的准确性高度依赖合理的模型常数,而这些常数多由平板边界层、自由剪切流等经典流动标定而来,这显然难以满足调节阀内部复杂流场预测的要求。通常,RANS模型计算只能定性描述阀门通流特性,定量误差则普遍高于10%[1-3]。毫无疑问,选择使用合适的湍流模型常数,对于准确预测调节阀门通流特性非常重要。
采用实验数据驱动的相关算法优化湍流模型常数是常用的优化策略[4],其中数据同化则是最重要的方法之一。数据同化,是实验观测和模型预测的融合,其三大要素为预测模型、观测数据和同化算法。该方法在模型预测中融入观测数据而改变模型运行轨迹,最终达到优化模型性能、提高预测精度的目的[5]。数据同化最早运用于气象预报[6],而后扩展至地质[7]、水文[8]、系统监测[9]等领域。近些年,数据同化被引入了湍流数值模拟,成为优化湍流模型常数的重要方法。Hiroshi Kato[10]等提出了基于数据同化的湍流模型常数标定方法。该方法将实验测量数据作为观测,运用集合变换卡尔曼滤波(Ensemble Transform Kalman Filter, ETKF)算法修正k-ω SST模型的
蒸汽调节阀内部的流动极为复杂,且在不同运行工况下呈现不同特征。Wang等[13-15]研究了蒸汽调节阀内部的不稳定流动,发现阀内流动中存在射流、回流、旋涡等多种复杂现象。曾立飞等[16]研究了雷诺数对于调节阀模化试验的影响。结果表明其所研究的阀门呈现出附阀座流、冲击射流和充满流三种情形。Domnick[17]等对调节阀内流场的研究发现了三种流态:大开度、极大压比条件下的扩散器充满流动,极小开度、中小压比条件下的壁面附着流动和较小开度、小压比条件下的分离流动。调节阀内部流动形态的多样性,说明难以存在普适模型常数向量。本文所研究的蒸汽阀,内部结构紧凑,阀内流场复杂,显然需要结合阀内流态找到针对性的湍流模型常数。
本文实现了数据同化技术在工业化情景下的应用。以含滤网蒸汽调节阀为研究对象,采用k-ω SST模型数值模拟,结合通流特性实验测量结果进行集合卡尔曼滤波的数据同化,修正了预测模型的常数向量。按照阀门开度的区别,标定了3组SST模型常数向量,并进行了相关的验算和流场参数对比,分析了标定常数的适用性,为调节阀数值模拟优化提供了重要参考。
1 数学原理 1.1 湍流模型方程RANS模型因其对计算时间和硬件成本的低要求,成为了阀门通流特性的重要预测工具。在众多RANS模型中,由Menter提出[18]的k-ω SST模型,是一种综合标准k-ε和标准k-ω的两方程混合模型。该模型既具有标准k-ω善于预测边界层内部区域流动的优点,又有标准k-ε善于预测外部区域和自由剪切流动的优势。因而,本文采用k-ω SST模型作为数值模拟的基础模型,并结合阀门特性实验测量结果对模型常数进行重新标定。
SST模型k-ω部分微分方程为:
| $ \frac{{\rm{D}}\rho k}{{\rm{D}}t}={\tau }_{ij}\frac{\partial {u}_{i}}{\partial {x}_{j}}-{\beta }^{*}\rho \omega k+ \frac{\partial }{\partial {x}_{j}}\left[\left(\mu +{\sigma }_{{k}_{1}}{\mu }_{t}\right)\frac{\partial k}{\partial {x}_{j}}\right] $ | (1) |
| $ \frac{{\rm{D}}\rho \omega }{{\rm{D}}t}=\frac{{\gamma }_{1}}{{\nu }_{t}}{\tau }_{ij}\frac{\partial {u}_{i}}{\partial {x}_{j}}-{\beta }_{1}\rho {\omega }^{2}+ \frac{\partial }{\partial {x}_{j}}\left[\left(\mu +{\sigma }_{{\omega }_{1}}{\mu }_{t}\right)\frac{\partial \omega }{\partial {x}_{j}}\right] $ | (2) |
SST模型k-ε部分微分方程为:
| $ \frac{{\rm{D}}\rho k}{{\rm{D}}t}={\tau }_{ij}\frac{\partial {u}_{i}}{\partial {x}_{j}}-{\beta }^{*}\rho \omega k+ \frac{\partial }{\partial {x}_{j}}\left[\left(\mu +{\sigma }_{{k}_{2}}{\mu }_{t}\right)\frac{\partial k}{\partial {x}_{j}}\right] $ | (3) |
| $ \begin{split} \frac{{\rm{D}}\rho \omega }{{\rm{D}}t}=& \frac{{\gamma }_{2}}{{\nu }_{t}}{\tau }_{ij}\frac{\partial {u}_{i}}{\partial {x}_{j}}-{\beta }_{2}\rho {\omega }^{2}+ \frac{\partial }{\partial {x}_{j}}\left[\left(\mu +{\sigma }_{{\omega }_{2}}{\mu }_{t}\right)\frac{\partial \omega }{\partial {x}_{j}}\right]+\\ &2\rho {\sigma }_{{\omega}_{2}}\frac{1}{\omega }\frac{\partial k}{\partial {x}_{j}}\frac{\partial \omega }{\partial {x}_{j}} \end{split} $ | (4) |
式(2、4)中涡黏度项
| $ {\nu }_{t}=\frac{{a}_{1}k}{{\rm{max}}({a}_{1}\omega ,{F}_{2}\varOmega )} $ | (5) |
式中,Ω为涡度的绝对值,
引入混合系数
| $ \frac{{\rm{D}}\rho k}{{\rm{D}}t}={\tau }_{ij}\frac{\partial {u}_{i}}{\partial {x}_{j}}-{\beta }^{*}\rho \omega k+ \frac{\partial }{\partial {x}_{j}}\left[\left(\mu +{\sigma }_{k}{\mu }_{t}\right)\frac{\partial k}{\partial {x}_{j}}\right] $ | (6) |
| $ \begin{split} \frac{{\rm{D}}\rho \omega }{{\rm{D}}t}=&\frac{\gamma }{{\nu }_{t}}{\tau }_{ij}\frac{\partial {u}_{i}}{\partial {x}_{j}}-\beta \rho {\omega }^{2}+ \frac{\partial }{\partial {x}_{j}}\left[\left(\mu +{\sigma }_{\omega }{\mu }_{t}\right)\frac{\partial \omega }{\partial {x}_{j}}\right]+ \\ &2\left(1-{F}_{1}\right)\rho {\sigma }_{{\omega}_{2}}\frac{1}{\omega }\frac{\partial k}{\partial {x}_{j}}\frac{\partial \omega }{\partial {x}_{j}} \end{split} $ | (7) |
其中,
| $ \left(\begin{array}{c}\gamma \\ \beta \\ {\sigma }_{k}\\ {\sigma }_{\omega }\end{array}\right)={F}_{1}\left(\begin{array}{c}{\gamma }_{1}\\ {\beta }_{1}\\ {\sigma }_{{k}_{1}}\\ {\sigma }_{{\omega }_{1}}\end{array}\right)+(1-{F}_{1})\left(\begin{array}{c}{\gamma }_{2}\\ {\beta }_{2}\\ {\sigma }_{{k}_{2}}\\ {\sigma }_{{\omega }_{2}}\end{array}\right) $ | (8) |
SST模型的
| 表 1 SST模型常数默认值 Table 1 Default SST model constant |
|
|
数据同化过程实质为反演过程。预测模型的形式确立了预测参数与模型常数间的映射关系(预测),而数据同化则是采用一定算法(同化算法)解析映射关系(分析),并综合相关测量数据(观测)反推和标定模型常数(更新)。
本文数据同化所采用的预测模型为SST模型,观测数据为实验所测得的阀门入口流量数据,同化算法主要采用集合Kalman滤波(Ensemble Kalman Filter, EnKF)算法[19]重新标定SST模型的相关模型常数,详细过程将于下文说明。
1.2.1 集合卡尔曼滤波数据同化所使用的算法种类繁多,包括三维变分、四维变分、粒子滤波(Particle Filter, PF)、扩展卡尔曼滤波(Extended Kalman Filter, EKF)、集合卡尔曼滤波、集合变换卡尔曼滤波(Ensemble Transform Kalman Filter, ETKF)等。变分类同化一般多依靠预测模型的伴随方程进行求解[20],不适合复杂模型的优化。粒子滤波对状态空间的搜索使用大量的随机样本[5],这容易导致算法计算量大,且大量资源浪费于无用的粒子上。而卡尔曼滤波类同化则相对简单地获得数值模型的先验统计信息[21],适合本文的湍流数值模型这类复杂模型的优化。其中,集合卡尔曼滤波算法由Evensen[22]于1994年提出,是该类同化方法中最常用的算法之一。该算法从经典卡尔曼滤波和扩展卡尔曼滤波算法发展而来,能够结合观测数据完成对预测模型的修正。同时,集合卡尔曼滤波算法采用了蒙特·卡洛方法的误差统计,使其不再具有经典卡尔曼滤波算法对于线性系统的要求和扩展卡尔曼滤波用于高阶非线性问题时存在较大误差的缺陷,在高阶非线性领域亦可使用。同时,相关研究指出,对于湍流数值模型优化问题,集合卡尔曼滤波的优化性能优于集合变换卡尔曼滤波[10]。综上所述,针对具有高阶非线性特点的湍流问题的数值模型优化,本文采用集合卡尔曼滤波算法作为同化算法。
算法考察对象为如下的非线性系统:
| $ {{x}}_{f}={{F}}({{x}}_{0},{{v}}) $ | (9) |
| $ {{y}}={{H}}{{x}}_{f}+{{w}} $ | (10) |
其中,式(9)为非线性系统的预测方程,式(10)为观测方程。式中
算法的主要流程包括预测过程和分析过程:
1)预测过程。预测过程中,每个集合成员中的状态参数向量将从初始状态开始利用SST模型迭代计算,直至湍流数值模拟计算收敛。状态参数由以下公式给定:
| $ {{x}}_{f}^{i}=F\left({{x}}_{0}^{i},{{{v}}}^{{i}}\right) $ | (11) |
其中,预测模型
集合成员的均值由下式给出:
| $ {\bar{{x}}}_{f}=\frac{1}{l}\sum \limits_{i=1}^{l}{{x}}_{f}^{i} $ | (12) |
此处,上标
2)分析过程。这一步是集合卡尔曼滤波的核心。算法通过整合观测信息的不确定度和集合成员的统计信息,从而确定卡尔曼增益并完成对集合成员的更新。该步骤的过程如下:
a. 预测误差的分析:
| $ {{P}}=\frac{1}{l-1}\sum\limits _{i=1}^{l}{({{x}}_{f}^{i}-{\bar{{x}}}_{f}){({{x}}}_{f}^{i}-{\bar{{x}}}_{f})}^{\rm{T}} $ | (13) |
| $ {{R}}=\frac{1}{l-1}{{W}}{{{W}}}^{\rm{T}} $ | (14) |
其中,
| $ {{W}}=({{{w}}}^{1}\;\;{{{w}}}^{2}\;\;\cdots \;\;{{{w}}}^{n}) $ | (15) |
b. 卡尔曼增益计算:
| $ {{K}}={{P}}{{{H}}}^{\rm{T}}{\left({{H}}{{P}}{{{H}}}^{\rm{T}}+{{R}}\right)}^{-1} $ | (16) |
c. 更新集合成员:
| $ {{x}}_{\rm{a}}^{i}={{x}}_{f}^{i}+{{K}}({{{y}}}_{\rm{exp}}+{{{w}}}^{{i}}-{{H}}{{x}}_{f}^{i}) $ | (17) |
对应新集合成员的均值:
| $ {\bar{{x}}}_{\rm{a}}=\frac{1}{l}\sum \limits_{i=1}^{l}{{x}}_{\rm{a}}^{i} $ | (18) |
针对稳态问题的求解,最优状态参数
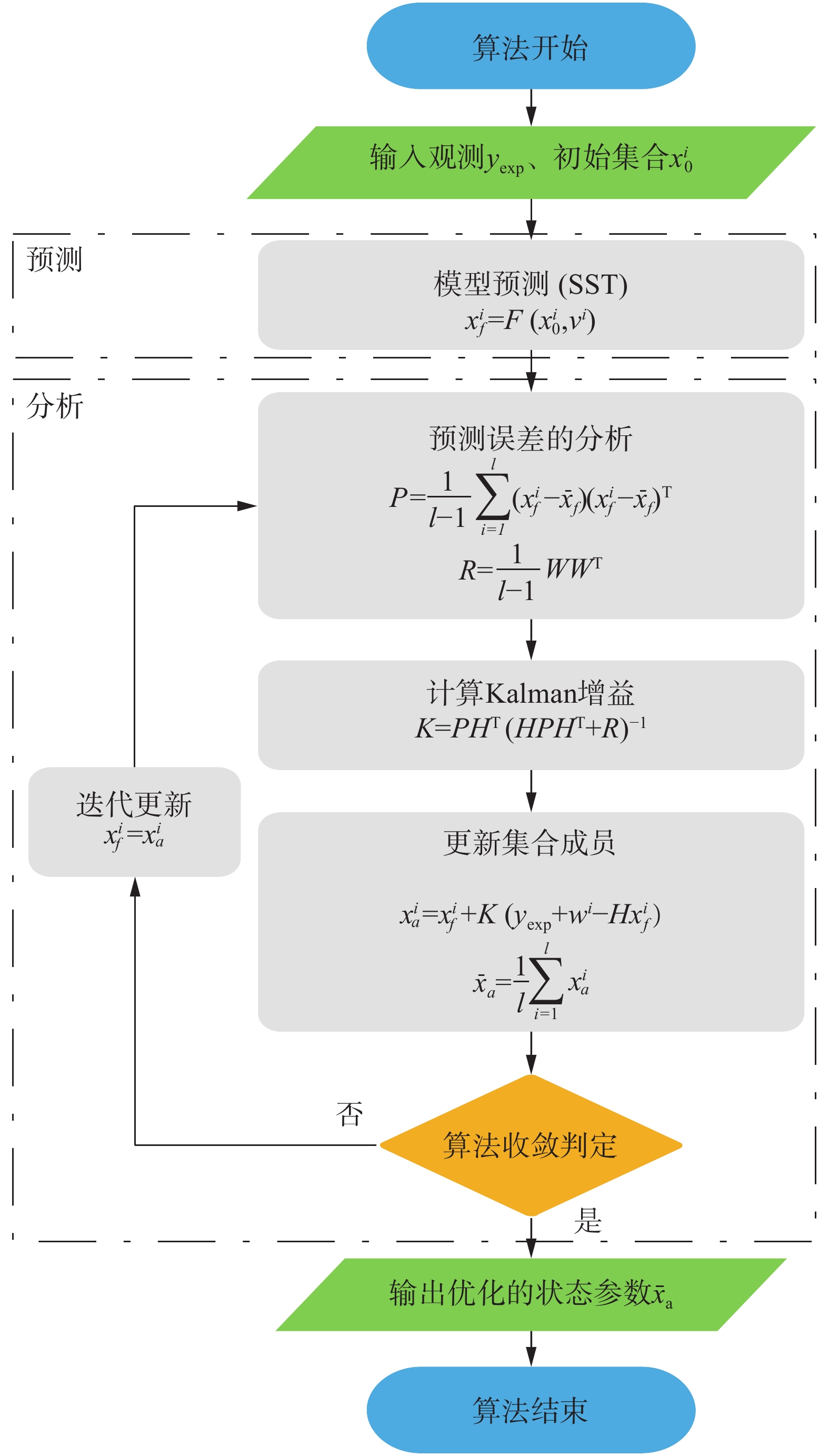
|
图 1 集合卡尔曼滤波算法流程图 Fig.1 Flow chart of EnKF Algorithm |
本文模型常数的标定基于集合卡尔曼滤波的数据同化方法。其中,集合的状态矩阵为:
| $\begin{split} {{{X}}_f} =& \left( {\begin{array}{*{20}{c}} {{{x}}_f^1}&{\begin{array}{*{20}{c}} {{{x}}_f^2}& \cdots &{{{x}}_f^l} \end{array}} \end{array}} \right)= \\& {\left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \!\!{{{{q}}^1}}\\ \!\!{{{{\theta }}^1}} \end{array}}&{\begin{array}{*{20}{c}} \!\!\!\!\!\!{{{{q}}^2}}\\ \!\!\!\!\!\!{{{{\theta }}^2}} \end{array}}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \!\!\!\!\!\!\!\!\!\!\!\!\!\cdots \\ \!\!\!\!\!\!\!\!\!\!\!\!\!\cdots \end{array}}&{\begin{array}{*{20}{c}} \!\!\!\!\!\!\!\!\!{{{{q}}^l}}\\ \!\!\!\!\!\!\!\!\!{{{{\theta }}^l}} \end{array}} \end{array}} \end{array}}\!\!\! \right)_{m \times l}} = \left( {\begin{array}{*{20}{c}} {{Q}}\\ {\bf{\varTheta }} \end{array}} \right) \end{split} $ | (19) |
实验流量观测数据为:
| $ {{{y}}}_{\rm{exp}}={\tilde{{q}}} $ | (20) |
同化观测矩阵为:
| $ \begin{split} {{Y}} =& {\left( {\begin{array}{*{20}{c}} {{{{y}}^1}}&{{{{y}}^2}}&{\begin{array}{*{20}{c}} \cdots &{{{{y}}^l}} \end{array}} \end{array}} \right)_{n \times l}}=\\& {\left( {\begin{array}{*{20}{c}} {{{{q}}^1}}&{{{{q}}^2}}&{\begin{array}{*{20}{c}} \cdots &{{{{q}}^l}} \end{array}} \end{array}} \right)_{n \times l}} = {{{y}}_{{\rm{exp}}}}{{\bf{1}}_{1 \times n}} + {{W}} \end{split} $ | (21) |
观测函数矩阵
| $ {{{H}}_{n \times m}} = \left( {\begin{array}{*{20}{c}} {{{{{{{{I}}}}}}_n}}&{{{\bf{0}}_{n \times \left( {m - n} \right)}}} \end{array}} \right) $ | (22) |
其中,
湍流模型常数标定流程如图2所示,选取的集合成员总数
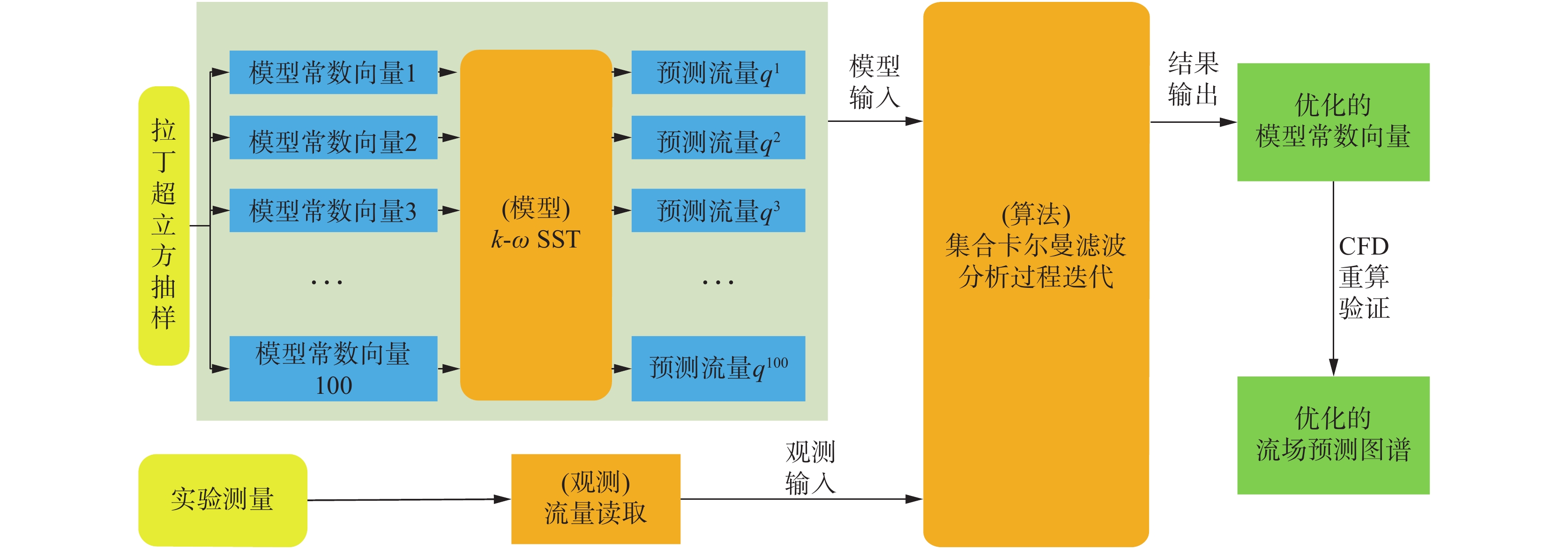
|
图 2 基于实验数据同化的湍流模型常数标定过程 Fig.2 Model constant calibration procedure based on experiment data assimilation |
可以看出,本文的湍流模型修正方法具有的两大优势。首先,该方法运用了数据同化方法,它是一类数据驱动的模型常数优化方法,可以实现对观测数据的充分利用,且实现上也相对简单;同时,本文所使用的集合卡尔曼滤波算法可以综合考虑模型预测和实验观测存在的误差,从而给出更准确的估计,相关结果更具有实际意义。
2 计算实例 2.1 研究对象本文的研究对象为如图3所示的蒸汽调节阀。图3(a)展示了阀门内部及附加管道流体域的正等测视图,图3(b)展示了阀门的z= 0截面示意图,其中阀内流体的路径如图中箭头所示。整个阀门结构包括调节阀结构(上)和主阀(截止阀)结构(下),二者具有共同的阀座。调节阀结构的阀腔与下游出口管道相连,阀塞(红色)作为实验的研究对象可以上下移动,达到调节阀组开度的目的。主阀结构的阀腔与上游入口管道相连,阀塞(蓝色)在整个实验中固定于开度最大的位置,从而使主阀始终保持全开状态;附加的滤网则位于在主阀阀芯的外侧,起到去除流体内杂质和整流的作用。
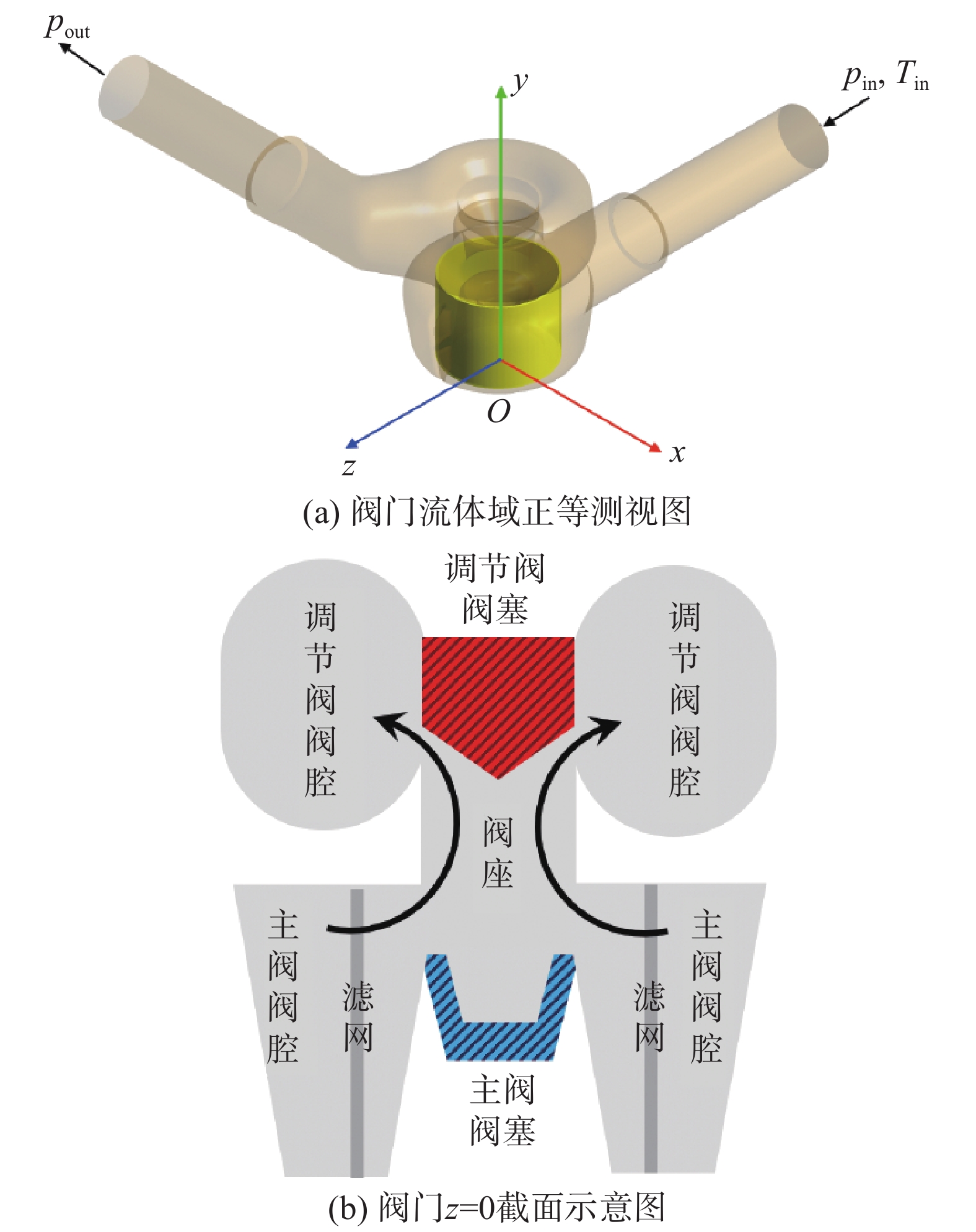
|
图 3 阀门几何结构示意图 Fig.3 Geometry sketch of valve 注:出于对商业敏感信息的保护,此处只展示了阀门结构简单示意图,实际计算采用真实阀门几何数据。 |
为了获取用于数据同化观测输入及后续验证的相关数据,本研究相关的通流特性实验已于前期进行。整体的管路图如图4所示,其中入口控制阀、出口调节阀用于调整被测阀门入、出口的压力,蒸汽加热器用于恒定阀门入口蒸汽温度并确保阀内的蒸汽始终具有一定的过热度。本研究中所涉及到的重点研究区域为图中虚线框内区域。实验中阀门保持一定开度(大/中/小),入口(温度计/压力计3)通入总压
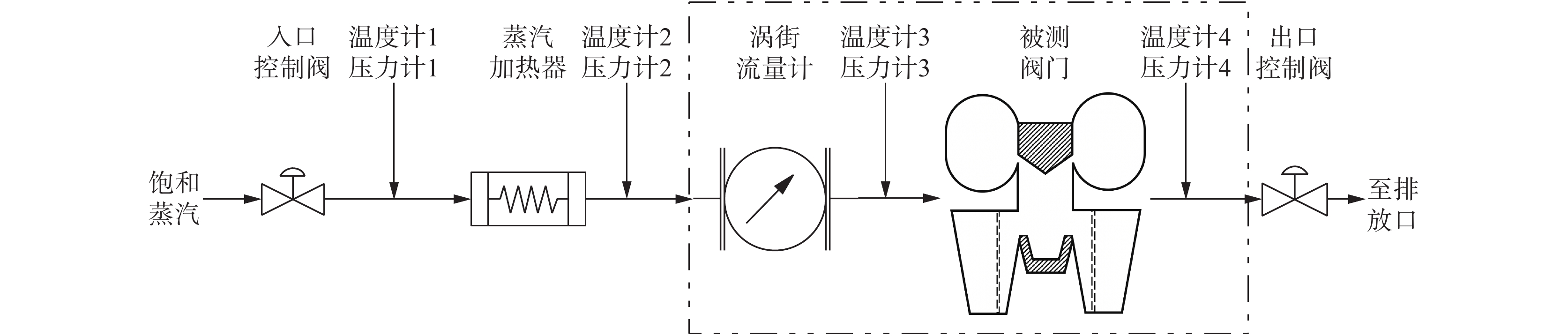
|
图 4 通流特性实验管路 Fig.4 Pipeline of flow characteristic experiment |
| 表 2 阀门实验数据 Table 2 Valve experiment data |
|
|
本文中数值模拟部分基于商业软件 ANSYS CFX。计算的流体域如图3(a)所示,包括两侧的出入口管道。计算的设置为稳态求解,基础湍流模型为SST模型,工作介质选用理想水蒸气。由于原型的滤网结构过于精细,无法完全按照几何结构进行模拟,因而采用文献[23, 24]中推荐使用的多孔介质模型处理。边界条件中入口边界条件总压
本文的数值计算边界条件依据相关实验测量的出入口数据设置。运用1.2.2节提出的模型常数标定方法,可由实验数据标定出三组模型常数矩阵,相关标定结果见表3,其中常数1,常数2,常数3分别对应大、中、小开度的阀门实验工况。
| 表 3 通过数据同化得到的湍流模型常数向量 Table 3 Calibrated model constant vectors using data assimilation |
|
|
为检验标定参数的可靠性及可拓展性,文中采用两种模型常数向量CFD验算的相关方案,具体见表4。方案1为按开度分组验算工况,每组仅使用组内工况标定的常数向量验算;方案2为所有验算工况仅使用中开度工况(M-1)标定的常数向量(常数2)验算。将相关的验算结果与实验记录对比,可得到对应的预测流量及误差,相关标准化分析结果于图5给出。
| 表 4 模型常数向量验算方案 Table 4 Validation cases for model constant vectors |
|
|
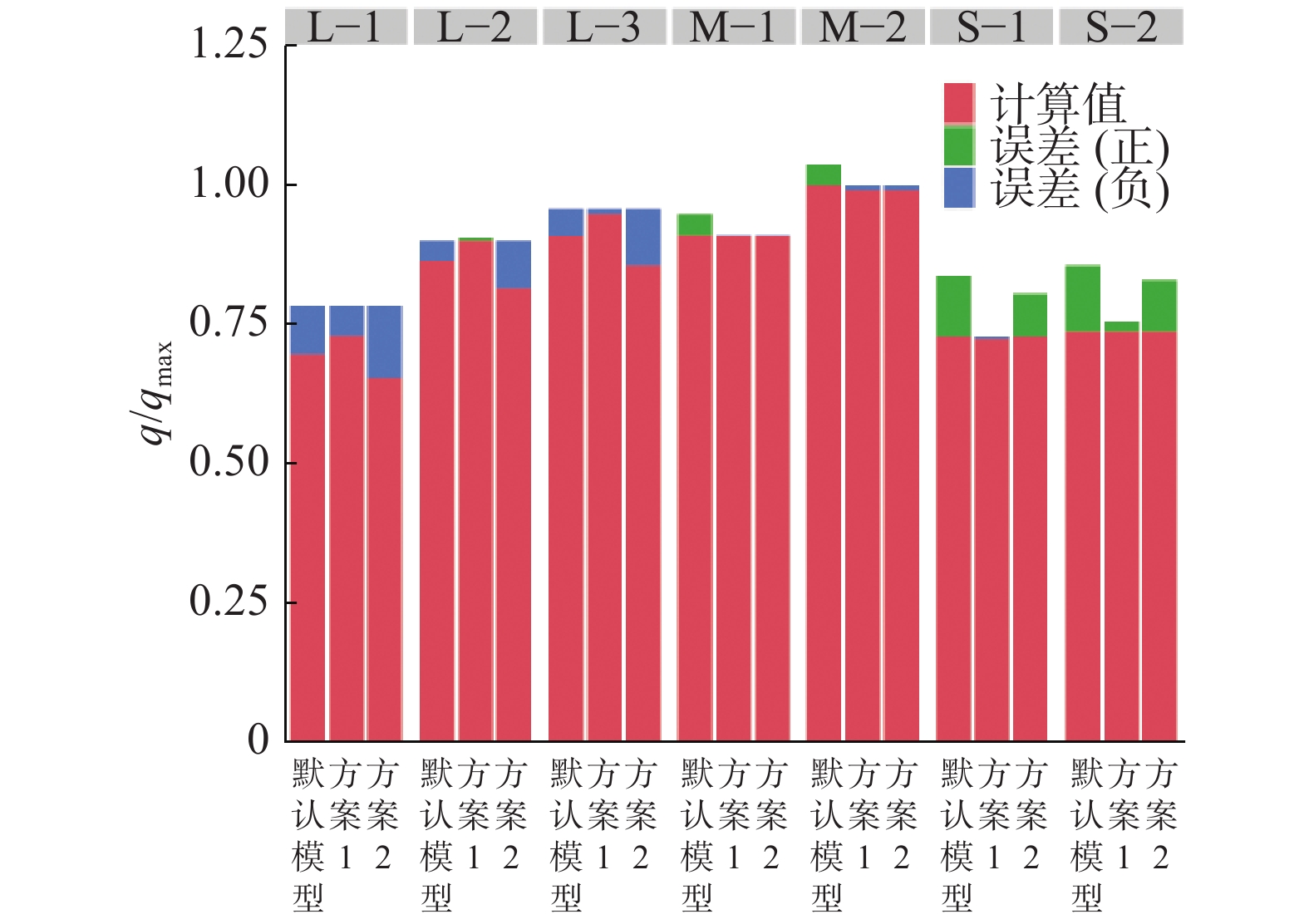
|
图 5 不同方案预测的标准化流量及与实验对比误差 Fig.5 Normalized flow rate by different prediction methods and relative errors against experimental measurementswith different methods |
从图5可看出,方案1选取的模型常数获得了最小的误差,且所有误差均小于默认SST模型的预测误差。这一点说明每一组工况的计算选择基于自身内部工况标定的常数的方案1是可行的。分析方案2,发现调节阀开度水平偏离常数的标定来源工况开度水平时,无论偏大还是偏小,都会出现显著的误差。这说明了最优湍流模型常数的选取需要依据阀门开度的大小进行。
3.2 内部流场分析为了从根本解释以上现象,本文分析了L-1、M-1和S-1三个工况的内部流场。在本文研究的范畴内,阀门在相似的开度、不同压比下的计算结果类似,因而相关流场不重复列举。
3.2.1 修正前不同工况阀内速度场对比图6展示了默认常数设置下阀内流动形态。由图6(a)可以看出,阀内高速区域的范围是不同开度下阀内速度场的重要区别。大开度下,如图6(a)左,高速区域填充了整个阀座和主阀阀口区域,并可以一直追溯到滤网内侧箭头指示位置。中开度下,如图6(a)中,高速区域仅可追溯到调节阀阀口,阀座内出现了“空心”。小开度下,阀内的高速流动区域仅填充了阀座内靠近壁面的小部分区域。此外,调节阀阀腔内的流动也存在显著区别。尽管图6(a)中三种开度下调节阀阀腔内高速流动区域均呈现圆环状,但该区域的厚度却有显著差异:大开度的高速区域厚度最高,中开度次之,小开度最低。

|
图 6 默认SST模型预测的阀门流动形态 Fig.6 Valve flow pattern predicted by default SST model |
图6(b)展示了调节阀阀口下游邻域的速度场和流线分布。大开度下,调节阀阀塞接近全开位置,其顶面与下游空腔壁几乎平齐,因而阀口下游高速区域较为宽广,流线方向恒定,且与壁面间几乎不存在低速带;中开度下,与前者类似,下游高速区域的流线方向较为恒定,但是阀塞锥面与下游壁面的相对偏离,导致高速区域与壁面间出现一个明显的低速带,且低速带一直延伸至壁面弯曲处;小开度下,下游高速区域在靠近阀口处与壁面明显分离,在远离阀口处出现明显的流线方向改变,导致很快出现再附着的现象。
以上现象说明不同开度水平下阀内流动形态存在明显的差异。流动形态的显著不同,必将导致最适模型常数存在一定的差异性,因不同阀门开度下最优的常数向量也必将不同。然而,以上的分析仅基于默认常数的计算,更可靠深入的分析还需要依据同化修正后的流场进行。
3.2.2 同工况修正前后阀内速度场对比图7~图9分别展示了M-1、S-1、L-1三种工况、不同模型常数下、阀门z= 0截面的标准化速度场对比。三个图(a)中默认常数的情形已于3.2.1节讨论,此处不再赘述。
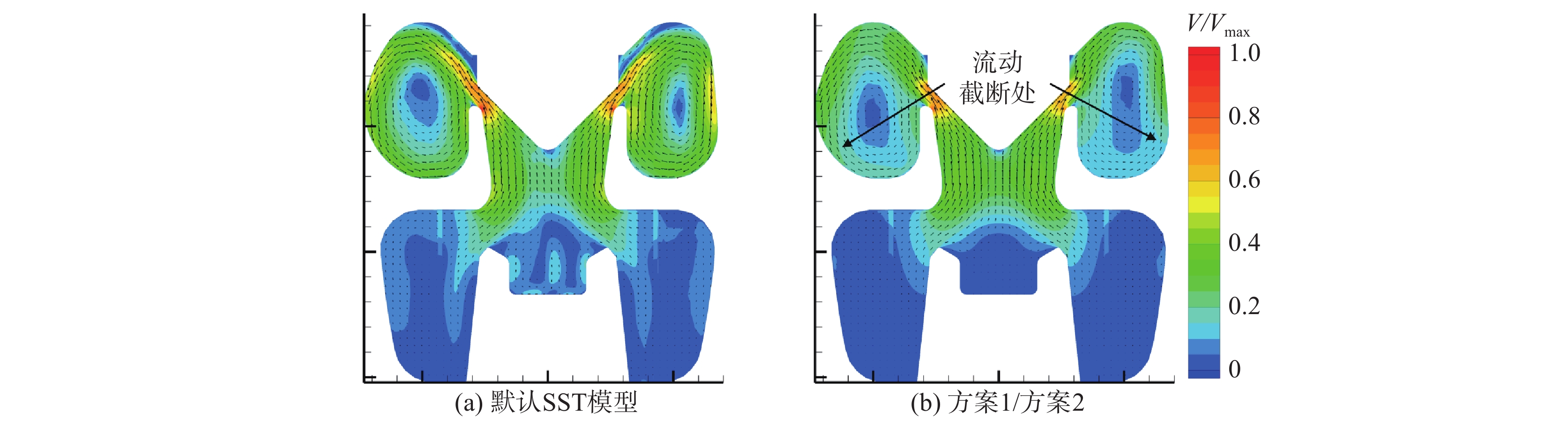
|
图 7 M-1工况z= 0截面不同模型常数预测的速度场 Fig.7 Predicted velocity field using different model constants on plane z= 0 at operating condition M-1 |
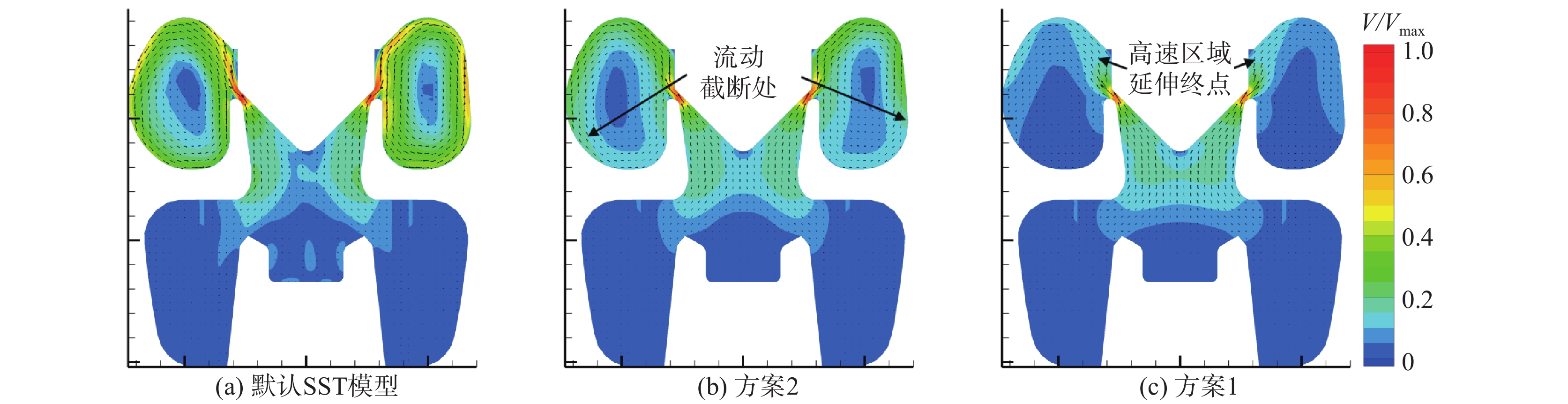
|
图 8 S-1工况z= 0截面不同模型常数预测的速度场 Fig.8 Predicted velocity field using different model constants on plane z= 0 at operating condition S-1 |
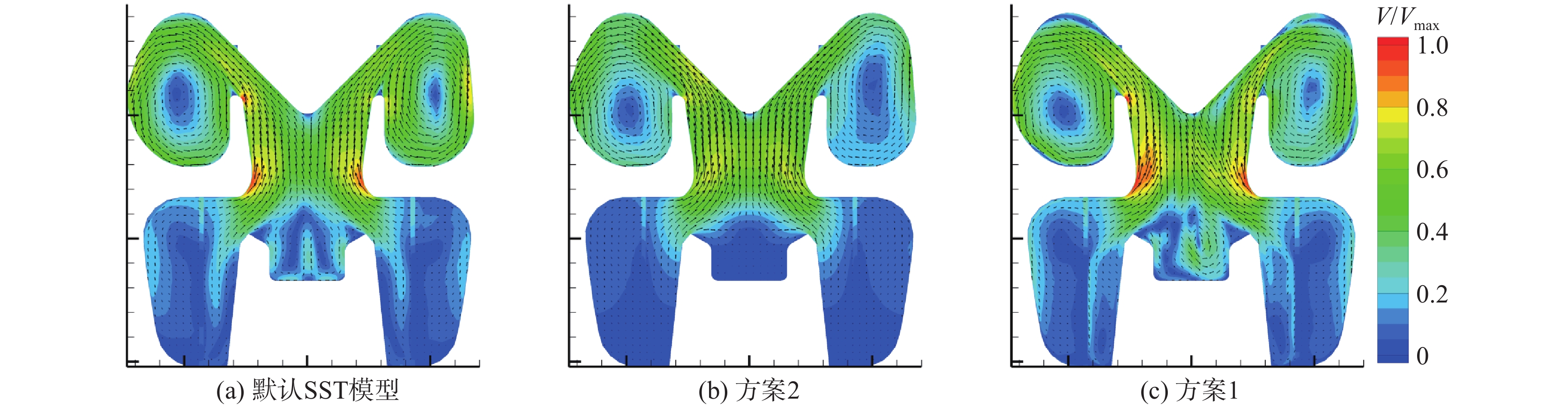
|
图 9 L-1工况z= 0截面不同模型常数预测的速度场 Fig.9 Predicted velocity field using different model constants on plane z= 0 at operating condition L-1 |
由图7(b)可以看出,修正后的流场存在两点显著区别:一是调节阀阀口最大流速一定程度的降低,且在下游邻域,流动不再分离,转化为贴壁流动;二是调节阀阀腔内的环状贴壁流动被削弱,流体沿着壁面到达图7(b)箭头所示位置时速度显著降低,呈现被截断的状态。对比二者综合而言,修正后的阀内流场的高速区域更小更规则,流动更简单、更均匀。
由图8(b)可以看出,运用方案2修正的阀内流场的均匀性被一定程度上提升,整体复杂程度类似图6(b),且高速区域在相似位点中断。由图8(c)则可以看出,运用方案1修正的阀内流动的均匀性被进一步提高。调节阀阀口下游的高速区呈贴壁流态,且于极短的距离内耗散,与低速区融合。综合对比,图8(a)到图8(b)到图8(c)流场的均匀性被逐步提高,阀内高速流动区域向阀口下游的流向延伸距离依次递减。
由图9(b)可以看出,采用方案2修正的阀内流场的均匀性被一定程度上提升,且调节阀阀腔内的旋涡状流动被截断,贴壁流动到达一定区域时速度显著降低,整体复杂程度与图6(b)相似。由图9(c)可以看出,采用方案1修正的阀内流场与图9(b)的趋势完全相反。阀内流动的均匀性被削弱,出现了更多的旋涡状结构;调节阀阀腔内的旋涡状流动不仅保持存在,且相对图9(a)更加复杂,出现多次分离和附着。因而,大开度情形下,默认模型和方案2的预测均无法捕捉阀内流场的细节。
分析以上现象可知,采用单一模型常数向量(默认SST模型、方案2),预测的流场具有相似的均匀度;而合理采用多种模型常数向量(方案1),预测的流场的均匀性随着开度的降低而增加。单一模型常数向量无法准确捕捉不同开度下阀内变化的速度复杂度,即无法实现对阀内速度场分布的合理预测。因而在通流特性预测上呈现出较大的局限性;而合理采用多种模型常数向量分别求解,可以适应多开度下阀内流场速度分布预测的需求,从而提高阀门数值模拟预测的准确度。
3.2.3 修正前后阀内涡黏度对比在利用RANS求解湍流问题的过程中,雷诺应力项的引入使得原方程组失去封闭性从而无法求解,而湍流模型的提出正是为了解决这一问题。湍流模型包括的物理项有对流项、生成项、耗散项等,在充分发展的湍流流场的控制区域内,湍流的流入、生成、耗散达到平衡。而这些湍流模型中的常数则是用来标定这些物理项相对贡献的大小,因而对前者的重新标定会打破原先的平衡并使其逐渐转移至一个新的平衡,这将改变流场内重要的湍流物理量的预测。其中,涡黏假设是一类湍流模型(涡黏模型)的重要处理方法,而涡黏度
图10展示了不同设置下z= 0截面预测的标准化涡黏度场,标准化涡黏度定义

|
图 10 z= 0截面不同模型常数预测的标准化涡黏度 Fig.10 Predicted normalized eddy viscosity using different model constants on plane z= 0 |
| $ {\nu _{t,n}} = \frac{{{\nu _t}}}{{{V_{{\rm{in}},{\rm{max}}}}{r_{{\rm{in}}}}}} = \frac{{{\nu _t} \cdot {\rm{{\text{π}} }}{r_{{\rm{in}}}}}}{{{q_{{\rm{max}}}}}} $ | (23) |
式中,
由图可得,采用默认常数模拟时,所有开度预测的的无量纲化涡黏度均处于
结合前文分析,可以看出速度场与涡黏度场间的关联性。基于默认常数,不同开度下阀内流动虽展现出多种不同的流态特征,但复杂程度相当;对应的,默认模型预测的阀内的涡黏度场强度相似。采用方案1,不同开度下阀内流动的复杂程度随着开度增加而逐渐提高;对应的,方案1预测的阀内涡黏度随着开度的提高而逐渐降低。更高的涡黏度表征湍流对时均流场更强的影响,一般来说促进湍流掺混,从而提高阀内流动均匀性。显然,对湍流掺混的修正,会改变阀内流动速度场的预测。由于阀门入口体积流量是阀门质量流量和入口处流体密度的函数,而阀门质量流量等于通过阀内任意完整曲面的流体质量之和,后者和曲面上流体的速度分布相关。因而,阀内速度场分布预测的改变,会影响阀门通流特性预测结果。同时,由相关文献分析可得知,模型常数
本文使用数据同化手段,以含滤网蒸汽阀门流动实验数据为观测数据,以集合卡尔曼滤波算法为同化算法,重新标定SST模型的常数向量,优化了蒸汽阀门流量特性数值预测的精度。主要结论如下:
1)采用数据同化方法可以有效标定蒸汽调节阀数值模拟的湍流模型常数向量,且标定的常数向量具有可拓展性,可以应用于计算相似开度的其它工况。这对数据同化的工业化应用和蒸汽调节阀通流特性的研究有重要的参考价值。
2)标定的常数向量的可拓展性是有限的。最优模型常数的选择需要依据阀门开度进行,强行将标定常数用于不同开度下的计算会导致误差的增加。
3)常数向量可拓展性的限制源于阀内流动形态特征的区别。不同开度下,阀内的流动特征不一致,而不同的流动特征对应不同的最优模型常数向量,因而将特定工况标定的常数向量运用于流动特征相异的工况往往无法实现同样的效果。
4) 模型常数修正能改变流场内部涡黏度的分布。涡黏度表征湍流对时均流场影响的强弱,从而直接改变阀内速度场的预测,这会对阀门通流特性的预测结果产生影响。
本文的工作是工业化背景下数据同化应用的一次重要尝试,实现了利用数据同化工具解决工程问题,扩展了数据同化的适用范围。后续工作可以从数据同化的同化算法入手,即通过对比不同算法对同一工程问题数值模型优化的性能和效率,评估不同算法的优劣,从而评估同化算法对特定工程问题的适用性。
| [1] |
QIAN J Y, WEI L, ZHANG M, et al. Flow rate analysis of compressible superheated steam through pressure reducing valves[J]. Energy, 2017, 135: 650-658. DOI:10.1016/j.energy.2017.06.170 |
| [2] |
HAJŠMAN M, KOVANDOVÁ D, MATAS R. Some aspects of numerical simulation of control valves for steam turbines[J]. EPJ Web of Conferences, 2012, 25: 01052. DOI:10.1051/epjconf/20122501052 |
| [3] |
HALIMI B, KIM S H, SUH K Y. Engineering of combined valve flow for power conversion system[J]. Energy Conversion and Management, 2013, 65: 448-455. DOI:10.1016/j.enconman.2012.09.012 |
| [4] |
机器学习在湍流模型构建中的应用进展[J]. 空气动力学学报, 2019, 37(3): 444-454. ZHANG W W, ZHU L Y, LIU Y L, et al. Progresses in the application of machine learning in turbulence modeling[J]. Acta Aerodynamica Sinica, 2019, 37(3): 444-454. DOI:10.7638/kqdlxxb-2019.0036 (in Chinese) |
| [5] |
马建文. 数据同化算法研发与实验[M]. 北京: 科学出版社, 2016.
|
| [6] |
LYNCH P. The origins of computer weather prediction and climate modeling[J]. Journal of Computational Physics, 2008, 227(7): 3431-3444. DOI:10.1016/j.jcp.2007.02.034 |
| [7] |
CANCHUMUNI S W A, EMERICK A A, PACHECO M A C. History matching geological facies models based on ensemble smoother and deep generative models[J]. Journal of Petroleum Science and Engineering, 2019, 177: 941-958. DOI:10.1016/j.petrol.2019.02.037 |
| [8] |
基于数据同化的珠江河口悬沙浓度多模型协同反演[J]. 泥沙研究, 2019, 44(4): 47-53. PAN H Z, YANG L Z, LIU C Q, et al. Muti-model collaborative retrieval of suspend sediment concentration in the estuary of Pearl River based on data assimilation[J]. Journal of Sediment Research, 2019, 44(4): 47-53. DOI:10.16239/j.cnki.0468-155x.2019.04.008 (in Chinese) |
| [9] |
应用新数据同化算法的桥梁极值应力预测[J]. 吉林大学学报(工学版), 2020, 50(2): 572-580. FAN X P, QU G, LIU Y F. Bridge extreme stress prediction based on new data assimilation algorithm[J]. Journal of Jilin University (Engineering and Technology Edition), 2020, 50(2): 572-580. DOI:10.13229/j.cnki.jdxbgxb20181017 (in Chinese) |
| [10] |
KATO H, OBAYASHI S. Data assimilation for turbulent flows[C]//16th AIAA Non-Deterministic Approaches Conference, National Harbor, Maryland. Reston, Virginia: AIAA, 2014.doi: 10.2514/6.2014-1177.
|
| [11] |
MARGHERI L, MELDI M, SALVETTI M V, et al. Epistemic uncertainties in RANS model free coefficients[J]. Computers & Fluids, 2014, 102: 315-335. DOI:10.1016/j.compfluid.2014.06.029 |
| [12] |
YANG M C, XIAO Z X. Parameter uncertainty quantification for a four-equation transition model using a data assimilation approach[J]. Renewable Energy, 2020, 158: 215-226. DOI:10.1016/j.renene.2020.05.139 |
| [13] |
WANG P, LIU Y Z. Unsteady flow behavior of a steam turbine control valve in the choked condition: Field measurement, detached eddy simulation and acoustic modal analysis[J]. Applied Thermal Engineering, 2017, 117: 725-739. DOI:10.1016/j.applthermaleng.2017.02.087 |
| [14] |
WANG P, MA H Y, LIU Y Z. Proper orthogonal decomposition and extended-proper orthogonal decomposition analysis of pressure fluctuations and vortex structures inside a steam turbine control valve[J]. Journal of Engineering for Gas Turbines and Power, 2019, 141(4). DOI:10.1115/1.4040903 |
| [15] |
WANG P, XU S, HE L, et al. Unsteady behavior of wall-detached flow inside a steam turbine control valve[J]. Physics of Fluids, 2019, 31(10): 105101. DOI:10.1063/1.5124359 |
| [16] |
雷诺数对调节阀模化试验影响的研究[J]. 中国电机工程学报, 2019, 39(5): 1405-1411. ZENG L F, GAO D P, QI W Y, et al. The influence of Reynolds number on modeling experiment of control valve[J]. Proceedings of the CSEE, 2019, 39(5): 1405-1411. DOI:10.13334/j.0258-8013.pcsee.180828 (in Chinese) |
| [17] |
DOMNICK C B, BENRA F K, BRILLERT D, et al. Numerical investigation on the time-variant flow field and dynamic forces acting in steam turbine inlet valves[J]. Journal of Engineering for Gas Turbines and Power, 2015, 137(8): 081601. DOI:10.1115/1.4029309 |
| [18] |
MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 |
| [19] |
DENG Z W, HE C X, WEN X, et al. Recovering turbulent flow field from local quantity measurement: turbulence modeling using ensemble-Kalman-filter-based data assimilation[J]. Journal of Visualization, 2018, 21(6): 1043-1063. DOI:10.1007/s12650-018-0508-0 |
| [20] |
RABIER F, LIU Z. Variational data assimilation: theory and overview [EB/OL]. https://www.ecmwf.int/sites/default/files/elibrary/2003/11805-variational-data-assimiltion-theory-and-overview.pdf, 2003.
|
| [21] |
MONS V, CHASSAING J C, GOMEZ T, et al. Reconstruction of unsteady viscous flows using data assimilation schemes[J]. Journal of Computational Physics, 2016, 316: 255-280. DOI:10.1016/j.jcp.2016.04.022 |
| [22] |
EVENSEN G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics[J]. Journal of Geophysical Research: Oceans, 1994, 99(C5): 10143-10162. DOI:10.1029/94JC00572 |
| [23] |
ZANAZZI G, RICE T, SELL M, et al. Experimental and numerical investigation into the aerodynamics of a novel steam turbine valve and its field application[J]. Journal of Engineering for Gas Turbines and Power, 2014, 136(9): 091601. DOI:10.1115/1.4026860 |
| [24] |
WANG P, LIU Y Z. Influence of a circular strainer on unsteady flow behavior in steam turbine control valves[J]. Applied Thermal Engineering, 2017, 115: 463-476. DOI:10.1016/j.applthermaleng.2016.12.073 |
| [25] |
CHATTOPADHYAY H, KUNDU A, SAHA B K, et al. Analysis of flow structure inside a spool type pressure regulating valve[J]. Energy Conversion and Management, 2012, 53(1): 196-204. DOI:10.1016/j.enconman.2011.08.021 |
| [26] |
EVANS S, LARDEAU S. Validation of a turbulence methodology using the SST k-ω model for adjoint calculation[C]//54th AIAA Aerospace Sciences Meeting, San Diego, California, USA. Reston, Virginia: AIAA, 2016. doi: 10.2514/6.2016-0585.
|
| [27] |
湍流模型封闭常数对S系列翼型CFD模拟的影响[J]. 太阳能学报, 2013, 34(10): 1690-1696. ZHONG W, WANG T G. Influence of closure coefficient of turbulence model on cfd simulations of s series airfoils[J]. Acta Energiae Solaris Sinica, 2013, 34(10): 1690-1696. DOI:10.3969/j.issn.0254-0096.2013.10.00 (in Chinese) |
 2021, Vol. 39
2021, Vol. 39


