爆轰波在传播时,其波阵面呈入射激波、反射激波和马赫干组成的三波结构,该结构是非定常的,三波点的轨迹构成了爆轰的胞格结构。胞格的尺寸作为爆轰本征值,反映了可燃系统气体动力学和化学反应动力学之间的非线性反馈作用,可以用来表征爆轰极限、爆轰临界直径和临界能量等爆轰动力学参数[1-5]。然而,胞格尺寸的测量主观性比较强。对于一个不规则的爆轰胞格,不同研究者测得的胞格尺寸可能相差较大。图1是C3H8+5O2在直径为52 mm的圆管内的实验胞格,8个实验人员对其进行了测量,得到的胞格尺寸分别为8、13.5、10、6.4、13、7.1、10、8.3 mm,最大值和最小值几乎相差了一倍[6]。这种研究者的主观因素带来的误差会明显影响到可燃系统的爆轰动力学参数的确定。因此,需要对爆轰胞格的尺寸进行客观的测量,以消除或减弱这种主观因素引起的误差,实现对爆轰过程的控制。

|
图 1 C3H8+5O2在直径52 mm圆管的爆轰胞格结构 Fig.1 Detonation cell structure of C3H8+5O2 in acircular tube with a diameter of 52 mm |
Shepherd[7]最早通过计算数字化胞格的能量谱,得到空间尺寸分布的频谱,根据谱的峰值来确定相应的尺寸为胞格尺寸。随后,Shepherd[8]采用该方法对不同燃料形成的爆轰的胞格尺寸进行了分析,比如氢气、乙炔、乙烯等。这种方法的缺点是对噪点很敏感,在对烟迹板上的胞格进行数字化处理时,烟迹板上的积碳会导致背景灰度值波动较大,进而影响该方法对胞格尺寸的预测。Lee[9]采用自相关函数法对实验胞格进行了分析,该方法的物理意义更加清晰,它可以提供x方向和y方向偏移量的相关性。作者对不同浓度氩气稀释的乙炔与氧气的混合物形成的爆轰胞格进行了讨论。对于不规则的胞格,该方法面临噪音干扰的问题。为了降低这种干扰的影响,Hebral[10]使用Photoshop和Matlab对图像进行降噪锐化处理,使迹线更加明显,提高胞格尺寸的统计效果。近来,Shepherd[6]采用概率密度函数法和自相关函数法对数值爆轰胞格进行了初步的统计分析,其中三波点轨迹的捕捉采用正涡量和负涡量,这样避免了三波点统计时的干扰。
以上研究表明,爆轰胞格尺寸的测量,尤其是不规则胞格,需要采用统计处理来摆脱人眼的主观性。本文采用两种统计方法:概率密度函数法和自相关函数法,对规则程度不同的数值胞格进行了统计分析,并对两种统计方法进行了比较。由于爆轰的稳定性对活化能比较敏感,本研究通过调整活化能的大小来形成规则程度不同的爆轰胞格。
1 物理模型和算法 1.1 控制方程和胞格的捕捉对于气相爆轰波而言,国内外普遍采用Euler方程进行数值研究,本文研究基于单步反应的Euler方程:
| $\frac{{\partial Q}}{{\partial t}} + \frac{{\partial F}}{{\partial x}} + \frac{{\partial G}}{{\partial y}} = S$ | (1) |
其中,
| $ Q = \left[ \begin{array}{l} \rho \\ \rho u \\ \rho v \\ \rho e \\ \rho Z \\ \end{array} \right]\;,\;\;\;\;F = \left[ \begin{array}{l} \rho u \\ \rho {u^2} + p \\ \rho uv \\ (\rho e + p)u \\ \rho Zu \end{array} \right] , $ |
| $ G = \left[ \begin{array}{l} \rho v \\ \rho uv \\ \rho {v^2} + p \\ (\;\rho e + p)v \\ \rho Zv \\ \end{array} \right]\;,\;\;\;S = \left[ \begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \\ \rho w \\ \end{array} \right] . $ |
式中,u和v分别为x和y方向的速度分量,t、p、ρ和Z分别表示时间、混合物的压力、混合物的密度和反应产物的质量分数。e为混合物单位质量的总能量,满足以下关系:
| $e = p/[\rho (\gamma - 1)] + ({u^2} + {v^2})/2 - Zq$ | (2) |
式中q为反应热。化学反应采用单步不可逆反应,反应速率满足:
| $w = (1 - Z)k\exp ( - {E_a}/RT)$ | (3) |
式中k、Ea和R分别表示指前因子、活化能和气体常数,其中k的选取是为了保证特征长度为半个反应区长度,即L1/2=1,其值与活化能有关,计算公式为:
| $k = \int_0^{{1 / 2}} {\frac{{u\exp ( - Ea/RT)}}{{1 - \lambda }}} {\rm{d}}\lambda $ | (4) |
为了捕捉流场中爆轰波的精细结构,本文采用分裂格式,方程(1)中的对流项采用5阶WENO格式(Weighted Essentially Non-Oscillatory)离散[11],时间项采用3阶TVD型的Runge-Kutta法[12]进行积分求解,化学反应源项采用五阶Runge-Kutta法进行求解。以上所提到的计算格式已经在相关的算例中经过了验证[13-15]。
爆轰胞格作为爆轰波阵面三波点的轨迹,其形成机理存在多种观点,Quirk[16]和Sharpe[17]认为实验中烟迹片上产生的胞格痕迹是由三波点处的最大涡量引起的,故本文在数值研究爆轰胞格时,采用记录每个网格点上达到的最大涡量
概率密度函数是用来描述随机变量在给定的样本空间中出现的可能性。概率密度函数范围介于样本空间中样本值的最大值和最小值之间,其峰值所对应的变量值表示最可能发生的事件。
随机变量x的累计分布函数F(x),存在非负函数f(x),使得对于任意实数有:
| $F(x) = \int_{- \infty}^x f(t){\rm{d}}t$ | (5) |
则称x为连续随机变量,其中f(x)称为x的概率密度函数,简称概率密度,存在:
| $f(t) \geqslant 0,\; \int_{- \infty}^{ + \infty} f(t){\rm{d}}t = 1{\text{}} $ |
对于爆轰胞格,通过跟踪三波点轨迹的涡量数据,计算任意相邻两条平行迹线间距。最终通过绘制相邻两条迹线间距的概率密度分布图,其中最大概率对应的三波点的间距可以定义为胞格的尺寸。
1.3 爆轰胞格尺寸的自相关函数法自相关函数主要应用在信号处理中,用来描述信号在一个时刻的取值与另一个时刻的取值的依赖关系。当信号中有周期性分量出现时,自相关函数分布的极大值能够很好的体现这种周期长度。
对于爆轰波的二维流场中,以涡量ω(x, y)为待处理的信号,其自相关函数R(dx, dy)可以定义为:
| $R({{{\rm{d}}}{x}},{{{\rm{d}}{{y}}}}) = \dfrac{1}{{MN}}\frac{{\displaystyle\sum\nolimits_{j = 1}^N {\displaystyle\sum\nolimits_{i = 1}^M {\omega (x,y)} } \omega (x + {\rm{d}}x,y + {\rm{d}}y)}}{{\displaystyle\sum\nolimits_{j = 1}^N {\displaystyle\sum\nolimits_{i = 1}^M {{\omega ^2}(x,y)} } }}$ | (6) |
其中,dx和dy分别表示x方向和y方向的信号的偏移。上述相关函数的定义表明,未偏移信号ω(x, y)与偏移信号ω(x+dx, y+dy)之间的关联程度。
2 结果与讨论 2.1 不同活化能的爆轰胞格结构本文采用的物理模型如图2所示,无量纲热力学参数分别为:初温T0 = 1,初压p0 = 1,比热比γ = 1.2,反应热Q = 50。以半个反应区长度L1/2为特征长度,采用的网格标准为64/L1/2(半个反应区里有64个计算网格),该网格精度足以描述爆轰的胞格特性[3]。计算区域纵向长度(y方向)为300L1/2,流向尺度(x方向)是爆轰波传播方向的尺度。在爆轰胞格的数值模拟中,需要足够长的时间和空间才能得到稳定的流场结构。为了节省计算资源,本文采用移动计算窗口(x方向尺度为1800L1/2),即爆轰波接近计算区域右端边界时,在计算区域最左端舍弃一部分网格,同时在右端增加一部分网格,这部分新增加的网格中的参数设置为新鲜的未燃气体。需要注意的是,这部分网格数量的选取要适当,如太多,左边界会影响爆轰波的结构,如太少,会导致舍弃网格和增加网格的操作太频繁,从而降低计算效率。经过本文的计算实验表明,这部分网格数量为500L1/2。

|
图 2 计算示意图 Fig.2 Schematic diagram of the computational domain |
为了表征爆轰胞格的规则程度,活化能选取了四种不同的情况,分别为Ea = 15、20、25和27,其中数值模拟的爆轰动力学参数已经在Sharp[6]的研究中验证过。图3为活化能为15时的不同时刻流场的变化图,左图为压力云图,右图为反应物质量分数云图。初始时刻,在管道左端的高温高压点火,如图3(a)所示,形成的压力波往周围传播,在管道上下壁面反射,形成反射激波,往管道右端传播,与此同时,激波后面的未燃气迅速燃烧,转变成燃烧产物,如图3(b)所示。随后,激波在往前传播的过程中,形成的横波往管道上下壁面之间来回反射,此时,波阵面只存在一组三波点(分别向上下传播的2个三波点),如图3(c)所示。经历一段时间后,波阵面开始出现多个子波,即多组三波点,如图3(d)所示。随着波阵面继续往前传播,经过上下壁面的多次反射,形成充分发展的爆轰波(具有完整的爆轰波波系的结构),如图3(e)所示。此时的爆轰波并不是最终的爆轰波,其胞格尺寸也不同于最终的胞格尺寸,该尺寸与数值计算的初始条件有关。由于爆轰波是一个非定常结构,必须要经过足够长的时间才能得到稳定的爆轰波,如图3(f)所示。

|
图 3 不同时刻爆轰波传播的流场图 Fig.3 Flow fields of the detonation wave at different time instances |
图4是当爆轰稳定传播时,根据网格点上的最大涡量绘制的三波点的迹线,由于涡量存在正负,图4(a、b、c)分别是根据正涡量最大值ω+、负涡量最大值ω−、正负涡量叠加(ω++|ω−|)/2绘制的三波点轨迹。涡量的符号代表三波点不同的传播方向,正涡量代表一组相互平行的向左传播的迹线(面向下游),负涡量代表一组相互平行的向右传播的迹线,正涡量与负涡量的叠加得到鱼鳞状的胞格结构。
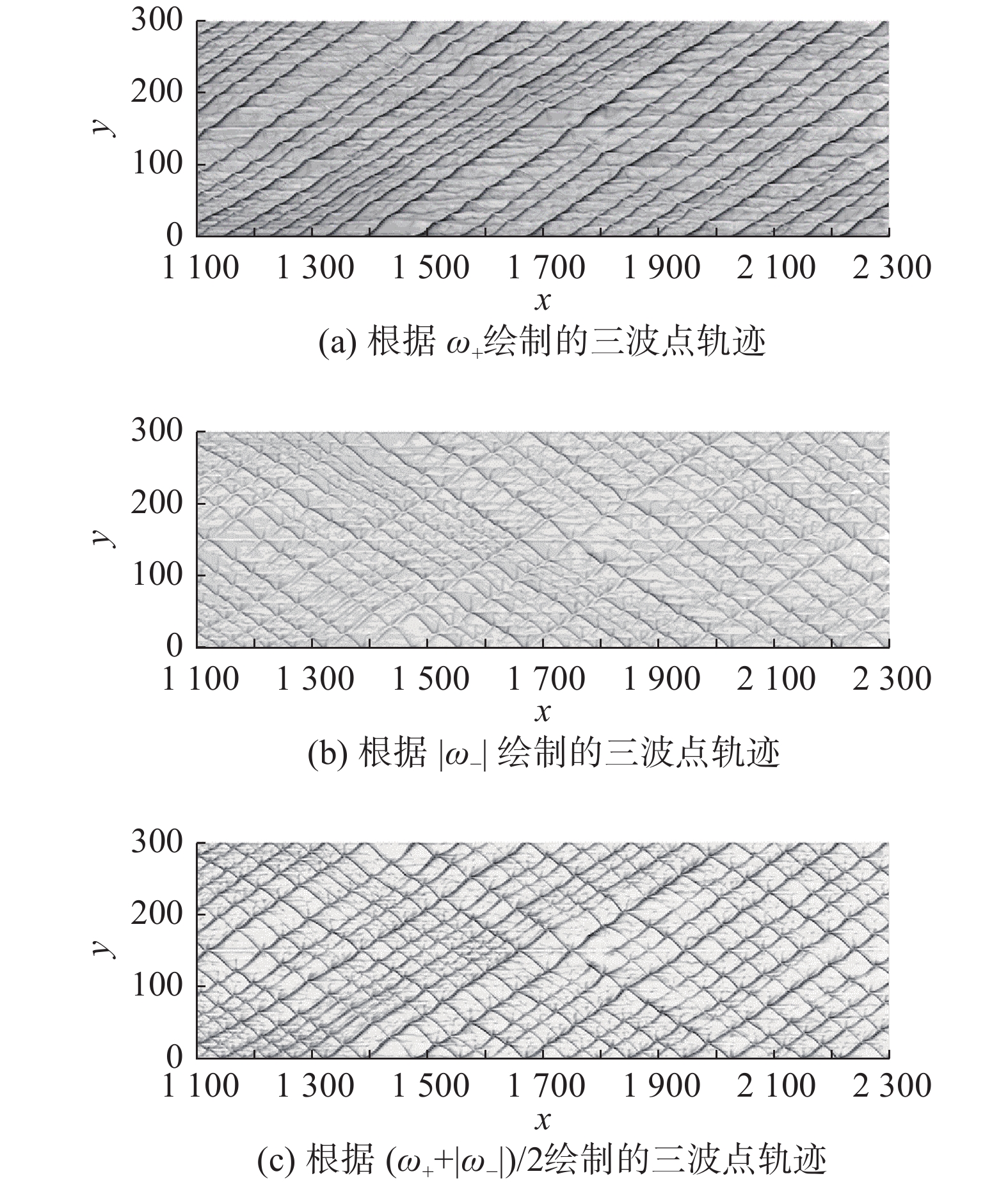
|
图 4 活化能Ea= 15时的三波点轨迹 Fig.4 Triple-point tracks for Ea= 15 |
图5是活化能Ea为20、25、27时,根据网格点上的正负涡量叠加(ω++|ω−|)/2绘制的数值胞格。随着活化能的增加,激波后的诱导区变长,反应区变短,能量释放越快,此时,诱导区的温度扰动对反应的影响越大,相应的爆轰越不稳定,形成的胞格也越不规则,流场达到稳定所需的时间也越长,数值胞格所选的区域也越靠后。为了排除初始流场的影响,数值胞格的统计处理需采用稳定的流场信息。因此,活化能为20、25和27时,选取的胞格区域为7200 ≤ x ≤ 9000。由图5,活化能为20时,胞格结构开始出现不规则,三波点的迹线出现相交的趋势,活化能增加到25时,三波点的迹线出现合并,胞格尺寸的取值范围明显增加,当活化能增加到27时,胞格极不规则,其尺寸的取值范围进一步扩大。
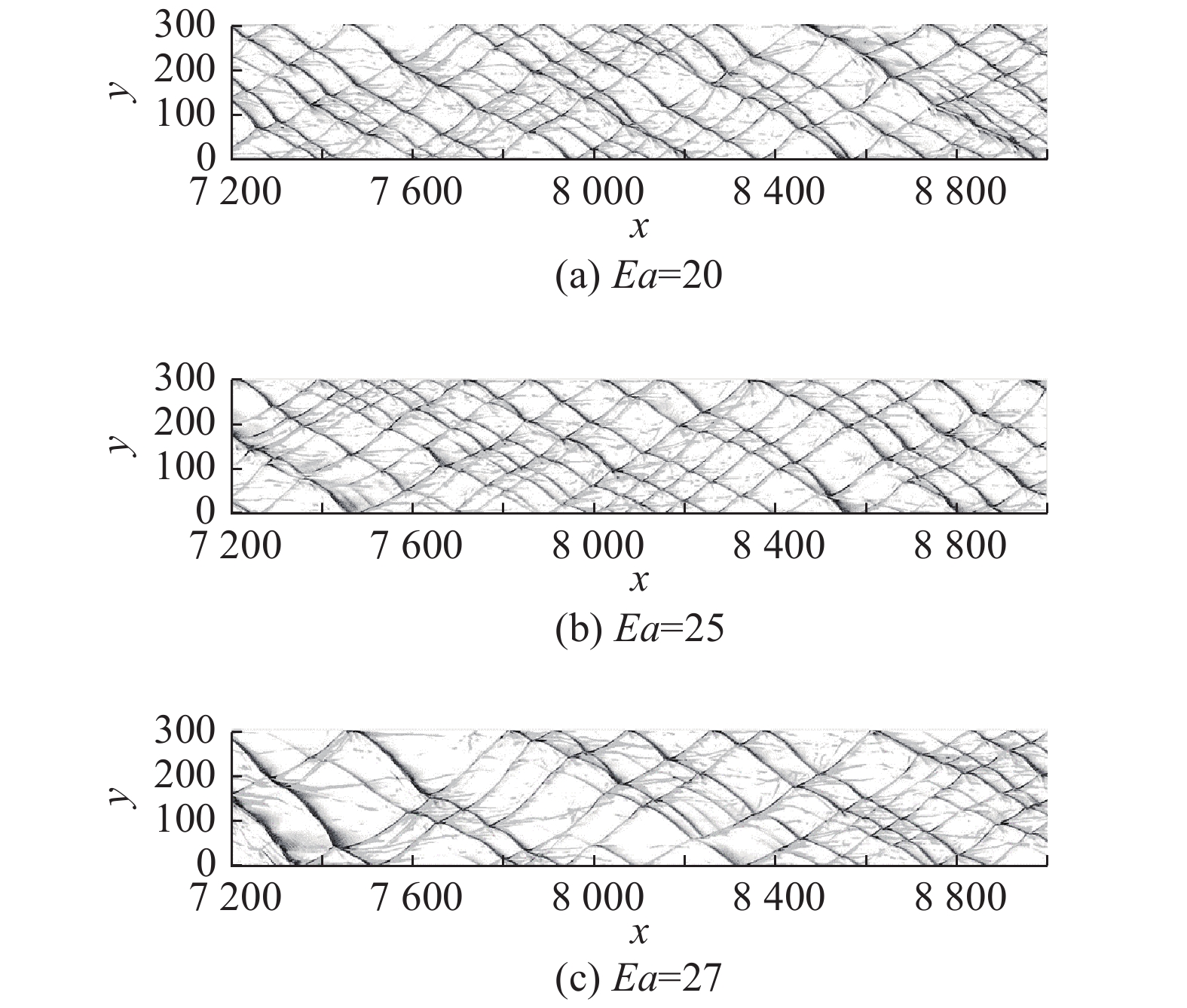
|
图 5 不同活化能的数值爆轰胞格结构 Fig.5 Numerical detonation cell structures for different activation energies |
对于规则胞格(Ea = 15),采用两种不同的统计方法对胞格尺寸进行处理。首先,采用概率密度函数法对规则胞格进行处理。基于图4(a)绘制的三波点迹线,利用Sharpe提出的全局阈值法提取胞格迹线,即对涡量的数值设置一个阈值,本研究采用的阈值为27,小于该阈值的涡量舍去,仅保留高于该阈值的涡量,得到图6所示的胞格迹线,此时的胞格较规则,三波点的迹线没有出现相交的情形。对相邻的胞格迹线间的距离进行概率统计,绘制概率曲线,如图7所示,此时,最大概率值所对应的迹线的距离约为28,该值即为胞格的尺寸。
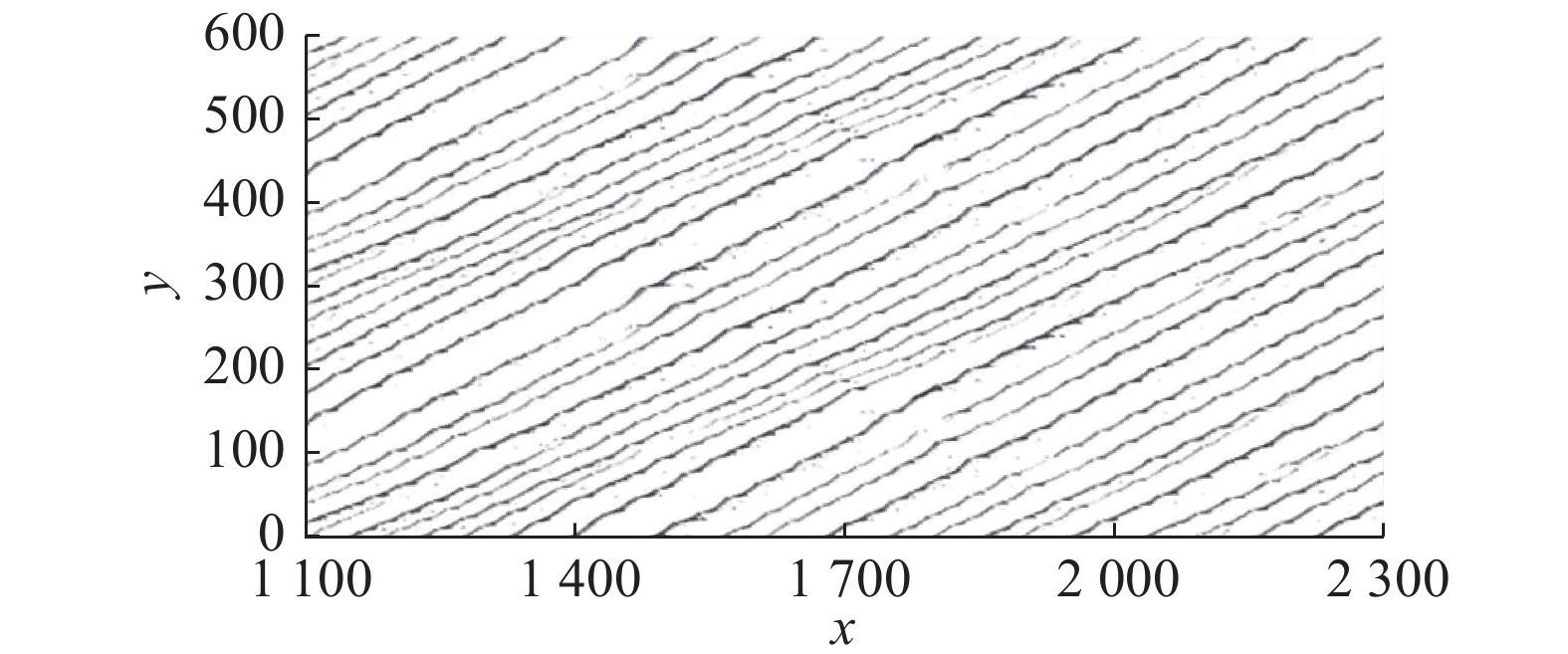
|
图 6 活化能Ea= 15时,根据全局阈值法提取的三波点的轨迹 Fig.6 Extracted triple-point tracks based on the globalthreshold method for Ea= 15 |
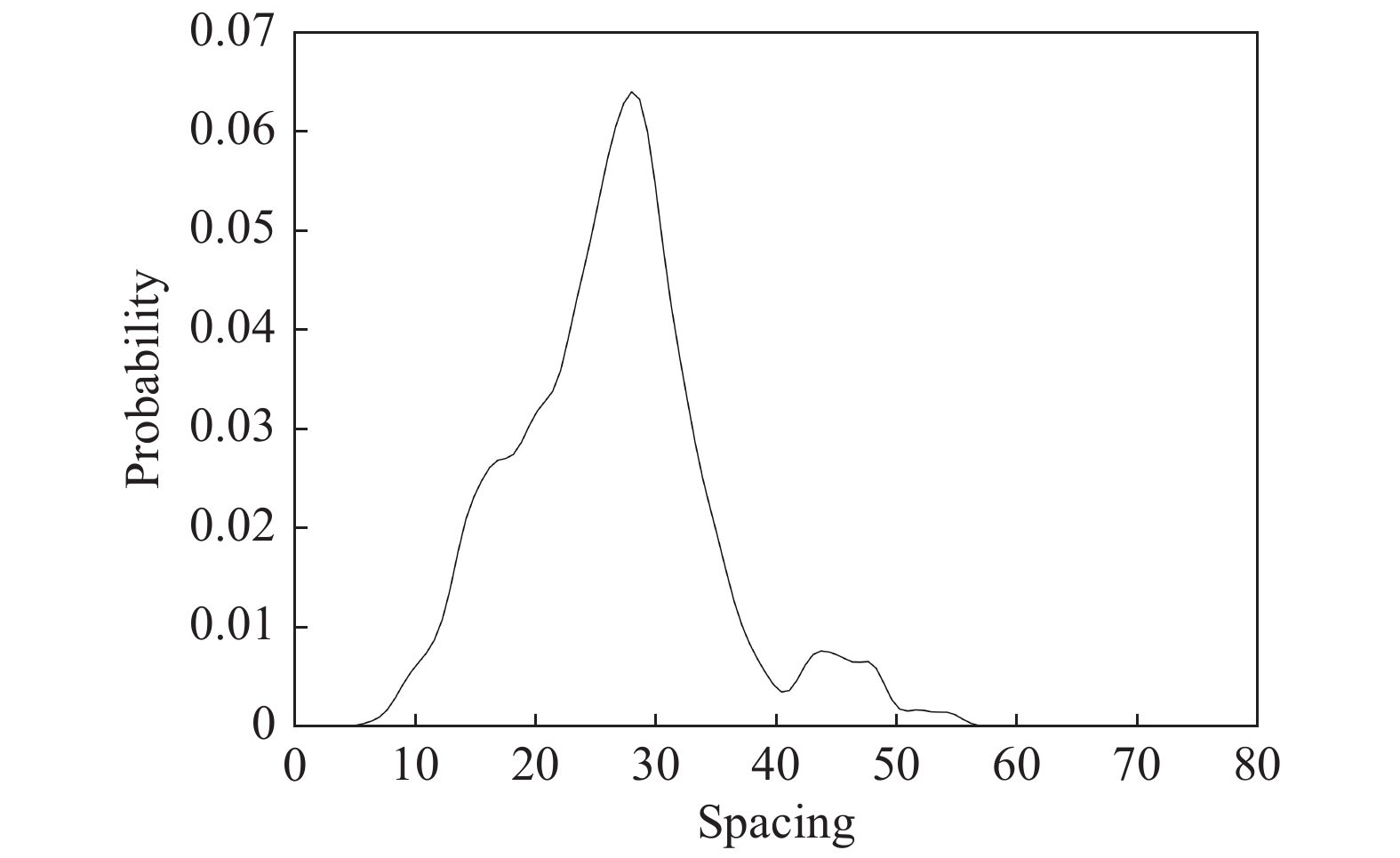
|
图 7 活化能Ea = 15时,三波点轨迹间距离的概率分布 Fig.7 Probability density function of thespacing between triple-point tracks for Ea= 15 |
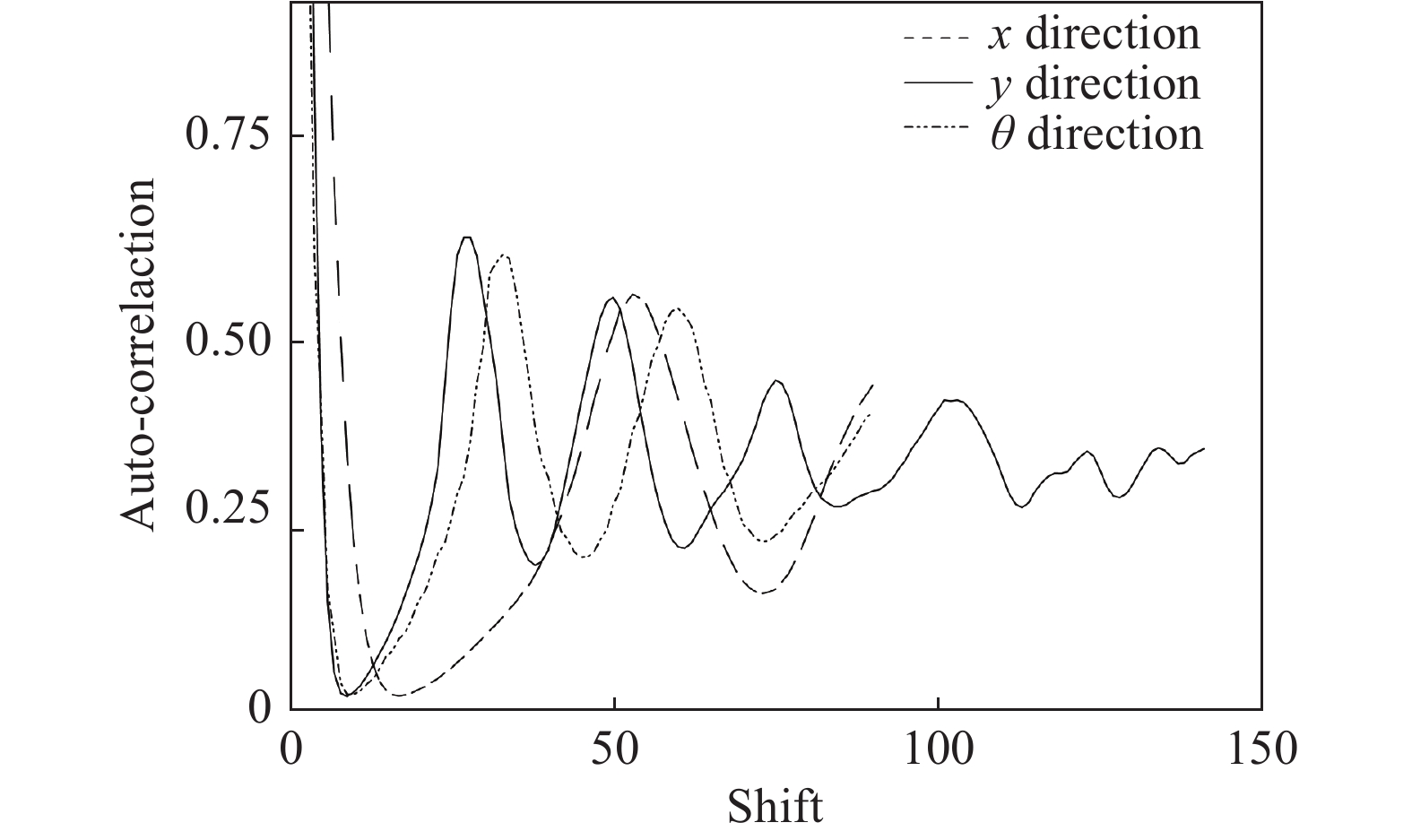
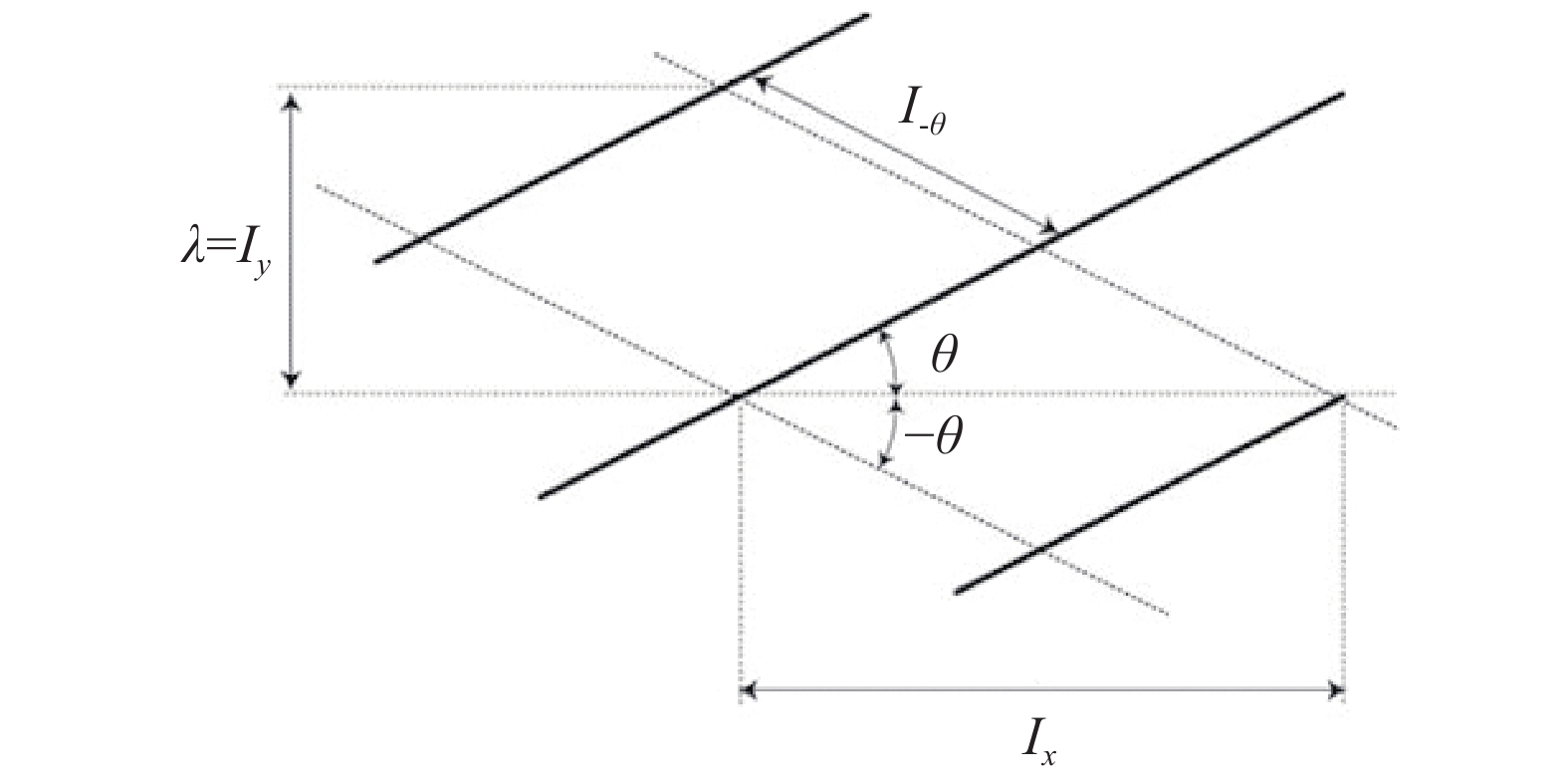
采用自相关函数法对规则胞格(Ea = 15)进行统计处理,图8代表自相关函数在不同偏移方向的变化,其中x方向表示爆轰波传播的方向,y方向表示爆轰波结构中横波的传播方向,θ方向是三波点迹线的方向。根据爆轰胞格特征尺度的定义,胞格横向的尺寸λ为爆轰胞格的尺寸(图9)。因此,自相关函数在y方向的变化体现了爆轰胞格的尺寸。根据图8所示,自相关函数在三个方向均呈现周期性的变化,且其峰值逐渐降低,在y方向出现的第一个峰值,也是最大值,其对应的偏移量为爆轰胞格的尺寸,该值约为29,与概率密度函数法得到的胞格尺寸接近。
|
图 8 活化能为15时,自相关函数在不同偏移方向的变化 Fig.8 Autocorrelation functions along differentshift directions for Ea= 15 |
|
图 9 爆轰胞格的尺寸示意图 Fig.9 Schematic diagram of the detonation cell size |
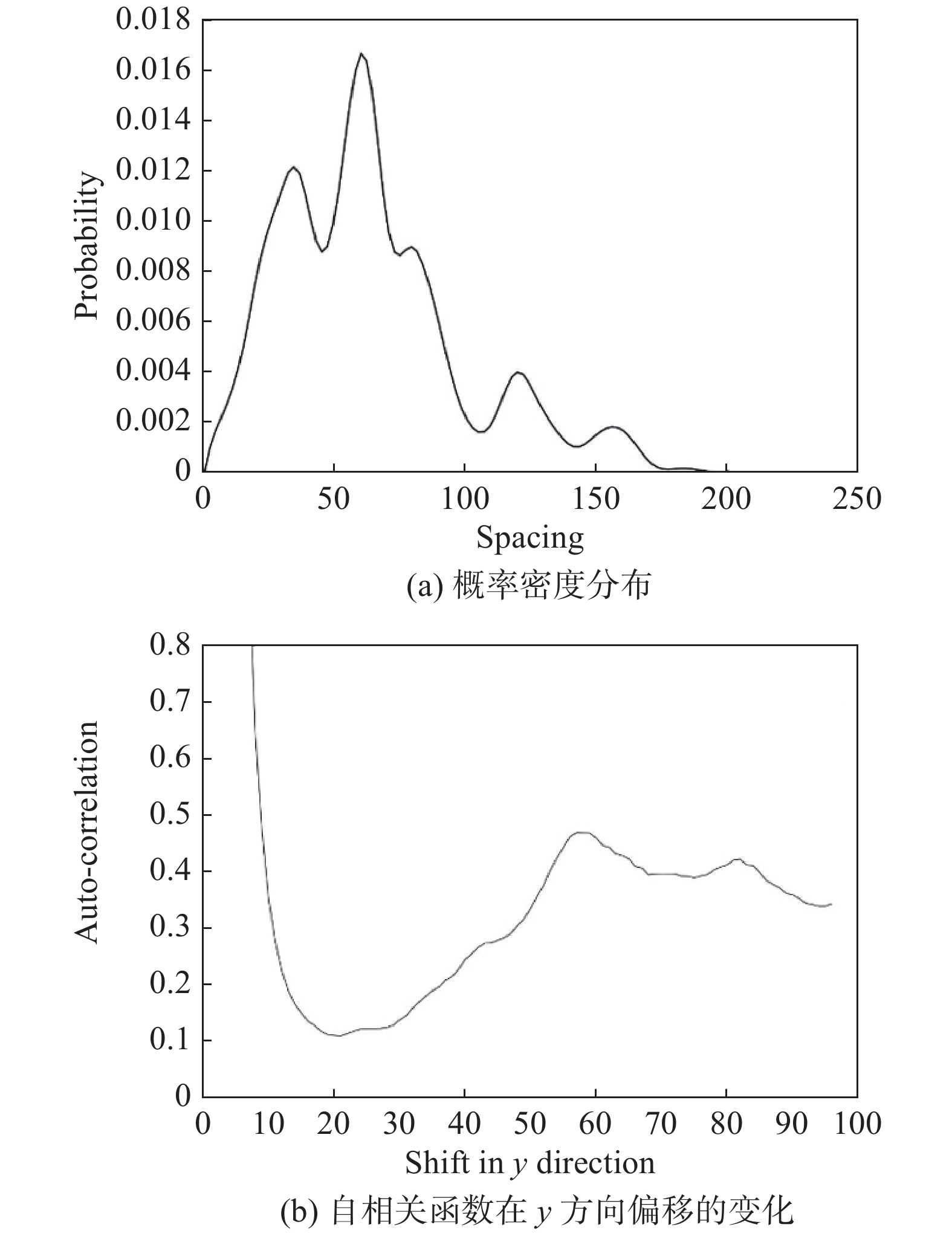
当活化能Ea = 20时,对数值胞格分别采用概率密度函数法和自相关函数法统计方法得到的变化曲线见图10所示。图10(a)是概率密度分布曲线,其最大峰值明显小于活化能Ea = 15时概率密度分布的最大峰值,这是因为爆轰胞格的不规则程度增加,胞格尺寸的取值范围增加,胞格的特征尺寸在所有胞格尺寸中占的比例有所下降,此时,胞格的特征尺寸约为60。图10(b)是自相关函数在y方向偏移的变化曲线,随着不规则程度的增加,自相关函数的周期性减弱,其峰值对应的爆轰胞格的特征尺寸为64。此时,两种统计方法得到的胞格尺寸基本一致。
|
图 10 活化能Ea = 20时爆轰胞格尺寸的统计分析 Fig.10 Statistical analysis of the detonation cell size for Ea= 20 |
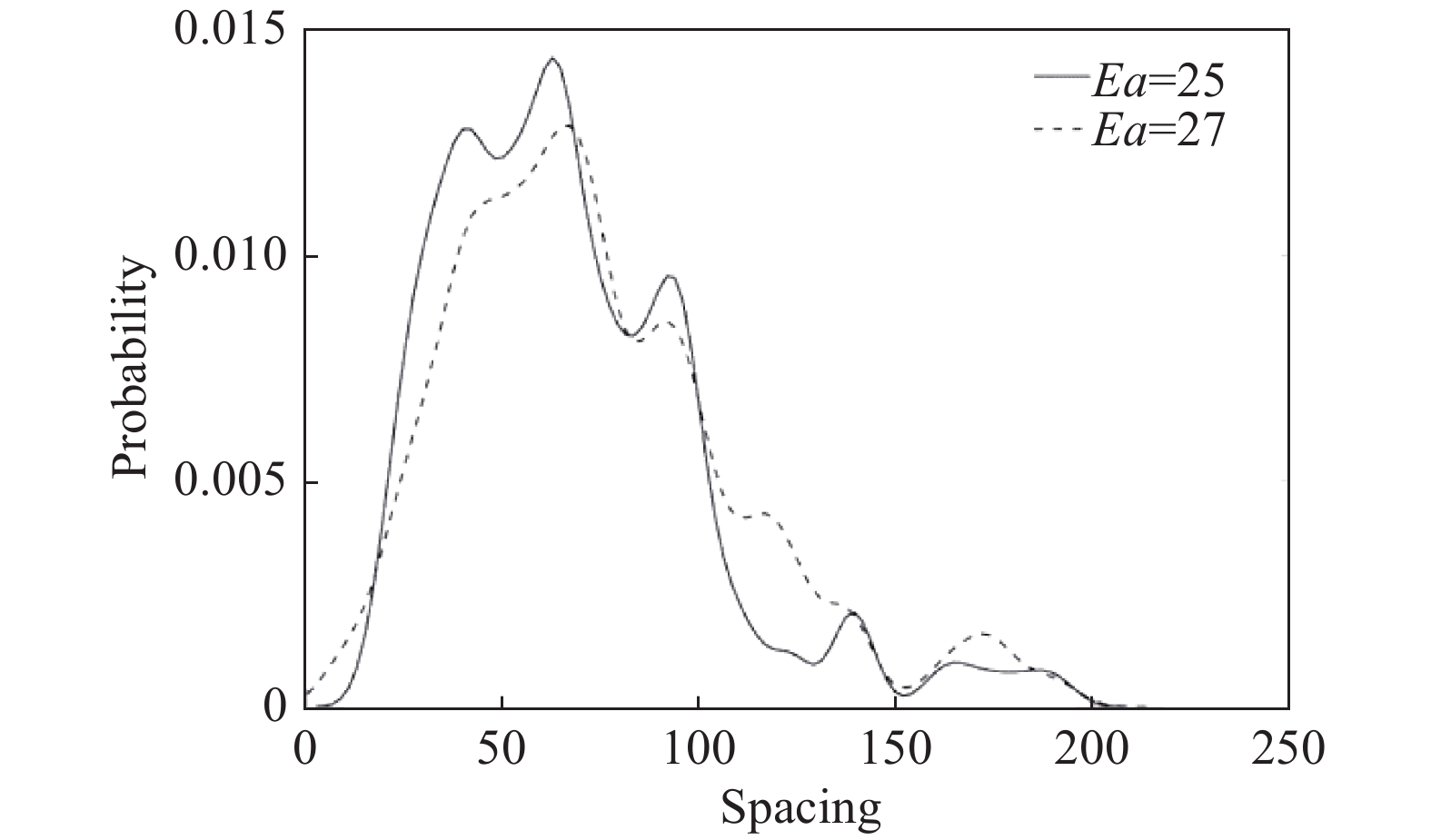
随着活化能的进一步增加,当活化能Ea = 25、27时,三波点的迹线开始出现合并,爆轰胞格非常不规则。图11为活化能为25和27时的概率密度分布曲线,两者的分布基本一致,分布范围和峰值出现位置基本相同。其中活化能为25时的胞格尺寸为62,活化能为27时胞格尺寸为67。
|
图 11 活化能Ea = 25、27时爆轰胞格尺寸的概率密度分布 Fig.11 Probability density functions of the detonationcell size for Ea= 25, 27 |
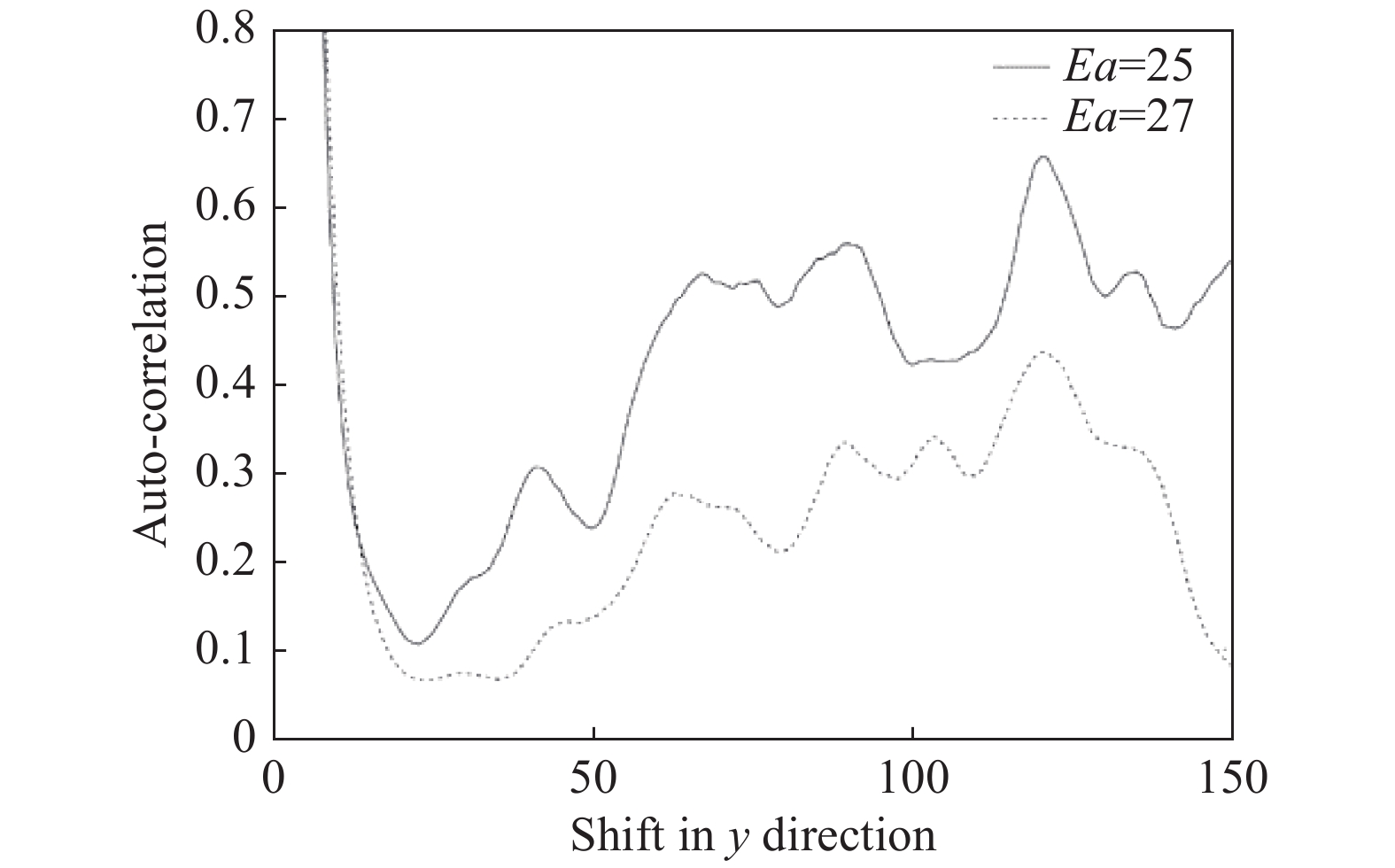
图12是活化能为25和27时的自相关函数在y方向的变化曲线。图中第一个峰值分别发生在胞格尺寸为43(Ea= 25)和63(Ea= 27)的位置。值得注意的是,与规则胞格不同,这两种不规则程度较高的胞格的自相关函数的第一个峰值不再是自相关性最高的值。在第一个峰值后,会再次出现峰值更高的自相关函数值,其值分别为121(Ea= 25)和120(Ea= 27),约为第一个峰值出现位置的两倍。根据自相关函数法对胞格尺寸的取值,自相关性最大的位置是胞格尺寸,因此,自相关法得到的胞格尺寸应是121(Ea= 25)和120(Ea= 27),其值约为概率密度法得到的尺寸的两倍。该现象与Shepherd[6]的研究工作是一致的。之所以出现这样大的偏差,这和两种统计方法的特性有关。
|
图 12 活化能Ea = 25、27时爆轰胞格尺寸的自相关函数 Fig.12 Autocorrelation functions of the detonation cellsize for Ea= 25, 27 |
概率密度法统计迹线间距时,忽略了迹线上能量的数值,也就是将迹线的能量以相同的权重进行统计,因此其峰值所对应的胞格尺寸是表观上看到的胞格的最大概率尺寸。而自相关法在统计涡量信号时,迹线上的涡量大小信息作为自相关函数的参数加入计算,涡量大的迹线权重大。因此得到的自相关峰值是考虑了迹线涡量的大小的峰值。
在不规则的爆轰胞格中,出现了横波的合并,使得三波点的涡量发生急剧变化,这种现象也体现在自相关函数值的变化上。而概率密度法仅能反映此时胞格大小出现的概率,无法体现这种横波合并引发的物理现象。因此,两种统计方法预测的胞格尺寸出现较大的偏差,而在规则胞格中,没有横波合并这种现象,故两种统计方法预测的胞格尺寸基本吻合。
3 结 论本文通过数值研究了不同活化能(Ea= 15、20、25、27)时的爆轰胞格,随着活化能的增加,胞格的不规则程度明显变大。同时,采用概率密度函数法和自相关函数法这两种统计方法对数值模拟得到的胞格尺寸进行统计处理。当活化能为15、20时,这两种统计方法得到的胞格尺寸较吻合。当活化能增加到25和27时,数值胞格出现横波合并现象,自相关函数法得到的胞格尺寸大约是概率密度函数得到的胞格尺寸的两倍。这是由于概率密度法没有考虑三波点迹线上的物理量分布,仅是一种表观上观测到的胞格尺寸出现的最大概率,而自相关函数法考虑了迹线上的涡量分布,进而能反映横波合并这种物理现象,因此,自相关函数法比传统的概率密度函数法更能体现爆轰胞格尺寸这种爆轰的本征值。
| [1] |
FICKETT W, DAVIS W C. Detonation[M]. Berkeley: University of California Press, 1979.
|
| [2] |
LEE J H S. The Detonation Phenomenon[M]. Cambridge: Cambridge University Press, 2008.
|
| [3] |
ZHAO H, LEE J H S, LEE J, et al. Quantitative comparison of cellular patterns of stable and unstable mixtures[J]. Shock Waves, 2016, 26(5): 621-633. DOI:10.1007/s00193-016-0673-9 |
| [4] |
XU H, MI X C, CHARLES B K, et al. The role of cellular instability on the critical tube diameter problem for unstable gaseous detonations[J]. Proceedings of the Combustion Institute, 2019, 37(3): 3545-3553. DOI:10.1016/j.proci.2018.05.133 |
| [5] |
与爆轰有关的湍流燃烧[J]. 空气动力学学报, 2020, 38(3): 515-531. GUI M Y, ZHANG L Y, CUI H, ZHANG H. Turbulent combustion related with detonaion[J]. Acta Aerodynamica Sinica, 2020, 38(3): 515-531. DOI:10.7638/kqdlxxb-2020.0066 (in Chinese) |
| [6] |
SHARPE G J, RADULESCU M I. Statistical analysis of cellular detonation dynamics from numerical simulations: one-step chemistry[J]. Combustion Theory and Modelling, 2011, 15(5): 691-723. DOI:10.1080/13647830.2011.558594 |
| [7] |
SHEPHERd J E, TIESZEN S R. Detonation cellular structure and image processing[R]. Albuquerque NM (USA): Sandia National Laboratories, 1986.
|
| [8] |
SHEPHERD J E, MOEN I O, MURRAY S B, et al. Analyses of the cellular structure of detonations[J]. Symposium (International) on Combustion, 1988, 21(1): 1649-1658. DOI:10.1016/s0082-0784(88)80398-9 |
| [9] |
LEE J J, GARINIS D, FROST D L, et al. Two-dimensional autocorrelation function analysis of smoked foil patterns[J]. Shock Waves, 1995, 5(3): 169-174. DOI:10.1007/bf01435524 |
| [10] |
HÉBRAL J P, SHEPHERD J E. User guide for detonation cell size measurement using Photoshop and Matlab[R]. Explosion Dynamics Laboratory Report FM00-6, 2000.
|
| [11] |
JIANG G S, SHU C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228. DOI:10.1006/jcph.1996.0130 |
| [12] |
SHU C W, OSHER S. Efficient implementation of essentially non-oscillatory shock-capturing schemes[J]. Journal of Computational Physics, 1988, 77(2): 439-471. DOI:10.1016/0021-9991(88)90177-5 |
| [13] |
PAN Z H, FAN B C, ZHANG X D, et al. Wavelet pattern and self-sustained mechanism of gaseous detonation rotating in a coaxial cylinder[J]. Combustion and Flame, 2011, 158(11): 2220-2228. DOI:10.1016/j.combustflame.2011.03.016 |
| [14] |
GUI M Y, FAN B C. Wavelet structure of wedge-induced oblique detonation waves[J]. Combustion Science and Technology, 2012, 184(10-11): 1456-1470. DOI:10.1080/00102202.2012.693414 |
| [15] |
GUI M Y, FAN B C, LI B M. Detonation diffraction in combustible high-speed flows[J]. Shock Waves, 2016, 26(2): 169-180. DOI:10.1007/s00193-015-0602-3 |
| [16] |
QUIRK J J. Godunov-type schemes applied to detonation flows[M]//ICASE/LaRC Interdisciplinary Series in Science and Engineering. Dordrecht: Springer Netherlands, 1994: 575-596. doi: 10.1007/978-94-011-1050-1_21
|
| [17] |
SHARPE G J, QUIRK J J. Nonlinear cellular dynamics of the idealized detonation model: Regular cells[J]. Combustion Theory and Modelling, 2008, 12(1): 1-21. DOI:10.1080/13647830701335749 |
 2021, Vol. 39
2021, Vol. 39


