0 引　言

随着空基大挂载需求的牵引，以双体飞机挂载大质量任务载荷的方式逐渐被多国重点关注。相比其他投射方式，以双体飞机为载机进行大质量空基投射具有生存能力强、威慑能力大和动能利用率高等明显优势^[1-2]。在民用航天领域，双体飞机也为卫星快速发射、卫星发射窗口延拓和发射成本降低提供了一种全新的途径。其中以美国的Stratolaunch、英国的Virgin与法国的ATLAIR最为典型^[3]。

国防科技大学Zhang^[4]等对基于双体飞机微纳卫星发射任务进行了概念设计，并对发射任务进行了多学科优化。意大利都灵理工大学Chiesa提出^[5]：相比重新设计，利用现有飞机制造满足大载荷任务双体飞机会使任务成本极大降低。弗吉尼亚理工学院WANG^[6]等使用非定常涡格法对双体飞机中间翼流场特性进行了研究，并得到了与试验一致的结果。亚利桑那州大学Spiller^[7]构建了与美国Stratolaunch双体飞机相似的模型，对其纵向动力学特性进行研究，预测了多种飞行条件下的动力学行为。法国贝尔坦公司Cédric Dupont^[8]对ALTAIR项目的设计思路与研究进展进行了介绍，建立了挂载组合体简化梁模型，分别计算了定常与非定常飞行环境下的轴向载荷分布，采用模块设计的思路对整体结构质量进行了优化。

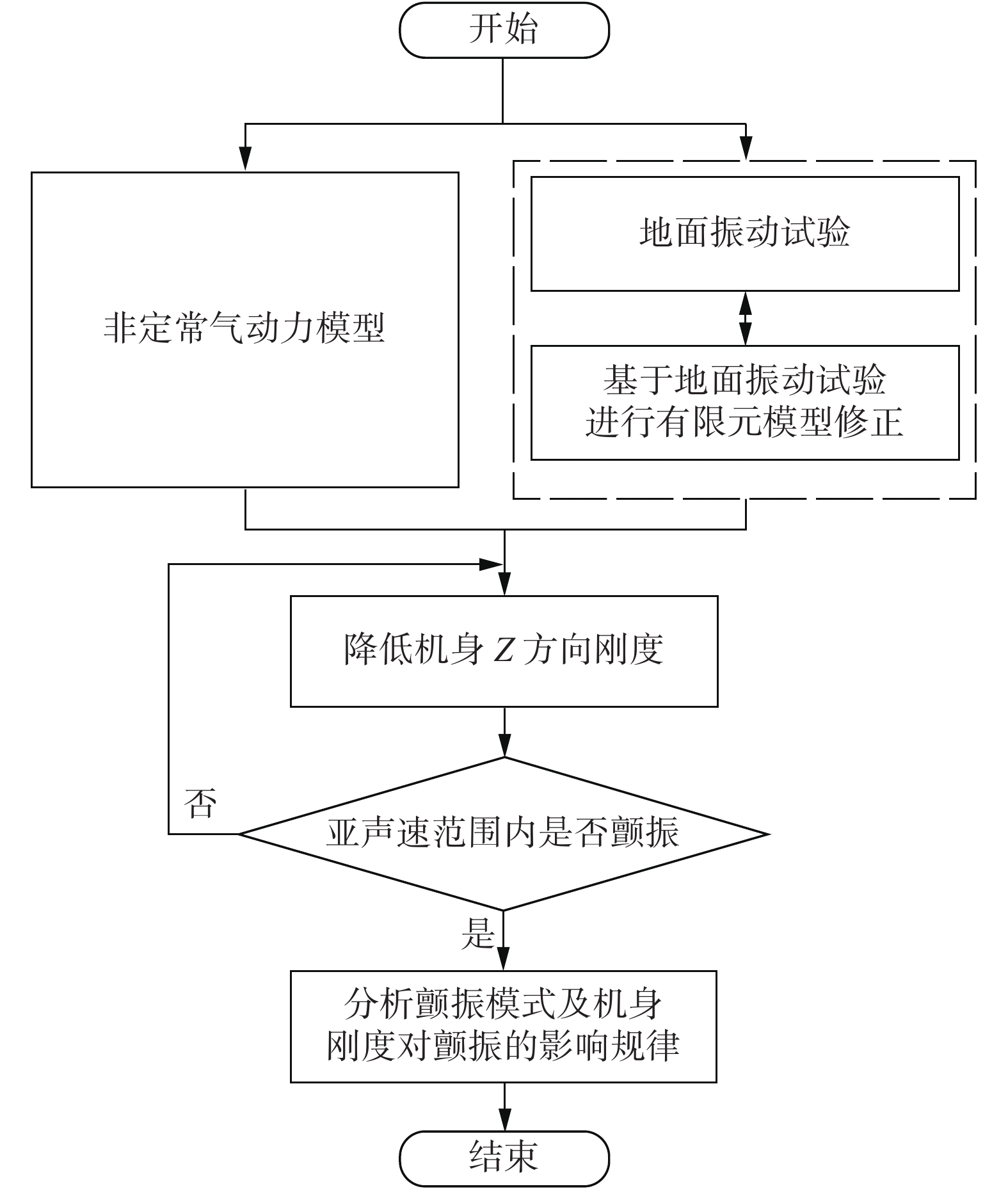
然而目前对于双体飞机的研究主要集中在：概念设计^[3-5]、气动性能分析^[6]与结构动力学分析方面^[7-8]。根据公开发表文献，还没有对双体飞机颤振特性的研究内容。针对双体飞机结构动力学特性复杂、气动干扰强烈，颤振模式复杂的问题，本文基于地面振动试验结果建立了变化刚度机身的双体飞机有限元简化模型，按照图1所示的逻辑对某双体飞机结构动力学特性和颤振模式开展研究，分析了机身刚度与机身布局对结构动力学和颤振特性的影响规律。

1 非定常气动力模型

基于线性化小扰动速度势方程的偶极子网格方法（Double-Lattice Method）^[9-10]是目前工程计算中应用最广泛的非定常气动力计算方法。但由于双体飞机所用的“T型”尾翼平尾与垂尾之间存在强烈的气动干扰，垂尾的运动会导致平尾产生较大的展向与弦向位移。Rodden^[11]与Jennings^[12]通过对某T型尾翼研究发现经典偶极子网格方法在未进行相关修正前无法满足非定常气动力计算精度要求。相关文献也表明，对于T尾这种尾部结构，常规计算方法得到的颤振边界与试验结果有一定偏差。

本文采用片条理论修正后的偶极子网格方法与考虑翼体干涉的偶极子网格方法对双体飞机非定常气动力进行计算^[13-14]：

$ \left[ \begin{array}{l} {Q_1} \\ {Q_2} \end{array} \right] = \left[ \begin{array}{l} {\;\;\;\;\;\;Q_{1}} \\ {Q_{20}} + \Delta {Q_2} \end{array} \right] $

(1)

式中： ${Q_1}$ 为双体飞机主机翼与机身非定常气动力部分； ${Q_2}$ 为双体飞机 $\Pi $ 型尾翼非定常气动力部分； ${Q_{20}}$ 为常规非定常气动力； $\Delta {Q_2}$ 为附加的 $\Pi $ 型尾翼特殊非定常气动力。

亚声速条件下，偶极子网格方法得到的常规非定常气动力可以表示为：

$ {Q_0} = \frac{1}{2}\rho {V^2}{{{A}}_0}{{q}} $

(2)

式中： ${Q_0}$ 为常规非定常气动力； $\rho $ 为来流密度； $V$ 为来流速度； ${{q}}$ 为广义位移列阵； ${{{A}}_0}$ 为广义气动力影响系数矩阵。

对于“ $\Pi $ 型”尾翼采用片条理论修正的非定常气动力部分，沿展向将平尾划分为一系列片条，忽略片条间弦向变形，对于任意片条，其所受非定常气动力可表示为：

$ L = \left[ {\begin{array}{*{20}{c}} {{F_x}} \\ {{F_y}} \\ {{F_z}} \\ {{M_x}} \\ {{M_y}} \\ {{M_z}} \end{array}} \right] =[{{B}}][d]= \left[ {\begin{array}{*{20}{c}} {{b_{11}}}& \cdots &{{b_{16}}} \\ \vdots & \ddots & \vdots \\ {{b_{61}}}& \cdots &{{b_{66}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\delta x} \\ {\delta y} \\ {\delta z} \\ \phi \\ \theta \\ \psi \end{array}} \right] $

(3)

式中： $L$ 为附加的特殊非定常气动力； ${{B }}$ 为片条气动力影响系数矩阵； $d$ 为运动自由度。

对于“ $\Pi $ 型”尾翼附加的特殊非定常气动力主要由片条的滚转运动、片条的弦向运动、片条的偏航运动和片条的侧向运动导致。在无阻尼小扰动谐振荡条件下，经过Theodorson修正后，可以得到“ $\Pi $ 型”尾翼附加非定常气动力影响系数矩阵：

$ {{B}} = \left[ {\begin{array}{*{20}{c}} {{b_{11}}}& \cdots &{{b_{16}}} \\ \vdots & \ddots & \vdots \\ {{b_{61}}}& \cdots &{{b_{66}}} \end{array}} \right] $

(4)

式（4）中元素有如下表示（未提及的其他元素为0）：

$ \begin{split} &{b_{24}} = {L_0} \\& {b_{31}} = - 2{L_0} \cdot \frac{{ik}}{b} \cdot C\left( k \right) \\& {b_{32}} = \frac{{ikC\left( k \right)}}{{{b_r}}} \cdot \left[ {\frac{{{L_0}\tan \varOmega }}{2} + \frac{{3q\left( {{c_1}{C_{L2}} - {c_2}{C_{L2}}} \right)}}{8}\left( {\frac{{{c_1} + {c_2}}}{2}} \right)} \right] \\& {b_{36}} = C\left( k \right) \cdot \left[ {\frac{{{L_0}\tan \varOmega }}{2} + \frac{{3q\left( {{c_1}{C_{L2}} - {c_2}{C_{L2}}} \right)}}{8}\left( {\frac{{{c_1} + {c_2}}}{2}} \right)} \right] \\& {b_{51}} = b\left( {0.5 + a} \right) \cdot {b_{31}} \\& {b_{52}} = b\left( {0.5 + a} \right) \cdot {b_{32}} \\& {b_{56}} = b\left( {0.5 + a} \right) \cdot {b_{36}} \\& {b_{64}} = b\left( {0.5 + a} \right) \cdot {b_{24}} \end{split} $

其中： ${L_0}$ 为偶极子网格方法计算得到的片条定常升力， $C\left( k \right)$ 为Theodorson函数， $k$ 为减缩频率； ${b_r}$ 为参考弦长，Ω为 ${1 / 4}$ 弦线处后掠角； $q$ 为来流动压， $c$ 为片条弦长， ${C_L}$ 为升力系数， $b$ 为片条当地弦长。

引入振动模态坐标后“ $\Pi $ 型”尾翼附加的特殊非定常气动力可以表达为：

$ \Delta Q = \frac{1}{2}\rho {V^2}\left( {\sum\limits_i {\varPhi _i^{\rm{T}}{{B}}{\varPhi _i}} } \right)q $

(5)

2 地面振动试验

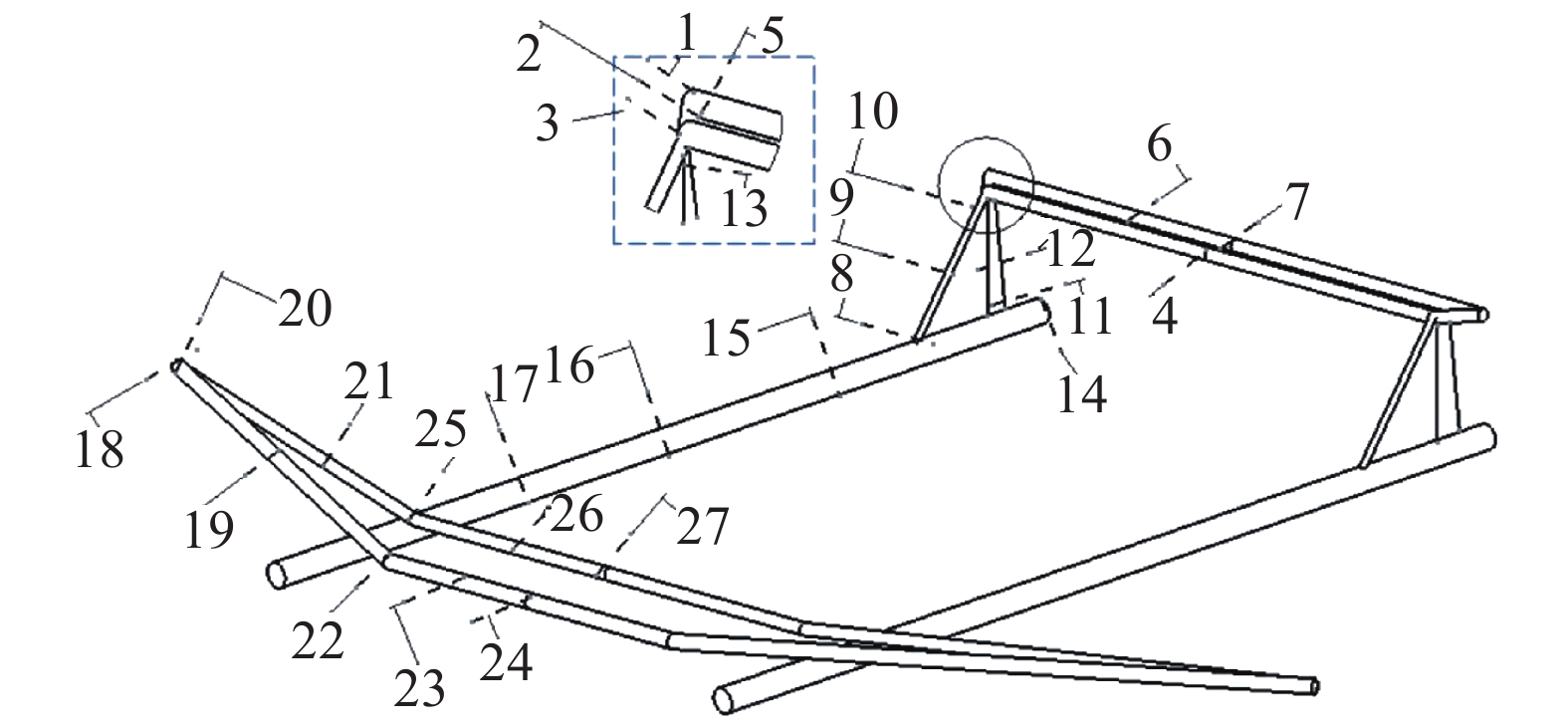
2018年12月在西安中国飞机强度研究所对本文研究的双体飞机验证样机进行地面振动试验（图2），采用不同截面刚度设计和集中质量的形式模拟双体飞机刚度/质量特性，建立了双体飞机等效梁（Equivalent Beam Model）模型^[15-16]（图3），并根据试验结果对模型进行修正，得到了双体飞机的典型模态频率与振型如表1所示。

试验结果表明：双体飞机在50 Hz以内具有多个典型模态，具有模态密集的特性；由于双体飞机特殊的结构布局，这些密集模态具有振型复杂的特点，且机身刚度与平尾与垂直的连接刚度对双体飞机结构动力学特性有较大影响。

3 数值计算 3.1 结构动力学影响规律探索

针对地面振动试验中发现的特点，调整有限元模型机身刚度及垂尾与平尾的连接刚度，进行数值计算。通过数值试验发现：机身垂向刚度对机身模态、平尾滚转模态影响较大，对主机翼弯曲模态基本无影响。具体变化规律如图4所示。

3.2 颤振计算

本文研究对象几何模型如图5所示。使用片条修正后的偶极子网格方法建立双体飞机“ $\Pi $ 型”尾翼非定常气动力模型^[17]，使用偶极子网格方法建立其余部分非定常气动力模型，图6为网格示意图。

使用样条插值方法实现非定常气动力模型与结构动力学耦合。使用P-K方法求解频域颤振方程，得到双体飞机“速度-阻尼”曲线与“速度-频率”曲线。

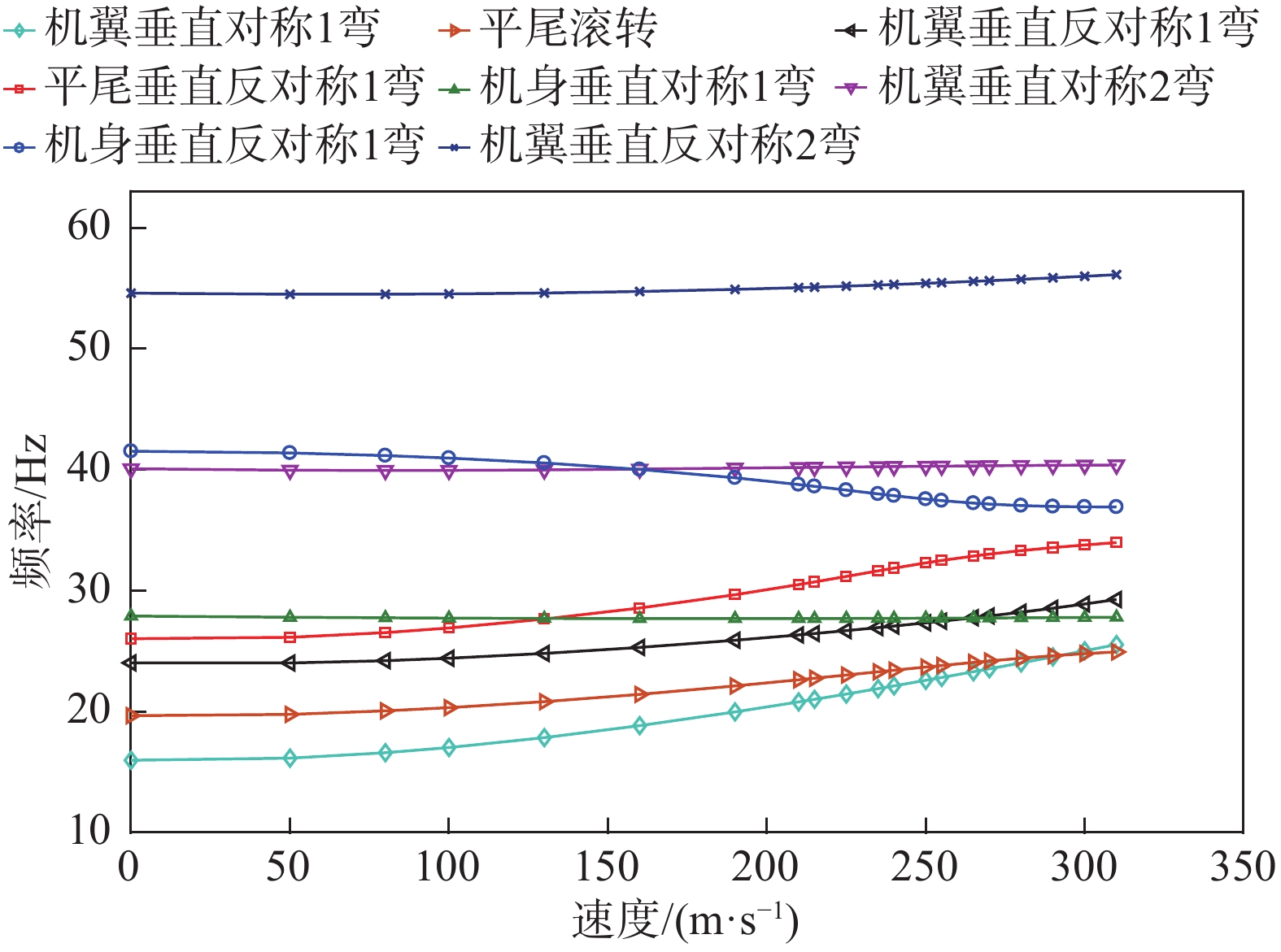
通过计算发现：随着双体飞机机身截面垂向刚度降低，机身垂直反对称一阶弯曲模态对平尾扭转效应增强^[15]，当机身截面垂向刚度降低到原设计刚度67%时，双体飞机平尾处发生颤振。此时双体飞机“速度-阻尼”曲线与“速度-频率”曲线如图7、图8所示。

由图7发现，机身截面垂向刚度降低到原设计刚度67%时，双体飞机机身垂直反对称一阶弯曲阻尼曲线在269.34 m/s时通过零点，在图8中，机翼垂直对称一阶弯曲模态、平尾滚转模态、平尾垂直反对称一阶弯曲模态、机翼垂直反对称一阶弯曲模态和机身垂直反对称一阶弯曲模态频率曲线相靠近，对应颤振频率为37.2 Hz。

通过模态剔除试验，发现其中平尾滚转、平尾垂直反对称一阶弯曲和机身垂直反对称一阶弯曲模态为颤振发生的必要模态，模态振型如图9所示。

仅保留颤振发生的必要模态与非定常气动力模型进行耦合计算，得到当机身截面垂向刚度降低到原设计刚度67%时双体飞机“速度-阻尼”曲线与“速度-频率”曲线如图10与图11所示。仅保留必要模态的数值试验得到的颤振速度260.55 m/s、颤振频率37.5 Hz与全模态颤振试验结果误差满足要求。仅保留必要模态的数值试验清晰反映了弱刚度机身双体飞机颤振模式是机身垂直反对称一阶弯曲导致的平尾扭转与平尾自身弯曲耦合。

4 结　论

本文采用地面振动试验修正后的等效梁模型建立双体飞机简化模型，通过有限元方法研究了机身刚度对双体飞机结构动力学影响规律。通过与片条修正偶极子网格方法建立的非定常气动力模型模型，研究了机身刚度对双体飞机这一特殊构型飞行器颤振的影响规律，得到以下结论：

1） 通过地面振动试验发现双体飞机具有模态密集、振型复杂的特点，在50 Hz以内具有多个模态，模态振型复杂；

2） 机身垂向刚度对机翼模态频率基本无影响，对机身模态频率影响较大，对平尾滚转模态频率有一定影响。机身垂向刚度降低为原刚度67%时，机身一阶垂直对称弯曲模态频率降低26.7%，机身一阶垂直反对称弯曲模态频率降低18.8%，平尾滚转模态频率降低4.63%；

3） 当机身垂向刚度降低为原刚度67%时，机身垂直反对称一阶弯曲模态对平尾扭转效应增强，导致双体飞机平尾发生颤振，颤振速度为269 m/s，颤振频率为37.2 Hz，颤振模式是由机身一阶反对称弯曲模态、平尾滚转模态和平尾垂直反对称一阶弯曲模态耦合。