在计算流体力学领域中,数值模拟是解决科研问题和实现工程应用的重要工具。然而,进行复杂系统的高精度数值模拟需要耗费大量的计算资源和时间。为了解决这一问题,Dowell[1]、Silva[2]等提出了基于数值模拟构造降阶模型(Reduced Order Model, ROM)的思路,能够在保证计算精度的同时,有效地节省计算成本。自提出以来,降阶模型的相关研究已经取得了一定的进展[3]。近年来,深度学习技术在基因学[4]、图像分类[5]、疾病诊断[6]等许多领域得到了广泛应用。随着相关技术的不断发展,深度学习也开始在流体力学领域中崭露头角[7-9]。深度学习能从数据中学习到相应的隐藏信息和特征,使其在学习非线性系统的多级表征和数据预测方面有着强大的优势。结合深度学习构建降阶模型也逐渐成为一个新的研究热点。
在现有的结合深度学习的降阶模型中,深度学习主要被应用于未来时刻流场的预测,即输入过去的一个或多个时刻的流场数据,输出未来时刻的流场。考虑到流场中离散点的数量,为了使数据便于处理并降低神经网络的复杂度,通常会先采用主成分分析(Principle Component Analysis, PCA)/本征正交分解(Proper Orthogonal Decomposition, POD)对数据进行降维。Wang[10]等在燃烧器的模型降阶中成功应用了前馈神经网络对POD基系数进行回归建模。在神经网络中,循环神经网络(Recurrent Neural Network, RNN)和长短期记忆(Long Short-Term Memory, LSTM)网络[11]在处理时间序列问题上有着独特的优势,也因此在模型降阶中备受青睐。Mannarino和Mantegazze[12]基于RNN,构建了连续时间的非定常非线性气动力降阶模型;Wang[13]等提出了一种基于PCA和LSTM的降阶模型,用于非定常流场控制方程的降阶;Mohan[14]等研究了LSTM和双向LSTM[15]在降阶模型中的应用,过拟合使双向LSTM的表现不及预期。Kani[16]等使用深度残差循环神经网络,与PCA相结合提出了一种非线性动力系统的模型降阶方法。Lindhorst等[17]组合了POD方法与递归RBF神经网络模型,在低维空间中建立了动态的非线性系统辨识模型。Yao和Marques[18]结合POD、离散经验插值和径向基函数(Radical Basis Function, RBF)神经网络,构建了针对气动弹性问题的非线性ROM。随着研究的不断深入,神经网络的拟合能力、泛化能力也为降阶模型的研究带来了新的课题。尹明朗[19]等在递归径向基函数(Recursive Radial Basis Function, RRBF)神经网络气动力模型中引入差分进化算法用于调整隐藏层中神经元的宽度,发展了一种具有高泛化能力的神经网络气动力降阶模型;Kou[20]等提出了多核神经网络并将其应用于降阶模型的构建,与基于单核RBF神经网络的降阶模型相比,基于多核神经网络的降阶模型在模型精度、泛化能力、抗噪能力上都得到了提升。
本文将多层自编码器和LSTM应用于降阶模型的构建,并与基于PCA的降阶模型进行了对比。实验表明使用多层自编码器和LSTM构建的降阶模型有着更高的精度,且通过微调,降阶模型的精度得到了进一步提升。深度学习可以优化和改进模型降阶方法,使降阶模型的精度更高。
1 模型降阶方法本文提出的模型降阶方法使用多层自编码器对数据进行降维和特征提取,应用LSTM构建预测模型,并通过微调改进模型性能。
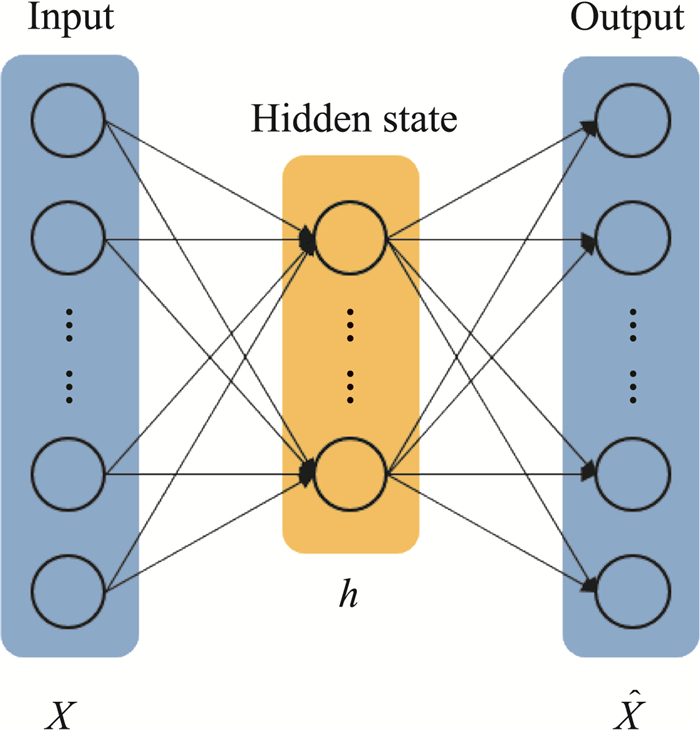
1.1 自编码器自编码器[21]是一种以最大程度还原原始输入数据为目标的神经网络。它能够从输入数据中学习到数据特征,并根据学习到的特征重构出原始数据。自编码器含有一个隐变量层h,将自编码器分为两部分:从输入层到隐变量层的部分被称为编码器、从隐变量层到输出层的部分是解码器。单层自编码器的结构如图 1所示。对于输入数据x,编码器可以由h
=f(x) 表示,解码器可以由
| $ Loss = \frac{{\sum\limits_{i = 1}^N {{{({x_i} - {{\hat x}_i})}^2}} }}{N} $ | (1) |
|
图 1 自编码器 Fig.1 Sketch of an autoencoder |
式中,N表示x的维度,下标i表示向量的第i个分量。
为了保证隐变量h中信息的有效性,在构建自编码器时,通常限制隐变量h的维度小于输入数据x的维度。这使得自编码器能够完成数据压缩的任务。自编码器作为深度学习中提取特征的一种有效手段,已经被证明可以应用于流场特征的提取[22]。
1.2 长短期记忆网络LSTM是RNN的变体,能够改善长期依赖和梯度消失/爆炸等问题。LSTM的内部结构中引入了三个门控单元:输入门、输出门和遗忘门,和记忆细胞ct。LSTM的门控单元采用了公式(2)所示的sigmoid激活函数,使得输出值在0~1之间,从而实现对信息的保留或丢弃,0表示完全丢弃信息,1表示完全保留。
| $ \sigma (z) = \frac{1}{{1 + {{\rm{e}}^{ - z}}}} $ | (2) |
式(2)中,z是激活函数的输入变量。三个门控单元中,遗忘门控制从前面的记忆中丢弃/继承多少信息;输入门决定了当前时刻的输入信息有多少被加入到记忆信息流中;输出门决定了当前时刻的记忆细胞中传输给隐藏状态的信息量。每个门都由上一时刻的隐藏状态mt-1、细胞状态ct-1和当前时刻的输入xt的线性组合及sigmoid函数构成。
利用三个门控单元更新当前时刻的隐藏状态和记忆细胞,LSTM中当前时刻的细胞状态和隐藏状态的计算过程如公式(3)~(7)。公式(3)~(5)分别是遗忘门、输入门和输出门的计算公式,公式(6)为细胞状态的计算公式,公式(7)计算当前时刻的隐藏状态。
| $ {{f^t} = \sigma \left( {{W_{fx}}{x^t} + {W_{fm}}{m^{t - 1}} + {W_{fc}}{c^{t - 1}} + {b_r}} \right)} $ | (3) |
| $ {{i^t} = \sigma \left( {{W_{ix}}{x^t} + {W_{im}}{m^{t - 1}} + {W_{ic}}{c^{t - 1}} + {b_i}} \right)} $ | (4) |
| $ {{o^t} = \sigma \left( {{W_{ox}}{x^t} + {W_{om}}{m^{t - 1}} + {W_{oc}}{c^{t - 1}} + {b_o}} \right)} $ | (5) |
| $ {{c^t} = {f^t}{c^{t - 1}} + {i^t}\tanh \left( {{W_{cx}}{x^t} + {W_{cm}}{m^{t - 1}} + {b_c}} \right)} $ | (6) |
| $ {{m^t} = {o^t}\tanh \left( {{c^t}} \right)} $ | (7) |
其中i、f、o、c、m分别表示输入门、遗忘门、输出门和细胞状态以及隐藏状态;W、b分别表示对应的权重系数矩阵和偏置;σ和tanh分别为sigmoid函数和公式(8)中的tanh函数:
| $ \tanh (z) = \frac{{{{\rm{e}}^z} - {{\rm{e}}^{ - z}}}}{{{{\rm{e}}^z} + {{\rm{e}}^{ - z}}}} $ | (8) |
其中,z表示函数的输入变量。
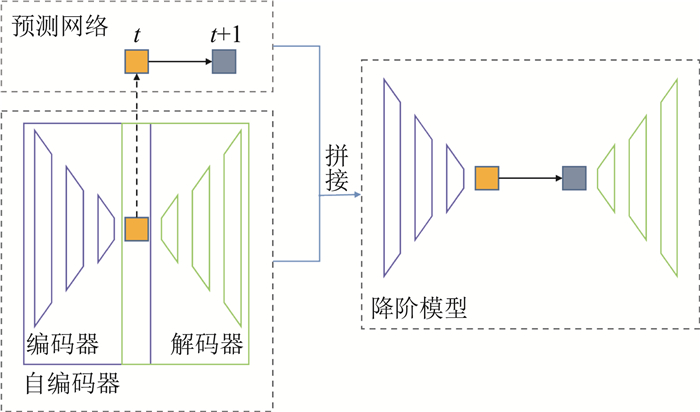
1.3 微调当模型参数采用随机初始化时,深层网络的训练很难进行,Hinton等[23]提出了逐层贪婪预训练,其主要思想是逐层地训练网络,将逐层训练好的网络参数作为整体网络参数的初始化,最后再对整体的网络进行微调。在本文中,我们将完整的降阶模型拆分成两个网络,多层自编码器和预测网络。先分别对两个网络进行训练,再将训练好的网络拼接在一起,构成降阶模型。对拼接后的网络进行微调,也就是对该网络再进行训练,得到最终的降阶模型。网络拼接的过程如图 2所示。
|
图 2 网络拼接 Fig.2 A sketch of the network stitching |
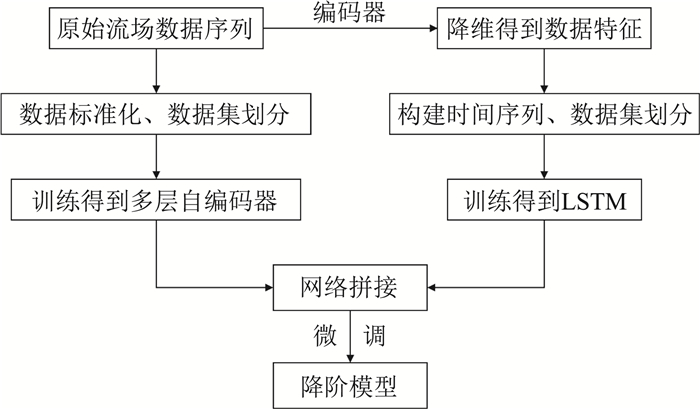
本文先分别训练多层自编码器和预测网络,将训练好的多层自编码器和LSTM拼接后,进行微调获得最终的降阶模型,降阶模型的构建流程如图 3。
|
图 3 降阶模型构建流程 Fig.3 A flow chart of the reduced order model construction |
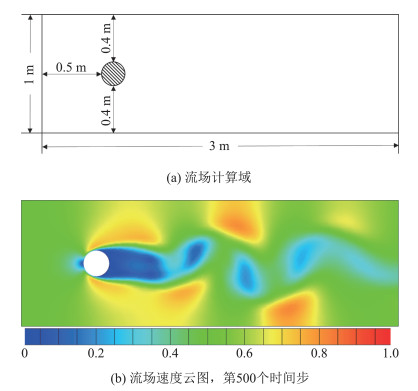
本文选取二维圆柱绕流算例,使用Fluent软件进行数值模拟以获取实验数据,构建降阶模型。流场的计算域如图 4(a)所示。流体的入场速度为v=0.5 m/s,流体的密度为1 kg/m3,雷诺数为150。流场计算域内的网格数量为6140。计算时间步长为2×10-2 s。第500个时间步时,流场的状态如图 4(b)所示。
|
图 4 二维圆柱绕流算例 Fig.4 The numerical simulation of flow past a cylinder |
特征提取方法应能从数据中提取有效的特征。在特征提取阶段,我们对三种降维方法的效果进行了比较和分析:单层自编码器(SAE, Single-layer AutoEncoder),多层自编码器(MAE, Multi-layer AutoEncoder)以及PCA。为了比较这三种方法在实际使用中的效果,我们设定了五个特征维度,ndim=8、16、32、48、64,并使用公式(9)均方根误差(Root Mean Square Error, RMSE)评估三种方法的数据降维和重构效果。
| $ {\rm{RMSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^N {{{({x_i} - {{\hat x}_i})}^2}} }}{N}} $ | (9) |
式中,N表示x的维度,下标i表示向量的第i个分量。
2.1.1 应用自编码器进行特征提取选择1000个时间步长的流场数据构造数据集,并将数据随机打乱,使其不再按时间顺序排列。按顺序依次将数据集划分为训练数据集、验证数据集和测试数据集,三个数据集的比例为6∶2∶2。此外,为了提升模型精度和收敛速度,我们在训练网络前对流场数据进行了标准化处理,将每个时刻的流场数据都缩放至[-1, 1]的范围中,标准化公式如下:
| $ {x^*} = \frac{{x - {x_{{\rm{mean}}}}}}{{{x_{{\rm{max}}}} - {x_{{\rm{min}}}}}} $ | (10) |
其中,xmean表示不同时刻流场数据的均值,xmax表示不同时刻流场数据中的最大值,xmin表示不同时刻流场数据中的最小值。
激活函数为神经网络引入了非线性,提高了模型的表达能力。在实验中,我们使用了两种激活函数,tanh函数和Relu函数,Relu函数见公式(11):
| $ {\rm{Relu}}(z) = {\rm{max}}\{ 0,z\} $ | (11) |
训练神经网络时,我们使用输入和输出之间的均方误差作为神经网络的损失函数;批大小为16,即每一次训练从训练集中取16个样本进行训练;训练150个时期,一个时期指对训练集所有数据进行一次前向和反向传播;并使用Adam[24]优化器。单层自编码器和多层自编码器内部均由全连接层构成,网络结构、节点数和激活函数的设置分别见表 1和表 2。
| 表 1 单层自编码器结构 Table 1 The structure of a SAE |
|
|
| 表 2 多层自编码器结构 Table 2 The structure of a MAE |
|
|
PCA方法对数据的协方差矩阵进行特征值分解,将特征值按照从大到小顺序排列,选择对应的特征向量组成投影矩阵,对原始数据进行投影,得到数据降维的结果。随着选取的特征值及特征向量数量的增加,PCA方法的效果也会不断提升。
实验中,我们选取与2.1.1节中相同的数据集进行PCA降维实验,即600条数据被用于PCA中的投影矩阵的构建,200条数据被用于测试PCA的降维效果。
2.1.3 实验结果分析表 3、图 6和图 7展示了三种方法对流场数据进行数据重构的效果。表 3是三种方法在测试集上均方根误差的平均值。从数值上看,在特征维度较低时,多层自编码器的效果最好;在特征维度较大时,PCA的效果最好;而由于模型的表达能力有限,单层自编码器的数据重构效果最差。随着特征维度的不断增加,各方法的性能都得到了不同程度的改善,尤其是PCA方法,特征维度的大小对其性能起决定性作用。而多层自编码器的性能主要由神经网络的结构决定,受特征维度的影响小,因此在特征维度增大时也没有得到较大的性能提升。
| 表 3 降维方法的均方根误差 Table 3 RMSE of dimensionality reduction methods |
|
|
|
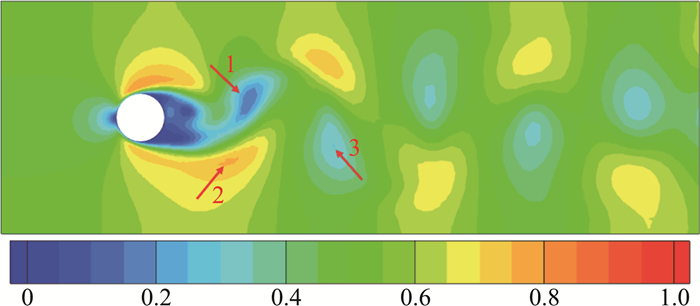
图 5 原始流场速度云图 Fig.5 Velocity of the original flow field |
|
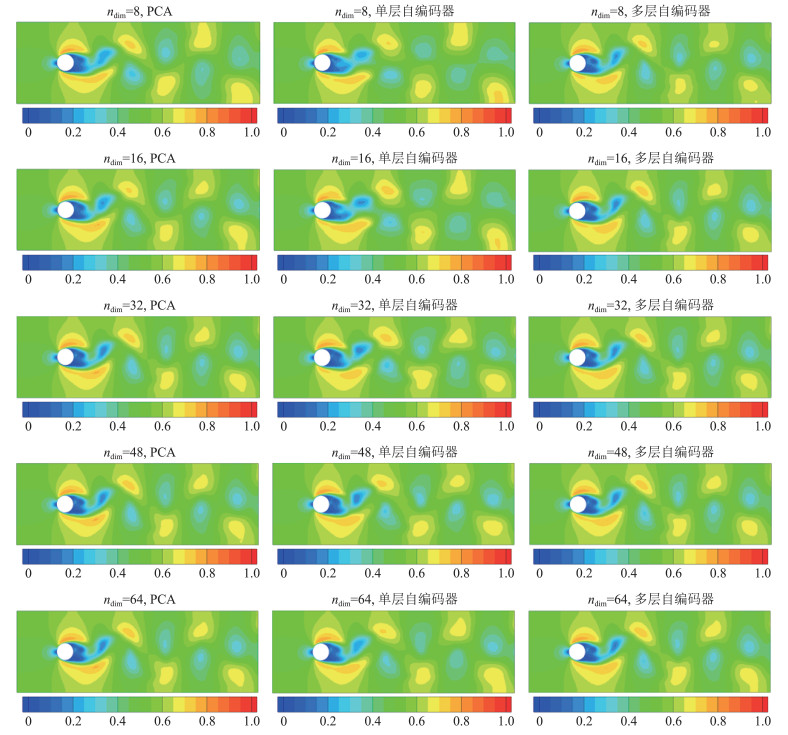
图 6 PCA、多层自编码器、单层自编码器的重构结果 Fig.6 The reconstructed velocity by three methods |
|
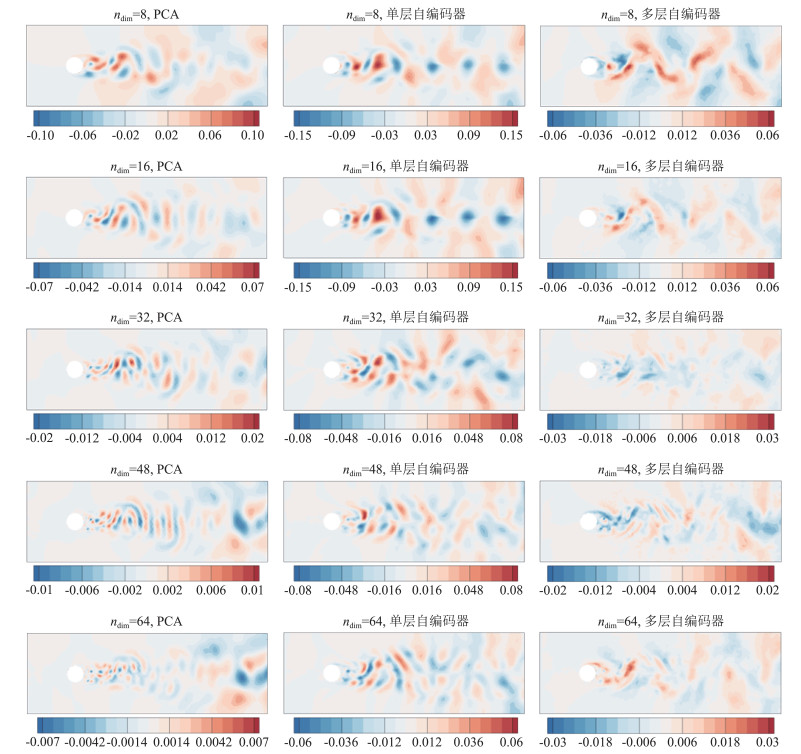
图 7 PCA、多层自编码器、单层自编码器的重构误差 Fig.7 Error between the original velocity and the reconstruction by three methods |
为了进一步评估三种方法的性能,我们选取第840个时间步的数据,通过数据可视化对三种方法进行直观的比较。选取的原始流场速度云图如图 5所示。
图 6是三种方法对图 5中的流场数据进行重构的结果,从左到右依次是PCA,单层自编码器和多层自编码器,从上到下依次是不同的特征维度,ndim= 8、16、32、48、64。由于三种方法的降维效果大致相近,直接根据流场数据的可视化结果难以进行比较,因此我们对原始流场数据和每种方法的重构结果之间的误差也进行了可视化,如图 7所示。图 7中数据的排列与图 6相同,在不同情况下,流场内误差的数值范围不同,颜色越浅表示误差越接近于0。
从图 6中可以看出,各种情况下三种方法都能重构流场的整体规律。它们之间的差别主要在于一些细节的重构,如图 5中红色箭头指向的三个位置。对于1号位置,多层自编码器在不同特征维度的情况中都有较好的刻画,而PCA和单层自编码器在特征维度较低时都不能重构出这一细节;在2号位置,只有PCA方法实现了重构;而3号位置,只有高特征维度的多层自编码器能进行较好的重构。
图 7展示了各种方法的重构数据和原始数据之间的误差。从图中可以看出,随着特征维度的增加,PCA方法的误差出现的区域逐渐缩小,且误差的数值不断降低,逐渐逼近0;自编码器中存在误差的区域则相对固定,误差的数值趋于稳定,如多层自编码器的误差范围稳定在[-0.03,0.03]。自编码器的性能受网络结构的限制,不能达到PCA方法不断降低误差的效果。
综合来看,在特征维度较小时,多层自编码器是三种方法中最优的选择,可以在确保较高精度的情况下提供较高的数据压缩率。
2.2 预测模型应用降维方法提取特征之后,我们需要对得到的低维特征建立预测模型。考虑到需要建模解决的问题是时间序列的预测问题,我们使用LSTM构建低维特征的预测模型。
由于2.1节中单层自编码器的表现较差,我们仅为多层自编码器和PCA方法的降维结果构建相应的预测模型。在实验中,综合考虑数据的复杂度、模型的精度和效率,我们使用两层LSTM构建预测网络。预测模型的结构如表 4所示。
| 表 4 预测模型结构 Table 4 Structure of the prediction model |
|
|
预测网络同样使用均方误差作为损失函数,训练的批大小为16,训练时期为150,使用Adam优化器。预测网络以过去五个时刻的低维特征为输入,输出下一个时刻的低维特征。对数据进行训练集,验证集和测试集的划分,数据比例为6∶2∶2。
对于PCA提取的特征,我们对其进行标准化,将数据缩放至[-1, 1],并将相应预测网络输出层的激活函数设为tanh。对于多层自编码器提取的特征,直接将编码器的输出作为预测网络的输入。由于在2.1.1节中编码器输出层的激活函数为Relu,因此对应的预测网络的输出层的激活函数也设置为Relu。
分别记PCA、多层自编码器对应的预测网络为P-LSTM和M-LSTM。表 5给出了两个预测模型在测试集上均方根误差的平均值。总体上,M-LSTM的误差大于P-LSTM,这是因为未对编码器提取的特征进行标准化,数值范围较大。而随着特征维度的增加,P-LSTM的预测误差不断增加,是因为P-LSTM的输入向量为稠密向量,需要建模的关系愈加复杂而预测网络的结构没有改变;同时,M-LSTM的误差更为稳定,甚至有一定程度的降低,是因为在编码器的输出层使用了Relu函数,特征表示是一个稀疏向量,特征维度的增长在为预测模型提供更多信息的同时未使数据关系过于复杂化。
| 表 5 两个预测模型的均方根误差 Table 5 RMSE of prediction models P-LSTM and M-LSTM |
|
|
数据降维方法和相应的预测网络共同构成了降阶模型。对于使用PCA降维的降阶模型,数据经过PCA变换后,将数据特征输入预测网络,对预测结果进行PCA的逆变换,得到降阶模型的预测结果;对于使用多层自编码器的降阶模型,将数据输入编码器,再将得到的低维特征输入预测网络,使用解码器将预测网络的输出结果重构为预测的流场数据。
对于基于多层自编码器和LSTM的降阶模型,我们可以按照编码器、预测网络、解码器的顺序将三个网络拼接成一个网络作为构建的降阶模型,并对拼接后的网络进行微调。因此,在本节中,我们将比较三种降阶模型。三种模型分别是基于PCA和LSTM的降阶模型(PCA and LSTM based ROM, PLRom)、基于MAE和LSTM的降阶模型(MAE and LSTM based ROM, MLRom)、微调后的基于MAE和LSTM的降阶模型(Fine-tuned MAE and LSTM based ROM, FMLRom)。在对MLRom进行微调时,使用的损失函数为均方误差,批大小为100,训练时期为10,使用Adam优化器。三个降阶模型在测试集上的均方根误差见表 6。
| 表 6 三个降阶模型的均方根误差 Table 6 RMSE of reduced order models PLRom, MLRom, and FMLRom |
|
|
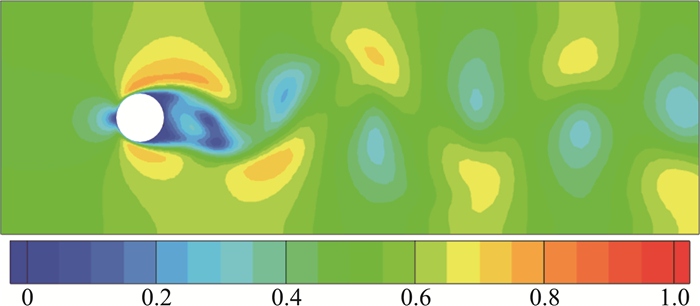
与之前实验中相同,为了进一步分析不同降阶模型的实际效果,我们选取第860个时间步的流场,对其进行预测和分析,原流场如图 8所示。
|
图 8 流场速度云图,时间步=860 Fig.8 The velocity field at time step=860 |
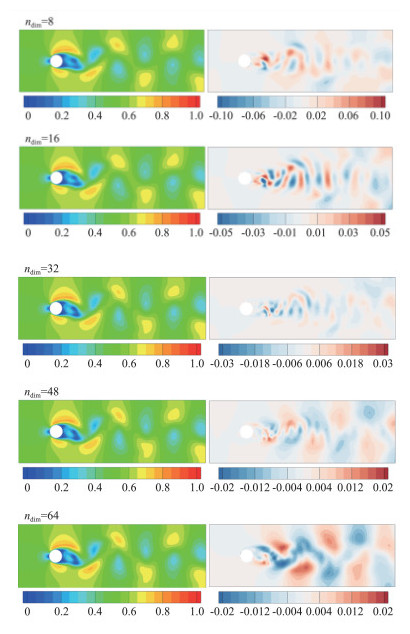
图 9、图 10、图 11分别展示了PLRom、MLRom、FMLRom的预测结果和误差,图中左侧为流场的预测结果,右侧为误差。综合表 6和图分析,FMLRom表现最好。总体上,三种降阶模型的预测性能相差较小。随着特征维度的增加,各个降阶模型的效果都有一定的提升,但由于预测网络性能的下降,当特征维度从48增加为64时,PLRom误差增大。微调使得FMLRom的性能较MLRom有一定提升。
|
图 9 PLRom的预测结果与误差 Fig.9 The prediction and error of PLRom |
|
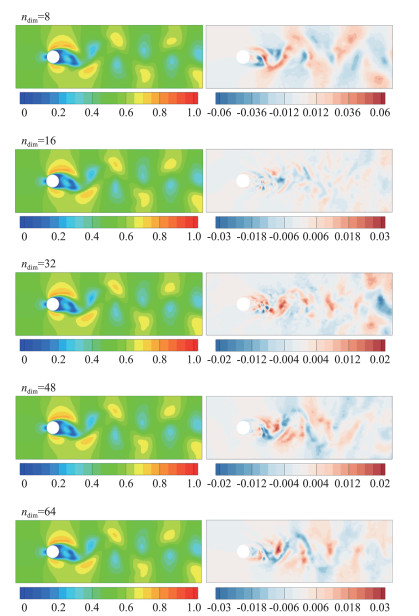
图 10 MLRom的预测结果与误差 Fig.10 The prediction and error of MLRom |
|
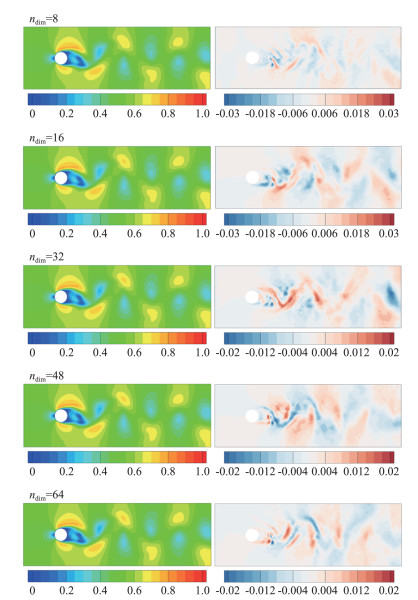
图 11 FMLRom的预测结果与误差 Fig.11 The prediction and error of FMLRom |
本文应用了多层自编码器和LSTM构建降阶模型,并以二维圆柱绕流为例验证了该降阶模型的有效性。降阶模型的预测流场和原始流场的RMSE降低至3×10-3左右。
本文比较了单层自编码器、多层自编码器和PCA等方法进行数据降维的效果。实验结果表明在特征维度较低时,多层自编码器的效果优于PCA方法。当特征维度为8时,多层自编码器在测试集上的RMSE为7.78×10-3,是PCA方法误差的一半,且多层自编码器性能受特征维度大小的影响较小。多层自编码器可以在较低的维度上更好地重构数据,在保证精度的同时有着较高的数据压缩率。
本文分别应用多层自编码器和PCA提取特征,利用LSTM构建预测网络,对低维特征进行预测,结合特征提取方法和预测网络即可得到构建的降阶模型。本文对多层自编码器和LSTM拼接后的网络进一步进行了微调,得到了精度更高的FMLRom。预测流场与原始流场之间的均方根误差降低至3×10-3左右。
对于构建复杂流场的降阶模型,应用多层自编码器进行数据降维能够提升降阶模型精度,使得基于LSTM的降阶模型具有更好的数据压缩效果和预测效果。此外,结合生成对抗网络、变分自编码器等方法进行流场数据的生成,可以进一步应用于构建适用于不同参数条件的降阶模型。
| [1] |
DOWELL E H. Eigenmode analysis in unsteady aerodynamics-Reduced-order models[J]. Applied Mechanics Reviews, 1997, 50(6): 371. DOI:10.1115/1.3101718 |
| [2] |
SILVA W A. Identification of linear and nonlinear aerodynamic impulse responses using digital filter techniques: AIAA-97-3712[R]. Reston: AIAA, 1997.
|
| [3] |
陈刚, 李跃明. 非定常流场降阶模型及应用研究进展与展望[J]. 力学进展, 2011, 41(6): 686-701. CHEN G, LI Y M. Advances and prospects of the reduced order model for unsteady flow and itsapplication[J]. Advances in Mechanics, 2011, 41(6): 686-701. (in Chinese) |
| [4] |
LIBBRECHT M W, NOBLE W S. Machine learning applications in genetics and genomics[J]. Nature Reviews Genetics, 2015, 16(6): 321. DOI:10.1038/nrg3920 |
| [5] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[C]//Advances in neural information processing systems. 2012: 1097-1105.
|
| [6] |
KOUROU K, EXARCHOS T P, EXARCHOS K P, et al. Machine learning applications in cancer prognosis and prediction[J]. Computational and Structural Biotechnology Journal, 2015, 13: 8-17. DOI:10.1016/j.csbj.2014.11.005 |
| [7] |
KUTZ J N. Deep learning in fluiddynamics[J]. Journal of Fluid Mechanics, 2017, 814: 1-4. DOI:10.1017/jfm.2016.803 |
| [8] |
张伟伟, 朱林阳, 刘溢浪, 等. 机器学习在湍流模型构建中的应用进展[J]. 空气动力学学报, 2019, 37(3): 444-454. ZHANG W W, ZHU L Y, LIU Y L, et al. Progresses in the application of machine learning in turbulence modeling[J]. Acta Aerodynamica Sinica, 2019, 37(3): 444-454. (in Chinese) |
| [9] |
TOMPSON J, SCHLACHTER K, SPRECHMANN P, et al. Accelerating eulerian fluid simulation with convolutional networks[C]//34th International Conference on Machine Learning-Volume 70. JMLR. org, 2017: 3424-3433.
|
| [10] |
WANG Q, HESTHAVEN J S, RAY D. Non-intrusive reduced order modeling of unsteady flows using artificial neural networks with application to a combustion problem[J]. Journal of Computational Physics, 2019, 384: 289-307. DOI:10.1016/j.jcp.2019.01.031 |
| [11] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [12] |
MANNARINO A, MANTEGAZZA P. Nonlinearaeroelastic reduced order modeling by recurrent neural networks[J]. Journal of Fluids and Structures, 2014, 48: 103-121. DOI:10.1016/j.jfluidstructs.2014.02.016 |
| [13] |
WANG Z, XIAO D, FANG F, et al. Model identification of reduced order fluid dynamics systems using deep learning[J]. International Journal for Numerical Methods in Fluids, 2018, 86(4): 255-268. DOI:10.1002/fld.4416 |
| [14] |
MOHAN A T, GAITONDE D V. A deep learning based approach to reduced order modeling for turbulent flow control using LSTM neural networks[EB/OL]. ArXiv Preprint ArXiv: 1804. 09269, 2018.
|
| [15] |
GRAVES A, SCHMIDHUBER J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures[J]. Neural Networks, 2005, 18(5-6): 602-610. DOI:10.1016/j.neunet.2005.06.042 |
| [16] |
KANI J N, ELSHEIKH A H. DR-RNN: A deep residual recurrent neural network for model reduction[EB/OL]. ArXiv Preprint ArXiv: 1709. 00939, 2017.
|
| [17] |
LINDHORST K, HAUPT M C, HORST P. Efficient surrogate modelling of nonlinear aerodynamics inaerostructural coupling schemes[J]. AIAA Journal, 2014, 52(9): 1952-1966. DOI:10.2514/1.J052725 |
| [18] |
YAO W, MARQUES S. Nonlinear aerodynamic andaeroelastic model reduction using a discrete empirical interpolation method[J]. AIAA Journal, 2017, 55(2): 1-14. |
| [19] |
尹明朗, 寇家庆, 张伟伟. 一种高泛化能力的神经网络气动力降阶模型[J]. 空气动力学学报, 2017, 35(2): 205-213. YIN M L, KOU J Q, ZHANG WW. A reduced-order aerodynamic model with high generalization capability based on neural network[J]. Acta Aerodynamica Sinica, 2017, 35(2): 205-213. DOI:10.7638/kqdlxxb-2015.0210 (in Chinese) |
| [20] |
KOU J, ZHANG W. Multi-kernel neural networks for nonlinear unsteady aerodynamic reduced-order modeling[J]. Aerospace Scienceand Technology, 2017, 67: 309-326. DOI:10.1016/j.ast.2017.04.017 |
| [21] |
RUMELHART D E, HINTON G E, WILLIAMS R J. Learning internal representations by error propagation[R]. California Univ San Diego La Jolla Inst for Cognitive Science, 1985.
|
| [22] |
叶舒然, 张珍, 宋旭东, 等. 自动编码器在流场降阶中的应用[J]. 空气动力学学报, 2019, 37(3): 498-504. YE S R, ZHANG Z, SONG X D, et al. Applications of autoencoder in reduced-order modeling of flow field[J]. Acta Aerodynamica Sinica, 2019, 37(3): 498-504. DOI:10.7638/kqdlxxb-2019.0039 (in Chinese) |
| [23] |
HINTON G E, OSINDERO S, TEH Y W. A fast learning algorithm for deep beliefnets[J]. Neural Computation, 2006, 18(7): 1527-1554. DOI:10.1162/neco.2006.18.7.1527 |
| [24] |
KINGMA D P, BA J. Adam: a method for stochastic optimization[J]. ArXiv Preprint ArXiv: 1412. 6980, 2014.
|
 2021, Vol. 39
2021, Vol. 39

