2. 空气动力学国家重点实验室, 绵阳 621000
2. State Key Laboratory of Aerodynamics, Mianyang 621000, China
现代运输机机翼普遍装配有增升装置,以确保飞机起降阶段有良好的升阻特性[1]。由于结冰条件通常发生在起降阶段,并且展开后的增升装置较展开前流动更加复杂,其结冰特性不同于单段翼,因此增升构型的结冰问题研究十分必要。然而,针对增升构型结冰试验的相似参数转换非常复杂,依靠风洞试验研究结冰问题存在较大的困难。随着结冰数值模拟理论的发展,数值计算已成为研究结冰问题的重要手段。
目前针对增升构型结冰计算问题,国内外开展了部分研究工作。Ozgen[2]、Cao[3]等人分别采用欧拉-拉格朗日和欧拉-欧拉框架实现了二维多段翼的结冰数值模拟。Dominik[4]、Sang[5]和Zhang[6]侧重分析了增升构型带冰后的气动特性,验证了积冰对增升效应造成的不利影响。在多段翼水滴撞击特性计算方面,Iuliano[7]、Yu[8]基于二维多段翼算例,对比了拉格朗日和欧拉法的水滴收集率计算结果。结果表明在黏性流场条件下,两者计算结果基本一致。由于拉格朗日方法算法通用性差,在计算复杂构型问题时普遍采用欧拉法进行分析[9-11]。但是,欧拉法自身存在缺陷,尤其针对复杂流动问题,欧拉法无法描述液滴轨迹交汇的现象,且计算结果受网格质量影响。
本文在拉格朗日框架下,发展了一套满足二维多段翼以及三维复杂构型的水滴收集率计算方法。通过与30P30N多段翼实验测量结果对比,验证了计算方法的准确性。在此基础上,开展了某大型商用运输机机翼增升构型及其翼型剖面的水滴收集率计算,重点针对缝翼背面缝道处的撞击特性进行了详细的分析。
1 计算方法欧拉-拉格朗日框架下水滴撞击特性计算流程分为四步[12]:1) 采用欧拉法计算空气流场;2) 液滴初始化;3) 在拉格朗日框架下计算水滴运动轨迹;4) 基于水滴撞击结果,计算壁面水滴收集率分布特性。
1.1 流场计算方法本文空气流场采用中国空气动力研究与发展中心(CARDC)自研的PHengLei流场解算器计算。该解算器采用基于非结构网格的有限体积法求解RANS方程。相关理论介绍可参阅文献[13]。
1.2 水滴运动方程及其求解方法基于球形假设,水滴运动的控制方程表达式如下:
| $ \frac{{{\rm{d}}{\mathit{\boldsymbol{u}}_{\rm{d}}}}}{{{\rm{d}}t}} = \frac{{\left( {{\rho _{\rm{d}}} - {\rho _{\rm{a}}}} \right)}}{{{\rho _{\rm{d}}}}}\mathit{\boldsymbol{g}} + \frac{{{C_{\rm{d}}} \cdot Re}}{{24}} \cdot \frac{{18{\mu _{\rm{a}}}}}{{{\rho _{\rm{d}}} \cdot {D^2}}}\left( {{\mathit{\boldsymbol{u}}_{\rm{a}}} - {\mathit{\boldsymbol{u}}_{\rm{d}}}} \right) $ | (1) |
上式等号右侧第一项表示水滴所受的重力和浮力,第二项表示水滴运动过程中所受的阻力。组合参数作为修正系数,仅由相对雷诺数决定。
| $ \frac{{{C_{\rm{d}}} \cdot \mathit{Re}}}{{24}} = 1.0 + 0.197R{e^{0.63}} + 2.6 \times {10^{ - 4}}\mathit{R}{\mathit{e}^{1.38}} $ | (2) |
| $ Re = \frac{{{\rho _{\rm{a}}} \cdot \left\| {{\mathit{\boldsymbol{u}}_{\rm{a}}} - {\mathit{\boldsymbol{u}}_{\rm{d}}}} \right\| \cdot D}}{{{\mu _{\rm{a}}}}} $ | (3) |
方程(1)为一阶常微分方程,在水滴初始速度已知的前提下,方程的解是存在且唯一的。可采用龙格库塔方法推进求解。
在采用拉格朗日法进行粒子跟踪计算的过程中,需要实时建立水滴颗粒坐标和包含该颗粒的网格单元的对应关系,并向水滴颗粒传递流场信息。为避免全局遍历带来的大量计算量,本文采用定向查找[14]的方法,以近乎最优的路径进行水滴颗粒的定位。确定了所处单元后,采用体积/面积加权的方式进行流场信息插值。
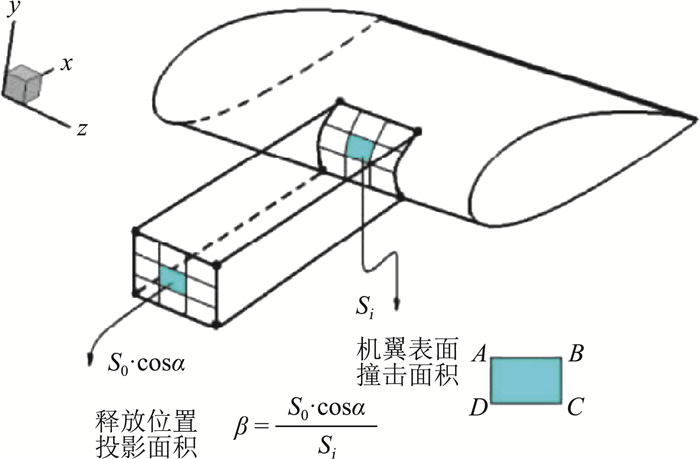
1.3 收集率计算水滴收集系数的定义为液滴在壁面与远场处单位面积上的质量通量比值。在拉格朗日框架下,可以根据水滴运动轨迹组成的颗粒流管的面积变形率近似表示撞击区域内的水滴收集率。如图 1所示。
|
图 1 三维水滴收集率计算示意图[15] Fig.1 A sketch of calculating the collection coefficient of water droplets under 3D condition[15] |
收集率计算表达式:
| $ \beta = {S_0} \cdot \cos \alpha /{S_{\rm{i}}} $ | (4) |
式中Si、S0、α分别表示撞击面积,远场水滴阵列所围面积,来流速度迎角。
由于流管假设模型成立的前提条件是要确保水滴轨迹不发生交叉。而本文的研究对象具有复杂的流动特征,因此在发生轨迹交叉后,采用“粒子统计法”[16]来评估壁面的水滴收集率。如下所示:
| $ \beta = \frac{{{n_{{\rm{inlet }}}} \cdot {m_d}/{A_{{\rm{wall }}}}}}{{{n_0} \cdot {m_d}/{A_0}}} $ | (5) |
式中Awall、A0、md分别表示壁面网格单元面积,远场水滴阵列所围面积,单个液滴粒子包所代表的质量。ninlet和n0分别为网格单元上的撞击粒子数和远场释放液滴粒子数。
上述两种方法各有其优劣。前者计算效率高,但是计算复杂外形时,算法复杂度高,普适性较差。后者,计算方法简单,普适性优异,然而该算法耗费计算资源,求解效率低。因此,需要根据具体问题来选取计算方法。
2 验证算例首先利用圆柱案例验证计算模型。圆柱直径为10.16 cm,分别采用“粒子统计法”和“面积率计算方法”计算其水滴收集系数。并与实验数据[17]进行对比验证。计算工况如下:迎角0°,速度80 m/s, 远场静压89 867 Pa,空气密度1.097 kg/m3,液滴直径16.0 μm。
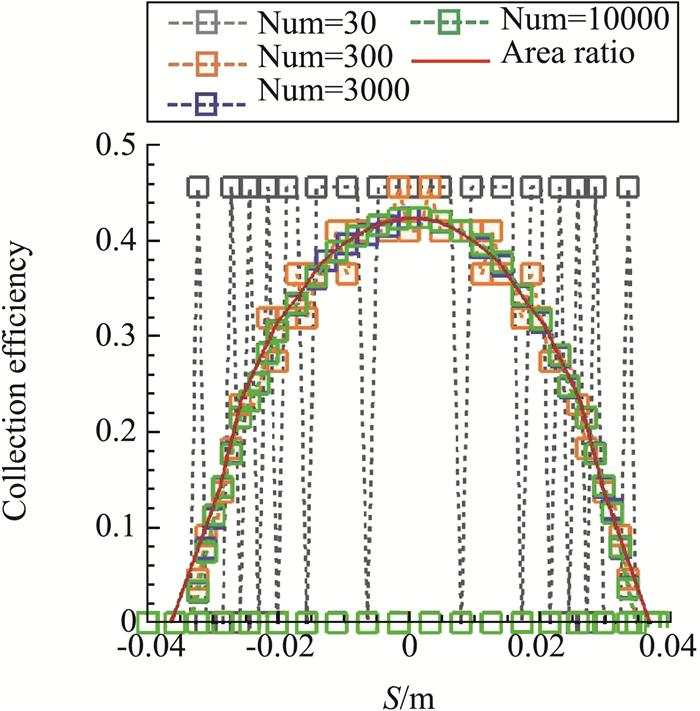
图 2给出了不同释放水滴数下的水滴收集率分布曲线。显而易见,计算误差随水滴数增加而减小,最终与“面积率计算方法”的计算结果趋于一致。由此推断出,在定常流场的条件下,本文方法的计算结果是随有效轨迹数增加而趋于收敛的。
|
图 2 不同水滴数下的收集系数分布曲线 Fig.2 The distribution of collection efficiency with different number of water droplets |
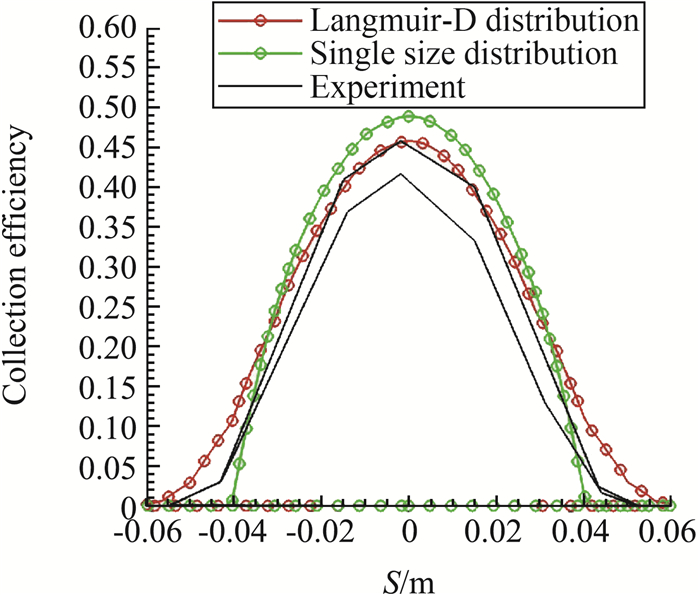
按照Langmuir-D粒径分布原则,对单一尺度粒径下的水滴收集率曲线进行修正,如图 3所示。修正后的曲线极限位置与实验结果基本一致,并且与参考区间吻合度更高。
|
图 3 水滴收集率计算结果与实验值对比 Fig.3 The comparison of computational and experimental collection efficiency of the cylinder case |
为测试本文方法在多段翼等复杂流动条件下计算能力,本文选用了30P30N多段翼型进行计算分析。30P30N是一种典型的运输类飞机着陆构型翼剖面,由前缘缝翼,主翼和后缘襟翼三部分组成。Bidwell[18]在报告中公开发布了该翼型的水滴撞击特性试验数据。其中壁面水滴收集率是通过水滴撞击染色纸对其着色后利用激光测量技术得到的。
算例计算工况如下:来流速度78 m/s,静压95 840 Pa,静温288.15 K,迎角(AoA)0°,液滴直径(MVD)11.5、21.0 μm,弦长111.44 mm。
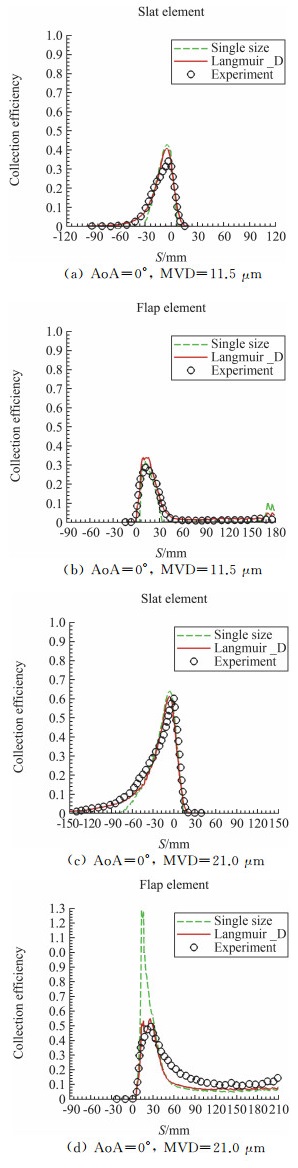
图 4给出了单尺度及多尺度粒径下的计算结果,并与实验测量结果进行了比较。由图可见,基于Langmuir_D分布原则修正的收集率分布曲线与实验值基本吻合。但是在图 4(d)中,后缘襟翼驻点附近的当地水滴收集率结果出现了明显的高点。产生这一现象的原因,是靠近物面的水滴受缝翼与主翼气动力耦合作用的影响,水滴流管被压缩,导致该区域内的液态水含量增加,进而造成襟翼上局部收集率激增。在多尺度条件下,由于不同粒径的流管撞击区域不一致,加权计算后该峰值便被抹平了。
|
图 4 收集率计算结果与实验测量数据的对比 Fig.4 The comparison of collection efficiencies between numerical simulation and experiment |
综上,本文采用计算方法具备分析增升构型水滴撞击特性的能力,计算结果具有工程参考意义。
3 某型飞机增升构型撞击特性计算当前关于缝翼的结冰特性研究主要集中在其迎风面的积冰特征及其造成的分离流动问题上,很少关注缝道处的水滴撞击情况。本文选用某大型运输机的增升构型作为分析对象,重点考察常规液滴粒径下的水滴撞击特性。该模型翼展约为16.8 m,弦长约为5.07 m。下文分别针对其二维翼剖面及三维构型的水滴收集率进行计算。
3.1 二维翼剖面撞击特性计算计算网格如图 5所示。
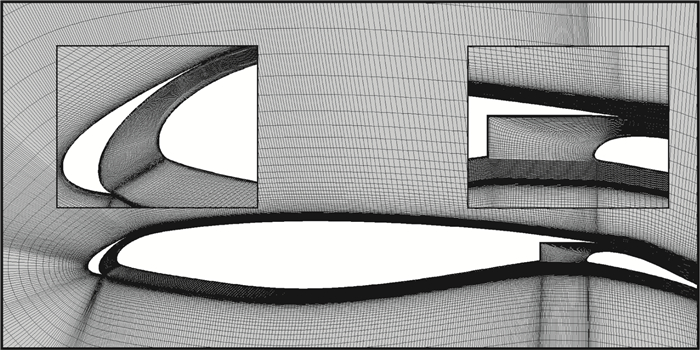
|
图 5 多段翼计算网格 Fig.5 The mesh for a multi-element airfoil |
计算工况如下:迎角选用4.5°、8.5°、12.5°,来流速度75 m/s,远场静压95 954.5 Pa,远场静温264.15 K,水滴粒径20.0~50.0 μm。
图 6中给出了各工况下的霜冰计算结果(单步,6 min),用来描述壁面水滴收集率的分布特性。结果显示,缝翼背面的水滴撞击情况非常严重。由于该区域通常处在机翼的防冰区之外,结冰风险非常高。
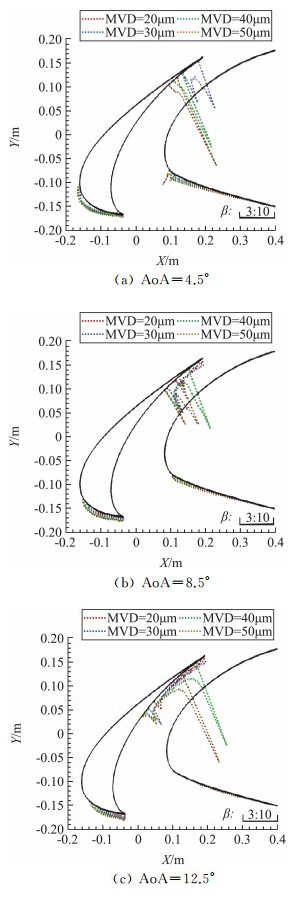
|
图 6 不同迎角和液滴粒径的缝翼水滴收集率计算结果 Fig.6 The Calculation Results of the collection efficiency of the slat wing with different AoAs and MVDs |
相比之下,缝翼迎风面和主翼下翼面的水滴收集率要小得多。并且随迎角增加,主翼表面的水滴收集量逐渐减小。当迎角达到12.5°时,没有水滴撞击在主翼上。
图 7展示了迎角8.5°下缝翼背面的水滴收集率分布情况。当水滴粒径大于33 μm时,收集率曲线呈双峰分布。这一现象恰好揭示了流经缝道水滴轨迹的复杂性。图 8给出了迎角8.5°下不同粒径下撞击缝翼的水滴轨迹。图 8(b、c、d)中上游两股水滴在缝道处交汇,这两股水滴分别受凹腔涡及主翼的气动特性影响,使水滴撞壁特性出现差异。
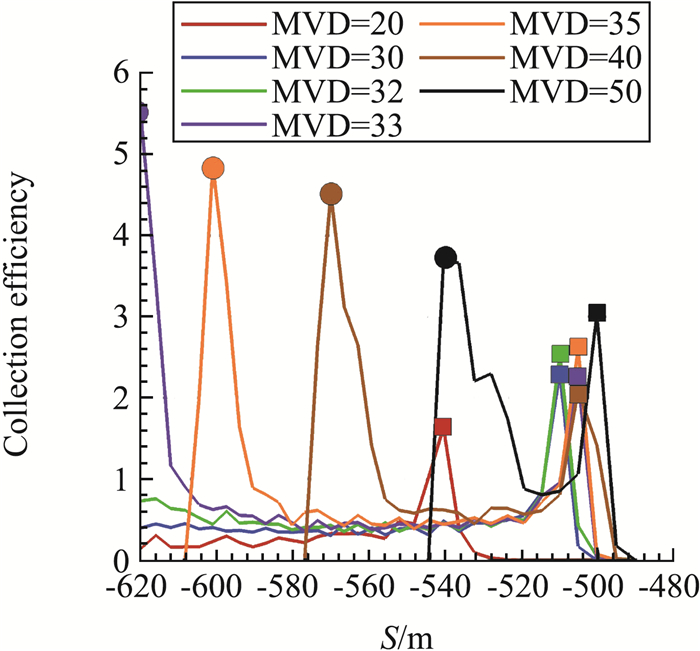
|
图 7 迎角8.5°缝翼背面水滴收集率分布曲线 Fig.7 The distribution of collection efficiency on the reverse side of the slat wing, AoA=8.5° |
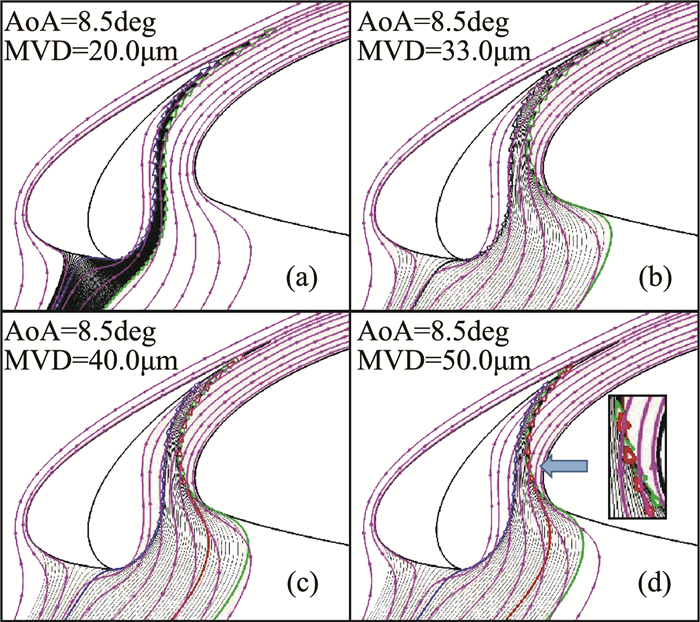
|
图 8 撞击缝翼的水滴轨迹 Fig.8 Trajectories of water droplets hit on the slat wing |
通过观察水滴的运动轨迹可以发现,当水滴粒径较小时,水滴的跟随性好,仅有靠近凹腔附近的水滴撞击缝翼壁面。然而,当粒径增大到某一条件时(图 7中,粒径为33 μm),主翼下表面由驻点向前缘点运动的水滴受惯性影响撞击到缝翼后缘。由于这部分液滴流管被严重压缩变形,使得此时缝翼后缘处的水滴收集率出现激增。另一方面,随粒径增加,绕过主翼前缘的水滴轨迹会逐渐减少,从而导致后缘点收集率峰值也随之减小。
在主翼前缘点附近,越靠近壁面流动变化越剧烈,使得液滴运动至该区域会发生轨迹交叉的现象,如图 8(d)中被红色和绿色标记的水滴轨迹。在水滴不发生碰撞的前提下,两条轨迹是相互独立的。此时,不可采用面积法和欧拉法分析水滴撞击特性。这一点突显了本文采用“粒子统计法”计算的优势。
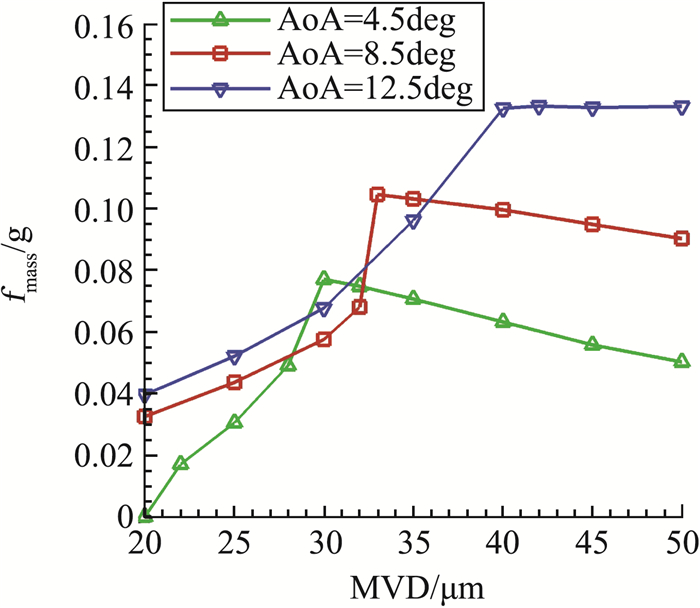
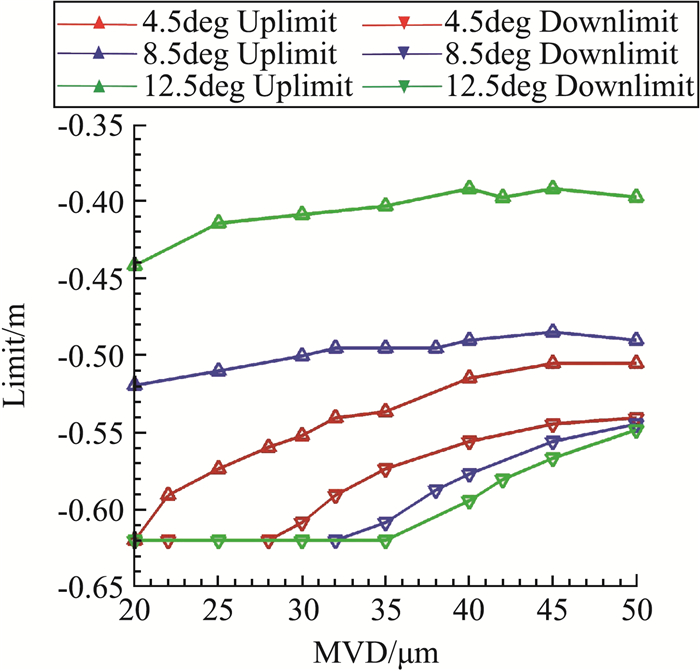
图 9中统计了不同条件下的缝翼背面水滴收集总量(假设来流液态水含量为1.0 g/m3)。图中纵轴表示单位时间内的水滴收集质量,单位为g,横轴表示液滴直径,单位为μm。结果显示,不同迎角下,缝翼背面液滴收集量随液滴直径增加呈现先增加后降低的规律。当迎角增大,收集总量变化拐点后移,且拐点后的水滴收集量对粒径变化的敏感度会随之越小。另外,图 10给出了不同迎角下的缝翼背面撞击极限随水滴粒径变化的分布结果,图中纵坐标表示距前缘点的壁面距离,单位为m。从图中可以总结得到以下规律:1)迎角越大,其上极限(靠近缝翼凹腔)受粒径影响较小。2)随粒径增大,上下极限向前(靠近凹腔方向)移动。
|
图 9 缝翼背面水滴收集总量 Fig.9 The total liquid water collection on the back of the slat wing |
|
图 10 不同工况下的缝翼背面撞击极限 Fig.10 The impingement limits on the back of slat wing under different conditions |
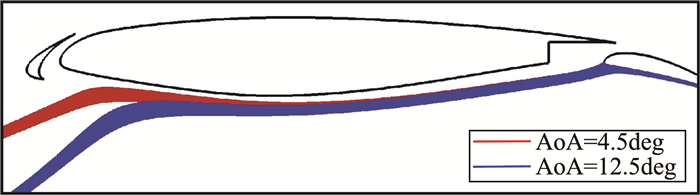
本节计算模型尺寸较大,主翼附近的流场特性对周围水滴运动起主导作用,使得常规粒径下的大部分液滴基本不会进入襟翼缝道。同时,主翼下翼面为水滴有足够的距离进行轨迹调整,如图 11所示,不同迎角下流经主翼下翼面的水滴轨迹最终趋于一致,进而使襟翼上的水滴收集率分布特性也基本相同。
|
图 11 不同迎角下撞击在襟翼上的液滴轨迹 Fig.11 The trajectories of water droplets hit on the flap wing with different AoAs |
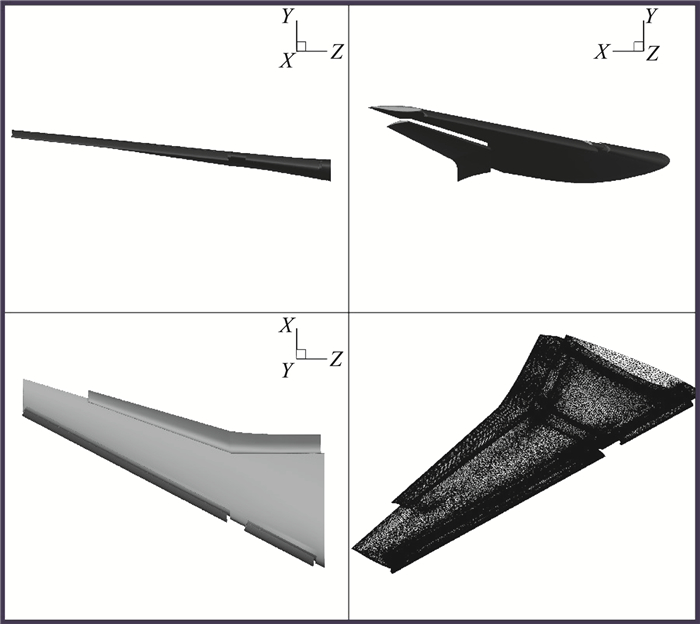
本节将传统欧拉拉格朗日计算方法推广到三维问题,并采用该方法考察外形更加复杂的某型带后掠的三维多段机翼的水滴撞击特性,以此验证本文方法在复杂构型算例下的可行性。模型网格如图 12。计算工况如下:马赫数0.23,雷诺数5.67×106,迎角8.5°,液态水含量1 g/m3,液滴直径50 μm。
|
图 12 三维多段机翼构型计算网格 Fig.12 The computational mesh of 3D multi-element wing |
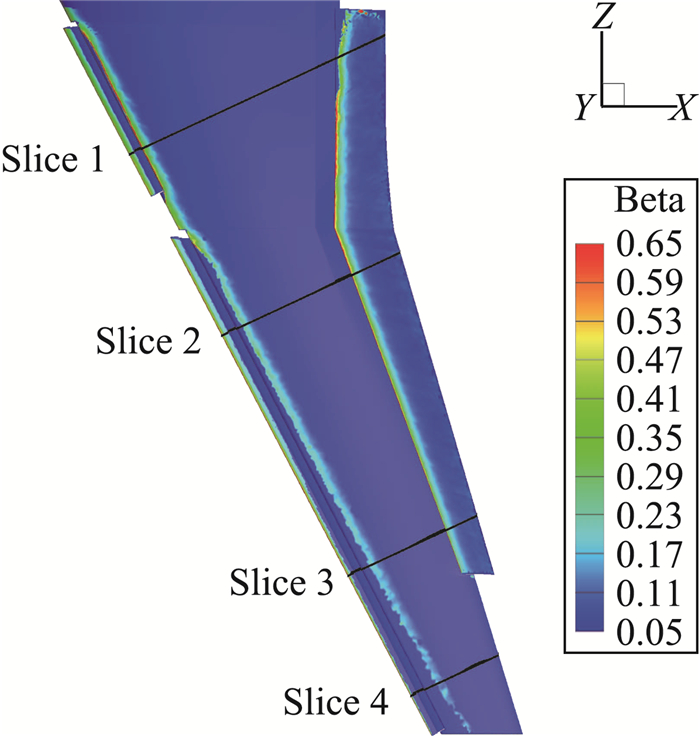
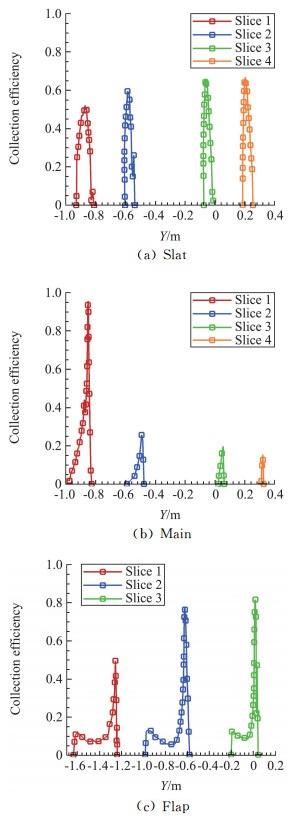
图 13给出了水滴收集系数分布云图,截取了机翼站位在25%、50%、80%、95%处的弦向收集系数分布曲线,如图 14所示。
|
图 13 水滴收集系数分布云图 Fig.13 The distribution of collection efficiency on the multi-element wing |
|
图 14 机翼沿展向不同站位的收集系数分布 Fig.14 The distribution of collection efficiencies at different spanwise locations of the wing |
图 14(a)、(b)、(c)分别描述了缝翼、主翼和襟翼上不同站位的收集率分布特性。当前工况下,前缘缝翼和后缘襟翼的水滴撞击范围及其收集率普遍偏大,在这些区域内发生结冰的风险较高。
水滴在缝翼上的撞击范围主要集中在迎风面上,越靠近翼梢收集系数峰值越大,对比各截面最大收集系数,翼梢比翼根处高出了近27%。主翼上的水滴收集率受三维流动效应的影响比较明显,越靠近翼梢其收集率峰值以及撞击范围呈减小的趋势,这一特性与二维翼剖面的分析结果相反。后缘襟翼上的水滴收集率主要集中在下翼面,且沿展向收集率峰值逐渐增加,而撞击范围逐渐减小。
4 结论本文基于欧拉-拉格朗日计算框架,建立了多体模型的水滴撞击特性计算方法。通过开展大型运输机增升构型机翼计算,获得了以下结论:
1) 当水滴轨迹发生交汇时,采用欧拉法和一般的“流管模型”计算水滴收集率都存在一定的缺陷。而本文采用的“粒子统计”法能够满足计算需求,计算过程不存在数值耗散,有良好的收敛特性,且结果准确性高。但是该方法进行三维问题计算时,在不清楚有效水滴释放位置的情况下,需要计算大量的水滴轨迹确保计算收敛,从而导致算法计算量会显著增加。因此,在水滴不发生交叉区域采用“流管模型”进行分析,而当轨迹发生交叉时,采用“粒子统计”方法计算。
2) 常规粒径条件下,缝翼和襟翼的水滴撞击情况比较严重。在特定的缝道参数及来流工况下,缝翼背面会有水滴撞击。并且受附近流场流动特性影响,缝道处有大量水滴轨迹聚集,造成局部水滴收集系数显著增加。
3) 缝翼背面结冰会导致缝道堵塞或缝翼作动机构卡死等问题,对飞机飞行安全带来巨大的安全隐患,需要引起重视。当防冰系统失效时,可适当减少飞机迎角,使其水滴收集量保持较低的状态。
本文方法具备模拟三维复杂外形水滴撞击特性的能力,能够为飞机结冰机理研究以及防除冰系统设计提供参考。
| [1] |
RECKZEH D. Aerodynamic design of the high-lift-wing for a Megaliner aircraft[J]. Aeropspace Science Technology, 2003, 7: 107-119. DOI:10.1016/S1270-9638(02)00002-0 |
| [2] |
OZGEN S, CANIBEK M. Ice accretion simulation on multi-element airfoils using extended Messinger model[J]. Heat and Mass Transfer, 2008, 45(3): 305-322. |
| [3] |
CAO Y H, ZHONG G, MA C. Numerical simulation of ice accretion prediction on multiple element airfoil[J]. Science China, 2011, 54(9): 2296-2304. DOI:10.1007/s11431-011-4434-9 |
| [4] |
DOMINIK C, SHIN J, MILLER D. Effect of in-flight ice accretion on the performance of a multi-element airfoil[R]. National Aeronautics and Space Administration, 1995.
|
| [5] |
SANG W M, JIANG S J, LI F W. Icing research for airfoil and multi-element airfoil[R]. Applied Aerodynamics Conference, AIAA 2006-3647, 2006.
|
| [6] |
张恒, 李杰, 龚志斌. 多段翼型缝翼前缘结冰大迎角分离流动数值模拟[J]. 航空学报, 2017, 38(2): 520733. ZHANG H, LI J, G ONG Z B. Numerical simulation of separated fliw around a multi-element airfoil at high angle of attack with iced slat[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(2): 520733. (in Chinese) |
| [7] |
IULIANO E, BRANDI V, MINGIONE G. Water impingement prediction on multi-element airfoils by means of Euerian and Lagrangian approach with viscous and inviscid air flow[R]. ASME paper AIAA 2006-1270, 2006.
|
| [8] |
YU C X, KE P, YU G F, et al. Investigation of water impingement on a multi-element high-lift airfoil by Lagrangian and Eulerian approach[J]. Propulsion and Power Research, 2015, 4(3): 161-168. DOI:10.1016/j.jppr.2015.07.001 |
| [9] |
RAJ L P, LEE J W, MYONG R S. Ice accretion and aerodynamic effects on a multi-element airfoil under SLD icing conditions[J]. Aerospace Science and Technology, 2018, P1: 1-14. |
| [10] |
易贤, 王开春, 林业伟. 结冰面水滴收集率欧拉计算方法研究及应用[J]. 空气动力学学报, 2010, 28(28): 596-601. YI X, WANG K C, GUI Y W. Study on Eulerian method for icing collection efficiency computation and its application[J]. Acta Aerodynamic Sinica, 2010, 28(5): 596-601. DOI:10.3969/j.issn.0258-1825.2010.05.019 (in Chinese) |
| [11] |
杨胜华, 林贵平, 申晓斌. 三维复杂表面水滴撞击特性计算[J]. 航空动力学报, 2010, 25(2): 284-290. YANG S H, LIN G P, SHEN X B. Water dropletimpingement prediction for three-dimension complex surfaces[J]. Journal of Aerospace Power, 2010, 25(2): 284-290. (in Chinese) |
| [12] |
WIDHALM M, RONZHEIMER A, MEYER J. Lagrangian particle tracking on large unstructured three-dimensional meshes[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada: AIAA-2008-472, 2008.
|
| [13] |
赵钟, 张来平, 何磊, 等. 适用于任意网格的大规模并行CFD计算框架PHengLei[J]. 计算机学报, 2019, 11(11): 2368-2383. ZHAO Z, ZHANG L P, HE L, et al. PHengLei: A large scale parallel CFD framework for arbitrary grids[J]. Chinese Journal of Computers, 2019, 11(11): 2368-2383. DOI:10.11897/SP.J.1016.2019.02368 (in Chinese) |
| [14] |
HASELBACHER A. An efficient and robust particle-localiztion algorithm for unstructured grids[J]. Journal of Computational Physics, 2007, 225: 2198-2213. DOI:10.1016/j.jcp.2007.03.018 |
| [15] |
孙志国, 朱春玲. 三维机翼表面水滴撞击特性计算[J]. 计算物理, 2011, 28(5): 677-685. SUN Z G, ZHU C L. Calculation of water-droplet impingement on wing surface[J]. Chinese Journal of Computational Physics, 2011, 28(5): 677-685. DOI:10.3969/j.issn.1001-246X.2011.05.006 (in Chinese) |
| [16] |
韩雅慧, 柯鹏, 杨春信, 等. 水滴撞击特性的粒子统计法研究[J]. 航空学报, 2013, 34(7): 1588-1595. HAN Y H, KE P, YANG C X, et al. Research on particle statistic method of water droplet impingement characteristics[J]. Acta Aeronautica Astronautica Sinica, 2013, 34(7): 1588-1595. (in Chinese) |
| [17] |
TONG X L, LUKE A. Eulerian simulations of icing collection efficiency using a singularity diffusion model: AIAA-2005-1246[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 2005.
|
| [18] |
BIDEWELL C S. Icing calculations for a 3D, high-lift wing configuration[R]. ASME paper AIAA 2005-1244, 2005.
|
 2021, Vol. 39
2021, Vol. 39


