为了提高隐身性和机动能力, 现代高性能作战飞机的机载导弹普遍采用舵面折叠+内埋的方式存储[1-2].当导弹在内埋弹舱内时舵面折叠, 待出舱之后再展开.在整个舵面展开的过程中, 导弹与载机的距离非常近, 而且还处在舱门开启之后的复杂流场当中[3-4], 舵面展开是否顺利, 展开的过程是否同步, 不仅会影响到导弹发射的成败, 更会影响到载机的飞行安全.
机载导弹一般由弹身+4片尾舵组成, 驱动方式有扭簧、扭杆及火工品作动筒等多种[7].展开过程会受到飞行高度、速度、迎角/侧滑角, 载机/导弹气动外形等多种因素的影响.展开过程中不仅要保证展开的同步性,而且还要保证到位后不能有过大的冲击载荷[10]。然而在展开的过程中,4片尾舵处于弹身的不同方位,其所受的气动载荷各不相同,而且随弹体滚转角而有较大的不同,要保证同步性和防冲击的要求,就必须要对折叠舵外翼的气动特性作全面深入的研究。
理论上来讲,开展折叠舵研究的最好的方法是飞行试验,这样可以模拟真实外形、真实动压情况以及真实驱动能量。然而飞行试验成本非常昂贵,所能获得的数据也非常有限,因此目前基本上是采用风洞试验[8-11]和CFD数值方法[12-13]来开展研究,且在型号设计中也主要是以风洞试验数据为准。然而,由于涉及到4片尾舵,不同迎角、Ma数以及折叠角,其组合状态非常庞大,全部状态开展风洞试验会使得试验成本和周期变得不可控制。这样就需要建立某种理论来统一这些数据的规律,形成设计的依据。前人的研究中,对舵面展开角、Ma数、迎角/侧滑角做过一些研究[8-9],但仍然缺少明显有规律性的结论。
其次,折叠舵的展开事实上是一个非定常的过程,目前风洞试验和数值计算主要采用定常方法,定常方法获得的结果在多大程度上能够应用于非定常过程是与实际问题本身直接相关的[14-15]。大量研究表明[16-18],当物体运动的减缩频率k < 0.05(k=ωb/V,其中ω为角速度,b为半展长,V为来流速度)时,其非定常的影响较弱,非定常效应基本可以忽略。
本文在前人研究的基础上通过风洞试验和数值计算的方法对折叠舵外翼气动特性进行了研究,通过大量数据分析了折叠角,迎角、Ma数及气动滚转角的影响,并在此基础上推导了影响折叠舵气动特性的预测公式,预测结果与样本点获得了较好的一致性。
1 折叠舵试验研究 1.1 试验风洞本试验在中国航天空气动力技术研究院的FD-12风洞进行。风洞试验段尺寸为1.2 m×1.2 m,Ma数范围为0.3~4.0,超声速试验段长度为2.4 m,亚跨声速试验段长度为3.8 m。
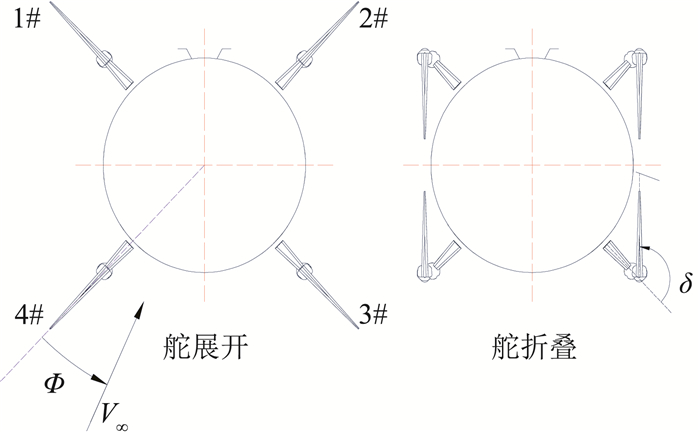
1.2 试验模型风洞试验模型见图 1。弹身为旋成体,顺航向,左上为1#舵,顺时针依次为2#,3#,4#舵。折叠舵外翼绕折叠轴朝弹体两侧折叠,完全折叠时折叠角δ=135°。气动滚转角Ф的定义为,当气流沿4#舵流向弹体时Ф=0°,沿逆时针方向Ф为正。合成迎角α为气流与弹轴的夹角,当气流从弹体下侧过来时迎角为正,从上侧过来时迎角为负。
|
图 1 试验模型(顺航向) Fig.1 Experimental model(Flow wise) |
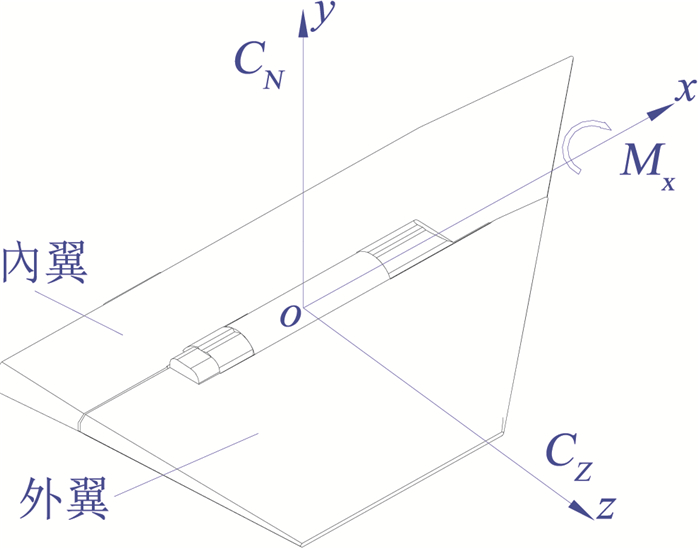
折叠舵模型见图 2。内翼与弹身固连,外翼绕折叠轴转动。舵面坐标系与外翼固连,坐标原点O位于折叠轴与铰链轴纵向平面的交点,Ox轴与折叠轴重合,Oy轴垂直于外翼中剖面,Oz轴按右手定则指向舵梢。气动力系数定义在舵面坐标系下。试验时采用杆式六分量天平测量外翼气动力和力矩。
|
图 2 折叠舵模型 Fig.2 A model of folding wing |
主要试验状态见表 1。导弹呈“×”型状态(Ф=45°),测量舵为3#舵,采用定常测力。
| 表 1 试验状态 Table 1 Experimental state |
|
|
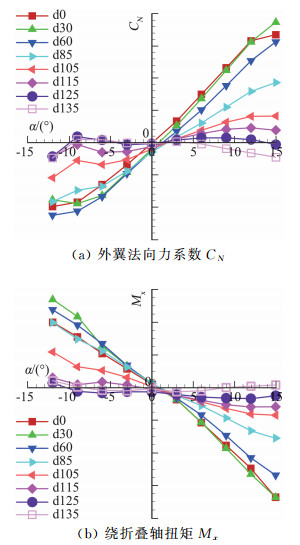
不同折叠角下外翼气动力/力矩系数随迎角的变化关系见图 3。当折叠角δ≥105°时,外翼靠近弹体,其与气流的夹角较小因从而法向力也较小。当δ<105°时,在迎角-9°~15°范围内法向力系数CN随迎角表现出良好的线性关系,在迎角小于-12°以后CN表现出明显的非线性。值得注意的是正迎角时测量舵处于迎风侧,负迎角时处于背风侧,在负迎角较大时会受到弹身及下侧舵面的干扰,该干扰使得气动力变小。扭矩系数的变化规律与法向力系数基本一致,在负迎角时扭矩受到的弹身及下侧翼的干扰没有法向力明显。
|
图 3 折叠舵气动力系数随迎角的关系 Fig.3 Aerodynamic coefficients vs.α |
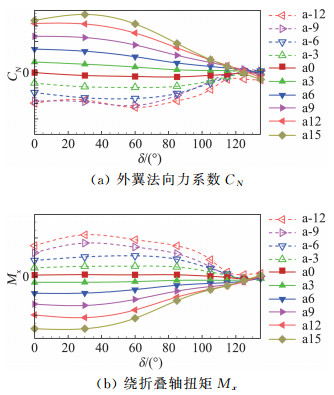
不同折叠角下外翼气动力系数随迎角的变化关系见图 4。图中实线为正迎角,虚线为负迎角。可以看出在不同迎角下当展开角很小时(δ≥105°)外翼气动载荷也小,随着外翼的展开气动载荷开始增大,折叠角δ从105°到60°气动载荷增加较快,δ < 60°以后变化平缓,外翼最大载荷出现在折叠角δ=30°附近。
|
图 4 折叠舵气动力特性随折叠角的关系 Fig.4 Aerodynamic coefficients vs.δ |
采用CFD方法开展折叠舵气动特性研究是进行折叠舵设计和优化的有效手段。本节针对第一节的试验模型开展了CFD计算研究。
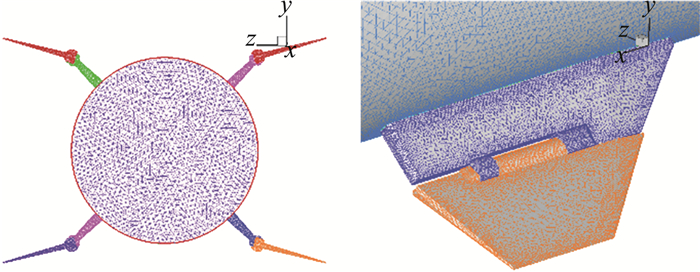
2.1 CFD计算验证计算数模采用第1节中的模型,对弹体模型进行了简化,略去了弹体表面突起物,仅保留弹身及折叠舵部件。计算模型表面网格见图 5,采用非结构网格,网格单元总数约190万。
|
图 5 CFD计算表面网格 Fig.5 Surface mesh of CFD calculation |
数值求解采用Fluent软件[19],控制方程采用可压缩雷诺平均NS方程。计算时湍流模型采用SA一方程模型,采用标准壁面函数。控制方程采用隐式格式求解。
计算状态参见表 1。为节省计算量,CFD计算时仅计算了δ=0°、30°和60°三个折叠角状态。
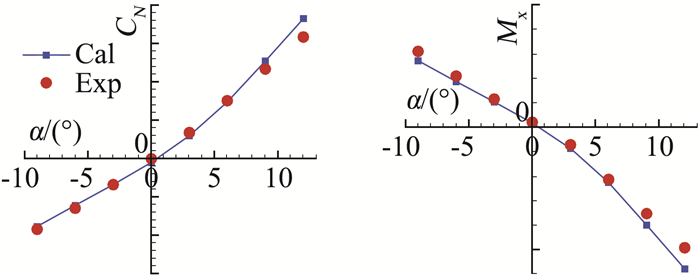
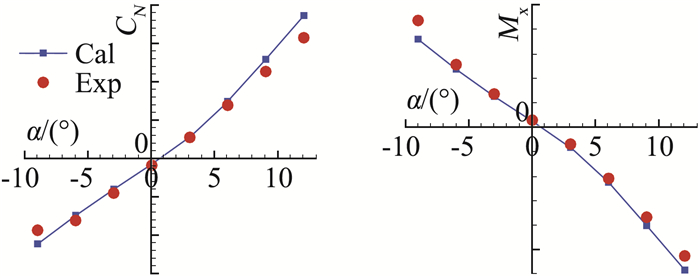
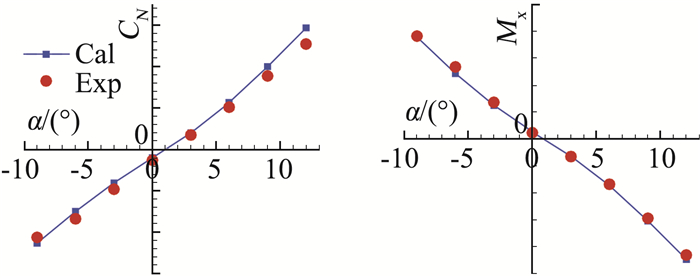
计算结果与试验结果的对比见图 6~图 8,不同折叠角下外翼气动力/力矩系数与试验值均吻合良好,小迎角下计算与试验值几乎完全重合,迎角较大时计算值略大于试验值。可见本文的CFD计算方法有较高的精度,计算与试验之间的差异可能与模型的简化有关。
|
图 6 δ=0°计算试验对比 Fig.6 Comparison of Cal. with Exp.(δ=0°) |
|
图 7 δ=30°计算试验对比 Fig.7 Comparison of Cal. with Exp. (δ=30°) |
|
图 8 δ=60°计算试验对比 Fig.8 Comparison of Cal. with Exp. (δ=60°) |
在2.1节的基础上针对δ=30°的状态对不同Ma下的外翼气动力/力矩进行了计算,计算Ma数为0.6、0.9、1.2、1.5。计算结果对比见图 9。
|
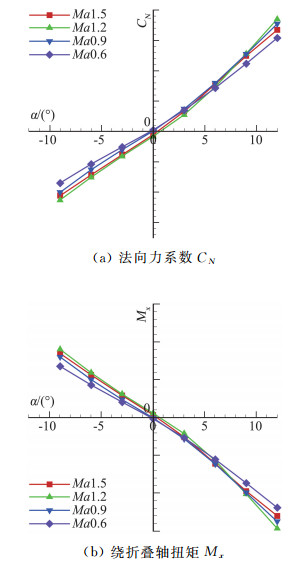
图 9 Ma数影响 Fig.9 The effect of Ma number |
相同迎角和折叠角下Ma 0.9和Ma 1.2拥有最大的法向力/力矩系数,且Ma 0.9和Ma 1.2的数据基本一致,该范围属于跨声速范围,这说明外翼在跨声速范围内有最大的气动力/力矩的系数值。Ma 0.6时系数最小。但从计算的4个Ma数来看,其数值都比较接近,这说明Ma数对外翼气动系数的影响有限,在实际工程设计时为缩短周期和节省成本可只选取某一Ma数开展试验或CFD计算。
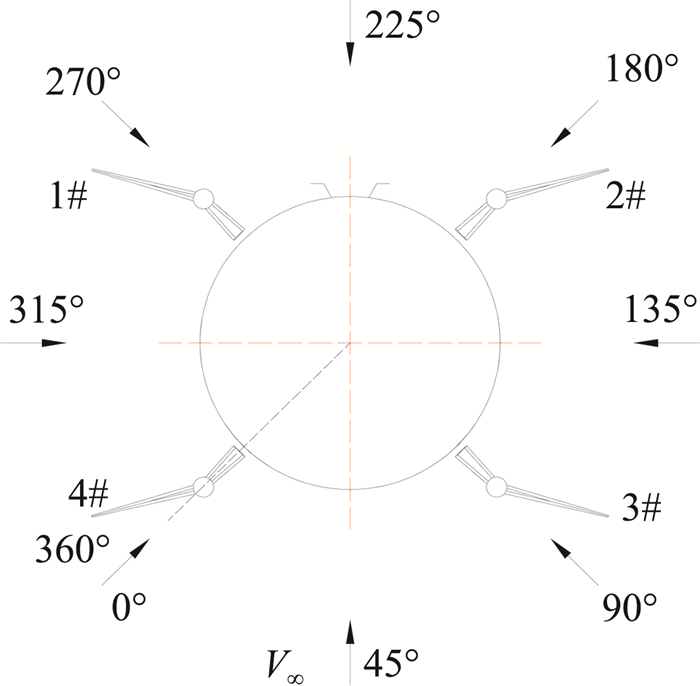
2.3 滚转角变化关系机载导弹一般包括弹身和4片尾舵,在展开过程中4片尾舵由于所处方位不同而受到气动载荷也不同,从而会影响到舵面展开的同步性。本节在上述章节的基础上对折叠舵外翼在气流绕弹体一周滚转角下的气动特性进行了研究,该计算可以得到某工况下4片舵的受载特性。计算舵面为3#舵,计算状态见表 2。其中Ф角取22.5°一个间隔,计算Ф角示意图见图 10。
| 表 2 计算状态 Table 2 Calculation state |
|
|
|
图 10 气动滚转角示意图 Fig.10 Map of aerodynamic roll angle |
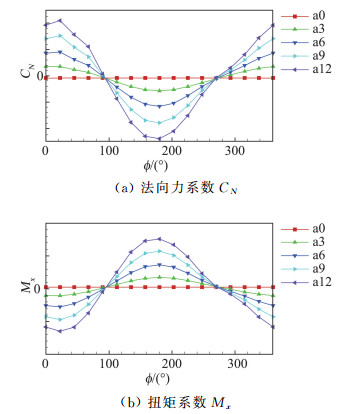
图 11给出了不同迎角下3#舵外翼法向力和扭矩系数随气动滚转角的变化关系。气动力/力矩在Ф=90°和Ф=270°附近最小,此时气流顺3#舵方向,气流与3#舵外翼在该Ф角附近夹角最小。从Ф=270°到Ф=90°范围内扭矩为负,该扭矩阻碍舵面展开,为阻尼力矩,且在Ф=22.5°附近有负的最大值。从Ф=90°到Ф=270°范围内扭矩为正,该扭矩驱动舵面展开,为驱动力矩,且在Ф=180°附近有正的最大值。
|
图 11 气动滚转角计算结果 Fig.11 Results of roll angle |
从周向角的情况来看,外翼气动载荷的大小与外翼当地气流夹角有关,气流越垂直于舵面则相应的载荷也就越大。但从图 11中可以看出,相同气流夹角下最大负扭矩的绝对值要小于正最大扭矩,这是由于受弹身和内翼的影响在Ф=22.5°附近时气流顺着外翼流出而在Ф=180°附近时气流被堵在弹身、内翼和外翼形成的局部区域内形成局布高压,因而载荷会更高一些。
从上述分析不难得到以下结论:折叠舵在展开过程中,4片舵面所受到的气动载荷是不相同的,载荷的大小与外翼当地气流夹角正相关,一般来讲气流越垂直于舵面所受到的载荷就会越大。同时气动载荷还受到弹身与内外翼构型的共同影响,气流受堵时载荷会更大一些。导弹上的4片舵面中,按图 10的折叠方式,Ф=45°正迎角时迎风舵受到的气动力矩为阻尼力矩,背风舵受到的力矩为驱动力矩,背风区的舵面会更容易展开。
2.4 气动力系数变化规律从2.3节中分析可知,外翼气动载荷与当地气流偏角存在某种关系,本节在2.3节的基础上对这上规律进行了推导。
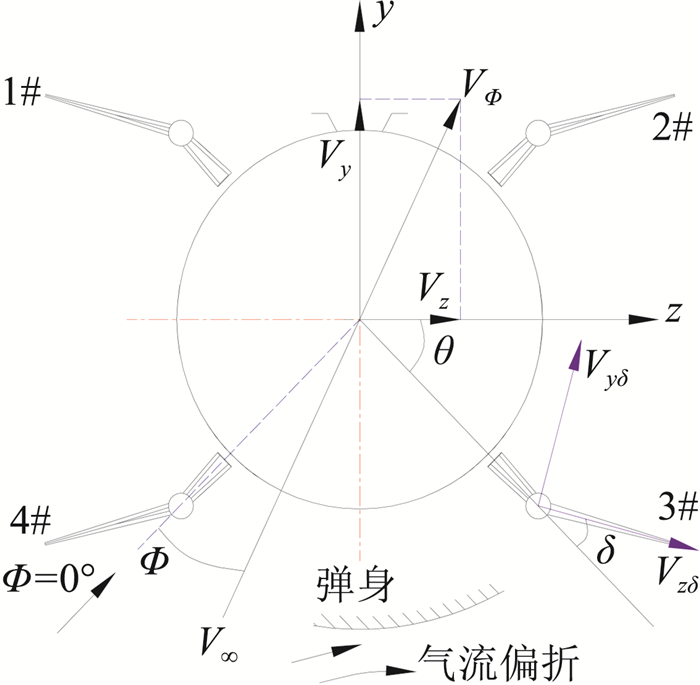
由图 12,可以推导出当地气流偏角的公式。将气流沿弹轴和垂直于弹轴的方向进行分解,见式(1):
| $ \left\{ {\begin{array}{*{20}{l}} {{V_x} = {V_\infty }\cos \alpha }\\ {{V_\varphi } = {V_\infty }\sin \alpha } \end{array}} \right. $ | (1) |
|
图 12 当地气流偏角 Fig.12 Local stream angle |
将速度分量分解到弹体坐标系,见式(2):
| $ \left\{\begin{array}{l} V_{y}=V_{\varphi} \cos \phi \\ V_{z}=V_{\varphi} \sin \phi \end{array}\right. $ | (2) |
分解到舵面坐标系,见式(3):
| $ \left\{\begin{array}{l} V_{y \delta}=V_{y} \cos (\theta-\delta)-V_{z} \sin (\theta-\delta) \\ V_{z \delta}=V_{z} \cos (\theta-\delta)+V_{y} \sin (\theta-\delta) \end{array}\right. $ | (3) |
根据迎角的定义[20]可得外翼当地气流偏角αT为:
| $ \tan \left(\alpha_{T}\right)=\frac{V_{y \hat{\delta}}}{V_{x}} $ | (4) |
再联立(1),(2),(3)式化简之后得到:
| $ \alpha_{T}=\arctan [\tan \alpha \cos (\phi+\theta-\delta)] $ | (5) |
可见,当地气流偏角αT是合成迎角α、合成滚转角ϕ,舵面方位角θ和外翼折叠角δ的函数,即:
| $ \alpha_{T}=\alpha_{T}(\alpha, \phi, \theta, \delta) $ | (6) |
根据薄翼理论[20-21]可以建立起折叠舵外翼气动力系数与当地气流偏角的如下关系:
| $ C_{F}=C \cdot \alpha_{T}(\alpha, \phi, \theta, \delta)+C_{0} $ | (7) |
其中,C表示与来流Ma数、弹外形及外翼外形有关的参数,C0则表示αT=0时弹身对外翼的初始干扰。
但是在实际使用公式(7)时发现气动载荷的最大值并非发生在αT为最大的时候,预测最大值与理论最大值在Φ轴上会有一个相移。其原因在于αT的计算是通过速度按理想无干扰的方式分解到舵面坐标系下的,而实际上气流在流过弹体时方向会发生偏折(图 12)。
按照图 12的解释,不难发现实际最大当地气流偏角应该比式(7)预估的要靠后,因此对式(7)进行修正,得到式(8)如下:
| $ \alpha_{T}=\alpha_{T}\left(\alpha, \phi-\phi^{\prime}, \theta, \delta\right) $ | (8) |
其中ϕ′表示考虑弹身干扰之后的合成ϕ角修正量。考虑ϕ修正之后的折叠舵外翼气动力计算公式则为:
| $ C_{F}=C \cdot \alpha_{T}\left(\alpha, \phi-\phi^{\prime}, \theta, \delta\right)+C_{0} $ | (9) |
进一步的,则可以将外翼法向力及扭矩系数写成式(10)的形式。
| $ \left\{\begin{array}{l} C_{n}=C \cdot \alpha_{T}\left(\alpha, \phi-\phi^{\prime}, \theta, \delta\right)+C_{0} \\ M_{x}=M \cdot \alpha_{T}\left(\alpha, \phi-\phi^{\prime}, \theta, \delta\right)+M_{0} \end{array}\right. $ | (10) |
通过有限的气动数据对式(10)中的参数进行辨识即可得到所有气动滚转角、合成迎角,舵片方位角和折叠角下的气动数据。
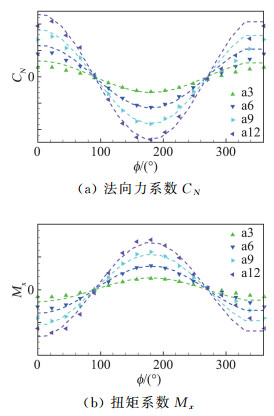
图 13给出了不同迎角下按式(10)给出的结果与样本数据的对比。在ϕ角0°~270°范围内预测值与样本值几乎完全重合,而在270°~360°范围内预测值存在一定误差。该误差产生的原因在于3#舵向上折,在该区间内外翼恰好处在受弹身干扰最为严重的区域,采用简单的当地气流偏角计算已不再适用,后续需对该部分的影响作进一步的研究。
|
图 13 预测值与样本值对比 Fig.13 Predict value vs. sample value |
本文采用风洞试验和CFD计算相结合的方法对机载导弹折叠舵外翼气动特性进行了研究,研究影响因素包括迎角、折叠角、Ma数气动滚转角等。通过研究可以得出以下结论:
1) “×”型状态下外翼在完全折叠时所受的气动载荷最小,随着外翼的展开气动载荷逐渐增大,在折叠角30°附近时载荷最大;
2) 外翼气动力系数受Ma数影响较小,从Ma=0.6到Ma=1.5范围之内Ma=1.2时的气动系数最大;
3) 外翼气动载荷与当地气流偏角存在正相关关系,可以写成合成迎角α、合成滚转角ϕ,舵面方位角θ和外翼折叠角δ的函数。受弹身干扰气动ϕ角需作适当平移。在ϕ角0°~270°范围内预测值与样本值几乎完全重合,在270°~360°范围内外翼处于背风区复杂流场之下,预测公式需做进一步的研究。
致谢: 感谢西北工业大学航空学院张伟伟教授在本文研究思路上给予的指导。
| [1] |
武文康, 张彬乾, 编著. 战斗机气动布局设计[M]. 西北工业大学出版社, 2005. WU W K, ZHANG B Q. Aerodynamic layout design for fighter aircraft[M]. Northwestern Polytechnical University Press, 2005. (in Chinese) |
| [2] |
BJORG S T. Flow around an obiect projected from a cavity into a supersonic freestream: AFIT/GAE/ENY/01-M02[R]. Ohio: Wright Patterson Air Force Base, 2004.
|
| [3] |
张培红, 王明, 邓有奇, 等. 武器分离及舱门开启过程数值模拟研究[J]. 空气动力学学报, 2013, 6(3): 277-281. ZHANG P H, WANG M, DENG Y Q, et al. Numerical simulation of store separation and door operation[J]. Acta Aerodynamica Sinica, 2013, 6(3): 277-281. (in Chinese) |
| [4] |
BAKER W B JR, KEEN K, MORGRET C. Validation of weapon separation predictions using F/A-22 flight test results: AIAA-2004-6803[R]. Restone: AIAA, 2004.
|
| [5] |
郭秋亭, 张来平, 常兴华, 等. 变形飞机动态气动特性数值模拟研究[J]. 空气动力学学报, 2011, 12(6): 744-750. GUO Q P, ZHANG L P, CHANG X H, et al. Numerical simulation of dynamic aerodynamic characteristics of a morphing aircraft[J]. Acta Aerodynamica Sinica, 2011, 12(6): 744-750. DOI:10.3969/j.issn.0258-1825.2011.06.010 (in Chinese) |
| [6] |
洪金森, 等译. 战术导弹空气力学[M]. 宇航出版社, 1999. 12. HONG J S, et al. Tactical missile aerodynamics[M]. China Aerospace Publishing House, 1999. 12. (in Chinese) |
| [7] |
李双江. 火箭弹折叠尾翼的设计与优化[D]. 中国工程物理研究院, 硕士论文, 2016. LI S J. The structure design and weight optimization of folding wing in rocket projectile[D]. Institute of Systems Engineering China Academy of Engineering Physics, 2016. (in Chinese) |
| [8] |
秦永明, 蔡琛芳, 董金刚. 机载导弹折叠舵展开气动特性试验研究[J]. 航空兵器, 2013(5): 3-6. QIN Y M, Cai C F, DONG J G. Experimental study on aerodynamics of airborne missile folding rudder[J]. Aero Weaponry, 2013(5): 3-6. (in Chinese) |
| [9] |
吕胜利, 刘平, 杨广珺, 等. 折叠机翼展开过程气动特性实验研究[J]. 飞行力学, 2013, 2(1): 80-83. LU S L, LIU P, YANG G J, et al. Experimental study of aerodynamic characteristics in folding wings deployment process[J]. Flight Dynamics, 2013, 2(1): 80-83. (in Chinese) |
| [10] |
贾毅, 李甘牛. 战术导弹折叠尾翼展开动态测力试验技术研究[J]. 实验流体力学, 2007, 6(2): 46-49. JIA Y, LI G N. The dynamic test of folded wing deploying of some tqctical missiles[J]. Journal of Experiments in Fluid Mechanics, 2007, 6(2): 46-49. (in Chinese) |
| [11] |
蒋坤, 钱丹丹, 吴凯, 等. 高速风洞折叠舵展开过程试验技术[C]//CARS-2013-1573.
|
| [12] |
YUAN Y, Li D, MA Y Y, et al. Numerical simulation of dynamic deployment of the folded wings[R]. AIAA 2017-2371.
|
| [13] |
JIANG K, ZHANG W, XU X W, et al. Investigation of dynamic characteristic of forward swept folding wing[C]//International Conference on Automation and Logistics, Chongqing, China, August 2011.
|
| [14] |
范国芳, 李强, 操小龙, 等. 折叠翼面展开过程中气动载荷特性数值模拟[J]. 气体物理, 2017, 11(6): 48-53. FAN G F, Li Q, CAO X L, et al. Numerical study on aerodynamics loads of a high-speed aircraft folding wing in its deploying procedure[J]. Physics of Gases, 2017, 11(6): 48-53. (in Chinese) |
| [15] |
单继祥, 甄文强, 石运国, 等. 气动效应对折叠翼展开过程影响研究[J]. 弹箭与制导学报, 2017, 10(5): 105-108. SAN J X, ZHEN W Q, SHI Y G, et al. Effects of aerodynamic moment on the folding-wing deployment process[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2017, 10(5): 105-108. (in Chinese) |
| [16] |
JAN R WRIGHT, JONATHAN E COPPER. Introduction to aircraft aeroelasticity and loads[M]. John Wiley & Sons, Ltd. 2007.
|
| [17] |
ZHANG W, GONG Y, LIU Y. Abnormal changes of dynamic derivatives at low reduced frequencies[J]. Chinese Journal of Aeronautics, 2018, 31(7): 1428-1436. DOI:10.1016/j.cja.2018.05.001 |
| [18] |
张伟伟, 等. 非定常流动与流动控制基础[M]. 科学出版社, 2020. ZHANG W W, et al. Basic of unsteady flow and flow control[M]. Science Press, 2020. (in Chinese) |
| [19] |
Fluent inc. Fluent user's guide[S]. 2006.
|
| [20] |
JOHN D ANDERSON, Jr. Fundamentals of aerodynamics[M]. Fifth Edition. McGraw-Hill Education 2010, 2.
|
| [21] |
李凤蔚, 主编. 空气与气体动力学引论[M]. 西北工业大学出版社, 2007, 5. LI F W. Introduction to aerodynamics and gas dynamics[M]. Northwestern Polytechnical University Press, 2007, 5. (in Chinese) |
 2021, Vol. 39
2021, Vol. 39

