2. 中国工程物理研究院研究生院, 北京 100088
2. Graduate School of China Academy of Engineering Physics, Beijing 100088, China
多介质可压缩流体动力学问题的数值计算方法主要分为两类:欧拉方法(Eulerian method)和拉氏方法(Lagrangian method)。欧拉方法采用固定的空间网格进行计算。拉氏方法的网格跟随流体一起运动。这两种方法各有利弊。欧拉方法易于处理流场大变形,但是难以精确地捕捉物质界面。拉氏方法能清晰地刻画、描述物质界面,但是当流场中发生大变形时,网格会严重扭曲,导致计算精度下降甚至计算终止。为了结合这两种方法的优点,Hirt等[1]提出了ALE(Arbitrary Lagrangian-Eulerian)方法,其中网格可以以任意指定的方式移动。大多数ALE算法[2-7]包括三步:拉氏步、重分步和重映步。传统的ALE方法用单元边描述物质界面,并且要求每个单元只有一种介质。当物质界面变形严重时,很难生成质量良好的新网格。为了解决这个问题,Peer等[8]将传统的ALE方法与界面捕捉方法相结合,提出了MMALE(Multi-material ALE)方法。这种方法引入了混合单元(一个单元中存在多种介质),在混合单元中重构物质界面,重分网格时可以跨过界面生成新的网格,因此比传统的ALE方法提供了额外的灵活性。MMALE方法的计算流程与传统的ALE方法类似。首先,在拉氏步更新每种介质的物理量以及网格坐标,其中对混合单元需要用热力学封闭模型来更新各种介质的物理量。当网格变形严重时,需要重构混合单元的物质界面,为后面重映步提供界面信息。然后,在重分步生成一个几何品质较好的新网格。最后, 在重映步将旧网格的物理量映射到新网格上。
在拉氏步,常用的离散方法有两种。一种是交错型格式[9-12],指的是速度定义在节点上,而其他变量(密度、压力和内能等)定义在单元中心。另一种是中心型格式[13-17],所有变量都定义在单元中心。中心型格式比交错型格式有一些优点。例如,交错型格式对变量使用不同的控制体, 很难对所有变量构建一致的高阶精度。本文采用中心型格式。中心型格式可以分为两类: 中心型有限体积方法[16-17]和中心型间断有限元方法[18-20]。有限体积方法需要较大的单元模板来构造高阶格式;而间断有限元是利用单元内的高阶插值多项式来构造高阶格式。因此,间断有限元方法比有限体积方法更具有发展高阶格式的前景。重映步通常采用两种方法。一种是对流重映[21-25],它要求新旧网格离得比较近,计算效率比较高.另一种是积分重映[26-31], 它对新旧网格的关联要求不高,但是需要计算新旧网格的交点,计算结果比较精确。近年来,在MMALE方法的研究上取得了一些进展[32-35]。Galera和Maire等[33-34]提出了一种单元中心型二维MMAIE方法,界面重构采用VOF(Volume of Fluid)或MOF方法。贾祖朋等[29]提出了一种基于MOF界面重构的交错型非结构MMALE方法,模拟涉及强剪切变形的多介质可压缩流动。后来,贾祖朋等[36]发展了一种基于改进的MOF方法的中心型MMALE方法。上面提到的MMALE方法在拉氏步都是用有限体积方法。
本文提出了一种二维中心型间断有限元MMALE方法。在拉氏步,使用间断有限元方法对流体力学方程组进行离散,选取文献[19]中的基函数。为了构造二阶积分重映算法,对拉氏步获得的物理量单元均值做分片线性重构。经典的限制方法是对重构多项式的梯度进行限制[26, 37]。近些年, Blanchard和Loubere[38]提出了基于MOOD (Multi-dimensional Optimal Order Detection)限制策略[39-40]的后验校正。本文采用后验校正,并做了一些改动以适应多介质计算。对新旧网格相交的计算,借鉴文献[31]的三维“剪裁投影”算法的基本思想,设计了二维“剪裁投影”算法,显著降低了多边形相交算法的复杂度。
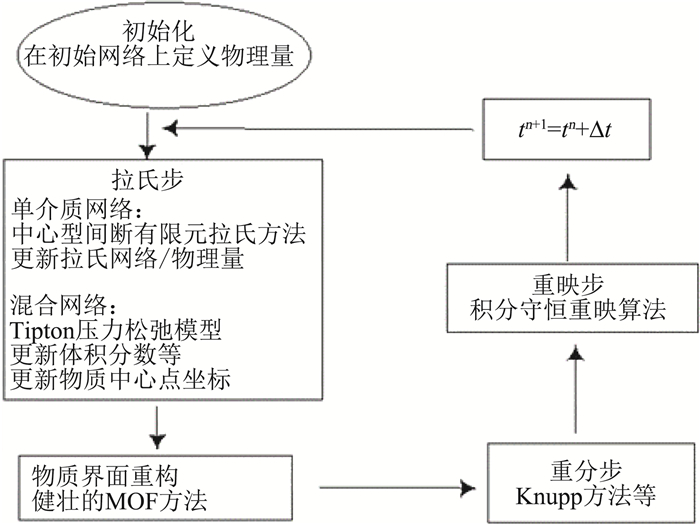
1 MMALE方法的计算步骤本文的MMALE方法的计算步骤如图 1所示。首先是初始化步:定义初始网格上所有物理量的分布,使用文献[41]中2.3.1节的方法定义初始网格中物质体积分数和中心坐标。在拉氏步,采用单元中心型间断有限元方法求解流体动力学方程,并将物理量和网格从时间tn更新到时间tn+1=tn+Δt上。混合单元的封闭模型采用Tipton压力松弛模型[42-43]。使用文献[44]中等参坐标方法更新物质的中心坐标。界面重构采用卿芳等提出的一种健壮的MOF算法[45]。在网格重分步,利用Knupp算法[46]对拉氏网格进行光滑处理;或者采用初始网格作为重分网格。最后,在重映步,使用二阶积分守恒重映方法,将时间tn+1的拉氏网格中的所有物理量映射到重分后的新网格上。
|
图 1 MMALE方法流程图 Fig.1 A flowchart of the multi-material ALE algorithm |
欧拉框架下的二维无粘可压缩Euler方程组的向量形式为:
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \nabla \cdot (\mathit{\boldsymbol{Uu}}) + \nabla \cdot (\mathit{\boldsymbol{F}},\mathit{\boldsymbol{G}}) = 0 $ | (1) |
其中
下面给出式(1)的弱形式。式(1)两边同时乘以函数φ,并经过微分运算,得:
| $ \begin{array}{l} \frac{{\partial (\varphi \mathit{\boldsymbol{U}})}}{{\partial t}} + \nabla \cdot (\varphi \mathit{\boldsymbol{Uu}}) - U\left( {\frac{{\partial \varphi }}{{\partial t}} + \mathit{\boldsymbol{u}} \cdot \nabla \varphi } \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \nabla \cdot (\varphi (\mathit{\boldsymbol{F}},\mathit{\boldsymbol{G}})) - (\mathit{\boldsymbol{F}},\mathit{\boldsymbol{G}}) \cdot \nabla \varphi = 0 \end{array} $ | (2) |
由于
| $ \begin{array}{*{20}{l}} {\int_{\mathit{\Omega }(t)} {\frac{{\partial (\varphi \mathit{\boldsymbol{U}})}}{{\partial t}}} {\rm{d}}\mathit{\Omega } + \int_{\mathit{\Omega }(t)} \nabla \cdot (\varphi \mathit{\boldsymbol{Uu}} + \varphi (\mathit{\boldsymbol{F}},\mathit{\boldsymbol{G}})){\rm{d}}\mathit{\Omega }}\\ {\quad - \int_{\mathit{\Omega }(t)} \mathit{\boldsymbol{U}} \frac{{{\rm{d}}\varphi }}{{{\rm{d}}t}}{\rm{d}}\mathit{\Omega } - \int_{\mathit{\Omega }(t)} {(\mathit{\boldsymbol{F}},\mathit{\boldsymbol{G}})} \nabla \varphi {\rm{d}}\mathit{\Omega } = 0} \end{array} $ | (3) |
对上式第一项用Reynolds输运定理以及对第二项用散度定理,最终得到:
| $ \begin{array}{c} \frac{{\rm{d}}}{{{\rm{d}}t}}\int_{\mathit{\Omega }(t)} \varphi \mathit{\boldsymbol{U}}{\rm{d}}\mathit{\Omega } = \int_{\mathit{\Omega }(t)} \mathit{\boldsymbol{U}} \frac{{{\rm{d}}\varphi }}{{{\rm{d}}t}}{\rm{d}}\mathit{\Omega } + \int_{\mathit{\Omega }(t)} {(\mathit{\boldsymbol{F}},\mathit{\boldsymbol{G}})} \cdot \nabla \varphi {\rm{d}}\mathit{\Omega }\\ - \int_{\partial \mathit{\Omega }(t)} {\left( {\varphi \mathit{\boldsymbol{F}}{n^x} + \varphi \mathit{\boldsymbol{G}}{n^y}} \right)} {\rm{d}}S \end{array} $ | (4) |
其中n=(nx, ny) 表示单元边界S的单位外法向量。
接下来对空间进行离散。假设初始时刻的计算区域为Wt=0=Ω0,Ω0被剖分成N个不重叠的四边形单元{Wk0,k=1, …, N}。在任意时刻t,这些四边形单元记为{Wk,k=1, …, N}。定义一个分片多项式有限元空间:
| $ \begin{array}{c} V_h^n = \left\{ {{\varphi _h} \in {L_2}(\mathit{\Omega }(t)):{\varphi _h}\mid {W_k} \in {P_n}\left( {{W_k}} \right),} \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\forall {W_k},k = 1, \cdots ,N} \right\} \end{array} $ | (5) |
其中Pn(Wk)为单元Wk上不超过n次多项式的全体集合。那么,对任意的单元Wk,下面的方程成立:
| $ \begin{array}{*{20}{c}} {\frac{{\rm{d}}}{{{\rm{d}}t}}\int_{{W_k}} {{\varphi _h}} {\mathit{\boldsymbol{U}}_h}{\rm{d}}{W_k} = \int_{{W_k}} {{\mathit{\boldsymbol{U}}_h}} \frac{{{\rm{d}}{\varphi _h}}}{{{\rm{d}}t}}{\rm{d}}{W_k} + }\\ {\int_{{W_k}} {\left( {{\mathit{\boldsymbol{F}}_h},{\mathit{\boldsymbol{G}}_h}} \right)} \cdot \nabla {\varphi _h}{\rm{d}}{W_k}}\\ { - \int_{\partial {W_k}} {\left( {{\varphi _h}{\mathit{\boldsymbol{F}}_h}{n^x} + {\varphi _h}{\mathit{\boldsymbol{G}}_h}{n^y}} \right)} {\rm{d}}l} \end{array} $ | (6) |
定义标准单元Ωst=[-1, 1]2,它的坐标记为(ξ, η),ξ, η[-1, 1]。对于任意的时间t,存在一个从Ωst到Wk的双线性映射Fk: (ξ, η)∈Ωst→(x, y)∈Wk:
| $ x = \sum\limits_{i = 1}^4 {{x_i}} {\psi _i}(\xi ,\eta ),\quad y = \sum\limits_{i = 1}^4 {{y_i}} {\psi _i}(\xi ,\eta ) $ | (7) |
其中(xi, yi)表示单元Wk的顶点Mi的坐标,
标准单元Ωst的四个基函数为σ1=1, σ2=ξ, σ3=η, σ4=ξη。由于Fk是光滑的可逆映射,因此:
| $ \begin{array}{*{20}{c}} {{\sigma _i}(\xi ,\eta ) = {\sigma _i}\left( {F_k^{ - 1}(x,y)} \right) \buildrel \Delta \over = {B_i}(x,y,t),}\\ {i = 1, \cdots ,4} \end{array} $ | (8) |
选取Bi, i=1, …, 4为有限元空间Vhn的基函数。这个基函数有个非常重要的性质,它的物质导数为零,即
| $ {{\mathit{\boldsymbol{U}}_h} = \sum\limits_{i = 1}^4 {{\mathit{\boldsymbol{U}}_{ki}}} {B_{ki}},\quad (x,y) \in {W_k}} $ | (9) |
| $ {{\varphi _h} = \sum\limits_{i = 1}^4 {{\varphi _{ki}}} {B_{ki}},\quad (x,y) \in {W_k}} $ | (10) |
用间断有限元方法对(1)进行空间离散,就是寻找数值解Uh=(ρh, (ρu)h, (ρv)h, (ρE)h)T∈Vhn,使得对所有的试探函数φh∈Vhn和所有单元Wk, k=1, …N,满足:
| $ \begin{array}{*{20}{l}} {\frac{{\rm{d}}}{{{\rm{d}}t}}\int_{{W_k}} {{\varphi _h}} {\mathit{\boldsymbol{U}}_h}{\rm{d}}{W_k} = \int_{{W_k}} {\left( {{\mathit{\boldsymbol{F}}_h},{\mathit{\boldsymbol{G}}_h}} \right)} \cdot \nabla {\varphi _h}{\rm{d}}{W_k}}\\ { - \int_{\partial {W_k}} {\left( {{\varphi _h}{\mathit{\boldsymbol{F}}_h}{n^x} + {\varphi _h}{\mathit{\boldsymbol{G}}_h}{n^y}} \right)} {\rm{d}}l} \end{array} $ | (11) |
由于对所有试探函数φh∈Vhn,上式都成立。因此上式等价于:
| $ \begin{array}{*{20}{c}} {\frac{{\rm{d}}}{{{\rm{d}}t}}\sum\limits_{i = 1}^4 {\int_{{W_k}} {{\mathit{\boldsymbol{U}}_{ki}}} } {B_{ki}}{B_{km}}{\rm{d}}{W_k} = \int_{{W_k}} {{\mathit{\boldsymbol{F}}_h}} \cdot {\partial _x}{B_{km}}{\rm{d}}{W_k} + }\\ {\int_{{W_k}} {{\mathit{\boldsymbol{G}}_h}} \cdot {\partial _y}{B_{km}}{\rm{d}}{W_k}}\\ { - \int_{\partial {W_k}} {\left( {{\mathit{\boldsymbol{F}}_h}{n^x} + {\mathit{\boldsymbol{G}}_h}{n^y}} \right)} {B_{km}}{\rm{d}}l,m = 1,2,3,4} \end{array} $ | (12) |
数值解在单元的交界面上可以是间断的。因此在单元边界上定义一个数值通量函数F*和G*来代替原来的通量函数F和G[20]。边[Mr, Mr+1]上的数值通量定义为:
| $ \left\{ {\begin{array}{*{20}{l}} {F_{r,r + 1}^{1,*} = 0}\\ {F_{r,r + 1}^{2,*} = p_{r,r + 1}^*}\\ {F_{r,r + 1}^{3,*} = 0}\\ {F_{r,r + 1}^{4,*} = (pu)_{r,r + 1}^*} \end{array}\left\{ {\begin{array}{*{20}{l}} {G_{r,r + 1}^{1,*} = 0}\\ {G_{r,r + 1}^{2,*} = 0}\\ {G_{r,r + 1}^{3,*} = p_{r,r + 1}^*}\\ {G_{r,r + 1}^{4,*} = (pv)_{r,r + 1}^*} \end{array}} \right.} \right. $ | (13) |
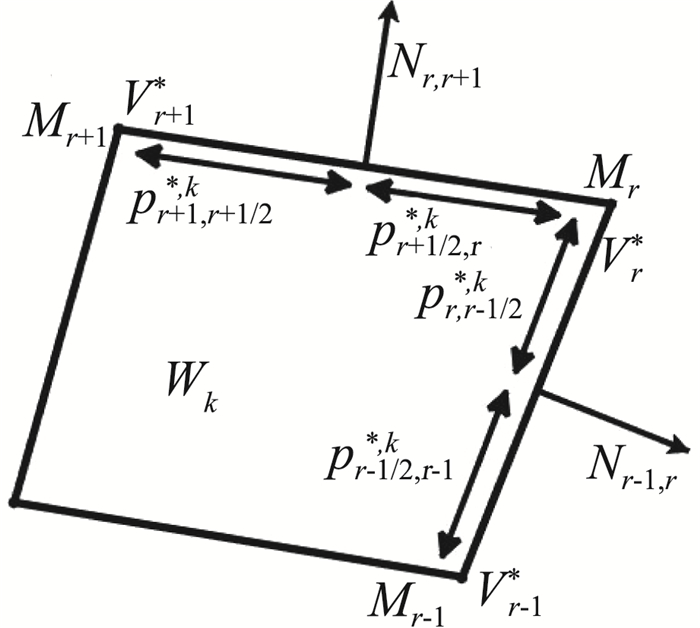
引入与文献[16]相同的记号。如图 2所示,在每条边上引入四个压力,其中每侧引入两个压力。
| $ {\mathit{\boldsymbol{V}}_{r,r + 1}^* = \frac{1}{2}\left( {\mathit{\boldsymbol{V}}_r^* + \mathit{\boldsymbol{V}}_{r + 1}^*} \right)} $ | (14) |
| $ {p_{r,r + 1}^{*,k} = \frac{1}{2}\left( {p_{r,r + \frac{1}{2}}^{*,k} + p_{r + \frac{1}{2},r + 1}^{*,k}} \right)} $ | (15) |
| $ {(p\mathit{\boldsymbol{V}})_{r,r + 1}^{*,k} = \frac{1}{2}\left( {p_{r,r + \frac{1}{2}}^{*,k}\mathit{\boldsymbol{V}}_r^* + p_{r + \frac{1}{2},r + 1}^{*,k}\mathit{\boldsymbol{V}}_{r + 1}^*} \right)} $ | (16) |
|
图 2 单元的记号 Fig.2 Notations in a quadrangular cell |
将(13)-(16)代入(12):
| $ {\frac{{\rm{d}}}{{{\rm{d}}t}}\sum\limits_{i = 1}^4 {\int_{W_{k}} {{\rho _{ki}}} } {B_{ki}}{B_{km}}{\rm{d}}{W_k} = 0,m = 1,2,3,4} $ | (17) |
| $ \begin{array}{*{20}{c}} {\frac{{\rm{d}}}{{{\rm{d}}t}}\sum\limits_{i = 1}^4 {\int_{W_{k}} {{{(\rho u)}_{ki}}} } {B_{ki}}{B_{km}}{\rm{d}}{W_k} = \int_{W_{k}} {{p_k}} {\partial _x}{B_{km}}{\rm{d}}{W_k}}\\ { - \sum\limits_{r = 1}^4 {\frac{1}{2}} \left( {p_{r,r + \frac{1}{2}}^{*,k} + p_{r + \frac{1}{2},r + 1}^{*,k}} \right)n_{r,r + 1}^x\int_{r,r + 1} {{B_{km}}} {\rm{d}}l,}\\ {m = 1,2,3,4} \end{array} $ | (18) |
| $ \begin{array}{*{20}{c}} {\frac{{\rm{d}}}{{{\rm{d}}t}}\sum\limits_{i = 1}^4 {\int_{W_{k}} {{{(\rho v)}_{ki}}} } {B_{ki}}{B_{km}}{\rm{d}}{W_k} = \int_{W_{k}} {{p_k}} {\partial _y}{B_{km}}{\rm{d}}{W_k}}\\ { - \sum\limits_{r = 1}^4 {\frac{1}{2}} \left( {p_{r,r + \frac{1}{2}}^{*,k} + p_{r + \frac{1}{2},r + 1}^{*,k}} \right)n_{r,r + 1}^y\int_{r,r + 1} {{B_{km}}} {\rm{d}}l,}\\ {m = 1,2,3,4} \end{array} $ | (19) |
| $ \begin{array}{c} \frac{\mathrm{d}}{\mathrm{d} t} \sum\limits_{i=1}^{4} \int_{W_{k}}(\rho E)_{k i} B_{k i} B_{k m} \mathrm{~d} W_{k}= \\ \int_{W_{k}}(p u)_{k} \partial_{x} B_{k m}+(p v)_{k} \partial_{y} B_{k m} \mathrm{~d} W_{k} \\ -\sum\limits_{r=1}^{4} \frac{1}{2}\left[\left(p_{r, r+\frac{1}{2}}^{*, k} u_{r}^{*}+p_{r+\frac{1}{2}, r+1}^{*, k} u_{r+1}^{*}\right) n_{r, r+1}^{x}+\right. \\ \left.\left(p_{r, r+\frac{1}{2}}^{*, k_{1}} v_{r}^{*}+p_{r+\frac{1}{2}, r+1}^{*, k} v_{r+1}^{*}\right) n_{r, r+1}^{y}\right] \\ \int_{r, r+1} B_{k m} \mathrm{~d} l, \quad m=1,2,3,4 \end{array} $ | (20) |
关于单元Wk的顶点速度Vq*和压力pq, k*, k(pq, k*, k-1)的计算,参考Maire的节点求解器[16-17]。
最后,如果令:
| $ {{\mathit{\boldsymbol{M}}_k} = \int_{{W_k}} {{B_{ki}}} {B_{km}}{\rm{d}}{W_k}(i = 1,2,3,4;m = 1,2,3,4)} $ | (21) |
| $ {{\mathit{\boldsymbol{u}}_{k1}} = \left[ {{\rho _{k1}},{\rho _{k2}},{\rho _{k3}},{\rho _{k4}}} \right]} $ | (22) |
| $ {{\mathit{\boldsymbol{u}}_{k2}} = \left[ {\rho {u_{k1}},\rho {u_{k2}},\rho {u_{k3}},\rho {u_{k4}}} \right]} $ | (23) |
| $ {{\mathit{\boldsymbol{u}}_{k3}} = \left[ {\rho {v_{k1}},\rho {v_{k2}},\rho {v_{k3}},\rho {v_{k4}}} \right]} $ | (24) |
| $ {{\mathit{\boldsymbol{u}}_{k4}} = \left[ {\rho {E_{k1}},\rho {E_{k2}},\rho {E_{k3}},\rho {E_{k4}}} \right]} $ | (25) |
将顶点速度(ur*, vr*)和压力pq, k*, k(pq, k*, k-1)代入(17)~(20),可以得到:
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}{\mathit{\boldsymbol{M}}_k} \cdot {\mathit{\boldsymbol{u}}_{kj}} = {L_{kj}},\quad j = 1,2,3,4 $ | (26) |
其中Lkj(j=1, 2, 3, 4)是(17)~(20)式空间离散算子得到的向量。
半离散格式(26)的时间离散采用二阶显式Runge-Kutta方法[48]。时间步长的估计遵循标准的CFL准则和每个时间步上限制单元面积的变化,详情请参考文献[16-17]。空间二阶重构采用最小二乘算法[17],并采用Barth-Jesperson限制器[49]抑制非物理的数值振荡。
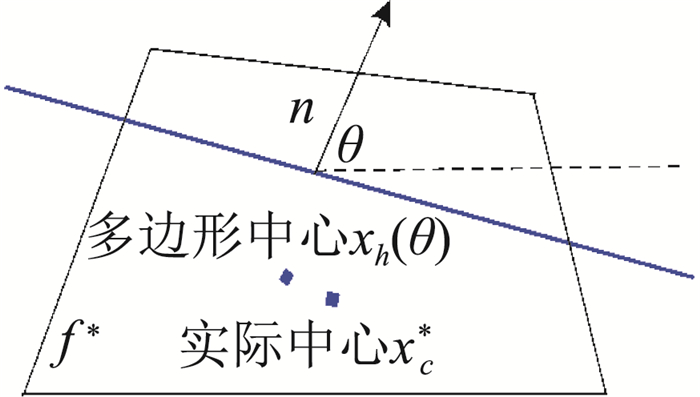
3 界面重构在拉氏步,需要对混合网格中的每种介质更新物质中心点坐标以及体积分数,以便在重映步之前用MOF方法重构物质界面。先来回顾一下经典的MOF方法[50]。如图 3所示,给定混合网格内的某种介质物质中心点坐标xc*和体积分数f*。n表示待确定的直线界面的单位法向量, θ表示向量n与x轴的夹角,即n=(cosθ, sinθ)。需要重构一条直线,使得该直线所截取的多边形的体积分数为f*,而中心点与xc*尽可能的接近。求重构直线的问题可以转化为极小化目标函数:
| $ f(\theta ) = \left\| {{x_h}(\theta ) - x_c^*} \right\|_2^2 $ | (27) |
|
图 3 MOF方法示意图 Fig.3 A sketch of the MOF method |
其中xh(θ)表示直线截取的多边形的中心点。文献[50]用最优化方法求解上述极小化问题,有可能收敛到局部极小值。因此,近年有学者对经典的MOF方法做了一些改进。
注意到f(θ)的一阶导数[50-51],f′(θ)=2(xh(θ)-xc*)·x′h(θ), 0≤θ≤2π文献[51]中提到f′(θ)是关于θ 的连续函数。因此,f(θ)的最小值点一定是f′(θ)的零点或者区间端点。文献[45]提出了一种健壮的算法计算f′(θ)的零点。本文采用这种健壮的MOF方法[45]。
4 重映为了便于描述,引入一些记号。假设计算区域划分成两套不重叠的网格。拉氏(旧)网格{W}由单元W组成;重分(新)网格
为了构造二阶重映算法,需要在旧单元上对每种介质的物理量g=ρ, ρu, ρe重构一个分片线性多项式。如果旧单元Wk是一个只含有介质i的纯网格单元,那么把它记为Pi, k;如果旧单元Wk是一个混合网格,需要用MOF方法重构物质界面,那么包含介质i的多边形记为Pi, k。设(xc, i, k, yc, i, k)是多边形Pi, k的中心坐标。物理量g在Pi, k的均值用gi, k表示.在Pi, k重构一个多项式gi, k(x, y):
| $ \begin{array}{l} {g_{i,k}}(x,y) = {{\bar g}_{i,k}} + {\left( {\frac{{\partial g}}{{\partial x}}} \right)_{i,k}}\left( {x - {x_{c,i,k}}} \right) + \\ {\left( {\frac{{\partial g}}{{\partial y}}} \right)_{i,k}}\left( {y - {y_{c,i,k}}} \right) \end{array} $ | (28) |
其中梯度
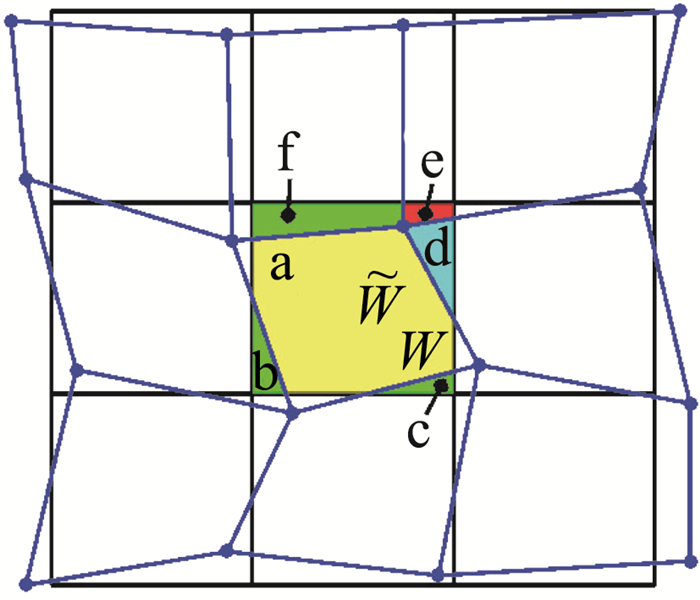
由于本文采用积分守恒重映方法,因此需要计算新单元
| $ \tilde{W}=\bigcup\limits_{i, k} \tilde{W} \cap P_{i, k}, \tilde{W} \cap P_{i, k} \neq \varnothing $ | (29) |
|
图 4 新单元 |
因此,新单元
| $ \tilde{V}_{\widetilde{W}}=\sum\limits_{i, k} V_{\widetilde{W} \cap P_{i, k}} $ | (30) |
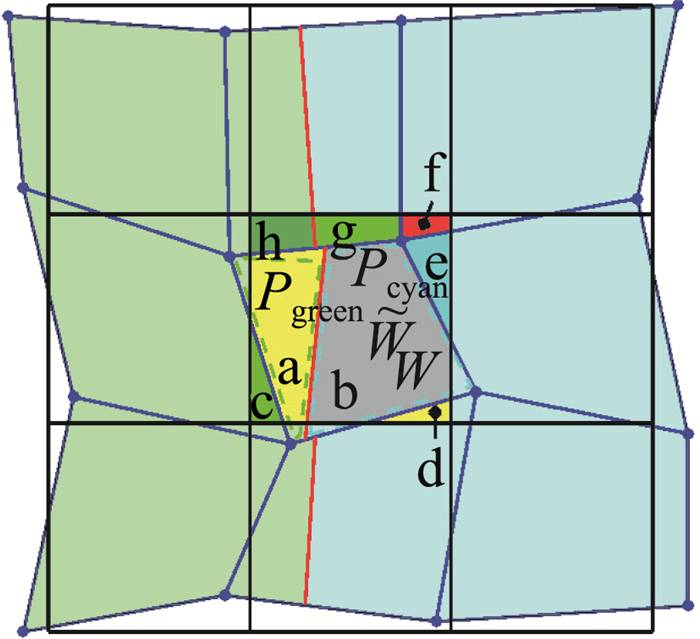
值得注意的是,每一个相交子多边形只包含一种介质。因此,如果旧单元是混合网格,那么需要计算新单元与混合网格中单介质子多边形的交点,而不是新单元与整个混合网格的交点。如图 5,3×3的网格由两种介质组成,物质界面用中间的粗实线来表示。界面的左边是第一种物质,界面的右边是第二种物质。正中间的新单元
|
图 5 单元内物质用物质界面(红线)分隔开。单介质子多边形用Pgreen,Pcyan表示 Fig.5 Materials are separated by material interface (red lines) in each cell. Pgreen and Pcyan are particular pure material sub-polygons |
下面介绍求相交子多边形的一个算法。这个算法遵循陈享等[31]的三维“剪裁投影”算法基本思想,并改为退化的二维“剪裁投影”算法。由于新单元是四边形,可以先把它分解成两个三角形。然后用这两个三角形分别和旧网格求相交子多边形,因而,新单元的面积等于这两个三角形分别得到的相交子多边形的面积之和。这个新旧网格相交的算法归结为求三角形与多边形的交点。算法分为以下三步:
1) 仿射变换
设参考坐标系为X,物理坐标系为x,参考坐标系中单位三角形
2) “剪裁投影”算法
我们提出了一种“剪裁投影”算法,高效、鲁棒地计算参考坐标系中单位三角形
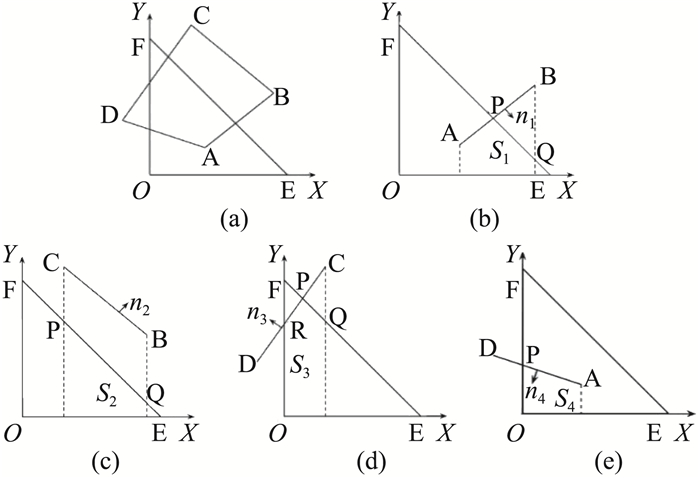
以图 6(a)为例, 单位三角形
| $ \begin{array}{*{20}{c}} {\int_S {{\rm{d}}} X{\rm{d}}Y = {\mathop{\rm sign}\nolimits} \left( {{n_{1Y}}} \right)\int_{{S_1}} {{\rm{d}}} X{\rm{d}}Y + {\mathop{\rm sign}\nolimits} \left( {{n_{2Y}}} \right)\int_{{S_2}} {{\rm{d}}} X{\rm{d}}Y}\\ {\quad + {\mathop{\rm sign}\nolimits} \left( {{n_{3Y}}} \right)\int_{{S_3}} {{\rm{d}}} X{\rm{d}}Y + {\mathop{\rm sign}\nolimits} \left( {{n_{4Y}}} \right)\int_{{S_4}} {{\rm{d}}} X{\rm{d}}Y = }\\ {\sum\limits_i {{\mathop{\rm sign}\nolimits} } \left( {{n_{iY}}} \right)\int_{{S_i}} {{\rm{d}}} X{\rm{d}}Y} \end{array} $ | (31) |
|
图 6 单位三角形和多边形的交点 Fig.6 Intersections of an unit triangle and a polygon |
相交多边形
| $ V(\mathbb{T} \cap \mathbb{P})=\sum\limits_{i} \operatorname{sign}\left(n_{i Y}\right) \int_{S_{i}} \mathrm{~d} X \mathrm{~d} Y $ | (32) |
同理,可以得到
| $ X(\mathbb{T} \cap \mathbb{P})=\frac{\sum\limits_{i} \operatorname{sign}\left(n_{i Y}\right) \int_{S_{i}} \mathrm{~d} X \mathrm{~d} Y}{V(\mathbb{T} \cap \mathbb{P})} $ | (33) |
3) 相交多边形的面积和中心坐标
最后,通过坐标变换,将参考坐标系中相交多边形的面积和中心坐标转换为物理坐标系中面积和中心坐标:
| $ V(\boldsymbol{T} \cap \boldsymbol{P})=\operatorname{det}(\boldsymbol{A}) \times V(\mathbb{T} \cap \mathbb{P}) $ | (34) |
| $ x(\boldsymbol{T} \cap \boldsymbol{P})=\boldsymbol{A}^{-1}(\boldsymbol{X}(\mathbb{T} \cap \mathbb{P})-b) $ | (35) |
由(29)可知,新单元
| $ \tilde{V}_{\widetilde{W}, i}=\sum\limits_{k} \int_{\widetilde{W} \cap P_{i, k}} 1 \mathrm{~d} x \mathrm{~d} y $ | (36) |
因而新单元
| $ \tilde{V}_{\widetilde{W}}=\sum\limits_{i} \tilde{V}_{\widetilde{W}, i} $ | (37) |
新单元
| $ \tilde{V}_{\widetilde{W}}=\sum\limits_{i} \tilde{V}_{\widetilde{W}, i} $ | (38) |
同理, 新单元
| $ \begin{array}{l} \tilde{x}_{c, \widetilde{W}, i}=\frac{\sum_{i} \int_{\widetilde{W} \cap P i, k} x \mathrm{~d} x \mathrm{~d} y}{\sum_{i} \int_{\widetilde{w} \cap P i, k} 1 \mathrm{~d} x \mathrm{~d} y}, \\ \tilde{y}_{c, \tilde{w}, i}=\frac{\sum_{i} \int_{\widetilde{w} \cap P_{i, k}} y \mathrm{~d} x \mathrm{~d} y}{\sum_{i} \int_{\tilde{w} \cap P_{i, k}} 1 \mathrm{~d} x \mathrm{~d} y} \end{array} $ | (39) |
对重构多项式(28)的密度进行积分,新单元
| $ \tilde{m}_{\widetilde{W}, i}=\sum\limits_{k} \int\limits_{\widetilde{W} \cap P_{i, k}} \rho_{i, k}(x, y) \mathrm{d} x \mathrm{~d} y $ | (40) |
因此,新单元
| $ {\tilde \rho _{\tilde W,i}} = \frac{{{{\tilde m}_{\tilde W,i}}}}{{{{\tilde V}_{\hat W,i}}}} $ | (41) |
同理, 分别对重构多项式(28)的动量和内能进行积分, 新单元
| $ {{{(\tilde m\tilde u)}_{\tilde W,i}} = \sum\limits_k {\int\limits_{\tilde W \cap {P_{i,k}}} {{\rho _{i,k}}} } (x,y){\mathit{\boldsymbol{u}}_{i,k}}(x,y){\rm{d}}x{\rm{d}}y} $ | (42) |
| $ {{{(\tilde m\tilde e)}_{\tilde W,i}} = \sum\limits_k {\int\limits_{\tilde W \cap {P_{i,k}}} {{\rho _{i,k}}} } (x,y){e_{i,k}}(x,y){\rm{d}}x{\rm{d}}y} $ | (43) |
因此, 新单元
| $ \tilde{\boldsymbol{u}}_{\widetilde{W}, i}=\frac{(\tilde{m} \tilde{\boldsymbol{u}})_{\widetilde{W}, i}}{\tilde{m}_{\widetilde{W}, i}}, \quad \tilde{e}_{\tilde{W}, i}=\frac{(\tilde{m} \tilde{e})_{\widetilde{W}, i}}{\tilde{m}_{\tilde{W}, i}} $ | (44) |
新单元
| $ \tilde{\boldsymbol{u}}_{\widetilde{W}}=\frac{\sum_{i}(\tilde{m} \tilde{\boldsymbol{u}})_{\widetilde{W}, i}}{\sum_{i} \tilde{m}_{\tilde{W}, i}} $ | (45) |
一般而言,重构多项式(28)需要一个限制器来抑制间断附近的振荡。本文采用文献[38]中提出的基于MOOD限制策略的后验校正。后验校正的原理是检测出“坏”单元,然后降低“坏”单元上重构多项式的次数,重复之前的步骤,直到这个单元是“好”单元为止。值得注意的是,文献[38]中提出的方法只适用于单介质流。为了使其适应于多介质流,我们对它做了一些小改动。对于纯(单介质)新单元,对新单元进行检测;对于混合(多介质)新单元,对所有单介质子多边形进行检测,而不是整个新单元。
检测的目的是过滤“好”单元,这些单元已经使用无限制的重构多项式进行精确积分守恒重映;而把存在一些问题(振荡,非物理等)的“坏”单元标识出来。检测准则有两个:
1) 物理相容性检验准则(PAD)
该准则的依据是密度、内能和压强的必须为正:
| $ C^{P A D}=\left\{\begin{aligned} 1, & \tilde{\rho}_{\widetilde{W}, i}>0 \ \text { and } \ \tilde{e}_{ \widetilde{w}, i} >0 \\ & \ \ \ \ \ \ \text { and } \ \ \tilde{p}_{\widetilde{w}, i} >0 \\ 0, & \ \ \ \ \ \ \ \ \ \ \ \ \ \text { else } \end{aligned}\right. $ | (46) |
2) 数值相容性检验准则(NAD)
该准则是为了检验数值解是否局部光滑:
| $ \begin{array}{c} D^{N A D}= \\ \left\{\begin{array}{l} 0, \widetilde{G}_{\widetilde{W}, i}<\min \limits_{k \in \widetilde{W} \cap P_{i, k} \neq \varnothing} \bar{g}_{i, k} \text { and } \max\limits _{k \in \widetilde{W} \cap P_{i, k} \neq \varnothing} \bar{g}_{i, k}<\widetilde{G}_{\widetilde{W}, i} \\ 1, \text { else } \end{array}\right. \end{array}. $ | (47) |
其中gi, k的定义在(28)中给出,
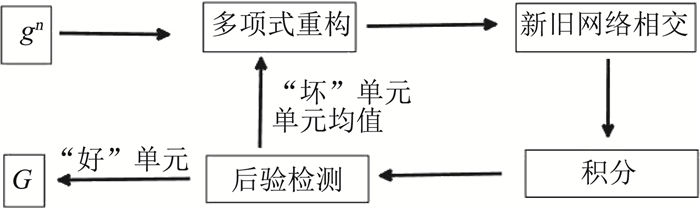
因此,如果CPAD和DNAD都等于1,那么单介质子多边形被认为是“好的”。如果一个新单元中所有单介质子多边形都是“好的”,那么它就被标记为“好”单元;否则,新单元是“坏”单元。当一个新单元
|
图 7 基于后验校正的重映算法示意图 Fig.7 A sketch of a posterior detection in a remapping algorithm |
有一个平均对角流ρ=1,p=1和(u, v)= (1, 1)。在这个平均流的速度(u, v)和温度T=ρ/p上加一个等熵涡扰动,对熵S=p/ρr不加扰动,即
| 表 1 误差及收敛阶(拉氏方法) Table 1 Errors and convergence orders (Lagrangian method) |
|
|
| 表 2 误差及收敛阶(MMALE方法) Table 2 Errors and convergence orders (MMALE method) |
|
|
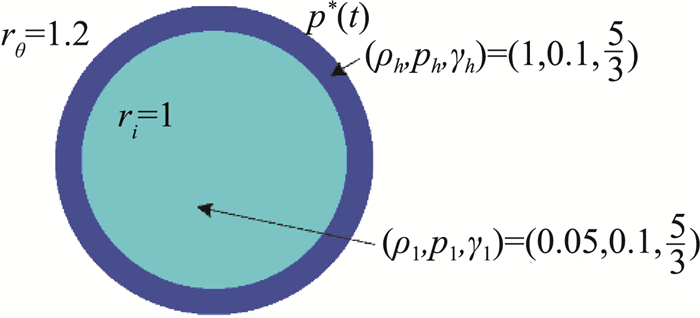
这是一个类似ICF的测试问题。初始状态如图 8所示,一团轻气体(R∈[0, 1])被一团重气体包围(R∈[0, 1.2]))。两种气体均为理想气体(绝热指数γl=γh=1.5)。轻气体的初始状态为(ρl, pl, Ul)=(0.05, 0.1, 0), 重气体为(ρh, ph, Uh)=(1, 0.1, 0)。在重气体外表面给定随时间变化的压力边界条件,
| $ p^{*}(t)=\left\{\begin{array}{ll} 13, & t \in[0,0.04] \\ 13-12.5 \frac{t-0.04}{0.125-0.04}, & t \in[0.04,0.12] \\ 0.5, & t \in[0.125,0.3] \end{array}\right. $ |
|
图 8 初始区域的几何数据 Fig.8 Geometrical parameters of the initial domain |
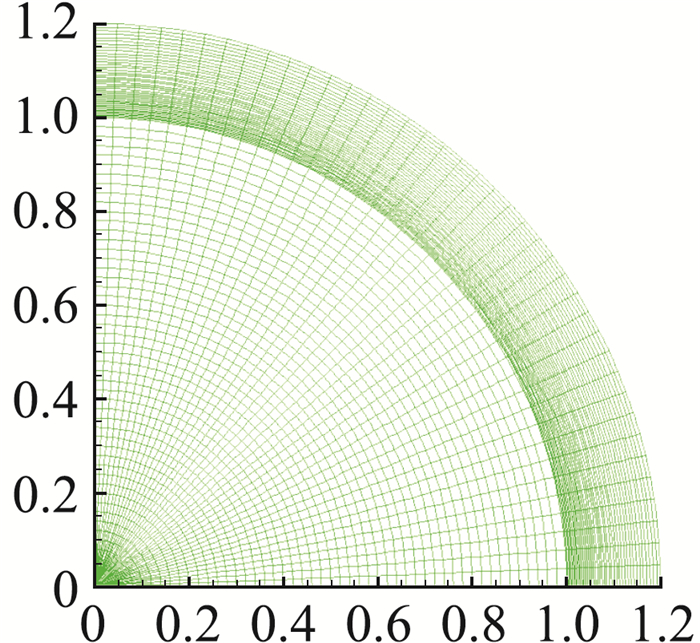
为了研究圆柱内爆中Rayleigh-Taylor不稳定性的时间演化,我们给出了轻、重气体界面的初始扰动,ripert=ri[1+acos(nθ)]。这里,ri和ripert分别表示无扰动和受扰动的半径。a表示扰动的振幅,整数n对应于扰动的模态。我们取模态n=8。两个不同的初始振幅a=2×10-4和a=10-3。初始时刻,采用射线网格把计算区域剖分成90×40个单元。如图 9所示,在径向上,轻气体均匀剖分成50份,重气体则剖分成不均匀的40份。将重气体中的单元按几何级数沿径向上进行分级,以便在界面处获得质量匹配网格。利用本文的间断有限元拉氏方法和MMALE方法分别计算这个问题。
|
图 9 初始网格 Fig.9 The initial mesh |
对于MMALE方法,在开始时初始网格没有混合单元,因此仅需执行拉氏步。当网格由于界面不稳定而发生严重变形时,需要进行重分和重映。如果网格中存在混合单元,采用Tipton压力松弛模型进行计算,并在重映步之前对这些混合单元执行MOF界面重构算法。
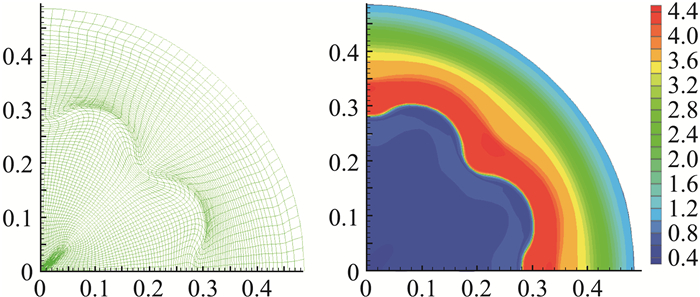
当取a=10-3时,图 10给出t=0.3时用拉氏方法计算的网格和密度图。注意到最终的网格质量保持很好,没有翻转单元。图 11给出的是t=0.3时用MMALE方法计算网格与界面和密度等值线图。从图 10和图 11可见,拉氏方法和MMALE方法的计算结果是非常相似的。
|
图 10 a=2×10-4,t=0.3时用间断有限元拉氏方法计算的网格(左)和密度图(右) Fig.10 Meshes (left) and density contours (right) at the final time t=0.3 calculated by Lagrangian discontinuous Galerkin method with a=2×10-4 |
|
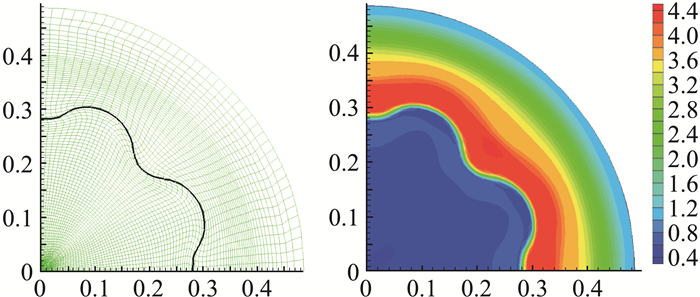
图 11 a=2×10-4,t=0.3时用MMALE方法计算的网格(左)和密度(右) Fig.11 The mesh and the interfaces (left) and density contours (right) at the final time t=0.3 calculated by MMALE method with a=2×10-4 |
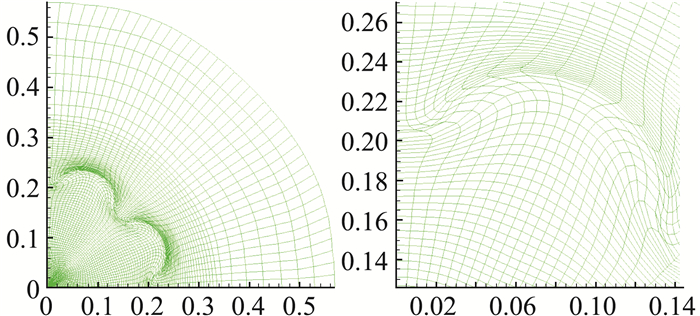
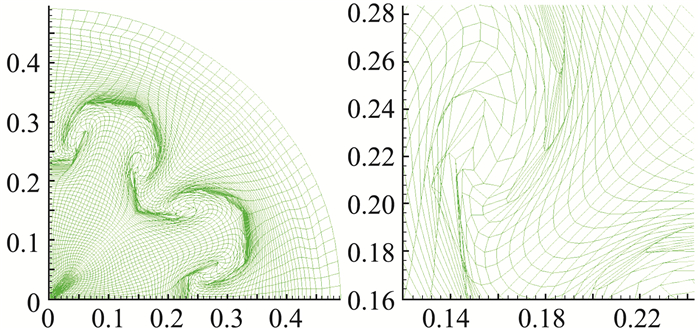
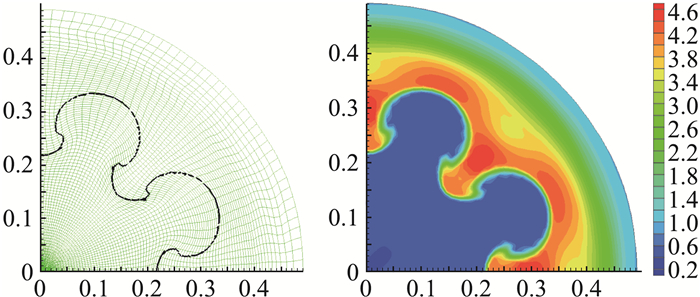
当取a=10-3时,图 12给出了t=0.25时用拉氏方法计算的网格和局部放大图,此时网格是没有翻转单元的。当t=0.3时,用拉氏方法计算的结果是不准确的,此时网格扭曲严重而且存在翻转单元,如图 13所示。然而,用MMALE方法运行到最终时刻没有任何问题。图 14给出的是t=0.3时用MMALE方法计算的网格与界面和密度等值线图。该算例的计算结果表明了MMALE方法具有较好的灵活性和鲁棒性。
|
图 12 a=10-3,t=0.25时用间断有限元拉氏方法计算的网格(左)和局部放大图(右) Fig.12 The meshes and its close-up view (left) and zoom of meshes (right) at the final time t=0.25 calculated by Lagrangian discontinuous Galerkin method with a=10-3 |
|
图 13 a=10-3,t=0.3时用间断有限元拉氏方法计算的网格(左)和局部放大图(右) Fig.13 The mesh (left)and its close-up view (right) at the final time t=0.3 calculated by Lagrangian discontinuous Galerkin method with a=10-3 |
|
图 14 a=10-3,t=0.3时用MMALE方法计算的网格(左)和密度(右) Fig.14 (left) The mesh and interfaces and (right) density contours at the final time t=0.3 calculated by MMALE method with a=10-3 |
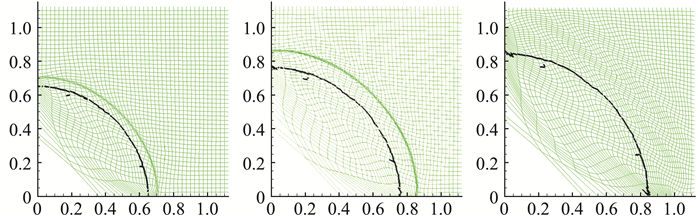
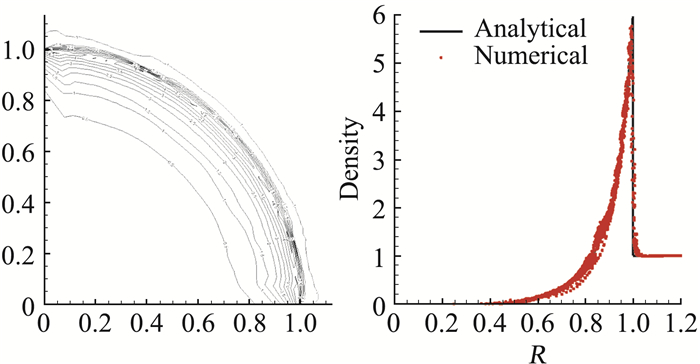
这是一个点爆炸问题。在原点处给定一个能量。随着时间的推进,一个圆柱型激波会向外传播。初始密度为ρ=1,速度为(u, v)=(0, 0)。在原点处,存在单位内能,并且在其它点处初始压力为p=0。这个问题的精确解由Sedov在文献[54]中给出:在时间t=1时,激波运动到离原点距离为1处,密度峰值达到6。使用本文的中心型MMALE方法进行计算。计算区域为Ω=[0, 1.125]×[0, 1.125],初始剖分为45×45的一致网格。在靠近原点的第一个单元上给定内能e0=400。在初始时刻,界面位于以原点为圆心,半径为0.43的圆上。注意到在混合单元中,这两种介质都是理想气体,具有相同的绝热指数γ=1.4。我们将它们视为混合单元,以便将数值解与精确解进行比较。图 15给出了t=0.5, 0, 75, 1时的网格和界面。图 16是t=1时刻的密度等值线图和以半径为变量的密度图。从图 16可知。计算得到的激波位置是准确的,数值解与精确解很接近。
|
图 15 t=0.5, 0, 75, 1时的网格和界面(从左到右) Fig.15 Meshes and interfaces at (left) t = 0.5, (middle) t=0.75, and (right) t=1 |
|
图 16 t=1时的密度等值线图(左)和以半径为变量的密度图(右) Fig.16 (left) Density contours and (right) density at centroids of all cells versus the distance of the centroids to the origin at t =1 |
计算区域为矩形[0, 1/3]×[0, 1].初始时刻将它剖分为35×100的均匀网格。初始时刻,密度为ρh=2的重气体和密度为ρl=1的轻气体被扰动界面分隔开,界面方程为yi(x)=0.5+0.01cos(6πx)。重气体在轻气体之上。这两种气体都有相同的绝热指数γ=1.4。重力场垂直向下,重力加速度为g=(gx, gy)T=(0, -0.1)T。初始时刻两种气体都处于静止状态。初始压力分布通过静压平衡条件推导出来:
| $ \left\{\begin{aligned} p_{h}(x, y)=& 1+\rho_{h} g(y-1), \quad y>y_{i}(x) \\ p_{l}(x, y)=& 1+\rho_{l} g_{y}\left(y_{i}(x)-1\right)+\\ & \rho_{l} g_{y}\left(y-y_{i}(x)\right), \quad y \leqslant y_{i}(x) \end{aligned}\right. $ |
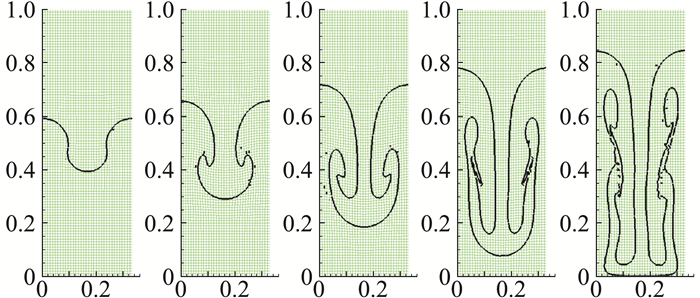
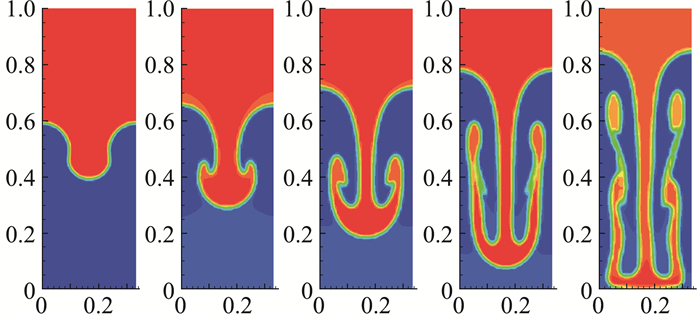
众所周知,这种状态是不稳定的。由于正弦界面的存在,在界面附近会产生旋涡。随着时间的推移,较重的气体会落入较轻的气体中形成一个尖钉;较轻的气体会上升到较重的气体中形成一个气泡。图 17给出了t=5, 7, 9, 11, 13时的网格和界面。图 18给出了t=5, 7, 9, 11, 13时的密度等值线图。从图 17和图 18可以看出,我们的结果与文献[6, 29]中的结果非常接近,这里的计算结果对称性好,界面清晰。
|
图 17 t=5, 7, 9, 11, 13时的网格和界面(从左到右) Fig.17 Meshes and interfaces at t= 5, 7, 9, 11, and 13 (from left to right) |
|
图 18 t=5, 7, 9, 11, 13时的密度等值线图(从左到右) Fig.18 Density contours at t = 5, 7, 9, 11, and 13 (from left to right) |
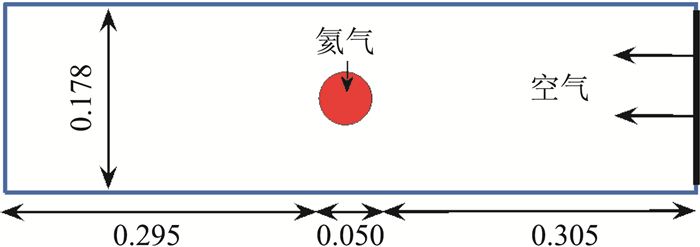
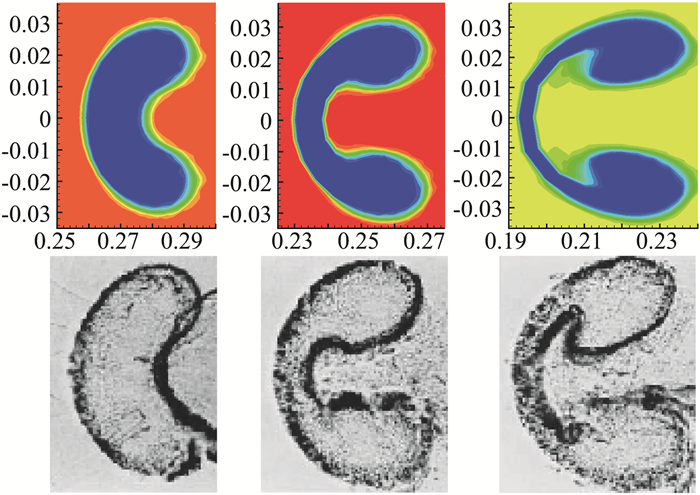
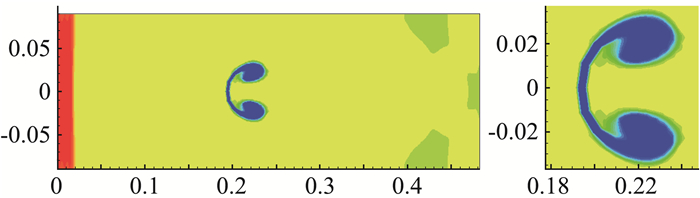
计算区域为[0, 0.65]×[-0.089, 0.089],初始时刻将它剖分成260×72个均匀单元。如图 19所示,气泡是由圆心(xc, yc)=(0.32, 0)和半径r=0.025定义的圆盘。在右边界(初始时刻位于x=0.65)上给出了一个类似活塞的边界条件,它以速度(u*, 0)向左移动。在其他边界上给固壁边界条件。入射激波的马赫数为Ms=1.22。氦气泡和空气在初始时刻处于静止状态。氦气泡和空气的初始数据分别为(ρ1, p1)=(0.182, 105), (ρ2, p2)=(1, 105);摩尔质量和绝热指数分别为(M1, γ1)=(5.269×10-3, 1.648),(M2, γ2)=(28.963×10-3, 1.4)。由Rankine-Hugoniot关系可以得到活塞在x方向的速度u*=-124.824。入射激波的x方向速度是Dc=-456.482。入射激波在ti=668.153×10-6时刻撞击氦气泡。计算终止时间tfinal=ti+674×10-6=1342.153×10-6。图 20给出了t1=ti+245×10-6=913.153×10-6,t2=ti+4247×10-6= 1095.153×10-6和tfinal三个时刻的网格和界面以及这三个时刻的试验纹影图[55]。图 21给出了tfinal时刻的密度等值线图以及局部放大图。从图 20和图 21可以看出,这里的计算结果与文献[55]中的试验纹影图符合的很好,与文献[6, 36]的数值结果非常接近。
|
图 19 初始区域的几何数据 Fig.19 Geometrical parameters of the initial domain |
|
图 20 t1,t2, tfinal时刻(从左到右)用MMALE方法计算的密度(上)和试验纹影图(下) Fig.20 Instantaneous density contours obtained by (top) the MMALE method and (bottom) Schlieren images from experiments at time instances (left) t1, (middle) t2, and (right) tfinal |
|
图 21 tfinal时刻的密度等值线图(左) 和局部放大图(右) Fig.21 The overview and a close-up view of density contours at tfinal |
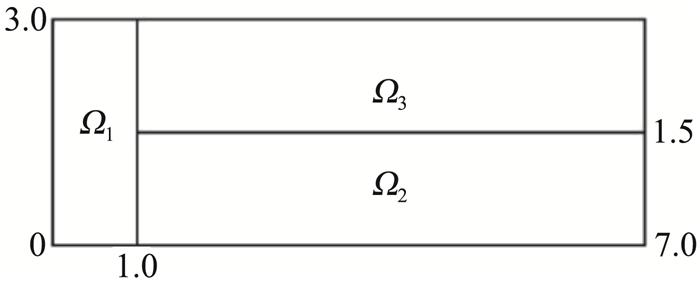
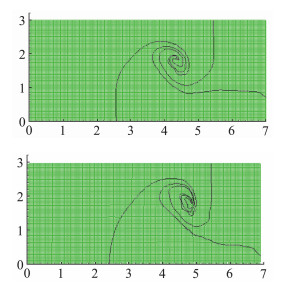
考虑如图 22所示矩形域中的三种状态的二维黎曼问题。初始区域Ω=[0, 7]×[0, 3]分为三个子区域Ω1=[0, 1]×[0, 3];Ω2=[1, 7]×[0, 1.5]和Ω3=[1, 7]×[1.5, 3]。Ω1中是初始状态为(ρ1, p1, U1)=(1, 1, 0)的高压高密度气体。Ω2中是初始状态为(ρ2, p2, U2)=(1, 0.1, 0)的低压高密度气体。Ω3中是初始状态为(ρ3, p3, U3)=(0.125, 0.1, 0)的低压低密度气体。Ω1和Ω3中物质的绝热指数均为γ1=γ3=1.5;Ω2中物质的绝热指数为γ2=1.4。边界条件均为固壁边界条件, 时间计算到tfinal=10。初始网格数为210×90。由于声阻抗的不同,Ω2和Ω3中的两个激波以不同的速度传播。这在Ω2和Ω3的界面处产生强剪切力。这种剪切作用产生Kelvin-Helmholtz不稳定性,并形成涡旋。用拉氏方法计算该问题时,在涡旋发展前由于网格扭曲缠结而导致计算终止。当使用经典的ALE方法时,捕获涡流是困难的。我们使用新的中心型MMALE方法计算此问题。图 23给出了t=5, 6时的网格和界面。
|
图 22 初始区域的几何数据 Fig.22 Geometrical parameters of the initial domain |
|
图 23 t=5, 6的网格和界面(从上到下) Fig.23 Meshes and interfaces at (up) t=5 and (down) t=6 |
本文提出了一种具有二阶精度的中心型间断有限元MMALE方法。在该方法中,拉氏步采用间断有限元方法求解可压缩欧拉方程。对于混合网格,采用Tipton压力松弛模型更新物理量。采用具有鲁棒性的MOF方法进行界面重构。针对重映步的多边形相交问题,提出了一种“裁剪投影”算法;在此基础上构建了一个基于后验校正的二阶积分守恒重映方法。数值试验的结果表明,该方法具有较好的鲁棒性和灵活性。
| [1] |
HIRT C W, AMSDEN A A, COOK J L. An arbitrary Lagrangian-Eulerian computing method for all flow speeds[J]. Journal of Computational Physics, 1974, 14(3): 227-253. DOI:10.1016/0021-9991(74)90051-5 |
| [2] |
BENSON D J. An efficient, accurate, simple ALE method for nonlinear finite element programs[J]. Computer Methods in Applied Mechanics and Engineering, 1989, 72(3): 305-350. DOI:10.1016/0045-7825(89)90003-0 |
| [3] |
BENSON D J. Computational methods in Lagrangian and Eulerian hydrocodes[J]. Computer Methods in Applied Mechanics and Engineering, 1992, 99: 235-394. DOI:10.1016/0045-7825(92)90042-I |
| [4] |
MARGOLIN L G. Introduction to "an arbitrary Lagrangian-Eulerian computing method for all flow speeds"[J]. Journal of Computational Physics, 1997, 135(2): 198-202. DOI:10.1006/jcph.1997.5727 |
| [5] |
MAIRE P H, BREIL J, GALERA S. A cell-centred arbitrary Lagrangian-Eulerian (ALE) method[J]. International Journal for Numerical Methods in Fluids, 2008, 56(8): 1161-1166. DOI:10.1002/fld.1557 |
| [6] |
LOUBERE R, MAIRE P H, SHASHKOV M, et al. ReALE: A reconnection-based arbitrary-Lagrangian-Eulerian method[J]. Journal of Computational Physics, 2010, 229(12): 4724-4761. DOI:10.1016/j.jcp.2010.03.011 |
| [7] |
BARLOW A J, MAIRE P H, RIDER W J, et al. Arbitrary Lagrangian-Eulerian methods for modeling high-speed compressible multimaterial flows[J]. Journal of Computational Physics, 2016, 322: 603-665. DOI:10.1016/j.jcp.2016.07.001 |
| [8] |
PEERY J S, CARROLL D E. Multi-Material ALE methods in unstructured grids[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 187(3-4): 591-619. DOI:10.1016/S0045-7825(99)00341-2 |
| [9] |
WILKINS M L. Use of artificial viscosity in multidimensional shock wave problems[J]. J Comput Phys, 1980, 36(3): 281-303. DOI:10.1016/0021-9991(80)90161-8 |
| [10] |
CARAMANA E J, BURTON D E, SHASHKOV M J, et al. The construction of compatible hydrodynamics algorithms utilizing conservation of total energy[J]. Journal of Computational Physics, 1998, 146(1): 227-262. DOI:10.1006/jcph.1998.6029 |
| [11] |
MAIRE P H, LOUBÈRE R, VÁCHAL P. Staggered Lagrangian discretization based on cell-centered Riemann solver and associated hydrodynamics scheme[J]. Communications in Computational Physics, 2011, 10(4): 940-978. DOI:10.4208/cicp.170310.251110a |
| [12] |
MORGAN N R, LIPNIKOV K N, BURTON D E, et al. ALagrangian staggered grid Godunov-like approach for hydrodynamics[J]. Journal of Computational Physics, 2014, 259: 568-597. DOI:10.1016/j.jcp.2013.12.013 |
| [13] |
GODUNOV S K. Reminiscences about difference schemes[J]. Journal of Computational Physics, 1999, 153(1): 6-25. DOI:10.1006/jcph.1999.6271 |
| [14] |
DESPRES B, MAZERAN C. Lagrangian gas dynamics in two dimensions and Lagrangian systems[J]. Archive for Rational Mechanics and Analysis, 2005, 178(3): 327-372. DOI:10.1007/s00205-005-0375-4 |
| [15] |
CHENG J, SHU C W. A high order ENO conservative Lagrangian type scheme for the compressible Euler equations[J]. Journal of Computational Physics, 2007, 227(2): 1567-1596. DOI:10.1016/j.jcp.2007.09.017 |
| [16] |
MAIRE P H, ABGRALL R, BREIL J, et al. A cell-centered Lagrangian scheme for two-dimensional compressible flow problems[J]. SIAM Journal on Scientific Computing, 2007, 29(4): 1781-1824. DOI:10.1137/050633019 |
| [17] |
MAIRE P H. A high-order cell-centered Lagrangian scheme for two-dimensional compressible fluid flows on unstructured meshes[J]. Journal of Computational Physics, 2009, 228(7): 2391-2425. DOI:10.1016/j.jcp.2008.12.007 |
| [18] |
LOUBERE R, OVADIA J, ABGRALL R. A Lagrangian discontinuous Galerkin-type method on unstructured meshes to solve hydrodynamics problems[J]. International Journal for Numerical Methods in Fluids, 2004, 44(6): 645-663. DOI:10.1002/fld.665 |
| [19] |
JIA Z, ZHANG S. A new high-order discontinuous Galerkin spectral finite element method for Lagrangian gas dynamics in two-dimensions[J]. Journal of Computational Physics, 2011, 230(7): 2496-2522. DOI:10.1016/j.jcp.2010.12.023 |
| [20] |
LI Z, YU X, JIA Z. The cell-centered discontinuousGalerkin method for Lagrangian compressible Euler equations in two-dimensions[J]. Computers & Fluids, 2014, 96: 152-164. |
| [21] |
KUCHARIK M, SHASHKOV M, WENDROFF B. An efficient linearity-and-bound-preserving remapping method[J]. Journal of Computational Physics, 2003, 188(2): 462-471. DOI:10.1016/S0021-9991(03)00187-6 |
| [22] |
GARIMELLA R, KUCHARIK M, SHASHKOV M. An efficient linearity and bound preserving conservative interpolation (remapping) on polyhedral meshes[J]. Computers & Fluids, 2007, 36(2): 224-237. |
| [23] |
LOUBERE R, SHASHKOV M J. Asubcell remapping method on staggered polygonal grids for arbitrary-Lagrangian-Eulerian methods[J]. Journal of Computational Physics, 2005, 209(1): 105-138. DOI:10.1016/j.jcp.2005.03.019 |
| [24] |
CHENG J, SHU C W. A high order accurate conservative remapping method on staggered meshes[J]. Applied Numerical Mathematics, 2008, 58(7): 1042-1060. DOI:10.1016/j.apnum.2007.04.015 |
| [25] |
KUCHARIK M, SHASHKOV M. One-step hybrid remapping algorithm for multi-material arbitrary Lagrangian-Eulerian methods[J]. Journal of Computational Physics, 2012, 231(7): 2851-2864. DOI:10.1016/j.jcp.2011.12.033 |
| [26] |
DUKOWICZ J K, KODIS J W. Accurate conservative remapping (rezoning) for arbitrary Lagrangian-Eulerian computations[J]. SIAM Journal on Scientific and Statistical Computing, 1987, 8(3): 305-321. DOI:10.1137/0908037 |
| [27] |
GRANDY J. Conservative remapping and region overlays by intersecting arbitrarypolyhedra[J]. Journal of Computational Physics, 1999, 148(2): 433-466. DOI:10.1006/jcph.1998.6125 |
| [28] |
MENON S, SCHMIDT D P. Conservative interpolation on unstructured polyhedral meshes: An extension of thesupermesh approach to cell-centered finite-volume variables[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(41-44): 2797-2804. DOI:10.1016/j.cma.2011.04.025 |
| [29] |
JIA Z, LIU J, ZHANG S. An effective integration of methods for second-order three-dimensional multi-material ALE method on unstructured hexahedral meshes using MOF interface reconstruction[J]. Journal of Computational Physics, 2013, 236: 513-562. DOI:10.1016/j.jcp.2012.11.004 |
| [30] |
KUCHARIK M, SHASHKOV M. Conservative multi-material remap for staggered multi-material Arbitrary Lagrangian-Eulerian methods[J]. Journal of Computational Physics, 2014, 258: 268-304. DOI:10.1016/j.jcp.2013.10.050 |
| [31] |
CHEN X, ZHANG X, JIA Z. A robust and efficient polyhedron subdivision and intersection algorithm for three-dimensional MMALE remapping[J]. Journal of Computational Physics, 2017, 338: 1-17. DOI:10.1016/j.jcp.2017.02.029 |
| [32] |
BARLOW A J. A compatible finite element multi-material ALE hydrodynamics algorithm[J]. International Journal for Numerical Methods in Fluids, 2008, 56(8): 953-964. DOI:10.1002/fld.1593 |
| [33] |
GALERA S, MAIRE P H, BREIL J. A two-dimensional unstructured cell-centered multi-material ALE scheme using VOF interface reconstruction[J]. Journal of Computational Physics, 2010, 229(16): 5755-5787. DOI:10.1016/j.jcp.2010.04.019 |
| [34] |
GALERA S, BREIL J, MAIRE P H. A 2D unstructured multi-material cell-centered arbitrary Lagrangian-Eulerian (CCALE) scheme using MOF interface reconstruction[J]. Computers & Fluids, 2011, 46(1): 237-244. |
| [35] |
BREIL J, GALERA S, MAIRE P H. Multi-material ALE computation in inertial confinement fusion code CHIC[J]. Computers & Fluids, 2011, 46(1): 161-167. |
| [36] |
贾祖朋, 孙宇涛. 一种基于MOF界面重构的二维中心型MMALE方法[J]. 计算物理, 2016, 33(5): 523-538. JIA Z P, SUN Y T. A 2D cell-centered MMALE method based on MOF interface reconstruction[J]. Chinese Journal of Computational Physics, 2016, 33(5): 523-538. DOI:10.3969/j.issn.1001-246X.2016.05.003 (in Chinese) |
| [37] |
RIDER W J, MARGOLIN L G. Simple modifications of monotonicity-preserving limiter[J]. Journal of Computational Physics, 2001, 174(1): 473-488. DOI:10.1006/jcph.2001.6914 |
| [38] |
BLANCHARD G, LOUBERE R. High order accurate conservative remapping scheme on polygonal meshes using a posteriori MOOD limiting[J]. Computers & Fluids, 2016, 136: 83-103. |
| [39] |
CLAIN S, DIOT S, LOUBERE R. A high-order finite volume method for systems of conservation laws-Multi-dimensional Optimal Order Detection (MOOD)[J]. Journal of computational Physics, 2011, 230(10): 4028-4050. DOI:10.1016/j.jcp.2011.02.026 |
| [40] |
DIOT S, CLAIN S, LOUBERE R. Improved detection criteria for the multi-dimensional optimal order detection (MOOD) on unstructured meshes with very high-order polynomials[J]. Computers & Fluids, 2012, 64: 43-63. |
| [41] |
AULISA E, MANSERVISI S, SCARDOVELLI R, et al. Interface reconstruction with least-squares fit and split advection in three-dimensional Cartesian geometry[J]. Journal of Computational Physics, 2007, 225(2): 2301-2319. DOI:10.1016/j.jcp.2007.03.015 |
| [42] |
TIPTON R E. CALE mixed zone pressure relaxation model[R]. Tech rep, Private communication, Lawrence Livermore National Laboratory, 1989: 82.
|
| [43] |
SHASHKOV M. Closure models formultimaterial cells in arbitrary Lagrangian-Eulerian hydrocodes[J]. International Journal for Numerical Methods in Fluids, 2008, 56(8): 1497-1504. DOI:10.1002/fld.1574 |
| [44] |
KUCHARIK M, GARIMELLA R V, SCHOFIELD S P, et al. A comparative study of interface reconstruction methods for multi-material ALE simulations[J]. Journal of Computational Physics, 2010, 229(7): 2432-2452. DOI:10.1016/j.jcp.2009.07.009 |
| [45] |
QING F, YU X, JIA Z. A robust MoF method applicable to severely deformed polygonal mesh[J]. Journal of Computational Physics, 2019, 377: 162-182. DOI:10.1016/j.jcp.2018.10.032 |
| [46] |
KNUPP P M. Achieving finite element mesh quality via optimization of the Jacobian matrix norm and associated quantities. Part I-A framework for surface mesh optimization[J]. International Journal for Numerical Methods in Engineering, 2000, 48(3): 401-420. DOI:10.1002/(SICI)1097-0207(20000530)48:3<401::AID-NME880>3.0.CO;2-D |
| [47] |
STROUBOULIS T, DEVLOO P, ODEN J T. A moving-grid finite element algorithm for supersonic flow interaction between moving bodies[J]. Computer Methods in Applied Mechanics and Engineering, 1986, 59(2): 235-255. DOI:10.1016/0045-7825(86)90104-0 |
| [48] |
COCKBURN B, SHU C W. The Runge-Kutta discontinuous Galerkin method for conservation laws V: multidimensional systems[J]. Journal of Computational Physics, 1998, 141(2): 199-224. DOI:10.1006/jcph.1998.5892 |
| [49] |
BARTH T J. Numerical methods for gasdynamic systems on unstructured meshes[M]//An introduction to recent developments in theory and numerics for conservation laws. Springer, Berlin, Heidelberg, 1999: 195-285.
|
| [50] |
DYADECHKO V, SHASHKOV M. Moment-of-fluid interface reconstruction[J]. Los Alamos Report LA-UR-05-7571, 2005. |
| [51] |
CHEN X, ZHANG X. An improved 2D MoF method by using high order derivatives[J]. Journal of Computational Physics, 2017, 349: 176-190. DOI:10.1016/j.jcp.2017.08.031 |
| [52] |
MAVRIPLIS D. Revisiting the least-squares procedure for gradient reconstruction on unstructured meshes[C]//16th AIAA Computational Fluid Dynamics Conference. 2003: 3986.
|
| [53] |
YOUNGS D L. Multi-mode implosion in cylindrical 3d geometry[C]//11th International Workshop on the Physics of Compressible Turbulent Mixing (IWPCTM11), Santa Fe. 2008.
|
| [54] |
SEDOV L I. Similarity and dimensional methods in mechanics[M]. New York: Academic Press, 1959.
|
| [55] |
QUIRK JJ, KARNI S. On the dynamics of a shock-bubble interaction[J]. Journal of Fluid Mechanics, 1996, 318: 129-163. DOI:10.1017/S0022112096007069 |
 2021, Vol. 39
2021, Vol. 39


