计算效率是CFD格式在复杂流动模拟中面临的核心问题。非结构网格能更好地适应复杂外形,网格生成和自适应动态调整自动化程度高,能极大地减少网格生成工作量。发展非结构网格上的高效数值格式,具有重要的理论研究和工程应用价值,也具有很大的挑战性。紧致高阶精度重构和高效通量演化方法是其中的关键。此外,还需要考虑格式的并行效率以及稳健性等因素。
传统有限体积法由于每个单元只包含单元平均值,难以实现紧致高阶重构。这里的紧致是指重构模板最多只包含面相邻单元。紧致的计算模板不仅能更好地与可压缩流动的局域性相容,而且能有效避免非紧致带来的一些弊端。例如,由于非结构网格分布的任意性,距离较远的模板单元的选取较为复杂。此外,模板单元过多也会导致缓存利用率和并行效率降低、计算域边界处理更加困难,而且网格质量对重构的影响较大。
内自由度方法通过在网格单元内设置足够的自由度来实现紧致重构,并利用控制方程对每个内自由度加以记录和更新。这里的自由度表示的是每个单元内记录的离散信息,如内点值、子单元平均值或多项式展开系数,与气体动理论中涉及的气体分子的自由度是不同的概念。内自由度方法中最具有代表性的是间断伽辽金(DG)方法[1-2],也是目前最为流行的非结构网格高精度方法。Huynh针对一维双曲守恒律提出了一种简单高效的内自由度方法,称为通量重构(Flux Reconstruction, FR)格式[3-4]。FR首先计算求解点(内点)上的通量值,并插值得到单元内的通量分布,再结合单元界面通量对其进行修正,从而可以直接计算通量散度值来更新守恒量。相比于传统的DG方法,FR方法具有很高的效率。LCP方法则通过引入提升算子的方式进行通量修正,从而使之适用于三角形和四面体网格[5]。FR和LCP后来统称CPR方法,为多种内自由度方法提供了一个统一框架[6-7]。
相比于传统有限体积法,内自由度方法不仅易于实现紧致重构,而且由于单元内多个自由度共享同一个连续的多项式分布,重构效率更高。同时,单元内的连续分布使得计算通量时不必求解Riemann问题,从而更为简单高效。但是,在捕捉流场间断时,单元内的连续分布难以描述间断结构,重构时需要针对单元整体进行限制,从而导致分辨率的降低,相当于损失了自由度。在这方面,谱体积方法(SV)具有独特的优势[8-9]。它结合了内自由度方法和有限体积法的特点,在每个单元内划分若干个子单元,将子单元平均值作为内自由度,按照有限体积法更新,保证了高阶重构的紧致性。由于可以分别对每个子单元进行限制,因而能够避免内自由度损失,实现在子单元尺度上捕捉间断[10]。已有研究对DG和SV进行了混合[11-12]。但SV格式对于子单元划分的要求十分苛刻,对格式稳定性影响较大,不易推广到四边形或六面体网格。
利用面相邻子单元参与重构,Pan等发展了针对一维及二维四边形网格上的双曲守恒方程的子单元有限体积法(Subcell Finite Volume, SCFV)。相比于SV,SCFV划分的子单元更少,也更简单灵活[13-14]。这种通过引入面相邻单元自由度参与重构的方法,集合了内自由度方法和有限体积方法的优势,与DG结合后也能有效降低计算量,增大时间步长[15-16]。为获得稳定的数值格式,重构时子单元的守恒性非常重要。SCFV通过一种简单的平移修正来间接保证守恒性。但是,这会在单元内部的子单元界面上额外引入间断,从而导致子单元界面的通量计算效率低于SV方法。
除了高精度重构外,通量求解器也对CFD方法的精度和效率起着重要的影响作用。传统CFD方法多是基于宏观Euler方程的Riemann解来计算数值通量。由于传统的Riemann解只有一阶时间精度,通常需要结合多步Runge-Kutta(R-K)方法进行时间推进。多步法中每个子步都需要进行重构、通量计算以及并行通信,影响格式的计算效率。Li和Du利用通量及其一阶时间导数,提出了两步四阶方法,通过两个子步达到四阶时间精度[17]。基于广义Riemann问题(GRP)通量求解器,两步四阶方法成功用于Euler方程的高效求解[18-19]。此外,传统高精度格式需要分别计算无黏和黏性通量。由于计算黏性通量需要用到单元界面上的物理量的一阶导数,而重构得到的两侧导数值通常是不连续的,从而使得计算往往较为复杂。
徐昆等提出的气体动理学格式(GKS)为发展高精度格式提供了一条新的途径[20-21]。GKS利用介观BGK方程的局部解析解来计算网格界面上的数值通量。该局部解在连续流区可以用平衡态分布及其时空导数,即宏观量及其时空导数来表示,因而GKS可以直接记录和更新宏观守恒量,避免了在微观速度空间离散导致的巨大计算资源开销。与N-S方程不同,BGK方程能描述任意重构初始间断的演化,因而GKS能够引入更为合理的数值耗散,具有很强的稳健性,同时也能更好地考虑多维特性[22]。由于缺乏多维Riemann解,这在传统格式中是难以做到的。此外,GKS通量自动耦合了无黏和黏性影响,且包含时间的演化,只需要单步即可达到二阶时间精度[23]。二阶GKS在高马赫数流动、多介质流动以及湍流等多种流动中显示了优异的性能[24-27]。
为进一步提高计算效率,可以基于时空二阶Taylor展开,利用BGK方程的局部解析解,建立时空三阶精度的动理学格式(HGKS)[28-29]。由于通量中包含了三阶时空演化,具有真正的多维特性,HGKS可以通过直接积分来计算界面通量,避免了采用数值积分时多个积分点上的通量计算[30-31]。同时,时间方向只需要单步推进即可达到三阶精度,避免了传统格式中采用多步法带来的不足[32-33]。
将高阶GKS拓展到非结构网格上时,同样面临紧致重构的问题。考虑到GKS构造了BGK方程的局部时空演化解来计算数值通量,该演化解可以用来直接计算界面上的宏观量,从而为重构提供额外的信息,提高紧致性[34-36]。按照这一思路,已建立了三角形网格上的紧致三阶HWENO-GKS[37-38]。如何更好地利用GKS提供的额外信息,进一步提高格式精度以及稳定性,是一个很有意思的研究方向。结合紧致最小二乘重构,也可以发展非结构网格上的高阶GKS[39],不过需要求解大型代数方程组,在显式格式中计算量相对较大。Ren等基于DG框架发展了非结构网格上的高阶GKS[40],能够有效保证紧致性。基于更加高效的内自由度方法,如CPR,有望发展更为高效的高阶GKS。
在时间推进格式方面,由于GKS通量包含时间演化,可以直接积分得到每个时间步内的数值通量,从而建立单步高精度格式[29]。也可以借鉴两步四阶方法,利用相对更为简单二阶GKS通量及其一阶时间导数,通过两个子步获得四阶时间精度[41]。考虑到重构过程通常需要较大的计算量,更少的子步意味着更小的计算量,以及更高的并行效率。同时,GKS无需额外计算黏性通量,且内涵自适应耗散机制,将其与高效紧致重构方法相结合,充分挖掘其多维及时空演化特性,有望构造出高精度、高效率和强稳健性的数值格式。
本文旨在探讨GKS通量求解器与高效紧致重构方法的有机结合,发展非结构网格上的高效高精度格式。首先将简要介绍课题组近年来发展的几种基于内自由度紧致重构的高精度动理学格式。将三阶GKS通量求解器与SCFV和CPR相结合,构造了两种单步时空三阶格式SCFV-GKS和CPR-GKS。进一步将二阶GKS通量与CPR结合,利用两步四阶方法构造了时空四阶格式CPR-GKS,并结合SCFV及曲边网格技术增强对流场间断和复杂外形的模拟能力。在此基础上,通过多种典型流动对这几种格式进行验证,对比分析不同格式的精度、效率以及激波捕捉性能。研究表明,结合高效的重构方法和时空演化的GKS通量,充分利用各自优势,能够建立更加高效、稳健的新型数值方法。
1 基于内自由度的紧致高精度GKS 1.1 GKS的基本原理GKS基于介观气体动理论中的Boltzmann-BGK方程,
| $ \begin{array}{*{20}{c}} {\frac{{\partial f}}{{\partial t}} + \mathit{\boldsymbol{u}} \cdot \frac{{\partial f}}{{\partial \mathit{\boldsymbol{x}}}} = \frac{{g - f}}{\tau }}\\ {g = \rho {{(2{\rm{ \mathsf{ π} }}RT)}^{ - (K + 3)/2}}{{\rm{e}}^{ - \left[ {({\boldsymbol{u}} - {\boldsymbol{U}})2 + {\xi ^2}} \right]/(2RT)}}} \end{array} $ | (1) |
其中,f=f(x, u, ξ, t)为气体分子速度分布函数,u为分子平动速度,ξ为内自由度,内自由度数为K。g为平衡态分布函数,(ρ, U, T)分别为气体的密度、速度和温度,τ为分子平均碰撞时间,R为气体常数。对BGK方程取矩,可以得到宏观守恒量Q及守恒方程:
| $ \begin{array}{c} \frac{\partial \boldsymbol{Q}}{\partial t}+\nabla \cdot \boldsymbol{F}=0 \\ \boldsymbol{Q}=(\rho, \rho \boldsymbol{U}, \rho E)^{\mathrm{T}}=\int f \boldsymbol{\psi} \mathrm{d} \varXi \triangleq\langle f\rangle \\ \boldsymbol{F}_{\alpha}=\left\langle u_{\alpha} f\right\rangle, \alpha=1,2,3 \\ \boldsymbol{\varPsi}=\left(1, \boldsymbol{u},\left(\boldsymbol{u}^{2}+\xi^{2}\right) / 2\right)^{\mathrm{T}} \end{array} $ | (2) |
在连续流区,通过一阶Chapmann-Enskog展开,
| $ f=\left[g-\tau\left(\frac{\partial g}{\partial t}+\boldsymbol{u} \cdot \frac{\partial g}{\partial \boldsymbol{x}}\right)\right] $ | (3) |
将分布函数近似用平衡态及其时空导数表示,可以导出宏观的N-S方程。由此可以建立逼近N-S方程的动理学格式,且只需要记录和更新宏观量(对应平衡态分布),避免在速度空间和内自由度空间的离散,使得计算量和传统直接基于宏观方程的CFD方法相当。
由方程(2)可以建立有限体积形式的GKS,
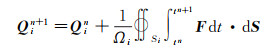
|
(4) |
其中,Si为离散物理空间上网格单元i的界面面积,Ωi为单元体积。为计算网格单元界面数值通量,GKS利用BGK方程(1)的形式解:
| $ \begin{array}{l} f(\mathit{\boldsymbol{x}},t,\mathit{\boldsymbol{u}},\xi ) = \frac{1}{\tau }\int_0^t g \left( {{\mathit{\boldsymbol{x}}^\prime },{t^\prime },\mathit{\boldsymbol{u}},\xi } \right){{\rm{e}}^{ - \left( {t - {t^\prime }} \right)/\tau }}{\rm{d}}{t^\prime } + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\rm{e}}^{ - t/\tau }}{f_0}(\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{u}}t,\mathit{\boldsymbol{u}},\xi ),\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{x}}^\prime } = \mathit{\boldsymbol{x}} - \mathit{\boldsymbol{u}}\left( {t - {t^\prime }} \right) \end{array} $ | (5) |
来描述界面上任意重构初值的演化,其中,x′=x-u(t-t′)。该演化解描述了从初始分布函数f0向平衡态分布的时空演化,自动耦合了分子的自由运动和相互碰撞,这是确保基于该演化解的GKS成为真正多尺度方法的关键[23]。从宏观上看,不仅耦合处理了无黏与黏性项,而且引入了随时间变化的自适应数值耗散,保证了其在可压缩黏性流动模拟中的优异性能。
在求解连续流区流动时,GKS基于式(3),结合时空Taylor展开来构造初始分布函数f0,并且相应地用Taylor展开构造平衡态分布g,从而可以借助式(5)获得界面上的演化解,进而直接计算数值通量。其中Taylor展开的阶数对应于重构多项式阶数,直接取决于格式精度的要求。通过二阶Taylor展开,可以得到单元界面上具有时间和空间三阶截断误差的分布函数(以二维为例,界面坐标x=0):
| $ \begin{array}{l} f(0, y, t, \boldsymbol{u}, {\xi})=f^{l} H(u)+f^{r}[1-H(u)]+f^{c}, \\ f^{s}=\mathrm{e}^{-t / \tau}\left\{1-C_{1} a_{k}^{s} u_{k}-\tau A^{s}+C_{2}\left(a_{k}^{s} a_{m}^{s}+d_{k m}^{s}\right) u_{k} u_{m}+\right. \\ \quad \quad C_{3}\left(A^{s} a_{k}^{s}+b_{k}^{s}\right) u_{k}+\left[a_{2}^{s}-C_{1}\left(a_{k}^{s} a_{2}^{s}+d_{k 2}^{s}\right) u_{k}-\right. \\ \quad \quad \left.\left.\left.\tau\left(A^{s} a_{2}^{s}+b_{2}^{s}\right)\right] y+\left[\left(a_{2}^{s}\right)^{2}+d_{22}^{s}\right] y^{2} / 2\right)\right\} g^{s}, \\ f^{c}=\left\{C_{4}+C_{5} a_{k} u_{k}+C_{6} A+C_{8}\left(A^{2}+B\right) / 2+\right. \\ \quad \quad C_{7}\left(a_{k} a_{m}+d_{k m}\right) u_{k} u_{m} / 2+C_{9}\left(A a_{k}+b_{k}\right) u_{k}+ \\ \quad \quad {\left[C_{4} a_{2}+C_{6}\left(A a_{2}+b_{2}\right)+C_{5}\left(a_{k} a_{2}+d_{k 2}\right) u_{k}\right] y+} \\ \quad \quad \left.\left.C_{4}\left(a_{2}\right)^{2}+d_{22}\right) y^{2} / 2\right\} g_{0} \end{array} $ | (6) |
其中H为Heaviside函数;上标s=l, r;下标k=1, 2;m=1, 2,系数:
| $ \begin{array}{c} C_{1}=\tau+t, \quad C_{2}=\tau t+t^{2} / 2, \quad C_{3}=\tau t, \\ C_{4}=1-\mathrm{e}^{-t / \tau}, \quad C_{5}=-\tau+(\tau+t) \mathrm{e}^{-t / \tau}, \\ C_{6}=t-\tau+\tau \mathrm{e}^{-t / \tau}, \quad C_{7}=-\left(t^{2}+2 \tau t\right) \mathrm{e}^{-t / \tau}, \\ C_{8}=t^{2}-2 \tau t, \quad C_{9}=-\tau t\left(1+\mathrm{e}^{-t / \tau}\right) \end{array} $ | (7) |
分布函数中的各项展开系数可以由重构出的宏观物理量各阶导数及相容条件给出:
| $ \begin{array}{c} \left\langle a_{k}\right\rangle=\partial \boldsymbol{Q} / \partial x_{k}, \\ \left\langle a_{k} a_{m}+d_{k m}\right\rangle=\partial^{2} \boldsymbol{Q} / \partial x_{k} \partial x_{m}, \\ \left\langle a_{k} u_{m}+A\right\rangle=0, \\ \left\langle\left(a_{k} a_{m}+d_{k m}\right) u_{k}+A a_{k}+b_{k}\right\rangle=0, \\ \left\langle\left(A a_{k}+b_{k}\right) u_{k}+A^{2}+B\right\rangle=0 \end{array} $ | (8) |
单元界面上的守恒量及其一、二阶导数可由高阶重构得到。对气体分布函数求矩即可得到二阶时空分布的守恒量通量F(0, y, t)。由于其中包含了高阶时空导数,只需要直接对时间和界面切向坐标积分就可以得到界面数值通量,从而建立单步时空三阶精度GKS,且不需要布置高斯积分点,计算量得到显著减少。
需要说明的是,式(6)中包含了界面两侧的初始间断分布,从而有利于捕捉流场间断。实际上,对于光滑区流动,比如CPR内点,式(6)可以简化为:
| $ \begin{array}{c} f(\boldsymbol{x}, t, \boldsymbol{u}, \xi)=\left\{1-\tau a_{k} u_{k}+(t-\tau) A-\right. \\ \tau t\left(A a_{k}+b_{k}\right) u_{k}+\left(t^{2} / 2-\tau t\right)\left(A^{2}+B\right)+ \\ {\left[a_{k}-\tau\left(a_{k} a_{m}+d_{k m}\right) u_{m}+\right.} \\ \left.(t-\tau)\left(A a_{k}+b_{k}\right)\right] x_{k}+ \\ \left.\left(a_{k} a_{m}+d_{k m}\right) x_{k} x_{m} / 2\right\} g_{0} \end{array} $ | (9) |
因此可以获得整个单元内通量的时空分布F(x, t),从而一次计算出所有内部点上的通量,减少计算量。
如果略去分布函数中的高阶展开项, 对应于二阶 GKS, 式(6) 可简化为:
| $ \begin{array}{l} f^{s}=\mathrm{e}^{-t / \tau}\left(1-C_{1} a_{k}^{s} u_{k}-\tau A^{s}+a_{2}^{s} y\right) g^{s}, \\ f^{c}=\left(C_{4}+C_{5} a_{k} u_{k}+C_{6} A+C_{4} a_{2} y\right) g_{0} \end{array} $ | (10) |
如果直接对时间积分,可以达到单步二阶时间精度。实际上,由于该分布函数包含了一阶时间导数项,可以结合两步四阶离散方法,从而高效地达到四阶时间精度。通过结合新型的紧致重构框架,可以充分发挥三阶GKS和二阶GKS的优势,构造出更加高效的高精度格式。
1.2 SCFV-GKSSCFV方法具有混合方法的思想,其放宽了子单元数的限制,同时将重构模板拓展到面相邻单元。这样能够有效避免SV方法划分子单元的瓶颈。如图 1所示,为了满足三阶和四阶紧致重构的需求,可以将每个单元(也称为主单元)均匀划分为4个子单元。子单元界面分为两种类型,当界面(实线)两侧为不同主单元时,将其称为Ⅰ-型界面,而对于主单元内部的界面(虚线)则称为Ⅱ-型界面。
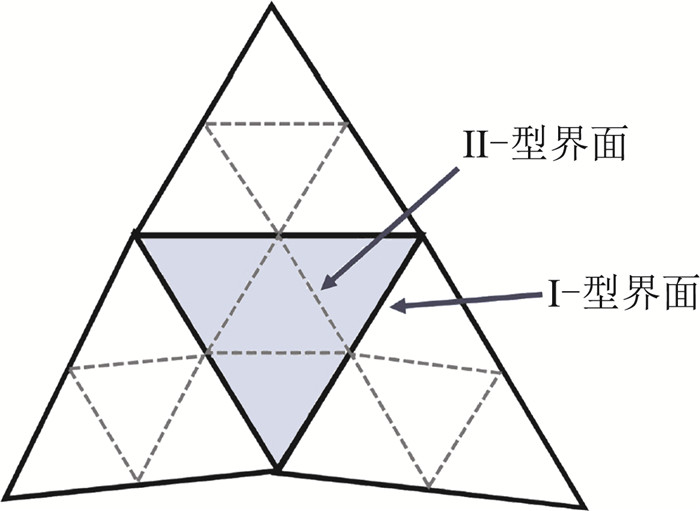
|
图 1 三阶SCFV方法的子单元划分 Fig.1 Partition of subcells in 3rd-order SCFV |
原始的SCFV方法采用加权最小二乘法重构单元内的分布,由此得到的多项式只能保证主单元的守恒性,其内部子单元的守恒性无法直接保证。Pan等采用了平移修正的方式对子单元守恒性进行修正,但这样会在子单元界面上额外引入间断,导致通量计算量的增大。
我们首先通过约束最小二乘重构对SCFV方法进行改进。在重构目标单元的多项式时,将目标单元的子单元平均值作为约束条件,并通过标准的拉格朗日乘子方法求解待定系数矩阵[42]。由此得到的多项式能够直接保证子单元的守恒性,而无需进行额外的修正。在此基础上,将紧致三阶SCFV与三阶GKS相结合,发展的了具有单步时空三阶精度的SCFV-GKS。紧致三阶重构模板仅包含目标主单元的4个子单元以及面相邻主单元内的9个子单元。子单元平均值按照式(4)分别更新。
为计算子单元界面上的数值通量,可以基于式(6),直接沿子单元界面切向和时间方向积分,从而不需要空间高斯积分点以及时间方向的R-K推进。值得注意的是,基于对SCFV方法的改进,仅I-型界面上保留了间断。而II-型界面上的分布则是连续的,因此可以基于简化的气体分布函数式(9)进行计算,从而有效降低通量的计算量。同时,在光滑区域,由于重构是针对大单元进行的,不需要对每个子单元分别进行重构,同样可以减小计算量。总之,SCFV-GKS不仅能保证紧致性,计算效率也能得到显著提高。
为了实现激波捕捉,可以通过激波探测器标记问题单元,并在问题单元上实施基于逐级重构的WENO限制器[43],该限制器能够在保证光滑区域高精度的同时,有效抑制激波附近的数值振荡。由于限制后的多项式无法直接保证子单元的守恒性,为简单起见,仍采用原始SCFV方法中的平移修正来间接保证子单元的守恒性,实现子单元尺度上的间断捕捉。SCFV-GKS的具体细节见文献[44]。
1.3 基于CPR框架的高精度GKSCPR框架的表达式如下:
| $ \frac{\partial \boldsymbol{Q}_{i j}}{\partial t}+\nabla \cdot \boldsymbol{F}\left(\boldsymbol{Q}_{i j}\right)+\delta_{i j}=0 $ | (11) |
其利用单元内设置的若干求解点可以插值得到守恒量和通量在单元内的分布,从而可以直接对通量函数多项式求散度,进而更新每个求解点上的守恒变量Qij。考虑到单元界面两侧可能存在间断,还需在每个单元界面上设置若干通量点,计算耦合相邻单元影响的通量值,并由此对单元内的通量分布进行修正,即式(11)中的修正项δij。三阶CPR的求解点和通量点分布如图 2所示,为减少计算量,求解点与通量点均采用Lobatto点,两者位置重合。
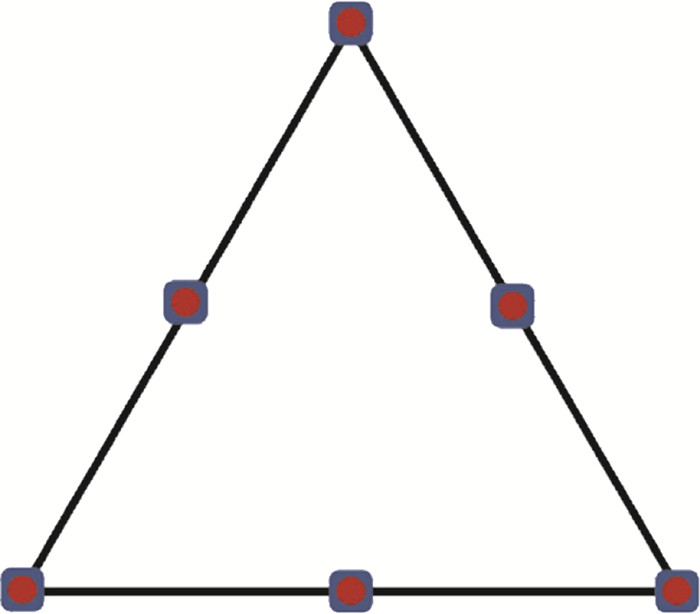
|
图 2 三阶CPR的求解点(圆形)和通量点分布(方形) Fig.2 The distribution of solution points and flux points in 3rd-order CPR |
我们首先基于CPR的紧致三阶重构,结合三阶GKS通量求解器,发展了单步时空三阶精度的CPR-GKS。充分利用三阶GKS的多维特性,基于单元界面中点,以及单元形心分别构造了时空二阶分布的气体分布函数,即式(6)和式(9),进而得到通量在单元界面以及单元内的时空二阶分布。由此可以同时确定单元界面上所有通量点,以及单元内所有求解点上的通量值。传统CPR则需要逐点计算数值通量。同时,由于通量包含了时间演化,因此可以沿时间积分单步更新求解点值,而不需要结合多步R-K方法。此外,由于GKS中自动耦合了无黏和黏性影响,毋须像传统CPR那样额外处理黏性通量。格式的具体细节见文献[45]。
为进一步提高格式精度,我们基于CPR的紧致四阶重构,结合二阶GKS通量及其时间导数,借助两步四阶离散,发展了两步四阶GKS,只需要两个子步即可达到时空四阶精度。而传统CPR则通常需要结合四步或五步R-K方法。相比于单步四阶GKS,采用两步四阶GKS能够有效简化气体分布函数的构造,降低通量的计算量。
两步四阶CPR-GKS的高效性,来源于对GKS通量中包含的丰富时空信息的充分利用。类似地,单步三阶CPR-GKS利用了GKS通量的多维时空特性,从而显著提高了计算效率。Xu等利用界面上的演化解直接计算下一时刻的宏观量,从而提高重构紧致性[34-38]。实际上,如果充分利用四阶GKS通量的时空信息,也有望建立更为高效的数值格式。
虽然基于CPR框架能够高效地实现紧致高阶重构,但在高速流动问题中的激波捕捉技术尚待进一步研究。通过借鉴SCFV方法在激波捕捉上的优势,我们进一步发展了CPR/SCFV混合算法。通过激波探测器区分流场中的光滑区域和包含间断的区域,前者采用CPR求解,而后者则采用SCFV求解。这样既能够保证光滑区域的高精度,同时兼顾激波捕捉的高分辨率和强稳健性。传统CPR限制器通常直接针对单元内的高阶多项式进行限制,难以在亚网格尺度上捕捉间断。而在CPR/SCFV混合算法中,通过将激波探测器标记的问题单元划分为一组子单元,并且针对每个子单元分别进行限制。如图 3所示,对于三阶CPR,将问题单元均匀划分为9个子单元,这样能够在保证原有内自由度的同时,避免子单元划分的复杂性。类似的,四阶CPR则将问题单元均匀划分为16个子单元。具体细节见文献[46]。
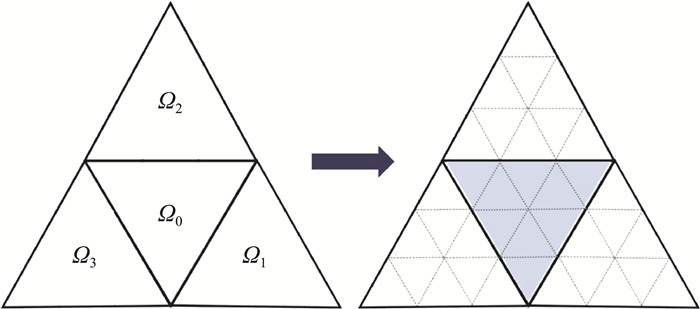
|
图 3 三阶CPR的子单元划分 Fig.3 Partition of subcells in 3rd-order CPR |
通过在子单元界面上引入间断,激波的厚度能够被有效地限制在大单元尺度范围内,从而实现子单元尺度上的激波捕捉。需要指出的是,我们在每个子单元上采用的是二阶TVD限制器[10],该限制器能够较好地抑制数值振荡,并且实现较为简单,但引入的数值耗散较大,也在一定程度上增加了对激波探测器的依赖性。在后续的研究中,可以考虑针对子单元实施高阶限制器。
高阶格式在处理曲面边界时,网格对物理边界的逼近程度会严重影响数值计算精度,有必要采用曲边网格。基于CPR框架发展的高精度GKS,能够比较方便地处理曲边网格。只需通过等参变换将物理空间的高阶网格单元变换到计算空间的标准单元上,并在标准单元实施CPR算法即可。同时,由一维CPR方法通过张量积的形式将其推广到六面体网格,从而建立适合复杂外形的三维CPR-GKS。
2 数值验证及对比分析通过典型算例对前面提到的几种格式进行验证,考察不同格式的精度、效率以及激波捕捉性能。为了说明与传统通量求解器的区别,还与传统CPR进行了一定的对比。二维问题中直接基于单元尺度计算的CFL数,SCFV-GKS取为0.2,CRP-GKS以及传统CPR均取0.1,三维问题中CFL数取值为0.05。
2.1 可压缩Couette流动考察在两无限长平行平板之间的流动,上板温度为T1 = 1,运动速度为U1 = 0.5,相应的马赫数为Ma=0.5,下板静止且绝热。雷诺数设为Re=500。黏性系数μ与温度呈线性关系μ=μ1T/T1,普朗特数为Pr=1。为了简单起见,边界条件按照解析解给定。需要说明的是,虽然流动定常,这里仍按非定常显式推进,计算至足够长的时间(t=300)后评估各格式所得结果的误差与所用CPU时间。图 4给出了速度的2-范数误差随网格尺度变化的曲线。其中传统CPR的无黏通量采用HLLC格式,黏性通量采用BR2格式,并且结合四步R-K方法进行时间推进。可以看出所有格式都达到了设计的精度阶数,绝对误差主要受重构阶数影响。相比于三阶格式,四阶格式具有显著更小的绝对误差,并且随着网格加密,绝对误差下降得更快。
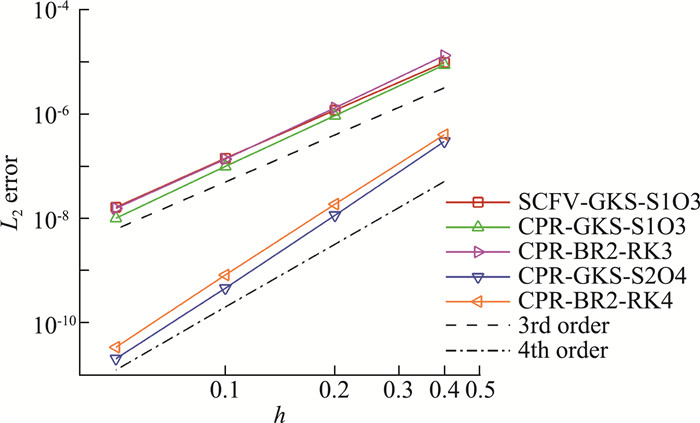
|
图 4 可压缩Couette流动:速度误差随网格尺度的变化 Fig.4 Compressible Couette flow: velocity error vs. mesh size |
为进一步考察格式的计算效率,图 5给出了绝对误差随计算所用CPU时间变化的曲线。虽然在相同网格尺度下,四阶格式的计算量大于三阶格式,但由于绝对误差明显更小,因此四阶格式相比于三阶格式具有明显的效率优势。对于传统CPR,虽然传统Riemann求解器的计算量较小,但在黏性问题中还需要额外处理黏性项,并且由于需要更多的子步,因此总的计算量与CPR-GKS相当。总之,基于CPR框架发展的两步四阶GKS具有最显著的优势。需要指出的是,本算例为光滑流动问题,因此没有施加限制器。对于高速流动问题,施加限制器往往带来较大的计算量,由于CPR-GKS能够采用更少的子步数达到高阶时间精度,因此其计算效率相比于传统CPR还能够进一步提高。此外,考虑到三阶CPR-GKS可以比四阶格式取更大的CFL数,此时效率会有一定的提升,但仍然显著低于四阶格式。不同格式CFL数取值大小的影响仍有待进一步研究。
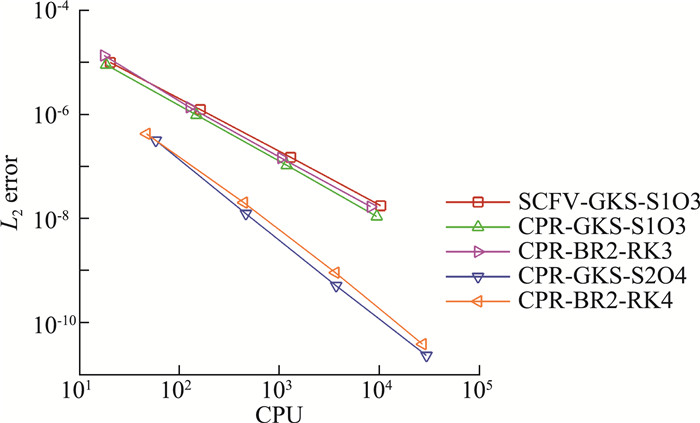
|
图 5 可压缩Couette流动:速度误差随CPU时间的变化 Fig.5 Compressible Couette flow: velocity error vs. CPU time |
马赫数Ma=10的正激波经过30°斜坡形成的双马赫反射是典型的二维强激波问题,可用于验证格式的稳健性和激波捕捉能力。初始流场为:
| $ (\rho ,U,V,p) = \left\{ {\begin{array}{*{20}{l}} {(1.4,0,0,1),}&{x < 0}\\ {(8,8.25,0,116.5),}&{x > 0} \end{array}} \right. $ | (12) |
计算时间为t=0.2,网格尺度为h=1/160。图 6给出了不同格式计算得到的三波点附近的密度等值线图,其中包含30条在2.0~22.5之间均匀分布的密度等值线。可以看出,两步四阶CPR-GKS的计算结果最好,激波的分辨率最高,并且在滑移线上捕捉到了一系列小尺度涡结构。相比于单步三阶CPR-GKS,单步三阶SCFV-GKS在滑移线上捕捉到的涡结构更加明显,但间断略显更宽。需要注意的是,与文献[45]不同,本文的三阶CPR-GKS由于在间断区域结合了SCFV,每个单元内包含了更多的内自由度,因此对间断的分辨率比SCFV-GKS更高。但是,两者在子单元上采用的限制器是不同的:CPR-GKS采用的是二阶TVD限制器,而SCFV-GKS则是HR-WENO,因此在滑移线附近,由于部分单元被标记为间断单元,高阶限制器使得SCFV-GKS得到的涡结构更加明显。计算结果表明三种高精度GKS都能够在激波捕捉中兼具高分辨率和强稳健性,并且两步四阶CPR-GKS的优势更加明显。
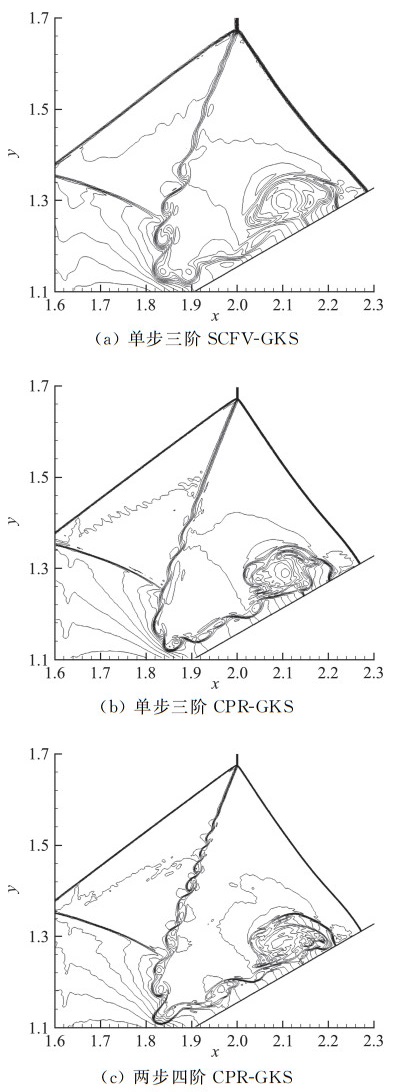
|
图 6 双马赫反射:密度等值线(t=0.2) Fig.6 Double Mach reflection: density contours at t=0.2 |
图 7给出了两步四阶CPR-GKS计算得到的密度等值线的全局视图,斜激波下方的等值线也比较光滑,说明格式能够有效抑制数值振荡。图 8进一步给出了由两步四阶CPR-GKS计算得到的马赫杆附近的密度等值线,且同时展示了主单元和子单元的分布。可以看出激波厚度被成功限制在主单元的尺度内,因此能够实现子单元尺度上的激波捕捉,验证了CPR/SCFV混合算法对间断的高分辨率。
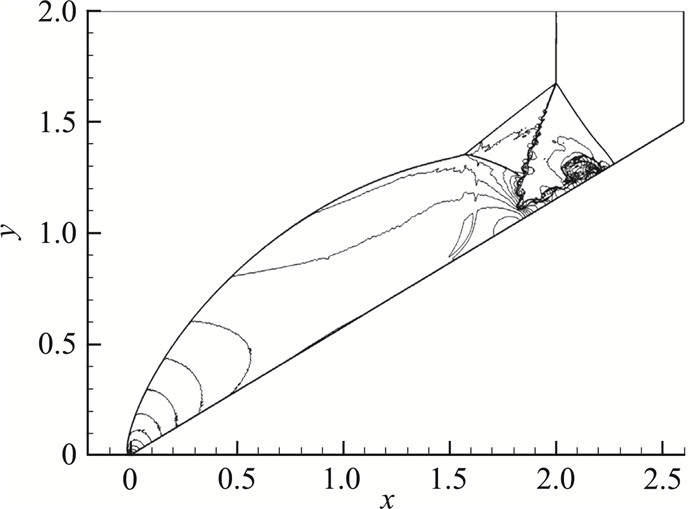
|
图 7 双马赫反射:密度等值线的全局视图(t=0.2),两步四阶CPR-GKS Fig.7 Double Mach reflection: global view of density contours at t=0.2 from fourth-order CPR-GKS |
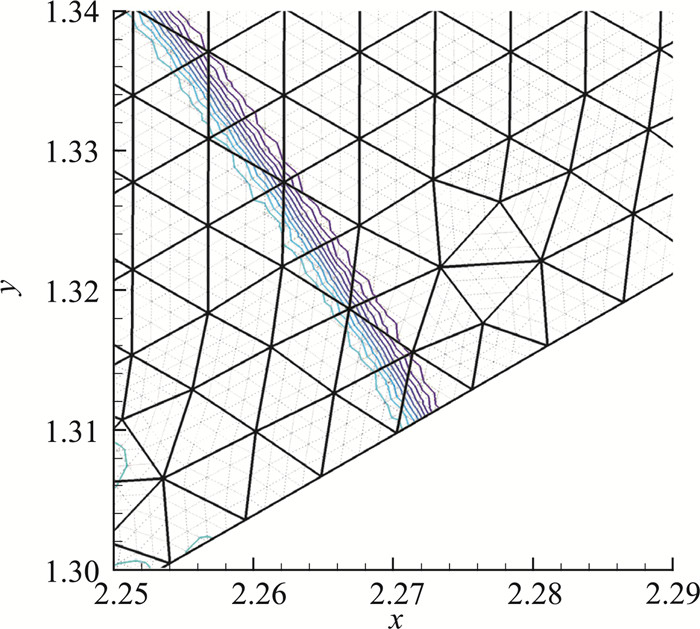
|
图 8 双马赫反射:马赫杆附近的等值线(t=0.2),两步四阶CPR-GKS Fig.8 Double Mach reflection: contours near the Mach stem at t=0.2 from fourth-order CPR-GKS |
超声速来流绕过圆球时,流场中包含复杂的波系和旋涡结构,对于数值方法具有较大的挑战性。来流马赫数取为Ma=1.2,雷诺数为Re=1000。计算网格如图 9所示,共88 128个单元,圆球表面附近的法向最小网格尺度为0.0365,拉伸率约为1.15,圆球表面为无滑移绝热壁。
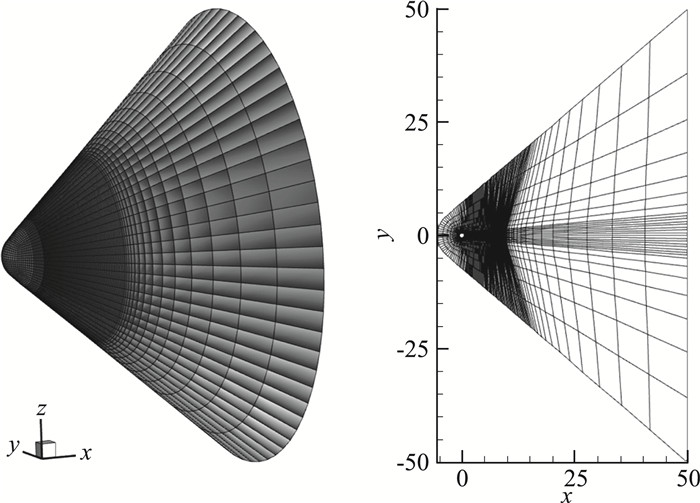
|
图 9 三维超声速圆球绕流:计算网格 Fig.9 Supersonic flow over a sphere: computational mesh |
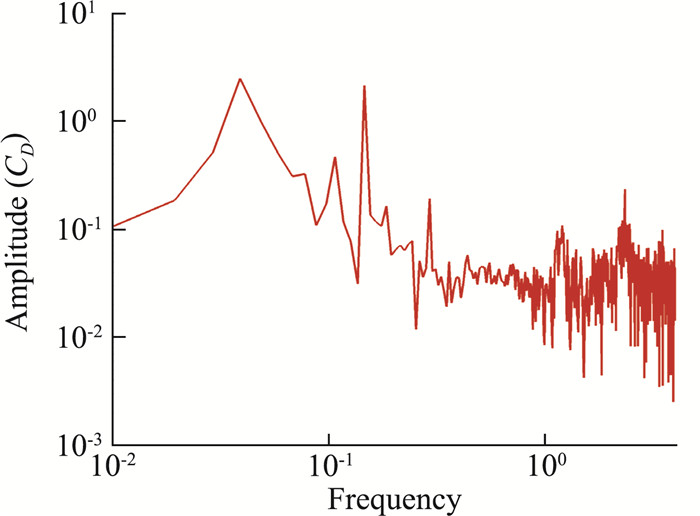
图 10给出了t=400的瞬时密度分布云图,其中可以看到圆球前面的弓形激波、后部的膨胀波及流动分离形成的回流区,以及回流区末端的再压缩波。在尾迹区则可以观察到有大尺度的涡脱落。图 11给出了t=400的瞬时Q判据等值面图,其中Q=0.001,并以马赫数着色。从图中可以看到,四阶CPR-GKS清晰地捕捉到了尾迹区的涡结构,且流场存在明显的对称面。图 12给出了阻力系数随时间变化的曲线,可以看出流动结构的演化过程仍然具有明显的周期性,但此时已出现较小的随机扰动。由阻力系数曲线得到的频谱如图 13所示,可以观察到两个主导的频率分别为0.039和0.145,此外还存在几个更小的峰值频率,并且都集中在低频区域。统计得到的阻力时均值为1.055,计算结果与Nagata等给出的结果1.054吻合得较好[47]。

|
图 10 三维超声速圆球绕流:密度分布云图(t=400) Fig.10 Supersonic flow over a sphere: density contours at t=400 |
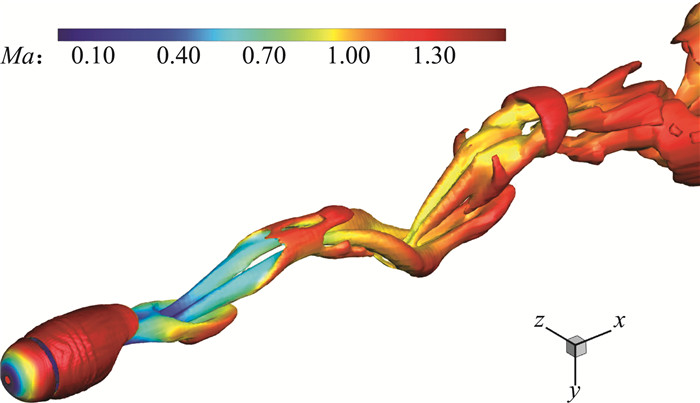
|
图 11 三维超声速圆球绕流:Q判据等值面图(t=400) Fig.11 Supersonic flow over a sphere: Q iso-surface at t=400 |
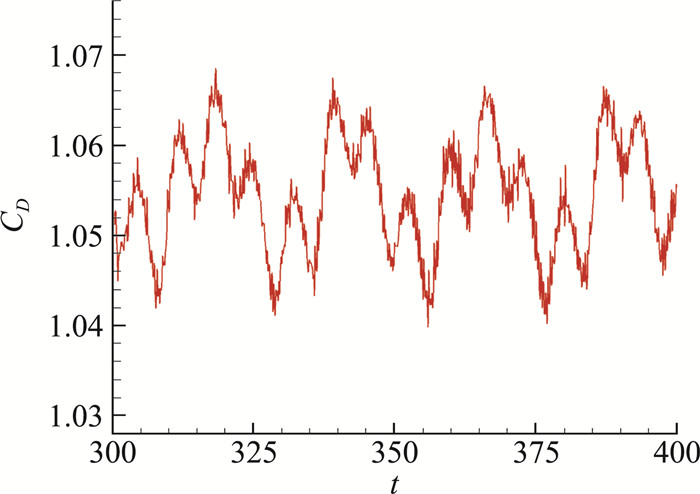
|
图 12 三维超声速圆球绕流:阻力系数随时间变化的曲线 Fig.12 Supersonic flow over a sphere: drag coefficient vs. time |
|
图 13 三维超声速圆球绕流:阻力频谱 Fig.13 Supersonic flow over a sphere: spectrum of drag coefficient |
本文介绍了近年来课题组在非结构网格高效高精度气体动理学格式上的研究进展。利用介观GKS通量求解器,结合基于内自由度的高效紧致重构方法,发展了单步时空三阶精度的SCFV-GKS和CPR-GKS,以及时空四阶精度的CPR-GKS。利用GKS通量的多维空间分布,结合单元内部的连续分布,减少通量的计算量,同时结合通量的时间演化特性减少或消除时间方向的推进子步,从而有效提高了计算效率。混合光滑区CPR和间断区域SCFV发展的两步四阶CPR-GKS,很好地兼顾了高精度、高分辨率和强稳健性。进一步结合曲边网格技术发展了六面体网格上的四阶CPR-GKS,有效增强了格式在复杂流动中的实用性能。
在此基础上,通过典型算例对几种格式进行验证和对比分析,考察了不同格式的精度、效率以及激波捕捉性能。结果表明,其中结合SCFV的两步四阶CPR-GKS具有显著的优势。基于气体动理论的GKS求解器包含丰富的时空演化信息,充分利用这些信息,结合高效的紧致重构方法,能够发展兼具高精度、高效率和强稳健性的新型数值方法,为新一代CFD软件开发提供有力支撑。
在后续的研究工作中,还需要对高阶GKS在三维流动问题,特别是包含强激波的流动问题中的计算性能做进一步的验证。同时,本文涉及到的均为显式格式,为增强对实际工程问题的模拟能力,有必要开展隐式高精度格式研究。此外,为模拟工程实际中面临的高雷诺数湍流问题,可以基于拓展BGK方程的跨尺度演化解发展新型的可压缩湍流多尺度模拟方法,并应用于典型高雷诺数工程湍流精细模拟。
致谢: 感谢清华探索100高性能计算平台、并行科技高性能计算支持服务为本文工作提供部分计算机时。
| [1] |
COCKBURN B, SHU C W. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws Ⅱ: General framework[J]. Mathematics of Computation, 1989, 52: 411-435. DOI:10.2307/2008474 |
| [2] |
COCKBURN B, HOU S, SHU C W. The Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. IV: the multidimensional case[J]. Mathematics of Computation, 1990, 54(190): 545-581. DOI:10.2307/2008501 |
| [3] |
HUYNH H T. A flux reconstruction approach to high-order schemes including discontinuous Galerkin methods[C]//18th AIAA Computational Fluid Dynamics Conference, Session: CFD-9: Higher-Order Methods I: Discontinuous Galerkin. Miami, Florida. Reston, Virginia: AIAA, 2007 doi: 10.2514/6.2007-4079
|
| [4] |
HUYNH H T. A reconstruction approach to high-order schemnes including discontinuous Galerkin for diffusion[C]//Proc of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, Florida. Reston, Virginia: AIAA, 2009 doi: 10.2514/6.2009-403
|
| [5] |
WANG Z J, GAO H Y. A unifying lifting collocation penalty formulation including the discontinuousGalerkin, spectral volume/difference methods for conservation laws on mixed grids[J]. Journal of Computational Physics, 2009, 228(21): 8161-8186. DOI:10.1016/j.jcp.2009.07.036 |
| [6] |
YU M, WANG Z J, LIU Y. On the accuracy and efficiency of discontinuousGalerkin, spectral difference and correction procedure via reconstruction methods[J]. Journal of Computational Physics, 2014, 259: 70-95. DOI:10.1016/j.jcp.2013.11.023 |
| [7] |
HUYNH H T, WANG Z J, Vincent P E. High-order methods for computational fluid dynamics: a brief review of compact differential formulations on unstructured grids[C]//Proc of the 21st AIAA Computational Fluid Dynamics Conference, Session: 40 Years of CFD (Invited). San Diego, CA. Reston, Virginia: AIAA, 2013. AIAA 2013-2564. doi: 10.2514/6.2013-2564
|
| [8] |
WANG Z J. Spectral (finite) volume method for conservation laws on unstructured grids. basic formulation[J]. Journal of Computational Physics, 2002, 178(1): 210-251. DOI:10.1006/jcph.2002.704 |
| [9] |
WANG Z J, LIU Y. Spectral (finite) volume method for conservation laws on unstructured grids: Ⅱ. Extension to two-dimensional scalar equation[J]. Journal of Computational Physics, 2002, 179(2): 665-697. DOI:10.1006/jcph.2002.7082 |
| [10] |
WANG Z J, ZHANG L P, LIU Y. Spectral (finite) volume method for conservation laws on unstructured grids IV: extension to two-dimensional systems[J]. Journal of Computational Physics, 2004, 194(2): 716-741. DOI:10.1016/j.jcp.2003.09.012 |
| [11] |
HUERTA A, CASONI E, PERAIRE J. A simple shock-capturing technique for high-order discontinuous Galerkin methods[J]. International Journal for Numerical Methods in Fluids, 2012, 69(10): 1614-1632. DOI:10.1002/fld.2654 |
| [12] |
SONNTAG M, MUNZ C D. Shock capturing for discontinuous Galerkin methods using finite volume subcells[M]//FUHRMANN J, OHLBERGER M, ROHDE C, (EDS). Finite Volumes for Complex Applications VⅡ-Elliptic, Parabolic and Hyperbolic Problems. Springer Proceedings in Mathematics & Statistics, Springer, Cham, 2014, 78: 945-953. doi: 10.1007/978-3-319-05591-6_96
|
| [13] |
PAN J H, REN Y X. High order sub-cell finite volume schemes for solving hyperbolic conservation laws I: basic formulation and one-dimensional analysis[J]. Science China Physics, Mechanics & Astronomy, 2017, 60(8): 084711. DOI:10.1007/s11433-017-9033-9 |
| [14] |
PAN J H, REN Y X, SUN Y T. High order sub-cell finite volume schemes for solving hyperbolic conservation laws Ⅱ: Extension to two-dimensional systems on unstructured grids[J]. Journal of Computational Physics, 2017, 338: 165-198. DOI:10.1016/j.jcp.2017.02.052 |
| [15] |
DUMBSER M, BALSARA D S, TORO E F, et al. A unified framework for the construction of one-step finite volume and discontinuous Galerkin schemes on unstructured meshes[J]. Journal of Computational Physics, 2008, 227(18): 8209-8253. DOI:10.1016/j.jcp.2008.05.025 |
| [16] |
DUMBSER M. Arbitrary high order PNPM schemes on unstructured meshes for the compressible Navier-Stokes equations[J]. Computers & Fluids, 2010, 39(1): 60-76. DOI:10.1016/j.compfluid.2009.07.003 |
| [17] |
LI J Q. Two-stage fourth order: temporal-spatial coupling in computational fluid dynamics (CFD)[J]. Advances in Aerodynamics, 2019, 1: 3. DOI:10.1186/s42774-019-0004-9 |
| [18] |
LI J Q, DU Z F. A two-stage fourth order time-accurate discretization for Lax-Wendroff type flow solvers I. hyperbolic conservation laws[J]. SIAM Journal on Scientific Computing, 2016, 38(5): A3046-A3069. DOI:10.1137/15m1052512 |
| [19] |
DU Z F, LI J Q. A two-stage fourth order time-accurate discretization for Lax-Wendroff type flow solvers Ⅱ: High order numerical boundary conditions[J]. Journal of Computational Physics, 2018, 369: 125-147. DOI:10.1016/j.jcp.2018.05.002 |
| [20] |
徐昆, 李启兵, 黎作武. 离散空间直接建模的计算流体力学方法[J]. 中国科学(物理学力学天文学), 2014, 44(5): 519-530. XU K, LI Q B, LI Z W. Direct modeling-based computational fluid dynamics[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2014, 44(5): 519-530. (in Chinese) |
| [21] |
XU K. Direct modeling for computational fluid dynamics: Construction and application of unified gas-kinetic schemes[M]. World Scientific, 2014.
|
| [22] |
XU K. Direct modeling for computational fluid dynamics[M]. Singapore: World Scientific Publishing, 2015.
|
| [23] |
李启兵, 徐昆. 气体动理学格式研究进展[J]. 力学进展, 2012, 42(5): 522-537. LI Q B, XU K. Progress ingas-kinetic scheme[J]. Advances in Mechanics, 2012, 42(5): 522-537. (in Chinese) |
| [24] |
XU K. A gas-kinetic BGK scheme for the Navier-Stokes equations and its connection with artificial dissipation and Godunov method[J]. Journal of Computational Physics, 2001, 171(1): 289-335. DOI:10.1006/jcph.2001.6790 |
| [25] |
李启兵. 应用BGK格式对可压缩混合层的数值研究[D]. 北京: 清华大学, 2002. LI Q B. Numerical study of compressible mixing layer with BGK scheme[D]. Beijing: Tsinghua University, 2002. (in Chinese) |
| [26] |
LI Q B, FU S, XU K. A compressibleNavier-Stokes flow solver with scalar transport[J]. Journal of Computational Physics, 2005, 204(2): 692-714. DOI:10.1016/j.jcp.2004.10.026 |
| [27] |
TAN S, LI Q B, XIAO Z X, et al. Gas kinetic scheme for turbulence simulation[J]. Aerospace Science and Technology, 2018, 78: 214-227. DOI:10.1016/j.ast.2018.04.022 |
| [28] |
谭爽, 李诗一, 李启兵, 等. 气体动理学格式与多尺度流动模拟[J]. 计算力学学报, 2017, 34(1): 88-94. TAN S, LI S Y, LI Q B, et al. Gas kinetic scheme and numerical simulation of multiscale flows[J]. Chinese Journal of Computational Mechanics, 2017, 34(1): 88-94. (in Chinese) |
| [29] |
LI Q B, FU S. A high-order accurate gas-kinetic BGK scheme[C]//5th International Conference on Computational Fluid Dynamics. Seoul, Korea, 2008.
|
| [30] |
LI Q B, XU K, FU S. A high-order gas-kinetic Navier-Stokes flow solver[J]. Journal of Computational Physics, 2010, 229(19): 6715-6731. DOI:10.1016/j.jcp.2010.05.019 |
| [31] |
LI Q B, XU K, FU S. A new high-order multidimensional scheme[C]//6th International Conference on Computational Fluid Dynamics. St Petersburg, Russia, 2010.
|
| [32] |
LI Q B, FU S. On the high-order multidimensional gas-kinetic scheme[C]//7th International Conference on Computational Fluid Dynamics. Big Island, Hawaii, 2012.
|
| [33] |
LUO J, XU K. A high-order multidimensional gas-kinetic scheme for hydrodynamic equations[J]. Science China Technological Sciences, 2013, 56(10): 2370-2384. DOI:10.1007/s11431-013-5334-y |
| [34] |
PAN L, XU K. A third-order gas-kinetic scheme for three-dimensional inviscid and viscous flow computations[J]. Computers & Fluids, 2015, 119: 250-260. DOI:10.1016/j.compfluid.2015.07.006 |
| [35] |
XU K. A slope-update scheme for compressible flow simulation[J]. Journal of Computational Physics, 2002, 178(1): 252-259. DOI:10.1006/jcph.2002.7027 |
| [36] |
PAN L, XU K. A compact third-order gas-kinetic scheme for compressible Euler and Navier-Stokes equations[J]. Communications in Computational Physics, 2015, 18(4): 985-1011. DOI:10.4208/cicp.141214.140715s |
| [37] |
PAN L, XU K. A third-order compact gas-kinetic scheme on unstructured meshes for compressible Navier-Stokes solutions[J]. Journal of Computational Physics, 2016, 318: 327-348. DOI:10.1016/j.jcp.2016.05.012 |
| [38] |
JI X, PAN L, SHYY W, et al. A compact fourth-order gas-kinetic scheme for the Euler and Navier-Stokes equations[J]. Journal of Computational Physics, 2018, 372: 446-472. DOI:10.1016/j.jcp.2018.06.034 |
| [39] |
JI X, ZHAO F X, SHYY W, et al. A HWENO reconstruction based high-order compact gas-kinetic scheme on unstructured mesh[J]. Journal of Computational Physics, 2020, 410: 109367. DOI:10.1016/j.jcp.2020.109367 |
| [40] |
LI J, ZHONG C W, ZHUO C S. A third order gas-kinetic scheme for unstructured grid[J]. Computers & Mathematicswith Applications, 2019, 78(1): 92-109. DOI:10.1016/j.camwa.2019.02.020 |
| [41] |
REN X D, XU K, SHYY W, et al. A multi-dimensional high-order discontinuous Galerkin method based on gas kinetic theory for viscous flow computations[J]. Journal of Computational Physics, 2015, 292: 176-193. DOI:10.1016/j.jcp.2015.03.031 |
| [42] |
PAN L, XU K, LI Q B, et al. An efficient and accurate two-stage fourth-order gas-kinetic scheme for the Euler andNavier-Stokes equations[J]. Journal of Computational Physics, 2016, 326: 197-221. DOI:10.1016/j.jcp.2016.08.054 |
| [43] |
SHI L, WANG Z J, FU S, et al. A PNPM-CPR method fornavier-stokes equations[C]//50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, Tennessee. Reston, Virigina: AIAA, 2012. AIAA 2012-0460. doi: 10.2514/6.2012-460
|
| [44] |
XU Z L, LIU Y J, SHU C W. Hierarchical reconstruction for discontinuous Galerkin methods on unstructured grids with a WENO-type linear reconstruction and partial neighboring cells[J]. Journal of Computational Physics, 2009, 228(6): 2194-2212. DOI:10.1016/j.jcp.2008.11.025 |
| [45] |
ZHANG C, LI Q B. A third-order subcell finite volume gas-kinetic scheme for the Euler and Navier-Stokes equations on triangular meshes[J]. Journal of Computational Physics, 2019(submitted).
|
| [46] |
ZHANG C, LI Q B, FU S, et al. A third-order gas-kinetic CPR method for the Euler and Navier-Stokes equations on triangular meshes[J]. Journal of Computational Physics, 2018, 363: 329-353. DOI:10.1016/j.jcp.2018.02.040 |
| [47] |
ZHANG C, LI Q B, WANG Z J, et al. A two-stage fourth-order gas-kinetic CPR method for the Navier-Stokes equations on triangular meshes[EB/OL]. arXiv: 2010.08914, 2020.
|
| [48] |
NAGATA T, NONOMURA T, TAKAHASHI S, et al. Direct numerical simulation of subsonic, transonic and supersonic flow over an isolated sphere up to a Reynolds number of 1000[J]. Journal of Fluid Mechanics, 2020, 904: A36. DOI:10.1017/jfm.2020.629 |
 2021, Vol. 39
2021, Vol. 39

