2. 军事科学院 系统工程研究院, 北京 100082;
3. 军事科学院, 北京 100091
2. Institute of System Engineering, Academy of Military Sciences, Beijing 100082, China;
3. Academy of Military Sciences, Beijing 100091, China
近年来,随着计算机浮点运算能力的逐步提升, 对湍流等包含时空多尺度流动结构的精细模拟成为研究热点,针对湍流流动的分离涡模拟(DES)[1-2]、大涡模拟(LES)[3-4]以及直接数值模拟(DNS)[5-6]等较为精细的数值模拟方法得到了进一步发展和完善。精细的湍流模拟方法需要严格控制所有离散过程中的数值误差,相较于传统的二阶精度计算方法,高阶精度的计算方法具有明显优势。
高阶精度应用场景的现实强烈需求催生了一系列的高阶精度计算方法。精度最高的谱方法[7]具有理想的指数阶精度,却难以应用于复杂外形的流动模拟中,目前谱方法多用于对其他高阶精度数值计算方法的考核与验证。其他的数值方法按照其离散框架大致可以分为基于有限差分方法的、基于有限体积方法的和基于有限元方法的高阶精度计算方法,以及近年来逐渐衍生出的DG方法[8-9]、谱差分方法[10-11]以及谱体积方法[12-13]。由于离散框架的不同,不同类型的高阶精度数值方法提高计算精度的方式迥异,尤其是在多维问题中。得益于逐维离散特性,有限差分方法能以较小计算代价实现多维问题的高阶精度计算[14-15],但适应复杂几何外形的能力较弱[16]。当网格不够光滑时,高阶精度有限差分方法还存在明显的降阶问题。因此,在相当长的一段时间内,基于有限差分方法的高阶精度算法多用于绕简单外形的类似于湍流等多尺度复杂流动问题的模拟中[17-18],鲜有在复杂外形流动中成功应用的例子。近年来的研究结果表明[19-22],基于有限差分方法的高阶精度计算格式对复杂网格的适应能力较差的主要原因是有限差分方法离散框架下的几何守恒律不易满足。
有限差分方法中几何守恒律(Geometry Conservation Law, GCL)的确切定义最早由Thomas和Lombard[23-24]于1978年提出,而由于几何守恒未满足而引起的几何守恒误差最早则由Steger于1977年发现[25-26]。几何守恒律一般可以分为体积守恒律(Volume Conservation Law, VCL)和面积守恒律(Surface Conservation Law, SCL)[27],体积守恒律表征了网格运动过程中网格变换雅克比和网格运动速度之间需满足的约束关系,面积守恒律则反映了网格变换导数各分量之间需满足的约束关系。
Thomas和Lombard[23-24]在首次明确几何守恒律概念时着重关注的正是运动网格下的体积守恒律问题。在有限差分离散框架下,Thomas等[23-24]在已知网格运动速度的情况下通过求解微分型的体积守恒律方程得到网格变换雅克比,从而使得体积守恒律得以满足。但网格变换雅克比在离散后的体积应由当前网格点的位置唯一确定,Thomas等通过求解体积守恒律方程得到的数值体积与其定义之间存在相容性的问题。针对有限差分方法中运动网格的体积守恒律问题,Abe等[28-29]通过改变与网格运动相关的导数(网格运动速度)的计算方式使得体积守恒律在有限差分离散下自动满足。在有限体积离散框架下,Wang[30]和Zhang[31]通过改变网格界面运动速度的计算方式来使得体积守恒律自动满足。最近Chang等[32]还对有限体积方法中运动网格的几种体积守恒解决方案进行了较为详细的分析与比较。从解决体积守恒律问题的角度,Abe等[28-29]的解决方案与Wang[30]和Zhang[31]的方案基本思路一致,只不过分别是在有限差分和有限体积的框架下实现的。
面积守恒律反映的是各网格变换导数分量之间需满足的约束关系。早在1977年Steger[25-26]就发现,在采用传统网格变换导数算法利用二阶中心有限差分格式离散计算坐标系下的守恒律方程时会面临自由流不守恒的问题,其守恒误差是以二阶精度趋于0的。传统的网格变换导数算法会导致流场中存在着完全由计算网格引起的误差源(Hindman[33-34]将其称为几何诱导误差),容易对计算流场产生非物理的干扰,严重时还会引起数值振荡[35]导致计算过程不稳定。为了有效解决这一问题,1978年Pulliam和Steger[36-37]给出了一种加权平均的网格变换导数算法,但美中不足的是Pulliam和Steger[36-37]的加权平均方法中同时包括二阶中心差分和二阶中心插值,其在网格块边界上的应用存在困难,且不具有普适性,不能直接推广到高阶精度有限差分方法的应用中。紧随其后,1979年Thomas和Lombard[24]首次提出了网格变换导数的守恒计算形式,并指出如果网格变换导数和对流通量导数均采用二阶中心差分离散,则能满足面积守恒律。尽管Thomas和Lombard[24]的面积守恒律解决方案是针对二阶精度有限差分格式提出的,但其在解决有限差分几何守恒律问题的历史上仍具有里程碑式的意义,其工作也被后续诸多研究人员所引用[27-29, 38-40]。关于高阶精度有限差分方法中的几何守恒律问题,直到二十多年后的2002年才由Visbal和Gaitonde[38]将Thomas和Lombard[24]的解决方案推广到高阶精度的有限差分格式计算中。Visbal和Gaitonde[38]再次重申了采用网格变换导数守恒计算形式的必要性,且明确指出网格变换导数和对流项必须采用相同的高阶差分格式离散,并成功将其应用到高阶紧致有限差分格式的计算中,后续研究人员将该解决思路称之为Visbal和Gaitonde的数值方法。2010年Nonomura等[39]将Visbal和Gaitonde的数值方法[38]首先应用到WCNS[41-43]中,模拟了三角翼的绕流问题,数值计算结果表明WCNS能够很好地满足面积守恒律。同时Nonomura等[39]还研究了有限差分的WENO格式[44-45]的面积守恒特性,发现由于在计算数值通量时采用了包含网格变换导数的混合通量分裂方法,导致非线性的WENO格式难以满足面积守恒律,其对复杂网格的适应能力不如WCNS[39]。为了能够适应绕复杂构型流动的数值模拟,计算格式必须满足面积守恒律[27]。为此Nonomura[46]和Jiang[47]均对WENO格式进行了一些改进,以便能够满足面积守恒律。
2011年Deng等[40]从理论上详细分析了面积守恒律的满足条件,并给出了满足几何守恒律的充分条件(Conservative Metric Method, CMM),同时还指出Thomas和Lombard[24]的解决方案是CMM条件的一个二阶精度特例,而Visbal和Gaitonde的数值方法[38]则是CMM条件的高阶精度紧致差分格式的应用实例,并首次将几何守恒律的满足范围从内点严格地扩展到边界和临近边界的计算点上。随后,Deng等[48]从几何意义的角度给出了满足几何守恒律的对称守恒网格导数算法(Symmetrical Conservative Metric Method, SCMM),解决了网格变换导数和雅克比计算形式的唯一性问题。
本文主要介绍有限差分方法中几何守恒律问题的研究进展,重点将集中在有限差分框架下的网格变换导数和雅克比的具体离散形式和几何守恒律对数值计算结果的影响。
1 几何守恒律问题笛卡尔坐标系(t, x, y, z)下的一般守恒律方程的微分形式可以表述为:
| $ \frac{{\partial \mathit{\boldsymbol{Q}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial y}} + \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial z}} = 0 $ | (1) |
其中Q为流场变量,E、F和G为关于Q的通量。为了便于在贴体结构网格中进行有限差分离散,需对守恒律方程(1)进行坐标变换。
| $ \left\{\begin{array}{l} \tau=\tau(t)=t \\ \xi=\xi(t, x, y, z) \\ \eta=\eta(t, x, y, z) \\ \zeta=\zeta(t, x, y, z) \end{array}\right. $ | (2) |
经坐标变换(2),计算坐标系下的守恒律方程可表述为:
| $ \frac{\partial \hat{\boldsymbol{Q}}}{\partial \tau}+\frac{\partial \hat{\boldsymbol{E}}}{\partial \xi}+\frac{\partial \hat{\boldsymbol{F}}}{\partial \eta}+\frac{\partial \hat{\boldsymbol{G}}}{\partial \zeta}=I_{t} \boldsymbol{Q}+I_{x} \boldsymbol{E}+I_{y} \boldsymbol{F}+I_{z} \boldsymbol{G} $ | (3) |
其中:
| $ \begin{array}{c} \hat{\boldsymbol{Q}}=J^{-1} {\boldsymbol{Q}} \\ \hat{\boldsymbol{E}}=\hat{\xi}_{t} Q+\hat{\xi}_{x} \boldsymbol{E}+\hat{\xi}_{y} \boldsymbol{F}+\hat{\xi}_{z} \boldsymbol{G} \\ \hat{\boldsymbol{F}}=\hat{\eta}_{t} \boldsymbol{Q}+\hat{\eta}_{x} \boldsymbol{E}+\hat{\eta}_{y} \boldsymbol{F}+\hat{\eta}_{z} \boldsymbol{G} \\ \hat{\boldsymbol{G}}=\hat{\zeta}_{t} \boldsymbol{Q}+\hat{\zeta}_{x} \boldsymbol{E}+\hat{\zeta}_{y} \boldsymbol{F}+\hat{\zeta}_{z} \boldsymbol{G} \end{array} $ | (4) |
以及:
| $ \begin{array}{c} I_{\mathrm{t}}=\frac{\partial \hat{\xi}_{t}}{\partial \xi}+\frac{\partial \hat{\eta}_{t}}{\partial \eta}+\frac{\partial \hat{\zeta}_{t}}{\partial \zeta}+\frac{\partial J^{-1}}{\partial \tau} \\ I_{x}=\frac{\partial \hat{\xi}_{x}}{\partial \xi}+\frac{\partial \hat{\eta}_{x}}{\partial \eta}+\frac{\partial \hat{\zeta}_{x}}{\partial \zeta}\\ I_{y}=\frac{\partial \hat{\xi}_{y}}{\partial \xi}+\frac{\partial \hat{\eta}_{y}}{\partial \eta}+\frac{\partial \hat{\zeta}_{y}}{\partial \zeta} \\ I_{z}=\frac{\partial \hat{\xi}_{z}}{\partial \xi}+\frac{\partial \hat{\eta}_{z}}{\partial \eta}+\frac{\partial \hat{\zeta}_{z}}{\partial \zeta} \end{array} $ | (5) |
网格变换导数的具体表达式:
| $ \left\{\begin{array}{l} \hat{\xi}_{x}=J^{-1} \frac{\partial \xi}{\partial x}=y_{\eta} z_{\zeta}-y_{\zeta} z_{\eta} \\ \hat{\xi}_{y}=J^{-1} \frac{\partial \xi}{\partial y}=z_{\eta} x_{\zeta}-z_{\zeta} x_{\eta} \\ \hat{\xi}_{z}=J^{-1} \frac{\partial \xi}{\partial z}=x_{\eta} y_{\zeta}-x_{\zeta} y_{\eta} \\ \hat{\eta}_{x}=J^{-1} \frac{\partial \eta}{\partial x}=y_{\zeta} z_{\xi}-y_{\xi} z_{\zeta} \\ \hat{\eta}_{y}=J^{-1} \frac{\partial \eta}{\partial y}=z_{\zeta} x_{\xi}-z_{\xi} x_{\zeta} \\ \hat{\eta}_{z}=J^{-1} \frac{\partial \eta}{\partial z}=x_{\zeta} y_{\xi}-x_{\xi} y_{\zeta} \\ \hat{\zeta}_{x}=J^{-1} \frac{\partial \zeta}{\partial x}=y_{\xi} z_{\eta}-y_{\eta} z_{\xi} \\ \hat{\zeta}_{y}=J^{-1} \frac{\partial \zeta}{\partial y}=z_{\xi} x_{\eta}-z_{\eta} x_{\xi} \\ \hat{\zeta}_{z}=J^{-1} \frac{\partial \zeta}{\partial z}=x_{\xi} y_{\eta}-x_{\eta} y_{\xi} \end{array}\right. $ | (6) |
以及网格变换雅克比为:
| $ J^{-1}=\left|\frac{\partial(t, x, y, z)}{\partial(\tau, \xi, \eta, \zeta)}\right|=\left|\begin{array}{lll} \frac{\partial x}{\partial \xi} & \frac{\partial x}{\partial \eta} & \frac{\partial x}{\partial \zeta} \\ \frac{\partial y}{\partial \xi} & \frac{\partial y}{\partial \eta} & \frac{\partial y}{\partial \zeta} \\ \frac{\partial z}{\partial \xi} & \frac{\partial z}{\partial \eta} & \frac{\partial z}{\partial \zeta} \end{array}\right| $ | (7) |
网格运动速度的具体表达式为:
| $ \begin{aligned} &\hat{\xi}_{t}=J^{-1} \frac{\partial \xi}{\partial t}=-\left|\begin{array}{lll} \frac{\partial x}{\partial \tau} & \frac{\partial x}{\partial \eta} & \frac{\partial x}{\partial \zeta} \\ \frac{\partial y}{\partial \tau} & \frac{\partial y}{\partial \eta} & \frac{\partial y}{\partial \zeta} \\ \frac{\partial z}{\partial \tau} & \frac{\partial z}{\partial \eta} & \frac{\partial z}{\partial \zeta} \end{array}\right|\\ &\hat{\eta}_{t}=J^{-1} \frac{\partial \eta}{\partial t}=-\left|\begin{array}{lll} \frac{\partial x}{\partial \tau} & \frac{\partial x}{\partial \xi} & \frac{\partial x}{\partial \zeta} \\ \frac{\partial y}{\partial \tau} & \frac{\partial y}{\partial \xi} & \frac{\partial y}{\partial \zeta} \\ \frac{\partial z}{\partial \tau} & \frac{\partial z}{\partial \xi} & \frac{\partial z}{\partial \zeta} \end{array}\right|\\ &\hat{\zeta}_{t}=J^{-1} \frac{\partial \zeta}{\partial t}=-\left|\begin{array}{lll} \frac{\partial x}{\partial \tau} & \frac{\partial x}{\partial \xi} & \frac{\partial x}{\partial \eta} \\ \frac{\partial y}{\partial \tau} & \frac{\partial y}{\partial \xi} & \frac{\partial y}{\partial \eta} \\ \frac{\partial z}{\partial \tau} & \frac{\partial z}{\partial \xi} & \frac{\partial z}{\partial \eta} \end{array}\right| \end{aligned} $ | (8) |
为了简化公式的表达形式,将笛卡尔坐标系下的坐标表示为矢量形式:
| $ \boldsymbol{r}=x \boldsymbol{e}_{x}+y \boldsymbol{e}_{y}+z \boldsymbol{e}_{z} $ | (9) |
其中矢量ex、ey和ez分别为笛卡尔坐标系下的三个不变的坐标基,x、y和z分别为矢量r在笛卡尔坐标系下三个坐标基方向上的分量。将网格变换导数(6)表示为矢量的分量形式:
| $ \begin{array}{l} \boldsymbol{\xi}=\hat{\xi}_{x} \boldsymbol{e}_{x}+\hat{\xi}_{y} \boldsymbol{e}_{y}+\hat{\xi}_{z} \boldsymbol{e}_{z} \\ \boldsymbol{\eta}=\hat{\eta}_{x} \boldsymbol{e}_{x}+\hat{\eta}_{y} \boldsymbol{e}_{y}+\hat{\eta}_{z} \boldsymbol{e}_{z} \\ \boldsymbol{\zeta}=\hat{\zeta}_{x} \boldsymbol{e}_{x}+\hat{\zeta}_{y} \boldsymbol{e}_{y}+\hat{\zeta}_{z} \boldsymbol{e}_{z} \end{array} $ | (10) |
则容易得到坐标变换导数(6)更为紧凑的矢量形式为:
| $ \boldsymbol{\xi}=\boldsymbol{r}_{\eta} \times \boldsymbol{r}_{\zeta}, \boldsymbol{\eta}=\boldsymbol{r}_{\zeta} \times \boldsymbol{r}_{\xi}, \zeta=\boldsymbol{r}_{\xi} \times \boldsymbol{r}_{\eta} $ | (11) |
以及网格变换雅克比(7)的紧凑表达形式:
| $ J^{-1}=\boldsymbol{r}_{\xi} \cdot \boldsymbol{\xi}=\boldsymbol{r}_{\eta} \cdot \boldsymbol{\eta}=\boldsymbol{r}_{\zeta} \cdot \boldsymbol{\zeta} $ | (12) |
类似的,网格运动速度(8)也可以表述为:
| $ \begin{array}{l} \hat{\xi}_{t}=-\left(x_{\tau} \hat{\xi}_{x}+y_{\tau} \hat{\xi}_{y}+z_{z} \hat{\xi}_{z}\right)=-\boldsymbol{r}_{\tau} \cdot \boldsymbol{\xi} \\ \hat{\eta}_{t}=-\left(x_{\tau} \hat{\eta}_{x}+y_{\tau} \hat{\eta}_{y}+z_{\tau} \hat{\eta}_{z}\right)=-\boldsymbol{r}_{\tau} \cdot \boldsymbol{\eta} \\ \hat{\zeta}_{t}=-\left(x_{z} \hat{\zeta}_{x}+y_{z} \hat{\zeta}_{y}+z_{z} \hat{\zeta}_{z}\right)=-\boldsymbol{r}_{\tau} \cdot \boldsymbol{\zeta} \end{array} $ | (13) |
对于流场变量ϕ和φ,在(偏)微分算子d的作用下满足:
| $ \mathrm{d}(\phi \varphi)=\varphi \mathrm{d} \phi+\phi \mathrm{d} \varphi $ | (14) |
在微分算子(14)作用下,将网格导数表达式(6)和(8)代入式(5)中,容易得到:
| $ I_{\mathrm{t}}=I_{x}=I_{y}=I_{z}=0 $ | (15) |
则可将计算坐标系下的守恒律控制方程(3)进一步表述为:
| $ \frac{\partial \hat{\boldsymbol{Q}}}{\partial \tau}+\frac{\partial \hat{\boldsymbol{E}}}{\partial \xi}+\frac{\partial \hat{\boldsymbol{F}}}{\partial \eta}+\frac{\partial \hat{\boldsymbol{G}}}{\partial \zeta}=0 $ | (16) |
采用有限差分方法离散守恒律控制方程(16)需满足的一个基本条件是均匀流保持:如果在计算域内给定初值为均匀来流,且计算域的所有边界也都为均匀来流边界(则流场中任意一点的变量Q、E、F和G均为常数),则数值离散守恒律控制方程(16)应该依然得到与初始值相同的均匀流。容易看出,均匀流问题本身是笛卡尔坐标系下守恒律控制方程(1)的解,同时也是计算坐标系下守恒律控制方程(16)的解。对于均匀流动问题,计算坐标系下守恒律控制方程(16)退化为:
| $ \frac{\partial \boldsymbol{Q}}{\partial \tau}=-\frac{1}{J^{-1}}\left(I_{t} \boldsymbol{Q}+I_{x} \boldsymbol{E}+I_{y} \boldsymbol{F}+I_{z} \boldsymbol{G}\right) $ | (17) |
均匀流保持要求变量Q恒为常数,即∂Q/∂τ=0对于任意的流场变量Q恒成立。方程(17)右端在微分意义下恒为0,均匀流保持要求方程(17)在有限差分离散下亦恒成立。守恒律控制方程(16)在有限差分算子离散下可以表述为:
| $ \delta_{\tau}^{1} \hat{\boldsymbol{Q}}+\delta_{\xi}^{1} \hat{\boldsymbol{E}}+\delta_{\eta}^{1} \hat{\boldsymbol{F}}+\delta_{\zeta}^{1} \hat{\boldsymbol{G}}=0 $ | (18) |
其中δ1为有限差分求导算子,下标表示求导方向。对于均匀流问题,式(18)退化为:
| $ I_{t}^{N} \boldsymbol{Q}+I_{x}^{N} \boldsymbol{E}+I_{y}^{N} \boldsymbol{F}+I_{z}^{N} \boldsymbol{G}=0 $ | (19) |
其中,
| $ \begin{array}{c} I_{t}^{N}=\delta_{\xi}^{1}\left(\hat{\xi}_{t}\right)+\delta_{\eta}^{1}\left(\hat{\eta}_{t}\right)+\delta_{\zeta}^{1}\left(\hat{\zeta}_{t}\right)+\delta_{\tau}^{1}\left(J^{-1}\right) \\ I_{x}^{N} =\delta_{\xi}^{1}\left(\hat{\xi}_{x}\right)+\delta_{\eta}^{1}\left(\hat{\eta}_{x}\right)+\delta_{\zeta}^{1}\left(\hat{\zeta}_{x}\right) \\ I_{y}^{N} =\delta_{\xi}^{1}\left(\hat{\xi}_{y}\right)+\delta_{\eta}^{1}\left(\hat{\eta}_{y}\right)+\delta_{\zeta}^{1}\left(\hat{\zeta}_{y}\right) \\ I_{z}^{N} =\delta_{\xi}^{1}\left(\hat{\xi}_{z}\right)+\delta_{\eta}^{1}\left(\hat{\eta}_{z}\right)+\delta_{\zeta}^{1}\left(\hat{\zeta}_{z}\right) \end{array} $ | (20) |
上标“N”表示有限差分离散。式(20)对于任意变量Q恒成立意味着:
| $ I_{t}^{N}=I_{x}^{N}=I_{y}^{N}=I_{z}^{N}=0 $ | (21) |
将离散网格变换导数(6)的有限差分求导算子记为δ2。以IxN为例,将网格导数(6)的离散形式代入式(20)有:
| $ \begin{array}{l}I_{x}^{N}=\delta_{\xi}^{1}\left[\left(\delta_{\eta}^{2} y\right)\left(\delta_{\zeta}^{2} z\right)-\left(\delta_{\zeta}^{2} y\right)\left(\delta_{\eta}^{2} z\right)\right]+\\ \ \ \ \ \ \ \ \ \ \ \delta_{\eta}^{1}\left[\left(\delta_{\zeta}^{2} y\right)\left(\delta_{\xi}^{2} z\right)-\left(\delta_{\xi}^{2} y\right)\left(\delta_{\zeta}^{2} z\right)\right]+ \\ \ \ \ \ \ \ \ \ \ \ \delta_{\zeta}^{1}\left[\left(\delta_{\xi}^{2} y\right)\left(\delta_{\eta}^{2} z\right)-\left(\delta_{\eta}^{2} y\right)\left(\delta_{\xi}^{2} z\right)\right] \end{array} $ | (22) |
一般情况下,差分算子δ具有以下性质:
| $ \begin{array}{c} \delta(\alpha \phi)=\alpha \delta \phi \\ \delta(\phi+\varphi)=\delta \phi+\delta \varphi \\ \delta_{\xi}\left(\delta_{\eta} \phi\right)=\delta_{\eta}\left(\delta_{\xi} \phi\right) \end{array} $ | (23) |
其中α为常数。值得特别指出的是:差分算子δ一般还存在如下不等式:
| $ \delta(\phi \varphi) \neq \varphi \delta \phi+\phi \delta \varphi $ | (24) |
微分算子的属性(14)能够严格导出式(15),差分算子δ的属性(23)和(24)却表明IxN≠0,即在上述有限差分格式离散下不能保持均匀流,存在完全由网格离散引起的几何守恒误差。这种误差的大小同网格质量紧密相关,高阶精度格式对这种误差较为敏感。当网格质量(特别是网格变化的连续性)低于格式精度要求时,不仅会导致计算结果精度下降,严重时还会引起计算不稳定的问题。
2 满足几何守恒律的条件为了满足式(21),需要采用在数学上与网格导数(6)等价的守恒计算形式(以上标“S1”表示):
| $ \left\{\begin{array}{l} \hat{\xi}_{x}^{S 1}=\left(y_{\eta} z\right)_{\zeta}-\left(y_{\zeta} z\right)_{\eta} \\ \hat{\xi}_{y}^{S 1}=\left(z_{\eta} x\right)_{\zeta}-\left(z_{\zeta} x\right)_{\eta} \\ \hat{\xi}_{z}^{S 1}=\left(x_{\eta} y\right)_{\zeta}-\left(x_{\zeta} y\right)_{\eta} \\ \hat{\eta}_{x}^{S 1}=\left(y_{\zeta} z\right)_{\xi}-\left(y_{\xi} z\right)_{\zeta} \\ \hat{\eta}_{y}^{S 1}=\left(z_{\zeta} x\right)_{\xi}-\left(z_{\xi} x\right)_{\zeta} \\ \hat{\eta}_{z}^{S 1}=\left(x_{\zeta} y\right)_{\xi}-\left(x_{\xi} y\right)_{\zeta} \\ \hat{\zeta}_{x}^{S 1}=\left(y_{\xi} z\right)_{\eta}-\left(y_{\eta} z\right)_{\xi} \\ \hat{\zeta}_{y}^{S 1}=\left(z_{\xi} x\right)_{\eta}-\left(z_{\eta} x\right)_{\xi} \\ \hat{\zeta}_{z}^{S 1}=\left(x_{\xi} y\right)_{\eta}-\left(x_{\eta} y\right)_{\xi} \end{array}\right. $ | (25) |
将网格导数的守恒计算形式(25)离散后代入式(20)有:
| $ \begin{array}{l} I_{x}^{N}=\delta_{\xi}^{1}\left[\delta_{\zeta}^{2}\left(z \delta_{\eta}^{3} y\right)-\delta_{\eta}^{2}\left(z \delta_{\zeta}^{3} y\right)\right]+ \\ \ \ \ \ \ \ \ \delta_{\eta}^{1}\left[\delta_{\xi}^{2}\left(z \delta_{\zeta}^{3} y\right)-\delta_{\zeta}^{2}\left(z \delta_{\xi}^{3} y\right)\right]+ \\ \ \ \ \ \ \ \ \delta_{\zeta}^{1}\left[\delta_{\eta}^{2}\left(z \delta_{\xi}^{3} y\right)-\delta_{\xi}^{2}\left(z \delta_{\eta}^{3} y\right)\right] \end{array} $ | (26) |
考虑到差分算子的性质(23),在满足下列条件:
| $ \delta_{\xi}^{1}=\delta_{\xi}^{2}, \quad \delta_{\eta}^{1}=\delta_{\eta}^{2}, \quad \delta_{\zeta}^{1}=\delta_{\zeta}^{2} $ | (27) |
并结合差分算子性质(23),容易得到IxN=0,同理也可以得到IyN=IzN=0。由于采用了网格导数的守恒计算形式(25),我们将上述解决均匀流保持问题的方案称之为守恒网格导数方法[40](Conservative Metric Method, CMM)。
在数学上与网格导数(6)等价的守恒计算形式并不唯一,类似于式(25),还存在另外一种守恒计算形式(以上标“S2”表示):
| $ \left\{\begin{array}{l} \hat{\xi}_{x}^{S 2}=\left(y z_{\zeta}\right)_{\eta}-\left(y z_{\eta}\right)_{\zeta} \\ \hat{\xi}_{y}^{S 2}=\left(z x_{\xi}\right)_{\eta}-\left(z x_{\eta}\right)_{\zeta} \\ \hat{\xi}_{z}^{S 2}=\left(x y_{\zeta}\right)_{\eta}-\left(x y_{\eta}\right)_{\zeta} \\ \hat{\eta}_{x}^{S 2}=\left(y z_{\xi}\right)_{\zeta}-\left(y z_{\zeta}\right)_{\xi} \\ \hat{\eta}_{y}^{S_{2}}=\left(z x_{\xi}\right)_{\zeta}-\left(z x_{\xi}\right)_{\xi} \\ \hat{\eta}_{z}^{S 2}=\left(x y_{\xi}\right)_{\zeta}-\left(x y_{\zeta}\right)_{\xi} \\ \hat{\zeta}_{x}^{S 2}=\left(y z_{\eta}\right)_{\xi}-\left(y z_{\xi}\right)_{\eta} \\ \hat{\zeta}_{y}^{S 2}=\left(z x_{\eta}\right)_{\xi}-\left(z x_{\xi}\right)_{\eta} \\ \hat{\zeta}_{z}^{S 2}=\left(x y_{\eta}\right)_{\xi}-\left(x y_{\xi}\right)_{\eta} \end{array}\right. $ | (28) |
类似于守恒计算形式S1(25),采用守恒计算形式S2(28)离散并满足CMM条件(27),也能够得到IxN=IyN=IzN=0。
还可以进一步证明,对于守恒计算形式S1(25)和S2(28)任意线性组合,在CMM条件(27)下都能够使得IxN=IyN=IzN=0。这种网格变换导数(6)的守恒计算形式的不唯一性在一定程度上会给实际计算过程带来不确定性。网格变换导数的对称守恒计算形式(以上标“S3”表示):
| $ \left\{\begin{array}{l} \hat{\xi}_{x}^{S 3}=\frac{1}{2}\left[\left(y_{\eta} z\right)_{\zeta}+\left(y z_{\zeta}\right)_{\eta}-\left(y_{\zeta} z\right)_{\eta}-\left(y z_{\eta}\right)_{\zeta}\right] \\ \hat{\xi}_{y}^{S 3}=\frac{1}{2}\left[\left(z_{\eta} x\right)_{\zeta}+\left(z x_{\zeta}\right)_{\eta}-\left(z_{\zeta} x\right)_{\eta}-\left(z x_{\eta}\right)_{\zeta}\right] \\ \hat{\xi}_{z}^{S 3}=\frac{1}{2}\left[\left(x_{\eta} y\right)_{\zeta}+\left(x y_{\zeta}\right)_{\eta}-\left(x_{\zeta} y\right)_{\eta}-\left(x y_{\eta}\right)_{\zeta}\right] \\ \hat{\eta}_{x}^{S 3}=\frac{1}{2}\left[\left(y_{\zeta} z\right)_{\xi}+\left(y z_{\xi}\right)_{\zeta}-\left(y_{\xi} z\right)_{\zeta}-\left(y z_{\zeta}\right)_{\xi}\right] \\ \hat{\eta}_{y}^{S 3}=\frac{1}{2}\left[\left(z_{\zeta} x\right)_{\xi}+\left(z x_{\xi}\right)_{\zeta}-\left(z_{\xi} x\right)_{\zeta}-\left(z x_{\zeta}\right)_{\xi}\right] \\ \hat{\eta}_{z}^{S 3}=\frac{1}{2}\left[\left(x_{\zeta} y\right)_{\xi}+\left(x y_{\xi}\right)_{\zeta}-\left(x_{\xi} y\right)_{\zeta}-\left(x y_{\zeta}\right)_{\xi}\right] \\ \hat{\zeta}_{x}^{S 3}=\frac{1}{2}\left[\left(y_{\xi} z\right)_{\eta}+\left(y z_{\eta}\right)_{\xi}-\left(y_{\eta} z\right)_{\xi}-\left(y z_{\xi}\right)_{\eta}\right] \\ \hat{\zeta}_{y}^{S 3}=\frac{1}{2}\left[\left(z_{\xi} x\right)_{\eta}+\left(z x_{\eta}\right)_{\xi}-\left(z_{\eta} x\right)_{\xi}-\left(z x_{\xi}\right)_{\eta}\right] \\ \hat{\zeta}_{z}^{S 3}=\frac{1}{2}\left[\left(x_{\xi} y\right)_{\eta}+\left(x y_{\eta}\right)_{\xi}-\left(x_{\eta} y\right)_{\xi}-\left(x y_{\xi}\right)_{\eta}\right] \end{array}\right. $ | (29) |
式(29)还可以表述为更为紧凑的矢量形式:
| $ \begin{array}{l} \boldsymbol{\xi}^{S 3}=\frac{1}{2}\left[\left(\boldsymbol{r} \times \boldsymbol{r}_{\zeta}\right)_{\eta}+\left(\boldsymbol{r}_{\eta} \times \boldsymbol{r}\right)_{\zeta}\right] \\ \boldsymbol{\eta}^{S 3}=\frac{1}{2}\left[\left(\boldsymbol{r} \times \boldsymbol{r}_{\xi}\right)_{\zeta}+\left(\boldsymbol{r}_{\zeta} \times \boldsymbol{r}\right)_{\xi}\right] \\ \boldsymbol{\zeta}^{S 3}=\frac{1}{2}\left[\left(\boldsymbol{r} \times \boldsymbol{r}_{\eta}\right)_{\xi}+\left(\boldsymbol{r}_{\xi} \times \boldsymbol{r}\right)_{\eta}\right] \end{array} $ | (30) |
在网格变换导数(6)的几种能满足几何守恒律的守恒计算形式中,本文推荐使用其对称守恒计算形式S3(29)和(30),原因在于S3能够较好反映计算网格的特性(离散后的网格变换导数表现为计算网格单元的矢量面积)。
如果网格导数(6)的所有方向上的δ2算子均为二阶中心差分时,在O点的矢量面积如图 1所示。
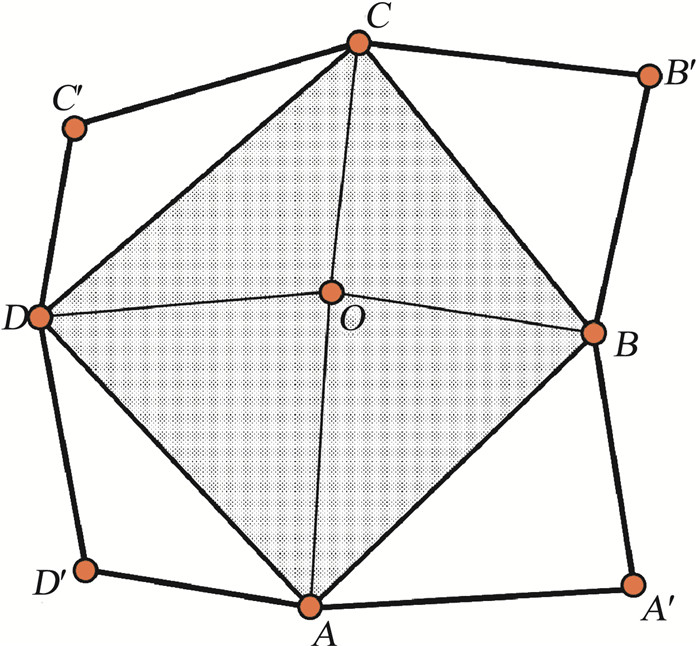
|
图 1 网格变换导数(6)在二阶中心差分离散下的面积示意图 Fig.1 A schematic diagram of the area based on metric (6) calculated by a 2nd-order central difference operator |
在对网格导数的守恒计算形式(25)、(28)和(29)进行离散时,记其内层的差分算子为δ3,当满足如下条件时:
| $ \delta_{\xi}^{3}=\delta_{\xi}^{2}, \quad \delta_{\eta}^{3}=\delta_{\eta}^{2}, \quad \delta_{\zeta}^{3}=\delta_{\zeta}^{2} $ | (31) |
结合CMM条件(27)容易得到:
| $ \delta^{1}=\delta^{2}=\delta^{3} $ | (32) |
类似的,如果网格导数的守恒计算形式(25)、(28)和(29)的所有方向上的δ2和δ3算子均为二阶中心差分时,在O点的矢量面积分别如图 2和图 3所示。对于质量不佳的网格分布情况,图 3所示的矢量面积能更好地反映计算网格的离散特性。
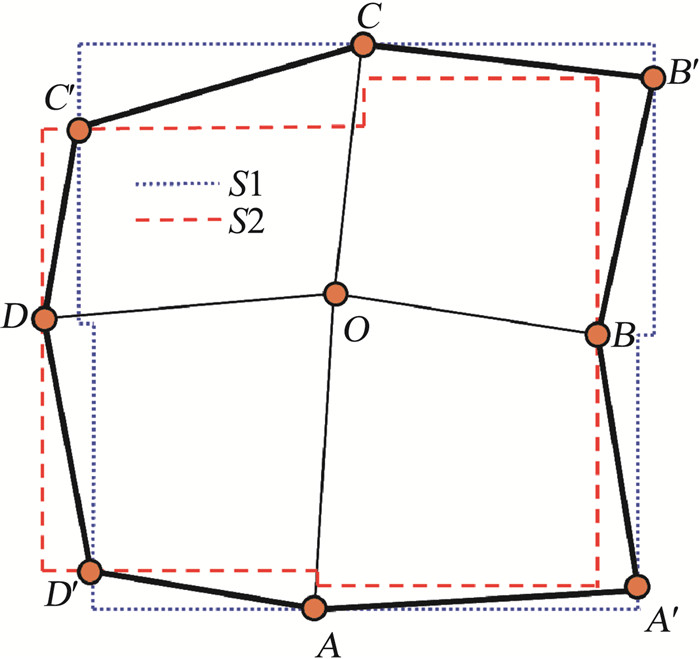
|
图 2 网格变换导数(25)和(28)在二阶中心差分离散下的面积示意图 Fig.2 A schematic diagram of the area based on metrics (25) and (28) calculated by a 2nd-order central difference operator |
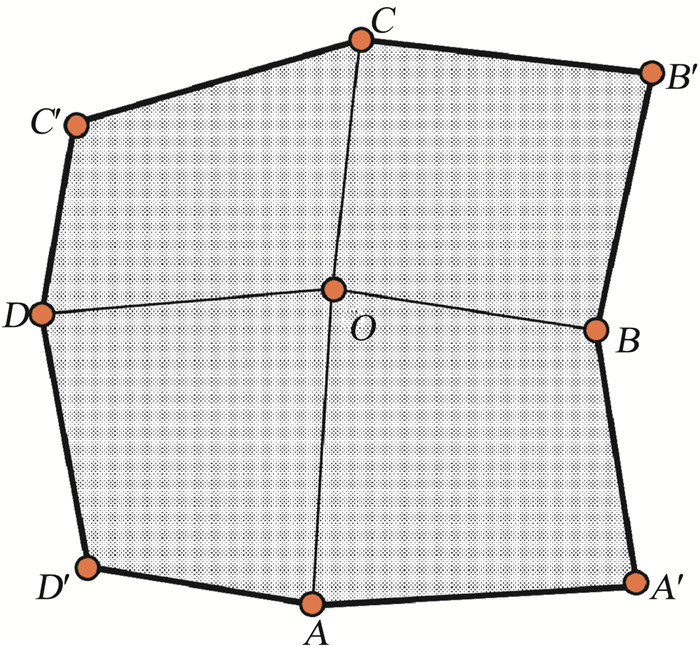
|
图 3 网格变换导数(29)在二阶中心差分离散下的面积示意图 Fig.3 A schematic diagram of the area based on metric (29)calculated by a 2nd-order central difference operator |
以二阶中心差分算子离散网格变换雅克比(7),其在O点的体积如图 4所示。基于网格变换雅克比的矢量形式(12)给出其对称计算形式:
| $ J^{-1}=\frac{1}{3}\left(\boldsymbol{r}_{\xi} \cdot \boldsymbol{\xi}+\boldsymbol{r}_{\eta} \cdot \boldsymbol{\eta}+\boldsymbol{r}_{\zeta} \cdot \boldsymbol{\zeta}\right) $ | (33) |
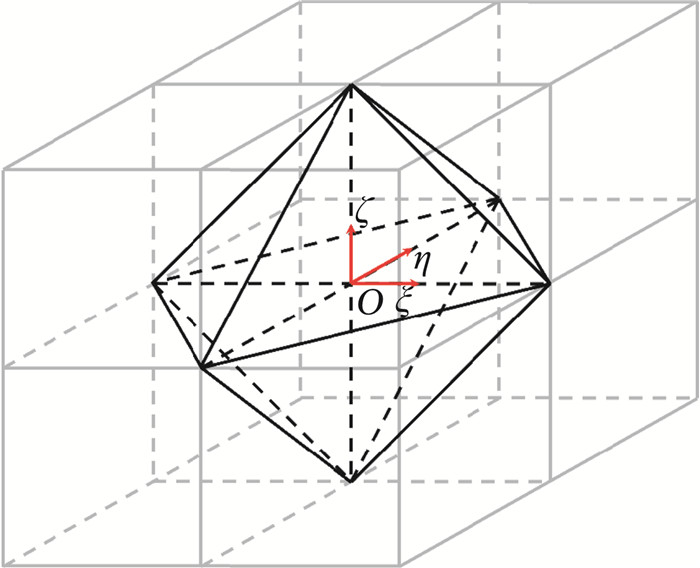
|
图 4 网格变换雅克比(7)在二阶中心差分离散下的体积示意图 Fig.4 A schematic diagram of the volume based on Jacobian(7) calculated by a 2nd-order central difference operator |
在二阶中心差分算子离散下,网格变换雅克比的对称计算形式(33)在O点的体积由六个部分体积组成,为叙述简洁,本文仅给出其在ξ负方向上的部分体积,如图 5所示。
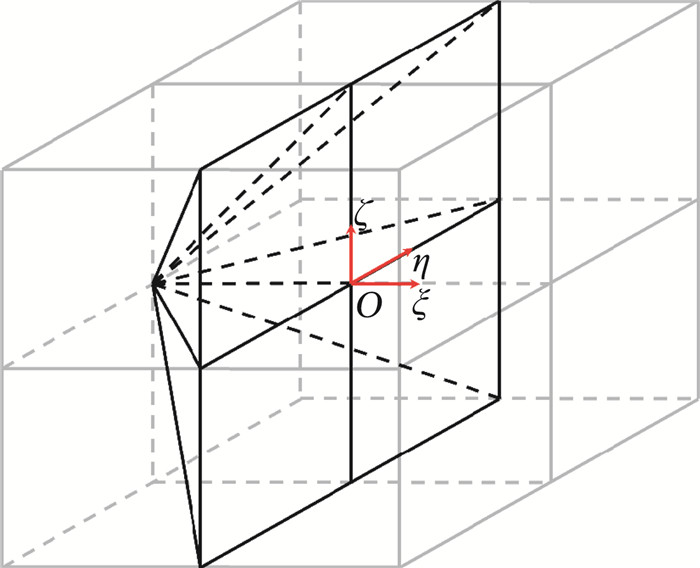
|
图 5 网格雅克比(33)在二阶中心差分离散下的部分体积示意图 Fig.5 A schematic diagram of the fractional volume based on Jacobian (33) calculated by a 2nd-order cental difference operator |
网格变换导数离散后表现为计算网格单元的矢量面积,网格变换雅克比离散后为网格单元的体积,且应为由矢量面积封闭包围的体积。由图 4和图 5可以看出,基于网格变换雅克比的定义式(7)和对称计算形式(33)离散后的体积均不能被网格变换导数离散后的矢量面积封闭和包围,据此本文给出网格变换雅克比的对称守恒计算形式:
| $ J^{-1}=\frac{1}{3}\left[(\boldsymbol{r} \cdot \xi)_{\xi}+(\boldsymbol{r} \cdot \boldsymbol{\eta})_{\eta}+(\boldsymbol{r} \cdot \boldsymbol{\zeta})_{\zeta}\right] $ | (34) |
类似的,在二阶中心差分算子离散下,网格变换雅克比的对称守恒计算形式(34)在O点的体积也由六个部分体积组成,为叙述简洁,本文仅给出其在ξ负方向上的部分体积,如图 6所示。不同于图 4和图 5所示的体积,基于网格变换雅克比的对称守恒计算形式(34)离散后的体积可由图 3所示的网格变换导数的对称守恒计算形式(29)离散后的矢量面积完全封闭和包围。
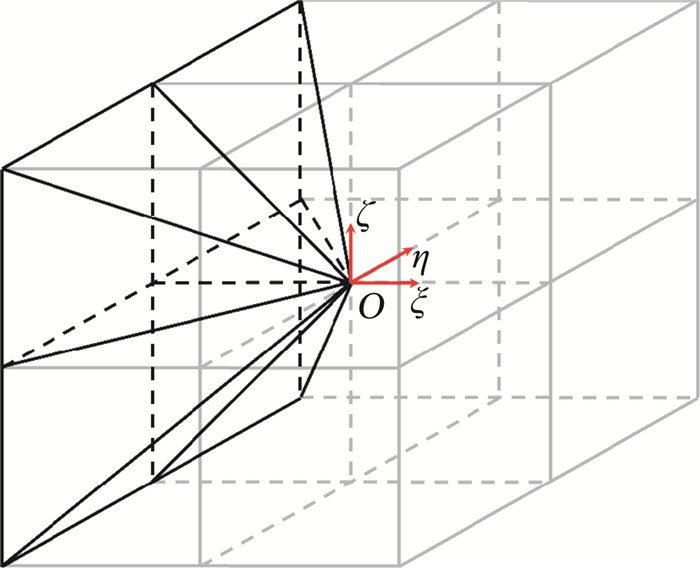
|
图 6 网格雅克比(34)在二阶中心差分离散下的部分体积示意图 Fig.6 A schematic diagram of the fractional volume based on Jacobian (34) calculated by a 2nd-order central difference operator |
鉴于采用了网格变换导数和网格变换雅克比的对称守恒计算形式,将上述满足几何守恒律的解决方案称之为网格变换系数的对称守恒计算方法[48](Symmetrical Conservative Metric Method, SCMM),其详细叙述如下:
(1) 网格变换导数采用其对称守恒计算形式S3(29)或(30);
(2) 网格变换雅克比采用其对称守恒计算形式(34);
(3) 方程(18)中通量差分算子和网格变换雅克比对称守恒计算形式(34)的外层差分算子δ1、网格变换导数的对称守恒计算形式(29)中外层差分算子δ2以及其内层差分算子δ3在同一计算坐标方向上完全相同,即同时满足条件(27)和(31)。
对称守恒网格导数算法(SCMM)是有限差分方法满足几何守恒律的充分条件,与网格质量无关。还可以进一步证明,在SCMM条件下采用高阶精度有限差分格式离散的网格变换导数和雅克比是若干个二阶精度格式离散值的线性组合[49-50]。
3 满足几何守恒律的特征对接边界技术将结构网格技术应用于绕复杂构型的流动模拟时,单块网格的适应能力极其有限,需要采用多块对接结构网格技术。高阶精度有限差分方法对数值误差的严格控制决定了其对网格对接边界的处理方法的要求更为苛刻,因此发展了一种能够满足几何守恒律的特征对接边界处理技术[51]。
对于静止网格而言,将计算坐标系下的守恒律控制方程(16)中空间导数项归类写为:
| $ \frac{\partial \boldsymbol{Q}}{\partial \tau}=-\frac{1}{J^{-1}}\left(\frac{\partial \hat{\boldsymbol{E}}}{\partial \xi}+\frac{\partial \hat{\boldsymbol{F}}}{\partial \eta}+\frac{\partial \hat{\boldsymbol{G}}}{\partial \zeta}\right)=R H S $ | (35) |
经过系列特征分析[51],在网格对接边界两端(下标L和R)的离散方程可以分别表述为:
| $ \begin{array}{l} \left.\frac{\partial \boldsymbol{Q}}{\partial \tau}\right|_{L}=A_{L}^{+} R H S_{L}+A_{L}^{-} R H S_{R} \\ \left.\frac{\partial \boldsymbol{Q}}{\partial \tau}\right|_{R}=A_{R}^{+} R H S_{R}+A_{R}^{-} R H S_{L} \end{array} $ | (36) |
其中:
| $ \begin{array}{l} A^{+}=P_{Q V} \operatorname{diag}\left[\frac{1+\operatorname{sign}\left(\lambda_{i}\right)}{2}\right] P_{Q V}^{-1} \\ A^{-}=P_{Q V} \operatorname{diag}\left[\frac{1-\operatorname{sign}\left(\lambda_{i}\right)}{2}\right] P_{Q V}^{-1} \end{array} $ | (37) |
λi为网格对接方向上的特征值,PQV为守恒变量对特征变量的导数矩阵,其在计算坐标系下的详细表达形式可参见Kim和Lee关于广义特征边界条件的文章[52]。
如果方程(35)中的右端项还存在黏性耗散项,则在对接边界处的黏性项取其左右值的平均:
| $ RH{S^v} = \frac{1}{2}(RHS_L^v + RHS_R^v) $ | (38) |
在上述离散下可以证明,QL和QR在数学上严格相等。在进行时间推进后将对边界上的流场变量Q取为左右值的算术平均以消除数值计算过程中舍入误差的影响:
| $ \mathit{\boldsymbol{Q}} = \frac{1}{2}({\mathit{\boldsymbol{Q}}_L} + {\mathit{\boldsymbol{Q}}_R}) $ | (39) |
基于上述特征对接边界处理技术和满足几何守恒律的WCNS-E-5格式,完成了若干复杂拓扑结构的对接网格算例,其中30P-30N三段翼的流动模拟结果如图 7所示。

|
图 7 30P-30N三段翼数值模拟结果(左:网格;右:压力) Fig.7 Numerical results of the 30P-30N three-element airfoil(left: grid; right: pressure) |
由图 7所示的流场等值线可以看出,即使网格对接不太光滑,由于采用了能够满足几何守恒律的特征对接边界处理技术,数值方法在边界附近也能保持精度不降,流场在对接边界附近也比较光滑(对接面两侧网格的粗细程度相差不大时)。4几何守恒律误差的影响研究
4.1 几何守恒律误差对数值解影响的理论分析众所周知,高阶精度有限差分格式可以成功应用于简单几何外形流动的精细模拟,但在复杂几何外形上的应用却遇到了很大的困难。我们认为其根本原因是复杂几何外形的网格质量难以满足高阶精度差分格式的要求。由此出发,我们开展了非充分光滑网格下,几何守恒律误差对数值计算结果精度影响的理论分析工作[53]。
以二维情况下流场变量u对笛卡尔坐标x的导数∂u/∂x为例说明:
| $ \frac{\partial \boldsymbol{u}}{\partial x}=\frac{1}{J^{-1}}\left(\frac{\partial \boldsymbol{u} \hat{\xi}_{x}}{\partial \xi}+\frac{\partial \boldsymbol{u} \hat{\eta}_{x}}{\partial \eta}\right)=\frac{1}{J^{-1}}\left(\frac{\partial \boldsymbol{u} y_{\eta}}{\partial \xi}-\frac{\partial \boldsymbol{u} y_{\xi}}{\partial \eta}\right) $ | (40) |
其在有限差分格式离散下的数值解∂uN/∂x可表述为:
| $ \left.\frac{\partial \boldsymbol{u}}{\partial x}\right|^{N}=\frac{1}{J^{-1, N}}\left[\delta_{\xi}^{1}\left(\boldsymbol{u} \delta_{\eta}^{2} y\right)-\delta_{\eta}^{1}\left(\boldsymbol{u} \delta_{\xi}^{2} y\right)\right] $ | (41) |
其中网格变换雅克比在二维情况下的对称守恒计算形式为:
| $ J^{-1, N}=\frac{1}{2}\left[\begin{array}{l} \delta_{\xi}^{1}\left(x \delta_{\eta}^{2} y\right)-\delta_{\xi}^{1}\left(y \delta_{\eta}^{2} x\right)+ \\ \delta_{\eta}^{1}\left(y \delta_{\xi}^{2} x\right)-\delta_{\eta}^{1}\left(x \delta_{\xi}^{2} y\right) \end{array}\right] $ | (42) |
如果计算网格为M阶连续,不妨设网格坐标y对计算坐标系ξ方向的导数为M阶连续,即:
| $ \begin{array}{c} \left(\frac{\partial^{n} y}{\partial \xi^{n}}\right)^{L}=\left(\frac{\partial^{n} y}{\partial \xi^{n}}\right)^{R}, \quad n \in[0,1,2, \cdots, M] \\ \left(\frac{\partial^{n} y}{\partial \xi^{n}}\right)^{L} \neq\left(\frac{\partial^{n} y}{\partial \xi^{n}}\right)^{R}, \quad n \geqslant M+1 \end{array} $ | (43) |
其余网格导数均足够光滑。通过Taylor展开,在N阶精度有限差分格式离散下,当几何守恒律不满足(δ1≠δ2)时,数值解的精度为:
| $ \left.\frac{\partial \boldsymbol{u}}{\partial x}\right|^{N}-\frac{\partial \boldsymbol{u}}{\partial x}=\mathrm{O}\left[(\Delta \xi)^{\min (M, N)}\right]+\mathrm{O}\left[(\Delta \eta)^{N}\right] $ | (44) |
其中(Δξ)M为几何守恒律误差IxN的精度。当几何守恒律满足(δ1=δ2)时,几何守恒律误差均为0,则数值解的精度为:
| $ \left.\frac{\partial \boldsymbol{u}}{\partial x}\right|^{N}-\frac{\partial \boldsymbol{u}}{\partial x}=\mathrm{O}\left[(\Delta \xi)^{\min (M+1, N)}\right]+\mathrm{O}\left[(\Delta \eta)^{N}\right] $ | (45) |
由上述分析的数值误差表达式(44)和式(45)可以看出,对于M阶连续的计算网格(43)而言,当几何守恒律满足时,基于SCMM方法离散的数值解的精度为M+1阶;如果几何守恒律不满足,则其数值精度同几何守恒律误差IxN的精度一样,均为M阶。换言之,对于不是足够光滑的计算网格,如果几何守恒律不满足,则其数值解的精度为M阶;而如果几何守恒律满足,其数值解的精度可以达到M+1阶。从另一个方面可以得知,对于设计精度为N阶的有限差分离散格式,几何守恒律的满足与否对计算网格光滑性的要求是有差别的,如果几何守恒律未能满足,则要求计算网格满足N阶连续条件;而如果几何守恒律能够满足,则计算网格只需满足N-1阶连续条件即可达到格式设计计算精度。更为详细的推导证明参阅文献[53]。
4.2 几何守恒律误差对计算精度的影响为了验证几何守恒律误差对计算精度的影响,采用三角函数生成不同连续程度的网格[53-54],三角函数的指数n代表网格波动的连续程度,如图 8所示。

|
图 8 网格波动示意图 Fig.8 A schematic diagram of mesh waves |
给定解析初场及其导数:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}} = \sin (2{\rm{ \mathsf{ π} }}x)\sin (2{\rm{ \mathsf{ π} }}y)}\\ {\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial x}} = 2{\rm{ \mathsf{ π} }}\cos (2{\rm{ \mathsf{ π} }}x)\sin (2{\rm{ \mathsf{ π} }}y)} \end{array} $ | (46) |
采用四阶中心差分格式计算得到导数∂uN/∂x,给出其相对于解析导数(46)的数值误差,逐步加密网格,其统计误差L∞范数的数值精度表现如图 9所示。
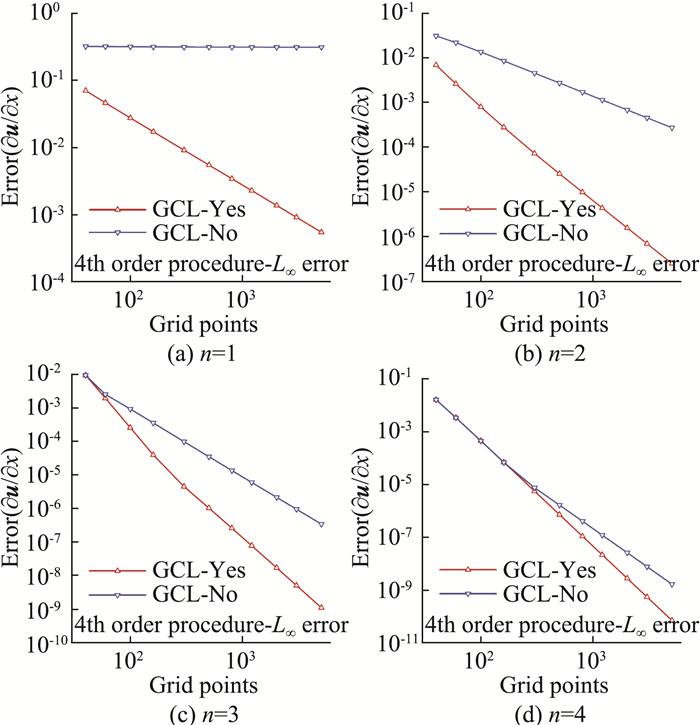
|
图 9 数值误差 Fig.9 Numerical errors |
通过图 9所示的不同连续程度的网格下的数值精度可以看出,当计算网格不是足够光滑时,几何守恒律的满足能够有效提升数值解的离散精度,其数值精度相较于几何守恒律不满足时要高出一阶精度,同理论分析结论一致[53]。
4.3 几何守恒律误差对计算稳定性的影响为了直观展现几何守恒律对计算过程及稳定性的影响,通过网格变换导数的传统计算形式(6)和对称守恒计算形式(29)的线性加权设计一种新的网格导数算法[55-56]。以
| $ {\hat \xi _x} = \sigma \hat \xi _x^T + (1 - \sigma )\hat \xi _x^{S3} $ | (47) |
其中
采用高阶精度有限差分格式(HDCS)模拟对数值误差敏感的双圆柱散射问题,在同一时刻的脉动压力均方根如图 10所示。
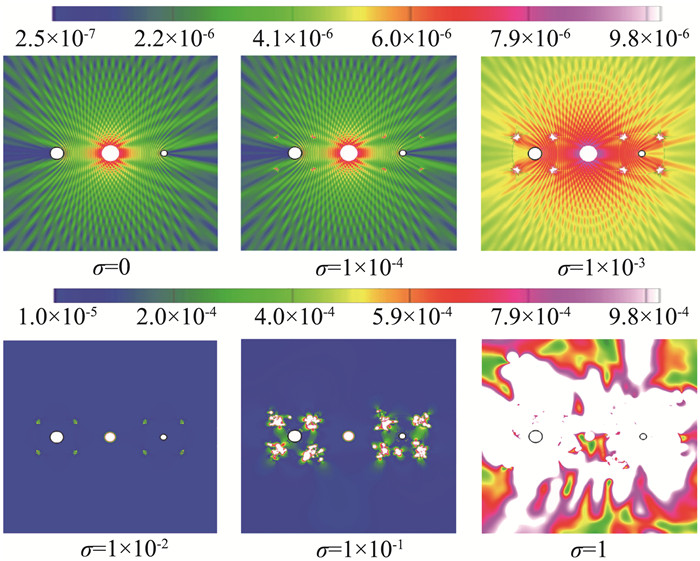
|
图 10 脉动压力均方根云图 Fig.10 Contours of the root-mean-square of fluctuating pressure |
从图 10可以看出,如果几何守恒律满足,声场光滑合理;如果几何守恒律不满足,声场会被几何守恒律误差所污染。σ较小时(σ≤1×10-3),污染主要集中在网格质量不佳的奇点附近;σ越大,声场被污染得越严重,σ>1×10-2时,整个声场都被污染,σ=1时声场已被严重污染而导致计算过程的不稳定。
通过对双圆柱散射问题的数值模拟,验证了几何守恒律对高阶精度有限差分格式计算的重要影响。当网格质量不佳时,由于几何守恒律不满足而引起的网格离散误差可能对流场产生比较明显的污染,严重时还可能引起计算过程的不稳定和计算结果的发散。几何守恒律的满足能够大幅提升高阶精度有限差分格式在复杂网格计算中的适应能力,计算结果也更为可信。
5 结论以实现高阶精度有限差分数值方法在绕复杂构型流动中的应用为目标,综合运用理论分析和数值验证手段,比较系统地研究了结构网格中高阶精度有限差分方法的几何守恒律问题,得到以下认识:
1) 满足几何守恒律的充分条件表明,不是所有的有限差分算子都能较为方便地满足几何守恒律,而邓小刚等提出的系列WCNS格式对于满足几何守恒律具有明显优势。
2) SCMM条件是满足几何守恒律的充分条件,同时网格变换导数和雅克比均采用其对称守恒计算形式,具有唯一性。基于SCMM条件离散的矢量面积(由网格变换导数分量组成)完全封闭,网格变换雅克比离散后体积恰好由矢量面积所围成,更符合计算网格的几何意义。
3) 自由流保持只是满足几何守恒律的一种表现形式,是几何守恒律满足的必要条件,而非充分条件。严格来讲,几何守恒律的本质含义应当包括矢量面积完全封闭、体积由矢量面积围成和确定以及在网格运动过程中依然维持上述关系等。在静止网格中SCMM条件能够完全满足几何守恒律。
4) 几何守恒律的满足能够有效提高高阶精度有限差分格式在质量欠佳网格中的计算精度,同时还能大幅提升高阶精度格式在复杂网格中的计算稳定性。
在下一步工作中,我们将继续完善几何守恒律的相关理论,同时重点开展几何守恒律研究成果的应用工作,如指导高阶精度有限差分格式的构造[55, 57]、结构网格质量的检测等,以继续提升高阶精度有限差分算法在绕复杂构型流动数值模拟的应用能力。
| [1] |
CARUELLE B, DUCROS F. Detached-eddy simulations of attached and detached boundary layers[J]. International Journal of Computational Fluid Dynamics, 2003, 17: 433-451. DOI:10.1080/10618560310001598880 |
| [2] |
PHILIPPE R SPALART. Detached-eddy simulation[J]. Annual Review of Fluid Mechanics, 2009, 41: 181-202. DOI:10.1146/annurev.fluid.010908.165130 |
| [3] |
UGOPIOMELLI, ELIAS BALARAS. Wall-layer models for large-eddy simulations[J]. Annual Review of Fluid Mechanics, 2002, 34: 349-374. DOI:10.1146/annurev.fluid.34.082901.144919 |
| [4] |
PIERRE SAGAUT. Large eddy simulation for incompressible flows-An introduction[M]. Third edition, Springer, 2006.
|
| [5] |
PARVIZ MOIN, KRISHNAN MAHESH. Direct numerical simulation: A tool in turbulence research[J]. Annual Review of Fluid Mechanics, 1998, 30: 539-578. DOI:10.1146/annurev.fluid.30.1.539 |
| [6] |
TAKASHI ISHIHARA, TOSHIYUKIGOTOH, YUKIO KANEDA. Study of high-Reynolds number isotropic turbulence by direct numerical simulation[J]. Annual Review of Fluid Mechanics, 2009, 41: 165-180. DOI:10.1146/annurev.fluid.010908.165203 |
| [7] |
SHEN J, TANG T, WANG L L. Spectral methods: Algorithms, analysis and applications[M]. Springer, 2011.
|
| [8] |
BERNARDO COCKBURN, SHU C W. The local discontinuous Galerkin method for time-dependent convection-diffusion systems[J]. SIAM Journal on Numerical Analysis, 1998, 35: 2440-2463. DOI:10.1137/S0036142997316712 |
| [9] |
BERNARDO COCKBURN, SHU C W. Runge-Kutta discontinuous Galerkin methods for convection-dominated problems[J]. Journal of Scientific Computing, 2001, 16(3): 173-261. DOI:10.1023/A:1012873910884 |
| [10] |
YEN LIU, MARCEL VINOKUR, WANG Z J. Spectral difference method for unstructured grids I: Basic formulation[J]. Journal of Computational Physics, 2006, 216: 780-801. DOI:10.1016/j.jcp.2006.01.024 |
| [11] |
WANG Z J, LIU Y, GEORG MAY, et al. Spectral difference method for unstructured grids Ⅱ: Extension to the Euler equations[J]. Journal of Scientific Computing, 2007, 32: 45-71. DOI:10.1007/s10915-006-9113-9 |
| [12] |
WANG Z J. Spectral (finite) volume method for conservation laws on unstructured grids: Basic formulation[J]. Journal of Computational Physics, 2002, 178: 210-251. DOI:10.1006/jcph.2002.7041 |
| [13] |
WANG Z J, LIU Y. Spectral (finite) volume method for conservation laws on unstructured grids Ⅱ: Extension to two-dimensional scalar equation[J]. Journal of Computational Physics, 2002, 179: 665-697. DOI:10.1006/jcph.2002.7082 |
| [14] |
DINSHAW S BALSARA, SHU C W. Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy[J]. Journal of Computational Physics, 2000, 160: 405-452. DOI:10.1006/jcph.2000.6443 |
| [15] |
DONG Y D, DENG X G, XU D, et al. Reevaluation of high-order finite difference and finite volume algorithms with freestream preservation satisfied[J]. Computers and Fluids, 2017, 156: 343-352. DOI:10.1016/j.compfluid.2017.07.020 |
| [16] |
JAY CASPER, SHU C W, ATKINS H. Comparison of two formulations for high-order accurate essentially non-oscillatory schemes[J]. American Institute of Aeronautics and Astronautics Journal, 1994, 32(10): 1970-1977. DOI:10.2514/3.12240 |
| [17] |
XU C Y, CHEN L W, LU X Y. Large-eddy simulation of the compressible flow past a wavy cylinder[J]. Journal of Fluid Mechanics, 2010, 665: 238-273. DOI:10.1017/S0022112010003927 |
| [18] |
ERIC LAMBALLAIS. Direct numerical simulation of a turbulent flow in a rotating channel with a sudden expansion[J]. Journal of Fluid Mechanics, 2014, 745: 99-131. |
| [19] |
HERVÉ GUILLARD, CHARBEL FARHAT. On the significance of the geometric conservation law for flow computations on moving meshes[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 190: 1467-1482. DOI:10.1016/S0045-7825(00)00173-0 |
| [20] |
DANIELE BOFFI, LUCIA GASTALDI. Stability and geometric conservation laws for ALE formulations[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193: 4717-4739. DOI:10.1016/j.cma.2004.02.020 |
| [21] |
DIMITRI J MAVRIPLIS, YANG Z. Construction of the discrete geometric conservation law for high-order time-accurate simulations on dynamic meshes[J]. Journal of Computational Physics, 2006, 213: 557-573. DOI:10.1016/j.jcp.2005.08.018 |
| [22] |
DIMITRI J MAVRIPLIS, CRISTIAN R NASTASE. On the geometric conservation law for high-order discontinuous Galerkin discretizations on dynamically deforming meshes[J]. Journal of Computational Physics, 2011, 230: 4285-4300. DOI:10.1016/j.jcp.2011.01.022 |
| [23] |
THOMAS P D, LOMBARD C K. The Geometric conservation law-a link between finite difference and finite volume methods of flow computation on moving grids: AIAA-78-1208[R]. American Institute of Aeronautics and Astronautics, 1978.
|
| [24] |
THOMAS P D, LOMBARD C K. Geometric conservation law and its application to flow computations on moving grids[J]. American Institute of Aeronautics and Astronautics Journal, 1979, 17(10): 1030-1037. DOI:10.2514/3.61273 |
| [25] |
STEGER J L. Implicit finite difference simulation of flow about arbitrary geometrics with application to airfoils: AIAA-77-665[J]. American Institute of Aeronautics and Astronautics, 1977. |
| [26] |
JOSEPH L STEGER. Implicit finite difference simulation of flow about arbitrary two dimensional geometries[J]. American Institute of Aeronautics and Astronautics Journal, 1978, 16(7): 679-686. DOI:10.2514/3.7377 |
| [27] |
ZHANG H, REGGIO M, TRÉPANIER J Y, et al. Discrete form of the GCL for moving meshes and its implementation in CFD schemes[J]. Computers and Fluids, 1993, 22(1): 9-23. DOI:10.1016/0045-7930(93)90003-R |
| [28] |
YOSHIAKI ABE, NOBUYUKⅢZUKA, TAKU NONOMURA, et al. Conservative metric evaluation for high-order finite difference schemes with the GCL identities on moving and deforming grids[J]. Journal of Computational Physics, 2013, 232: 14-21. DOI:10.1016/j.jcp.2012.08.031 |
| [29] |
YOSHIAKI ABE, TAKU NONOMURA, NOBUYUKI ⅡZUKA, et al. Geometric interpretations and spatial symmetry property of metrics in the conservative form for high-order finite-difference schemes on moving and deforming grids[J]. Journal of Computational Physics, 2014, 260: 163-203. DOI:10.1016/j.jcp.2013.12.019 |
| [30] |
WANG Z J, YANG H Q. Unsteady flow simulation using a zonal multi-grid approach with moving boundaries: AIAA-94-0057[R]. American Institute of Aeronautics and Astronautics, 1994.
|
| [31] |
ZHANG L P, WANG Z J. A block LU-SGS implicit dual time-stepping algorithm for hybrid dynamic meshes[J]. Computers and Fluids, 2004, 33: 891-916. DOI:10.1016/j.compfluid.2003.10.004 |
| [32] |
CHANG X H, MA R, ZHANG L P, et al. Further study on the geometric conservation law for finite volume method on dynamic unstructured mesh[J]. Computers and Fluids, 2015, 120: 98-110. DOI:10.1016/j.compfluid.2015.07.023 |
| [33] |
RICHARD G HINDMAN. Geometrically induced errors and their relationship to the form of the governing equations and the treatment of generalized mappings: AIAA-81-1008[R]. American Institute of Aeronautics and Astronautics, 1981.
|
| [34] |
RICHARD G HINDMAN. Generalized coordinate forms of governing fluid equations and associated geometrically induced errors[J]. American Institute of Aeronautics and Astronautics Journal, 1982, 20(10): 1359-1367. DOI:10.2514/3.51196 |
| [35] |
HENRIVIVIAND, WALID GHAZZI. Numerical solution of the compressible Navier-Stokes equations at high Reynolds numbers with applications to the blunt body problem[J]. Lecture Notes in Physics, 1976, 59: 434-439. |
| [36] |
PULLIAM T H, STEGER J L. On implicit finite-difference simulations of three dimensional flow: AIAA-78-10[R]. American Institute of Aeronautics and Astronautics, 1978.
|
| [37] |
THOMAS H PULLIAM, JOSEPH L STEGER. Implicit finite-difference simulation of three dimensional compressible flow[J]. American Institute of Aeronautics and Astronautics Journal, 1980, 18(2): 159-167. DOI:10.2514/3.50745 |
| [38] |
MIGUEL R VISBAL, DATTA V GAITONDE. On the use of higher-order finite-difference schemes on curvilinear and deforming meshes[J]. Journal of Computational Physics, 2002, 181: 155-185. DOI:10.1006/jcph.2002.7117 |
| [39] |
TAKU NONOMURA, NOBUYUKI ⅡZUKA, KOZO FUJⅡ. Free-stream and vortex preservation properties of high-order WENO and WCNS on curvilinear grids[J]. Computers and Fluids, 2010, 39: 197-214. DOI:10.1016/j.compfluid.2009.08.005 |
| [40] |
DENG X G, MAO M L, TU G H, et al. Geometric conservation law and applications to high-order finite difference schemes with stationary grids[J]. Journal of Computational Physics, 2011, 230: 1100-1115. DOI:10.1016/j.jcp.2010.10.028 |
| [41] |
DENG X G, ZHANG H X. Developing high-order weighted compact nonlinear schemes[J]. Journal of Computational Physics, 2000, 165: 22-44. DOI:10.1006/jcph.2000.6594 |
| [42] |
邓小刚. 高阶精度耗散加权紧致非线性格式[J]. 中国科学(A辑), 2001, 31(12): 1104-1117. |
| [43] |
TAKU NONOMURA, KOZO FUJⅡ. Effects of difference scheme type in high-order weighted compact nonlinear schemes[J]. Journal of Computational Physics, 2009, 228: 3533-3539. DOI:10.1016/j.jcp.2009.02.018 |
| [44] |
JIANG G S, SHU C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126: 202-228. DOI:10.1006/jcph.1996.0130 |
| [45] |
SHU C W. High order weighted essentially non-oscillatory schemes for convection dominated problems[J]. SIAM Review, 2009, 51: 82-126. DOI:10.1137/070679065 |
| [46] |
TAKU NONOMURA, DAIKI TERAKADO, YOSHIAKI ABE, et al. A new technique for freestream preservation of finite difference WENO on curvilinear grid[J]. Computers and Fluids, 2015, 107: 242-255. DOI:10.1016/j.compfluid.2014.09.025 |
| [47] |
JIANG Y, SHU C W, ZHANG M P. Free-stream preserving finite difference schemes on curvilinear meshes[R]. Brown University, Scientific Computing Group Report 2013-10, 2013.
|
| [48] |
DENG X G, MIN Y B, MAO M L, et al. Further studies on Geometric conservation law and applications to high-order finite difference schemes with stationary grids[J]. Journal of Computational Physics, 2013, 239: 90-111. DOI:10.1016/j.jcp.2012.12.002 |
| [49] |
DENG X G, ZHU H J, MIN Y B, et al. Symmetric conservative metric method: A link between high order finite-difference and finite-volume schemes for flow computations around complex geometries[C]//Eighth International Conference on Computational Fluid Dynamics, Chengdu, China, ICCFD8-2014-0005, 2014.
|
| [50] |
DENG X G, ZHU H J, Min Y B, et al. High-order finite difference schemes based on symmetric conservative metric method: Decomposition, geometric meaning and connection with finite volume schemes[J]. Advances in Applied Mathematics and Mechanics, 2020, 12(2): 436-479. DOI:10.4208/aamm.OA-2017-0243 |
| [51] |
DENG X G, MAO M L, TU G H, et al. Extending weighted compact nonlinear schemes to complex grids with characteristic-based interface conditions[J]. American Institute of Aeronautics and Astronautics Journal, 2010, 48(12): 2840-2851. DOI:10.2514/1.J050285 |
| [52] |
KIM J W, LEE D J. Generalized characteristic boundary conditions for computational aeroacoustics, Part 2[J]. American Institute of Aeronautics and Astronautics Journal, 2004, 42(1): 47-55. DOI:10.2514/1.9029 |
| [53] |
MAO M L, ZHU H J, DENG X G, et al. Effect of geometric conservation law on improving spatial accuracy for finite difference schemes on two-dimensional nonsmooth grids[J]. Communications in Computational Physics, 2015, 18(3): 673-706. DOI:10.4208/cicp.250614.060215a |
| [54] |
闵耀兵, 马燕凯, 李松. CFD中统计误差的数值精度分析[J]. 航空学报, 2020, 41(4): 123554. MIN Y B, MA Y K, LI S. Accuracy analysis of numerical error with statistical forms in CFD[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(4): 123554. (in Chinese) |
| [55] |
DENG X G, YI Y, MAO M L, et al. A family of hybrid cell-edge and cell-node dissipative compact schemes satisfying geometric conservation law[J]. Computers and Fluids, 2015, 116: 29-45. DOI:10.1016/j.compfluid.2015.04.015 |
| [56] |
姜屹, 邓小刚, 毛枚良, 等. 基于HDCS-E8T7格式的气动噪声数值模拟方法研究进展[J]. 空气动力学学报, 2014, 32(5): 559-574. JIANG Y, DENG X G, MAO M L., et al. Progress of aeroacoustic simulation method based on HDCS-E8T7 scheme[J]. Acta Aerodynamica Sinica, 2014, 32(5): 559-574. (in Chinese) |
| [57] |
YI Y, MAO M L, DENG X G, et al. Extending seventh-order dissipative compact scheme satisfying geometric conservation law to large eddy simulation on curvilinear grids[J]. Advances in Applied Mathematics and Mechanics, 2015, 7(4): 407-429. DOI:10.4208/aamm.2013.m404 |
 2021, Vol. 39
2021, Vol. 39


