2. 火箭军工程大学, 西安 710025;
3. 北京应用物理与计算数学研究所, 北京 100094
2. Rocket Force University of Engineering, Xi'an 710025, China;
3. Institute of Applied Physics and Computational Mathematics, Beijing 100094, China
超声速流中,多尺度结构(如湍流)、间断(如激波)以及这些结构之间的相互作用同时存在,给数值模拟带来很大的挑战。一方面,多尺度结构要求数值格式具有较小的色散耗散误差以精确地捕捉幅值和相位,另一方面,间断附近需要格式具有足够的耗散以抑制数值振荡。这两种矛盾的要求使得构造高分辨率的激波捕捉格式非常困难。目前最具代表性的高精度激波捕捉格式是WENO格式,它最初由Liu等[1]提出,之后被Jiang和Shu[2]改进。WENO格式可以根据流场局部的光滑性,动态调整候选模板的权重来无振荡地捕捉激波,但是这一非线性机制也使得格式在光滑区的耗散过大,特别是在计算可压缩流动的多尺度结构时,数值耗散可能会高于物理耗散[3]。
解决这一问题的一种方法是改进WENO或ENO格式的非线性机制,更好地实现光滑区和间断的尺度分离。Henrick等[4]提出了WENO-M格式,通过映射非线性权解决了WENO-JS在极点处不满足五阶收敛条件的问题。Borgers等[5]提出的WENO-Z格式采用了一种归一化的光滑因子,可以使非线性权在光滑区更快地恢复到线性权。该格式在极点处也满足五阶收敛条件,且计算量远小于WENO-M格式。刘朋欣等[6]参考Henrick等[4]提出的映射函数的思想,将一种五次分段多项式映射函数应用于一种由NND格式改型得到的中心型三阶格式,构造出SWENO3-PPM5格式,算例测试结果表明该格式具有比WENO3更高的分辨率。Taylor等[7]基于一种相对光滑限制器构造得到WENO-RL格式,当光滑因子间的比值较小时直接采用线性权,这种方法可以使格式在中低波数段的色散耗散特性和对应的线性格式一致,从而改善格式的谱特性。WENO-SYMBO格式[8]将对应的线性格式由迎风改为中心格式,并通过求解一个积分形式目标函数的最小值,对格式的谱特性进行优化。Hu和Adams等[9]发展了一种自适应的中心迎风六阶WENO格式(WENO-CU6),采用新的光滑因子控制格式在中心和迎风之间切换。最近发展的TENO格式[10]采用新的模板选择和加权策略,来实现光滑区和间断的有效区分,从而改善分辨率。
另外一种方法是利用间断探测器,将激波捕捉格式和谱特性良好的格式结合起来,构造混合格式。混合格式在流场光滑区采用低耗散的格式以提高分辨率,而在间断附近采用激波捕捉格式以避免数值振荡。混合格式首先由Adams和Shariff[11]提出,他们将非守恒形式的紧致格式与ENO格式相结合,用于激波湍流相互作用流场的模拟。Pirozzoli[12]将守恒的紧致格式与WENO格式相结合,构造了一种守恒的紧致-WENO混合格式。该工作由Ren等[13]进一步发展,他设计了一种新的间断探测器,并采用加权的方式将守恒的紧致格式和WENO格式混合,避免了两种格式的突然切换。武从海等[14]将Ren等[13]提出的间断探测器进行改进,构造了基于WENO-Z格式和五阶守恒紧致格式的混合格式,并且通过仅对混合格式中WENO部分进行特征投影处理,提高了计算效率。对于混合格式,间断探测器的精度对格式的谱特性有很大影响。传统的间断探测器通常采用流场解的一阶导数或二阶导数来判断流场的光滑性[13, 15-16]。此外,近年来还发展了基于非正交小波基函数[15, 17]以及WENO非线性权[18-21]的间断探测器。然而,如何将间断和高频成分以及极点进行区分仍然是一个困难的问题。
上述两种方法改善计算效果的主要思路都是在流场光滑区尽可能地优先采用线性格式,因此,线性格式的性能对最终计算结果有直接影响。例如,WENO-M和WENO-Z等的线性格式是五阶迎风格式,而WENO-SYMBO格式对应的线性格式是六阶中心格式。混合格式的线性部分则多采用紧致格式和中心格式。当线性格式是迎风格式时,对湍流直接数值模拟等应用而言,耗散还是较大;当线性格式为中心格式时,耗散则不足。Pirozzoli[12]指出,为了减少数值振荡,格式需要具有一定的耗散以抑制色散误差较大的高波数成分。但是,如何合理地确定线性格式的耗散大小仍然是一个开放问题。
我们最近的工作,就是解决混合格式中线性部分的色散优化和耗散控制问题。关于色散优化的方法,已经开展了较多研究,但是线性格式的耗散控制相关的研究还比较少。本文综述了我们近期的相关研究工作。首先,Sun等[22]提出了一类色散耗散相互独立的有限差分格式,在优化色散同时,耗散可以通过一个参数调节,从而得到了色散最小、耗散可控(Minimized Dispersion and Controllable Dissipation, MDCD)格式。但是MDCD格式耗散参数的设置依赖于具体问题,需要基于经验人工进行选取,而在大型的数值计算如直接数值模拟中,参数的调试会花费大量的时间。Hu等[23]认为,格式的耗散大小应该与色散误差相关。他们据此得到一个色散耗散条件,来确定足够的耗散以抑制非物理的高频振荡。Sun等[24]根据这一关系,确定了六阶MDCD格式的耗散参数,在多个测试算例中,格式均表现出较好的鲁棒性。这种方法虽然可以得到具有合适耗散的格式,但它只能调节格式耗散的整体水平,而没有考虑解的局部尺度。
理想的格式耗散应该是与数值解的局部尺度相关的。在解的局部尺度远大于网格尺度时,线性格式的耗散应该很小甚至为0。当解的局部尺度与网格尺度接近时,此时格式的色散误差已非常大,应当将耗散增加到足以抑制高波数振荡的水平。根据这一思想,Li等[25]发展了一类具有最小色散、自适应耗散特性(Minimized Dispersion and Adaptive Dissipation, MDAD)的格式。
自适应耗散的差分格式包含以下要素。首先,为了保证耗散的自适应不影响格式的色散特性,选择色散和耗散相互独立的四阶MDCD格式作为自适应耗散格式的基础。其次,为了识别数值解的局部尺度,Li等[25]提出了一种基于流场解的导数的尺度识别器,可用来得到数值解局部的等效无量纲波数。最后,采用Hu等[23]提出的色散耗散条件,设计出耗散参数与局部等效无量纲波数之间的关系,从而构造得到具有自适应耗散特性的MDAD格式。
为了使格式具有激波捕捉能力,通过将MDAD格式的数值通量表示为一系列候选模板上的低阶多项式的线性组合,并引入WENO格式的非线性权,发展了MDAD-WENO格式。之后将MDAD格式与MDAD-WENO格式相结合,构造了一种混合格式,记为MDAD-HY。采用近似色散关系[26]分析MDAD-HY格式与其他激波捕捉格式的近似谱特性,发现MDAD-HY格式相比基于MDCD的混合格式MDCD-HY,在中低波数段的耗散更小,而在高波数段有相近的耗散,说明格式在数值解尺度较大的区域分辨率较高,而在间断区也有较好的鲁棒性。构造混合格式的一个关键问题是合理的间断探测器。为此,Li等[25]将传统间断探测器[13]与尺度识别器相结合,提出了一种新的间断探测器,能够有效减少对光滑区的极点的误判。
本文介绍了MDCD格式、MDAD格式、混合格式MDCD-HY和MDAD-HY,以及MDCD格式的应用情况和MDAD格式的测试算例,最后作出了总结。
1 色散最小、耗散可控有限差分格式本文以一维线性波动方程为例,介绍高精度有限差分格式的色散优化和耗散控制方法。方程形式如下:
| $ \frac{{\partial u}}{{\partial t}} + \frac{{\partial f}}{{\partial x}} = 0 $ | (1) |
其中, u为守恒量,f=au为通量且a为常数。考虑在均匀网格上,采用半离散有限差分格式对式(1)在(xj, t)处进行离散,得到:
| $ \frac{{\partial {u_j}}}{{\partial t}} + f_\Delta ^\prime ({x_j}) = 0 $ | (2) |
其中Δx为网格长度,f′Δ(xj)为有限差分格式对空间一阶偏导数
| $ f_\Delta ^\prime ({x_j}) = \frac{1}{{\Delta x}}\sum\limits_{m = - r}^s {{b_m}} {f_{j + m}} $ | (3) |
其中fj+m=f(xj+mΔx)。式(3)可改写为守恒形式,即:
| $ f_\Delta ^\prime ({x_j}) = \frac{1}{{\Delta x}}({\hat f_{j + \frac{1}{2}}} - {\hat f_{j - \frac{1}{2}}}) $ | (4) |
其中
常规的数值格式色散和耗散特性是相互关联的,但是MDCD格式具有色散、耗散相互独立的特性,这就使得它可以对色散进行单独优化,而耗散也可以根据不同工况进行调节。为了简洁,本文将只介绍四阶MDCD格式[22],六阶MDCD格式的具体细节参见文献[24]。
1.1 MDCD格式的半离散特性当空间有限差分格式包含对称的(2r+1)个模板点时,式(3)可写为:
| $ f_\Delta ^\prime ({x_j}) = \frac{1}{{\Delta x}}\sum\limits_{m = - r}^r {{b_m}} {f_{j + m}} $ | (5) |
通过对bm的合理选取,格式最高可以达到2r阶精度。Sun等在文献[22]中证明,当式(5)中的f′Δ(xj)达到(2r-2)阶精度时,格式的色散和耗散特性将分别由两个自由参数γdisp和γdiss单独控制。通过求解一个积分型目标函数的最小值问题,可以得到最优的色散参数γdisp,而耗散参数γdiss需要根据具体问题来确定,从而得到具有低色散、可控耗散特性(MDCD)的有限差分格式。
当r=3时,四阶的MDCD格式[22]形式如下:
| $ \begin{array}{c} f_{\Delta}^{\prime}\left(x_{j}\right)=\frac{1}{\Delta x}\left[\left(-\frac{1}{2} \gamma_{\mathrm{disp}}-\frac{1}{2} \gamma_{\mathrm{diss}}\right) f_{j-3}+\right. \\ \left(2 \gamma_{\mathrm{disp}}+3 \gamma_{\mathrm{diss}}+\frac{1}{12}\right) f_{j-2}+ \\ \left(-\frac{5}{2} \gamma_{\mathrm{disp}}-\frac{15}{2} \gamma_{\mathrm{diss}}-\frac{2}{3}\right) f_{j-1}+ \\ 10 \gamma_{\mathrm{diss}} f_{0}+\left(\frac{5}{2} \gamma_{\mathrm{disp}}-\frac{15}{2} \gamma_{\mathrm{diss}}+\frac{2}{3}\right) f_{j+1}+ \\ \left(-2 \gamma_{\mathrm{disp}}+3 \gamma_{\mathrm{diss}}-\frac{1}{12}\right) f_{j+2}+ \\ \left.\left(\frac{1}{2} \gamma_{\mathrm{disp}}-\frac{1}{2} \gamma_{\mathrm{diss}}\right) f_{j+3}\right] \end{array} $ | (6) |
将该格式写为守恒格式,数值通量
| $ \begin{array}{c} \hat{f}_{j+\frac{1}{2}}=\frac{1}{\Delta x}\left[\left(\frac{1}{2} \gamma_{\text {disp }}+\frac{1}{2} \gamma_{\text {diss }}\right) f_{j-2}+\right. \\ \left(-\frac{3}{2} \gamma_{\text {disp }}-\frac{5}{2} \gamma_{\text {diss }}-\frac{1}{12}\right) f_{j-1}+ \\ \left(\gamma_{\text {disp }}+5 \gamma_{\text {diss }}+\frac{7}{12}\right) f_{j}+ \\ \left(\gamma_{\text {disp }}-5 \gamma_{\text {diss }}+\frac{7}{12}\right) f_{j+1}+ \\ \left(-\frac{3}{2} \gamma_{\text {disp }}+\frac{5}{2} \gamma_{\text {diss }}-\frac{1}{12}\right) f_{j+2}+ \\ \left.\left(\frac{1}{2} \gamma_{\text {disp }}-\frac{1}{2} \gamma_{\text {diss }}\right) f_{j+3}\right] \end{array} $ | (7) |
不论γdisp和γdiss如何选取,格式都有四阶精度。
下面分析式(6)所示四阶MDCD的半离散色散耗散特性。考虑单一的简谐波,
| $ f(x)=\hat{u}_{0} \mathrm{e}^{\mathrm{i} \omega x} $ | (8) |
则空间一阶偏导数有精确解
| $ \frac{\partial f}{\partial x}=\frac{\mathrm{i} k}{\Delta x} \hat{u}_{0} \mathrm{e}^{\mathrm{i} \omega x} $ | (9) |
其中k=ωΔx为无量纲波数。将式(8)代入式(6)并写为:
| $ f_{\Delta}^{\prime}\left(x_{j}\right)=\frac{\mathrm{i} k^{\prime}}{\Delta x} \hat{u}_{0} \mathrm{e}^{\mathrm{i} \omega x_{j}} $ | (10) |
其中
| $ \begin{array}{c} \Re\left(k^{\prime}\right)=\gamma_{\text {disp }} \sin 3 k-\left(4 \gamma_{\text {disp }}+\frac{1}{6}\right) \sin 2 k+ \\ \left(5 \gamma_{\text {disp }}+\frac{4}{3}\right) \sin k \\ \mathfrak{J}\left(k^{\prime}\right)=\gamma_{\text {diss }}(\cos 3 k-6 \cos 2 k+15 \cos k-10) \end{array} $ | (11) |
显然格式的色散特性只与γdisp有关,耗散特性只与γdiss有关,从而实现了对格式色散和耗散的单独控制。
MDCD格式的色散和耗散特性是相互独立的,因此可以对色散进行单独优化而不影响耗散。通常认为格式的色散误差应当在选定的标准下达到最小。文献[8]设计了一种加权积分形式的优化目标函数:
| $ E=\int_{0}^{\rm{ \mathsf{ π} }} \mathrm{e}^{-\nu k}[\Re(k)-k]^{2} \mathrm{~d} k $ | (12) |
其中e-νk用于控制不同波数下色散误差的相对权重,通过求解使目标函数式(12)最小的优化问题,可以得到最优的色散参数γdisp。为了使格式在尽可能大的波数范围内都有较小的色散误差,文献[22]最终采用了ν=8下的最优色散参数,
| $ {\gamma _{{\rm{disp}}}} = 0.046{\kern 1pt} {\kern 1pt} 378{\kern 1pt} {\kern 1pt} 3 $ | (13) |
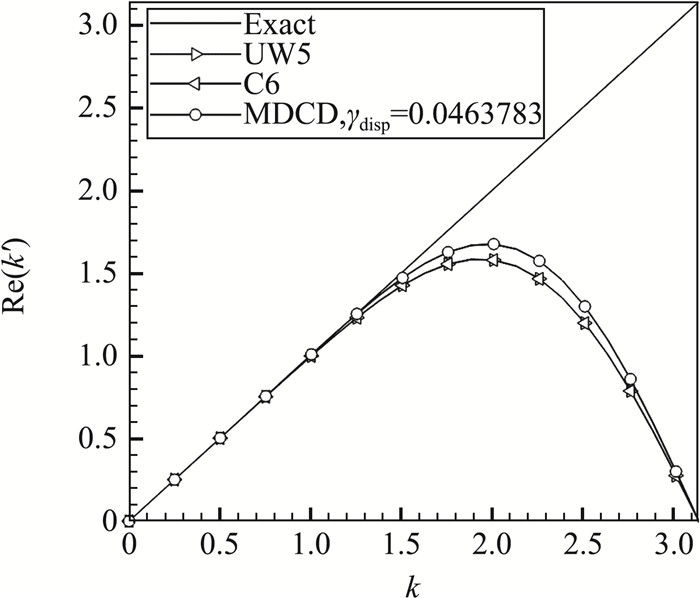
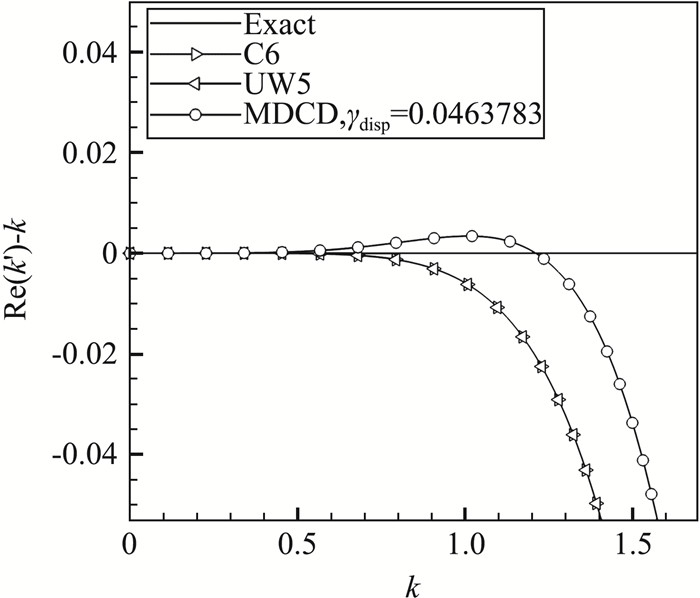
图 1展现了优化后的四阶MDCD格式的色散特性,并与五阶迎风格式(UW5,五阶WENO格式的线性部分)和六阶中心差分格式(C6)进行比较。可以看到UW5和C6的色散特性完全一致,而优化后的四阶MDCD格式则在更长的波数范围内有较好的色散特性。为了更清楚地展示中低波数段各个格式的色散特性差异,我们采用绝对色散误差
|
图 1 不同格式的色散特性 Fig.1 Comparison of dispersion properties of various linear schemes |
|
图 2 不同格式的色散误差 Fig.2 Comparison of dispersion errors of various linear schemes |
对于耗散特性,为了使格式保持稳定,所有波数下的耗散都应非负。由式(11)所示,MDCD格式的耗散大小只与γdiss有关,虚部
| $ \mathfrak{J}\left(k^{\prime}\right)=\gamma_{\text {diss }} g(\cos k) $ | (14) |
其中,
| $ g(x)=4 x^{3}-12 x^{2}+12 x-4 $ | (15) |
由于g′(x)=12(x-1)2≥0,为单调非减函数,易证g(cosk)≤0。因此当a>0时,如果γdiss≥0,则MDCD格式有非负耗散,格式是稳定的,且随着γdiss的增大,格式的耗散增加。当耗散参数取0时,MDCD为中心格式,此时格式分辨率最高,但是无法抑制高波数的非物理振荡。
在实际计算中,正如文献[12]提到的,格式需要具有一定的耗散。对于四阶MDCD格式,Sun等[22]对不同算例采用试错的方法确定合适的耗散参数γdiss进行计算。而在文献[24]中,Sun等采用Hu等[23]提出的色散耗散条件确定了六阶MDCD格式的耗散参数。多个数值实验结果显示该六阶MDCD格式表现出较好的鲁棒性,没有出现明显的数值振荡。Hu等[23]提出的色散耗散条件具体形式如下:
| $ r=\frac{\left|\frac{\partial \Re\left(k^{\prime}\right)}{\partial k}-1\right|}{\left|\mathfrak{J}\left(k^{\prime}\right)\right|} \sim 1<10 $ | (16) |
Hu等认为格式的耗散应当与色散误差相关,在式(16)中,给定波数下的色散耗散比值r越小表示格式对该波数的波耗散越大。当r < 10时,格式的耗散基本可以抑制非物理的高频波动。这里我们采用与文献[24]相同的做法确定四阶MDCD格式的通用耗散参数γdiss。考虑到k=π时格式的耗散最大,我们采用r(π)来确定γdiss。本文选择r≤9作为限制条件,此时满足条件的最小耗散参数为:
| $ {\gamma _{{\rm{diss}}}} = 0.012 $ | (17) |
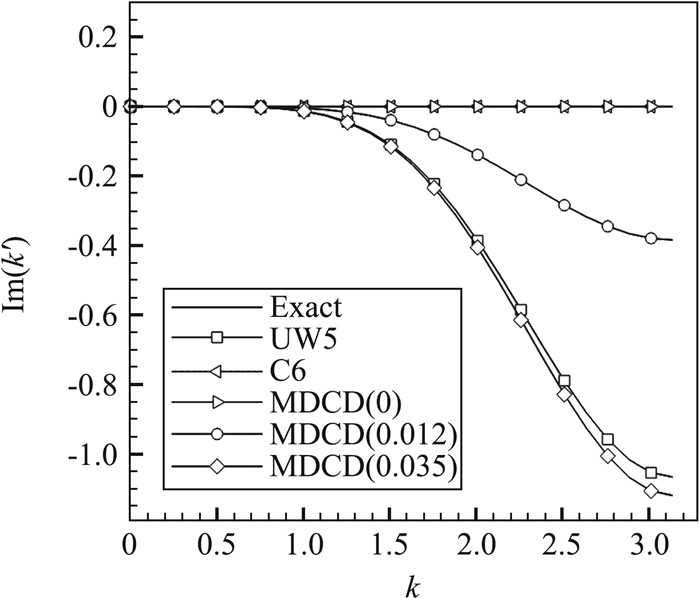
图 3展示了不同耗散参数下的MDCD格式与UW5以及C6格式的半离散耗散特性对比,其中括号内的数字为耗散参数的大小。可以看到C6和MDCD(0)均为零耗散,MDCD(0.035)的耗散特性与UW5接近,而MDCD(0.012)的耗散介于C6和UW5之间。MDCD(0.012)在中低波数段耗散较小,格式有较高的分辨率,在高波数段,格式的色散误差变大时,也能提供足够的耗散来抑制振荡,有较好的鲁棒性。因此,对于大多数工况,我们推荐采用MDCD(0.012)。在本文中,如无特殊说明,MDCD格式的耗散参数均采用γdiss=0.012。
|
图 3 不同格式的耗散特性 Fig.3 Comparison of dissipation properties of various linear schemes |
上一节中我们提到,MDCD格式的半离散色散耗散特性相互独立,分别受色散参数γdisp和耗散参数γdiss控制。但实际计算中,结果同时受到空间离散和时间离散的影响,因此分析格式的全离散特性是有必要的。
考虑线性对流方程:
| $ \frac{{\partial u}}{{\partial t}} + a\frac{{\partial u}}{{\partial x}} = 0 $ | (18) |
当初始值为
| $ u_{e x}=\mathrm{e}^{-\mathrm{i} k c} \hat{u}_{0} \mathrm{e}^{\mathrm{i} \omega x} $ | (19) |
其中c=aΔt/Δx为库朗数,k=ωΔx为无量纲波数。而半离散方程式(4)的解为:
| $ u_{s}=\mathrm{e}^{-\mathrm{i} k^{\prime} c} \hat{u}_{0} \mathrm{e}^{\mathrm{i} \omega x} $ | (20) |
其中k′为1.1节中所述的无量纲修正波数。对比式(19)和式(20),可以发现空间离散格式引入的误差为:
| $ r_{s}=\mathrm{e}^{-\mathrm{i}\left(k^{\prime}-k\right) c}=\mathrm{e}^{\mathfrak{J}\left(k^{\prime}\right) c} \mathrm{e}^{-\mathrm{i}\left(\Re\left(k^{\prime}\right)-k\right) c} $ | (21) |
其中
| $ u_{t}=G(k, c) \hat{u}_{0} \mathrm{e}^{\mathrm{i} \omega x} $ | (22) |
其中G(k, c)为放大因子,具体形式为一个s阶多项式,其中s为龙格库塔格式的级数。对比式(22)和式(19),可以发现G(k, c)为精确的放大因子e-ikc的近似。因此,格式的全离散误差为:
| $ {r_t} = |{r_t}|{{\rm{e}}^{ - {\rm{i}}{\delta _t}}} = \frac{{G(k,c)}}{{{{\rm{e}}^{ - {\rm{i}}kc}}}} $ | (23) |
其中|rt|=|G(k, c)|为全离散耗散误差,δt=-δG-kc为全离散色散误差。考虑到1.1节中分析半离散色散耗散特性时采用的是
| $ \begin{array}{l} \Re\left(k_{t}\right)=-\delta_{G} / c \\ \mathfrak{J}\left(k_{t}\right)=\lg (|G(k, c)|) / c \end{array} $ | (24) |
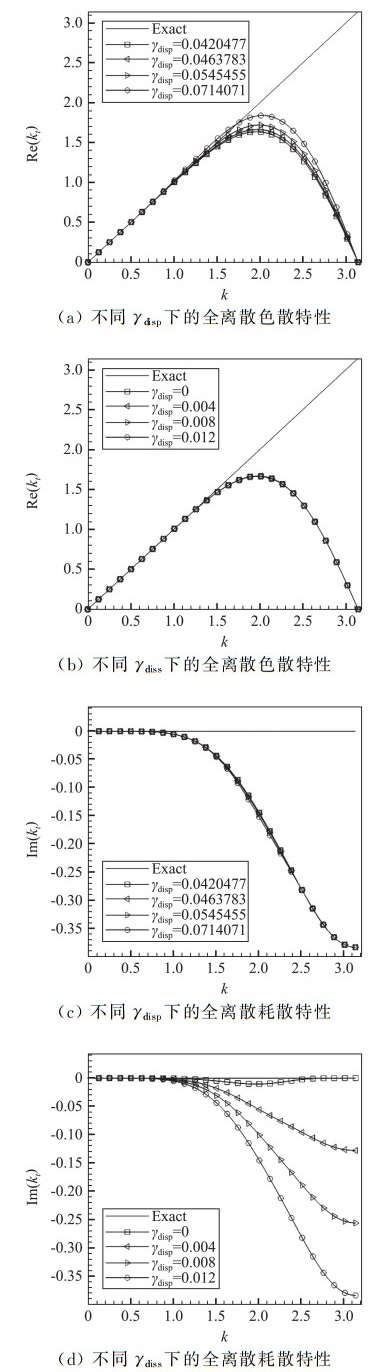
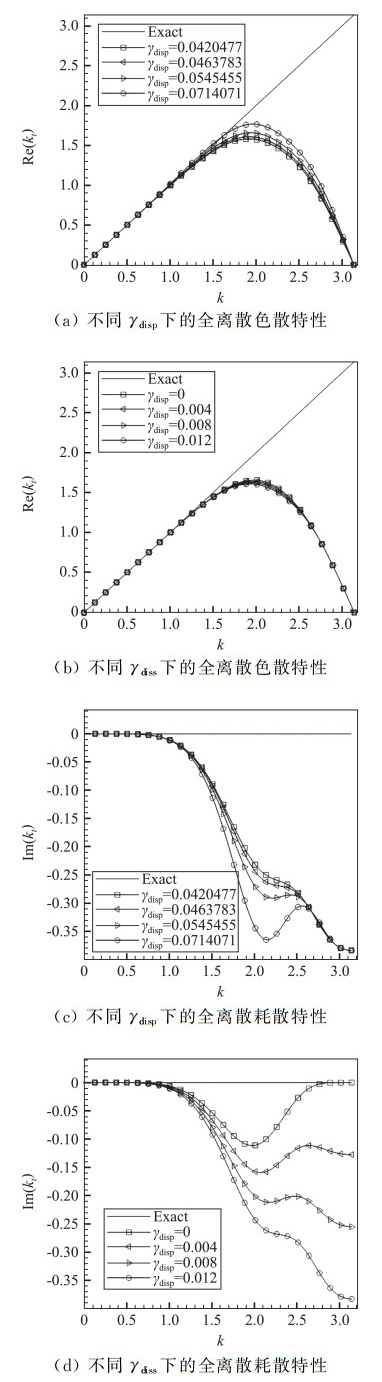
其中kt为全离散情况下的等效无量纲修正波数。由式(24)可知,全离散的色散耗散特性均与库朗数c有关。为了不失一般性,我们采用c=0.3、0.6、1.0三种条件,对全离散色散耗散特性关于γdisp和γdiss的灵敏度进行测试,结果如图 4~图 6所示。
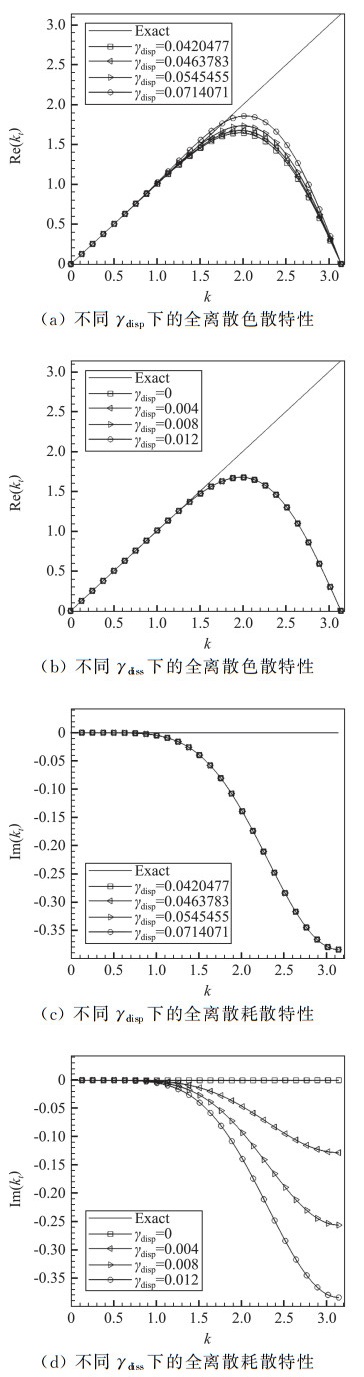
|
图 4 c=0.3时的全离散色散耗散特性 Fig.4 Total dispersion and dissipation properties with the Courant number c=0.3 |
|
图 5 c=0.6时的全离散色散耗散特性 Fig.5 Total dispersion and dissipation properties with the Courant number c=0.6 |
|
图 6 c=1.0时的全离散色散耗散特性 Fig.6 Total dispersion and dissipation properties with the Courant number c=1.0 |
可以看到,当库朗数较小(c=0.3、0.6)时,格式的全离散色散耗散特性受时间离散影响尚不明显,主要由空间离散决定[24],此时全离散色散特性主要受色散参数γdisp控制,对耗散参数γdiss不敏感,而全离散耗散特性主要受耗散参数γdiss影响,对色散参数γdisp不敏感。但当库朗数c=1.0时,时间离散带来的误差与空间离散相当,此时全离散色散耗散特性表现出同时受色散参数γdisp和耗散参数γdiss影响。但是色散参数γdisp对耗散的影响仍比耗散参数γdiss小得多,而耗散参数γdiss对色散的影响也比色散参数γdisp小得多。因此可以认为,在全离散意义下,MDCD格式仍是可用的。
2 色散最小、耗散自适应有限差分格式在1.1节中,我们采用Hu等[23]提出的色散耗散条件确定了一个通用的四阶MDCD格式的耗散参数。但是我们也注意到,当流场尺度较大时,可以采用更小的数值耗散,因为此时物理耗散可被准确地预测以使计算稳定。在某些情况下,对于可精确分辨的解,采用中心格式计算已经足够[9]。因此,当全场采用相同的耗散参数时,在流场尺度较大的光滑区,可能出现耗散过大的情况。
理想的耗散参数应该随着解的局部尺度而自动调节。为了实现这一目标,必须发展数值解的尺度识别器,并在此基础上构造具有最小色散、自适应耗散特性(Minimized Dispersion and Adaptive Dissipation, MDAD)的格式[25]。本节综述这方面工作的最新进展。
2.1 数值解尺度识别器原则上,在解的局部尺度远大于网格尺度时,线性格式的耗散应该很小甚至为0,以提高格式的分辨率。而当解的局部尺度与网格尺度接近时,应该将耗散增加到足以抑制高波数振荡的水平。如果能够实现这一点,则MDCD格式在鲁棒性不下降时,分辨率将得到进一步改善。为此,本节将提出一种数值解局部尺度识别器,用于识别数值解局部的等效长度尺度,作为构造自适应耗散格式的第一步。
数值解尺度的确定是一个开放性的问题,目前相关的研究很少。Li等[28]提出了一种尺度识别器,用于优化一种五点非线性格式,以计算扩散方程中的二阶导数项。而文献[25]提出了一种新的数值解局部波数识别器,用于自适应耗散格式的构造。
设计尺度识别器的难点在于定量描述尺度时看似矛盾的两个要求。一方面,考虑到我们关注的是解的局部特性,尺度识别器应该作用于局部的物理空间。另一方面,为了将尺度识别器用于耗散控制,需要将其表示为波数的形式,而波数是傅里叶空间中的概念。为了满足上述两个条件,文献[25]提出一种两步的构造校准方法,即首先基于物理空间构造一种尺度识别器,之后再采用正弦波来校准尺度识别器中的参数。
第一步:构造。考虑光滑函数f(x),为了估计其在x0附近的长度尺度,将其在x0处作Taylor展开,有:
| $ f(x) - f({x_0}) = \sum\limits_{p = 1}^\infty {\frac{1}{{p!}}} {f^{(p)}}\Delta {x^p} $ | (25) |
其中
| $ \Delta {f_p} = \frac{1}{{p!}}{f^{(p)}}\Delta {x^p} $ | (26) |
当数值解的尺度较大时,低阶导数对函数变化的影响比高阶导数大。例如,当解为直线分布时,只有Δf1对解的变化有贡献。而x0附近如果出现小尺度结构,则说明高阶导数项产生的影响足够大。因此,原则上数值解的无量纲尺度可以用不同Δfp的比值来表示:
| $ \delta = \alpha {\left| {\frac{{\Delta {f_q}}}{{\Delta {f_p}}}} \right|^{\frac{1}{{p - q}}}} $ | (27) |
其中δ为局部无量纲尺度,且p>q。将式(26)代入式(27)得到:
| $ \delta = \frac{\beta }{{\Delta x}}{\left| {\frac{{{f^{(q)}}}}{{{f^{(p)}}}}} \right|^{\frac{1}{{p - q}}}} $ | (28) |
其中β是待定参数。考虑到四阶MDCD格式数值通量的模板点为6个,可以数值计算的导数f(p)的阶数为p=1~5,这里选取p=1~4构造尺度识别器,但此时仍然有多种可能的p-q组合方式。为了解决这个问题,可以采用如下的校准步骤。
第二步:校准。在这一步中,采用正弦波来确定式(28)中的参数。若将式(28)定义的长度尺度校准为精确的正弦波无量纲波长,最简单的方式是令p=q+2,此时p-q只剩如下两种组合方式:
| $ \delta=\frac{\beta}{\Delta x} \sqrt{\frac{\left|f^{(1)}\right|}{\left|f^{(3)}\right|}}, \quad \text { 或 } \delta=\frac{\beta}{\Delta x} \sqrt{\frac{\left|f^{(2)}\right|}{\left|f^{(4)}\right|}} $ | (29) |
证明过程如下。考虑单一正弦波,
| $ f=A \sin (\omega x+\varphi) $ | (30) |
可以得到它的各阶导数:
| $ \begin{array}{l} f^{(1)}=A \omega \cos (\omega x+\varphi) \\ f^{(2)}=-A \omega^{2} \sin (\omega x+\varphi) \\ f^{(3)}=-A \omega^{3} \cos (\omega x+\varphi) \\ f^{(4)}=A \omega^{4} \sin (\omega x+\varphi) \end{array} $ | (31) |
将式(31)代入式(29),并考虑波数ω和波长λ之间的关系
| $ \delta=\frac{\beta}{\Delta x} \sqrt{\frac{\left|f^{(1)}\right|}{\left|f^{(3)}\right|}}=\frac{\beta}{\Delta x} \sqrt{\frac{\left|f^{(2)}\right|}{\left|f^{(4)}\right|}}=\frac{\beta}{\Delta x} \frac{1}{\omega}=\frac{\beta}{2 {\rm{ \mathsf{ π} }}} \frac{\lambda}{\Delta x} $ | (32) |
因此,当β=2π时,无量纲尺度δ即为精确的无量纲波长,
| $ \delta=\frac{\lambda}{\Delta x} $ | (33) |
基于式(33),定义解的等效无量纲波数k,
| $ k=\omega \Delta x=\frac{2 {\rm{ \mathsf{ π} }} \Delta x}{\lambda}=\frac{2 {\rm{ \mathsf{ π} }}}{\delta} $ | (34) |
将式(29)代入式(34),并令β=2π,则有:
| $ k=\sqrt{\frac{\left|f^{(3)}\right|}{\left|f^{(1)}\right|}} \Delta x, \quad \text { 或 } k=\sqrt{\frac{\left|f^{(4)}\right|}{\left|f^{(2)}\right|}} \Delta x $ | (35) |
需要注意的是,式(35)定义的等效无量纲波数并不是傅里叶空间中的波数,而是局部长度尺度的倒数,是一个物理空间中局部的定义。对于单一正弦波,它可以得到精确的正弦波无量纲波数。为了避免式(35)在极值点和拐点附近的奇异性,可以把该式的两种情况相结合,从而有:
| $ k=\sqrt{\frac{\left|f^{(3)}\right|+\left|f^{(4)}\right| \Delta x}{\left|f^{(1)}\right|+\left|f^{(2)}\right| \Delta x+\varepsilon}} \Delta x $ | (36) |
其中ε为防止分母为0的小量,取ε=1×10-3。
在自适应耗散格式中,数值通量中的耗散参数γdiss由尺度识别器得到的等效无量纲波数确定。因此,式(36)应当在界面
| $ \begin{aligned} f_{j+\frac{1}{2}}^{(1)}=& \frac{1}{\Delta x}\left(-\frac{3}{640} f_{j-2}+\frac{25}{384} f_{j-1}-\frac{75}{64} f_{j}+\right.\\ &\left.\frac{75}{64} f_{j+1}-\frac{25}{384} f_{j+2}+\frac{3}{640} f_{j+3}\right) \\ f_{j+\frac{1}{2}}^{(2)}=& \frac{1}{\Delta x^{2}}\left(-\frac{5}{48} f_{j-2}+\frac{13}{16} f_{j-1}-\frac{17}{24} f_{j}-\right.\\ &\left.\frac{17}{24} f_{j+1}+\frac{13}{16} f_{j+2}-\frac{5}{48} f_{j+3}\right) \\ f_{j+\frac{1}{2}}^{(3)}=& \frac{1}{\Delta x^{3}}\left(\frac{1}{8} f_{j-2}-\frac{13}{8} f_{j-1}+\frac{17}{4} f_{j}-\right.\\ &\left.\frac{17}{4} f_{j+1}+\frac{13}{8} f_{j+2}-\frac{1}{8} f_{j+3}\right) \\ f_{j+\frac{1}{2}}^{(4)}=& \frac{1}{\Delta x^{4}}\left(\frac{1}{2} f_{j-2}-\frac{3}{2} f_{j-1}+f_{j}+\right.\\ &\left.f_{j+1}-\frac{3}{2} f_{j+2}+\frac{1}{2} f_{j+3}\right) \end{aligned} $ | (37) |
根据式(36),
| $ k_{j+\frac{1}{2}}=\sqrt{\frac{\left|f_{j+\frac{1}{2}}^{(3)}\right|+\left|f_{j+\frac{1}{2}}^{(4)}\right| \Delta x}{\left|f_{j+\frac{1}{2}}^{(1)}\right|+\left|f_{j+\frac{1}{2}}^{(2)}\right| \Delta x+\varepsilon}} \Delta x $ | (38) |
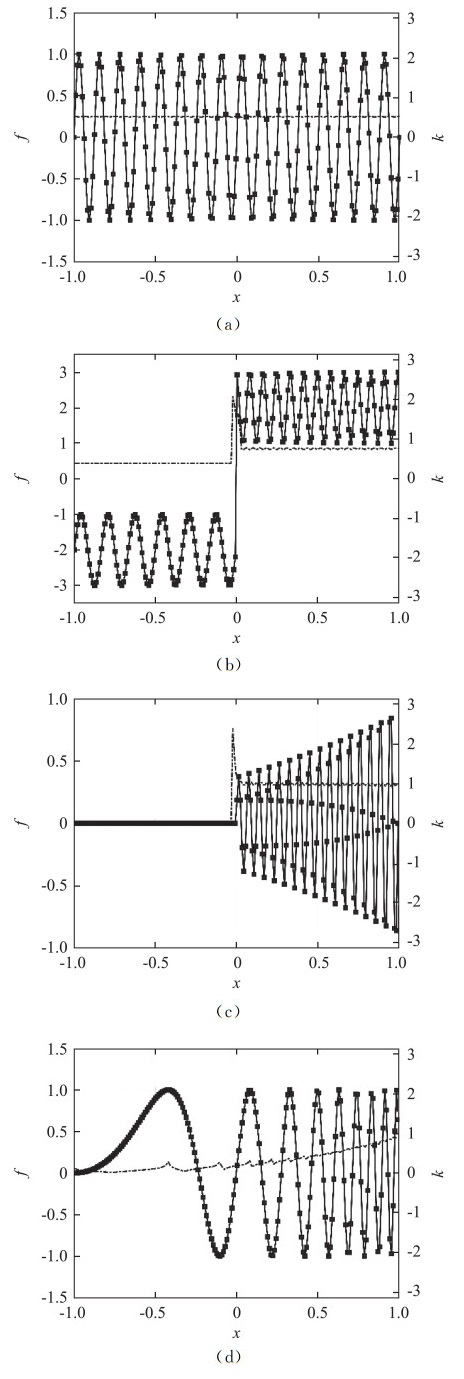
为了验证尺度识别器在流场中的效果,Li等[25]采用如下四组指定的函数进行静态测试,其中包括:
| $ \text { (a) }\ \ f=\sin (16 {\rm{ \mathsf{ π} }} x) \quad\quad\ , \ \ -1 \leqslant x \leqslant 1 $ |
| $ \text { (b) }\ \ f=\left\{\begin{array}{l} \sin (12 {\rm{ \mathsf{ π} }} x)-2 & , & -1 \leqslant x<0 \\ \left(\sin 24 {\rm{ \mathsf{ π} }}+\frac{{\rm{ \mathsf{ π} }}}{2}\right)+2 & , & 0 \leqslant x \leqslant 1 \end{array}\right. $ |
| $ \text { (c) }\ \ f=\left\{\begin{array}{lll}0 & , & -1 \leqslant x<0 \\ \mathrm{e}^{x-1} \sin (32 {\rm{ \mathsf{ π} }} x) & , & 0 \leqslant x \leqslant 1\end{array}\right. $ |
| $ \text { (d) }\ \ f=\sin \left(2 {\rm{ \mathsf{ π} }} \mathrm{e}^{x+1} x\right) \quad\quad\ , \ \ -1 \leqslant x \leqslant 1 $ |
测试所用网格数均为N=192。(a)用于验证尺度识别器对于标准的正弦波(
|
图 7 尺度识别器测试结果 Fig.7 Distributions of the scale sensor for assigned functions (方块实线为指定函数,点划线为等效无量纲波数) (the square symbols). Dash-dotted lines represent the effective scaled wavenumbers. The triangle symbols (see scale on the right axis) denote values of the scale sensor. |
由测试结果可知,尺度识别器能够准确地识别标准正弦波的无量纲波数,对于幅值增加和频率增加的正弦波识别效果也很好。式(38)通过各阶导数的恰当组合,有效抑制了等效无量纲波数在极值点和拐点处的振荡。而对于间断,尺度识别器往往将其识别为一个高频成分,这也与物理事实相吻合。
2.2 MDAD格式2.1节已经介绍了可以用于判断流场局部等效无量纲波数的尺度识别器,为了构造耗散自适应的MDAD格式,需要根据等效无量纲波数对式(7)中的耗散参数γdiss进行动态的调整。此时,γdiss在全场不再是一个常数。为了更清楚地介绍MDAD格式的构造过程,可以将式(7)改写为:
| $ \begin{array}{l} \hat{f}_{j+\frac{1}{2}}=\frac{1}{\Delta x}\left[\left(\frac{1}{2} \gamma_{\text {disp }}+\frac{1}{2}\left(\gamma_{\text {diss }}\right)_{j+\frac{1}{2}}\right) f_{j-2}+\right. \\ \quad\quad\ \ \left(-\frac{3}{2} \gamma_{\text {disp }}-\frac{5}{2}\left(\gamma_{\text {diss }}\right)_{j+\frac{1}{2}}-\frac{1}{12}\right) f_{j-1}+ \\ \quad\quad\ \ \left(\gamma_{\text {disp }}+5\left(\gamma_{\text {diss }}\right)_{j+\frac{1}{2}}+\frac{7}{12}\right) f_{j}+ \\ \quad\quad\ \ \left(\gamma_{\text {disp }}-5\left(\gamma_{\text {diss }}\right)_{j+\frac{1}{2}}+\frac{7}{12}\right) f_{j+1}+ \\ \quad\quad\ \ \left(-\frac{3}{2} \gamma_{\text {disp }}+\frac{5}{2}\left(\gamma_{\text {diss }}\right)_{j+\frac{1}{2}}-\frac{1}{12}\right) f_{j+2}+ \\ \quad\quad\ \ \left.\left(\frac{1}{2} \gamma_{\text {disp }}-\frac{1}{2}\left(\gamma_{\text {diss }}\right)_{j+\frac{1}{2}}\right) f_{j+3}\right] \end{array} $ | (39) |
为了实现自适应耗散,
| $ {({\gamma _{{\rm{diss}}}})_{j + \frac{1}{2}}} = {\gamma _{{\rm{diss}}}}({k_{j + \frac{1}{2}}}) $ | (40) |
其中
Li等[25]采用Hu等[23]提出的色散耗散条件指导式(40)的设计。需要注意的是色散耗散条件是在傅里叶空间中的关系,然而自适应耗散应该在物理空间中实施。因此,使用该条件时需要格外小心。不过对于单一正弦波,等效无量纲波数即为精确的正弦波波数,此时色散耗散条件可以很容易的使用。从这个角度考虑,使用色散耗散条件设计式(40)也可以看作是一个校准的过程,即以单一正弦波为例,采用色散耗散条件构造耗散参数与等效无量纲波数之间的关系,并应用于更一般的情况。需要注意的是,式(40)也可以基于经验或者物理意义进行设计,这一问题将在接下来的工作中继续研究。
1.1节中提到,当限制色散耗散比值r(π)≤9时,满足条件的最小耗散参数为γdiss=0.012。考虑到MDCD格式的色散和耗散特性均为已知函数,则当r固定时,可以反推不同波数下所需的耗散参数。将式(14)代入式(16)可以得到耗散参数与波数的关系式:
| $ \gamma_{\text {diss }}=\frac{\left|\frac{\partial \Re\left(k^{\prime}\right)}{\partial k}-1\right|}{r|g[\cos (k)]|} $ | (41) |
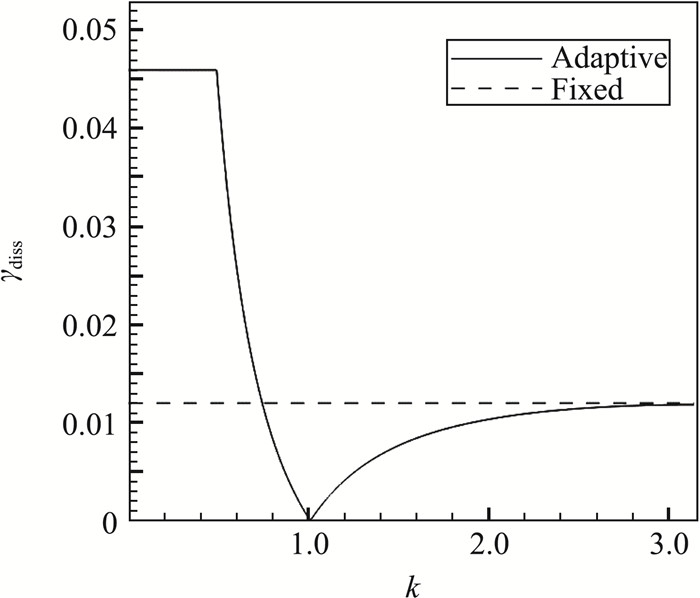
令r=9并限制
|
图 8 耗散参数与波数的关系 Fig.8 The relation between the dissipation parameter and the wave number. The solid and dashed lines are respectively the adaptive and fixed dissipation parameter. (实线为自适应耗散参数,虚线为固定的耗散参数0.012) |
由图可知,耗散参数随波数的变化可以分为左右两支,交点为(1.012, 0)。在低波数段(k≤1.012),由于|g[cos(k)]|较小,反解得到的γdiss一开始较大,之后逐渐减小为0。而在高波数段k>1.012,随着波数的增高,色散误差增加变快,
| $ \left(\gamma_{\text {diss }}\right)_{j+\frac{1}{2}}=\left\{\begin{array}{lc} 0 \quad \quad \quad \quad \quad , \quad 0 \leqslant k_{j+\frac{1}{2}} \leqslant 1.012 \\ 0.00862 \arctan \left(2.594\left(k_{j+\frac{1}{2}}-1.012\right)\right) \\ \quad \quad \quad \quad \quad\ \ , \quad 1.012<k_{j+\frac{1}{2}} \leqslant {\rm{ \mathsf{ π} }} \\ 0.012 \ \quad \quad \quad , \quad k_{j+\frac{1}{2}}>{\rm{ \mathsf{ π} }} \end{array}\right. $ | (42) |
通过式(38)计算等效无量纲波数,再采用式(42)得到式(39)中的耗散参数
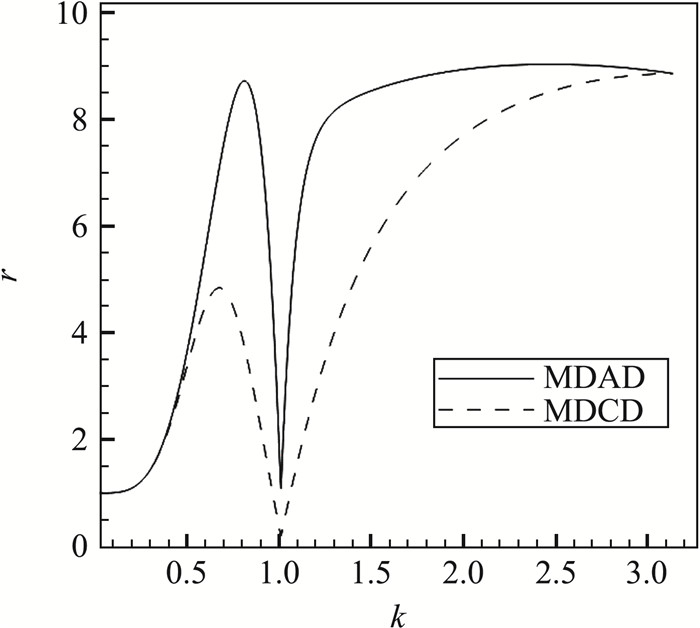
为了验证MDAD格式相对于MDCD的优越性,图 9展示了这两种格式的色散耗散比值r随波数的变化(r采用
|
图 9 色散耗散比值r随波数的变化曲线 Fig.9 The dispersion-dissipation ratio computed with r |
虽然MDCD格式和MDAD格式有很好的色散耗散特性,但它们不能直接用于含间断流场的数值模拟。为了使这些格式具有激波捕捉的能力,Sun等[22, 24]和Li等[25]的方案是首先将这些格式与WENO格式相结合,发展相应的非线性格式,之后将线性格式与非线性格式相结合,构造混合格式。由于MDCD格式与MDAD格式在混合格式构造方面基本一致,本文我们只介绍MDAD格式对应的混合格式MDAD-HY。本节将首先介绍MDAD-WENO格式,之后介绍一种新的间断探测器用于MDAD-HY格式的构造,并用近似色散关系(ADR)[26]对混合格式的谱特性进行分析。需要注意的是,引入自适应耗散机制后,MDAD格式实际上是非线性的,但为了简便,在后文我们仍然称其为线性格式。
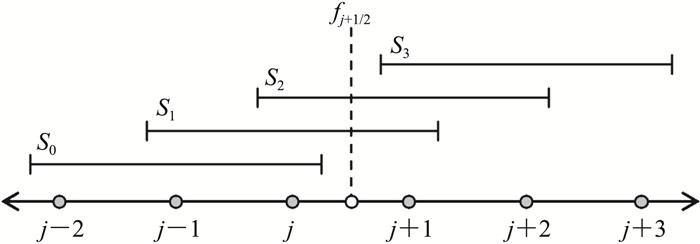
3.1 MDAD-WENO格式WENO格式[2]是一类代表性的非线性激波捕捉格式,在含间断流场的数值模拟中有广泛的应用。WENO格式的基本思想是通过对一系列候选模板上低阶多项式的非线性组合,实现无振荡的激波捕捉能力。为了构造MDAD-WENO格式,可以采用包含对称的6个模板点的MDAD格式作为它的线性部分,这些模板点被划分如图 10所示的四条候选模板{S0, S1, S2, S3},则MDAD格式的数值通量可以改写为:
| $ \hat{f}_{j+\frac{1}{2}}^{\mathrm{MDAD}}=\sum\limits_{k=0}^{3} C_{k} q_{k}\left(x_{j+\frac{1}{2}}\right) $ | (43) |
|
图 10 MDAD格式数值通量 |
其中
| $ \left\{\begin{array}{l} q_{0}\left(x_{j+\frac{1}{2}}\right)=\frac{1}{6}\left(2 f_{j-2}-7 f_{j-1}+11 f_{j}\right) \\ q_{1}\left(x_{j+\frac{1}{2}}\right)=\frac{1}{6}\left(-f_{j-1}+5 f_{j}+2 f_{j+1}\right) \\ q_{2}\left(x_{j+\frac{1}{2}}\right)=\frac{1}{6}\left(2 f_{j}+5 f_{j+1}-f_{j+2}\right) \\ q_{3}\left(x_{j+\frac{1}{2}}\right)=\frac{1}{6}\left(11 f_{j+1}-7 f_{j+2}+2 f_{j+3}\right) \end{array}\right. $ | (44) |
通过对比式(43)和式(39),可以得到线性权Ck是关于γdisp和
|
表 1 线性权Ck关于γdisp和 |
|
|
可以看到,2.2节中提到的限制条件
| $ \hat f_{j + \frac{1}{2}}^{{\rm{MDAD - WENO}}} = \sum\limits_{k = 0}^3 {{\omega _k}} {q_k}\left( {{x_{j + \frac{1}{2}}}} \right) $ | (45) |
其中qk与式(43)意义相同,ωk为WENO格式的非线性权,与对应候选模板Sk上解的光滑性有关。MDAD-WENO的非线性权采用与Jiang和Shu[2]相同的形式:
| $ {\omega _k} = \frac{{\frac{{{C_k}}}{{{{\left( {{\beta _k} + \varepsilon } \right)}^p}}}}}{{\sum\limits_{k = 0}^3 {\frac{{{C_k}}}{{{{\left( {{\beta _k} + \varepsilon } \right)}^p}}}} }} $ | (46) |
其中Ck采用表 1中的关系计算,因此MDAD-WENO格式也是耗散自适应的。ε为防止分母为0的小量,p与候选模板自适应的敏感性有关,通常取p=2,而βk为对应候选模板上解的光滑因子:
| $ {\beta _k} = \sum\limits_{m = 1}^2 {\int_{{x_{j - 1/2}}}^{{x_{j + \frac{1}{2}}}} {{{(\Delta x)}^{2m - 1}}} } {\left[ {\frac{{{\partial ^m}{q_k}(x)}}{{\partial {x^m}}}} \right]^2}{\rm{d}}x $ | (47) |
代入每个候选模板得到:
| $ \left\{ {\begin{array}{*{20}{l}} {{\beta _0} = \frac{1}{4}{{\left( {{f_{j - 2}} - 4{f_{j - 1}} + 3{f_j}} \right)}^2} + \frac{{13}}{{12}}{{\left( {{f_{j - 2}} - 2{f_{j - 1}} + {f_j}} \right)}^2}}\\ {{\beta _1} = \frac{1}{4}{{\left( {{f_{j - 1}} - {f_{j + 1}}} \right)}^2} + \frac{{13}}{{12}}{{\left( {{f_{j - 1}} - 2{f_j} + {f_{j + 1}}} \right)}^2}}\\ {{\beta _2} = \frac{1}{4}{{\left( {3{f_j} - 4{f_{j + 1}} + {f_{j + 2}}} \right)}^2} + \frac{{13}}{{12}}{{\left( {{f_j} - 2{f_{j + 1}} + {f_{j + 2}}} \right)}^2}}\\ {{\beta _3} = \frac{1}{4}{{\left( {5{f_{j + 1}} - 8{f_{j + 2}} + 3{f_{j + 3}}} \right)}^2} + \frac{{13}}{{12}}{{\left( {{f_{j + 1}} - 2{f_{j + 2}} + {f_{j + 3}}} \right)}^2}} \end{array}} \right. $ | (48) |
然而需要注意的是,与WENO-JS不同,MDAD-WENO是采用对称的模板,正如文献[8]中所说,它的候选模板S3包含的全部为顺风模板点,当该模板的非线性权ω3大于其他非线性权时,有可能会引起格式的不稳定,因此,在式(48)计算完所有非线性权之后,需要对β3增加额外的限制,
| $ {\beta _3} = \mathop {{\rm{max}}}\limits_{0 \le k \le 3} {\beta _k} $ | (49) |
以此来限制非线性权ω3不大于其他线性权,保证格式的稳定。
3.2 MDAD-HY格式WENO格式能够很好地捕捉流场中的间断,但是相比对应的线性格式,由于引入了非线性机制,色散耗散特性往往会变差[26]。为了在提高格式分辨率的同时仍然保持良好的间断捕捉能力,一种思路是采用合适的方法将WENO格式与谱特性良好的线性格式进行混合,在流场光滑区采用线性格式,在间断附近采用WENO格式。文献[25]对MDAD格式和MDAD-WENO格式进行组合,构造了具有耗散自适应、低色散特性的四阶有限差分混合格式(MDAD-HY)。
MDAD-HY格式的数值通量可表示为:
| $ \hat{f}_{j+\frac{1}{2}}=\sigma_{j+\frac{1}{2}} \hat{f}_{j+\frac{1}{2}}^{\mathrm{MDAD}}+\left(1-\sigma_{j+\frac{1}{2}}\right) \hat{f}_{j+\frac{1}{2}}^{\mathrm{MDAD}-\mathrm{WENO}} $ | (50) |
其中
| $ \sigma_{j+\frac{1}{2}}=\min \left(1, \frac{\psi_{j+\frac{1}{2}}}{\psi_{c}}\right) $ | (51) |
式(51)中的
| $ \psi_{j+\frac{1}{2}}=\min \left(\psi_{j}, \psi_{j+1}\right) $ | (52) |
其中,
| $ \psi_{j}=\frac{\left|2\left(f_{j+1}-f_{j}\right)\left(f_{j}-f_{j-1}\right)\right|+\varepsilon}{\left(f_{j+1}-f_{j}\right)^{2}+\left(f_{j}-f_{j-1}\right)^{2}+\varepsilon} $ | (53) |
ε为防止分母为0的小量,
| $ \varepsilon=\frac{0.9 \psi_{c}}{1-0.9 \psi_{c}} \xi^{2} $ | (54) |
其中ξ=1×10-3。由式(53)可知,ψj∈[0, 1],且可以反映xj左右两侧一阶导数绝对值的变化情况,当一阶导数绝对值变化大时,ψj趋于0,而一阶导数绝对值变化很小时,ψj趋于1。ψc为一个常数,当
在文献[21]中,Zhao等对一些常见的间断探测器进行了分析。他们的结论是, Ren等[13]提出的间断探测器构造得到的混合格式谱特性较好,但有可能把光滑解的极值点误判为激波。为了解决极点处容易出现误判的问题,Li等[25]在Ren等[13]提出的间断探测器基础上,结合尺度识别器,提出了一种新的间断探测器。其基本思路是在进行间断探测前,先利用尺度识别器将大尺度的光滑区分离。当尺度识别器识别得到的等效无量纲波数较低(k≤kc)时,可以认为流场的局部长度尺度较大,处在光滑区,此时直接令
| $ \begin{array}{c} \sigma_{j+\frac{1}{2}}=\frac{1+\operatorname{sign}\left(k_{c}-k\right)}{2}+ \\ \frac{1-\operatorname{sign}\left(k_{c}-k\right)}{2} \min \left(1, \frac{\psi_{j+\frac{1}{2}}}{\psi_{c}}\right) \end{array} $ | (55) |
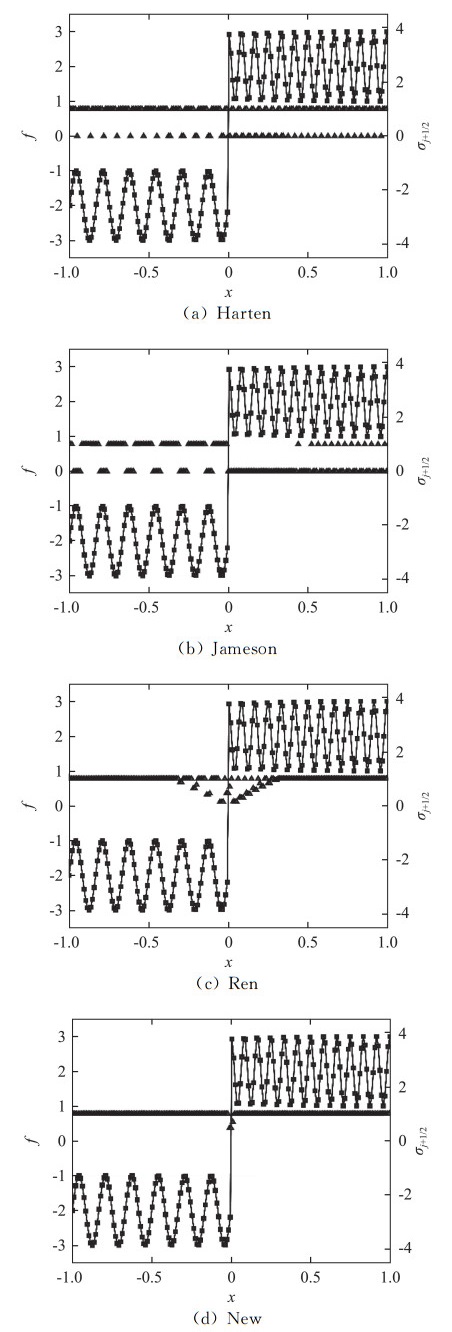
为了验证新的间断探测器的效果,我们将其与Harten[15]、Jameson等[16]以及Ren等[13]提出的基于一阶导或者二阶导的间断探测器进行比较。Harten的间断探测器同样基于流场梯度的变化,具体形式如下:
| $ \psi_{j+\frac{1}{2}}=1-\frac{\left|f_{j-1}-2 f_{j}+f_{j+1}\right|}{\left|f_{j-1}-f_{j}\right|+\left|f_{j}-f_{j+1}\right|+\varepsilon} $ | (56) |
| $ \sigma_{j+\frac{1}{2}}=\left\{\begin{array}{ll} 0 \quad, \quad \psi_{j+\frac{1}{2}}<\psi_{c} \\ 1 \quad, \quad \text { otherwise } \end{array}\right. $ | (57) |
其中, 阈值ψc=0.3,ε为防止分母为0的小量。而Jameson提出的间断探测器基于归一化的二阶导数:
| $ \begin{aligned} \psi_{j+\frac{1}{2}}=1-\frac{\left|f_{j-1}-2 f_{j}+f_{j+1}\right|}{\left|f_{j-1}\right|+2\left|f_{j}\right|+\left|f_{j+1}\right|+\varepsilon} \end{aligned} $ | (58) |
| $ \sigma_{j+\frac{1}{2}}=\left\{\begin{array}{ll} 0 \quad, \quad \psi_{j+\frac{1}{2}}<\psi_{c} \\ 1 \quad, \quad \text { otherwise } \end{array}\right. $ | (59) |
其中, 阈值
采用2.1节中的(b)算例对间断探测器进行静态测试,结果如图 11所示。可以看到,Harten和Jameson的间断探测器能够识别间断,但是在正弦波光滑区都出现大量误判,这将严重影响混合格式的分辨率。Ren提出的间断探测器识别效果相对较好,但在光滑区部分极点附近也存在误判。Li提出的新的间断探测器不仅能够准确识别间断,而且由于引入了尺度识别器的结果进行截断,光滑区的识别结果得到很大改善。
|
图 11 间断探测器静态测试结果 Fig.11 Distributions of shock detectors for test (b) in Section 2.2 (the square symbols). The triangle symbols (see scale on the right axis) denote values of shock detectors. (方块实线为指定函数,三角为 |
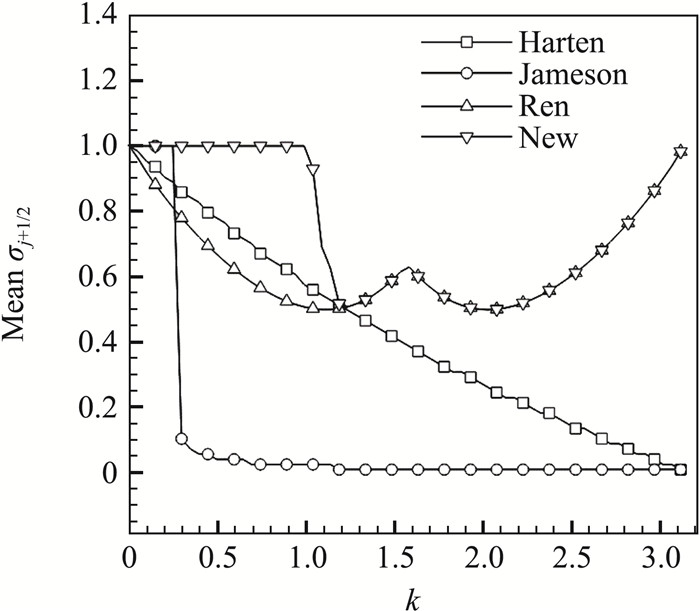
为了进一步验证间断探测器的效果,可以在整个波数空间内对其进行测试。类似于文献[21]中的方法,图 12展示了间断探测器对于不同波数的正弦波测试得到的所有网格上的
|
图 12 间断探测器在不同波数下测试得到的 |
线性格式的色散耗散特性可由傅里叶分析得到,但是对于非线性格式,目前还没有解析的分析谱特性的方法。Pirozzoli[26]提出一种近似色散关系(Approximate Dispersion Relation, ADR),可以数值地计算非线性的激波捕捉格式的修正波数,从而得到非线性格式近似的色散耗散特性。本节将利用ADR分析MDAD-HY格式的色散耗散特性,并与原始的MDCD-HY格式[22]进行对比。
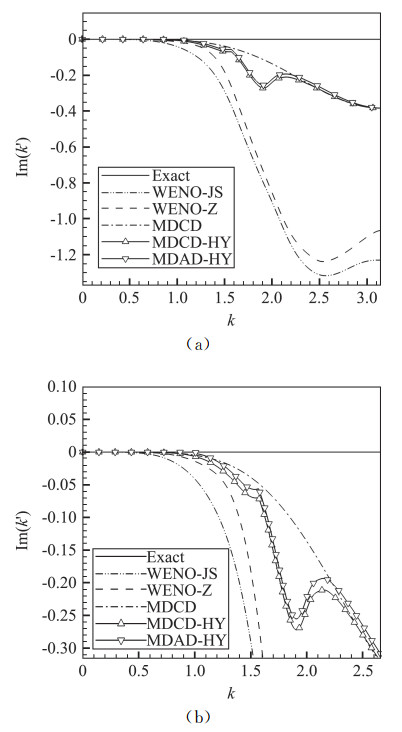
图 13展示了不同格式的近似耗散特性,Jiang和Shu[2]提出的WENO格式(即图中的WENO-JS),Borgers[5]提出的WENO-Z格式,以及Sun等[22]提出的线性MDCD格式也被引入作为参考。可以看到,WENO-Z的耗散小于WENO-JS,但是仍比两种混合格式要大。混合格式MDCD-HY和MDAD-HY的耗散特性在低波数和高波数段与线性MDCD格式接近,但在中波数段耗散变大。通过局部放大,可以观察到MDAD-HY在k < 1.04时耗散为0,小于MDCD-HY的耗散,之后随着波数的增加,耗散逐渐增大,直到k>2.5后MDAD-HY的耗散特性曲线与MDCD-HY基本接近。这就说明MDAD-HY格式在低波数段相比MDCD-HY有更好的分辨率,而在高波数段能提供和MDCD-HY相似的耗散来抑制数值振荡,具有较好的鲁棒性。
|
图 13 不同格式的近似耗散特性(其中(b)是(a)的局部放大) Fig.13 Comparisons of dissipation properties for various nonlinear schemes. (b) is the enlarged portion of (a) in the low to medium wavenumber range |
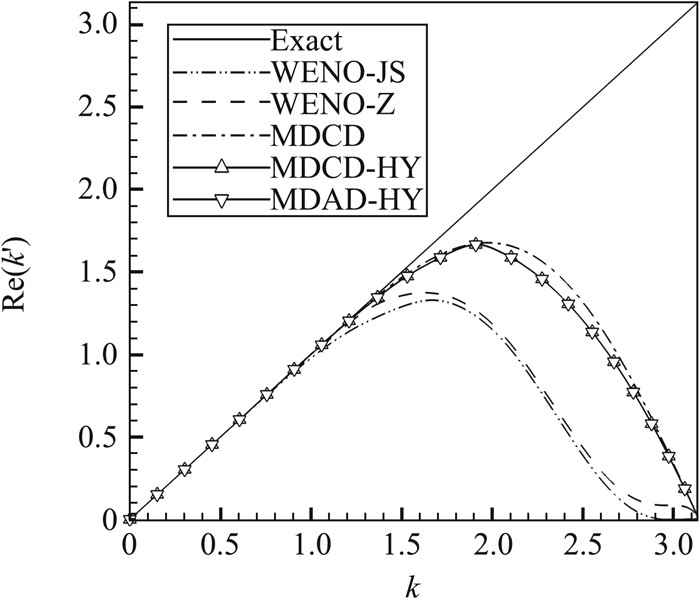
图 14为不同格式的近似色散特性对比,可以看到MDAD-HY和MDCD-HY的色散特性非常接近,在高波数段稍差于MDCD,但远好于WENO-JS和WENO-Z。
|
图 14 不同格式的近似色散特性 Fig.14 Comparisons of dispersion properties for various nonlinear schemes |
前面我们以线性波动方程为例介绍了MDCD和MDAD格式,这些算法很容易推广到Euler方程和N-S方程。具体方案是:采用特征分解[29]的方法计算无黏数值通量,尺度识别器和间断探测器都作用于特征分解后的局部特征通量。更多细节可以参考文献[22, 30]。而黏性通量采用文献[31]中的方法进行计算。时间积分采用低存储的四阶龙格-库塔格式[32],也可以采用常见的隐式格式。
MDCD格式自提出以来,得到了持续的发展和广泛的应用,而MDAD格式及其对应的混合格式MDCD-HY最近才被提出。因此在本节中,对于MDCD格式我们主要介绍其发展和应用,而对于MDAD格式,我们主要介绍其在求解一些标准算例中的表现。
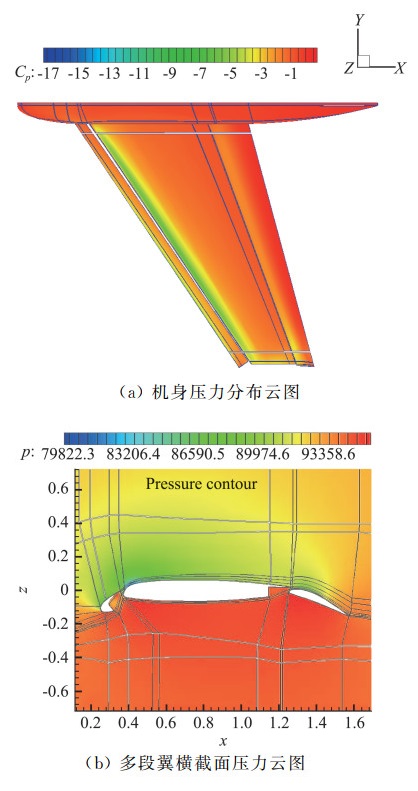
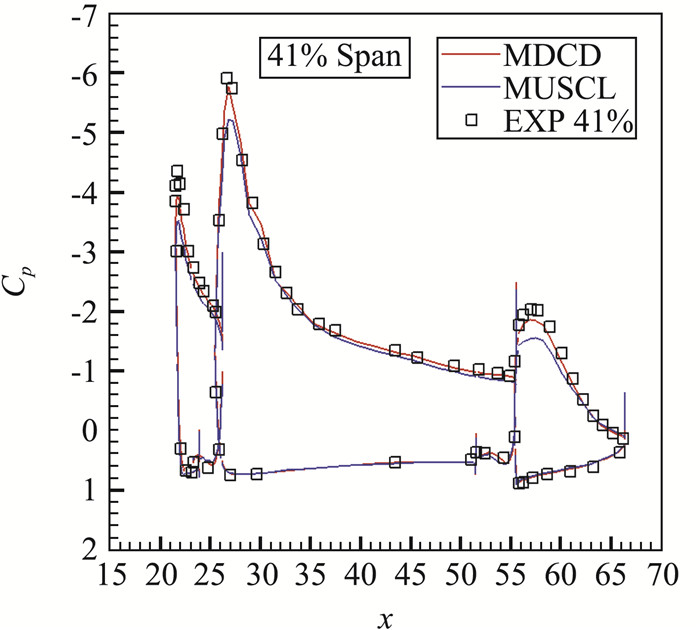
4.1 MDCD格式的发展及应用MDCD格式[22]自提出以来,得到了一定的发展和应用。原始MDCD格式是四阶精度的,Sun等[24]研究了六阶精度的MDCD格式,并初步研究了耗散控制问题。Wang等[33]将MDCD格式推广到有限体积格式,通过采用多块结构网格,使算法具备了模拟复杂几何外形的能力。图 15是用有限体积MDCD格式得到的AIAA CFD HiLiftPW-1多段翼模型标准算例的压力分布云图。图 16是41%翼展的压力系数分布,对比同样网格上MUSCL格式的计算结果,可以看到MDCD格式预测的压力分布更接近实验结果。
|
图 15 多段翼算例压力分布 Fig.15 The pressure distribution of a multi segment wing |
|
图 16 41%翼展压力系数分布 Fig.16 The pressure coefficient distribution of the 41% span |
文献[34-35]将MDCD格式发展到求解多介质复杂流动,并研究了激波与多物质界面作用产生的界面不稳定性和湍流混合问题。图 17是激波与氦气泡作用后,界面失稳的形态。

|
图 17 激波与氦气泡作用后的界面不稳定性 Fig.17 The interface instability due to the interaction between a helium bubble and a shock wave |
此外,Li等[36]、Chen等[37]利用MDCD格式耗散可调的特点,研究了MDCD格式的耗散对隐式大涡模拟的影响。Jiang等[38]把MDCD格式与SIMPLE算法相结合,将MDCD格式推广到求解不可压缩流动,显著提高了算法的分辨率。Duan等[39-40]把MDCD格式应用于高超声速边界层粗糙元诱发转捩问题的直接数值模拟,Jiang等[41]把MDCD格式应用于低压涡轮分离诱导转捩的预测,Yang等[42]把MDCD格式应用于基于涡流发生器的流动控制研究。这些应用充分说明了MDCD格式解决实际科学与工程问题的能力。
4.2 MDAD格式算例测试MDAD格式是MDCD格式的进一步发展,本节通过典型算例说明MDAD格式具有比采用传统耗散控制方法的MDCD格式具有更好的性能。由于篇幅的限制,我们只介绍二维无黏和黏性流动两个算例,更多的测试算例请参见文献[25]。
4.2.1 双马赫反射问题考虑文献[43]中提到的双马赫反射问题作为二维验证算例。该算例的控制方程为二维Euler方程。一个马赫数为10、与x轴夹角为60°的激波向右移动,并与下壁面发生反射。初始条件如下:
| $ (\rho, u, v, p)=\left\{\begin{array}{l} (1.4,0,0,1.0) \\ \quad \quad \quad \quad \ \quad, \quad x>x_{0}+\sqrt{3} / 3 y \\ (8.0,7.1447,-4.125,116.5) \\ \quad \quad \quad \quad \ \quad, \quad \text { otherwise } \end{array}\right. $ |
其中x0=1/6,计算域为(x, y)∈[0, 4]×[0, 1]。边界条件方面,在下边界,为了使激波附着在壁面前缘,x∈[0, x0]段采用激波后的参数,而x∈[x0, 4]段为滑移壁面。入口和出口分别采用来流和出流边界条件。上边界采用精确的波前波后参数,并随着激波的移动而变化。
图 18展现了计算时间t=0.18时不同格式的密度等值线,网络量采用800×200,库朗数Nc=0.3。可以看到,WENO-JS、WENO-Z、MDCD-HY和MDAD-HY均能很好地捕捉到流场结构,包括马赫杆和壁面射流。但是,MDAD-HY在第二个三波点附近的涡结构明显更加细致,对小尺度结构捕捉更好。这说明相比于其他三种格式,MDAD-HY格式有着更高的分辨率。
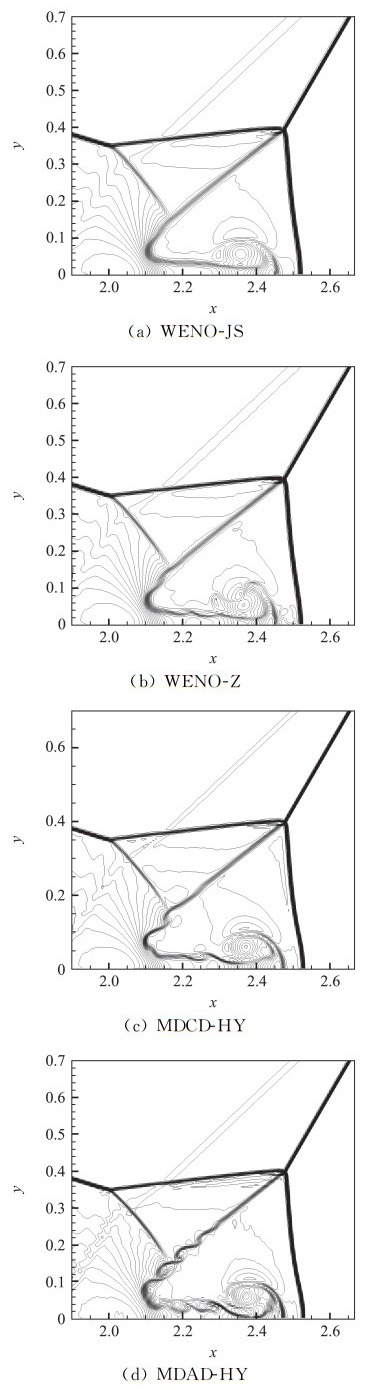
|
图 18 双马赫反射算例t=0.18时的密度等值线(50等分) Fig.18 Density contours for the double Mach reflection problem at t=0.18. Contour levels are equally spaced. |
为了研究不同格式在二维N-S方程中的效果,可以考察带有黏性的弱激波与等熵涡的相互作用问题[44]。该算例的计算域为[0, 2L0]×[0, 2L0],其中参考长度L0=1.0。一个静止的平面激波位于x=1.0,波前来流参数为ρ0=1.0,p0=1/γ,预设的激波前后压差为Δp/p0=0.4,对应的激波强度为M0=1.1588,其余的流场参数由Rankine-Hugoniot关系确定。雷诺数Re=5000,它的参考长度为L0,参考密度和参考速度均为来流参数。初始状态下,一个孤立的等熵涡被叠加在来流中,涡中心位于(x0, y0)=(0.5, 1.0),它表现为速度(u, v)和温度T=γp/ρ的扰动,而熵S=p/ργ为常数。
| $ (\delta u,\delta v) = \frac{{{U_c}}}{{{R_c}}}{{\rm{e}}^{0.5\left( {1 - \frac{{{r^2}}}{{R_c^2}}} \right)}}( - \bar y,\bar x) $ |
| $ \delta T = - \frac{{\gamma - 1}}{2}U_c^2{{\rm{e}}^{1 - \frac{{{r^2}}}{{R_c^2}}}} $ |
其中Rc=0.075,Uc=0.25,而
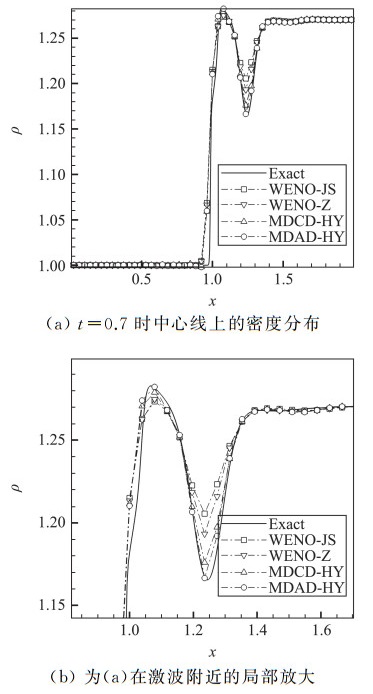
|
图 19 弱激波等熵涡相互作用算例 Fig.19 The weak shock/vortex interaction problem |
本文综述了我们在有限差分格式的色散优化和耗散控制等方面的工作。相应的计算格式可以计算无激波的光滑解,也可以作为非线性激波捕捉格式(如WENO格式)或者混合格式的线性部分。
在理论上,我们得到了半离散格式色散、耗散独立的充分条件,使色散优化和耗散控制不相互干扰,为格式性能优化打下了基础。进一步的分析表明,即使对于全离散格式,上述充分条件也可以保证色散和耗散近似独立。
以此为基础,我们得到了色散最小、耗散可控的MDCD格式,该格式的优良性能已经在一系列应用中得到了验证,并被推广到有限体积方法,以及求解多介质流动、不可压流动等。MDCD格式的主要缺点在于耗散控制。无论是采用试错方法还是基于色散、耗散条件确定通用耗散参数,得到的格式在耗散特性方面仍有很大的改进空间。
为了解决耗散控制问题,我们提出了将数值耗散与数值解的尺度相关联的思路。为此,我们首先提出了一种基于数值通量模板点上导数的尺度识别器,用于判断流场局部的等效无量纲波数。然后通过色散耗散条件[23],设计出耗散参数与等效无量纲波数之间的关系,从而实现耗散参数的自适应调节,提出了色散最小、耗散自适应的MDAD格式。
我们通过所发展的格式与WENO格式相混合的方法,使MDCD和MDAD格式在能够高精度、高分辨率的求解光滑流动的同时,具有鲁棒的激波捕捉能力。我们发现,通过在混合格式的激波探测器中,引入基于尺度识别器的修正,可以进一步提高混合格式的性能。
由于MDCD格式的性能已经得到了充分的验证,且MDAD格式在多个标准算例中都表现出优于MDCD格式的性能,可以预见,MDAD格式及其对应的混合格式MDAD-HY在求解含激波的复杂多尺度流动中也有很好的应用前景。
致谢: 李万爱、潘建华、曾卫刚、黄文锋、李星辉、张宏杰、李俊涛、张润东等参与了计算程序开发、验证、应用等工作,特致感谢。
| [1] |
LIU X D, OSHER S, CHAN T. Weighted essentially non-oscillatory schemes[J]. Journal of Computational Physics, 1994, 115: 200-212. DOI:10.1006/jcph.1994.1187 |
| [2] |
JIANG G S, SHU C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126: 202-228. DOI:10.1006/jcph.1996.0130 |
| [3] |
JOHNSEN E, LARSSON J, BHAGATWALA A V, et al. Assessment of high-resolution methods for numerical simulations of compressible turbulence with shock waves[J]. Journal of Computational Physics, 2010, 229(4): 1213-1237. DOI:10.1016/j.jcp.2009.10.028 |
| [4] |
HENRICK A K, ASLAM T A, POWERS J M. Mapped weighted essentially non-oscillatory schemes: achieving optimal order near critical points[J]. Journal of Computational Physics, 207(2): 542-567. DOI:10.1016/j.jcp.2005.01.023 |
| [5] |
BORGES R, CARMONA M, COSTA B, et al. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws[J]. Journal of Computational Physics, 2008, 227: 3191-3211. DOI:10.1016/j.jcp.2007.11.038 |
| [6] |
刘朋欣, 李沁, 张涵信. 基于映射函数的中心型三阶格式[J]. 空气动力学学报, 2017, 35(1): 71-77. LIU P X, LI Q, ZHANG H X. A kind of third order central scheme based on mapping functions[J]. Acta Aerodynamics Sinica, 2017, 35(1): 71-77. DOI:10.7638/kqdlxxb-2015.0172 (in Chinese) |
| [7] |
TAYLOR E M, WU M, MARTIN M P. Optimization of nonlinear error for weighted essentially non-oscillatory methods in direct numerical simulations of compressible turbulence[J]. Journal of Computational Physics, 2007, 223: 384-397. DOI:10.1016/j.jcp.2006.09.010 |
| [8] |
MARTIN M P, TAYLOR E M, WU M, et al. A bandwidth-optimized WENO scheme for effective direct numerical simulation of compressible turbulence[J]. Journal of Computational Physics, 2006, 220: 270-289. DOI:10.1016/j.jcp.2006.05.009 |
| [9] |
HU X Y, WANG Q, ADAMS N A. An adaptive central-upwind weighted essentially non-oscillatory scheme[J]. Journal of Computational Physics, 2010, 229: 8952-8965. DOI:10.1016/j.jcp.2010.08.019 |
| [10] |
FU L, HU X Y, ADAMS N A. A family of high-order targeted ENO schemes for compressible-fluid simulations[J]. Journal of Computational Physics, 2016, 305: 333-359. DOI:10.1016/j.jcp.2015.10.037 |
| [11] |
ADAMS N A, SHARIFF K. A high-resolution hybrid compact-ENO scheme for shock/turbulence interaction problems[J]. Journal of Computational Physics, 1996, 127: 27-51. DOI:10.1006/jcph.1996.0156 |
| [12] |
PIROZZOLI S. Conservative hybrid compact-WENO schemes for shock-turbulence interaction[J]. Journal of Computational Physics, 2002, 178: 81-117. DOI:10.1006/jcph.2002.7021 |
| [13] |
REN Y X, LIU M, ZHANG H X. A characteristic-wise compact WENO scheme for solving hyperbolic conservation laws[J]. Journal of Computational Physics, 2003, 192: 365-386. DOI:10.1016/j.jcp.2003.07.006 |
| [14] |
武从海, 赵宁, 田琳琳. 一种改进的紧致WENO混合格式[J]. 空气动力学学报, 2013, 31(4): 477-481. WU C H, ZHAO N, TIAN L L. An improved hybrid compact-WENO scheme[J]. Acta Aerodynamics Sinica, 2013, 31(4): 477-481. (in Chinese) |
| [15] |
HARTEN A. The artificial compression method for computation of shocks and contact discontinuities. Ⅲ. Self-adjusting hybrid schemes[J]. Mathematics of Computation, 1978, 32(142): 363-389. |
| [16] |
JAMESON A, SCHMIDT W, TURKEL E. Numerical solution of the Euler equations by finite volume methods using Runge-Kutta time stepping schemes[C]//Proceeding of the 14th AIAA Fluid and Plasma Dynamics Conference, 1981.
|
| [17] |
SJOGREEN B, YEE H C. Multiresolution wavelet based adaptive numerical dissipation control for shock-turbulence computations[J]. Research Institute for Advanced Computer Science, 2001, 1: 1-43. |
| [18] |
HILL D J, PULLIN D I. Hybrid tuned center-difference-WENO method for large eddy simulations in the presence of strong shocks[J]. Journal of Computational Physics, 2004, 194(2): 435-450. DOI:10.1016/j.jcp.2003.07.032 |
| [19] |
VISBAL M, GAITONDE D. Shock capturing using compact-differencing-based methods[C]//Proceeding of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, 2005.
|
| [20] |
MOVAHED P, JOHNSEN E. A solution-adaptive method for efficient compressible multifluid simulations with application to the Richtmyer-Meshkov instability[J]. Journal of Computational Physics, 2013, 239: 166-186. DOI:10.1016/j.jcp.2013.01.016 |
| [21] |
ZHAO G Y, SUN M B, PIROZZOLI S. On shock sensors for hybrid compact/WENO schemes[J]. Computers and Fluids, 2020, 199: 104439. DOI:10.1016/j.compfluid.2020.104439 |
| [22] |
SUN Z S, REN Y X, LARRICQ C, et al. A class of finite difference scheme with low dispersion and controllable dissipation for DNS of compressible turbulence[J]. Journal of Computational Physics, 2011, 230: 4616-4635. DOI:10.1016/j.jcp.2011.02.038 |
| [23] |
HU X Y, ADAMS N A. Dispersion-dissipation condition for finite difference schemes[EB/OL]. https://www.researchgate.net/publication/224812783, 2012-04-23/2020-08-18.
|
| [24] |
SUN Z S, LUO L, REN Y X, et al. A sixth order hybrid finite difference scheme based on the minimized dispersion and controllable dissipation technique[J]. Journal of Computational Physics, 2014, 270: 238-254. DOI:10.1016/j.jcp.2014.03.052 |
| [25] |
LI Y H, CHEN C W, REN Y X. A class of high-order finite difference schemes with minimized dispersion and adaptive dissipation for solving compressible flows[J]. Submitted to Journal of Computational Physics. |
| [26] |
PIROZZOLI S. On the spectral properties of shock-capturing schemes[J]. Journal of Computational Physics, 2006, 219: 489-497. DOI:10.1016/j.jcp.2006.07.009 |
| [27] |
HU F Q, HUSSAINI M Y, MANTHEY J L. Low-dissipation and low-dispersion Runge-Kutta schemes for computational acoustics[J]. Journal of Computational Physics, 1996, 124: 177-191. DOI:10.1006/jcph.1996.0052 |
| [28] |
LI L, YU C P, CHEN Z, et al. Resolution-optimised nonlinear scheme for secondary derivatives[J]. International Journal of Computational Fluid Dynamics, 2016, 30(2): 107-119. DOI:10.1080/10618562.2016.1164849 |
| [29] |
SHU C W. High order ENO and WENO schemes for computational fluid dynamics[M]. Berlin: Springer, 1999: 439-582.
|
| [30] |
SUN Z S, REN Y X. The development of the characteristic-wise hybrid compact-WENO scheme for solving the Euler and Navier-Stokes equations[J]. Computational Fluid Dynamics Review 2010, 2010, 1: 279-297. |
| [31] |
SHEN Y Q, YANG B Y, ZHA G C. Implicit WENO scheme and high order viscous formulas for compressible flows[C]//Proceeding of the 25th AIAA Applied Aerodynamics Conference, 2007.
|
| [32] |
SHU C W. Advanced numerical approximation of nonlinear hyperbolic equations[M]. Berlin: Springer, 2006: 325-432.
|
| [33] |
WANG Q J, REN Y X, SUN Z S, et al. Low dispersion finite volume scheme based on reconstruction with minimized dispersion and controllable dissipation[J]. Science China Physics, Mechanics & Astronomy, 2013, 56: 423-431. DOI:10.1007/s11433-012-4987-z |
| [34] |
WANG Q J, DEITERDING R, PAN J H, et al. Consistent high resolution interface-capturing finite volume method for compressible multi-material flows[J]. Computers and Fluids, 2020, 202: 104518. DOI:10.1016/j.compfluid.2020.104518 |
| [35] |
ZENG W G, PAN J H, SUN Y T, et al. Turbulent mixing and energy transfer of reshocked heavy gas curtain[J]. Physics of Fluids, 2018, 30(6): 064106. DOI:10.1063/1.5032275 |
| [36] |
LI Z, ZHANG Y, CHEN H. A low dissipation numerical scheme for implicit large eddy simulation[J]. Computers & Fluids, 2015, 117: 233-246. |
| [37] |
CHEN H, LI Z, ZHANG Y. U or V shape: dissipation effects on cylinder flow implicit large-eddy simulation[J]. AIAA Journal, 2017, 55(2): 459-473. DOI:10.2514/1.J055278 |
| [38] |
JIANG S, FU S. Modifications to the SIMPLE algorithm with the MDCD approach for incompressible flow simulation[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2018. |
| [39] |
DUAN Z W, XIAO Z X, FU S. Direct numerical simulation of hypersonic transition induced by an isolated cylindrical roughness element[J]. SCIENCE CHINA Physics, Mechanics & Astronomy, 2014, 57(12): 2330-2345. |
| [40] |
段志伟, 肖志祥. 粗糙元诱导的高超声速边界层转捩[J]. 航空学报, 2016, 37(8): 2454-2463. DUAN Z W, XIAO Z X. Roughness element induced hypersonic boundary layer transition[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2454-2463. (in Chinese) |
| [41] |
JIANG S Y, FU S. Numerical investigation of separation-induced transition in a low-pressure turbine cascade in a low-disturbance environment[J]. SCIENCE CHINA Physics, Mechanics & Astronomy, 2020, 63(6): 1-17. |
| [42] |
YANG J, ZHANG Y, CHEN H, et al. Unsteady flow control of a plane diffuser based on a Karman-vortex generator[J]. AIP Advances, 2020, 10(5): 055314. DOI:10.1063/5.0004559 |
| [43] |
WOODWARD P, COLELLA P. The numerical simulation of two-dimensional fluid flow with strong shocks[J]. Journal of Computational Physics, 1984, 54: 115-173. DOI:10.1016/0021-9991(84)90142-6 |
| [44] |
TENAUD C, GARNIER E, SAGAUT P. Evaluation of some high-order shock capturing schemes for direct numerical simulation of unsteady two-dimensional free flows[J]. International Journal for Numerical Methods in Fluids, 2000, 33: 249-278. DOI:10.1002/(SICI)1097-0363(20000530)33:2<249::AID-FLD17>3.0.CO;2-Z |
 2021, Vol. 39
2021, Vol. 39


