0 引言

可压缩流体的运动变化规律是空气动力学的主要研究内容。伴随高马赫数流动产生的激波等不连续现象使得可压缩流动的流场结构更为复杂，并同时包含连续与间断解，给理论和实验研究带来很多本质性的困难。在过去的数十年中，由于计算机硬件的飞速发展，以及相关领域实际应用的巨大需求，计算流体力学作为最活跃的科学研究领域之一，取得了重大进展，并已成为空气动力学非常重要的研究手段。

针对描述可压缩流体的欧拉方程，至今已提出了各种数值算法。其中，以具有严格守恒特性的Godunov格式^[1]为基础开发的各类高阶守恒格式已成为求解可压缩流体运动的主流算法。基于Godunov格式的高阶守恒格式一般包括重构和演化两个重要步骤。其中，演化是根据重构得到的离散变量，利用控制方程的物理性质计算相应时间步长内的数值通量，进而预报下一时刻的物理量变化。关于欧拉方程及其黏性扩展情形下的数值通量计算，可参阅有关专著及论文^[2-5]。本文集中讨论如何进行物理变量的空间重构。

作为构造高阶Godunov方法的关键，空间重构一直是关注的焦点。至今已提出了针对不同空间离散框架的各种重构方法^[6]，包括有限体积或有限差分格式^[7-19]、紧致格式^[20-22]等基于单个单元自由度的方法，也有间断伽列金方法^[23-24]、间断伽列金/有限体积混合方法^[25-27]、通量重构方法^[28-30]、多矩有限体积方法^[31-34]等包含多个局地自由度的高精度方法，并已被用于求解各类实际问题。这些方法通常采用高阶多项式进行重构，在用于计算解较为光滑的问题时，能够得到较高收敛率和较精确的数值结果。然而，当求解的物理问题含有激波或多相复杂介质界面等强间断时，必须使用非线性限制映射或限制器来抑制虚假的数值振荡。其中，使用WENO(weighted essentially non-oscillatory) ^[12-13]思想构造的高分辨格式既可有效地抑制数值振荡又能对光滑解获得较高的收敛精度，在可压缩流体的数值模拟中得到广泛应用。现有算法中设计非线性限制器的基本做法是，在解较光滑的区域尽量保持高阶多项式的性质，而在解出现间断处采用更平直或较低阶的重构函数。这类做法通常在抑制数值振荡与控制数值耗散之间，在计算鲁棒性和求解精度等方面无法兼顾，很难对光滑和间断解同时给出令人满意的计算结果。在实际应用中主要表现为：(1)存在显著的数值耗散，会抹平接触间断和较小尺度的流场结构；(2)多数非线性权函数无法使重构函数在光滑情形下完全恢复到原来的常系数高阶多项式插值函数，且依赖于一些人为确定的参数，给实际应用带来不便。作为相关领域长期以来一个未能很好解决的问题，如何构造能同时精确捕捉光滑和间断解的高保真空间重构方法，一直是可压缩流体数值方法研究的热点。

为了更好地模拟包含间断解的可压缩复杂流动，我们近年提出了以减小空间重构在网格单元边界上的变差为原则设计数值格式的思想，即，BVD(Boundary Variation Diminishing)原理。根据此原理，我们发展了一类可用于求解单相和多相可压缩流体的高保真数值算法^[35-46]。这些算法能有效克服其他现有高分辨格式存在的问题，可以同时精确捕捉光滑和间断解。各种标准算例结果表明，BVD格式在模拟各种具有强间断的可压缩流体运动方面，与其他的现有格式相比具有明显的优势。利用BVD原理进行空间重构可望成为构建可压缩流体新型高保真数值方法的有效途径。

本文对BVD格式研发的已有工作做一个简要综述，内容包括BVD的基本思想介绍、几个具有实用意义BVD算法、有代表性的标准算例结果，以及简短总结和展望。

1 BVD的基本思想 1.1 Godunov方法概要

我们考虑双曲标量守恒律:

$ \frac{{\partial u}}{{\partial t}} = - \frac{{\partial f(u)}}{{\partial x}} $

(1)

式中，u(x, t) 为守恒变量，f(u)为通量函数，且特征速度 $\alpha = \frac{{\partial f}}{{\partial u}}$ 为实数。

采用有限体积方法对其进行离散。离散网格单元${\mathit{\Omega }_i}: = \left[ {{x_{i - \frac{1}{2}}}, {x_{i + \frac{1}{2}}}} \right]$内守恒变量的单元体积分平均值定义为:

$ \bar{u}_{i}(t)=\frac{1}{\Delta x_{i}} \int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} u(x, t) \mathrm{d} x $

这里$\Delta {x_i} = {x_{i + \frac{1}{2}}} - {x_{i - \frac{1}{2}}}$为网格间距。将守恒方程(1)对网格单元Ω_i进行体积分可得到以下有限体积方法的一般形式:

$ \frac{\mathrm{d} \bar{u}_{i}}{\mathrm{~d} t}=-\frac{1}{\Delta x_{i}}\left(\hat{f}(u)_{i+\frac{1}{2}}-\hat{f}(u)_{i-\frac{1}{2}}\right) $

(2)

如何计算(2)中的数值通量$\hat f{\left( u \right)_{i + \frac{1}{2}}}$成为有限体积方法的核心问题。

求解双曲守恒律的有限体积方法可追溯到早期的一阶Godunov方法^[1]。现在广泛采用的高阶Godunov方法通过以下两个主要步骤计算数值通量$\hat f{\left( u \right)_{i + \frac{1}{2}}}$。

(Ⅰ) 空间重构。利用定义在Ω_i及其相邻单元构成的模板上的积分平均值构造表示相关物理量空间分布的重构函数${{\tilde u}_i}\left( x \right)$，并获得网格单元边界${{x_{i + \frac{1}{2}}}}$上的物理变量值。针对双曲型方程，为使数值格式具有迎风性质，通常采用偏心模板分别计算单元边界左侧和右侧的值，$u_{i + \frac{1}{2}}^L = {{\tilde u}_i}\left( {{x_{i + \frac{1}{2}}}} \right){\rm{和}}u_{i + \frac{1}{2}}^R = {{\tilde u}_{i + 1}}\left( {{x_{i + \frac{1}{2}}}} \right)$。一般来讲，$u_{i + \frac{1}{2}}^L{\rm{和}}u_{i + \frac{1}{2}}^R$不相等。我们将其差的绝对值定义为边界变差，$B{V_{i + \frac{1}{2}}} = \left| {u_{i + \frac{1}{2}}^R - u_{i + \frac{1}{2}}^L} \right|$。

(Ⅱ) 近似黎曼算子。利用空间重构(Ⅰ)得到的网格单元边界${{x_{i + \frac{1}{2}}}}$左右两侧的值$u_{i + \frac{1}{2}}^L{\rm{和}}u_{i + \frac{1}{2}}^R$计算通过该单元边界的数值通量$\hat f{\left( u \right)_{i + \frac{1}{2}}}$。针对双曲守恒律的近似黎曼算子基于波或流的传播方向采用迎风型格式，其代表形式可写为:

$ \begin{aligned} \hat{f}(u)_{i+\frac{1}{2}}=& \frac{1}{2}\left(f\left(u_{i+\frac{1}{2}}^{L}\right)+f\left(u_{i+\frac{1}{2}}^{R}\right)\right)-\\ & \frac{1}{2}\left|\alpha_{i+\frac{1}{2}}\right|\left(u_{i+\frac{1}{2}}^{R}-u_{i+\frac{1}{2}}^{L}\right) \end{aligned} $

(3)

通过以上步骤(Ⅰ)和(Ⅱ)获得边界数值通量后，一般可以通过线方法，采用常微分方程的数值解法对半离散方程(2)进行时间积分, 得到下一时刻的数值解。

至今的高分辨数值方法研究，基本集中于开发具备更好数值性能的空间重构(Ⅰ)和黎曼算子(Ⅱ)。

1.2 BVD方法的基本思想

从近似黎曼算子的基本形式(3)可以看出，数值通量一般由中心格式(右端第一项)和数值耗散/数值黏性(右端第二项)两部分组成。如果在构造数值格式时，能够减小数值耗散项，将有效降低格式的数值耗散，从而改善计算结果。

由数值耗散项的表达式不难看出，减小数值耗散可从两方面入手，即:

(A) 减小代表耗散系数的特征速度${\alpha _{i + \frac{1}{2}}}$；

(B) 减小空间重构得到的边界变差值

$ B{V_{i + \frac{1}{2}}} = \left| {u_{i + \frac{1}{2}}^R - u_{i + \frac{1}{2}}^L} \right|。$

各类黎曼算子的研究开发在一定意义上可以看作是为实现目标(A)所做的努力。围绕在保证计算稳定的条件下，如何控制减小数值耗散系数，提出了各类近似黎曼算子。这方面的研究可参阅相关专著^[2]。

关于空间重构，在至今的研究工作中并没有把边界变差值$B{V_{i + \frac{1}{2}}}$最小化作为一个明确的目标或指导方针来设计格式。现有的数值方法基本局限于多项式插值以及如何设计为避免数值振荡的非线性限制映射方面，其代表性的工作包括TVD(total variation diminishing)或保单调类的限制器^[7-9]和(W)ENO类限制器^[10-19]。众所周知，这类方法通常都会产生较大的数值耗散。

为了在空间重构过程中有效地减小数值耗散，我们提出以下设计空间重构格式的一般性原理。

BVD原理：空间重构应该选用能使边界变差值$B{V_{i + \frac{1}{2}}}$最小化的许容函数。

这里所指的许容函数可以广义地包括所有可以用于计算$u_{i + \frac{1}{2}}^L{\rm{和}}u_{i + \frac{1}{2}}^R\left( {u_{i + \frac{1}{2}}^L \ne u_{i + \frac{1}{2}}^R} \right)$的偏心重构函数。

如果在开发空间重构算法时能有意识地根据BVD原理，尽可能地减小边界变差值，则可以有效抑制格式的数值耗散，改进数值计算结果。我们注意到，文献[47]通过边界变差最小化的变分约束关系构造了紧致有限体积方法。

2 BVD混合格式的构建

基于BVD原理，我们提出了构建高保真数值格式的基本框架，并发展了一类基于BVD原理的混合格式。BVD格式主要包括BVD许容重构函数集和BVD选择算法两个部分。

2.1 BVD许容重构函数集

流体力学问题解的空间分布极为复杂，既包括各种尺度的涡和波动等相对光滑的流场结构，也包括激波、接触间断、不同流体间的物质界面等不连续结构。很难用一类插值函数准确描述各种不同的流场结构。在以往的研究中，各种重构函数和重构方法被相继开发出来，并用于针对不同应用问题的高分辨格式。我们把一些有代表性的重构函数分为以下三类BVD许容函数。

2.1.1 第一类：常系数多项式

这类重构函数用于逼近光滑解。包括各阶泰勒多项式、紧致格式^[48-49]以及各种频散/耗散优化格式^[50-54]等。作为例子，我们具体给出针对网格单元Ω_i的四阶多项式:

$ u_i^{{P_4}}(x) = \sum\limits_{k = 0}^4 {{c_k}} {(x - {x_i})^k} $

(4)

其中系数c_k(k=0, 1, …, 4)通过以下约束条件求出:

$ \frac{1}{{\Delta x}}\int_{{x_{j - \frac{1}{2}}}}^{{x_{j + \frac{1}{2}}}} {\tilde u_i^{{P_4}}(x)} {\rm{d}}x = {\bar u_j},\quad (j = i,i \pm 1,i \pm 2) $

(5)

为书写简便，我们在此采用等网格距，Δx_i=Δx。由此可以直接得到:

$ \begin{aligned} u_{i+\frac{1}{2}}^{L}=& \widetilde{u}_{i}^{P_{4}}\left(x_{i+\frac{1}{2}}\right)=\frac{1}{60}\left(2 \bar{u}_{i-2}-13 \bar{u}_{i-1}+\right.\\ &\left.47 \bar{u}_{i}+27 \bar{u}_{i+1}-3 \bar{u}_{i+2}\right) \\ u_{i-\frac{1}{2}}^{R}=& \widetilde{u}_{i}^{P_{4}}\left(x_{i-\frac{1}{2}}\right)=\frac{1}{60}\left(-3 \bar{u}_{i-2}+27 \bar{u}_{i-1}+\right.\\ &\left.47 \bar{u}_{i}-13 \bar{u}_{i+1}+2 \bar{u}_{i+2}\right) \end{aligned} $

(6)

2.1.2 第二类：非线性系数多项式

在高分辨激波捕捉格式的发展过程中，为避免高阶多项式在间断解附近出现的非物理振荡，提出了许多非线性限制投影算法。例如，采用TVD限制器的2阶MUSCL格式^[7]，可将网格单元边界左右两侧的变量值写为：

$ \begin{array}{l} u_{i+\frac{1}{2}}^{L}=\widetilde{u}_{i}^{M}\left(x_{i+\frac{1}{2}}\right)=\bar{u}_{i}+\frac{1}{2} \varphi\left(r_{i+\frac{1}{2}}^{L}\right)\left(\bar{u}_{i+1}-\bar{u}_{i}\right) \\ u_{i-\frac{1}{2}}^{R}=\tilde{u}_{i}^{M}\left(x_{i-\frac{1}{2}}\right)=\bar{u}_{i}-\frac{1}{2} \varphi\left(r_{i-\frac{1}{2}}^{R}\right)\left(\bar{u}_{i}-\bar{u}_{i-1}\right) \end{array} $

(7)

其中，φ(r)为空间重构的梯度限制器。$r_{i + \frac{1}{2}}^L = \frac{{{{\bar u}_i} - {{\bar u}_{i - 1}}}}{{{{\bar u}_{i + 1}} - {{\bar u}_i}}}, r_{i - \frac{1}{2}}^R = \frac{{{{\bar u}_{i + 1}} - {{\bar u}_i}}}{{{{\bar u}_i} - {{\bar u}_{i - 1}}}}$。

如果采用WENO类算法，则可将插值函数写成非线性加权系数多项式的形式。以下给出5阶WENO格式计算网格单元边界左右两侧变量值的算式。

$ \begin{array}{l} u_{i+\frac{1}{2}}^{L}=\widetilde{u}_{i}^{W_{4}}\left(x_{i+\frac{1}{2}}\right)=\omega_{0} u_{i+\frac{1}{2}}^{(0)}+\omega_{1} u_{i+\frac{1}{2}}^{(1)}+\omega_{2} u_{i+\frac{1}{2}}^{(2)} \\ u_{i-\frac{1}{2}}^{R}=\widetilde{u}_{i}^{W_{4}}\left(x_{i-\frac{1}{2}}\right)=\omega_{0} u_{i-\frac{1}{2}}^{(0)}+\omega_{1} u_{i-\frac{1}{2}}^{(1)}+\omega_{2} u_{i-\frac{1}{2}}^{(2)} \end{array} $

(8)

其中,

$ \left\{\begin{array}{l} u_{i \pm \frac{1}{2}}^{(0)}=\frac{1}{3} \bar{u}_{i \mp 2}-\frac{7}{6} \bar{u}_{i \mp 1}+\frac{11}{6} \bar{u}_{i} \\ u_{i \pm \frac{1}{2}}^{(1)}=-\frac{1}{6} \bar{u}_{i \mp 1}+\frac{5}{6} \bar{u}_{i}+\frac{1}{3} \bar{u}_{i \pm 1} \\ u_{i \pm \frac{1}{2}}^{(2)}=\frac{1}{3} \bar{u}_{i}+\frac{5}{6} \bar{u}_{i \pm 1}-\frac{1}{6} \bar{u}_{i \pm 2} \end{array}\right. $

关于非线性权重系数ω_j(j=0, 1, 2)的计算方法，至今已提出了各种方案^{[12-19, 24]}。

2.1.3 第三类: 非多项式类插值函数

采用某些具有单调特性的非多项式类插值函数能够避免空间重构中的数值振荡。例如，采用双曲函数、有理函数或对数函数^[55-57]可以有效地抑制数值振荡。文献[58-61]使用双曲正切函数拟合跃阶型间断，并发展了一类可用于捕捉移动界面的代数VOF(Volume of Fluid)方法^[62]，称为THINC(Tangent of Hyperbola for INterface Capturing)方法。和其他Sigmoid函数一样，THINC重构函数具有严格的单调性，并能很好地模拟激波、接触间断以及多相流中的物质界面等具有跃阶分布的变量。

已知u_i-1、u_i、u_i+1，定义在网格单元Ω_i上的THINC重构函数可表示成以下形式：

$ \widetilde{u}_{i}^{T}(x)=\bar{u}_{\min }+\frac{\Delta u}{2}\left\{1+\theta \tanh \left[\beta\left(\frac{x-x_{i-\frac{1}{2}}}{\Delta x_{i}}-\tilde{x}_{i}\right)\right]\right\} $

这里，u_min=min(u_i-1, u_i+1)，Δu=max(u_i-1, u_i+1)-u_min，θ=sgn(u_i+1-u_i-1)。其中β为控制间断厚度的参数，称为陡度参数，当其取较大值时，可以精确地逼近具有台阶分布的Heaviside函数。${{\tilde x}_i}$是跃阶的中心位置，通过以下守恒限制条件确定:

$ \frac{1}{\Delta x_{i}} \int_{x_{i-} \frac{1}{2}}^{x_{i+\frac{1}{2}}} \tilde{u}_{i}^{T}(x) \mathrm{d} x=\bar{u}_{i} $

(9)

由此，可以将通过THINC重构得到的网格单元左右两端的值写为:

$ \begin{aligned} u_{i+\frac{1}{2}}^{L}=& \tilde{u}_{i}^{T}\left(x_{i+\frac{1}{2}}\right)=\bar{u}_{\min }+\frac{\Delta u}{2}\left(1+\theta \frac{\tanh (\beta)+A}{1+A \tanh (\beta)}\right) \\ & u_{i-\frac{1}{2}}^{R}=\tilde{u}_{i}^{T}\left(x_{i-\frac{1}{2}}\right)=\bar{u}_{\min }+\frac{\Delta u}{2}(1+\theta A) \end{aligned} $

(10)

这里，

$ A=\frac{1}{\tanh (\beta)}\left(\frac{B}{\cosh (\beta)}-1\right) $

$ B=e^{\theta \beta(2 C-1)} $

$C = \frac{{\bar u - {{\bar u}_{\min }} + \varepsilon }}{{\Delta u + \varepsilon }}$，其中ε为小正数。

在实际应用中，可以通过调节陡度参数β的值，使THINC重构函数适用于各类数值解分布。数值频散/耗散分析表明，如果β取值于1和1.3之间，则THINC重构可以表示一类MUSCL格式^[37]。取较大β值，则可以很好地拟合跃阶间断分布，并有效地抑制数值扩散。

对于多维情形，可将THINC重构函数表示为:

$ \begin{array}{c} \tilde{u}_{i}^{T}(x, y, z)= \\ \bar{u}_{\min }+\frac{\Delta u}{2}\left\{1+\tanh \left[\beta\left(P_{i}(x, y, z)+d_{i}\right)\right]\right\} \end{array} $

其中，P_i(x, y, z)+d_i=0为界面方程。d_i通过与式(9)类似的多维体积分约束关系计算。P_i(x, y, z)可采用高阶多项式，以更准确地描述界面的几何形状。关于多维高阶THINC重构可参阅相关文献[60-61]。

从以上三类许容函数中选取适当的候补函数构成BVD许容函数集，记为

$ \begin{array}{c} \varPi:=\left\{\tilde{u}_{i}^{(1)}(x), \cdots, \tilde{u}_{i}^{\langle\xi\rangle}(x), \cdots, \tilde{u}_{i}^{(\varXi)}(x)\right\}, \\ \xi=1,2, \cdots, \varXi \end{array} $

这里Ξ表示BVD许容函数集里所包含的候补函数的个数，通常Ξ≥2。

一般根据流场结构的主要特征以及希望改善的数值解性质选取候补函数。例如，针对以间断解为主的应用问题，可以选取非线性限制多项式(第二类)和THINC函数(第三类)构成BVD许容函数集^{[35-36, 43]}。或选取采用不同β值的THINC函数构成BVD许容函数集^[37]。针对以声场或旋涡为主的应用问题，为了充分利用高阶常系数多项式的良好性质，可以避开非线性限制多项式，只选取高阶常系数多项式(第一类)和THINC函数(第三类)构成BVD许容函数集^{[38-42, 44-46]}。研究表明，通过构造合适的BVD算法，即使不采用非线性限制多项式，也能有效地抑制数值振荡，如后叙的PnTm-BVD格式。

2.2 BVD选择算法

在选定BVD许容函数后，需要建立合理的选择算法，以确定合适的重构函数。可以根据BVD原理，设计各种能够有效减小边界变差的BVD选择算法(以下称BVD算法)。为使用方便，除单元边界${x_{i + \frac{1}{2}}}$的变差

$ \begin{array}{c} B{V_{i + \frac{1}{2}}} = \left| {u_{i + \frac{1}{2}}^R - u_{i + \frac{1}{2}}^L} \right|\\ = \left| {{{\tilde u}_{i + 1}}\left( {{x_{i + \frac{1}{2}}}} \right) - {{\tilde u}_i}\left( {{x_{i + \frac{1}{2}}}} \right)} \right| \end{array} $

之外，我们还定义单元Ω_i边界x_i-12和x_i+12的变差之和，即单元边界总变差(TBV_i)，

$ TB{V_i} = B{V_{i + \frac{1}{2}}} + B{V_{i - \frac{1}{2}}}。$

我们对各类BVD许容函数用于连续和间断分布重构时产生的BV或TBV值进行了分析及数值实验，得到以下主要结论：

(1) 对于光滑分布，采用第一类许容重构函数(常系数多项式)能够得到更小的BV或TBV值。且多项式阶数越高，边界变差值越小。与Weierstrass多项式逼近定理一致。

(2) 对于跃阶型间断解，在第二类许容重构函数(带限制器的非线性系数多项式)中，高阶格式的TBV值小于低阶格式的TBV值。数值耗散较大的格式产生较大的TBV值。与基于非线性系数多项式重构相比，采用较大β值的THINC重构可以获得更小的TBV值。

(3) 对间断进行插值时，THINC函数产生的BV只出现在空间较窄区域，而基于多项式的重构函数则会导致较宽区域内出现明显的BV。

由此，我们提出了各种选择算法。下面列举几个有较强实用意义的BVD算法。

2.2.1 BVD算法Ⅰ

BVD许容函数集包括两个候补函数，即

$ \mathit{\Pi }: = \{ \tilde u_i^{(1)}(x),\tilde u_i^{(2)}(x)\} $

其中，$\tilde u_i^{\left\langle 1 \right\rangle }\left( x \right)$可采用一个基于高阶多项式的重构函数，$\tilde u_i^{\left\langle 2 \right\rangle }\left( x \right)$可采用一个阶数较低但单调性较好的重构函数。则BVD算法Ⅰ可由以下步骤组成:

(1) 针对单元边界${x_{i + \frac{1}{2}}}$，找出$\tilde u_i^{\left\langle \xi \right\rangle }\left( x \right){\rm{和}}\tilde u_i^{\left\langle \eta \right\rangle }\left( x \right)$使得$B{V_{i + \frac{1}{2}}} = \left| {\tilde u_{i + 1}^{\left\langle \eta \right\rangle }\left( {{x_{i + \frac{1}{2}}}} \right) - \tilde u_i^{\left\langle \xi \right\rangle }\left( {{x_{i + \frac{1}{2}}}} \right)} \right|$最小。这里ξ和η分别为1或2。

(2) 针对单元边界${x_{i - \frac{1}{2}}}$，如果使$B{V_{i - \frac{1}{2}}}$最小的$\tilde u_i^{\left\langle \eta \right\rangle }\left( x \right)$和从步骤(1)得到的$\tilde u_i^{\left\langle \eta \right\rangle }\left( x \right)$相同，则，${{\tilde u}_i}\left( x \right) = \tilde u_i^{\left\langle \xi \right\rangle }\left( x \right)$，否则

$ \tilde{u}_{i}(x)=\left\{\begin{array}{ll} \tilde{u}_{i}^{\langle 1\rangle}(x), & \text { if } \quad\left(\bar{u}_{i+1}-\bar{u}_{i}\right)\left(\bar{u}_{i}-\bar{u}_{i-1}\right)<0 \\ \tilde{u}_{i}^{\langle 2\rangle}(x), & \text { otherwise } \end{array}\right. $

(3) 采用${{\tilde u}_i}\left( x \right)$作为网格单元Ω_i最终的重构函数，并用其计算网格单元左右边界的值。

$ \left\{ {\begin{array}{*{20}{l}} {u_{i + \frac{1}{2}}^L = {{\tilde u}_i}({x_{i + \frac{1}{2}}})}\\ {u_{i - \frac{1}{2}}^R = {{\tilde u}_i}({x_{i - \frac{1}{2}}})} \end{array}} \right. $

文献[35]分别采用WENO多项式(8)和THINC函数(10)作为候补函数，即$\tilde u_i^{\left\langle 1 \right\rangle }\left( x \right) = \tilde u_i^{W4}\left( x \right), \tilde u_i^{\left\langle 2 \right\rangle }\left( x \right) = \tilde u_i^T\left( x \right)$，所得到的WENO-THINC-BVD格式能有效地改善原有的WENO格式的数值耗散，很好地捕捉间断结构。

2.2.2 BVD算法Ⅱ

采用包含两个候补函数的BVD许容函数集，通过以下步骤确定重构函数。

(1) 针对各个候补函数$\tilde u_i^{\left\langle \xi \right\rangle }\left( x \right), \xi = 1, 2$，分别计算其与相邻网格候补重构函数之间产生的TBV最小值。

$ mTBV_i^\xi = {\rm{min}}\left( {\begin{array}{*{20}{r}} {\left| {\tilde u_{i - 1}^{\langle 1\rangle }\left( {{x_{i - \frac{1}{2}}}} \right) - \tilde u_i^{\langle \xi \rangle }\left( {{x_{i - \frac{1}{2}}}} \right)} \right| + }\\ {\left| {\tilde u_{i + 1}^{\langle 1\rangle }\left( {{x_{i + \frac{1}{2}}}} \right) - \tilde u_i^{\langle \xi \rangle }\left( {{x_{i + \frac{1}{2}}}} \right)} \right|,}\\ \begin{array}{r} \begin{array}{*{20}{r}} {\left| {\tilde u_{i - 1}^{\langle 2\rangle }\left( {{x_{i - \frac{1}{2}}}} \right) - \tilde u_i^{\langle \xi \rangle }\left( {{x_{i - \frac{1}{2}}}} \right)} \right| + }\\ {\left| {\tilde u_{i + 1}^{\langle 2\rangle }\left( {{x_{i + \frac{1}{2}}}} \right) - \tilde u_i^{\langle \xi \rangle }\left( {{x_{i + \frac{1}{2}}}} \right)} \right|,} \end{array}\\ \begin{array}{*{20}{r}} {\left| {\tilde u_{i - 1}^{\langle 1\rangle }\left( {{x_{i - \frac{1}{2}}}} \right) - \tilde u_i^{\langle \xi \rangle }\left( {{x_{i - \frac{1}{2}}}} \right)} \right| + }\\ {\left| {\tilde u_{i + 1}^{\langle 2\rangle }\left( {{x_{i + \frac{1}{2}}}} \right) - \tilde u_i^{\langle \xi \rangle }\left( {{x_{i + \frac{1}{2}}}} \right)} \right|,}\\ {\begin{array}{*{20}{r}} {\left| {\tilde u_{i - 1}^{\langle 2\rangle }\left( {{x_{i - \frac{1}{2}}}} \right) - \tilde u_i^{\langle \xi \rangle }\left( {{x_{i - \frac{1}{2}}}} \right)} \right| + }\\ {\left| {\tilde u_{i + 1}^{\langle 1\rangle }\left( {{x_{i + \frac{1}{2}}}} \right) - \tilde u_i^{\langle \xi \rangle }\left( {{x_{i + \frac{1}{2}}}} \right)} \right|} \end{array}} \end{array} \end{array} \end{array}} \right) $

(2) 选取mTBV_i^ξ更小的候补函数作为最终的重构函数，

$ \tilde{u}_{i}(x)=\left\{\begin{array}{ll} \tilde{u}_{i}^{\langle 1\rangle}(x), & \text { if }\ m T B V_{i}^{\langle 1\rangle} \leqslant m T B V_{i}^{\langle 2\rangle} \\ \tilde{u}_{i}^{\langle 2\rangle}(x), & \text { otherwise } \end{array}\right. $

使得边界总变差最小。

文献[36]分别采用MUSCL插值函数(7)和THINC函数(10)作为候补函数，即$\tilde u_i^{\left\langle 1 \right\rangle }\left( x \right) = \tilde u_i^M\left( x \right), \tilde u_i^{\left\langle 2 \right\rangle }\left( x \right) = \tilde u_i^T\left( x \right)$，得到了MUSCL-THINC-BVD格式。用该格式求解自由界面多项流问题，能有效地抑制自由界面的扩散和捕捉各种复杂的流场结构，并且具有很好的稳定性和鲁棒性。

2.2.3 BVD算法Ⅲ

针对包含两个候补函数的BVD许容函数集，通过以下步骤确定重构函数。

(1) 针对各候补函数，分别计算单元Ω_i边界${x_{i - \frac{1}{2}}}{\rm{和}}{x_{i + \frac{1}{2}}}$的变差之和，即边界总变差(TBV_i)，

$ T B V_{i}^{\langle\xi\rangle}=B V_{i+\frac{1}{2}}^{\langle\xi\rangle}+B V_{i-\frac{1}{2}}^{(\xi)}。$

其中，$BV_{i + \frac{1}{2}}^{\left\langle \xi \right\rangle } = \left| {\tilde u_{i + 1}^{\left\langle \xi \right\rangle }\left( {{x_{i + \frac{1}{2}}}} \right) - \tilde u_i^{\left\langle \xi \right\rangle }\left( {{x_{i + \frac{1}{2}}}} \right)} \right|, \xi = 1$。

(2) 选取使得边界总变差最小的函数作为最终的重构函数，

$ \tilde{u}_{i}(x)=\left\{\begin{array}{ll} \tilde{u}_{i}^{\langle 1\rangle}(x), & \text { if } T B V_{i}^{\langle 1\rangle} \leqslant T B V_{i}^{\langle 2\rangle} \\ \tilde{u}_{i}^{\langle 2\rangle}(x), & \text { otherwise } \end{array}\right. $

(3) 采用${{\tilde u}_i}\left( x \right)$作为其最终的重构函数，计算网格单元左右边界的值。

$ \left\{ {\begin{array}{*{20}{l}} {u_{i + \frac{1}{2}}^L = {{\tilde u}_i}({x_{i + \frac{1}{2}}})}\\ {u_{i - \frac{1}{2}}^R = {{\tilde u}_i}({x_{i - \frac{1}{2}}})} \end{array}} \right. $

针对多个候补函数构成的BVD许容函数集(Ξ≥3)，算法Ⅲ可写成更一般的形式:

$ \begin{aligned} \tilde{u}_{i}(x)=& \tilde{u}_{i}^{\langle\xi\rangle}(x), \quad \text { if }\ T B V_{i}^{\langle\xi\rangle} \leqslant T B V_{i}^{\langle\eta\rangle} \\ & \text { for all } \ \tilde{u}_{i}^{\langle\eta\rangle}(x) \in \varPi ; \eta \neq \xi \end{aligned} $

(11)

文献[43]采用三个候补函数建立了非结构网格的BVD格式，能很好地捕捉间断和涡结构。

2.2.4 BVD算法Ⅳ

当BVD许容函数集包括3个以上候补函数时，可通过多步BVD算法确定重构函数。其一般步骤如下:

(1) 首先对BVD许容函数$\tilde u_i^{\left\langle \xi \right\rangle }\left( x \right){\rm{从}}\tilde u_i^{\left\langle 1 \right\rangle }\left( x \right){\rm{到}}\tilde u_i^{\left\langle\mathit{\Xi }\right\rangle}\left( x \right)$编号。一般可以先按照从高阶到低阶、从振荡到单调的顺序进行排列，这样可以通过合适的BVD选择算法首先获得一套基本无振荡的重构函数，以此为基础可进一步引入使用具有较大β值的THINC函数，以消除针对不连续解的数值耗散。

(2) 选取$ \tilde u_{}^{\left\langle 1 \right\rangle }{\;_i}\left( x \right)$作为起始候补函数，$\tilde u_i^{\left( 1 \right)}\left( x \right) = \tilde u_i^{\left\langle 1 \right\rangle }\left( x \right)$。

(3) 通过BVD判据，将$\tilde u_i^{\left\langle 1 \right\rangle }\left( x \right)$与其他候补函数逐个进行比较，

$ \begin{array}{*{20}{l}} \begin{array}{l} {\rm{ for }}\left( {\xi = 2;\xi \le \mathit{\Xi };{\xi ^{ + + }}} \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \{ \end{array}\\ {\begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde u_i^\xi (x) = BV{D_\xi }\left( {\tilde u_i^{(\xi - 1)}(x),\tilde u_i^{\langle \xi \rangle }(x)} \right)}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\tilde u}_i}(x) = \tilde u_i^{(\mathit{\Xi })}(x)} \end{array}} \end{array} $

其中，BVD_ξ(·, ·)表示基于BVD原理，针对两个候补函数的选择算法，如上述的算法Ⅰ至算法Ⅲ。

(4) 采用${{\tilde u}_i}\left( x \right)$作为其最终的重构函数，计算网格单元左右边界的值。

$ \left\{\begin{array}{l} u_{i+\frac{1}{2}}^{L}=\tilde{u}_{i}\left(x_{i+\frac{1}{2}}\right) \\ u_{i-\frac{1}{2}}^{R}=\widetilde{u}_{i}\left(x_{i-\frac{1}{2}}\right) \end{array}\right. $

作为BVD算法Ⅳ的一个具体范例，下面给出PnTm-BVD格式的计算步骤。这里，Pn代表n次常系数多项式(第一类BVD许容函数)，Tm代表采用m个不同β值(β₁，β₂，…, β_m)的THINC函数，记为$\tilde u_i^{T\left( {\beta \varepsilon } \right)}\left( x \right), \xi = 1, \cdots , m$。该算法的计算步骤为：

(1) 选多项式为初始候补函数，$\tilde u_i^{\left\langle 1 \right\rangle }\left( x \right) = \tilde u_i^{{\rm{Pn}}}\left( x \right)$。

(2) 对ξ=1，…, m-1循环计算

$ \begin{array}{*{20}{c}} {TBV_i^{\left\langle \xi \right\rangle } = \left| {\tilde u_{i - 1}^{\left\langle \xi \right\rangle }\left( {{x_{i - \frac{1}{2}}}} \right) - \tilde u_i^{\left\langle \xi \right\rangle }\left( {{x_{i - \frac{1}{2}}}} \right)} \right| + }\\ {\left| {\tilde u_{i + 1}^{\left\langle \xi \right\rangle }\left( {{x_{i + \frac{1}{2}}}} \right) - \tilde u_i^{\left\langle \xi \right\rangle }\left( {{x_{i + \frac{1}{2}}}} \right)} \right|} \end{array} $

和

$ \begin{array}{*{20}{c}} {TBV_i^{T\left( {{\beta _\xi }} \right)} = \left| {\tilde u_{i - 1}^{T\left( {{\beta _\xi }} \right)}\left( {{x_{i - \frac{1}{2}}}} \right) - \tilde u_i^{T\left( {{\beta _\xi }} \right)}\left( {{x_{i - \frac{1}{2}}}} \right)} \right| + }\\ {\left| {\tilde u_{i + 1}^{T\left( {{\beta _\xi }} \right)}\left( {{x_{i + \frac{1}{2}}}} \right) - \tilde u_i^{T\left( {{\beta _\xi }} \right)}\left( {{x_{i + \frac{1}{2}}}} \right)} \right|} \end{array} $

根据以下判据更新$\tilde u_i^{\left\langle \xi \right\rangle }\left( x \right){\rm{A}}\tilde u_{i \pm 1}^{\left\langle \xi \right\rangle }\left( x \right)$,

$ \begin{array}{c} \tilde{u}_{j}^{\langle\xi\rangle}(x)=\left\{\begin{array}{l} \tilde{u}_{j}^{T(\beta _\xi)}(x), & \text { if } \ T B V_{i}^{T(\beta_ \xi)} \leqslant T B V_{i}^{\langle\xi\rangle} \\ \tilde{u}_{j}^{\langle\xi\rangle}(x), & \text { otherwise } \end{array}\right. \\ j=i-1, i, i+1。\end{array} $

(3) 由上述步骤得到$\tilde u_i^{\left( {m - 1} \right)}\left( x \right)$后，再引入一个采用较大β值(β_m)的THINC函数，$\tilde u_i^{T\left( {\beta m} \right)}\left( x \right)$，通过以下BVD算法获得最后的重构函数。

$ \tilde{u}_{i}(x)=\left\{\begin{array}{ll} \tilde{u}_{i}^{T\left(\beta_{m}\right)}(x), & \text { if } \ T B V_{i}^{T(\beta m)} \leqslant T B V_{i}^{(m-1)} \\ \widetilde{u}_{i}^{(m-1)}(x), & \text { otherwise } \end{array}\right. $

文献[38-40]分别给出了P4T2-BVD、P6T3-BVD、P8T3-BVD、P10T3-BVD、P12T3-BVD和P14T3-BVD等高阶BVD格式。这些格式对光滑解可以得到对应的常系数多项式的最高收敛阶数，亦即，PnTm-BVD格式具有n+1阶。同时，能有效避免数值振荡。与其他现有的高阶方法不同，这类BVD格式完全不需要使用传统的非线性限制映射来消除数值振荡。

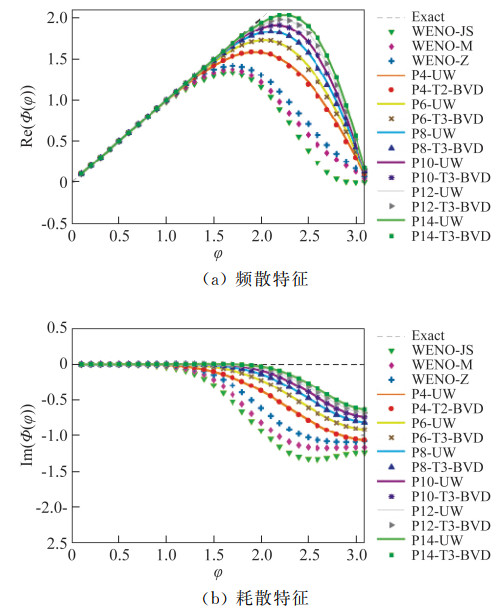
使用ADR(Approximate Dispersion Relation)方法^[63]可以分析数值格式的频散和耗散性质。图 1显示各阶PnTm-BVD格式的数值频散和耗散特征。为了比较，这里还显示了WENO-JS^[13]、WENO-M^[14]、WENO-Z^[15]以及基于各阶格式对应的常系数多项式的线性格式的频散/耗散关系。对于所有波数，PnTm-BVD可以回复其对应高阶线性格式的频散/耗散关系，而采用非线性限制多项式的高阶格式则在高波数区明显偏离线性格式。

此外，文献[44]还提出了以4次常系数多项式和采用可变β值的THINC作为候补函数的BVD格式。其中，网格单元Ω_i的THINC函数的β值通过以下算式给出:

$ \beta_{i}=\frac{\beta_{\text {low }}+\beta_{\text {high }}}{2}+\frac{\beta_{\text {high }}-\beta_{\text {low }}}{2} \tanh \left(\varphi\left(\left|\ln r_{i}\right|-r_{0}\right)\right) $

这里，${r_i} = \frac{{{{\bar u}_i} - {{\bar u}_{i - 1}}}}{{{{\bar u}_{i + 1}} - {{\bar u}_i}}}, {\beta _{{\rm{low }}}} = 1.1, {\beta _{{\rm{high }}}} = 1.6, \varphi = 2.0, {r_0} = \frac{1}{4}\ln 2$。由此得到的THINC函数计为$\tilde u_i^{{T_{\beta v}}}\left( x \right)$。

采用四阶多项式(6)和$\tilde u_i^{{T_{\beta v}}}\left( x \right)$作为候补函数，可得到下列的BVD格式，

$ \begin{array}{c} \tilde{u}_{j}(x)=\left\{\begin{array}{l} \tilde{u}_{j}^{T \beta v}(x), & \text { if }\ T B V_{i}^{T_{\beta v}} \leqslant T B V_{i}^{P_{4}} \\ \tilde{u}_{j}^{P_{4}}(x), & \ \ \ \text { otherwise } \end{array}\right. \\ j=i-1, i, i+1 \end{array} $

该格式称为P4Tβ_v-BVD格式。

2.3 多维BVD格式的构建

上述构建一维BVD格式的思路原则上都可以推广到多维情形。对于结构网格可以采用方向分离方法，通过一维格式进行空间重构。对于非结构网格，文献[43]用重构函数沿网格单元各边界的积分值计算BV。针对网格单元Ω_i和与其相邻的单元Ω_ij，沿单元边界Γ_ij的BV值由下式计算，

$ B V_{i j}^{\langle\xi\rangle}=\left|\tilde{u}_{i}^{\langle\xi\rangle}\left(\varGamma_{i j}\right)-\tilde{u}_{i j}^{\langle\xi\rangle}\left(\varGamma_{i j}\right)\right| $

这里$\tilde u_i^{\left\langle \xi \right\rangle }\left( {{\mathit{\Gamma }_{ij}}} \right){\rm{和}}\tilde u_{ij}^{\left\langle \xi \right\rangle }\left( {{\mathit{\Gamma }_{ij}}} \right)$分别表示定义在Ω_i和Ω_ij上的重构函数$\tilde u_i^{\left\langle \xi \right\rangle }\left( x \right){\rm{和}}\tilde u_{ij}^{\left\langle \xi \right\rangle }\left( x \right)$沿单元边界Γ_ij的积分值。其对应的单元边界总变差为$TBV_i^{\left\langle \xi \right\rangle } = \sum\limits_{j = 1}^J {BV_{ij}^{\left\langle \xi \right\rangle }} $。其中，J表示构成单元Ω_i表面的线(两维)或面(三维)的个数。如两维三角单元，J=3；三维四面体单元，J=4。在得到各重构函数的单元边界总变差TBV后，可以基于前述的BVD准则，最后确定重构函数。

需要指出，BVD算法在同一网格单元上要对所有候补函数进行重构，并储存相应的BV或TBV值，会增加计算量和存储量。然而，由于各网格单元间的计算过程相互独立，BVD算法不会给并行处理带来不利影响。

3 数值结果

我们利用标量守恒律和欧拉方程的各种标准算例，对BVD算法进行了系统的检验，并与其他现有方法进行了比较。

3.1 精度检验

对于光滑解，BVD格式一般都能从候补函数中选择高阶重构，从而获得高收敛率。以下列举采用不同阶数常系数多项式作为候补函数的BVD格式的收敛检验算例。文献[38-40]分别针对平流和欧拉方程进行了网格收敛率检验。对于一维平流方程，选用以下具有一定光滑度的初始条件，

$ u(x,0) = \sin \left( {{\rm{ \mathsf{ π} }}x - \frac{{\sin ({\rm{ \mathsf{ π} }}x)}}{{\rm{ \mathsf{ π} }}}} \right),x \in [ - 1,1] $

对于二维欧拉方程的密度扰动传播算例, 初始条件设为:

$ \begin{array}{c} \left\{ {\begin{array}{*{20}{l}} {\rho (x,y,0) = 1 + 0.2\sin (2{\rm{ \mathsf{ π} }}(x + y))}\\ {u(x,y,0) = 0.7}\\ {v(x,y,0) = 0.3}\\ {p(x,y,0) = 1.0} \end{array}} \right.\\ (x,y) \in [ - 1,1] \times [ - 1,1] \end{array} $

表 1给出各阶PnTm-BVD格式的误差及收敛率，均能达到相对应的常系数多项式的阶数。其误差的绝对值与采用常系数多项式作为重构函数的结果基本一致。

3.2 Jiang-Shu平流实验

作为检验数值格式是否能够同时捕捉连续和间断解的算例，文献[13]设计了一个既包括光滑分布又包括间断解的平流初始条件。

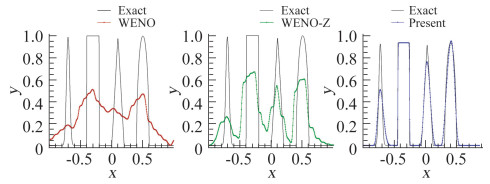
图 2分别显示了经过一百万步后WENO-JS^[13]，WENO-Z^[15]和P4T2-BVD格式^[38]的计算结果。可以看出，由于数值误差的不断积累，WENO-JS和WENO-Z格式已无法保持初始分布的特征。而P4T2-BVD格式则能很好保持初始分布，对连续和间断解都能得到高保真的计算结果。P4T2-BVD格式既能有效地避免数值振荡，又可以消除数值耗散，使解的结构在长期积分后仍能可靠再现。这是现有其他方法很难做到的。

3.3 一维欧拉方程的数值实验

对于一维欧拉方程，我们利用各类标准算例对BVD格式进行了检验，在抑制数值振荡的同时，对间断和光滑解均能得到高保真的计算结果。以下给出几个具体算例的结果。

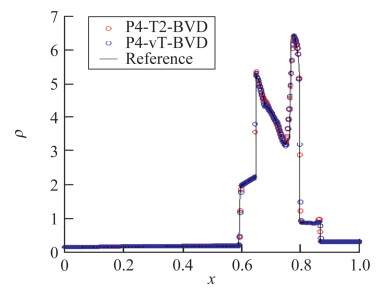
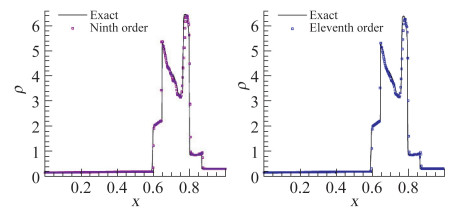
3.3.1 双激波相互作用^[64]

本算例通过两个激波的相互作用及边界反射产生复杂的流场结构，包括激波、接触间断和膨胀波，被广泛用于检验数值方法是否产生数值振荡，以及对各类间断和连续解的捕捉能力。图 3给出了P4T2-BVD以及P4Tβ_v-BVD格式的计算结果。可以看到BVD格式能够精确地得到各类特征的数值解。在图 4中我们进一步显示9阶和11阶BVD格式的计算结果，高阶BVD格式也能有效抑制数值振荡，保持良好的鲁棒性，并得到高保真的数值计算结果。在上述结果中，BVD格式能够有效地控制数值耗散，可使最左端的接触间断厚度保持在3至4个网格之内。这是现有基于多项式重构及非线性限制映射的高分辨格式难以实现的。

3.3.2 激波与密度扰动相互作用^[65]

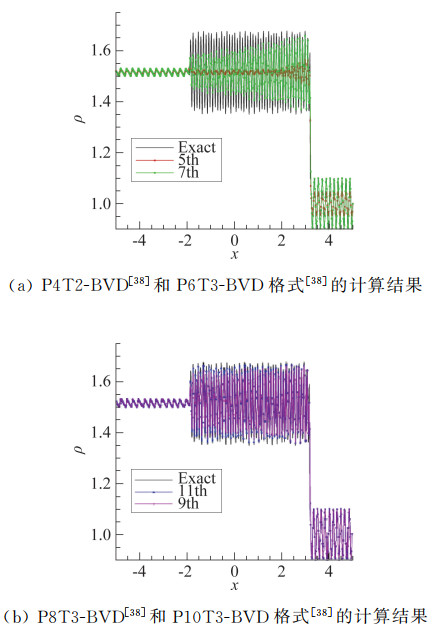
为了进一步检验BVD格式对高频周期波的捕捉能力，我们计算了激波与密度扰动相互作用的算例。图 5显示不同阶数BVD格式的计算结果。可以看到，不同阶数的BVD格式都能抑制数值振荡，并在光滑区正确地选择多项式作为重构函数。随着多项式阶数的提高，BVD能有效减小数值耗散，更精确地捕捉高频波动^[40]。

3.3.3 Le Blanc激波管问题^[66]

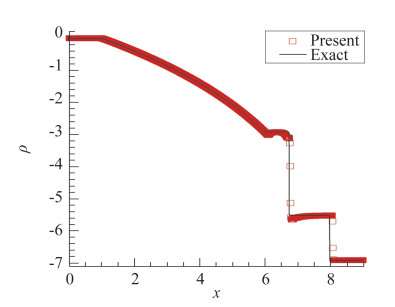
作为一个较困难的标准算例，Le Blanc激波管问题的解包括非常强的激波和稀疏波，经常用来检验算法的鲁棒性^[66]。图 6给出了P4T2-BVD的计算结果(密度)。没有出现明显的数值振荡。并能很好再现稀疏波、接触间断和激波^[46]。数值实验表明，随着网格分辨率的提高，右行激波能够收敛到相应精确解的位置。

3.3.4 刚性爆轰波^[67]

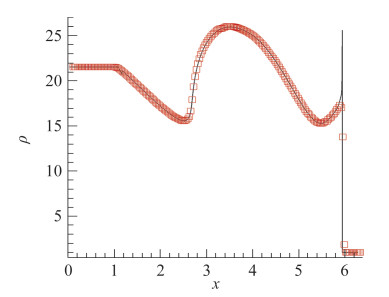
与现有的数值方法相比，BVD格式能够消除数值耗散，精确地捕捉不连续界面。图 7显示了包括刚性化学反应的爆轰波计算结果。P4T2-BVD格式能有效控制反应面的温度跃阶厚度，从而保证反应面始终以正确的速度传播^{[42, 46]}。

3.4 二维欧拉方程的数值实验 3.4.1 双马赫反射^[64]

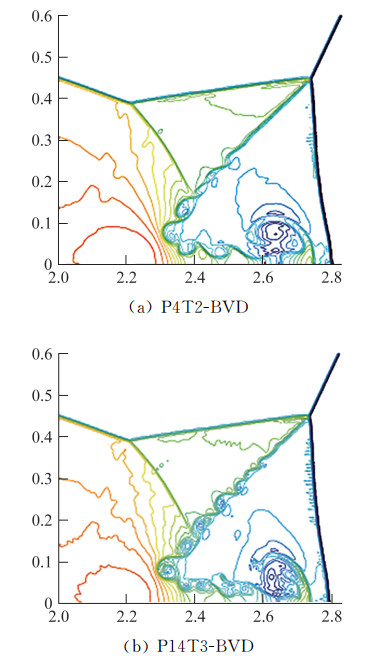
作为检验二维算法的标准算例，双马赫反射问题自提出以来，在相关文献中得到广泛应用。在本算例中，沿两个反射激波间的滑移线会出现开尔文-亥姆霍兹不稳定，进而产生涡列。在数值计算中，这些涡列是否出现和发展取决于数值耗散的大小。图 8分别给出了P4-T2-BVD和P14-T3-BVD格式的计算结果。由于BVD原理旨在减小格式的数值耗散，以此为基础设计的格式都能更多地保留流场的细微结构，捕捉到更小尺度的流体运动。与其他五阶格式相比，P4-T2-BVD格式的结果显示了充分发展的涡列。随着精度提高，十五阶的P14-T3-BVD格式可以捕捉到更多旋涡结构^[44]。

3.4.2 爆轰波扰流问题^[68]

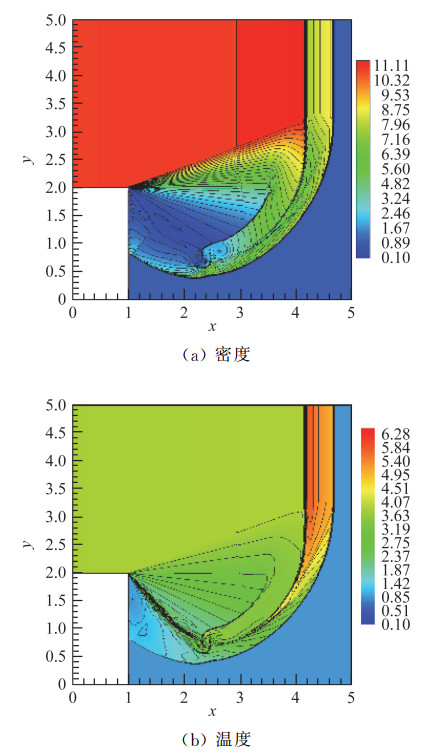
二维爆轰波的90°凸角绕流在绕角下流区域会产生密度和压力的低值区，极易在数值结果中出现负值，导致计算失败。文献[46]在P4-T2-BVD格式中引入了MOOD(Multi dimensional Optimal Order Detection)正定修正算法^[69]，从而保证了热力学变量数值解的正定性。图 9显示二维爆轰波90°凸角绕流的密度和温度分布，对于反应区和各种流场结构均获得较精确的计算结果。

3.4.3 空气激波与水柱相互作用^[70]

采用THINC函数作为候补重构函数的BVD格式可以有效控制数值耗散，从而避免接触间断和物质界面在计算过程中被平滑扩散的现象。文献[36]采用MUSCL-THINC-BVD格式对各类两项可压缩流动进行了模拟，取得了良好的计算结果。

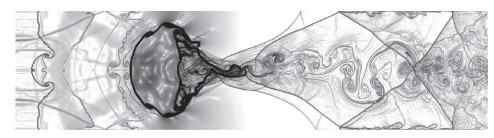
图 10给出了空气与水柱相互作用的计算结果。BVD格式能有效地保持水/气界面的厚度，并对各种流场结构都能得到高保真的计算结果。与文献[70]及其他现有算法相比，BVD格式能在抑制数值振荡的同时，获得间断解的高保真计算结果，显示出在模拟可压缩多相介质等具有显著间断解结构特征应用问题时的明显优势和潜力。文献[43]将基于MUSCL和THINC的BVD格式扩展到非结构网格，并计算了包含移动界面的可压缩多相流算例，获得了良好的数值结果。

4 结论

本文概述了BVD方法的基本思想，设计相关格式的基本思路，以及一些具有很强实用价值的BVD格式。并通过单相和两相可压缩流动的一些典型算例验证了BVD格式的特点和优势。

BVD方法把减小数值耗散作为设计空间重构算法的指导思想，具有明确的物理含义和普遍性，是一条设计和改进数值格式的新途径。针对研究对象，选用合适的BVD许容函数作为空间重构的候补选项，并设计相应的BVD算法可以构建一类全新的数值格式。这些格式与基于多项式重构和非线性限制修正的传统方法有本质区别。数值实验结果表明，BVD格式可以得到明显优于已有算法的计算结果，能同时对各种尺度的连续和间断结构都获得高保真的数值解。

采用THINC或类似的Sigmoid函数作为候补重构函数可以明显改善基于欧拉网格的数值方法对接触间断和物质界面在计算过程中被平滑扩散的问题，对解决含有化学反应面或移动物质界面流动问题的实际应用具有重要意义。

相关研究工作仍在继续，例如，可以通过BVD判据，在光滑区引入中心格式进一步控制数值耗散^[71]，以及将BVD格式扩展到间断伽列金的数值框架^[72]。希望通过不断努力和持续发展，能够提出具有更好性能的BVD格式，并成为解决实际应用问题的有力工具。

致谢: 邓希、谢彬、孙紫尧、程李东、金鹏、陈春刚、Shimizu、Inaba、Tann、Wakimura等东京工业大学工学院肖研究室的学生以及合作者姜振华、Loubère、Abe等对本项研究工作做出了重要贡献，特此致谢。