0 引言

可压缩湍流在高超声速飞行器设计、高温化学反应流动、激光核聚变、超新星爆炸等各种工程问题和自然现象中起到关键作用，不仅是流体力学中的基础科学问题，也是国家重大工程中的重点研究课题^[1-10]。与不可压缩湍流相比，可压缩湍流更加复杂，包含了旋涡、声波、激波、膨胀波等丰富的流动结构。在可压缩湍流中，动能和内能之间通过压力做功相互转化，密度、速度、压力和温度之间相互耦合。可压缩湍流的复杂性给理论分析、数值模拟和实验研究带来了巨大的挑战。因此，非常有必要系统地研究可压缩湍流的流动机理，为进一步发展更可靠的可压缩湍流模型提供理论支持^[11-23]。

由于可压缩湍流包含了丰富的物理过程，一种有效的方法是将可压缩湍流分解为不同的部分，然后研究每一部分的性质以及各部分之间的相互作用。Moyal在1952年通过亥姆霍兹分解，将可压缩湍流的速度场分解为剪切部分和胀压部分，并指出，速度场的剪切部分类似于不可压缩湍流场，而速度场的胀压部分可以看做是随机噪声^[24]。Kavasznay在1953年对可压缩流动的控制方程做了线性假设，将可压缩流动分解为三种相互正交的模态：涡模态、声模态和熵模态，分别对应于可压缩流动的剪切过程、胀压过程和热力学过程^[25]。

亥姆霍兹分解方法已被广泛应用于可压缩均匀各向同性湍流的研究中。在1991年，Sarkar等采用了声波理论来描述弱可压缩各向同性湍流速度场的胀压部分^[26]。在1997年，Ristorcelli使用了伪声理论来研究弱可压缩各向同性湍流速度场的胀压部分^[27]。当湍流马赫数比较高的时候，湍流场中的旋涡运动会诱导产生小尺度激波，也称为小激波(shocklet)。在1991年，Lee等首次通过数值模拟研究了可压缩各向同性湍流中的小激波结构，发现在小激波前后的物理量变化近似满足激波跳跃关系式^[28]。Samtaney等在2001年采用小激波识别方法研究了可压缩各向同性湍流场中的小激波的统计规律^[29]。Jagannathan和Donzis在2016年，通过亥姆霍兹分解研究了可压缩性对各向同性湍流场的影响，并指出当湍流马赫数高于临界值0.3时，胀压部分会对整个流场有较明显的影响^[30]。

李新亮、傅德薰和马延文在2002年，通过数值模拟研究了可压缩各向同性衰减湍流，并指出湍流间歇性是可压缩湍流中出现小激波的重要原因^[31]。他们分析了可压缩各向同性湍流辐射声波的性质，并和Lilley模型、Poudman模型做了比较^[32]。李虎和张树海在2012年，通过数值模拟研究了可压缩各向同性衰减湍流，发现可压缩性会加快从大尺度脉动到小尺度脉动的湍动能输运^[33]。何国威课题组在2013年研究了可压缩各向同性湍流的速度场的时间关联性质^[34]。他们对速度的胀压部分发展了新的时间关联模型，并通过直接数值模拟作了验证。

陈十一研究团队在2010年到2015年期间，发展了紧致差分和WENO格式相结合的混合方法，并对可压缩均匀各向同性湍流开展了一系列的研究，包括：小激波和可压缩性对速度梯度和流场小尺度脉动的影响、速度散度的概率分布以及和一维Burgers湍流的比较、能量级串过程、可压缩湍流中的粒子运动规律等^[35-43]。这部分研究内容主要在2015年的一篇文章中作了总结^[43]。

本文主要介绍陈十一研究团队自2017年以来在可压缩湍流的流动机理方面的研究进展，包括：可压缩湍流的多过程分解、各类可压缩条件下的速度和热力学量的谱的标度律、动能和热力学量的多尺度传输、大尺度剪切流的作用、高温非平衡效应、化学反应的影响等^[44-56]。

1 基本方程和流动参数

经过无量纲化后的描述理想气体的可压缩流体力学基本方程组如下^{[1, 35, 47]}:

$ {\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}} \right)}}{{\partial {x_j}}} = 0} $

(1)

$ {\frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j} + p{\delta _{ij}}} \right)}}{{\partial {x_j}}} = \frac{1}{{Re}}\frac{{\partial {\sigma _{ij}}}}{{\partial {x_j}}} + {F_i}} $

(2)

$ \begin{array}{*{20}{c}} {\frac{{\partial E}}{{\partial t}} + \frac{{\partial \left[ {(E + p){u_j}} \right]}}{{\partial {x_j}}} = }\\ {\frac{1}{\alpha }\frac{\partial }{{\partial {x_j}}}\left( {\kappa \frac{{\partial T}}{{\partial {x_j}}}} \right) + \frac{1}{{Re}}\frac{{\partial \left( {{\sigma _{ij}}{u_i}} \right)}}{{\partial {x_j}}} - \mathit{\Lambda } + {F_j}{u_j}} \end{array} $

(3)

$ {p = \frac{{\rho T}}{{\gamma {M^2}}}} $

(4)

其中，ρ、u_i、p、T分别表示密度、速度、压力、温度。黏性应力张量σ_ij定义为：

$ {\sigma _{ij}} = \mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{2}{3}\mu \theta {\delta _{ij}} $

(5)

其中，速度散度θ=∂u_j/∂x_j。F_i表示加在动量上的大尺度驱动力，Λ表示大尺度冷却函数^{[35, 47]}。单位体积的总能量定义为：

$ E = \frac{p}{{\gamma - 1}} + \frac{1}{2}\rho {u_j}{u_j} $

(6)

我们采用了一系列的参考量对可压缩流动的相关物理量做无量纲化，包括：参考长度L_r，参考速度U_r，参考密度ρ_r，参考压力p_r=ρ_rU_r²，参考温度T_r，参考能量e_r=ρ_rU_r²，参考黏性系数μ_r，参考热传导系数κ_r。通过无量纲化，可以得到三个重要的无量纲参数：参考雷诺数Re=ρ_rU_rL_r/μ_r，参考马赫数M=U_r/c_r和参考普朗特数Pr=μ_rC_p/κ_r。设参考普朗特数为Pr=0.7。参考声速定义为${c_r} = \sqrt {\gamma R{T_r}} $；γ=C_p/C_v是比热比，这里取γ=1.4。R是气体常数。参数α定义为α=(γ-1)M²PrRe。采用Sutherland公式计算无量纲化后的动力学黏性和热传导系数^{[35, 47]}。

采用紧致差分与WENO格式相结合的混合格式，在一个立方体内采用周期性边界条件开展三维可压缩各向同性湍流的数值模拟^[35]。通过固定前两个波数上的能谱，对速度场加入了大尺度的驱动力^{[35, 47]}，又采用了空间均匀分布的冷却函数，使平均内能达到统计定常^{[35, 47]}。

湍流的泰勒雷诺数Re_λ定义为^{[35, 47]}：

$ R{e_\lambda } = Re\frac{{\langle \rho \rangle {u^\prime }\lambda }}{{\sqrt 3 \langle \mu \rangle }} $

(7)

其中，尖括号表示空间平均。速度大小的均方根为${u^\prime } = \sqrt {\left\langle {u_1^2 + u_2^2 + u_3^2} \right\rangle } $。泰勒微尺度定义为：

$ \lambda = \sqrt {\frac{{\left\langle {u_1^2 + u_2^2 + u_3^2} \right\rangle }}{{\left\langle {{{\left( {\frac{{\partial {u_1}}}{{\partial {x_1}}}} \right)}^2} + {{\left( {\frac{{\partial {u_2}}}{{\partial {x_2}}}} \right)}^2} + {{\left( {\frac{{\partial {u_3}}}{{\partial {x_3}}}} \right)}^2}} \right\rangle }}} $

(8)

湍流马赫数M_t定义为^{[35, 47]}：

$ {M_t} = M\frac{{{u^\prime }}}{{\langle \sqrt T \rangle }} $

(9)

湍流马赫数表示湍流脉动速度相对平均声速的大小。一般情况下，湍流马赫数越大，湍流场的可压缩性越强。另外，湍流场的可压缩性还依赖于剪切部分的动能与胀压部分的动能之比。

两个重要的特征尺度分别定义如下: 柯尔莫哥洛夫尺度定义为$\eta = {\left[ {{{\langle \mu /\mathit{Re}\rho \rangle }^3}/\varepsilon } \right]^{1/4}}$, 积分尺度定义为${L_I} = \frac{{3{\rm{ \mathsf{ π} }}}}{{2{{\left( {{u^\prime }} \right)}^2}}}\int_0^\infty {\frac{{E(k)}}{k}} {\rm{d}}x$, 其中单位质量的耗散率为ε=〈μσ_ijS_ij/(Reρ)〉，单位质量的能谱满足$\int_0^\infty E (k){\rm{d}}x{\rm{ = }}{\left( {{u^\prime }} \right)^2}$。

2 多过程分解和物理量的谱 2.1 可压缩湍流的多过程分解

在这一节中，介绍可压缩湍流的多过程分解方法。目前，该方法已被系统地应用于可压缩各向同性湍流和均匀剪切湍流的研究。我们将在后续的工作中用该方法研究更复杂的可压缩湍流。

我们采用亥姆霍兹分解，将速度场分解为剪切部分u^s和胀压部分u^d。其中，$\nabla \cdot {\mathit{\boldsymbol{u}}^s} = 0, \nabla \times {\mathit{\boldsymbol{u}}^d} = 0$。速度场的剪切部分代表了湍流的剪切过程，和旋涡结构相对应。速度场的胀压部分代表了湍流的胀压过程，对应于声波、膨胀波、激波等可压缩流动结构。

我们将密度、压力和温度分解为平均值和脉动值，即^[44]：$\rho = {\rho _0} + {\rho ^\prime }, p = {p_0} + {p^\prime }, T = {T_0} + {T^\prime }$。其中，压力场的脉动可以分解为剪切部分p^s和胀压部分p^d[44]：p′=p^s+p^d。压力的剪切部分p^s满足泊松方程：$\frac{{{\partial ^2}{p^s}}}{{\partial x_i^2}} = - {\rho _0}\frac{{\partial u_i^s}}{{\partial {x_j}}}\frac{{\partial u_j^s}}{{\partial {x_i}}}$。

对于弱可压缩湍流，在伪声模态假设下，有：${\mathit{\boldsymbol{u}}^d} \sim M_t^2{\mathit{\boldsymbol{u}}^s} \ll {\mathit{\boldsymbol{u}}^s}, {p^d} \sim M_t^2{p^s} \ll {p^s}$。从而可以推出伪声模态关系式^[44]：

$ \gamma {p_0}\frac{{\partial u_j^d}}{{\partial {x_j}}} \approx - \left( {\frac{{\partial {p^s}}}{{\partial t}} + u_j^s\frac{{\partial {p^s}}}{{\partial {x_j}}}} \right) $

(10)

$ \begin{array}{c} \frac{1}{{{\rho _0}}}\frac{{\partial {p^d}}}{{\partial {x_i}}} \approx - \left( {\frac{{\partial u_i^d}}{{\partial t}} + \mathit{\Pi }\left\{ {u_j^s\frac{{\partial u_i^d}}{{\partial {x_j}}} + u_j^d\frac{{\partial u_i^s}}{{\partial {x_j}}}} \right\}} \right) + \\ \frac{1}{{2\gamma {\rho _0}{p_0}}}\frac{\partial }{{\partial {x_i}}}\left[ {{{\left( {{p^s}} \right)}^2}} \right] \end{array} $

(11)

可以进一步对速度场和压力场的胀压部分作分解：${\mathit{\boldsymbol{u}}^d} = {\mathit{\boldsymbol{u}}^{ds}} + {\mathit{\boldsymbol{u}}^{dd}}, {p^d} = {p^{ds}} + {p^{dd}}$。其中，速度场和压力场的伪声模态满足：

$ \gamma {p_0}\frac{{\partial u_j^{ds}}}{{\partial {x_j}}} = - \left( {\frac{{\partial {p^s}}}{{\partial t}} + u_j^s\frac{{\partial {p^s}}}{{\partial {x_j}}}} \right) $

(12)

$ \begin{array}{c} \frac{1}{{{\rho _0}}}\frac{{\partial {p^{ds}}}}{{\partial {x_i}}} = - \left( {\frac{{\partial u_i^{ds}}}{{\partial t}} + \mathit{\Pi }\left\{ {u_j^s\frac{{\partial u_i^{ds}}}{{\partial {x_j}}} + u_j^{ds}\frac{{\partial u_i^s}}{{\partial {x_j}}}} \right\}} \right) + \\ \frac{1}{{2\gamma {\rho _0}{p_0}}}\frac{\partial }{{\partial {x_i}}}\left[ {{{\left( {{p^s}} \right)}^2}} \right] \end{array} $

(13)

伪声速度场的谱满足：

$ \int_0^\infty {{E^{ds}}} (k){\rm{d}}k = \left\langle {\frac{{{{\left( {{\mathit{\boldsymbol{u}}^{ds}}} \right)}^2}}}{2}} \right\rangle $

(14)

设在波数k上的时间尺度为τ_k。对伪声速度场的谱作量纲分析：${E^{ds}}(k) \sim \frac{{\rho _0^2}}{{p_0^2}}\frac{1}{{{k^7}\tau _k^6}}$。根据柯尔莫戈洛夫理论得：${E^{ds}}(k) \sim \frac{{\rho _0^2}}{{p_0^2}}\frac{{{\varepsilon ^2}}}{{{k^3}}}$。其中，ε表示动能耗散率。热力学量满足：$\frac{{\rho _0^2}}{{p_0^2}} \sim \frac{{M_t^4}}{{{{\left( {{u^\prime }} \right)}^4}}} \sim \frac{{M_t^4}}{{{{\left( {{L_I}\varepsilon } \right)}^{\frac{4}{3}}}}}$。因此，伪声速度谱在惯性区上的标度关系如下^[44]：

$ {E^{ds}}(k) = C_v^{PS}M_t^4L_I^{ - 4/3}{\varepsilon ^{2/3}}{k^{ - 3}} \sim M_t^4{k^{ - 3}} $

(15)

采用Kavasznay分解将密度、压力和温度的脉动值进一步分解为声模态(等熵模态)和熵模态。声模态的计算公式如下^[49]：

$ {p^I} = p - {p_0},{\rho ^I} = \frac{{{\rho _0}{p^I}}}{{\gamma {p_0}}},{T^I} = \frac{{(\gamma - 1){T_0}{p^I}}}{{\gamma {p_0}}} $

(16)

熵模态的计算公式如下：

$ {p^E} = 0,{\rho ^E} = \rho - {\rho _0} - {\rho ^I},{T^E} = T - {T_0} - {T^I} $

(17)

其中，压力的脉动部分都属于声模态，没有熵模态。

2.2 可压缩湍流的物理量的谱

我们在表 1中列出了不同情况下速度的胀压部分u^d、压力p、密度ρ和温度T的谱在惯性区上的标度指数。速度和热力学量的胀压过程、声模态、熵模态等在不同可压缩条件下表现出了不同的统计特点。可压缩湍流的速度及其剪切部分的谱具有-5/3标度律^[44-50]。

不同情况下的物理量的谱的标度律如下：

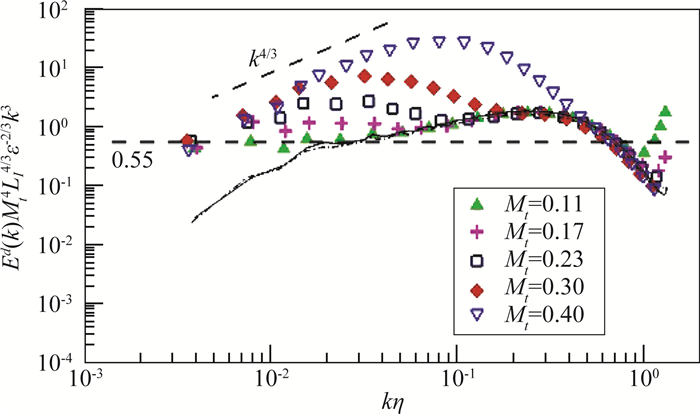
1) 大尺度剪切力驱动下的弱可压缩湍流^[44]。速度的胀压部分由伪声模态占主导，相应的谱具有-3标度律(见图 1)。压力由剪切部分占主导，压力谱具有-7/3标度律。温度和密度的谱也具有-7/3标度律。

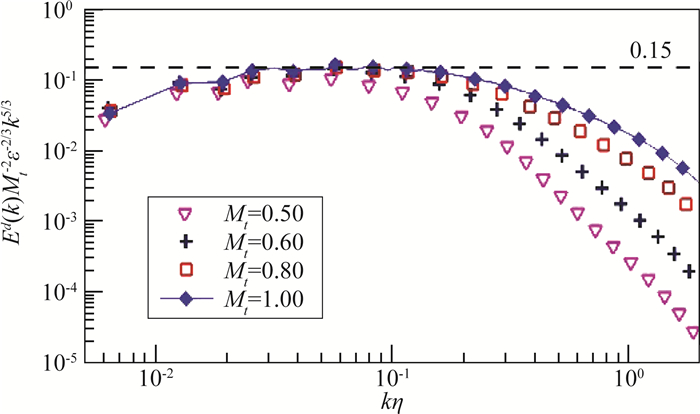
2) 大尺度剪切力驱动下的强可压缩湍流^{[44-47, 50]}。速度的胀压部分由声模态占主导，相应的谱具有-5/3标度律(见图 2)。温度、密度和压力都由声模态占主导，在惯性区上近似满足等熵关系式。温度、密度和压力的谱都具有-5/3标度律。

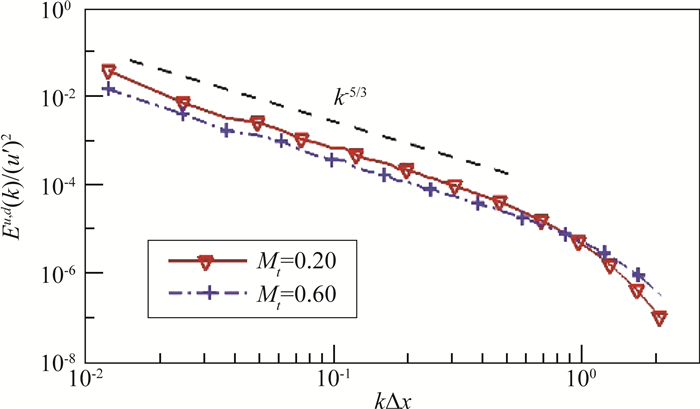
3) 大尺度剪切力和胀压力同时驱动下的可压缩湍流^[48]。流场出现了大激波结构。速度的胀压部分的谱具有-2标度律(见图 3)。温度、密度和压力的谱也都具有-2标度律。

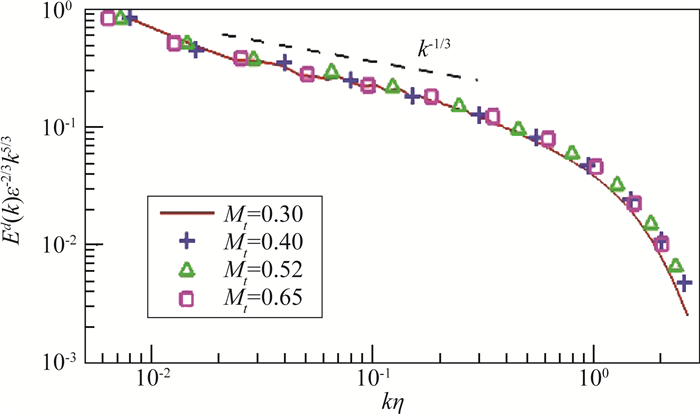
4) 大尺度剪切力驱动下的有热源的可压缩湍流^[49]。速度的胀压部分和压力都由声模态占主导。温度和密度由熵模态占主导。速度的胀压部分的谱具有-5/3标度律(见图 4)。温度、密度和压力的谱也都具有-5/3标度律。

3 动能和热力学量的多尺度传输 3.1 动能的多尺度传输

在这一节中，我们采用滤波方法分析可压缩各向同性湍流的动能的多尺度传输^{[47, 50]}。

对于任意一个函数f(x)，滤波后的函数f(x)定义如下：$\bar f(\mathit{\boldsymbol{x}}) = \int {{d^3}} \mathit{\boldsymbol{r}}{G_l}(\mathit{\boldsymbol{r}})f(\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{r}})$。这里，G_l(r)=l^-3G(r/l)表示滤波函数，G(r)表示归一化后的窗口函数，l表示滤波尺度。Favre滤波(密度加权的滤波) ${\tilde f}$定义为：$\tilde f = \overline {\rho f} /\bar \rho $。

设密度加权的速度场为：${{\tilde w}_i} = \sqrt {\bar \rho } {{\tilde u}_i}$。作空间平均后的动能的滤波方程如下^{[47, 50]}：

$ \frac{\partial }{{\partial t}}\left\langle {\frac{1}{2}{{\left( {{{\tilde w}_i}} \right)}^2}} \right\rangle = - \left\langle {{\mathit{\Phi }_l}} \right\rangle - \left\langle {{\mathit{\Pi }_l}} \right\rangle - \left\langle {{D_l}} \right\rangle $

(18)

其中，压力做功项Φ_l、亚格子动能流量Π_l和黏性耗散项D_l分别为：${\mathit{\Phi }_l} = - \bar p\frac{\partial }{{\partial {x_j}}}\left( {\frac{{{{\tilde w}_j}}}{{\sqrt {\bar \rho } }}} \right), {\mathit{\Pi }_l} = - \bar \rho {{\tilde \tau }_{ij}} \cdot $$\frac{\partial }{{\partial {x_j}}}\left( {\frac{{{{\tilde w}_i}}}{{\sqrt {\bar \rho } }}} \right), {D_l} = \frac{{{{\bar \sigma }_{ij}}}}{{\mathit{Re}}}\frac{\partial }{{\partial {x_j}}}\left( {\frac{{{{\tilde w}_i}}}{{\sqrt {\bar \rho } }}} \right)$。

对密度加权的速度场做亥姆霍兹分解：

$ {{\tilde w}_i} = \tilde w_i^s + \tilde w_i^d,\nabla \cdot {{\mathit{\boldsymbol{\tilde w}}}^s} = 0,\nabla \times {{\mathit{\boldsymbol{\tilde w}}}^d} = 0 $

(19)

亥姆霍兹分解后的滤波动能方程如下^{[47, 50]}：

$ \frac{\partial }{{\partial t}}\left\langle {\frac{1}{2}{{\left( {\tilde w_i^X} \right)}^2}} \right\rangle = \left\langle {A_l^X} \right\rangle - \left\langle {\mathit{\Phi }_l^X} \right\rangle - \left\langle {\mathit{\Pi }_l^X} \right\rangle - \left\langle {D_l^X} \right\rangle $

(20)

其中，上标X=s, d。非线性对流项A_l^X、压力做功项Φ_l^X、亚格子动能流量Π_l^X和黏性耗散项D_l^X分别为：$A_l^X = - \tilde w_i^X\left( {{{\tilde u}_j}\frac{{\partial {{\tilde w}_i}}}{{\partial {x_j}}} + \frac{{{{\tilde w}_i}}}{2}\frac{{\partial {{\tilde u}_j}}}{{\partial {x_j}}}} \right)$，$\mathit{\Phi }_l^X = - \bar p\frac{\partial }{{\partial {x_i}}}\left( {\frac{{\tilde w_j^X}}{{\sqrt {\bar \rho } }}} \right)$，$\mathit{\Pi }_l^X = - \bar \rho {{\tilde \tau }_{ij}}\frac{\partial }{{\partial {x_j}}}\left( {\frac{{\tilde w_i^X}}{{\sqrt {\bar \rho } }}} \right)$，$D_l^X = \frac{{{{\bar \sigma }_{ij}}}}{{\mathit{Re}}}\frac{\partial }{{\partial {x_j}}}\left( {\frac{{\tilde w_i^X}}{{\sqrt {\bar \rho } }}} \right)$。

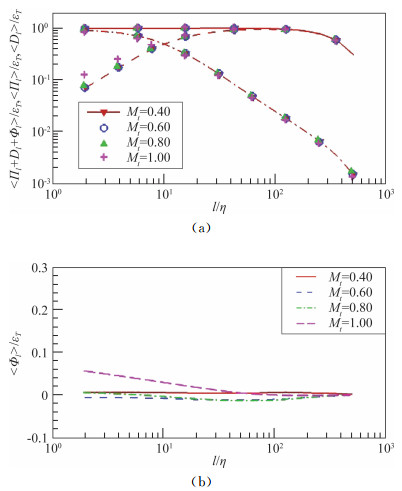
压力做功、亚格子动能流量、黏性耗散等各个项在动能的多尺度传输过程中所起的作用如图 5所示。在惯性区，亚格子流量在动能的多尺度传输过程中起主导作用。压力做功会引起动能和内能在局部区域内的相互转化，但经过平均后对动能传输的作用比较小。黏性耗散主要集中在小尺度上，将动能以不可逆的形式转化为内能^[47]。

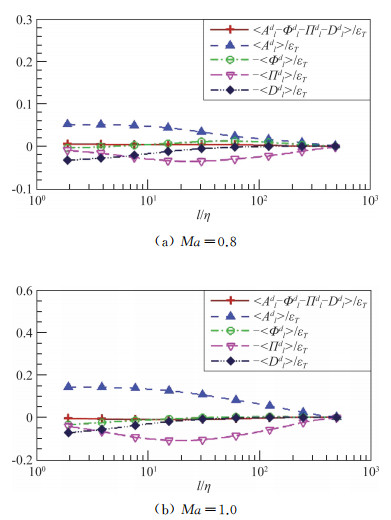
动能胀压部分的多尺度传输规律如图 6所示。在惯性区，动能的胀压部分通过非线性对流从剪切部分中得到能量，然后通过亚格子流量往小尺度传输，在小尺度上通过黏性耗散转化为内能^[47]。

3.2 热力学量的多尺度传输

在这一节中，我们采用滤波方法分析可压缩各向同性湍流的热力学量的多尺度传输^[49]。

温度可以分解为平均温度T₀和脉动温度T₁两部分：T=T₀+T₁，其中，T₀=〈T〉。滤波后温度的均方根的方程如下^[49]：

$ \frac{\partial }{{\partial t}}\left\langle {\tilde T_1^2} \right\rangle = - \left\langle {\mathit{\Phi }_l^T + \mathit{\Pi }_l^T + D_l^T + F_l^T} \right\rangle $

(21)

其中，Φ_l^T表示胀压项，Π_l^T表示亚格子项，D_l^T表示热扩散和黏性耗散的作用，F_l^T表示大尺度力的作用。速度散度的滤波记作${\theta _l} = \partial {{\tilde u}_j}/\partial {x_j}$。胀压项可表示为$\mathit{\Phi }_l^T = - (3 - 2\gamma )\tilde T_1^2{\theta _l} + 2(\gamma - 1){T_0}{{\tilde T}_1}{\theta _l}$，亚格子项为Π_l^T=Π_l^{T, 1}+Π_l^{T, 2}。其中，两个亚格子项分别为$\mathit{\Pi }_l^{T \cdot 1} = - 2\left[ {\bar \rho \left( {\widetilde {{T_1}{u_j}} - {{\tilde T}_1}{{\tilde u}_j}} \right)} \right]\frac{\partial }{{\partial {x_j}}}\left( {\frac{{{{\tilde T}_1}}}{{\bar \rho }}} \right)$，以及$\mathit{\Pi }_l^{T \cdot 2} = 2(\gamma - 1){{\tilde T}_1}\left( {\widetilde {{T_1}\theta } - {{\tilde T}_1}{\theta _l}} \right)$。

类似地，滤波后熵的均方根的方程如下^[49]：

$ \frac{\partial }{{\partial t}}\left\langle {\tilde s_1^2} \right\rangle = - \left\langle {\mathit{\Phi }_l^s + \mathit{\Pi }_l^s + D_l^s + F_l^s} \right\rangle $

(22)

其中，Φ_l^s表示胀压项，Π_l^s表示亚格子项，D_l^s表示热扩散和黏性耗散的作用，F_l^s表示大尺度力的作用。胀压项可表示为$\mathit{\Phi }_l^s = - \tilde s_1^2{\theta _l}$。亚格子项可表示为$\mathit{\Pi }_l^s = - 2\left[ {\bar \rho \left( {\widetilde {{s_1}{u_j}} - {{\tilde s}_1}{{\tilde u}_j}} \right)} \right]\frac{\partial }{{\partial {x_j}}}\left( {\frac{{{{\tilde s}_1}}}{{\bar \rho }}} \right)$。

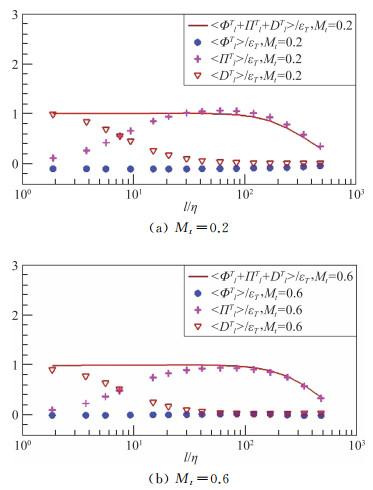
亚格子流量、胀压项、热扩散和黏性耗散等各个项在温度的多尺度传输过程中所起的作用如图 7所示。在惯性区，亚格子流量在温度脉动的多尺度传输过程中起主导作用，胀压、热扩散和黏性耗散的作用可忽略。温度的脉动在惯性区上存在从大尺度向小尺度的级串现象^[49]。

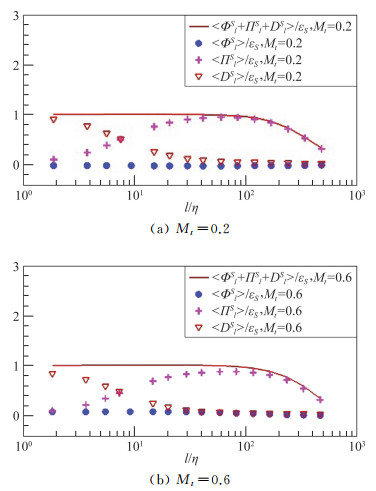
亚格子流量、胀压项、热扩散和黏性耗散等各个项在熵的多尺度传输过程中所起的作用如图 8所示。在惯性区，亚格子流量在熵的脉动的多尺度传输过程中起主导作用，其他项的作用可忽略^[49]。

4 统计定常的可压缩均匀剪切湍流

均匀剪切湍流是最简单的剪切湍流。利用雷诺分解，均匀剪切湍流的瞬时速度可以分解为平均速度U=(Sx₂, 0, 0) 和脉动速度u_i，在数值模拟中只计算脉动速度，则控制方程(1-3)变为以下形式^[52-53]：

$ {\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}} \right)}}{{\partial {x_j}}} + S{x_2}\frac{{\partial \rho }}{{\partial {x_1}}} = 0} $

(23)

$ \begin{array}{*{20}{c}} {\frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j} + p{\delta _{ij}}} \right)}}{{\partial {x_j}}} + S{x_2}\frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial {x_1}}} + S\rho {u_2}{\delta _{i1}}}\\ { = \frac{1}{{Re}}\frac{{\partial {\sigma _{ij}}}}{{\partial {x_j}}}} \end{array} $

(24)

$ \begin{array}{*{20}{c}} {\frac{{\partial E}}{{\partial t}} + \frac{{\partial \left[ {(E + p){u_j}} \right]}}{{\partial {x_j}}} + S{x_2}\frac{{\partial E}}{{\partial {x_1}}} + S\rho {u_1}{u_2}}\\ { = \frac{1}{\alpha }\frac{\partial }{{\partial {x_j}}}\left( {\kappa \frac{{\partial T}}{{\partial {x_j}}}} \right) + \frac{1}{{Re}}\frac{{\partial \left( {{\sigma _{ij}}{u_i}} \right)}}{{\partial {x_j}}} + \frac{{S{\sigma _{12}}}}{{Re}} - \mathit{\Lambda }} \end{array} $

(25)

因为以上方程中显含x₂，导致其在法向并不满足周期边界条件。通常采用被称为“剪切边界条件”的方法将其变换至动坐标系中进行求解^[57]。均匀剪切湍流可以从平均速度获得能量，仍需要在能量方程中加入冷却项Λ使其达到统计定常^[51]。

由于既具有空间均匀的统计特性，又有与其他复杂剪切湍流类似的湍动能生成的机制，均匀剪切湍流被认为是研究剪切湍流的重要模型。早期，对均匀剪切湍流的研究主要针对各向同性湍流受到均匀剪切后的初始阶段，分析湍动能的时间演化、各向异性和流场结构等。Pumir^[58]延长了不可压缩均匀剪切湍流的数值模拟时间，大尺度流动结构受到计算域的约束，湍动能不再增长，最终得到了统计定常的流场。相比各向同性湍流，统计定常的均匀剪切湍流的明显特征是具有很强的脉动，这是由于在均匀剪切湍流中存在类似边界层湍流中的猝发过程，而在统计定常的情况下该猝发过程的尺度达到了计算域尺度。统计定常均匀剪切湍流的很多统计特征和拟序结构都与壁湍流的对数区非常相似^[58-60]。目前对统计定常的均匀剪切湍流的研究主要针对不可压流动，对于可压缩的统计定常均匀剪切湍流的研究屈指可数^[51-54]。运用Helmholtz分解，可将速度场分解为剪切部分和胀压部分，进而研究剪切过程和胀压过程以及两者的相互作用。可压缩的统计定常均匀剪切湍流中, 剪切湍动能和胀压湍动能均存在很强的脉动^[51]。

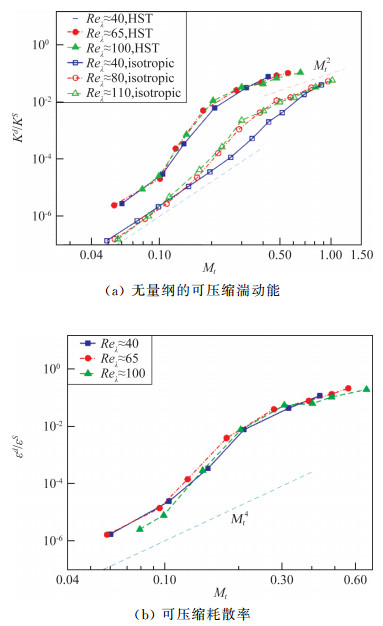
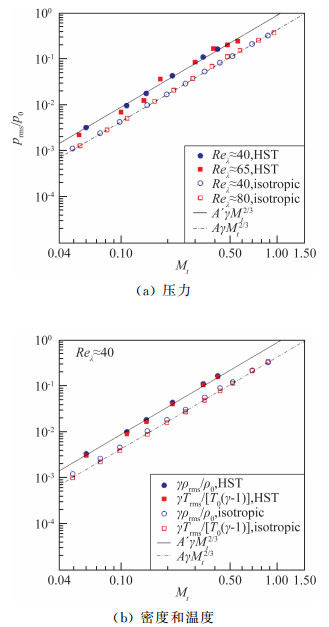
4.1 马赫标度率和能谱

流动的可压缩性随着湍流马赫数的增大而变强。在可压缩均匀剪切湍流中，剪切速度场的各种统计特性对湍流马赫数不敏感，而胀压速度场的能谱和统计量的标度律等则明显依赖湍流马赫数。如图 9所示，在马赫数较小时，均匀剪切湍流的可压缩速度场由伪声模态主导，可压缩湍动能和耗散率呈M_t⁴的标度关系；在马赫数较大时，则由声模态主导，可压缩湍动能呈M_t²的标度关系。同时可以看出，在相同的湍流马赫数下，均匀剪切湍流中的可压缩湍动能和耗散率均明显大于各向同性湍流。Chen^[54]发现增加流体的体积黏性后，各向同性湍流和均匀剪切湍流的可压缩湍动能都会受到抑制，同时导致伪声模态向声模态的转变明显滞后。密度，压力和温度等热力学量的均方根值在低马赫数和高马赫数时均呈M_t²的标度关系，如图 10所示。

4.2 可压缩性对小尺度结构的影响

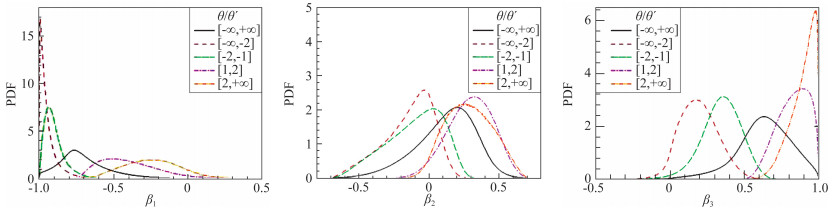
湍流小尺度结构一般用速度梯度张量来描述，它的动力学特性对理解能量级串、间歇性、标量的输运等各种湍流现象非常关键。可压缩性的影响主要体现在速度场的胀压分量，对速度场剪切部分的影响很微弱^[55]。湍流马赫数较小时，变形速度张量S_ij的概率最大的三个特征值之比约为-4∶1∶3，这与不可压缩湍流类似。随着马赫数增大，该比值逐渐趋于-1∶0∶0，表明激波结构的出现。相同的马赫数下，均匀剪切湍流的可压缩性强于各向同性湍流，小尺度结构对马赫数更加敏感^[52]。速度散度θ/θ′的大小描述流场的局部压缩程度。在M_t≈0.6时，均匀剪切湍流的不同压缩程度的区域中，变形速度张量三个特征值的概率分布和条件概率密度分布如图 11所示，可见在θ/θ′≤-2的强压缩区间，大部分特征值的比值都很接近-1∶0∶0，这与各向同性湍流在M_t≈1.0时的结果类似^[37]。在流体的体积黏性较大时，强压缩和强膨胀区间各特征值的概率密度会明显减小^[54]。

分析流场的局部拓扑结构可以进一步了解压缩性对湍流小尺度结构的影响。根据Chong等^[61]提出的拓扑学分类方法，局部流动结构可以通过速度梯度张量A_ij的三个不变量来描述。为了方便分析并与不可压缩流动做比较，一般可以用变形速度偏张量S_ij^*=S_ij-S_kkδ_ij/3 (其第一不变量为0)来分析拓扑结构^{[37, 62]}，它的第二、第三不变量的联合概率密度分布具有一定的普适性。与可压缩各向同性湍流类似^[37], 在均匀剪切湍流中，变形速度偏张量S_ij^*的第二、第三不变量(R^*, Q^*)的联合概率密度分布也具有泪滴状分布，在高马赫数时第四象限会增强，泪滴状分布的尾巴变长^[53]。

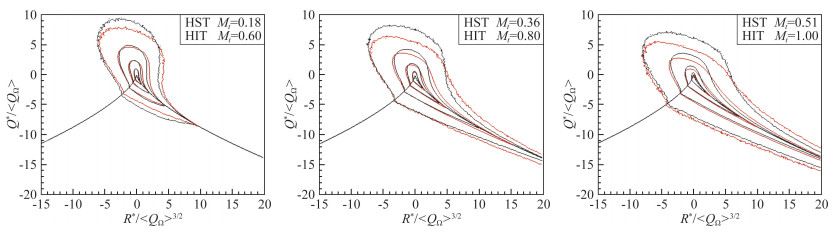
在强压缩区间，均匀剪切湍流和各向同性湍流的(R^*, Q^*)的联合概率密度分布具有明显的相似性，如图 12所示^[53]，并且在均匀剪切湍流中压缩性对(R^*, Q^*)的联合概率密度的影响更加明显。

5 振动非平衡可压缩各向同性湍流

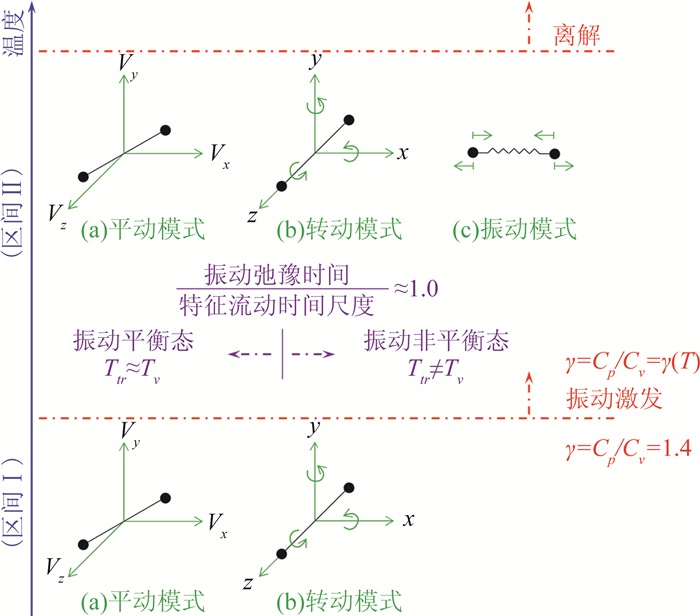
高温气体流动是指在高速高温等极端条件下，气体微团具有分子内部自由度激发，原子、分子间不断发生离解、电离和复合等化学反应，乃至出现辐射和电磁效应等物理化学过程的复杂气体介质流动^[63-65]。高温气体流动在自然界和航空航天等工业领域都极为常见。最典型的例子是通过激波的高超声速流动，高速流体大部分动能被转化为内能并导致流体微团压强和温度急剧增大。当流体微团的压强和温度突然增大时，原本处于平衡状态的振动模式与化学性质将发生变化，并通过分子间碰撞实现新的平衡，因此需要一个特征时间(弛豫时间)来完成。在经历足够长的时间和足够多的碰撞使流体微团达到新的平衡状态后，流体微团已经运动到激波下游一定远距离的位置。因此，在激波后会有一个尚未达到平衡状态的区域——非平衡区。如图 13所示，振动能级被激发后，气体分子的内能添加了振动模式。与平动和转动模式非平衡的弛豫时间相比，振动模式非平衡的弛豫时间要长得多(振动弛豫时间约高出平动与转动弛豫时间4个数量级)。因此，在研究振动能级被激发的可压缩湍流时，通常假设内能的平动和转动模式处于平衡态，而振动模式处于非平衡态，并分别用平动-转动温度(T_tr)和振动温度(T_v)表征(即双温模型^[63])。在激波后很大范围内，平动-转动温度与振动温度存在明显滞后现象^[66]。

当前大部分可压缩各向同性湍流的研究没有考虑振动能级被激发的情况^{[29-30, 37, 39, 44, 50]}，关于振动非平衡和湍流脉动相互作用的研究很少。Donzis和Maqui^[67]通过直接数值模拟方法研究了统计稳态的振动能级被激发的可压缩各向同性湍流，揭示了由于振动非平衡和有限的弛豫时间，内能的平动-转动模式和振动模式之间存在强烈的能量传递。Khurshid和Donzis^[68]进一步研究了自由衰减的振动能级被激发的可压缩各向同性湍流中湍流脉动和振动非平衡的相互作用。研究发现湍流脉动和振动非平衡相互作用的强度取决于振动非平衡的初始程度和弛豫时间的大小。本课题组也开展了振动非平衡的可压缩各向同性湍流统计特性的研究，探讨了湍流马赫数、振动弛豫时间和特征温度、压缩性对振动弛豫率和振动能脉动的影响^[56]。本节主要介绍振动非平衡可压缩湍流的一些基本概念和控制方程，以及大湍流马赫数(M_t=1.09)下的部分研究结果。

5.1 基本控制方程

图 13展示的是振动能级被激发的双原子分子气体内能模式与热非平衡态概念示意图。常温下内能主要包括平动模式和转动模式，在这种情况下比热比等于1.4。当气体振动能级被激发后，内能则添加了振动模式，并根据振动弛豫时间与特征流动时间尺度的关系可分为振动平衡态和振动非平衡态。振动非平衡态气体内能的无量纲形式可表示为：

$ {\varepsilon _{{\rm{in }}}} = \frac{\rho }{{{\gamma _r}{M^2}}}\left[ {\frac{3}{2}{T_{tr}} + {T_{tr}} + \frac{{{\theta _v}}}{{\exp \left( {\frac{{{\theta _v}}}{{{T_v}}}} \right) - 1}}} \right] $

(26)

在这种情况下，气体比热比是温度的函数，而不再为常数。其中θ_v为气体的无量纲振动特征温度。

振动非平衡态下湍流的总能量和振动能的控制方程以及气体状态方程如下所示：

$ \begin{array}{*{20}{c}} {\frac{{\partial \varepsilon }}{{\partial t}} + \frac{{\partial \left[ {(\varepsilon + p){u_j}} \right]}}{{\partial {x_j}}} = \frac{1}{\alpha }\frac{\partial }{{\partial {x_j}}}\left( {{k_{tr}}\frac{{\partial {T_{tr}}}}{{\partial {x_j}}} + {\kappa _v}\frac{{\partial {T_v}}}{{\partial {x_j}}}} \right)}\\ { + \frac{1}{{Re}}\frac{{\partial \left( {{\sigma _{ij}}{u_i}} \right)}}{{\partial {x_j}}} - \mathit{\Lambda } + {{\cal F}_I} + {{\cal F}_j}{u_j}} \end{array} $

(27)

$ {\frac{{\partial {E_v}}}{{\partial t}} + \frac{{\partial \left( {{E_v}{u_j}} \right)}}{{\partial {x_j}}} = \frac{1}{\alpha }\frac{\partial }{{\partial {x_j}}}\left( {{\kappa _v}\frac{{\partial {T_v}}}{{\partial {x_j}}}} \right) + \frac{{E_v^* - {E_v}}}{{{\tau _v}}}} $

(28)

$ {p = \rho {T_{tr}}/\left( {{\gamma _r}{M^2}} \right)} $

(29)

值得注意的是，由于气体压力主要来自分子的平动运动，与分子的转动和振动运动无关。因此气体状态方程中只考虑了平动-转动温度的影响^[69]。振动能控制方程右侧的第二项(振动弛豫率)Q_v=(E_v^*-E_v)/τ_v采用了Landau-Teller弛豫模型^[69]。其中，平衡态和非平衡态的单位体积振动能分别表示为：

$ E_v^* = \frac{{\rho {\theta _v}}}{{{\gamma _r}{M^2}\left[ {\exp \left( {{\theta _v}/{T_{tr}}} \right) - 1} \right]}} $

(30)

$ {E_v} = \frac{{\rho {\theta _v}}}{{{\gamma _r}{M^2}\left[ {\exp \left( {{\theta _v}/{T_v}} \right) - 1} \right]}} $

(31)

τ_v是无量纲的振动弛豫时间，它是局部温度和压力的函数，通常可由如下的关系式获得：

$ {\tau _v} = (C/p)\exp {\left( {{K_2}/{T_{tr}}} \right)^{1/2}} $

(32)

其中，C和K₂是无量纲常数，依赖于气体分子的物理性质。通常可固定K₂的数值并修改C的取值得到不同的振动弛豫时间^{[56, 67-68]}。受限于篇幅，更详细的参数含义和表达式，比如平动-转动温度和振动温度的热传导系数(κ_tr和κ_v)，请参考文献[56]。

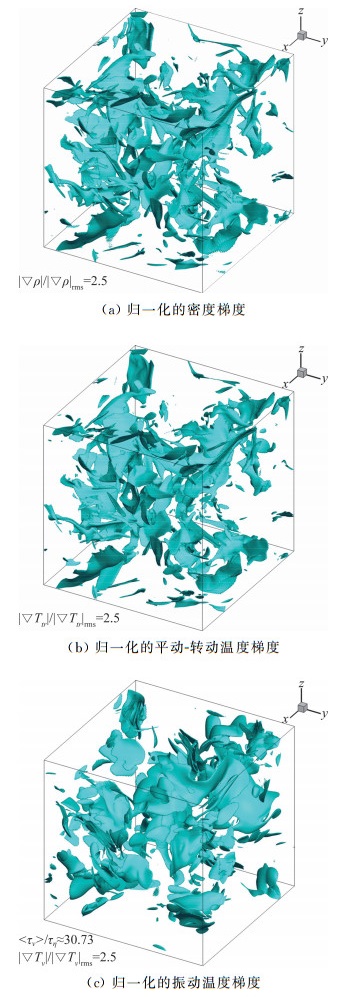
5.2 振动弛豫时间对物理量梯度方向的影响

通常情况下, 在可压缩各向同性湍流流动中密度梯度与速度散度的等值面是重合的，且常用于刻画微型激波的结构。流动中的压缩和膨胀运动对流体微团做功，尤其是激波的强压缩作用，使得可压缩湍流中物理量的变化与气体的压缩性紧密相关，并体现为物理量的梯度和速度散度的等值面重合。图 14展示了归一化的密度梯度、平动-转动温度梯度和转动温度梯度的等值面。在振动非平衡可压缩湍流流动中，压缩和膨胀运动对流体微团做功直接改变的是平动-转动温度，之后通过内能中平动-转动模式和振动模式的弛豫现象，进而改变振动温度。如图 14所示，在归一化弛豫时间〈τ_v〉/τ_η≈30.73时，密度梯度和平动-转动温度梯度的等值面基本重合；而由于有限的弛豫时间，密度梯度与振动温度梯度的等值面则完全不重合。

为了进一步量化密度梯度与振动温度梯度夹角随振动弛豫时间的变化，可通过计算振动温度梯度和密度梯度夹角cosine函数值的概率密度分布函数。振动温度梯度和密度梯度可分别表示为：

$ \begin{aligned} \boldsymbol{G}_{T_{v}}^{*} &=\left(G_{T_{v, 1}}^{*}, G_{T_{v}, 2}^{*}, G_{T_{v, 3}}^{*}\right) \\ \boldsymbol{G}_{\rho}^{*} &=\left(G_{\rho 1}^{*}, G_{\rho 2}^{*}, G_{\rho 3}^{*}\right) \end{aligned} $

(33)

其中，$\mathit{\boldsymbol{G}}_{\phi i}^* = \frac{{\frac{{\partial \phi }}{{\partial {x_i}}}}}{{\sqrt {{{\left( {\frac{{\partial \phi }}{{\partial {x_1}}}} \right)}^2} + {{\left( {\frac{{\partial \phi }}{{\partial {x_2}}}} \right)}^2} + {{\left( {\frac{{\partial \phi }}{{\partial {x_3}}}} \right)}^2}} }}$

振动温度梯度和密度梯度夹角的cosine函数值可表示为:

$ \cos \left\langle\boldsymbol{G}_{T_{v}}^{*}, \boldsymbol{G}_{\rho}^{*}\right\rangle=\left(\boldsymbol{G}_{T_{v}}^{*} \cdot \boldsymbol{G}_{\rho}^{*}\right) /\left(\left|\boldsymbol{G}_{T_{v}}^{*}\right|\left|\boldsymbol{G}_{\rho}^{*}\right|\right) $

(34)

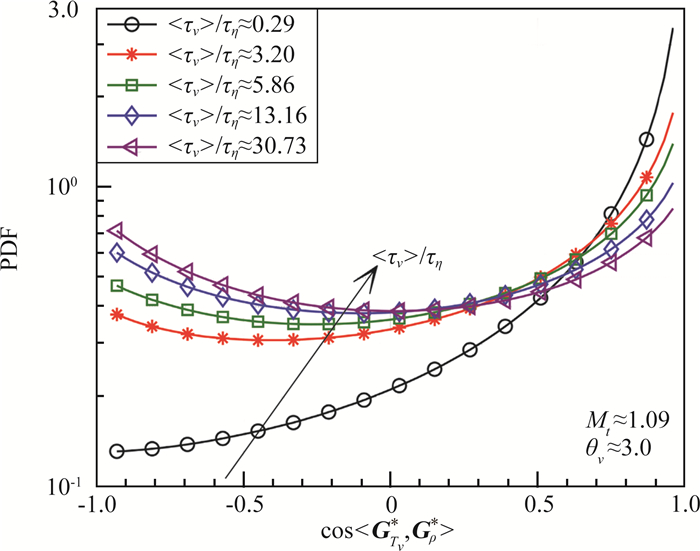
图 15展示的是振动温度梯度和密度梯度夹角cosine函数值的概率密度分布函数随归一化振动弛豫时间的变化规律。显然，在归一化弛豫时间〈τ_v〉/τ_η≈0.29时，振动温度梯度和密度梯度方向近乎重合；随着弛豫时间的增大，振动温度梯度和密度梯度方向逐渐偏离。当〈τ_v〉/τ_η≈30.73时，PDF曲线近乎水平，意味着振动温度梯度和密度梯度方向已完全偏离。

5.3 振动弛豫时间对弛豫率的影响

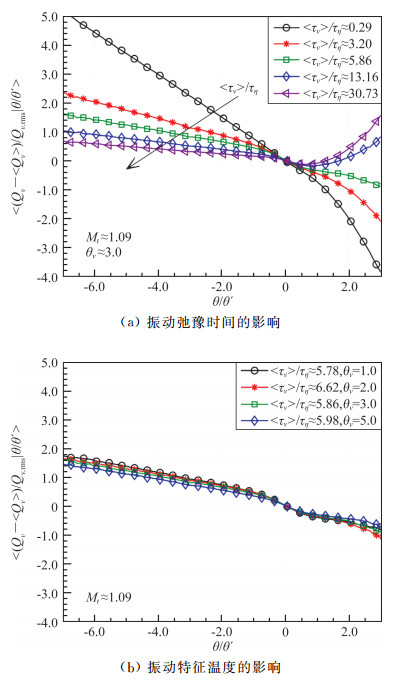
振动弛豫率Q_v=(E_v^*-E_v)/τ_v代表内能中平动-转动模式和振动模式能量交换的速率。对于统计稳态的可压缩各向同性湍流而言，振动弛豫率的系综平均值〈Q_v〉等于0。正的弛豫率代表能量从平动-转动模式向振动模式转化，负的弛豫率则表示反向的能量转化。因此振动弛豫率的均方根值可用于评估内能模式间的能量转化强度。图 16展示的是归一化的振动弛豫率关于速度散度的条件平均。显然，对于高湍流马赫数的情况，压缩性和振动弛豫时间对振动弛豫率均有很大影响。在归一化弛豫时间〈τ_v〉/τ_η≈0.29时，〈(Q_v-〈Q_v〉)/Q_{v, rms}|θ/θ′〉在压缩区域(θ/θ′ < 0)为正值，在膨胀区域(θ/θ′>0)为负值，且随着压缩性的增强而数值逐渐增大。这表明从平均的角度上讲，当弛豫时间较小时，在压缩区域能量从平动-转动模式向振动模式转化，在膨胀区域能量则反向转化；且转化速率随着压缩性的增强而变大。

随着弛豫时间的增大，振动弛豫率的数值逐渐变小，甚至当弛豫时间足够大时，比如〈τ_v〉/τ_η≥13.16，在强膨胀区域甚至出现了反向的能量转化(图 16a)。这是因为如5.2小节所述，当弛豫时间较大时，振动温度梯度和平动-转动温度梯度不再重合，流动的压缩运动无法保证平动-转动温度在平均的角度上大于转动温度；同理，也无法保证在膨胀区域的反向温度差。因此，可以认为弛豫效应弱化了压缩性对振动弛豫率统计特性的影响。图 16(b)则是展示了振动特征温度对归一化弛豫率的影响。不同的振动特征温度对应的曲线相互重叠，即振动特征温度对归一化弛豫率的影响几乎可以忽略。

6 可压缩化学反应湍流

化学反应湍流存在于多种实际流动中，涉及能源、环境、化工、航空航天等领域^[70-72]。湍流-化学反应的时间和空间多尺度相互作用对湍流的动力学性质以及能量传递有重要影响^[73-75]。化学反应湍流的时空多尺度特性以及化学反应与流动的耦合作用对机理研究提出了挑战。目前，采用直接数值模拟手段针对不可压和弱可压缩湍流-化学反应相互作用的研究已有大量的成果^[72-85]。本课题组的研究进一步考虑湍流的可压缩性，探索强可压缩湍流与化学反应的相互作用。

6.1 控制方程

可压缩化学反应均匀各向同性湍流无量纲守恒形式的Navier-Stokes方程组^{[35, 76-77]}如下所示：

$ {\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}} \right)}}{{{x_j}}} = 0} $

(35)

$ {\frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j} + p{\delta _{ij}}} \right)}}{{\partial {x_j}}} = \frac{1}{{Re}}\frac{{\partial {\sigma _{ij}}}}{{\partial {x_j}}} + {\mathit{\Gamma }_i}} $

(36)

$ \begin{array}{*{20}{c}} {\frac{{\partial \varepsilon }}{{\partial t}} + \frac{{\left. {\partial \left[ {(\varepsilon + p){u_j}} \right)} \right]}}{{\partial {x_j}}} = \frac{1}{\alpha }\frac{\partial }{{\partial {x_j}}}\left( {\kappa \frac{{\partial T}}{{\partial {x_j}}}} \right) + }\\ {\frac{1}{{Re}}\frac{{\partial \left( {{\sigma _{ij}}{u_i}} \right)}}{{\partial {x_j}}} + Q - \mathit{\Lambda } + {\mathit{\Gamma }_i}{u_j}} \end{array} $

(37)

$ \begin{array}{*{20}{c}} {\frac{{\partial \left( {\rho {Y_s}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {Y_s}{u_j}} \right)}}{{\partial {x_j}}} = \frac{1}{{Re}}\frac{1}{{Sc}}\frac{\partial }{{\partial {x_j}}}\left( {\mu \frac{{\partial {Y_s}}}{{\partial {x_j}}}} \right) + {{\dot \omega }_s},}\\ {s = 1, \cdots ,{n_s} - 1} \end{array} $

(38)

$ {p = \frac{{\rho T}}{{\left( {\gamma {M^2}} \right)}}} $

(39)

其中，ρ为混合气体密度，u_i为速度分量，p为混合气体压力，T为温度，黏性应力σ_ij根据下式计算得到：

$ {\sigma _{ij}} = \mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{2}{3}\mu \theta {\delta _{ij}} $

(40)

其中，θ=∂u_k/∂x_k为速度散度，Q为化学反应热，Y_s为组分质量分数，${{\dot \omega }_s}$为组分质量变化率，n_s为总的组分数量。单位体积的总能量通过下式计算得到：

$ \varepsilon = \frac{p}{{\gamma - 1}} + \frac{1}{2}\rho \left( {{u_j}{u_j}} \right) $

(41)

为了探索化学反应的能量释放对可压缩湍流的影响，我们选用了单步不可逆简单化学反应来获得化学反应过程中组分的变化以及能量的释放。化学反应方程^[76-77]如下所示：

$ A + B \to 2P $

(42)

反应物和产物的质量变化以及总的能量释放可以通过下式^[76-77]计算得到：

$ \dot{\omega}_{A}=\dot{\omega}_{B}=-\frac{1}{2} \dot{\omega}_{P}=-D a \rho^{2} Y_{A} Y_{B} \exp \left(-\frac{Z e}{T}\right) $

(43)

$ Q=\frac{C e}{(\gamma-1) M^{2}} \dot{\omega}_{P} $

(44)

式中Da为Damköhler数，Ze为Zeldovich数，这两个参数共同控制反应物和产物的组分变化，Ce为放热系数，与产物的组分变化率共同控制反应吸/放热速率。

6.2 流场结构

化学反应对可压缩均匀各向同性湍流不同尺度的流场结构均有影响。尤其对于放热反应而言，化学反应释放的能量首先通过压力膨胀做功传递给动能的胀压部分，进一步，通过对流运动将能量由动能的胀压部分传递给剪切部分^[73]。在能量的传递过程中，胀压运动将导致流场的膨胀和压缩都急剧的增大^{[75, 78]}，流场结构随之发生改变。

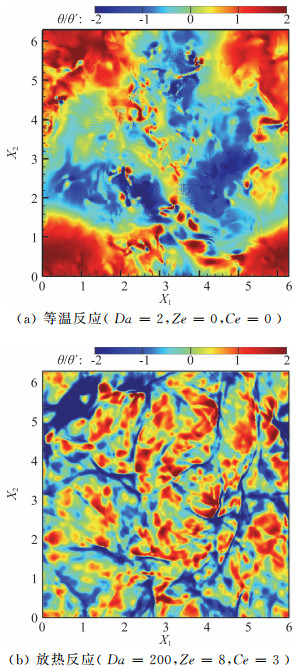
如图 17所示，在低湍流马赫数M_t=0.2状态下，等温反应(Da=2，图 17(a))中，速度散度云图呈现大范围交替出现的压缩和膨胀区域。在放热反应中(Da=200，图 17(b))，流场中出现蓝色条纹状结构。这些条纹状结构对应流场的强压缩区域，为小激波结构。这意味着在弱可压缩湍流中，化学反应放热可以导致小激波这种强压缩结构的出现。

6.3 能谱与标度律

化学反应对可压缩湍流中速度以及热力学量的能谱有重要影响。我们发现，对于放热反应而言，在能量的传递过程中，速度、密度、温度和压力的能谱在所有尺度均有不同程度的增加，并且，在放热反应中，弱可压缩和强可压缩湍流的主导模态均为声学模态^[55]。

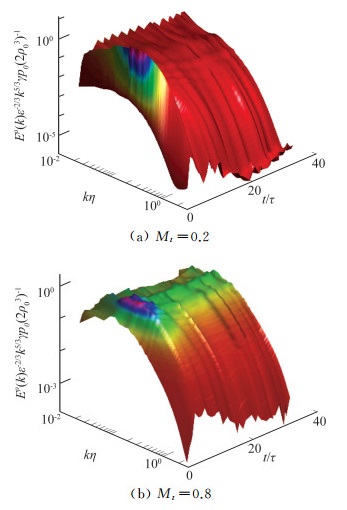
图 18所示为放热反应中(Da=200), 密度归一化能谱随无量纲化学反应时间t/τ的变化，其中τ为大涡翻转时间，t/τ=0对应化学反应的起始时刻。可以看到，在化学反应的初期(0 < t/τ < 5)，密度归一化能谱在所有kη范围均出现大幅度阶跃式增加。随着化学反应的进行，在不同马赫数状态，能谱在各尺度均有所下降，但与反应开始时的初始能谱相比均增大。

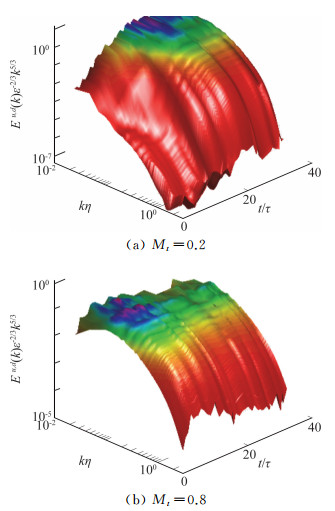
流场压力膨胀做功在可压缩化学反应湍流的能量传输中具有重要作用，因此，进一步分析在放热反应中(Da=200)的速度的胀压分量能谱(图 19)可以得到，速度胀压分量的能谱在放热化学反应中同样呈现在所有尺度范围的增加，但与热力学量能谱的阶跃式增加不同，速度胀压分量能谱呈渐进式增加，在t/τ>20达到统计稳定状态。

密度和速度胀压分量的归一化能谱在化学反应过程中的增加形式进一步说明化学反应使热力学量的能谱能在极短的时间内发生改变，而速度胀压分量能谱的增加依赖于能量传递过程。同时可以发现，弱可压缩湍流中能谱的变化受反应放热的影响大于强可压缩湍流，弱可压缩湍流中能谱的增加更明显。

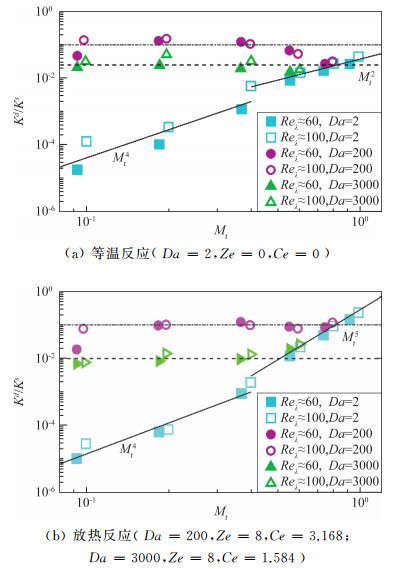
通过分析动能胀压部分与剪切部分比值K^d/K^s以及动能耗散的胀压部分与剪切部分的比值ε^d/ε^s随湍流马赫数的变化，拟合得到了K^d/K^s和ε^d/ε^s的马赫数标度率。如图 20所示，在等温反应中(Da=2)，在弱可压缩范围(M_t < 0.4)，K^d/K^s和ε^d/ε^s均满足M_t⁴标度率。在强可压缩(M_t≥0.4)范围，K^d/K^s满足M_t²标度率，ε^d/ε^s满足M_t⁵标度率。上述标度率与无化学反应的可压缩各向同性湍流的标度率一致^[44]。对于放热反应(Da=200, 3000)而言，K^d/K^s和ε^d/ε^s均表现出湍流马赫数无关性。这表明，在放热反应中，湍流马赫数对动能和动能耗散的影响减弱，而反应放热成为主要影响因素。

7 结论

可压缩湍流包含了丰富的流动结构和物理现象，既有旋涡运动，又包含了膨胀和压缩运动，而且动力学过程和热力学过程相互耦合。我们采用亥姆霍兹分解方法，将可压缩湍流的速度和压力分解为剪切过程和胀压过程，并将胀压过程分解为伪声模态和声模态。我们采用了Kavasznay分解方法，将热力学量的脉动分解为声模态和熵模态。

我们通过研究可压缩湍流的不同物理过程和流动模态的多尺度性质及其相互作用，得到了各类可压缩条件对湍流的速度和热力学量的谱、动能的多尺度传输等物理规律的影响。在弱可压缩湍流中，当伪声模态占主导时，可压缩部分的速度谱在惯性区上具有-3标度律，压力、密度和温度的谱具有-7/3标度律。对于中等可压缩湍流，当声模态占主导时，可压缩部分的速度谱以及热力学量的谱都具有-5/3标度律。对于强可压缩湍流，当大激波结构占主导时，可压缩部分的速度谱以及热力学量的谱都具有-2标度律。随着可压缩性的增强，有更多的动能从速度场的剪切部分传递到胀压部分。然后这些胀压部分的动能通过亚格子流量往小尺度传输，在小尺度上通过黏性耗散转化为内能。

我们进一步讨论了大尺度剪切运动、体积黏性系数、高温非平衡效应、化学反应对可压缩湍流的多尺度性质的影响。在相同湍流马赫数情况下，大尺度的剪切运动会增强湍流的可压缩性。体积黏性会抑制湍流的可压缩性，使得胀压部分更容易被伪声模态占主导。在振动非平衡可压缩湍流中，当弛豫时间较大时，密度梯度与振动温度梯度的等值面完全不重合。弛豫效应弱化了可压缩性对振动弛豫率统计特性的影响。在弱可压缩湍流中，化学反应放热可以极大地增强流动的可压缩性，使得流场出现小激波。在放热反应中，湍流马赫数对动能和动能耗散的影响减弱。

通过这些研究，我们系统地建立和完善了充分发展的可压缩湍流的基本理论，为进一步研究更复杂条件下的可压缩湍流的流动机理以及发展高精度的可压缩湍流大涡模拟方法奠定了坚实的基础。

致谢: 本研究工作得到南方科技大学科学与工程计算中心的支持。