2. 湍流与复杂系统国家重点实验室, 北京 100871
2. State Key Laboratory for Turbulence and Complex Systems, Peking University, Beijing 100871, China
边界层从层流向湍流的转捩问题是一个著名的科学与工程难题。在科学上,转捩是流动从有序向无序转化的过程,是一个典型的强非平衡物理过程。在这一过程中,有序和无序二面达到一定的平衡,这一平衡集中体现了系统的自组织。至今,对这一自组织原理的认识还很不够。具体的科学问题包括:层流边界层平均速度的布拉休斯剖面怎样发展到充分发展湍流边界层的剖面?湍动能(或湍流度)剖面是如何形成和发展的?背后的物理机制和动力学过程是怎样的?控制转捩发生的相似参数及其临界数值是什么?等等。这些都还是尚未解决的问题。在航空航天工程上,气动力和气动热对转捩非常敏感,所以准确预测转捩成为气动设计的关键[1]。而要做到这一点却非常困难,因为转捩机制复杂,受到各种控制参数和环境因素的显著影响[2-4]。目前人们对这种复杂性依然缺乏认识和系统化的描述,难以给出适用性和精准度都满足要求的转捩预测模型。
以往对转捩的研究分别在科学与工程两条线上几乎平行地展开,交集很小,反映出对湍流基本原理认识的不足[5-6]。转捩首先被认为是流动失稳的结果[2],于是长期以来成为线性稳定性理论研究的核心课题。但受限于小扰动假设,以及理论上所设想的扰动形式过于简单,基于稳定性理论的研究与有效预测工程实际中的边界层转捩存在一定距离。非线性方法和其它稳定性理论弱化了解析性,更多依赖经验数据和定性描述,虽然与真实的边界层更加靠近,依然难以实现对转捩的定量精准的理论预测,特别是无法预测转捩中后期的演化。最近由于计算技术的飞速发展,人们通过直接数值模拟(DNS)来研究转捩[7]。DNS以极大计算代价获得与实际比较接近的流动细节,本质上属于数值实验,因为它只能开展一例例实际工况的模拟而不具有超越实验的预测功能。而如何从数据中提炼流动规律并将其转化为具有预测功能的转捩理论和转捩模型,至今依然是未解难题[6]。此外,长期以来经典流体力学研究所关注的特征流动结构(相干结构)的思路,虽然在发现T-S波、流向涡、条带结构、发卡涡和发卡涡包、湍流斑等诸多典型转捩流动结构中有许多收获[8-10],也总结出了猝发、扫掠、涡断裂和重联等动力学过程,却依然没有能够捕捉到工程上关心的转捩特征量(如转捩雷诺数)随物理控制参数变化的普遍性规律,形成普适可靠的工程转捩模型。因此,突破传统稳定性理论的框架、创新湍流流动结构的概念成为突破转捩难题基础研究的关键。
受到应用的驱动,人们发展了许多转捩工程预测方法[2, 11-12],包括经验的转捩关联式、结合稳定性理论和经验数据的eN方法[2]、低雷诺数湍流模型、层流脉动能模型,以及基于间歇因子输运的转捩模型[13-14]等。这些方法的普遍特征是存在过多的变化规律未知的经验参数。尽管这些参数可以通过实验或计算数据来标定,但其普适性并没有得到充分论证,尤其是无法确定在控制参数和环境因素变化时是否具有相似性,因此当向工程复杂边界层推广时,模型的可靠性便成为关键疑点。并且,由于模型方程的高度非线性,以及模型参数与边界层的流动物理之间缺乏直接联系,工程师难以基于对流动物理的理解来调节参数,也无法通过实验对改进参数的验证来增进对流动物理的理解。正因为缺乏基础理论的指导,工程CFD计算强烈依赖个人经验,成为气动设计中的一个突出问题。突破这一问题的根本途径是“从根子上”认识边界层湍流的本质,在基础理论指导下构建工程转捩模型,这样才有望获得参数物理含义清晰的可靠的转捩模型。
本课题组近些年来发展的湍流边界层的结构系综理论(Structural Ensemble Dynamics,SED)[15-19]提供了刻画边界层转捩的新思路,为构建新型工程转捩模型提供了新视角[5-6, 20-23]。首先,SED创新了流动结构概念。它以结构系综的新概念来替代传统的瞬时涡结构,用来刻画一个个包含相似性特征的、由湍流涡集合所填充的空间区域。SED提出的最重要的命题是:任何(复杂的)有统计定态的边界层流动皆拥有少数几个结构系综,每一个结构系综稳定占据一定的流动区域,具有特定的湍流动量和动能的输运性质。其次,SED提出,结构系综必然受到来自环境(固壁)的(对称性)约束。固壁对于边界层流动的约束来自于拉伸对称性,其结果是同一个结构系综所占据的区域内,涡特征尺度随空间坐标满足幂次律(即拉伸对称性成立)。进一步,涡特征尺度由雷诺应力张量和平均剪切根据量纲原理唯一确定,被称为应力长函数。SED的一个重要发现是,相邻结构系综之间应力长函数满足普适的幂次律跃迁形式,称为广义对称性原理。这一原理使得理论上能解析地将空间不同的结构系综连接起来,实现能够覆盖湍流边界层垂向全域的多层结构的解析表述,从而形成描述湍流边界层平均速度和湍动能全剖面的SED解析理论。每一个结构系综由其特征位置、特征标度指数等物理参数所刻画,获得这些参数值便实现了对边界层的完整的物理数学描述。
文献[17-18]以大量的实验和计算数据证明了SED对于槽道、圆管和边界层湍流的精确刻画。将结构系综概念延伸到描述具有显著流向演化的边界层转捩流动,逻辑上非常简单,因为在流向同样存在以边界层前缘为中心的拉伸对称群,只需在流向引进层流区、过渡区和湍流区三大结构系综即可[22-23](与沿垂向的黏性底层、过渡区、对数区非常相似)。这一思路与稳定性理论明显不同,强调的是流动系统的全流域自组织性,物理上对应于一系列不稳定事件在强非线性作用下达到动态平衡时涌现的结构系综,具有只有在系综层面上才会呈现的相似性。因此,采取这一视角来描述转捩过程几乎是不可避免的。传统理论对转捩的刻画在边界层流向的不同发展阶段是由不同的理论和方法来处理的,从而削弱了系统层面的相似性,导致转捩描述和转捩预测问题长期没有得到解决。所以,SED对转捩过程的系统性刻画开启了转捩研究的新模式。它的突出优势在于,针对不同的转捩机制(自然转捩或旁路转捩)和不同的转捩影响因素(来流湍流度、压力梯度等),结构系综是相当稳定的,而且相似性特征非常明显。这一点对于研究工程复杂转捩尤为重要,譬如高超声速转捩涉及几十个影响因素[3, 24],确定相似性是开展高超声速转捩预测的核心,而新型相似性规律将可能在结构系综的描述下诞生。
最近在SED理论指导下诞生了SED-SLT系列代数转捩模型[22-23, 25]。最初的SED-SLT1.0将边界层转捩仅划分为两个流向结构系综——层流系综和湍流系综。在定量描述上,将边界层的两个关键垂向多层结构参数沿流向的演化过程写成从层流系综到湍流系综的两层结构的变化形式。SED-SLT1.0已经可以实现对边界层转捩的摩阻曲线的准确描述;应用到翼型等航空标模的计算中,给出了阻力系数的精准预测,显著超越了以往的模型[22-23]。一个令人鼓舞的发现是,在自由来流湍流(FST)影响的零压力梯度不可压缩光滑平板边界层转捩中,从层流系综向湍流系综跃迁的中心位置(转捩中心,这是对转捩位置的新刻画)相对FST的湍流度呈现出两层结构的标度律[22]。该标度律区别了自然转捩和FST诱发的旁路转捩,描述了两者的过渡过程,与其它转捩经验关联式相比, 与实验数据更加吻合。由于幂次律是相似性规律的呈现形式,这个发现证明了多层结构物理参数的确能够抓住转捩随流动控制参数和环境因素变化时的相似性,从而为SED-SL模型在更宽参数域内保持有效性提供了理论依据。
本文将介绍近期对SED-SLT1.0的进一步发展。我们更加细致地识别和确定了由FST诱发的边界层强迫转捩的各个流向结构系综,因此获得了对转捩中雷诺应力和湍动能各个分量的精准刻画。这一进展对于人们理解转捩中湍流脉动量的生成与演化机制,以及构建基于湍动能的转捩模型都具有重要意义。由于结构系综的稳定性,新确定的转捩结构系综也为研究其他类型的边界层转捩奠定了基础,本文通过将SED-SLT模型应用于计算带攻角的高超声速尖锥转捩流动初步证明了这一点。此外,为了方便读者理解和掌握SED的研究方法,本文还特别介绍了从实验和计算数据出发,构建工程湍流模型的完整的研究步骤,以期为学界和业界发展和应用SED理论,针对各种工程复杂流动开展湍流模型创新,提供较为系统的技术方案。
1 结构系综理论新思路 1.1 结构系综理论对转捩边界层的描述结构系综是我们针对壁湍流研究所提出的一个重要概念。它从边界层方程所满足的拉伸对称性出发,提出不同流动区域的湍流脉动自组织成不同的结构系综,其统计特性由应力长的广义拉伸对称性所刻画,即在结构系综内应力长随空间坐标以幂次律变化,跨系综则遵循普适的跃迁函数形式。这一概念成为构建壁湍流平均场理论的基础。
应力长是对普朗特混合长的概念拓展,定义为:
| $ {\ell _{ij}} = \frac{{\sqrt {\langle |{u_i}{u_j}|\rangle } }}{{\frac{{\partial U}}{{\partial y}}}} $ | (1) |
其中ui(i=1, 2, 3)为脉动速度分量,U为平均流向速度,y为垂向坐标,| |表示绝对值,〈〉表示系综平均。在平板边界层中存在四个非零的应力长:ℓ12称剪切应力长(即混合长),用其封闭涡黏系数可以求解边界层的平均速度分布;ℓ11、ℓ22、ℓ33分别为流向、垂向和展向的动能长,它们与平均速度剪切一起决定了湍动能各个分量的分布。SED确定的湍流边界层的应力长剖面的表达式为:
| $ \ell _{ij}^ + = {\varPhi _{ij}}({y^ + })\varPsi (r) $ | (2) |
其中加号表示以壁面尺度归一化;Ψ(r)为外区剖面,是SED给出的新的尾流函数。对于剪切应力长和三个动能长,Ψ(r)的形式是一致的:
| $ \varPsi (r) = \frac{{1 - {r^4}}}{{4(1 - r)}} $ | (3) |
其中r为边界层外区坐标,r=1-y/δe,δe为外区拉伸对称中心的位置。在充分发展湍流边界层中δe约等于边界层厚度δ99。Φij(y+)为内区剖面,表达式分别为:
| $ {\varPhi _{12}}({y^ + }) = \ell _{12 - 0}^ + {\left( {\frac{{{y^ + }}}{{9.7}}} \right)^{\frac{3}{2}}}{\left[ {1 + {{\left( {\frac{{{y^ + }}}{{9.7}}} \right)}^4}} \right]^{\frac{1}{8}}}{\left[ {1 + {{\left( {\frac{{{y^ + }}}{{y_{{\rm{ buf }}}^ + }}} \right)}^4}} \right]^{ - \frac{1}{4}}} $ | (4a) |
| $ {\varPhi _{11}}({y^ + }) = \ell _{11 - 0}^ + {\left( {\frac{{{y^ + }}}{{9.7}}} \right)^1}{\left[ {1 + {{\left( {\frac{{{y^ + }}}{{9.7}}} \right)}^4}} \right]^{\frac{1}{8}}}{\left[ {1 + {{\left( {\frac{{{y^ + }}}{{y_{{\rm{ buf }}}^ + }}} \right)}^4}} \right]^{ - \frac{1}{8}}} $ | (4b) |
| $ {\varPhi _{22}}({y^ + }) = \ell _{22 - 0}^ + {\left( {\frac{{{y^ + }}}{{9.7}}} \right)^2}{\left[ {1 + {{\left( {\frac{{{y^ + }}}{{9.7}}} \right)}^4}} \right]^{\frac{1}{8}}}{\left[ {1 + {{\left( {\frac{{{y^ + }}}{{y_{{\rm{ buf }}}^ + }}} \right)}^4}} \right]^{ - \frac{3}{8}}} $ | (4c) |
| $ {\varPhi _{33}}({y^ + }) = \ell _{33 - 0}^ + {\left( {\frac{{{y^ + }}}{{9.7}}} \right)^1}{\left[ {1 + {{\left( {\frac{{{y^ + }}}{{9.7}}} \right)}^4}} \right]^{\frac{1}{4}}}{\left[ {1 + {{\left( {\frac{{{y^ + }}}{{y_{{\rm{ buf }}}^ + }}} \right)}^4}} \right]^{ - \frac{1}{4}}} $ | (4d) |
式(4)分别描述了四个应力长在黏性底层的标度律,以及之上向缓冲层和对数区的两次标度跃迁。标度跃迁满足如下的普适函数形式(SED基函数):
| $ {\left[ {1 + {{\left( {\frac{{{y^ + }}}{{y_c^ + }}} \right)}^n}} \right]^{\frac{\varDelta }{n}}} $ | (5) |
其中yc+为跃迁发生的空间位置,n为刻画跃迁快慢的参数,Δ为标度指数的跃迁量。式(4)具有非常简单的解析构造——新的结构系综通过以普适跃迁函数为乘子的方式逐层引入。这种连乘形式与量纲分析极其类似,本质上两者都源于拉伸对称性原理。在式(4)中,9.7是SED确定的黏性底层的厚度,由于非常靠近壁面,在固壁的强约束下黏性底层具有一定的普适性,其厚度可认为在各种流动中基本保持不变;ybuf+是缓冲层的厚度,即近壁拟序涡层的厚度,受到各种边界层效应的显著影响,对于充分发展的规范湍流边界层,ybuf+=ybuf∞+≈41。lij-0+为近壁涡特征尺度,其中l12-0+=κ9.72/ybuf+,在充分发展的湍流边界层中,卡门常数κ=0.45[26],l12-0+=l12-0∞+≈1.03。
以剪切应力长封闭湍流涡黏系数,通过数值求解边界层方程,即可给出充分发展的湍流边界层平均场的精确预测,这是得到一系列数据支撑的结论[17-18, 26]。在转捩中,边界层由层流的垂向单层结构(布拉休斯自相似解)演变为湍流的垂向四层结构(式(3)和式(4a))。这个流向演化过程在SED-SLT1.0中,被模化为两个关键多层结构参数ybuf+和l12-0+所满足的相对于边界层前缘的流向两层结构的变化[22]:
| $ {l_{12 - 0}^ + = l_{12 - 0\infty }^ + {{\left( {\frac{x}{{{x_{{\rm{ tran }}}}}}} \right)}^{{\gamma _l}}}{{\left[ {1 + {{\left( {\frac{x}{{{x_{{\rm{ tran }}}}}}} \right)}^{10}}} \right]}^{ - \frac{{\gamma l}}{{10}}}}} $ | (6a) |
| $ {y_{{\rm{ buf }}}^ + = y_{{\rm{ buf }}\infty }^ + {{\left( {\frac{x}{{{x_{{\rm{ tran }}}}}}} \right)}^{{\gamma _b}}}{{\left[ {1 + {{\left( {\frac{x}{{{x_{{\rm{ tran }}}}}}} \right)}^{10}}} \right]}^{ - \frac{{\gamma b}}{{10}}}}} $ | (6b) |
式(6a)描述了l12-0+在层流区以xγl的标度律增长,之后趋于充分发展湍流边界层的常值,其中xtran是从层流区到湍流区的跃迁中心,是对转捩位置的新的刻画——它介于摩阻曲线的最低点(传统上的转捩起始位置)和最高点(传统上的转捩结束位置)之间。式(6b)描述了ybuf+的两层结构流向演化,与l12-0+类似。两个标度指数γl和γb是与转捩类型相关的经验参数。在外界扰动较小的情况下(如湍流度不太大的FST),l12-0+与层流边界层厚度的增长速度一致,即γl=0.5;对于由粗糙度或壁面吹吸等强扰动诱发的强迫转捩,γl会显著大于0.5。γb刻画了缓冲层厚度的增长率,反映了不同转捩因素对转捩拟序涡结构的影响。
式(6)中最关键也是工程上最关心的参数是转捩中心位置xtran。与Menter的γ-Reθ四方程转捩模型类似,为了使模型封闭,需要发展xtran所对应的转捩雷诺数Rextran的经验关联式。对于FST诱发的平板边界层转捩,我们基于实验和计算数据提出了Rextran随湍流度Tu变化的如下式[22]:
| $ R{e_{x{\rm{ trans }}}} = 3.3 \times {10^6}{\left[ {1 + {{\left( {\frac{{Tu}}{{0.65}}} \right)}^4}} \right]^{ - \frac{{1.5}}{4}}} $ | (7) |
式(7)显示Rextran随Tu的增加呈现两层结构的广义标度律:自然转捩时(Tu0.65%)Rextran为常值;强FST时(Tu0.65%)时Rextran随Tu的增加以-1.5次方的标度律减小。与以往的经验关联式相比,式(7)不仅定量更加精准,还给出了转捩雷诺数随Tu的多层结构相似律,这表明xtran是对转捩位置更加物理的刻画。
式(2)~式(7)构成了求解转捩边界层全流域平均速度分布的SED-SLT1.0代数转捩模型。肖梦娟和佘振苏成功地将SED-SLT1.0用于平板、翼型等标模流动的计算,准确预测了边界层转捩的摩阻系数分布[22-23],与经典模型相比,将翼型阻力的计算误差降低了约一个数量级[23]。
式(6)对转捩过程的流向结构系综划分是初步的,还不能准确描述摩阻系数和雷诺应力分布的更加细节的变化,也就是说,在边界层转捩中还存在一些次导的结构系综。仔细识别和确定这些次导结构系综,形成对转捩边界层“逐级近似”的认识,对于构建边界层转捩的理论框架、研究更复杂的工程转捩边界层具有重要意义。此外,转捩最重要的特征是湍流脉动能的形成与发展,这些信息包含在三个动能长函数的多层结构的演化之中,没有被SED-SLT1.0模型所描述。针对湍动能分布开展理论描述,对于理解转捩中湍流脉动量的生成与演化机制、构建基于湍动能的转捩模型和湍流模型都具有重要意义。本文将简要介绍近期在这两方面研究内容上取得的进展,并将新的SED-SL模型用于一种典型的工程复杂边界层转捩流动——有攻角的高超声速尖锥。
以上研究采用了同样的研究方法,即从实验和高精度计算数据中挖掘流动的结构系综,通过应力长的广义拉伸对称性实现对结构系综的全流域解析描述和对复杂转捩边界层平均场的理论预测,进而构建适用于该类型流动的新型SED-SL代数转捩模型。下面我们来介绍这一SED的湍流研究方法。
1.2 研究复杂转捩边界层的SED方法如前所述,我们认为湍流研究的一个重要课题是基于实验和高质量的计算数据确定实际流动中的结构系综,从而形成对复杂边界层的统计特性的精准描述,在此基础上产生可靠的工程计算模型。这里高质量的计算数据包括DNS、高分辨率的LES,以及经验证确认可靠的RANS算例等。
DNS包含了所有的流动细节,但通常雷诺数不够大,模型的几何构型相对简单,工况数目极为有限。但是,由于结构系综抓住了边界层流动的相似性,通常具有宽幅的雷诺性不变性,因此,对DNS数据开展SED分析,能够提供许多工程边界层流动的结构系综的定量信息,为构建可靠的工程转捩模型奠定基础。在SED理论的发展过程中,我们建立了一套对DNS湍流大数据开展结构系综分析的方法,总结为序函数分析三部曲:(1)针对DNS数据开展应力长函数的广义拉伸不变性分析,确定结构系综及其个数;(2)具体测量实际流动的多层结构参数,并验证多层结构表达式对平均场的预测精度;(3)针对流动条件的变化,确定多层结构参数的变化规律,实现具有预测性功能的工程模型,同时给出对实际边界层流动的物理刻画(与其他边界层流动的定量区别)。SED在上述序函数分析的各个阶段都发展了一系列具体的方法,包括定义序函数的准则、确定多层结构参数的诊断函数和测量方法、构建参数物理模型的理论构思,等等,详细内容可参考陈曦、唐帆等人的博士论文[25-26]。
大量的工程复杂边界层湍流(尤其是高超声速飞行器流动)通常只能提供不完整的流场测量数据。在这种情况下,结构系综研究需要采取一种后验的策略,即基于已有的经验,考虑从已有流动到新的流动中多层结构物理的变化,人为地设置多层结构的修正,将新的预测与有限的实验或(可靠的)计算数据进行比较,来确定新参数的有效性。这种后验方法的适用性更强,对面向工程实际问题的研究更有价值。下面介绍这种工程化的分析方法。
这种方法面向常规的实验数据类型,比如流场空间几个位置的平均速度剖面,或者壁面若干位置的压强、温度、摩阻或热流分布,以及一系列工况下的升阻力和力矩等,都可以应用该方法。这是因为流动的结构系综数目通常为少数几个,且多层结构随空间有缓变的特征,多层结构参数的总数是极为有限的,因此有一定空间分布的实验数据会对多层结构参数形成强约束,可以通过不断优化预测结果与实验数据的相似度实现对多层结构参数的确定。
以边界层转捩中壁面摩阻或热流的实验或计算曲线为例,SED-SLT1.0假定了层流边界层和湍流边界层两个主导的流向结构系综,再通过两个关键的垂向多层结构参数在流向相对边界层前缘的两层结构演化形式(式(6b))来对转捩边界层进行定量描述,其中包含了xtran、l12-0∞+、ybuf∞+、γl和γb共计5个多层结构参数,它们相对独立其具有清晰的物理内涵:xtran决定了转捩位置;l12-0∞+和ybuf∞+分别刻画了转捩后湍流边界层的近壁涡尺度和涡层厚度(在翼型等流动中它们受到压力梯度等效应的影响,可能偏离规范湍流边界层的理论值),主要影响转捩后边界层的发展;γl和γb分别描述了近壁涡尺度和涡层厚度在转捩过程中的增长速度,决定了转捩的快慢。对这几个模型参数进行预设后,通过求解基于SED-SLT1.0模型的RANS方程可以得到对转捩边界层摩阻系数分布的预测,与实验数据进行比较,进而通过调节模型参数使计算误差逐步达到最小。这一过程可以在人为的干预下快速迭代完成,原因是SED-SL的模型参数具有显著的物理含义,工程师可以基于对流动物理的判断(快了?慢了?厚了?薄了?)理性地调节这些参数。在以上述方式确定模型参数之后,就可以进一步构建模型参数随流动控制参数(如马赫数、攻角、壁温等)变化的相似性规律,实现完整的转捩模型,对其他工况下的边界层转捩开展预测。
本文以FST诱发的平板边界层强迫转捩和有攻角的高超声速尖锥转捩两种复杂边界层转捩流动为例来展示上述分析过程。
针对FST诱发的平板边界层强迫转捩,我们发现SED-SLT1.0还不能精准预测摩阻曲线的所有细致变化,原因是存在层流边界层和湍流边界层之外的其它次导的流向结构系综。这些次导系综现在被辨识为转捩过冲系综、外区发展系综和转捩弛豫系综(或有限雷诺数湍流系综)等。新系综的引入遵循了普适的对称破缺法则,即在原流向两层结构模型中引入新的普适跃迁函数乘子,刻画相应结构系综的平均场效应。新结构系综的存在性和参数的独立性以能够唯一精准刻画实验或计算曲线(包括但不限于摩阻曲线)为依据,以流动物理为支撑。包含转捩过冲系综的SED-SL模型称为SED-SLT2.0,它实现了对转捩过冲现象的描述。包含全部三个次导流向系综的SED-SL模型称为SED-SLT3.0,它实现了对FST诱发的平板边界层强迫转捩的摩阻系数、平均速度和雷诺应力在转捩全流域的精准描述。3.0模型的所有结构系综一起构成了对转捩边界层的多层结构更加完整的刻画,为研究其他复杂转捩边界层奠定了基础。类似的分析还被拓展到湍动能各个分量的研究,首次形成了对湍动能在转捩全流域的精准理论描述。
有攻角的高超声速尖锥转捩流动是受到广泛研究的航天标模,也是挑战转捩模型的难题。我们针对不同攻角下高超声速尖锥转捩的表面红外图像数据实践了上述研究框架。通过与实验数据的比较确定了SED-SL模型的多层结构参数随攻角和周向角的变化,准确复现了尖锥表面的实验数据。进一步的研究正在提炼多层结构参数与流场局部流动参量的关联关系,使得模型具备在宽参数域内对尖锥转捩流动的精准预测能力。下面简要介绍这些结果。
2 对平板转捩的全分量和全流域的刻画FST诱导的零压力梯度不可压缩光滑平板边界层转捩被认为是研究转捩的标准模型,长期以来积累了大量的实验和计算数据,包括一些基准实验,如S & K实验和T3系列平板转捩实验[27],被广泛用于转捩模型的验证。目前人们针对这些实验已开展了不少的DNS、LES和RANS计算,但尚未形成转捩理论或转捩模型能够描述所有的实验数据,尤其是针对大湍流度下的平板转捩数据,尚不存在精准可靠的转捩模型。此外,更没有理论或模型能预测湍流脉动量的演化。这里我们结合实验和DNS数据,细致研究了有较大来流湍流度的T3B平板转捩流动的各个流向结构系综,形成了对FST诱导边界层转捩流动开展全分量、全流域精准描述的SED-SLT3.0代数转捩模型。
2.1 SED-SLT2.0和SED-SLT3.0代数转捩模型T3B是较大来流湍流度(~6.5%)诱发的平板边界层强迫转捩。当前流行的一些转捩模型,如Menter的四方程转捩模型[13],难以准确预测T3B的实验摩阻曲线(图 1)。T3B摩阻曲线的一个重要特征是所谓转捩过冲现象,即摩阻系数的峰值显著超越了湍流边界层的摩阻曲线在该雷诺数下的数值。转捩过冲的出现反映了转捩中涡结构出现了过度发展,通常源于强外界扰动,如壁面有粗糙度或边界层吹吸、存在来流强湍流等情况。在高速流动中,当热流出现显著的转捩过冲时,固壁的热负荷会大大增加,需要进行热防护,因此转捩过冲受到了气动设计部门的重视。近年来阎超等针对转捩过冲的模拟做了一系列富有成效的工作[28]。转捩过冲也会带来明显的转捩后湍流边界层的弛豫过程。
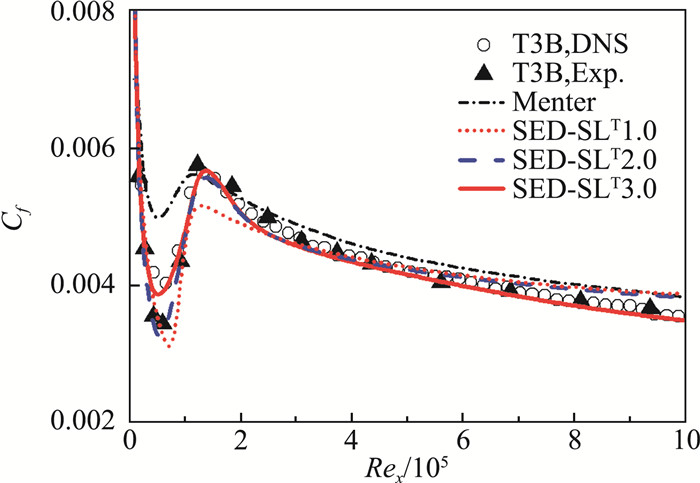
|
图 1 SED-SLT3.0对T3B摩阻曲线的计算结果与T3B的实验、DNS,以及SED-SLT1.0、SED-SLT2.0和Menter转捩模型计算结果的比较.值得指出的是,实验与DNS计算在转捩区还是稍有差别,而SED-SL模型是可以描述这一差别的 Fig.1 Comparisons between the skin friction coefficients of T3B calculated by SED-SLT1.0, SED-SLT2.0, SED-SLT3.0, Menter's model, and those measured in experiment (Exp.) and DNS. It is worthy pointing out that subtle difference exists between EXP and DNS, which can be described both by the SED-SLT3.0 model |
我们发现SED-SLT1.0不能给出转捩过冲的预测。从物理上看,转捩过冲出现的原因是,在强FST扰动下转捩边界层中的涡结构与来流湍流脉动发生了强相互作用,于是出现了过度发展的情况,即在转捩区存在一个强湍流激发态,形成了显著增强的动量和能量输运。这一强激发态是一个新的流向结构系综,主要发生在涡结构最强的缓冲层的变化上,可以通过在ybuf+中引入新的普适跃迁函数乘子给予刻画:
| $ \begin{array}{l} y_{{\rm{ buf }}}^ + = y_{{\rm{ buf }}\infty }^ + {a^{\Delta \gamma }}{(\frac{x}{{{x_{{\rm{ tran }}}}}})^{{\gamma _b}}}{[1 + {(\frac{x}{{{x_{{\rm{ tran }}}}}})^{10}}]^{ - \frac{{(\gamma b + \Delta \gamma )}}{{10}}}} \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left[ {1 + {{\left( {\frac{x}{{a{x_{{\rm{ tran }}}}}}} \right)}^{10}}} \right]^{\frac{{\Delta \gamma }}{{10}}}} \end{array} $ | (8) |
与式(6b)相比,式(8)为流向三层结构,分别为x≤xtran、xtran≤x≤axtran和x≤axtran。式(8)中Δγ为描述转捩过冲强度的奇异标度指数;a>1为转捩过冲结束位置相对转捩中心位置的比例因子。γb、Δγ和a目前都是与具体流动有关的经验参数,在T3B中,γb≈5.5,Δγ≈1.2,a≈1.5。我们把式(8)的修正称为SED-SLT2.0,它对T3B的预测结果如图 1所示。可以看到SED-SLT2.0抓住了摩阻曲线的转捩过冲,但对转捩后期湍流边界层摩阻的预测仍然出现一定程度的偏差。
这种偏差源于转捩后湍流边界层仍然需要经历一个较长的弛豫过程,才能进入充分发展的相似区(即多层结构沿流向不再变化)。在这个驰豫过程中,l12-0+和ybuf+依然存在流向的缓慢变化,之后才达到SED所预测的常值l12-0∞+和ybuf∞+。这种弛豫过程实际上就是有限雷诺数的湍流边界层,也就是说,有限雷诺数湍流边界层可看作是转捩的后期演化。因此,为刻画转捩后的有限雷诺数湍流边界层效应,有必要在l12-0+和ybuf+的流向演化中(分别为式(6a)和式(8))分别引入描述转捩弛豫系综的普适跃迁函数乘积因子:
| $ {{\theta _l} = {{\left[ {1 + {{\left( {\frac{x}{{{x_1}}}} \right)}^4}} \right]}^{ - \frac{{0.2}}{4}}}{{\left[ {1 + {{\left( {\frac{x}{{1.9{x_1}}}} \right)}^4}} \right]}^{ - \frac{{0.2}}{4}}}} $ | (9a) |
| $ {{\theta _b} = {{\left[ {1 + {{\left( {\frac{x}{{{x_1}}}} \right)}^4}} \right]}^{\frac{{0.1}}{4}}}{{\left[ {1 + {{\left( {\frac{x}{{2.4{x_1}}}} \right)}^4}} \right]}^{ - \frac{{0.1}}{4}}}} $ | (9b) |
之前在规范湍流边界层的研究中我们已发现l12-0+和ybuf+有显著的有限雷诺数效应:随雷诺数的增加,l12-0+逐渐减小而ybuf+逐渐增加,直至趋于充分发展湍流边界层的常值。式(9a)和式(9b)分别通过引入-0.2和0.1两个小的经验奇异标度指数修正描述了这种变化趋势。式(9)中x1是有限雷诺数湍流边界层进入奇异标度区的起点,在T3B的流动中被经验地确定为Rex1=6.5×105(见图 1)。式(9)中1.9x1和2.4x1分别标志了近壁涡尺度和缓冲层厚度趋于充分发展的位置,它们是与x1相关的,并非独立参数。这里需要再次强调的是,式(9)是对转捩后湍流边界层的有限雷诺数效应的一个经验刻画,建立在对T3B摩阻系数的精确预测基础之上。湍流边界层的有限雷诺数效应是一个被广泛讨论的重要科学问题,式(9)还需要在一般情况下,结合更多的观测数据进行研究。
此外,在边界层转捩的前期,各种实验和DNS均表明湍流首先从近壁开始发展,逐渐扩散到边界层外区,最后才形成外区的亏损型标度律(式(3))。SED-SLT1.0模型未考虑垂向外区结构在转捩中的生成过程,导致了雷诺应力在边界层转捩的前期被显著低估。为了表达外区结构从无到有的生长过程,我们引入了外区发展系综的经验刻画:
| $ \sigma = \frac{{{\delta _e}}}{{{\delta _{99}}}} = 1.6{\left[ {1 + {{\left( {\frac{x}{{0.5{x_{{\rm{ tran }}}}}}} \right)}^4}} \right]^{ - \frac{1}{4}}}{\left[ {1 + {{\left( {\frac{x}{{{x_{{\rm{ tran }}}}}}} \right)}^4}} \right]^{\frac{1}{4}}} $ | (10) |
式(10)在定量上的表现为:在层流区,外区拉伸对称中心δe远在边界层厚度(δ99)之外,因此在边界层内Ψ(r)≈1,外区结构不存在;转捩后,外区拉伸对称中心趋于边界层厚度,外区结构形成。
包含以上转捩过冲系综、转捩弛豫系综和外区发展系综的SED-SL模型称为SED-SLT3.0模型,它能够精确描述不同湍流度的FST诱发的平板边界层转捩流动的摩阻、雷诺应力和平均速度在转捩全流域的分布。图 1为SED-SLT3.0对T3B摩阻系数的模拟结果。图 2和图 3分别为SED-SLT3.0对平均速度和雷诺应力剖面在转捩各个阶段的模拟结果。模型预测结果与DNS吻合非常好,说明SED-SLT3.0抓住了FST诱发转捩的全部结构系综。这些结构系综可以作为转捩多层结构的基本设置,用于研究其它类型的边界层转捩。
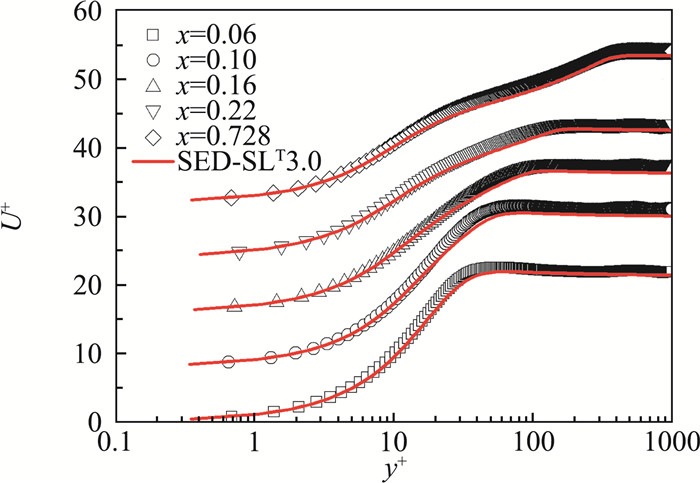
|
图 2 SED-SLT3.0对T3B平均速度剖面的计算结果与T3B DNS的比较.五条曲线分别为五个流向不同位置,覆盖了从转捩极早期到转捩后期 Fig.2 Comparisons between the SED-SLT3.0 calculated mean velocity profiles and the DNS data at five streamwise locations covering the laminar region, the transition region and the turbulent boundary layer region |
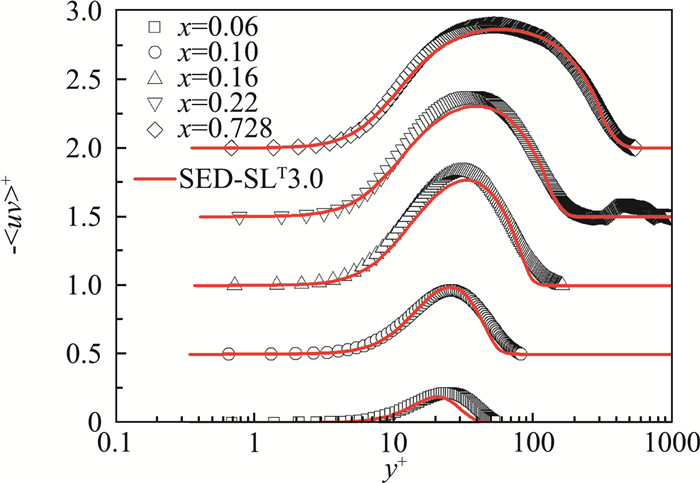
|
图 3 SED-SLT3.0对T3B雷诺应力剖面的计算结果与T3B DNS的比较.五条曲线分别为五个流向不同位置,覆盖了从转捩极早期到转捩后期 Fig.3 Comparisons between the SED-SLT3.0 calculated Reynolds shear stress profiles and the DNS data at five streamwise locations |
边界层转捩最明显的特征是脉动量从层流区到湍流区的极大增长,因此研究湍动能(或湍流度)剖面在边界层流向的发展对理解转捩物理具有重要意义。并且,湍动能作为一个局部流动参量也是众多湍流模型和转捩模型所模拟的关键变量,发展湍动能剖面的理论描述对转捩模型研究也具有重要价值。我们基于结构系综概念对湍动能在平板转捩全流域的分布实现了初步的定量理论描述,这是转捩研究中的首次。
根据动能长的定义(式(1)),对湍动能的预测可以由动能长和(已计算得到的)平均剪切来实现。由于三个动能长具有极为类似的垂向和流向多层结构,为简洁起见,这里仅以流向动能长为例进行说明。计算流向湍动能的理论公式为:
| $ {\langle uu\rangle ^ + } = {\left( {l_{11}^ + \frac{{{\rm{d}}{U^ + }}}{{{\rm{d}}{y^ + }}}} \right)^2} + {U^{ + 2}}\frac{{{{\langle uu\rangle }_\infty }}}{{{U^2}}}f(\frac{{{y^ + }}}{{R{e_\tau }}}) $ | (11) |
其中式(11)等号右侧第二项描述了FST在流向和垂向的衰减,我们称之为自由来流湍流衰减系综。式(11)中,
| $ \frac{{{{\langle uu\rangle }_\infty }}}{{{U^2}}} = a{\left( {\frac{{x - {x_0}}}{l}} \right)^{ - n}} $ | (12a) |
| $ f(\frac{{{y^ + }}}{{R{e_\tau }}}) = \left( {\frac{{{y^ + }}}{{0.5R{e_\tau }}}} \right){\left[ {1 + {{\left( {\frac{{{y^ + }}}{{0.5R{e_\tau }}}} \right)}^4}} \right]^{ - \frac{1}{4}}} $ | (12b) |
式(12a)为文献上普遍采用的刻画均匀各向同性湍流自由衰减过程的经验表达式[29],其中几个参数由DNS数据来确定。式(12b)描述了FST向边界层内的贯穿,它被模化为由垂向的线性壁面律和边界层之上的均匀湍流两层结构构成。注意到FST对边界层内湍动能的贡献与边界层自身的湍动能分布存在耦合,要在定量上对二者进行区分尚需要深入的研究,式(12b)提供了一个初步的模型,对湍动能预测可能带来一定误差。与剪切应力长的流向演化类似,流向动能长也存在三个主导多层结构参数(ℓ11-0+,ybuf+,σ)的多层结构形式的流向变化,其中ybuf+和σ与剪切应力长相同,ℓ11-0+的表达式为流向三层结构:
| $ \begin{array}{l} \ell _{11 - 0}^ + = \ell _{11 - 0\infty }^ + {0.8^{ - 0.2}}{\left( {\frac{x}{{0.8{x_{{\rm{tran}}}}}}} \right)^{1.0}}{\left[ {1 + {{\left( {\frac{x}{{0.8{x_{{\rm{tran}}}}}}} \right)}^{10}}} \right]^{ - \frac{{1.2}}{{10}}}} \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left[ {1 + {{\left( {\frac{x}{{{x_{{\rm{ tran }}}}}}} \right)}^{10}}} \right]^{\frac{{0.2}}{{10}}}} \end{array} $ | (13) |
我们将对湍动能的预测模型也称为SED-SLT3.0。针对T3B的湍动能的预测结果如图 4~6所示。SED-SLT3.0的预测结果与T3B的DNS数据在转捩全流域都符合良好,这是首次由转捩模型给出在边界层转捩全流域的湍动能分布的定量精准的预测结果。SED-SLT3.0对湍动能剖面的参数化, 对后续理解转捩物理,预测转捩中湍流脉动量的生成和发展机制,以及评估和修正基于湍动能输运方程的转捩模型都具有极重要的意义。
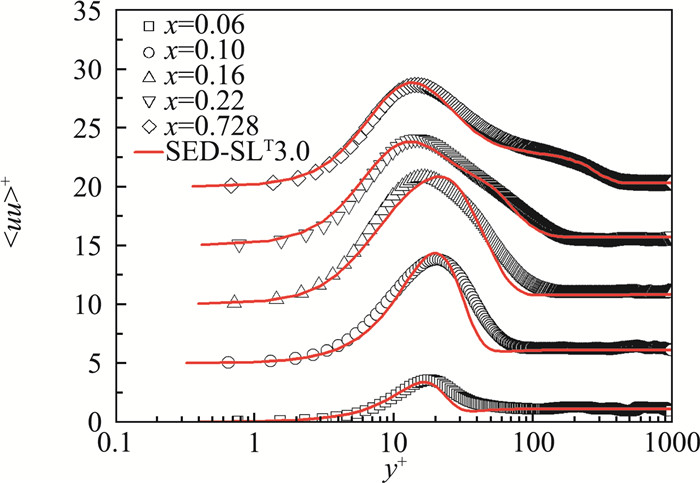
|
图 4 SED-SLT3.0计算的流向湍动能与T3B的DNS的对比.流向位置覆盖从层流到转捩最终到充分发展区的全部流域 Fig.4 Comparisons between the SED-SLT3.0 calculated streamwise turbulent kinetic energy profiles and the DNS data at five streamwise locations |
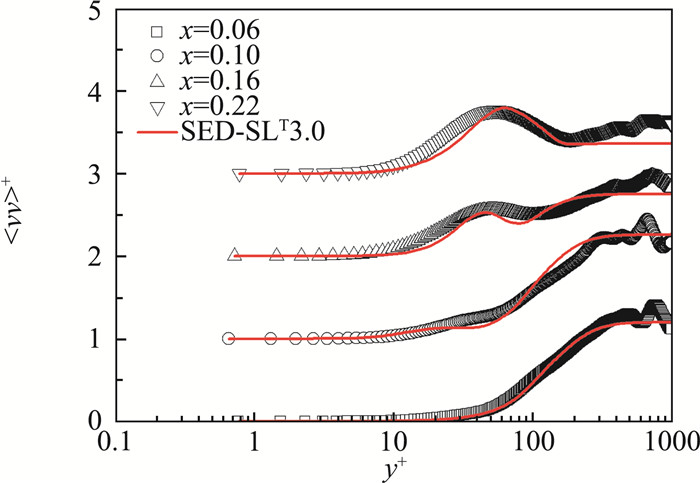
|
图 5 SED-SLT3.0计算的垂向湍动能与T3B的DNS的对比 Fig.5 Comparisons between the SED-SLT3.0 calculated wall-normal turbulent kinetic energy profiles and the DNS data at four streamwise locations |
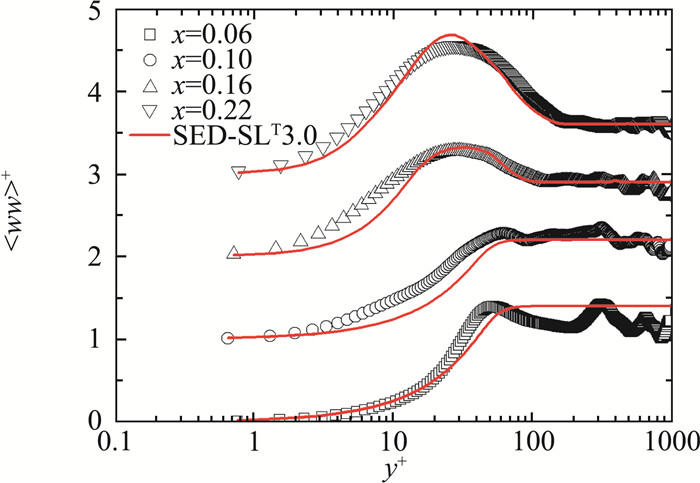
|
图 6 SED-SLT3.0计算的展向湍动能与T3B的DNS的对比 Fig.6 Comparisons between the SED-SLT3.0 calculated transversal turbulent kinetic energy profiles and the DNS data at four streamwise locations |
高超声速边界层转捩是制约高速飞行器气动设计的瓶颈难题。近些年来,由于我国国防工业和航天事业的重大需求,高超声速边界层转捩受到了政府部门、学术界和工程设计单位的重视。国家通过重点研发计划支持国内多个优势单位开展高超声速边界层转捩的研究[4],国家数值风洞工程也将高超声速边界层转捩的CFD预测作为优先发展的重点方向。与低速边界层转捩相比,高超声速边界层转捩难在转捩机制更加复杂,影响因素更多,流动环境更加特殊,流动状态敏感多变,不确定性因素也更多。与之相应的是,支持高超声速边界层转捩基础研究和工程应用发展的实验和计算数据也更加难以获取,成本非常高昂[1-4]。在这种情况下,特别需要湍流基础理论研究成果的支撑,来厘清各种复杂性。
尖锥是研究高超声速边界层转捩的一个标模,与航天飞行器联系非常紧密。它的几何构型简单,但呈现了高超声速转捩的各种复杂性,几十年来也积累了较为丰富的实验和计算数据,成为验证高超声速边界层转捩理论和转捩模型的一个基准模型。我们基于结构系综的研究方法对尖锥转捩流动初步开展了SED-SL模型的计算。
3.1 适用于高超声速尖锥的SED-SL模型我们具体针对有中等攻角、马赫数6、锥度0.05 mm的7°半锥角圆锥开展了RANS计算,并与红外热图实验数据[30]进行了对比。
对RANS计算的设定描述如下。计算网格由CARDC提供,为周向半模模型。网格数为173×31×131(轴向×周向×垂向)。在尖锥轴向和周向为均匀网格,壁面垂向为指数拉伸网格,垂向第一层网格的y+ < 1。入口条件为自由来流条件,尖锥表面为黏附条件和等温壁,出口采用外插边界条件。在计算方法上,采用了总变差减小的隐式LU-SGS格式进行时间推进,在用有限体积法分裂后,无黏通量采用三阶MUSCL格式来求解,黏性通量采用Van-Leer格式求解,在边界点附近采用了迎风格式求解。计算在工作站上开展,计算平台为中科院力学所李新亮研究员等开发的OpenCFD-EC软件,并在CFL3D平台上进行了验证。SED-SL转捩模型模块在平台原有的B-L湍流模型模块的基础上开发而成。需要指出的是,为了简化计算,在SED-SL模型中x方向被指定为尖锥母线方向,这将在大攻角的情况下偏离物理真实。在本文计算的6°攻角之下,流向拉伸原点相距尖锥顶点偏离不大,其定量影响是有限的,并被多层结构参数的变化所反映。对于更大攻角的计算,宜考虑流线相对母线的变化。
通过前述的结构系综的多次迭代分析过程,我们获得了该超声速尖锥转捩边界层的多层结构参数,反映在SED-SLT3.0的模型设置中(其中未考虑有限雷诺数系综,源于湍流边界层在尖锥中极短),由此取得了对尖锥表面热流分布的精准预测。
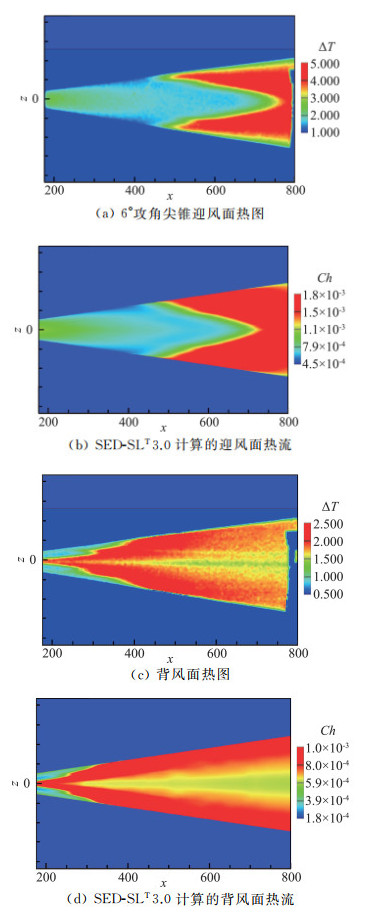
图 7和图 8分别给出了2°和6°攻角由SED-SLT3.0预测的尖锥迎风面和背风面的热流云图,与实验的红外热图做了对比,两者高度一致。注意到实验是对转捩边界层瞬时温升的测量,它与热流在定量上有相似性。在中等攻角的情况下,转捩线随攻角增大在背风面前移,在迎风面后移,这是尖锥转捩的典型特征。
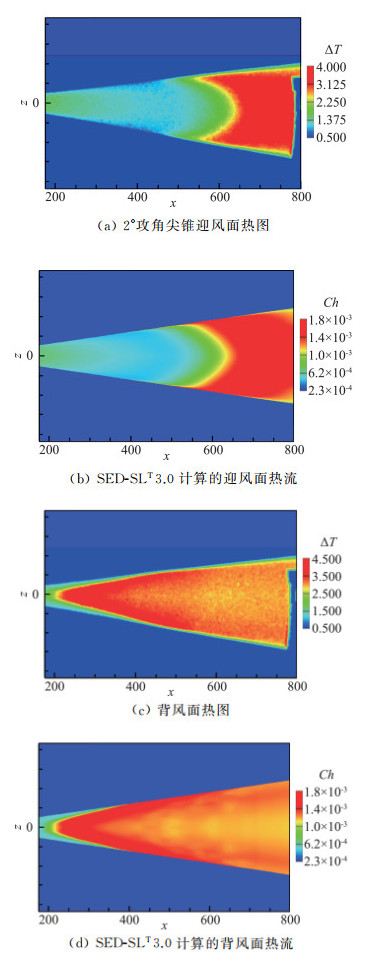
|
图 7 SED-SLT 3.0计算的2°攻角尖锥迎风和背风面的热流云图与实验测量的红外热图的比较 Fig.7 The heat fluxes on the windward and leeward surfaces of the sharp cone at calculated by the SED-SLT 3.0, compared with the corresponding infrared thermal images measured in wind tunnel |
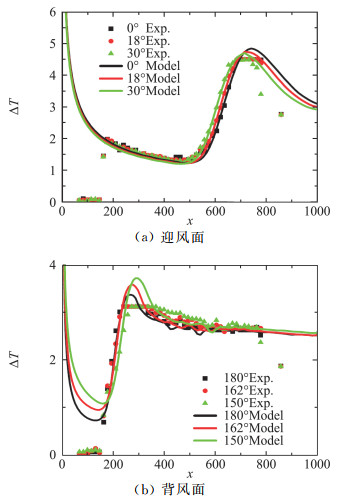
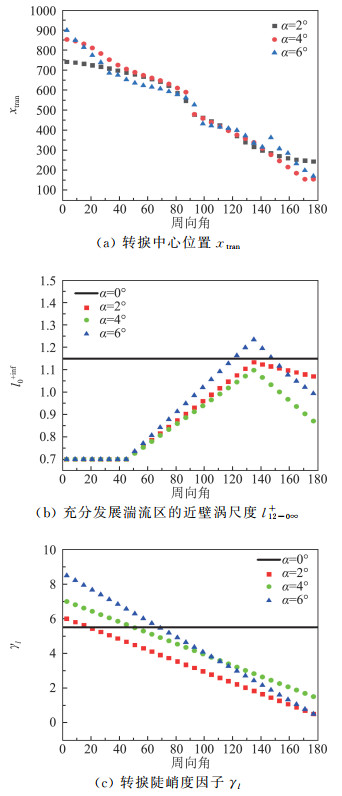
图 9给出了2°攻角下尖锥迎风面和背风面各三个周向角的、由SED-SLT3.0计算的热流数据(经定量调整)与实验的实测温差数据的对比。可以看到,随着攻角的出现,在迎风面和背风面,除了转捩中心位置发生移动之外(图 10a),迎风面的转捩温差曲线在转捩后期(即温差峰值位置之后)趋于更快地衰减,背风面的转捩温差曲线在转捩区变得更加陡峭(转捩雷诺数小的原因)。计算发现,影响转捩后期发展的主要是近壁涡尺度l12-0∞+(ybuf+的流向多层结构基本不变),它在中等攻角的尖锥的迎风区变化不大(图 10b)。描述转捩发展快慢的多层结构参数是γl,它与转捩中心点位置的变化规律相似,两者有明显的依赖性,可通过构建与当地流动控制参数(动量厚度雷诺数和横流雷诺数)的关联关系一并处理。图 10是在与实验数据比较下形成的对尖锥高超转捩中SED-SLT3.0模型的几个主导多层结构参数的经验设定。特别从l12-0∞+的周向角变化中,我们可以推测尖锥转捩在迎风面、背风面和侧向具有不同的变化趋势,这与人们认为在这三个区域转捩机理存在不同相映照[30]。因此,通过多层结构参数有可能对转捩类型进行区分和判定,这还需要进一步的研究来确认。
|
图 9 2°攻角尖锥迎风面和背风面各三个周向角的温差沿尖锥轴向的变化曲线.点为实验数据;线为SED-SLT3.0模型计算结果,后者从热流推出.周向角0°(180°)为迎风面(背风面)中心线 Fig.9 The temperature increases measured at three circumferential angles on each of the windward and leeward surfaces of the sharp cone at α=2° (symbols), compared with the SED-SLT3.0 predictions (lines) |
|
图 10 SED-SLT3.0的模型参数对攻角和周向角的变化 Fig.10 Variations of the multi-layer parameters in the SED-SLT3.0 with the angle of attack and the circumferential angle |
现阶段由于缺乏实验和可靠的计算数据,我们对尖锥高超转捩中多层结构参数的变化规律还没有形成完整的认识,这需要一段时间的积累。这里再次谈一谈我们对包括高超尖锥转捩在内的复杂边界层研究的整体构思。
高超声速边界层转捩是一个异常复杂的科学与工程难题,其突破需要丰富的经验数据与深刻的理论构思相结合[31]。目前国家在高超声速飞行器研究方面的投入增加,风洞实验数据和飞行试验数据正逐步积累,但是,对这些数据依然缺乏有效的理论分析,仅仅从中提炼工程设计所需要的经验参数是远远不够的。另一方面,随着近些年来计算能力和计算技术的飞速提升,湍流的高精度、大规模数值模拟得以广泛开展,使湍流研究快速进入到大数据的时代,但对这些大数据的分析也严重不够。在这种情况下,发展深刻的理论构思,从湍流大数据中既验证普适的物理原理,又提炼具体流动的与工程相关的参数,才能真正实现将基础理论研究和应用研究结合起来,推动工程技术进步的目标。随着SED理论的日益成熟,离这一时机的到来越来越近。我们特别希望能受到学界和业界的关注,积极组织力量来实现这一融合。建立在SED理论基础上的SED-SL系列代数转捩模型,其物理图像清晰,在一系列标模转捩流动中显示了精准的预测能力,有可能成为湍流基础理论和工程应用研究相结合而结出的硕果。
就高超声速边界层转捩难题而言,要取得突破,还需要一定的时间和耐心。首先需要综合集成各方面的数据,包括风洞实验数据、飞行试验数据、DNS数据、LES数据等,还包括研究者和工程师的知识和经验。再通过对这些数据开展SED分析,揭示高超声速转捩边界层的结构系综的特性,它将展示相对各种控制参数和环境因素变化的相似性,由多层结构参数的理论和经验公式表达出来,体现在SED-SL模型的参数设定之中,最终实现对高超声速飞行器全包线的精准模拟。
就本文所介绍的内容而言,目前的成果仍然是非常初步的。但重要的一点是,我们对转捩实现了一个非常普适的参数化方案,从而可以考虑各种边界层转捩效应,这在之前是无法做到的。未来我们希望能够与国内工程单位开展合作,对更多的实验数据展开分析,尤其是对当前工程上极关心的几个重要的高超声速边界层转捩效应开展攻关,完成针对锥度效应、横流效应、再层流化效应等的刻画,也解答困惑学界的一些转捩问题。
4 结论与展望本文提出了一个构建典型工程边界层转捩模型的崭新思路:通过实验和可靠的计算数据确定转捩边界层的结构系综,提炼反映转捩边界层物理状态和相似性的多层结构参数,进而形成物理图像清晰、定量描述精确的新型转捩模型。我们将这个思路成功应用到刻画由自由来流湍流诱发的平板边界层强迫转捩和有攻角的高超声速尖锥转捩两类流动,获得了对大湍流度下平板转捩的全分量、全流域的精准理论描述,对高超声速尖锥的计算也得到了与实验一致的计算结果。该研究对研发可靠、物理内涵清晰的转捩模型具有重要的指引作用。
目前的成果仍然是初步的,距离一个可工程化应用的转捩模型尚有一段距离。这里,总结并对今后工程转捩模型的研究做出如下展望:
1) 在实验和计算数据日益丰富的今天,转捩模型应该全面刻画典型流场的全部信息,即转捩过程中除了摩擦速度(摩阻曲线)以外,还应该刻画雷诺应力、湍动能剖面沿流向的发展。只有完整刻画所有雷诺应力分量的演化,才能保证转捩过程刻画的可靠性,也才能奠定转捩模型的可靠性。
2) 转捩模型中参数随流动工况参数变化是否具有不变性,是考验转捩模型的核心要素。除了有限的后验验证以外,还应该对参数不变性有独立的(先验)验证。这就要求转捩模型的参数具有物理意义。目前绝大多数转捩模型不满足这一条件,难以成为工程师可以放心使用的理想模型。转捩模型的创新势在必行。
3) 本文所介绍的新思路还很初步,还需针对实际应用(例如包含各类复杂性的尖锥流动),一步步展开,以详细的对比来证明,结构系综的概念可以将多数复杂流动因素(如横流、攻角效应等)逐一以普适简略的形式包括进来,在高级近似中给出对转捩过程的精准的刻画。
4) 更为重要的是,本文所介绍的从DNS/LES和实验的大数据分析建立流动的结构系综的方法,有待于在实际应用中丰富和发展,成为复杂边界层湍流研究的基本方法,这是本文最重要的意义。
| [1] |
周恒, 张涵信. 空气动力学的新问题[J]. 中国科学:物理学力学天文学), 2015, 45(10): 104709. ZHOU H, ZHANG H X. New problems of aerodynamics[J]. SCIENTIA SINICA Physica, Mechanica & Astronomica, 2015, 45(10): 104709. DOI:10.1360/SSPMA2015-00402 (in Chinese) |
| [2] |
周恒, 苏彩虹, 张永明. 超声速/高超声速边界层的转捩机理及预测[M]. 北京: 科学出版社, 2015.
|
| [3] |
陈坚强, 涂国华, 张毅锋, 等. 高超声速边界层转捩研究现状与发展趋势[J]. 空气动力学学报, 2017, 35(3): 311-337. CHEN J Q, TU G H, ZHANG Y F, et al. Hypersnonic boundary layer transition:what we know, where shall we go[J]. Acta Aerodynamica Sinica, 2017, 35(3): 311-337. DOI:10.7638/kqdlxxb-2017.0030 (in Chinese) |
| [4] |
陈坚强, 袁先旭, 涂国华, 等. 高超声速边界层转捩的几点认识[J]. 中国科学:物理学力学天文学, 2019, 49(11): 114701. CHEN J Q, YUAN X X, TU G H, et al. Recent progresses on hypersonic boundary-layer transition[J]. SCIENTIA SINICA Physica, Mechanica & Astronomica, 2019, 49(11): 114701. DOI:10.1360/SSPMA-2019-0071 (in Chinese) |
| [5] |
佘振苏, 陈曦, 未波波, 等. 应用结构系综理论发展壁湍流工程湍流模型[J]. 中国科学:物理学力学天文学, 2015, 45(12): 124703. SHE Z S, CHEN X, WEI B B, et al. SED-based studies of turbulence models for wall flows[J]. SCIENTIA SINICA Physica, Mechanica & Astronomica, 2015, 45(12): 124703. DOI:10.1360/SSPMA2015-00444 (in Chinese) |
| [6] |
佘振苏, 唐帆, 肖梦娟. 面向精准工程湍流模型的理论研究[J]. 空气动力学学报, 2019, 37(1): 1-18. SHE Z S, TANG F, XIAO M J. Structural ensemble dynamics theory for engineering turbulenc models[J]. Acta Aerodynamica Sinica, 2019, 37(1): 1-18. DOI:10.7638/kqdlxxb-2018.0249 (in Chinese) |
| [7] |
LI X L, FU D X, MAY W. Direct numerical simulation of hypersonic boundary layer transition over a blunt cone with a small angle of attack[J]. Physics of Fluids, 2010, 22(2): 025105. DOI:10.1063/1.3313933 |
| [8] |
EMMONS H W. The laminar-turbulent transition in a boundary layer-part I[J]. Journal of the Aeronautical Sciences, 1951, 18(7): 490-498. DOI:10.2514/8.2010 |
| [9] |
SCHUBAUER G B, KLEBANOFF P S. Contributions on the mechanics of boundary layer transition[R]. NACA TR-1289, 1955.
|
| [10] |
LEE C, CHEN S Y. Recent progress in the study of transition in the hypersonic boundary layer[J]. National Science Review, 2019, 6(1): 155-170. DOI:10.1093/nsr/nwy052 |
| [11] |
阎超, 于剑, 徐晶磊, 等. CFD模拟方法的发展成就与展望[J]. 力学进展, 2011, 41(5): 562-589. YAN C, YU J, XU J L, et al. On the achievements and prospects for the methods of computational fluid dynamics[J]. Advances in Mechanics, 2011, 41(5): 562-589. (in Chinese) |
| [12] |
DURBIN P A. Some recent developments in turbulence closure modeling[J]. Annual Review of Fluid Mechanics, 2018, 50(1): 77-103. DOI:10.1146/annurev-fluid-122316-045020 |
| [13] |
MENTER F R, LANGTRY R, VOLKER S. Transition modelling for general purpose CFD codes[J]. Flow, Turbulence and Combustion, 2006, 77(1): 277-303. DOI:10.1007/s10494-006-9047-1 |
| [14] |
FU S, WANG L. RANS modeling of high-speed aerodynamic flow transition with consideration of stability theory[J]. Progress in Aerospace Sciences, 2013, 58: 36-59. DOI:10.1016/j.paerosci.2012.08.004 |
| [15] |
SHE Z S, HU N, WU Y. Structural ensemble dynamics based closure model for wall-bounded turbulent flow[J]. Acta Mechanica Sinica, 2009, 25(5): 731-736. DOI:10.1007/s10409-009-0282-2 |
| [16] |
SHE Z S, CHEN X, WU Y, et al. New perspective in statistical modeling of wall-bounded turbulence[J]. Acta Mechanica Sinica, 2010, 26(6): 847-861. DOI:10.1007/s10409-010-0391-y |
| [17] |
SHE Z S, CHEN X, HUSSAIN F. Quantifying wall turbulence via a symmetry approach:a Lie group theory[J]. Journal of Fluid Mechanics, 2017, 827: 322-356. DOI:10.1017/jfm.2017.464 |
| [18] |
CHEN X, HUSSAIN F, SHE Z S. Quantifying wall turbulence via a symmetry approach. Part 2. Reynolds stresses[J]. Journal of Fluid Mechanics, 2018, 850: 401-438. DOI:10.1017/jfm.2018.405 |
| [19] |
CHEN X, HUSSAIN F, SHE Z S. Non-universal scaling transition of momentum cascade in wall turbulence[J]. Journal of Fluid Mechanics, 2019, 871: R2. DOI:10.1017/jfm.2019.309 |
| [20] |
CHEN X, HUSSAIN F, SHE Z S. Predictions of canonical wall-bounded turbulent flows via a modified k-ω equation[J]. Journal of Turbulence, 2017, 18(1): 1-35. DOI:10.1080/14685248.2016.1243244 |
| [21] |
SHE Z S, ZOU H Y, XIAO M J, et al. Prediction of compressible turbulent boundary layer via a symmetry-based length model[J]. Journal of Fluid Mechanics, 2018, 857: 449-468. DOI:10.1017/jfm.2018.710 |
| [22] |
XIAO M J, SHE Z S. Symmetry-based description of laminar- turbulent transition[J]. Science China Physics, Mechanics & Astronomy, 2019, 62(9): 994711. DOI:10.1007/s11433-018-9377-0 |
| [23] |
XIAO M J, SHE Z S. Precise drag prediction of airfoil flows by a new algebraic model[J]. Acta Mechanica Sinica, 2020, 36(1): 35-43. DOI:10.1007/s10409-019-00911-9 |
| [24] |
ANDERSON J D Jr. Hypersonic and high-temperature gas dynamics[M]. third edition. Washington, DC: AIAA, Inc., 2019. DOI:10.2514/4.105142
|
| [25] |
唐帆. k-ω模型与边界层转捩流动中的结构系综研究[D].北京: 北京大学, 2020.
|
| [26] |
陈曦.壁湍流的结构系综理论[D].北京: 北京大学, 2012.
|
| [27] |
SAVILL A M. Evaluating turbulence model predictions of transition[J]. Applied Scientific Research, 1993, 51(1-2): 555-562. DOI:10.1007/bf01082590 |
| [28] |
QIN Y P, YAN C, HAO Z H, et al. An intermittency factor weighted laminar kinetic energy transition model for heat transfer overshoot prediction[J]. International Journal of Heat and Mass Transfer, 2018, 117: 1115-1124. DOI:10.1016/j.ijheatmasstransfer.2017.10.081 |
| [29] |
KROGSTAD PÅ, DAVIDSON P A. Freely decaying, homogeneous turbulence generated by multi-scale grids[J]. Journal of Fluid Mechanics, 2011, 680: 417-434. DOI:10.1017/jfm.2011.169 |
| [30] |
陈久芬, 凌岗, 张庆虎, 等. 7°尖锥高超声速边界层转捩红外测量实验[J]. 实验流体力学, 2020, 34(1): 60-66. CHEN J F, LING G, ZHANG Q H, et al. Infrared thermography experiments of hypersonic boundary-layer transition on a 7°half-angle sharp cone[J]. Journal of Experiments in Fluid Mechanics, 2020, 34(1): 60-66. DOI:10.11729/syltlx20180172 (in Chinese) |
| [31] |
陈坚强.国家数值风洞(NNW)工程关键技术研究进展[J].中国科学: 技术科学, 2020(在线发表). CHEN J Q. Advances in the key technologies of Chinese National Numerical Windtunnel project[J]. Scientia Sinica Technologica, 2020(online). (in Chinese) DOI: 10.1360/SST-2020-0334 |
 2020, Vol. 38
2020, Vol. 38