2. 中国科学院大学 工程科学学院, 北京 100049
2. School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
流动噪声既是流体力学基础研究的重要难题,又是航空工程中的重要问题。Ffowcs Williams and Hawkings (FW-H)方程[1]是目前计算流动噪声的重要工具。随着计算流体力学的发展,FW-H方程已被成功地应用于直升机旋翼[2-3]、增升装置[4-5]、和飞机起落架[6]等产生的流动噪声研究。特别是近年来,数值风洞[7]的发展更是为流动噪声的预测提供了有力的支撑。
FW-H方程通过引入广义函数将自由空间的Lighthill声比拟方程推广至有壁面的流动问题,其中的壁面(下文中称为FW-H积分面)既可以是真实的固体边界,也可以是流动中的虚拟边界。FW-H方程是一个关于密度(或压力)脉动的非齐次波动方程。远场的噪声可在形式上表示为流场变量和格林函数的积分(下文中称为FW-H积分)。根据FW-H积分,远场噪声为单极子声源、偶极子声源和四极子声源三部分贡献的叠加。其中,与单极子声源和偶极子声源相关的积分分别涉及积分面上的质量通量和非定常载荷,是相关量在FW-H积分面上的面积分。与四极子声源相关的积分是涉及Lighthill应力张量的体积分,其积分域应该包含Lighthill应力张量不为零的所有区域。计算四极子声源相关的积分所需要的计算量和存储量远大于偶极子声源和单极子声源相关的积分。并且,常用的实验测量和数值模拟数据难以包含Lighthill应力张量不为零的全部区域。Lighthill应力张量从FW-H积分面穿出,常会引起四极子声源对远场噪声的虚假贡献[8-9]。
在低马赫数流动中,相对于非定常载荷对应的偶极子声源产生的远场噪声,Lighthill应力张量对应的四极子声源产生的噪声所占比例相对较小,通常做法是忽略四极子声源体积分项。但是,随着来流马赫数的增加或流动边界的复杂化,四极子声源的影响逐渐不可忽略[10-14]。Yao等[13]研究了来流马赫数为0.3的半球扰流,发现回流区尾端的四极子声源是远场噪声的主要来源,Tomoaki Ikeda等[10]计算了来流马赫数为0.2、雷诺数为1×104、攻角为2°的二维NACA0012翼型绕流,结果显示,在部分观测点四极子声源穿出FW-H面造成的虚假声源与偶极子声源的贡献处于同一量级。
为了解决四极子积分项引起的虚假声源问题,Shur等[15]通过在接近控制面处添加人工黏性的方法耗散Lighthill应力张量。但是,Nitzkorski等[9]认为这种方法使得被打开面的法向的辐射噪声被低估。为了避免引入人工黏性,Wang等[11]曾在Curle积分的框架下提出了一种修正四极子声源计算的模型。该模型利用冻结流假设将所选声源区外的Lighthill应力张量的体积分对远场噪声的贡献转换为计算域边界上四极子声源流量的面积分,有效地恢复了低马赫数翼型绕流问题中产生的四极子声源对远场噪声的贡献。Wang等[11]的工作中使用缩放的均匀来流速度作为Lighthill应力张量穿过计算域边界的对流速度,需要将声源区的边界取至下游足够远处,以消除近场尾迹中的Lighthill应力张量对流速度的非均匀性对修正模型的影响。随后,Nitzkorski等[9]将Wang等[11]的思路推广至FW-H积分,并通过利用多出口面之间的交叉关联函数构建Lighthill应力张量的通量在FW-H积分面上的对流速度,避免了依赖于经验的缩放均匀来流作为对流速度。
上述工作在时域方法框架下修正计算四极子声源对远场噪声的贡献,有效地抑制了Lighthill应力张量穿过控制面引起的虚假声源问题。但由于FW-H积分面的运动和对流速度的计算方式等问题,这些方法没有被广泛地应用在频域方法中。Lockard等[16]提出了频域方法框架下的四极子声源积分项的计算模型。该模型通过连续使用分部积分,将四极子声源的体积分近似表达为一系列面积分的和,避免了在整个计算域内存储和计算Lighthill应力张量,并且抑制了四极子声源体积分计算中对远场噪声的虚假贡献。在这一过程中,Lockard等[16]根据Wang等[11]的工作以对流方程的形式描述Lighthill应力张量通过积分面的过程,并假设对流速度取为均匀来流的速度。该假设没有考虑积分面上的Lighthill应力张量对流速度的非均匀性,一般难以将积分面取在近尾迹区域。
针对这一问题,本文发展一种可以在FW-H积分面上计算非均匀对流速度的模型,用于改进Lockard等[16]提出的四极子修正方法中的均匀对流速度假设。该模型受时域方法中Nitzkorski等[9]的工作的启发,基于FW-H积分面上的关联函数计算对流速度。与Nitzkorski等[9]的工作不同的是,我们根据Lighthill应力张量的关联函数,而不是Lighthill应力张量的通量的关联函数,来计算对流速度,避免了依赖于经验选用的均匀来流作为对流速度,并考虑了对流速度空间分布的非均匀性。
本文第1部分简要地给出FW-H方程在频域的解,第2部分给出FW-H积分四极子声源项修正模型以及四极子声源项的对流速度的具体计算方法,第3部分用二维对流涡以及低马赫数圆柱绕流两个标准算例检验所发展的模型,第4部分为结论。
1 FW-H方程及其解常用的FW-H方程的微分形式:
| $ \begin{array}{l} \left( {\frac{{{\partial ^2}}}{{\partial {t^2}}} - c_o^2\frac{{{\partial ^2}}}{{\partial {z_i}\partial {z_i}}}} \right)(H(f){\rho ^\prime }) = \\ \frac{{{\partial ^2}}}{{\partial {z_i}\partial {z_j}}}({T_{ij}}H(f)) - \frac{\partial }{{\partial {z_i}}}({F_i}\delta (f)) + \frac{\partial }{{\partial t}}(Q\delta (f)) \end{array} $ | (1) |
其中,
| $ \begin{array}{*{20}{l}} {Q = ({\rho _o}{v_i} + \rho ({u_i} - {v_i})){{\hat n}_i}}\\ {{F_i} = (\rho {u_i}({u_j} - {v_j}) + {P_{ij}}){{\hat n}_j}}\\ {{T_{ij}} = \rho {u_i}{u_j} + {P_{ij}} - c_o^2{\rho ^\prime }{\delta _{ij}}} \end{array} $ | (2) |
式中,密度与压力扰动分别定义为ρ′=ρ-ρo与p′=p-po,ρo、co、po分别为无穷远场的密度、声速与压力,ρ、p为总的密度与压力。
| $ \begin{array}{l} (\frac{{{\partial ^2}}}{{\partial {t^2}}} + {U_i}{U_j}\frac{{{\partial ^2}}}{{\partial {y_i}\partial {y_j}}} + 2{U_i}\frac{{{\partial ^2}}}{{\partial {y_i}\partial t}} - c_o^2\frac{{{\partial ^2}}}{{\partial {y_i}\partial {y_i}}})(H(f){\rho ^\prime })\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{{\partial ^2}}}{{\partial {y_i}\partial {y_i}}}({T_{ij}}H(f)) - \frac{\partial }{{\partial {y_i}}}({F_i}\delta (f)) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\partial }{{\partial t}}(Q\delta (f)) \end{array} $ | (3) |
其中,yi=zi+Uit是随FW-H积分面运动的坐标下的空间位置变量,Ui为无穷远来流在yi方向的速度。不影响一般性,在本文中按照Wang等[11]和Lockard等[16]的处理方式,取无穷远来流仅沿y1方向,即U=(U1, 0, 0)。则声源项变为
| $ \begin{array}{*{20}{l}} {Q = [ - {\rho _o}{U_i} + \rho ({u_i} + {U_i})]{{\hat n}_i}}\\ {{F_i} = [{\rho _o}{U_i}{U_j} + {p^\prime }{\delta _{ij}} + \rho ({u_i} - {U_i})({u_j} + {U_j})]{{\hat n}_j}}\\ {{T_{ij}} = \rho {u_i}{u_j}} \end{array} $ | (4) |
式中的速度ui和uj皆为减去无穷远来流后的速度扰动。为了将对流波动方程变化到频域,我们根据Lockard [17]的工作定义傅里叶变换对如下:
| $ \begin{array}{*{20}{l}} {\mathcal{F}\{ q(t)\} = q(\omega ) = \int_{ - \infty }^\infty q (t)\exp ( - {\rm{i}}\omega t){\rm{d}}t}\\ {{\mathcal{F}^{ - 1}}\{ q(\omega )\} = q(t) = \frac{1}{{2\pi }}\int_{ - \infty }^\infty q (\omega )\exp ({\rm{i}}\omega t){\rm{d}}\omega } \end{array} $ | (5) |
利用式(5),频域中的FW-H方程可写为:
| $ \begin{array}{l} ( - {k^2} - {M_i}{M_j}\frac{{{\partial ^2}}}{{\partial {y_i}\partial {y_j}}} - 2{\rm{i}}{M_i}k\frac{\partial }{{\partial {y_i}}} + \frac{{{\partial ^2}}}{{\partial {y_i}\partial {y_i}}}) \cdot \\ (H(f)c_o^2{\rho ^\prime }(y,\omega )) = - \frac{{{\partial ^2}}}{{\partial {y_i}\partial {y_j}}}({T_{ij}}(y,\omega )H(f)) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\partial }{{\partial {y_i}}}({F_i}(y,\omega )\delta (f)) - {\rm{i}}\omega Q(y,\omega )\delta (f) \end{array} $ | (6) |
其中k=ω/co为波数,Mi=Ui/co为马赫数。
| $ H(f)c_o^2{\rho ^\prime }(x,\omega ) = {I_T} + {I_L} + {I_Q} $ | (7) |
其中IT、IL分别为厚度声源与载荷声源,分别对应于单极子声源和偶极子声源,表达式如下:
| $ \begin{array}{*{20}{l}} {{I_T}(x,\omega ) = - \int_{f = 0} {\rm{i}} \omega Q(y,\omega )G(x;y){\rm{d}}S}\\ {{I_L}(x,\omega ) = - \int_{f = 0} {{F_i}} (y,\omega )\frac{{\partial G(x;y)}}{{\partial {y_i}}}{\rm{d}}S} \end{array} $ | (8) |
其中x、y分别表示观测点与声源所在位置。
四极子声源积分项为:
| $ {I_Q}(x,\omega ) = - \int_{f > 0} {{T_{ij}}} (y,\omega )\frac{{{\partial ^2}G(x;y)}}{{\partial {y_i}\partial {y_j}}}{\rm{d}}V $ | (9) |
准确求解四极子声源对远场噪声的贡献需要保存FW-H积分面以外的所有Lighthill应力张量不为零的区域流场,如式(9)所示。当四极子声源的积分域不能包含所有的Lighthill应力张量不为零的区域时,Lighthill应力张量会穿过FW-H积分面,导致四极子声源对远场噪声的虚假贡献。Lockard等[16]通过分部积分的方法将四极子体积分项(式(9))近似地表达为面积分的和:
| $ \begin{array}{*{20}{l}} {{I_Q}(x;\omega ) \approx }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{l = 1}^n - \int_{f = 0} {{{(\frac{{ - {\rm{i}}{U_c}}}{\omega })}^l}} {T_{ij}}(y,\omega )\frac{{{\partial ^{l - 1}}}}{{\partial y_1^l}}(\frac{{{\partial ^2}G(x;y)}}{{\partial {y_i}\partial {y_j}}}){\rm{d}}S} \end{array} $ | (10) |
在计算中一般取前三项。Uc为Lighthill应力张量的输运速度,表示四极子声源穿出FW-H积分面的速度,注意,式(10)在推导过程中假设对流速度沿流向与时间的变化可以忽略不计。Lighthill应力张量穿出FW-H积分面的过程用如下方程模化:
| $ \frac{{\partial {T_{ij}}(y,t)}}{{\partial t}} + {U_c}(y,t)\frac{{\partial {T_{ij}}(y,t)}}{{\partial {y_1}}} = 0 $ | (11) |
按照式(10)计算四极子声源项对远场噪声的贡献的关键是计算对流速度Uc。Lockard等[16]选取对流速度为均匀来流速度。以均匀来流为对流速度没有考虑FW-H积分面上的对流速度的非均匀性,会导致远场噪声依赖于FW-H的位置。不同于Lockard的选用均匀来流为对流速度,我们采用多个出口面Lighthill应力张量的关联函数构建对流速度,其基本思想是利用关联函数得到四极子声源在出口面之间的输运时间,继而根据出口面之间的距离得到穿出出口面的速度。与直接选用均匀来流为对流速度相比,此方法不仅提高了远场噪声指向性预测的准确性,而且减小了预测结果对FW-H面选取位置的依赖性。
构建对流速度Uc的Lighthill应力张量的关联函数为:
| $ \begin{array}{*{20}{l}} {{R_{xy}}(\tau ) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int_0^T {{T_{ij}}} ({y_1},{y_2},t){T_{ij}}({y_1} + \Delta {y_1},{y_2},t + \tau ){\rm{d}}t} \end{array} $ | (12) |
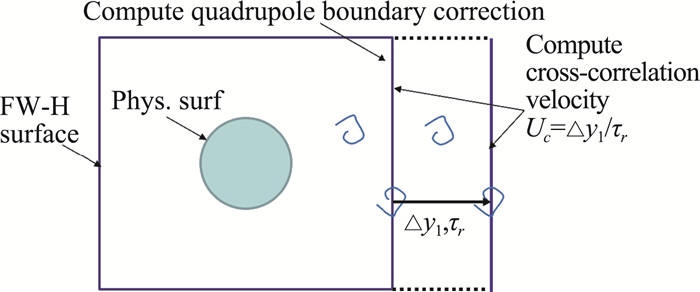
其中,Tij(y1, y2, t)与Tij(y1+Δy1, y2, t+τ)分别为上下游两个面对应位置的信号,Δy1为所选取的两出口面之间的距离。T为用来计算Uc的采样时间,在文中,我们取Uc仅随空间位置变化。如图 1所示,基于泰勒冻结假设,涡在输运过程中不发生变形。因此,Lighthill应力张量的输运速度Uc与涡的运动速度保持一致,并且本文考虑的涡沿方向穿过出口面,对应单元的位置仅在流向变化。需要注意的是,由于使用了泰勒冻结流假设,下游出口面的位置应取在速度梯度较小的区域[14],并且用于求解出口速度的两个出口面之间的距离不能太大。在3.2节的圆柱绕流算例中,第一个出口面到圆柱中心的距离大于或等于2.5D,两个出口面的间距为0.1D。为了便于计算,本文用于计算出口速度的两个出口面都垂直于流向。式(12)的离散形式写为:
| $ \begin{array}{*{20}{l}} {{{\hat R}_{xy}}(j{\varDelta ^\prime }) = \frac{1}{N}\sum\limits_{i = 1}^N {{T_{ij}}} ({y_1},{y_2},i{\varDelta ^\prime })}\\ {{T_{ij}}({y_1} + \varDelta {y_1},{y_2},i{\varDelta ^\prime } + j{\varDelta ^\prime })} \end{array} $ | (13) |
|
图 1 四极子声源修正模型的求解示意图 Fig.1 Schematics of the quadrupole source term correction model |
其中Δ′为采样的时间步长,N为总的采样步数。根据文献[19],信号在上下游两个面之间的输运时间τr由
| $ {U_c} = \Delta {y_1}/{\tau _r} $ | (14) |
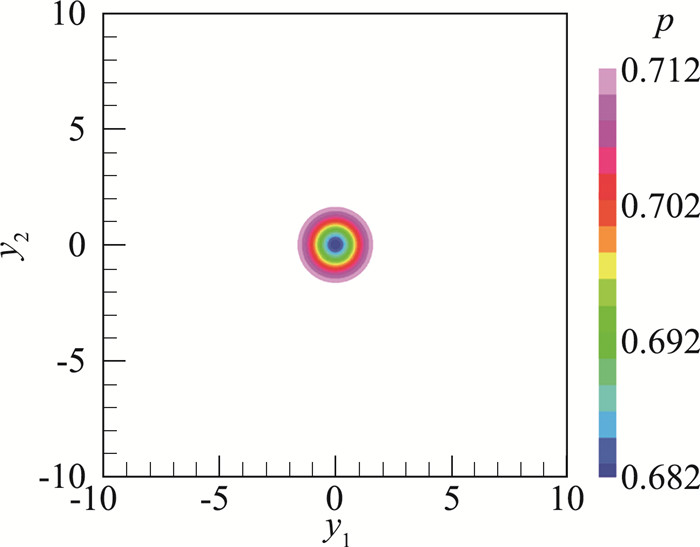
二维对流涡为可压缩欧拉方程的一个精确解,是检验FW-H积分修正方法的正确性的典型算例[16, 20-21]。在图 2和图 3所示的对流涡算例中,涡以匀速直线运动沿y1方向向下游运动,严格满足冻结流假设。压力与速度场的表达式为:
| $ \begin{array}{*{20}{l}} {p = \frac{1}{\gamma }{{[1 - {a_2}\exp (1 - {r^2})]}^{\frac{\gamma }{{\gamma - 1}}}}}\\ {\rho = {{(\frac{p}{{{p_o}}})}^{\frac{1}{\gamma }}}}\\ {u = M - {a_0}{a_1}{y_2}\exp ((1 - {r^2})/2)}\\ {v = {a_0}{a_1}({y_1} - Mt)\exp ((1 - {r^2})/2)} \end{array} $ | (15) |
|
图 2 初始时刻二维对流涡压力分布云图 Fig.2 Initial distribution of the pressure of the 2-D covecting vortex |
|
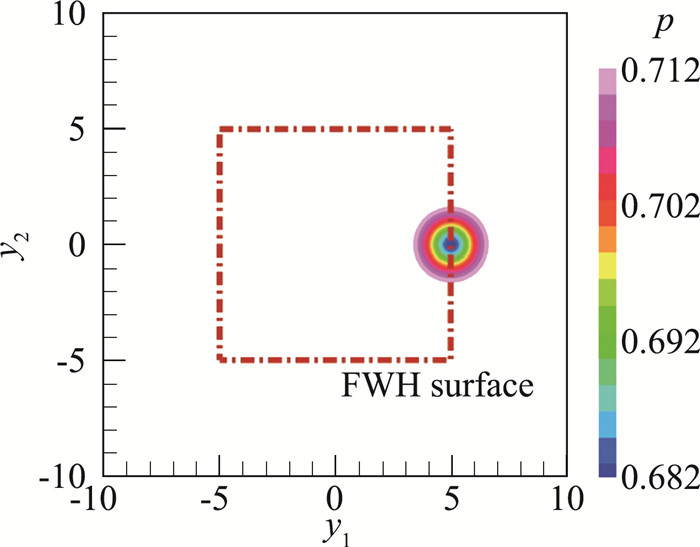
图 3 无量纲时刻t=25时二维对流涡压力分布云图 Fig.3 Distribution of the pressure the 2-D convecting vortex at t=25 |
其中,po为无穷远处的压力;γ为空气的热容比, 取1.4;y1、y2表示二维笛卡尔坐标系;M为对流马赫数;t为时间。
| $ \begin{array}{*{20}{l}} {{a_0} = 1,{a_1} = 1/(2{\rm{ \mathsf{ π} }}),\quad {a_2} = (\gamma - 1)a_0^2a_1^2/2,}\\ {{r^2} = {{({y_1} - Mt)}^2} + y_2^2} \end{array} $ | (16) |
式(15)式(16)所有的量皆经过无量纲化,参考物理量为单位长度L、声速co以及密度ρ。Lighthill应力张量满足:
| $ \frac{{\partial {T_{ij}}(y,t)}}{{\partial t}} + M\frac{{\partial {T_{ij}}(y,t)}}{{\partial {y_1}}} = 0 $ | (17) |
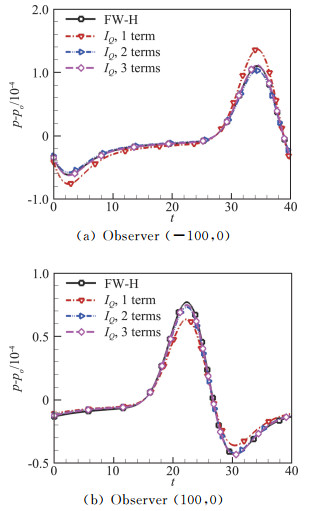
不失一般性,我们在计算中将FW-H积分面取为矩形,其在y1、y2方向的取值范围分别为[-5L, 5L]、[-5L, 5L],如图 3所示。当来流马赫数为0.2时,在无量纲时刻t=25,仅有一部分四极子声源在FW-H积分面内,穿出下游出口面的四极子声源使常规的FW-H积分的计算结果产生误差。我们采用式(10)和式(14)修正了Lighthill应力张量穿出FW-H积分面所引起的误差,如图 4所示。需要注意的是,图中的黑色实线表示FW-H方程所计算出的(IT+IL)的相反数。由于观察点的真实压力脉动趋于0,则不进行修正的FW-H方程的解实际上远远高估了压力脉动的大小,因此误差近似为此解的相反数,四极子声源修正模型所得结果应逼近于此误差。在计算式(10)的过程中,我们取了不同的n值,当n=3时(与Lockard等[16]所取的n值相同),我们的方法在二维涡的上下游远场观测点均能够修正Lighthill应力张量穿出FW-H积分面引起的误差。这一结论证实了我们的模型在二维对流涡运动中的有效性。
|
图 4 马赫数0.2的二维对流涡当中,FW-H积分修正项IQ与FW-H方程计算结果的误差的对比 Fig.4 Comparison of the quadrupole corrections with the FW-H errors for the 2-D convecting vortex |
低雷诺数圆柱绕流的远场辐射噪声是一个广泛应用的检验流动噪声计算模型和方法的算例。直接数值模拟[22]、FW-H方程[9]以及精确格林函数[23]等方法皆被应用于此问题当中,并且相应的结果显示出一致性。其中,Inoue等[22]较早地利用直接数值模拟的手段系统研究了雷诺数150下,二维圆柱绕流辐射噪声的指向性、远场衰减特性以及远场压力脉动关于马赫数的标度率,并常被用作比对算例。本文的结果将与Inoue等[22]的直接数值模拟结果进行比较,以检验所发展的模型的有效性。
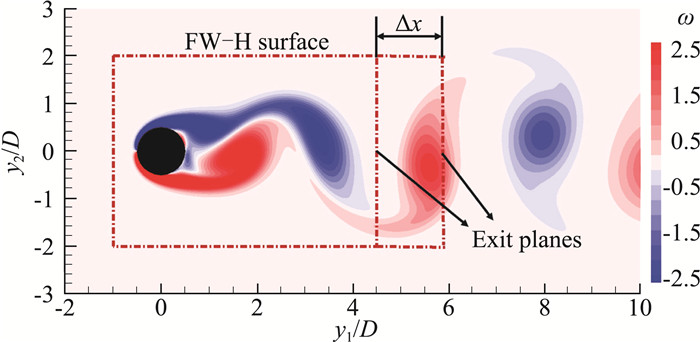
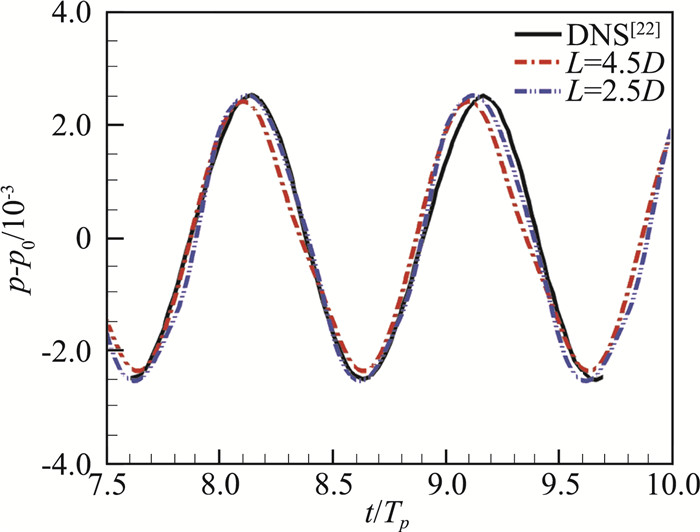
我们通过数值求解不可压流动的Navier-Stokes方程作为远场噪声的声源。声源数值模拟的设置如图 5所示,圆柱中心在原点,直径为D,来流速度为U0,基于来流速度与圆柱直径定义的雷诺数为150,坐标轴y1、y2分别对应流向与垂向。流场计算采用浸入边界方法,计算区域为[-10D, 15D],[-12D, 12D],均匀网格的尺度为0.01D,流场计算的时间步长为0.001D/U0。FW-H积分面选为长方形,上游以及两侧的面位置分别为y1=-D与y2=±2D,计算声场的采样步长为0.027D/U0。为了检验结果对出口面位置的敏感度,我们选取了不同位置的出口面,分别为y1=4.5D、y1=2.5D,计算了马赫数为0.2下,位于(0D, 100D)处观测点的压力脉动,并与Inoue等[22]的直接数值模拟结果进行了对比。结果如图 6所示,其中Tp为所选观察点处压力脉动的周期,对于不同位置的出口面,我们的模型均能够消除四极子声源穿出FW-H积分面引起的误差,与直接数值模拟的结果相符。此结果表明我们的模型不依赖于出口面位置的选取。
|
图 5 二维圆柱绕流涡量分布云图与远场噪声计算所用FW-H面的位置示意图 Fig.5 Schematics of the FW-H integral surface for the flows around a circular cylinder |
|
图 6 马赫数0.2下,不同位置的出口面得到的(0D, 100D)处观测点的压力脉动,并与Inoue的直接数值模拟结果对比 Fig.6 Pressure fluctuations at (0D, 100D) computed with different distances from the FW-H integral surface (M=0.2) |
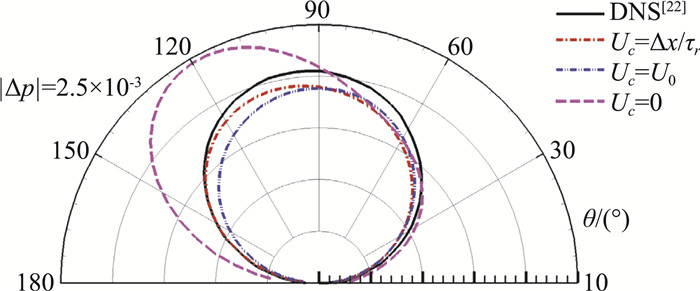
图 7比较了利用各种方法得到的远场压力脉动的指向性,|Δp|为压力脉动幅值的均方根。参考Inoue等[22]对观测点位置的选取,图 7中的观测点到圆柱中心的距离定义为75[1+Mcos(θ)]D,其中M为来流马赫数,此处为M=0.2,方向角θ为观测点位置对应向量与y1轴正向的夹角。图中的黑色实线为Inoue等[22]的直接数值模拟的结果。红色点划线为利用本文所发展的模型的计算结果,蓝色双点划线为四极子声源对流速度取为来流速度的结果,紫色虚线为未经FW-H积分四极子声源修正的结果。在本文所选用的FW-H积分面下,如果在用FW-H方程计算远场噪声中不考虑四极子声源修正,将会引起指向性和压力脉动幅值严重偏离DNS值。如表 1所示,在本文坐标系下,Inoue等[22]给出的最大压力脉动在101.5°,未经修正的结果在120.0°,经均匀来流为对流速度的四极子声源修正后,最大压力脉动在92.0°处,可经本文所发展的方法修正后,最大压力脉动在100.0°,指向性的最大误差降至2°以下。在压力脉动幅值误差明显的120°方向角处,未经修正的幅值的误差为31%,经均匀来流为对流速度的四极子声源修正后,误差为12%,可经本文所发展的方法修正后,误差则降为4%以下。这一结果表明了本文所提出的四极子声源修正模型的有效性,并且本文所提出的模型改进了Lockard等[16]所提出的频域FW-H积分修正方法。
|
图 7 二维圆柱绕流中,利用各种方法计算出的远场压力脉动指向性 Fig.7 Directivity of the sound generated by the flows around a circular cylinder |
| 表 1 最大压力脉动方向 Table 1 Angles of the maximum pressure fluctuations |
|
|
针对FW-H积分中的四极子声源项常在远场噪声的计算中引起虚假声源的问题,本文在频域方法的框架下改进了四极子声源项的修正模型,用于修正Lighthill应力张量穿过积分域边界引起的误差。该工作基于泰勒冻结流假设模化Lighthill应力张量穿过积分域边界的过程,特色是基于关联函数计算Lighthill应力张量的对流速度,而不是将对流速度取为均匀来流。所提出的模型考虑了对流速度的空间非均匀性,改善了非均匀流动区域FW-H积分面对远场噪声的影响。利用二维对流涡算例以及低雷诺数圆柱绕流算例检验了所提出的模型,结果表明模型准确修正了四极子声源穿出FW-H积分面所导致的远场噪声计算误差。作为在频域方法中考虑FW-H积分面上的非均匀对流速度的第一步工作,我们在二维流动的例子中验证了基于关联函数构建Lighthill应力张量的可行性,并将进一步把该模型用于三维流动的四极子声源的修正。
| [1] |
FFOWCS WILLIAMS J E, HAWKINGS D L. Sound generation by turbulence and surfaces in arbitrary motion[J]. Philosophical Transactions of the Royal Society of London Series A, Mathematical and Physical Sciences, 1969, 264(1151): 321-342. DOI:10.1098/rsta.1969.0031 |
| [2] |
段广战, 陈平剑. 基于CFD的直升机旋翼噪声计算[J]. 空气动力学学报, 2009, 27(3): 314-319. DUAN G Z, CHEN P J. Research of helicopter rotor aeroacoustic noise based on CFD technics[J]. Acta Aerodynamica Sinica, 2009, 27(3): 314-319. DOI:10.3969/j.issn.0258-1825.2009.03.009 (in Chinese) |
| [3] |
贺祥, 史勇杰, 徐国华. 基于声压相消的旋翼厚度噪声控制机理[J]. 空气动力学学报, 2019, 37(6): 893-900. HE XI, SHI Y J, XU G H. Control mechanism of the thickness noise based on sound pressure cancellation[J]. Acta Aerodynamica Sinica, 2019, 37(6): 893-900. DOI:10.7638/kqdlxxb-2018.0049 (in Chinese) |
| [4] |
卢清华, 陈宝. 基于LES方法的增升装置气动噪声特性分析[J]. 空气动力学学报, 2016, 34(4): 448-455. LU Q H, CHEN B. Analysis ofaeroacoustics characteristics of high lift device using LES method[J]. Acta Aerodynamica Sinica, 2016, 34(4): 448-455. DOI:10.7638/kqdlxxb-2014.0140 (in Chinese) |
| [5] |
刘志仁, 王福新, 宋文滨, 等. 二维增升装置前缘缝翼的远场噪声分析[J]. 空气动力学学报, 2012, 30(3): 388-393. LIU Z R, WANG F X, SONG W B, et al. Far-field aeroacoustic analysis for slat of a two-dimensional high-lift configuration[J]. Acta Aerodynamica Sinica, 2012, 30(3): 388-393. DOI:10.3969/j.issn.0258-1825.2012.03.018 (in Chinese) |
| [6] |
WANG L, MOCKETT C, KNACKE T, et al. Detached-eddy simulation of landing-gear noise[C]//Proc of the 19th AIAA/CEAS Aeroacoustics Conference, Berlin, Germany. Reston, Virginia: AIAA, 2013.
|
| [7] |
陈坚强.国家数值风洞(NNW)工程关键技术研究进展[J].中国科学:技术科学, 2020(在线发表). CHEN J Q. Advances in the key technologies of Chinese National Numerical Windtunnel project[J]. Scientia Sinica Technologica, 2020(online). (in Chinese) DOI:10.1360/SST-2020-0334 |
| [8] |
IKEDA T, ENOMOTO S, YAMAMOTO K, et al. On the modification of the ffowcs williams-hawkings integration for jet noise prediction[C]//Proc of the 19th AIAA/CEAS Aeroacoustics Conference, Berlin, Germany. Reston, Virginia: AIAA, 2013. DOI: 10.2514/6.2013-2277
|
| [9] |
NITZKORSKI Z, MAHESH K. A dynamic end cap technique for sound computation using the Ffowcs Williams and Hawkings equations[J]. Physics of Fluids, 2014, 26(11): 115101. DOI:10.1063/1.4900876 |
| [10] |
IKEDA T, ENOMOTO S, YAMAMOTO K, et al. Quadrupole effects in the ffowcs williams-hawkings equation using permeable control surface[C]//Proc of the 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), Colorado Springs, CO. Reston, Virigina: AIAA, 2012. DOI: 10.2514/6.2012-2069
|
| [11] |
WANG M, LELE S K, MOIN P. Computation of quadrupole noise using acoustic analogy[J]. AIAA Journal, 1996, 34(11): 2247-2254. DOI:10.2514/3.13387 |
| [12] |
RAHIER G, HUET M, PRIEUR J. Additional terms for the use of Ffowcs Williams and Hawkings surface integrals in turbulent flows[J]. Computers & Fluids, 2015, 120: 158-172. DOI:10.1016/j.compfluid.2015.07.014 |
| [13] |
YAO H D, DAVIDSON L, ERIKSSON L E. Noise radiated by low-Reynolds number flows past a hemisphere at Ma=0.3[J]. Physics of Fluids, 2017, 29(7): 076102. DOI:10.1063/1.4994592[LinkOut |
| [14] |
MAO Y J, HU Z W. Analysis of spurious sound due to vortical flow through permeable surfaces[J]. Aerospace Science and Technology, 2020, 96: 105544. DOI:10.1016/j.ast.2019.105544 |
| [15] |
SHUR M L, SPALART P R, STRELETS M K, et al. Towards the prediction of noise from jet engines[J]. International Journal of Heat and Fluid Flow, 2003, 24(4): 551-561. DOI:10.1016/s0142-727x(03)00049-3 |
| [16] |
LOCKARD D, CASPER J. Permeable surface corrections for ffowcs williams and hawkings integrals[C]//Proc of the 11th AIAA/CEAS Aeroacoustics Conference, Monterey, California. Reston, Virigina: AIAA, 2005. DOI: 10.2514/6.2005-2995
|
| [17] |
LOCKARD D P. An efficient, two-dimensional implementation of the ffowcs williams and hawkings equation[J]. Journal of Sound and Vibration, 2000, 229(4): 897-911. DOI:10.1006/jsvi.1999.2522 |
| [18] |
LOCKARD D. A comparison of ffowcs williams-hawkings solvers for airframe noise applications[C]//Proc of the 8th AIAA/CEAS Aeroacoustics Conference & Exhibit, Breckenridge, Colorado. Reston, Virigina: AIAA, 2002. DOI: 10.2514/6.2002-2580
|
| [19] |
ZHANG W B, WANG C, WANG Y L. Parameter selection in cross-correlation-based velocimetry using circular electrostatic sensors[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(5): 1268-1275. DOI:10.1109/TIM.2010.2040901 |
| [20] |
CHEUNG L, LELE S. Evaluation of far-field sound with open surface corrections to lighthill's equation[C]//Proc of the 12th AIAA/CEAS Aeroacoustics Conference (27th AIAA Aeroacoustics Conference), Cambridge, Massachusetts. Reston, Virigina: AIAA, 2006. DOI: 10.2514/6.2006-2488
|
| [21] |
IKEDA T, ENOMOTO S, YAMAMOTO K, et al. Quadrupole corrections for the permeable-surface Ffowcs Williams-Hawkings equation[J]. AIAA Journal, 2017, 55(7): 2307-2320. DOI:10.2514/1.J055328 |
| [22] |
INOUE O, HATAKEYAMA N. Sound generation by a two-dimensional circular cylinder in a uniform flow[J]. Journal of Fluid Mechanics, 2002, 471: 285-314. DOI:10.1017/s0022112002002124 |
| [23] |
GLOERFELT X, PÉROT F, BAILLY C, et al. Flow-induced cylinder noise formulated as a diffraction problem for low Mach numbers[J]. Journal of Sound and Vibration, 2005, 287(1-2): 129-151. DOI:10.1016/j.jsv.2004.10.047 |
 2020, Vol. 38
2020, Vol. 38


