2. 中国空气动力研究与发展中心 气动噪声控制重点实验室, 绵阳 621000
2. Key Laboratory of Aerodynamics Noise Control, China Aerodynamics Research and Development Center, Mianyang 621000, China
气动声学问题通常要求数值格式具有良好的多尺度分辨率。高精度紧致差分格式由于其良好的谱分辨率,在计算气动声学中得到了广泛应用[2-3]。但是紧致格式在使用时一般需要求解全局方程组,这会导致计算效率的降低和并行处理上的困难。
优化差分格式是另一类常用于气动声学问题的数值格式[4]。优化差分格式分为中心型和迎风型两种。中心型格式不含耗散,在实际应用中需要增加滤波过程。而迎风型优化格式由于其内在的耗散一般无需滤波。Tam认为迎风型优化格式通常会存在一定程度的不稳定性[5]。文献[6]给出了一种稳定性判据,发现了两种迎风型优化格式存在不稳定性,并采用这个判据作为约束条件分别构造了相应的稳定优化格式。但是,构造迎风优化格式首先需要设计一个综合考虑耗散误差与色散误差的目标函数,而该目标函数的设计存在较大的经验性成分。
优化格式通过牺牲收敛精度的阶数而对某一特定范围波数的波形(比如短波)的分辨率进行优化[4]。但是损失的精度阶数会导致格式在波数0附近的波数误差增大,因而格式在含大量低频成分波形的远距离传播问题中表现不佳。文献[1]中,通过将优化格式和最高阶格式加权组合,得到的格式达到了最优阶收敛精度,并且对于无量纲波数不大于π/3的单色波的波数误差几乎为0。
由于该格式相比普通优化格式具有更好的谱分辨率性质,这里称其为增强优化差分格式(下文简写为增强优化格式)。增强优化格式由优化格式和最高阶格式非线性加权组合得到。本文将基于不同的线性优化格式构造增强优化格式,并通过线性传播方程的数值测试选取表现较优的格式,最后针对声散射问题进行数值模拟与分析。
1 增强优化格式 1.1 差分格式的波数误差本文讨论的格式均为中心格式,采用的模板为7点对称等距模板,网格间距为h。这种差分格式可写为:
| $ \tilde f_j^\prime = \frac{1}{h}\sum\limits_{l = - 3}^3 {{a_l}} {f_{j + l}} $ | (1) |
中心格式的系数满足反对称条件,即:
| $ {a_0} = 0,{a_1} = - {a_{ - 1}},{a_2} = - {a_{ - 2}},{a_3} = - {a_{ - 3}} $ |
对于波数为k的单色波,
| $ f = {{\rm{e}}^{{\rm{i}}kx}} $ |
其导函数
| $ {f^\prime } = {\rm{i}}kf(x) $ |
对于格式(1),我们可以在节点处得到类似的公式:
| $ \tilde f_j^\prime = {\rm{i}}\tilde k{\kern 1pt} f({x_j}) $ |
若记κ=kh为无量纲波数,
| $ \tilde \kappa = 2\sum\limits_{l = 1}^3 {{a_l}} \sin (l\kappa ) $ | (2) |
记
考虑光滑函数f(x),其傅立叶变换为:
| $ \mathscr{F}(f(x)) = F(k) $ |
则
| $ \mathscr{F}({f^\prime }(x)) = {\rm{i}}kF(k) $ | (3) |
若逼近f′(x)的某差分格式为q阶精度,将逼近式从网格点拓展到实数域,则可得到一个关于x的函数,记为
| $ \mathscr{F}({\tilde f^\prime }(x)) = {\rm{i}}\tilde k{\kern 1pt} F(k) $ | (4) |
根据泰勒展开,差分格式的截断误差为:
| $ \begin{array}{*{20}{l}} {{T_h} = {{\tilde f}^\prime }(x) - {f^\prime }(x)}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = M{f^{(q + 1)}}(x){h^q} + {\rm{O}}({f^{(q + 2)}}(x){h^{q + 1}})} \end{array} $ | (5) |
其中M是由差分格式决定的常数。对上式做傅立叶变换得:
| $ \begin{array}{*{20}{l}} {\mathscr{F}({{\tilde f}^\prime }(x) - {f^\prime }(x)) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} M{{({\rm{i}}k)}^{q + 1}}F(k){h^q} + {\rm{O}}({k^{q + 2}}{h^{q + 1}})} \end{array} $ | (6) |
结合几个傅立叶变换的等式(3)、(4)、(6)以及κ=kh,
| $ \tilde \kappa - \kappa = M{{\rm{i}}^q}{\kappa ^{q + 1}} + {\rm{O}}({\kappa ^{q + 2}}) $ | (7) |
由该式可知,高阶精度的格式在波数0附近的波数误差更小。
1.2 线性优化差分格式本小节讨论7点对称模板上的最高阶格式及优化格式。在该模板上的最高阶显式差分格式为六阶。根据泰勒展开,六阶格式的系数(用上标S表示)需满足:
| $ \begin{array}{*{20}{l}} {2 \cdot 1 \cdot a_1^S + 2 \cdot 2 \cdot a_2^S + 2 \cdot 3 \cdot a_3^S = 1}\\ {2 \cdot {1^3} \cdot a_1^S + 2 \cdot {2^3} \cdot a_2^S + 2 \cdot {3^3} \cdot a_3^S = 0}\\ {2 \cdot {1^5} \cdot a_1^S + 2 \cdot {2^5} \cdot a_2^S + 2 \cdot {3^5} \cdot a_3^S = 0} \end{array} $ | (8) |
求解得到的结果为:
| $ a_1^S = \frac{3}{4},\quad a_2^S = - \frac{3}{{20}},\quad a_3^S = \frac{1}{{60}} $ | (9) |
该格式在公式中记为
这里考虑的优化格式为四阶精度的中心格式,且满足在某无量纲波数为κ0∈[0, π]时波数误差为0。根据泰勒展开和有效波数的计算公式可得到系数(用上标O表示)满足的方程组:
| $ \begin{array}{*{20}{l}} {2 \cdot 1 \cdot a_1^O + 2 \cdot 2 \cdot a_2^O + 2 \cdot 3 \cdot a_3^O = 1}\\ {2 \cdot {1^3} \cdot a_1^O + 2 \cdot {2^3} \cdot a_2^O + 2 \cdot {3^3} \cdot a_3^O = 0}\\ {2\sin ({\kappa _0})a_1^O + 2\sin (2{\kappa _0})a_2^O + 2\sin (3{\kappa _0})a_3^O = {\kappa _0}} \end{array} $ | (10) |
文献[5]中的七点色散关系保持(Dispersion Relation Preserving, DRP)格式可由κ0取1.42151084298得到,下文用DRP4表示。文献[1]中的优化格式为无量纲波数κ0取π/3时的情况,对应单位波长所含网格点数(Points Per Wavelength, PPW)[8]PPW=6。六阶中心格式Cen6也可视为κ0趋于0的极限情况。
令κ0分别取π/2、π/3和π/4(分别对应PPW=4, 6, 8),求解方程组(10)得到的优化格式分别记为Opt1、Opt2和Opt3。这三个优化格式以及DRP4在下文的公式中统一用
| $ \begin{array}{*{20}{l}} {a_1^{O1} = 0.8150810376}\\ {a_2^{O1} = - 0.2020648301}\\ {a_3^{O1} = 0.0296828742} \end{array} $ | (11) |
Opt2的系数为:
| $ \begin{array}{*{20}{l}} {a_1^{O2} = 0.7729989404}\\ {a_2^{O2} = - 0.1683991523}\\ {a_3^{O2} = 0.0212664547} \end{array} $ | (12) |
Opt3的系数为:
| $ \begin{array}{*{20}{l}} {a_1^{O3} = 0.7620318401}\\ {a_2^{O3} = - 0.1596254721}\\ {a_3^{O3} = 0.0190730347} \end{array} $ | (13) |
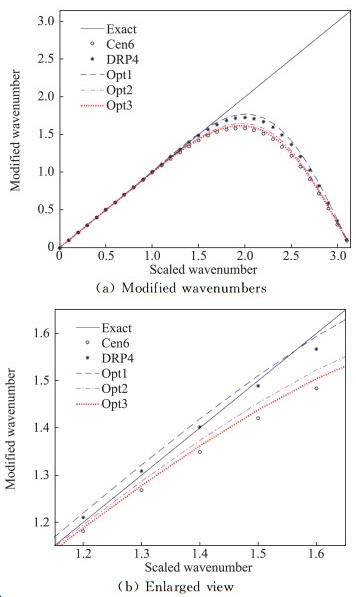
图 1(a)为几种格式的谱分辨率图,图 1(b)为局部放大图。图 1中用Exact表示理论值,后文图例中Exact均表示理论值或精确值。从图 1中可以看出,除去两端,无量纲波数从大到小依次为Opt1、DRP4、Opt2、Opt3和Cen6,这也与其相应κ0的大小顺序一致。另外,几种优化格式的修正波数
|
图 1 几种格式的谱分辨率 Fig.1 Spectral properties of some schemes |
增强优化格式是优化格式和最高阶格式的凸加权组合,即
根据下文中该格式的设计,其波数误差在[0, κ0]中非常小,而对于更高波数的单色波,其表现与普通的优化格式无异。而对于更一般的波形,如果将波形的每一小段(如四个节点)当作单色波,由于相位误差小,各段的波形应可以得到较好的保持,那么整体波形理应可以得到保持。而实际的波形中,由于一些非常高波数成分的存在,这使得该格式的表现不如在单色波中突出。
构造增强优化格式时,首先仿照文献[9]给出一种局部波数指示子:
| $ \begin{array}{*{20}{l}} {I{W_j} = [{{({f_{j - 2}} - 4{f_{j - 1}} + 6{f_j} - 4{f_{j + 1}} + {f_{j + 2}})}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{( - {f_{j - 2}} + 2{f_{j - 1}} - 2{f_{j + 1}} + {f_{j + 2}})}^2}]/}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [{{({f_{j - 1}} - 2{f_j} + {f_{j + 1}})}^2} + {{( - {f_{j - 1}} + {f_{j + 1}})}^2} + \varepsilon ]} \end{array} $ | (14) |
ε是一个小的正数,用来防止分母为0,这里取1×10-40。那么对于单色波f=sin(kx+φ)+C(C为常数项),
| $ I{W_j} = 16{\sin ^4}\left( {\frac{\kappa }{2}} \right) $ | (15) |
其中κ=kh为无量纲波数。
对于如何由IWj构造单色波相位误差较小的权值,最直接的方法是先求解无量纲波数κ,再构造权系数。令:
| $ {\lambda _0} = \frac{{\kappa - {{\tilde \kappa }^S}}}{{{{\tilde \kappa }^O} - {{\tilde \kappa }^S}}} $ | (16) |
其中
从IWj得到λ0的过程需要计算反三角函数和几个三角函数,计算量相对较大。因此采用一个简单的公式来逼近:
| $ {\lambda _j} = \min (1,{\gamma _j}) $ | (17) |
这里min表示两者的较小值,其中
| $ {\gamma _j} = \sqrt {I{W_j}} a + I{W_j}b $ | (18) |
则λj在0到1之间,这使得增强优化格式为两个子格式的凸组合。
下面讨论参数a和参数b的取值。参数a的设计目标是将
| $ IW = {\rm{O}}({\kappa ^4}),\sqrt {IW} = {\kappa ^2} + {\rm{O}}({\kappa ^4}) $ |
并且,
| $ {\lambda _j} = a{\kappa ^2} + {\rm{O}}({\kappa ^4}) $ |
设最高阶格式
| $ {T_h^S = {C_6}{f^{(7)}}(x){h^6} + {\rm{O}}({h^8})} $ |
| $ {T_h^O = {C_4}{f^{(5)}}(x){h^4} + {\rm{O}}({h^6})} $ |
其中系数C6和C4可由泰勒展开计算得到。
根据截断误差与波数误差之间的关系式(7),两个子格式的波数误差为:
| $ {{{\tilde \kappa }^S} - \kappa = - {C_6}{\kappa ^7} + {\rm{O}}({\kappa ^9})} $ |
| $ {{{\tilde \kappa }^O} - \kappa = {C_4}{\kappa ^5} + {\rm{O}}({\kappa ^7})} $ |
那么增强优化格式的波数误差为:
| $ \begin{array}{*{20}{l}} {\tilde \kappa - \kappa = (1 - {\lambda _j})({{\tilde \kappa }^S} - \kappa ) + {\lambda _j}({{\tilde \kappa }^O} - \kappa )}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = - {C_6}(1 - {\lambda _j}){\kappa ^7} + {C_4}{\lambda _j}{\kappa ^5} + {\rm{O}}({\kappa ^9})}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = (a{C_4} - {C_6}){\kappa ^7} + {\rm{O}}({\kappa ^9})} \end{array} $ |
为了减小波数误差,令首项系数为0,则:
| $ a = \frac{{{C_6}}}{{{C_4}}} $ | (19) |
对于参数b,我们要求当无量纲波数为κ0时γj为1。那么:
| $ 4{\sin ^2}\left( {\frac{{{\kappa _0}}}{2}} \right)a + 16{\sin ^4}\left( {\frac{{{\kappa _0}}}{2}} \right)b = 1 $ |
则:
| $ b = \frac{{1 - 4{{\sin }^2}\left( {\frac{{{\kappa _0}}}{2}} \right)a}}{{16{{\sin }^4}\left( {\frac{{{\kappa _0}}}{2}} \right)}} $ | (20) |
本文构造的增强优化格式为:
| $ {\tilde f^\prime } = (1 - {\lambda _j}){\tilde f^{\prime S}} + {\lambda _j}{\tilde f^{\prime O}} $ | (21) |
其中
| 表 1 几种优化格式对应的参数a和b的值 Table 1 Parameters a and b for some optimized schemes |
|
|
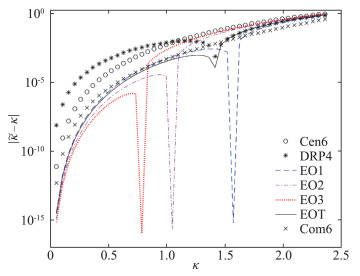
图 2给出了几种格式在0≤κ≤3π/4之间波数误差的绝对值,横坐标为无量纲波数,间隔π /60,纵坐标采用对数坐标。其中Com6表示6阶中心紧致格式[2]。从图 2中可以看出,在波数0附近DRP格式由于只有四阶精度因而误差最大,其次是Cen6,再次是Com6,而几种增强优化格式的误差较小。在优化格式及增强优化格式各自的κ0处,根据其设计原理,波数误差为机器0。而DRP和EOT由于相应的κ0不在采样点上,图中该处仅出现小幅下探。对于几种增强优化格式,随着相应κ0的变大,格式在无量纲波数较小时的误差随之变大,而在无量纲波数较大时误差则会变小。
|
图 2 几个格式波数误差绝对值的比较 Fig.2 Absolute values of wavenumber errors for some schemes |
注意上述波数误差的结果是基于单色波得到的。对于更一般的波形,其各单色波成分的波数误差与图 2所示并不一致。
2 收敛精度验证文献[1]中已经对增强优化格式的收敛精度进行了分析,其结论对于本文中几种增强优化格式依然成立。增强优化格式在流场光滑区域基本为6阶精度,但是由于格式的非线性性质,其收敛精度可能会在极值点附近降低。具体为:若求解问题是光滑的,且极值点处二阶导数不为0,则增强优化格式除极值点附近为5阶外均为6阶,则L1收敛精度为6阶,L∞收敛精度为5阶;若极值点处二阶导数为0,则增强优化格式L1收敛精度为5阶,L∞收敛精度为4阶。
下面通过数值实验验证收敛精度。考虑如下线性对流方程的初值问题:
| $ \left\{ {\begin{array}{*{20}{l}} {{u_t} + {u_x} = 0}&{, - 1 \le x \le 1}\\ {u(x,0) = {u_0}(x)}&{,{\rm{周期函数}}} \end{array}} \right. $ | (22) |
计算终止时间为T=1。采用的初值条件为u0(x)=
| 表 2 增强优化格式收敛精度测试 Table 2 Accuracy tests of two enhanced optimized schemes |
|
|
本节通过一维算例来测试对比几种增强优化格式,同时参与计算的还有六阶中心格式Cen6、优化格式DRP4及六阶中心紧致格式Com6。时间格式采用三阶TVD龙格库塔方法[10]。在实际计算中常常采用低耗散低色散龙格库塔方法[11-12]。
3.1 正弦波传播问题采用对流方程进行测试,对流速度设为1,其方程为:
| $ {u_t} + {u_x} = 0 $ | (23) |
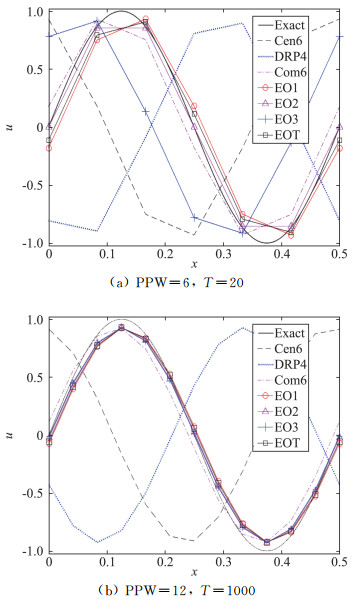
初值为u0(x)=sin (4πx),求解区域为[0, 1],计算的CFL数均取0.1,PPW分别取6和12,推进的时间分别为T=20和1000。图 3中给出了[0, 0.5]间的计算结果。两种情况下,六阶中心格式Cen6和优化格式DRP4的误差都较大。当PPW为6时,其它格式除EO3之外均得到了较好的结果,相比而言,EO2更为准确。这是由于EO3仅对无量纲波数在[0, π/4]的单波误差很小,PPW=6的正弦波的无量纲波数为π/3,超出了此范围,从图 2中也可以看出此时EO3的波数误差较大。当正弦波的PPW为12时,四种增强优化格式及紧致格式均取得了较好的结果。
|
图 3 正弦波的传播问题 Fig.3 Advection of sine waves |
两种情况下,EOT的结果大幅均优于其组成成分格式DRP4。实际上,从图 2的结果可以看出,二者的波数误差相差至少一个量级。这也说明了增强优化格式在单色波问题中有着上佳的表现。
3.2 高斯波传播问题这里计算一个高斯波的传播问题[13],其控制方程与前一问题一致,而初始波形为:
| $ {u_0} = 0.5\exp \left( { - \ln 2{{\left( {\frac{x}{{3h}}} \right)}^2}} \right) $ | (24) |
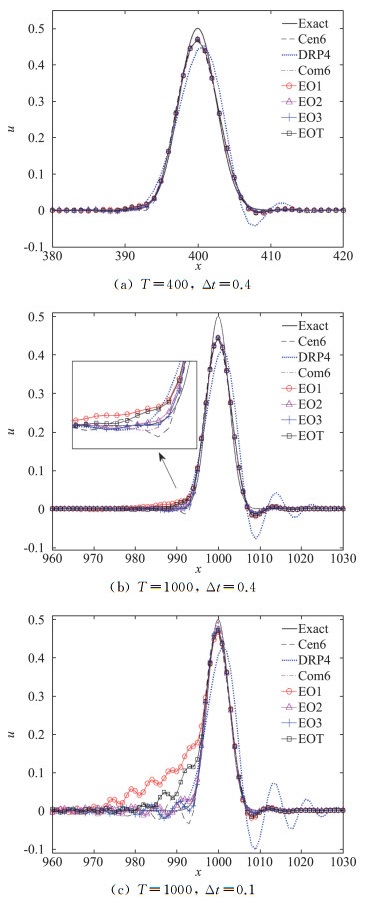
其中h=1为空间步长,取时间步长Δt=0.4。计算终止时间为T=400和1000, 计算结果显示在图 4中。整体而言,除优化格式DRP4外,几种格式均获得了较好的结果,其中六阶紧致格式Com6的结果最接近精确解。优化格式DRP4在波后发生了较明显的数值波动,这是由于这些波动的成分对应的相速度偏大所致。图 4(b)中局部的放大图中可以看到六阶中心格式Cen6存在相对明显的数值波动,与DRP4格式相反,其原因为相应成分的相速度偏小。四种增强优化格式中,其结果最好的是EO3,然后依次是EO2、EOT和EO1,其中EOT和EO1偏离精确解较大。这是由于该高斯波在步长为1时主要由长波(波数较小)构成,而此时这两种格式有一定的过度优化,导致对PPW较大的波数误差相对较大。
|
图 4 高斯波的传播问题 Fig.4 Advection of a Gaussian wave |
图 4(c)给出了时间步长取Δt=0.1时T=1000的计算结果。相比图 4(b),计算结果在高斯波两端的振荡幅度明显加大。这说明当Δt=0.4时,时间格式的耗散较大,消除了部分振荡。该算例中,EO2和EO3取得了相对较好的结果。由于中心格式没有耗散,实际计算中通常采用滤波方法[2, 14]来消除这种连续流场中的非物理振荡。
4 声散射问题数值研究当声波穿过旋涡时,会发生强烈的非线性散射现象,声波的幅值和相位都会发生显著的变化[15]。下面采用增强优化差分格式及其他常用的气动声学计算格式直接数值求解二维欧拉方程,计算平面声波穿过等熵涡的散射问题。
以无穷远处声速和密度对问题进行无量纲化。背景流动中二维等熵泰勒涡的涡心位于计算区域的中心(0, 0),其流动参数如下[16]:
| $ {{u_\theta } = {M_v}r{\kern 1pt} {\kern 1pt} \exp [(1 - {r^2})/2]} $ | (25) |
| $ {{u_r} = 0} $ | (26) |
| $ {\rho = {{\left[ {1 - \frac{{\gamma - 1}}{2}M_v^2{\kern 1pt} {\kern 1pt} {\kern 1pt} \exp (1 - {r^2})} \right]}^{\frac{1}{{\gamma - 1}}}}} $ | (27) |
| $ {p = \frac{{{\rho ^\gamma }}}{\gamma }} $ | (28) |
其中,uθ为背景流动切向速度,ur为径向速度,ρ和p分别为密度和压强。最大马赫数Mv=0.125,γ为气体绝热指数(空气中一般取为1.4)。
如图 5所示,计算区域为-20, 20 × -20, 20。左边界入射平面波形式为:
|
图 5 平面声波穿过泰勒涡示意图 Fig.5 Diagram of plane wave propagating through Taylor vortex |
| $ \left[ {\begin{array}{*{20}{c}} {{\rho ^\prime }}\\ {{u^\prime }}\\ {{v^\prime }}\\ {{p^\prime }} \end{array}} \right] = \varepsilon \left[ {\begin{array}{*{20}{l}} 1\\ 1\\ 0\\ 1 \end{array}} \right]\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }(x - t)} \right) $ | (29) |
其中,ρ′、u′、v′、p′分别为入射声波的密度、x方向速度、y方向速度、压强。声压振幅ε=1×10-5,波长λ分别为0.8和1。在计算区域右侧和上下两边设置吸收层,减小反射声波对计算的影响,满足无反射边界条件,具体形式参见文献[17-18]。
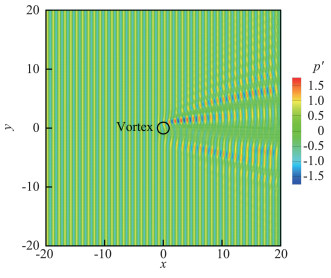
根据一维算例的结果,我们采用综合表现最好的EO2格式计算此问题。为了进行比较,同时还采用了六阶中心格式Cen6、优化格式DRP4以及六阶紧致格式Com6进行计算。为了便于比较,计算中统一采用了8阶紧致滤波格式[2]进行滤波。由于该问题没有理论精确解,这里采用时间步长为0.004,空间步长为0.02的六阶紧致格式计算结果作为该问题的参考精确解(图中用Ref.表示)。λ取0.8和1时计算终止时间分别取t=56和60。图 6给出了λ=1、t=60时参考精确解的声压分布。可以看到声波穿过旋涡后会发生明显的畸变。在旋涡正后方有明显的相移,声波幅值快速衰减,在局部形成“寂静区”。下游±15°的方向形成两条一级强噪声干扰条带,在一级条带外侧,形成若干个次级噪声干扰条带,强度依次减弱。由于泰勒涡逆时针旋转,干扰条带关于y轴不对称,且旋涡上方干扰强度大于下方。
|
图 6 λ=1、t=60时声压云图 Fig.6 Contour of the acoustic fluctuating pressure at t=60 for λ=1 |
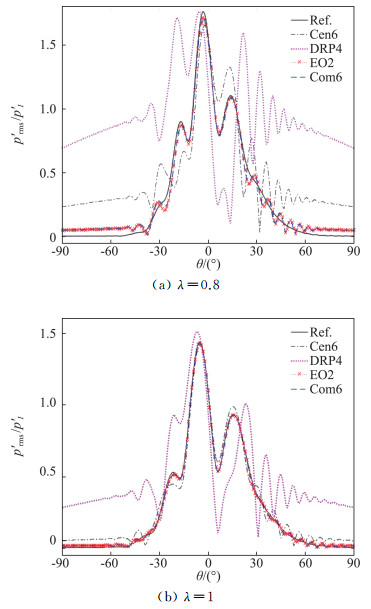
该问题计算时间步长和空间步长分别取0.02和0.1。图 7给出了r=10的圆周上散射声压的指向性分布。首先我们取入射波波长为0.8。图 7(a)为几种格式在各个方向的散射声压均方根。从图 7(a)中可以看出,在这种相对较粗的网格下,数值结果相比参考解有较明显的误差。其中增强优化格式EO2与紧致格式Com6的结果相差很小,它们与参考解之间的差距较小。在声波散射的主要区域,其幅值与参考解基本符合,在25°到70°之间,其幅值随角度变化有一定幅度的振荡。声波散射影响较小的区域,其结果的幅值误差略微偏大。六阶中心格式的误差较大,而优化格式DRP4表现最差。然后我们将入射波波长设为1,图 7(b)给出了计算结果散射声压均方根的指向性分布。结果与图 7(a)相似,但是误差变得更小了。说明对于该问题,随着入射波的波长的增加,数值计算更容易获得好的结果。
|
图 7 RMS压力指向性分布 Fig.7 Directivity distributions of RMS values of fluctuating pressure |
本文数值模拟均采用Fortran程序在CPU为Intel Core i7 6700K@4GHz的台式机上单线程计算。编译优化选项为“-O2”。
对于3.2节中高斯波传播问题Δt=0.1、T=1000的情况,即图 4(c)对应的算例,我们记录了几种格式该算例的计算时间。然后将空间间距两次减半,分别记录了其计算时间,三次计算的时间均列入表 3中。从表 3中可以看出增强优化格式EO2仅需紧致格式Com6不到一半的时间。
| 表 3 几种格式计算高斯波传播问题所需时间(Δt=0.1, T=1000, 单位: s) Table 3 Computational time of advection of Gaussian wave (Δt=0.1, T=1000, unit: s) |
|
|
表 4中给出了声散射问题几种格式的计算时间。从表 4中可以看出增强优化格式EO2所需时间少于紧致格式Com6,但是该算例中EO2取得了与紧致格式相近的结果。并且,EO2是显式格式,相比紧致格式更容易处理边界条件并且更适于并行计算。
| 表 4 几种格式计算声波散射问题所需时间(单位:s) Table 4 Computational time of the sound scattering problem (unit: s) |
|
|
增强优化格式为最高阶格式与线性优化格式的加权平均。加权系数通过极小化单色波的相位误差得到,加权的过程保证了格式的最优阶收敛精度,并且提高了分辨率。该类格式对于单色波问题的误差很小,而对于其它连续波形的传播问题,也有较好表现。
本文给出了七点增强优化格式的统一构造方法,并比较了几种增强优化格式。线性传播问题的数值实验表明增强优化格式EO2综合表现相对较好。针对平面声波穿过泰勒涡的散射问题,采用了增强优化格式EO2进行数值模拟,并比较了几种不同类型的格式。结果表明增强优化格式EO2的结果与六阶中心紧致格式相近,但是需要的计算时间更少。另外,由于该格式为显式格式,因此相比紧致格式更容易处理边界条件,并且更适于并行计算。
下一步将采用更多算例对该格式进行进一步测试,并将相应算法加入国家数值风洞(NNW)工程拟开发的气动噪声数值模拟软件。NNW工程是我国在2018年底启动的项目,旨在自主研发功能先进、种类齐全的CFD软件系统,相关介绍及详细进展参见文献[19]。
| [1] |
武从海, 王益民, 张树海. 一种混合优化差分格式[J]. 气体物理, 2019, 4(6): 22-28. WU C H, WANG Y M, ZHANG S H. A hybrid optimized difference scheme[J]. Physics of Gases, 2019, 4(6): 22-28. (in Chinese) |
| [2] |
LELE S K. Compact finite difference schemes with spectral-like resolution[J]. Journal of Computational Physics, 1992, 103(1): 16-42. DOI:10.1016/0021-9991(92)90324-R |
| [3] |
姜屹, 邓小刚, 毛枚良, 等. 基于HDCS-E8T7格式的气动噪声数值模拟方法研究进展[J]. 空气动力学学报, 2014, 32(5): 559-574. JIANG Y, DENG X G, MAO M L, et al. Progress of aeroacoustic simulation method based on HDCS-E8T7 scheme[J]. Acta Aerodynamica Sinica, 2014, 32(5): 559-574. DOI:10.7638/kqdlxxb-2014.0103 (in Chinese) |
| [4] |
TAM C K W. Recent advances in computational aeroacoustics[J]. Fluid Dynamics Research, 2006, 38(9): 591-615. DOI:10.1016/j.fluiddyn.2006.03.006 |
| [5] |
TAM C K W, WEBB J C. Dispersion-relation-preserving finite difference schemes for computational acoustics[J]. Journal of Computational Physics, 1993, 107(2): 262-281. DOI:10.1006/jcph.1993.1142 |
| [6] |
WU C H, ZHAO N. A stability criterion for semi-discrete difference schemes of hyperbolic conservation laws on uniformgrids[J]. Journal of Scientific Computing, 2014, 58(2): 450-471. DOI:10.1007/s10915-013-9742-8 |
| [7] |
VICHNEVETSKY R, BOWLES J B. Fourier analysis of numerical approximations of hyperbolic equations[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1982. DOI:10.1137/1.9781611970876
|
| [8] |
LOCKARD D P, BRENTNER K S, ATKINS H L. High-accuracy algorithms for computational aeroacoustics[J]. AIAA Journal, 1995, 33(2): 246-251. DOI:10.2514/3.12436 |
| [9] |
武从海.流体力学高精度高分辨率差分格式的研究[D].南京: 南京航空航天大学, 2012. WU C H. Research on high order accurate and high resolution difference methods of fluid dynamics[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012.(in Chinese) |
| [10] |
SHU C W. Total-variation-diminishing time discretizations[J]. SIAM Journal on Scientific and Statistical Computing, 1988, 9(6): 1073-1084. DOI:10.1137/0909073 |
| [11] |
HU F Q, HUSSAINI M Y, MANTHEY J L. Low-dissipation and low-dispersion Runge-Kutta schemes for computational acoustics[J]. Journal of Computational Physics, 1996, 124(1): 177-191. DOI:10.1006/jcph.1996.0052 |
| [12] |
BERLAND J, BOGEY C, BAILLY C. Low-dissipation and low-dispersion fourth-order Runge-Kutta algorithm[J]. Computers & Fluids, 2006, 35(10): 1459-1463. DOI:10.1016/j.compfluid.2005.04.003[LinkOut |
| [13] |
HARDIN J C, RISTORCELLI J R, TAM C K W. ICASE/LaRC Workshop on Benchmark Problems in Computational Aeroacoustics (CAA)[C]//Proceedings of a workshop sponsored by the National Aeronautics and Space Administration, Washington, D.C., and the Institute for Computer Applications in Science and Engineering (ICASE). Hampton, Virginia, 1994. NASA CP 1995-3300, 1995.
|
| [14] |
KOUTSAVDIS E K, BLAISDELL G A, LYRINTZIS A S. Compact schemes with spatial filtering in computational aeroacoustics[J]. AIAA Journal, 2000, 38(4): 713-715. DOI:10.2514/2.1016 |
| [15] |
COLONIUS T, LELE S K, MOIN P. The scattering of sound waves by a vortex:Numerical simulations and analytical solutions[J]. Journal of Fluid Mechanics, 1994, 260: 271-298. DOI:10.1017/s0022112094003514 |
| [16] |
INOUE O, HATTORI Y. Sound generation by shock-vortex interactions[J]. Journal of Fluid Mechanics, 1999, 380: 81-116. DOI:10.1017/s0022112098003565 |
| [17] |
王益民.声波在典型流场中传播的畸变特性[D].绵阳: 中国空气动力研究与发展中心, 2017. WANG Y M. Distortion characteristics of wave propagation in typical flow structure[D]. Mianyang: China Aerodynamics Research and Development Center, 2017. (in Chinese) |
| [18] |
ABARBANEL S, DITKOWSKI A. Wave propagation inadvected acoustics within a non-uniform medium under the effect of gravity[J]. Applied Numerical Mathematics, 2015, 93: 61-68. DOI:10.1016/j.apnum.2014.04.003 |
| [19] |
陈坚强.国家数值风洞(NNW)工程关键技术研究进展[J].中国科学: 技术科学, 2020(在线发表). CHEN J Q. Advances in the key technologies of Chinese National Numerical Windtunnel project[J]. Scientia Sinica Technologica, 2020(online). (in Chinese) DOI: 10.1360/SST-2020-0334 |
 2020, Vol. 38
2020, Vol. 38


