2. 中南大学 高速铁路建造技术国家工程实验室, 长沙 410075
2. National Engineering Laboratory for High-speed Railway Construction, Central South University, Changsha 410075, China
工程中经常会遇到一端固定于壁面的有限长柱体绕流的问题,如高层建筑等。有限长柱体的流动是高度三维的,与二维流动存在很大差异[1-3]。通常,有限长柱体的流动结构可分为顶部涡或者拖曳涡、展向涡以及底部涡[2, 4-5]。顶部涡和底部涡分别诱导产生的沿展向的下扫流和上扫流会减弱展向周期性的旋涡脱落[3, 6]。对于有限长柱体,随着壁面边界层厚度的增加,底部涡以及相应的上扫流将会增强[4];而展向涡的强弱主要取决于柱体的高宽比H/d。当H/d小于临界值时,展向涡由交错排列变为对称排列状态[7-8],Sakamoto和Arie[7]给出了H/d临界值的建议值,圆柱为3.0,方柱为2.5。
基于时均尾流场的分析,Tanaka和Murata[9]计算了有限长柱体下游的平均涡线。对于H/d分别为1.25和10两种情况,他们发现柱体两侧的涡线在自由端附近相互连接,形成拱形结构。Wang和Zhou[5]对H/d=7的有限长方柱尾流进行了展向和横向的同步流动可视化,发现从瞬时角度看,展向剪切流与自由端剪切流也相互连接,形成拱形结构。Kawai[2]等用三维立体PIV对H/d=2.7的有限长柱体尾流进行的测试验证了上述结论。
在高层建筑的设计中,风荷载和风致振动是至关重要的[10-11]。外形优化是降低高层建筑风荷载和振动最常用的措施之一[11-14]。Kim[12]等探究了棱柱的边数和螺旋化对高层建筑风荷载的影响。结果表明,增加建筑物的棱柱边数,其抗风稳定性会增强,且边数为3和4的高层建筑物的螺旋化处理对其脉动力有明显的抑制效果。Tanaka[13]等利用风洞实验研究了方形截面高层建筑物切角、圆角、开洞、螺旋化以及沿高度方向改变其截面积等措施对其气动力、风压特性的影响。发现这些被动控制措施对其风荷载、风致振动均起到了一定的抑制作用。Dutton[14]等通过风洞实验研究了H/d=9的方柱上半部分沿高度方向开洞的控制效果。发现贯穿开洞可以有效地减小高层建筑模型的气动力和横风向风致振动。但是上述外形优化方法对高层建筑结构设计和内部空间有很大的影响。
近年来,将主动控制方法应用于抑制高层建筑风荷载与风致振动也逐渐受到关注。Zhang[15]等通过实验研究了在H/d=6的高层建筑物侧面和背面定常吸气对其气动力的控制效果,发现两者对模型气动力都有一定的优化,但侧面吸气控制效果更佳。Zheng[16-17]等通过数值模拟研究了H/d=3.7的高层建筑物侧面全高定常吹气的控制效果。并对比了吹气角、开孔宽度、开孔位置和吹气流量系数等对模型的气动力的影响效果,发现吹气流量对控制效果起了主导作用。郑朝荣[18]等通过在H/d=3.7的高层建筑物在模型上部施加吸气控制,研究了风向角和吸气系数等参数对模型时均气动力的影响规律。发现吸气高度范围内模型气动力变化显著,但其它区域气动力变化较小,且吸气流量越大,模型侧面风压和顺风向风荷载折减越显著。郑朝荣[19]等尝试了在H/d=5的凹角方形截面柱体展向分离点附近施加定常吸气的控制方法,发现吸气能起到减阻效果,且吸气流量系数越大,减阻效果越显著,时均气动阻力最多可减小62%。上述主动控制均是沿柱体展向布置,与传统的二维柱体绕流控制在本质上是相似的。
文献[2-4, 20]指出,有限长柱体绕流中自由端剪切流与沿展向剪切流相互连接,并构成了一个封闭的拱门形涡结构。因此有可能通过控制自由端剪切流达到控制整个尾流的目的。Park[21]等研究了H/d=6圆柱自由端形状对其尾流的影响,发现由半球型顶端代替平面型顶端后可以削弱圆柱体尾流中有规则的涡脱落,减小模型后方回流区长度。文献[3-4]指出H/d=5的有限长柱体尾流中下扫流对其展向涡中反对称涡脱落形态起到抑制作用,从而具有削弱模型的气动力的作用。最近,Wang[22]等报道了通过自由端定常狭缝吸气可以明显抑制H/d=5的方柱的脉动升力,但控制的机理尚不清楚。
本文通过大涡模拟(LES)研究了自由端定常狭缝吸气对H/d=5方形柱体绕流与气动力的影响,对比了三种典型吸气系数下的模拟结果。为揭示有限长柱体顶部吸气这一新型控制方法的作用机理,进行了气动力分析、时均流场分析以及λ2准则分析。
1 数值模拟介绍 1.1 模拟方法采用LES对计算域内非稳态流动问题进行求解。LES以空间特征尺度Δ对不可压N-S方程和连续方程进行过滤,得到式(1)、式(2)所示控制方程:
| $\frac{\partial \overline{u_{i}}}{\partial t}+\frac{\partial\left(u_{i} u_{j}\right)}{\partial x_{j}}=-\frac{1}{\rho} \frac{\partial \bar{p}}{\partial x_{i}}+\nu \frac{\partial^{2} \overline{u_{i}}}{\partial x_{j}}-\frac{\partial \tau_{i j}}{\partial x_{j}} $ | (1) |
| $\frac{\partial \bar{u}_{i}}{\partial x_{i}}=0 $ | (2) |
其中,i、j=1, 2, 3;xi为三个方向的坐标;ui为过滤特征后三个方向的速度,p为过滤后的压力;ρ为流体的密度,ν为气体的运动黏性系数;τij为亚网格剪切应力;t为时间。LES是基于对大尺度运动直接求解,对小尺度运动通过亚网格应力(subgrid-scale stress, SGS)模型进行模拟求解。式(1)中τij反映了亚网格湍流对于大尺度湍流的作用。本文选用Smagorinsky[23]亚网格应力模型,如式(3)所示。
| $\tau_{i j}=\overline{u_{i} u_{j}}-\overline{u_{i}} \overline{u_{j}}=-2 \nu_{s g s} \bar{S}_{i j}+\tau_{k k} \delta_{i j} / 3 $ | (3) |
式中
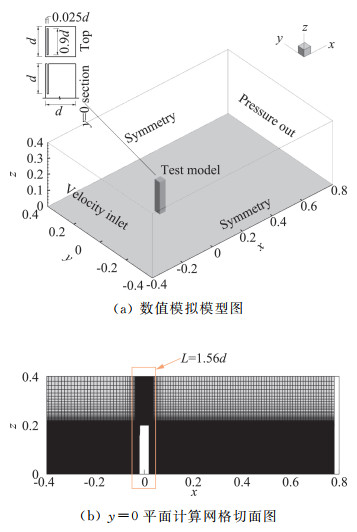
计算域和坐标定义如图 1(a)所示,坐标原点在柱体底面中心。柱体高宽比H/d=5,宽度d=40 mm。计算域长30 d,宽20 d,高10 d。柱体中心距离计算域入口10 d。柱体吸气狭缝在顶面的长度为0.9 d,宽为0.025 d,距离顶面前缘0.025 d,吸气狭缝深度为d,如图 1(a)所示。由文献[25]可知,将边界条件定义在狭缝底部,这样可以避免将吸气狭缝边界条件定义在模型顶面上而造成的对计算结果的影响。采用结构化网格对计算域离散,模型周边网格进行局部加密,在模型两侧各0.78 d范围进行加密,如图 1(b)示。对于800万网格工况,最小网格尺寸为0.01 mm,相当于0.025% d。
|
图 1 数值计算域及计算网格 Fig.1 Numerical calculation domain and calculation grid |
计算域入口为均匀速度入口,自由来流速度U∞=10 m/s,雷诺数Re=2.78×104,入口湍流强度为0.5%。出口为压力出口,计算域顶面和侧面为对称边界条件,柱体表面与计算域底面为无滑移壁面,吸气狭缝底部为速度出口。
由文献[22]可知,有限长正方形柱体的斯特劳哈尔数(St)略小于对应的二维方柱,为0.11左右。因此,计算时间步长选为0.001 s,约为涡脱周期的0.86%。定义吸气系数Q=U/U∞,其中U为吸气狭缝入口风速,U∞为自由来流速度,吸气流量系数Qv是从流量的角度定义吸气强度,A为吸气狭缝的面积,其计算公式如式(4)所示。本文研究了三种典型吸气系数(Q=0,1和3,此时Qv分别为0、0.18、0.54)下的柱体尾流与气动力特性。
| $Q_{v}=\frac{U A}{U_{\infty} d H} $ | (4) |
共选用了三套网格,总网格数约分别为400万、700万和800万。三套网格均满足模型表面y+ < 1,其主要区别在于模型周边网格加密程度。表 1将三套网格的计算结果与文献[22]中实验结果进行对比。三套网格的St变化幅度不大,对于时均阻力
| 表 1 结果对比 Table 1 Results comparison |
|
|
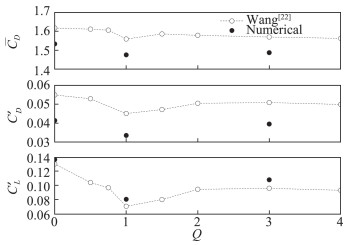
图 2将不同吸气系数Q下大涡模拟所得的
|
图 2 整体阻力 |
| 表 2 有无控制计算结果比较 Table 2 Comparison of calculated results with or without suction control |
|
|
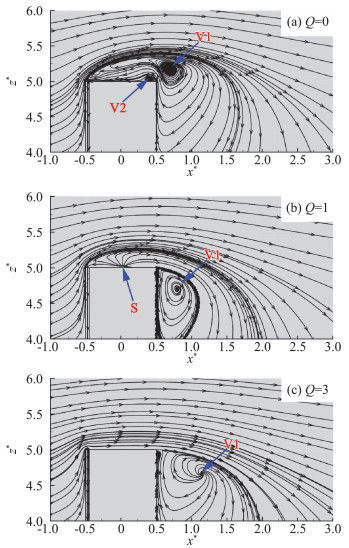
图 3分别给出了模型尾流y=0平面内的时均流线图。当Q=0时,来流在模型顶部前边缘发生分离,由于柱体背面负压的作用,分离流绕过模型后在其下游形成明显的下扫流。部分下扫流进入柱体尾流,并沿柱体背面向上运动至其自由端,该流动在柱体自由端附近形成一主旋涡“V1”,沿柱体背面的上升流在其自由端后边缘形成次旋涡“V2”,如图 3 (a)所示。此时,除V2范围外,柱体顶部都处于分离流所形成的回流区内。当Q=1时,来流仍在前边缘发生了分离,但自由端上出现一个源点“S”,如图 3(b)所示。显然,仅S上游部分的自由端仍处于回流区内。自由端剪切流在Q=1的吸气作用下明显向下倾斜,主旋涡V1的高度明显降低。当Q=3时,在强烈的狭缝吸气作用下,分离流被彻底抑制,来流紧贴自由端向下游运动,主旋涡V1进一步向下游运动,如图 3(c)所示。
|
图 3 y=0平面不同吸气系数下模型的时均流线图 Fig.3 Time-averaged flow chart of the model at different suction ratios in the plane of y=0 |
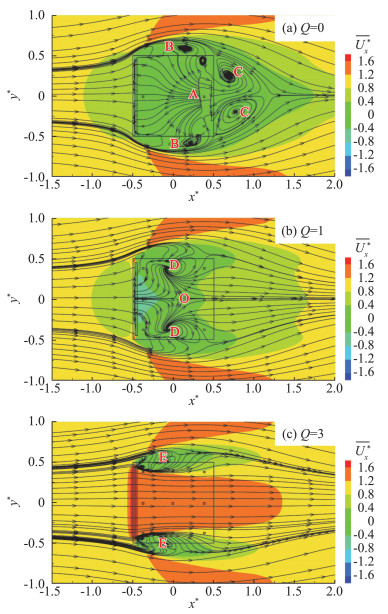
为进一步显示吸气作用下自由端分离流的变化情况,图 4给出了紧贴柱体顶部的水平面内的时均流线图。Q=0时,柱体两侧与柱体下游各出现了一对旋涡B和C,其中C为柱体尾流中展向涡的时均结果。自由端后边缘附近出现一分离线A。当从y=0平面进行观察的时候,这一分离线对应了图 3(a)中自由端后边缘旋涡“V2”的前侧分离点。当Q=1时,顶面中心线上出现一鞍点O,左右两侧流动汇聚于O,并在其上、下游分别形成回流和紧贴顶面的流动,如图 4(b)所示。O点位置即为图 3(b)所示中心截面内所显示的源点S。当Q=1时,尾流中与柱体侧面的旋涡(即图 5(a)中所示B与C)都完全消失了,这一现象说明自由端附近展向涡脱落被显著抑制了。当Q=3时,除自由端两侧局部旋涡之外,边缘处的流动分离被完全抑制,来流紧贴模型顶端表面流过柱体。
|
图 4 顶面时均流场图 Fig.4 Time averaged flow field on the top |
|
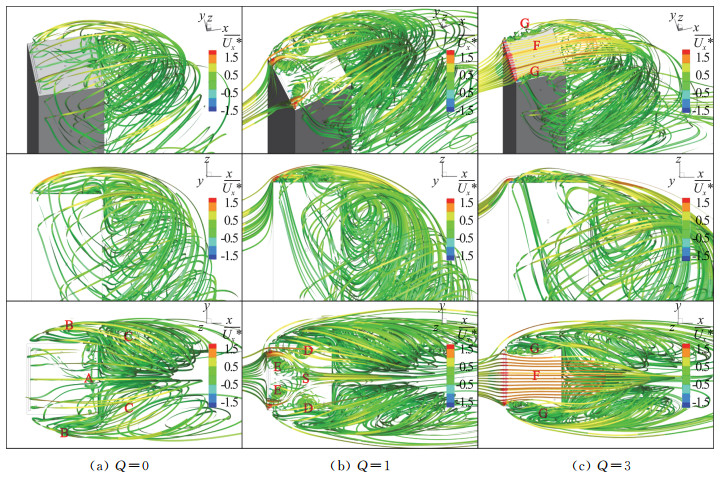
图 5 Q=0, 1和3下顶部流场三维流线示意图 Fig.5 Three-dimensional streamline diagram of flow field at the top under Q=0, 1 and 3 |
图 5给出了不同吸气系数时,柱体顶部附近的三维流线图,并采用了流向速度对流线进行了着色。在Q=1时, 在顶部负压的作用下柱体两侧流动会沿侧面向上运动进入顶面分离流区域, 在顶面形成D和E两对旋涡。柱体两侧出现了较强的上升流动,这一上升流动将抑制展向的旋涡脱落强度并削弱柱体的气动力,如图 5(b)所示。Q=3时的流线如图 5(c)所示,其中G点表示在方柱顶部两侧对称出现的旋涡,其对应着图 4(c)中E点;方柱顶部大部分区域内流动分离完全被抑制,流线紧贴顶面向下游发展,如F所示区域。
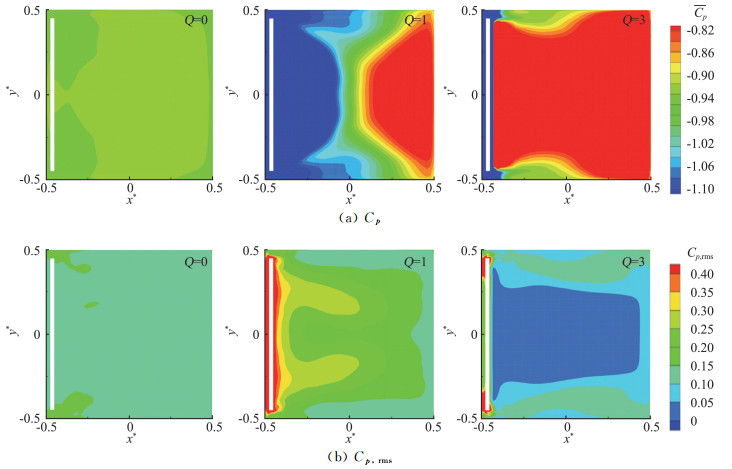
图 6给出了柱体自由端上的时均与脉动风压分布。Q=0时,顶面的
|
图 6 柱体顶面时均与脉动风压 Fig.6 Top surface time-averaged pressureand rms pressure of cylinder |
|
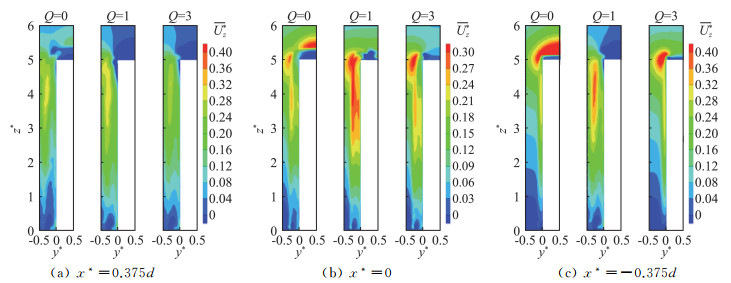
图 7 x*=0.375 d, 0, -0.375 d截面 |
为了说明吸气作用下顶面风压分布与侧面流动情况的关系,图 7给出了三种吸气系数Q下x方向三个不同截面内的时均展向速度
为了突出顶部狭缝吸气对柱体尾流的影响,图 8给出了尾流中λ2等值面,其定义为:
|
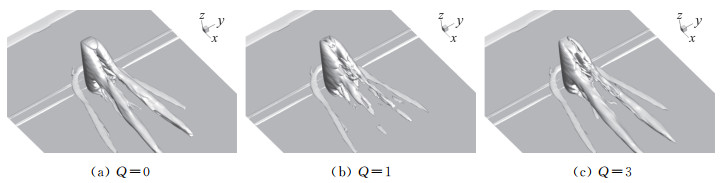
图 8 λ2=0.4的时均等值面图 Fig.8 Time-averaged iso-surface of λ2=0.4 |
| $\lambda_{2}=0.5\left(R_{i j} R_{i j}-S_{i j} S_{i j}\right)\\ R_{i j}=0.5\left(\frac{\partial u_{i}}{\partial x_{j}}-\frac{\partial u_{j}}{\partial x_{i}}\right)\\ S_{i j}=0.5\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right) $ | (5) |
式中,Rij为斜对称旋转张量;Sij为对称应变张量;i, j=1, 2, 3;u1、u2和u3分别是笛卡尔坐标系中沿x1、x2和x3方向的速度分量。λ2不变量是常见的几个Galilean不变量之一,是基于Rij和Sij常见的一种涡结构提取方法[20, 30]。图 8给出了Q=0,1和3下λ2=0.4的时均等值面。从图 8可以观察到柱体附近产生的马蹄形涡,而尾流上半部分则由对称的流向涡所控制,即顶部涡,这与文献[20]的规律是一致的。当Q=1时,尾流上半部分的顶部涡被显著削弱;而当Q=3时,顶部涡又一次出现,且其强度与无控制工况相当。上述规律与柱体顶面风压与流动情况是一致的,即Q=1时的狭缝吸气对尾流的抑制作用是最显著的。
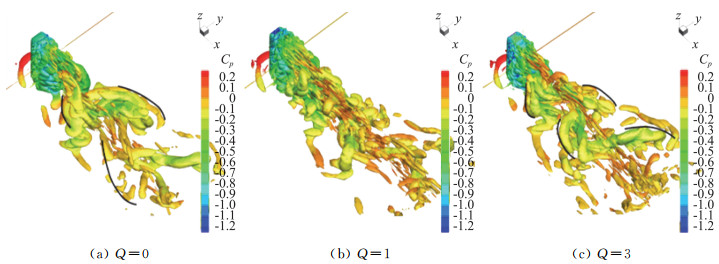
为了突出顶部狭缝吸气对柱体展向涡强度的影响,图 9给出了λ2=0.6的瞬时特征等值面图,并以风压进行着色。图 9(a)、9(c)中,用黑色的线条大致表示出展向涡的发展趋势,为反对称分布形态。而Q=1时,展向涡的强度和两侧发展程度明显减弱,说明当展向涡的强度减弱的时候,气动力(脉动升力和脉动阻力)也会随之明显减弱。由前文介绍可知,有限长柱体绕流中自由端剪切流与沿展向剪切流是相互连接的并构成了一个封闭的拱门形涡结构,因此顶部狭缝吸气通过对展向涡强度的控制,可以达到对整体气动力控制的效果。
|
图 9 不同吸气系数下典型时刻λ2=0.6等值面图 Fig.9 Iso-surface of λ2=0.6 at typical moment with different suction coefficients Q |
利用LES对H/d=5的有限长正方形截面柱体顶部定常狭缝吸气对其气动力和绕流特性的影响进行了研究,重点分析了不同吸气系数Q下自由端剪切流变化情况,得出如下结论:
1) 顶部狭缝定常吸气这一新型主动控制措施对气动力控制起到了一定的作用,但是并不是吸气强度越大,控制效果越好,模型整体的气动力控制效果在Q=1时最佳,相对于无控制工况,时均阻力、脉动阻力和脉动升力分别减少了3.92%、19.08%和40.88%。
2) 从流动控制角度而言,相对于无控制工况,Q =1时模型顶部负压和压力脉动最为显著,模型自由端前半部处于分离区内,而后半部流动则附着于顶面,此时尾流中顶部涡被明显削弱。当吸气系数增大到Q=3时,顶部流动分离被完全抑制,顶面负压强度和压力脉动明显减弱,尾流中顶部涡强度又有所增强,与无控制工况基本一致。
3) Q=1时,顶面较强的负压有利于柱体两侧形成向上的流动,从而削弱柱体展向涡结构并抑制柱体气动力;此外,顶部强烈的压力脉动增强了自由端剪切流和尾流间的动量交换,有效地削弱了尾流中的流向顶部涡结构。
| [1] |
SATTARI P, BOURGEOIS J A, MARTINUZZI R J. On the vortex dynamics in the wake of a finite surface-mounted square cylinder[J]. Experiments in Fluids, 2012, 52(5): 1149-1167. DOI:10.1007/s00348-011-1244-6 |
| [2] |
KAWAI H, OKUDA Y, OHASHI M. Near wake structure behind a 3D square prism with the aspect ratio of 2.7 in a shallow boundary layer flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 104-106: 196-202. DOI:10.1016/j.jweia.2012.04.019 |
| [3] |
WANG H F, PENG S, ZHOU Y, et al. Transition along a finite-length cylinder in the presence of a thin boundary layer[J]. Experiments in Fluids, 2016, 57(5): 66. DOI:10.1007/s00348-016-2160-6 |
| [4] |
WANG H F, ZHOU Y, CHAN C K, et al. Effect of initial conditions on interaction between a boundary layer and a wall-mounted finite-length-cylinder wake[J]. Physics of Fluids, 2006, 18(6): 065106. DOI:10.1063/1.2212329 |
| [5] |
WANG H F, ZHOU Y. The finite-length square cylinder near wake[J]. Journal of Fluid Mechanics, 2009, 638: 453-490. DOI:10.1017/s0022112009990693 |
| [6] |
PORTEOUS R, MOREAU D J, DOOLAN C J. A review of flow-induced noise from finite wall-mounted cylinders[J]. Journal of Fluids and Structures, 2014, 51: 240-254. DOI:10.1016/j.jfluidstructs.2014.08.012 |
| [7] |
SAKAMOTO H, ARIE M. Vortex shedding from a rectangular prism and a circular cylinder placed vertically in a turbulent boundary layer[J]. Journal of Fluid Mechanics, 1983, 126: 147-165. DOI:10.1017/s0022112083000087 |
| [8] |
PATTENDEN R J, TURNOCK S R, ZHANG X. Measurements of the flow over a low-aspect-ratio cylinder mounted on a ground plane[J]. Experiments in Fluids, 2005, 39(1): 10-21. DOI:10.1007/s00348-005-0949-9 |
| [9] |
TANAKA S, MURATA S. An investigation of the wake structure and aerodynamic characteristics of a finite circular cylinder. Time-averaged wake structures behind circular cylinders with various aspect ratios[J]. JSME International Journal Series B, 1999, 42(2): 178-187. DOI:10.1299/jsmeb.42.178 |
| [10] |
GU M, QUAN Y. Across-wind loads of typical tall buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92(13): 1147-1165. DOI:10.1016/j.jweia.2004.06.004 |
| [11] |
QUAN Y, GU M. Across-wind equivalent static wind loads and responses of super-high-rise buildings[J]. Advances in Structural Engineering, 2012, 15(12): 2145-2155. DOI:10.1260/1369-4332.15.12.2145 |
| [12] |
KIM Y C, BANDI E K, YOSHIDA A, et al. Response characteristics of super-tall buildings-Effects of number of sides and helical angle[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 145: 252-262. DOI:10.1016/j.jweia.2015.07.001 |
| [13] |
TANAKA H, TAMURA Y, OHTAKE K, et al. Experimental investigation of aerodynamic forces and wind pressures acting on tall buildings with various unconventional configurations[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 107-108: 179-191. DOI:10.1016/j.jweia.2012.04.014 |
| [14] |
KWOK K C S, BAILEY P A. Aerodynamic devices for tall buildings and structures[J]. Journal of Engineering Mechanics, 1987, 113(3): 349-365. DOI:10.1061/(asce)0733-9399(1987)113:3(349) |
| [15] |
ZHANG H F, XIN D B, OU J P. Steady suction for controlling across-wind loading of high-rise buildings[J]. The Structural Design of Tall and Special Buildings, 2016, 25(15): 785-800. DOI:10.1002/tal.1283 |
| [16] |
ZHENG C R, ZHANG Y C. Computational fluid dynamics study on the performance and mechanism of suction control over a high-rise building[J]. The Structural Design of Tall and Special Buildings, 2012, 21(7): 475-491. DOI:10.1002/tal.622 |
| [17] |
郑朝荣, 张耀春. 高层建筑风荷载减阻的吸气方法数值研究[J]. 应用基础与工程科学学报, 2010, 18(1): 80-90. ZHENG C R, ZHANG Y C. Numerical investigation of the wind-load reduction for a high-rise building by suction[J]. Journal of Basic Science and Engineering, 2010, 18(1): 80-90. DOI:10.1631/jzus.A0900593 (in Chinese) |
| [18] |
郑朝荣, 任凯, 武岳, 等. 上部吸气控制下超高层建筑的平均风荷载特性研究[J]. 武汉理工大学学报, 2015, 37(6): 60-65. ZHENG C R, REN K, WU Y, et al. Experimental research on the characteristics of mean wind loads of high-rise buildings controlled by upper-surface suction[J]. Journal of Wuhan University of Technology, 2015, 37(6): 60-65. DOI:10.3963/j.issn.1671-4431.2015.06.012 (in Chinese) |
| [19] |
郑朝荣, 张继同, 张智栋. 凹角与吸气控制下高层建筑平均风荷载特性试验研究[J]. 建筑结构学报, 2016, 37(10): 125-131. ZHENGC R, ZHANG J T, ZHANG Z D. Experimental investigation on characteristics of mean wind loads of high-rise buildings controlled by corner recession and air-suction[J]. Journal of Building Structures, 2016, 37(10): 125-131. DOI:10.14006/j.jzjgxb.2016.10.015 (in Chinese) |
| [20] |
ZHANG D, CHENG L, AN H W, et al. Direct numerical simulation of flow around a surface-mounted finite square cylinder at low Reynolds numbers[J]. Physics of Fluids, 2017, 29(4): 045101. DOI:10.1063/1.4979479 |
| [21] |
PARK C W, LEE S J. Effects of free-end corner shape on flow structure around a finite cylinder[J]. Journal of Fluids and Structures, 2004, 19(2): 141-158. DOI:10.1016/j.jfluidstructs.2003.12.001 |
| [22] |
WANG H F, PENG S, LI Y, et al. Control of the aerodynamic forces of a finite-length square cylinder with steady slot suction at its free end[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 179: 438-448. DOI:10.1016/j.jweia.2018.06.016 |
| [23] |
SMAGORINSKY J. General circulation experiments with the primitive equations[J]. Monthly Weather Review, 1963, 91(3): 99-164. DOI:10.1175/1520-0493(1963)091<0099:gcewtp>2.3.co;2 |
| [24] |
KRAJNOVIC S, DAVIDSON L. Large-eddy simulation of the flow around a bluff body[J]. AIAA Journal, 2002, 40: 927-936. DOI:10.2514/3.15142 |
| [25] |
崔文诗.基于合成射流技术的汽车非定常流动控制研究[D].上海: 同济大学, 2017.
|
| [26] |
OGUNREMI A, SUMNER D. On the effects of incidence angle on the mean wake of a surface-mounted finite-height square prism[C]//Proceedings of ASME/JSME/KSME 2015 Joint Fluids Engineering Conference, Seoul, South Korea, 2015. DOI: 10.1115/AJKFluids2015-15011
|
| [27] |
王汉封, 赵东伟, 邹超, 等. 高宽比为5的悬臂正方形棱柱气动力特性[J]. 实验流体力学, 2015, 29(6): 8-15. WANG H F, ZHAO D W, ZOU C, et al. Aerodynamic forces of a cantilevered square prism with aspect ratio of 5[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(6): 8-15. DOI:10.11729/syltlx20150040 (in Chinese) |
| [28] |
MCCLEAN J F, SUMNER D. An experimental investigation of aspect ratio and incidence angle effects for the flow around surface-mounted finite-height square prisms[J]. Journal of Fluids Engineering, 2014, 136(8): 081206. DOI:10.1115/1.4027138 |
| [29] |
SAHA A K. Unsteady flow past a finite square cylinder mounted on a wall at low Reynolds number[J]. Computers & Fluids, 2013, 88: 599-615. DOI:10.1016/j.compfluid.2013.10.010 |
| [30] |
解利军, 张帅, 张继发, 等. 基于特征的流场数据挖掘[J]. 空气动力学学报, 2010, 28(5): 540-546. XIE L J, ZHANG S, ZHANG J F, et al. A feature-based data mining method for fluid dynamics[J]. Acta Aerodynamica Sinica, 2010, 28(5): 540-546. DOI:10.3969/j.issn.0258-1825.2010.05.010 (in Chinese) |
 2020, Vol. 38
2020, Vol. 38


